Темы школьной программы — математика 5-11 класс. Найдите корень уравнения — Задание 5 ЕГЭ
Сегодня мы будем тренировать навык решения задания 5 ЕГЭ — найдите корень уравнения. Будем искать корень уравнения. Рассмотрим примеры решения такого рода заданий. Но для начала, давайте вспомним — что значит — найти корень уравнения?
Это значит найти такое, зашифрованное под х число, которое мы подставим вместо x и наше уравнение будет верным равенством.
Например, 3x=9 — это уравнение, а 3.3=9 — это уже верное равенство. То есть в данном случае, мы вместо x подставили число 3 — получили верное выражение или равенство, это означает, что мы решили уравнение, то есть нашли данное число x=3, которое превращает уравнение в верное равенство.
Вот этим мы и займемся — будем находить корень уравнения.
Содержание
Задание 1 — найдите корень уравнения 2
1-4x=32Это показательное уравнение. Оно решается следующим образом — нужно чтобы и слева, и справа от знака «равно» была степень с одинаковым основанием.
Слева у нас основание степени 2, а справа — степени нет вовсе. Но мы знаем, что 32 — это 2 в пятой степени. То есть, 32=25
Таким образом, наше уравнение будет выглядеть так: 21-4х=25
Слева и справа у нас основания степени одинаковы, значит, чтобы у нас было равенство, должны быть равны и показатели степени:
1-4х=5
Получаем обыкновенное уравнение. Решаем обычным способом — все неизвестные оставляем слева, а известные переносим вправо, получим:
-4х=5-1
-4х=4
х=-1.
Делаем проверку: 21-4(-1)=32
25=32
32=32
Мы нашли корень уравнение. Ответ: х=-1.
Самостоятельно найдите корень уравнения в следующих заданиях:
а) 25-х=64
б) 21-3х=128
Задание 2 — найдите корень уравнения 2
5-x = 1/16Уравнение решаем аналогично — путем приведения левой и правой частей уравнения к одному основанию степени. В нашем случае — к основанию степени 2.
Используем следующее свойство степени:
По этому свойству мы получим для правой части нашего уравнения:
Тогда наше уравнение запишется в виде:
Если равны основания степени, значит, равны и показатели степени:
5-х=-4
-х=-4-5
х=9
Ответ: х=9.
Сделаем проверку — подставим найденное значение х в исходное уравнение — если мы получим верное равенство, значит, мы решили уравнение правильно.
25-9=1/16
2-4=1/16
1/16=1/16
Мы нашли корень уравнения правильно.
Задание 3 — найдите корень уравнения
Заметим, что справа у нас стоит 1/8, а 1/8 — это
Тогда наше уравнение запишется в виде:
Если основания степени равны, значит, равны и показатели степени, получим простое уравнение:
3х-12=3
3х=15
х=5
Ответ: х=5. Проверку сделайте самостоятельно.
Задание 4 — найдите корень уравнения log
3(15-х)=log32Это уравнение решается также как и показательное. Нам нужно, чтобы основания логарифмов слева и справа от знака «равно» были одинаковыми. Сейчас они одинаковы, значит, приравниваем те выражения, которые стоят под знаком логарифмов:
Нам нужно, чтобы основания логарифмов слева и справа от знака «равно» были одинаковыми. Сейчас они одинаковы, значит, приравниваем те выражения, которые стоят под знаком логарифмов:
15-х=2
-х=2-15
-х=-13
х=13
Ответ: х=13
Задание 5 — найдите корень уравнения log
3(3-x)=3Число 3 — это log327. Чтобы было понятно внизу нижним индексом под знаком логарифма стоит число которое возводится в степень, в нашем случае 3, под знаком логарифма стоит число, которое получилось при возведении в степень — это 27, а сам логарифм — это показатель степени, в которую нужно возвести 3, чтобы получить 27.
Смотрите на картинке:
Таким образом, любое число можно записать в виде логарифма. В данном случае очень удобно записать число 3 в виде логарифма с основанием 3. Получим:
log3(3-x)=log327
Основания логарифмов равны, значит, равны и числа, стоящие под знаком логарифма:
3-х=27
Получим,
-х=27-3
-х=24
х=-24
Сделаем проверку:
log3(3-(-24))=log327
log3(3+24)= log327
log327=log327
3=3
Ответ: x=-24.
Задание 6. Найдите корень уравнения log(x+3)=log
2(3x-15).log2(x+3)=log2(3x-15)
Решение:
x+3=3x-15
x-3x=-3-15
-2x=-18
x=9
Проверка: log2(9+3)=log2(27-15)
log212=log212
Ответ: x=9.
Задание 7. Найдите корень уравнения log
2(14-2x)=2log23log2(14-2x)=2log23
log2(14-2x)=log232
14-2x=32
14-2x=9
-2x=9-14
-2x=-5
x=2,5
Проверка: log2(14-5)=2log23
log29=2log23
log232=2log23
2log23=2log23
Ответ: x=2,5
Подготовьтесь к ЕГЭ и к ОГЭ -посмотрите предыдущие темы Найдите значение выражения и Как решать неравенства .
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения . | Найдите корень уравнения: |
Найдите корень уравнения | Найдите корень уравнения . | Найдите корень уравнения | Найдите корень уравнения: |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения . |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения: | Найдите корень уравнения: |
Найдите корень уравнения . | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения . | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения: |
Найдите корень уравнения | Найдите корень уравнения . | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения . | Найдите корень уравнения . | Найдите корень уравнения | Найдите корень уравнения . |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения: |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения . | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
| Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения Если уравнение имеет более одного корня, в ответе укажите
меньший из них.
| Найдите корень уравнения Если уравнение имеет более одного корня, в ответе укажите больший из них.
| Найдите корень уравнения Если уравнение имеет более одного корня, в ответе укажите меньший из них
| Найдите корень уравнения Если уравнение имеет более одного корня, в ответе укажите больший из них
|
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения Если уравнение имеет более одного корня, укажите меньший из них. | Найдите корень уравнения Если уравнение имеет более
одного корня, укажите меньший из них. | Найдите корень уравнения Если уравнение имеет более одного корня, укажите меньший из них. | Найдите корень уравнения Если уравнение имеет более одного корня, укажите меньший из них. |
Найдите корень уравнения В ответе запишите наибольший отрицательный корень. | Найдите корень уравнения В ответе запишите наибольший отрицательный корень. | Найдите корень уравнения В ответе запишите наибольший отрицательный корень. | Найдите корень уравнения В ответе запишите наибольший отрицательный корень. |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения . | Найдите корень уравнения | Найдите корень уравнения . |
Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите больший из корней. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите меньший из корней. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите меньший из корней. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите больший из корней. |
Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите меньший из корней. | Найдите корень уравнения . Если уравнение имеет более
одного корня, в ответе запишите больший из корней. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите больший из корней. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите меньший из корней. |
Найдите корень уравнения | Найдите корень уравнения . | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения . | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите больший из корней. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите больший из корней. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите больший из корней. |
Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите больший из корней. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите больший из корней. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите больший из корней. | Найдите корень уравнения . |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите меньший из корней. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите больший из корней. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите меньший из корней. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе запишите больший из корней. |
Найдите корень уравнения . В ответе
напишите наибольший отрицательный корень. | Найдите корень уравнения . В ответе напишите наименьший положительный корень. | Найдите корень уравнения . В ответе напишите наибольший отрицательный корень. | Найдите корень уравнения . В ответе напишите наибольший отрицательный корень. |
Найдите корень уравнения . В ответе напишите наименьший положительный корень. | Найдите корень уравнения . В ответе напишите наибольший отрицательный корень. | Найдите корень уравнения . В ответе напишите наименьший положительный корень. | Найдите корень уравнения . В ответе напишите наибольший отрицательный корень. |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения . | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них. |
Найдите корень уравнения . | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них. | Найдите корень уравнения . Если уравнение имеет более одного корня, в ответе укажите меньший из них. |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения . | Найдите корень уравнения . |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения . | Найдите корень уравнения . | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения . | Найдите корень уравнения | Найдите корень уравнения . |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения . | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения | Найдите корень уравнения |
Задание №5.
 Простые уравнения. Профильный ЕГЭ по математике
Простые уравнения. Профильный ЕГЭ по математикеВ задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.
Вот список тем, которые стоит повторить:
Квадратные уравнения
Арифметический квадратный корень
Корни и степени
Показательная функция
Показательные уравнения
Логарифмическая функция
Логарифмические уравнения
Тригонометрический круг
Формулы приведения
Формулы тригонометрии
Простейшие тригонометрические уравнения 1
Уравнения, сводящиеся к квадратным
1. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.
Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.
С левой частью уравнения все понятно. Дробь умножается на А в правой части — смешанное число Его целая часть равна 19, а дробная часть равна Запишем это число в виде неправильной дроби:
Получим:
или
Выбираем меньший корень.
Ответ: -6,5.
2. Решите уравнение
Возведем в квадрат левую часть уравнения. Получим:
Ответ: -6.
Дробно-рациональные уравнения
3. Найдите корень уравнения
Перенесем единицу в левую часть уравнения. Представим 1 как и приведем дроби к общему знаменателю:
Ответ: -2.
Это довольно простой тип уравнений. Главное — внимательность.
Иррациональные уравнения
Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.
4. Решите уравнение:
Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.
Значит, .
Возведём обе части уравнения в квадрат:
Решим пропорцию:
Условие при этом выполняется.
Ответ: 87.
5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.
Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:
.
Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:
.
Мы получили, что . Это единственный корень уравнения.
Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:
Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни: или Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.
В итоге ноль баллов.
Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.
Ответ: 8.
6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Запишем решение как цепочку равносильных переходов:
.
Ответ: 9.
Показательные уравнения
При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.
7. Решите уравнение
Вспомним, что Уравнение приобретает вид: Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
откуда
Ответ: 4.
8. Решите уравнение
Представим как
Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
Ответ: 7,5.
9.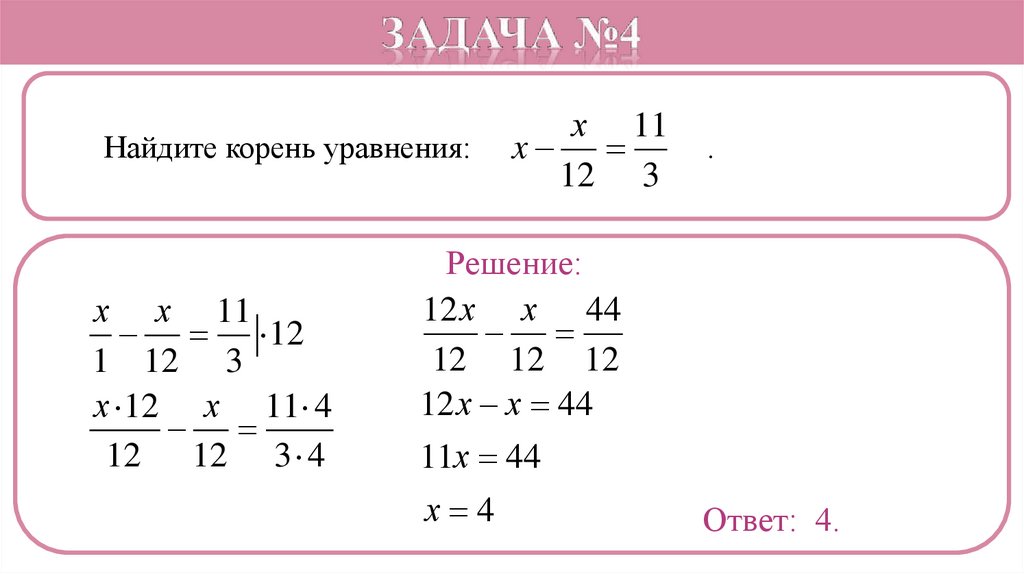 Решите уравнение
Решите уравнение
Представим в виде степени с основанием 3 и воспользуемся тем, что
Ответ: 12,5.
Логарифмические уравнения
Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.
И конечно, помним про область допустимых значений логарифма:
Логарифмы определены только для положительных чисел.
Основание логарифма должно быть положительно и не равно единице.
10. Решите уравнение:
Область допустимых значений: . Значит,
Представим 2 в правой части уравнения как , чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом
Ответ: 21.
11. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:
.
Ответ: -4.
12. Решите уравнение:
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Записываем решение как цепочку равносильных переходов.
.
Ответ: 19.
13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.
Получим систему:
Первое уравнение мы получили просто из определения логарифма.
Квадратное уравнение имеет два корня: и
Очевидно, корень является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения:
Ответ: 12.
Тригонометрические уравнения (Часть 1 ЕГЭ по математике)
Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.
Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.
14. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.
Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.
Сделаем замену Получим:
Получаем решения: Вернемся к переменной x.
Поделим обе части уравнения на и умножим на 4.
Первой серии принадлежат решения
Вторая серия включает решения
Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это
Ответ: -2.
15. Решите уравнение: В ответе напишите наименьший положительный корень.
Решение:
Сделаем замену Получим: Решения этого уравнения:
Вернемся к переменной х:
Умножим обе части уравнения на 4 и разделим на . 2
2
Найдите корень уравнения. 1) 9(x-1)=x+15 2) (11x+14)-(5x-8)=25 3) 12-4(x-3)=39-9x 4) 2(3x+5)-3(4x-1)=11,8 решите уравнение: 1) -7(2-3x)=56 2) (5+7a)*15= -30 решите уравнение: 1) 0,4(x-3)-1,6=5(0,1x-0,5) 2) 1,5(2x-5)+2x=5(0,5x-1,5)-10 3) 2/3 (1 1/2x+3/5)-4/5(5/12x-1/2)=1 3/5 чему равен корень уравнения: 1) x-8/x+2=7/3 2) 4/x-12=15/x-10 /
Все предметы
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Информатика
Українська література
Қазақ тiлi
Экономика
Музыка
Беларуская мова
Французский язык
Немецкий язык
Психология
Оʻzbek tili
Кыргыз тили
Астрономия
Физкультура и спорт
Решите уравнение:
1) -7(2-3x)=56
2) (5+7a)*15= -30
Решите уравнение:
1) 0,4(x-3)-1,6=5(0,1x-0,5)
2) 1,5(2x-5)+2x=5(0,5x-1,5)-10
3) 2/3 (1 1/2x+3/5)-4/5(5/12x-1/2)=1 3/5
Чему равен корень уравнения:
1) x-8/x+2=7/3
2) 4/x-12=15/x-10
/ — дробная черта
Ответ дан
jekadva
Ответ:
Пошаговое объяснение:
Найдите корень уравнения.
1)
9(x-1)=x+15
9x — 9 = x + 15
9x — x = 15 + 9
8x = 24
x = 24 : 8
x = 3
2)
(11x+14)-(5x-8)=25
11x + 14 — 5x + 8 = 25
6x + 22 = 25
6x = 25 — 22
6x = 3
x = 3 : 6
x = 0,5
3)
12-4(x-3)=39-9x
12 — 4x + 12 = 39 — 9x
24 — 4x = 39 — 9x
9x — 4x = 39 — 24
5x = 15
x = 15 : 5
x = 3
4)
2(3x+5)-3(4x-1)=11,8
6x + 10 — 12x + 3 = 11,8
-6x + 13 = 11,8
6x = 13 — 11,8
6x = 1,2
x = 1,2 : 6
x = 0,2
Решите уравнение:
1)
-7(2-3x)=56
-14 + 21x = 56
21x = 56 + 14
21x = 70
x = 70 : 21
x = 3 1/3
2)
(5+7a)*15= -30
75 + 105a = -30
105a = -30 — 75
105a = -105
a = -1
Решите уравнение:
1)
0,4(x-3)-1,6=5(0,1x-0,5)
0,4x — 1,2 — 1,6 = 0,5x — 2,5
0,4x — 2,8 = 0,5x — 2,5
0,5x — 0,4x = -2,8 + 2,5
0,1x = -0,3
x = -0,3 : 0,1
x = -3
2)
1,5(2x-5)+2x=5(0,5x-1,5)-10
3x — 7,5 + 2x = 2,5x — 7,5 — 10
5x — 7,5 = 2,5x — 17,5
5x — 2,5x = -17,5 + 7,5
2,5x = -10
x = -10 : 2,5
x = -4
3)
2/3 (1 1/2x+3/5)-4/5(5/12x-1/2)=1 3/5
x + 2/5 — 1/3x + 2/5 = 1 3/5
2/3x + 4/5 = 1 3/5
2/3x = 1 3/5 — 4/5
2/3x = 4/5
x = 4/5 * 3/2
x = 6/5
x = 1 1/5
Чему равен корень уравнения:
1)
(x-8)/(x+2)=7/3
7*(x+2) = 3*(x-8)
7x + 14 = 3x — 24
7x — 3x = -24 — 14
4x = -38
x = -38 : 4
x = -9 1/2
2)
4/(x-12)=15/(x-10)
15*(x-12) = 4*(x-10)
15x — 180 = 4x — 40
15x — 4x = 180 — 40
11x = 140
x = 140 : 11
x = 12 8/11
Найдите корень уравнение: 1)9(х+1)=х+15 2)(11x+-8)=25
Математика, 2022-06-17 11:59:23, yulenkaradosti
Ответ
Ответ разместил: find1337
1)9x+9=x+15
9x-x=15-9
8x=6
X=6/8
X=3/4
2)11x+14-5x+8=25
6x=25-14-8
6x=3
X=3/6=1/2
Ответ
Ответ разместил: Artemkotkot20
1) 9(х-1)=х+15; 9х-9=х+15; 8х=24; х=3.
2) 11х+14-5х+8=25; 6х=3; х=0.5
Ответ
Ответ разместил: natasha8750p092ef
1) 9х-9=х+15
9х-х=15+9
8х=24
х=24/8
х=3
2) 11х+14-5х+8=25
6х=3
х=3/6
х=0,5
3) 12-4х+12=39-9х
-4х+9х=39-12-12
5х=15
х=15/5
х=3
4) 6х+10-12х+3=11,8
-6х=11,8-10-3
-6х=-1,2
х=-1,2/(-6)
х=0,2
Ответ
Ответ разместил: даша3609
1) х=3
и подставь в уравнение 3 вот тебе и проверка
2) х=3
Ответ
Ответ разместил: goida82
1)9(x-2)=x+15
9x-18=x+15
9x-x=15+18
8x=33
x=4.125
2)11x+14-5x+8=25
11x-5x=25-8-14
6x=3
x=0.5
Ответ
Ответ разместил: baus100
1)9(х-1)=х+15
9x-9=x+15
9x-x=15+9
8x=24
x=3
2)(11х+14)-(5х-8)=25
11x+14-5x+8=25
11x-5x=25-14-8
6x=3
x=0.5
3)12-4(х-3)=39-9х
12-4x+12=39-9x
-4x+9x=39-12-12
5x=14
x=3
4)2(3х+5)-3(4х-1)=11,8
6x+10-12x+3=11. 8
8
6x-12x=11.8-10-3
-6x=-1.2
x=0.2
Ответ
Ответ разместил: artamasvan
1)
9x-9=x+15
9x-x=15+9
8x=24
x=3
2)
(11x+14)-(5x-8)=25
11x+14-5x+8=25
6x+22=25
6x=25-22
6x=3
x=3:6
x=0,5
3)
12-4(x-3)=39-9x
12-4x+12=39-9x
-4x+9x=39-12-12
5x=15
x=15:5
x=3
Ответ
Ответ разместил: Книга086
9(x-1)=x+15 (11x+14)-(5x-8)=25 12-4(x-3)=39-9x -3(4-5y)+2(3-6y)=-3,9
9x-9=x+15 11x+14-5x+8=25 12-4x+12=39-9x -12+15y+6-12y=-3,9
8x=24 6x=3 5x=15 3y=2,1
x=3 x=0.5 x=3 y=0,7
Ответ
Ответ разместил: Nodukam
9(х-1)=х-15 9х-9=х+15 9х-х=9+15 8х=24 Х=3 (11х+14)-(5х-8)=25 11х+14-5х+8=25 6х=3 х=1/2 12-4(х-3)=39-9х 12-4х+12=39-9х 5х=15 х=3
Ответ
Ответ разместил: belanvlabimir
9*(x-1)=x+15
9*x-9-x-15=0
8*x-9-15=0
8*x-24=0
x=24/8=3.
11*x+14-(5*x-8)=25
6*x+14+8-25=0
6*x-3=0
x=3/6=1/2~~0.5.
12-4(х-3)=39-9х
24-4*x-39+9*x=0
-15+5*x=0
x=15/5=3.
-3(4-5у)+2(3-6у)=-3,9
-6+15*y-12*y+3.9=0
-6+3*y+39/10=0
-21/10+3*y=0
y=21/10/3=7/10~~0.7.
Другие вопросы по: Математика
.(Если в некоторых десятичных дроби перенесли запятую через один знак влево, то она увеличится на 32,13. найдите эту дробь)….
Опубликовано: 27.02.2019 13:30
Ответов: 2
7121350-(15125: 25+302×804-986: 17)x9= 1092322: 574+152×93-(96×125-82215: 9)= решить!…
Опубликовано: 28.02.2019 04:40
Ответов: 3
.(Пісня- душа народу твір надо решите только на укр. мове)….
Опубликовано: 28.02.2019 17:10
Ответов: 3
Напишите,, сочинение на тему «почему мы изучаем язык» (7-10 предложений.)…
Опубликовано: 28.02.2019 22:10
Ответов: 1
Два тела массами 3кг и 7кг и скоростями 2м/с и 3м/с соответсвенно движутся навстречу друг другу и испытывают абсолютное столкновение. 2…
2…
Опубликовано: 02.03.2019 12:50
Ответов: 3
Найти и разобрать сложное слово по составу. лучи солнца, белоснежный ландыш, вещ подружки, положил в борщ, много трудных ,талантливый скрипач, летит среди туч, серьезная молодеж, к…
Опубликовано: 03.03.2019 09:30
Ответов: 1
Угол a ромба abcd на 24 градусов больше угла b. найдите угол c…
Опубликовано: 03.03.2019 22:00
Ответов: 1
Напишите, к то-нибудь, ! охарактезируйте каждую часть предложения. укажите, чем каждая часть осложнена. спишите предложения, расставляя знаки препинания. составьте схемы предложени…
Опубликовано: 04.03.2019 08:00
Ответов: 1
:перед ремонтом зоопарка животных вывезли в специальных автофургонах. было сделано 150 рейсов. каждым рейсом отправлялось одно и то же количество животных. после ремонта зоопарка с…
Опубликовано: 04. 03.2019 09:50
03.2019 09:50
Ответов: 1
Криголам за 3 дні пробивав собі дорогу серед крижин. першого дня він пройшов 2/5 всього шляху, другого дня — 5/8трешти шляху, а третього дня- 90 км, які залишились. який шлях подол…
Опубликовано: 04.03.2019 11:00
Ответов: 1
Укажите реактивы, используя которые можно распознать растворы кислот состава hcl, h3so4,hno3.напишите сокращенные ионно-молекулярные уравнения…
Опубликовано: 07.03.2019 14:30
Ответов: 3
Больше вопросов по предмету: Математика Случайные вопросы
Полиномиалы
Проект улучшения математического образования в школах (Times)
Возврат к индексу
Полиномии
Номер и алгебра: модуль 39 лет: 9-10
июня 2011 г.
PDF версия модуля
Assuded
PDF версия модуля
.

y = x2.
Мотивация
Полиномы представляют следующий уровень алгебраической сложности после квадратичных. Действительно, квадратное число — это многочлен степени 2. Мы можем факторизовать квадратные выражения, решать квадратные уравнения и строить графики квадратичных функций, возникает очевидный вопрос о том, как эти вещи могут быть выполнены с алгебраическими выражениями более высокой степени.
Квадратичный x2 − 5x + 6 размножается как (x − 2)(x − 3). Следовательно, уравнение x2 − 5x + 6 = 0
имеет решения x = 2 и x = 3,9.0003
Точно так же мы можем разложить кубик x3 − 6×2 + 11x − 6 как (x − 1)(x − 2)(x − 3), что позволяет нам показать, что решения x3 − 6×2 + 11x − 6 = 0 x = 1, x = 2 или x = 3. В этом модуле мы увидим, как получить эту факторизацию.
Многочлены во многих отношениях ведут себя как целые числа или целые числа. Мы можем складывать, вычитать и умножать два или более многочлена вместе, чтобы получить другой многочлен. Точно так же, как мы можем разделить одно целое число на другое, получив частное и остаток, мы можем разделить один многочлен на другой и получить частное и остаток, которые также являются многочленами.
Точно так же, как мы можем разделить одно целое число на другое, получив частное и остаток, мы можем разделить один многочлен на другой и получить частное и остаток, которые также являются многочленами.
Квадратное уравнение вида ax2 + bx + c имеет 0, 1 или 2 решения в зависимости от того, является ли дискриминант отрицательным, нулевым или положительным. Число решений этого уравнения помогло нам нарисовать график квадратичной функции y = ax2 + bx + c. Точно так же информация о корнях полиномиального уравнения позволяет нам дать грубый набросок соответствующей полиномиальной функции.
Помимо того, что полиномы представляют интерес по своей сути, они имеют важные приложения в реальном мире. Одно такое приложение к кодам исправления ошибок обсуждается в Приложении к этому модулю.
Содержание
Терминология
Полиномом является такое выражение, как x5 − 2×3 + 8x + 3 или x4 − x2 + 1. Может быть любое количество членов, но каждый член должен быть кратен целой степени числа Икс. Таким образом, 2×3 − x не является полиномом.
Таким образом, 2×3 − x не является полиномом.
Член с наибольшей степенью называется ведущим членом, а его коэффициент называется старшим коэффициентом. Если старший коэффициент равен 1, то полином называется моническим. Индекс старшего члена называется степенью многочлена. Член, не зависящий от, называется постоянным членом.
Таким образом, x5 − 2×3 + 8x + 3 является унитарным многочленом степени 5 с постоянным членом 3, а
x4 − x2 + 1 является немоническим многочленом степени 4 со старшим коэффициентом и постоянным членом 1.
В первый многочлен, все коэффициенты целые, а второй многочлен имеет иррациональный коэффициент. По большей части мы будем рассматривать только многочлены первого типа, но многое из того, что будет сказано ниже, в равной степени применимо и ко второму типу.
Чтобы назвать многочлены, мы будем использовать обозначение функции, такое как p(x) или q(x). Таким образом, мы можем записать p(x) = x5 − 2×3 + 8x + 3 или q(x) = x4 − x2 + 1. Это позволяет нам удобно подставлять значения x, когда это необходимо.
Это позволяет нам удобно подставлять значения x, когда это необходимо.
Общий многочлен имеет вид
p(x) = anxn − an − 1xn − 1 + … + a1x + a0,
, где an ≠ 0, а n — целое число. Коэффициенты, как правило, действительные числа.
УПРАЖНЕНИЕ 1
Запишите старший член, старший коэффициент, степень и постоянный член в приведенном выше общем многочлене.
Для полиномов малых степеней мы используем следующие имена.
- многочлен степени 1 называется линейным
- полином второй степени называется квадратичным
- многочлен степени 3 называется кубическим
- многочлен степени 4 называется квартикой
- многочлен степени 5 называется квинтикой
Многочлен, состоящий только из ненулевой константы, называется постоянным многочленом и имеет степень 0. Многочлен p(x) = 0 называется нулевым многочленом. У него нет терминов, а значит, нет и ведущего термина. Лучше не определять степень нулевого полинома. В некоторых книгах его степень указывается как −1 или −∞.
В некоторых книгах его степень указывается как −1 или −∞.
Сложение, вычитание и умножение многочленов
Чтобы сложить или вычесть два многочлена, собираем одинаковые члены.
ПРИМЕР
Пусть p(x) = 3×4 − 2×2 + x − 1, q(x) = 7×5 + 2×2.
Найдите a p(x) + q(x) b p(x) − q(x) c2p(x) − 3q(x).
Решение
a p(x) + q(x) = 7×5 + 3×4 + x − 1
b p(x) − q(x) = −7×5 + 3×4 − 4×2 − 1
c2p(x) − 3q (x) = 14×5 − 9×4 + 10×2 − 3x + 3.
Обратите внимание, что мы обычно записываем члены полинома от наибольшей степени к наименьшей. Это иногда называют стандартной формой многочлена.
Чтобы умножить два многочлена, мы умножаем каждый член первого многочлена на второй многочлен и собираем одинаковые члены.
ПРИМЕР
Многочлены P(x), Q(x) и R(x) задаются как P(x) = x3 − 2×2 + x − 1, Q(x) = 3×3 − 2×2 и R(x) = −x4 + 2×3 − 3×2. Найти:
a P(x)Q(x) b Q(x)R(x)
Решение
| a | П(х)В(х) | = (х3 — х2 + х — 1)(3х3 — 2х2) | |
| = х3(3х2 — 2х2) — х2(3х3 — 2х2) + х(3х3 — 2х2) — (3х3 — 2х2) | |||
| = 3×6 — 2×5 — 3×5 + 2×4 + 3×4 — 2×3 — 3×3 + 2×2 | |||
| = 3×6 — 5×5 + 5×4 — 5×3 + 2×2 | |||
| б | В(х)Р(х) | = (3×3 — 2×2)(-x4 + 2×3 — 3×2) | |
| = 3×3(−x4 + 2×3 − 3×2) − 2×2(−x4 + 2×3 − 3×2) | |||
| = -3×7 + 6×6 — 9×5 + 2×6 — 4×5 + 6×4 | |||
| = -3×7 + 8×6 — 13×5 + 6×4 |
УПРАЖНЕНИЕ 2
a Возведение в квадрат многочлена p(x) = 2×3 − x + 1.
b Закончите утверждения:
i При перемножении двух ненулевых многочленов степень произведения равна .. …..
ii Постоянный член произведения двух многочленов равен ……….
Деление многочленов
При делении одного целого числа на другое получается частное и остаток. Таким образом, получается 7, остаток 2. Есть разные способы записать этот результат.
- 37 ÷ 5 равно 7 остаток 2
- 37 ÷ 5 = 7
- 37 = 7 × 5 + 2
В выражении 37 ÷ 5 равно 7 остаток 2
- число 5, на которое мы делим, называется делителем
- число 37, на которое мы делим, называется делимым
- число 7 называется частным
- число 2 называется остатком
Ключевым моментом остатка является то, что он неотрицательный, но строго меньше делителя. Таким образом, используя третье представление, при делении двух целых чисел p и d > 0 мы можем записать
p = dq + r, где 0 ≤ r ≤ d.
Если остаток равен нулю, то мы можем сказать, что d является множителем p.
У этих основных утверждений относительно арифметики есть аналоги, когда мы приходим к делению одного многочлена на другой. Мы будем использовать ту же терминологию при обсуждении полиномиального деления. Процесс выполнения этого смоделирован на длинном делении.
Деление многочлена p(x) на многочлен d(x) также дает частное q(x) и остаток r(x), поэтому мы можем записать
p(x) = d(x)q (х) + г(х).
Основная идея при выполнении деления состоит в том, чтобы продолжать работать с ведущими терминами, как показано в следующем примере.
ПРИМЕР
Разделим полином p(x) = 5×4 −7×3 + 2x − 4 на многочлен d(x) = x − 2, а затем представим деление в виде p(x) = d(x )q(x) + r(x).
Решение
| 5×3 | + | 3×2 | + | 6x | + | 14 | |||||
| х — 2 | 5×4 | − | 7×3 | + | 2x | − | 4 | (Разделить x на 5×4, получится 5×3. ) ) | |||
| 5×4 | − | 10×3 | (Умножить x − 2 на 5×3 и затем вычесть.) | ||||||||
| 3х3 | + | 2x | − | 4 | (Разделить x на 3×3, получится 3×2.) | ||||||
| 3х3 | − | 6×2 | (Умножить x − 2 на 3×2 и затем вычесть. ) ) | ||||||||
| 6×2 | + | 2x | − | 4 | (Разделить х на 6х2, получится 6х.) | ||||||
| 6×2 | − | 12x | (Умножьте x − 2 на 6x, а затем вычтите.) | ||||||||
| 14x | − | 4 | (Разделить х на 14х, получится 14. ) ) | ||||||||
| 14x | − | 28 | (Умножьте x − 2 на 14, а затем вычтите.) | ||||||||
| 24 | (Это последний остаток.) |
Следовательно, 5×4 − 7×3 + 2x − 4 = (x − 2)(5×3 + 3×2 + 6x + 14) + 24. (1)
(1)
В этом примере мы видим, что частное равно q(x) = 5×3 + 3×3 + 6x − 14, а остаток равен r(x) = 24.
Мы можем выполнить частичную проверку, подставив x = 2 в последнюю строку.
Из приведенного примера видно, что степень остатка меньше степени делителя, так как в противном случае мы могли бы продолжить деление. Таким образом, в случае, когда — линейный множитель, остаток будет постоянным, и поэтому мы можем записать его как .
В общем, теперь мы можем написать p(x) = d(x)q(x) + r(x), где r(x) = 0, или 0 ≤ степеней (r(x)) < степеней ( д(х)).
УПРАЖНЕНИЕ 3
Разделите p(x) = 5×4 − 7×3 + 2x − 4 на d(x) = x2 − 2. Результат представим в виде
p(x) = d(x)q(x) + r(x), где степень r(x) меньше степени d(x).
Обратите внимание, что в этом случае, поскольку делитель имеет степень 2, остаток будет либо равен 0, либо будет иметь степень не более 1.
Теорема об остатках интересует остаток. Это не появляется до конца вычисления. Когда мы делим многочлен p(x) на линейный множитель (x − a), мы можем довольно легко найти остаток.
Поскольку делитель линейный, p(x) = (x − a)q(x) + r, где r — константа. Подставив x = a в обе части, мы получим r = p(a).
Таким образом, остаток равен многочлену, вычисленному при x = a.
Этот удивительный результат называется теоремой об остатках. Мы должны иметь в виду, что он вообще ничего не говорит о частном q(x) и работает только тогда, когда мы делим на линейный множитель (x − a).
ПРИМЕР
Найдите остаток при делении p(x) = x4 − 3×2 − 10x + 2 на 9.0003
а (х — 3) б (х + 4) в (2х — 1)
Раствор
- а
- Остаток равен p(3) = 81 − 27 − 30 + 2 = 26
- b
- Поскольку (x + 4) = (x − (−4)), остаток равен p(−4) = 256 − 48 + 40 + 2 = 250
- c
- Запишите p(x) = (2x − 1)q(x) + r, так что мы можем получить r, подставив x = в обеих частях. Следовательно, остаток равен r = − − 5 + 2 = −.
УПРАЖНЕНИЕ 4
Многочлен p(x) = x5 − 7×3 + ax + 1 имеет остаток 13 после деления на x − 1.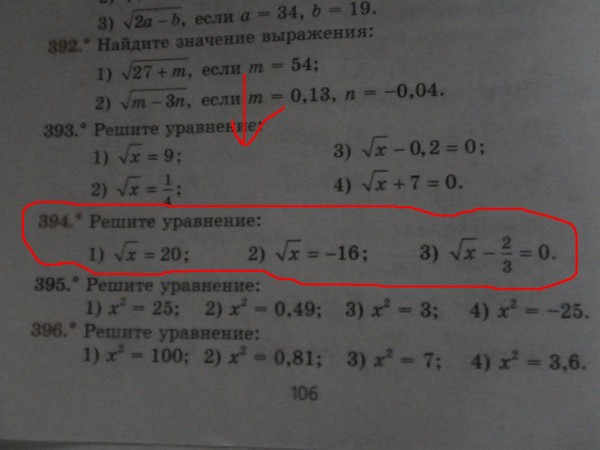 Найдите значение коэффициента a.
Найдите значение коэффициента a.
Факторная теорема
Квадратичная факторизация — важный метод, который мы использовали для решения квадратных уравнений. Аналогичным образом мы хотели бы иметь возможность разработать некоторые методы факторизации многочленов.
Если линейный полином (x − a) является фактором многочлена p(x), то мы можем написать
p(x) = q(x)(x − a), и поэтому остаток, когда p(x) равно деленное на (x − a), равно 0.
Используя теорему об остатках, мы доказали:
Теорема
(x − a) является фактором полинома p (x), если p (a) = 0. Если p (a) ≠ 0, то
(x − a) не является фактором p (x).
Число a, которое дает p(a) = 0, называется нулем многочлена.
ПРИМЕР
Что из следующего является множителями p(x) = x3 − 6×2 + 11x − 6?
а(х — 2) б (х + 1) с (х — 1).
Раствор
- и
- p(2) = 8 − 24 + 22 − 6 = 0, поэтому (x − 2) является множителем p(x).
- б
- p(−1) = − 1 − 6 − 11 − 6 ≠ 0, поэтому (x + 1) не является множителем p(x).

- с
- p(1) = 1 − 6 + 11 − 6 = 0, поэтому (x − 1) является множителем p(x).
Обратите внимание, что поскольку (x − 2) и (x − 1) оба являются множителями p(x), то их произведение равно
(x − 2)(x − 1) = x2 − 3 x + 2. Мы могли бы таким образом, найдите третий множитель делением в длину.
Деление p(x) на x2 − 3x + 2 дает (x − 3) в качестве третьего множителя, и, таким образом, мы имеем
после факторизации,
р(х) = х3 — 6х2 + 11х — 6 = (х — 1)(х — 2)(х — 3).
Альтернативный метод
Поскольку p(2) = 0 и p(1) = 0, а p(x) имеет степень 3, мы можем записать p(x) = (x − 2)(x − 1) (x − а)
Где а — число, подлежащее определению. Так как p(0) = −6, то −2a = −6, поэтому a = 3.
УПРАЖНЕНИЕ 5
Многочлен p(x) = 3×6 − 5×3 + ax2 + bx + 10 делится на x + 1 и x − 2. Найдите значения коэффициентов a и b.
Факторные полиномы
Наша цель — взять многочлен с целыми коэффициентами и записать его как произведение многочленов меньшей степени, которые также имеют целые коэффициенты. Этот процесс называется факторингом целых чисел.
Этот процесс называется факторингом целых чисел.
Факторная теорема позволяет нам проверить, имеет ли многочлен p(x) линейный множитель (x − a). Если это так, то мы можем использовать длинное деление, чтобы найти полином q(x) такой, что p(x) = (x − a)q(x) и q(x) имеет степень на единицу меньше, чем степень p(x ). Таким образом, мы можем повторять процесс над q(x) и так далее как можно чаще, чтобы получить полную факторизацию p(x).
Например,
Начнем с многочлена p(x) = x3 + 4×2 — 7x — 10.
- Мы систематически ищем один линейный множитель, проверяя числа a = 1, — 1, 2, -2 , … пока не найдем целочисленное значение a такое, что p(a) = 0,
p(1) = −12 ≠ 0, p(−1) = 0, поэтому (x + 1) является множителем.
- Затем мы используем длинное деление, чтобы разделить p(x) на (x + 1), чтобы получить p(x) = (x + 1)(x2 + 3x — 10).
Теперь квадратное число q(x) = x2 + 3x − 10 можно разложить на множители, используя наши знания о квадратичных уравнениях, как (x + 5)(x − 2), и поэтому полная факторизация p(x) равна
р(х) = (х+1)(х + 5)(х — 2).
Чтобы помочь нам найти целочисленный нуль полинома, мы используем следующий результат.
Теорема
Если многочлен
p(x) = anxn + an−1xn−1 + … + a1x + a0
имеет целочисленный нуль a, то a является множителем постоянного члена a0.
Таким образом, в приведенном выше примере единственными возможными целыми нулями являются ±1, ±2, ±5 или ±10.
УПРАЖНЕНИЕ 6
Объясните, почему приведенная выше теорема верна.
ПРИМЕР
Факторизируем многочлен p(x) = x4 − 2×3 − 8x + 16.
Решение
- Нам нужно только проверить положительные и отрицательные множители числа 16.
P(1) = 1 − 2 − 8 + 16 ≠ 0, поэтому x — 1 не является множителем p (x).
P(−1) = 1 + 2 + 8 + 16 ≠ 0, поэтому x + 1 не является фактором p(x).
P(2) = 16 − 16 − 16 + 16 = 0, поэтому x − 2 является множителем.
После длинного деления p(x) на x − 2, p(x) = (x − 2)(x3 − 8) - Пусть Q(x) = x3 − 8,
x − 1 и x + 1 не являются факторами Q(x), поскольку P(x) = (x − 2)Q(x), и они не являются факторами P(x).
Однако Q(2) = 8 − 8 = 0, поэтому x − 2 также является фактором Q(x).
После длинного деления Q(x) на x − 2 получается Q(x) = (x − 2) (x2 + 2x + 4). - Квадратное число x2 + 2x + 4 нельзя разложить на множители, см. ниже.
Следовательно, P(x) = (x − 2)2(x2 + 2x + 4) является полной факторизацией P(x).
Обратите внимание, что квадратное число x2 + 2x + 4 = (x + 1) 2 + 3, которое всегда больше или равно 3, следовательно, квадратичное число не имеет множителей.
УПРАЖНЕНИЕ 7
Сначала удалив очевидный общий множитель, разложите многочлен
p(x) = 2×5 − 22×4 + 78×3 − 90×2.
Полиномиальные уравнения
Одним из основных методов решения квадратных уравнений был метод факторизации. Точно так же одно из основных применений факторинговых полиномов — решение полиномиальных уравнений.
ПРИМЕР
Решить x3 + 4 x2 — 7x — 10 = 0
Решение
В предыдущем примере мы разложили полином 9 на множители. 0020 p(x) = x3 + 4 x2 — 7x — 10 = 0 как (x + 1)(x + 5)(x — 2).
0020 p(x) = x3 + 4 x2 — 7x — 10 = 0 как (x + 1)(x + 5)(x — 2).
Таким образом, уравнение x3 + 4 x2 — 7x — 10 = 0 становится (x + 1)(x + 5)(x — 2) = 0
Поскольку произведение трех множителей равно нулю, мы можем приравнять каждое фактор к нулю, чтобы найти решения. Таким образом, x + 1 = 0 или x — 2 = 0 или x + 5 = 0, что дает x = -1, x = 2 или x = -5.
Примечание. Полином p(x) = (x − 1)(x − 2) 2(x − 4) 3 имеет степень 6, но уравнение полинома (x − 1)(x − 2)2(x − 4) 3 = 0 имеет только 3 (различных) решения x = 1 или x = 2 или x = 4. Таким образом, количество (различных) решений может быть меньше степени, но никогда не может превышать степень.
УПРАЖНЕНИЕ 8
Используйте факторизацию p(x) = 2×5 − 22×4 + 78×3 −90×2 из приведенного выше упражнения, чтобы решить уравнение 2×5 − 22×4 + 78×3 − 90×2 = 0.
В некоторых ситуациях результаты факторизации в квадратном уравнении, не имеющем действительных решений или иррациональных решений. В этом случае нам может понадобиться завершить задачу, используя квадратичную формулу.
ПРИМЕР
Решить x4 + 7×3 − 2×2 − 7x + 1 = 0 1).
Следовательно, уравнение принимает вид (x − 1)(x + 1)( x2 + 7x − 1) = 0.
Таким образом, решения равны x = 1, x = −1, а решения x2 + 7x − 1 = 0.
Используя формулу квадратного уравнения, b2 − 4ac = 49 + 4 = 53, поэтому квадратное уравнение имеет решения
x = и x = .
Следовательно, квартика имеет четыре решения x = 1, −1 и x = .
Обратите внимание, что существуют полиномиальные уравнения с иррациональными корнями, которые нельзя решить с помощью описанной выше процедуры. Например, многочлен p(x) = x5 − 3×3 − 2×2 + 6 делит на
(x2 − 3)(x3 − 2), поэтому уравнение x5 − 3×3 − 2×2 + 6 = 0 имеет решения, x = , x = − и x = .
В общем, разложение многочленов на множители над целыми числами — трудная задача. Многочлен
x3 − 2, например, нельзя разложить на множители по целым числам, но он имеет одно действительное решение, x = .
Зарисовка полиномиальных функций
Полиномиальная функция — это функция вида y = p(x), где p(x) — полином.
В модуле «Квадратичные функции» мы увидели, как нарисовать график квадратичной
, найдя
- точки пересечения
- найти вершину.
Вершина является примером поворотной точки.
Для многочленов степени больше 2 нахождение точек поворота не является элементарной процедурой и обычно требует использования исчисления, однако:
Возьмем многочлен y = x3 + x2 − 6x = x(x − 2)(x − 3).
Пересечение по оси y равно 0, а пересечение по оси x происходит, когда x(x − 2)(x − 3) = 0, то есть когда x = 0, 2 и 3.
Чтобы получить представление об общей форме кривой, мы можем заменить некоторые контрольные точки.
Мы можем представить знак y, используя диаграмму знаков:
Имея эту информацию, мы можем начать рисовать график y = x(x − 2)(x + 3).
Диаграмма знаков говорит нам о том, что график пересекает ось x в точках x = −3, 0 и 2, а также о том, находится ли график выше или ниже оси a по обе стороны от этих точек. Он не сообщает нам максимальное и минимальное значения y между нулями.
Он не сообщает нам максимальное и минимальное значения y между нулями.
Обратите внимание, что если x — большое положительное число, то p(x) также большое и положительное число. Например, если x = 10, то y = 1040. Если x — большое отрицательное число, то p(x) — также большое отрицательное число. Например, если x = -10, то y = -840.
УПРАЖНЕНИЕ 9
Нарисуйте график y = (x + 2)(x + 1)(x − 1)(x − 2).
Графики многочленов с повторяющимися множителями
Полиномиальные функции, такие как p(x) = 3(x − 1)2(x + 3)5(x − 4), которые содержат повторяющиеся множители, требуют особого внимания.
Если мы рассмотрим, например, размер x4 для различных значений x, мы заметим, что
- x4 положителен как для положительных, так и для отрицательных значений x
- для значений x от −1 до 1 размер x4 меньше, чем значение x.
Графически это говорит нам о том, что график y = x4 имеет минимум при x = 0 и что вблизи x = 0 график довольно плоский, но начинает резко возрастать при x > 1 и при x < −1.
Графики y = x2 и y = x4 показаны для сравнения.
Оба этих графика имеют минимум при x = 0. В случае параболы мы называем это вершиной, но обычно не используем это слово для многочленов более высокой степени. Вместо этого мы говорим о поворотной точке и далее классифицируем ее как максимум или минимум.
Графики y = −x2 и y = −x4 имеют максимум при x = 0.
Четные степени
То же самое происходит для всех положительных четных степеней x и для четных степеней (x − а). Следовательно, вблизи нуля полинома, который возникает из множителя с четной степенью, график имеет минимум или максимум и является «плоским» вблизи этого нуля.
Нечетные степени
График y = (x − 2) пересекает ось x в точке x = 2, но не имеет там ни максимума, ни минимума. Поскольку это прямая линия, график в этой точке не плоский, а имеет уклон в 45°. С другой стороны, график y = (x − 2)3 ведет себя несколько иначе при
x = 2. В дальнейшем мы будем рассматривать нечетные степени, большие или равные 3.
В дальнейшем мы будем рассматривать нечетные степени, большие или равные 3.
Поскольку нечетная степень отрицательного числа отрицательна, диаграмма знаков показывает, что
значений y графика y = x3 перемещаются от от отрицательного к положительному по мере того, как значения x изменяются от -1 до 1. Как и выше, график плоский вблизи начала координат.
Отсюда график y = x3 выглядит так:
В начале координат нет ни максимума, ни минимума. Точка x = 0 называется точкой заражения кривой.
ПРИМЕР
Постройте график y = 2×3(x − 2)2.
Решение
График проходит через начало координат и пересекает ось x в точках x = 0 и x = 2. При x = 0 график имеет точку перегиба, а при x = 2 имеет минимум. Схема знака есть.
График:
УПРАЖНЕНИЕ 10
Нарисуйте график полиномиальной функции p(x) = (x + 3)3(x − 1)3. (Вы должны обнаружить, что граф симметричен относительно x = −1, понимаете, почему?)
Ссылки Вперед
Основная теорема алгебры
Нули полинома также называют корнями соответствующего полиномиального уравнения.
Полиномиальное уравнение x2− 4 = 0 имеет два целых корня, x = 2, x = −2, а уравнение x2 − 2 = 0 имеет два действительных корня, x = , x = −. С другой стороны, уравнение x2 + 2 = 0 не имеет действительных корней. Более того, уравнение x3 − 1 = 0, которое факторизуется как (x − 1)(x2 + x + 1 = 0), имеет только один действительный корень, поскольку квадратное выражение x2 + x + 1 = 0 не имеет решений.
Чтобы правильно понять, сколько решений может иметь полиномиальное уравнение, нам нужно ввести комплексные числа. Комплексное число — это число вида a + ib, где a, b — действительные числа, а i2 = − 1. Комплексное число i часто называют мнимым числом. Обратите внимание, что если мы положим b = 0, мы получим действительное число, и поэтому комплексные числа содержат множество всех действительных чисел.
Таким образом, хотя уравнение x2 + 1 = 0 не имеет действительных решений, оно имеет два комплексных решения, x = i и x = −i, и многочлен x2 + 1 можно разложить на множители как (x − i)( х + я).
Великий математик Гаусс (1777−1855) впервые доказал следующий удивительный результат, известный как Основная теорема алгебры.
Теорема
Каждое полиномиальное уравнение степени больше 0 имеет хотя бы одно комплексное решение.
Учитывая этот результат, несложно показать, что:
Следствие
Каждое полиномиальное уравнение степени n, большей 0, имеет ровно n решений, учитывая кратность, над комплексными числами.
УПРАЖНЕНИЕ 11
Объясните, как можно вывести следствие из теоремы.
Следовательно, каждый многочлен степени n, большей 0, может быть разложен на n линейных множителей с использованием комплексных чисел.
Обратите внимание, что выражение с подсчетом кратности означает, что, например, для полиномиального уравнения (x − 2)3(x + 1) 2 = 0 мы говорим, что его корни равны x = 2, 2, 2, −1, − 1. Таким образом, мы говорим, что x = 2 является корнем кратности 3, а x = −1 является корнем кратности 2. Однако уравнение имеет только два (различных) корня.
Поворотные точки
Вершина параболы является примером поворотной точки. Координата x точки поворота параболы y = ax2 + bx + c определяется выражением x = −. Координаты x точек поворота многочлена найти не так просто и требуют использования дифференциального исчисления, которое изучается в высшей математике.
Корни многочлена
Предположим, что мы можем разложить моническую квадратичную функцию x2 + bx + c как (x − α)(x − β). Раскрывая, мы видим, что сумма корней α + β равна −b, а произведение корней ab равно c.
Мы можем выполнить аналогичное упражнение на моник-кубиках. То есть, если корнями кубического
x3 + bx2 + cx + d являются α, β, γ, то можно показать, что
α + β + γ = −b, αβ + αγ + βγ = c и αβγ = −d,
Эти тождества задают отношения между корнями многочлена и его коэффициентами.
УПРАЖНЕНИЕ 12
Выведите приведенные выше формулы.
История
Изучение уравнений степени больше двух восходит к арабской математике. Омар Хайям (1048–1141 гг.) провел большую часть своей жизни, пытаясь решить различные случаи кубического уравнения. Только в эпоху Возрождения было получено общее решение кубического. Точные детали отрывочны, но итальянский математик Кардано (1501–1576 гг.) сумел разгадать секрет решения кубического уравнения своего соотечественника Тартальи и включил его в свой труд «Ars Magna» («Великое искусство»), опубликованный в 1545 г.
Омар Хайям (1048–1141 гг.) провел большую часть своей жизни, пытаясь решить различные случаи кубического уравнения. Только в эпоху Возрождения было получено общее решение кубического. Точные детали отрывочны, но итальянский математик Кардано (1501–1576 гг.) сумел разгадать секрет решения кубического уравнения своего соотечественника Тартальи и включил его в свой труд «Ars Magna» («Великое искусство»), опубликованный в 1545 г.
Кубик
Кардано показал, как привести любое кубическое уравнение к виду x3 + px + c = 0, а затем, сделав замену x = u − v, свести задачу к решению квадратного уравнения. На практике проще положить x = u + v.
УПРАЖНЕНИЕ 13
Положим x = y − в уравнение x3 + ax2 + bx + c = 0, чтобы показать, что полученное уравнение не содержит членов степени 2.
ПРИМЕР
Решите x3 + 3x — 1 = 0, используя замену x = u + v.
Решение
Преобразовывая уравнение и подставляя, мы имеем
(u + v)3 = −3(u + v) + 1.
Теперь мы расширяем левую часть и делим 3uv от двух членов, чтобы получить
u3 + v3 + 3uv(u + v) = 1 −3(u + v).
Приравнивая коэффициенты (u + v) с обеих сторон и приравнивая остальные члены,
получаем
u3 + v3 = 1 , 3uv = −3.
Кубирование второго уравнения дает
u3 + v3 = 1 , u3v3 = −1 ,
На этом этапе у нас есть два числа u3, v3, сумма и произведение которых нам известны. Отсюда
они будут удовлетворять квадратному уравнению z2 − z − 1 = 0, имеющему решения z = или
z = . Эти решения представляют числа u3 + v3 в любом порядке, поэтому, взяв кубические корни, мы получим следующее решение исходного уравнения:
x = u + v = + .
Это единственное реальное решение уравнения.
УПРАЖНЕНИЕ 14
Воспользуйтесь калькулятором, чтобы выразить это в десятичной форме и проверить, удовлетворяет ли оно исходному уравнению
.
Квартика
Решение общего уравнения четвертой степени вскоре было найдено учеником и протеже Кардано Феррари. Он открыл способ сведения задачи решения
квартики к задаче решения кубики.
В обоих случаях решение данного уравнения можно выразить с помощью квадратных и высших корней и обычных арифметических действий (сложения, вычитания, умножения и деления). Такой раствор часто называют раствором с использованием радикалов. Решения квадратного уравнения ax2 + bx + c = 0 равны x = и x = −, поэтому квадратное уравнение также можно решить с помощью радикалов.
Прошло несколько сотен лет, прежде чем Абель (1802−1829) и Галуа (1811−1832) поняли, что невозможно найти решение общего уравнения пятой степени или общего уравнения более высокой степени, используя радикалы. Очевидно, что некоторые уравнения более высоких степеней можно решить с помощью радикалов, например, x5 − 32 = 0, но в общем случае это невозможно.
Корни многочленов
Несмотря на то, что работа Кардано стала крупным прорывом, оставалось еще много вопросов, касающихся многочленов, без ответа. В 17 веке Декарт нашел критерий, известный как правило знаков Декарта, для определения числа положительных действительных корней многочлена, а Ньютон открыл так называемые тождества Ньютона, которые находят и связывают формулы для суммы k-х степеней. корней многочлена. В 18 и 19века великие математики Эйлер, Лагранж, Эйзенштейн и Гаусс еще больше расширили наше понимание полиномов и полиномиальных уравнений. Это привело к развитию того, что сегодня называется современной алгеброй, которая занимается изучением алгебраических структур.
корней многочлена. В 18 и 19века великие математики Эйлер, Лагранж, Эйзенштейн и Гаусс еще больше расширили наше понимание полиномов и полиномиальных уравнений. Это привело к развитию того, что сегодня называется современной алгеброй, которая занимается изучением алгебраических структур.
Разложение полиномов на множители
Выше мы видели, что при изучении полинома нам нужно указать, какие решения/факторы мы ищем. В частности, предположим, что p(x) — полином со степенью больше 0 и действительными коэффициентами
- комплексные числа p(x) делят на линейные множители
- над действительными числами p(x) имеет все свои множители либо линейные, либо квадратичные
- над рациональными числами можно найти полиномы сколь угодно большой
-й степени, которые являются неприводимыми, то есть они не могут быть выражены в виде произведения
двух многочленов с рациональными коэффициентами, каждый меньшей степени.
Основная теорема алгебры используется для демонстрации первого из этих утверждений. Чтобы получить второе, нам нужно знать тот факт, что, когда у нас есть многочлен с действительными коэффициентами, любые комплексные корни будут встречаться парами, известными как сопряженные пары. То есть, если a + ib — корень, то и a — ib тоже. Этот факт можно использовать для доказательства второго утверждения.
Чтобы получить второе, нам нужно знать тот факт, что, когда у нас есть многочлен с действительными коэффициентами, любые комплексные корни будут встречаться парами, известными как сопряженные пары. То есть, если a + ib — корень, то и a — ib тоже. Этот факт можно использовать для доказательства второго утверждения.
УПРАЖНЕНИЕ 15
(Требуется небольшое знание комплексных чисел.)
Предположим, что все коэффициенты многочлена p(x) = anxn − an − 1xn − 1 + … + a1x + a0 действительны.
- и
- Если α = a + ib является решением полиномиального уравнения, p(x) = anxn − an − 1xn − 1 + … + a1x + a0 = 0, покажи, что = a − ib также является решением.
- б
- Покажите, что если x − α является множителем p(x), где α = a + ib является комплексным числом, то квадратное (x − α)(x − ) также является множителем p(x) и что (x − α)(x − ) имеет действительные коэффициенты.
- в
- Сделайте вывод, что каждый многочлен с действительными коэффициентами теоретически может быть разложен на множители как произведение линейных и/или квадратичных множителей с действительными коэффициентами.
 (Обратите внимание, что на практике это может быть очень сложной задачей.)
(Обратите внимание, что на практике это может быть очень сложной задачей.)
Эйзенштейн (ок. 1850 г.) предложил следующий остроумный тест на неприводимость полиномов над рациональными числами.
Рассмотрим многочлен p(x) = anxn − an − 1xn − 1 + … + a1x + a0, где все коэффициенты целые. Предположим, что мы можем найти простое число p, которое не делится на старший коэффициент an, но делит все остальные коэффициенты. Тест говорит, что если квадрат того же простого числа не делит постоянный член, т. е. p2 + a0, то p(x) неприводимо над рациональными числами.
ПРИМЕР
Многочлен p(x) = 5×7 + 6×6 − 15x 4 + 12x − 21 удовлетворяет критерию Эйзенштейна с простым числом p = 3, поэтому p(x) не может быть выражен в виде произведения двух многочленов, каждый из которых имеет меньшую степень с целыми коэффициентами. То есть р(х) неприводим.
УПРАЖНЕНИЕ 16
Объясните, как построить многочлен произвольно большой степени, который нельзя разложить на множители по рациональным числам.
Серия Маклорена
В 17-м и 18-м веках математики сделали замечательное открытие, что такие функции, как y = sin x и y = cos x, могут быть выражены с помощью «бесконечных многочленов», то есть многочленов, степени x которых продолжаются бесконечно. . Они называются силовыми рядами. Так, например,
sin x = x − + − + …,
, где очевидная закономерность сохраняется навсегда. Обозначение n! (читается как n факториал) — это сокращение от n(n − 1)(n − 2) … 3.2.1. Таким образом 5! = 5 × 4 × 3 × 2 × 1 = 120. Эти бесконечные ряды часто называют рядами Маклорена, и они имеют очень широкое применение как в математике, так и в физике.
До сих пор остаются нерешенными проблемы, связанные с полиномами. В приложении ниже в общих чертах обсуждается замечательное применение полиномов в современных телекоммуникациях.
Приложение
Применение полиномов к кодам с исправлением ошибок
Оцифровка информации
Информация обычно оцифровывается путем преобразования ее в последовательность нулей и единиц. Например, код ASCII для цифры 1 и буквы A — «1» 1000110 и «A» 1000001. Здесь мы будем предполагать, что все рассматриваемые сообщения представляют собой конечные последовательности нулей и единиц.
Например, код ASCII для цифры 1 и буквы A — «1» 1000110 и «A» 1000001. Здесь мы будем предполагать, что все рассматриваемые сообщения представляют собой конечные последовательности нулей и единиц.
Когда ваш мобильный телефон отправляет или получает сообщения или данные отправляются со спутников, находящихся глубоко в космосе, информация может быть потеряна или повреждена по пути к месту назначения.
Поскольку информация отправляется в виде последовательностей 0 и 1, «искаженный» 0 становится 1 и наоборот.
Простая проверка на наличие ошибок заключается в добавлении контрольной цифры, чтобы в строке было четное количество единиц и, следовательно, сумма цифр была четной.
Таким образом, мы кодируем 1 как 10001101, а A как 10000010.
Теперь, если байт передан и один из битов поврежден, количество единиц становится нечетным, и получатель может запросить повторную передачу.
Этот код может обнаружить одну ошибку, но не может ее исправить.
Многочлены по модулю 2
Многочлены по модулю 2 — это многочлены, коэффициенты которых равны 0 или 1. Затем выполняются арифметические действия по модулю 2, так что 0 + 1 = 1 + 0 = 1 и 1 + 1 = 2 = 0.
Затем выполняются арифметические действия по модулю 2, так что 0 + 1 = 1 + 0 = 1 и 1 + 1 = 2 = 0.
Выполняем сложение по модулю 2.
ПРИМЕР
Если p(t) = t3 + 1 + 1, q(t) = t4 + t3 + t2 + 1
Тогда p(t) + q(t) = t4 + 2t3 + t2 + 2t + 2 = t4 + t2.
Умножение выполняется аналогично.
Решение
p(t) = t3 + 1 + 1, q(t) = t + 1, тогда
p(t) × q(t) = (t3 + t + 1)(t + 1) = t4 + t3 + t2 + 2t + 1 = t4 + t3 + t2 + 1
Кодирование
Зафиксируем теперь многочлен m1(t) = t3 + t + 1.
Этот многочлен нельзя факторизовать по модулю 2, поскольку возможны только корни 0 и 1, и ни один из них не работает.
Теперь предположим, что многочлен m1(t) имеет корень a. То есть a обладает тем свойством, что
α3 + α + 1 = 0 или α3 = α + 1 (напомним, что по модулю 2, −1 = 1)
Это число α очень интересно, и, используя приведенное выше уравнение, мы можем составить таблицу его степеней.
Мощность | Упрощенная форма
| α | | α | |
| α2 | | α2 | |
| α3 | | α + 1 | |
| α4 | | α2 + α | |
| α5 | | α2 + α + 1 | |
| α6 | | α2 + 1 | |
| α7 | | 1 |
Например, чтобы получить α5, мы умножаем α4 = α2 + α на α5 = α3 + α2 и заменяем α3 на α + 1, чтобы получить α5 = α + 1 + α2.
Таким образом, мы можем записать все степени α как комбинации 1, α и α2 (!!)
Теперь о кодах.
Мы начинаем с сообщения (a, b, c, d) в двоичном формате длиной 4, добавляем 3 контрольных цифры, чтобы получить
(a, b, c, d, x, y, z). Мы используем их как коэффициенты многочлена
p(t) = at6 + bt5 + ct4 + dt3 + xt2 + yt + z.
Цифры x, y, z выбраны так, что p(t) делится на полином m1(t) = t3 + t + 1
Поскольку a является корнем m1(t), он также является корнем p(t) и поэтому p(a) = 0.
ПРИМЕР
Возьмите сообщение (1, 0, 0, 1) и закодируйте его как (1, 0, 0, 1, x, y, z). Преобразуя в многочлен, имеем
| п(т) | = t6 + t3 + xt2 + yt + z. | |
| Подставив t = a и упростив таблицу, мы получим | ||
| р(а) | = а6 + а3 + ха2 + уа + з. | |
| = (а2 + 1) + (а + 1) + ха2 + уа + г | ||
| = а2 (х + 1) + а (у + 1) + z. | ||
Теперь, если мы возьмем x = 1, y = 1, z = 0, то p(a) будет равно нулю. Следовательно, мы кодируем сообщение
(1, 0, 0, 1) как (1, 0, 0, 1, 1, 1, 0). Мы назовем полином, соответствующий отправленному сообщению, C(t), поэтому C(a) = 0.
Исправление ошибок
Предположим, что в пятом числе слева возникает одна ошибка, поэтому мы получаем сообщение (1, 0 , 1, 1, 1, 1, 0).
Таким образом, коэффициент t4 неверен и полином для полученного сообщения равен
R(t) = C(t) + t4
Подставляя t = α, мы получаем
R(α) = C(α) + α4 = α4
и, таким образом, мы знаем, где ошибка.
В общем случае, если бы в й цифре была ровно одна ошибка, мы бы получили
R(t) = C(t) + ti.
Тогда R(α) = C(α) + αi = αi, и вычисление R(a) дает позицию неправильной цифры.
Если R(α) = 0, то ошибок не было. Этот процесс, конечно, предполагает, что произошло не более 1
ошибок.
ПРИМЕР
Допустив не более одной ошибки, исправьте и расшифруйте сообщение (1, 0, 0, 1, 0, 0, 1).
Решение
Преобразуя в многочлены, имеем
R(t) = t6 + t3 + 1
и, следовательно,
R(α) = α6 + α3 + 1 = α2 + 1 + α + 1 + 1 = α2 + α + 1 = α5
Итак, исправленное сообщение было (1, 1, 0, 1, 0, 0, 1), которое расшифровывается как (1, 1, 0, 1).
Исправление более одной ошибки
Описанная выше процедура кодирования и исправления работает только в том случае, если при передаче произошла не более одной ошибки.
Полиномиальный метод может быть расширен для обнаружения и исправления более чем одной ошибки.
Детали этих кодов немного сложнее, но в них используются те же идеи, что и выше.
Коды, используемые для исправления множественных ошибок, называются кодами БЧХ и были открыты (независимо) Боузом и Чаудхури (в 1960 г.) и Хоквингемом (в 1959 г.) — отсюда и название БЧХ.
Хотя арифметика теперь становится очень сложной, она легко выполняется компьютером, и могут быть созданы коды, которые могут обнаруживать и исправлять произвольное количество ошибок.
Современные коды исправления ошибок, используемые в мобильных телефонах, снова более сложны, но в основном используют механизмы, описанные выше.
В последнее время коды Рида-Соломона, которые являются типом кода BCH, использовались в таких приложениях, как спутниковая связь, проигрыватели компакт-дисков, DVD и дисководы.
ОТВЕТЫ НА УПРАЖНЕНИЯ
УПРАЖНЕНИЕ 1
Старший член: anxn
Старший коэффициент: an
Степень: n
Постоянный член: a0
УПРАЖНЕНИЕ 2
a 4×6 − 4×4 + 4×3 + x2 − 2x + 1
b i…. сумма степеней многочленов
сумма степеней многочленов
ii… произведение констант
УПРАЖНЕНИЕ 3
5×4 − 7×3 + 2x − 4 = (x2 − 2)(5×2 − 7x + 10) + (−12x + 16)
УПРАЖНЕНИЕ 4
a = 18
УПРАЖНЕНИЕ 5
a = −33 и b = −15 −а1а. Следовательно, а делит а0.
Упражнение 7
2×2 (x — 3) 2 (x — 5)
Упражнение 8
x = 0 или x = 3 или x = 5
Упражнение 9
Упражнение 10
Упражнение 11
Для полиномиального уравнения P(x) = 0 существует решение x = a по теореме. Следовательно, x − a является фактором P(x) и P(x) = (x − a)Q(x). Уравнение Q(x) = 0 также имеет решение, поэтому по теореме можно найти новый линейный множитель.
УПРАЖНЕНИЕ 12
(x − α)(x − β)(x − γ) = x3 − (α + β + γ)x2 + (αβ + αγ + βγ)x + αβγ = x3 + bx2 + cx + д
Отсюда результат: b = −(α + β + γ), c = (αβ + αγ + βγ) и d = αβγ

Проект улучшения математического образования в школах (TIMES) на 2009–2011 годы финансировался Министерством образования, занятости и трудовых отношений правительства Австралии.
Мнения, выраженные здесь, принадлежат автору и не обязательно отражают точку зрения Министерства образования, занятости и трудовых отношений правительства Австралии.
© Мельбурнский университет от имени Международного центра передового опыта в области образования в области математики (ICE-EM), образовательного подразделения Австралийского института математических наук (AMSI), 2010 г. (если не указано иное). Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons. org/licenses/by-nc-nd/3.0/
org/licenses/by-nc-nd/3.0/
Как найти решение квадратного уравнения
Все математические ресурсы PSAT
10 диагностических тестов 421 практический тест Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
PSAT Math Help » Алгебра » Уравнения / Неравенства » Квадратные уравнения » Как найти решение квадратного уравнения
Если f(x) = -x 2 + 6x — 5, то каким может быть значение a, если f(a) = f(1,5)?
Возможные ответы:
3,5
1
4
2,5
4,5
3 Правильный ответ: 40 6 57 90 9,3713 Объяснение:Нам нужно ввести 1,5 в нашу функцию, затем нам нужно ввести в нашу функцию «а» и установить эти результаты равными.
f(а) = f(1,5)
f(а) = -(1,5) 2 +6(1,5) -5
f(a) = -2,25 + 9 — 5
f(a) = 1,75
-a 2 + 6a -5 = 1,75
Умножить обе части на 4, так что мы можем работать только с целыми числами коэффициентов.
-4а 2 + 24а — 20 = 7
Вычесть 7 с обеих сторон.
-4a 2 + 24a — 27 = 0
Умножьте обе части на отрицательную, просто чтобы получить больше положительных коэффициентов, с которыми обычно легче работать.
4а 2 — 24a + 27 = 0
Чтобы разложить это на множители, нам нужно умножить внешние коэффициенты, что дает нам 4 (27) = 108. Нам нужно подумать о двух числах, которые умножаются, чтобы дать нам 108, но добавьте, чтобы дать нам -24. Эти два числа равны -6 и -18. Теперь мы перепишем уравнение как:
4a 2 — 6a -18a + 27 = 0
Теперь мы можем сгруппировать первые два члена и два последних члена, а затем мы можем факторизовать.
(4а 2 — 6а )+(-18а + 27) = 0
2a(2a-3) + -9(2a — 3) = 0
(2a-9)(2a-3) = 0
Это означает, что 2a — 9 = 0 или 2a — 3 = 0.
2a — 9 = 0
2a = 9
a = 9/2 = 4,5
2a — 3 = 0
a = 3/2 = 1,5
Таким образом, a может быть либо 1,5, либо 4,5.
Единственный доступный вариант ответа, который может быть 4.5.
Сообщить об ошибке
Найдите x: 2(x + 1) 2 – 5 = 27
Возможные ответы:
3 или –5
3 или 4
–2 или 5
–3 или 2
–2 или 4
Правильный ответ:
3 или –5
Пояснение:
Квадратные уравнения обычно имеют два ответа. Мы добавляем 5 к обеим частям, а затем делим на 2, чтобы получить квадратное выражение в одной части уравнения: (x + 1) 2 = 16. Извлекая квадратный корень из обеих частей, мы получаем x + 1 = –4 или x + 1 = 4. Затем мы вычитаем по 1 с обеих сторон, чтобы получить x = –5 или x = 3,
Сообщить об ошибке
Произведение двух последовательных положительных чисел, кратных трем, равно 54. Какова сумма этих двух чисел?
Возможные ответы:
3
6
12
15
9
Правильный ответ:
15
Объяснение:
Определим переменные как x = первое кратное трем и x + 3 = следующее последовательное кратное 3.
Зная, что произведение этих двух чисел равно 54, мы получаем уравнение x(x + 3) = 54 , Чтобы решить это квадратное уравнение, нам нужно умножить его и приравнять к нулю, а затем разложить на множители. Так х 2 + 3x – 54 = 0 становится (x + 9)(x – 6) = 0. Решая для x, мы получаем x = –9 или x = 6, и только положительное число является правильным. Таким образом, эти два числа равны 6 и 9, а их сумма равна 15.
Сообщить об ошибке
Решите 3x 2 + 10x = –3
Возможные ответы:
x = –1/3 или –3
x = –2/3 или –2
x = –1/9 или –9
x = –1/6 или –6
x = –4/3 или –1
Правильный ответ:
х = –1/3 или –3
Объяснение:
Как правило, квадратные уравнения имеют два ответа.
Во-первых, уравнения должны быть представлены в стандартной форме: 3x 2 + 10x + 3 = 0
Во-вторых, попробуйте разложить квадратное число на множители; однако, если это невозможно, используйте квадратичную формулу.
В-третьих, проверьте ответ, подставив ответы обратно в исходное уравнение.
Сообщить об ошибке
3x 2 – 11x = –10
Какое из следующих значений является допустимым для x?
Возможные ответы:
-5 / 3
5 /3
Ни один из других ответов
3
-2
Правильный ответ:
5 /3 7 Объяснение:
Начнем с того, что приведем наше уравнение к следующему виду: Ax 2 + BX + C = 0:
3x 2 – 11x + 10 = 0
Теперь, если разложить левое число, можно найти ответ. . Начните с рассмотрения двух групп. Они должны будут начинаться соответственно с 3 и 1 в качестве коэффициентов для вашего значения x. Точно так же, глядя на последний элемент, вы можете сказать, что оба должны иметь + или -, поскольку коэффициент C положительный. Наконец, поскольку коэффициент B отрицателен, мы знаем, что он должен быть равен –. Итак, мы знаем:
Итак, мы знаем:
(3x – ?)(x – ?)
Потенциальные множители 10: 10, 1; 1, 10; 2, 5; 5, 2
5 и 2 работают:
(3x – 5)(x – 2) = 0, потому что вы можете СЛОГАТЬ (3x – 5)(x – 2) обратно в 3x 2 – 11x + 10.
Теперь осталось присвоить каждому из факторов значение 0, потому что, если какая-либо из групп равна 0, все уравнение будет равно 0:
3x – 5 = 0 → 3x = 5 → x = 5/3
x – 2 = 0 → x = 2
Следовательно, x равно 5/3 или 2. Первое представляется как ответ.
Сообщить об ошибке
Какова сумма значений x, удовлетворяющих следующему уравнению:
16 x – 10(4) x + 16 = 0.
8 Возможные ответы: 3 5/2 4 3/2 1 Правильный ответ: 2 Объяснение: Уравнение, которое нам нужно решить, 16 x – 10(4) x + 16 = 0,9. Уравнения этого типа часто можно «преобразовать» в другие уравнения, такие как линейные или квадратные уравнения, если мы перепишем некоторые термины. Во-первых, мы можем заметить, что 16 = 4 2 . Таким образом, мы можем записать 16 x как (4 2 ) x или как (4 x ) 2 . Теперь уравнение (4 x ) 2 – 10(4) x + 16 = 0 Введем переменную u и приравняем ее к 4 x . Преимущество этого в том, что он позволяет нам «преобразовать» исходное уравнение в квадратное уравнение. u 2 – 10u + 16 = 0 Это уравнение нам знакомо гораздо лучше. Чтобы решить ее, нам нужно разложить ее на множители и приравнять каждый множитель к нулю. Чтобы разложить его на множители, мы должны подумать о двух числах, которые при умножении дают нам 16, а при сложении дают -10. Эти два числа -8 и -2. Таким образом, мы можем разложить u 2 – 10u + 16 = 0 следующим образом: (u – 8)(u – 2) = 0 Затем приравняем каждый коэффициент к 0. u – 8 = 0 Прибавим 8. Добавить 2. u = 2. Таким образом, u должно равняться 2 или 8. Однако мы хотим найти x, а не u. Поскольку мы определили u равным 4 x , уравнения примут вид: 4 x = 2 или 4 x = 8 Сначала решим 4 x = 2. Мы можем переписать 4 x как (2 2 ) x = 2 2x , так что основания совпадают. 2 2x = 2 = 2 1 2x = 1 x = 1/2 Наконец, мы решим 4 x x 4 9 9 3 4 = 1. Еще раз, пусть 13 9 9 4 = 8. 2x . Мы также можем записать 8 как 2 3 . 2 2x = 2 3 2x = 3 x = 3/2 В исходном вопросе нам предлагается найти сумму значений x, которые решают уравнение. Поскольку х может быть 1/2 или 3/2, сумма 1/2 и 3/2 равна 2. Ответ: 2. Сообщить об ошибке Если x > 0, какие значения x удовлетворяют неравенству x 2 > x ? Возможные ответы: Все положительные реальные числа Все идеальные квадраты Все положительные целые числа Нет значений x SATIFY. Все реальные числа больше одного 77777777777777777777 годы. Правильно: .1378 Все действительные числа больше единицы Объяснение: Есть два значения, где x 2 = x , а именно x = 0 и x = 1. Все значения от 0 до 1 уменьшаются после возведения в квадрат. Все значения больше 1 становятся больше после возведения в квадрат. Сообщить об ошибке.1367 х ) = ( х 2 + 16) (1/2) . Если k — отрицательное число такое, что f ( k ) = 31, то каково значение ( f ( g ( k ))? 31 25 -35 5 -81 Правильный ответ: 31 Объяснение: Чтобы найти значение f ( g ( k )), нам сначала нужно будет найти k . f ( x ) = 2 x 2 – 4 x + 1 f ( k ) = 2 k 2 – 4 k + 1 = 31 Вычесть 31 с обеих сторон. 2 K 2 — 4 K — 30 = 0 Разделите обе стороны на 2. K 2 — 2 K — 15 = 0 . для этого нужно подумать о двух числах, которые умножаются, чтобы дать -15, и складываются, чтобы дать -2. Эти два числа равны –5 и 3. 0, чтобы найти значения для к . k – 5 = 0 Добавьте 5 к обеим сторонам. k = 5 Теперь положим k + 3 = 0. Вычтем 3 с обеих сторон. k = –3 Это означает, что k может быть либо 5, либо –3. Наконец, мы можем вычислить выражение f ( g (–3)). Сначала нам нужно найти г (–3). g ( x ) = ( x 2 + 16) (1/2) G (–3) = (–3) 9137 2 7 413467 (–3) = (–3) 9137 2 74174 (–3) = (–3) 9137 2 2 . (1/2) = (9 + 16) (1/2) = 25 (1/2) Возведение чего-либо в половинную степень равносильно извлечению квадратного корня . 25 (1/2) = 5 Теперь, когда мы знаем, что g (–3) = 5, мы должны найти f (5). f (5) = 2(5) 2 – 4(5) + 1 = 2(25) – 20 + 1 = 31 Ответ: 31. Сообщить об ошибке 3 II. рациональный III. отдельные Какое из описаний характеризует решения уравнения 2x 2 – 6x + 3 = 0? Возможные ответы: Только I и III Только I Только II Только I и II Только II и III Правильный ответ: Только I и III Пояснение: Уравнение в задаче квадратное, поэтому для его решения можно использовать квадратичную формулу. В этой конкретной задаче a = 2, b = –6 и c = 3. дискриминанта, и это дает нам важную информацию о природе решений квадратного уравнения. Если дискриминант меньше нуля, то корни недействительны, потому что нам пришлось бы брать квадратный корень из отрицательного числа, что дает мнимый результат. Дискриминант уравнения, которое нам дано, равен (–6) 2 – 4(2)(3) = 36 – 24 = 12 > 0. Поскольку дискриминант неотрицательный, решения уравнения будут действительными. Таким образом, вариант I правильный. Дискриминант также может сказать нам, являются ли решения уравнения рациональными или нет. Если мы возьмем квадратный корень из дискриминанта и получим рациональное число, то решения уравнения должны быть рациональными. Наконец, дискриминант сообщает нам, различны ли корни уравнения (отличны ли они друг от друга). Если дискриминант равен нулю, то решения x становятся (– b + 0)/2 a и (– b – 0)/2 a , поскольку квадратный корень из нуля равно 0. Обратите внимание, что (– b + 0)/2 a совпадает с (– b – 0)/2 a . Таким образом, если дискриминант равен нулю, то корни уравнения одинаковые, т.е. нечеткие. В этой конкретной задаче дискриминант = 12, что не равно нулю. Это означает, что два корня будут разными, т.е. различными. Следовательно, применяется вариант III. Ответ только на варианты I и III. Сообщить об ошибке Решить для x . 3 x 2 + 15 x – 18 = 0. Possible Answers: x = 5 or x = 1 x = –6 or x = 1 х = 6 или х = –1 х = –2 или х = 3 х = 2 или 21367 х = –3 Правильный ответ: х = –6 или х = 1 Объяснение: Сначала посмотрим, есть ли общий термин. 3 x 2 + 15 x — 18 = 0 Мы можем вытащить 3: 3 ( x 2 + 5 x — 6) = 0,00003 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 + 5 x — 61373. Нам нужны два числа, которые в сумме дают 5 и умножаются на –6. 6 и –1 работают. ( x + 6) ( x — 1) = 0 x = –6 или x = 1 Отчет о ошибке ° С. Уведомление об авторских правах 10 Диагностические тесты
421 практический тест
Вопрос дня
Карточки
Learn by Concept Например, если ваше число равно 1, вы прибавляете 4, удваиваете это число, вычитаете 7, и вы получаете 3. Все, что нужно сделать компьютеру, это решить задачу в обратном порядке. Луиджи из Humanitree и Karrthic из Австралийской международной школы в Малайзии нашли алгебраическое выражение для конечного числа. Это работа Каррича: Furkan из TED Ankara Koleji в Турции, Bernd и Qianwei из Humanitree и Shriya из International School Frankfurt в Германии показали, что компьютер делает алгебраически. Это работа Цяньвэя: Фуркан и Шрия упростили уравнение перед тем, как «обратить» его. Это работа Фуркана: Алекс из Humanitree и Фернандо из Британской академии Кускатлека в Сальвадоре заметили другую закономерность в цифрах, полученных с компьютера. Это работа Фернандо: Однако, если мы начнем с 1 и попытаемся довести до пяти, вы заметите последовательность: Следовательно, в инструкции прямо 0,5$n-0,5$ ! Видите, как этот результат связан с уравнением Фуркана? Ваше число был Таким образом, если бы окончательное число было 19, сначала вам нужно было бы вычесть 1. Это будет равно 18. Затем вам нужно будет добавить 2, что будет равно 20. И [наконец] вам нужно будет разделить его на 4. Это равно 5, поэтому первое число будет 5. Федерико из Humanitree использовал алгебру: Если число было $n$ $(n-5) \times4 +10 = $ end number ($x$) Затем компьютер проделает эту операцию, чтобы получить исходное значение $n:$ Эта операция даст исходные результаты. Абдулла из Польши написал программу на Python для угадывания вашего числа: number = float(input(«Теперь введите число, которое вы закончили, и нажмите Enter. answer = ((( number + 23) / 3) + 6) * 4 — 9 print(«Вы выбрали число %s» % ответ) Leila C и Scarlett K из Westridge School for Girls и KSc из Cheadle Academy прислали интересные наборы инструкций, которые всегда будут давать один и тот же результат, как в задаче Your Number Is… Математика Часть I (решения) Решения для 10 класса Математика Глава 2 Квадратные уравнения представлены здесь с простыми пошаговыми объяснениями. Напишите любые два квадратных уравнения. Два квадратных уравнения: Определите, какие из следующих уравнений являются квадратными. (1) x 2 + 5 x – 2 = 0 (2) г 2 = 5 г – 10 (3) y2+1y=2 (4) x+1x=-2 (5) ( м + 2) ( м – 5) = 0 (6) м 3 + 3 м 2 – 2 = 3 м 3 Напишите следующие уравнения в форме AX 2 + BX + C = 0, тогда напишите значения A A A A A A A . (1) 2 y = 10 – y 2 (2) ( x – 1) 2 = 2 x + 3 (3) x 2 + 5 x = –(3 – x ) (4) 3 M 2 = 2 M 2 = 2 M 2 = 2 M 2 = 2 M 2 = 2 M 2 = 2 M 2 . 9 (6) x 2 – 9 = 13 Определите, являются ли значения, заданные для каждого квадратного уравнения, корнями уравнения. (1) x 2 + 4 x – 5 = 0 , x = 1, –1 (2) 2 м 2 – 5 м = 0, m=2, 52 Найти K IF x = 3 — корень уравнения KX 2 — 10 x + 3 = 0 — 10 x + 3 = 0 — 10 x + 3 = 09373 — 10 x + 3 = 0 — 10 x + 3 = 09373 — 10 . Один из корней уравнения 5 m 2 + 2 m + k = 0 равно -75 . Выполните следующее действие, чтобы найти значение « k ». -75 является корнем квадратного уравнения 5 м 2 + 2 м + k = 0. Решите следующие квадратные уравнения методом факторизации. (1) x 2 – 15 x + 54 = 0 (2) x 2 + x – 20 = 0 (3) 2 y 2 + 27 y + 13 = 0 (4) 5 м 2 = 22 м + 15 (5) 2 x 2 – 2 x + 12 = 0 (6) 6x-2x=1 (7) 2×2+7x+52=0 (8) 3×2-26x+2=0 ( 9) 2мм-24=50 (10) 25m2=9 (11) 7м2=21м (12) м2-11=0 Решите следующие квадратные уравнения, выполнив квадратный метод. (1) x 2 + x – 20 = 0 (3) м 2 – 5 м = –3 (4) 9 y 2 – 12 y + 2 = 0 (5) 2 г 2 + 9 г +10 = 0 Сравните данные квадратные уравнения с общим видом и запишите значения a , b , c . (1) x 2 – 7 x + 5 = 0 2 2: 0003
0003
 Неравенство
Неравенство Нам говорят, что f ( k ) = 31, поэтому мы можем написать выражение для f ( k ) и найти k .
Нам говорят, что f ( k ) = 31, поэтому мы можем написать выражение для f ( k ) и найти k . Однако нам говорят, что k — отрицательное число, что означает k = –3.
Однако нам говорят, что k — отрицательное число, что означает k = –3. I. реальный
 Если уравнение имеет вид x 2 + bx + c = 0, где a , b и c — константы, то приведенная ниже квадратичная формула дает нам решения х .
Если уравнение имеет вид x 2 + bx + c = 0, где a , b и c — константы, то приведенная ниже квадратичная формула дает нам решения х . В этой задаче нам нужно будет извлечь квадратный корень из 12. Однако 12 не является полным квадратом, поэтому извлечение его квадратного корня даст иррациональное число. Поэтому решения уравнения в задаче не могут быть рациональными. Это означает, что вариант II неверен.
В этой задаче нам нужно будет извлечь квадратный корень из 12. Однако 12 не является полным квадратом, поэтому извлечение его квадратного корня даст иррациональное число. Поэтому решения уравнения в задаче не могут быть рациональными. Это означает, что вариант II неверен.
 на 3: x 2 + 5 x – 6 = 0
на 3: x 2 + 5 x – 6 = 0 Все математические ресурсы PSAT
Mathway | Популярные проблемы
1 93-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92 Ваш номер был.
 ..
.. Возраст от 11 до 14 лет
Уровень сложности
Ученицы Westridge School for Girls в США, Cedric из Australian International School Malaysia, Poppy and Gracie из Walton High School в Англии, ученики из Humanitree в Мексике, Флоренс из начальной школы Walthamstow Hall в Великобритании, Эрик и Люсия из школы Willowbank в Новой Зеландии, Абдулла из Польши, ученики англиканской школы Frederick Irwin.
в Австралии, Джон из Пулсвилля ES в США, Брача и Антуан из начальной школы St Philip’s CofE в Кембридже в Великобритании, Парк из Международной школы Ренессанса Сигон в Корее, Дия из Великобритании, Дениз из школы Норт-Лемингтон в Великобритании, Ира из Coldspring3 и Ади из New Beacon в Великобритании описали, как компьютер вычисляет ваш стартовый номер.
Кристин из Вестриджской школы для девочек прислала это объяснение:
Все, что вам нужно сделать, это решить задачу в обратном порядке.
3$+$7 (против $-$7) равно 10.
10$\div$2 (противоположно $\times$2) равно 5.
$-$4 (противоположно $+$4) равно 1, что было моим исходным количество.
Операция
$(x +4) \times 2 -7= y$
Например,
$(5 + 4) = 9\\
9 \times2 = 18\\
18-7=11$
Когда вы делаете операцию в обратном порядке, вы получаете $x$
$(x+4) \times 2 — 7=y$
Если мы хотим получить $x$, нам нужно сделать противоположное этому уравнению.
Начните с $y.$ В уравнении $7$ [было вычтено], поэтому нам нужно добавить $7$ к $y$
$(7+y)$
В уравнении $(x+4)$ было удвоено, нам нужно разделить его на два, чтобы получить обратное.
$(7+y)\div2$
В уравнении $x$ прибавили [к] $4$, чтобы получить обратное, нужно из $x отнять $4$.$
$(y+7) \div2-4$
Наконец, уравнение, которое мы использовали для нахождения $x$, будет таким:
$(y+7)\div2-4=x$
$(x+4) \times2 — 7$ равно $2x + 1,$, поэтому мы вычитаем из результата $1$ и делим на $2$, чтобы получить начальное число.
Если следовать инструкциям, приведенным в задаче, если [вы зададите компьютеру случайные целые числа в результате вычислений], вы получите случайные числа. Число, которое вы сообщаете компьютеру, было вашим ответом Номер, который, по словам компьютера, вы начали с .
1 0 2 0,5 3 1 4 1,5 5 2
Как видите, последовательность прогрессирует на 0,5, то есть является линейной. Это добавляет 0,5, поэтому мы видим, что когда 0,5$\times n$ выполнено, последовательность теперь выглядит следующим образом: Число, которое вы сообщаете компьютеру, было вашим ответом ($n$) Номер, который, по словам компьютера, вы начали с . 0,5$\times n$ 1 0 0,5 2 0,5 1 3 1 1,5 4 1,5 2 5 2 2,5
Ответ на подстановку всегда на 0,5 больше фактического ответа,
поэтому надо всегда вычитать 0,5
Мы получили множество наборов инструкций для подобных действий.
Эти инструкции от Тамары из Humanitree:
.Задумайте число
.умножьте его на 4
.вычтите 2
.прибавьте 1
Вычесть 10
Разделить на 4
Прибавить 5
Вы должны сделать
$(x-10 )\div4 +5 =$ начальный номер
input(«Задумайте число.»
print()
input(«Добавить 9»)
print()
input(«Разделить на 4»)
print()
input(«Вычесть 6»)
print()
input(«Утроить»)
print()
input(«Вычесть 23») «))
«))
print(«Обработка…»)
=Если вы будете следовать этим инструкциям, сможет ли компьютер определить, с какого числа вы начали?
Это инструкции KSc: Математика Часть I (решения) для 10 класса Математика Глава 2
 Эти решения для квадратных уравнений чрезвычайно популярны среди учащихся 10 класса по математике. Решения для квадратных уравнений пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из книги по математике, часть I (решения) для 10 класса, глава 2, предоставляются здесь для вас бесплатно. Вам также понравится отсутствие рекламы в решениях Meritnation по математике, часть I (решения). Вся математика Часть I (решения) Решения для класса 10 по математике подготовлены экспертами и на 100% точны.
Эти решения для квадратных уравнений чрезвычайно популярны среди учащихся 10 класса по математике. Решения для квадратных уравнений пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из книги по математике, часть I (решения) для 10 класса, глава 2, предоставляются здесь для вас бесплатно. Вам также понравится отсутствие рекламы в решениях Meritnation по математике, часть I (решения). Вся математика Часть I (решения) Решения для класса 10 по математике подготовлены экспертами и на 100% точны. Страница № 34:
Вопрос 1:
Ответ:
x2+10x-200=0 и x2+5x-6=0. Страница № 34:
Вопрос 2:
(1) х 2 + 5 х – 2 = 0
(2) у 2 = 5 у – 10 х 91 2 2 (1)
(3) у +1x=-2
(5) ( м + 2) ( m – 5) = 0
(6) m 3 + 3 m 2 – 2 = 3 m 3 Answer:
Только одна переменная x.
Максимальный индекс = 2
Итак, это квадратное уравнение.
Только одна переменная г.
Максимальный индекс = 2
Итак, это квадратное уравнение.
⇒y3+1=2y
Только одна переменная y.
Максимальный индекс = 3
Итак, это не квадратное уравнение.
⇒x2+1=-2x
Только одна переменная x.
Максимальный индекс = 2
Итак, это квадратное уравнение.
⇒м2-3м-10=0
Только одна переменная м.
Максимальный индекс = 2
Итак, это квадратное уравнение.
Только одна переменная м.
Максимальный индекс = 3
Итак, это не квадратное уравнение. Страница № 34:
Вопрос 3:
 , c для каждого уравнения.
, c для каждого уравнения.
(1) 2 у = 10 — Y 2
(2) ( x — 1) 2 = 2 x + 3
(3) x 2 9374 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 . – x )
(4) 3 м 2 = 2 м 2 – 9
(5) P(3+6 p ) = –5 Ответ:
⇒y2+2y=10⇒y2+2y-10=0 1374 имеет вид ax 2 + bx + c = 0, где a = 1, b = 2 и c
⇒x2-2x+1=2x+3⇒x2-4x-2=0
Итак, 4 913 форма ax 2 + bx + c = 0, где a = 1, b = −4 и c =
⇒x2+5x+3-x=0⇒x2+4x+3=0
Итак, имеет вид ax 23 4 3 + BX + C = 0, где A = 1, B = 4 и C = 3.
⇒ 3m2-2m2+9=0⇒m2+0m+9=0
Итак, имеет вид ax 2 + bx + c = 90 36 9 где1367 a = 1, b = 0 и c = 9. +5 = 0
SO, Это форма AX 2 + BX + C = 0, где A = 6, B = 3 и C = 6, B = 3 и C = 6, B = 3 и C = 6, B = 3 и C = 6, B = 3 и .
⇒x2-9-13=0⇒x2-22=0⇒x2+0x-22=0
Итак, имеет вид 2 + bx + c = 0, где a = 1, b = 0 и c = -22. Страница № 34:
Вопрос 4:

(1) х 2 + 4 х – 5 = 0 , х = 1, –1
(2) 2 м 2 , м = 2 Ответ:
Итак, x = 1 является решением данного уравнения.
Для x = –1
-12+4-1-5=0⇒1-4-5=0⇒-3-5=0⇒-8≠0
Итак, x = –1 не является решение заданного уравнения.
Таким образом, только x = 1 является корнем данного уравнения.
При m=2222-52=0⇒8-10=0⇒-2≠0
Итак, м = 2 не является решением данного уравнения.
Когда m=522522-552=0⇒252-252=0
Итак, m=52 является решением данного квадратного уравнения.
Таким образом, только m=52 является корнем данного квадратного уравнения. Стр. № 34:
Вопрос 5:
 x = 3 — это корень уравнения 9.1367 kx 2 – 10 x + 3 = 0
x = 3 — это корень уравнения 9.1367 kx 2 – 10 x + 3 = 0
Таким образом, x = 3 должны удовлетворять заданному квадратичному уравнению.
k32-103+3=0⇒9k-30+3=0⇒9k-27=0⇒9k=27⇒k=279=3
Таким образом, k = 3. Страница № 34:
Вопрос 6:
Ответ:
∴ Поместите м = -75 в уравнение.
5×-752+2×-75+k=0495+-145+k=07+k=0k=-7 Страница № 36:
Вопрос 1:
(1) x 2 – 15 x + 54 = 0
(2) x 2 + x – 20 = 0
(3) 2 y 2 + 27 г + 13 = 0
(4) 5 м 2 = 22 м + 15
(5) 2 x 2 – 2 x + 12 = 0
(6) 6x21x1 (7) 6x21x1 (7) 6x21x1 7 52=0
Чтобы решить это квадратное уравнение с помощью факторизации, выполните следующее задание.
(8) 3×2-26x+2=0
(9) 2мм-24=50
(10) 25м2=9
(11) 7м2=21м
(12) м2-11=0
Ответ:
⇒x2-9x-6x+54=0⇒xx-9-6x-9=0⇒x-6x-9=0⇒x- 6=0 или х-9=0⇒x=6 или x=9
Итак, 6 и 9 являются корнями данного квадратного уравнения.
⇒x2+5x-4x-20=0⇒xx+5-4x+5=0⇒x-4x+5=0⇒x -4=0 или x+5=0⇒x=4 или x=-5
Итак, 4 и -5 являются корнями данного квадратного уравнения.
2y2+26y+y+13=0⇒2yy+13+y+13=0⇒2y+1y+13=0⒒ 2y+1=0 или y+13=0⇒y=-12 или y=-13
Итак, -12 и -13 – это корни данного квадратного уравнения.
⇒5м2-22м-15=0⇒5м2-25м+3м-15=0⇒5мм-5+3м-5=0⇒5м +3m-5=0⇒5m+3=0 или m-5=0⇒m=-35 или m=5
Итак, -35 и 5 – это корни данного квадратного уравнения.
⇒4×2-4x+1=0⇒2×2-2×1×2x+1=0Используя тождество, a-b2=a2 +b2-2ab2x2-2×1×2x+1=0⇒2x-12=0⇒x=12,12
Итак, 12 и 12 – это корни данного квадратного уравнения.
⇒6×2-2=1x⇒6×2-1x-2=0⇒6×2-4x+3x-2=0⇒2x3x-2+13x-2=0⇒3x-22x+ 1=0⇒3x-2=0 или 2x+1=0⇒x=23 или x=-12
23 и -12 являются корнями данного квадратного уравнения.
2×2+5x+2x+52=0x2x+5+22x+5=02x+5x+2=02x+5=0 или x+2=0∴x=- 52 или x=-2∴-52 и -2 являются корнями уравнения.
⇒3×2-6x-6x+2=0⇒3x3x-2-23x-2=0⇒3x-23x-2=0⇒x=23,23
⇒мм-24=25⇒м2-24м=25⇒м2-24м-25=0⇒м2-25м+м-25=0⇒мм-25+1м-25=0⇒м +1m-25=0⇒m=-1,25
⇒25m2-9=0⇒5m2-32=0⇒5m-35m+3=0 ∵x-ax+a=x2 -a2⇒5m-3=0 или 5m+3=0⇒m=35,-35
⇒7м2-21м=0⇒7мм-3=0⇒7м=0 или м-3=0⇒м=0 или м=3
⇒m2-112=0⇒m-11m+11=0⇒m=11, -11 Страница № 39:
Вопрос 1:
(1) x 2 + x — 20 = 0
(2) x 2 + 2 x — 5 = 0
(3) M — 5 = 0
(3) M — 5 = 0
(3) M 2 2 2 2 — 5 2 — 5 — 5 — 5 — 5 — 5 — 5 — 5 — 5 — 5 — 5 — 5 . м = –3
м = –3
(4) 9 y 2 – 12 y + 2 = 0
(5) 2 y 2 + 9 y +10 = 0
(6) 5 x 2 = 4 x + 7 Ответ:
x2+x+122-122-20=0⇒x+1222=12 =14+20⇒x+122=814⇒x+12=92 или x+12=-92 ⇒x=4 или x=-5
(2) x 2 + 2 x – 5 = 0
⇒x2+2x+222-222-5=0⇒x2+2x+1-1-5=0⇒x+12-6=0⇒x+12=6⇒x+12=62⇒x+1 =6 или x+1=-6⇒x=6-1 или x=-6-1
⇒m2-5m+-522—522=-3⇒m2-5m+254-254=-3⇒m-522=-3 +254⇒m-522=134⇒m-522=1322⇒m-52=132 или m-52=-132⇒m=132+52 или m=-132+52⇒m=13+52 или m=5 -132
⇒y2-129y+29=0⇒y2-43y+29=0⇒y2-43y+4222+4222 =0⇒y2-43y+232-232+29=0
⇒y2-43y+49-49+29=0⇒y-232-29=0⇒y-232=29⇒y-232=232
⇒y -23=23 или y-23=-23⇒y=23+23 или y=-23+23⇒y=2+23 или y=-2+23
⇒y2+92y+5=0⇒y2+92y+9222-9222+5=0⇒y2+92y+942-942+5=0⇒y +942=8116-5⇒y+942=116
⇒y+942=142⇒y+94=14 или y+94=-14⇒y=14-94=-84=-2 или y=-14- 94=-104=-52⇒y=-2,-52
(6) 5 x 2 = 4 x + 7
⇒5×2-4x-7=0⇒x2-45x-75=0 ⇒x2-45x+4522-4522-75=0⇒x2-45x+252-252-75=0⇒x-252=75+425=35+425=3925⇒x-252=3925
⇒x-252= 3952⇒x-25=395 или x-25=-395⇒x=2+395 или x=2-395 Страница № 43:
Вопрос 1:

(1) x 2 – 7 x + 5 = 0
(2) 2 m 2 = 5 m – 5
(3) y 2 = 7 y
Ответ:
Общая форма квадратного уравнения: ax2+bx+c=0.
Сравнение x 2 – 7 x + 5 = 0 with the general form we have a = 1, b = -7 and c = 5.
(2) 2 m 2 = 5 м – 5
⇒ 2m2-5m+5=0
Общая форма квадратного уравнения: ax2+bx+c=0.
Сравнение 2 M 2 = 5 M -5 с общей формой.1368 2 = 7 y
⇒y2-7y+0=0
Общая форма квадратного уравнения: ax2+bx+c=0.
Сравнение Y2-7Y+0 = 0 с общей формой мы имеем A = 1, B = -7 и C = 0, Страница № 43:
2:
.
 Решить по формуле.
Решить по формуле.
(1) x 2 + 6 x + 5 = 0
(2) x 2 – 3 x – 2 = 0 7
(3)1368 2 + 2 м – 7 = 0
(4) 5 м 2 – 4 м – 2 = 0
(5) 6 7 х 3 915 2
Ответ:
(1) x 2 + 6 x + 5 = 0
Onax+ 5 = 0
Onax+ 5 = 0
a = 1, b = 6 и c = 5
Теперь b2-4ac=62-4×1×5=36-20=16
x=-b±b2-4ac2a
x=- 6±162×1=-6±42⇒x=-6+42 или x=-6-42⇒x=-1 или x=-5
(2) x 2 – 3 x – 2 = 0
При сравнении с уравнением = -2
Теперь b2-4ac=-32-4×1×-2=9+8=17
x=-b±b2-4ac2a
x=3±172×1=3±172⇒x=3 +172 или x=3-172
(3) 3 м 2 + 2 м – 7 = 0
При сравнении с уравнением ах2+bх+с=0,
а = 3,368 b = 2 и c = -7
Теперь b2-4ac=22-4×3×-7=4+84=88
x=-b±b2-4ac2a
x=-2±882×3=-2±886⇒x=-2+886 или x=-2-886⇒x=-1+223 или -1-223
(4) 5 м 2 – 4 м – 2 = 0
При сравнении с уравнением ax2+bx+c=0,
а = 5, -2
Теперь b2-4ac=-42-4×5×-2=16+40=56
x=-b±b2-4ac2a
x=-4±562×5=-4±5610⇒x= -4+5610 или x=-4-5610⇒x=-2+145 или -2-145
(5) y2+13y=2
Умножение уравнения на 3
3y2+y=6⇒3y2+y- 6=0
При сравнении с уравнением ax2+bx+c=0,
a = 3, b = 1 и c = -6
Теперь b2-4ac=12-4×3×-6=1+72=73
x=-b±b2-4ac2a
x =-1±732×3=-1±736⇒x=-1+736 или x=-1-736
(6) 5 x 2 + 13 x + 8 = 0
При сравнении с уравнением ax2+bx+c=0,
a = 5, b = 13 и c = 8
Теперь b2-4ac=132-4×5×8=169-160=9
x =-b±b2-4ac2a
x=-13±92×5=-13±310⇒x=-13+310 или x=-13-310⇒x=-1010 или x=-1610⇒x=-1 или x=-85
Страница № 44:
Вопрос 3:
С помощью приведенной ниже блок-схемы решите уравнение x2+23x+3=0 по формуле.
Ответ:
Сравните уравненияx2+23x+3=0 иax2+bx+c=0, найдите значения a,b,c. →Найти значение b2-4ac→Написать формулу для решенияквадратичного уравнения.→Подставить значения a,b,c и найти корни
, сравнивая x2+23x+3=0 с ax2+bx+c=0, получаем
a=1,b=23 и c=3
b2-4ac=232-4×1×3=12-12=0
Формула для решения квадратного уравнения будет
x=-b±b2-4ac2a⇒x=-23±02×1=-232=-3
Таким образом, x=-3,-3.
Страница № 49:
Вопрос 1:
Заполните пропуски и закончите.
(3) Если α, β — корни квадратного уравнения,
Ответ:
Если α и β — корни квадратного уравнения, то квадратное уравнение можно записать в виде
x2-α +βx+αβ=0
Итак, квадратное уравнение с суммой корней α+β=-7 и произведением корней αβ=5 будет равно
x2+7x+5=0
Сумма корней = -ba=—42=2
Произведение корней = ca=-32
Страница № 49:
Вопрос 2:
Найдите значение дискриминант.
(1) x 2 + 7 x – 1 = 0
(2) 2 y 2 – 5 y + 10 = 0 3
Ответ:
(1) x 2 + 7 x – 1 = 0
Сравнение данного уравнения с ax2+bx+c=0,
a=1,b=7 и c=-1
Итак, дискриминант b2-4ac=72-4×1×-1=49+4=53
(2) 2 y 2 – 5 y + 10 = 0
Сравнивая данное уравнение с 10=25-80=-55
(3) 2×2+4x+22=0
Сравнивая данное уравнение с ax2+bx+c=0,
a=2,b=4 и c=22
Итак, дискриминант b2-4ac=42-4×2×22=16-16=0
Страница № 49:
Вопрос 3:
Определите природу корней следующих квадратных уравнений.
(1) x 2 — 4 x + 4 = 0
(2) 2 Y 2 — 7 Y +2 = 0
(3) M 2 2 2 2 2 2 2 2 2 2 2 2 . 2 м + 9 = 0
Ответ:
(1) x 2 – 4 x + 4 = 0
Сравнивая данное уравнение с квадратным уравнением a=1,b=-4,c=4
Дискриминант, △=b2-4ac=-42-4×1×4=16-16=0
Поскольку дискриминант = 0, то корни данного квадратного уравнения действительны и равны.
(2) 2 y 2 – 7 y +2 = 0
Сравнение данного уравнения с квадратным уравнением ax2+bx+c=0,
a=2,b=-7,c= 2
Дискриминант, △=b2-4ac=-72-4×2×2=49-16=33
Поскольку дискриминант > 0, значит, корни данного квадратного уравнения действительны и неравны.
(3) м 2 + 2 м + 9 = 0
Сравнивая данное уравнение с квадратным уравнением ax2+bx+c=0,
a=1,b=2,c=9
Дискриминант, △=b2-4ac=22-4×1×9=4-36=-32
Поскольку дискриминант < 0, значит, корни данного квадратного уравнения не вещественны.
Страница № 50:
Вопрос 4:
Составьте квадратное уравнение из приведенных ниже корней.
(1) 0 и 4
(2) 3 и –10
(3) 12,-12
(4) 2-5,2+5
Ответ:
(1) 0 и 4
Сумма корней = 0 + 4 = 4
Произведение корней = 0 × 4 = 0
Общая форма квадратного уравнения: x2-Сумма корнейx+Произведение корней=0 0
⇒x2-4x=0⇒xx-4=0
(2) 3 и –10
Сумма корней = 3 + (–10) = −7
Произведение корней = 3 × –10 = –30
общая форма квадратного уравнения: x2-Сумма корнейx+Произведение корней=0
Таким образом, полученное квадратное уравнение имеет вид x2—7x+-30=0
x2+7x-30=0
(3) 12,- 12
Сумма корней = 12+-12=0
Произведение корней = 12×-12=-14
Общая форма квадратного уравнения: x2-Сумма корнейx+Произведение корней=0
Итак, квадратное уравнение получено x2-0x+-14=0
⇒x2-14=0
(4) 2-5,2+5
Сумма корней = 2-5+2+5=4
Произведение корней = 2-52+5=4-5=-1
Общая форма квадратного уравнения: x2-Сумма корнейx+Произведение корней=0
Итак, полученное квадратное уравнение:
Вопрос 5:
Сумма корней квадратного уравнения равна удвоенному их произведению. Найдите k , если уравнение x 2 – 4k x + k +3 = 0
Найдите k , если уравнение x 2 – 4k x + k +3 = 0
Ответ:
Пусть корнями квадратного уравнения будут α и β.
Сумма корней = α+β
Произведение корней = αβ
Учитывая, что сумма корней = удвоенному произведению
⇒α+β=2αβ k x + k +3 = 0 …..(II)
Общая форма квадратного уравнения: =0⇒x2-2αβx+αβ=0 …..III
При сравнении (II) и (III) имеем
4k=2αβ и k+3=αβ
Решая эти уравнения, имеем
4k=2k+3⇒2k=k+3⇒2k-k=3⇒k=3
Стр. № 50:
Вопрос 6:
α, β — корни Y 2 — 2 Y –7 = 0 Найти, α, β — корни3161 a=1,b=-2,c=-7a=1,b=-2,c=-7 (2) Корни каждого из следующих квадратных уравнений действительны и равны, найдите k. Ответ: 10632 10632 у 2 + k y +12 = 0 (2) k x ( x – 2) + 6 = 0 Произведение возраста Прагати 2 года назад и 3 года спустя равно 84. Найдите ее настоящий возраст. Пусть нынешний возраст Прагати будет х лет. Сумма квадратов двух последовательных натуральных чисел равна 244; найти числа. Отказ от ответственности: В данном вопросе есть ошибка. Здесь это должны быть два последовательных четных натуральных числа. В Мадхусудане 150 апельсиновых деревьев. Пусть количество деревьев в каждом столбце равно x . Вивек старше Кишора на 5 лет. Сумма обратных величин их возрастов равна 16. Найдите их настоящий возраст. Пусть нынешний возраст Кишора будет х лет. Суяш набрал на 10 баллов больше во втором тесте, чем в первом. В 5 раз результат второго теста равен квадрату результата первого теста. Найдите его результат в первом тесте. Пусть результат первого теста будет x . Мистер Касам занимается изготовлением глиняных горшков. Он делает определенное количество горшков ежедневно. Стоимость производства каждого горшка составляет 40 рупий, что более чем в 10 раз превышает общее количество горшков, которые он производит за один день. Пусть количество горшков, которое г-н Касам делает за один день, равно x. Пратику требуется 8 часов, чтобы пройти 36 км вниз по течению и вернуться на то же место. Скорость лодки в стоячей воде 12 км. Пусть скорость течения = y км/ч Пинту требуется на 6 дней больше, чем у Нишу, чтобы выполнить определенную работу. Если они работают вместе, они закончат его за 4 дня. За сколько дней они выполнят работу, если они будут работать в одиночку. Пусть число дней, потраченных Нишу, равно 9.1367 х . Если 460 разделить на натуральное число, то частное будет больше делителя, умноженного на 6, а остаток равен 1. Найдите частное и делитель. Пусть делитель будет х .
(1) α 2 –7 = 0,
(1) α 2 –7. Ответ:
(1)
α+β=-ba=—21=2αβ=ca=-71=- 7
α2+β2=α+β2-2αβ=22-2-7=4+14=18
α3+β3=α+β3-3αβα+β=23-3-72=8+42 =50
Страница № 50:
Вопрос 7:

(1) 3 y 2 + k y +12 = 0
(2) k x ( x – 2) + 6 = 0
Корни данного квадратного уравнения действительны и равны. Таким образом, дискриминант будет равен 0.
b2-4ac=0⇒k2-4×3×12=0⇒k2-144=0⇒k2=144⇒k=±12
⇒kx2-2kx+6=0
Корни данного квадратного уравнения действительны и равны. Таким образом, дискриминант будет равен 0.
b2-4ac=0⇒-2k2-4×k×6=0⇒4k2-24k=0⇒4kk-6=0⇒4k=0 или k-6=0⇒k= 0 или k=6
Но k не может быть равно 0, так как тогда не будет никакого квадратного уравнения.
Итак, k = 6
Страница № 52:
Вопрос 1:
Ответ:
Ее возраст 2 года назад = x-2
Ее возраст через 3 года = x+3
Произведение возраста Прагати 2 года назад и через 3 года равно 84.
x-2x+3=84⇒x2+x-6= 84⇒x2+x-90=0x=-b±b2-4ac2a⇒x=-1±12-4×1×-902=-1±3612x=-1-192 или -1+192⇒x=-10 или 9
Но возраст не может быть отрицательным, поэтому x = 9.
Таким образом, нынешний возраст Прагати составляет 9 лет.
Страница № 52:
Вопрос 2:
Ответ:
Пусть два последовательных натуральных числа равны x и x+2.
Сумма квадратов этих двух последовательных натуральных чисел равна 244
x2+x+22=244⇒x2+x2+4+4x=244⇒2×2+4x-240=0⇒x2+2x-120=0⇒x=-b±b2-4ac2a⇒x=-2±22 -4×1×-1202⇒x=-2±4+4802
⇒x=-2±4842⇒x=-2±222⇒x=-2+222,-2-222⇒x=202,-242 ⇒x=10,-12
Но натуральное число не может быть отрицательным, поэтому
Два числа 10 и 10 + 2 = 12.
Страница № 52:
Вопрос 3:
 Количество деревьев в каждой строке на 5 больше, чем в каждом столбце. Найдите количество деревьев в каждой строке и каждом столбце с помощью следующей блок-схемы.
Количество деревьев в каждой строке на 5 больше, чем в каждом столбце. Найдите количество деревьев в каждой строке и каждом столбце с помощью следующей блок-схемы. Ответ:
Количество деревьев в строке = x + 5
Всего деревьев = Количество строк × Количество столбцов = xx+5 = 150
⇒xx+5=150⇒x2+5x-150=0⇒x2+15x- 10x-150=0⇒xx+15-10x+15=0⇒x+15x-10=0⇒x=10,-15
Но количество столбцов не может быть отрицательным, поэтому количество столбцов = 10.
Количество строк = 10 + 5 = 15
Страница № 52:
Вопрос 4:
Ответ:
Вивек старше Кишора на 5 лет.
Итак, возраст Вивека будет x + 5.
Сумма обратных величин их возрастов равна 16.
1x+1x+5=16⇒x+5+xxx+5=16⇒5+2xx2+5x= 16⇒30+12x=x2+5x⇒x2-7x-30=0⇒x2-10x+3x-30=0⇒xx-10+3x-10=0⇒x+3x-10=0⇒x=-3 ,10
Но возраст не может быть отрицательным, поэтому возраст Кишора 10 лет, а возраст Вивека 10 + 5 = 15 лет.
Страница № 52:
Вопрос 5:
Ответ:
Результат Суяша во втором тесте на 10 больше, чем в первом.
Итак, его результат во втором тесте = x + 10
5 умноженный на балл во втором тесте равен квадрату балла в первом тесте.
5x+10=x2⇒5x+50=x2⇒x2-5x-50=0⇒x2-10x+5x-50=0⇒xx-10+5x-10=0⇒x+5x-10=0⇒x =10,-5
Результат не отрицательный, поэтому Суяш набрал 10 баллов в первом тесте.
Страница № 52:
Вопрос 6:
 Если стоимость производства всех горшков в день составляет 600 рупий, найдите стоимость производства одного горшка и количество горшков, которые он производит в день.
Если стоимость производства всех горшков в день составляет 600 рупий, найдите стоимость производства одного горшка и количество горшков, которые он производит в день. Ответ:
Себестоимость производства каждого горшка составляет 40 рупий более чем в 10 раз больше общего количества горшков, которое он производит за один день = 10 x + 40
Себестоимость производства всех горшков в день составляет 600
рупий (10 x + 40 ) x = 600
10×2+40x=600⇒x2+4x-60=0⇒x2+10x-6x-60=0⇒xx+10-6x+10=0⇒x-6x+10=0⇒x =6,-10
Но количество горшков не может быть отрицательным, поэтому
x≠-10⇒x=6
Стоимость производства 1 горшка = 10×6+40=60+40=100 9 рупий.3161 Страница № 52:
Вопрос 7:
 в час. Найдите скорость течения воды.
в час. Найдите скорость течения воды. Ответ:
Скорость лодки в стоячей воде = 12 км/ч
Скорость вверх по течению = 12-y
Скорость вниз по течению = 12 + y = 36 км вниз по течению и 36 км вверх по течению
Скорость = РасстояниеВремя⇒Время=РасстояниеСкорость =24×4⇒y2=36⇒y2-36=0⇒y=±6
Скорость не может быть отрицательной, поэтому скорость течения воды = 6 км/ч. Страница № 52:
Вопрос 8:
Ответ:
Таким образом, количество дней, затраченных Пинту, будет x + 6
1-дневная работа Нишу = 1x
1-дневная работа Пинту = 1x+6
Работа, выполненная вместе за 4 дня = 14
1x+1x+6=14⇒ х+6+ххх+6=14⇒6+2хх2+6х=14⇒24+8х=х2+6х⇒х2-2х-24=0⇒х2-6х+4х-24=0⇒х-6х+4= 0⇒x=6,-4
Количество дней не может быть отрицательным, поэтому x = 6.
Таким образом, количество дней, затраченных Нишу = 6, а количество дней Пинту = 6 + 6 = 12. Страница № 52 :
Вопрос 9:
Ответ:
Делимое = 460
Частное = 5 x + 6
Остаток = 1
Мы знаем
Делимое = Делитель × Частное + Остаток =0⇒x=-b±b2-4ac2a⇒x=-6±62-4×5×-4592×5⇒x=-6±36+
⇒x=-6± 9610⇒x=-6+9610,-6-9610⇒x=9,-10,2
Таким образом, делитель = 9, частное = 5 x + 6 = 5×9+6=45+6=51
Страница № 52:
Вопрос 10:
На приложенном рис. □ABCD — трапеция AB || CD и его площадь 33 см 2 . По информации, представленной на рисунке, найдите длины всех сторон □ABCD. Заполните пустые поля, чтобы получить решение.
Ответ:
□ABCD — трапеция.
АБ || CD
A(□ABCD) = 12AB+CD×AM
33=12x+2x+1×x-4∴33×2=3x+1×x-4∴3×2+11x-70=0∴3xx-7+ 10x-7=0∴3x+10x-7=0∴3x+10=0 или x-7=0∴x=-103 или x=7
Но длина никогда не бывает отрицательной.
∴x≠-103 ∴x=7
AB = 7, CD = 15, BC = 5
Страница № 53:
Вопрос 1:
Выберите правильные ответы на следующие вопросы.
(1) Какое из них является квадратным уравнением?
| (А) 5x-3=x2 | (Б) х ( х + 5) = 2 | (С) n – 1 = 2 n | (Д) 1x2x+2=x |
(2) Какое из следующих уравнений не является квадратным уравнением?
| (А) x 2 + 4 х = 11 + х 2 | (Б) x 2 = 4 x | (С) 5 х 2 = 90 | (D) 2 x – x 2 = x 2 + 5 |
(3) Корни x 2 + kx + k = 0 действительны и равны, найдите k.
| (А) 0 | (Б) 4 | (С) 0 или 4 | (Д) 2 |
(4) Для 2×2-5x+2=0 найти значение дискриминанта.
| (А) –5 | (Б) 17 | (С) 2 | (Д) 22-5 |
(5) Какое из следующих квадратных уравнений имеет корни 3,5 ?
| (А) x 2 – 15 х + 8 = 0 | (Б) х 2 – 8 х + 15 = 0 |
| (С) х 2 + 3 х + 5 = 0 | (Г) х 2 + 8 х – 15 = 0 |
(6) Из следующих уравнений найдите уравнение, имеющее сумму корней –5.
| (А) 3 x 2 – 15 х + 3 = 0 | (Б) х 2 – 5 х + 3 = 0 |
| (С) х 2 + 3 х – 5 = 0 | (D) 3x 2 + 15 x + 3 = 0 |
(7) 5m2-5m+5=0 какое из следующих утверждений верно для данного уравнения?
| (А) Действительные и неправильные корни | (B) Действительные и равные корни |
| (C) Корни не настоящие | (D) Три корня. |
(8) Один из корней уравнения x 2 + m x – 5 = 0 равен 2; найти м.
| (А) –2 | (Б)-12 | (С) 12 | (Д) 2 |
Ответ:
(1) Общая форма квадратного уравнения: ax2+bx+c=0.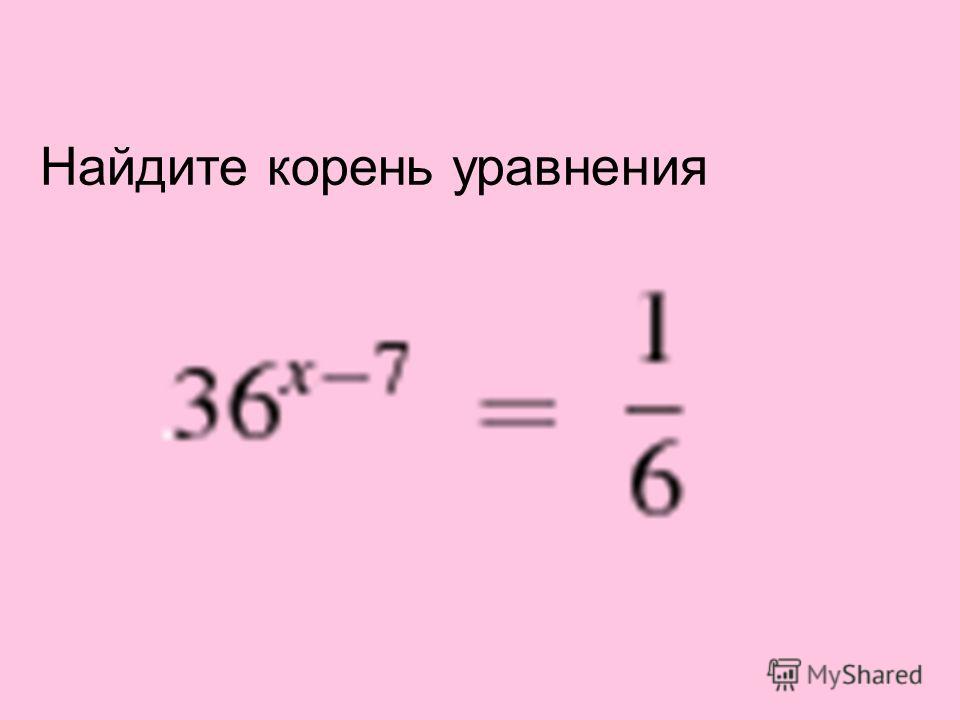
Для (А), 5x-3=x2
5-3x=x3
Таким образом, (A) не является квадратным уравнением.
Для (B) x ( x + 5) = 2
x2+5x-2=0
Таким образом, (B) является квадратным уравнением.
(C) также не является квадратным уравнением.
(D) 1x2x+2=x
x+2=x3 что также не является квадратичным.
Значит, правильный ответ — вариант (Б).
(2) (A) x 2 + 4 x = 11 + x 2
⇒ 4x=11
Таким образом, (A) не является квадратным уравнением.
(B) и (C) можно записать как x2-4x+0=0 и 5×2-90+0=0 соответственно.
Итак, B и C являются квадратными уравнениями.
(D) 2 x – x 2 = x 2 + 5 можно записать как 2×2-2x+5=0.
Таким образом, это также образует квадратное уравнение.
Следовательно, правильный ответ — вариант (А).
(3) Данное квадратное уравнение имеет вид 0⇒k2-4k=0⇒kk-4=0⇒k=0,k=4
Следовательно, правильный ответ — вариант C.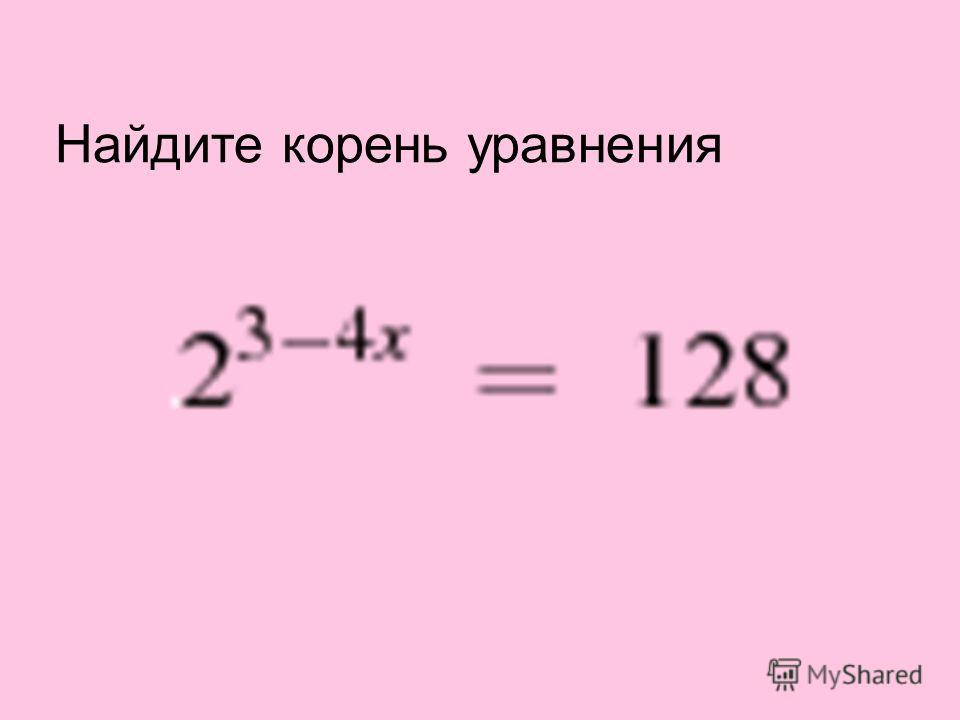
(4) 2×2-5x+2=0
a=2,b=-5,c=2D=b2-4ac=-52-4×2×2=25-8=17
Следовательно, правильный ответ вариант B.
(5) Корни квадратного уравнения 0⇒x-3x-5=0⇒x=3,5
Следовательно, правильный ответ — вариант B.
(6) Для уравнения 3 x 2 + 15 x + 3 = 0
Сумма корней=-ba=-153=-5
Следовательно, правильный ответ — вариант D.
(7) Для заданного квадратного уравнения 5m2-5m+5=0
D=b2-4ac=-52-4×5×5=5-20=-15
Так как D < 0, значит, корни недействительны .
Следовательно, правильный ответ — вариант C.
(8) Для уравнения x 2 + m x – 5 = 0
один из корней равен 2. Значит, 2 должно удовлетворять данному уравнению.
22+m×2-5=0⇒4+2m-5=0⇒2m-1=0⇒m=12
Следовательно, правильный ответ — вариант C.
Страница № 54:
Вопрос 2:
Какое из следующих уравнений является квадратным?
(1) x2+2x+11=0
(2) x2-2x+5=x2
(3) x+22=2×2
Ответ:
Общая форма квадратного уравнения:
ax2+bx+c =0
(1) x2+2x+11=0 представляет собой общее квадратное уравнение.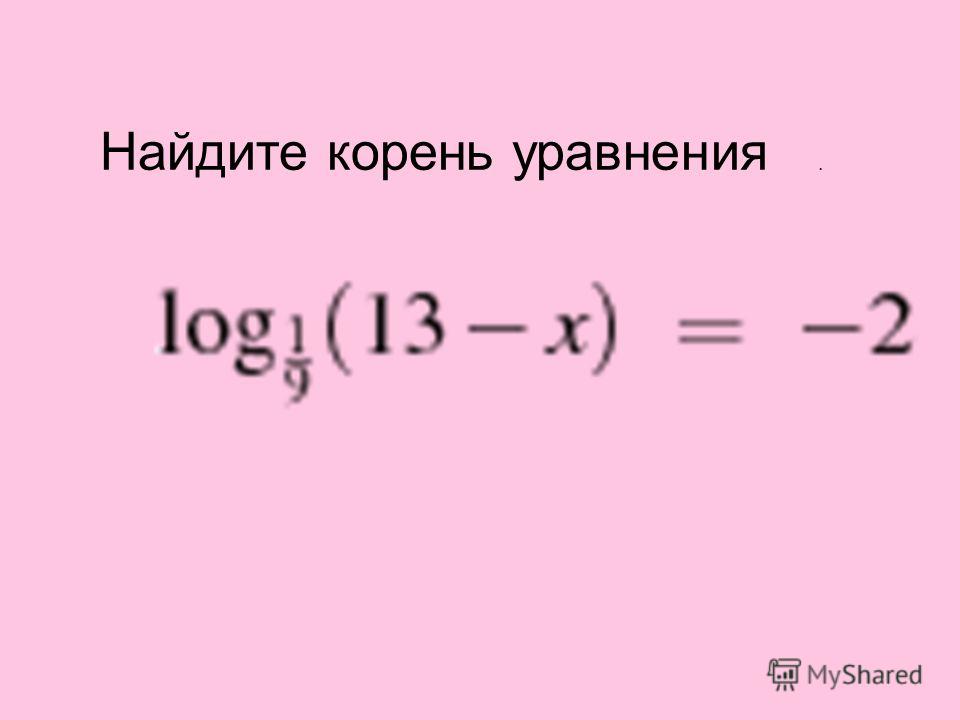
(2) x2-2x+5=x2
⇒-2x+5=0
Это не форма квадратного уравнения.
(3) x+22=2×2
⇒x2+4+4x=2×2⇒x2-4x-4=0
Оно также имеет форму квадратного уравнения.
Следовательно, (1) и (3) являются квадратными уравнениями.
Страница № 54:
Вопрос 3:
Найдите значение дискриминанта для каждого из следующих уравнений.
(1) 2y2-y+2=0
(2) 5m2-m=0
(3) 5×2-x-5=0
Ответ:
(1) 2y2-y+2=0
Для квадратное уравнение, ax2+bx+c=0
D=b2-4ac
Здесь,
a=2,b=-1,c=2D=-12-4×2×2=1-16=-15
(2) 5m2-m=0
Для квадратного уравнения ax2+bx+c=0
D=b2-4ac
Здесь
m=5,b=-1,c=0D=-12-4×5 ×0=1
(3) 5×2-x-5=0
Для квадратного уравнения: ax2+bx+c=0
D=b2-4ac
Здесь
a=5,b=-1,c=-5D=-12-4×5×-5=1+20=21
Страница № 54:
Вопрос 4:
Один из корней квадратного уравнения 2×2+kx-2=0 равен –2. найти к .
Ответ:
2×2+kx-2=0
Один из корней равен –2, поэтому он удовлетворяет данному уравнению.
2-22+k-2-2=0⇒8-2k-2=0⇒6-2k=0⇒6=2k⇒k=3
Страница № 54:
Вопрос 5:
Два корня из даны квадратные уравнения; составить уравнение.
(1) 10 и –10
(2) 1–35 и 1+35
(3) 0 и 7
Ответ:
(1) 10 и –10
Сумма корней = 10 + (–10) = 0
Произведение корней = 10 ×-10=-100
Общая форма квадратного уравнения:
x2-Сумма корнейx+произведение корней=0
Итак, квадратное уравнение будет
x2-0x-100=0⇒x2-100=0
(2) 1-35 и 1+35
Сумма корней = 1-35+1+35=2
Произведение корней = 1-351+35=1-45=-44
Общий вид квадратного уравнения равно
x2-Сумма корнейx+произведение корней=0
Таким образом, квадратное уравнение будет иметь вид
x2-2x-44=0
(3) 0 и 7
Сумма корней = 0 + 7 = 7
Произведение корней = 0×7=0
Общий вид уравнения квадратное уравнение
x2-Сумма корнейx+произведение корней=0
Итак, квадратное уравнение будет
x2-7x+0=0⇒x2-7x=0
Страница № 54:
Вопрос 6:
Определите характер корней для каждого квадратного уравнения.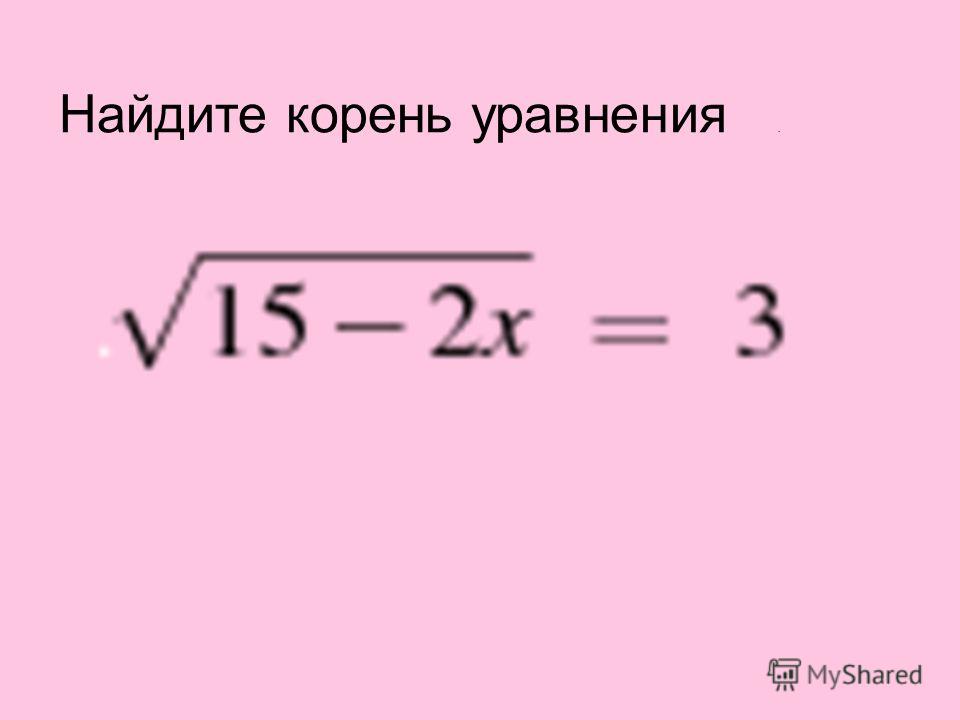
(1) 3×2-5x+7=0
(2) 3×2+2x-23=0
(3) м2-4x-3=0
Ответ:
(1) 3×2-5x+7=0
Чтобы найти природу корней, нам нужно найти дискриминант.
D=b2-4aca=3,b=-5,c=7D=-52-4×3×7=25-84=-59
Так как D < 0, то настоящего корня нет.
(2) 3×2+2x-23=0
Чтобы найти природу корней, нам нужно найти дискриминант.
D=b2-4aca=3,b=2,c=-23D=22-4×3×-23=2+24=26>0
Так как D > 0, значит, действительные и неравные корни.
(3) m2-4x-3=0
Чтобы найти природу корней, нам нужно найти дискриминант.
D=b2-4aca=1,b=-4,c=-3D=-42-4×1×-3=16+12=28
Так как D > 0, значит, действительные и неравные корни.
Страница № 54:
Вопрос 7:
Решите следующие квадратные уравнения.
(1) 1x+5=1×2
(2) x2-3×10-110=0
(3) 2x+32=25
(4) м2+5м+5=0
(5) 5м2+2м+1= 0
(6) x2-4x-3=0
Ответ:
(1) 1x+5=1×2
⇒x2=x+5⇒x2-x-5=0⇒x=—1±-12 -4×1×-52×1⇒x=1±1+202=1±212
(2) x2-3×10-110=0
⇒10×2-3x-1=0⇒x=—3±-32 -4×10×-12×10⇒x=3±9+4020=3±4920⇒x=3±720⇒x=3+720,3-720⇒x=1020,-420⇒x=12,-15
(3) 2x+32=25
⇒4×2+ 9+12x=25⇒4×2+12x-16=0⇒x2+3x-4=0⇒x2+4x-x-4=0⇒xx+4-1x+4=0⇒x-1x+4=0⇒ x=1,-4
(4) m2+5m+5=0
⇒m=-5±52-4×1×52⇒m=-5±25-202⇒m=-5±52
(5) 5m2+2m+1=0
⇒m=-2±22-4×1×52⇒m=-2±4-202⇒m=-2±-162
Итак, корни недействительны, поскольку дискриминант отрицателен.
(6) x2-4x-3=0
⇒x=—4±-42-4×1×-32×1⇒x=4±16+122⇒x=4±282⇒x=4± 272⇒x=2±7
Страница № 54:
Вопрос 8:
Найдите m, если ( m – 12) x 2 + 2( m –12) x + 2 = 0 имеет действительные и равные корни.
Ответ:
Для реальных и равных корней, дискриминант должен составлять 0.
( M — 12) x 2 + 2 ( M –12) x + 2 = 0
61616161616161616 гг. =b2-4ac=0a=m-12,b=2m-12,c=2
2m-122-4m-12×2=0⇒4m2+576-96m-8m+96=0⇒4m2-104m+672 =0⇒м2-26м+168=0⇒м2-14м-12м+168=0⇒мм-14-12м-14=0⇒м-14м-12=0м=12,14
Но если m = 12, то будет составлено квадратное уравнение, следовательно, значение m равно 14.
Страница № 54:
Вопрос 9:
Сумма двух корней квадратного уравнения равна 5 и сумма их кубов равна 35, найдите уравнение.
Ответ:
Пусть корнями будут α и β.
Сумма корней = 5
α+β=5
Кроме того,
α3+β3=35⇒α3+β3=α+β3-3αβα+β⇒35=53-3αβ5⇒15αβ=125-35⇒αβ=6
Общее квадратное уравнение:
x2-α+βx+αβ=0
Таким образом, искомое квадратное уравнение будет иметь вид
x2-5x+6=0⇒x2-5x+6=0
Страница № 54:
Вопрос 10:
Найдите квадратное уравнение, корни которого равны квадрату суммы корни и квадрат разности корней уравнения 2×2+2p+qx+p2+q2=0
Ответ:
2×2+2p+qx+p2+q2=0
Пусть корни данного квадратного уравнения равны α и β.
Сумма корней, α + β = -2p+q2=-p+q
⇒α+β2=p+q2 …..( A )
αβ=p2+q22
α-β2=α+β2-4αβ=p+q2-4p2+q22=p+q2-2p2+q2=-p-q2 p+q2-p-q2=p+q-p+qp+q+p-q ∵x2-y2=x-yx+y=4pq
AB=p+q2-p-q2=-p2+q2+2pqp2+q2 -2pq=-p22+q22-2p2q2=-p2-q22
Общая форма квадратного уравнения:
x2-A+Bx+AB=0
Подставляя значения A и B, получаем
x2-4pq-p2-q22= 0.
Страница № 54:
Вопрос 11:
У Мукунда на 50 рупий больше, чем у Сагара. Произведение суммы, которую они имеют, равно 15 000. Найдите сумму, которая есть у каждого.
Ответ:
Пусть сумма с Сагаром будет x рупий.
Сумма с Мукундом = рупий x + 50
Произведение суммы, которую они имеют, равно 15 000.
хх+50=15000⇒х2+50х=15000⇒х2+50х-15000=0⇒х2+150х-100х-15000=0⇒хх+150-100х+150=0⇒х-100х+150=0⇒х =100,-150
Но сумма не может быть отрицательной, поэтому
Сумма с Сагаром = 100 рупий, а сумма с Мукундом — 150 рупий. 120. Квадрат меньшего числа в два раза больше большего числа. Найдите числа.
120. Квадрат меньшего числа в два раза больше большего числа. Найдите числа.
Ответ:
Пусть меньшее число будет x .
Большее число должно быть и .
Квадрат меньшего числа в два раза больше большего числа.
x2=2y
Разница между квадратами двух чисел равна 120.
y2-x2=120⇒y2-2y-120=0⇒y2-12y+10y-120=0⇒yy-12+10y-12=0⇒ y+10y-12=0⇒y=12,-10
Таким образом, большее число равно 12, а меньшее число равно
x2=2×12=24⇒x=±24
Страница № 54:
Вопрос 13:
Ранджана хочет раздать ученикам 540 апельсинов. Если бы 30 учеников было больше, каждый получил бы на 3 апельсина меньше. Найдите количество учеников.
Ответ:
Всего апельсинов = 540
Пусть общее количество учеников равно x .
Апельсин, который получит каждый ученик, будет 540x
Если будет еще 30 учеников, то общее количество учеников будет x + 30
Количество апельсинов на человека будет 540x+30.
Если бы студентов было на 30 больше, каждый получил бы на 3 апельсина меньше = 540x-3
540x+30 = 540x-3
⇒3=5401x-1x+30⇒1=180x+30-xxx+30⇒1=18030×2+30x⇒ х2+30х=5400⇒х2+30х-5400=0⇒х2+90х-60х-5400=0⇒хх+90-60х+90=0⇒x-60x+90=0⇒x=60,-90
Но количество студентов не может быть отрицательным, поэтому количество студентов равно 60. Динеш владеет сельскохозяйственной фермой в деревне Талвель. Длина фермы на 10 метров больше ширины в два раза. Для сбора дождевой воды он выкопал на ферме пруд квадратной формы. Сторона пруда – 13 ширины фермы. Площадь фермы в 20 раз больше площади пруда. Найдите длину и ширину фермы и пруда.
Ответ:
Ширина фермы = x
Длина фермы = 2x+10
Площадь фермы = lb=x2x+10=2×2+10x
Сторона пруда = x3
Площадь пруда = s2=x32
Площадь фермы = 2(Площадь пруда)
⇒2×2+10x=20×x29⇒18×2+90x=20×2⇒9×2+45x=10×2⇒x2-45x=0⇒xx-45=0⇒x=0,45
Длина фермы = 2×45+10=100 единиц
Ширина фермы = 45 единиц
Сторона пруда = 453=15 единиц
Калькулятор дробей
Этот калькулятор выполняет основные и расширенные операции с дробями, выражения с дробями в сочетании с целыми числами , десятичные и смешанные числа. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т. е. 1,45 .
е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример |
|---|---|---|---|
| + | плюс знак | Дополнение | 1/2 + 1/3 |
| — | Минус. | multiplication | 2/3 * 3/4 |
| × | times sign | multiplication | 2/3 × 5/6 |
| : | division sign | division 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
|


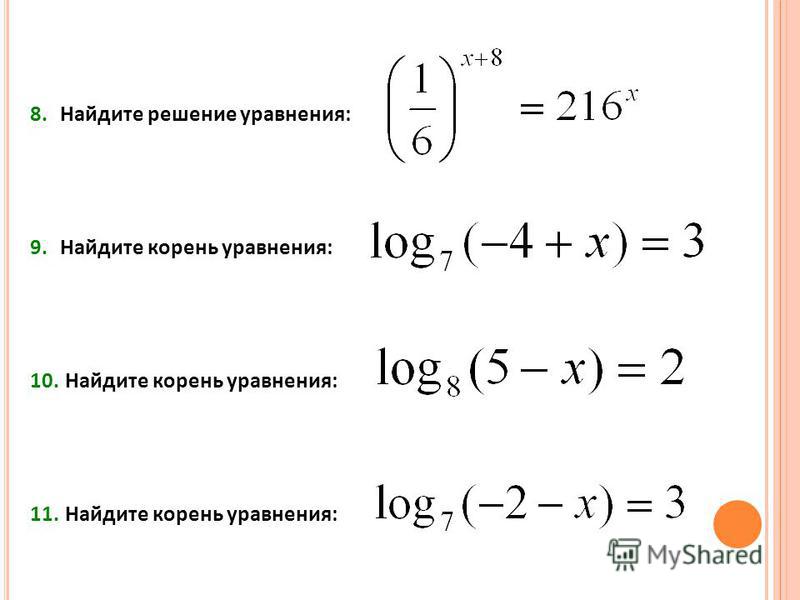




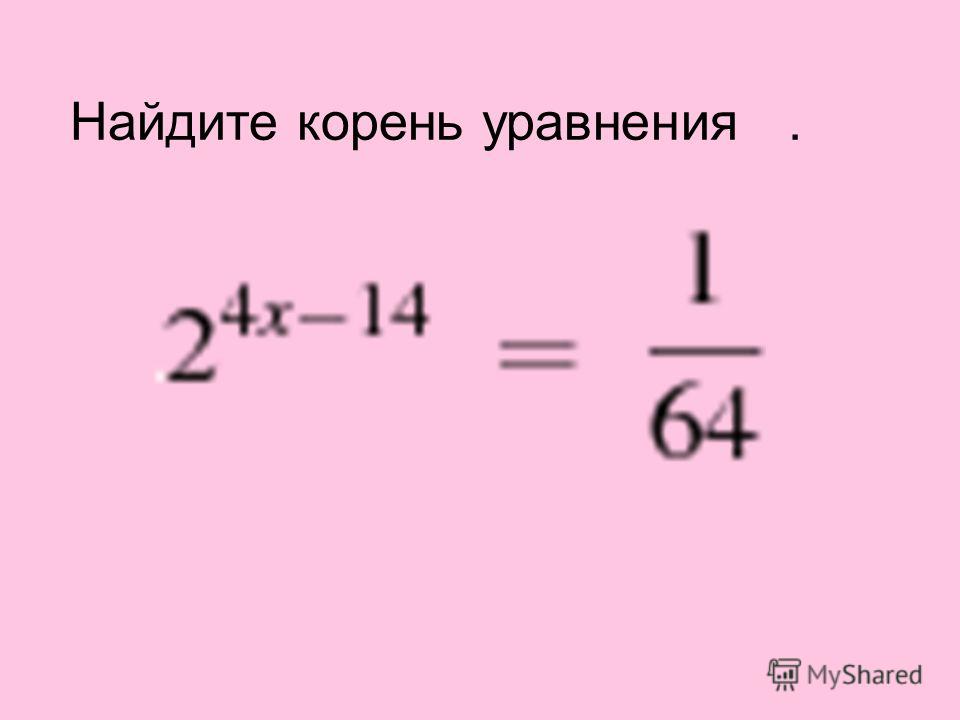
 Если уравнение
имеет более одного корня, в ответе запишите меньший из корней.
Если уравнение
имеет более одного корня, в ответе запишите меньший из корней. Если
уравнение имеет более одного корня, в ответе запишите больший из корней.
Если
уравнение имеет более одного корня, в ответе запишите больший из корней.

 Если уравнение имеет более
одного корня, в ответе укажите меньший из них.
Если уравнение имеет более
одного корня, в ответе укажите меньший из них.


 (Обратите внимание, что на практике это может быть очень сложной задачей.)
(Обратите внимание, что на практике это может быть очень сложной задачей.) Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Отсюда шесть пар синих, три пары коричневых, две черных и две белых. Какая часть носков Макса коричневого или черного цвета?
Отсюда шесть пар синих, три пары коричневых, две черных и две белых. Какая часть носков Макса коричневого или черного цвета?