Длина вектора — как найти? Формулы и примеры
Что такое векторы и какими они бывают
Как обычно, мы начнем с самого важного: с определения.
Вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.
Вектор обозначают знаком →, например . Как вы заметили, вектор можно выразить одной латинской буквой, а можно — сочетанием двух букв, которыми мы назовем точками начала и конца вектора.
Нулевой вектор — вектор, начало которого совпадает с его концом. Обозначается он так: .
Как вы уже знаете, векторы бывают коллинеарными и неколлинеарными, сонаправленными и противоположно направленными. Теперь давайте подумаем, что объединяет все виды векторов без исключения. Правильно, у всех есть длина! О том, что это такое, мы и поговорим дальше.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Запишитесь и участвуйте в розыгрыше 8 уроков
Длина вектора
Длиной или модулем вектора называется длина направленного отрезка, определяющего вектор.
Иногда в математике длину вектора называют модулем. Это легко запомнить, так как длина вектора обозначается с помощью знака | |. Например: . Альтернативное название длины вектора дает нам отличную подсказку: она не может быть отрицательной, в какую бы сторону вектор ни был направлен. А вот нулевой — пожалуйста!
Длина нулевого вектора всегда равна нулю.
Здесь вам может стать интересно, зачем нам нужно знать, как найти длину вектора, и это очень хороший вопрос. Причин может быть множество, но мы выделим несколько главных:
Чтобы определить равенство векторов, необходимо знать их длины. Векторы являются равными, если равны их длины, и сами векторы — сонаправленные.
Вычислив модуль вектора, мы можем рассчитать другие величины.
Например, в физике сила — это векторная величина, т.

В геометрии с помощью длины векторов мы можем определить угол между ними, их скалярное произведение.
Достаточно весомые аргументы для нахождения этой величины, правда? Самое время перейти от слов к делу: давайте научимся вычислять длину вектора через свои координаты!
Как можно найти длину вектора по его координатам
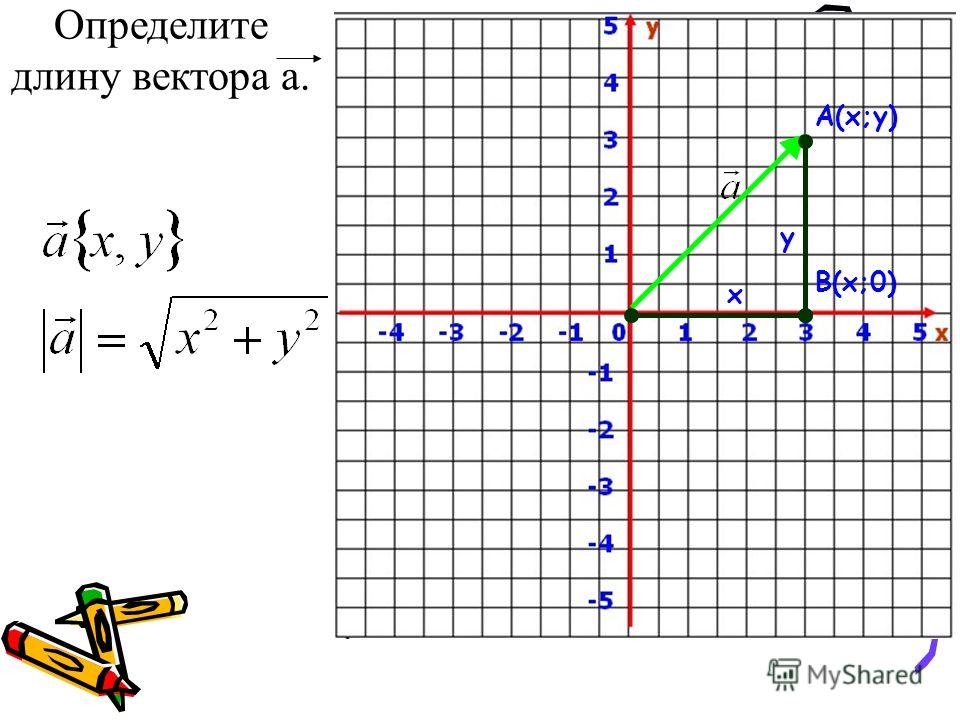
Используя прямоугольную систему координат, нарисуем вектор АВ (х, у) из точки (0; 0). Тогда его можно будет считать радиус-вектором для векторов АВ1 и АА1.
Давайте обозначим длину вектора |АВ1| = у, длину вектора |АА1| = х. Треугольники АА1В и АВ1В являются прямоугольными, где АВ — гипотенуза. Теперь вспомните, как можно найти длину гипотенузы, зная длины катетов. Верно, через теорему Пифагора! Составим выражение для АВ:
Это значит, чтобы найти длину вектора нужно взять квадратный корень из суммы квадратов его координат.
Если мы будем рассматривать векторы в трехмерном пространстве, формулу нахождения длины вектора можно рассчитать так:
Давайте разберемся, как работают эти формулы для нахождения длины вектора, на примерах. Вы можете решать задания самостоятельно, а потом свериться с нами: так будет еще эффективнее!
Пример № 1
Найдите модуль вектора .
Решение:
Ответ:
Пример № 2
Проведите вычисление длины вектора по его координатам {-2; 0; 5}.
Решение:
Ответ:
Пример № 3
Определите координату х вектора , если его координата по у равна 6, а длина вектора 10.
Решение:
,
,
,
.
,
,
,
.
Ответ: .
Уверены, что у вас все блестяще получилось!
Как найти длину вектора по двум точкам
Давайте подумаем, как решать задачи, если нам не даны координаты вектора. Для этого нужно понять, как найти длину вектора по двум точкам — координатам начала и конца. Вспомним: координаты вектора с точкой А (х_а; у_а) и В (х_в; у_в) можно рассчитать так: (х_в – х_а; у_в – у_а). А значит, длину вектора мы определим, если подставим эти выражения в формулу для ее нахождения:
Для этого нужно понять, как найти длину вектора по двум точкам — координатам начала и конца. Вспомним: координаты вектора с точкой А (х_а; у_а) и В (х_в; у_в) можно рассчитать так: (х_в – х_а; у_в – у_а). А значит, длину вектора мы определим, если подставим эти выражения в формулу для ее нахождения:
Пример № 4
Найти длину вектора , если В (4; 6), С (-2; 0).
Решение:
Ответ:
Как найти длину вектора по теореме косинусов
Пришло время разобраться, как длина вектора связана с теоремой косинусов. К сожалению, не во всех задачах дано нужное количество информации, чтобы определить длину вектора — тут-то нам и поможет теорема. Вспомним ее!
Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Итак, чтобы определить длину стороны треугольника, нужно сложить квадраты двух других сторон, вычесть удвоенное произведение длин сторон на косинус угла между ними и взять корень из полученного числа. Так мы получим формулу нахождения длины вектора через теорему косинусов.
Так мы получим формулу нахождения длины вектора через теорему косинусов.
Предположим, что нам необходимо узнать длину вектора или . Тогда, чтобы воспользоваться теоремой косинусов, нам нужно найти длину векторов и и угол между ними.
Пример № 5
Длины векторов и равны 5 и 12 соответственно, а угол между ними равен π/3. Проведите вычисление длины вектора .
Решение:
Ответ:
Сегодня мы обсудили с вами все основные моменты, которые касаются длины вектора: изучили теорию и дополнили ее базовыми задачами. Дело осталось за малым — выучить весь материал и практиковаться! В этом вам помогут курсы по профильной математике в школе Skysmart. Уникальная платформа, учителя-профессионалы, индивидуальная программа — уроки просто созданы для того, чтобы стать уверенными в математике. Ждем вас на занятиях и до новых встреч!
Нахождение длины вектора через координаты начала и. Вектор. Координаты вектора
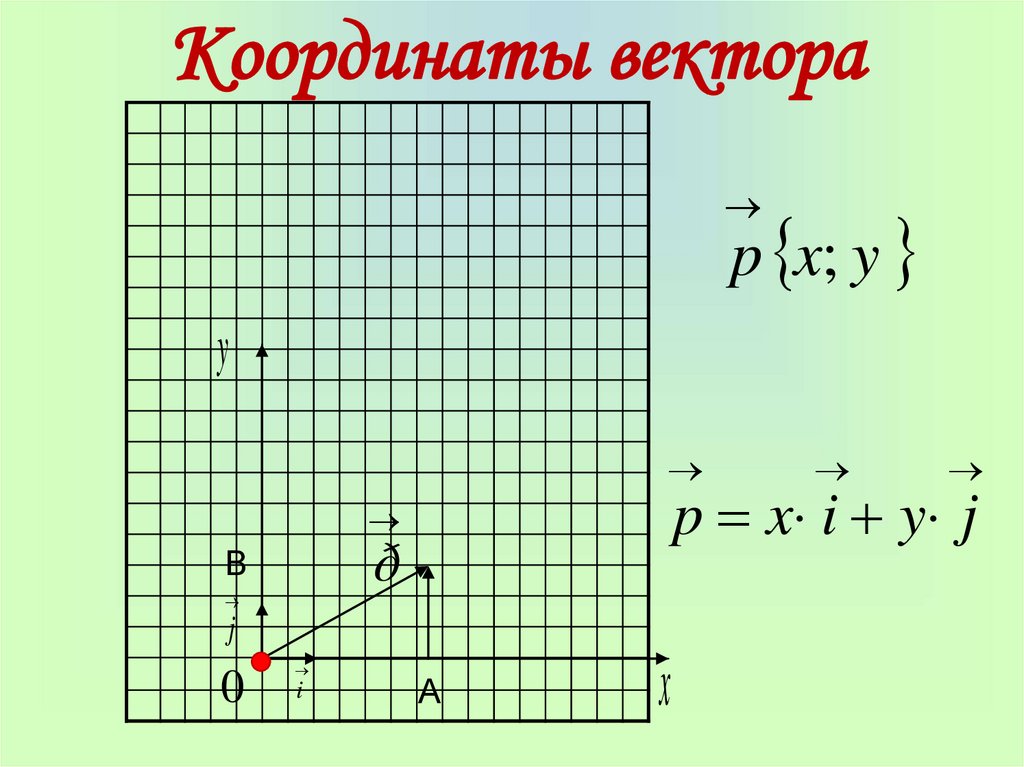
На оси абсцисс и ординат называются координатами вектора . Координаты вектора общепринято указывать в виде (х, у) , а сам вектор как: =(х, у).
Координаты вектора общепринято указывать в виде (х, у) , а сам вектор как: =(х, у).
Формула определения координат вектора для двухмерных задач.
В случае двухмерной задачи вектор с известными координатами точек A(х 1 ;у 1) и B(x 2 ; y 2 ) можно вычислить:
= (x 2 — x 1 ; y 2 — y 1).
Формула определения координат вектора для пространственных задач.
В случае пространственной задачи вектор с известными координатами точек A(х 1 ;у 1 ; z 1 ) и B(x 2 ; y 2 ; z 2 ) можно вычислить применив формулу:
= (
x 2 — x 1 ; y 2 — y 1 ; z 2 — z 1 ).Координаты дают всеобъемлющую характеристику вектора, поскольку по координатам есть возможность построить и сам вектор. Зная координаты, легко вычислить и длину вектора . (Свойство 3, приведенное ниже).
Зная координаты, легко вычислить и длину вектора . (Свойство 3, приведенное ниже).
Свойства координат вектора.
1. Любые равные векторы в единой системе координат имеют равные координаты .
2. Координаты коллинеарных векторов пропорциональны. При условии, что ни один из векторов не равен нулю.
3. Квадрат длины любого вектора равен сумме квадратов его координат .
4.При операции умножения вектора на действительное число каждая его координата умножается на это число.
5. При операции сложения векторов вычисляем сумму соответствующие координаты векторов
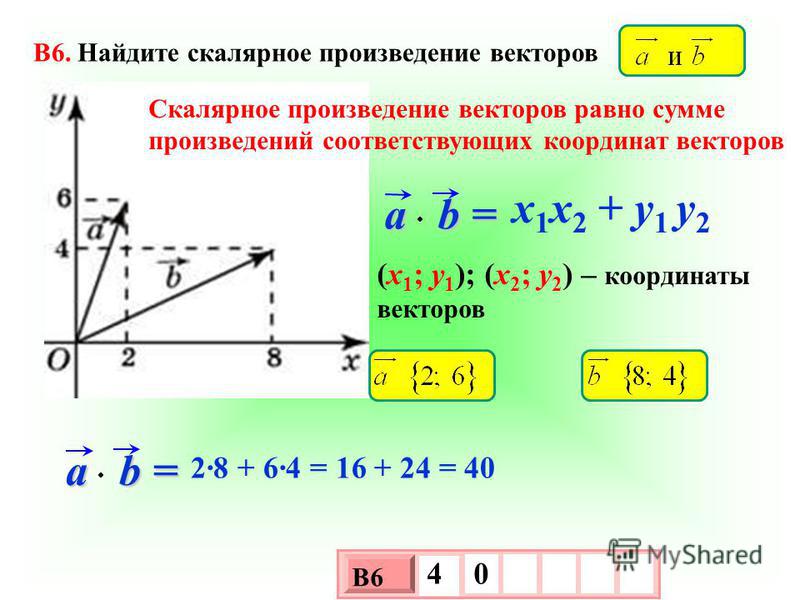
6. Скалярное произведение двух векторов равняется сумме произведений их соответствующих координат.
Векторы. Действия с векторами. В этой статье мы поговорим о том, что такое вектор, как находить его длину, и как умножать вектор на число, а также как находить сумму, разность и скалярное произведение двух векторов.
Как обычно, немного самой необходимой теории.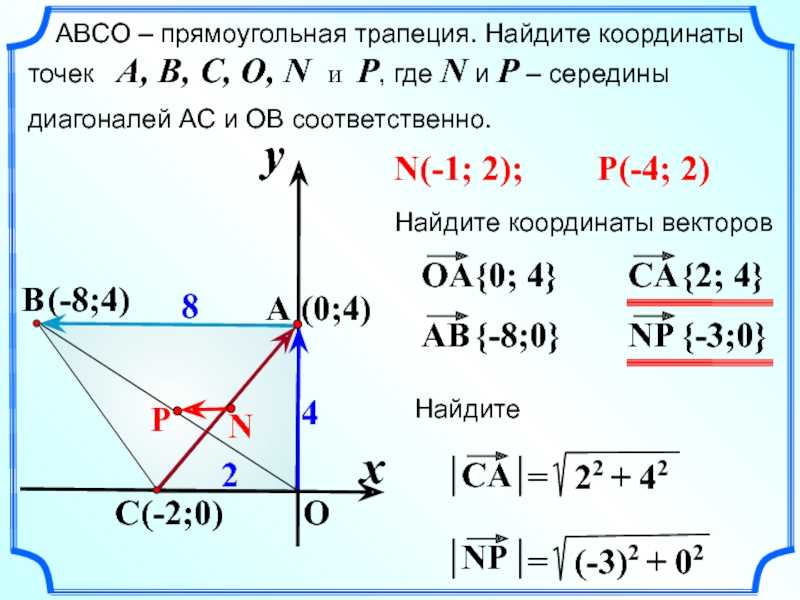
Вектор — это направленный отрезок, то есть такой отрезок, у которого есть начало и конец:
Здесь точка А — начало вектора, а точка В — его конец.
У вектора есть два параметра: его длина и направление.
Длина вектора — это длина отрезка, соединяющего начало и конец вектора. Длина вектора обозначается
Два вектора называются равными , если они имеют одинаковую длину и сонаправлены.
Два вектора называются сонаправленными , если они лежат на параллельных прямых и направлены в одну сторону: вектора и сонаправлены:
Два вектора называются противоположно направленными, если они лежат на параллельных прямых и направлены в противоположные стороны: вектора и , а также и направлены в противоположные стороны:
Вектора, лежащие на параллельных прямых называются коллинеарными : вектора , и — коллинеарны.
Произведением вектора на число называется вектор, сонаправленный вектору , если title=»k>0″>, и направленный в противоположную сторону, если , и длина которого равна длине вектора , умноженной на :
Чтобы сложить два вектора
и , нужно начало вектора соединить с концом вектора .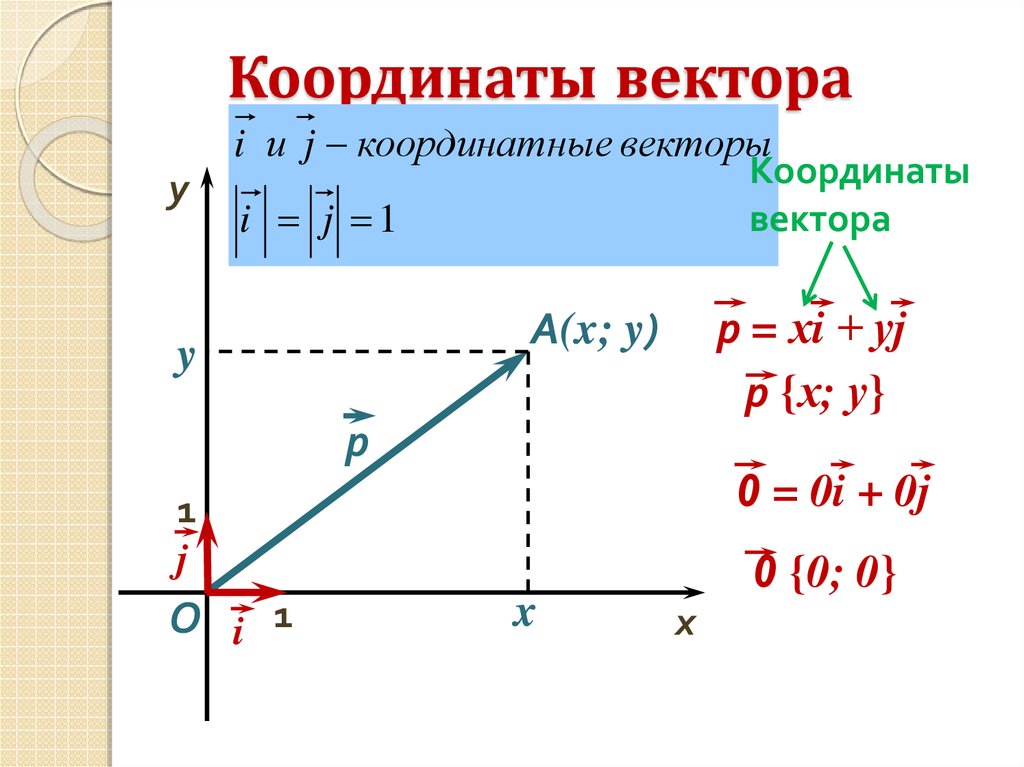 Вектор суммы соединяет начало вектора с концом вектора :
Вектор суммы соединяет начало вектора с концом вектора :
Это правило сложения векторов называется правилом треугольника .
Чтобы сложить два вектора по правилу параллелограмма , нужно отложить вектора от одной точки и достроить до параллелограмма. Вектор суммы соединяет точку начала векторов с противоположным углом параллелограмма:
Разность двух векторов определяется через сумму: разностью векторов и называется такой вектор , который в сумме с вектором даст вектор :
Отсюда вытекает правило нахождения разности двух векторов : чтобы из вектора вычесть вектор , нужно отложить эти вектора от одной точки. Вектор разности соединяет конец вектора с концом вектора (то есть конец вычитаемого с концом уменьшаемого):
Чтобы найти угол между вектором и вектором , нужно отложить эти вектора от одной точки. Угол, образованный лучами, на которых лежат вектора, называется углом между векторами:
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
Предлагаю вам решить задачи из Открытого банка заданий для , а затем сверить све решение с ВИДЕОУРОКАМИ:
1
. Задание 4 (№ 27709)
Задание 4 (№ 27709)
Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов и .
2 . Задание 4 (№ 27710)
Две стороны прямоугольника ABCD равны 6 и 8. Найдите скалярное произведение векторов и . (чертеж из предыдущей задачи).
3 . Задание 4 (№ 27711)
Две стороны прямоугольника ABCD O . Найдите длину суммы векторов и .
4 . Задание 4 (№ 27712)
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O . Найдите длину разности векторов и . (чертеж из предыдущей задачи).
5 . Задание 4 (№ 27713)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора .
6 . Задание 4 (№ 27714)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора + .
7 .Задание 4 (№ 27715)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора — .(чертеж из предыдущей задачи).
8 .Задание 4 (№ 27716)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора — .
Найдите длину вектора — .
9 . Задание 4 (№ 27717)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора + .
10 . Задание 4 (№ 27718)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора — .(чертеж из предыдущей задачи).
11 .Задание 4 (№ 27719)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите скалярное произведение векторов и .(чертеж из предыдущей задачи).
12 . Задание 4 (№ 27720)
ABC равны Найдите длину вектора +.
13 . Задание 4 (№ 27721)
Стороны правильного треугольника ABC равны 3. Найдите длину вектора -.(чертеж из предыдущей задачи).
14 . Задание 4 (№ 27722)
Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов и . (чертеж из предыдущей задачи).
Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачать
Firefox
Oxy
О А ОА .
, откуда ОА .
Таким образом, .
Рассмотрим пример.
Пример.
Решение.
:
Ответ:
Oxyz в пространстве.
А ОА будет диагональю.
В этом случае (так как ОА ОА .
Таким образом, длина вектора .
Пример.
Вычислите длину вектора
Решение.
, следовательно,
Прямая на плоскости
Общее уравнение
Ax + By + C ( > 0).
Вектор = (А; В) — нормальный вектор прямой.
В векторном виде: + С = 0 , где — радиус-вектор произвольной точки на прямой (рис. 4.11).
Частные случаи:
1) By + C = 0 — прямая параллельна оси Ox ;
2) Ax + C = 0 — прямая параллельна оси Oy ;
3) Ax + By = 0 — прямая проходит через начало координат;
4) y = 0 — ось Ox ;
5) x = 0 — ось Oy .
Уравнение прямой в отрезках
где a, b — величины отрезков, отсекаемых прямой на осях координат.
Нормальное уравнение прямой (рис. 4.11)
где — угол, образуемый нормально к прямой и осью Ox ; p — расстояние от начала координат до прямой.
Приведение общего уравнения прямой к нормальному виду:
Здесь — нормируемый множитель прямой; знак выбирается противоположным знаку C , если и произвольно, если C = 0 .
Нахождение длины вектора по координатам.
Длину вектора будем обозначать . Из-за такого обозначения длину вектора часто называют модулем вектора.
Начнем с нахождения длины вектора на плоскости по координатам.
Введем на плоскости прямоугольную декартову систему координат Oxy . Пусть в ней задан вектор и он имеет координаты . Получим формулу, позволяющую находить длину вектора через координаты и .
Отложим от начала координат (от точки О ) вектор .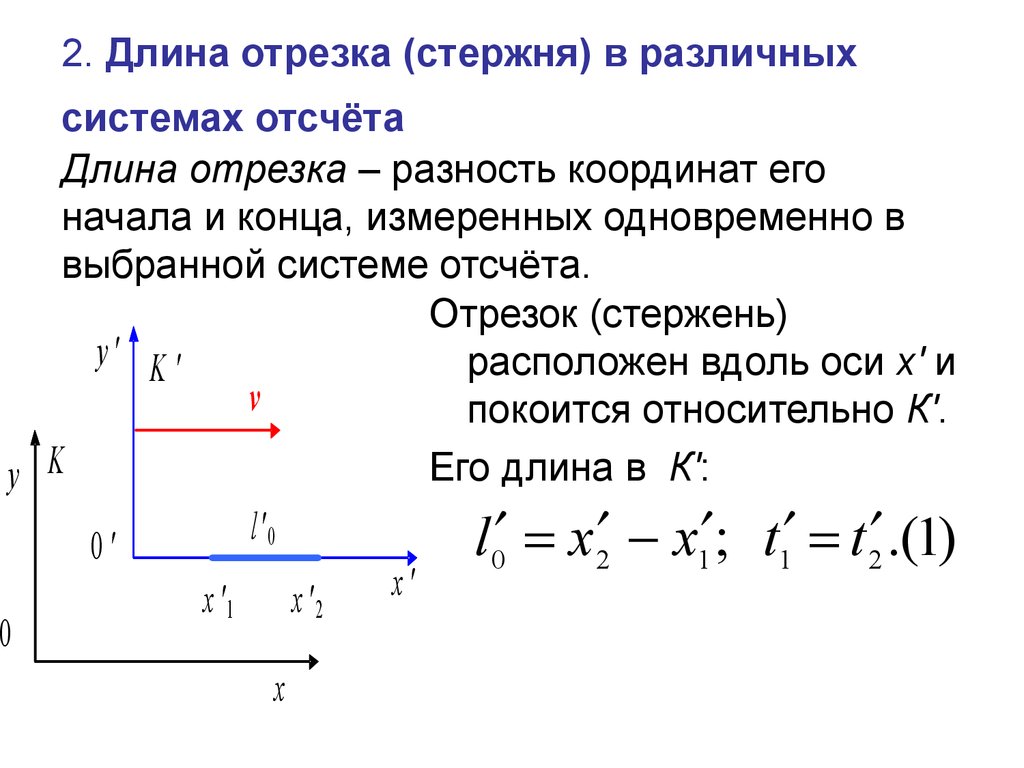 Обозначим проекции точки А на координатные оси как и соответственно и рассмотрим прямоугольник с диагональю ОА .
Обозначим проекции точки А на координатные оси как и соответственно и рассмотрим прямоугольник с диагональю ОА .
В силу теоремы Пифагора справедливо равенство , откуда . Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что и , а по построению длина ОА равна длине вектора , следовательно, .
Таким образом, формула для нахождения длины вектора по его координатам на плоскости имеет вид .
Если вектор представлен в виде разложения по координатным векторам , то его длина вычисляется по этой же формуле , так как в этом случае коэффициенты и являются координатами вектора в заданной системе координат.
Рассмотрим пример.
Пример.
Найдите длину вектора , заданного в декартовой системе координат.
Решение.
Сразу применяем формулу для нахождения длины вектора по координатам :
Ответ:
Теперь получим формулу для нахождения длины вектора по его координатам в прямоугольной системе координат Oxyz в пространстве.
Отложим от начала координат вектор и обозначим проекции точки А на координатные оси как и . Тогда мы можем построить на сторонах и прямоугольный параллелепипед, в котором ОА будет диагональю.
В этом случае (так как ОА – диагональ прямоугольного параллелепипеда), откуда . Определение координат вектора позволяет нам записать равенства , а длина ОА равна искомой длине вектора, следовательно, .
Таким образом, длина вектора в пространстве равна корню квадратному из суммы квадратов его координат , то есть, находится по формуле .
Пример.
Вычислите длину вектора , где — орты прямоугольной системы координат.
Решение.
Нам дано разложение вектора по координатным векторам вида , следовательно, . Тогда по формуле нахождения длины вектора по координатам имеем .
Прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем теперь, непосредственно, понятие длин вектора.
Определение 3
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.
Определение 4
Два вектора будем называть равными, если они удовлетворяют двух условиям:
1.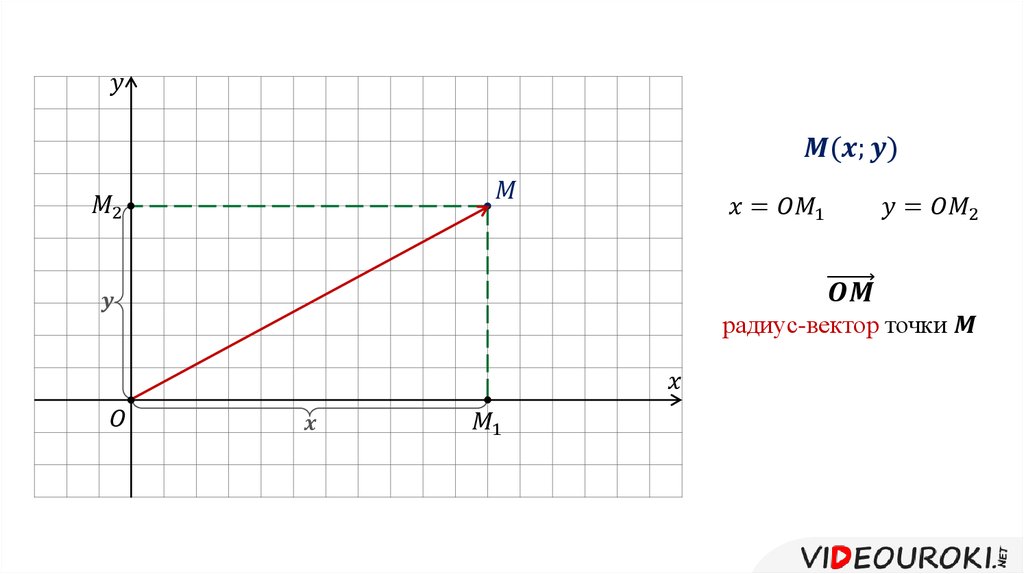 Они сонаправлены;
1. Их длины равны (рис. 2).
Они сонаправлены;
1. Их длины равны (рис. 2).
Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.
Определение 5
Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:
$\overline{c}={m,n}$
Как найти длину вектора?
Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:
Пример 1
Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.
Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $\overline{OA}=\overline{a}$. 2}$.
2}$.
Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.
Пример задач
Пример 2
Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.
Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что
Сумма векторов. Длина вектора. Дорогие друзья, в составе типов задний экзамена присутствует группа задач с векторами. Задания довольно широкого спектра (важно знать теоретические основы). Большинство решается устно. Вопросы связаны с нахождением длины вектора, суммы (разности) векторов, скалярного произведения. Так же много заданий, при решении которых необходимо осуществить действия с координатами векторов.
Теория касающаяся темы векторов несложная, и её необходимо хорошо усвоить. В этой статье разберём задачи связанные с нахождением длины вектора, также суммы (разности) векторов. Некоторые теоретические моменты:
В этой статье разберём задачи связанные с нахождением длины вектора, также суммы (разности) векторов. Некоторые теоретические моменты:
Понятие вектора
Вектор — это направленный отрезок.
Все векторы, имеющие одинаковое направление и равные по длине являются равными.
*Все представленные выше четыре вектора равны!
То есть, если мы будем при помощи параллельного переноса перемещать данный нам вектор, то всегда получим вектор равный исходному. Таким образом, равных векторов может быть бесчисленное множество.
Обозначение векторов
Вектор может быть обозначен латинскими заглавными буквами, например:
При данной форме записи сначала записывается буква обозначающая начало вектора, затем буква обозначающая конец вектора.
Ещё вектор обозначается одной буквой латинского алфавита (прописной):
Возможно также обозначение без стрелок:
Суммой двух векторов АВ и ВС будет являться вектор АС .
Записывается как АВ +ВС =АС .
Это правило называется – правилом треугольника .
То есть, если мы имеем два вектора – назовём их условно (1) и (2), и конец вектора (1) совпадает с началом вектора (2), то суммой этих векторов будет вектор, начало которого совпадает с началом вектора (1), а конец совпадает с концом вектора (2).
Вывод: если мы имеем на плоскости два вектора, то всегда сможем найти их сумму. При помощи параллельного переноса можно переместить любой из данных векторов и соединить его начало с концом другого. Например:
Перенесём вектор b , или по-другому – построим равный ему:
Как находится сумма нескольких векторов? По тому же принципу:
* * *
Правило параллелограмма
Это правило является следствием изложенного выше.
Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.
Построим вектор равный вектору b так, чтобы его начало совпадало с концом вектора a , и мы можем построить вектор, который будет являться их суммой:
Ещё немного важной информации, необходимой для решения задач.
Вектор, равный по длине исходному, но противоположно направленный, обозначается также но имеет противоположный знак:
Эта информация крайне полезна для решения задач, в которых стоит вопрос о нахождении разности векторов. Как видите, разность векторов это та же сумма в изменнёном виде.
Пусть даны два вектора, найдём их разность:
Мы построили вектор противоположный вектору b, и нашли разность.
Координаты вектора
Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала:
То есть, координаты вектора представляют собой пару чисел.
Если
И координаты векторов имеют вид:
То c 1 = a 1 + b 1 c 2 = a 2 + b 2
Если
То c 1 = a 1 – b 1 c 2 = a 2 – b 2
Модуль вектора
Модулем вектора называется его длина, определяется по формуле:
Формула для определения длины вектора, если известны координаты его начала и конца:
Рассмотрим задачи:
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке О. Найдите длину разности векторов АО
и ВО
.
Диагонали пересекаются в точке О. Найдите длину разности векторов АО
и ВО
.
Найдём вектор, который будет являться результатом АО –ВО:
АО –ВО =АО +(–ВО )=АВ
То есть разность векторов АО и ВО будет являться вектор АВ. А его длина равна восьми.
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ +AD .
Найдём вектор, который будет являться суммой векторов AD и AB BC равен вектору AD . Значит AB +AD =AB +BC =AC
AC это длина диагонали ромба АС , она равна 16.
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО +ВО .
Найдём вектор, который будет являться суммой векторов АО и ВО ВО равен вектору OD, з начит
AD это длина стороны ромба. Задача сводится к нахождению гипотенузы в прямоугольном треугольнике AOD. Вычислим катеты:
По теореме Пифагора:
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16.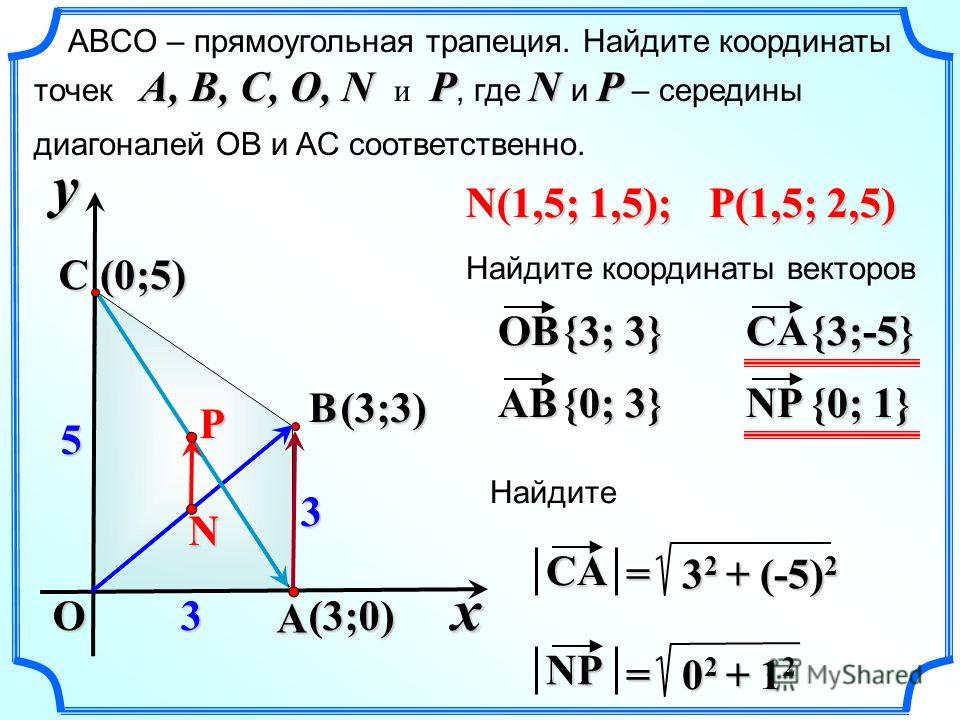 Найдите длину вектора АО
–ВО
.
Найдите длину вектора АО
–ВО
.
Найдём вектор, который будет являться результатом АО –ВО :
АВ это длина стороны ромба. Задача сводится к нахождению гипотенузы АВ в прямоугольном треугольнике AOB. вычислим катеты:
По теореме Пифагора:
Стороны правильного треугольника ABC равны 3.
Найдите длину вектора АВ –АС .
Найдём результат разности векторов:
СВ равна трём, так как в условии сказано, что треугольник равносторонний и его стороны равны 3.
27663. Найдите длину вектора а (6;8).
27664. Найдите квадрат длины вектора АВ .
Формула вычисления длины вектора по его координатам. Как найти координаты вектора. Вычисление углов между двумя плоскостями
Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).
Вектор – это направленный отрезок прямой. Длина этого отрезка определяет числовое значение вектора и называется
длиной вектора или модулем вектора.
Длина этого отрезка определяет числовое значение вектора и называется
длиной вектора или модулем вектора.
1. Вычисление длины вектора по его координатам
Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a x и a y , то длину вектора можно найти по формуле
В случае вектора в пространстве добавляется третья координата
В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9)) позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9 , см. файл примера ).
Функция СУММКВ() возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле =B8*B8+B9*B9 .
В файле примера также вычислена длина вектора в пространстве.
Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)) .
2. Нахождение длины вектора через координаты точек
Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))
В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно.
Функция СУММКВРАЗН() в озвращает сумму квадратов разностей соответствующих значений в двух массивах.
По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.
3. Нахождение длины вектора по теореме косинусов
Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).
Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))
В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 — угол между ними в радианах (в долях числа ПИ() ).
Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))
Примечание : для наглядности в ячейке со значением угла в градусах можно применить , см. например, статью
На оси абсцисс и ординат называются координатами вектора . Координаты вектора общепринято указывать в виде (х, у) , а сам вектор как: =(х, у).
Координаты вектора общепринято указывать в виде (х, у) , а сам вектор как: =(х, у).
Формула определения координат вектора для двухмерных задач.
В случае двухмерной задачи вектор с известными координатами точек A(х 1 ;у 1) и B(x 2 ; y 2 ) можно вычислить:
= (x 2 — x 1 ; y 2 — y 1).
Формула определения координат вектора для пространственных задач.
В случае пространственной задачи вектор с известными координатами точек A(х 1 ;у 1 ; z 1 ) и B(x 2 ; y 2 ; z 2 ) можно вычислить применив формулу:
= (x 2 — x 1 ; y 2 — y 1 ; z 2 — z 1 ).
Координаты дают всеобъемлющую характеристику вектора, поскольку по координатам есть возможность построить и сам вектор.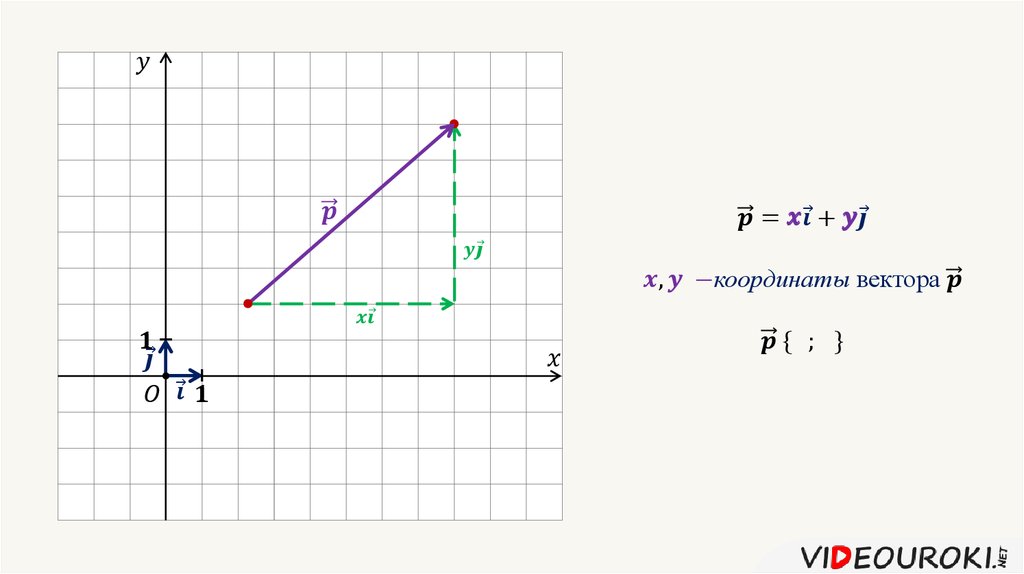 Зная координаты, легко вычислить и длину вектора . (Свойство 3, приведенное ниже).
Зная координаты, легко вычислить и длину вектора . (Свойство 3, приведенное ниже).
Свойства координат вектора.
1. Любые равные векторы в единой системе координат имеют равные координаты .
2. Координаты коллинеарных векторов пропорциональны. При условии, что ни один из векторов не равен нулю.
3. Квадрат длины любого вектора равен сумме квадратов его координат .
4.При операции умножения вектора на действительное число каждая его координата умножается на это число.
5. При операции сложения векторов вычисляем сумму соответствующие координаты векторов .
6. Скалярное произведение двух векторов равняется сумме произведений их соответствующих координат.
Прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.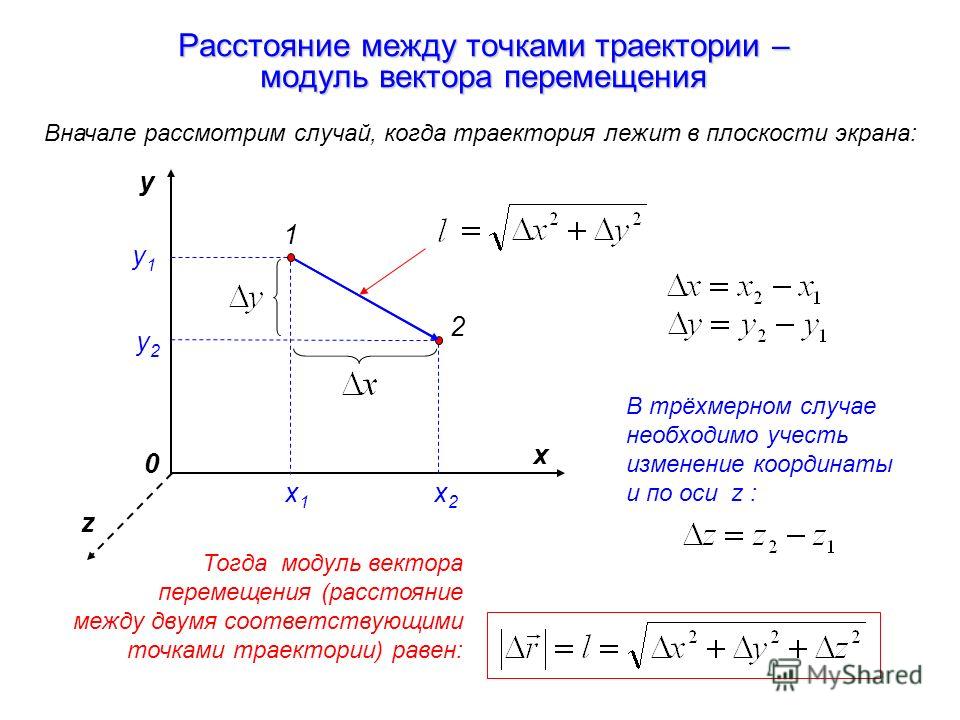
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем теперь, непосредственно, понятие длин вектора.
Определение 3
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.
Определение 4
Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).
Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.
Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.
Определение 5
Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:
$\overline{c}={m,n}$
Как найти длину вектора?
Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:
Пример 1
Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.
Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $\overline{OA}=\overline{a}$. Построим проекции $OA_1$ и $OA_2$ построенного вектора на оси $Ox$ и $Oy$, соответственно (рис. 3).
Построенный нами вектор $\overline{OA}$ будет радиус вектором для точки $A$, следовательно, она будет иметь координаты ${x,y}$, значит
$=x$, $[ OA_2]=y$
Теперь мы легко можем найти искомую длину с помощью теоремы Пифагора, получим
$|\overline{α}|^2=^2+^2$
$|\overline{α}|^2=x^2+y^2$
$|\overline{α}|=\sqrt{x^2+y^2}$
Ответ: $\sqrt{x^2+y^2}$.
Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.
Пример задач
Пример 2
Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.
Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что
Прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем теперь, непосредственно, понятие длин вектора.
Определение 3
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.
Определение 4
Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).
Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.
Определение 5
Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:
$\overline{c}={m,n}$
Как найти длину вектора?
Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:
Пример 1
Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.
Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $\overline{OA}=\overline{a}$. Построим проекции $OA_1$ и $OA_2$ построенного вектора на оси $Ox$ и $Oy$, соответственно (рис. 3).
Построенный нами вектор $\overline{OA}$ будет радиус вектором для точки $A$, следовательно, она будет иметь координаты ${x,y}$, значит
$=x$, $[ OA_2]=y$
Теперь мы легко можем найти искомую длину с помощью теоремы Пифагора, получим
$|\overline{α}|^2=^2+^2$
$|\overline{α}|^2=x^2+y^2$
$|\overline{α}|=\sqrt{x^2+y^2}$
Ответ: $\sqrt{x^2+y^2}$.
Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.
Пример задач
Пример 2
Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.
Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что
вектор длина
Вы искали вектор длина? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление длины вектора, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.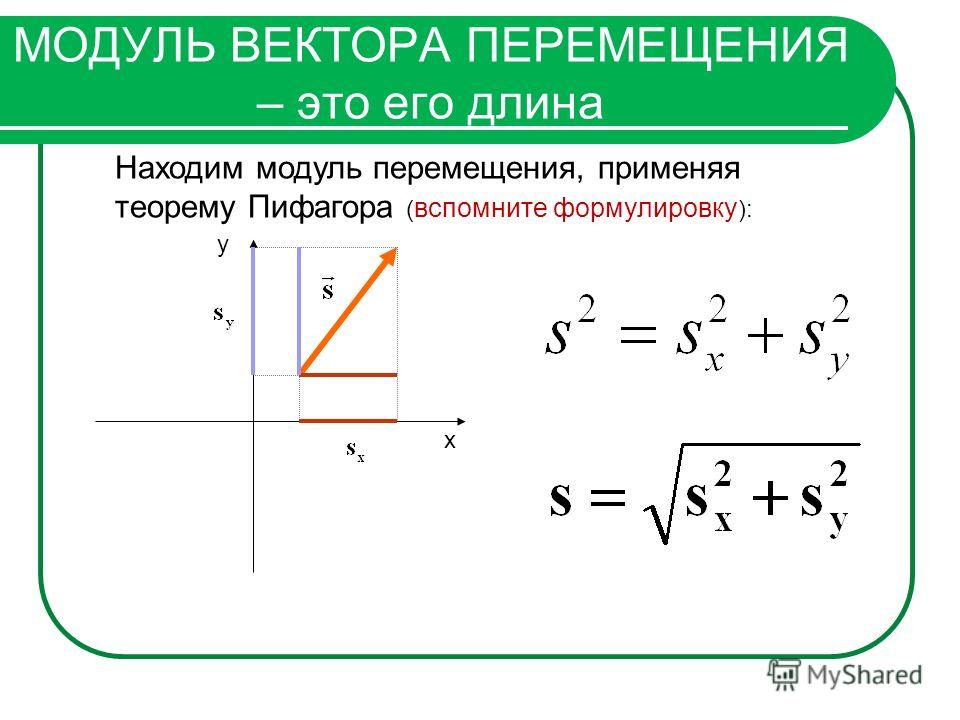 Например, «вектор длина».
Например, «вектор длина».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вектор длина,вычисление длины вектора,вычисление длины вектора по его координатам,вычисление длины вектора по его координатам доказательство,вычислить длину вектора,длина вектор,длина вектора,длина вектора c,длина вектора в пространстве,длина вектора как найти,длина вектора как обозначается,длина вектора модуль вектора,длина вектора определение,длина вектора по двум точкам,длина вектора по его координатам,длина вектора по координатам,длина вектора по координатам начала и конца,длина вектора по координатам точек,длина вектора по координатам формула,длина вектора равна,длина вектора равна квадратному корню из суммы его координат,длина вектора формула,длина вектора формула по координатам,длина вектора через координаты,длина вектора это,длина векторов,длина векторов по координатам,длина через координаты вектора,длину вектора,длины векторов,длины векторов как найти,как в прямоугольнике найти длины векторов,как вычислить длину вектора,как вычислить длину вектора по координатам,как зная координаты вектора найти его длину,как зная координаты найти длину вектора,как найти длина вектора,как найти длину вектора,как найти длину вектора ав,как найти длину вектора если известны его координаты,как найти длину вектора если известны координаты вектора,как найти длину вектора зная его координаты,как найти длину вектора зная его координаты начала и конца,как найти длину вектора зная координаты,как найти длину вектора зная координаты его начала и конца,как найти длину вектора и координаты,как найти длину вектора по двум точкам,как найти длину вектора по его координатам,как найти длину вектора по координатам,как найти длину вектора по координатам двух точек,как найти длину вектора по координатам начала и конца,как найти длину вектора формула,как найти длину вектора через координаты,как найти длину векторов,как найти длину и координаты вектора,как найти длины векторов,как найти длины векторов по координатам,как найти квадрат длины вектора,как найти координаты вектора если известна длина вектора,как найти координаты вектора зная длину,как найти координаты вектора зная его длину,как найти координаты вектора зная его длину и координаты начала,как найти координаты вектора и длину,как найти координаты вектора через длину,как найти координаты и длину вектора,как находить длину вектора,как обозначается длина вектора,как определить длину вектора,как определить длину вектора по координатам,как узнать длину вектора,как узнать длину вектора по координатам,квадрат длины вектора формула,координаты вектора длина вектора,модуль вектора длина вектора,модуль вектора определение,найдите длину и координаты вектора,найдите длины векторов,найти длину вектора,найти длину вектора по координатам,найти длину вектора по координатам точек,найти длину и координаты вектора,найти длину по координатам точек вектора,найти длины векторов,найти координаты вектора и длину,найти координаты и длину вектора,нахождение длины вектора,нахождение длины вектора по его координатам,определение вектора длина вектора,определение вектора длины,определение вектора длины вектора,определение длина вектора,определение длины вектора,определение модуль вектора,по координатам точек найти длину вектора,формула вычисления длины вектора,формула вычисления длины вектора по его координатам,формула длина вектора,формула длины вектора,формула длины вектора по его координатам,формула для вычисления длины вектора по его координатам,формула для нахождения длины вектора,формула как найти длину вектора,формула квадрат длины вектора,формула модуля вектора,формула нахождения длины,формула нахождения длины вектора,формула нахождения длины вектора по его координатам,чему равна длина вектора,что такое длина вектора. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вектор длина. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычисление длины вектора по его координатам).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вектор длина. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычисление длины вектора по его координатам).
Решить задачу вектор длина вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Что значит найти вектор — dj-sensor.ru
Содержание
- Длина вектора — основные формулы
- Длина вектора через координаты точек его начала и конца
- Нахождение длины вектора по теореме косинусов
Если вектор (x,y,z) перпендикулярен вектору (u,v,w), то их скалярное произведение, т. е. произведение длины первого на длину второго на косинус угла между ними, равно 0 (нулю), поскольку косинус 90 градусов равен 0. Скалярное произведение двух векторов по определению = x*u + y*v + z*w. Соответственно у вас система уравнений для искомого (x,y,z):
е. произведение длины первого на длину второго на косинус угла между ними, равно 0 (нулю), поскольку косинус 90 градусов равен 0. Скалярное произведение двух векторов по определению = x*u + y*v + z*w. Соответственно у вас система уравнений для искомого (x,y,z):
-6*x + 4*y + 2*z = 0 (1ое уравнение, перпендикулярность A)
3*x + 1*y + 5*z = 0 (2ое уравнение, перпендикулярность B)
Умножаем второе уравнение с двух сторон на 2 и прибавляем к первому. Получаем:
-6x + 6x +4y + 2y +2z+10z = 0, т.е.
z = -1/2 *y = — 0.5 * y
Подставляем этот z в первое уравнение, получаем:
Соответственно z= -0.5y = -0.5*(2x) = -x.
Отсюда ответ: вектор (x, 2x, -x), где x любое число, будет перпендикулярен и А, и В.
(Можно подставить в уравнения 1 и 2 и проверить)
Длина вектора — основные формулы
Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .
Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .
От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .
Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .
Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .
Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.
Читайте также: Школьница наносит ответный удар фильм
Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.
Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2 : a → = 7 2 + e 2 = 49 + e
Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)
В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .
Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .
Вычислить длину вектора a → = 4 · i → — 3 · j → + 5 · k → , где i → , j → , k → — орты прямоугольной системы координат.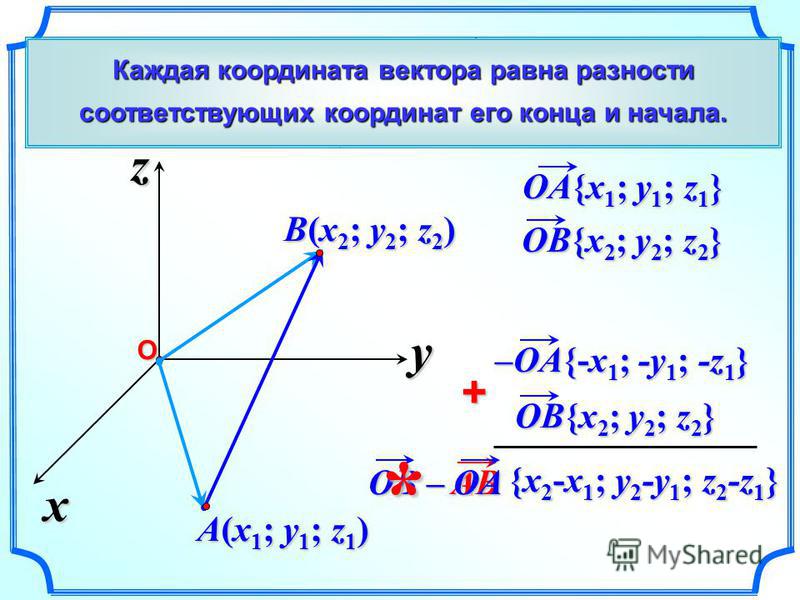
Дано разложение вектора a → = 4 · i → — 3 · j → + 5 · k → , его координаты равны a → = 4 , — 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + ( — 3 ) 2 + 5 2 = 5 2 .
Длина вектора через координаты точек его начала и конца
Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.
Итак, даны точки с заданными координатами A ( a x ; a y ) и B ( b x ; b y ) , отсюда вектор A B → имеет координаты ( b x — a x ; b y — a y ) значит, его длина может быть определена по формуле: A B → = ( b x — a x ) 2 + ( b y — a y ) 2
А если даны точки с заданными координатами A ( a x ; a y ; a z ) и B ( b x ; b y ; b z ) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле
A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2
Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B — 3 , 1 .
Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = ( b x — a x ) 2 + ( b y — a y ) 2 : A B → = ( — 3 — 1 ) 2 + ( 1 — 3 ) 2 = 20 — 2 3 .
Читайте также: Что лучше 360 total security или касперский
Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = ( — 3 — 1 ; 1 — 3 ) = ( — 4 ; 1 — 3 ) ; A B → = ( — 4 ) 2 + ( 1 — 3 ) 2 = 20 — 2 3 . —
Ответ: A B → = 20 — 2 3 .
Определить, при каких значениях длина вектора A B → равна 30 , если A ( 0 , 1 , 2 ) ; B ( 5 , 2 , λ 2 ) .
Для начала распишем длину вектора A B → по формуле: A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2 = ( 5 — 0 ) 2 + ( 2 — 1 ) 2 + ( λ 2 — 2 ) 2 = 26 + ( λ 2 — 2 ) 2
Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ :
26 + ( λ 2 — 2 ) 2 = 30 26 + ( λ 2 — 2 ) 2 = 30 ( λ 2 — 2 ) 2 = 4 λ 2 — 2 = 2 и л и λ 2 — 2 = — 2 λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .
Ответ: λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .
Нахождение длины вектора по теореме косинусов
Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.
Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.
Рассмотрим такой случай на следующем примере.
Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .
Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 — 2 · A B · A C · cos ∠ ( A B , → A C → ) = 3 2 + 7 2 — 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .
Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = ( b x — a x ) 2 + ( b y — a y ) 2 или A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2 , в некоторых случаях следует использовать теорему косинусов.
Читайте также: Чем отличается код бодо от азбуки морзе
Здравствуйте!
Помогите решить два задания:
«В прямоугольной ДСК на плоскости Oxy заданы две точки M(11; –17) и F(–23; –37). Найдем координаты векторов ОМ и МF в данной системе координат».
«В трехмерном пространстве в прямоугольной системе координат Oxyz заданы координаты точки С(11; 13; 17) и координаты вектора СК = (–8; 18; –23). Найдем координаты конца вектора СК».
Спасибочки за помощь!
Пример 1.
В прямоугольной ДСК на плоскости Oxy заданы две точки M(11; –17) и F(–23; –37). Найдем координаты векторов ОМ и МF в данной системе координат.
Решение.
Вектор ОМ является радиус-вектором точки М, а значит, его координаты совпадут с координатами точки М, таким образом, ОМ = (11; –17).
Координаты вектора MF найдем как разность соответствующих координат заданных точек F и M:
MF = (–23–11; –37–(–17)) = (–34; –20).
Ответ. ОМ = (11; –17), MF = (–34; –20).
Пример 2.
В трехмерном пространстве в прямоугольной системе координат Oxyz заданы координаты точки С(11; 13; 17) и координаты вектора СК = (–8; 18; –23). Найдем координаты конца вектора СК.
Решение.
Известно, что координаты вектора СК равняются разности координат точек конца и начала вектора соответственно, то координаты вектора . Подставим известные координаты точки С:
.
Из условия задачи известно, что СК = (–8; 18; –23).
В прямоугольной системе координат равность векторов подтверждается равностью их соответствующих координат.
Поэтому приравняем соответствующие координаты вектора и получим следующую систему уравнений:
Из данной системы уравнений найдем неизвестные координаты точки К:
- Автор: Мария Сухоруких
- Распечатать
Оцените статью:
(0 голосов, среднее: 0 из 5)
Поделитесь с друзьями!
Модуль вектора примеры.
 Вычисление длины (модуля) вектора в MS EXCEL. Понятие вектора. Свободный вектор
Вычисление длины (модуля) вектора в MS EXCEL. Понятие вектора. Свободный вектормодуль вектора — величина вектора — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы величина вектора EN absolute value of a vector …
модуль вектора — vektoriaus modulis statusas T sritis fizika atitikmenys: angl. absolute value of vector vok. Vektorbetrag, m rus. длина вектора, f; модуль вектора, m pranc. module d’un vecteur, m … Fizikos terminų žodynas
— (от лат. modulus «маленькая мера»): В Викисловаре есть статья «модуль» Мо … Википедия
Модуль (от лат. modulus «маленькая мера») составная часть, отделимая или хотя бы мысленно выделяемая из общего. Модульной обычно называют вещь, состоящую из чётко выраженных частей, которые нередко можно убирать или добавлять, не разрушая вещь… … Википедия
Абсолютная величина или модуль вещественного или комплексного числа x есть расстояние от x до начала координат. Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… … Википедия
Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… … Википедия
модуль волнового вектора — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN magnitude of propagation vector … Справочник технического переводчика
модуль конвольвера кодового вектора огибающей — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN shape codevector convolution module … Справочник технического переводчика
Модулем комплексного числа называется длина вектора, соответствующего этому числу: . Модуль комплексного числа z обычно обозначается | z | или r. Пусть и вещественные числа такие, что комплексное число (обычные обозначения). Тогда Числа … Википедия
Модуль в математике, 1) М. (или абсолютная величина) комплексного числа z = х + iy есть число ═(корень берётся со знаком плюс). При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… … Большая советская энциклопедия
При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… … Большая советская энциклопедия
Абелева группа с кольцом операторов. М. является обобщением (линейного) векторного пространства над полем Кдля случая, когда Кзаменяется нек рым кольцом. Пусть задано кольцо А. Аддитивная абелева группа Мназ. левым А модулем, если определено… … Математическая энциклопедия
Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).
Вектор – это направленный отрезок прямой. Длина этого отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.
1. Вычисление длины вектора по его координатам
Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a x и a y , то длину вектора можно найти по формуле
В случае вектора в пространстве добавляется третья координата
В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9))
позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9 , см. файл примера
).
файл примера
).
Функция СУММКВ() возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле =B8*B8+B9*B9 .
В файле примера также вычислена длина вектора в пространстве.
Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)) .
2. Нахождение длины вектора через координаты точек
Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))
В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно.
Функция СУММКВРАЗН() в озвращает сумму квадратов разностей соответствующих значений в двух массивах.
По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.
3. Нахождение длины вектора по теореме косинусов
Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).
Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))
В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 — угол между ними в радианах (в долях числа ПИ() ).
Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))
Примечание : для наглядности в ячейке со значением угла в градусах можно применить , см. например, статью
Характеризующийся величиной и направлением. Например, в геометрии и в естественных науках вектор есть направленный отрезок прямой в евклидовом пространстве (или на плоскости) .
Является одним из основополагающих понятий линейной алгебры . При использовании наиболее общего определения векторами оказываются практически все изучаемые в линейной алгебре объекты, в том числе матрицы , тензоры , однако, при наличии в окружающем контексте этих объектов, под вектором понимаются соответственно вектор-строка или вектор-столбец , тензор первого ранга. Свойства операций над векторами изучаются в векторном исчислении .
Свойства операций над векторами изучаются в векторном исчислении .
Обозначения [ | ]
Вектор, представленный набором n {\displaystyle n} элементов (компонент) a 1 , a 2 , … , a n {\displaystyle a_{1},a_{2},\ldots ,a_{n}} обозначают следующими способами:
⟨ a 1 , a 2 , … , a n ⟩ , (a 1 , a 2 , … , a n) , { a 1 , a 2 , … , a n } {\displaystyle \langle a_{1},a_{2},\ldots ,a_{n}\,\rangle ,\ \left(a_{1},a_{2},\ldots ,a_{n}\,\right),\{a_{1},a_{2},\ldots ,a_{n}\,\}} .
Для того, чтобы подчеркнуть, что это вектор (а не скаляр), используют черту сверху, стрелочку сверху, жирный или готический шрифт:
a ¯ , a → , a , A , a . {\displaystyle {\bar {a}},\ {\vec {a}},\mathbf {a} ,{\mathfrak {A}},\ {\mathfrak {a}}.}
Сложение векторов почти всегда обозначается знаком плюс:
a
→
+
b
→
{\displaystyle {\vec {a}}+{\vec {b}}}
.
Умножение на число — просто написанием рядом, без специального знака, например:
k b → {\displaystyle k{\vec {b}}} ,
причём число при этом обычно пишут слева.
Общепринятых обозначений вектора не существует, используются жирный шрифт, черта или стрелка над буквой, готический алфавит и др.
В геометрии [ | ]
В геометрии под векторами понимают направленные отрезки. Эту интерпретацию часто используют в компьютерной графике , строя карты освещения , с помощью нормалей к поверхностям. Так же с помощью векторов можно находить площади различных фигур, например треугольников и параллелограммов , а также объёмы тел: тетраэдра и параллелепипеда .
Иногда с вектором отождествляют направление.
Вектор в геометрии естественно сопоставляется переносу (параллельному переносу), что, очевидно, проясняет происхождение его названия (лат. vector
, несущий ). Действительно, любой направленный отрезок однозначно определяет собой какой-то параллельный перенос плоскости или пространства, и обратно, параллельный перенос однозначно определяет собой единственный направленный отрезок (однозначно — если считать равными все направленные отрезки одинакового направления и длины — то есть рассматривать их как свободные векторы).
Интерпретация вектора как переноса позволяет естественным и интуитивно очевидным способом ввести операцию сложения векторов — как композиции (последовательного применения) двух (или нескольких) переносов; то же касается и операции умножения вектора на число.
В линейной алгебре [ | ]
Общее определение [ | ]
Наиболее общее определение вектора даётся средствами общей алгебры :
- Обозначим F {\displaystyle {\mathfrak {F}}} (готическая F) некоторое поле с множеством элементов F {\displaystyle F} , аддитивной операцией + {\displaystyle +} , мультипликативной операцией ∗ {\displaystyle *} , и соответствующими нейтральными элементами : аддитивной единицей и мультипликативной единицей 1 {\displaystyle 1} .
- Обозначим
V
{\displaystyle {\mathfrak {V}}}
(готическая V) некоторую абелеву группу с множеством элементов
V
{\displaystyle V}
, аддитивной операцией
+
{\displaystyle +}
и, соответственно, с аддитивной единицей
0
{\displaystyle \mathbf {0} }
.

Иначе говоря, пусть F = ⟨ F ; + , ∗ ⟩ {\displaystyle {\mathfrak {F}}=\langle F;+,*\rangle } и V = ⟨ V ; + ⟩ {\displaystyle {\mathfrak {V}}=\langle V;+\rangle } .
Если существует операция F × V → V {\displaystyle F\times V\to V} , такая что для любых a , b ∈ F {\displaystyle a,b\in F} и для любых x , y ∈ V {\displaystyle \mathbf {x} ,\mathbf {y} \in V} выполняются соотношения:
Вектор как последовательность [ | ]
Вектор — (последовательность , кортеж) однородных элементов. Это наиболее общее определение в том смысле, что может быть не задано обычных векторных операций вообще, их может быть меньше, или они могут не удовлетворять обычным аксиомам линейного пространства . Именно в таком виде вектор понимается в программировании , где, как правило, обозначается именем-идентификатором с квадратными скобками (например, object ). Перечень свойств моделирует принятое в
Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .
От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .
Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .
Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .
Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.
Пример 1
Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.
Решение
Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2: a → = 7 2 + e 2 = 49 + e
Ответ: a → = 49 + e .
Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)
В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .
Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .
Пример 2
Вычислить длину вектора a → = 4 · i → — 3 · j → + 5 · k → , где i → , j → , k → — орты прямоугольной системы координат.
Решение
Дано разложение вектора a → = 4 · i → — 3 · j → + 5 · k → , его координаты равны a → = 4 , — 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + (- 3) 2 + 5 2 = 5 2 .
Ответ: a → = 5 2 .
Длина вектора через координаты точек его начала и конца
Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.
Итак, даны точки с заданными координатами A (a x ; a y) и B (b x ; b y) , отсюда вектор A B → имеет координаты (b x — a x ; b y — a y) значит, его длина может быть определена по формуле: A B → = (b x — a x) 2 + (b y — a y) 2
А если даны точки с заданными координатами A (a x ; a y ; a z) и B (b x ; b y ; b z) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле
A B → = (b x — a x) 2 + (b y — a y) 2 + (b z — a z) 2
Пример 3
Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B — 3 , 1 .
Решение
Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = (b x — a x) 2 + (b y — a y) 2: A B → = (- 3 — 1) 2 + (1 — 3) 2 = 20 — 2 3 .
Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = (- 3 — 1 ; 1 — 3) = (- 4 ; 1 — 3) ; A B → = (- 4) 2 + (1 — 3) 2 = 20 — 2 3 . —
Ответ: A B → = 20 — 2 3 .
Пример 4
Определить, при каких значениях длина вектора A B → равна 30 , если A (0 , 1 , 2) ; B (5 , 2 , λ 2) .
Решение
Для начала распишем длину вектора A B → по формуле: A B → = (b x — a x) 2 + (b y — a y) 2 + (b z — a z) 2 = (5 — 0) 2 + (2 — 1) 2 + (λ 2 — 2) 2 = 26 + (λ 2 — 2) 2
Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ:
26 + (λ 2 — 2) 2 = 30 26 + (λ 2 — 2) 2 = 30 (λ 2 — 2) 2 = 4 λ 2 — 2 = 2 и л и λ 2 — 2 = — 2 λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .
Ответ: λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .
Нахождение длины вектора по теореме косинусов
Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.
Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.
Рассмотрим такой случай на следующем примере.
Пример 5
Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .
Решение
Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 — 2 · A B · A C · cos ∠ (A B , → A C →) = 3 2 + 7 2 — 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .
Ответ: B C → = 37 .
Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = (b x — a x) 2 + (b y — a y) 2 или A B → = (b x — a x) 2 + (b y — a y) 2 + (b z — a z) 2 , в некоторых случаях следует использовать теорему косинусов.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
\circ)$ как представляющий «5 км к северо-востоку», т. е. этот вектор может быть смещением вектор , указывая, скажем, на то, что ваша бабушка прошла 5 километров в сторону северо-восток в школу в снегу. С другой стороны, тот же вектор может обозначать скорость, указывая на то, что ваша бабушка шла со 5 км/ч на северо-восток. То, что вектор не указывает, где произошло это блуждание: вектор представляет величину, а направление, но не место. Наглядно полезно изобразить вектор в виде стрелки; направление вектора, естественно, направление, в котором указывает стрелка; величина вектора отражается на длине стрелы.
Оказывается, многие величины ведут себя как векторы, например,
перемещение, скорость, ускорение, сила. Мы уже можем получить некоторые
представление об их полезности с использованием векторов смещения. Предположим, что ваш
бабушка прошла 5 км на СВ и 2 км на ЮЮВ; если позволяет местность,
и, возможно, вооружившись компасом, как могла ваша бабушка
шел прямо к месту назначения? Мы можем использовать векторы (и немного
геометрия), чтобы ответить на этот вопрос. Начнем с того, что отметим, что поскольку
векторы не включают спецификацию положения, мы можем «поместить»
их в любом удобном месте. Таким образом, мы можем представить вашу бабушку
путешествие в виде двух векторов смещения, проведенных лоб в лоб:
9\circ$
к северу от востока (примерно на восток-восток) доставит вашу бабушку
школа. Этот вид расчетов настолько распространен, что мы удостоим его
имя: мы говорим, что третий вектор является суммой двух других векторов. Есть
еще один распространенный способ изобразить сумму двух векторов. \circ)$. Давайте
нарисуйте его снова, но наложите систему координат. Если мы положим хвост
стрелка в начале координат, конец стрелки заканчивается в
точка $\ds (5/\sqrt2,5/\sqrt2)\приблизительно(3.54, 3.54)$.
\circ)$. Давайте
нарисуйте его снова, но наложите систему координат. Если мы положим хвост
стрелка в начале координат, конец стрелки заканчивается в
точка $\ds (5/\sqrt2,5/\sqrt2)\приблизительно(3.54, 3.54)$.
стрелка, при условии, что мы знаем, что конец стрелки был помещен в $(0,0)$. Тогда на самом деле вектор всегда можно определить как $(3.54,3.54)$, где бы он ни находился; мы просто должны помнить что цифры 3.54 должны интерпретироваться как изменение от положение хвоста, а не фактические координаты наконечника стрелки; чтобы подчеркнуть это, мы будем писать $\langle 3.54,3.54\rangle$, чтобы обозначить вектор и $(3.54,3.54)$ для обозначения точки. Тогда, если вектор $\langle 3.54,3.54\rangle$ нарисован хвостом в $(1,2)$, это выглядит как это:
вектор, представляющий первую часть пути, равен $\ds \langle 5/\sqrt2,5/\sqrt2\rangle$, а вторая часть пути представлен $\langle 2\cos(-3\pi/8),2\sin(-3\pi/8)\rangle \приблизительно\угол 0,77,-1,85 \угл$. Мы можем представить сумму этих с обычной картинкой головы до хвоста:
точки $\ds (5/\sqrt2+2\cos(-3\pi/8),5/\sqrt2+2\sin(-3\pi/8))$ или
приблизительно $(4.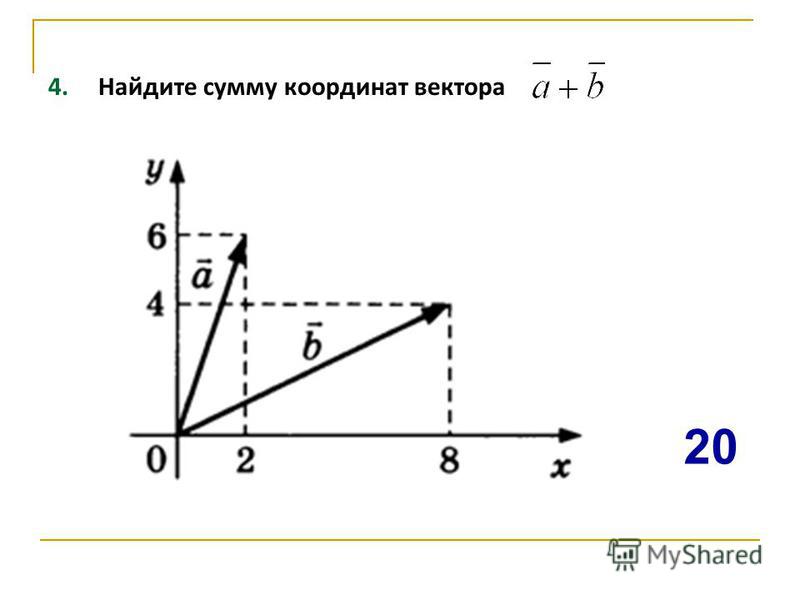 2}$.
2}$.
В трех измерениях векторы по-прежнему являются величинами, состоящими из
величина и направление, но, конечно, возможно гораздо больше
направления. Неясно, как мы могли бы представить направление
явно, но координатная версия векторов делает столько же
смысл в трех измерениях, как в двух. Под $\langle 1,2,3\rangle$ мы подразумеваем
вектор, голова которого находится в $(1,2,3)$, если его хвост находится в начале координат. В качестве
раньше мы могли разместить вектор где угодно; если у него есть хвост
в $(4,5,6)$, то его голова находится в $(5,7,9))$. Остается верным, что
арифметика легко выполняется с векторами в такой форме:
$$\выравнивание{
&a\langle v_1,v_2,v_3\rangle=\langle av_1,av_2,av_3\rangle\cr
&\langle v_1,v_2,v_3\rangle + \langle w_1,w_2,w_3\rangle
=\langle v_1+w_1,v_2+w_2,v_3+w_3\rangle\cr
&\langle v_1,v_2,v_3\rangle — \langle w_1,w_2,w_3\rangle
=\лангле v_1-w_1,v_2-w_2,v_3-w_3\рангл\кр}
$$
Величина вектора снова равна расстоянию от начала координат до
наконечник стрелы или
$\ds |\langle v_1,v_2,v_3\rangle|=\sqrt{v_1^2+v_2^2+v_3^2}$.
Рисунок 12.2.1. Вектор $\langle 2,4,5\rangle$ с хвостом в начале координат.
Три особенно простых вектора оказываются весьма полезными: ${\bf i}=\langle1,0,0\rangle$, ${\bf j}=\langle0,1,0\rangle$ и ${\bf k}=\langle0,0,1\rangle$. Они играют почти ту же роль для векторы, которые оси играют за точки. В частности, обратите внимание, что $$\выравнивание{ \langle v_1,v_2,v_3\rangle &= \langle v_1,0,0\rangle + \langle 0,v_2,0\rangle + \langle 0,0,v_3\rangle\cr &=v_1\langle1,0,0\rangle + v_2\langle0,1,0\rangle + v_3\langle0,0,1\rangle\cr &= v_1{\bf i} + v_2{\bf j} + v_3{\bf k}\cr }$$
Мы часто хотим создать вектор, который указывает из одной точки другому. То есть, если $P$ и $Q$ — точки, мы ищем вектор $\bf x$ такой, что когда хвост $\bf x$ помещается в $P$, его голова находится в $Q$; мы называем этот вектор как $\ds \overrightarrow{\strut PQ}$. Если мы знаем координаты $P$ и $Q$, координаты вектора легко найти.
Пример 12.2.1
Предположим, что $P=(1,-2,4)$ и $Q=(-2,1,3)$. Вектор
$ \ ds \ overrightarrow {\ распорка PQ} $
является
$\langle -2-1,1- -2,3-4\rangle=\langle -3,3,-1\rangle$ и
$\ds \overrightarrow{\strut QP}=\langle 3,-3,1\rangle$.
Обратите внимание, что это то же самое, что вычитание векторов с хвостами в точках.
начало координат и головы в $P$ и $Q$:
$\langle -2,1,3\rangle-\langle 1,-2,4\rangle=\langle -3,3,-1\rangle$.
$\квадрат$
Вектор
$ \ ds \ overrightarrow {\ распорка PQ} $
является
$\langle -2-1,1- -2,3-4\rangle=\langle -3,3,-1\rangle$ и
$\ds \overrightarrow{\strut QP}=\langle 3,-3,1\rangle$.
Обратите внимание, что это то же самое, что вычитание векторов с хвостами в точках.
начало координат и головы в $P$ и $Q$:
$\langle -2,1,3\rangle-\langle 1,-2,4\rangle=\langle -3,3,-1\rangle$.
$\квадрат$
Арифметика с векторами обладает некоторыми знакомыми свойствами, перечисленными в следующая теорема. Все это довольно легко доказать, просто представление векторов в стандартной форме.
Теорема 12.2.2. Если ${\bf u}$, ${\bf v}$ и ${\bf w}$ — векторы, а $a$ и $b$ — вещественные числа, затем
1. $\ds {\bf u}+{\bf v}={\bf v}+{\bf u}$
2. $a{\bf u}={\bf u}a$
3. $a({\bf u}+{\bf v})=a{\bf u}+a{\bf v}$
4. $(a+b){\bf u}= a{\bf u} + b{\bf u}$
5. $({\bf u}+{\bf v})+{\bf w}={\bf u}+({\bf v}+{\bf w})$
6. $|a{\bf u}|=|a||{\bf u}|$
Доказательство. Мы делаем один из них в качестве примера, часть 3. Пишем
${\bf u}=\langle x_1, y_1, z_1\rangle$,
${\bf v}=\langle x_2, y_2, z_2\rangle$. затем
$$\выравнивание{
a ({\ bf u} + {\ bf v}) & = a (\ langle x_1, y_1, z_1 \ rangle + \ langle x_2, y_2, z_2 \ rangle) \ cr
&=a\langle x_1+x_2,y_1+y_2,z_1+z_2\rangle\cr
&=\langle a(x_1+x_2),a(y_1+y_2),a(z_1+z_2)\rangle\cr
&=\langle ax_1+ax_2,ay_1+ay_2,az_1+az_2\rangle\cr
&=\langle ax_1,ay_1,az_1\rangle+\langle ax_2,ay_2,az_2\rangle\cr
&=a\langle x_1,y_1,z_1\rangle+a\langle x_2,y_2,z_2\rangle\cr
& = а {\ bf и} + а {\ bf v} \ cr
}$$
$\qed$
Мы делаем один из них в качестве примера, часть 3. Пишем
${\bf u}=\langle x_1, y_1, z_1\rangle$,
${\bf v}=\langle x_2, y_2, z_2\rangle$. затем
$$\выравнивание{
a ({\ bf u} + {\ bf v}) & = a (\ langle x_1, y_1, z_1 \ rangle + \ langle x_2, y_2, z_2 \ rangle) \ cr
&=a\langle x_1+x_2,y_1+y_2,z_1+z_2\rangle\cr
&=\langle a(x_1+x_2),a(y_1+y_2),a(z_1+z_2)\rangle\cr
&=\langle ax_1+ax_2,ay_1+ay_2,az_1+az_2\rangle\cr
&=\langle ax_1,ay_1,az_1\rangle+\langle ax_2,ay_2,az_2\rangle\cr
&=a\langle x_1,y_1,z_1\rangle+a\langle x_2,y_2,z_2\rangle\cr
& = а {\ bf и} + а {\ bf v} \ cr
}$$
$\qed$
Вы можете использовать Sage для выполнения векторной арифметики.
Пример 12.2.1 Нарисуйте вектор $\langle 3,-1\rangle$ хвостом в источник.
Пример 12.2.2 Нарисуйте вектор $\langle 3,-1,2\rangle$ хвостом в источник.
Пример 12.2.3 Пусть ${\bf A}$ — вектор с хвостом в начале координат и головой
в $(1,2)$; пусть ${\bf B}$ — вектор с хвостом в начале координат и головой
в $(3,1)$. Нарисуйте ${\bf A}$ и ${\bf B}$, а также вектор ${\bf C}$ с
хвост в $(1,2)$ и голова в $(3,1)$. Нарисуйте $\bf C$ хвостом в начале координат.
Нарисуйте ${\bf A}$ и ${\bf B}$, а также вектор ${\bf C}$ с
хвост в $(1,2)$ и голова в $(3,1)$. Нарисуйте $\bf C$ хвостом в начале координат.
Пример 12.2.4 Пусть ${\bf A}$ — вектор с хвостом в начале координат и головой в $(-1,2)$; пусть ${\bf B}$ — вектор с хвостом в начале координат и головой в $(3,3)$. Нарисуйте ${\bf A}$ и ${\bf B}$, а также вектор ${\bf C}$ с хвост в $(-1,2)$ и голова в $(3,3)$. Нарисуйте $\bf C$ хвостом в начале координат.
Пример 12.2.5 Пусть ${\bf A}$ — вектор с хвостом в начале координат и головой в $(5,2)$; пусть ${\bf B}$ — вектор с хвостом в начале координат и головой в $(1,5)$. Нарисуйте ${\bf A}$ и ${\bf B}$, а также вектор ${\bf C}$ с хвост в $(5,2)$ и голова в $(1,5)$. Нарисуйте $\bf C$ хвостом в начале координат.
Пример 12.2.6 Найти $|{\bf v}|$, ${\bf v}+{\bf w}$, ${\bf v}-{\bf w}$,
$|{\bf v}+{\bf w}|$, $|{\bf v}-{\bf w}|$ и $-2{\bf v}$ для
${\bf v} = \langle 1,3\rangle$ и ${\bf w} = \langle -1,-5\rangle$. (отвечать)
(отвечать)
Пример 12.2.7 Найти $|{\bf v}|$, ${\bf v}+{\bf w}$, ${\bf v}-{\bf w}$, $|{\bf v}+{\bf w}|$, $|{\bf v}-{\bf w}|$ и $-2{\bf v}$ для ${\bf v} = \langle 1,2,3\rangle$ и ${\bf w} = \langle -1,2,-3\rangle$. (отвечать)
Пример 12.2.8 Найти $|{\bf v}|$, ${\bf v}+{\bf w}$, ${\bf v}-{\bf w}$, $|{\bf v}+{\bf w}|$, $|{\bf v}-{\bf w}|$ и $-2{\bf v}$ для ${\bf v} = \langle 1,0,1\rangle$ и ${\bf w} = \langle -1,-2,2 \rangle$. (отвечать)
Пример 12.2.9 Найти $|{\bf v}|$, ${\bf v}+{\bf w}$, ${\bf v}-{\bf w}$, $|{\bf v}+{\bf w}|$, $|{\bf v}-{\bf w}|$ и $-2{\bf v}$ для ${\bf v} = \langle 1,-1,1\rangle$ и ${\bf w} = \langle 0,0,3\rangle$. (отвечать)
Пример 12.2.10 Найти $|{\bf v}|$, ${\bf v}+{\bf w}$, ${\bf v}-{\bf w}$, $|{\bf v}+{\bf w}|$, $|{\bf v}-{\bf w}|$ и $-2{\bf v}$ для ${\bf v} = \langle 3,2,1\rangle$ и ${\bf w} = \langle -1,-1,-1\rangle$. (отвечать)
Пример 12.2.11 Пусть $P=(4,5,6)$, $Q=(1,2,-5)$.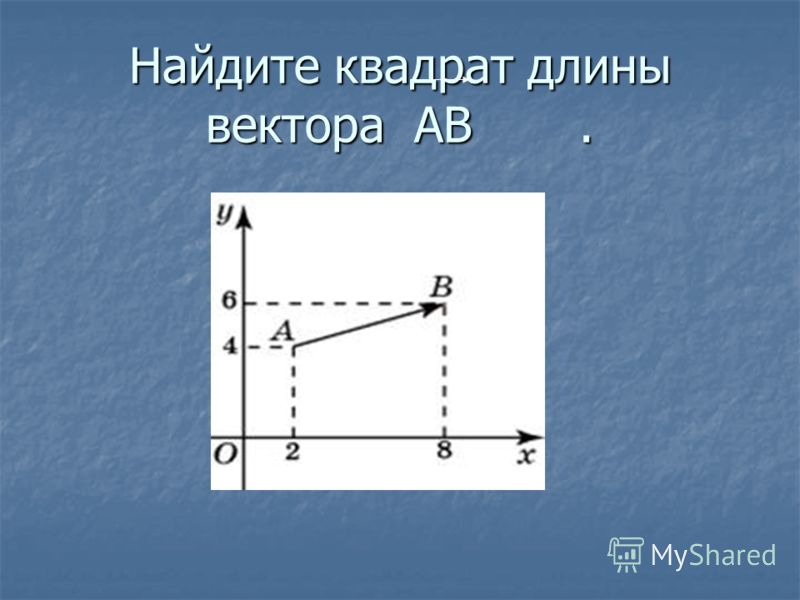 Находить
$\ds \overrightarrow{\strut PQ}$. Найдите вектор с
в том же направлении, что и $\ds \overrightarrow{\strut PQ}$
но с длиной 1. Найдите вектор с
в том же направлении, что и $\ds \overrightarrow{\strut PQ}$
но с длиной 4.
(отвечать)
Находить
$\ds \overrightarrow{\strut PQ}$. Найдите вектор с
в том же направлении, что и $\ds \overrightarrow{\strut PQ}$
но с длиной 1. Найдите вектор с
в том же направлении, что и $\ds \overrightarrow{\strut PQ}$
но с длиной 4.
(отвечать)
Пример 12.2.12 Если $A, B$ и $C$ — три точки, найдите $ \ ds \ overrightarrow {\ распорка AB} + \overrightarrow{\распорка до н.э.}+ \overrightarrow{\распорка CA}$. (отвечать)
Пример 12.2.13 Рассмотрим 12 векторов, хвосты которых находятся в центре часы и их соответствующие головки на каждой из 12 цифр. Что такое сумма этих векторов? Что, если мы удалим вектор, соответствующий до 4 часов? Что, если вместо этого все векторы имеют свои решки на 12 часов, а головы на остальные цифры? (отвечать)
Пример 12.2.14 Пусть $\bf a$ и $\bf b$ — ненулевые векторы в двух измерениях.
которые не параллельны и не антипараллельны. Покажите алгебраически, что если
$\bf c$ — любой двумерный вектор, существуют скаляры $s$ и $t$
такое, что ${\bf c}=s{\bf a}+t{\bf b}$.
Пример 12.2.15 Верно ли утверждение из предыдущего упражнения, если векторы $\bf a$, $\bf b$ и $\bf c$ — трехмерные векторы? Объяснять.
Пример 12.2.16 Докажите остальные части Теорема 12.2.2.
Положение и смещение
Положение и смещениеМногие предметы, с которыми мы сталкиваемся в повседневной жизни, находятся в движении или состоят из частей. которые находятся в движении. Движение – это правило, а не исключение. Физические законы, управляющие движением этих объектов универсальны, т.е. все объекты движутся по одним и тем же правилам, и одна из целей этого класса состоит в том, чтобы понять эти правила.
Когда объект движется, его положение изменяется как функция времени.
Положение объекта
дано относительно некоторой согласованной точки отсчета. Недостаточно просто
укажите расстояние от
ориентир. Мы также должны указать направление . Расстояние скаляр количество, это число, выраженное в некоторых единицах . Позиция — это вектор количество. Он также имеет величину
как направление. Величина векторной величины представляет собой число (с единицами)
сообщая вам, сколько есть количества, и направление говорит вам, какое
как он указывает. А единичный вектор — это направление
индикатор. Это безразмерный вектор с величиной 1, используемый для указания
направление. В тексте векторные величины обычно выделяются жирным шрифтом.
введите или со стрелкой над символом. Таким образом, хотя d = расстояние, d = смещение.
Позиция — это вектор количество. Он также имеет величину
как направление. Величина векторной величины представляет собой число (с единицами)
сообщая вам, сколько есть количества, и направление говорит вам, какое
как он указывает. А единичный вектор — это направление
индикатор. Это безразмерный вектор с величиной 1, используемый для указания
направление. В тексте векторные величины обычно выделяются жирным шрифтом.
введите или со стрелкой над символом. Таким образом, хотя d = расстояние, d = смещение.
Ссылки:
Скаляры и векторы (пожалуйста, изучите!)
Направление вектора
Позиция
Удобный способ указать положение объекта
это с помощью система координат .
Мы выбираем фиксированную точку, называемую началом координат .
и три направленные линии, которые проходят через начало координат и
перпендикулярны друг другу. Эти линии называются осями координат трехмерной прямоугольной (декартовой) системы координат и помечены
оси x, y и z. Три числа с единицами определяют положение
точка P. Эти числа представляют собой координаты x, y и z точки P.
Координаты точки P на
на диаграмме справа (а, б, в).
Три числа с единицами определяют положение
точка P. Эти числа представляют собой координаты x, y и z точки P.
Координаты точки P на
на диаграмме справа (а, б, в).
Координаты точки P являются компонентами вектора положения. Единичный вектор указание в направлении x имеет x-компоненту 1 и y- и z-компоненты нуль. Обозначается i . Точно так же единичный вектор , указывающий в направлении y, обозначается j , а единичный вектор направление в направлении z обозначается как k . Единичные векторы являются указателями поворота.
Компоненты любого вектора в сумме образуют
сам вектор. Вектор положения точки P с координатами (a, b, c)
может быть записано с точки зрения его компонентов как
г = а i + б j +
с к .
Величина вектора положения равна его длине r. Это зависит от выбора начала системы координат. Это — прямолинейное расстояние P от начала координат.
Ниже приведено трехмерное представление вектора положения. r = a i + b j + c k . Пожалуйста, нажмите
на рисунке!
r = a i + b j + c k . Пожалуйста, нажмите
на рисунке!
(Используйте современный браузер. 3D-приложения не работают в Internet Explorer.
или более старые браузеры.)
Чтобы получить наилучший вид, измените окно просмотра, перетащив мышь и
увеличить или уменьшить масштаб по мере необходимости.
Нажмите кнопки, чтобы выбрать другой вектор
или другая схема добавления векторов компонентов.
Пример:
Вектор положения здания Nielsen Physics Building на небольшой карте с левым нижним углом в качестве начала координат.
Рабочий объем
Изменение положения называется смещением . На приведенной ниже диаграмме показано позиции P 1 и P 2 игрока в два разных момента времени.
Стрелка, указывающая от P 1 к P 2 , является вектор смещения .
Его величина — прямая линия расстояние между P 1 и P 2 .
Компоненты вектора смещения от P 1 до
P 2 (x 2 — x 1 ) вдоль оси x, (y 2 —
y 1 ) по оси Y.
Вектор смещения d от P 1 до P 2 может
можно записать как d = (x 2 — x 1 ) i + (y 2 -у 1 ) у .
Объем двигателя d составляет (x 2 — x 1 ) единиц в
направление x плюс (y 2 — y 1 ) единицы измерения в направлении y.
Величина смещения d = ((x 2 — х 1 ) 2 + (у 2 — у 1 ) 2 ) ½ . Это следует из
пифагорейский
теорема.
Расстояние между двумя точками P 1 с координатами (x 1 , y 1 ,
я 1 ) и P 2 с координатами (x 2 , y 2 , z 2 ) равно
d = ((x 2 — х 1 ) 2 + (у 2 — у 1 ) 2 + (z 2 — z1) 2 )½ .
- Расстояние d является величиной вектора смещения d .
- направление вектора смещения d – направленный отрезок прямой от Р 1 к P 2 .
- Мы называем этот направленный отрезок геометрической или графической представление вектора d .
- Мы рисуем стрелку на P 2 , чтобы указать что сегмент линии начинается с P 1 и заканчивается на P 2 .
Тройка действительных чисел d x = (x 2 — x 1 ), d y = (у 2 — у 1 ), d z = (z 2 — z 1 ) называются декартовыми компонентами числа d .
Ссылка: Расстояние и смещение (Пожалуйста, изучите!)
Проблема:
Футбольный защитник бежит 15,0 м
прямо на игровом поле (в
положительное направление x) за 2,50 с.
Затем его ударили и толкнули на 3,00 м. прямо назад за 1,75 с. Он
ломает снасть и бежит прямо
вперед еще 21,0 м за 5,20 с.
Вычислите его вектор смещения и
общее пройденное расстояние.
прямо назад за 1,75 с. Он
ломает снасть и бежит прямо
вперед еще 21,0 м за 5,20 с.
Вычислите его вектор смещения и
общее пройденное расстояние.
Решение:
Проблема:
Во время движения по прямому межгосударственному шоссе вы обратите внимание, что на отметке 260 миль. отметку, а затем вернитесь к отметке 175 миль. Что это величина вашего результирующего смещения от 260-мильной отметки?
Решение:
- Обоснование:
Результирующее смещение есть вектор d , сумма двух векторов г 1 и d 2 , которые указывают в противоположных направлениях. - Детали расчета:
Результирующее смещение представляет собой вектор d , сумму двух векторов г 1 и d 2 , которые указывают в противоположных направлениях.
Проблема:
Кончик лопасти вертолета 5,00 м от центра вращения. За один оборот лезвия вычислить вектор смещения и общее расстояние, пройденное наконечником лезвия.
Решение:
- Обоснование:
После одного оборота наконечник возвращается в исходное положение. Вектор его смещения d = 0. - Детали расчета:
Общее пройденное расстояние кончик равен окружности окружности радиусом r = 5 м.
Окружность = 2πr = 31,42 м.
Общее расстояние, пройденное вершина 31,42 м.
Вектор смещения имеет одинаковую величину и направление независимо от выбор начала системы координат. Величина и направление вектор смещения, однако, зависят от система отсчета , в которой система координат закреплена и находится в состоянии покоя.
Пример:
Автомобиль двинулся вперед
расстояние 6 м, пока ребенок переместился с заднего сиденья на переднее
сидеть на расстоянии 1 м.
- Использование автомобиля в качестве системы отсчета и привязка системы координат в машине перемещение ребенка d (автомобиль) = (1 м) i .
- Использование дороги в качестве системы отсчета и привязка системы координат на дороге перемещение ребенка d (дорога) = (6 м) i + (1 м) i = (7 м) i .
Векторная алгебра:
ВЕКТОРНЫЕ МЕТОДЫ
векторное сложение
Векторы и сложение векторов:
Скаляр — это величина, подобная массе или температуре, которая имеет только величину. С другой стороны, вектор — это математический объект, который имеет величину и
направление. Линия заданной длины, указывающая в заданном направлении, например
стрелка, является типичным представлением вектора. Типичные обозначения для
обозначить вектор жирным шрифтом, символом и стрелкой на нем,
или символ с чертой под ним (т. е. ). Величина вектора
его длины и обычно обозначается или А .
С другой стороны, вектор — это математический объект, который имеет величину и
направление. Линия заданной длины, указывающая в заданном направлении, например
стрелка, является типичным представлением вектора. Типичные обозначения для
обозначить вектор жирным шрифтом, символом и стрелкой на нем,
или символ с чертой под ним (т. е. ). Величина вектора
его длины и обычно обозначается или А .
Сложение двух векторов выполняется сложением векторов голова к хвосту последовательно, чтобы создать треугольник, как показано на рисунке.
В векторной алгебре применяются следующие правила.
где P и Q — векторы, а a — скаляр.
Единичные векторы: 9″О сочетании с жирным шрифтом (т.е.). Следовательно,
Любой вектор может быть введен в единый вектор путем его деления на его длину.
может быть вектор. полностью представлен путем предоставления его величины и единицы измерения
вектор вдоль его направления.
полностью представлен путем предоставления его величины и единицы измерения
вектор вдоль его направления.
Базовые векторы и компоненты вектора:
Базовые векторы — это набор векторов, выбранных в качестве основы для представления всех остальных векторы. Идея состоит в том, чтобы построить каждый вектор из сложения векторов по основным направлениям. Например, вектор на рисунке можно записать в виде суммы трех векторов u 1 , u 2 и u 3 , каждая вдоль направления одного из базовых векторов e 1 , e 2 , and e 3 , so that
Each one of the vectors u 1 , u 2 , and у 3 параллелен одному из базовых векторов и может быть записан как скаляр, кратный
эта база. Пусть и 1 , и 2 , и и 3 обозначим эти скалярные множители, такие что
Пусть и 1 , и 2 , и и 3 обозначим эти скалярные множители, такие что
Исходный вектор u может now be written as
The scalar multipliers u 1 , u 2 , and u 3 известны как компоненты и в базе, описываемой базой векторы e 1 , e 2 и e 3 . Если базовые векторы являются единичными векторами, то компоненты представляют длины соответственно трех векторов u 1 , u 2 , и у 3 . Если базовые векторы являются единичными векторами и взаимно ортогонален, то основание известно как ортонормированное, евклидово или декартово база.
Вектор можно разложить по любым двум направлениям в плоскости, содержащей его. На рисунке показано, как правило параллелограмма используется для построения векторов и и b , которые в сумме дают c .
На рисунке показано, как правило параллелограмма используется для построения векторов и и b , которые в сумме дают c .
В трех измерениях вектор можно разрешить по любым трем некомпланарным линии. На рисунке показано, как вектор может быть разрешен по трем направлениям. сначала найдя вектор в плоскости двух направлений, а затем разрешение этого нового вектора вдоль двух направлений на плоскости.
Когда векторы представлены в терминах базовых векторов и компонентов, сложение двух векторов приводит к сложению компонентов векторы. Следовательно, если два вектора A и B представлены
, затем
прямоугольный компоненты в 2D:
Базовые векторы прямоугольной системы координат x-y задаются формулой
единичные векторы и вдоль x и y направления соответственно.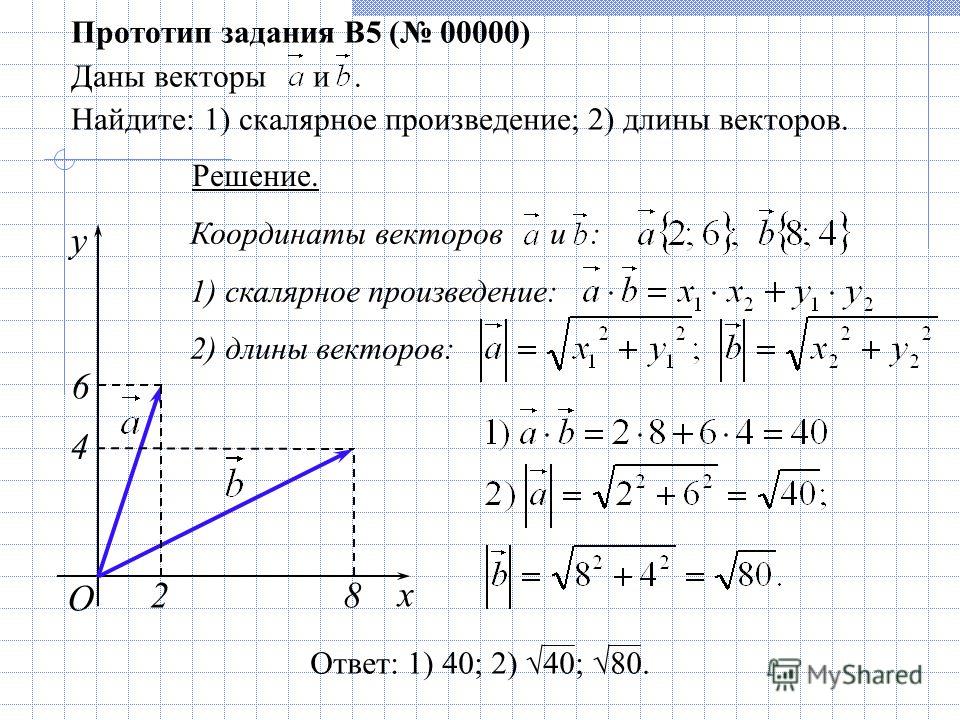
.
Прямоугольный координаты в 3D:
Базовые векторы прямоугольной системы координат задаются набором три взаимно ортогональных единичных вектора, обозначенных , , и что находятся вдоль x , y и z направления координат, соответственно, как показано на рисунке.
Показанная система является правосторонней, начиная с большого пальца правой руки указывает в направлении z , если пальцы таковы, что представляют вращение вокруг оси z от x до y . Эта система может превратить в левостороннюю систему, изменив направление любого из координатные линии и связанный с ними базовый вектор.
В прямоугольной системе координат компонентами вектора являются
проекции вектора вдоль x , y и z направления.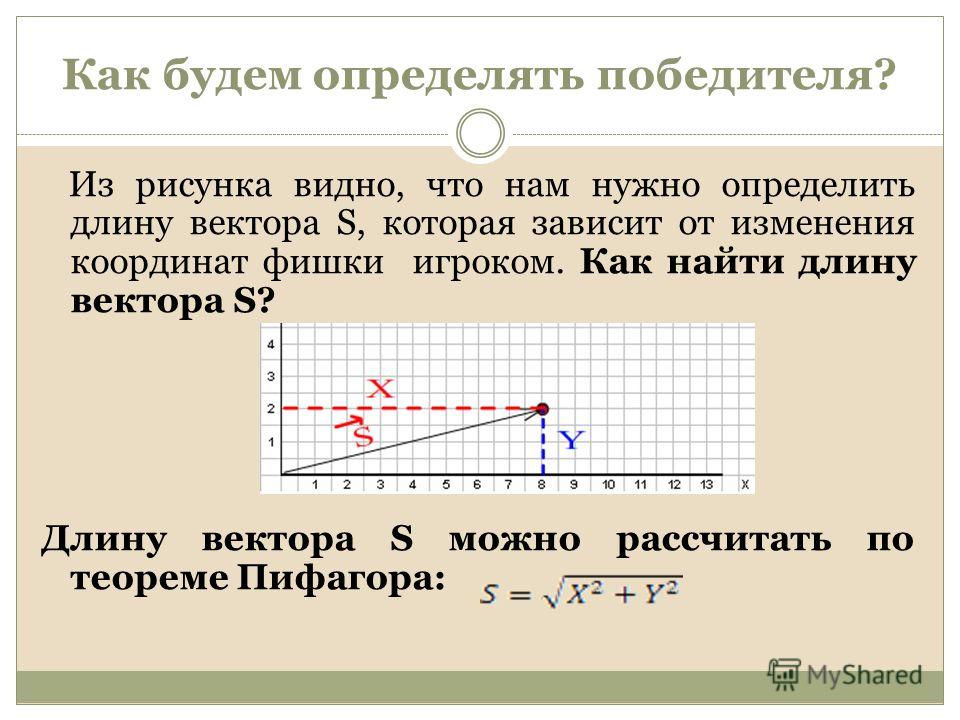 Например, на рисунке проекции вектора A по направлениям x, y, и z задаются A x , A y , и A z соответственно.
Например, на рисунке проекции вектора A по направлениям x, y, и z задаются A x , A y , и A z соответственно.
В силу теоремы Пифагора и ортогональности основания векторов, величина вектора в прямоугольной системе координат может быть calculated by
Direction cosines:
Direction cosines are defined as
where the angles , , and are the углы, показанные на рисунке. Как показано на рисунке, направляющие косинусы представляют собой косинусы углов между вектором и тремя согласовывать направления.
Направляющие косинусы можно вычислить из
компоненты вектора и его модуль через соотношения
и должно удовлетворять соотношению
используя направляющие косинусы в качестве составляющих вдоль х , и и z направлений.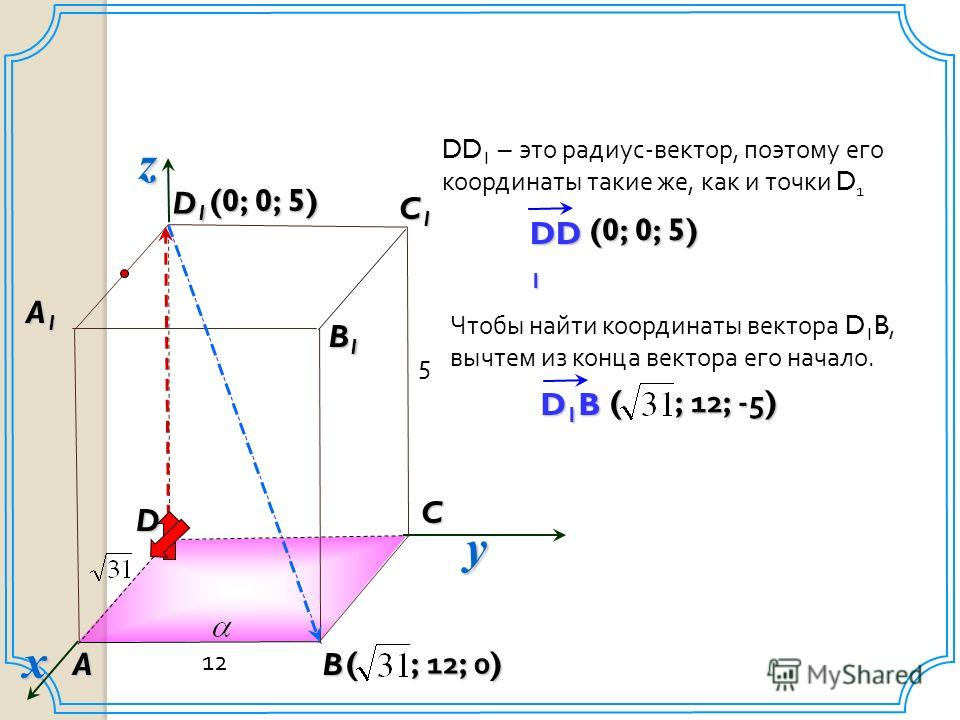 Например, единичный вектор вдоль вектора A получается из
Например, единичный вектор вдоль вектора A получается из
Следовательно,
2
5 вектор
соединение двух точек:
Вектор, соединяющий точку A с точкой Б задан
A Единый вектор вдоль линии A-B может быть получен с
A Vector F
A Vector F
8
A Vector F
8
A. F банка
таким образом, можно получить из отношения
Скалярный продукт:
Скалярный продукт обозначается «» между двумя векторами.
скалярное произведение векторов A и B дают скалярную величину, заданную
отношение
где угол между двумя векторами. Порядок не важен в
скалярный продукт, как видно из определения скалярных продуктов. В результате один
получает
Порядок не важен в
скалярный продукт, как видно из определения скалярных продуктов. В результате один
получает
Скалярный продукт обладает следующими свойствами.
Поскольку косинус 90 o равно нулю, точечному произведению двух
ортогональные векторы приведут к нулю.
Поскольку угол между вектором и самим собой равен нулю, а косинус нуля
равно единице, величина вектора может быть записана в терминах скалярного произведения
по правилу
Прямоугольные координаты:
При работе с векторами, представленными в
прямоугольная система координат по компонентам
, то скалярное произведение можно вычислить из
отношение
Это можно проверить прямым умножением
векторов и отметив, что из-за ортогональности базовых векторов
прямоугольная система
получается перемещением одного конца вектора на прямую и опусканием
перпендикулярно линии с другого конца вектора. Результирующий
отрезок на прямой является ортогональной проекцией вектора или просто его
проекция.
Результирующий
отрезок на прямой является ортогональной проекцией вектора или просто его
проекция.
Скалярная проекция вектора A вдоль
единичный вектор – это длина ортогональной проекции A вдоль линии, параллельной , и может быть оценено с помощью скалярного произведения.
соотношение для проекции:
Векторная проекция A вдоль единицы
вектор просто умножает скалярную проекцию на единичный вектор, чтобы
получить вектор вместе. Это дает соотношение
Крест
произведение:
Произведение векторов a и b является перпендикулярным вектором
как a , так и b и имеет величину, равную площади
параллелограмм, полученный из a и b . Направление креста
произведение определяется по правилу правой руки. Перекрестное произведение обозначается
«» между векторами
В векторном произведении важен порядок. Если порядок действий изменится
в векторном произведении направление результирующего вектора меняется на противоположное. То есть
Если порядок действий изменится
в векторном произведении направление результирующего вектора меняется на противоположное. То есть
Перекрестное произведение обладает следующими свойствами.
Прямоугольные координаты:
При работе в прямоугольных системах координат,
векторное произведение векторов A и B , приведенные
можно оценить с использованием правила
Один также можно использовать прямое умножение базы.
векторов с использованием соотношений
произведение:
Тройное произведение векторов a , b и c задается как
Значение тройного произведения равно объему параллелепипеда
построенный из векторов. Это можно увидеть на рисунке с
Тройной продукт имеет следующие свойства
Прямоугольные координаты:
Рассмотрены Vectors. система координат как
система координат как
Тройное произведение можно вычислить с помощью
отношение
Тройной вектор
Продукт:
Продукт с тройным вектором обладает свойствами
направление, ориентация, добавление, умножение, скаляры
. быть двумя различными точками плоскости. Направленный отрезок $\overrightarrow{AB}$ – это отрезок, в котором мы точно знаем, какая точка является начальной, а какая конечной.
Два направленных отрезка эквивалентны, если существует перевод, при котором один переводится в другой.
Вектор – это набор всех направленных отрезков, которые эквивалентны друг другу.
Любой направленный отрезок мы будем называть вектором из-за простоты речи. Векторы мы будем обозначать через $\overrightarrow{AB}, \overrightarrow{CD}, \ldots$ или просто как $\overrightarrow{a}, \overrightarrow{b}, \ldots$.
Векторы однозначно определяются своей величиной, направлением и ориентацией.
Рисование векторов в двумерных декартовых координатах
Каждый вектор определяется двумя точками. Это делает их рисование в координатной плоскости довольно простым. Например, если нам даны две точки с их координатами $A=(1, 2)$ и $B = (5, 6)$ и наша задача состоит в том, чтобы нарисовать вектор $\overrightarrow{AB}$, мы должны сначала нарисовать отрезок $\overline{AB}$, а затем просто нарисуйте стрелку, обозначающую нашу конечную точку.
Каждой точке плоскости может быть поставлен в соответствие уникальный вектор, начальная точка которого находится в начале координат, а конечная точка находится в данной точке. Эти векторы очень важны в векторной геометрии, и они называются координатами или радиус-векторами .
Величина векторов
Величина вектора $\overrightarrow{AB}$ равна длине отрезка $\overline{AB}$.
Некоторые дополнительные имена для величин векторов, такие как: норма вектора, модуль вектора или абсолютное значение вектора.
Величина любого вектора определяется положением его начальной и конечной точки и рассчитывается точно так же, как длина отрезка. Величина вектора всегда либо положительное число, либо ноль. Величина вектора равна нулю тогда и только тогда, когда начальная точка равна конечной точке.
Если у нас есть две точки с их координатами $ A = (x_1, y_1)$ и $ B = (x_2, y_2)$, тогда величина вектора $\overrightarrow{AB}$ равна: 92}.$$
Нулевой вектор или нулевой вектор — это вектор, длина которого равна $0$. Нулевой вектор обозначается $\overrightarrow{0}$.
Единичный вектор — это вектор, длина которого равна $1$, однако он может двигаться в любом направлении. Для вектора $\overrightarrow{a}$ длины $|\overrightarrow{a}|$ единичный вектор $\overrightarrow{a_0}$ определяется как
$$\overrightarrow{a_0} = \frac{\overrightarrow {а}}{|\overrightarrow{а}|}. $$ 92} = \sqrt{50} = \sqrt{2 \cdot 25} = 5\sqrt{2}$.
$$ 92} = \sqrt{50} = \sqrt{2 \cdot 25} = 5\sqrt{2}$.
3. $\overrightarrow{EF} = 0$, потому что $E=F$.
Направление векторов
Направление вектора — это мера угла, заключенного с осью $y$. Его можно наблюдать как наклон линии, на которой он лежит, потому что его наклон вычисляется так же, как мы вычисляем наклон линии. Мы будем отмечать направление вектора с помощью $\varphi$.
Если у нас есть вектор $\overrightarrow{PQ}$, $P = (x_1, y_1)$, $ Q = (x_2, y_2)$, то 9{\circ}$.
Ориентация векторов
Ориентация вектора относится исключительно к коллинеарным векторам. Коллинеарные векторы – это векторы, лежащие на одной прямой или параллельной одной и той же прямой. Например, если у нас есть два вектора $\overrightarrow{AB}$ и $\overrightarrow{CD}$, то их ориентация может быть только равной или противоположной.
Как мы можем таким образом определить ориентацию, если предположить, что эти два вектора коллинеарны? Сначала мы должны взять один вектор и перевести его так, чтобы его начальная точка попала в начальную точку другого вектора. Это означает, что мы переносим вектор $\overrightarrow{CD}$ так, что $C = A$. Если точки $B$ и $D$ лежат по одну сторону от точки $A$, то они обе имеют одинаковую ориентацию, если же они находятся по разные стороны от точки $A$, то они имеют противоположную ориентацию. .
Это означает, что мы переносим вектор $\overrightarrow{CD}$ так, что $C = A$. Если точки $B$ и $D$ лежат по одну сторону от точки $A$, то они обе имеют одинаковую ориентацию, если же они находятся по разные стороны от точки $A$, то они имеют противоположную ориентацию. .
Векторы с одинаковой ориентацией:
Векторы с противоположной ориентацией:
Примечание. Два вектора равны, если они имеют одинаковую величину, направление и ориентацию. Если два коллинеарных вектора имеют одинаковую длину, хотя и разную ориентацию, они называются противоположными векторами . Если $\overrightarrow{a}$ — вектор, который мы наблюдаем, то его противоположный вектор обозначается $\overrightarrow{- a}$.
Сложение векторов
Складывая векторы $\overrightarrow{AB}$ и $\overrightarrow{CD}$, мы получим новый вектор $\overrightarrow{AD}$, начальная точка которого совпадает с первым слагаемым, а конец точка нового вектора совпадает со вторым слагаемым. Применяя это правило, получается треугольник. Вот почему этот метод сложения называется правилом треугольника . Когда у нас есть два вектора, которые мы должны сложить, сначала мы переводим один вектор на другой таким образом, чтобы конечная точка первого была начальной точкой второго. Затем все, что осталось, это завершить треугольник и отметить ориентацию нашего нового вектора.
Применяя это правило, получается треугольник. Вот почему этот метод сложения называется правилом треугольника . Когда у нас есть два вектора, которые мы должны сложить, сначала мы переводим один вектор на другой таким образом, чтобы конечная точка первого была начальной точкой второго. Затем все, что осталось, это завершить треугольник и отметить ориентацию нашего нового вектора.
Сложение с нулевым вектором:
$\overrightarrow{a}$ + $\overrightarrow{0}$ = $\overrightarrow{a}$
$\overrightarrow{0}$ + $\overrightarrow{ а}$ = $\overrightarrow{а}$.
Закон параллелограмма сложения векторов Если у нас есть два вектора, имеющих одну и ту же начальную точку, то мы можем использовать закон параллелограмма вектора сложения . Мы просто рассматриваем эти два вектора как смежные стороны параллелограмма, их сумма будет диагональю параллелограмма. Начальная точка суммы этих двух векторов будет их начальной точкой.
Шаг за шагом:
Свойства сложения
Для любых двух векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ верно:
$$\overrightarrow{a}\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}.$$
Это означает, что сложение векторов коммутативно.
Для любых трех векторов $\overrightarrow{a}$, $\overrightarrow{b}$ и $\overrightarrow{c}$ допустимо:
$$(\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c}).$$
Следовательно, сложение векторов ассоциативно.
Сложение более двух векторов
Сложение $n$ взаимосвязанных векторов $\overrightarrow{A_1 A_2}, \overrightarrow{A_2 A_3}, \overrightarrow{A_3 A_4}, … , \overrightarrow{ A_{n-1}A_n}$ равен вектору $\overrightarrow{A_1 A_n}$
Примечание: Как мы уже знаем, $\overrightarrow{-a}$ — это вектор, ориентация которого противоположна ориентации вектора $\overrightarrow{a}$, однако их величина и направление равны. Используя это утверждение, мы знаем, как вычитать векторы. Если у нас есть два вектора, $\overrightarrow{a}$ и $\overrightarrow{b}$, и нам нужно вычесть $\overrightarrow{b}$ из $\overrightarrow{a}$ $ (\overrightarrow{a} – \overrightarrow{b})$, мы просто меняем ориентацию вектора $\overrightarrow{b}$ и добавляем их как таковые $\overrightarrow{a} + (\overrightarrow{-b})$.
Используя это утверждение, мы знаем, как вычитать векторы. Если у нас есть два вектора, $\overrightarrow{a}$ и $\overrightarrow{b}$, и нам нужно вычесть $\overrightarrow{b}$ из $\overrightarrow{a}$ $ (\overrightarrow{a} – \overrightarrow{b})$, мы просто меняем ориентацию вектора $\overrightarrow{b}$ и добавляем их как таковые $\overrightarrow{a} + (\overrightarrow{-b})$.
Умножение векторов на действительные числа
Произведение действительного числа $ k \not = 0$ на вектор $\overrightarrow{a}$ представляет собой вектор, который мы обозначаем как $ k \overrightarrow{a}$ , с правилами:
- Векторы $\overrightarrow{a}$ и $k \vec{a}$ являются коллинеарными векторами одной ориентации, если $k > 0$, и противоположной ориентации, если $k < 0$
- Величина вектора $ k \overrightarrow{a}$ равно $\mid k \mid \cdot\mid \overrightarrow{a} \mid$
- Произведение вектора на ноль является нуль-вектором
- Произведение вектора на $1$ является одним и тем же вектором
Например, если у нас есть вектор $\overrightarrow{AB}$, где $ A = (2, 4)$, $ B = (5, 6)$, вычислить $2\overrightarrow{AB}$ и $-2\overrightarrow{AB}$, произведение вектора на действительное число всегда будет расположено на линии, на которой лежит наблюдаемый вектор. Поэтому первое, что мы должны сделать, это провести линию, на которой лежит вектор $\overrightarrow{AB}$.
Поэтому первое, что мы должны сделать, это провести линию, на которой лежит вектор $\overrightarrow{AB}$.
Теперь нам нужно вычислить $ 2\overrightarrow{AB}$. Его величина будет в два раза больше, чем у вектора $\overrightarrow{AB}$. Вектор будет расположен на той же прямой и будет иметь ту же ориентацию, потому что $2 > 0$. Теперь у нас есть все необходимые данные:
Теперь нам нужно вычислить $-2 \cdot\vec{AB}$. Поскольку $-2 < 0$, этот вектор будет иметь противоположную вектору $\overrightarrow{AB}$ ориентацию, двойную величину и то же направление.
Свойства умножения вектора на вещественное число
Справедливо для любых двух действительных чисел $k$ и $l$ и для любых двух векторов $\overrightarrow{a}$ и $\overrightarrow{b }$:
$ k (\overrightarrow{a} + \overrightarrow{b}) = k \overrightarrow{a} + k \overrightarrow{b}$
$ (k + l) \overrightarrow{a} = k \overrightarrow{a} + l \overrightarrow{a}$
$(kl) \overrightarrow{a} = k (l \overrightarrow{a})$
Линейная комбинация – линейная зависимость и независимость
Если $\overrightarrow{a}$ и $\overrightarrow{b}$ являются векторами и $\alpha$ и $\beta$ вещественными числами, то вектор
$\overrightarrow{ c} = \alpha \overrightarrow{a} + \beta \overrightarrow{b}$
называется линейной комбинацией векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ с коэффициентами $\alpha$ и $\бета$.
Если $\overrightarrow{a}$ и $\overrightarrow{b}$ — два коллинеарных, а не нуль-вектора с одинаковой ориентацией, где $\overrightarrow{a}$ в $k$ раз длиннее, чем $\overrightarrow{b }$, то мы можем написать:
Это означает, что один вектор может быть представлен с помощью другого и что $\overrightarrow{a}$ и $\overrightarrow{b}$ являются линейно зависимыми .
Векторы $\overrightarrow{a_1}, \overrightarrow{a_2} … , \overrightarrow{a_n}$ называются линейно зависимыми, если существуют действительные числа $\alpha_1, \alpha_2, … , \alpha_n$ такие, что:
$\overrightarrow{0} = \alpha_1 \overrightarrow{a_1} + \alpha_2 \overrightarrow{a_2}, … , \alpha_n \overrightarrow{a_n}$.
Если линейная комбинация $\alpha_1 \overrightarrow{a_1} + \alpha_2 \overrightarrow{a_2}, … , \alpha_n \overrightarrow{a_n}$ равна $\overrightarrow{0}$ только тогда, когда $\alpha_1, \alpha_2 , … , \alpha_n$ равны нулю, то говорят, что векторы $\overrightarrow{a_1}, \overrightarrow{a_2} … , \overrightarrow{a_n}$ линейно независимы .
Любые два коллинеарных вектора на плоскости линейно зависимы, а каждые два неколлинеарных вектора линейно независимы.
Каждый вектор на плоскости может быть представлен уникальным образом как линейная комбинация двух неколлинеарных векторов.
Векторы в координатной плоскости
Пусть $E$ — единичная точка на оси $x$, $F$ — единичная точка на оси $y$, а точка $O$ — начало координат. Тогда радиус-вектор $\overrightarrow{OE}$ равен единичному вектору $\overrightarrow{i}$, а радиус-вектор $\overrightarrow{OF}$ равен единичному вектору $\overrightarrow{j}$.
Используя эти два вектора, мы можем представить любой вектор на плоскости уникальным образом.
Если точка $P$ имеет координаты $(x, y)$, то радиус-вектор $\overrightarrow{OP}$ имеет представление $\overrightarrow{OP} = x \overrightarrow{i} + y \overrightarrow{j}$ .
Если $A_1 = (x_1, y_1)$ и $A_2 = (x_2, y_2)$ две точки плоскости, то: $\overrightarrow{A_1A_2} = (x_2 – x_1) \overrightarrow{i} + (y_2 – y_1) \overrightarrow{j}$.
Например, если у нас есть две точки $ A = (1, 3)$ и $ B = (2 , 5)$, то вектор $\overrightarrow{AB}$ равен:
$\overrightarrow{AB} = (x_2 – x_1) \vec{i} + (y_2 – y_1) \overrightarrow{j} = (2 – 4) \overrightarrow{i} + (5 – 3) \overrightarrow{ j} = \overrightarrow{i} + 2 \overrightarrow{j}$.
Скалярное или скалярное произведение
Предположим, что на плоскости есть два вектора, оба отличные от $\overrightarrow{0}$. Если они не имеют одной и той же начальной точки, мы просто переводим один вектор в другой таким образом, чтобы у них была одна и та же начальная точка.
Угол между этими двумя векторами — это меньший угол из двух углов, заключенных между полупрямыми, на которых лежат эти два вектора.
Если $\overrightarrow{a}$ и $\overrightarrow{b}$ — два вектора, отличные от $\overrightarrow{0}$, произведение
$$\overrightarrow{a} \cdot \overrightarrow{b } = |\overrightarrow{a}| \cdot |\overrightarrow{b}| cos \angle (\overrightarrow{a}, \overrightarrow{b})$$
называется скаляром или скалярным произведением векторов $\overrightarrow{a}$ и $\overrightarrow{b}$.
Свойства скалярного произведения
1. $ \cdot \overrightarrow{a} \cdot \overrightarrow{b} = \overrightarrow{b} \cdot \overrightarrow{a}$ для любых двух векторов $\overrightarrow{a}$ и $\overrightarrow{b }$
2. $ (\overrightarrow{a} + \overrightarrow{b}) \cdot \overrightarrow{c} = \overrightarrow{a} \cdot \overrightarrow{c} + \overrightarrow{b} \cdot \overrightarrow {c}$, для каждых трех векторов $\overrightarrow{a}$, $\overrightarrow{b}$ и $\overrightarrow{c}$
3. $(\alpha \cdot \overrightarrow{a}) \cdot \overrightarrow{b} = \overrightarrow{a}\cdot (\alpha \cdot \overrightarrow{b}) = \alpha \cdot (\overrightarrow{a} \cdot \overrightarrow{b})$ , для любых двух векторов $ \overrightarrow{a}$ и $\overrightarrow{b}$ и $\forall \alpha \in \mathbb{R}$ 92$, для каждого вектора $\overrightarrow{a}$
5. $\overrightarrow{a} \cdot \overrightarrow{b} = 0$ , если $\cos \angle(\overrightarrow{a}, \overrightarrow{ b}) = 0$
Для единичных векторов $\overrightarrow{i}$ и $\overrightarrow{j}$ справедливо:
$$\overrightarrow{i} \cdot \overrightarrow{j} = \overrightarrow{j } \cdot \overrightarrow{i} = 0. $$
$$
Рабочие листы
Именование вершин и векторов (419,4 КиБ, 720 совпадений)
Vectors measurement of angles (490.3 KiB, 10,170 hits)
How to Multiply Vectors — Scalar (dot) product
How to Multiply Vectors
Key Terms
Unit vector Scalar (точечный) продукт
Цели
Определение концепции единичных векторов Использование единичных векторов для алгебраического представления векторов Определение умножения скаляра на вектор Использование скалярного произведения для вычисления длины вектора
В этой статье мы рассмотрим другое представление векторов, а также основы умножения векторов.
Единичные векторы
Хотя форма координат для представления векторов ясна, мы также можем представить их в виде алгебраических выражений, используя единичные векторы. В наших стандартных прямоугольных (или евклидовых) координатах ( x, y, и z ), единичный вектор — это вектор длины 1, параллельный одной из осей. В двумерной координатной плоскости единичные векторы часто называют i и j, , как показано на графике ниже. Для трех измерений мы добавляем единичный вектор k , соответствующий направлению оси z . Эти векторы определяются алгебраически следующим образом.
В наших стандартных прямоугольных (или евклидовых) координатах ( x, y, и z ), единичный вектор — это вектор длины 1, параллельный одной из осей. В двумерной координатной плоскости единичные векторы часто называют i и j, , как показано на графике ниже. Для трех измерений мы добавляем единичный вектор k , соответствующий направлению оси z . Эти векторы определяются алгебраически следующим образом.
i = (1, 0) или (1, 0, 0)
j = (0, 1) или (0, 1, 0)
k = (0,135 , 1)
Перед тем, как мы представим алгебраическое представление векторов с помощью единичных векторов, мы должны ввести алгебраическое представление векторов с помощью векторов-умножений.
Умножение векторов на скаляры
Умножение с участием векторов сложнее, чем просто скаляров, поэтому мы должны относиться к этому вопросу внимательно. Начнем с самого простого случая: умножения вектора на скаляр. Ниже приведено определение умножения скаляра c на вектор a, , где a = ( x, y ). (Опять же, мы можем легко распространить эти принципы на три измерения.)
Начнем с самого простого случая: умножения вектора на скаляр. Ниже приведено определение умножения скаляра c на вектор a, , где a = ( x, y ). (Опять же, мы можем легко распространить эти принципы на три измерения.)
Скалярное умножение является коммутативным, поэтому . Но что означает это умножение? Как оказалось, умножение на скаляр c увеличивает длину вектора в c раз. Это лучше всего видно для единичных векторов, но это применимо к любому вектору. (Однако умножение на отрицательную скалярную величину меняет направление вектора на противоположное.) На приведенном ниже графике показаны некоторые примеры с использованием c = 2. (Напомним, что положение вектора не влияет на его значение.)
Практическая задача: , задан вектор
5 a 3, найти вектор в том же направлении, что и на , но в два раза длиннее.
Решение: Когда мы умножаем вектор на скаляр, направление вектора произведения совпадает с направлением множителя. Единственная разница в том, что длина умножается на скаляр. Итак, чтобы получить вектор, длина которого в два раза больше A , но в том же направлении, что и A, просто умножьте на 2.
2 A = 2 • (3, 1) = (2 • 3, 2 • • 1) = (6, 2)
Алгебраическое представление векторов
Мы можем использовать скалярное умножение с векторами для представления векторов в алгебральном плане. Заметим, что любой двумерный вектор v можно представить как сумму длины, умноженной на единичный вектор i , и другой длины, умноженной на единичный вектор j. Например, рассмотрим вектор (2, 4). Примените правила векторов, которые мы уже изучили:
(2, 4) = (2, 0) + (0, 4) (правило сложения для векторов)
(2, 4) = 2 • (1, 0) + 4 • (0, 1) (правило умножения скаляров и векторов)
(2, 4) = 2 i + 4 j
Графически мы добавляем два вектора в единичных направлениях, чтобы получить наши произвольные направления.
Хотите узнать больше? Почему бы не пройти онлайн-курс Precalculus?
Обратите внимание, что единичные векторы действуют почти так же, как переменные. Таким образом, мы можем сложить два вектора a и b следующим образом.
a = 3 i – 2 j b = i + 3 j
a + b = (3 i – 2 i ) + ( i + 3 j ) = 3 i + i 3 6 9 903 1 – 5 3 9 9 0 3 10135 j = 4 i + j
Это представление координат обеспечивает большую гибкость, чем представление координат, но оно обеспечивает большую гибкость, чем представление координат.
Практическая задача: Рассчитайте сумму и разницу ( T — U ) Векторов T = -2 I +
+ + I + + + + + + + + + + + + + + + + + + и ).0135 u = 6 i — 4 j.
Решение: Мы можем довольно легко решить эту задачу алгебраически.
T + U = (-2 I + 3 J ) + (6 I — 4 J ) = I — 4 J ) = I — 4 J ) = I — 4 j ) = I — 4 j ) = I — 4 j ) = I — 4 J ) = I — 4 J ). (4, -1)
(4, -1)
t — u = (-2 i + 3 j ) — (6 i — 4 j ) = -2 i + 3 j — 6 i + 4 j = -8 i 6-
+ 3 5 j + 3 7 , 7) Порядок не важен в
скалярный продукт, как видно из определения скалярных продуктов. В результате один
получает
Порядок не важен в
скалярный продукт, как видно из определения скалярных продуктов. В результате один
получает Результирующий
отрезок на прямой является ортогональной проекцией вектора или просто его
проекция.
Результирующий
отрезок на прямой является ортогональной проекцией вектора или просто его
проекция. Если порядок действий изменится
в векторном произведении направление результирующего вектора меняется на противоположное. То есть
Если порядок действий изменится
в векторном произведении направление результирующего вектора меняется на противоположное. То есть система координат как
система координат как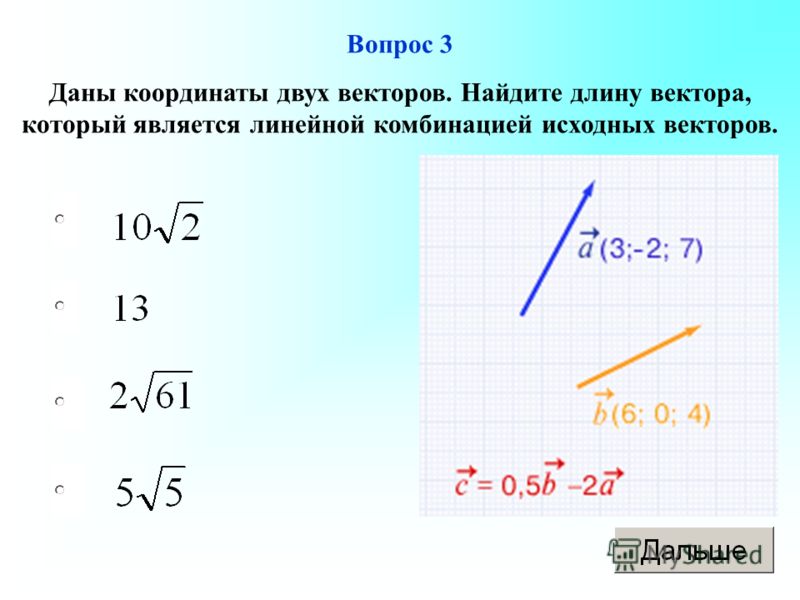

 $$ 92} = \sqrt{50} = \sqrt{2 \cdot 25} = 5\sqrt{2}$.
$$ 92} = \sqrt{50} = \sqrt{2 \cdot 25} = 5\sqrt{2}$. Это означает, что мы переносим вектор $\overrightarrow{CD}$ так, что $C = A$. Если точки $B$ и $D$ лежат по одну сторону от точки $A$, то они обе имеют одинаковую ориентацию, если же они находятся по разные стороны от точки $A$, то они имеют противоположную ориентацию. .
Это означает, что мы переносим вектор $\overrightarrow{CD}$ так, что $C = A$. Если точки $B$ и $D$ лежат по одну сторону от точки $A$, то они обе имеют одинаковую ориентацию, если же они находятся по разные стороны от точки $A$, то они имеют противоположную ориентацию. . Применяя это правило, получается треугольник. Вот почему этот метод сложения называется правилом треугольника . Когда у нас есть два вектора, которые мы должны сложить, сначала мы переводим один вектор на другой таким образом, чтобы конечная точка первого была начальной точкой второго. Затем все, что осталось, это завершить треугольник и отметить ориентацию нашего нового вектора.
Применяя это правило, получается треугольник. Вот почему этот метод сложения называется правилом треугольника . Когда у нас есть два вектора, которые мы должны сложить, сначала мы переводим один вектор на другой таким образом, чтобы конечная точка первого была начальной точкой второго. Затем все, что осталось, это завершить треугольник и отметить ориентацию нашего нового вектора.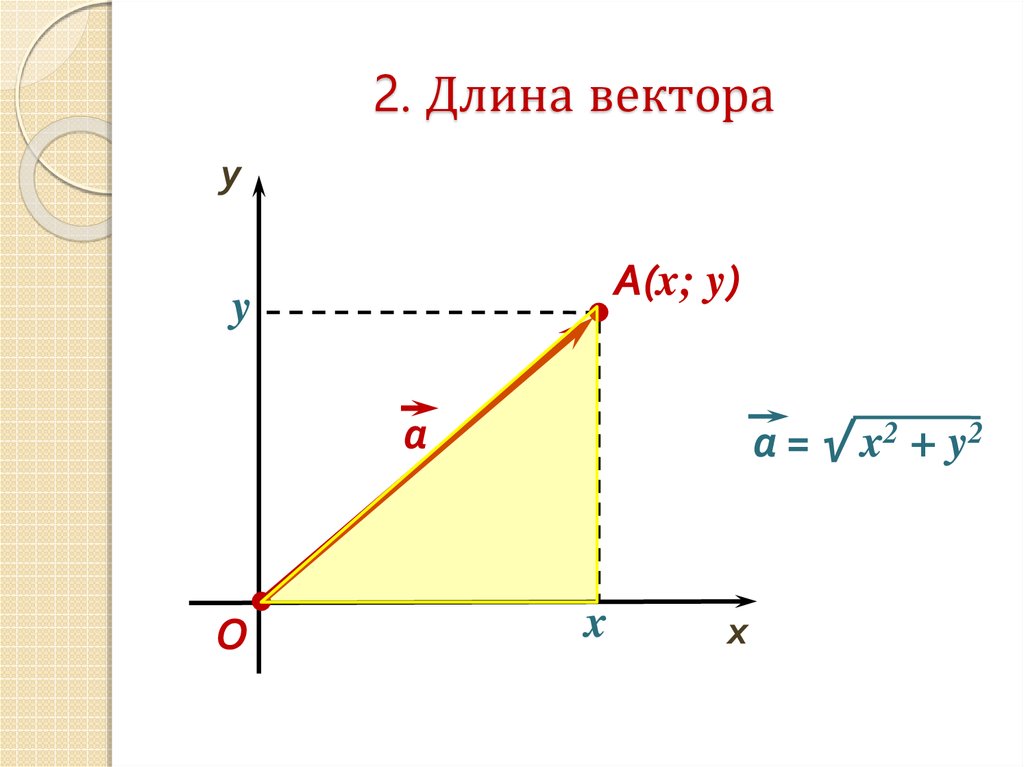
 Используя это утверждение, мы знаем, как вычитать векторы. Если у нас есть два вектора, $\overrightarrow{a}$ и $\overrightarrow{b}$, и нам нужно вычесть $\overrightarrow{b}$ из $\overrightarrow{a}$ $ (\overrightarrow{a} – \overrightarrow{b})$, мы просто меняем ориентацию вектора $\overrightarrow{b}$ и добавляем их как таковые $\overrightarrow{a} + (\overrightarrow{-b})$.
Используя это утверждение, мы знаем, как вычитать векторы. Если у нас есть два вектора, $\overrightarrow{a}$ и $\overrightarrow{b}$, и нам нужно вычесть $\overrightarrow{b}$ из $\overrightarrow{a}$ $ (\overrightarrow{a} – \overrightarrow{b})$, мы просто меняем ориентацию вектора $\overrightarrow{b}$ и добавляем их как таковые $\overrightarrow{a} + (\overrightarrow{-b})$. Поэтому первое, что мы должны сделать, это провести линию, на которой лежит вектор $\overrightarrow{AB}$.
Поэтому первое, что мы должны сделать, это провести линию, на которой лежит вектор $\overrightarrow{AB}$.


Угол между этими двумя векторами — это меньший угол из двух углов, заключенных между полупрямыми, на которых лежат эти два вектора.

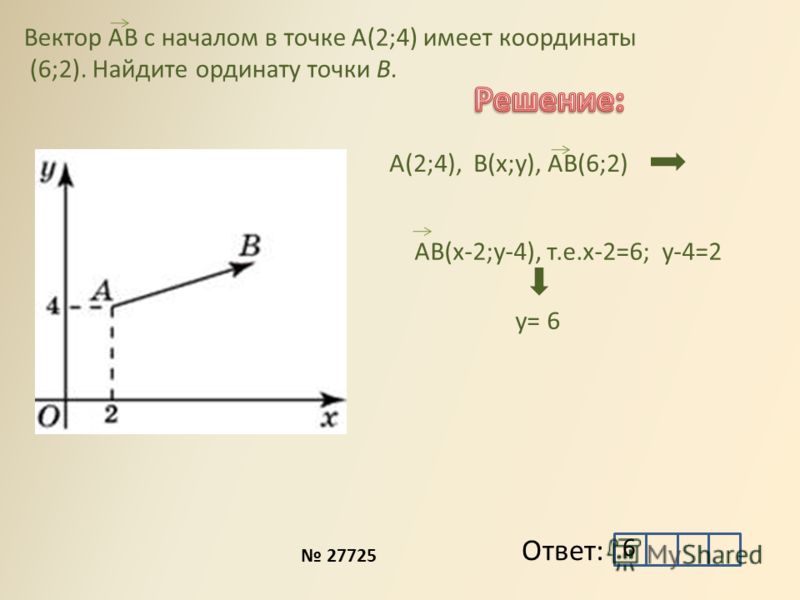 $$
$$
 В наших стандартных прямоугольных (или евклидовых) координатах ( x, y, и z ), единичный вектор — это вектор длины 1, параллельный одной из осей. В двумерной координатной плоскости единичные векторы часто называют i и j, , как показано на графике ниже. Для трех измерений мы добавляем единичный вектор k , соответствующий направлению оси z . Эти векторы определяются алгебраически следующим образом.
В наших стандартных прямоугольных (или евклидовых) координатах ( x, y, и z ), единичный вектор — это вектор длины 1, параллельный одной из осей. В двумерной координатной плоскости единичные векторы часто называют i и j, , как показано на графике ниже. Для трех измерений мы добавляем единичный вектор k , соответствующий направлению оси z . Эти векторы определяются алгебраически следующим образом.= (0,135 , 1)
Перед тем, как мы представим алгебраическое представление векторов с помощью единичных векторов, мы должны ввести алгебраическое представление векторов с помощью векторов-умножений.
Умножение векторов на скаляры
Умножение с участием векторов сложнее, чем просто скаляров, поэтому мы должны относиться к этому вопросу внимательно. Начнем с самого простого случая: умножения вектора на скаляр. Ниже приведено определение умножения скаляра c на вектор a, , где a = ( x, y ). (Опять же, мы можем легко распространить эти принципы на три измерения.)
Начнем с самого простого случая: умножения вектора на скаляр. Ниже приведено определение умножения скаляра c на вектор a, , где a = ( x, y ). (Опять же, мы можем легко распространить эти принципы на три измерения.)
Скалярное умножение является коммутативным, поэтому . Но что означает это умножение? Как оказалось, умножение на скаляр c увеличивает длину вектора в c раз. Это лучше всего видно для единичных векторов, но это применимо к любому вектору. (Однако умножение на отрицательную скалярную величину меняет направление вектора на противоположное.) На приведенном ниже графике показаны некоторые примеры с использованием c = 2. (Напомним, что положение вектора не влияет на его значение.)
Практическая задача: , задан вектор
5 a 3, найти вектор в том же направлении, что и на , но в два раза длиннее.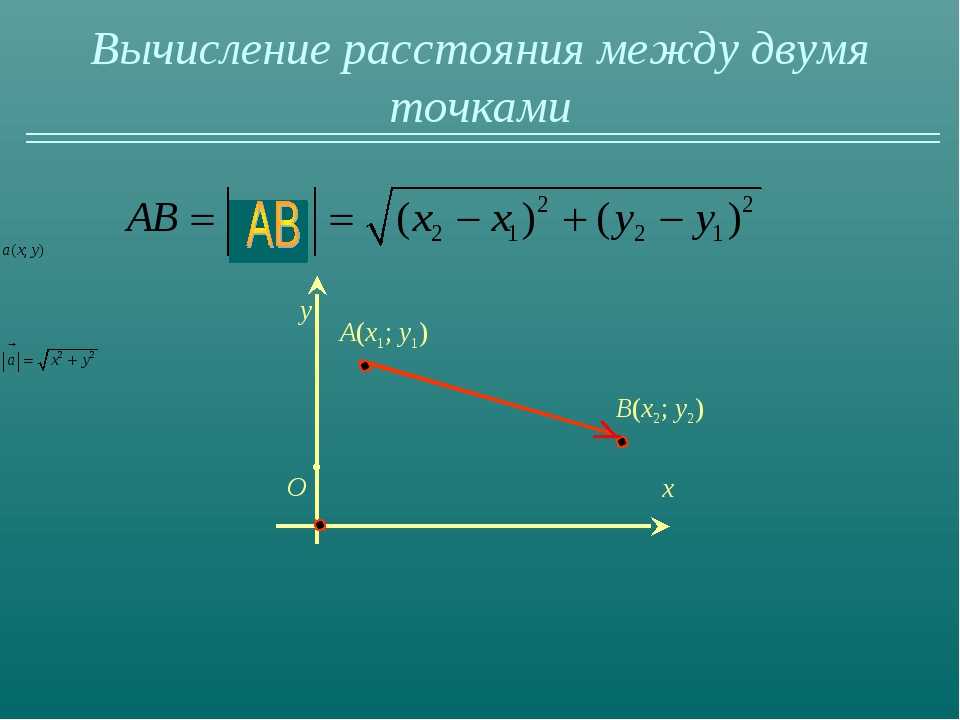
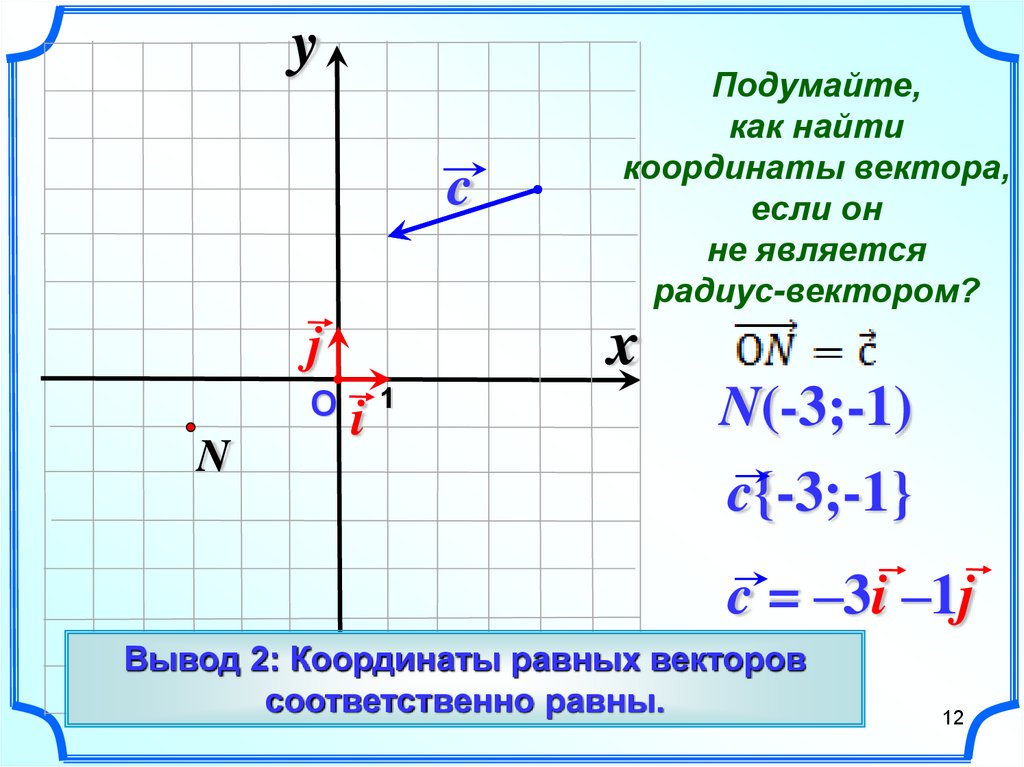

 (4, -1)
(4, -1)Умножение вектора: Скалярное (точечное) Продукт
Многочисленное количество. . Определены два типа умножения с участием двух векторов: так называемое скалярное произведение (или «точечный продукт») и так называемое векторное произведение (или «перекрестное произведение»). Для простоты мы обратимся только к скалярному произведению, но на этом этапе у вас должна быть достаточная математическая база, чтобы понимать и векторное произведение. 9Скалярное произведение 0135 (или скалярное произведение ) двух векторов определяется следующим образом в двух измерениях. Как всегда, это определение можно легко распространить на три измерения — просто следуйте шаблону. Обратите внимание, что операция всегда должна обозначаться точкой (•), чтобы отличить ее от векторного произведения, в котором используется символ умножения () — отсюда и названия — скалярное произведение и перекрестное произведение .
Как всегда, это определение можно легко распространить на три измерения — просто следуйте шаблону. Обратите внимание, что операция всегда должна обозначаться точкой (•), чтобы отличить ее от векторного произведения, в котором используется символ умножения () — отсюда и названия — скалярное произведение и перекрестное произведение .
Однако на данный момент значение этого продукта может быть вам не совсем ясно. Мы можем проиллюстрировать это, рассмотрев простой случай: скалярное произведение произвольного вектора v и единичных векторов i и j.
0222
Thus, v • i is the «part» of vector v in the direction of I.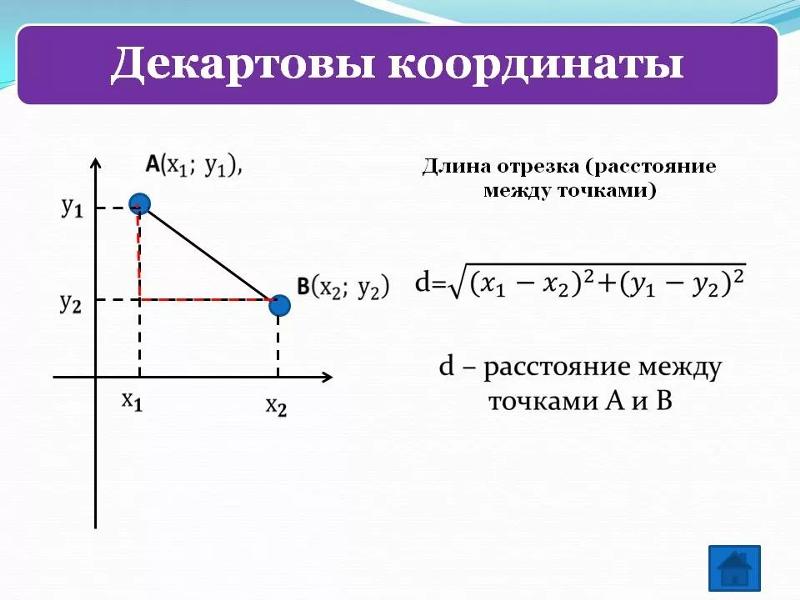
Однако это объяснение работает только для векторов длины 1. Когда два произвольных вектора перемножаются, скалярное произведение имеет аналогичный смысл, но величина числа немного отличается. Мы не будем углубляться в это, но мы можем рассмотреть частный случай, когда скалярное произведение дает ценную информацию.
Длина вектора
Рассмотрим случай скалярного продукта вектора V .
Посмотреть на эту ситуацию Графически.
Результатом здесь является прямоугольный треугольник с горизонтальной стороной длиной x и вертикальной стороной длиной y. Эти длины соответствуют длинам составляющих векторов x i и y j, соответственно.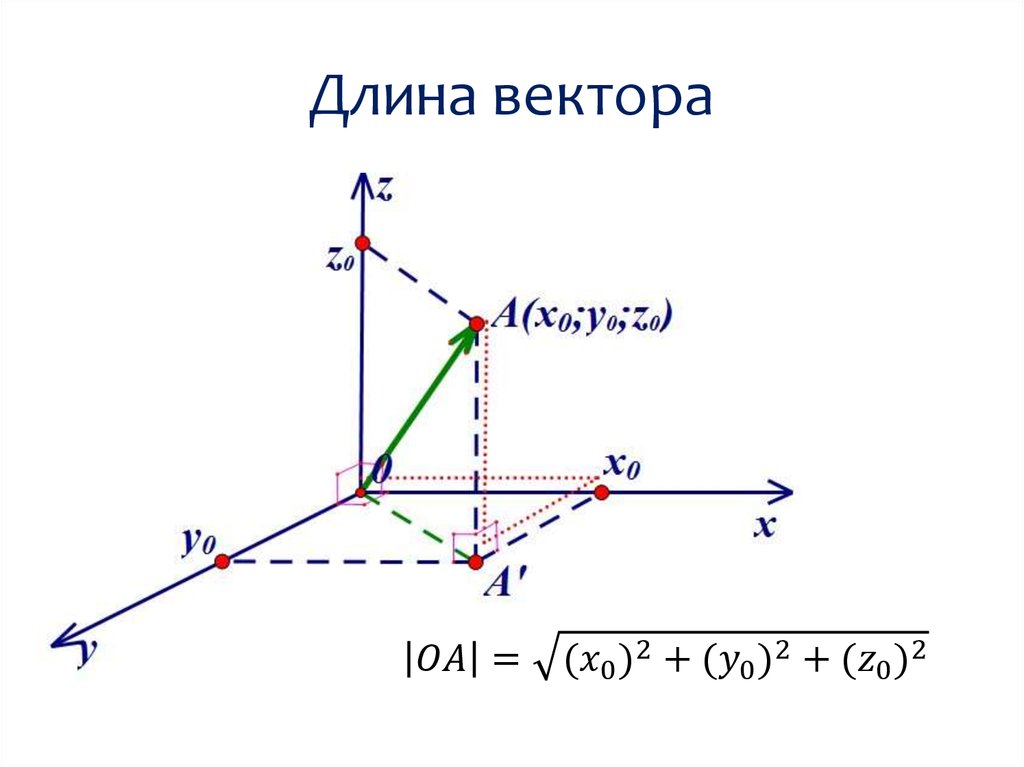 Но мы знаем из теоремы Пифагора, что есть квадрат длины вектора против . Не случайно это то же самое, что и скалярное произведение в сам с собой. Таким образом, длина любого вектора v, , записанного как (или иногда ), является квадратным корнем скалярного произведения.
Но мы знаем из теоремы Пифагора, что есть квадрат длины вектора против . Не случайно это то же самое, что и скалярное произведение в сам с собой. Таким образом, длина любого вектора v, , записанного как (или иногда ), является квадратным корнем скалярного произведения.
In the simple case of the unit vectors,
Эти простые случаи помогают проверить эту интерпретацию скалярного произведения.
Практическая задача: Вычислите длины следующих векторов.
а. б. 3 i + 2 j – k c.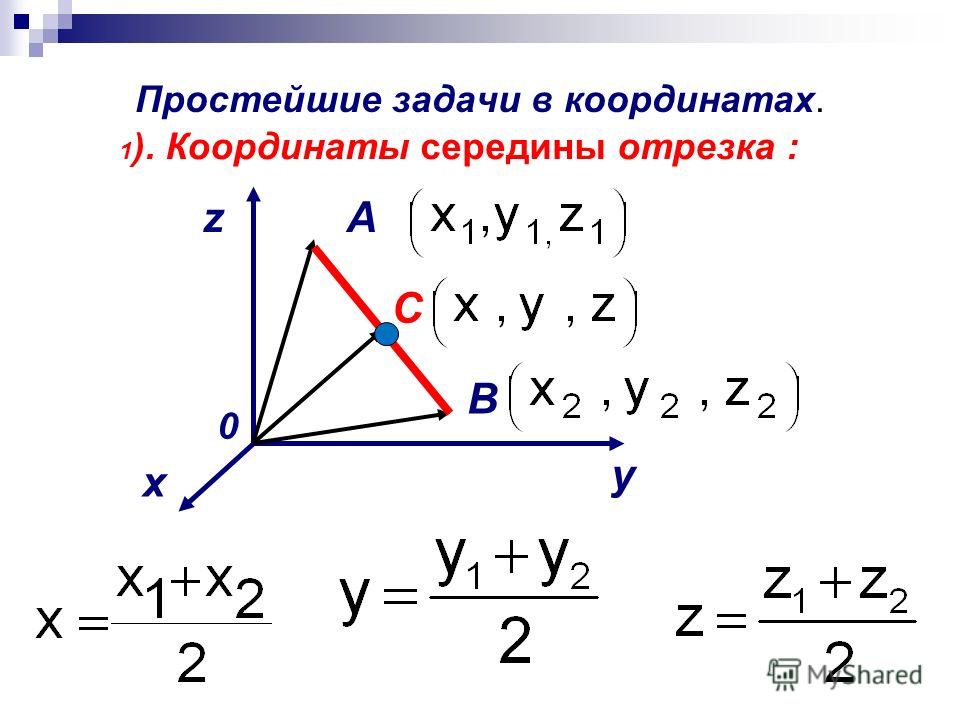 (2, –1) д. 5 к
(2, –1) д. 5 к
Решение: В каждом случае просто возьмите квадратный корень из скалярного произведения вектора на самого себя. Результатом является длина вектора в каждом случае. Для части b просто расширьте определение скалярного произведения до трех измерений.
а.
б.
c.
д.
Операции над векторами, сложение векторов, умножение векторов на действительное число.
Рассмотрим вектор v, начальная точка которого начало координат в xy-системе координат, а конечная точка . Мы говорим, что вектор находится в стандартной позиции и называем его вектором положения. Обратите внимание, что упорядоченная пара однозначно определяет вектор. Таким образом, мы можем использовать для обозначения вектора.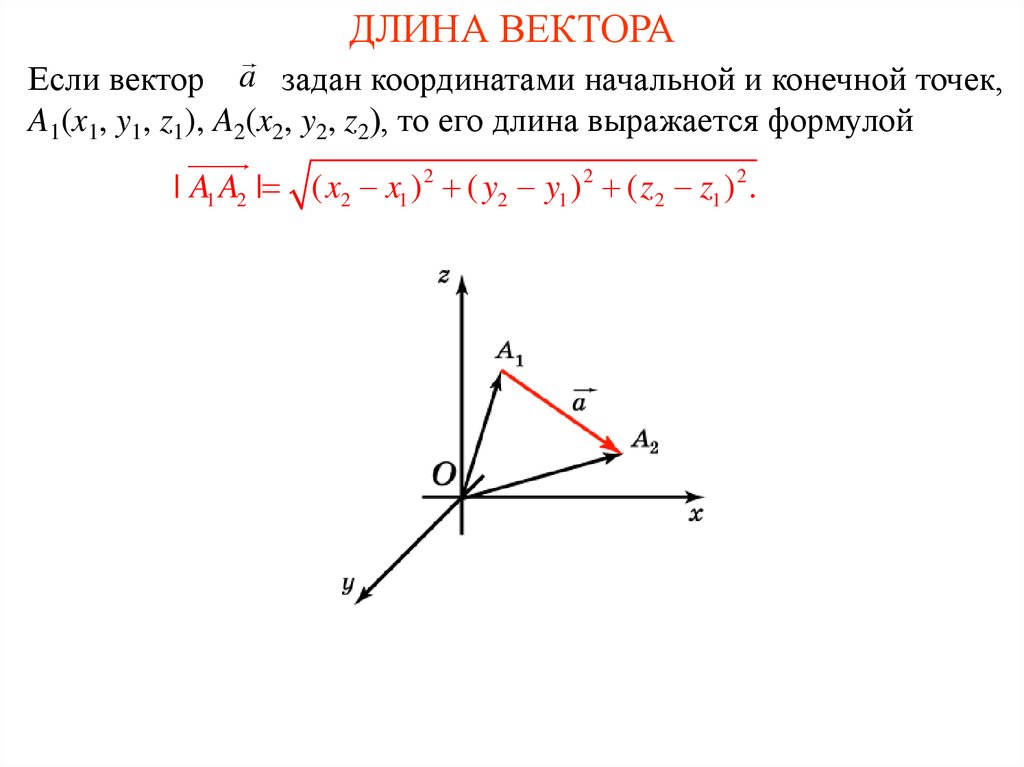 Чтобы подчеркнуть, что мы думаем о векторе, и избежать путаницы с упорядоченно-парными и интервальными обозначениями, мы обычно пишем
Чтобы подчеркнуть, что мы думаем о векторе, и избежать путаницы с упорядоченно-парными и интервальными обозначениями, мы обычно пишем
v = .
Координата a является скалярной горизонтальной составляющей вектора, а координата b является скалярной вертикальной составляющей вектора. Под скаляром мы подразумеваем числовую величину, а не векторную величину. Таким образом, считается компонентом формы v. Обратите внимание, что a и b НЕ являются векторами, и их не следует путать с определением компонента вектора.
Теперь рассмотрим с A = (x 1 , y 1 ) и C = (x 2 , y 2 ). Давайте посмотрим, как найти вектор положения, эквивалентный . Как вы можете видеть на рисунке ниже, начальная точка A перемещена в начало координат (0, 0). Координаты P находятся путем вычитания координат A из координат C. Таким образом, P = (x 2 — x 1 , y 2 — y 1 ), а вектор положения равен .
Можно показать, что и имеют одинаковую величину и направление и, следовательно, эквивалентны. Таким образом, = = 2 — х 1 , у 2 — у 1 >.
Форма компонента с A = (x 1 , Y 1 ) и C = (x 2 , Y 2 ) —
= 2 — x 1 1 , y 222222222). — у 1 >.
Пример 1 Найдите компонентную форму, если C = (- 4, — 3) и F = (1, 5).
Решение У нас есть
== .
Обратите внимание, что вектор эквивалентен вектору положения, как показано на рисунке выше.
Теперь, когда мы знаем, как записывать векторы в компонентной форме, давайте переформулируем некоторые определения.
Длину вектора v легко определить, если известны компоненты вектора. Для v = 1, v 2 >, имеем
|v| 2 = v 2 1 + v 2 2 Используя теорему Пифагора
|v| = √v 2 1 + v 2 2 .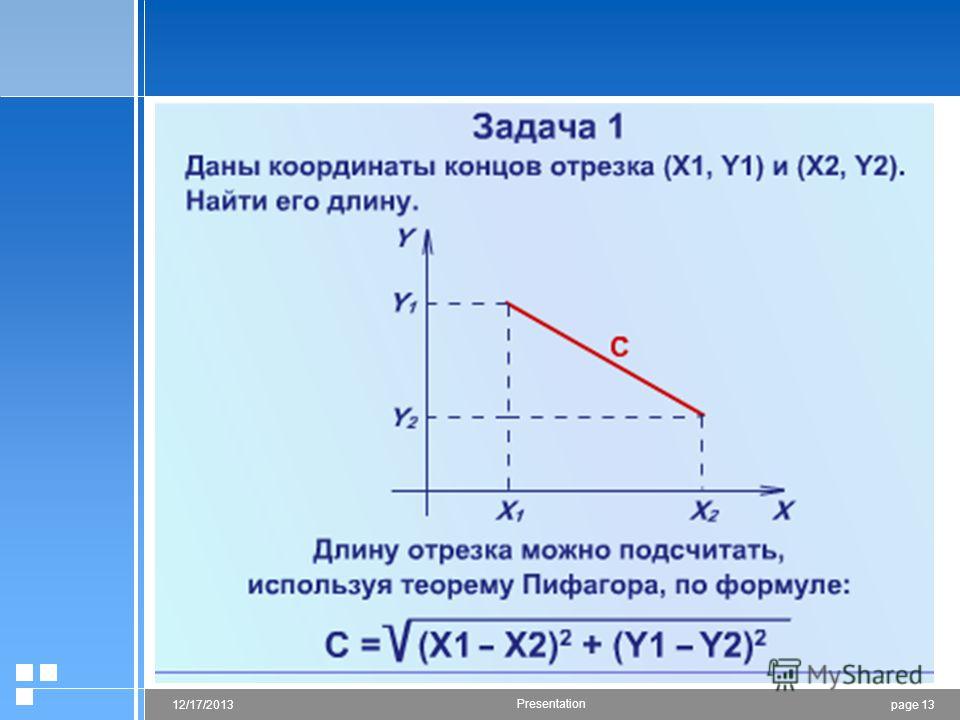
длина или величина вектора v = 1, v 2 > задается как |v| = √v 2 1 + v 2 2 .
Два вектора эквивалентны , если они имеют одинаковую величину и одно и то же направление.
Пусть u = 1, u 2 > и v = 1, v 2 >. Тогда
1, u 2 > = 1, v 2 > тогда и только тогда, когда u 1 = v 1 и и 2 = v 2 .
Операции над векторами
Чтобы умножить вектор v на положительное действительное число, мы умножаем его длину на это число. Его направление остается прежним. Когда вектор v умножается, например, на 2, его длина удваивается, а его направление не меняется. Когда вектор умножается на 1,6, его длина увеличивается на 60%, а направление остается прежним. Чтобы умножить вектор v на отрицательное действительное число, мы умножаем его длину на число и меняем его направление на обратное.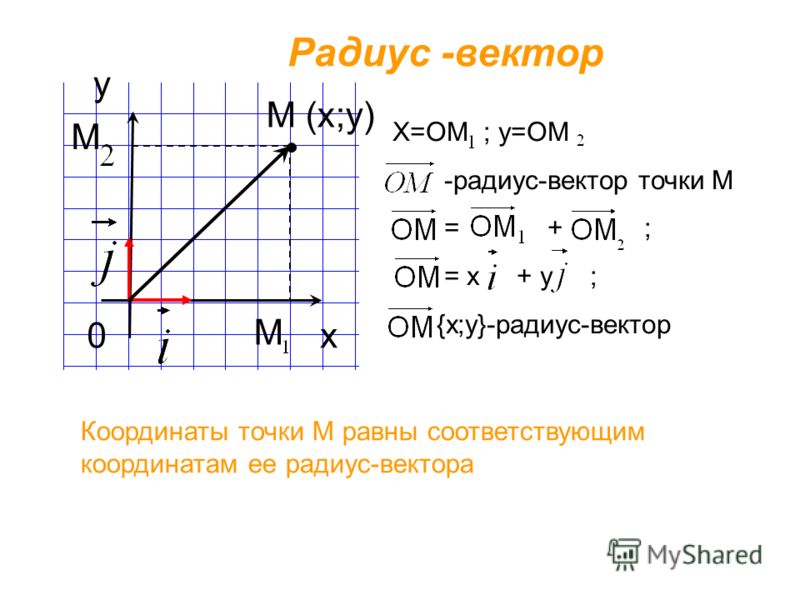 Когда вектор умножается на 2, его длина удваивается, а направление меняется на противоположное. Поскольку действительные числа работают как коэффициенты масштабирования при умножении векторов, мы называем их 9.0528 скаляры и произведения kv называются скалярными множителями v.
Когда вектор умножается на 2, его длина удваивается, а направление меняется на противоположное. Поскольку действительные числа работают как коэффициенты масштабирования при умножении векторов, мы называем их 9.0528 скаляры и произведения kv называются скалярными множителями v.
Для действительного числа k и вектора v = 1, v 2 >, скалярное произведение k и v равно
kv = k.1, v 2 > = 1, kv 2 >.
Вектор kv является скалярным числом, кратным вектора v.
Пример 2 Пусть u = и w = . Найдите — 7w, 3u и — 1w.
Решение
— 7w = — 7. = ,
3u = 3. = ,
— 1w = — 1. = .
Теперь мы можем сложить два вектора, используя компоненты. Чтобы сложить два вектора, заданных в компонентной форме, мы добавляем соответствующие компоненты. Пусть u = 1, u 2 > и v = 1, v 2 >. Тогда
u + v = 1 + v 1 , u 2 + v 2 >
Например, если v = и w = , то
v + w = =
Если u = 1, u 2 > и v = 1, v 2 >, тогда
и + v = 1 + v 1 , и 2 + v 2 >.
Прежде чем мы определим вычитание векторов, нам нужно определить — v. Противоположность v = 1, v 2 >, показанная ниже, равна
— v = (- 1).v = (- 1)1, v 2 > = 1, — v 2 >
Вычитание векторов, таких как u — v, включает вычитание соответствующих компонентов. Мы покажем это, переписав u — v как u + (- v). Если u = 1, u 2 > и v = 1, v 2 >, то
u — v = u + (- v) = 1, u 2 > + 1, — v 2 > = 1 + (- v 1 ), u 2 + (- v 2 ) > = 1 — v 1 , u 2 — v 2 >
Мы можем проиллюстрировать вычитание векторов параллелограммами так же, как мы делали сложение векторов.
Вычитание векторов
Если u = 1, u 2 > и v = 1, v 2 >, то
u — v = 1 — v 1 , у 2 — в 2 >.
Интересно сравнить сумму двух векторов с разностью тех же двух векторов в одном и том же параллелограмме. Векторы u + v и u — v являются диагоналями параллелограмма.
Векторы u + v и u — v являются диагоналями параллелограмма.
Пример 3 Выполните следующие вычисления, где u = и v = .
а) и + в
б) и — 6в
в) 3и + 4в
г) |5в — 2и|
Раствор
а) u + v = + = = ;
б)и — 6в = — 6. = — = ;
в) 3и + 4в = 3. + 4. = + = ;
г) |5в — 2у| = |5. — 2.| = | — | = || = √(- 29) 2 + 21 2 = √1282 ≈ 35,8
Прежде чем мы сформулируем свойства векторного сложения и скалярного умножения, нам нужно определить еще один специальный вектор — нулевой вектор. Вектор, начальная и конечная точки которого оба являются нулевым вектором , обозначается как O или . Его величина равна 0. При сложении векторов нулевой вектор является вектором аддитивной идентичности:
v + O = v. 1, v 2 > + = 1, v 2 >
Операции над векторами во многом схожи с операциями над действительными числами.
Для всех векторов u, v и w и для всех скаляров b и c:
1. u + v = v + u.
u + v = v + u.
2. и + (v + w) = (u + v) + w.
3. v + O = v.
4 1.v = v; 0.v = O.
5. v + (-v) = O.
6. b(cv) = (bc)v.
7. (b + c)v = bv + cv.
8. b(u + v) = bu + bv.
Единичные векторы
Вектор величины или длины 1 называется единичным вектором . Вектор v = является единичным, поскольку
|v| = || = √(- 3/5) 2 + (4/5) 2 = √9/25 + 16/25 = √25/25 = √1 = 1,
Пример 4 Найдите единичный вектор, который имеет то же направление, что и вектор w = .
Решение Сначала найдем длину w:
|w| = √(- 3) 2 + 5 2 = √34. Таким образом, нам нужен вектор, длина которого составляет 1/√34 длины w, а направление совпадает с направлением вектора w. Этот вектор равен
u = w/√34 = /√34 = .
Вектор u является единичным, поскольку
|u| = | ш / √ 34 | = = √9/34 + 25/34 = √34/34 = √1 = 1,
Если v — вектор и v ≠ O, то
(1/|v|) • v, или v/|v|,
— это единичный вектор в направлении v.
Хотя единичные векторы могут иметь любое направление, единичные векторы, параллельные осям x и y, особенно полезны. Они определены как
i = и j = .
Любой вектор может быть выражен как линейная комбинация единичных векторов i и j. Например, пусть v = 1, v 2 >. Тогда
v = 1, v 2 > = 1, 0 > + 2 > = v 1 + v 2 = v 1 i + v 2 j.
Пример 5 Выразите вектор r = в виде линейной комбинации i и j.
Решение
r = = 2i + (- 6)j = 2i — 6j.
Пример 6 Запишите вектор q = — i + 7j в компонентной форме.
Решение q = — i + 7j = -1i + 7j =
Операции с векторами также можно выполнять, когда векторы записываются как линейные комбинации i и j.
Пример 7 Если a = 5i — 2j и b = -i + 8j, найти 3a — b.
Раствор
3a — b = 3(5i — 2j) — (- i + 8j) = 15i — 6j + i — 8j = 16i — 14j.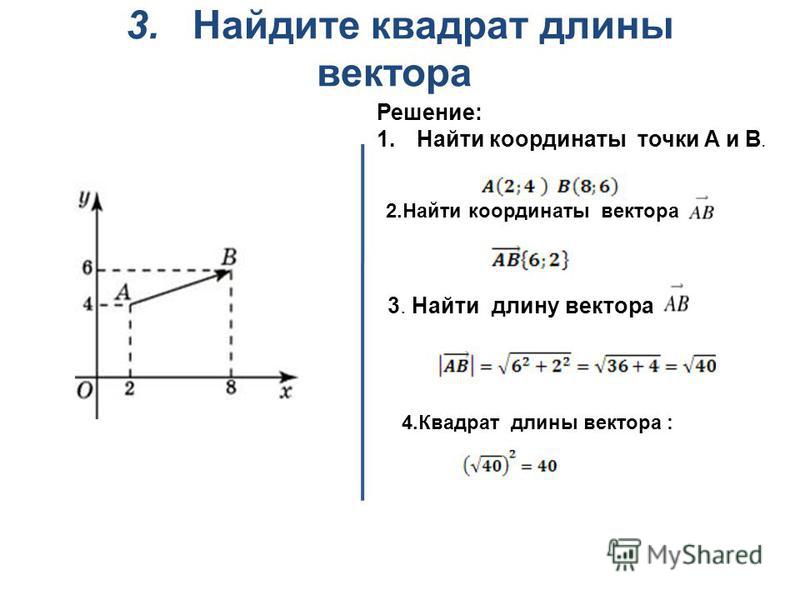
Углы направления
Конечная точка P единичного вектора в стандартном положении — это точка на единичной окружности, обозначенная (cosθ, sinθ). Таким образом, единичный вектор может быть выражен в компонентной форме
u = ,
или как линейная комбинация единичных векторов i и j,
u = (cosθ)i + (sinθ)j,
где компоненты u являются функциями направления угла θ, измеренного против часовой стрелки от оси x к вектору. Поскольку θ изменяется от 0 до 2π, точка P описывает окружность x 2 + y 2 = 1. Это принимает во всех возможных направлениях единичные векторы, поэтому уравнение u = (cosθ)i + (sinθ)j описывает каждый возможный единичный вектор на плоскости.
Пример 8 Вычислите и зарисуйте единичный вектор u = (cosθ)i + (sinθ)j для θ = 2π/3. Включите единичный круг в свой эскиз.
Решение
u = (cos(2π/3))i + (sin(2π/3))j = (- 1/2)i + (√3/2)j
Пусть v = 1, v 2 > с дирекционным углом θ. Используя определение функции тангенса, мы можем определить направляющий угол по составляющим v:
Используя определение функции тангенса, мы можем определить направляющий угол по составляющим v:
Пример 9 Определить направляющий угол θ вектора w = — 4i — 3j.
Решение Мы знаем, что
w = — 4i — 3j = .
Таким образом, мы имеем
тангенс θ = (- 3)/(- 4) = 3/4 и θ = тангенс — 1 (3/4).
Поскольку w находится в третьем квадранте, мы знаем, что θ является углом третьего квадранта. Опорный угол равен
tan — 1 (3/4) ≈ 37°, и θ ≈ 180° + 37° или 217°.
Удобно для работы с прикладными задачами и в последующих курсах, таких как исчисление, иметь способ выразить вектор так, чтобы можно было легко определить или прочитать как его величину, так и его направление. Пусть v — вектор. Тогда v/|v| является единичным вектором в том же направлении, что и v. Таким образом, мы имеем
в/|в| = (cosθ)i + (sinθ)j
v = |v|[(cosθ)i + (sinθ)j] Умножение на |v|
v = |v|(cosθ)i + |v|(sinθ)j.
Пример 10 Скорость и направление полета самолета. Самолет движется по азимуту 100° со скоростью 190 км/ч при скорости ветра 48 км/ч с направления 220°. Найдите путевую скорость самолета и направление его следа или курса относительно земли.
Решение Сначала делаем чертеж. Ветер представлен, а вектор скорости самолета — . Результирующий вектор скорости есть v, сумма двух векторов:
v = + .
Азимут (измеренный с севера) вектора воздушной скорости составляет 100°. Его направляющий угол (измеряемый против часовой стрелки от положительной оси абсцисс) равен 350°. Азимут (измеренный с севера) вектора ветра составляет 220°. Его направляющий угол (отсчитываемый против часовой стрелки от положительной оси x) равен 50°. Величины и равны 190 и 48 соответственно. Имеем
= 190(cos350°)i + 190(sin350°)j и
= 48(cos50°)i + 48(sin50°)j.
Таким образом,
v = +
= [190(cos350°)i + 190(sin350°)j] + [48(cos50°)i + 48(sin50°)j]
= [190(cos350°)i + 48(cos50°)i] + [ 190(sin350°)j + 48(sin50°)j]
≈ 217,97i + 3,78j.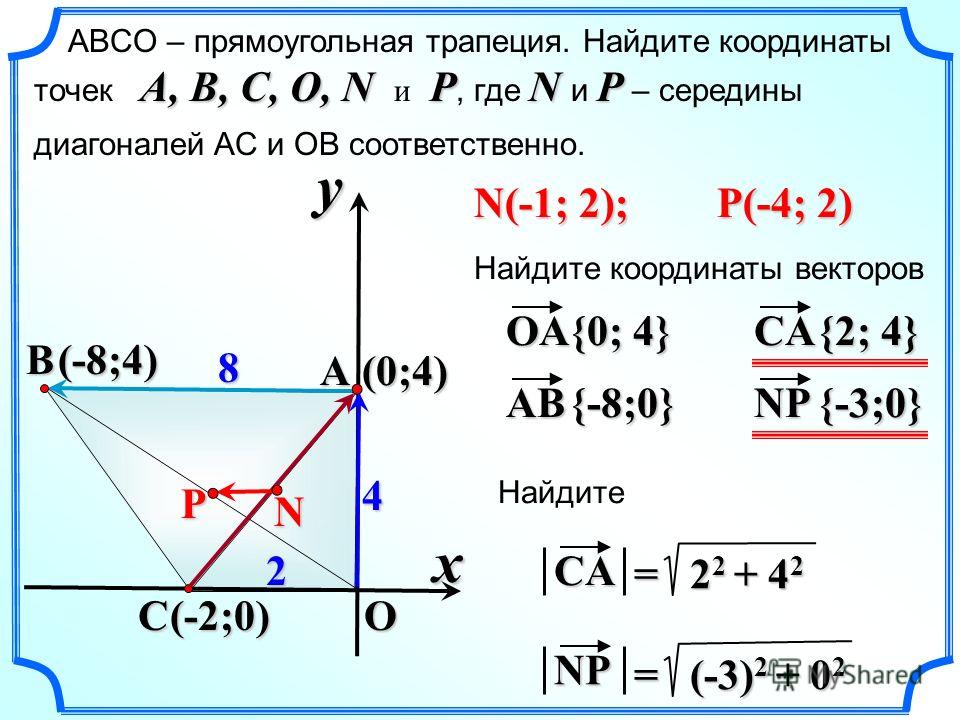
Из этой формы мы можем определить путевую скорость и курс:
Путевая скорость ≈ √(217,97) 2 + (3,78) 2 ≈ 218 км/ч.
Пусть α будет углом направления v. Тогда
tanα = 3,78/217,97
α = tan — 1 3,78/217,97 ≈ 1°.
Таким образом, курс самолета (направление с севера) равен 90° — 1° или 89°.
Угол между векторами
Когда вектор умножается на скаляр, результатом является вектор. При сложении двух векторов результатом также является вектор. Таким образом, мы могли бы ожидать, что произведение двух векторов тоже будет вектором, но это не так. скалярное произведение двух векторов является действительным числом или скаляром. Этот продукт полезен при нахождении угла между двумя векторами и при определении того, перпендикулярны ли два вектора.
скалярное произведение двух векторов u = 1, u 2 > и v = 1, v 2 > равно
u • v = u 1 .v 1 + u 2 .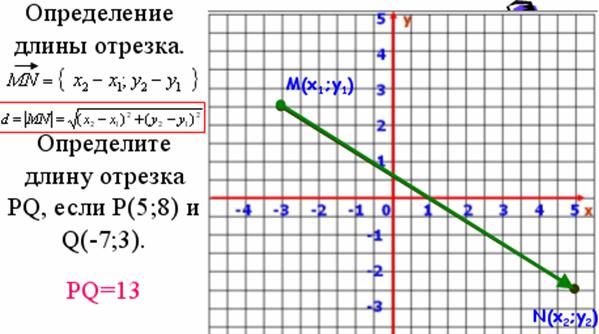 2 .
2 .
(Обратите внимание, что u 1 v 1 + u 2 v 2 является скаляром , а не вектором.)
Пример 11 Найдите указанное скалярное произведение, когда
u = , v = и w = .
а)у • ш
б) ш • в
Раствор
а) и • ш = 2(- 3) + (- 5)1 = — 6 — 5 = — 11;
б) ш • v = (- 3)0 + 1(4) = 0 + 4 = 4.
Скалярное произведение можно использовать для нахождения угла между двумя векторами. Угол между двумя векторами является наименьшим положительным углом, образованным двумя направленными отрезками прямой. Таким образом, угол θ между u и v — это тот же угол, что и между v и u, и 0 ≤ θ ≤ π.
Если θ — угол между двумя ненулевыми векторами u и v, то
cosθ = (u • v)/|u||v|.
Пример 12 Найдите угол между u = и v = .
Решение Начнем с нахождения u • v, |u| и |v|:
u • v = 3(- 4) + 7(2) = 2,
|u| = √3 2 + 7 2 = √58 и
|v| = √(- 4) 2 + 2 2 = √20.
Тогда
cosα = (u • v)/|u||v| = 2/√58,√20
α = cos — 1 (2/√58,√20)
α ≈ 86,6°.
Силы в равновесии
Когда несколько сил действуют через одну и ту же точку на объекте, их векторная сумма должна быть равна O, чтобы возник баланс. Когда возникает равновесие, то объект либо неподвижен, либо движется прямолинейно без ускорения. Тот факт, что для баланса векторная сумма должна быть равна O, и наоборот, позволяет решать многие прикладные задачи, связанные с силами.
Пример 13 Подвесной блок. Блок весом 350 фунтов подвешен на двух тросах, как показано слева. В точке А действуют три силы: W, тянущая блок вниз, и R и S, два троса, тянущие вверх и наружу. Найдите натяжение каждого троса.
Решение Рисуем силовую диаграмму с начальными точками каждого вектора в начале координат. Чтобы был баланс, сумма векторов должна быть вектором O:
R + S + W = O.
Мы можем выразить каждый вектор через его величину и угол направления:
R = |R|[(cos125°)i + (sin125°)j],
S = |S|[(cos37°)i + (sin37°)j] и
W = |W|[(cos270 °)i + (sin270°)j]
= 350(cos270°)i + 350(sin270°)j
= -350j cos270° = 0; sin270° = — 1.