Онлайн калькулятор матриц метод крамера: Онлайн калькулятор. Решение систем линейных уравнений. Метод Крамера

Метод крамера подробное решение. Метод крамера решения систем линейных уравнений

В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.

А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера.

Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

;

Ответ : ,

Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод,

обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .

Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений

x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .

А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!

2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:

Сделаем аналогичное действие, заменив в первом определителе второй столбец:

Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.

Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Решение систем методом подстановки.

Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.

и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Применять формулы Крамера нельзя. Решим эту систему методом подстановки

Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет

Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.

Теорема 1

Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений: $x_i = \frac{D_i}{D}$

В чем заключается метод Крамера

Суть метода Крамера в следующем:

1. Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
2. Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
3. Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ — номер крайнего справа столбца.
4. После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.

Приёмы для вычисления определителя матрицы

Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:

• Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей — со знаком минус.

Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера

• С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
• При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.

Решение систем уравнений методом Крамера

Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:

$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$

Отобразим её в расширенной форме для удобства:

$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$

Найдём определитель основной матрицы, также называемый главным определителем системы:

$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$

Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:

$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$

$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$

Теперь найдём неизвестные $x_1$ и $x_2$:

$x_1 = \frac {D_1}{D}$

$x_2 = \frac {D_2}{D}$

Пример 1

Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.

Решите систему уравнений:

$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 — x_3 = 10 \\ \end{cases}$

Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:

$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 3 = — 12 – 8 -12 -32 – 6 + 6 = — 64$

А теперь три других детерминанта:

$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 21 = — 84 – 40 – 36 – 160 – 18 + 42 = — 296$

$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = — 27 + 120 + 84 – 72 + 63 – 60 = 108$

$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 — (-2) \cdot 3 \cdot 10 — (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = — 60$

Найдём искомые величины:

$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$

$x_2 = \frac{D_1} {D} = \frac{108} {-64} = — 1 \frac {11} {16}$

$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

.

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

.

На основании теоремы Крамера

………….
,

где
—

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы — (2; -1; 1).

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко ходить не надо.

Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Калькулятор системы уравнений — MathCracker.com

Инструкции: Используйте этот калькулятор системы уравнений для решения предоставленной вами общей системы уравнений с тем же количеством уравнений и переменных, показывающим все шаги. Сначала нажмите на одну из кнопок ниже, чтобы указать размерность системы (количество уравнений и переменных). Например, «2×2» означает «2 уравнения и 2 переменные».

Затем заполните коэффициенты, связанные со всеми переменными и правым размером, для каждого из уравнений. Если переменная отсутствует в одном конкретном уравнении, введите «0» или оставьте поле пустым.

Подробнее об этом решателе системы уравнений

Этот калькулятор позволяет вычислить решение системы линейных уравнений при условии, что количество уравнений совпадает с количеством переменных, и вы можете определить систему до пяти переменных и пяти уравнений.

Решение системы уравнений может быть трудоемким и требует большого количества вычислений, особенно для больших систем.

Как решить систему уравнений

Существует несколько стратегий, но чаще всего используются следующие:

• графический метод
• метод замены
• метод исключения

Эти методы широко используются, особенно для системы 2×2 (это системы с 2 переменными и 2 уравнениями). Проблема с этими методами заключается в том, что они становятся громоздкими для больших систем.

А графический метод применим только для систем 2х2. Для больших систем можно использовать более систематические правила, такие как исключение Гаусса и Метод Крамера .

Существует несколько методов, которые можно использовать для вычисления решений систем линейных уравнений, но мы предпочитаем использовать Правило Крамера подход, так как это один из самых простых способов вспомнить расчет решений системы.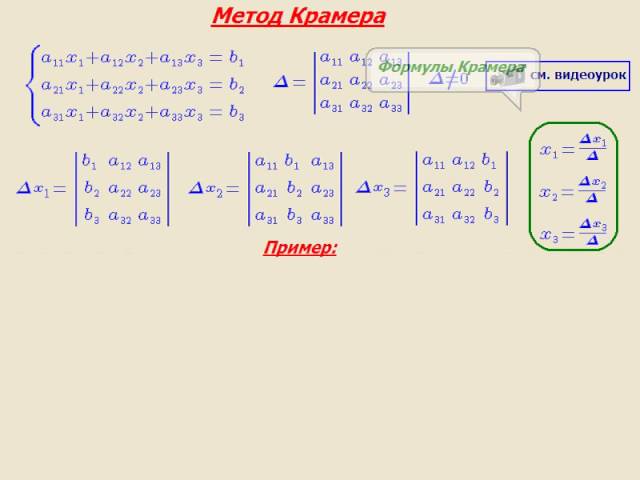

Как решить систему уравнений с помощью этого калькулятора

1. Определите размер системы (количество переменных и количество уравнений). Варианты: системы 2×2, 3×3, 4×4 и 5×5.
2. После того, как размер указан, вам нужно указать коэффициенты, связанные с каждой переменной.
3. Если коэффициент не используется, оставьте его пустым или введите 0
4. Нажмите «Рассчитать», и этот решатель покажет вам все шаги и решения.

Правило Крамера тесно связано с этим калькулятор решений системы уравнений с использованием матриц , так что вы также можете использовать этот маршрут.

Это решатель системы 5 уравнений?

Да, с помощью этого решателя вы можете получить решения систем, содержащих до 5 уравнений и 5 переменных. Методика для большего количества переменных и уравнений на самом деле не меняется, но ручные вычисления становятся очень длинными. Таким образом, для более чем 5 уравнений вы можете решить их с помощью компьютера.

Как решить систему уравнений с помощью этого решателя?

Шаг 1: Вам нужно указать систему уравнений, которую вы хотите решить, заполнив пропуски коэффициентами системы. Обратите внимание, что если в уравнении нет переменной, ее коэффициент должен быть равен нулю.

Шаг 2: Просто нажмите «Рассчитать», и этот решатель сделает все остальное. Сначала калькулятор найдет форму матрицы.

Шаг 3: Решатель вычислит определитель матрицы A. Если det(A) = 0, мы знаем, что система не будет иметь единственного решения.

Шаг 4: Калькулятор вычислит сопряженную матрицу. j) }{\det(A)}\]

Итак, как бы вы решили уравнение с 6 переменными?

Это был бы точно такой же подход, только вычисление сопряженной матрицы было бы потенциально очень трудоемким. Вам было бы лучше использовать CAS, такую как Mathematica или Matlab, чтобы получать решения, пропуская все шаг за шагом, что может быть слишком обширным.

Можно ли использовать Excel для решения системы уравнений?

Технически вы можете, используя некоторые специальные групповые функции, такие как «=MMULT», но обычно средний пользователь Excel обычно не знает, как это сделать.

Преимущество этого решателя системы уравнений с шагами заключается в том, что все, что вам нужно сделать, это указать Система уравнений вы хотите решить, используя визуально интуитивно понятный из.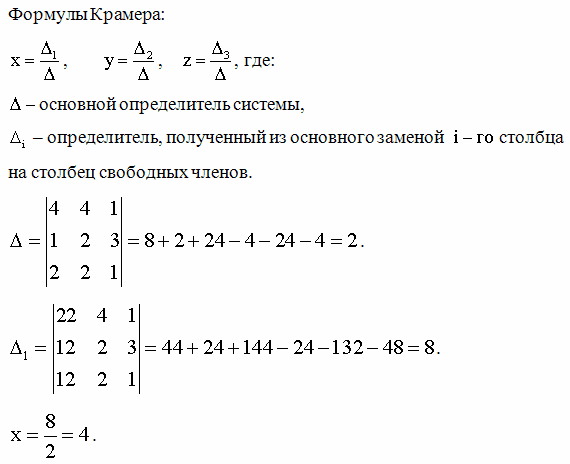 С этого момента все, что вам нужно сделать, это нажать «Рассчитать», чтобы получить пошаговый расчет.

Пример решения системы уравнений

Рассмотрим следующую систему уравнений

\[ \begin{aligned} 2 x&\, + \, &3 y&\, + \, & z & \, = \,3\\2 x&\, + \, &2 y&\, + \, &4 z & \, = \,1\\ x&\, + \, & y&\, + \, & z & \, = \,2 \end{aligned}\]

Решите приведенную выше систему, используя правило Крамера, показав все шаги.

Отвечать: Была предоставлена система линейных уравнений \(3 \times 3\).

Шаг 1: Найдите соответствующую матричную структуру

Первый шаг состоит в нахождении соответствующей матрицы \(A\) и вектора \(b\), которые позволяют записать систему в виде \(A x = b\).

В этом случае и исходя из коэффициентов приведенных уравнений получаем, что

\[ A = \begin{bmatrix} \displaystyle 2&\displaystyle 3&\displaystyle 1\\[0.6em]\displaystyle 2&\displaystyle 2&\displaystyle 4\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 1 \end{bmatrix} \]

и

\[ b = \begin{bmatrix} \displaystyle 3\\[0. 6em]\displaystyle 1\\[0.6em]\displaystyle 2 \end{bmatrix} \]

Шаг 2: вычислить определитель матрицы

Теперь нам нужно вычислить определитель \(A\), чтобы узнать, можем ли мы использовать правило Крамера:

По формуле субдетерминанта получаем:

\[ \begin{vmatrix} \displaystyle 2&\displaystyle 3&\displaystyle 1\\[0.6em]\displaystyle 2&\displaystyle 2&\displaystyle 4\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 1 \end{vmatrix} = 2 \cdot \left( 2 \cdot \left( 1 \right) — 1 \cdot \left(4 \right) \right) — 3 \cdot \left( 2 \cdot \left( 1 \right) — 1 \cdot \left(4 \right) \right) + 1 \cdot \left( 2 \cdot \left( 1 \right) — 1 \cdot \left(2 \right) \right)\] \[ = 2 \cdot \left( -2 \right) — 3 \cdot \left( -2 \right) + 1 \cdot \left( 0 \right) = 2\]

Поскольку \(\det(A) = \displaystyle 2 \ne 0\), мы заключаем, что матрица обратима, и мы можем продолжить использование правила Крамера. j\) точно соответствует матрице \(A\), за исключением того, что столбец j заменен на \(b\).

Для \(x\):

По формуле субдетерминанта получаем:

\[ \begin{vmatrix} \displaystyle 3&\displaystyle 3&\displaystyle 1\\[0.6em]\displaystyle 1&\displaystyle 2&\displaystyle 4\\[0.6em]\displaystyle 2&\displaystyle 1&\displaystyle 1 \end{vmatrix} = 3 \cdot \left( 2 \cdot \left( 1 \right) — 1 \cdot \left(4 \right) \right) — 3 \cdot \left( 1 \cdot \left( 1 \right) — 2 \cdot \left(4 \right) \right) + 1 \cdot \left( 1 \cdot \left( 1 \right) — 2 \cdot \left(2 \right) \right)\] \[ = 3 \cdot \left( -2 \right) — 3 \cdot \left( -7 \right) + 1 \cdot \left( -3 \right) = 12\]

Теперь мы находим, что по формуле Крамера \(x\) вычисляется как

\[x = \displaystyle \frac{\det(A^{ 1}) }{\det(A)} = \displaystyle \frac{ \begin{vmatrix} \displaystyle 3&\displaystyle 3&\displaystyle 1\\[0. 6em]\displaystyle 1&\displaystyle 2&\displaystyle 4\\[0.6em]\displaystyle 2&\displaystyle 1&\displaystyle 1 \end{vmatrix} }{ \begin{vmatrix} \displaystyle 2&\displaystyle 3&\displaystyle 1\\[0.6em]\displaystyle 2&\displaystyle 2&\displaystyle 4\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 1 \end{vmatrix} } = \displaystyle \frac{ \displaystyle 12 }{ \displaystyle 2} = 6 \]

Для \(y\):

По формуле субдетерминанта получаем:

\[ \begin{vmatrix} \displaystyle 2&\displaystyle 3&\displaystyle 1\\[0.6em]\displaystyle 2&\displaystyle 1&\displaystyle 4\\[0.6em]\displaystyle 1&\displaystyle 2&\displaystyle 1 \end{vmatrix} = 2 \cdot \left( 1 \cdot \left( 1 \right) — 2 \cdot \left(4 \right) \right) — 3 \cdot \left( 2 \cdot \left( 1 \right) — 1 \cdot \left(4 \right) \right) + 1 \cdot \left( 2 \cdot \left( 2 \right) — 1 \cdot \left(1 \right) \right)\] \[ = 2 \cdot \left( -7 \right) — 3 \cdot \left( -2 \right) + 1 \cdot \left( 3 \right) = -5\]

Теперь мы находим, что по формуле Крамера \(y\) вычисляется как

\[y = \displaystyle \frac{\det(A^{ 2}) }{\det(A)} = \displaystyle \frac{ \begin{vmatrix} \displaystyle 2&\displaystyle 3&\displaystyle 1\\[0. 6em]\displaystyle 2&\displaystyle 1&\displaystyle 4\\[0.6em]\displaystyle 1&\displaystyle 2&\displaystyle 1 \end{vmatrix} }{ \begin{vmatrix} \displaystyle 2&\displaystyle 3&\displaystyle 1\\[0.6em]\displaystyle 2&\displaystyle 2&\displaystyle 4\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 1 \end{vmatrix} } = \displaystyle \frac{ \displaystyle -5 }{ \displaystyle 2} = -\frac{5}{2} \]

Для \(z\):

По формуле субдетерминанта получаем:

\[ \begin{vmatrix} \displaystyle 2&\displaystyle 3&\displaystyle 3\\[0.6em]\displaystyle 2&\displaystyle 2&\displaystyle 1\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 2 \end{vmatrix} = 2 \cdot \left( 2 \cdot \left( 2 \right) — 1 \cdot \left(1 \right) \right) — 3 \cdot \left( 2 \cdot \left( 2 \right) — 1 \cdot \left(1 \right) \right) + 3 \cdot \left( 2 \cdot \left( 1 \right) — 1 \cdot \left(2 \right) \right)\] \[ = 2 \cdot \left( 3 \right) — 3 \cdot \left( 3 \right) + 3 \cdot \left( 0 \right) = -3\]

Теперь мы находим, что по формуле Крамера \(z\) вычисляется как

\[z = \displaystyle \frac{\det(A^{ 3}) }{\det(A)} = \displaystyle \frac{ \begin{vmatrix} \displaystyle 2&\displaystyle 3&\displaystyle 3\\[0. 6em]\displaystyle 2&\displaystyle 2&\displaystyle 1\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 2 \end{vmatrix} }{ \begin{vmatrix} \displaystyle 2&\displaystyle 3&\displaystyle 1\\[0.6em]\displaystyle 2&\displaystyle 2&\displaystyle 4\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 1 \end{vmatrix} } = \displaystyle \frac{ \displaystyle -3 }{ \displaystyle 2} = -\frac{3}{2} \]

Следовательно, и резюмируя, решение

\[ \begin{bmatrix} \displaystyle x\\\\\displaystyle y\\\\\displaystyle z \end{bmatrix} = \begin{bmatrix} \displaystyle 6\\\\\displaystyle -\frac{ 5}{ 2}\\\\\displaystyle -\frac{ 3}{ 2} \end{bmatrix} \]

что завершает вычисление решений для данной линейной системы.

Решить слу методом крамера. Линейные уравнения. Решение систем линейных уравнений. Метод Крамера. В чем заключается метод Крамера

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

.

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

.

На основании теоремы Крамера

………….
,

где
—

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы — (2; -1; 1).

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко ходить не надо.

Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .

А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!

Рассмотрим систему 3-х уравнений с тремя неизвестными

Используя определители 3-го порядка, решение такой системы можно записать в таком же виде, как и для системы двух уравнений, т. е.

(2.4)

если 0. Здесь

Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .

Пример 2.3. Решить систему линейных уравнений при помощи правила Крамера:

Решение . Находим определитель основной матрицы системы

Поскольку 0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще три определителя:

Проверка:

Следовательно, решение найдено правильно. 

Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, наводят на мысль, что такие же правила можно сформулировать и для линейных систем любого порядка. Действительно имеет место

Теорема Крамера. Квадратная система линейных уравнений с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение и это решение вычисляется по формулам

(2.5)

где  – определитель основной матрицы ,  i – определитель матрицы , полученной из основной, заменой i -го столбца столбцом свободных членов .

Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо не имеет вообще решений, либо имеет бесконечно много решений.

Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.

2.4. Определители n-го порядка

Дополнительным минором M ij элемента a ij называется определитель, получаемый из данного путем вычеркивания i -й строки и j -го столбца. Алгебраическим дополнением A ij элемента a ij называется минор этого элемента, взятого со знаком (–1) i + j , т.е. A ij = (–1) i + j M ij .

Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя

Получаем



Используя понятие алгебраического дополнения можно сформулировать теорему о разложении определителя n -го порядка по строке или столбцу .

Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:

(2.6)

Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка . В результате разложения определителя n -го порядка по какой-либо строке или столбцу, получается n определителей (n –1)-го порядка. Чтобы таких определителей было меньше, целесообразно выбирать ту строку или столбец, в которой больше всего нулей. На практике формулу разложения определителя обычно записывают в виде:

т.е. алгебраические дополнения записывают в явном виде через миноры.

Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.



2.

5. Основные свойства определителей

Разлагая определитель по какой-либо строке или столбцу, мы получим n определителей (n –1)-го порядка. Затем каждый из этих определителей (n –1)-го порядка также можно разложить в сумму определителей (n –2)-го порядка. Продолжая этот процесс, можно дойти до определителей 1-го порядка, т.е. до элементов матрицы, определитель которой вычисляется. Так, для вычисления определителей 2-го порядка придется вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых. Число слагаемых будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, непосильной даже для ЭВМ. Однако вычислять определители можно и по-другому, используя свойства определителей.

Свойство 1 . Определитель не изменится, если в нем поменять местами строки и столбцы, т. е. при транспонировании матрицы :

.

Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.

Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).

Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.

Свойство 3 . Общий множитель всех элементов в какой-либо строке (столбце) можно вынести за знак определителя .

Например,

Следствие . Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю .

Свойство 4 . Определитель не изменится, если к элементам одной строки (столбца), прибавить элементы другой строки (столбца), умноженной на какое-либо число .

Например,

Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:

В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.

А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

;

Ответ : ,

Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

Решение систем квадратных уравнений по формулам крамера.

Линейные уравнения

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

.

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

.

На основании теоремы Крамера

………….
,

где
—

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы — (2; -1; 1).

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко ходить не надо.

Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т.е. имеет вид

Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,

. (1.6)

Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:

(j = 1, 2, …, n ). (1.7)

Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:

(1.8)

Пример 1.5. Методом Крамера решить систему уравнений

.

Вычислим главный определитель системы:

Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):

Таким образом,

Действия над матрицами

1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.

2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть

. (1.9)

Пример 1.6. .

Сложение матриц.

Данная операция вводится только для матриц одного и того же порядка.

Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:

(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.

Пример 1.7. .

Умножение матриц.

Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:

2

Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:

Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :

Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :

2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .

Обратная матрица. Решение систем линейных уравнений матричным способом

Матрица A — 1 называется обратной к квадратной матрице А , если выполнено равенство:

где через I обозначается единичная матрица того же порядка, что и матрица А :

.

Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:

, (1.13)

где A ij — алгебраические дополнения к элементам a ij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).

Пример 1.9. Найти обратную матрицу A — 1 к матрице

.

Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:

.

Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 — 3 × 3 × 3 — 1 × 5 × 4 — 2 × 2 × 8 = 24 + 30 + 24 — 27 — 20 — 32 = — 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.

1) Найдем алгебраические дополнения A ij :

Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.

Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:

Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:

где

Умножая обе части равенства (1.14) слева на A — 1 , мы получим решение системы:

, откуда

Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.

Задача 1.10. Решить систему линейных уравнений

с помощью обратной матрицы.

Решение. Запишем систему в матричном виде: ,

где — основная матрица системы, — столбец неизвестных и — столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :

Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:

Решение системы находим по формуле (1.15):

Таким образом,

Решение систем линейных уравнений методом обыкновенных жордановых исключений

Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:

(1.16)

Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.

При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.

Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.

Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.

В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.

Пример 1.11.

x

После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:

Выразим y из второго уравнения и подставим его в первое уравнение:

Запомним второе уравнение, а из первого найдем z :

Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :

.

Затем подставим и в первое запомненное уравнение , откуда найдем x :

Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:

. (1.17)

Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

.

Запомним первое уравнение

В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.

Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.

Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.

Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:

. (1.18)

Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

.

Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:

Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.

В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда

Подставим y и z в первое запомненное равенство и найдем x :

.

Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :

(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1.18).

В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.

Пусть дана система линейных форм (уравнений):

, (1.20)
где x j — независимые (искомые) переменные, a ij — постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.

Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.

Мы получим следующую систему:

. (1.21)

Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.

Вычислим коэффициенты полученной системы (1. 21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:

Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:

(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):

После приведения подобных членов, получим:

(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):

(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».

Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:

Таблица 1. 1

	x 1	x 2	…	x j	…	x s	…	x n
y 1 =	a 11	a 12		a 1j		a 1s		a 1n
…………………………………………………………………..
y i =	a i 1	a i 2		a ij		a is		a in
…………………………………………………………………..
y r =	a r 1	a r 2		a rj		a rs		a rn
………………………………………………………………….
y n =	a m 1	a m 2		a mj		a ms		a mn

Жорданова таблица 1. 1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.

Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:

Таблица 1.2

	x 1	x 2	…	x j	…	y r	…	x n
y 1 =	b 11	b 12		b 1 j		b 1 s		b 1 n
…………………………………………………………………. .
y i =	b i 1	b i 2		b ij		b is		b in
…………………………………………………………………..
x s =	b r 1	b r 2		b rj		b rs		b rn
………………………………………………………………….
y n =	b m 1	b m 2		b mj		b ms		b mn

Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.

Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).

1. Разрешающий элемент заменяется обратным числом:

2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:

3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:

4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:

Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:

-21-26-13-37

Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т.к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.

Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1.4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: x 1 = — 3 + 2x 5 .

Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:

Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:

x 1 = — 3 + 2t

x 2 = — 1 — 3t

x 3 = — 2 + 4t . (1.27)
x 4 = 4 + 5t

x 5 = t

Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; — 1; — 2; 4; 0).

С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).

Теорема Крамера.

Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :

где Δ — определитель матрицы системы ,

Δ i — определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.

Когда определитель системы нулевой, значит, система может стать совместной или несовместной.

Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.

Описание метода Крамера.

Есть система уравнений:

Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.

Составляем определитель из коэффициентов у неизвестных:

Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:

,,

Решаем систему по формулам Крамера :

Примеры решения систем уравнений методом Крамера.

Пример 1 .

Дана система:

Решим ее методом Крамера.

Сначала нужно вычислить определитель матрицы системы:

Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:

Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .

А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!

Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

;

Ответ : ,

Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.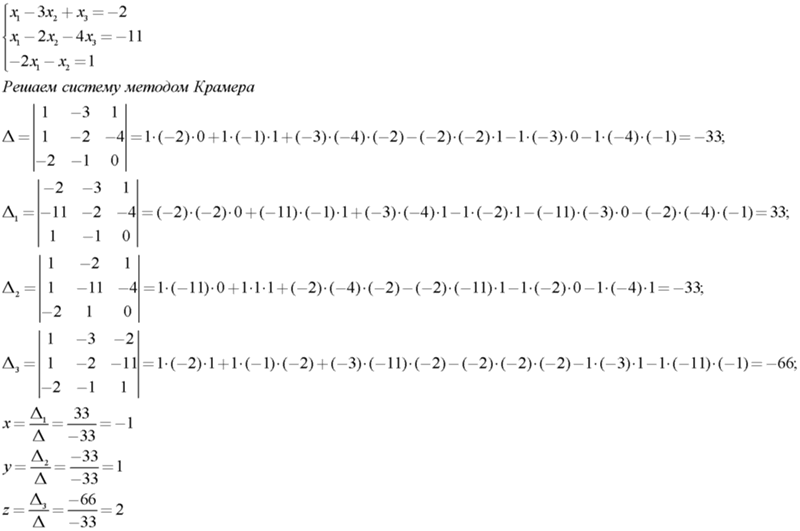

решаем системы линейных алгебраических уравнений (слау)

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .

А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

.

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

.

На основании теоремы Крамера

………….
,

где
—

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы — (2; -1; 1).

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко ходить не надо.

Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:

Сделаем аналогичное действие, заменив в первом определителе второй столбец:

Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.

Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Решение систем методом подстановки.

Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.

и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Применять формулы Крамера нельзя. Решим эту систему методом подстановки

Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет

Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.

Теорема 1

Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений: $x_i = \frac{D_i}{D}$

В чем заключается метод Крамера

Суть метода Крамера в следующем:

1. Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
2. Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
3. Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ — номер крайнего справа столбца.
4. После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.

Приёмы для вычисления определителя матрицы

Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:

• Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей — со знаком минус.

Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера

• С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
• При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.

Решение систем уравнений методом Крамера

Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:

$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$

Отобразим её в расширенной форме для удобства:

$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$

Найдём определитель основной матрицы, также называемый главным определителем системы:

$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$

Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:

$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$

$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$

Теперь найдём неизвестные $x_1$ и $x_2$:

$x_1 = \frac {D_1}{D}$

$x_2 = \frac {D_2}{D}$

Пример 1

Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.

Решите систему уравнений:

$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 — x_3 = 10 \\ \end{cases}$

Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:

$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 3 = — 12 – 8 -12 -32 – 6 + 6 = — 64$

А теперь три других детерминанта:

$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 21 = — 84 – 40 – 36 – 160 – 18 + 42 = — 296$

$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = — 27 + 120 + 84 – 72 + 63 – 60 = 108$

$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 — (-2) \cdot 3 \cdot 10 — (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = — 60$

Найдём искомые величины:

$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$

$x_2 = \frac{D_1} {D} = \frac{108} {-64} = — 1 \frac {11} {16}$

$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$

Рассмотрим систему 3-х уравнений с тремя неизвестными

Используя определители 3-го порядка, решение такой системы можно записать в таком же виде, как и для системы двух уравнений, т. е.

(2.4)

если 0. Здесь

Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .

Пример 2.3. Решить систему линейных уравнений при помощи правила Крамера:

Решение . Находим определитель основной матрицы системы

Поскольку 0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще три определителя:

Проверка:

Следовательно, решение найдено правильно. 

Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, наводят на мысль, что такие же правила можно сформулировать и для линейных систем любого порядка. Действительно имеет место

Теорема Крамера. Квадратная система линейных уравнений с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение и это решение вычисляется по формулам

(2.5)

где  – определитель основной матрицы ,  i – определитель матрицы , полученной из основной, заменой i -го столбца столбцом свободных членов .

Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо не имеет вообще решений, либо имеет бесконечно много решений.

Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.

2.4. Определители n-го порядка

Дополнительным минором M ij элемента a ij называется определитель, получаемый из данного путем вычеркивания i -й строки и j -го столбца. Алгебраическим дополнением A ij элемента a ij называется минор этого элемента, взятого со знаком (–1) i + j , т.е. A ij = (–1) i + j M ij .

Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя

Получаем



Используя понятие алгебраического дополнения можно сформулировать теорему о разложении определителя n -го порядка по строке или столбцу .

Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:

(2.6)

Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка . В результате разложения определителя n -го порядка по какой-либо строке или столбцу, получается n определителей (n –1)-го порядка. Чтобы таких определителей было меньше, целесообразно выбирать ту строку или столбец, в которой больше всего нулей. На практике формулу разложения определителя обычно записывают в виде:

т.е. алгебраические дополнения записывают в явном виде через миноры.

Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.



2.

5. Основные свойства определителей

Разлагая определитель по какой-либо строке или столбцу, мы получим n определителей (n –1)-го порядка. Затем каждый из этих определителей (n –1)-го порядка также можно разложить в сумму определителей (n –2)-го порядка. Продолжая этот процесс, можно дойти до определителей 1-го порядка, т.е. до элементов матрицы, определитель которой вычисляется. Так, для вычисления определителей 2-го порядка придется вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых. Число слагаемых будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, непосильной даже для ЭВМ. Однако вычислять определители можно и по-другому, используя свойства определителей.

Свойство 1 . Определитель не изменится, если в нем поменять местами строки и столбцы, т. е. при транспонировании матрицы :

.

Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.

Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).

Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.

Свойство 3 . Общий множитель всех элементов в какой-либо строке (столбце) можно вынести за знак определителя .

Например,

Следствие . Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю .

Свойство 4 . Определитель не изменится, если к элементам одной строки (столбца), прибавить элементы другой строки (столбца), умноженной на какое-либо число .

Например,

Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:

решаем системы линейных алгебраических уравнений (слау)

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .

А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

.

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

.

На основании теоремы Крамера

………….
,

где
—

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы — (2; -1; 1).

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко ходить не надо.

Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:

Сделаем аналогичное действие, заменив в первом определителе второй столбец:

Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.

Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Решение систем методом подстановки.

Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.

и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Применять формулы Крамера нельзя. Решим эту систему методом подстановки

Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет

Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т.е. имеет вид

Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,

. (1.6)

Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:

(j = 1, 2, …, n ). (1.7)

Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:

(1.8)

Пример 1.5. Методом Крамера решить систему уравнений

.

Вычислим главный определитель системы:

Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1. 8):

Таким образом,

Действия над матрицами

1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.

2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть

. (1.9)

Пример 1.6. .

Сложение матриц.

Данная операция вводится только для матриц одного и того же порядка.

Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:

(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.

Пример 1.7. .

Умножение матриц.

Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:

2

Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:

Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :

Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :

2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .

Обратная матрица. Решение систем линейных уравнений матричным способом

Матрица A — 1 называется обратной к квадратной матрице А , если выполнено равенство:

где через I обозначается единичная матрица того же порядка, что и матрица А :

.

Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:

, (1.13)

где A ij — алгебраические дополнения к элементам a ij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).

Пример 1.9. Найти обратную матрицу A — 1 к матрице

.

Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:

.

Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 — 3 × 3 × 3 — 1 × 5 × 4 — 2 × 2 × 8 = 24 + 30 + 24 — 27 — 20 — 32 = — 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.

1) Найдем алгебраические дополнения A ij :

Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.

Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:

Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:

где

Умножая обе части равенства (1. 14) слева на A — 1 , мы получим решение системы:

, откуда

Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.

Задача 1.10. Решить систему линейных уравнений

с помощью обратной матрицы.

Решение. Запишем систему в матричном виде: ,

где — основная матрица системы, — столбец неизвестных и — столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :

Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:

Решение системы находим по формуле (1. 15):

Таким образом,

Решение систем линейных уравнений методом обыкновенных жордановых исключений

Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:

(1.16)

Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.

При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.

Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.

Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.

В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.

Пример 1.11.

x

После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:

Выразим y из второго уравнения и подставим его в первое уравнение:

Запомним второе уравнение, а из первого найдем z :

Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :

.

Затем подставим и в первое запомненное уравнение , откуда найдем x :

Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:

. (1.17)

Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

.

Запомним первое уравнение

В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.

Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.

Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.

Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:

. (1.18)

Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

.

Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:

Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.

В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда

Подставим y и z в первое запомненное равенство и найдем x :

.

Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :

(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1. 18).

В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.

Пусть дана система линейных форм (уравнений):

, (1.20)
где x j — независимые (искомые) переменные, a ij — постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.

Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.

Мы получим следующую систему:

. (1.21)

Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.

Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:

Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:

(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):

После приведения подобных членов, получим:

(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):

(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».

Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:

Таблица 1.1

	x 1	x 2	…	x j	…	x s	…	x n
y 1 =	a 11	a 12		a 1j		a 1s		a 1n
…………………………………………………………………. .
y i =	a i 1	a i 2		a ij		a is		a in
…………………………………………………………………..
y r =	a r 1	a r 2		a rj		a rs		a rn
………………………………………………………………….
y n =	a m 1	a m 2		a mj		a ms		a mn

Жорданова таблица 1.1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.

Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:

Таблица 1.2

	x 1	x 2	…	x j	…	y r	…	x n
y 1 =	b 11	b 12		b 1 j		b 1 s		b 1 n
…………………………………………………………………..
y i =	b i 1	b i 2		b ij		b is		b in
…………………………………………………………………..
x s =	b r 1	b r 2		b rj		b rs		b rn
………………………………………………………………….
y n =	b m 1	b m 2		b mj		b ms		b mn

Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.

Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).

1. Разрешающий элемент заменяется обратным числом:

2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:

3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:

4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:

Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:

-21-26-13-37

Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т. к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.

Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1. 4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: x 1 = — 3 + 2x 5 .

Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:

Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:

x 1 = — 3 + 2t

x 2 = — 1 — 3t

x 3 = — 2 + 4t . (1.27)
x 4 = 4 + 5t

x 5 = t

Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; — 1; — 2; 4; 0).

Калькулятор решения методом наименьших квадратов

+ онлайн-решатель с бесплатными шагами

Калькулятор решения методом наименьших квадратов используется для решения системы линейных уравнений, которые не имеют полного ранга в матричной форме. Полный ранг матрицы соответствует квадратной матрице с ненулевым определителем.

Таким образом, метод наименьших квадратов используется для решения не квадратных, а прямоугольных матриц. Решение таких матриц может быть немного сложным, но калькулятор наименьших квадратов здесь, чтобы помочь с этим.

Что такое калькулятор решения методом наименьших квадратов?

A Калькулятор решения методом наименьших квадратов — это инструмент, который предоставит вам решения методом наименьших квадратов для ваших прямоугольных матриц прямо здесь, в вашем браузере. Вы можете использовать этот онлайн-калькулятор и очень легко решать задачи методом наименьших квадратов.

Этот калькулятор предназначен специально для решения матричных задач 3 x 2, поскольку их нельзя решить с помощью обычного метода квадратной матрицы. Эта матрица порядка 3 x 2 описывает матрицу с 3 строками и 2 столбцами. Вы можете просто ввести элементы матрицы мест в поля ввода калькулятор для использования.

Как пользоваться калькулятором решения методом наименьших квадратов?

Калькулятор решения методом наименьших квадратов можно использовать, сначала поставив задачу, которую вы хотите решить, а затем следуя инструкциям по его использованию. Важно отметить, что этот калькулятор работает только для матричных задач 3 x 2.

Чтобы найти решение с помощью этого калькулятора , у вас должна быть матрица 3 x 2 A и матрица 3 x 1 b , которую необходимо решить для полученного 2 x 1 9Матрица 0029 X . Теперь выполните приведенные ниже шаги, чтобы получить наилучшие результаты от этого калькулятора:

Шаг 1:

Вы можете начать с ввода заданных A записей матрицы в поля ввода, а именно «Строка 1 из A», «Строка 2 А» и «3-й ряд А» соответственно.

Шаг 2:

За этим следует шаг, включающий ввод матрицы b в поле ввода, помеченное «b».

Шаг 3:

После того, как вы ввели все входные данные, вы можете просто нажать « Submit », чтобы получить желаемое решение из калькулятора. Этот шаг открывает решение проблемы в новом интерактивном окне.

Шаг 4:

Наконец, вы можете продолжать решать свои проблемы в новом интерактивном окне, если хотите. Вы также можете в любой момент закрыть это окно, нажав кнопку с крестиком в правом верхнем углу.

Важно отметить, что этот калькулятор не будет эффективен против задач с матрицей порядка, отличной от 3 x 2. Порядок матрицы 3 x 2 является очень распространенным порядком для задач без полного ранга. Поэтому он служит отличным инструментом для решения подобных задач.

Как работает калькулятор решения методом наименьших квадратов?

Калькулятор решения методом наименьших квадратов работает путем решения системы линейных уравнений матрицы A 3 x 2 для значения вектора b. Чтобы решить матрицу без полного ранга, важно отметить, имеет ли матрица ранг, равный 2.

Ранг матрицы

Ранг матрицы A определяется как соответствующая размерность векторного пространства. Чтобы определить ранг, сначала применяют элементарные преобразования к матрице. Преобразование должно привести к нормальной форме матрицы, включая единичную матрицу я .

Порядок результирующей единичной матрицы I представляет числовое значение ранга данной матрицы.

Метод наименьших квадратов

Метод наименьших квадратов используется для решения системы линейных уравнений, с которыми не связана квадратная матрица. Еще один важный факт, который следует помнить, заключается в том, что вы можете применять метод наименьших квадратов только к матрицам с рангом выше 1.

Теперь предположим, что имеется матрица A 3 x 2 и вектор b, который также может быть представлен в виде Матрица 3 х 1. Эти две матрицы можно связать вместе, используя третью матрицу, а именно X порядка 2 x 1, которая неизвестна. {-1} \begin{bmatrix}1&3&-2 \\ 5&1&4\end{bmatrix}\begin{bmatrix}4 \\ -2 \\ 3\end{bmatrix}\]

Наконец, решение этого уравнения приводит к ответу по методу наименьших квадратов матрицы 3 x 2. Его можно выразить следующим образом:

\[x = \frac{1}{14} \bigg( \begin{bmatrix}1&3&-2 \\ 5&1&4\end{bmatrix}\begin{bmatrix}4 \\ -2 \ \ 3\end{bmatrix}\bigg), y = \frac{1}{42} \bigg( \begin{bmatrix}1&3&-2 \\ 5&1&4\end{bmatrix}\begin{bmatrix}4 \\ -2 \\ 3\end{bmatrix}\bigg) \]

Пример № 2

Рассмотрим матрицу A и вектор b, заданные как:

\[A=\begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix}, b=\begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\]

Найдите матрицу X для приведенной выше задачи.

Решение

Начнем с составления матриц в виде уравнения AX = b.

\[\begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix} X = \begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\]

Сейчас возьмите транспонирование A и умножьте его на обе части уравнения:

\[\begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix}^{T} \begin{bmatrix}2&- 2 \\ -2&2 \\ 5&3\end{bmatrix} X = \begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix}^{T} \begin{bmatrix}-1 \\ 7 \ \-26\конец{bmatrix}\]

\[\begin{bmatrix}2&-2&5 \\ -2&2&3\end{bmatrix} \begin{bmatrix}2&-2 \\ -2&2 \\ 5&3\end{bmatrix} X = \begin{bmatrix}2&- 2&5 \\ -2&2&3\end{bmatrix}\begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\]

После выполнения матричного умножения необходимо взять обратное значение и получить значения Х можно рассчитать. {-1} \begin{bmatrix}2&-2&5 \\ -2&2&3\end{bmatrix}\begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\]

Наконец, решение этого уравнения приводит к ответу по методу наименьших квадратов матрицы 3 x 2. Его можно выразить следующим образом:

\[x = \frac{5}{256} \bigg( \begin{bmatrix}2&-2&5 \\ -2&2&3\end{bmatrix}\begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\bigg), y = \frac{13}{256} \bigg( \begin{bmatrix}2&-2&5 \\ -2&2&3\end{bmatrix}\begin{bmatrix}-1 \\ 7 \\ -26\end{bmatrix}\bigg) \]

Список математических калькуляторов

Математический калькулятор — онлайн-калькуляторы для решения математических задач шаг за шагом

Математический калькулятор: Математика всегда сложна!! Это уже не то же самое с нашим математическим калькулятором, универсальным средством для решения всех ваших трудных и сложных математических задач. Сэкономьте время на длительных расчетах и ​​воспользуйтесь бесплатными онлайн-инструментами. Простой инструмент не только избавит вас от хлопот, связанных с решением сложных задач во время домашней работы, но также очистит ваши вопросы, и вы сможете перепроверить свои ответы.

Взгляните на обширный набор калькуляторов и легко решайте сложные задачи. Будь то любой математический калькулятор, который вы называете, и он у нас есть. Получите доступ к бесплатным онлайн-калькуляторам по предоставленным прямым ссылкам и получите точные, но прямые описания, чтобы получить полное представление о концепции.

• Maths Formulas
• Math Tables
• Cubes and Cube Roots List
• Table of Squares and Square Roots
• Percentages Table
• Percentages Formulas
• Percentages calculators
• Arithmetic calculators
• Калькуляторы координатной геометрии
• Калькуляторы линейной алгебры
• Калькулятор алгебры
• Калькулятор геометрии
• Polynomials Calculator
• Decimals Calculator
• Rational Numbers Calculator
• GCF and LCM Calculator
• Fractions Calculator
• Sequences Calculator
• Sequence and Series Formulas
• Trigonometry Calculator
• Trigonometry Formulas
• Калькулятор статистики
• Калькулятор преобразований
• Калькулятор дискретной математики
• Other Math calculators
• Long Addition Calculator
• Long Subtraction Calculator
• Long Multiplication Calculator
• Long Division Calculator
• Long Division with Decimals Calculator
• Partial Quotient Division Calculator
• Age Difference Калькулятор
• Калькулятор определенных интегралов
• Как вычислить проценты
• Age Calculator
• NEET Percentile Calculator
• Ratio Calculator
• Sum Calculator
• Product Sum Calculator
• Sum of Even Numbers Calculator
• Sum of Odd Numbers Calculator
• Standard Form Calculator
• Онлайн-калькулятор скидок
• Калькулятор линейного программирования
• Калькулятор базовой точки
• Калькулятор прибыли
• Percentile Calculator
• Remainder Calculator
• Percentage Calculator
• Percentage Change Calculator
• Percent Grade to Degree Calculator
• Degree to Percent Grade Calculator
• Adding Square Root Calculator
• Math Equation Solver
• Калькулятор умножения решеток
• Калькулятор значащих цифр
• Калькулятор скорости, расстояния, времени
• Unit Rate Calculator
• Mod Calculator
• Estimate the Difference Calculator
• Ratio Calculator Online
• Common Factors Calculator
• Diamond Problem Solver
• Distance Calculator
• Adding Percentage Calculator
• Калькулятор умножения квадратных корней
• Калькулятор перестановок и комбинаций

Таблица процентов

Fraction	Decimal	Percent
1/2	0. 5	50%
1/3	0.333…	33.333…%
2/3	0.666… ​​	66.666…%
1/4	0.25	25%
3/4	0.75	75%
1 /5	0,2	20%
2/5	0.4	40%
3/5	0.6	60%
4/5	0.8	80%
1/ 6	0.1666… ​​	16.666…%
5/6	0.8333…	83.333…%
1/8	0.125	12.5% ​​
3/8	0,375	37,5%

Fraction	Decimal	Percent
5/8	0.625	62. 5%
7/8	0.875	87.5%
1/	0,111 …	11,111 …%
2/9	0,222 …	22.222 …%
999999494					994	969.94	49494		494	9	.		4				9	9949	.2222. …%
5/9	0,555 …	55,555 …%
7/9	0,777 …	77,777 …%
77,777 …%
77,777 …%
77,777 …%	77	77,777 …%	88.888…%
1/10	0.1	10%
1/12	0.08333…	8.333…%
1/16	0,0625	6,25%
1/32	0,03125	3,125%
1/50	0,02	2%

Процент Formulas

y = P% * x

9002 9002 y = P% * x

.

Y составляет 25% от 150

Уравнение: Y = P% * X

Решение нашего уравнения для Y

р = 25%/100 = 0,25

Y = 0,25 * 150

Y = 37,5

35 сколько процентов от 175?

35 есть P% от 175

Уравнение: Y = P% * X

Решение нашего уравнения для P десятичная дробь в процентах:

P% = 0,2 * 100 = 20%

35 составляет 12% от чего?

35 составляет 12% от X

Уравнение: Y = P% * X

Решение нашего уравнения для X0005

p = 12%/100 = 0,12

X = 35/0,12

X = 291,6667

---

P% * X = Y

P% от 2400 равно 360

Уравнение: P% * X = Y

Решение нашего уравнения для P десятичная дробь в процентах:

P% = 0,15 * 100 = 15%

35% что такое 560?

35% X равно 560

Уравнение: P% * X = Y

Решение нашего уравнения для X

X = Y/P%

X = 560/35%

Преобразование процентов в десятичные числа:

p = 35%/100 = 0,35

X = 560/0,35

X = 1600

32% от 560 это что?

32% от 560 равно Y

Уравнение: P% * X = Y

Решение нашего уравнения для Y

Y = P% * X

Y = 32% * 560

Преобразование процентов в десятичное:

р = 32%/100 = 0,32

Y = 0,32 * 560

Y = 179,2

---

Y ÷ X= P%

350 из чего 15%?

350 из X равно 15%

Уравнение: Y/X = P%

Решение нашего уравнения для X

X = Y/P%

X = 350/15%

p = 15%/100 = 0,15

X = 350/0,15

X = 2333,3333

Сколько из 450 составляет 12%?

Y из 450 составляет 12%

Уравнение: Y/X = P%

Решение нашего уравнения для Y

Y = P% * X

Y = 12% * 450

Преобразование процентов в десятичные числа:

p = 12%/100 = 0,12

Y = 402009 * 0 0,12 = 54

570 из 850 это сколько %?

570 из 850 равно P%

Уравнение: Y/X = P%

Решение нашего уравнения для P

P% = Y/X

P% = 570/850

2 p =

6 Преобразовать десятичная дробь в процентах:

P% = 0,6706 * 100 = 67,06%

---

X + (X × P%) = Y

Пример: Сколько будет 25% от 150?

350 плюс 12% это что?

350 плюс 12% равно Y

Уравнение:

X + (X × P%) = Y

X(1 + P%) = Y

Решение нашего уравнения для Y

Y = X(1 + P%)

Y = 350(1 + 12%)

Преобразование процентов в десятичные числа:

p = 12%/100 = 0,12

Y = 350(1 + 0,12)

Y = 350(

)

Д = 392

420 плюс сколько процентов составляет 560?

420 плюс P% равно 560

Уравнение:

X + (X × P%) = Y

X(1 + P%) = Y

Решение нашего уравнения для P

P% = Y/X — 1

P% = 560/420 — 1

p = 0,3333

Преобразовать десятичную дробь в проценты:

P% = 0,3333 * 100 = 33,33%

Сколько плюс 25% будет 450?

X плюс 25% равно 450

Уравнение:

X + (X × P%) = Y

X(1 + P%) = Y

Решение нашего уравнения для X

X = Y/(1 + P%)

X = 450/(1 + 25%)

Преобразование процентов в десятичные числа:

p = 25%/100 = 0,25

X = 450/(1 + 0,25)

X = 450/1,25

X = 360

---

X — (X × P%) = Y

450 минус 12% это что?

450 минус 12% равно Y

Уравнение:

X — (X × P%) = Y

X(1 — P%) = Y

Решение нашего уравнения для Y

Y = X(1 — П%)

Д = 450(1 — 12%)

Преобразование процентов в десятичные числа:

p = 12%/100 = 0,12

Y = 450(1 — 0,12)

Y = 450(0,88)

Y = 396

чему равно 3 минус 2?

650 минус P% равно 325

Уравнение:

X — (X × P%) = Y

X(1 — P%) = Y

Решение нашего уравнения для P

P% = 1 — Y /X

P% = 1 — 325/650

p = 0,5

Преобразовать десятичную дробь в проценты:

P% = 0,5 * 100 = 50%

Сколько минус 2% будет 490?

X минус 2% равно 490

Уравнение:

X — (X × P%) = Y

X(1 — P%) = Y

Решение нашего уравнения для X

X = Y/(1 — P%)

X = 490/(1 — 2%)

Преобразование процентов в десятичные числа:

p = 2%/100 = 0,02

X = 490/(1 — 0,02)

X = 490/ 0,98

X = 500

---

Формула изменения в процентах

Изменение в процентах = [ (Новое_значение — Исходное_значение) / |Исходное_значение| ] * 100

Пример: Процентное изменение с 250 на 350?

Решение: Новое_значение = 350, Исходное_значение = 250

Процентное изменение = [ (Новое_значение — Исходное_значение) / |Исходное_значение| ] * 100

Подставьте данные значения в формулу.

Процентное изменение = (350 — 250) / |250| * 100

Процентное изменение = (100/250) * 100 = (2/5) * 100 = 0,4 * 100

Процентное изменение = 40%

∴ Процентное изменение с 250 на 350 составляет 40%

---

Формула ошибки в процентах

Ошибка

процентов = [(AV — OV) / | АВ | ] * 100%

где: AV — фактическое значение, а OV — наблюдаемое значение.

Пример: Процентная ошибка от 200 до 250?

Решение: фактическое значение = 200, наблюдаемое значение = 250

Ошибка в процентах = [(AV — OV) / | АВ | ] * 100%

Подставьте данные значения в формулу.

Процент ошибки = (250 — 200) / |200| * 100

Ошибка в процентах = (50/200) * 100 = (1/4) * 100 = 0,25 * 100

Процентная ошибка = 25%

∴ Процентная ошибка от 200 до 250 составляет 25% СВ | ] * 100%

где: FV — конечное значение, а SV — начальное значение.

Пример: Процентное увеличение с 90 до 108?

Решение: начальное значение = 90, конечное значение = 108

увеличение в процентах = [(FV — SV) / ​​| СВ | ] * 100%

Подставьте данные значения в формулу.

Увеличение в процентах = (108 — 90) / |90| * 100

Увеличение в процентах = (18/90) * 100 = (1/5) * 100 = 0,2 * 100

Увеличение в процентах = 20%

∴ Увеличение в процентах с 90 до 108 составляет 20%

---

0 Формула уменьшения

Процентное уменьшение = [(SV — FV) / | СВ | ] * 100%

где: FV — конечное значение, а SV — начальное значение.

Пример: Процентное уменьшение с 80 до 68?

Решение: начальное значение = 80, конечное значение = 68

Увеличение в процентах = [ (SV — FV) / | СВ | ] * 100%

Подставьте данные значения в формулу.

Пер. Уменьшение = (80 — 68) / |80| * 100

Пер. Уменьшение = (12/80) * 100 = (3/20) * 100 = 0,15 * 100

Пер. Уменьшение =

∴ Процент Уменьшение с 80 до 68 составляет 15%

---

Формула разницы в процентах

Разница в процентах = 100 * |a — b| / ((a + b) / 2)

Пример: Процентная разница от 300 до 200?

Решение: a = 300, b = 200

Разница в процентах = 100 * |a — b| / ((a + b) / 2)%

Подставить данные значения в формулу.

Разница в процентах = 100 * |300 — 200| / ((300+200) / 2)%

P.D = 100 * |100| / (500/2)

P.D = (10000/250)%

P.D = 40%

∴ Процент разница с 300 до 200 — 40%

---

процент процентной формулы

процент процента. = (pct1 ÷ 100) × (pct2 ÷ 100) × 100

где: pct1 — процент 1, а pct2 — процент 2.

Пример: найти 25% от 60%

Решение: pct1 = 300, pct2 = 200

p = (pct1 ÷ 100) × (pct2 ÷ 100) × 100

p = (25 ÷ 100) × (60 ÷ 100) × 100

p = 0,25 × 0,6 × 100

p = 0,15 × 100

p = 15%

∴ 25% от 60% равно 15%

---

Формула времени удвоения

время удвоения = log(2) / log(1 + r)

Где: r = постоянная скорость роста

Growth Rate	Doubling Time
0.1	693.49
0.2	346. 92
0.3	231.4
0.4	173.63
0.5	138.98
0.6	115.87
0.7	99.36
0.8	86.99
0.9	77.36
1	69.66
1.1	63.36
1.2	58.11
1.3	53.66
1.4	49.86
1.5	46.56
1.6	43.67
1.7	41.12
1.8	38.85
1.9	36.83
2	35

Growth Rate	Doubling Time
2. 1	33.35
2.2	31.85
2.3	30.48
2.4	29.23
2.5	28.07
2.6	27
2.7	26.02
2.8	25.1
2.9	24.25
3	23.45
3.1	22.7
3.2	22.01
3.3	21.35
3.4	20.73
3.5	20.15
3.6	19.6
3.7	19.08
3.8	18.59
3.9	18.12
4	17.67

Growth Rate	Doubling Time
4. 1	17.25
4.2	16.85
4.3	16.46
4.4	16.1
4.5	15.75
4.6	15.41
4.7	15.09
4.8	14.78
4.9	14.49
5	14.21
5.5	12.95
6	11.9
6.5	11.01
7	10.24
7.5	9.58
8	9.01
8.5	8.5
9	8.04
9.5	7.64
10	7.27

---

Преобразование дроби в проценты

Простая формула для преобразования дроби в проценты

(n / d) * 100 = P

, где n — числитель, d — знаменатель, а p — знаменатель.

---

Percentages Calculators 💯

• Percentage Calculator
• Percent error Calculator
• Percentage change Calculator
• Percentage increase Calculator
• Percentage difference Calculator
• Doubling time Calculator
• Convert fraction в проценты Калькулятор
• Процентное уменьшение Калькулятор
• Процент в процентах Калькулятор

Arithmetic calculators ➗

• Average Calculator
• Geometric mean Calculator
• Harmonic mean Calculator
• Mean Calculator
• Root mean square Calculator
• Factor Calculator
• Modulo Calculator
• Калькулятор простых чисел
• Калькулятор GCF
• Калькулятор LCM
• Калькулятор простой факторизации
• Absolute value Calculator
• Addition Calculator
• Binary subtraction Calculator
• GCF and LCM Calculator
• Long division Calculator
• Pascal’s triangle Calculator
• Reciprocal Calculator
• Standard form Calculator
• Калькулятор дополнения до двух
• Калькулятор средневзвешенного значения
• e мощность x Калькулятор

Coordinate Geometry Calculators 📈

• Rise over run calculator Calculator
• Slope Calculator
• Perpendicular line Calculator
• Distance Calculator
• Angle between two vectors Calculator
• Dot product Calculator
• Калькулятор перекрестного произведения
• Калькулятор средней скорости изменения
• Калькулятор цилиндрических координат
• Equation of a circle Calculator
• Gradient Calculator
• Least squares regression line Calculator
• Linear interpolation Calculator
• Midpoint Calculator
• Parabola Calculator
• Parallel line Calculator
• Polar coordinates Калькулятор
• Форма пересечения уклона Калькулятор
• Сферические координаты Калькулятор
• Three-dimensional distance Calculator

Linear algebra calculators 🔢

• (Reduced) row echelon form Calculator
• Characteristic polynomial Calculator
• Cramer’s rule Calculator
• Diagonalize matrix Calculator
• Eigenvalue Калькулятор собственных векторов
• Калькулятор Грамма-Шмидта
• Калькулятор обратной матрицы
• Калькулятор линейной независимости
• Matrix addition and subtraction Calculator
• Matrix determinant Calculator
• Matrix multiplication Calculator
• Matrix rank Calculator
• Matrix transpose Calculator
• Systems of equations Calculator
• Unit vector Calculator
• Калькулятор векторной величины
• Калькулятор проекции вектора

Другие математические калькуляторы

• Significant figures Calculator
• Scientific notation Calculator
• Golden ratio Calculator

2 x 5 = 10 9

Multiplication Table of 2
2 x 1 = 2
2 x 2 = 4
2 x 3 = 6
2 x 4 = 8
2 x 5 = 10
0
2 x 7 = 14
2 x 8 = 16
2 x 9 = 18
2 x 10 = 20
2 x 10 = 20
2 x 10 =
2 x 10 =
2 x 10 =
2 x 10 =
2 x 10 =
2 x. x 12 = 24
2 x 13 = 26
2 x 14 = 28
2 x 15 = 30
2 x 15 2
2 x 152
2 x 152
2 x 15 2
2 x 15 = 30
2 x 15 = 30
2 x 15.
2 х 18 = 36
2 х 19 = 38
2 x 20 = 40

. = 45

Multiplication Table of 3
3 x 1 = 3
3 x 2 = 6
3 x 3 = 9
3 x 4 = 12
3 x 5 = 15
3 x 6 = 18
3 x 7 = 21
3 x 8 = 24
3 х 9 = 27
3 x 10 = 30
3 x 11 = 33
3 x 12 = 36
3 x 13 = 39
3 x 13 = 39
3 x 13 = 39
3 39
3 39
3 39
3 39
3 x 16 = 48
3 x 17 = 51
3 x 18 = 54
3 x 18 = 54
3 x 18 = 54
3 x 18 = 54
3 x 18.

.. 44. x 19 = 76

Таблица умножения 4
4 x 1 = 4
4 x 2 = 8
4 x 3 = 12
4 x 3 = 12
4 x 3 = 12
4 x 3 = 12
4 x 3 = 12	4 x 6 = 24
4 x 7 = 28
4 x 8 = 32
4 x 9 = 36
4 4
4 4
4 4. 36
4 4
4 9.
4 х 12 = 48
4 х 13 = 52
4 x 14 = 56
4 x 15 = 60
4 x 16 = 64
4 x 17 =
4 x 17 = 64
4 = 64
4 = 64
4 x 20 = 80

Multiplication Table of 5
5 x 1 = 5
5 x 2 = 10
5 х 3 = 15
5 x 4 = 20
5 x 5 = 25
5 x 6 = 30
5 x 7 = 35
5 x 7 = 35
5 x 7 = 35
5 x 7. 9 = 45
5 x 10 = 50
5 x 11 = 55
5 x 12 = 60
5 x 12 = 60390
5 x 12 = 60390
5 x.
5 х 15 = 75
5 х 16 = 80
5 x 17 = 85
5 x 18 = 90
5 x 19 = 95
5 x 20 = 100

Multiplication Table of 6
6 x 1 = 6
6 x 2 = 12
6 x 3 = 18
6 x 4 = 24
6 x 5 = 30
6 х 6 = 36
6 x 7 = 42
6 x 8 = 48
6 x 9 = 54
6 x 10 = 60
6 x 10 = 60
6 x 10 = 60390
6. 60390
6. 72
6 x 13 = 78
6 x 14 = 84
6 x 15 = 90
6 x 16 = 96
6 x 17 = 102
6 х 18 = 108
6 х 19 = 114
6 x 20 = 120

9. 9.

Multiplication Table of 7
7 x 1 = 7
7 x 2 = 14
7 x 3 = 21
7 x 4 = 28
7 x 5 = 35
7 x 6 = 42
7 x 7 = 49
7 x 7 = 49
7 x 7. 4
7.
7
9
7
7 x 6. 9 = 63
7 х 10 = 70
7 x 11 = 77
7 x 12 = 84
7 x 13 = 91
7 x 14 = 98
7 x 15 = 105
7 x 16 = 112
7 x 17 = 119
7 x 18 = 126
7 x 19 = 133
7 x 20 = 140

Таблица умножения 8
8 x 1 = 8
8 x 2 = 16
8 x 3 = 24
8 x 4 = 32
8 x 4 = 32
8 x 4 = 32
8 x 4 = 24
8.
. x 6 = 48
8 x 7 = 56
8 x 8 = 64
8 x 9 = 72
8 x 9 =
8 x
8. 8
8.
.
8 х 12 = 96
8 х 13 = 104
8 x 14 = 112
8 x 15 = 120
8 x 16 = 128
8 x 17 =
8 x 176
8. x 19 = 152
8 x 20 = 160

Multiplication Table of 9
9 x 1 = 9
9 x 2 = 18
9 х 3 = 27
9 x 4 = 36
9 x 5 = 45
9 x 6 = 54
9 x 7 = 63
9 x 8 = 72
9 x 9 = 81
9 x 10 = 90
9 x 11 = 99
9 x 12 = 108
9 x.
9 х 15 = 135
9 х 16 = 144
9 x 17 = 153
9 x 18 = 162
9 x 19 = 171
9 x 20 = 180

. x 12 = 120

Multiplication Table of 10
10 x 1 = 10
10 x 2 = 20
10 x 3 = 30
10 x 4 = 40
10 x 5 = 50
10 х 6 = 60
10 x 7 = 70
10 x 8 = 80
10 x 90
10 x 10 =
10 x 10 =
10 =
10 =
10
10 =
10
10 =
10 x 13 = 130
10 x 14 = 140
10 x 15 = 150
10 x 15 = 150
10 x 150
10 x 150
10 x 150
.
10 х 18 = 180
10 x 19 = 190
10 x 20 = 200

Multiplication Table of 11
11 x 1 = 11
11 x 2 = 22
11 x 3 = 33
11 x 4 = 44
11 x 5 = 55
11 x 66
11 x 66
11 x 66
8 = 88
11 x 9 = 99
11 x 10 = 110
11 x 11 = 121
11 x 12 = 132
11 x 12 = 132
11 x 12 = 132
11
11	89.	9.
9	9389	. 154
11 x 15 = 165
11 x 16 = 176
11 x 17 = 187
11 x 18 = 198
11 x 19 = 209
11 х 20 = 220

Multiplication Table of 12
12 x 1 = 12
12 x 2 = 24
12 x 3 = 36
12 x 4 = 48
12 x 5 = 60
12 x 6 = 72
12 x 7 = 84
12 x 8 = 96
12 x 8 = 96
12 x 8 = 96
12 x 8 = 96
120
12 х 11 = 132
12 x 12 = 144
12 x 13 = 156
12 x 14 = 168
12 x 15 = 180
12 x 16 = 192
12 x 17 = 204
12 x 18 = 216
12 x 19 = 228
12 x 20 = 240

Multiplication Table of 13
13 x 1 = 13
13 x 2 = 26
13 x 3 = 39
13 x 4 = 52
13 x 4 = 52
13 x 4 = 52
13 x 4 = 52
13 x 7 = 91
13 x 8 = 104
13 x 9 = 117
13 x 10 = 130
13 x 11 = 143
13 х 12 = 156
13 х 13 = 169
13 x 14 = 182
13 x 15 = 195
13 x 16 = 208
13 x 17 = 221
13 x 17 = 221
13 x 17 = 221
13 x 17 = 221
13. = 247
13 x 20 = 260

Multiplication Table of 14
14 x 1 = 14
14 x 2 = 28
14 х 3 = 42
14 x 4 = 56
14 x 5 = 70
14 x 6 = 84
14 x 7 = 98
14 x 8 = 112
14 x 9 = 126
14 x 10 = 140
14 x 11 = 154
14 x 12 = 168
14 x 12 = 168
14 x 12 = 168
14 x 12 = 168
14 x
14 х 15 = 210
14 x 16 = 224
14 x 17 = 238
14 x 18 = 252
14 x 19 = 266
14 x 20 = 280

Multiplication Table of 7
15 x 1 = 15
15 x 2 = 30
15 x 3 = 45
15 x 4 = 60
15 x 5 = 75
15 x 6 = 90
15 x 7 = 105
15 x 8 = 120
15 x 9 = 135
15 x 10 = 150
15 x 11 = 165
15 x 12 = 180
15 x 13 = 195
15 x 14 = 210
15 x 15 = 225
15 x 16 = 240
15 х 17 = 255
15 х 18 = 270
15 x 19 = 285
15 x 20 = 300

7

Multiplication Table of 16
16 x 1 = 16
16 x 2 = 32
16 x 3 = 48
16 x 4 = 64
16 x 5 = 80
16 x 5 =
16 x 5 =
16 = 969390
16 =
16 =
16 =
16 =
.	16 х 8 = 128
16 x 9 = 144
16 x 10 = 160
16 x 11 = 176
16 x 12 = 192
16 x 13 = 208
16 x 14 = 224
16 x 15 = 240
16 x 16 = 256
16 x 17 = 272
16 x 17 = 272
16 x 17 = 272
16 x 17 = 272
16 x 17 = 272
16 x 17 = 272
16 x 17 = 272
16.
16 х 20 = 320

Multiplication Table of 17
17 x 1 = 17
17 x 2 = 34
17 x 3 = 51
17 x 4 = 68
17 x 5 = 85
17 x 6 = 102
17 x 7 = 119
17 x 8 = 136
17 x 9 = 153
17 х 10 = 170
17 x 11 = 187
17 x 12 = 204
17 x 13 = 221
17 x 14 = 238
17 x 14 = 238
17 x 14 = 238
17. = 272
17 x 17 = 289
17 x 18 = 306
17 x 19 = 323
17 x 20 = 340

Multiplication Table из 2
18 x 1 = 18
18 x 2 = 36
18 x 3 = 54
18 x 4 = 72
18 x 5 = 90
18 x 6 = 108
18 x 7 = 126
18 x 8 = 144
18 x 9 = 162
18 x 9 = 162
18 x
18 x
.
18 х 12 = 216
18 x 13 = 234
18 x 14 = 252
18 x 15 = 270
18 x 16 = 288
18 x 16 = 288
18 x 16 =
18.
18 x 19 = 342
18 x 20 = 360

Multiplication Table of 19
19 x 1 = 19
19 x 2 = 38
19 x 3 = 57
19 x 4 = 76
19 x 5 = 95
19 x 6 = 114
19 x 7 = 133
19 x 8 = 152
19 x 9 = 171
19 x 10 = 190
19 x 11 = 209
19 x 12 = 228
19 x 13 = 247
19 х 14 = 266
19 х 15 = 285
19 x 16 = 304
19 x 17 = 323
19 x 18 = 342
19 x 19 = 361
19 x 20 = 380

Multiplication Table of 20
20 x 1 = 20
20 x 2 = 40
20 x 3 = 60
20 x 4 = 80
20 х 5 = 100
20 x 6 = 120
20 x 7 = 140
20 x 8 = 160
20 x
20 x
20 x
20 = 160
. x 11 = 220
20 x 12 = 240
20 x 13 = 260
20 x 14 = 280
20 x 14 = 280
20 x 14 = 280
20 x 140
.
20 х 17 = 340
20 x 18 = 360
20 x 19 = 380
20 x 20 = 400

.

Multiplication Table of 30
30 x 1 = 30
30 x 2 = 60
30 x 3 = 90
30 x 4 = 120
30 x 5 = 150
30 x 6 = 180
30 х 7 = 210
30 x 8 = 240
30 x 9 = 270
30 x 10 = 300
30 x 11 = 330
30 x 11330 360387787787880	30 x. 13 = 390
30 x 14 = 420
30 x 15 = 450
30 x 16 = 480
30 x 16 = 480
30 x 16 = 480
30 = 480
30 = 480
30 = 480
30 = 480
30 = 480
30 х 19 = 570
30 x 20 = 600

Number	Cube(a 3 )	Cube root ∛a
1	1	1.000
2	8	1.260
3	27	1.442
4	64	1.587
5	125	1.710
6	216	1.817
7	343	1.913
8	512	2.000
9	729	2.080
10	1000	2.154
11	1331	2.224
12	1728	2.289
13	2197	2. 351
14	2744	2.410
15	3375	2.466

Number	Square	Square Root
1	1	1
2	4	1.414
3	9	1.732
4	16	2
5	25	2.236
6	36	2.449
7	49	2.646
8	64	2.828
9	81	3
10	100	3.162
11	121	3.317
12	144	3.464
13	169	3. 606
14	196	3.742
15	225	3.873
16	256	4
17	289	4.123
18	324	4.243
19	361	4.359
20	400	4.472
21	441	4.583
22	484	4.69
23	529	4.796
24	576	4.899
25	625	5
26	676	5.099
27	729	5.196
28	784	5.292
29	841	5.385
30	900	5. 477
31	961	5.568
32	1,024	5.657
33	1,089	5.745
34	1,156	5.831
35	1,225	5.916
36	1,296	6
37	1,369	6.083
38	1,444	6.164
39	1,521	6.245
40	1,600	6.325
41	1,681	6.403
42	1,764	6.481
43	1,849	6.557
44	1,936	6.633
45	2,025	6.708
46	2,116	6. 782
47	2,209	6.856
48	2,304	6.928
49	2,401	7
50	2,500	7.071
51	2,601	7.141
52	2,704	7.211
53	2,809	7.28
54	2,916	7.348
55	3,025	7.416
56	3,136	7.483
57	3,249	7.55
58	3,364	7.616
59	3,481	7.681
60	3,600	7.746
61	3,721	7.81
62	3,844	7. 874
63	3,969	7.937
64	4,096	8
65	4,225	8.062
66	4,356	8.124
67	4,489	8.185
68	4,624	8.246
69	4,761	8.307
70	4,900	8.367
71	5,041	8.426
72	5,184	8.485
73	5,329	8.544
74	5,476	8.602
75	5,625	8.66
76	5,776	8.718
77	5,929	8.775
78	6,084	8. 832
79	6,241	8.888
80	6,400	8.944
81	6,561	9
82	6,724	9.055
83	6,889	9.11
84	7,056	9.165
85	7,225	9.22
86	7,396	9.274
87	7,569	9.327
88	7,744	9.381
89	7,921	9.434
90	8,100	9.487
91	8,281	9.539
92	8,464	9.592
93	8,649	9.644
94	8,836	9. 695
95	9,025	9.747
96	9,216	9.798
97	9,409	9.849
98	9,604	9.899
99	9,801	9,95
100	10 000	10

9002 9.1029.

Onlinecalculator.guru — это надежный веб-сайт, который предлагает математические калькуляторы для всех понятий, чтобы облегчить вашу работу.

---

2. Как слишком легко решать сложные математические задачи?

Воспользуйтесь помощью бесплатных онлайн-калькуляторов по математике в одном месте и получите точные и понятные описания.

---

3. Где я могу получить разработанную процедуру для математических понятий?

На нашей странице вы можете получить подробную процедуру разработки математических понятий.

---

4. Могу ли я полагаться на доступные здесь математические калькуляторы при выполнении домашних заданий?

Да, вы можете положиться на доступные здесь математические калькуляторы во время выполнения домашних заданий, так как все они даны после огромных исследований и дают точные результаты.

сообщите об этом объявлении

Правило Крамера с двумя переменными

Поиск

Правило Крамера — это еще один метод, позволяющий решать системы линейных уравнений с использованием определителей.

Что касается обозначений, a 9Матрица 0029 представляет собой массив чисел, заключенный в квадратные скобки, а определитель представляет собой массив чисел, заключенный в две вертикальные черты.

Обозначения

---

Формула для нахождения определителя матрицы 2 x 2 очень проста.

Краткий обзор:

Определитель матрицы 2 x 2

---

Краткие примеры поиска определителей матрицы 2 x 2

Пример 1 : Найдите определитель матрицы A ниже .

---

Пример 2 : Найдите определитель матрицы B ниже.

---

Пример 3 : Найдите определитель матрицы C ниже.

Узнав, как найти определитель матрицы 2 x 2, вы теперь готовы изучить процедуры или шаги по использованию правила Крамера. Вот так!

---

Правила Крамера для систем линейных уравнений с двумя переменными

• Дана линейная система

• Назовите каждую матрицу

Матрица коэффициента:

x — Матрица:

Y — Матрица:

для решения для переменной x:

до Solve For For For For the Variable Y:

9 . моменты, которые следует учитывать при рассмотрении формулы:

1) Столбцы \large{x}, \large{y} и постоянные члены \large{c} получаются следующим образом:

2) Оба знаменателя в решения \large{x} и \large{y} совпадают. Они берутся из столбцов \large{x} и \large{y}.

3) Глядя на числитель при решении для \large{x}, коэффициенты столбца \large{x} заменяются постоянным столбцом (красным).

4) Таким же образом, чтобы найти \large{y}, коэффициенты \large{y}-столбца заменяются константным столбцом (красным).

---

Примеры решения системы линейных уравнений с двумя переменными с использованием правила Крамера

Пример 1 : Решение системы с двумя переменными с помощью правила Крамера

Начните с извлечения трех соответствующих матриц: коэффициента, \large{x} и \large{y}. Затем решите каждый соответствующий определитель.

• для матрицы коэффициента

• для x — Матрица

• для Y — Matrix

для Y — MATRIX

для Y — Matrix

. } и \large{y}  с помощью приведенной выше формулы.

Я могу записать окончательный ответ как \large{\left( {x,y} \right) = \left({2, — 1} \right)}.

---

Пример 2 : Решите систему с двумя переменными по правилу Крамера

Настройте матрицы коэффициентов, \large{x} и \large{y} из заданной системы линейных уравнений. Затем вычислите их определители соответственно.

Помните, что мы всегда вычитаем произведений диагональных элементов.

• Для матрицы коэффициентов (используйте коэффициенты переменных x и y)

• Для X – матрица (столбец x замените столбцом констант)

• Для  Y – матрица (столбец y замените столбец констант)

Надеюсь, вы привыкли к вычислениям для определитель двумерной матрицы. Чтобы окончательно решить требуемые переменные, я получаю следующие результаты.

Записав окончательный ответ в виде точек, я получил \large{\left( {x,y} \right) = \left({6, — 5} \right)}.

---

Пример 3 : Решить систему с двумя переменными по правилу Крамера

Эту задачу можно довольно легко решить с помощью метода исключения. Это связано с тем, что коэффициенты переменной x «одинаковые», но только противоположные по знаку ( +1 и −1 ). Чтобы решить эту проблему с помощью метода исключения, вы добавляете соответствующие столбцы, и переменная x исчезает – остается одношаговое уравнение в \large{y}. Я говорю об этом, потому что у каждой техники есть недостатки, и лучше выбрать самую эффективную. Всегда получайте разъяснения от своего учителя, можно ли использовать другой подход, если метод не указан для данной проблемы.

В любом случае, поскольку мы учимся решать по правилу Крамера, давайте продолжим и поработаем с этим методом.

Я построю три матрицы (коэффициент, \large{x} и \large{y}) и оценю их соответствующие определители.

• Для матрица коэффициентов

• Для X – матрица (записывается прописной D с нижним индексом x)

• Для Y – матрица (записывается заглавной D)0172

После получения значений трех необходимых определителей я вычислю \large{x} и \large{y} следующим образом.

Окончательный ответ в точечной форме: \large{\left( {x,y} \right) = \left( { — 1,2} \right)} .

---

Пример 4 : Решение системы с двумя переменными по правилу Крамера

Поскольку мы уже рассмотрели несколько примеров, я предлагаю вам решить эту задачу самостоятельно. Затем сравните свои ответы с решением ниже.

Если вы сделаете это правильно с первого раза, это означает, что вы становитесь «профессионалом» в отношении правила Крамера. Если вы этого не сделали, попытайтесь выяснить, что пошло не так, и научитесь не совершать ту же ошибку в следующий раз. Так вы станете лучше в математике. Изучайте различные виды задач и, что более важно, выполняйте много самостоятельной практики.

• Для матрица коэффициентов

• Для X – матрица

• Для Y – матрица

Вы должны получить ответ ниже…

---

Пример 5 : Решить систему с двумя переменными по правилу Крамера

В нашем последнем примере я включил ноль в столбец констант. Каждый раз, когда вы видите число ноль в столбце констант, я настоятельно рекомендую использовать правило Крамера для решения системы линейных уравнений. Почему? Потому что вычисление определителей для матриц \large{x} и \large{y} становится очень простым. Проверьте сами!

• для коэффициента матрицы

• для x — Матрица

• для Y — Matrix

.

Правило Крамера 3×3

Fortis и Visual Matrix объединяются для предоставления комплексной интегрированной системы оплаты для операционных систем гостиничного бизнеса

НОВИ, штат Мичиган, 21 сентября 2022 г. /PRNewswire/ — Fortis, лидер в области платежных и коммерческих технологий для поставщиков программного обеспечения, торговых площадок и масштабирующих компаний, сегодня объявила о своем партнерстве с Visual Matrix, ведущей системой управления гостиничной собственностью. Оба партнера обладают глубокими знаниями в области гостиничного бизнеса, что делает партнерство идеальным решением, которое улучшит качество обслуживания гостей и операторов отелей за счет интеграции отмеченной наградами коммерческой платформы Fortis с ведущей в отрасли гостиничной операционной системой Visual Matrix.

«Наше партнерство с Fortis дает пользователям Visual Matrix возможность предоставлять гостям больше вариантов оплаты», — сказала Джорджин Мунц, генеральный директор Visual Matrix. «Команда Fortis понимает уникальные проблемы индустрии гостеприимства и предоставляет платформу, которая упрощает платежи для гостей и расширяет возможности оплаты по мере появления новых вариантов. Это также помогает оптимизировать процессы работы отеля, такие как сверка, за счет интеграции с нашим программным обеспечением».

Best Western и другие ведущие гостиничные бренды используют операционную систему Visual Matrix для гостиниц, поскольку она объединяет различные компоненты гостиничных операций в одном месте, упрощая рабочие процессы и экономя время и деньги. Visual Matrix будет использовать технологию Fortis, позволяющую гостям платить удобным для них способом, а также исключать двойную запись платежей на стойке регистрации.

«Как и Fortis, команда Visual Matrix руководствуется инновациями, чтобы помочь операторам отелей подготовиться к тому, что будет дальше, поскольку ожидания гостей меняются, а индустрия гостеприимства развивается», — сказал Грег Коэн, генеральный директор Fortis. «Мы очень рады сотрудничать с лидером отрасли, таким как Visual Matrix, и органично интегрировать платформу Fortis в их систему управления недвижимостью, чтобы дать владельцам отелей больше возможностей для максимизации доходов и расширения вариантов оплаты».

Fortis предлагает индивидуальные платежные решения для гостиничного бизнеса, предлагая надежные функции, такие как несколько вариантов оплаты, повышенную безопасность, улучшенное управление возвратом платежей и прозрачное ценообразование. В качестве предпочтительного платежного решения для бизнес-лидеров, которые превращают коммерцию в конкурентное преимущество, Fortis по-прежнему привержена инновациям, которые предвосхищают растущий спрос на новые способы оплаты, в том числе в сфере гостеприимства.

Узнайте больше о Fortis на сайте fortispay.com. Для получения дополнительной информации о Visual Matrix посетите сайт visualmatrix.com/fortis.

О Fortis

Fortis предоставляет комплексные платежные решения и возможности для коммерции партнерам и разработчикам программного обеспечения, ежегодно обрабатывая миллиарды долларов. Миссия компании состоит в том, чтобы создать целостный опыт коммерции, помогая компаниям достичь невиданного роста и масштабирования. В качестве предпочтительного решения для будущих платежей Fortis приближает коммерцию к невидимости с помощью собственной платформы, которая поддерживает и укрепляет возможности коммерции и платежей партнеров по программному обеспечению. Для получения дополнительной информации посетите сайт fortispay.com.

О Visual Matrix

Более 3000 отелей в более чем 30 странах мира выбирают операционную систему Visual Matrix для гостиничного бизнеса, чтобы оптимизировать работу отеля и обслуживать гостей от бронирования до возвращения. Наша система включает революционную PMS и независимую мобильную операционную платформу (MOP) для использования с Visual Matrix и большинством других систем PMS. Наша PMS предлагает мощные функции и ключевые интеграции, которые просты в использовании, такие как управление доходами с автоматическим распределением ставок/скидок, полностью интегрированный менеджер каналов и мобильное приложение для отслеживания эффективности на ходу. MOP автоматизирует рутинные задачи и оптимизирует общение, чтобы сотрудники стойки регистрации, горничных и обслуживающего персонала могли сосредоточиться на гостях.

No related posts.