Гаусса онлайн – Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса — «Шпаргалка ЕГЭ»
Гаусса онлайн – Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса — «Шпаргалка ЕГЭ»
- by alexxlab
- Советы абитуриенту
Содержание
Решение системы линейных уравнений методом Гаусса с нахождением общего решения
Вообще говоря, на сайте уже есть один калькулятор, решающий СЛАУ методом Гаусса — Решение системы линейных алгебраических уравнений методом Гаусса. Он даже расписывает решение пошагово.
Однако, у него есть некоторые недостатки, которые будет решать новый калькулятор из этой статьи:
Во-первых, предыдущий калькулятор выдает решение в формате с плавающей запятой, тогда как во многих задачниках ответ обычно дается в виде дроби.
Во-вторых, предыдущий калькулятор только определяет факт наличия бесконечного множества решений (неопределенная система), но не выдает решение в общем виде.
В-третьих, предыдущий калькулятор работает только в случае когда число уравнений совпадает с числом неизвестных, и таким образом, не может решать недоопределенных (число неизвестных больше числа уравнений) и переопределенных систем (число неизвестных меньше числа уравнений).
Что касается, второго и третьего пунктов, то универсальность метода Гаусса состоит в том, что на самом деле он годится для систем линейных уравнений с любым числом уравнений и неизвестных, просто это не было использовано.
Описание самого метода Гаусса можно посмотреть по ссылке выше, а под калькулятором подробнее рассмотрены разные случаи (виды систем).
Сам калькулятор, помимо нахождения единственного решения, может находить и общее решение в случае неопределенной системы уравнений.
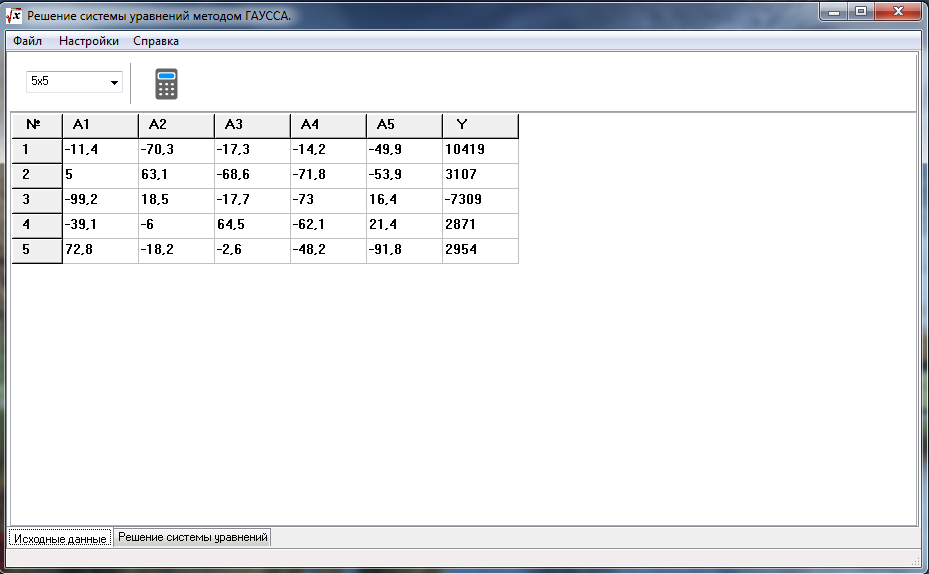
Матрица уравнений из случая 2 ниже (совместная неопределенная система линейных уравнений) использована в нем в качестве входных данных по умолчанию:
1 2 -3 5 1 1 3 -13 22 -1 3 5 1 -2 5 2 3 4 -7 4СЛАУ в матричном виде
Количество решений
Коэффициенты решения
Сохранить share extension
1.
 Совместная определенная система линейных уравнений (имеющая одно решение)
Совместная определенная система линейных уравнений (имеющая одно решение)Пример: пусть дана система линейных уравнений
После приведения матрицы к трапециевидной форме методом Гаусса получим:
Откуда обратным ходом находим единственное решение:
Система совместна и определена.
2. Совместная неопределенная система линейных уравнений (имеющая бесконечное множество решений)
Пример: пусть дана система линейных уравнений:
После приведения матрицы к трапециевидной форме методом Гаусса получим:
В результате приходим к системе:
Последние два уравнения верны при любых значениях переменных:
поэтому их можно отбросить.
Чтобы найти решения оставшихся двух уравнений, x1 и x2 можно выразить через x3 и x4.
При этом сами x3 и x4 могут принимать любые значения
Полученная эквивалентная система совместна, но неопределена. Формулы:
;
при произвольных x3 и x4 описывают бесконечное множество решений заданной системы.
3. Несовместная система линейных уравнений (не имеющая решений)
Пример: пусть дана система линейных уравнений:
Полученная эквивалентная система несовместна, так как последнее уравнение:
не может быть удовлетворено никакими значениями неизвестных.
Эта система несовместна, т. е. не имеет решения.
4. Переопределенная система линейных уравнений (число неизвестных меньше числа уравнений)
Пример: пусть дана система линейных уравнений
После приведения матрицы к трапециевидной форме методом Гаусса получим
Как видим, в данном случае «лишнее» уравнение можно просто отбросить. Также в результате преобразований можно получить одинаковые строки, «лишние» из которых тоже можно отбросить — после чего задача сводится к случаям 1 или 2.
5. Недоопределенная система линейных уравнений (число неизвестных больше числа уравнений)
Пример: пусть дана система линейных уравнений:
После приведения матрицы к трапециевидной форме методом Гаусса получим:
Полученная эквивалентная система имеет вид:
Как видно, в ней отсутствуют уравнения, дающие однозначные значения для x3 и x4, что равносильно появлению уравнений вида:
которые можно отбросить.
Таким образом этот случай сводится к случаю 2 с бесконечным множеством решений, которые описываются следующими формулами:
planetcalc.ru
Решить линейное уравнение методом Гаусса онлайн решателем
Карл Фридрих Гаусс – немецкий математик, механик, физик, астроном и геодезист. Он считается одним из
величайших математиков всех времён, «королём математиков». И даже избирался иностранным почетным членом
Петербургской академии наук. Для творчества Гаусса характерна органическая связь между теоретической и
прикладной математикой, широта проблематики. Труды Гаусса оказали большое влияние на развитие алгебры,
теории чисел, дифференциальной геометрии, математической физики, теории электричества и магнетизма, геодезии
и многих разделов астрономии. Метод Гаусса является самым действующим способом решения систем линейных
уравнений, поскольку ни метод Крамера, ни матричный метод не работают в условиях, когда система имеет
бесконечное количество решений или несовместна.
Так же читайте нашу статью “Решить логарифмическое уравнение онлайн решателем”
Решим следующую систему линейных уравнений методом Гаусса:
\[\left\{\begin{matrix} x_1+2x_2+3x_3-2_x4=1\\ 2x_1-x2-2x_3-3x_4=2\\ 3×1+2x_2-x_3+2x_4=-5\\ 2x_1-3x_2+2x_3+x_4=11 \end{matrix}\right.\]
Сделаем расширенную матрицу:
\[\begin{pmatrix} 1&2&3&-2\\ 2&-1&-2&-3\\ 3&2&-1&2\\ -2&-3&2&1 \end{pmatrix}\sim \\ \sim \begin{pmatrix} 1&2&3&-2\\ 0&-5&-8&1\\ 0&-4&-10&8\\ 0&-7&-4&5 \end{pmatrix}\]
Используя 2 уравнение, избавимся от переменной \[x_2\] в последующих уравнениях:
\[\begin{pmatrix} 1&2&3&-2\\ 0&-5&-8&1\\ 0&-4&-10&8\\ 0&-7&-4&5 \end{pmatrix}\sim \\ \sim \begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&-4&-10&8\\0&-7&-4&5 \end{pmatrix}\]
Выполним исключение переменной \[x_2\] из 3 и 4 уравнений. К 3 строке добавим 2, умноженную на \[\frac{1}{4},
\] а к \[4 – 2,\] умноженную на \[\frac{7}{1}. \]
К 3 строке добавим 2, умноженную на \[\frac{1}{4},
\] а к \[4 – 2,\] умноженную на \[\frac{7}{1}. \]
\[\begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&-4&-10&8\\ 0&-7&-4&5 \end{pmatrix}\sim \\ \sim \begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&0&-18&36\\ 0&0&-18&54 \end{pmatrix}\]
Теперь с помощью третьего уравнения исключим переменную \[x_3\] из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на \[-\frac{18}{18}=-1.\] Получаем расширенную матрицу трапециевидной формы.
\[\begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&0&-18&36\\ 0&0&-18&54 \end{pmatrix}\sim \\ \sim \begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&0&-18&36\\ 0&0&0&18 \end{pmatrix}\]
Заданная система эквивалентна, таким образом, следующей:
\[\left\{\begin{matrix} x_1+2x_2+3x_3-2x_4=1\\ x_2-2x_3+7x_4=-8\\ -18x_3+36x_4=-40\\ 18x_4-7
\end{matrix}\right. \]
\]
Основываясь на полученных данных, делаем вывод, что полученная и данная системы – совместны и определённы. Искомое решение находим “с конца”. Из четвёртого уравнения имеем
\[x_4=-\frac{7}{18}.\]
Это значение подставляем в третье уравнение системы и получаем
\[-18x_3+36(-\frac{7}{18})=-40,\]
откуда
\[x_3=\frac{13}{9}.\]
Далее, подставляем значения \[x_3\] и \[x_4\] во второе уравнение системы:
\[x_2=2\frac{13}{9}+7(-\frac{7}{18})-8,\]
т.е.
\[x_2=-\frac{43}{18}.\]
Наконец, подстановка значений \[x_2, x_3, x_4\] в первое уравнение даёт:
\[x_1+2(-\frac{43}{18})+3(\frac{13}{9})-2(-\frac{7}{18})=1,\]
Получаем:
\[x_1=\frac {2}{3}.\]
Ответ:
\[(x_1=\frac {2}{3}, x_2=-\frac{43}{18}, x_3=\frac{13}{9}, x_4=-\frac{7}{18}).\]
Где можно решить линейные уравнения методом Гаусса онлайн?
Решить систему уравнений вы можете на нашем сайте pocketteacher.ru. Бесплатный онлайн
решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо
сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео
инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы
можете задать их в нашей групе Вконтакте: pocketteacher. Вступайте
в нашу группу, мы всегда рады помочь вам.
Все, что вам необходимо
сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео
инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы
можете задать их в нашей групе Вконтакте: pocketteacher. Вступайте
в нашу группу, мы всегда рады помочь вам.
pocketteacher.ru
Решить уравнение Гаусса онлайн решателем
Карл Фридрих Гаусс – немецкий математик, механик, физик, астроном и геодезист. Он считается одним из величайших математиков всех времён, «королём математиков». И даже избирался иностранным почетным членом Петербургской академии наук. Для творчества Гаусса характерна органическая связь между теоретической и прикладной математикой, широта проблематики. Труды Гаусса оказали большое влияние на развитие алгебры, теории чисел, дифференциальной геометрии, математической физики, теории электричества и магнетизма, геодезии и многих разделов астрономии. Метод Гаусса идеально подходит для решения систем линейных уравнений, поскольку он имеет большее количество преимуществ по сравнению с другими методами, а именно:
– универсальность;
– не требует проверки системы на совместимость;
– минимальное количество математических операций.
Так же читайте нашу статью “Решить неравенство онлайн решателем”
Если возникли сомнения касательно конечного результата, то всегда можно узнать онлайн решение уравнения методом Гаусса и сравнить ответы.
Решим следующее уравнение методом Гаусса:
\[\left\{\begin{matrix} x_1+2x_2+3x_3-2_x4=1\\ 2x_1-x2-2x_3-3x_4=2\\ 3×1+2x_2-x_3+2x_4=-5\\ 2x_1-3x_2+2x_3+x_4=11 \end{matrix}\right.\]
Составляем расширенную матрицу системы
\[\begin{pmatrix} 1&2&3&-2\\ 2&-1&-2&-3\\ 3&2&-1&2\\ -2&-3&2&1 \end{pmatrix} \begin{pmatrix} 1&2&3&-2\\ 0&-5&-8&1\\ 0&-4&-10&8\\ 0&-7&-4&5 \end{pmatrix}\]
Далее необходимо с помощью второго уравнения исключить переменную \[x_2\] из:
\[\begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&-4&-10&8\\ 0&-7&-4&5 \end{pmatrix}\]
Сделаем собственно исключение переменной\[ x_2\] из 3 и 4 уравнений. Для этого к третьей строке прибавим
вторую, умноженную на \[\frac{1}{4},\] а к четвёртой – вторую, умноженную на\[ \frac{7}{1}.\]
Для этого к третьей строке прибавим
вторую, умноженную на \[\frac{1}{4},\] а к четвёртой – вторую, умноженную на\[ \frac{7}{1}.\]
\[\begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&-4&-10&8\\ 0&-7&-4&5 \end{pmatrix} \begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&0&-18&36\\ 0&0&-18&54 \end{pmatrix}\]
Теперь с помощью третьего уравнения исключим переменную \[x_3\] из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на \[ -\frac{18}{18}=-1\]. Получаем расширенную матрицу трапециевидной формы.
\[\begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&0&-18&36\\ 0&0&0&18 \end{pmatrix}\]
Заданная система эквивалентна, таким образом, следующей:
\[ \left\{\begin{matrix} x_1+2x_2+3x_3-2x_4=1\\ x_2-2x_3+7x_4=-8\\ -18x_3+36x_4=-40\\ 18x_4-7 \end{matrix}\right.\]
Следовательно, полученная и данная системы являются совместными и определёнными. Искомое решение находим “с
конца”. Из четвёртого уравнения имеем
Искомое решение находим “с
конца”. Из четвёртого уравнения имеем
\[x_4=-\frac{7}{18}\]
Это значение подставляем в третье уравнение системы и получаем
\[-18x_3+36(-\frac{7}{18})=-40\]
откуда
\[x_3=\frac{13}{9}\]
Далее, подставляем значения\[ x_3\]и \[x_4\] во второе уравнение системы:
\[x_2=2\frac{13}{9}+7(-\frac{7}{18})-8\]
т.е.
\[x_2=-\frac{43}{18},\]
Наконец, подстановка значений
\[x_1+2(-\frac{43}{18})+3(\frac{13}{9})-2(-\frac{7}{18})=1\]
Получаем:
\[x_1=\frac {2}{3}\]
Итак, данная система уравнений имеет единственное решение \[(x_1=\frac {2}{3}, x_2=-\frac{43}{18}, x_3=\frac{13}{9}, x_4=-\frac{7}{18})\].
Где можно решить методом Гаусса систему уравнений онлайн?
Решить систему матричных уравнений онлайн вы можете на нашем сайте pocketteacher.ru.
Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что
вам необходимо сделать – это просто ввести свои данные в решателе.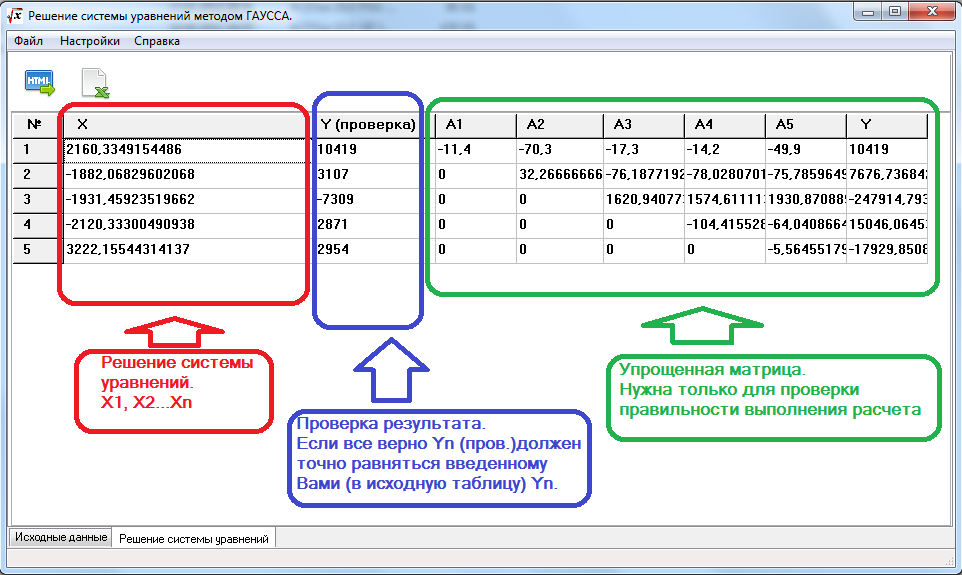 Так же вы можете посмотреть
видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы
можете задать их в нашей групе Вконтакте: pocketteacher. Вступайте
в нашу группу, мы всегда рады помочь вам.
Так же вы можете посмотреть
видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы
можете задать их в нашей групе Вконтакте: pocketteacher. Вступайте
в нашу группу, мы всегда рады помочь вам.
pocketteacher.ru
Гауссом решение онлайн: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса — ЭкоДом: Дом своими руками
Содержание
Как решить систему уравнений. Руководство к онлайн сервису
Построить график функции
Точки разрыва функции
Построение графика методом дифференциального исчисления
Упростить выражение
Примеры решенийРанг матрицыМетод КрамераУмножение матриц
Определитель матрицы
Метод обратной матрицы
Обратная матрица
Метод Гаусса онлайн
LU разложение матрицы
Производная онлайн
В указанных онлайн-калькуляторах решение сохраняется в формате Word со всеми выкладками. Также доступна проверка решений в Excel.
Также доступна проверка решений в Excel.
Прямые методы
- Решение СЛАУ методом Гаусса. Этот сервис также используется для исследования системы алгебраических уравнений с помощью теоремы Кронекера-Капелли.
- Решение СЛАУ методом Крамера происходит через нахождение определителей матрицы.
- Метод обратной матрицы. Также смотрите онлайн-калькулятор по нахождению матричных уравнений (
A*X = B,X*A = B, и других).
Исследование системы линейных уравнений
- Базисные решения системы линейных уравнений.
- Исследование системы линейных уравнений на совместность и определенность.
- Решение системы линейных однородных уравнений позволяет найти нетривиальное и фундаментальное решения.
- Координаты вектора в базисе. В естественном базисе заданы векторы a=(1,1,0)T, b=(1,-1,1)T, c=(-3,5,-6)T, d=(4,-4,5)T.
 Показать, что векторы образуют базис.
Показать, что векторы образуют базис.
Итерационные методы
- Решения СЛАУ методом простой итерации.
- Решения СЛАУ методом Зейделя.
- Решения системы методом декомпозиции (LU-разложение).
см. также раздел Высшая математика онлайн: онлайн-сервисы по аналитической геометрии, линейной алгебре, теории вероятности и другим.
Методы нахождения определителей
- Определитель матрицы разложением по строкам и столбцам через миноры.
- Определитель матрицы методом треугольников
- Определитель матрицы методом понижения порядка
- Определитель методом приведения к треугольному виду (методом Гаусса)
- Определитель матрицы методом декомпозиции
При изучении данной темы могут понадобится следующие онлайн-калькуляторы:
- Ранг матрицы
- Обратная матрица через алгебраические дополнения .Определение миноров матрицы, алгебраических дополнений, транспонированной матрицы
- Обратная матрица методом Жордано-Гаусса
- Умножение матриц
- Преобразование матрицы до треугольной
- LU разложение матрицы
Калькулятор по аналитической геометрии и векторной алгебре
- Помощь в решении
- Поиск
- Поддержать проект
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Системы линейных однородных уравнений онлайн
Системы линейных однородных уравнений — имеет вид ∑akixi = 0.
где m > n или m n.
Однородная система линейных уравнений всегда совместна, так как rangA = rangB. Она заведомо имеет решение, состоящее из нулей, которое называется тривиальным.
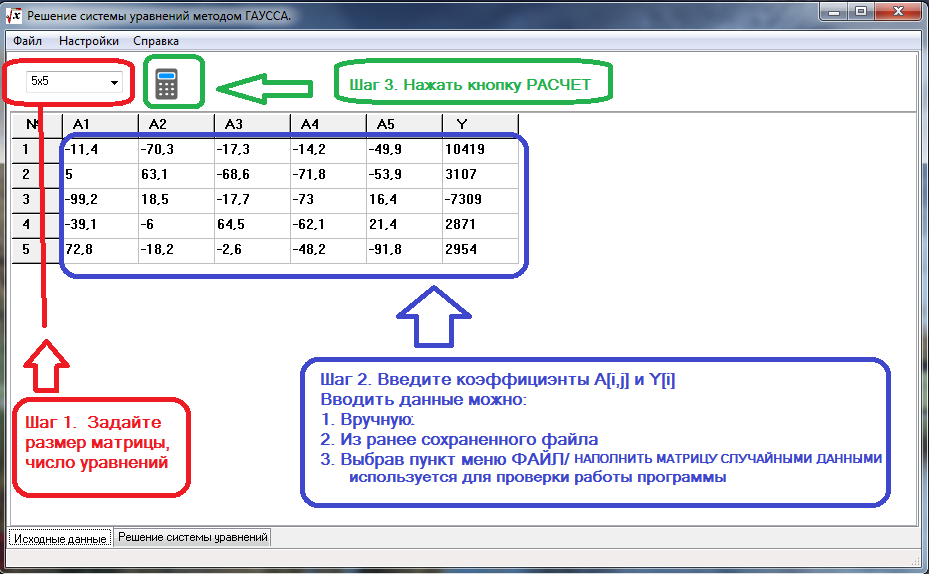
Назначение сервиса. Онлайн-калькулятор предназначен для нахождения нетривиального и фундаментального решения СЛАУ. Полученное решение сохраняется в файле Word (см. пример решения).
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Инструкция. Выберите размерность матрицы:
количество переменных:
2345678
и количество строк
23456
Свойства систем линейных однородных уравнений
Для того чтобы система имела нетривиальные решения, необходимо и достаточно, чтобы ранг ее матрицы был меньше числа неизвестных.
Теорема. Система в случае m=n имеет нетривиальное решение тогда и только тогда, когда определитель этой системы равен нулю.
Теорема. Любая линейная комбинация решений системы также является решением этой системы.
Определение. Совокупность решений системы линейных однородных уравнений называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы является линейной комбинацией этих решений.
Теорема. Если ранг r матрицы системы меньше числа n неизвестных, то существует фундаментальная система решений, состоящая из (n-r) решений.
Алгоритм решения систем линейных однородных уравнений
- Находим ранг матрицы.
- Выделяем базисный минор. Выделяем зависимые (базисные) и свободные неизвестные.
- Вычеркиваем те уравнения системы, коэффициенты которых не вошли в состав базисного минора, так как они являются следствиями остальных (по теореме о базисном миноре).

- Члены уравнений, содержащие свободные неизвестные, перенесем в правую часть. В результате получим систему из r уравнений с r неизвестными, эквивалентную данной, определитель которой отличен от нуля.
- Решаем полученную систему методом исключения неизвестных. Находим соотношения, выражающие зависимые переменные через свободные.
- Если ранг матрицы не равен количеству переменных, то находим фундаментальное решение системы.
- В случае rang = n имеем тривиальное решение.
Пример. Найти базис системы векторов (а1, а2,…,аm), ранг и выразить векторы по базе. Если а1=(0,0,1,-1), а2=(1,1,2,0), а3=(1,1,1,1), а4=(3,2,1,4), а5=(2,1,0,3).
Выпишем основную матрицу системы:
| 0 | 0 | 1 | -1 |
| 1 | 1 | 2 | 0 |
| 1 | 1 | 1 | 1 |
| 3 | 2 | 1 | 4 |
| 2 | 1 | 0 | 3 |
| x1 | x2 | x3 | x4 |
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 2-ую строку на (-1). Добавим 3-ую строку к 2-ой:
| 0 | 0 | 1 | -1 |
| 0 | 0 | -1 | 1 |
| 1 | 1 | 1 | 1 |
| 3 | 2 | 1 | 4 |
| 2 | 1 | 0 | 3 |
Умножим 3-ую строку на (-3). Добавим 4-ую строку к 3-ой:
| 0 | 0 | 1 | -1 |
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 3 | 2 | 1 | 4 |
| 2 | 1 | 0 | 3 |
Умножим 4-ую строку на (-2). Умножим 5-ую строку на (3). Добавим 5-ую строку к 4-ой:
Добавим 5-ую строку к 4-ой:
| 0 | 0 | 1 | -1 |
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
Умножим 3-ую строку на (-1). Добавим 4-ую строку к 3-ой:
| 0 | 0 | 1 | -1 |
| 0 | 0 | -1 | 1 |
| 0 | 0 | 0 | 0 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
В матрице B 1-ая строка нулевая, следовательно, вычеркиваем ее. Это равносильно вычеркиванию 1-го уравнения системы.
| 0 | 0 | 1 | -1 |
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
Добавим 2-ую строку к 1-ой:
| 0 | 0 | 0 | 0 |
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
В матрице B 1-ая строка нулевая, следовательно, вычеркиваем ее. Это равносильно вычеркиванию 1-го уравнения системы.
Это равносильно вычеркиванию 1-го уравнения системы.
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
Найдем ранг матрицы.
| 0 | 0 | -1 | 1 |
| 0 | -1 | -2 | 1 |
| 2 | 1 | 0 | 3 |
| x1 | x2 | x3 | x4 |
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно rang(A) = 3.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x1,x2,x3, значит, неизвестные x1,x2,x3 – зависимые (базисные), а x4 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.
| 0 | 0 | -1 | -1 |
| 0 | -1 | -2 | -1 |
| 2 | 1 | 0 | -3 |
| x1 | x2 | x3 | x4 |
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
— x3 = — x4
— x2 — 2x3 = — x4
2x1 + x2 = — 3x4
Методом исключения неизвестных находим нетривиальное решение:
Получили соотношения, выражающие зависимые переменные x1,x2,x3 через свободные x4, то есть нашли общее решение:
x3 = x4
x2 = — x4
x1 = — x4
M.
7 Исключение Гаусса-Джордана | СТАТ ОНЛАЙН
Исключение Гаусса-Жордана — это алгоритм, который можно использовать для решения систем линейных уравнений и поиска обратной любой обратимой матрицы. Он основан на трех элементарных операциях со строками , которые можно использовать с матрицей:
Он основан на трех элементарных операциях со строками , которые можно использовать с матрицей:
- Поменять местами две строки
- Умножить одну из строк на ненулевой скаляр.
- Добавить или вычесть скалярное число, кратное одной строке, другой строке.
В качестве примера операции с первой элементарной строкой поменяйте местами 1-ю и 3-ю строки.
\[ \begin{pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \end{pmatrix}\Стрелка вправо \begin{pmatrix} 7 & 5 & 0 \\ 2 & -2 & 3 \\ 4 & 0 & -1 \end{pmatrix} \]
В качестве примера операции со второй элементарной строкой умножьте вторую строку на 3.
\[ \begin{pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \end{pmatrix} \Стрелка вправо \begin{pmatrix} 4 & 0 & -1 \\ 6 & -6 & 9\\ 7 & 5 & 0 \end{pmatrix} \]
В качестве примера операции с третьей элементарной строкой дважды добавьте 1-ю строку ко 2-й строке.
\[ \begin{pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \end{pmatrix}\Стрелка вправо \begin{pmatrix} 4 & 0 & -1 \\ 10 & -2 & 1 \\ 7 & 5 & 0 \end{pmatrix} \]
Эшелонная форма с уменьшенной строкой
Цель исключения Гаусса-Жордана состоит в использовании трех элементарных операций над строками для преобразования матрицы в ступенчато-редуцированная форма. Матрица в Эшелонная форма с уменьшенной строкой , также известная как каноническая форма строки , если выполняются следующие условия:
- Все строки только с нулевыми элементами находятся внизу матрицы
- Первая ненулевая запись в строке, называемая ведущей записью или опорной , каждой ненулевой строки находится справа от ведущей записи строки над ней.
- Начальная запись, также называемая сводной, в любой ненулевой строке равна 1.
- Все остальные записи в столбце, содержащие ведущую единицу, равны нулю.

Например,
\[A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 3 \\ 0 & 0 & 0 \end{pmatrix}, B = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}, C = \begin{pmatrix} 0 & 7 & 3 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end {pmatrix}, D = \begin{pmatrix} 1 & 7 & 3 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \]
Матрицы A и B имеют эшелонированную форму с уменьшенными строками, а матрицы C и D — нет. C не находится в форме эшелона с уменьшенным рядом, потому что нарушает два и три условия. D не находится в форме эшелона с уменьшенным рядом, потому что нарушает условие четыре. Кроме того, элементарные операции со строками можно использовать для сведения матрицы D к матрице B .
Этапы исключения Гаусса-Жордана
Чтобы выполнить исключение Гаусса-Жордана:
- Поменять местами строки так, чтобы все строки со всеми нулевыми элементами были внизу
- Поменяйте местами строки так, чтобы строка с самой большой, самой левой ненулевой записью была наверху.

- Умножить верхнюю строку на скаляр, чтобы первая запись верхней строки стала равной 1.
- Прибавьте/вычтите несколько значений из верхней строки к другим строкам, чтобы все остальные записи в столбце, содержащем ведущую запись из верхней строки, были равны нулю.
- Повторяйте шаги 2–4 для следующей крайней слева ненулевой записи, пока все ведущие записи не будут равны 1.
- Поменяйте местами строки так, чтобы начальный элемент каждой ненулевой строки находился справа от ведущего элемента строки над ним.
Ниже показаны избранные примеры видео:
- Исключение Гаусса-Джордана — Джонатан Митчелл (YouTube)
- Использование Гаусса-Жордана для решения системы трех линейных уравнений — пример 1 — patrickJMT (YouTube)
- Алгебра — Матрицы — Метод Гаусса Джордана, часть 1 Расширенная матрица — IntuitiveMath (YouTube)
- Исключение Гаусса — patrickJMT (YouTube)
Чтобы получить обратную матрицу n × n A :
- Создайте разбитую матрицу \(( A | I )\) , где I — единичная матрица.
 {-1} )\) 9{-1} = I\).
{-1} )\) 9{-1} = I\).
GAUSS ELMANICATE CALCUTUTUTOR
x = 0,087
Y = 2,6087
z = -1,1304
Рассчитайте
Отчет об этом AD
Рассчитайте
leminic линейных уравнений. Этот метод также называется методом исключения Гаусса-Жордана. Он представлен последовательностью операций, выполняемых над матрицей. Метод назван в честь Карла Фридриха Гаусса (1777-1855), хотя был известен китайским математикам.
Метод решения системы линейных уравнений методом исключения Гаусса аналогичен методу решения матриц. Например, существует связь между системой трех линейных уравнений и ее матрицей коэффициентов.
$$\begin{align} &a_1x+b_1y+c_1z={ d_1}\\
&a_2x+b_2y+c_2z={ d_2}\\
&a_3x+b_3y+c_3z={ d_3}\\
\end{выравнивание} \quad\longmapsto \left(
\begin{массив}{ccc}
{a_1} и b_1 &c_1\\
{a_2} &b_2 &c_2\\
{a_3} &b_3 &c_3\\
\конец{массив}
\справа)$$
Существует три типа операций с элементарными строками:
- Замена двух рядов;
- Умножение строки на ненулевое число;
- Добавление кратного одной строки к другой строке.

Метод исключения Гаусса состоит из двух частей. Первая часть сводит данную систему к \underline{эшелонной форме строк}. Из эшелонированной формы строки мы можем сделать вывод, имеет ли система решения, единственное решение или бесконечно много решений. Вторая часть использует операции со строками до тех пор, пока не будет найдено решение.
Эшелонная форма строки удовлетворяет следующим свойствам:
- Старший коэффициент каждой строки должен быть равен $1$;
- Все элементы в столбце ниже начального $1$ должны быть $0$;
- Все строки, содержащие нули, находятся внизу матрицы.
Например, следующие матрицы имеют эшелонированную форму строк.
$$\слева(
\begin{массив}{cc}
1 и 5 \\
0 и 1 \\
\конец{массив}
\право), \четверо \лево(
\begin{массив}{cccc}
1 и 1 и 0 и 5 \\
0 и 1 и 3 и 4 \\
0&0 & 1 & 2 \\
\конец{массив}
\право), \четверо \лево(
\begin{массив}{cccc}
1 и 2 и 3 и 4 \\
0 и 1 и 3 и 4 \\
0&0 & 1 & 2 \\
0&0 & 0 &0 \\
\конец{массив}
\справа)$$
Матрица в
сокращенный эшелон строки
форма, если, кроме того, в каждом столбце, содержащем старший коэффициент, все остальные элементы в этом столбце равны нулю.
Например, матрицы, показанные ниже, являются примерами матриц в сокращенной эшелонированной форме строк.
$$\слева(
\begin{массив}{cc}
1 и 0 \\
0 и 1 \\
\конец{массив}
\право), \четверо \лево(
\begin{массив}{cccc}
1 и 0 и 0 и 7 \\
0 и 1 и 0 и -2 \\
0&0 & 1 & 2 \\
\конец{массив}
\право), \четверо \лево(
\begin{массив}{cccc}
1 и 0 и 0 и 2 \\
0 и 1 и 0 и -2 \\
0&0 & 1 & 2 \\
0&0 & 0 &0 \\
\конец{массив}
\справа)$$
Расширенная матрица
— это матрица, полученная путем сложения столбцов двух заданных матриц. В случае решения системы нам необходимо увеличить матрицу коэффициентов и матрицу констант. Вертикальная линия указывает на разделение между матрицей коэффициентов и постоянной матрицей. Итак, для системы трех уравнений
$$\begin{align} &a_1x+b_1y+c_1z={ d_1}\\
&a_2x+b_2y+c_2z={ d_2}\\
&a_3x+b_3y+c_3z={ d_3}\\
\end{выравнивание}$$
расширенная матрица
$$\слева(
\begin{массив}{ccc|c}
a_1 & b_1 & c_1 & d_1 \\
а_2 и б_2 и с_2 и d_2 \\
a_3&b_3&c_3&d_3\\
\конец{массив}
\справа)$$
Количество решений системы зависит только от ранга матрицы, представляющей систему, и ранга соответствующей расширенной матрицы. Согласно теореме Кронекера-Капелли любая система из трех линейных уравнений не имеет решений, если ранг расширенной матрицы больше ранга матрицы коэффициентов. Если ранги этих двух матриц равны, то система должна иметь хотя бы одно решение. Решение единственно тогда и только тогда, когда ранг равен количеству переменных, в данном случае, если ранг равен $3$.
Согласно теореме Кронекера-Капелли любая система из трех линейных уравнений не имеет решений, если ранг расширенной матрицы больше ранга матрицы коэффициентов. Если ранги этих двух матриц равны, то система должна иметь хотя бы одно решение. Решение единственно тогда и только тогда, когда ранг равен количеству переменных, в данном случае, если ранг равен $3$.
Например, решим решение системы методом исключения Гаусса
$$\begin{align} &4x+5y+3z={ 10}\\
&3x+6y+7z={ 8}\\
&2x+3y+0z={ 8}\\
\end{выравнивание}$$
Коэффициенты и постоянные члены системы дают матрицы
$$\слева(
\begin{массив}{ccc}
4 и 5 и 3\\
3 &6 &7\\
2 &3&0\\
\конец{массив}
\право),\четверо\лево(
\начать{массив}{с}
10\
8\
8\
\конец{массив}
\справа)$$
Расширенная матрица
$$\слева(
\begin{массив}{ccc|c}
4 и 5 &3&10\\
3 &6 &7&8\\
2 &3&0&8\\
\конец{массив}
\справа)$$
Чтобы решить систему, приведите расширенную матрицу к уменьшенной ступенчатой форме строки следующим образом.
- Разделите строку $1$ на $4$ ($R_1=\frac {R_1}4)$, чтобы получить
$$\слева(
\begin{массив}{ccc|c}
1 & \ гидроразрыв 54 & \ гидроразрыв 34 & \ гидроразрыв {5} 2 \\
3 &6 &7&8\\
2 &3&0&8\\
\конец{массив}
\right)$$ - Вычесть строку $1$, умноженную на $3$, из строки $2$ ($R_2=R_2-3R_1$), чтобы получить
$$\слева(
\begin{массив}{ccc|c}
1 & \ гидроразрыв 54 & \ гидроразрыв 34 & \ гидроразрыв {5} 2 \\
0 &\frac 94 &\frac{19}4&\frac 12\\
2 &3&0&8\\
\конец{массив}
\right)$$ - Вычесть строку $1$, умноженную на $2$, из строки $3$ ($R_3=R_3-2R_1$), чтобы получить
$$\слева(
\begin{массив}{ccc|c}
1 & \ гидроразрыв 54 & \ гидроразрыв 34 & \ гидроразрыв {5} 2 \\
0 &\ гидроразрыв 94 &\ гидроразрыв{19}4&\ гидроразрыв 12\\
0 &\frac12 &-\frac 32&3\\
\конец{массив}
\right)$$ - Умножьте строку $2$ на $\frac 49$ ($R_2=\frac49 R_2$), чтобы получить
$$\слева(
\begin{массив}{ccc|c}
1 & \ гидроразрыв 54 & \ гидроразрыв 34 & \ гидроразрыв {5} 2 \\
0 &1 &\frac{19}9&\frac 29\\\
0 &\frac12 &-\frac 32&3\\
\конец{массив}
\right)$$ - Вычесть строку $2$, умноженную на $\frac 54$, из строки $1$ ($R_1=R_1-\frac54 R_2$), чтобы получить
$$\слева(
\begin{массив}{ccc|c}
1 & 0 &-\frac {17}9&\frac{20}9\\
0 &1 &\frac{19}9&\frac 29\\
0 &\frac12 &-\frac 32&3\\
\конец{массив}
\right)$$ - Вычесть строку $2$, умноженную на $\frac 12$, из строки $3$ ($R_3=R_3-\frac12R_2$), чтобы получить
$$\слева(
\begin{массив}{ccc|c}
1 & 0 &-\frac {17}9&\frac{20}9\\
0 &1 &\frac{19}9&\frac 29\\
0 &0&-\frac{23}9&\frac{26}9\\
\конец{массив}
\right)$$ - Умножьте строку $3$ на $-\frac9{23}$ ($R_3=-\frac9{23}R_3$), чтобы получить
$$\слева(
\begin{массив}{ccc|c}
1 и 0 &-\фракция {17}9&\ гидроразрыв{20}9\\
0 &1 &\frac{19}9&\frac 29\\
0 &0&1&-\фракция{26}{23}\\
\конец{массив}
\right)$$ - Добавьте строку $3$, умноженную на $\frac{17}9$, к строке $1$ ($R_1=R_1+\frac{17}9R_3$), чтобы получить
$$\слева(
\begin{массив}{ccc|c}
1 & 0 &0&\frac2{23}\\
0 &1 &\frac{19}9&\frac 29\\
0 &0&1&-\фракция{26}{23}\\
\конец{массив}
\right)$$ - Вычесть строку $3$, умноженную на $\frac {19}9$, из строки $2$ ($R_2=R_2-\frac{19}9R_3$), чтобы получить
$$\слева(
\begin{массив}{ccc|c}
1 & 0 &0&\frac2{23}\\
0 &1 &0&\фракция {60}{23}\\
0 &0&1&-\фракция{26}{23}\\
\конец{массив}
\справа)$$
Таким образом, решение системы $(x, y, z) = (\frac{2}{23},\frac{60}{23}, -\frac{26}{23})$.
Работа по исключению Гаусса с шагами показывает полный пошаговый расчет для нахождения решения линейной системы из трех уравнений с использованием метода исключения Гаусса. Для любой другой системы просто введите двенадцать действительных чисел в качестве коэффициентов линейных уравнений и нажмите кнопку «Создать работу». Учащиеся начальной школы используют этот калькулятор исключения Гаусса для создания работы, проверки результатов решения систем линейных уравнений, полученных вручную, или для эффективного решения домашних задач. Во многих приложениях необходимо вычислить исключение матрицы, где этот онлайн-калькулятор исключения матрицы Гаусса может помочь легко упростить вычисления для соответствующих входных данных.
Практические задачи на исключение Гаусса
Практическая задача 1:
Используя метод исключения Гаусса, решите систему уравнений
$$\begin{align} &2x+4y-z=-1\\
&х+3у+7г=2\\
&х+2у+г=-5\\
\end{выравнивание} $$
Практическая задача 2:
Математическая библиотека хочет купить книги по 25$ за 2800$.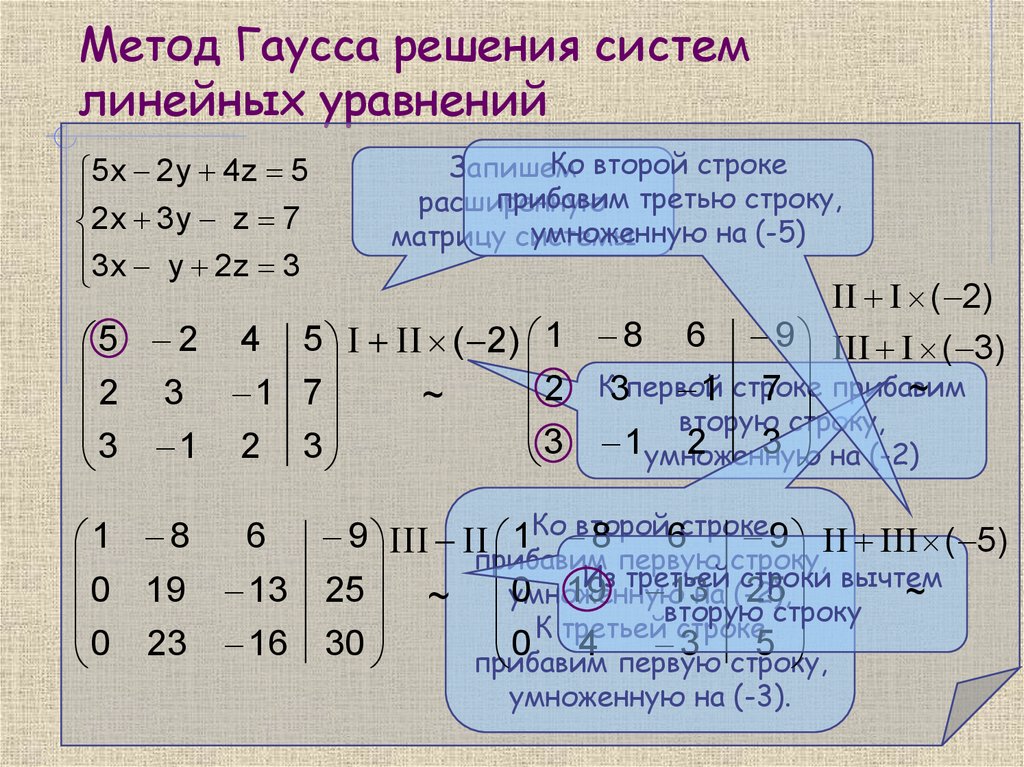
Решение линейных систем: исключение Гаусса
Вы здесь
Главная » Решение линейных систем: исключение Гаусса
Уменьшенная ступенчатая форма матрицы уникальна: простое доказательство
Капсулы MAA для занятий в классе и заметки
Исключение Гаусса в целочисленной арифметике: применение факторизации \(L\)-\(U\)
капсулы MAA для занятий в классе и заметки
Использование условий согласованности для решения линейных систем
Капсулы MAA для занятий в классе и заметки
Редукция Гаусса-Жордана: краткая история
Сообщество курсов
Исключение Гаусса
Сообщество курсов
Демонстрации линейной алгебры, Drexel Univ
Сообщество курса
Концептуальная линейная алгебра онлайн
Сообщество курсов
Онлайн-лаборатория математики в Калифорнийском университете в Санта-Барбаре
Сообщество курсов
Набор инструментов для линейной алгебры
Сообщество курсов
Апплет исключения Гаусса
Курс Сообщество
Math 220 Tutorials — Коллекция анимаций для матричных и векторных операций.

Сообщество курсов
Конечная математика 6e
Сообщество курсов
Плоскости, решения и исключение по Гауссу линейной системы \(3\x3\)
Сообщество курсов
Линейные уравнения: представление строк и столбцов
Сообщество курсов
Поворот и инструмент Gauss-Jordan
Сообщество курсов
Редуктор ряда
Сообщество курсов
Поворот и инструмент Gauss-Jordan
Сообщество курсов
Матричный калькулятор
Сообщество курсов
Калькулятор исключения Гаусса Джордана
Сообщество курсов
Матричный онлайн-калькулятор
Сообщество курсов
Форма эшелона рядов
Сообщество курсов
Матричный калькулятор
Сообщество курсов
Исключение Гаусса-Джордана
Сообщество курсов
Онлайн-калькулятор матриц
Сообщество курсов
Апплеты Теренса Тао
Сообщество курсов
Поворотный двигатель Previte
Сообщество курсов
LAVA: помощник по визуализации линейной алгебры
Сообщество курсов
Множитель матрицы
Сообщество курсов
Простое решение для «мини-выключения света»
Капсулы MAA для занятий в классе и заметки
Капсулы для занятий и заметки для решения линейных систем: исключение Гаусса в линейной алгебре
Сообщество курса
Страницы
- 1
- 2
- следующий ›
- последний »
Пустой вид — НЕ УДАЛИТЬ
Зарегистрируйтесь сейчас для AMC 8 и 12/10
Ваш новый портал для участников MAA запущен!
подписчикам скидка 25%
▷Step by Step Приложения для TI-Nspire CX и CX CAS Скачать бесплатно.
 Получите высшие баллы по математике, естественным наукам и бизнесу
Получите высшие баллы по математике, естественным наукам и бизнесуДля подготовки к экзаменам по математике и естественным наукам, домашнее задание. Проверьте свою работу.
— Шаг за шагом к успеху. Приложения запускаются за считанные минуты. Сначала протестируйте наши бесплатные пробные версии.—
| 95% купили больше ПРИЛОЖЕНИЙ. | 97% сообщили об улучшении результатов. | Рейтинг: 4,89 из 5 звезд. | Доступно 46 ПРИЛОЖЕНИЙ. |
КОВИД СПЕЦИАЛЬНЫЙ
Купите 3 приложения Made Easy по цене 2 приложений.
Выберите 3 приложения. EasyBusiness Stats Made EasyCalculus with Physics Apps Calculo de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht Gemacht DiscreteMDisateM de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenieu r Mathematik Leicht GemachtFinance Made EasyКонечная математика Made EasyGeometry Made EasyGeometrie Leicht GmachtGeometria de Manera FacilLand Survey Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GmachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyЧисленный анализ Made EasyТеория чисел Made EasyPhysik LeachPhysich Research Made EasyPhysik Research Made EasyPhysik GemachtFisica de Manera FacilPortfolio & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathSignals and Systems Made EasyStatistics and Probability Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatic and Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equation Solver Ecuaciones de Manera FacilПошаговый конвертер единиц измеренияThermodynamic Made EasyThermodynamik Leicht GemachtTransforms Made EasyTrigonometry Made EasyTrigonometri a de Manera FacilTrigonometrie Leicht GemachtVector Calculus Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht
Calculus Made EasyACT Made EasyAccounting Made EasyAerodynamic Made EasyAnalysis Leicht GemachtAnalysis mit PhysikAlgebra Made Easy CX CASAlgebra Made Easy CXAlgebra Leicht Gemacht CX CASAlgebra de Manera FacilAlgebra de Manera Facil CXApplications and Optimizations Made EasyBiology Made EasyBiostatistics AppBusiness Calculus Made EasyBusiness Stats with Physics de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht GemachtDiscrete Math Made EasyMatematicas Discretas de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenieur Mathematik Leicht GemachtFinance Mad e EasyFinite Math Made EasyGeometry Made EasyGeometrie Leicht GemachtGeometria de Manera FacilLand Surveying Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GemachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyNumerical Analysis Made EasyNumber Theory Made EasyProperties Research Made EasyPhysik Made EasyPhysik Leicht Gemacht & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathСигналы и системы Made EasyСтатистика и вероятность Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatik und Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equal SolverSolucionador de EcuacionesStep de Manera Facil by Step Unit ConverterThermodynamic Made EasyThermodynamik Leicht GemachtTransforms Made EasyTrigonometry Made EasyTrigonometria de Manera FacilTrigonometrie Leicht GemachtVector Calculus Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht
Calculus Made EasyACT Made EasyAccounting Made EasyAerodynamic Made EasyAnalysis Leicht GemachtAnalysis mit PhysikAlgebra Made Easy CX CASAlgebra Made Easy CXAlgebra Leicht Gemacht CX CASAlgebra de Manera FacilAlgebra de Manera Facil CXApplications and Optimizations Made EasyBiology Made EasyBiostatistics AppBusiness Calculus Made EasyBusiness Stats with Physics de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht GemachtDiscrete Math Made EasyMatematicas Discretas de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenieur Mathematik Leicht GemachtFinance Mad e EasyFinite Math Made EasyGeometry Made EasyGeometrie Leicht GemachtGeometria de Manera FacilLand Surveying Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GemachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyNumerical Analysis Made EasyNumber Theory Made EasyProperties Research Made EasyPhysik Made EasyPhysik Leicht Gemacht & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathСигналы и системы Made EasyСтатистика и вероятность Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatik und Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equal SolverSolucionador de EcuacionesStep de Manera Facil by Step Unit ConverterThermodynamic Made EasyThermodynamik Leicht GemachtTransforms Made EasyTrigonometry Made EasyTrigonometria de Manera FacilTrigonometrie Leicht GemachtVector Calculus Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht
Введите последние 8 цифр вашего 27-значного идентификатора продукта TI-Nspire.
Находится в разделе 5:Настройки → 4:Статус → О программе
ID может выглядеть так: 1008000007206E210B0 BD92F455 .
ПОМОГИТЕ НАЙТИ ID.
Если бы это был ваш ID, вы бы набрали только BD92F455.
или на международном уровне:
В конце оплаты PayPal вам будет отправлено электронное письмо, содержащее ваш ключ и программное обеспечение.
Хотите купить TI-калькулятор?
Получите самые низкие цены на TI-Calculators
(со сравнением цен)
СРАВНИТЕ лучшие цены на Amazon, Ebay, Target, Walmart, Office Max, Best Buy.
Сравните лучшие цены на Amazon, Walmart, Ebay, Target, Best Buy и т. д.
Изучите историю цен калькуляторов за последние несколько месяцев.
Установите оповещение по электронной почте при снижении цен, чтобы получать уведомления.
Сравните различные модели, чтобы найти калькулятор, который лучше всего соответствует вашим потребностям.
Найдите новые, обновленные, отремонтированные, подержанные калькуляторы.
Смотрите обучающие видео и читайте руководства по калькуляторам.
Читайте последние новости о калькуляторах в Интернете.
БЕСПЛАТНАЯ загрузка:
Решатель квадратных уравнений (шаг за шагом)
Загрузите пошаговый решатель квадратных уравнений
. Этот решатель является частью приложения Algebra Made Easy.
— Загрузите бесплатные пробные версии здесь.
-Пробные и платные приложения не имеют срока действия.
— Будущие обновления бесплатны — навсегда!
Онлайн-репетиторство по математике
Получите онлайн-репетиторство.
Репетиторы с отличными оценками по математике будут рады помочь вам.
Получите индивидуальную помощь по математике.
Мы используем Zoom для обучения онлайн, мы шаг за шагом объясняем, как решать математические задачи.

 Показать, что векторы образуют базис.
Показать, что векторы образуют базис.



 {-1} )\) 9{-1} = I\).
{-1} )\) 9{-1} = I\).