Переходные неравенства: онлайн калькулятор | BBF.RU
Понятие неравенство связано со сравнением двух числовых объектов или алгебраических выражений. Смысл неравенства познается вместе со смыслом таких определений как больше или меньше, выше или ниже, дороже или дешевле, дальше или ближе, холоднее или теплее.
Определение неравенства
Два любых числа или алгебраических выражения, которые соединены знаками отношения «больше» (>), «меньше» (<), «больше либо равно» (≥), «меньше либо равно» (≤) или «неравно» (≠), образуют неравенства. Знаки неравенства в их сегодняшнем виде предложил английский математик Томас Гарриот, который работал над развязыванием систем неравенств и опубликовал свои труды в печати. Обозначения «>» и «<» приглянулись не только математикам, но и книгопечатникам, так как знаки представляли собой просто перевернутую на 90 градусов литеру V.
Существует два фундаментальных класса неравенств. Неравные выражения со знаками «больше» и «меньше» считаются строгими и записываются как:
5 > 3 или 34 < 56
Нестрогие неравенства — это соотношения со знаком равно, которые обычно используются в буквенных неравенствах, когда значение одного аргумента неизвестно.
Например, в выражении:
x + 3 ≥ 4,
при x = 1 неравенство тождественно и выглядит как 4 = 4, а при всех x > 1 выражение также тождественно и принимает выражения 5 > 4, 6 > 4 и так далее.
При решении неравенств с неизвестными строгие и нестрогие знаки крайне важны при определении области допустимых значений функции. Например, если x > 3, то это означает, что он хоть на одну миллиардную долю, но больше 3, следовательно, тройка никогда не входит в область допустимых значений. При нестрогом неравенстве x≥3 включает в диапазон решений собственно тройку и все, что больше нее.
Виды неравенств
Выражения вида a > b и c > d называются неравенствами одинакового смысла. Такое название выражения получили из-за одинаковых знаков. Если же выражения выглядят как a > b и c < d, то такие числовые объекты считаются неравенствами противоположного смысла. К примеру, два выражения x > 3 и y > 4 считаются неравенствами одного смысла, а вот x > 3 и y < 5 — противоположного.
Буквенные неравенства противоположного смысла могут объединяться в двойные. Например, если x > 3 и x < 5, то такое выражение можно переписать как двойное неравенство 3 < x < 5. Это означает, что аргумент функции лежит строго в пределах от 3 до 5.
Свойства неравенств
Неравенства обладают несколькими полезными свойствами. Рассмотрим подробнее.
Свойство №1
Если a > b, то a + c > b + c. Если к обеим сторонам неравного соотношения прибавить одно и то же число или алгебраическое выражение, то знак неравенства не изменится.
Пример
Пусть есть выражение 10 > 5. Добавим к каждой части по 5. Получим 15 > 10, что верно. Добавим к каждой части по отрицательному числу, например, по — 2. Получим 8 > 3, и вновь верно. Точно также можно добавлять неизвестные аргументы и целые полиномы.
Свойство №2
Если a > b и n > 0, то a×n > b×n. Если обе части неравного соотношения умножить на одно и то же положительное число, то знак останется прежним.
Пример
Вновь посмотрим на числовое соотношение 10 > 5. Примем n = 2 и умножим обе части выражения на n. Получим 20 > 10. Очевидно, что все сходится.
Свойство №3
Если a < b и n < 0, то a × n > b × n. Если обе стороны неравенства умножить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.
Пример
Пусть у нас есть неравенство 10 > 5 и n = -2. Умножим обе части на минус 2 и получим, что -20 < -10. С отрицательными числами не всегда очевидно, ведь даже при сравнении температуры мы говорим, что мороз «увеличился», в то время как показатели на градуснике уменьшились. Тем не менее минус 20 явно меньше минус 10.
Свойство №4
Если a > b и b > c, то верно выражение a > c. Такое выражение называется переходным неравенством, и наш калькулятор работает именно с такими числовыми объектами. Задаваясь значениями переменных a, b, c мы можем составить переходное неравенство, которое соответствует свойству всех числовых соотношений.
Пример
Допустим есть выражение 10 > 5 и 5 > 3. В этом случае a = 10, b = 5, c = 3. Согласно четвертому свойству в результате получится, что a > c или 10 > 3. Вполне логично.
Наша программа представляет собой калькулятор, определяющий соотношения чисел в качестве переходного неравенства. Для работы с онлайн-инструментом требуется ввести значения a, b и c, после чего программа решит, составляют ли введенные значения переходное неравенство или нет.
Заключение
Неравные числовые или буквенные соотношения и их системы широко используются в самых разных прикладных науках. Например, изучение проблем макроэкономики осуществляется путем составления и решения систем нелинейных неравенств. Классические неравенства используются в высшей математике: неравенство Коши применяется при сравнении площадей, а неравенство Бернулли — для сравнения иррациональных чисел. Кроме того, существуют неравенства, которые являются однозначным способом доказательства существования некоторых объектов.
Используйте наши инструменты для работы с переходными неравенствами.
Решебник Неравенств Онлайн – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
Решебник Неравенств Онлайн
Подробное решение любых неравенств онлайн . Шаг 1 . Введите неравенство . Подробно решает любые неравенства онлайн с возможностью изобразить неравенство на рисунке .
Используя наш онлайн калькулятор, вы без труда получите решение любой своей задачи на тему неравенств . Решение неравенств происходит за считанные секунды .
Калькулятор онлайн . Решение неравенств : линейные, квадратные и дробные . Программа решения неравенств не просто даёт ответ задачи, она приводит подробное решение с . .
Решение неравенств онлайн . Неравенства — это выражения вида Решить приведённое выше неравенство, означает найти совокупность всех значений переменной x при которых . .
Онлайн калькулятор подходит для решения любых неравенств , если Вы не нашли подходящего калькулятора в разделе решения неравенств, то попробуйте воспользоваться данным .
.
Неравенства по-шагам . В неравенстве неизвестная . Результат . Примеры неравенств . Логарифмические неравенства . log(x + 27) — log(16-2*x) > log(x) .
Неравенства . Тождества . Неравенства любого вида . Тригонометрическое тождество . Матрицы .
Решение любых неравенств онлайн — неравенства с модулем, алгебраические Неравенства онлайн для решения математики . Быстро найти решение неравенства в режиме онлайн .
Любое неравенство или система неравенств может быть решена на нашем сайте используя Калькулятор за пару секунд . Решить неравенство с помощью калькулятора просто .
Онлайн решение задач, решение уравнений онлайн , решение неравенств онлайн , решение интегралов онлайн , решение логарифмов онлайн , решение пределов онлайн, нахождение . .
Неравенства в математике являются утверждением о порядке двух объектов (один из Неравенство – это два математических выражения, соединенных одним из таких знаков, как . .
Бесплатный сервис по решению математических задач даст ответы к вашему домашнему заданию по алгебре с пошаговым объяснением .
Здесь можно решить неравенство онлайн с подробным ответом . 23,852 просмотров всего, 11 просмотров сегодня .
Используйте наш бесплатный алгебраический калькулятор, чтобы получить пошаговые решения математических задач . Поддерживаются начальная математика, начальная алгебра, алгебра . .
Линейные, иррациональные, квадратные, логарифмические, рациональные, дробнорациональные неравенства ; решение неравенств . Калькуляторы по алгебре .
Подробное решение любых неравенств онлайн . Шаг 1 . Введите неравенство . Подробно решает любые неравенства онлайн с возможностью изобразить неравенство на рисунке .
Используя наш онлайн калькулятор, вы без труда получите решение любой своей задачи на тему неравенств . Решение неравенств происходит за считанные секунды .
Калькулятор онлайн . Решение неравенств : линейные, квадратные и дробные . Программа решения неравенств не просто даёт ответ задачи, она приводит подробное решение с . .
Решение неравенств онлайн .
Неравенства — это выражения вида Решить приведённое выше неравенство, означает найти совокупность всех значений переменной x при которых . .
Онлайн калькулятор подходит для решения любых неравенств , если Вы не нашли подходящего калькулятора в разделе решения неравенств, то попробуйте воспользоваться данным . .
Неравенства по-шагам . В неравенстве неизвестная . Результат . Примеры неравенств . Логарифмические неравенства . log(x + 27) — log(16-2*x) > log(x) .
Неравенства . Тождества . Неравенства любого вида . Тригонометрическое тождество . Матрицы .
Решение любых неравенств онлайн — неравенства с модулем, алгебраические Неравенства онлайн для решения математики . Быстро найти решение неравенства в режиме онлайн .
Любое неравенство или система неравенств может быть решена на нашем сайте используя Калькулятор за пару секунд . Решить неравенство с помощью калькулятора просто .
Онлайн решение задач, решение уравнений онлайн , решение неравенств онлайн , решение интегралов онлайн , решение логарифмов онлайн , решение пределов онлайн, нахождение .
.
Неравенства в математике являются утверждением о порядке двух объектов (один из Неравенство – это два математических выражения, соединенных одним из таких знаков, как . .
Бесплатный сервис по решению математических задач даст ответы к вашему домашнему заданию по алгебре с пошаговым объяснением .
Здесь можно решить неравенство онлайн с подробным ответом . 23,852 просмотров всего, 11 просмотров сегодня .
Используйте наш бесплатный алгебраический калькулятор, чтобы получить пошаговые решения математических задач . Поддерживаются начальная математика, начальная алгебра, алгебра . .
Линейные, иррациональные, квадратные, логарифмические, рациональные, дробнорациональные неравенства ; решение неравенств . Калькуляторы по алгебре .
ГДЗ По Математике 4 Класса Демидовой
ГДЗ По Русскому Бунеев
City Stars 6 Класс Учебник ГДЗ Ответы
Решебник 3 Класс Бененсон
ГДЗ По Огэ 3000 Задач Ященко 2020
ГДЗ По Дидактике Математике 5 Класс
ГДЗ 4 Класс Иванова Ленара
История России 7 Класс Пчелова ГДЗ
ГДЗ По Геометрии Бутузов Кадомцев
ГДЗ Афанасьева 7 Класс Часть 1
Русский Язык 9 Класс Бархударов ГДЗ 24
ГДЗ По Истории Класс Юдовская
Николина 7 Класс ГДЗ Рабочая Тетрадь
ГДЗ 1 Класс Климова
ГДЗ По Литературному Чтению Кубасова Рабочая
ГДЗ Алгебра 8 Мерзляк Якир
Арефьев 7 Класс Решебник
Решебник 8 Звавич
ГДЗ По Биологии Беляев Учебник
ГДЗ По Математике Учебник Фгос
ГДЗ По Алгебре 10 11 Кл Мордкович
Решение Математики ГДЗ
ГДЗ По Русскому 7 Класс Богдановой
ГДЗ По Английскому Языку 10 Учебник
ГДЗ По Русскому Языку 6 Класс Женский
ГДЗ Комарова 10 Класс Углубленный Уровень
Решебник Математика 1 Класс Башмаков
ГДЗ По Истории Нового Времени
ГДЗ Матем Раб
7 Класс Алгебра Мордкович ГДЗ 2 Часть
ГДЗ По Русскому Языку Учебник Канакина
ГДЗ По Геометрии 9 Класс Якир
6 Класс Русский Язык Капинос Решебник
ГДЗ Учебно Методический Материал Перышкин
ГДЗ По Англ 4 Класс Афанасьева
Решебник По Английскому 5 Класс Афанасьева 1
ГДЗ По Математике По Тестам 6
Решебник По Математике 6 Класс Гимназия
ГДЗ Английский Язык 10 Класс Spotlight Афанасьева
ГДЗ Окружающий Мир Плешаков Крючков
ГДЗ По Геометрии 7 Класс Мерзляк Дидактика
ГДЗ По Алгебре 10 Класс Моркодович
Верещагина Афанасьева 5 Класс Английский Язык ГДЗ
Петерсон 5 6 Лет Решебник
ГДЗ Шестой Класс Мерзляк Полонский
ГДЗ По Алгебре 7 Класс Номер 1.
19
ГДЗ По Математике 5 Мерзляк Полонский Якир
Решебник По Математике 4 Класс Автор
ГДЗ По Английскому Баранова Тетрадь
ГДЗ По Математике Муравина
ГДЗ По Алгебре 3
Решебник Моро
ГДЗ По Английскому Афанасьева 2013
ГДЗ По Химии 8 Габриэлян
Решебник По Физике 11 Касьянов
Решение абсолютных неравенств — MathCracker.com
Алгебра Учебники
Неравенство абсолютных ценностей — это неравенство, в котором есть одно или несколько
абсолютная величина
.
Напомним, неравенство почти похоже на уравнение, но вместо знака «=» стоит «≤» или «≥».
Это различие приводит к тому, что набор решений обычно представляет собой область, как и для большинства неравенств. И тот факт, что речь идет об абсолютных величинах, указывает на особый подход к их разрешению.
В этом руководстве мы сконцентрируемся на конкретных навыках, необходимых для разрешения этого типа неравенства, содержащего одно или несколько абсолютных значений. Также предположим, что в неравенстве участвуют одна или две переменные, \(x\) и / или \(y\).
Что такое абсолютное неравенство?
Для целей этого анализа мы будем рассматривать неравенство по абсолютной величине как неравенство, включающее одну или две переменные, по крайней мере, с одним абсолютным значением.
Например, ниже у нас есть неравенство абсолютных значений с двумя переменными \(x\) и \(y\):
\[|3x+2y-1| \ge 1\]Или, кроме того, мы могли бы иметь следующее неравенство по абсолютным значениям только с одной переменной:
\[|3x-1| \le 2\]Для наших целей и для целей методов, используемых для их разрешения, мы будем иметь дело с неравенствами обоих типов (одна и две переменные)
Как разрешить абсолютное неравенство ценностей?
При решении уравнений или неравенств на самом деле не существует серебряной пули, которая решает все.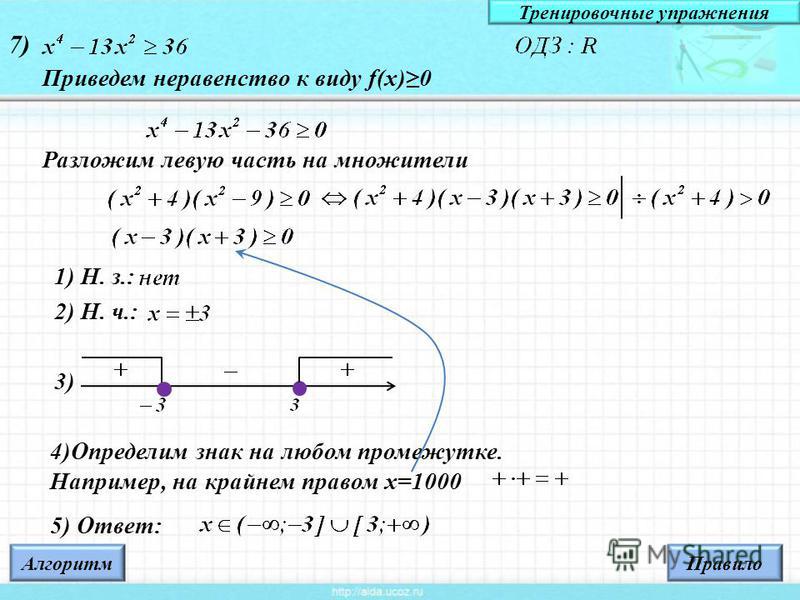
Каждая проблема индивидуальна и может иметь свои особенности.
Лучшее, что мы можем сделать, — это предложить серию шагов, которые помогут вам в процессе разрешения неравенства.
Шаг 1: Для каждого абсолютного значения определите области, в которых аргумент абсолютного значения отрицательный, а где неотрицательный.
Шаг 2:
Если в неравенстве есть только одно абсолютное значение, решите его в обеих областях (где аргумент абсолютного значения отрицательный, а где он неотрицательный).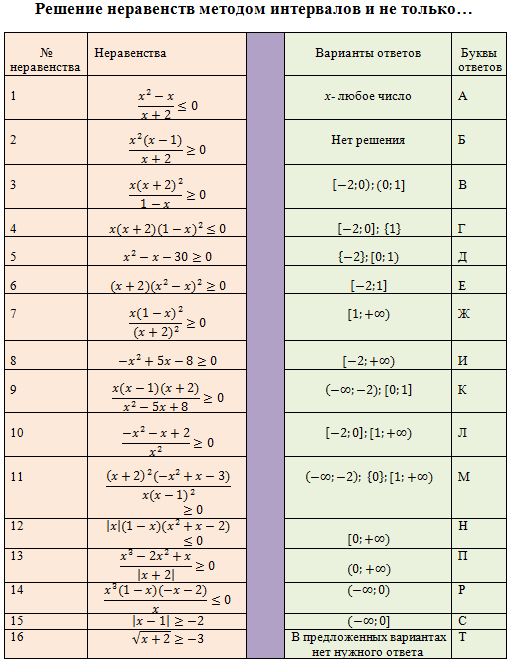
Шаг 4:
Как только вы получите частичное решение, которое находится в каждой из областей, окончательное решение будет простым объединением этих частичных решений.
Проще говоря: вам нужно выяснить области, в которых вы точно знаете знак аргумента абсолютных значений (чтобы от них можно было избавиться).
Несколько примеров должны прояснить эти шаги.
ПРИМЕР 1
Решите следующее неравенство
\[| 2x + 4y — 1 | \ge 2\]ОТВЕЧАТЬ:
Чтобы решить неравенство, нам нужно использовать шаги, указанные выше.
Шаг 1: Существует только одно абсолютное значение, поэтому нам нужно определить, является ли аргумент отрицательным или неотрицательным. Следовательно, нам нужно сначала решить:
\[2x + 4y — 1 \ge 0\]Есть несколько стратегий для решения вышеуказанного, но самый простой — сначала решить уравнение
\[2x + 4y — 1 = 0\]
что означает, что \(4y = -2x + 1\) или то же самое, что и \(y = -\frac{1}{2}x + \frac{1}{4}\), что соответствует линии с уклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = \frac{1}{4}\).
Теперь, чтобы позаботиться о \(2x + 4y — 1 \ge 0\), мы проверяем, удовлетворяет ли точка \((0,0)\) неравенству:
\[2(0) + 4(0) — 1 = -1 < 0\]Итак, \((0,0)\) удовлетворяет или не удовлетворяет неравенству. Напрашивается вывод, что линия с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = \frac{1}{4}\) делит плоскость на две области:
Для точек ниже линии (мы называем эту область 1, \(R_1\)) мы получаем, что \(2x + 4y — 1 < 0\)
Для точек над линией, включая саму линию (мы называем эту область 2, \(R_2\)), мы получаем, что \(2x + 4y — 1 \ge 0\)
Почему это важно? Почему мы берем на себя все эти проблемы? Потому что на \(R_1\) мы получаем это с \( 2x + 4y — 1 < 0\), затем \(| 2x + 4y — 1 | = -(2x + 4y — 1) \).
Шаг 2: Теперь нам нужно решить неравенство на участке 1, \(R_1\) :
\[| 2x + 4y — 1 | \ge 2\] \[\Rightarrow -(2x + 4y — 1) \ge 2\] \[\Rightarrow 2x + 4y — 1 \le -2 \text{ (multiplying by (-1) changes the direction of the inequality)}\] \[\Rightarrow 2x + 4y \le -1\] \[\Rightarrow 4y \le -2x — 1\] \[\Rightarrow y \le -\frac{1}{2}x — \frac{1}{4} \]
Но не забывайте, что вы находитесь на \(R_1\), и эта линия, которую мы обнаружили, находится НИЖЕ границы \(R_1\) (см. График ниже).
Чтобы уточнить, поскольку мы находимся в предположении, что мы находимся в \(R_1\), нам нужно, чтобы мы были НИЖЕ линией с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = \frac{1}{4}\). Исходя из этого предположения, мы решили исходное неравенство, и нам также необходимо находиться ниже линии с наклоном \(m = -\frac{1}{2}\) и точкой пересечения по оси Y \(n = -\frac{1}{4}\). Эти два условия должны выполняться одновременно, поэтому мы получаем пересечение двух областей.
Итак, частичное решение в этом случае соответствует всем точкам ниже или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = -\frac{1}{4}\).
Теперь нам нужно решить неравенство в области 2, \(R_2\) :
\[| 2x + 4y — 1 | \ge 2\] \[\Rightarrow 2x + 4y — 1 \ge 2\] \[\Rightarrow 2x + 4y \ge 3\] \[\Rightarrow 4y \ge -2x + 3\] \[\Rightarrow y \ge -\frac{1}{2}x + \frac{3}{4} \]
Это соответствует всем точкам выше или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = \frac{3}{4}\).
Но не забывайте, что вы находитесь на \(R_2\), и эта линия находится НАД границей \(R_2\) (см. График ниже).
Находя пересечение между \(R_2\) и областью выше, мы получаем, что решение части в этом случае — это все точки выше или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = \frac{3}{4}\).
Шаг 4:
Теперь окончательное решение — это объединение всех решений частей из предыдущих частей: окончательное решение — это все точки НИЖЕ или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = -\frac{1}{4}\), ПЛЮС все точки НАДЕЖДА или на линии с наклоном \(m = -\frac{1}{2}\) и Y-перехват \(n = \frac{3}{4}\).
Графически получаем
что завершает разрешение неравенства.
ПРИМЕР 2
Решите следующее двойное неравенство абсолютных значений
\[| 2x — 1 | \ge |x + 3|\]ОТВЕЧАТЬ:
Это двойное неравенство по абсолютным значениям, потому что существует 2 абсолютных значения.
Это означает, что поиск регионов потребует немного больше работы (условно говоря).
Шаг 1: Для первого абсолютного значения мы решаем:
\[2x- 1 \ge 0\] \[\Rightarrow \,\, 2x \ge 1\] \[\Rightarrow \,\, x \ge \frac{1}{2}\]
Итак, мы получаем \(2x- 1 \ge 0\) на \([\frac{1}{2}, +\infty)\) и \(2x- 1 < 0\) на \((-\infty, \frac{1}{2})\).
Для второго абсолютного значения решаем:
\[x+3 \ge 0\] \[\Rightarrow \,\, x \ge -3\]Итак, мы получаем \(x+3 \ge 0\) на \([-3, +\infty)\) и \(x+3 < 0\) на \((-\infty, -3)\).
Итак, мы определяем 4 региона:
\(R_1 = [\frac{1}{2}, +\infty) \cap [-3, +\infty) = [\frac{1}{2}, +\infty)\). В этом регионе мы получаем: \(2x- 1 \ge 0\) AND \(x+3 \ge 0\).
\(R_2 = [\frac{1}{2}, +\infty) \cap (-\infty, -3) = \varnothing\).
В этой области мы получаем: \(2x- 1 \ge 0\) AND \(x+3 < 0\), хотя эта область пуста.
\(R_3 = (-\infty, \frac{1}{2}) \cap [-3, +\infty) = [-3, \frac{1}{2})\). На этом участке получаем: \(2x- 1 < 0\) AND \(x+3 \ge 0\)
\(R_4 = (-\infty, \frac{1}{2}) \cap (-\infty, -3) = (-\infty, -3)\). В этом регионе мы получаем: \(2x- 1 < 0\) AND \(x+3 < 0\).
Шаг 2: Теперь нам нужно решить двойное неравенство по абсолютным значениям для каждой из четырех областей:
• \(R_1\):
Здесь мы получаем \(2x- 1 \ge 0\) AND \(x+3 \ge 0\), так что тогда
\[| 2x — 1 | \ge |x + 3|\] \[\Rightarrow \,\, 2x — 1 \ge x + 3\] \[\Rightarrow \,\, 2x — x \ge 3 — (-1)\] \[\Rightarrow \,\, x \ge 4\]
Итак, чтобы получить частичное решение, нам нужно пересечь \(x \ge 4\) или \([4, +\infty)\) с \(R_1\).
Следовательно, соответствующее решение детали: \([\frac{1}{2}, +\infty) \cap [4, +\infty) = [4, +\infty)\)
• \(R_2\):
Эта часть решения пуста (\(\varnothing\)).
• \(R_3\):
Здесь мы получаем \(2x- 1 < 0\) AND \(x+3 \ge 0\), так что тогда
\[| 2x — 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x — 1) \ge x + 3\] \[\Rightarrow \,\, 2x — 1 \le -x — 3\] \[\Rightarrow \,\, 2x — (-x) \le -3 — (-1)\] \[\Rightarrow \,\, 3x \le -2\] \[\Rightarrow \,\, x \le -\frac{2}{3}\]
Итак, чтобы получить это частичное решение, нам нужно пересечь \( x \le -\frac{2}{3}\) или \( (-\infty, -\frac{2}{3}]\) с \(R_3\).
Следовательно, соответствующее решение детали: \((-\infty, -\frac{2}{3}] \cap [-3, \frac{1}{2}) = [-3, -\frac{2}{3}] \)
• \(R_4\):
Здесь мы получаем \(2x- 1 < 0\) AND \(x+3 < 0\), так что тогда
\[| 2x — 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x — 1) \ge -(x + 3)\] \[\Rightarrow \,\, 2x — 1 \le x + 3\] \[\Rightarrow \,\, 2x — x \le 3 — (-1)\] \[\Rightarrow \,\, x \le 4\]
Итак, чтобы получить это частичное решение, нам нужно пересечь \( x \le 4 \) или \((-\infty, 4]\) с \(R_4\).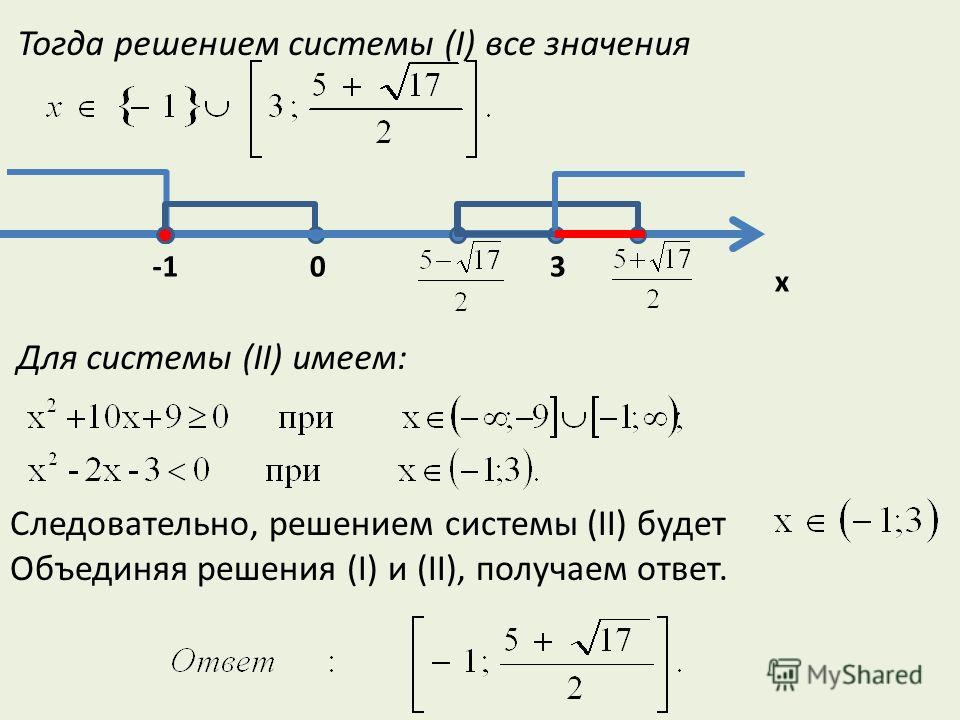
Следовательно, соответствующее решение детали: \((-\infty, -3) \cap (-\infty, 4] = (-\infty, -3) \)
Шаг 4: Наконец, мы получаем объединение частичных решений, чтобы получить, что решение начального данного неравенства
\[(-\infty, -3) \cup [-3, -\frac{2}{3}] \cup [4, +\infty) = (-\infty, -\frac{2}{3}] \cup [4, +\infty) \]
Никто не сказал, что это будет коротко, правда? Хорошо. Это не очень сложно, просто нужно действовать систематически и придерживаться плана.
Подробнее о неравенствах с абсолютным значением
Почему мы вообще беспокоимся о подобном неравенстве? Нам это не безразлично, потому что у них действительно есть приложения на практике.
Например, в геометрии расстояния на реальной прямой должны быть представлены как абсолютные значения, поскольку они должны быть неотрицательными.
Может возникнуть определенная геометрическая ситуация, в которой вам нужно найти все точки на реальной прямой, которые находятся на расстоянии как минимум 2 от точки 3. Такая ситуация может быть описана следующим неравенством:
\[| x-3 |\ge 2\]
Давайте разберемся в указанном выше неравенстве.
Точка \(x\) — это точка, в которой мы хотим удовлетворить неравенство. Расстояние от \(x\) до точки 3 обозначается как \(|x — 3|\).
Затем мы пытаемся найти точки, которые находятся на расстоянии не менее 2 от точки 3, поэтому расстояние \(|x — 3|\) должно быть не менее 2, что объясняет \(|x — 3| \ge 2.\)
Это всего лишь один из видов проблем неравенства абсолютных ценностей, с которыми вы можете столкнуться на практике.
Можете ли вы найти абсолютные неравенства без решения?
Вы делаете ставку. Вот вам один \(|2x| < |x|\). Неравенство может оказаться просто невыполнимым, как в случае с тем, которое я вам только что привел.
Как насчет графического отображения неравенства абсолютных значений?
Процесс их построения графиков по существу идет рука об руку с процессом их решения: вам нужно найти области, в которых вы точно знаете, являются ли аргументы абсолютных значений положительными или отрицательными, а затем неравенства абсолютных значений превращаются в простые неравенства, что тривиально изображено на графике.
Затем все кусочки полученных областей просто соединяются.
Абсолютное неравенство проблемы абсолютного неравенства Учебники по алгебре
Калькулятор уравнений и неравенств
!
| Тысячи пользователей используют наше программное обеспечение, чтобы выполнить домашнее задание по алгебре. Вот некоторые из их опытов: Наше вспомогательное программное обеспечение по алгебре помогает многим людям преодолеть страх перед алгеброй. Вот несколько выбранных ключевых слов, используемых сегодня для доступа к нашему сайту:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
..
алгебра-answer.com Все права защищены.
Copyright 2005-2022
Решатель полиномиального неравенства
|
Наших пользователей: У меня были проблемы с изучением квадратных уравнений, пока я не купил вашу программу. Мои методы обучения никогда не были достаточно хорошими; таким образом, я всегда ищу более легкий метод обучения, и я настоятельно рекомендую Алгебратор. Я использовал вашу программу для подготовки к экзамену по алгебре. Мне очень нравится пошаговый процесс решения и пояснения. Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение может спасти им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?Поисковые фразы, использованные в 2009 г.-12-13:
  
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Теперь я знаю, как делать не только квадратные уравнения, но и на пошаговых примерах научился решать другие, более сложные уравнения и неравенства. Отличный продукт! Калькулятор неравенства
Тысячи пользователей используют наше программное обеспечение, чтобы выполнить домашнее задание по алгебре. Вот некоторые из их впечатлений: Наше вспомогательное программное обеспечение по алгебре помогает многим людям преодолеть страх перед алгеброй. Вот несколько выбранных ключевых слов, используемых сегодня для доступа к нашему сайту:
|
..