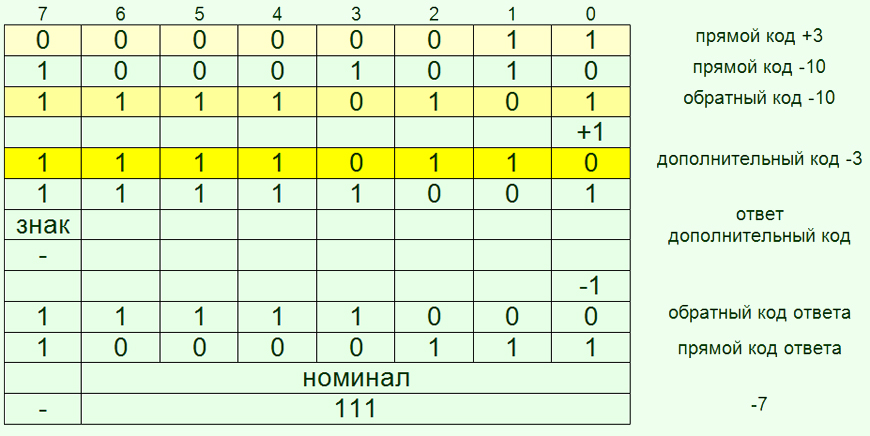
Коды двоичных чисел
- Виды кодов отрицательных чисел
- Прямой код двоичного числа
- Обратный код двоичного числа
- Дополнительный код двоичного числа
В принципы работы вычислительных машин заложен принцип двоичного кодирования: все данные представлены в виде закодированных некоторым образом двоичных чисел. коды двоичных чисел необходимы для того, чтобы производить над данными логические и арифметические операции.
В статье «Системы счисления» мы рассматривали только положительные числа. При записи двоичных чисел со знаком в их формате необходимо предусмотреть два поля: поле, определяющее знак числа, и поле, характеризующее модуль числа. Под знак числа отводится специальный знаковый бит (двоичный разряд). Остальные разряды определяют модуль числа. Знаковый разряд приписывается слева от модуля числа, причём знаку «+» соответствует нулевое значение знакового бита, а знаку «-» — единичное.
В истории развития компьютеров использовались три основных варианта представления знаковых чисел:
- прямой код или знак и величина;
- обратный код или код с дополнением до единицы;
- дополнительный код или код с дополнением до двух.
Во всех трёх кодах положительные числа выглядят одинаково. Различия в форме записи отрицательных чисел в обратном и дополнительном кодах касаются только способа представления модуля числа, а способ кодирования и место расположения знакового бита остаются неизменными.
В системе представления в прямом коде число состоит из кода знака и модуля числа, причём обе эти части обрабатываются по отдельности.
Примеры прямого кода для правильных дробей:
Примеры прямого кода для целых чисел:
Представление чисел в прямом коде имеет существенный недостаток — формальное суммирование чисел с различающимися знаками даёт неверный результат. Пример — сложение двух чисел и . В прямом коде эти числа имеют вид: и . Очевидно, что результат должен быть равен -2, что в прямом коде может быть записано как 1.010. В то же время при непосредственном сложении получаем
,
то есть значение, существенно отличающееся от ожидаемого.
Процедура для корректного сложения чисел в прямом коде всё же существует, но она очень громоздка. Прямой код имеет ещё один недостаток — нуль имеет два различных представления, а именно и , что математически не имеет смысла.
По причине отмеченных недостатков в вычислительных машинах используется не прямой код, а обратный и дополнительный коды.
В этих системах кодирования чисел место расположения знакового разряда и способ кодирования остаются теми же, что и в прямом кодировании. Однако знаковый разряд уже не рассматривается как обособленный, а считается неотъемлемой частью числа аналогично разрядам модуля числа и совместно с ними.
Для отрицательных двоичных чисел процедура получения обратного кода следующая: в знаковой разряд записывается единица, а в цифровых разрядах прямого кода единицы заменяются нулями, а нули единицами.
Примеры обратного кода для правильных дробей:
.
Примеры обратного кода для целых чисел:
.
Как нетрудно заметить, положительные числа в прямом и обратном кодах выглядят одинаково.
Хотя обратный код и позволяет решить проблему сложения и вычитания чисел с различными знаками, он имеет и недостатки. Во-первых, процесс суммирования чисел является двухэтапным, что увеличивает время выполнения этой операции. Во-вторых, как и в прямом коде, в обратном — два представления нуля: и .
Дополнительный код отрицательного двоичного числа формируется по следующему правилу: в цифровых разрядах прямого кода единицы заменить нулями, а нули — единицами, после чего к младшему разряду прибавить единицу.
Для примера рассмотрим число X, которое в прямом коде имеет вид:
.
Тогда обратный код можно записать как
.
Для получения дополнительного кода прибавим 1 к младшему разряду обратного кода:
.
Примеры дополнительного кода для правильных дробей:
.
Примеры дополнительного кода для целых чисел:
.
Положительные числа в дополнительном коде записываются так же, как и в прямом. При представлении чисел в дополнительном коде есть только одна форма записи нуля: 0.0…00, причём ноль считается положительным числом, так как его знаковый бит равен 0.
В большинстве вычислительных машин отрицательные числа представлены в дополнительном коде.
Сложение и вычитание чисел в обратном и дополнительном кодах
Вычитание производится как сложение чисел, одно из которых с отрицательным знаком.
При выполнении алгебраического сложения знаковый разряд и цифры модуля рассматриваются как
единое целое и обрабатываются совместно. Перенос из старшего (знакового) разряда в обратном и дополнительном кодах
учитывается по-разному.
В случае обратного кода единица переноса из знакового разряда прибавляется
к младшему разряду суммы. При использовании дополнительного кода единица переноса из знакового разряда отбрасывается.
Пример 1. Сложить числа и
При использовании обратного кода получим:
При использовании дополнительного кода получим:
Если знаковый разряд результата равен нулю, это означает, что получено положительное число, которое выглядит так же, как и в прямом коде. Единица в знаковом разряде означает, что результат отрицательный и его запись соответствует представлению в том коде, в котором производилась операция.
К началу страницы
8.Модифицированный дополнительный и обратный коды чисел. Примеры…
Привет, Вы узнаете про модифицированный код, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
модифицированный код, дополнительный код, обратный код , настоятельно рекомендую прочитать все из категории Цифровые устройства.
В лекции описаны модифицированные необязательные и обратные коды. Приведены методы умножения чисел с фиксированной запятой в прямом и дополнительном кодах, а также алгоритмы сдвига. Важной особенностью рассматриваемых кодов является то, что во время операции сложения-вычитания цифровая часть номера не переполняется и переносится в цифру знака. Переполнение происходит только при знаковом разряде. Это происходит потому, что сумма двух слагаемых по абсолютной величине меньше единицы. При решении реальных проблем зачастую трудно заранее определить, меньше ли сумма двух слагаемых, чем единица. В любом случае, чтобы предотвратить переполнение, вы можете ввести дополнительные ограничения на количество терминов, которые сужают диапазон чисел, с которыми работает машина. Оба недопустимы.
Рассмотрим такой пример:
То есть получаем неправильный результат как по знаку, так и в цифровой части.
Рассмотрим еще один пример:
То есть в этом случае возникающее переполнение в цифровой части искажает результат операции.
Можно отметить, что переполнение числовой сетки происходит в случае идентичных знаков терминов, поскольку именно в этом случае модуль результата превосходит модули каждого из терминов, факт переполнения можно исправить, изменив знак результата. Таким образом, одним из способов устранения переполнения является автоматическое определение перехода от одних и тех же знаков слагаемых к противоположному знаку результата. Однако такой способ устранения переполнения неудобен, поскольку ранее признаки терминов нужно запоминать, сравнивать друг с другом и после получения результата. Есть еще один принцип для устранения переполнения. Этот принцип основан на использовании так называемых модифицированных кодов. Очевидно, что когда сетка разгрузки переполнена, вычисления должны быть остановлены или, по крайней мере, должен быть разработан специальный признак переполнения, и решение о прекращении расчетов должно быть назначено программисту..
Существо модифицированных кодов состоит в том, что к знаковому разряду добавляется еще один разряд:
» + » ставится в соответствие 00
» – » ставится в соответствие 11
Тогда, по определению модифицированным дополнительным кодом числа называется
Возникающий в знаковых разрядах перенос теряется.
В целом же
модифицированный код не отличается от простого дополнительного. Аналогично, по определению, обратным кодом является:
Как и в случае простого обратного кода, возникающая единица переноса в знаковых разрядах по цепи циклического переноса добавляется в младший разряд цифровой части числа.
Так как в сложении по-прежнему участвуют только числа меньше единицы, то
S = X + Y < 2
Поэтому старший знаковый разряд не может быть искажен переносом из цифровой части числа, с другой стороны, перенос, возникающий при сложении чисел в случае, когда
S = X + Y > 1
искажает младший знаковый разряд.
Несовпадение знаковых разрядов после выполнения операции указывает на факт наличия переполнения.
При этом различают два типа переполнения:
- » 01 » — положительное
- » 10 » — отрицательное.
Первому ставится в соответствие комбинация 01 в знаковых разрядах, а второму – 10.
Примеры
Модифицированный дополнительный код :
Модифицированный обратный код
Умножение чисел со старших разрядов в прямом коде
Это есть аналитическая запись алгоритма умножения двух чисел, начиная со старших разрядов множителя.
Алгоритм:
Пример:
Видно, что в общем случае нужно иметь для точного результата сетку с числом разрядов, равным сумме разрядностей сеток сомножителей.
Если нужно получать произведение с точностью не хуже, чем 2-n, то достаточно иметь не удвоенную величину разрядной сетки, а лишь увеличенную на
Умножение с младших разрядов в прямом коде
Напишем выражение для произведения двух чисел в несколько измененном виде, а именно:
Это выражение называется преобразованием по схеме Горнера и задает алгоритм умножения с младших разрядов множителя.
Таким образом, для умножения должна выполняться следующая последовательность действий:
- Анализируется младшая цифра множителя. Если она равна «1», то множимое участвует в формировании части произведения. В противном случае – не участвует.
- Полученное частичное произведение сдвигается вправо на 1 разряд.
- Операции по пунктам 1 и 2 выполняются до старшего разряда.
Пример:
Замечание.
Для получения произведения с точностью не ниже, чем 2-n нужно иметь только «n»– разрядную сетку.
Итак, видим, что для получения произведения как при умножении со старших,так и младших разрядов необходимо выполнять двемикрооперации: суммирование чисел в позиционной системе счисления и сдвига.
Однако, известно, что числа могут быть представлены в различных кодах(это, прежде всего, отрицательные числа).
Мы уже знаем, как выполняется операция суммирования чисел (в том числе и с разными знаками).
Однако микрооперация сдвига имеет некоторые особенности:
Сдвиг вправо:
Сдвиг влево возможен только в случае, если сдвинутое число меньше единицы по модулю:
Исходные числа:
Если чисто формально сделать преобразование выражения некоторого числа, записанного в прямом коде до выполнения сдвига и после выполнения микрооперации сдвига, в обратный модифицированный код, то:
То есть при сдвиге вправо отрицательного числа старшие разряды заполняются единицами.
При сдвиге влево в старшие и младшие разряды пишутся единицы.
Пользуясь аналогичными правилами, нетрудно установить, что при сдвиге влево отрицательного числа в модифицированномдополнительном коде младшие разряды сдвинутого числа нужно заполнить нулями.
Умножение с младших разрядов в дополнительном коде
Алгоритм:
Пример:
Умножение со старших разрядов в дополнительном коде
вопрос
В чем заключаются причины использования модифицированных кодов чисел?
ответ
Для обнаружения переполнения разрядной сетки можно использовать модифицированные коды. Модифицированные коды отличаются от обычных кодов тем, что знак числа кодируется двумя разрядами. При выполнении алгебраического сложения или вычитания два знаковых разряда участвуют в операции как равноправные цифровые разряды. После выполнения операции содержимое знаковых разрядов определяет знак результата (левый знаковый разряд) и наличие переполнения (несовпадение знаковых разрядов): комбинация 01 фиксирует переполнение при сложении положительных чисел (положительное переполнение), а 10 – отрицательных (отрицательное переполнение).
К сожалению, в одной статье не просто дать все знания про модифицированный код. Но я — старался. Если ты проявишь интерес к раскрытию подробностей,я обязательно напишу продолжение! Надеюсь, что теперь ты понял что такое модифицированный код, дополнительный код, обратный код и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровые устройства. Микропроцессоры и микроконтроллеры. принципы работы ЭВМ
Reverse Binary Number — Reverse Bits — Online
Самый простой в мире реверсер двоичных битов для веб-разработчиков и программистов. Просто вставьте свои двоичные числа в форму ниже, нажмите Reverse Bits, и вы получите перевернутые двоичные строки. Нажмите кнопку, обратный двоичный код. Никакой рекламы, ерунды или мусора.
Объявление : Мы только что запустили Online Math Tools — набор утилит для решения математических задач.
Проверьте это!
(отменить)
Хотите инвертировать двоичные числа?
Используйте инструмент «Двоичный инвертор»!
Хотите вращать двоичные числа?
Используйте инструмент Binary Rotator!
Ищете дополнительные инструменты для веб-разработчиков? Попробуйте это!
URL Encoder
Decoder URL
Parser
HTML Encoder
HTML Decoder
BASE64
HASE64 DECODER
HTML PRETTIFIE0003
JSON Unescaper
JSON Validator
JS Prettifier
JS Minifier
JS Validator
CSS Prettify
CSS Minifier
XML Prettifier
XML Minifier
XML to JSON Converter
JSON to XML Converter
Преобразователь XML в CSV
Преобразователь CSV в XML
Преобразователь XML в YAML
Преобразователь YAML в XML
Преобразователь YAML в TSV
Преобразователь TSV в YAML
XML to TSV Converter
TSV to XML Converter
XML to Text Converter
JSON to CSV Converter
CSV to JSON Converter
JSON to YAML Converter
YAML to JSON Converter
JSON to TSV Converter
Конвертер TSV в JSON
Конвертер JSON в текст
Конвертер CSV в YAML
Конвертер YAML в CSV
Конвертер TSV в CSV
Конвертер CSV в TSV
90 Text002 Конвертер CSV в столбецТекстовые столбцы в CSV преобразователь
TSV в текстовые столбцы преобразователь
Текстовые столбцы в TSV преобразователь
CSV Transposer
CSV COLBERS TO ROWS CUSTRETE
Средство замены столбцов CSV
Средство добавления столбцов CSV
Средство добавления столбцов CSV
Средство вставки столбцов CSV
Средство удаления столбцов CSV
Устройство смены разделителей CSV
TSV Transposer
Столбки TSV в строки преобразователя
TSV строки в столбцы преобразователь
TSV Column Swapper
Deporter Column
TSV Column.
Средство удаления столбцов TSV
Средство смены разделителей TSV
Средство экспорта столбцов с разделителями
Средство удаления столбцов с разделителями
Средство замены столбцов с разделителями
Текстовый транспозер
Текстовые столбцы к конвертеру строк
Текстовые строки в столбцы преобразователь
Текстовый столбец Swapper
Текстовый столбец Delimiter Changer
HTML TO Markdown Converter
Markdown к HTML Converter
HTML TO Daydow Преобразователь HTML
Преобразователь BBCode в HTML
Преобразователь BBCode в Jade
Преобразователь BBCode в текст
Преобразователь HTML в текст
HTML Stripper
Преобразователь текста в HTML
Преобразователь времени UNIX во время UTC
Преобразователь времени UTC во время UNIX
Преобразователь IP в двоичный код
Преобразователь двоичного кода в IP
Преобразователь десятичных чисел в IP
Преобразование IP в шестнадцатеричный
Преобразователь шестнадцатеричного в IP
Сортировщик IP-адресов
Генератор паролей MySQL
Генератор паролей MariaDB
Postgres Password Generator
Bcrypt Password Generator
Bcrypt Password Checker
Scrypt Password Generator
Scrypt Password Checker
ROT13 Encoder/Decoder
ROT47 Encoder/Decoder
Punycode Encoder
Punycode Decoder
Base32 Encoder
Декодер Base32
Кодировщик Base58
Декодер Base58
Кодировщик Ascii85
Декодер Ascii85
Кодировщик UTF8
UTF8 Decoder
UTF16 Encoder
UTF16 Decoder
Uuencoder
Uudecoder
Morse Code Encoder
Morse Code Decoder
XOR Encryptor
XOR Decryptor
AES Encryptor
AES Decryptor
RC4 Encryptor
RC4 Decryptor
DES Encryptor
DES Decryptor
Triple DES Encryptor
Triple DES Decryptor
Rabbit Encryptor
Rabbit Decryptor
NTLM Hash Calculator
MD2 Hash Calculator
MD4 Hash Calculator
MD5 Hash Calculator
MD6 Hash Calculator
RipeMD128 Hash Calculator
RipeMD160 Hash Calculator
RipeMD256 Hash Calculator
RipeMD320 Hash Calculator
Калькулятор хэша SHA1
Калькулятор хэша SHA2
Калькулятор хэша SHA224
Калькулятор хэша SHA256
Калькулятор хэша SHA384
SHA512 Hash Calculator
Hash Calculator
CRC16 Хэш -калькулятор
CRC32 Хэш -калькулятор
Adler32 Hash Calculator
Hash Calculator
All Hashes Calculator
Seconds To H: H: M: M.
NERCUTURE
Second Seconds To H: M: M: M. NERCUTUTURE
Seconds To H: M: M: M: M: M. NERCUTUTOR
Seconds To H: M: M: M: M. NERCUTUTURE
.
Конвертер секунд в удобочитаемое время
Конвертер двоичного кода в восьмеричный
Конвертер двоичного кода в десятичный
Конвертер двоичного кода в шестнадцатеричный
Конвертер двоичного кода в двоичный
Октальный в десятичный преобразователь
Октальный в шестнадцатеричный преобразователь
Десятичный в двоичный преобразователь
Десятичный к октальному преобразованию
Десятичный в гекс конвертер
Hex в бинарный конвертер
Hex в Octal
Hex Decimame
Hex в Octal
Hex Decimamer
Hex в Octal
. Конвертер десятичных чисел в двоично-десятичные
Конвертер двоично-десятичных чисел
Конвертер восьмеричных чисел в двоично-десятичные
Конвертер двоично-десятичных чисел в восьмеричные
Конвертер шестнадцатеричных чисел в двоично-десятичные
Конвертер двоично-десятичных чисел
Binary to Gray Converter
Gray to Binary Converter
Octal to Gray Converter
Gray to Octal Converter
Decimal to Gray Converter
Gray to Decimal Converter
Hexadecimal to Gray Converter
Gray to Hexadecimal Converter
Калькулятор двоичной суммы
Калькулятор двоичного произведения
Калькулятор двоичного побитового И
Калькулятор двоичного побитового И-НЕ
Калькулятор двоичного побитового ИЛИ
двоичный битвей битовой норкол
Бинарный бить калькулятор XOR
Бинарный бить калькулятор XNOR
Бинальный бить.
Не калькулятор
Бинальный битовый инвертор
Бинальный битевой реверсер
Бинарный ротатор
Бинарный битец. Вз. Вращатель битов вправо
Преобразователь числа
Преобразователь римских чисел в десятичные
Преобразователь десятичных чисел в римские
Преобразователь чисел в слова
слова для преобразователя чисел
круглые числа в
круглые числа вниз
UTF8 в шестнадцатеричный преобразователь
Hex в UTF8 преобразователь
Текст в коды ASCII преобразователь
BIN Преобразователь текста в текст
Преобразователь текста в восьмеричный
Преобразователь восьмеричного в текст
Преобразователь текста в десятичный
Преобразователь десятичного в текст
Преобразователь текста в шестнадцатеричный
Hex в текстовый преобразователь
Текст в нижний конвертер
Текст в верхний преобразователь
Текст в Randomcase Converter
Текст TITTELECASE TUSTECASE
СЛОЖИТЕЛЬНЫЕ СЛОВА В ТЕКСТ
Текстовый чехол.
Lines
Преобразователь пробелов в символы табуляции
Преобразователь символов табуляции в пробелы
Преобразователь пробелов в новые строки
Преобразователь новых строк в пробелы
Средство удаления акцента
Extra WhiteSpaces Remover
All WhiteSpaces Remover
Партовая отметка
тысячи сепараторов Adder
СЕРВИС BACKSLASH
БАКСЛАШКА ДЛЯ СЛАЗА
ТЕКСТРЕСС
TEXT
Текст
Текст
Text -Text -Textavers
. Вращатель текстовых символов влево
Вращатель текстовых символов вправо
Калькулятор длины текста
Алфавитный сортировщик текста
Числовой текст сортировщика
Текст по длине сортировщик
Текст из генератора REGEX
Центральный текст
Текст правой кнопки
Текст левого столбца
Текст правой падки
Обоснованный текст
Текст.
Regex Match Extractor
Regex Match Replacer
Email Extractor
URL Extractor
Number Extractor
List Merger
List Zipper
List Intersection
Разница в списках
Printf Formatter
Текст GREP
Текстовая головка
Текст хвост
Экстрактор линии
Сортер Word
Word Wrapper
Сплиттер Word
Добавить номера линии
Добавить линию
Добавить линейные номера
Добавить линию
Добавить линейные номера
Добавить линию
Добавить линейные номера
Добавить линию
. Суффиксы строк
Добавление префикса и суффикса
Поиск самой длинной текстовой строки
Поиск самой короткой текстовой строки
Удаление повторяющихся строк
Удаление пустых строк
Текстовая линия Rampodizer
Letter Ramdigizer
Text Line Joiner
Строковой разветвитель
Text Line Reverser
ФИЛЬТР ТЕКСТРАЦИЯ ЛИНИЯ
Номер буквы в текстовом счетчике
Номер слова в текстовом счетчике
Номер строк в строках в Счетчик текста
Счетчик количества абзацев в тексте
Калькулятор частоты букв
Калькулятор частоты слов
Калькулятор частоты фраз
Text Statistics
Random Element Picker
Random JSON Generator
Random XML Generator
Random YAML Generator
Random CSV Generator
Random TSV Generator
Random Password Generator
Random String Generator
Random Number Generator
Генератор случайных дробей
Генератор случайных бинов
Генератор случайных чисел
Генератор случайных чисел
Генератор случайных шестнадцатеричных чисел
Random Byte Generator
Random IP Generator
Random MAC Generator
Random UUID Generator
Random GUID Generator
Random Date Generator
Random Time Generator
Prime Number Generator
Fibonacci Number Generator
Pi Digit Generator
E Генератор цифр
Преобразователь десятичных чисел в научные
Преобразователь научных чисел в десятичные
Преобразователь JPG в PNG
PNG в JPG Converter
GIF TO PNG Converter
GIF для JPG Converter
BMP в PNG Converter
BMP в JPG Converter
Image To Base64
Файл в Base64 Converter
JSON JSSON JANSON DOVERTER
.
Преобразователь XML в Base64
Преобразователь Hex в RGB
Преобразователь RGB в Hex
Преобразователь CMYK в RGB
Преобразователь RGB в CMYK
Преобразователь CMYK в Hex
HEX в CMYK Converter
IDN Encoder
IDN Декодер
миль до километра преобразователя
километров в миль
Celsius Converter.
Конвертер фунтов в килограммы
Конвертер килограммов в фунты
Мой IP-адрес
Все инструменты
Совет: вы можете использовать аргумент запроса ?input=text для передачи текста в инструменты.
Калькулятор обратного налога с продаж | Расчет налога с продаж
Калькуляторы » Финансы » Обратный калькулятор налога с продаж
Калькулятор обратного налога с продаж
Налог с продаж, % (т.е. 6):
Окончательная цена:
loading…
Поблагодарите нас «Нравится»:
Получите этот калькулятор для своего сайта:
Базовый
Расчеты — 100/мес.
Обязательная ссылка обратно.
или
Настроить
Расчеты — не ограничены. Настраиваемый. Нет ссылки.
Цена продажи = Окончательная цена / 1 + Налог с продаж
Задумывались ли вы когда-нибудь, сколько вы заплатили за товар до уплаты налога с продаж или правильно ли указан налог с продаж в вашей квитанции? Теперь вы можете узнать это с помощью нашего «Калькулятора обратного налога с продаж».
Наш «Калькулятор обратного налога с продаж» принимает два входа. Все, что вам нужно ввести, это сумма налога с продаж, которую вы заплатили, и окончательная цена в квитанции.
Например:
Если общая сумма вашего чека составляет 57,98 долларов США, и вы уплатили 1,07 процента налога с продаж, вы просто подставите эти цифры в наш калькулятор, чтобы узнать, что ваша первоначальная цена до налогообложения составляла 57,37 долларов США. Отсюда можно с помощью простой задачи на вычитание выяснить, что вы заплатили 0,61 цента в виде налога с продаж.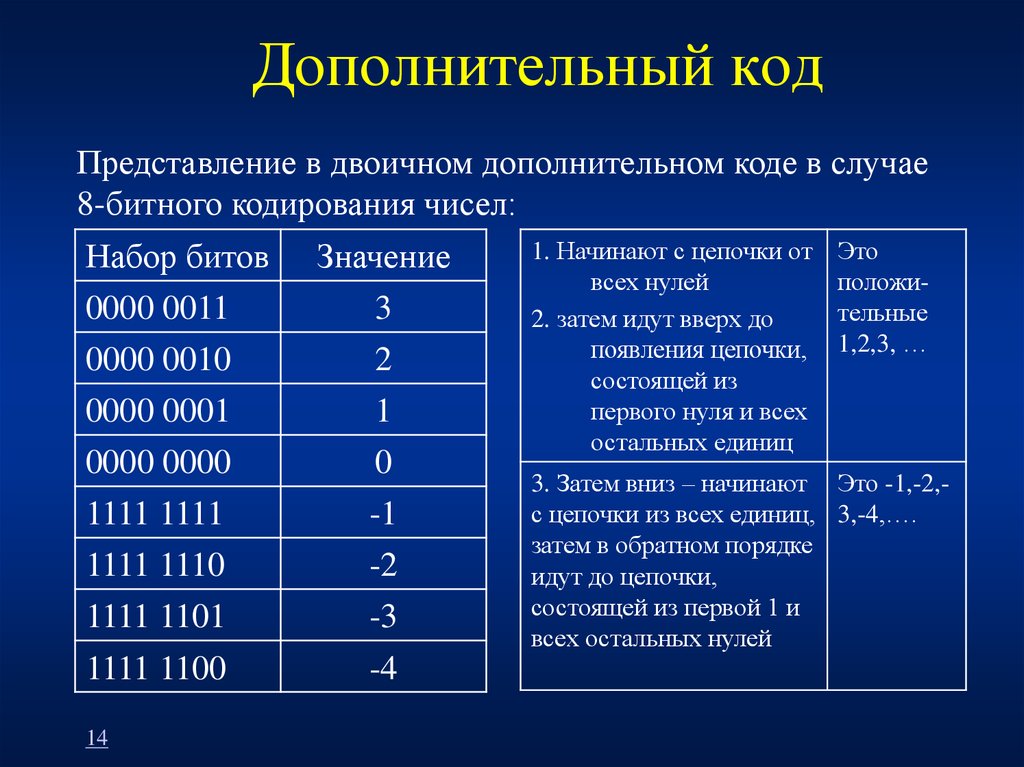
Единственное, что нужно помнить в нашем «Калькуляторе обратного налога с продаж», это то, что верхнее поле ввода предназначено для процента налога с продаж, а нижнее поле ввода — для общей стоимости покупки.
Чем полезен «Калькулятор обратного налога с продаж»
«Калькулятор обратного налога с продаж» полезен, если вы перечисляете свои отчисления и заявляете о переплате местных налогов и налогов с продаж за пределами штата по вашим налогам. Единственное, что нужно помнить о подаче заявления о налоге с продаж и налоговых формах, — это сохранять каждую квитанцию для каждой покупки, на которую вы собираетесь претендовать.
Большинство штатов и местных органов власти взимают налог с продаж товаров, продаваемых в магазинах. Для некоторых людей знание того, сколько они заплатили за продажи, необходимо для заполнения правильных налоговых деклараций и получения денежного кредита за переплаченный налог с продаж. Это особенно полезно, если вам нужно перечислить свои покупки за пределами штата с указанием текущего штата проживания и налогов, уплаченных с этих покупок.