Как построить график функции онлайн по уравнению с подробным решением
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Что такое график функций
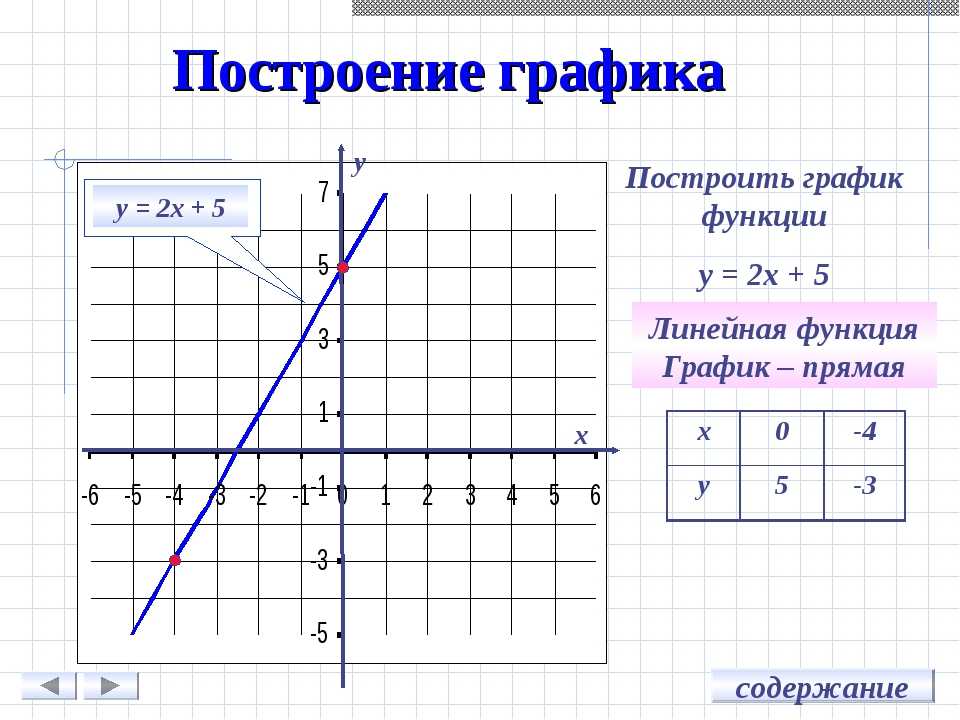
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
Пример:
На рисунке мы видим график функции y = x. Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y. Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y.
Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y. Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y.
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Umath.ru
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака =.
- Нажмите кнопку «Построить график».
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
Перейти на официальный сайт Umath
Yotx.ru
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить».
Огромным плюсом этого сайта можно считать визуализацию графика. Удобно реализована возможность построения нескольких графиков на одной координатной плоскости: можно назначить каждому свой уникальный цвет, толщину линии.
Перейти на официальный сайт Yotx
Graph.reshish.ru
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:».
- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Перейти на официальный сайт сервиса
Desmos.com
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).

- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
Перейти на официальный сайт Desmos
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Квадратичная и кубическая функции. Построение графиков онлайн Основные свойства квадратичной функции
Построить функцию
Мы предлагаем вашему вниманию сервис по потроению графиков функций онлайн, все права на который принадлежат компании Desmos . Для ввода функций воспользуйтесь левой колонкой. Вводить можно вручную либо с помощью виртуальной клавиатуры внизу окна. 2/16=1)
2/16=1)
С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.
Разделы: Математика
Тема: “Построение графика квадратной
функции, содержащей модуль”.
(На примере графика функции у = х 2 — 6x + 3.)
Цель.
- Исследовать расположение графика функции на координатной плоскости в зависимости от модуля.
- Развить навыки построения графика функции, содержащей модуль.
Ход урока.
1. Этап актуализации знаний.
а) Проверка домашнего задания.
Пример 1. Построить график функции у = х 2 — 6х + 3. Найти нули функции.
Решение.
2. Координаты вершины параболы: х= — b/2а = — (-6)/2=3, у(3) = 9 – 18 + 3 = — 6, А(3; -6).
4. Нули функции: у(х) = 0, х 2 — 6х + 3 = 0, D = 36 — 4·3 = 36 – 12 = 24, D>0,
x 1,2 = (6 ± )/2 = 3 ± ; В(3 — ;0), С(3 + ;0).
График на рис.1.
Алгоритм построения графика квадратной функции.
1. Определить направление “ветвей” параболы.
2. Вычислить координаты вершины параболы.
3. Записать уравнение оси симметрии.
4. Вычислить несколько точек.
б) Рассмотрим построение графиков линейных функций, содержащих модуль:
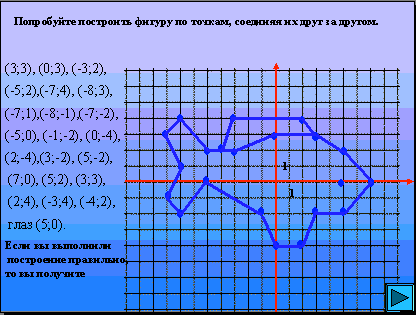
1. у = |х|. График функции на рисунке 2.
у = |х|. График функции на рисунке 2.
2.у = |х| + 1. График функции на рисунке 3.
3. у = |х + 1|. График функции рисунке 4.
Вывод.
1. График функции у = |х| + 1 получается из графика функции у = |х| параллельным переносом на вектор {0;1}.
2. График функции у = |х + 1| получается из графика функции у = |х| параллельным переносом на вектор {-1;0}.
2.Опирационно-исполнительная часть.
Этап исследовательской работы. Работа в группах.
Группа 1. Построить графики функций:
а) у = х 2 — 6|x| + 3,
б) у = |х 2 — 6х + 3|.
Решение.
1.Построить график функции у = х 2 -6х+3.
2. Отобразить его симметрично относительно оси Оу.
График на рисунке 5.
б) 1. Построить график функции у = х 2 — 6х + 3.
2. Отобразить его симметрично относительно оси Ох.
График функции на рисунке 6.
Вывод.
1.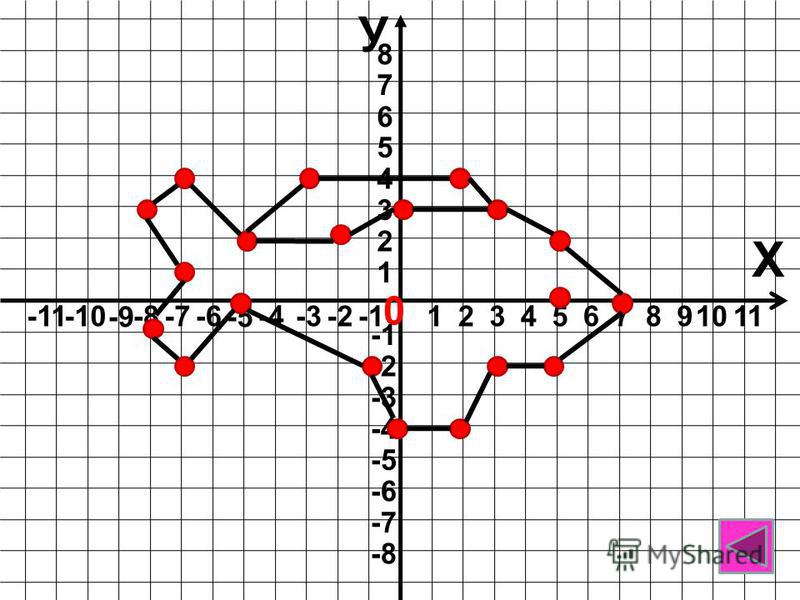 График функции у = f(|x|) получается из графика
функции у = f(x), отображением относительно оси Оу.
График функции у = f(|x|) получается из графика
функции у = f(x), отображением относительно оси Оу.
2. График функции у = |f(x)| получается из графика функции у = f(x), отображением относительно оси Ох.
Группа 2.Построить графики функций:
а) у = |x 2 — 6|x| + 3|;
б) y = |x 2 — 6x + 3| — 3.
Решение.
1. График функции у = х 2 + 6x + 3 отображаем относительно оси Оу, получается график функции у = х 2 — 6|x| + 3.
2. Полученный график отображаем симметрично относительно оси Ох.
График функции на рисунке 7.
Вывод.
График функции y = |f (|x|)| получается из графика функции у = f(х), последовательным отображением относительно осей координат.
1. График функции у = х 2 — 6х + 3 отображаем относительно оси Ох.
2. Полученный график переносим на вектор {0;-3}.
График функции на рисунке 8.
Вывод. График функции у = |f(x)| + a
получается из графика функции у = |f(x)|
параллельным переносом на вектор {0,a}.
Группа 3.Построить график функции:
а) у = |x|(х — 6) + 3; б) у = х|x — 6| + 3.
Решение.
а) у = |x| (x — 6) + 3, имеем совокупность систем:
Строим график функции у = -х 2 + 6x + 3 при х
График функции на рисунке 9.
б) у = х |х — 6| + 3, имеем совокупность систем:
Строим график функции у = — х 2 + 6х + 3 при х 6.
2. Координаты вершины параболы: х = — b/2a = 3, у(3) =1 2, А(3;12).
3. Уравнение оси симметрии: х = 3.
4. Несколько точек: у(2) = 11, у(1) = 3; у(-1) = — 4.
Строим график функции у = х 2 — 6х + 3 при х = 7 у(7) = 10.
График на рис.10.
Вывод. При решении данной группы уравнений необходимо рассматривать нули модулей, содержащихся в каждом из уравнений. Затем строить график функции на каждом из полученных промежутков.
(При построении графиков данных функций каждая
группа исследовала влияние модуля на вид графика
функции и сделала соответствующие заключения. )
)
Получили сводную таблицу для графиков функций, содержащих модуль.
Таблица построения графиков функций, содержащих модуль.
Группа 4.
Построить график функции:
а) у = х 2 — 5x + |x — 3|;
б) у = |x 2 — 5x| + x — 3.
Решение.
а) у = х 2 — 5х + |х — 3|, переходим к совокупности систем:
Строим график функции у = х 2 -6х + 3 при х 3,
затем график функции у = х 2 — 4х — 3 при х > 3 по
точкам у(4) = -3, у(5) = 2, у(6) = 9.
График функции на рисунке 11.
б) у = |х 2 — 5х| + х — 3, переходим к совокупности систем:
Строим каждый график на соответствующем интервале.
График функции на рисунке 12.
Вывод.
Выяснили влияние модуля в каждом слагаемом на вид графика.
Самостоятельная работа.
Построить график функции:
а) у = |х 2 — 5х + |x — 3||,
б) у= ||x 2 — 5x| + х — 3|.
Решение.
Предыдущие графики отображаем относительно оси Ох.
Группа.5
Построить график функции: у =| х — 2| (|x| — 3) — 3.
Решение.
Рассмотрим нули двух модулей: x = 0, х – 2 = 0. Получим интервалы постоянного знака.
Имеем совокупность систем уравнений:
Строим график на каждом из интервалов.
График на рисунке 15.
Вывод. Два модуля в предложенных уравнениях существенно усложнили построение общего графика, состоящего из трех отдельных графиков.
Учащиеся записывали выступления каждой из групп, записывали выводы, участвовали в самостоятельной работе.
3. Задание на дом.
Построить графики функций с различным расположением модуля:
1. у = х 2 + 4х + 2;
2. у = — х 2 + 6х — 4.
4. Рефлексивно – оценочный этап.
1.Оценки за урок складываются из отметок:
а) за работу в группе;
б) за самостоятельную работу.
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }
Построение точек в прямоугольной системе координат
Графический онлайн-калькулятор для построения точек в прямоугольной системе координат. С помощью этих учебных пособий вы сможете изучить свойства точек и квадрантов в прямоугольных системах координат. При необходимости предоставляется бесплатная миллиметровка.
Определение прямоугольной системы координат
Прямоугольная система координат, или декартова плоскость, представляет собой набор двух пересекающихся и перпендикулярных осей, образующих плоскость xy. Горизонтальные оси обычно обозначаются осью x, а вертикальные оси обычно обозначаются осью y. Две оси делят плоскость на четыре части, называемые квадрантами.Любая точка на плоскости соответствует упорядоченной паре (x,y) действительных чисел x и y. x называется координатой x, а y называется координатой y. Ниже представлен апплет, который можно использовать для интерактивного исследования точек в прямоугольной системе координат.
Построение точек в прямоугольной системе координат
введите координаты x и y и нажмите «Построить точку».х = 1 у = 2
Наведите муссовый курсор на точку, чтобы прочитать координаты.
Наведите указатель мыши в правом верхнем углу графика, чтобы получить возможность загрузить график в виде файла png.Урок 1.
Квадранты в прямоугольной системе координат Для каждой точки или упорядоченной пары введите x и y и начертите соответствующую точку. Определите квадрант или ось, на которой расположена каждая точка.
(2 , 3) , (-2 , -1) , (0 , -2) , (2 , -1) , (0 , 0) , (-2 , 3) , (2 , 0)
(-2 , 2) , (0 , 3) , (1 , -2) , (2 , 1) , (-3 , 0) , (-2 , -3) , (2 , -2)Часть 1 вопроса — (см. ответы ниже)
Используйте результаты из приведенного выше руководства и, возможно, некоторые другие моменты, чтобы ответить на следующие вопросы.
1 — При каких значениях x и y точка (x,y) находится в квадранте I?
2 — При каких значениях x и y точка (x,y) находится в квадранте II?
3 — При каких значениях x и y точка (x,y) находится в квадранте III?
4 — При каких значениях x и y точка (x,y) находится в квадранте IV?
5 — При каких значениях x и y точка (x,y) находится на оси x?
6 — При каких значениях x и y точка (x,y) находится на оси y?Вопрос, часть 2
Для каждой ситуации укажите координаты точки и используйте апплет, чтобы проверить свой ответ.(Примечание: эти вопросы имеют бесконечное количество возможных ответов).
1 — точка (x,y) находится в квадранте II.
2 — точка (x,y) находится в квадранте IV.
3 — точка (x,y) находится на оси x.
4 — точка (x,y) находится в квадранте III.
5 — точка (x,y) расположена в квадранте I.
6 — точка (x,y) находится на оси y.Ответы на вышеуказанные вопросы в части 1
1 — Точка (x,y), такая что x > 0 и y > 0, расположена в квадранте I.
2 — Точка (x,y), такая что x < 0 и y > 0, находится в квадранте II.
3 — Точка (x,y), такая что x < 0 и y < 0, расположена в квадранте III.
4 — Точка (x,y), такая что x > 0 и y < 0, расположена в квадранте IV.
5 — Точка (x,y), такая что y = 0, расположена на оси x?
6 — Точка (x,y) такая, что x = 0 расположена на оси y?Дополнительные справочные материалы и ссылки
Графические калькуляторы.Координатные графики
Координатная геометрия предназначена для построения графиков (или построения графиков) и анализа точек, линий и областей на координатной плоскости (координатный график). Каждой точке на числовой прямой присваивается номер. Точно так же каждой точке на плоскости ставится в соответствие пара чисел. Эти числа представляют размещение точки относительно двух пересекающихся линий. В координатных графиков (см. рис. 1), используются две перпендикулярные числовые линии, которые называются координатными осями . Одна ось является горизонтальной и называется осью x . Другая — вертикальная и называется осью y . Точка пересечения двух числовых линий называется началом координат и представлена координатами (0, 0).
Рис. 1. График координат x-y .
Каждая точка на плоскости определяется уникальной упорядоченной парой чисел, называемой координатами.
Некоторые координаты отмечены на Рисунке 2.
Рис. 2. Нанесение координат на график.
Обратите внимание, что на оси x числа справа от 0 положительные, а слева от 0 отрицательные. На оси y числа выше 0 являются положительными, а ниже 0 — отрицательными. Также обратите внимание, что первое число в упорядоченной паре называется 9.0057 x – координата, или – абсцисса, , а второе число – это y – координата, или – ордината. Координата x показывает направление вправо или влево, а координата y показывает направление вверх или вниз.
График координат разделен на четыре четверти, называемые квадрантами. Эти квадранты помечены на рис. 3.
Рис. 3. График координат с помеченными квадрантами.
Обратите внимание на следующее:
- В квадранте I x всегда положительно, а y всегда положительно.
- В квадранте II x всегда отрицательно, а y всегда положительно.
- В квадранте III оба числа x и y всегда отрицательны.
- В квадранте IV x всегда положительно, а y всегда отрицательно.
Графические уравнения на координатной плоскости
Чтобы построить уравнение на координатной плоскости , найдите координату, задав значение одной переменной и решив полученное уравнение для другого значения. Повторите этот процесс, чтобы найти другие координаты. (При задании значения одной переменной вы можете начать с 0, затем попробовать 1 и т. д.) Затем нарисуйте решения.
Пример 1
Нарисуйте уравнение x + y = 6.
Полезно использовать простую диаграмму.
x
y
| 0 | 6
| 1 | 5
| 2 | 4Теперь нанесите эти координаты, как показано на рисунке 4.
Рисунок 4. Нанесение координат (0,6), (1,5), (2,4)
Обратите внимание, что эти решения при построении образуют прямую линию.
Уравнения, множества решений которых образуют прямую линию, называются линейными уравнениями. Дополните график x + y = 6, проведя линию, проходящую через эти точки (см. рис. 5).
Рисунок 5. Линия, проходящая через точки, изображенные на рисунке 4.
Уравнения, в которых переменная возводится в степень, показывают деление на переменную, включают переменные с квадратными корнями или имеют переменные, умноженные вместе, не будут образуют прямую линию, когда их решения изображаются на графике. Они называются нелинейными уравнениями.
Пример 2
Нарисуйте уравнение y = x 2 + 4.
Используйте простую диаграмму.
x
y
| -2 | 8
| -1 | 5
| 0 | 4
| 1 | 5
| 2 | 8Теперь нанесите эти координаты, как показано на рисунке 6.
Обратите внимание, что эти решения при построении не образуют прямую линию.
Эти решения при построении дают кривую линию (нелинейную). Чем больше точек нанесено, тем проще увидеть и описать набор решений.
Рис. 6. Нанесение координат на простой график.
Дополните график y = x 2 + 4, соединив эти точки плавной кривой, проходящей через эти точки (см. рис. 7).
Рис. 7. Линия, проходящая через точки, изображенные на рис. 6.
Наклон и точка пересечения линейных уравнений
Между графиком линейного уравнения и самим уравнением существуют две зависимости, на которые следует обратить внимание. Один включает наклон линии , , а другой включает точку, где линия пересекает ось Y. Чтобы увидеть любое из этих соотношений, члены уравнения должны стоять в определенном порядке.
(+)(1) y = ( ) x + ( )
Когда члены записаны в таком порядке, говорят, что уравнение имеет форму y . Y ‐ форма написана y = m x + b , а два соотношения включают m и b .
Пример 3
Запишите уравнения в форме y .
- y = -2 x + 1 (уже в форме y )
Как показано на графиках трех задач на рисунке 8, линии пересекают ось y в точках –3, +1 и –2, последнем члене в каждом уравнении.
Если линейное уравнение записать в виде y = mx + b, b — точка пересечения y .
Наклон линии определяется как
, а слово «изменение» относится к разнице значений y (или x ) между двумя точками на линии.
Примечание: Точки A и B могут быть любыми двумя точками на линии; разницы в наклоне не будет.
Рисунок 8. Графики, показывающие линии, пересекающие и – ось.
Пример 4
Найдите наклон x – y = 3, используя координаты.
Чтобы найти наклон линии, выберите любые две точки на линии, например A (3, 0) и B (5, 2), и рассчитайте наклон.
Пример 5
Найдите наклон y = –2 x – 1, используя координаты.
Выберите две точки, например A (1, –3) и B (–1, 1) и рассчитайте наклон.
Пример 6
Найдите наклон x – 2 y = 4, используя координаты.
Выберите две точки, например A (0, –2) и B (4, 0), и рассчитайте наклон.
Возвращаясь к уравнениям для примера (a), (b) и (c), записанным в форме y , должно быть очевидно, что наклон линии равен числовому коэффициенту x ‐ термин.
Построение графика линейных уравнений с использованием наклона и точки пересечения
Построение графика уравнения с использованием его наклона и y‐ точки пересечения обычно довольно просто.
- Запишите уравнение в форме y‐ .
- Найдите точку пересечения и на графике (то есть одну из точек на линии).
- Запишите наклон в виде отношения (доли) и используйте его для поиска других точек на линии.
- Проведите линию через точки.
Пример 7
Нарисуйте уравнение x – y = 2, используя наклон и точку пересечения y- .
Найдите –2 на оси y‐ и от этой точки посчитайте, как показано на рисунке 9:
наклон = 1
Рисунок 9. График линии y – 3 x 9006 Пример 80063 ‐перехват.
Найдите +4 на оси y и от этой точки отсчитайте, как показано на рисунке 10:
наклон = 2
4.
Пример 9
Нарисуйте уравнение x + 3 y = 0, используя наклон и y — точку пересечения.
Найдите 0 на оси y и отсчитайте от этой точки, как показано на рисунке 11:
Рис. 11. График прямой x + 3 y = 0.
Нахождение уравнения прямой
Нахождение уравнения прямой при работе с упорядоченными парами, наклонами и точками пересечения , используйте один из следующих подходов в зависимости от того, какую форму уравнения вы хотите иметь.
Существует несколько форм, но наиболее распространенными являются три формы: форма с пересечением наклона , форма с точкой и наклоном и стандартная форма . Форма пересечения наклона выглядит следующим образом: y = м x + b , где м — это наклон линии, а b — это y — точка пересечения. Форма точечной склоны выглядит как Y — Y 1 = M ( x — x 1 ), где M является склоном линии и ( x 905 2 9062 M — это склон и ( x 9062 9. 1002. M . , y 1 ) — любая точка на прямой. Стандартная форма выглядит как Ax + By = C , где, если возможно, A , B и C являются целыми числами.
Форма пересечения наклона.
- Найти уклон, м .
- Найдите точку пересечения и , b .
- Подставьте наклон и y ‐отрезок в форму наклона отрезка, y = m x + b .
Точечно-наклонная форма.
- Найти уклон, м .
- Используйте любую точку на линии.
- Подставить наклон и упорядоченную пару точек в форму точка-наклон: y – y 1 = м ( x – x 1 ).
Примечание: Вы можете начать с формы точка-наклон для уравнения прямой, а затем решить уравнение для y. Вы получите форму пересечения наклона без необходимости сначала находить г ‐перехват.
Стандартная форма.
- Найдите уравнение прямой, используя либо форму пересечения наклона, либо форму точка-наклон.
- Используя соответствующую алгебру, постарайтесь получить x членов и y членов с одной стороны уравнения и константу с другой стороны уравнения.
- Если необходимо, умножьте каждую часть уравнения на наименьший общий знаменатель всех знаменателей, чтобы получить все целые коэффициенты для переменных.
Пример 10
Найдите уравнение линии в форме точки пересечения, когда м = – 4 и b = 3. Затем преобразуйте его в стандартную форму.
- Найти уклон, м .
- м = – 4 (дано)
- Найдите точку пересечения с осью Y, b .
- б = 3 (дано)
- Замените наклон и y -пересечение в форме наклон-пересечение, y = м х + б .
- y = – 4 x + 3 (форма пересечения наклона)
- Используя соответствующую алгебру, постарайтесь получить x членов и y членов с одной стороны уравнения и константу с другой стороны уравнения.
Пример 11
Найдите уравнение прямой в форме точка-наклон, проходящей через точку (6, 4) с наклоном –3. Затем преобразовать его в стандартный вид.
- Найти уклон, м .
- м = –3 (дано)
- Используйте любую точку на линии.
- (6, 4) (дано)
- Подставить наклон и упорядоченную пару точек в форму точка-наклон,
- Используя соответствующую алгебру, постарайтесь получить x членов и y членов с одной стороны уравнения и константу с другой стороны уравнения.
Пример 12
Найдите уравнение прямой, в форме точки и точки пересечения, проходящей через точки (5, –4) и (3, 7). Затем преобразовать его в стандартный вид.
Пуск с пересечением наклона:
- Найдите точку пересечения и , b .
- Подставьте наклон и любую точку в форму пересечения наклона.
- Замените наклон и y -отрезок в форму наклона-перехвата, y = м х + б.
- Используя соответствующую алгебру, постарайтесь получить x членов и y членов с одной стороны уравнения и константу с другой стороны уравнения.
- Если необходимо, умножьте каждую часть уравнения на наименьший общий знаменатель всех знаменателей, чтобы получить все целые коэффициенты для переменных.


 2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
 Любая точка на плоскости соответствует упорядоченной паре (x,y) действительных чисел x и y. x называется координатой x, а y называется координатой y. Ниже представлен апплет, который можно использовать для интерактивного исследования точек в прямоугольной системе координат.
Любая точка на плоскости соответствует упорядоченной паре (x,y) действительных чисел x и y. x называется координатой x, а y называется координатой y. Ниже представлен апплет, который можно использовать для интерактивного исследования точек в прямоугольной системе координат. Квадранты в прямоугольной системе координат Для каждой точки или упорядоченной пары введите x и y и начертите соответствующую точку. Определите квадрант или ось, на которой расположена каждая точка.
Квадранты в прямоугольной системе координат Для каждой точки или упорядоченной пары введите x и y и начертите соответствующую точку. Определите квадрант или ось, на которой расположена каждая точка. 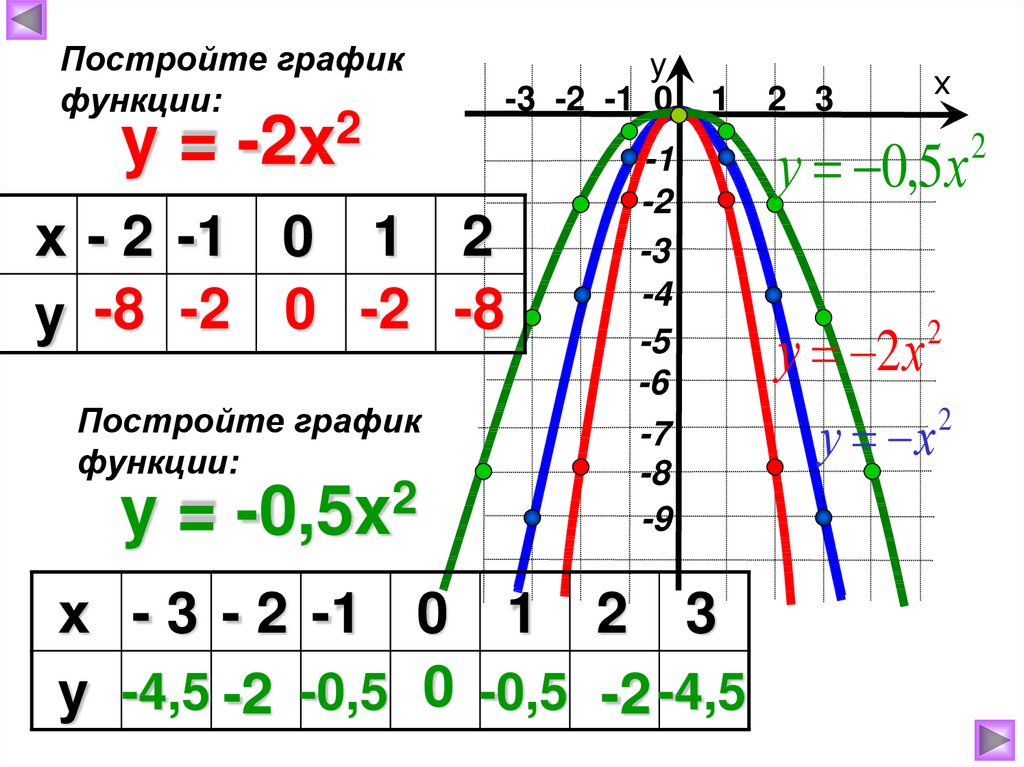 (Примечание: эти вопросы имеют бесконечное количество возможных ответов).
(Примечание: эти вопросы имеют бесконечное количество возможных ответов). 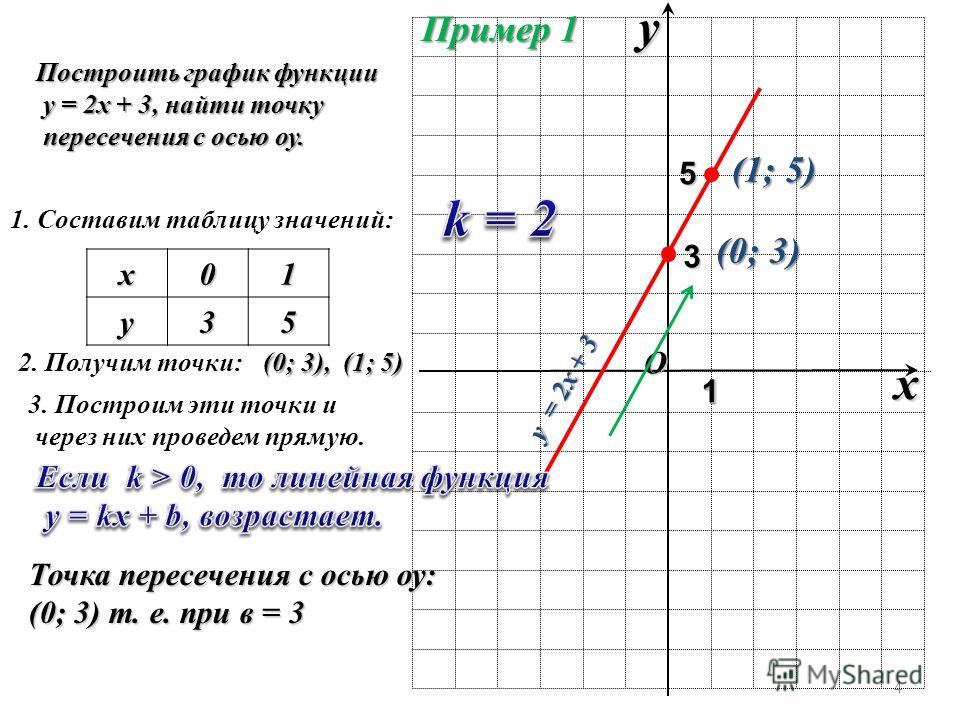
 Некоторые координаты отмечены на Рисунке 2.
Некоторые координаты отмечены на Рисунке 2. 
 Уравнения, множества решений которых образуют прямую линию, называются линейными уравнениями. Дополните график x + y = 6, проведя линию, проходящую через эти точки (см. рис. 5).
Уравнения, множества решений которых образуют прямую линию, называются линейными уравнениями. Дополните график x + y = 6, проведя линию, проходящую через эти точки (см. рис. 5).


 Существует несколько форм, но наиболее распространенными являются три формы: форма с пересечением наклона , форма с точкой и наклоном и стандартная форма . Форма пересечения наклона выглядит следующим образом: y = м x + b , где м — это наклон линии, а b — это y — точка пересечения. Форма точечной склоны выглядит как Y — Y 1 = M ( x — x 1 ), где M является склоном линии и ( x 905 2 9062 M — это склон и ( x 9062 9. 1002. M . , y 1 ) — любая точка на прямой. Стандартная форма выглядит как Ax + By = C , где, если возможно, A , B и C являются целыми числами.
Существует несколько форм, но наиболее распространенными являются три формы: форма с пересечением наклона , форма с точкой и наклоном и стандартная форма . Форма пересечения наклона выглядит следующим образом: y = м x + b , где м — это наклон линии, а b — это y — точка пересечения. Форма точечной склоны выглядит как Y — Y 1 = M ( x — x 1 ), где M является склоном линии и ( x 905 2 9062 M — это склон и ( x 9062 9. 1002. M . , y 1 ) — любая точка на прямой. Стандартная форма выглядит как Ax + By = C , где, если возможно, A , B и C являются целыми числами.