Радио для всех — Лаборатория
В разделе представлены on-line калькуляторы
Цветовая маркировка резисторов
Расчет индуктивности
Расчёт реактивного сопротивления конденсатора C и реактивного сопротивления катушки L
Расчёт параллельного соединения резисторов и последовательного конденсаторов
Расчёт резистивного и ёмкостного делителей
Расчёт частоты колебательного контура и цепочки RC. Частота среза фильтра ФНЧ и ФВЧ
Компенсация реактивной мощности
Закон Ома. Расчёт напряжения, сопротивления, тока, мощности
Расчет элементов J антенны
Расчет резонансной частоты LC-контура
Расчет резистивного Пи аттенюатора
Делитель напряжения
Цветовой код конденсаторов
Стабилизация напряжения
Дроссели, намотанные на резисторах МЛТ
Реактивное сопротивление конденсатора
Реактивное сопротивление катушки индуктивности
Калькулятор определения номинала SMD-резистора
Расчет значения резистора для LM317
Расчет «Cantenna» (баночной антенны) для Wi Fi
Расчет усилителя на биполярном транзисторе
Калькулятор расчета компактных монолитных усилителей
Расчет силового трансформатора
Расчет дискоконусной антенны
Сопротивления для согласующего трансформатора
Расчет для тороидальных (ферритовых) сердечников Amidon
Расчет петлевого вибратора
Калькулятор DC-DC преобразователя MC34063A
Расчет выпрямителя для блока питания
Расчет гасящего конденсатора в блоке питания
Расчет резистора для подключения светодиода
Расчет индуктивности
Длинна l=мсммм
Число витков w=
Магнитная проницаемость материала сердечника=Гн/м
(Магнитная проницаемость материала сердечника=1 если его нет как в примере)
Площадь витков=мсммм2
Индуктивность=ГнмГнмкГннГн
Расчёты электронных цепей.

Вписываем значения и кликаем мышкой в таблице
Расчёт реактивного сопротивления конденсатора C и реактивного сопротивления катушки LРеактивное сопротивление ёмкости
| Реактивное сопротивление индуктивности
|
Параллельное соединение двух сопротивлений
| Последовательное соединение двух ёмкостей
|
Расчёт резистивного и ёмкостного делителей
Расчёт резистивного делителя напряжения
| Расчёт ёмкостного делителя напряжения
|
Расчёт частоты колебательного контура и цепочки RC.
 Частота среза фильтра ФНЧ и ФВЧ
Частота среза фильтра ФНЧ и ФВЧЧастота резонанса колебательного контура LC
| Пост. времени τ RC и частота среза RC-фильтра
|
Компенсация реактивной мощности
Реактивная мощность Q = √((UI)²-P²) |
Закон Ома.
 тут будет результат
тут будет результат- 4-полоски
- 5-полосок
- 6-полосок
Резисторы с четырмя полосками
1-я цифра
2-я цифра
Множитель
Погрешность
1-я цифра 1 Коричневый2 Красный3 Оранжевый4 Желтый5 Зеленый6 Синий7 Фиолетовый8 Серый9 Белый
2-я цифра 0 Черный1 Коричневый2 Красный3 Оранжевый4 Желтый5 Зеленый6 Синий7 Фиолетовый8 Серый9 Белый
Множитель x1 Черныйx10 Коричневыйx100 Красныйx1k Оранжевыйx10k Желтыйx100k Зеленыйx1M Синийx10M Фиолетовыйx100M Серыйx1G Белый?10 Золотой?100 Серебристый
Погрешность ± 1% Коричневый± 2% Красный± 3% Оранжевый± 4% Желтый± 0.5% Зеленый± 0.25% Синий± 0.10% Фиолетовый± 0.05% Серый± 5% Золотой± 10% Серебристый
Сопротивление:
Ом (?)
Погрешность:
Минимум:
Ом (?)
Максимум:
Ом (?)
Резисторы с пятью полосками
1-я цифра
2-я цифра
3-я цифра
Множитель
Погрешность
1-я цифра 1 Коричневый2 Красный3 Оранжевый4 Желтый5 Зеленый6 Синий7 Фиолетовый8 Серый9 Белый
2-я цифра 0 Черный1 Коричневый2 Красный3 Оранжевый4 Желтый5 Зеленый6 Синий7 Фиолетовый8 Серый9 Белый
3-я цифра 0 Черный1 Коричневый2 Красный3 Оранжевый4 Желтый5 Зеленый6 Синий7 Фиолетовый8 Серый9 Белый
Множитель x1 Черныйx10 Коричневыйx100 Красныйx1k Оранжевыйx10k Желтыйx100k Зеленыйx1M Синийx10M Фиолетовыйx100M Серыйx1G Белый?10 Золотой?100 Серебристый
Погрешность ± 1% Коричневый± 2% Красный± 3% Оранжевый± 4% Желтый± 0. 5% Зеленый± 0.25% Синий± 0.10% Фиолетовый± 0.05% Серый± 5% Золотой± 10% Серебристый
5% Зеленый± 0.25% Синий± 0.10% Фиолетовый± 0.05% Серый± 5% Золотой± 10% Серебристый
Сопротивление:
Ом (?)
Погрешность:
Минимум:
Ом (?)
Максимум:
Ом (?)
Резисторы с шестью полосками
1-я цифра
2-я цифра
3-я цифра
Множитель
Погрешность
ТКС
1-я цифра 1 Коричневый2 Красный3 Оранжевый4 Желтый5 Зеленый6 Синий7 Фиолетовый8 Серый9 Белый
2-я цифра 0 Черный1 Коричневый2 Красный3 Оранжевый4 Желтый5 Зеленый6 Синий7 Фиолетовый8 Серый9 Белый
3-я цифра 0 Черный1 Коричневый2 Красный3 Оранжевый4 Желтый5 Зеленый6 Синий7 Фиолетовый8 Серый9 Белый
Множитель x1 Черныйx10 Коричневыйx100 Красныйx1k Оранжевыйx10k Желтыйx100k Зеленыйx1M Синийx10M Фиолетовыйx100M Серыйx1G Белый?10 Золотой?100 Серебристый
Погрешность ± 1% Коричневый± 2% Красный± 3% Оранжевый± 4% Желтый± 0.5% Зеленый± 0.25% Синий± 0.10% Фиолетовый± 0.05% Серый± 5% Золотой± 10% Серебристый
ТКС 100 Коричневый50 Красный15 Оранжевый25 Желтый10 Синий5 Фиолетовый
Сопротивление:
Ом (?)
Погрешность:
Минимум:
Ом (?)
Максимум:
Ом (?)
ppm/°C
Резервный калькулятор
4 полосы 5 полос
± 20%10%5%2%1%0. 5%0.25%0.1%
5%0.25%0.1%
Расчёт электрических цепей.
Калькулятор последовательной и параллельной цепи
Калькулятор эквивалентной последовательной и параллельной цепи
Здесь мы изучаем расчет эквивалентной или общей последовательной и параллельной цепи.
Во-первых, вы должны знать об основных понятиях, таких как последовательное и параллельное соединение цепи с подключенными различными элементами.
В одном из предыдущих уроков я объяснял последовательную и параллельную цепи на примере.
1. Калькулятор последовательной цепи —
При последовательном соединении несколько электрических элементов или компонентов соединяются последовательно или последовательно.
Например, данная цепь называется последовательной, когда компоненты электроники (такие как сопротивления R1, R2 и R3) соединены в одну цепь с подключенным источником напряжения (Vs).
Когда в цепь подается источник напряжения, течет тот же ток (I). Но разное (или падение) напряжение (V1, V2 и V3) возникало на всех последовательно подключенных сопротивлениях.
Но разное (или падение) напряжение (V1, V2 и V3) возникало на всех последовательно подключенных сопротивлениях.
Сумма падений напряжения на отдельных последовательно соединенных сопротивлениях равна приложенному напряжению (т. е. V= V1+V2+V3).
Давайте проверим здесь несколько важных формул для различных компонентов, соединенных последовательно.
Для расчета последовательного тока:
Суммарный ток, (Ieq) = (I1= I2 = I3 = I4 = 15 = ......= In) (Единица измерения - Ампер)
Примечание: Один и тот же ток протекает или возникает на разных соединенных компонентах в последовательной цепи.
Для расчета напряжения в серии:
Суммарный ток, (Veq) = (V1+ V2 + V3 + V4 = V5 = ......= Vn) (Unit-Volt)
Для расчета последовательного сопротивления:
Общее сопротивление, (треб.) = (R1+ R2 + R3 + R4 + R5 +......+ Rn) (Единица измерения – Ом)
Для расчета проводимости в Серия:
Общая проводимость, (Geq) = [1 / ((1/G1) + (1/G2) + (1/G3) + (1/G4) + (1/G5) +... ...+ (1/Gn))] (Единица измерения – Сименс)
Для расчета последовательной емкости:
Общая емкость, (Ceq) = [1 / ((1/C1) + (1/C2) + (1/C3) + (1/C4) + ( 1/C5) +......+ (1/Cn))] (Единица-Фарад)
Для расчета последовательной индуктивности:
Суммарная индуктивность, (Leq) = (L1 + L2 + L3 + L4 + L5......+ Ln) (Unit-Henry)
Это простое описание последовательной цепи с различными формулами.
2. Калькулятор параллельной цепи:
При параллельном соединении несколько электрических элементов или компонентов соединены параллельно.
Например, когда компоненты электроники (такие как резисторы R1, R2 и R3) соединены в параллельную ветвь с подключенным источником напряжения (Vs).
Когда в цепь подается источник напряжения, течет тот же ток (I). Но разное (или падение) напряжение (V1, V2 и V3) произошло на всех параллельно подключенных сопротивлениях.
Сумма падений напряжения на отдельных параллельно соединенных сопротивлениях равна приложенному напряжению (т. е. V= V1+V2+V3).
е. V= V1+V2+V3).
Давайте проверим, вот некоторые важные формулы для различных подключенных компонентов в параллельной цепи.
Для расчета параллельного тока:
Общий ток, (Ieq) = (I1 + I2 + I3 + I4 + 15 + ......+ In) (Единица измерения - Ампер)
Для расчета напряжения при параллельном подключении:
Общее напряжение, (Veq) = (V1 = V2 = V3 = V4 = V5 =......+ Vn) (Единица измерения – вольт)
Примечание. различные связанные компоненты.
Для расчета сопротивления параллельно:
Общее сопротивление, (треб.) = [1/((1/R1) + (1/R2) + (1/R3) + (1/R4) + (1/R5) +......+ (1/Rn))] (Единица-Ом)
Для расчета проводимости последовательно:
Суммарная проводимость, (Geq) = (G1 + G2 + G3 + G4 + G5 +......+ Gn) (Единица измерения – Сименс)
Для расчета последовательной емкости: (Ceq) = (C1 + C2 + C3 + C4 + C5 +.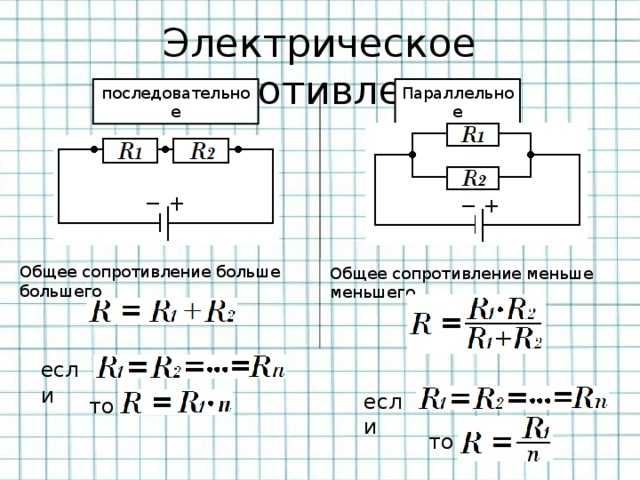 …..+ Cn) (Unit-Farad)
…..+ Cn) (Unit-Farad)
Для расчета последовательной индуктивности:
Суммарная индуктивность, (Leq) = [1 / ((1/L1) + (1/L2) + (1/L3) + (1/L4) + (1/L5) +......+ (1/Ln))] (Единица измерения — Генри )
Это простое описание параллельной схемы с различными формулами.
Рассчитайте сопротивление цепи резистора в режиме онлайн. Последовательное соединение проводников. Параллельное соединение различных сопротивлений
Определение параллельного соединения
Параллельное соединение Электрические элементы (проводники, сопротивления, конденсаторы, индуктивности) — такое соединение, при котором соединяемые элементы цепи имеют две общие точки соединения.
Другое определение: сопротивления соединены параллельно, если они подключены к одной и той же паре узлов.
Графическое обозначение схемы параллельного соединения
На рисунке ниже представлена схема параллельного соединения сопротивлений R1, R2, R3, R4.
В электротехнике принято, но строго не требуется, рисовать провода горизонтально и вертикально. Поэтому можно изобразить ту же схему, что и на рисунке ниже. Это тоже параллельное соединение одинаковых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина эквивалентного сопротивления равна сумме обратных величин всех параллельно соединенных сопротивлений. Эквивалентная проводимость равна сумме всех одновременно связанных проводимостей. электрическая цепь.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае, когда два резистора соединены параллельно:
Эквивалентное сопротивление цепи определяется по формуле:
В случае соединения «n» с одинаковым сопротивлением эквивалентное сопротивление можно рассчитать по специальной формуле:
Формулы для частных расчетов выводятся из основной формулы.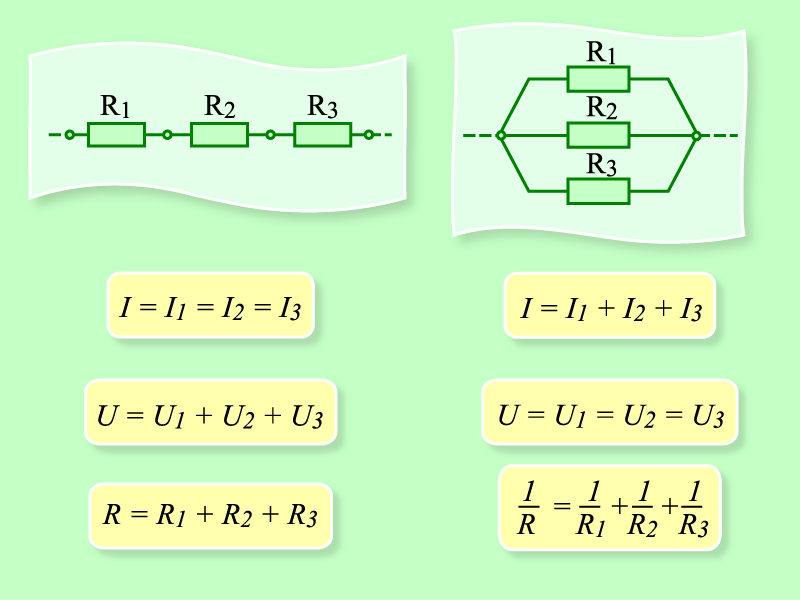
Формула расчета параллельного соединения конденсаторов (конденсаторов)
При параллельном соединении конденсаторов (конденсаторов) эквивалентная емкость равна сумме параллельно соединенных конденсаторов:
Формула для расчета индуктивностей параллельного соединения
При параллельном соединении индуктивностей эквивалентная индуктивность рассчитывается так же, как эквивалентное сопротивление при параллельном соединении:
Необходимо обратить внимание, что в формуле не учитываются взаимные индуктивности.
Пример коагуляции параллельного сопротивления
Для построения электрической цепи необходимо найти параллельное соединение сопротивлений, чтобы преобразовать их в одно.
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллелен, так как одним концом подключен к E1. R1 — один конец подключен к R5, а не к узлу. R5 — одним концом подключен к R1, а не к узлу. Можно также сказать, что последовательное соединение сопротивлений R1 и R5 подключается параллельно с R2 и R4.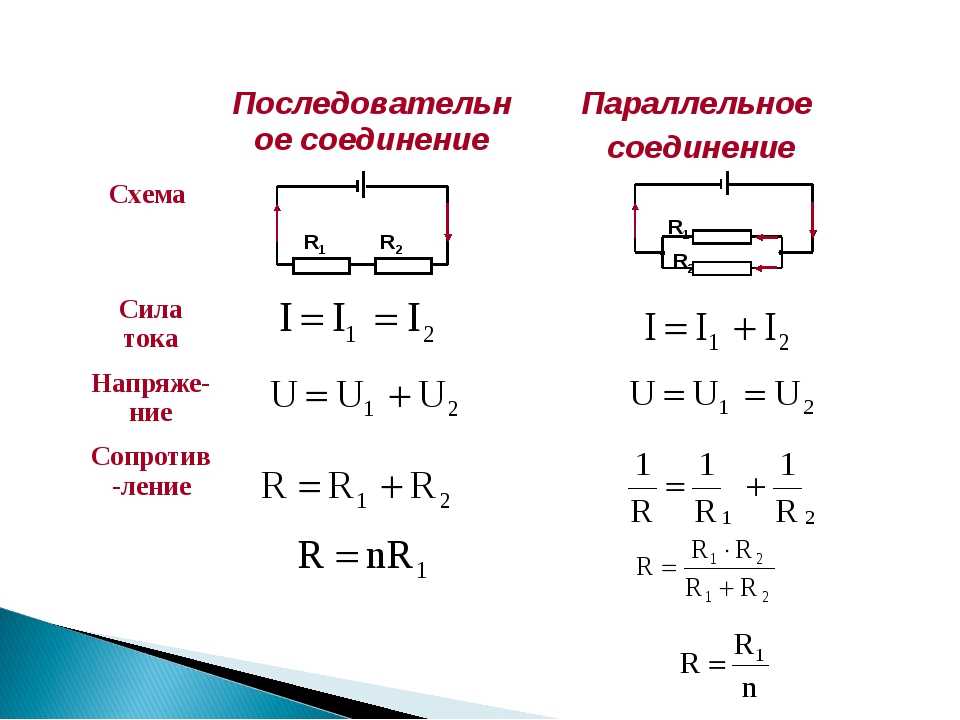
Параллельный ток
При параллельном соединении сопротивлений ток через каждое сопротивление вообще разный. Величина тока обратно пропорциональна величине сопротивления.
Напряжение при параллельном соединении
При параллельном соединении разность потенциалов между узлами, соединяющими элементы схемы, одинакова для всех элементов.
Приложение для параллельного подключения
1. В промышленности изготавливаются сопротивления в определенных количествах. Иногда необходимо получить значение сопротивления вне этих рядов. Для этого можно соединить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше наибольшего значения сопротивления.
2. Делитель тока.
Параллельное соединение резисторов — один из двух видов электрического соединения, когда оба вывода одного резистора соединяются с соответствующими выводами другого резистора или резисторов. Часто или параллельно для создания более сложных электронных схем.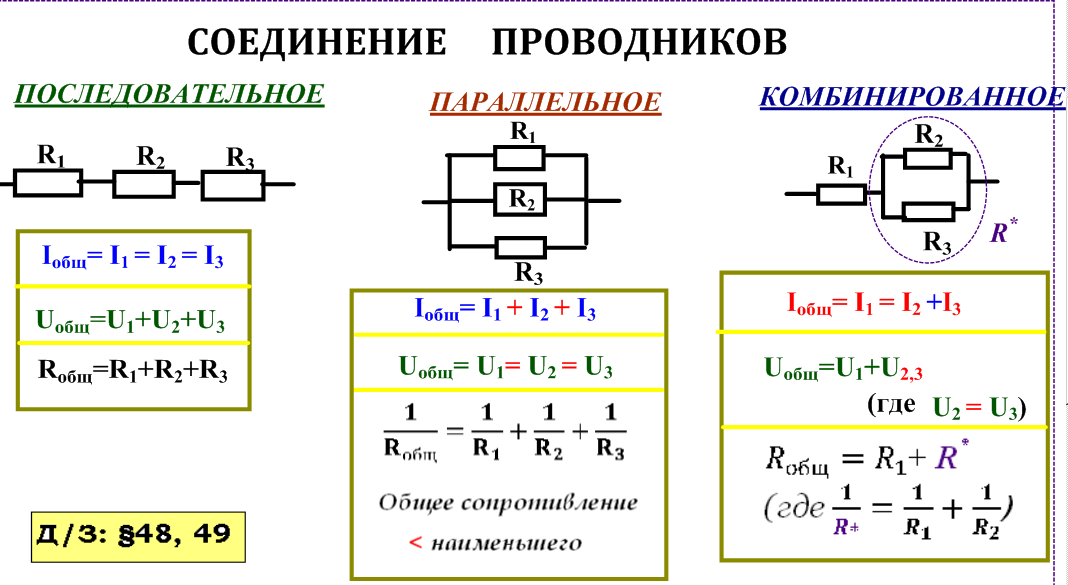
Схема параллельного подключения показана на рисунке ниже. При параллельном соединении резисторов напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула для параллельного соединения резисторов
Суммарное сопротивление нескольких параллельно соединенных резисторов определяется по следующей формуле:
Ток, протекающий через одиночный резистор, согласно, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства возникла необходимость установки резистора сопротивлением 8 Ом. Если просмотреть весь номинальный ряд стандартных номиналов резисторов, то мы увидим, что в нем нет ни одного резистора с сопротивлением 8 Ом.
Выход из этой ситуации — использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух параллельно соединенных резисторов рассчитывается следующим образом:
Это уравнение показывает, что если R1 равно R2, то сопротивление R равно половине сопротивления одного из двух резисторов.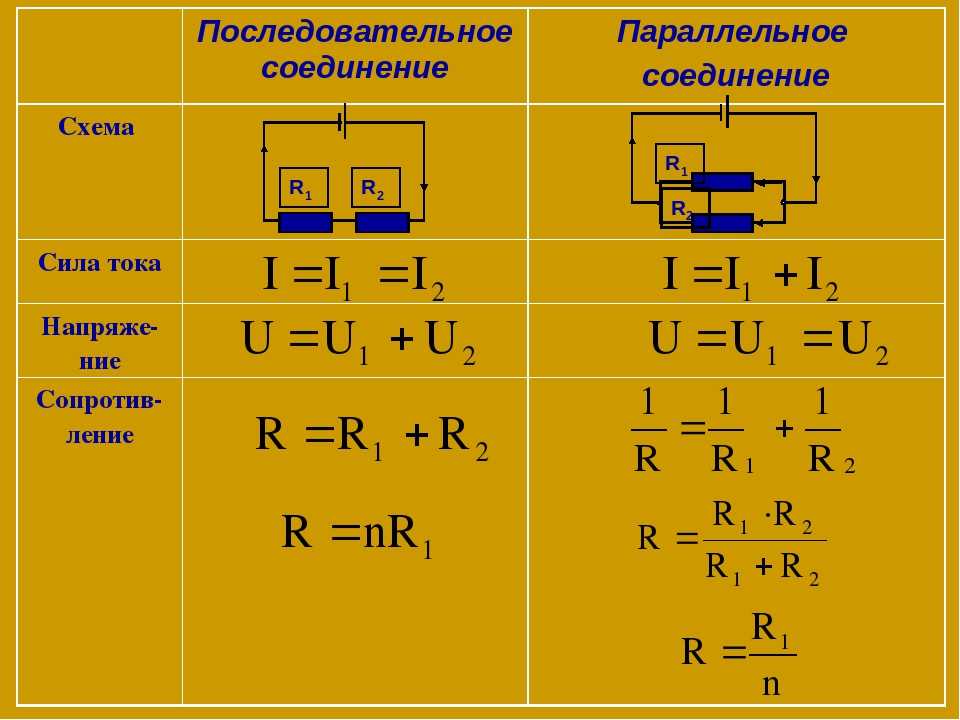 Следовательно, когда R = 8 Ом, R1 и R2 должны иметь значение 2 × 8 = 16 Ом.
Следовательно, когда R = 8 Ом, R1 и R2 должны иметь значение 2 × 8 = 16 Ом.
Теперь проверим, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета № 2
Найдите общее сопротивление R трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета можно использовать для расчета любого количества отдельных сопротивлений, соединенных параллельно.
Один важный момент, который необходимо помнить при расчете параллельно соединенных резисторов, заключается в том, что общее сопротивление всегда будет меньше значения наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы подключения резисторов
Более сложные соединения резисторов можно рассчитать путем систематического группирования резисторов. На рисунке ниже нужно рассчитать общее сопротивление цепи, состоящей из трех резисторов:
На рисунке ниже нужно рассчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета мы сначала сгруппируем резисторы по параллельному и последовательному соединению.
Резисторы R2 и R3 соединены последовательно (группа 2). Они, в свою очередь, включены параллельно резистору R1 (группа 1).
Последовательное соединение резисторов группы 2 рассчитывается как сумма сопротивлений R2 и R3:
В итоге упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей цепи можно рассчитать следующим образом:
Расчет более сложных соединений резисторов можно производить по законам Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторов
Общий ток I, протекающий в цепи параллельных резисторов, равен сумме отдельных токов, протекающих во всех параллельных ветвях, и ток в одной ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, на каждый резистор подается одинаковое напряжение.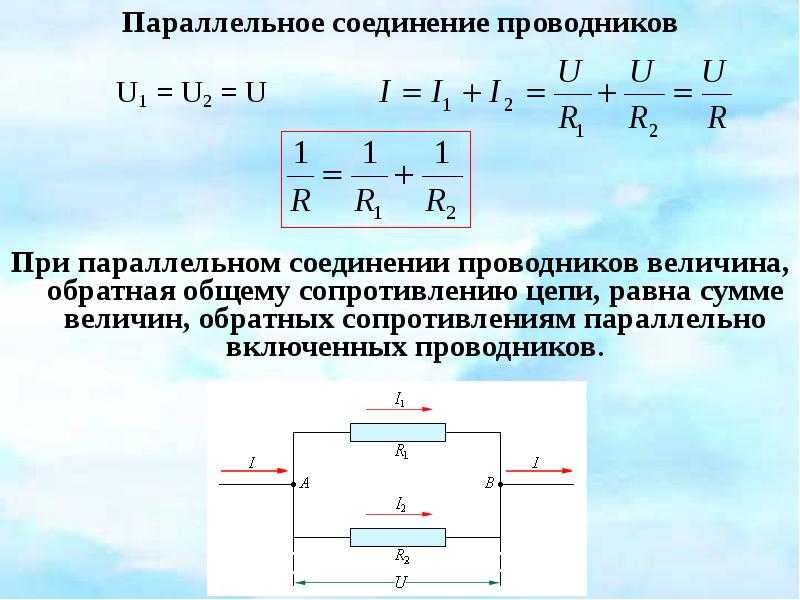 А так как величина сопротивления в параллельной цепи может быть разной, то и величина тока, протекающего через каждый резистор, тоже будет разной (по определению закона Ома).
А так как величина сопротивления в параллельной цепи может быть разной, то и величина тока, протекающего через каждый резистор, тоже будет разной (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, протекающий через каждый из резисторов (I1 и I2), будет отличаться друг от друга, так как сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который входит в цепь в точке «А», должен выйти из цепи в точке «В».
Первое правило Кирхгофа гласит: «Суммарный ток, выходящий из цепи, равен току, входящему в цепь».
Таким образом, общий ток в цепи можно определить как:
Затем, используя закон Ома, мы можем рассчитать ток, протекающий через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить с помощью закона Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
, где 15 кОм — общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в заключение следует отметить, что большинство современных резисторов обозначены цветными полосками и их назначение можно найти.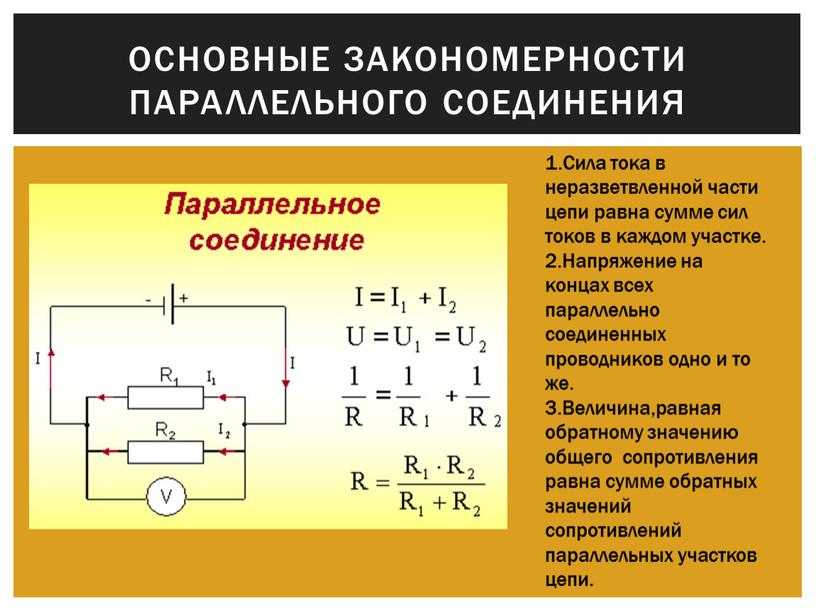
Параллельное соединение резисторов — онлайн калькулятор
Для быстрого расчета общего сопротивления двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн-калькулятором:
Суммировать
Когда два или более резистора соединены так, что оба контакта одного резистора соединены с соответствующими контактами другого резистора или резисторов, говорят, что они соединены параллельно друг другу. Напряжение на каждом резисторе внутри параллельной комбинации одинаково, но токи, протекающие через них, могут отличаться друг от друга в зависимости от сопротивления каждого резистора.
Эквивалент или импеданс параллельной комбинации всегда будет меньше минимального сопротивления резистора, включенного в параллельное соединение.
В каждой цепи есть резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. При разработке любой электрической схемы и ремонте электронных изделий часто возникает необходимость использовать резистор, имеющий необходимый номинал.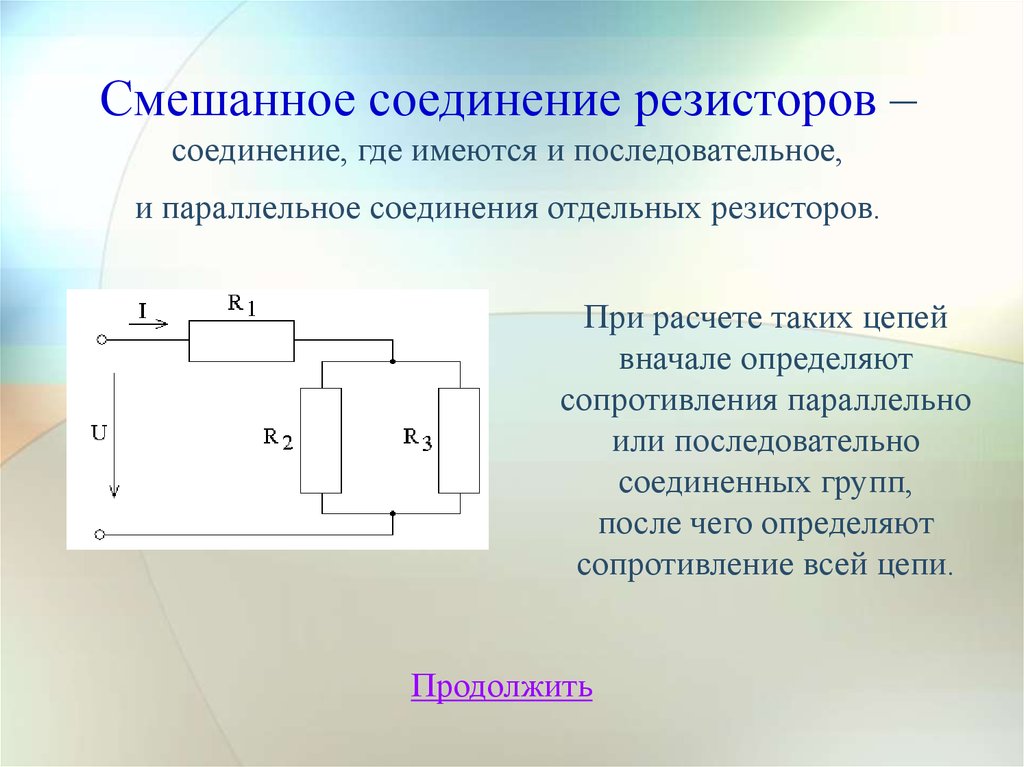
Несмотря на то, что для резисторов есть разные номиналы может случиться так, что не удастся найти нужный или даже не один элемент не сможет обеспечить требуемый показатель.
Решением этой проблемы может быть использование последовательного и параллельного соединений. Прочитав эту статью, вы узнаете об особенностях расчета и подбора различных значений сопротивления.
Часто при изготовлении каких-либо устройств используют резисторы, которые подключаются по последовательной схеме. Эффект от использования такого варианта сборки сводится к увеличению общего сопротивления цепи. Для этого варианта соединительных элементов создаваемое ими сопротивление рассчитывается как сумма номинальных значений. Если сборка деталей выполняется по параллельной схеме, то здесь необходимо рассчитать сопротивление по приведенным ниже формулам.
К схеме параллельного соединения прибегают в ситуации, когда стоит задача уменьшить общее сопротивление, а, кроме того, увеличить мощность для группы элементов, соединенных параллельно, которая должна быть больше, чем при их раздельном соединении.
Расчет сопротивления
В случае соединения деталей между собой, при использовании параллельной схемы расчета общего сопротивления будет использоваться следующая формула:
Р (всего) = 1/(1/Р1+1/Р2+1/Р3+1/Рн).
- R1- R3 и Rn — резисторы, соединенные по параллельной схеме.
При этом, если схема создается на основе всего двух элементов, то для определения общего номинального сопротивления используют следующую формулу:
Р (всего) = Р1 * Р2 / Р1 + Р2.
- R (общий) — общее сопротивление;
- R1 и R2 — резисторы, включенные по параллельной схеме.
Универсальная схема расчета
Применительно к радиотехнике следует обратить внимание на одно важное правило: если элементы, соединенные друг с другом по параллельной цепи имеют одинаковый показатель , то для расчета общего номинала общее значение следует разделить на количество подключенных узлов:
- R (общий) — суммарное значение сопротивления;
- Ом – номинал резистора, включенного параллельно;
- n — количество подключенных узлов.

Особое внимание следует обратить на то, что итоговый показатель сопротивления в случае использования схемы параллельного подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключенного к цепи.
Пример расчета
Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, номиналы которых соответственно 100, 150 и 30 Ом. Если мы воспользуемся первой формулой для определения общей стоимости, то получим следующее:
R (всего) = 1/(1/100 + 1/150 + 1/30) = 1/(0,01 + 0,007 + 0,03) = 1/0,047 = 21,28 Ом.
Если произвести несложные расчеты, то можно получить следующее: для цепи, включающей три части, где наименьшее значение сопротивления равно 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального номинала в цепи почти на 30%.
Важные нюансы
Обычно для резисторов используется параллельное соединение, когда стоит задача создать сопротивление большей мощности. Для ее решения потребуются резисторы, которые должны иметь равное сопротивление и мощность. С этим вариантом можно определить общую мощность следующим образом : мощность одного элемента необходимо умножить на общее количество всех резисторов, составляющих цепь, соединенных друг с другом в соответствии с параллельной схемой.
Для ее решения потребуются резисторы, которые должны иметь равное сопротивление и мощность. С этим вариантом можно определить общую мощность следующим образом : мощность одного элемента необходимо умножить на общее количество всех резисторов, составляющих цепь, соединенных друг с другом в соответствии с параллельной схемой.
Допустим, если использовать пять резисторов номиналом 100 Ом и мощностью каждого 1 Вт, которые соединены между собой по параллельной схеме, то общее сопротивление будет равно 20 Ом, а мощность составит 5 Вт.
Если взять те же резисторы, но соединить их в соответствии с последовательной схемой, то итоговая мощность будет 5 Вт, а суммарный номинал будет равен 500 Ом.
Заключение
Параллельное соединение резисторов очень востребовано по той причине, что часто возникает задача создания такого номинала, которого невозможно добиться с помощью простого параллельного соединения. При этом процедура расчета этого параметра достаточно сложная где необходимо учитывать разные параметры.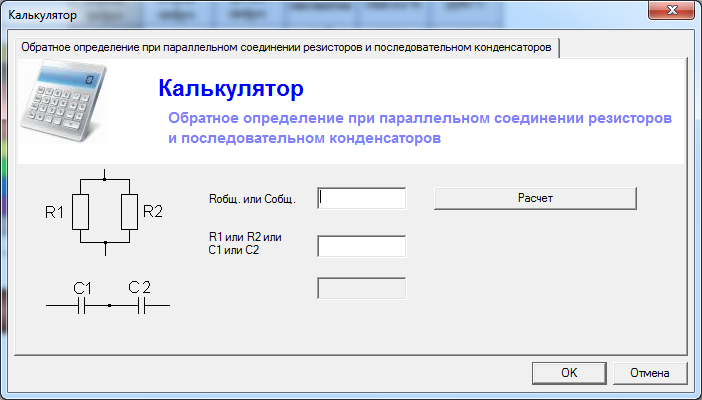
Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — в первую очередь сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий индикатор, то это не решит эффективно проблему создания в схеме нужного номинала.
Последовательное соединение – это соединение двух или более резисторов в виде цепи, в которой каждый отдельный резистор соединен с другим отдельным резистором только в одной точке.
Общее сопротивление R общее
При таком соединении через все резисторы проходит одинаковый электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» протекать по нему току. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор по закону Ома:
Т. е. чем больше сопротивление резистора, тем больше на нем падает напряжение.
е. чем больше сопротивление резистора, тем больше на нем падает напряжение.
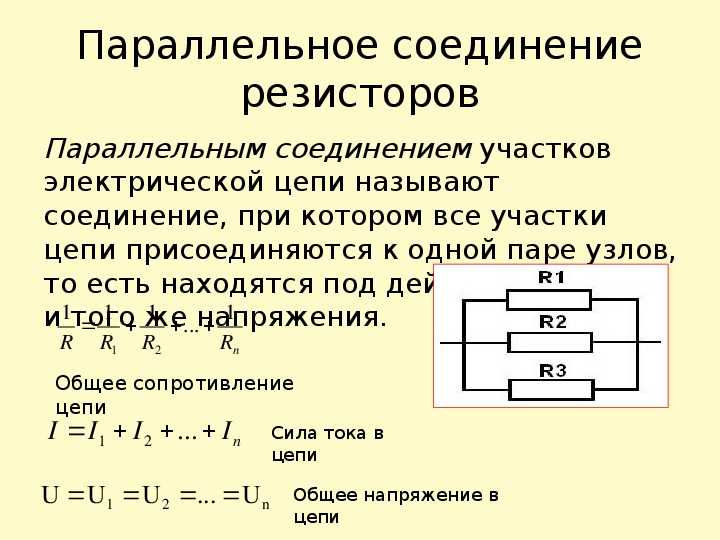
Параллельное соединение – это соединение, при котором резисторы соединяются друг с другом обоими контактами. В результате к одной точке (электрическому узлу) можно подключить несколько резисторов.
Общее сопротивление R общее
При таком подключении через каждый резистор будет протекать отдельный ток. Сила этого тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном соединении резисторов с разным сопротивлением общее сопротивление всегда будет меньше номинала наименьшего отдельного резистора.
Формула для общей проводимости при параллельном соединении резисторов:
Формула эквивалентного полного сопротивления для параллельного соединения резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине сопротивления одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно номиналу одного резистора, деленному на n.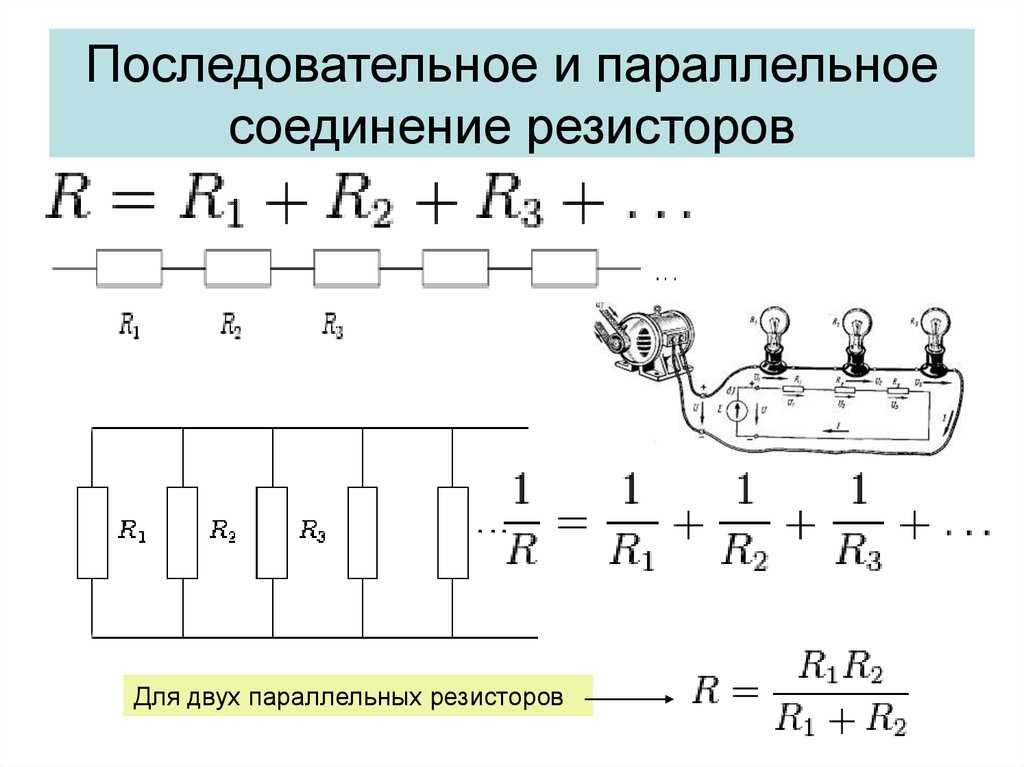
Напряжение при параллельном соединении
Напряжение между точками А и В является как суммарным напряжением для всего участка цепи, так и напряжением, приходящимся на каждый резистор в отдельности. Следовательно, при параллельном подключении ко всем резисторам будет падать одинаковое напряжение.
Через каждый резистор протекает ток, мощность которого обратно пропорциональна сопротивлению резистора. Для того, чтобы узнать, какой ток протекает через конкретный резистор, можно воспользоваться законом Ома:
Смешанным соединением называют участок цепи, на котором часть резисторов соединена друг с другом последовательно, а часть — параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление R общее
- Цепь делится на секции только с параллельным или только с последовательным соединением.
- Рассчитайте общее сопротивление для каждой отдельной области.

- Рассчитайте общее сопротивление для всей смешанной цепи.
Существует также более быстрый способ расчета общего сопротивления для смешанного состава. Можно в соответствии со схемой сразу написать формулу так:
- Если резисторы соединены последовательно, сложите.
- Если резисторы соединены параллельно — используйте символ «||».
- Подставить формулу параллельного соединения, где символ «||» стоит.
Значит будет искать Схема 1:
В этой теме можно привести множество примеров из нашей повседневной жизни, касающихся параллельного соединения сопротивлений. Параллельное соединение одинаковых сопротивлений — наглядный пример соединения люстры с n-м количеством ламп и с одинаковым сопротивлением для каждой лампы \рис.1\.
Если предположить в люстре, состоящей из нескольких ламп \с одинаковым сопротивлением\, перегорела одна лампа и была заменена лампа другой мощности на лампу другой мощности — в этом случае подключение люстры будет иметь вид параллельное соединение с разным сопротивлением.
Какие еще примеры можно привести из практики — с параллельным соединением сопротивлений? Предположим, вы подключили в своей квартире через удлинитель три бытовых электроприбора:
- электрическая плита;
- стиральная машина;
- телевизор.
Характер этого соединения будет таким же, как параллельное соединение, сопротивление отличается по размеру. То есть для каждого прибора сопротивление имеет свое значение.
Расчет сопротивления при параллельном соединении
Как уже было сказано, расчеты сопротивления при параллельном соединении выполняются:
- с таким же сопротивлением;
- с разным сопротивлением
а также, проводятся расчеты сопротивлений для смешанных соединений резисторов, при последовательном и параллельном соединении \ для одной цепи\. Расчет сопротивления для смешанных соединений резисторов, больше подходит для различных блок-схем:
- звуковое оборудование;
- видеооборудование.

К данной теме расчеты для смешанных соединений отношения не имеют.
Параллельное соединение одинаковых сопротивлений
Представьте себе параллельное соединение, например, трех сопротивлений \рис.2\равных по величине, где R1=R2=R3=36 Ом\сопротивление 9Лампа накаливания 5 Вт. К двум узловым точкам \A, B\ подключено напряжение 220 В. Необходимо рассчитать общее сопротивление всех трех ламп.
Для расчета общего сопротивления \Rобщ\ нам нужно 36 Ом разделить на количество сопротивлений. Решение простое, Rобщ = 12 Ом. То есть формула расчета таких расчетов выглядит так:
Р общ = Р/н
Параллельное соединение различных сопротивлений
Допустим возьмем выборочно три резистора, сопротивление:
- R1 = 20 Ом;
- R2 = 40 Ом;
- R3 = 10 Ом.
Необходимо определить общее сопротивление резисторов при параллельном соединении. Для этого расчета мы используем формулу:
1 / R всего = 1 / R1 + 1 / R2 + 1 / R3.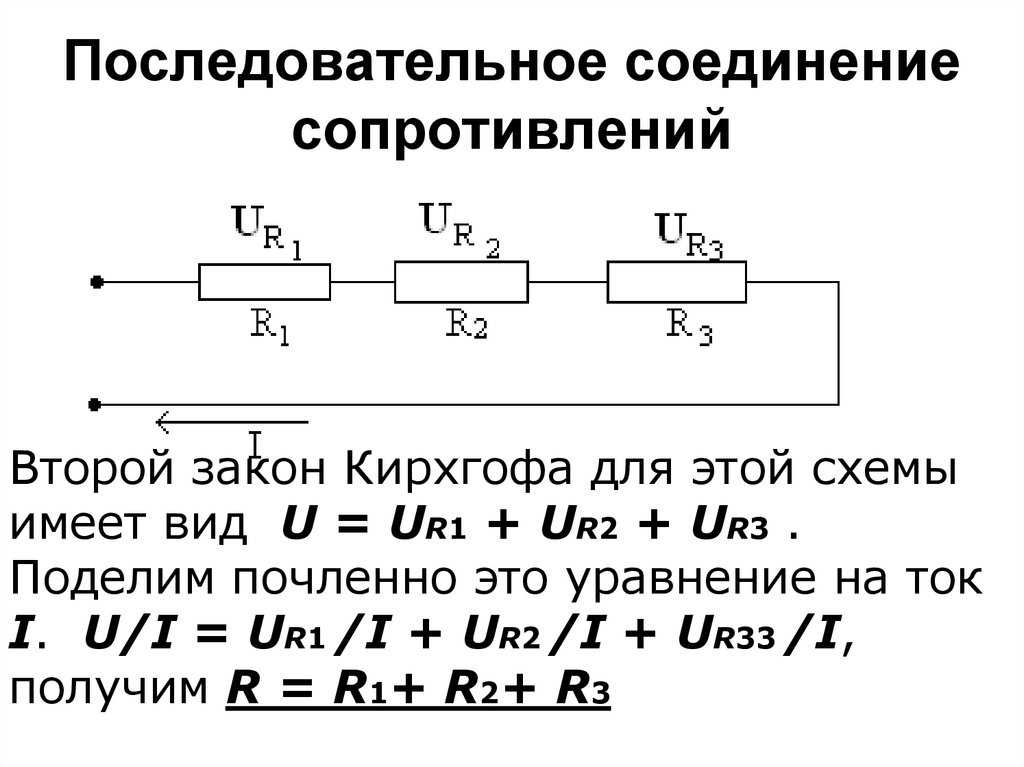

 .. ...+ (1/Gn))] (Единица измерения – Сименс)
.. ...+ (1/Gn))] (Единица измерения – Сименс)