Онлайн калькулятор решение задач по эконометрике: Онлайн-калькулятор по эконометрике

Содержание

решение задач. Контрольные по эконометрике.

Главная

Предметы

Эконометрика

«Студенты, изучающие эконометрику, это почти христианские мученики» — В. Черняк

Эконометрика – сравнительно молодой раздел науки, в котором произошел синтез экономической теории с современными прикладными статистическими методами исследования процессов. Это прикладная наука, и признаком её успешного изучения является умение решать задачи. Для приобретения практических навыков необходимо не только изучить объёмный и сложный материал, но понять суть проблемы, поставить правильно задачу для исследования. Для многих студентов решение задач по эконометрике представляет большую сложность — по сравнению, например, с контрольными по высшей математике и статистике. Мы предлагаем услугу решения задач по эконометрике на заказ. Возможно оказание помощи в режиме онлайн — вы присылаете задачу, мы в течении заранее оговоренного срока высылаем решение задачи. Также поможем в сдаче дистанционного тестирования по эконометрике.

Для тех специальностей, в вузах с более углубленным изучением курса эконометрики, где предусмотрено выполнение курсовой работы по эконометрике — свяжитесь с нами через форму заказа или любым удобным для вас способом, и наши специалисты окажут помощь в ее выполнении. При этом могут быть использованы прикладные программы, указанные вашем преподавателем.

Стоимость решения задач по эконометрике — от 300р, в зависимости от сложности. Онлайн помощь — от 1500р за билет.

Для тех, кто не смог подготовиться к экзамену предлагаем:

помощь на экзамене, зачете по эконометрике онлайн!

Примеры выполненных работ по эконометрике:

Пример решенных задач по эконометрике — регрессионный анализ в Excel
Пример решенного билета с экзамена по эконометрике — тест + задачи
Контрольная работа по эконометрике в Excel
Творческая работа по эконометрике — анализ социально-экономических показателей по ряду регионов РФ
Анализ зависимости смертности в субъектах РФ от некоторых социально-экономических факторов

При решении задач по эконометрике часто необходимо использовать прикладные эконометрические пакеты программ. Отметим наиболее распространенные:
— пакет анализа данных в Microsoft Excel;
— программа Gretl;
— эконометрический пакет Eviews;
— пакет Statistica
— программа для статистической обработки данных SPSS.

Ниже представлены в свободном доступе примеры решения задач по эконометрике в этих программных средствах, которые будут содержать отчет по решению задачи и файл реализации задачи в эконометрическом пакете. Так же на этой странице выложены бесплатные версии программ Gretl и Eviews3.

Пример выполненной работы по эконометрике в Excel
Анализ панельных данных в Eviews
Регрессионный анализ в SPSS
Построение уравнения множественной регрессии со всеми факторами матричным методом и с помощью надстройки «Анализ данных» MS Excel

Возможно выполнение работ на английском, немецком, французском и испанском языках!

Вы можете связаться с нами, уточнить стоимость и сроки, заказать услуги через наши контакты либо заполнив данную форму.

Логистическая регрессия и ROC-анализ — математический аппарат

Математический аппарат и назначение бинарной логистической регрессии — популярного инструмента для решения задач регрессии и классификации. ROC-анализ тесно связан с бинарной логистической регрессией и применяется для оценки качества моделей: позволяет выбрать аналитику модель с наилучшей прогностической силой, проанализировать чувствительность и специфичность моделей, подобрать порог отсечения.

Введение
Логистическая регрессия
ROC-анализ
Канонический алгоритм построения ROC-кривой

Введение

Логистическая регрессия — полезный классический инструмент для решения задачи регрессии и классификации. ROC-анализ — аппарат для анализа качества моделей. Оба алгоритма активно используются для построения моделей в медицине и проведения клинических исследований.

Логистическая регрессия получила распространение в скоринге для расчета рейтинга заемщиков и управления кредитными рисками. Поэтому, несмотря на свое «происхождение» из статистики, логистическую регрессию и ROC-анализ почти всегда можно увидеть в наборе Data Mining алгоритмов.

Логистическая регрессия

Логистическая регрессия — это разновидность множественной регрессии, общее назначение которой состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной. Бинарная логистическая регрессия применяется в случае, когда зависимая переменная является бинарной (т.е. может принимать только два значения). С помощью логистической регрессии можно оценивать вероятность того, что событие наступит для конкретного испытуемого (больной/здоровый, возврат кредита/дефолт и т.д.).

Все регрессионные модели могут быть записаны в виде формулы:

y = F (x_1,\, x_2, \,\dots, \, x_n)

В множественной линейной регрессии предполагается, что зависимая переменная является линейной функцией независимых переменных, т.е.:

y = a\,+\,b_1\,x_1\,+\,b_2\,x_2\,+\,\dots\,+\,b_n\,x_n

Можно ли ее использовать для задачи оценки вероятности исхода события? Да, можно, вычислив стандартные коэффициенты регрессии. {-y}}

где P — вероятность того, что произойдет интересующее событие e — основание натуральных логарифмов 2,71…; y — стандартное уравнение регрессии.

Зависимость, связывающая вероятность события и величину y, показана на следующем графике (рис. 1):

Рис. 1 — Логистическая кривая

Поясним необходимость преобразования. Предположим, что мы рассуждаем о нашей зависимой переменной в терминах основной вероятности P, лежащей между 0 и 1. Тогда преобразуем эту вероятность P:

P’ = \log_e \Bigl(\frac{P}{1-P}\Bigr)

Это преобразование обычно называют логистическим или логит-преобразованием. Теоретически P’ может принимать любое значение. Поскольку логистическое преобразование решает проблему об ограничении на 0-1 границы для первоначальной зависимой переменной (вероятности), то эти преобразованные значения можно использовать в обычном линейном регрессионном уравнении. А именно, если произвести логистическое преобразование обеих частей описанного выше уравнения, мы получим стандартную модель линейной регрессии. {-1}\,g_t(W_t)\,=\,W_t\,-\,\Delta W_t

Логистическую регрессию можно представить в виде однослойной нейронной сети с сигмоидальной функцией активации, веса которой есть коэффициенты логистической регрессии, а вес поляризации — константа регрессионного уравнения (рис. 2).

Рис. 2 — Представление логистической регрессии в виде нейронной сети

Однослойная нейронная сеть может успешно решить лишь задачу линейной сепарации. Поэтому возможности по моделированию нелинейных зависимостей у логистической регрессии отсутствуют. Однако для оценки качества модели логистической регрессии существует эффективный инструмент ROC-анализа, что является несомненным ее преимуществом.

Для расчета коэффициентов логистической регрессии можно применять любые градиентные методы: метод сопряженных градиентов, методы переменной метрики и другие.

ROC-анализ

ROC-кривая (Receiver Operator Characteristic) — кривая, которая наиболее часто используется для представления результатов бинарной классификации в машинном обучении. Название пришло из систем обработки сигналов. Поскольку классов два, один из них называется классом с положительными исходами, второй — с отрицательными исходами. ROC-кривая показывает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров.

В терминологии ROC-анализа первые называются истинно положительным, вторые — ложно отрицательным множеством. При этом предполагается, что у классификатора имеется некоторый параметр, варьируя который, мы будем получать то или иное разбиение на два класса. Этот параметр часто называют порогом, или точкой отсечения (cut-off value). В зависимости от него будут получаться различные величины ошибок I и II рода.

В логистической регрессии порог отсечения изменяется от 0 до 1 — это и есть расчетное значение уравнения регрессии. Будем называть его рейтингом.

Для понимания сути ошибок I и II рода рассмотрим четырехпольную таблицу сопряженности (confusion matrix), которая строится на основе результатов классификации моделью и фактической (объективной) принадлежностью примеров к классам.

Модель	Фактически положительно	Фактически отрицательно
Положительно	TP	FP
Отрицательно	FN	TN

TP (True Positives) — верно классифицированные положительные примеры (так называемые истинно положительные случаи).
TN (True Negatives) — верно классифицированные отрицательные примеры (истинно отрицательные случаи).
FN (False Negatives) — положительные примеры, классифицированные как отрицательные (ошибка I рода). Это так называемый «ложный пропуск» — когда интересующее нас событие ошибочно не обнаруживается (ложно отрицательные примеры).
FP (False Positives) — отрицательные примеры, классифицированные как положительные (ошибка II рода). Это ложное обнаружение, т.к. при отсутствии события ошибочно выносится решение о его присутствии (ложно положительные случаи).

Что является положительным событием, а что — отрицательным, зависит от конкретной задачи.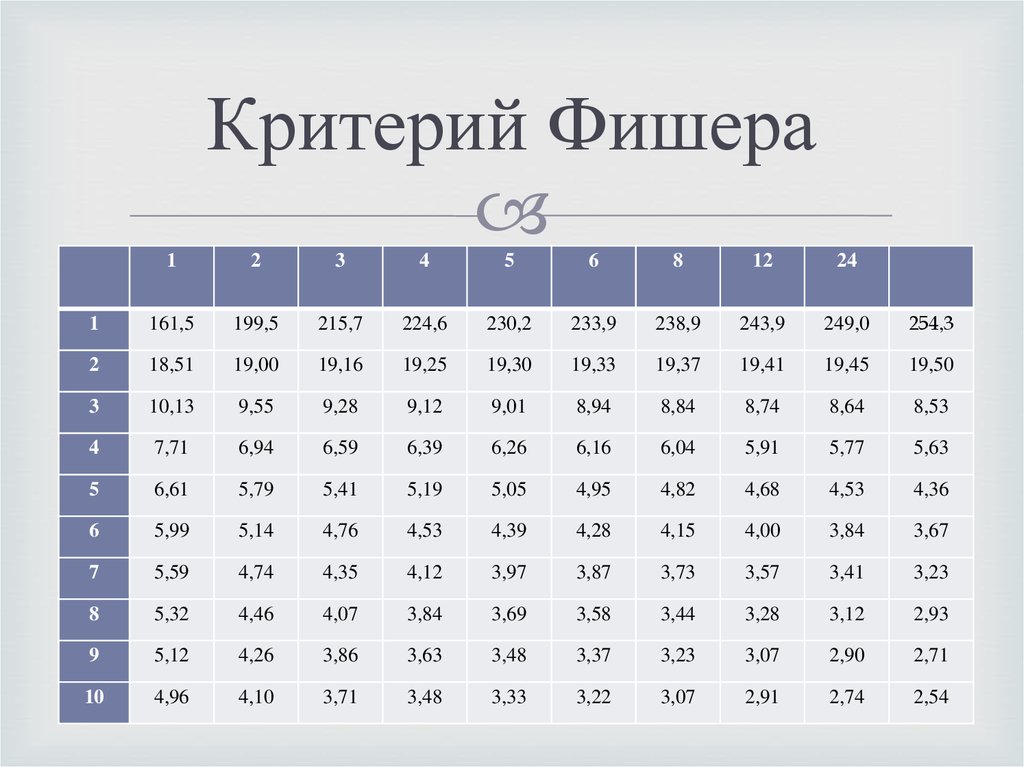 Например, если мы прогнозируем вероятность наличия заболевания, то положительным исходом будет класс «Больной пациент», отрицательным — «Здоровый пациент». И наоборот, если мы хотим определить вероятность того, что человек здоров, то положительным исходом будет класс «Здоровый пациент», и так далее.

При анализе чаще оперируют не абсолютными показателями, а относительными — долями (rates), выраженными в процентах:

Доля истинно положительных примеров (True Positives Rate): TPR = \frac{TP}{TP\,+\,FN}\,\cdot\,100 \,\%
Доля ложно положительных примеров (False Positives Rate): FPR = \frac{FP}{TN\,+\,FP}\,\cdot\,100 \,\%

Введем еще два определения: чувствительность и специфичность модели. Ими определяется объективная ценность любого бинарного классификатора.

Чувствительность (Sensitivity) — это и есть доля истинно положительных случаев:

S_e = TPR = \frac{TP}{TP\,+\,FN}\,\cdot\,100 \,\%

Специфичность (Specificity) — доля истинно отрицательных случаев, которые были правильно идентифицированы моделью:

S_p = \frac{TN}{TN\,+\,FP}\,\cdot\,100 \,\%

Заметим, что FPR=100-Sp

Попытаемся разобраться в этих определениях.

Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицины — задачи диагностики заболевания, где модель классификации пациентов на больных и здоровых называется диагностическим тестом, то получится следующее:

Чувствительный диагностический тест проявляется в гипердиагностике — максимальном предотвращении пропуска больных.
Специфичный диагностический тест диагностирует только доподлинно больных. Это важно в случае, когда, например, лечение больного связано с серьезными побочными эффектами и гипердиагностика пациентов не желательна.

ROC-кривая получается следующим образом:

Для каждого значения порога отсечения, которое меняется от 0 до 1 с шагом d_x (например, 0,01) рассчитываются значения чувствительности Se и специфичности Sp. В качестве альтернативы порогом может являться каждое последующее значение примера в выборке.
Строится график зависимости: по оси Y откладывается чувствительность Se, по оси X — FPR=100-Sp — доля ложно положительных случаев.

Канонический алгоритм построения ROC-кривой

Входы: L — множество примеров f[i] — рейтинг, полученный моделью, или вероятность того, что i-й пример имеет положительный исход; min и max — минимальное и максимальное значения, возвращаемые f; d_x — шаг; P и N — количество положительных и отрицательных примеров соответственно.

t=min
повторять
FP=TP=0
для всех примеров i принадлежит L {
если f[i]>=t тогда // этот пример находится за порогом
если i положительный пример тогда
{ TP=TP+1 }
иначе // это отрицательный пример
{ FP=FP+1 }
}
Se=TP/P*100
point=FP/N // расчет (100 минус Sp)
Добавить точку (point, Se) в ROC-кривую
t=t+d_x
пока (t>max)

В результате вырисовывается некоторая кривая (рис. 2): для каждого порога необходимо «пробегать» по записям и каждый раз рассчитывать TP и FP. Если же двигаться вниз по набору данных, отсортированному по убыванию выходного поля классификатора (рейтингу), то можно за один проход вычислить значения всех точек ROC-кривой, последовательно обновляя значения TP и FP.

Для идеального классификатора график ROC-кривой проходит через верхний левый угол, где доля истинно положительных случаев составляет 100% или 1,0 (идеальная чувствительность), а доля ложно положительных примеров равна нулю. Поэтому чем ближе кривая к верхнему левому углу, тем выше предсказательная способность модели. Наоборот, чем меньше изгиб кривой и чем ближе она расположена к диагональной прямой, тем менее эффективна модель. Диагональная линия соответствует «бесполезному» классификатору, т.е. полной неразличимости двух классов.

При визуальной оценке ROC-кривых расположение их относительно друг друга указывает на их сравнительную эффективность. Кривая, расположенная выше и левее, свидетельствует о большей предсказательной способности модели.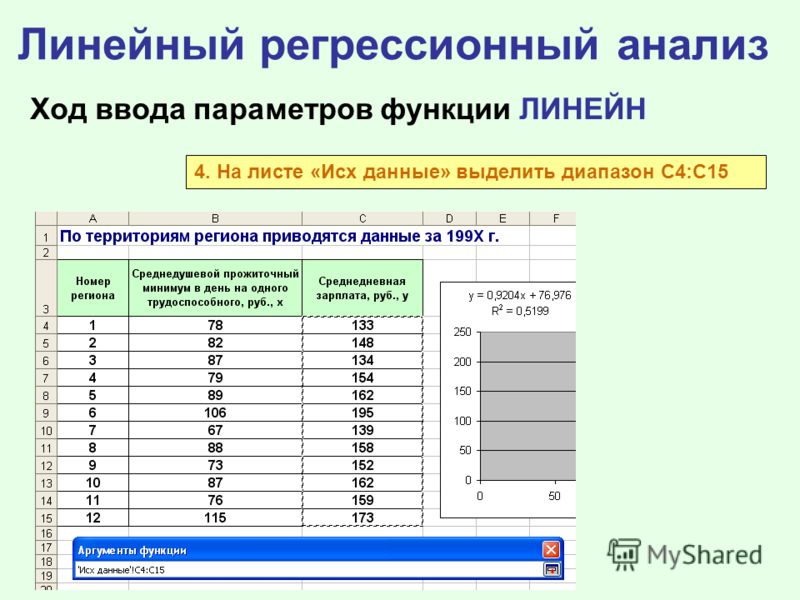 Так, на рис. 4 две ROC-кривые совмещены на одном графике. Видно, что модель «A» лучше.

Рис. 4 — Сравнение ROC-кривых

Визуальное сравнение кривых ROC не всегда позволяет выявить наиболее эффективную модель. Своеобразным методом сравнения ROC-кривых является оценка площади под кривыми. Теоретически она изменяется от 0 до 1,0, но, поскольку модель всегда характеризуются кривой, расположенной выше положительной диагонали, то обычно говорят об изменениях от 0,5 («бесполезный» классификатор) до 1,0 («идеальная» модель).

Эта оценка может быть получена непосредственно вычислением площади под многогранником, ограниченным справа и снизу осями координат и слева вверху — экспериментально полученными точками (рис. 5). Численный показатель площади под кривой называется AUC (Area Under Curve). Вычислить его можно, например, с помощью численного метода трапеций:

AUC = \int f(x)\,dx = \sum_i \Bigl[ \frac{X_{i+1}\,+\,X_i}{2}\Bigr]\,\cdot \,(Y_{i+1}\,-\, Y_i)

Рис. 5 — Площадь под ROC-кривой

С большими допущениями можно считать, что чем больше показатель AUC, тем лучшей прогностической силой обладает модель. Однако следует знать, что:

показатель AUC предназначен скорее для сравнительного анализа нескольких моделей;
AUC не содержит никакой информации о чувствительности и специфичности модели.

В литературе иногда приводится следующая экспертная шкала для значений AUC, по которой можно судить о качестве модели:

Интервал AUC	Качество модели
0,9-1,0	Отличное
0,8-0,9	Очень хорошее
0,7-0,8	Хорошее
0,6-0,7	Среднее
0,5-0,6	Неудовлетворительное

Идеальная модель обладает 100% чувствительностью и специфичностью. Однако на практике добиться этого невозможно, более того, невозможно одновременно повысить и чувствительность, и специфичность модели. Компромисс находится с помощью порога отсечения, т.к. пороговое значение влияет на соотношение Se и Sp. Можно говорить о задаче нахождения оптимального порога отсечения (optimal cut-off value).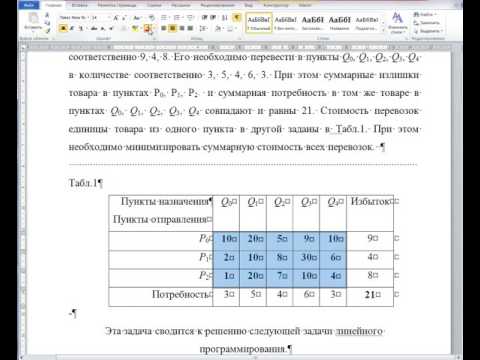

Порог отсечения нужен для того, чтобы применять модель на практике: относить новые примеры к одному из двух классов. Для определения оптимального порога нужно задать критерий его определения, т.к. в разных задачах присутствует своя оптимальная стратегия. Критериями выбора порога отсечения могут выступать:

Требование минимальной величины чувствительности (специфичности) модели. Например, нужно обеспечить чувствительность теста не менее 80%. В этом случае оптимальным порогом будет максимальная специфичность (чувствительность), которая достигается при 80% (или значение, близкое к нему «справа» из-за дискретности ряда) чувствительности (специфичности).
Требование максимальной суммарной чувствительности и специфичности модели, т.е. Cutt\underline{\,\,\,}off_o = \max_k (Se_k\,+\,Sp_k)
Требование баланса между чувствительностью и специфичностью, т.е. когда Se \approx Sp: Cutt\underline{\,\,\,}off_o = \min_k \,\bigl |Se_k\,-\,Sp_k \bigr |

Второе значение порога обычно предлагается пользователю по умолчанию. В третьем случае порог есть точка пересечения двух кривых, когда по оси X откладывается порог отсечения, а по оси Y — чувствительность или специфичность модели (рис. 6).

Рис. 6 — «Точка баланса» между чувствительностью и специфичностью

Существуют и другие подходы, когда ошибкам I и II рода назначается вес, который интерпретируется как цена ошибок. Но здесь встает проблема определения этих весов, что само по себе является сложной, а часто не разрешимой задачей.

Литература

Цыплаков А. А. Некоторые эконометрические методы. Метод максимального правдоподобия в эконометрии. Учебное пособие.
Fawcett T. ROC Graphs: Notes and Practical Considerations for Researchers // 2004 Kluwer Academic Publishers.
Zweig M.H., Campbell G. ROC Plots: A Fundamental Evaluation Tool in Clinical Medicine // Clinical Chemistry, Vol. 39, No. 4, 1993.
Davis J., Goadrich M. The Relationship Between Precision-Recall and ROC Curves // Proc. Of 23 International Conference on Machine Learning, Pittsburgh, PA, 2006.

Другие материалы по теме:

Применение логистической регрессии в медицине и скоринге

Machine learning в Loginom на примере задачи c Kaggle

Проверка гипотез, t-критерий, хи-квадрат, регрессия, корреляция, дисперсионный анализ, кластерный анализ

Вставить данные

Скопируйте свои данные в калькулятор статистики.

Выберите область

Выберите, что вы хотите сделать с вашими данными.

Выберите переменные

Выберите интересующие вас переменные.

Готово!

DATAtab выбирает соответствующий метод и интерпретирует ваши результаты.

Онлайн-калькулятор статистики

Что вы хотите рассчитать онлайн? Онлайн-калькулятор статистики прост и несложный! Здесь вы можете найти список всех реализованных методов!

Описательная статистика Калькулятор Параметр местоположения Калькулятор Среднее, Медиана, Мода, Модальное значение Калькулятор Параметр дисперсии Калькулятор Калькулятор стандартного отклонения и дисперсии Калькулятор диапазона Таблица частот Калькулятор Таблица сопряженности Калькулятор Калькулятор проверки гипотез Калькулятор p-значения Одновыборочный t-критерий Калькулятор-тест для независимых выборок Калькулятор-тест для зависимых выборок | paired CalculatorBinomial test CalculatorChi-square test CalculatorMann-Whitney U Test CalculatorWilcoxon-Test CalculatorANOVA CalculatorANOVA with repeated measures CalculatorTwo factor ANOVA CalculatorTwo factor ANOVA repeated measures CalculatorFriedman Test CalculatorKruskal-Wallis Test CalculatorCorrelation CalculatorCovariance CalculatorPearson correlation CalculatorSpearman correlation CalculatorPoint biserial correlation CalculatorRegression CalculatorLinear Regression CalculatorLogistic Regression CalculatorModeration analysis КалькуляторАнализ посредниковКалькуляторАнализ основных компонентов | СПС | Калькулятор исследовательского факторного анализаКалькулятор анализа надежностиКалькулятор альфа-альфа КронбахаКалькулятор каппы КоэнаКалькулятор каппы ФлейссаКалькулятор тау КендаллаКалькулятор W КендаллаКалькулятор внутриклассовой корреляцииКластерный анализКалькулятор кластерного анализа k-среднихКалькулятор Иерархический кластерный анализКалькуляторКалькулятор анализа возможностей процессаАнализ системы измерения | Калькулятор MSAКалькулятор критерия эквивалентности и не меньшей эффективностиКалькулятор дерева решений (CHAID)КалькуляторАнализ правил ассоциации (анализ рыночной корзины)КалькуляторАнализ выживания (Каплана-Мейера)КалькуляторКалькулятор регрессии КоксаROC (рабочая характеристика приемника)Калькулятор

Создание диаграмм онлайн с помощью DATAtab

Создавайте свои диаграммы для своих данных прямо в Интернете и несложно. Для этого вставьте свои данные в таблицу в разделе «Диаграммы» и выберите нужную диаграмму.

Создание диаграмм онлайн

Создание гистограмм онлайн Сделать боксплот онлайн Сделать гистограмму онлайн Создавайте диаграммы рассеяния онлайн

Преимущества DATAtab

Статистика проста как никогда.

DATAtab — это современное статистическое программное обеспечение с уникальным удобством для пользователя. Статистический анализ выполняется всего несколькими щелчками мыши, поэтому DATAtab идеально подходит как для новичков в статистике, так и для профессионалов, которые хотят более плавного взаимодействия с пользователем.

Непосредственно в браузере, полностью гибкий.

Непосредственно в браузере, полностью гибкий. DATAtab работает непосредственно в вашем веб-браузере. У вас нет никаких усилий по установке и обслуживанию. Где бы и когда бы вы ни захотели использовать DATAtab, просто зайдите на веб-сайт и начните работу.

Все необходимые статистические методы.

DATAtab предлагает широкий выбор статистических методов. Мы выбрали для вас наиболее важные и известные статистические методы и не перегружаем вас частными случаями.

Безопасность данных превыше всего.

Все данные, которые вы вставляете и оцениваете в DATAtab, всегда остаются на вашем конечном устройстве. Данные не отправляются на какой-либо сервер и не хранятся у нас (даже временно). Кроме того, мы не передаем ваши данные третьим лицам для анализа вашего пользовательского поведения.

Множество руководств с простыми примерами.

Для облегчения ознакомления DATAtab предлагает большое количество бесплатных руководств с подробными пояснениями на простом языке.

Мы объясняем статистическую подоплеку методов и даем пошаговые объяснения выполнения анализа в калькуляторе статистики.

Практический автопомощник.

DATAtab поможет вам в мире статистики. При принятии статистических решений, таких как выбор шкалы или уровня измерения или выбор подходящих методов, автопомощники обеспечивают быстрое получение правильных результатов.

Графики, простые и понятные.

Визуализация данных с DATAtab доставляет удовольствие! Здесь вы можете легко создавать содержательные диаграммы, которые оптимально иллюстрируют ваши результаты.

Новое в мире статистики?

DATAtab в первую очередь был разработан для людей, для которых статистика является новой территорией. Новички не перегружены множеством сложных опций и флажков, но им рекомендуется выполнять их анализ шаг за шагом.

Очень простой онлайн-опрос.

DATAtab предлагает вам возможность легко создать онлайн-опрос, который вы можете сразу оценить с помощью DATAtab.

Наши ссылки

Альтернатива статистическому программному обеспечению, такому как SPSS и STATA

DATAtab был разработан для простоты использования и является привлекательным альтернатива — статистические программы , такие как SPSS и STATA. На datatab.net, данные могут быть статистически оценены напрямую онлайн и очень легко (например, t-критерий, регрессия, корреляция и др.). Цель DATAtab — сделать мир

статистический анализ данных максимально простой, без установки и простой в использовании.

Обширные учебные пособия

Описательная статистика

Здесь вы можете узнать все о параметрах местоположения и параметрах рассеивания, а также о том, как вы можете описать и наглядно представить свои данные, используя характеристические значения.

Проверка гипотезы

Здесь вы найдете все о проверке гипотез: одновыборочный t-критерий, непарный t-критерий, парный t-критерий и критерий хи-квадрат. Вы также найдете учебные пособия по непараметрическим статистическим процедурам, таким как u-критерий Манна-Уитни и критерий Уилкоксона. U-критерий Манна-Уитни и критерий Уилкоксона

Регрессия

Регрессия предоставляет информацию о влиянии одной или нескольких независимых переменных на зависимую переменную. Вот простые объяснения линейной регрессии и логистической регрессии.

Корреляция

Корреляционный анализ позволяет анализировать линейную связь между переменными. Узнайте, когда использовать корреляцию Пирсона или ранговую корреляцию Спирмена. С помощью частичной корреляции вы можете вычислить корреляцию между двумя переменными, исключая третью переменную.

Частичная корреляция

Частичная корреляция показывает корреляцию между двумя переменными с исключением третьей переменной.

Левен Тест

Тест Левена проверяет ваши данные на равенство дисперсий. Таким образом, тест Левена используется в качестве предварительного теста для многих тестов гипотез.

р-значение

Значение p необходимо для каждой проверки гипотезы, чтобы иметь возможность сделать вывод о том, принимается или отвергается нулевая гипотеза.

Распределения

DATAtab содержит таблицы с распределениями и полезные пояснения функций распределения. К ним относятся Таблица t-распределения и Таблица распределения хи-квадрат

Таблица сопряженности

С помощью таблицы непредвиденных обстоятельств вы можете получить обзор двух категориальных переменных в статистике.

Эквивалентность и не меньшая ценность

В испытании на эквивалентность статистический тест направлен на то, чтобы показать, что два метода лечения не слишком отличаются по характеристикам, а исследование не меньшей эффективности должно показать, что экспериментальное лечение не хуже, чем установленное лечение.

причинность

Если существует четкая причинно-следственная связь между двумя переменными, то можно говорить о причинно-следственной связи. Узнайте больше о причинно-следственной связи в нашем уроке.

Мультиколлинеарность

Мультиколлинеарность — это когда две или более независимых переменных имеют высокую корреляцию.

Величина эффекта для независимого t-теста

Узнайте, как рассчитать размер эффекта для t-критерия для независимых выборок.

Калькулятор анализа надежности

На DATAtab Каппа Коэна может быть легко рассчитана онлайн в Калькуляторе Каппа Коэна. есть также калькулятор Fleiss Kappa Calculator. Конечно, альфа Кронбаха также может быть рассчитана в Калькуляторе альфа Кронбаха.

Дисперсионный анализ с повторным измерением

Повторные измерения ANOVA проверяет наличие статистически значимых различий в трех или более зависимых выборках.

Пошаговый калькулятор линейной регрессии — MathCracker.com

Решатели Статистика

Инструкции: Проведите регрессионный анализ с помощью Калькулятор линейной регрессии , где будет найдено уравнение регрессии и предоставлен подробный отчет о расчетах вместе с точечной диаграммой. Все, что вам нужно сделать, это ввести данные X и Y. При желании вы можете добавить заголовок и добавить имя переменных.

Данные X (разделенные запятой или пробелом)

Данные Y (разделенные запятой или пробелом)

Введите заголовок (необязательно)

Имя переменной X (необязательно)

Имя переменной Y (необязательно)

А модель линейной регрессии соответствует модели линейной регрессии, которая минимизирует сумму квадратов ошибок для набора пар \((X_i, Y_i)\).

Уравнение линейной регрессии, также известное как уравнение наименьших квадратов, имеет следующую форму: \(\hat Y = a + b X\), где коэффициенты регрессии \(a\) и \(b\) вычисляются этим регрессионным калькулятором следующее:

\[b = \frac{SS_{XY}}{SS_{XX}}\] \[a = \bar Y — \bar X \cdot b \]

Коэффициент \(b\) известен как коэффициент наклона, а коэффициент \(a\) известен как точка пересечения по оси y.

Если вместо линейной модели вы хотите использовать нелинейную модель, то вам следует вместо этого рассмотреть калькулятор полиномиальной регрессии , что позволяет использовать степени независимой переменной.

Калькулятор линейной регрессии Шаги

Шаги для проведения регрессионного анализа:

(1) Получите данные для зависимой и независимой переменной в формате столбца.

(2) Введите данные в формате, разделенном запятыми или пробелами.

(3) Нажмите «Рассчитать».

Остатки регрессии

Как мы оцениваем, хороша ли модель линейной регрессии? Вы можете подумать: «Легко, просто взгляните на диаграмма рассеяния «. В действительности математика и статистика, как правило, выходят за рамки того, что видно на графике. Обычно полагаться исключительно на диаграмму рассеяния для оценки качества модели рискованно.

С точки зрения качества подгонки, один из способов оценки качества подгонки модели линейной регрессии заключается в следующем. расчет коэффициента детерминации , указывает долю вариации зависимой переменной, которая объясняется независимой переменной.

В линейной регрессии выполнение допущений имеет решающее значение, чтобы оценки коэффициента регрессии имели хорошие свойства (среди прочего, беспристрастность, минимальная дисперсия).

Чтобы оценить предположения о линейной регрессии, вам нужно будет взглянуть на остатки. Для этого вы можете ознакомиться с нашим остаточный калькулятор .

Другие калькуляторы, связанные с линейной регрессией

Вас также могут заинтересовать вычисление коэффициента корреляции , или к построить точечную диаграмму с предоставленными данными.