Онлайн калькулятор системы неравенств с решением: Калькулятор систем неравенств

alexxlab / / Разное

Как решать систему линейных неравенств с одной переменной

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Решение системы неравенств

В данной публикации мы рассмотрим, что такое система линейных неравенств, как она решается методом интервалов на числовой оси. Также разберем практические примеры по этой теме.

  • Определение системы неравенств
  • Решение системы линейных неравенств

Определение системы неравенств

Для решения системы неравенств необходимо иметь навыки, позволяющие справиться с линейными неравенствами. Мы подробно рассмотрели этот вопрос в отдельной публикации.

Система неравенств – это два или более неравенства, объединенные фигурной скобкой. Например:

Т.е. она чем-то похожа на систему уравнений, в которых “равно” заменено на один из знаков сравнения (“больше”, “меньше”, “больше или равно”, “меньше или равно”).

Примечание: в системе линейных неравенств все они, соответственно, являются линейными. Обычно неизвестная переменная в них всего одна (чаще всего обозначается как “x”).

Решение системы линейных неравенств

Алгоритм состоит из двух основных шагов:

  1. По отдельности решаем каждое неравенство.
  2. Сопоставляем полученные решения на числовой оси методом интервалов, после чего выводим общий ответ.

Пример 1
Давайте попробуем решить систему, приведенную выше.

Решение:

x + 2 > 7 верно при x > 5
x – 1 ≥ 9 имеет решение x ≥ 10.

Теперь отметим на числовой оси полученные результаты, разделив области решений разными цветами для удобства восприятия.

Нам нужен участок, где присутствуют оба решения. Как мы видим на рисунке, он начинается с числа 10 включительно.

Таким образом, решением заданной системы неравенств: x ≥ 10.

Пример 2
Найдем решение системы неравенств ниже:

Решение:

2x – 5 < 11
2x < 11 + 5
2x < 16
x < 8

3 (x – 1) + 2 ≥ -13
3x – 3 + 2 ≥ -13
3x ≥ -13 + 3 – 2
3x ≥ -12
x ≥ -4

Перенесем найденные решения на числовую ось и нарисуем соответствующие им интервалы:

Как мы видим, общая область решения, удовлетворяющая обеим неравенствам, находится между числами -4 включительно и 8 исключительно.

Ответ: -4 ≤ x < 8.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Основные понятия, решение систем линейных неравенств 9 класс онлайн-подготовка на Ростелеком Лицей

 

 

Тема: Рациональные неравенства и их системы

 

Урок: Основные понятия, решение систем линейных неравенств

 

1.

Тема урока, введение

 

 

До сих пор мы решали отдельные неравенства и применяли к ним метод интервалов, это могли быть и линейные неравенства, и квадратные и рациональные. Теперь перейдем к решению систем неравенств – сначала линейных систем. Посмотрим на примере, откуда берется необходимость рассматривать системы неравенств.

 

 

2. Знакомство с графическим решением системы на примере

 

 

Найти область определения функции 

 

 

Найти область определения функции 

 

Найти область определения функции

Функция существует, когда существуют оба квадратних корня, т.е.

 

Как решать такую систему? Необходимо найти все x, удовлетворяющие и первому и второму неравенству.

Изобразим на оси ox множество решений первого и второго неравенства.

Промежуток пересечения двух лучей и есть наше решение.

Ответ:

Такой метод изображения решения системы неравенств иногда называют методом крыш.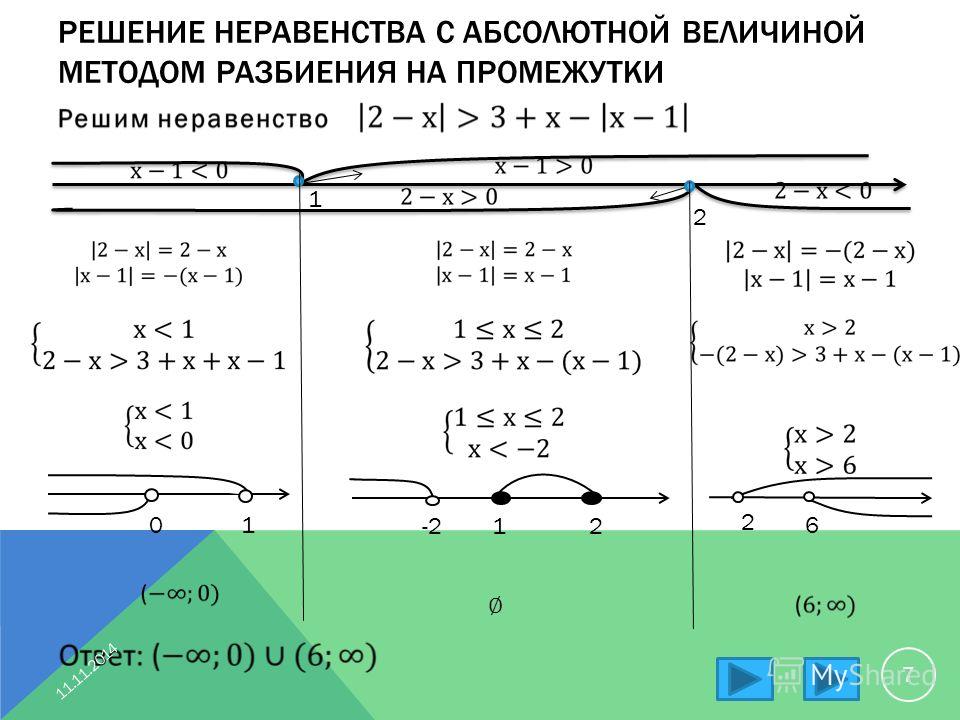

Решением системы является пересечение двух множеств.

Изобразим это графически. Имеем множество А произвольной природы и множество В произвольной природы, которые пересекаются.

 

3. Определение пересечения множеств

 

 

Определение: Пересечением двух множеств А и В называется такое третье множество, которое состоит из всех элементов, входящих и в А и в В.

 

Рассмотрим на конкретных примерах решения линейных систем неравенств, как находить пересечения множеств решений отдельных неравенств, входящих в систему.

 

4. Решение типовых стандартных задач

 

 

Решить систему неравенств:

 

1.

 

Ответ:

2.

Ответ: (7; 10].

3.

Ответ:

4. Решить систему

Откуда может взяться второе неравенство системы? Например, из неравенства

 

Графически обозначим решения каждого неравенства и найдем промежуток их пересечения.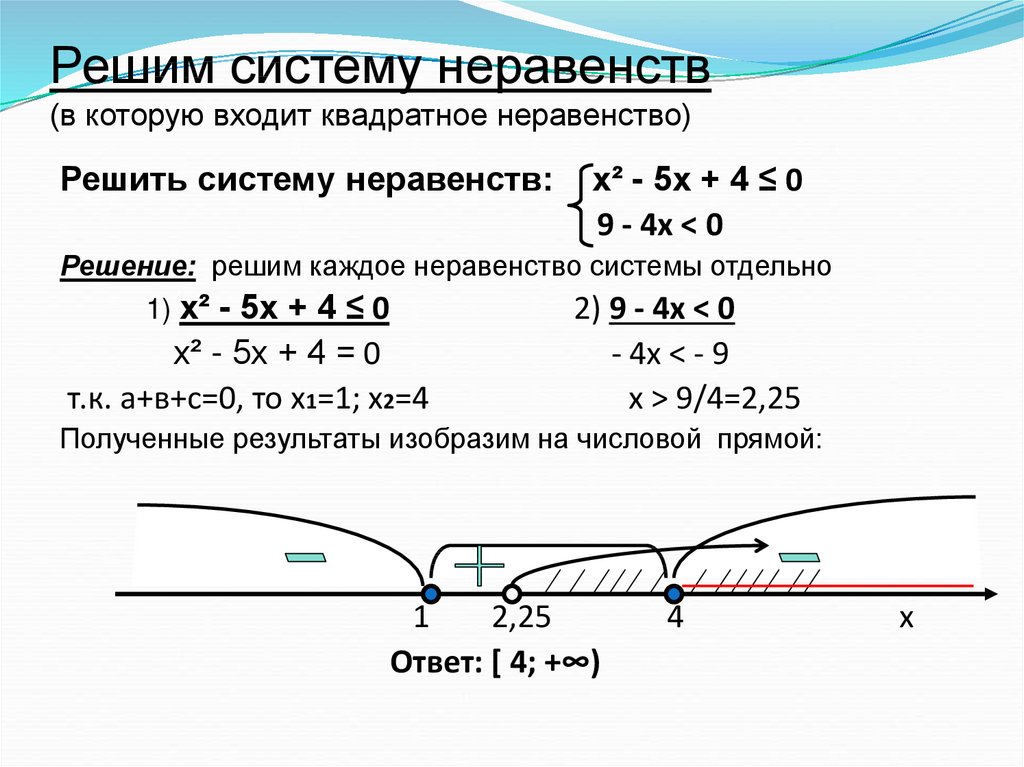

Ответ:

Таким образом, если мы имеем систему, в которой одно из неравенств удовлетворяет любому значению x, то его можно исключить.

 

5. Решение задач

 

 

5.

 

Ответ: система противоречива.

6.

Ответ:

Мы рассмотрели типовые опорные задачи, к которым сводится решение любой линейной системы неравенств.

Рассмотрим следующую систему.

7.

 

Ответ:

Иногда линейная система задается двойным неравенством, рассмотрим такой случай.

8.

 

 

 

Ответ:

 

6. Заключение

 

 

Мы рассмотрели системы линейных неравенств, поняли, откуда они появляются, рассмотрели типовые системы, к которым сводятся все линейные системы, и решили некоторые из них.

 

 

Список рекомендованной литературы

1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.

2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.

3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.

4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.

5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.

6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.

 

Рекомендованные ссылки на интернет-ресурсы

1. Портал Естественных Наук (Источник).

2. Электронный учебно-методический комплекс для подготовки 10-11 классов к вступительным экзаменам по информатике, математике, русскому языку (Источник).

3. Виртуальный репетитор (Источник).

4. Центр образования «Технология обучения» (Источник).

5. Раздел College.ru по математике (Источник).

 

Рекомендованное домашнее задание

1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. №№ 53; 54; 56; 57.

 

Equation calculator for inequalities online

  • Expression
  • Equation
  • Inequality
  • Contact us
  • Simplify
  • Factor
  • Expand
  • GCF
  • LCM
  • Solve
  • Graph
  • System
  • Решение
  • График
  • Система
  • Математический решатель на вашем сайте

Наших пользователей:

Не могу передать, как я счастлива, что наконец-то нашла программу, которая меня действительно чему-то учит!!!
Клара Джонсон, Северная Дакота

Это программное обеспечение для алгебры обладает исключительными возможностями для индивидуальных пользователей. Предлагая помощь с домашним заданием по алгебре, он также заставляет ученика изучать основы математики. Часть программного обеспечения для репетитора по алгебре предоставляет простые для понимания объяснения для каждого шага решения задачи по алгебре.

CP, Массачусетс

Как ни гордилась моя мама каждый раз, когда я видел, как она подбадривает меня после того, как я пробежал тачдаун с 5 ярдов, она всегда так же беспокоилась о моих оценках. Она сказала, что если я не подниму свои оценки, никто никогда не даст мне стипендию, независимо от того, сколько ярдов я наберу. Даже когда мой тренер показал мне вашу программу, я не захотел в ней участвовать. Но это начало обретать смысл. Теперь я занимаюсь алгеброй так же уверенно, как играю в футбол, и мой выпускной год будет моим лучшим!
Уоррен Миллс, Калифорния

Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение может спасти им жизнь.

Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?
Поисковые фразы, использованные 01.07.2011:
  • как решить систему уравнений в excel
  • Найти решатель недостающего угла
  • apptitude and buzzles question+pdf
  • практические задачи для 6-го класса nj ask test
  • помощь с домашним заданием алгебра 2 прентис холл математика
  • Практика решения и баланса химических уравнений рабочий лист
  • дифференциальное состояние второго порядка
  • онлайн-викторина на склоне 9 класса
  • бесплатные программы для решения математических задач
  • алгебра гленко 2 ответы
  • образец девятого теста по математике
  • одновременных уравнений с ограничениями Matlab
  • Matlab решает смешанную линейную систему
  • TI-84 плюс приложения алгебры
  • Факторинг с использованием коэффициентного метода
  • y7 бесплатные документы по английскому языку
  • бесплатный тестовый лист GMAT
  • Учебное пособие по алгебре 1 для 8-го класса по сложению и вычитанию радикалов
  • система уравнений сложения и вычитания
  • калькулятор, решающий многочлены
  • Рабочие листы с целыми числами для 7 класса
  • нелинейное алгебраическое уравнение, переменная Matlab
  • ks2 вопросы по математике на рассуждения уровень 5 сб
  • решатель линейного уравнения
  • калькулятор экстраполяции
  • Трехмерная координатная сетка
  • образец плана урока 1 класса
  • Бесплатные рабочие листы Алгебраические выражения
  • Рабочие листы дерева факторов
  • бесплатные онлайн-прайс-листы
  • ТИ-89 . pdf
  • онлайн калькулятор разложения неполных дробей
  • рабочих листа перестановок
  • метрические рабочие листы 6 класс
  • фольгирование корнеплодов
  • рабочие листы координатной плоскости
  • Рабочие листы TI 84
  • упростить параболу
  • бесплатный решатель алгебры
  • помощь с обратными задачами по алгебре FOIL
  • ответа на практический урок уравнения номер 12
  • бесплатный онлайн математический калькулятор со скобками
  • онлайн-решатель тригонометрических идентификаторов
  • решение квадратных уравнений с использованием идеальных квадратов
  • дивизионные рабочие листы
  • как использовать квадратные вычисления в языке C
  • абсолютное значение и радикалы
  • 4-й класс рисует график с бесплатными рабочими листами
  • умножение и деление одночленов, рабочий лист для печати
  • десятичных знака от наименьшего до наибольшего для третьего класса
  • исследовательские задачи
  • excel радикальный расчет
  • степени с корнями
    • Калькулятор целых дробей
  • репетитор по математике вычитает отрицательные числа
  • бесплатные тетради для первоклассников
  • бесплатное решение задач по алгебре
  • решить для 4 неизвестных
  • решить одновременную TI 89 и команду
  • репетиторские программы средней школы
  • вопросы по математике ks2 онлайн
  • Рабочий лист по химии Prentice Hall 11-3
  • графические параболы + преобразования + практические рабочие листы
  • третий класс tx работа
    • Рабочий лист линейных уравнений
  • 3-й
  • рабочих листа по алгебре II
  • математические задачи. com
  • рационализация числителя
  • бесплатных онлайн-книг по преалгебре
  • построение базовой параболы
  • факторизация трехчленов алгебра Гленко Макгроу-Хилла 1
  • бесплатных рабочих листа по элементарной вероятности
  • как упростить экспоненциальные члены
  • изменить основание логарифма
  • лист викторины по порядку операций
  • что эквивалентно смешанному десятичному числу
  • упражнения на склоне для 5 класса
  • калькулятор переменных алгебра
  • хранить образ на ti-89
  • игры по алгебре для печати
  • нью регенты выпустили тесты по алгебре 2
  • «вампирские числа» и «простые числа»
    • 9Рабочий лист десятичных эквивалентов десятичных дробей процентов 0003
  • онлайн калькулятор умножения рациональных выражений
  • рабочих листа по алгебре пиццы
  • Распечатка домашних заданий для 6-го класса на негативах #
  • учебник по простым вопросам о способностях
  • Калькулятор рационального наименьшего члена
  • matlab + нелинейное уравнение
  • нужна помощь в преобразовании смешанных дробей в десятичные
  • простой рабочий лист экспоненты только с переменными
  • Алгебра 8 класс 1 уравнения [дистрибутив]
Предыдущая Далее

Калькулятор линейных уравнений и неравенств

Онлайн-калькулятор линейных уравнений и неравенств LinearEquationCalcutor помогает детям и учителям решать задачи линейного неравенства. Введите данное линейное уравнение с неравенствами в качестве входных данных в названное поле и нажмите кнопку расчета, чтобы сгенерировать результат в течение доли секунды.

Калькулятор линейных уравнений и неравенств: Знание линейных уравнений и неравенств полностью улучшит ваше понимание концепции. Что ж, предоставленное пошаговое руководство по построению графиков неравенств и линейных уравнений с одной переменной и неравенств с примерами прольет свет на ваши расчеты. Используйте наш удобный и бесплатный онлайн-калькулятор линейных уравнений и неравенств, чтобы получить и проверить свои ответы за меньшее время.

Уравнения, в которых неизвестные появляются только в первой степени, называются линейными уравнениями. Общая форма линейного уравнения с одной переменной: ax + b = 0, где x — переменная.

Линейное неравенство напоминает уравнение заменой знака равенства на символ неравенства. Как правило, диапазон значений, а не одно конкретное значение, будет решением линейного неравенства.

Некоторые из примеров линейного неравенства перечислены ниже.