Как делать дроби на телефонном калькуляторе: лучшее руководство —
Общеизвестно, что изучение дробей может быть сложной задачей. Для объяснения этих трудностей были выдвинуты следующие теории: дроби могут обозначать множество понятий; их понимание требует концептуальной реорганизации по отношению к натуральным числам, а использование дробей требует выражения концептуального знания посредством эффективных процедурных манипуляций.
Мы предлагаем провести различие между концептуальным и процедурным знанием, чтобы охватить ключевые аспекты частичного знания. Кроме того, мы также рекомендуем использовать лучшие калькулятор дроби как разработана calculate-online.net, чтобы сократить дроби за считанные секунды.
Помимо всего этого, давайте познакомим вас с приведенной ниже статьей, которая наполнена надежными знаниями, необходимыми для понимания упрощения дробей вручную или с помощью калькулятора дробей. В конце концов, вы поймете, как делать дроби на телефонном калькуляторе.
Оставайся сфокусированным!!!
Определение дроби:По отношению к математике:
Дробь – это отношение числителя к знаменателю, выраженное математически.
Вы можете быстро и эффективно перечислить множество простых и сложных арифметических запросов дробей, используя онлайн-калькулятор кратных дробей. Какой звук он производит для вас?
Компоненты фракции:Компоненты дроби, которые вы должны сначала понять, прежде чем продолжить, перечислены ниже.
Числитель:Числитель — это часть дроби, которая находится сверху.
Знаменатель:Знаменатель — это наименьшее число, лежащее под чертой.
Винкулум:Линия между числителем и знаменателем известна как винкулум.
Упрощение дробей с помощью калькуляторов дробей:Мы все слышали о передовых инструментах, которые могут помочь вам вычислить дробные числа за считанные секунды. Некоторые из них хороши, а другие не так хороши с менее точными расчетами.
Некоторые из них хороши, а другие не так хороши с менее точными расчетами.
Но, тем не менее, мы собираемся провести вас через содержательную часть ниже, которая обогащена лучшими калькуляторами дробей, используемыми для наиболее точного уменьшения отношений.
Калькулятор-онлайн.net:Вы можете складывать, вычитать, умножать, делить и выполнять все эти операции с двумя или тремя дробями с помощью нашего бесплатного онлайн-калькулятора кратных дробей.
Кроме того, этот калькулятор поможет вам в следующем:
- С помощью этого калькулятора вы можете комбинировать дроби с одинаковыми и разными знаменателями.
- Сложение и вычитание дробей с разными и близкими знаменателями
- Он объединяет числитель и знаменатель вместе, чтобы упростить дробь до ее простейшей формы.
- Он разбивает дроби, чтобы привести результат к его простейшей форме.
К этому калькулятору прилагается соответствующее руководство пользователя, которое мы кратко опишем здесь:
- Сначала запишите числитель каждой дроби.

- аналогично со знаменателями
- Определите знак операции, который вы хотите использовать с дробями.
- Вы получаете подробное пошаговое объяснение того, как упростить указанные дроби, когда нажимаете кнопку вычисления.
Без сомнения, Calculatorsoup стремится предоставить учащимся метод упрощения дробей. Поскольку он, несомненно, дает точные результаты, он выделяется среди ученых и используется для подготовки к экзаменам. Этот инструмент является не только одним из лучших калькуляторов дробей, но и стоит особняком.
Руководство по использованию:Поэтому мы бесплатно предоставляем следующее руководство пользователя по использованию этого калькулятора дробей. Теперь давайте посмотрим на это:
- Введите числители и знаменатели обеих дробей, затем выберите оператор.
- Просто нажмите кнопку рассчитать, чтобы получить результат.
Эта платформа имеет собственную видимость в поисковых системах и является одним из калькуляторов дробей, который настоятельно рекомендуется для использования. Вместо этого в нем есть несколько калькуляторов для деления дробей, собранных на одной платформе. Теперь учащиеся могут свободно использовать этот упроститель дробей для решения любых проблем, связанных с дробями, и сразу же получать соответствующие решения. Итак, что вы обдумываете? Просто идите вперед и воспользуйтесь шансом в соответствии с вашими предпочтениями.
Вместо этого в нем есть несколько калькуляторов для деления дробей, собранных на одной платформе. Теперь учащиеся могут свободно использовать этот упроститель дробей для решения любых проблем, связанных с дробями, и сразу же получать соответствующие решения. Итак, что вы обдумываете? Просто идите вперед и воспользуйтесь шансом в соответствии с вашими предпочтениями.
Мы предоставим вам подробные инструкции для всех калькуляторов вычитания дробей, потому что многие из них доступны на одном веб-сайте. Двигайтесь!
- Во-первых, определите, какой из доступных калькуляторов вам нужно использовать.
- После этого приступайте к вводу всех параметров в соответствующие поля.
- Чтобы получить точные и исчерпывающие ответы, нажмите кнопку вычисления.
Калькулятор можно использовать как для простых, так и для сложных дробных операций, а также операторов, содержащих как дроби, так и целые, десятичные и смешанные числа.
Кроме того, он содержит исчерпывающие пошаговые инструкции по вычислению дробей. Почти каждый пример понятия дроби, связанный с этим калькулятором, был показан пользователю. Кроме того, на веб-сайте подчеркнуты все рекомендации по упрощению дробей. Проще говоря, использование этого инструмента просто фантастика.
Руководство пользователя:Используя его, вы заметите, что этот калькулятор дробей весьма привлекателен. Вы не ограничены простым сложением, вычитанием, умножением или делением двух или трех дробей.
- Перед вами квадрат, и вы можете добавить столько дробей, сколько захотите. Просто сделайте это, упростив дроби, используя соответствующие знаки операции.
- Наконец, просто нажмите кнопку вычисления, чтобы получить немедленные результаты.
Это полезный инструмент, который используют многие ученые по всему миру для решения дробей. Визуальное представление результатов является единственным уникальным аспектом этого онлайн-калькулятора.
Числителям присвоены разные цвета и знаменатели. При этом результаты ясны, а решения просты для понимания.
Руководство по использованию:Интерфейс этого инструмента для вычислений такой же, как у калькулятора-online.net, но он также включает в себя визуализацию в качестве дополнения. Посмотрим, как он будет работать.
- Поставьте знаменатели и числители на соответствующие места.
- Вы сразу увидите изображение каждой фракции.
- Когда вы выбираете операцию и нажимаете кнопку расчета, рядом с результатами отображается тот же эскиз изображения, который поможет вам лучше понять ее.
Учить детей дробям уже не сложно. Теперь вы можете упростить дроби, используя бесплатный калькулятор кратных дробей.
С другой стороны, крайне важно понять и научиться выполнять вычисления вручную. Поэтому давайте приблизимся к ним.
Дополнение дроби:Вы также можете складывать дроби с помощью бесплатного калькулятора сложения дробей. Однако давайте также рассмотрим ручные расчеты концепции.
Однако давайте также рассмотрим ручные расчеты концепции.
- Поставьте знак сложения между каждой дробью, которая у вас стоит первой.
- После этого определите знаменатель с наименьшим общим множителем среди всех них.
- Запишите числители после завершения этого шага и любых других необходимых шагов.
- Разделите полученное число, применяя наименьший общий знаменатель ко всем знаменателям дробей по одному. Затем умножьте результат на соответствующие числители.
- После этого сложите все числители вместе, чтобы получить окончательную дробь.
- Ищите способы, возможно, еще больше уменьшить эту долю.
- Для начала составьте список всех дробей со знаком вычитания.
- Следующим шагом является определение знаменателя, который имеет наименьший общий знаменатель со всеми остальными.
- Пришло время написать числители, когда этот шаг будет завершен.

- Разделите знаменатели дробей на наименьший общий знаменатель по одному, а затем умножьте ответ на числители.
- Вычтите все числители вместе, чтобы получить окончательную дробь.
- Изучите возможность дальнейшего снижения этой доли.
Позвольте бесплатному калькулятору дробей позаботиться о любых проблемах, возникающих во время вычислений.
Умножение дроби:Эта операция невероятно увлекательна и проста в освоении. Да, умножение различных дробей просто требует, чтобы вы помнили следующие важные моменты:
- Запишите каждую дробь в строке, содержащей символ умножения.
- После этого умножьте каждый из числителей и знаменателей по отдельности.
- Так выполняется умножение, и полученная дробь является новой.
- Наконец, вы должны определить, можете ли вы еще больше уменьшить эту пропорцию до значительной доли.
Деление дробей — это обратная операция умножения. Все вычисления соответствуют критериям, которые мы изложили для умножения дробей, за исключением первого шага. Давайте двигаться дальше от этого, а также!
Все вычисления соответствуют критериям, которые мы изложили для умножения дробей, за исключением первого шага. Давайте двигаться дальше от этого, а также!
- Все дроби со знаком деления должны быть записаны.
- Переверните числители и знаменатели всех оставшихся дробей, кроме начальной дроби.
- Повторите те же действия, что и для продукта дроби.
Дроби могут показаться менее сложными, чем десятичные, но они могут быть довольно проблематичными при использовании в реальных вычислениях.
Это происходит из-за вашего непонимания и образа мышления. Это руководство было создано в определенном контексте, чтобы помочь вам научиться решать дроби естественным и правдивым образом.
Кроме того, Калькулятор смешанных чисел упростил остальные вычисления. Мы очень надеемся, что эта статья окажется для вас очень полезной при подготовке к следующим экзаменам. Вы узнали, как делать дроби на телефонном калькуляторе? Пожалуйста, оставьте комментарий ниже.
- 3 секретных совета по обучению
- Улучшите свои навыки английского языка — 3 лучших способа, которые обязательно нужно использовать
НРАВИТСЯ:
подобно Загрузка…
Сложение дробей с разными знаменателями — алгоритмы и примеры решения
Пожалуй, одной из самых распространённых операций в алгебре является сложение дробей с разными знаменателями. Это довольно простое действие, с основами которого знакомят в седьмом классе среднеобразовательной школы. Единственная сложность, которая может возникнуть при решении, заключается в нахождении общего знаменателя и упрощения выражения. При этом, конечно же, необходимо знать порядок выполнения арифметических действий.
Содержание
- Общие сведения
- Правило действий
- Алгоритм решения
- Примеры заданий
- Использование онлайн-калькулятора
Общие сведения
Под дробью в математике принято понимать число, включающее в себя одну или несколько равных долей. Фактически это какая-то количественная часть от определённого числового или буквенного выражения. Существует два тип записи дробей: классически вид — a/b и десятичный — 0,345. В обыкновенном виде чёрточка обозначает деление. Число, стоящее над ней или с левой стороны, называется числителем, а внизу или справа от неё знаменателем. Первое является делимым, а второе делителем.
Фактически это какая-то количественная часть от определённого числового или буквенного выражения. Существует два тип записи дробей: классически вид — a/b и десятичный — 0,345. В обыкновенном виде чёрточка обозначает деление. Число, стоящее над ней или с левой стороны, называется числителем, а внизу или справа от неё знаменателем. Первое является делимым, а второе делителем.
Ещё в Древнем Вавилоне и Греции философы и учёные начали отличать части от целых значений. Надписи дробных выражений встречаются и в папирусах Древнего Египта. Египтяне умели делить и умножать дроби, но складывать их не могли. Вавилоняне использовали шестидесятеричные дроби, у которых в знаменателе могли стоять числа 60, 600, 602 и так далее. Такая запись была частным случаем и не могла описывать выделение других частей.
Поэтому итальянский математик Симон Стевин предложил использовать десятичную запись. То есть изображать дробь так, чтобы в его знаменателе стояла единица с последующими нулями. Своё изображение дробей использовали и в Индии. Их особенностью было расположение знаменателя сверху. Современную же запись предложили арабы, она оказалась настолько удачной, что её используют и до сих пор.
Своё изображение дробей использовали и в Индии. Их особенностью было расположение знаменателя сверху. Современную же запись предложили арабы, она оказалась настолько удачной, что её используют и до сих пор.
Существует три вида дробей:
Кроме этого, существует понятие правильной дроби — это выражение, в котором числитель меньше знаменателя, и неправильной — в ней знаменатель меньше числителя или равный ему.
При этом любую неправильную дробь можно преобразовать в сумму натурального числа с правильным выражением.
Правило действий
По сути, дробь — это вид записи числа. Причём одно и то же число может быть записано по-разному. Например, четыре можно представить как 4/1, 8/2, 4,0. Основное правило, использующееся при сложении дробей с разными числителями и знаменателями, заключается в том, что, если верхнюю и нижнюю часть умножить или разделить на одно и то же число, количественный результат не изменится. Это легко проверить, выполнив простые алгебраические вычисления.
Пусть имеется дробь 3/6. Для того чтобы переписать выражение в десятичный вид, нужно тройку разделить на шесть. В итоге получится ответ: ноль целых пять десятых. Записать его можно как 0,5. Теперь, чтобы проверить утверждение, нужно умножить числитель и знаменатель на одно и то же число. Пусть это будет двойка. Таким образом, выражение примет вид: 3 * 2 / 6 * 2 = 6/12. После деления шести на двенадцать ответ не изменится. Он будет равен 0,5.
Пусть это будет двойка. Таким образом, выражение примет вид: 3 * 2 / 6 * 2 = 6/12. После деления шести на двенадцать ответ не изменится. Он будет равен 0,5.
Аналогично можно проверить и операцию деления. При этом если верхнюю и левую часть можно разделить на одно и то же число, то выполнение такого действия называют сокращением. А когда числитель и знаменатель не имеют общего делимого (числа, на которое можно сократить), то дробь называют несократимой.
С дробями можно выполнять любые действия: прибавлять, вычитать, перемножать, делить, возводить в степень, извлекать корень. Для всех этих действий существуют строгие правила. Прибавление и вычитание относят к элементарным операциям. Для выполнения этих действий не нужно знать сложные формулы и теоремы. Следует лишь запомнить простое правило: для того чтобы сложить дроби с разными знаменателями, нужно привести их к общему делителю, а после просто выполнить складывание числителей без изменения нижней дробной части.
Хотя с первого взгляда это правило кажется замысловатым, на самом деле оно очень простое и доступное любому для понимания.
Чтобы его усвоить и разобраться, следует знать алгоритм действий и принцип нахождения общего знаменателя. Он основан на главном свойстве дроби.
Алгоритм решения
Решить пример или задачу — найти количественный ответ или привести его к простому виду. Поэтому применяют различные способы преобразования заданной дроби к простой записи. Складывать, впрочем, как и вычитать, две и более дроби между собой можно лишь при условии приведения их к общему знаменателю. Под ним понимают такое число, которое является кратным к любому знаменателю в складываемых выражениях. Чтобы найти наименьшее общее число, нужно подобрать значение, на которое любой из знаменателей будет делиться без остатка.
Вычислить его можно двумя способами: найти наибольший общий делитель или использовать каноническое разложение на простые множители. Например, для цифр 12 и 20 он будет равный 60. Для нахождения методом разложения нужно 12 представить в виде произведения 2*2*3, а 20 как 2*2*5. Затем объединить их без повторения и выполнить действие: 2*2*3*5 = 60.
Для нахождения методом разложения нужно 12 представить в виде произведения 2*2*3, а 20 как 2*2*5. Затем объединить их без повторения и выполнить действие: 2*2*3*5 = 60.
Другой вариант выполняется методом перебора. Сначала проверяют делимость без остатка 20 на 12. Так как действие невыполнимо, 20 умножают на два и снова проверяют. Действие снова невозможно. Теперь 20 умножают на три. Деление без остатка допустимо, таким образом, искомое число будет равно 20*3 = 60. Какой метод применять, зависит от предпочтения считающего и принципиального значения не имеет.
После того как обоюдный знаменатель определён, нужно это значение разделить на каждый делитель, а полученное число записать как соответствующий дополнительный множитель числителя. Далее, на каждое делимое умножить свой коэффициент и плюсовать полученные результаты.
Таким образом, алгоритм сложения неправильных дробей с разными знаменателями, впрочем, как и правильных, можно представить в следующем виде:

Этот подход применим к любой дроби, даже содержащей буквенные или неопределённые значения. Следует отметить, что при выполнении действий над смешанными отношениями целые части будут складываться отдельно от дробных членов. Если же после сложения получится неправильная дробь, то нужно выделить целую часть и при необходимости прибавить её к имеющейся. Тогда решение будет считаться правильным.
Примеры заданий
Понять принцип сложения дробей, проще всего выполнив несколько практических заданий. Начинать нужно с простых, постепенно переходя к более сложным.
Начинать нужно с простых, постепенно переходя к более сложным.
Например, нужно сложить два выражения 2/3 и 4/5. Это простое задание, обычно предлагающееся на школьных уроках. Для того чтобы его выполнить, необходимо воспользоваться алгоритмом решения. Первое что нужно, это найти общий множитель. Пять на три без остатка не делится, десять тоже, а вот число 15 подойдёт. Теперь нужно вычислить дополнительный коэффициент. Для этого первый и второй знаменатели делят на 15. Таким образом, получится: 2 / 3 + 4 / 5 = (2 * 5 + 4 * 3) / 15 = (10 + 12) / 15 = 22/15. В ответе получилась неправильная дробь, поэтому её нужно переписать, выделив целую часть. В итоге решением будет: 2 / 3 + 4 / 5 = 1 7/15.
Более сложные задания обычно включают в себя несколько членов, при этом выражения в них могут быть любыми. Пусть нужно найти решение математической задачи следующего вида: 5/12 — 7/18 + 2/36 + 3 5/6 + 7/4. В этом примере содержится неправильная дробь и смешанная. Согласно правилу, неправильное выражение нужно привести к нормальному виду: 7/4 = (1 * 4 +3) / 4 = 1 * 4 / 4 + (3 / 4) = 1 + ¾ = 1 ¾.
Подставив найденное выражение вместо неправильной дроби, пример примет вид: 5/12 — 7/18 + 2/36 + 3 5/6 + 1 ¾. Самым большим числом в знаменателе является тридцать шесть, оно же будет и общим знаменателем. Каждый знаменатель нужно разделить на 36. Полученное число добавить как коэффициент в числитель, а целые части сложить отдельно: 1 (5 * 3 — 7 * 2 + 5 * 6 + 9 * 3) / 36 = 1 (15 — 14 + 30 + 27) / 36 = 1 (58 / 36). Для того чтобы правильно записать ответ, полученное значение нужно преобразовать в смешанное выражение: 1 (58 / 36) = (1 * 36 + 58) / 36 = 94 / 26 = (94 / 2) / (36 / 2) = 47 / 18 = 2 11/18.
То есть при решении обычным способом важно привести дроби к упрощённому виду, найти общий знаменатель и при необходимости преобразовать выражение к смешанной дроби.
Использование онлайн-калькулятора
В реальных расчётах довольно часто приходится сталкиваться с формулами, содержащими большое количество членов. Чтобы самостоятельно в таких случаях найти общий знаменатель при сложении дробей, понадобится затратить много времени. При этом и в самих расчётах легко можно допустить ошибку. Поэтому совсем не зазорно будет воспользоваться специальными онлайн-калькуляторами.
Чтобы самостоятельно в таких случаях найти общий знаменатель при сложении дробей, понадобится затратить много времени. При этом и в самих расчётах легко можно допустить ошибку. Поэтому совсем не зазорно будет воспользоваться специальными онлайн-калькуляторами.
Это обыкновенные сайты, на страницах которых находятся формы для расчёта выражений любой сложности. Всё что требуется от пользователя — вести исходные данные и нажать кнопку «Рассчитать». Система буквально за несколько секунд автоматически выполнит вычисления, за правильность которых можно не переживать. Что примечательно, кроме итогового результата, пользователю будет доступна вся цепочка решения. Это даёт возможность, даже не зная правил, наглядно увидеть, как нужно находить сумму дробей.
Из всего множества сайтов можно выделить следующие три:
 Чтобы онлайн-калькулятор правильно распознал сложные выражения, их части нужно включать в скобки. Количество членов можно добавлять до бесконечности. С ключевыми моментами расчёта можно ознакомиться ниже строчки с ответом.
Чтобы онлайн-калькулятор правильно распознал сложные выражения, их части нужно включать в скобки. Количество членов можно добавлять до бесконечности. С ключевыми моментами расчёта можно ознакомиться ниже строчки с ответом.Воспользовавшись любым из этих онлайн-калькуляторов, не придётся скрупулёзно и монотонно искать ответ на поставленную задачу. Она будет решаться автоматически. Всё что будет нужно, так это переписать ответ и при желании изучить алгоритм вычисления.
Предыдущая
МатематикаИррациональные числа — определение, свойства и примеры
Следующая
МатематикаНеизвестное слагаемое — правила нахождения
Решение столбиком онлайн калькулятор с запятыми.
 Обыкновенные и десятичные дроби и действия над ними. Где можно решить десятичные уравнения онлайн
Обыкновенные и десятичные дроби и действия над ними. Где можно решить десятичные уравнения онлайнОнлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей.
Дробью в математике называется число, представляющее часть единицы или несколько её частей.
Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.
Дроби бывают правильными и неправильными.
- Правильной называется дробь, у которой числитель меньше знаменателя.

- Неправильная дробь – если у дроби числитель больше знаменателя.
Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть, называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь.
Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя:
Как перевести обыкновенную дробь в смешанную
Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:
- Поделить числитель дроби на её знаменатель
- Результат от деления будет являться целой частью
- Остаток отделения будет являться числителем
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
Как перевести дробь в проценты
Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.
Как перевести проценты в дробь
Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
- Выполнить сложение дробей путем сложения их числителей.
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Умножение дробей
Алгоритм действий при умножении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Деление дробей
Алгоритм действий при делении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Онлайн калькуляторы и конвертеры:
Калькулятор в столбик для Андроид устройств станет замечательным помощником для современных школьников. Программа не только дает правильный ответ на математическое действие, но и наглядно демонстрирует его пошаговое решение. Если же вам нужны более сложные калькуляторы – можете посмотреть или же продвинутый инженерный калькулятор.
Особенности
Главной особенностью программы является уникальность расчета математических операций. Отображение процесса вычислений столбиком дает возможность школьникам более подробно с ним ознакомиться, понять алгоритм решения, а не просто получить готовый результат и переписать его в тетрадь. Эта особенность имеет огромное преимущество перед другими калькуляторами, т.к. достаточно часто в школе учителя требуют расписать промежуточные вычисления, чтобы удостовериться, что школьник производит их в уме и действительно понимает алгоритм решения задач. Кстати, у нас есть еще одна программа похожего рода – .
Чтобы начать пользоваться программой, необходимо скачать калькулятор в столбик на Андроид. Сделать это можно на нашем сайте абсолютно бесплатно без дополнительных регистраций и смс. После установки откроется главная страница в виде тетрадного листа в клетку, на котором, собственно, и будут отображаться результаты вычислений и их подробное решение. Внизу располагается панель с кнопками:
- Цифры.
- Знаки арифметических действий.
- Удаление раннее введенных символов.
Ввод осуществляется по тому же принципу, что и на . Все отличие состоит только в интерфейсе приложения – все математические вычисления и их результат отображаются в виртуальной ученической тетради.
Приложение позволяет быстро и правильно выполнить стандартные для школьника математические вычисления столбиком:
- умножение;
- деление;
- сложение;
- вычитание.
Приятным дополнением в приложении является функция ежедневного напоминания о домашнем задании по математике.
Достоинства и недостатки
- Помогает школьнику не просто быстро получить правильный результат математических вычислений, но и понять сам принцип расчета.
- Очень простой, интуитивно понятный интерфейс для каждого пользователя.
- Установить приложение можно даже на самое бюджетное Андроид устройство с операционной системой 2.2 и более поздней версией.
- Калькулятор сохраняет историю проведенных математических вычислений, которую можно в любой момент очистить.
Калькулятор ограничен в математических операциях, поэтому применить его для сложных расчетов, с какими мог бы справиться инженерный калькулятор, не получится. Однако учитывая назначение самого приложения – наглядно продемонстрировать учащимся младшей школы принцип расчета в столбик, считать это недостатком не стоит.
Приложение также станет отличным помощником не только для школьников, но и для родителей, которые желают заинтересовать своего ребенка математикой и научить его правильно и последовательно производить вычисления. Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.
Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Линейное уравнение с десятичными дробями решается точно так же, как и множество других уравнений, однако их решение нужно начинать с сокращения уравнения и избавления от десятичных дробей.
Допустим, дано уравнение следующего вида:
Данное уравнение можно решить двумя разными способами.
Способ № 1:
Решение начинаем с упрощения уравнения с помощью открытия скобок, а поскольку перед скобками у нас стоит число, то умножаем это число на каждый член в скобках:
Сейчас наше уравнение имеет линейный вид, благодаря чему мы производим перенос неизвестных в одну сторону, целый числе в другую:
\[ — 7,2x + 5,2x = 1,7 — 14,4 — 4,3\]
Делим 2 части на число перед \
\[ — 2x = — 17\]
Ответ: \
Способ № 2:
В этом способе умножим левую и правую части на 10:
Это линейное уравнение, которое решается по аналогии с 1 способом:
\[ — 72x + 52x = 17 — 144 — 43\]
\[ — 20x = — 170\]
Ответ: \
Где можно решить десятичные уравнения онлайн?
Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто вdести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто вdести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
В этом уроке мы рассмотрим каждую из этих операций по отдельности.
Содержание урока
Сложение десятичных дробейКак мы знаем, десятичная дробь состоит из целой и дробной части. При сложении десятичных дробей, целые и дробные части складываются по отдельности.
Например, сложим десятичные дроби 3,2 и 5,3. Десятичные дроби удобнее складывать в столбик.
Запишем сначала эти две дроби в столбик, при этом целые части обязательно должны быть под целыми, а дробные под дробными. В школе это требование называют «запятая под запятой» .
Запишем дроби в столбик так, чтобы запятая оказалась под запятой:
Складываем дробные части: 2 + 3 = 5. Записываем пятёрку в дробной части нашего ответа:
Теперь складываем целые части: 3 + 5 = 8. Записываем восьмёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой» :
Получили ответ 8,5. Значит, выражения 3,2 + 5,3 равно 8,5
3,2 + 5,3 = 8,5
На самом деле не всё так просто как кажется на первый взгляд. Здесь тоже имеются свои подводные камни, о которых мы сейчас поговорим.
Разряды в десятичных дробяхУ десятичных дробей, как и у обычных чисел, есть свои разряды. Это разряды десятых, разряды сотых, разряды тысячных. При этом разряды начинаются после запятой.
Первая цифра после запятой отвечает за разряд десятых, вторая цифра после запятой за разряд сотых, третья цифра после запятой за разряд тысячных.
Разряды в десятичных дробях хранят в себе нéкоторую полезную информацию. В частности, они сообщают сколько в десятичной дроби десятых частей, сотых частей и тысячных частей.
В частности, они сообщают сколько в десятичной дроби десятых частей, сотых частей и тысячных частей.
Например, рассмотрим десятичную дробь 0,345
Позиция, где находится тройка, называется разрядом десятых
Позиция, где находится четвёрка, называется разрядом сотых
Позиция, где находится пятёрка, называется разрядом тысячных
Посмотрим на данный рисунок. Видим, что в разряде десятых располагается тройка. Это говорит о том, что в десятичной дроби 0,345 содержится три десятых .
Если мы сложим дроби , и то получим изначальную десятичную дробь 0,345
Сначала мы получили ответ , но перевели его в десятичную дробь и получили 0,345 .
При сложении десятичных дробей соблюдаются те же правила что и при сложении обычных чисел. Сложение десятичных дробей происходит по разрядам: десятые части складываются с десятыми частями, сотые с сотыми, тысячные с тысячными.
Поэтому при сложении десятичных дробей требуют соблюдать правило «запятая под запятой» . Запятая под запятой обеспечивает тот самый порядок, в котором десятые части складываются с десятыми, сотые с сотыми, тысячные с тысячными.
Запятая под запятой обеспечивает тот самый порядок, в котором десятые части складываются с десятыми, сотые с сотыми, тысячные с тысячными.
Пример 1. Найти значение выражения 1,5 + 3,4
В первую очередь складываем дробные части 5 + 4 = 9. Записываем девятку в дробной части нашего ответа:
Теперь складываем целые части 1 + 3 = 4. Записываем четвёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»:
Получили ответ 4,9. Значит значение выражения 1,5 + 3,4 равно 4,9
Пример 2. Найти значение выражения: 3,51 + 1,22
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»
В первую очередь складываем дробную часть, а именно сотые части 1+2=3. Записываем тройку в сотой части нашего ответа:
Теперь складываем десятые части 5+2=7. Записываем семёрку в десятой части нашего ответа:
Теперь складываем целые части 3+1=4. Записываем четвёрку в целой части нашего ответа:
Отделяем запятой целую часть от дробной, соблюдая правило «запятая под запятой»:
Получили ответ 4,73. Значит значение выражения 3,51 + 1,22 равно 4,73
Значит значение выражения 3,51 + 1,22 равно 4,73
3,51 + 1,22 = 4,73
Как и в обычных числах, при сложении десятичных дробей может произойти . В этом случае в ответе записывается одна цифра, а остальные переносят на следующий разряд.
Пример 3. Найти значение выражения 2,65 + 3,27
Записываем в столбик данное выражение:
Складываем сотые части 5+7=12. Число 12 не поместится в сотой части нашего ответа. Поэтому в сотой части записываем цифру 2, а единицу переносим на следующий разряд:
Теперь складываем десятые части 6+2=8 плюс единица, которая досталась от предыдущей операции, получим 9. Записываем цифру 9 в десятой части нашего ответа:
Теперь складываем целые части 2+3=5. Записываем цифру 5 в целой части нашего ответа:
Получили ответ 5,92. Значит значение выражения 2,65 + 3,27 равно 5,92
2,65 + 3,27 = 5,92
Пример 4. Найти значение выражения 9,5 + 2,8
Записываем в столбик данное выражение
Складываем дробные части 5 + 8 = 13. Число 13 не поместится в дробной часть нашего ответа, поэтому сначала записываем цифру 3, а единицу переносим на следующий разряд, точнее переносим её к целой части:
Число 13 не поместится в дробной часть нашего ответа, поэтому сначала записываем цифру 3, а единицу переносим на следующий разряд, точнее переносим её к целой части:
Теперь складываем целые части 9+2=11 плюс единица, которая досталась от предыдущей операции, получаем 12. Записываем число 12 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 12,3. Значит значение выражения 9,5 + 2,8 равно 12,3
9,5 + 2,8 = 12,3
При сложении десятичных дробей количество цифр после запятой в обеих дробях должно быть одинаковым. Если цифр не хватает, то эти места в дробной части заполняются нулями.
Пример 5 . Найти значение выражения: 12,725 + 1,7
Прежде чем записывать в столбик данное выражение, сделаем количество цифр после запятой в обеих дробях одинаковым. В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять:
Складываем тысячные части 5+0=5. Записываем цифру 5 в тысячной части нашего ответа:
Записываем цифру 5 в тысячной части нашего ответа:
Складываем сотые части 2+0=2. Записываем цифру 2 в сотой части нашего ответа:
Складываем десятые части 7+7=14. Число 14 не поместится в десятой части нашего ответа. Поэтому сначала записываем цифру 4, а единицу переносим на следующий разряд:
Теперь складываем целые части 12+1=13 плюс единица, которая досталась от предыдущей операции, получаем 14. Записываем число 14 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 14,425. Значит значение выражения 12,725+1,700 равно 14,425
12,725+ 1,700 = 14,425
Вычитание десятичных дробейПри вычитании десятичных дробей нужно соблюдать те же правила что и при сложении: «запятая под запятой» и «равное количества цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
Вычисляем дробную часть 5−2=3. Записываем цифру 3 в десятой части нашего ответа:
Записываем цифру 3 в десятой части нашего ответа:
Вычисляем целую часть 2−2=0. Записываем ноль в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 0,3. Значит значение выражения 2,5 − 2,2 равно 0,3
2,5 − 2,2 = 0,3
Пример 2. Найти значение выражения 7,353 — 3,1
В этом выражении разное количество цифр после запятой. В дроби 7,353 после запятой три цифры, а в дроби 3,1 только одна. Значит в дроби 3,1 в конце нужно добавить два нуля, чтобы сделать количество цифр в обеих дробях одинаковым. Тогда получим 3,100.
Теперь можно записать в столбик данное выражение и вычислить его:
Получили ответ 4,253. Значит значение выражения 7,353 − 3,1 равно 4,253
7,353 — 3,1 = 4,253
Как и в обычных числах, иногда придётся занимать единицу у соседнего разряда, если вычитание станет невозможным.
Пример 3. Найти значение выражения 3,46 − 2,39
Вычитаем сотые части 6−9. От число 6 не вычесть число 9. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда число 6 обращается в число 16. Теперь можно вычислить сотые части 16−9=7. Записываем семёрку в сотой части нашего ответа:
Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда число 6 обращается в число 16. Теперь можно вычислить сотые части 16−9=7. Записываем семёрку в сотой части нашего ответа:
Теперь вычитаем десятые части. Поскольку мы заняли в разряде десятых одну единицу, то цифра, которая там располагалась, уменьшилась на одну единицу. Другими словами, в разряде десятых теперь не цифра 4, а цифра 3. Вычислим десятые части 3−3=0. Записываем ноль в десятой части нашего ответа:
Теперь вычитаем целые части 3−2=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,07. Значит значение выражения 3,46−2,39 равно 1,07
3,46−2,39=1,07
Пример 4 . Найти значение выражения 3−1,2
В этом примере из целого числа вычитается десятичная дробь. Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,23 оказалась под числом 3
Теперь сделаем количество цифр после запятой одинаковым. Для этого после числа 3 поставим запятую и допишем один ноль:
Для этого после числа 3 поставим запятую и допишем один ноль:
Теперь вычитаем десятые части: 0−2. От нуля не вычесть число 2. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда, 0 обращается в число 10. Теперь можно вычислить десятые части 10−2=8. Записываем восьмёрку в десятой части нашего ответа:
Теперь вычитаем целые части. Раньше в целой располагалось число 3, но мы заняли у него одну единицу. В результате оно обратилось в число 2. Поэтому из 2 вычитаем 1. 2−1=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,8. Значит значение выражения 3−1,2 равно 1,8
Умножение десятичных дробейУмножение десятичных дробей это просто и даже увлекательно. Чтобы перемножить десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые.
Получив ответ, необходимо отделить запятой целую часть от дробной. Чтобы сделать это, надо посчитать количество цифр после запятой в обеих дробях, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Пример 1. Найти значение выражения 2,5 × 1,5
Перемножим эти десятичные дроби как обычные числа, не обращая внимания на запятые. Чтобы не обращать внимания на запятые, можно на время представить, что они вообще отсутствуют:
Получили 375. В этом числе необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в дробях 2,5 и 1,5. В первой дроби после запятой одна цифра, во второй дроби тоже одна. Итого две цифры.
Возвращаемся к числу 375 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 3,75. Значит значение выражения 2,5 × 1,5 равно 3,75
2,5 × 1,5 = 3,75
Пример 2. Найти значение выражения 12,85 × 2,7
Перемножим эти десятичные дроби, не обращая внимания на запятые:
Получили 34695. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 12,85 и 2,7. В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры.
В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры.
Возвращаемся к числу 34695 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую:
Получили ответ 34,695. Значит значение выражения 12,85 × 2,7 равно 34,695
12,85 × 2,7 = 34,695
Умножение десятичной дроби на обычное числоИногда возникают ситуации, когда требуется умножить десятичную дробь на обычное число.
Чтобы перемножить десятичную дробь и обычное число, нужно перемножить их, не обращая внимания на запятую в десятичной дроби. Получив ответ, необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в десятичной дроби, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Например, умножим 2,54 на 2
Умножаем десятичную дробь 2,54 на обычное число 2, не обращая внимания на запятую:
Получили число 508. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры.
Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры.
Возвращаемся к числу 508 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 5,08. Значит значение выражения 2,54 × 2 равно 5,08
2,54 × 2 = 5,08
Умножение десятичных дробей на 10, 100, 1000Умножение десятичных дробей на 10, 100 или 1000 выполняется таким же образом, как и умножение десятичных дробей на обычные числа. Нужно выполнить умножение, не обращая внимания на запятую в десятичной дроби, затем в ответе отделить целую часть от дробной, отсчитав справа столько же цифр, сколько было цифр после запятой в десятичной дроби.
Например, умножим 2,88 на 10
Умножим десятичную дробь 2,88 на 10, не обращая внимания на запятую в десятичной дроби:
Получили 2880. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,88. Видим, что в дроби 2,88 после запятой две цифры.
Видим, что в дроби 2,88 после запятой две цифры.
Возвращаемся к числу 2880 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 28,80. Отбросим последний ноль — получим 28,8. Значит значение выражения 2,88×10 равно 28,8
2,88 × 10 = 28,8
Есть и второй способ умножения десятичных дробей на 10, 100, 1000. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается вправо на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 2,88×10 этим способом. Не приводя никаких вычислений, сразу же смотрим на множитель 10. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 2,88 передвигаем запятую вправо на одну цифру, получим 28,8.
2,88 × 10 = 28,8
Попробуем умножить 2,88 на 100. Сразу же смотрим на множитель 100. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 2,88 передвигаем запятую вправо на две цифры, получаем 288
2,88 × 100 = 288
Попробуем умножить 2,88 на 1000. Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.
Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.
2,88 × 1000 = 2880
Умножение десятичных дробей на 0,1 0,01 и 0,001Умножение десятичных дробей на 0,1, 0,01 и 0,001 происходит таким же образом, как и умножение десятичной дроби на десятичную дробь. Необходимо перемножить дроби, как обычные числа, и в ответе поставить запятую, отсчитав столько цифр справа, сколько цифр после запятой в обеих дробях.
Например, умножим 3,25 на 0,1
Умножаем эти дроби, как обычные числа, не обращая внимания на запятые:
Получили 325. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 3,25 и 0,1. В дроби 3,25 после запятой две цифры, в дроби 0,1 одна цифра. Итого три цифры.
Возвращаемся к числу 325 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую:
Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую:
Получили ответ 0,325. Значит значение выражения 3,25 × 0,1 равно 0,325
3,25 × 0,1 = 0,325
Есть и второй способ умножения десятичных дробей на 0,1, 0,01 и 0,001. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается влево на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 3,25 × 0,1 этим способом. Не приводя никаких вычислений сразу же смотрим на множитель 0,1. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 3,25 передвигаем запятую влево на одну цифру. Передвинув запятую на одну цифру влево мы видим, что перед тройкой больше нет никаких цифр. В этом случае дописываем один ноль и ставим запятую. В результате получаем 0,325
3,25 × 0,1 = 0,325
Попробуем умножить 3,25 на 0,01. Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325
Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325
3,25 × 0,01 = 0,0325
Попробуем умножить 3,25 на 0,001. Сразу же смотрим на множитель 0,001. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 3,25 передвигаем запятую влево на три цифры, получаем 0,00325
3,25 × 0,001 = 0,00325
Нельзя путать умножение десятичных дробей на 0,1, 0,001 и 0,001 с умножением на 10, 100, 1000. Типичная ошибка большинства людей.
При умножении на 10, 100, 1000 запятая переносится вправо на столько же цифр сколько нулей во множителе.
А при умножении на 0,1, 0,01 и 0,001 запятая переносится влево на столько же цифр сколько нулей во множителе.
Если на первых порах это сложно запомнить, можно пользоваться первым способом, в котором умножение выполняется как с обычными числами. В ответе нужно будет отделить целую часть от дробной, отсчитав справа столько же цифр, сколько цифр после запятой в обеих дробях.
В одном из предыдущих уроков мы сказали, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.
Например, чтобы разделить одно яблоко на двоих, нужно в числитель записать 1 (одно яблоко), а в знаменатель записать 2 (двое друзей). В результате получим дробь . Значит каждому другу достанется по яблока. Другими словами, по половине яблока. Дробь это ответ к задаче «как разделить одно яблоко на двоих»
Оказывается, можно решать эту задачу и дальше, если разделить 1 на 2. Ведь дробная черта в любой дроби означает деление, а значит и в дроби это деление разрешено. Но как? Мы ведь привыкли к тому, что делимое всегда больше делителя. А здесь наоборот, делимое меньше делителя.
Всё станет ясным, если вспомнить, что дробь означает дробление, деление, разделение. А значит и единица может быть раздроблена на сколько угодно частей, а не только на две части.
При разделении меньшего числа на большее получается десятичная дробь, в которой целая часть будет 0 (нулевой). Дробная часть же может быть любой.
Итак, разделим 1 на 2. Решим этот пример уголком:
Единицу на два просто так нацело не разделить. Если задать вопрос «сколько двоек в единице» , то ответом будет 0. Поэтому в частном записываем 0 и ставим запятую:
Теперь как обычно умножаем частное на делитель, чтобы вытащить остаток:
Настал момент, когда единицу можно дробить на две части. Для этого справа от полученной единички дописываем ещё один ноль:
Получили 10. Делим 10 на 2, получаем 5. Записываем пятёрку в дробной части нашего ответа:
Теперь вытаскиваем последний остаток, чтобы завершить вычисление. Умножаем 5 на 2, получаем 10
Получили ответ 0,5. Значит дробь равна 0,5
Половину яблока можно записать и с помощью десятичной дроби 0,5. Если сложить эти две половинки (0,5 и 0,5), мы опять получим изначальное одно целое яблоко:
Этот момент также можно понять, если представить, как 1 см делится на две части. Если 1 сантиметр разделить на 2 части, то получится 0,5 см
Если 1 сантиметр разделить на 2 части, то получится 0,5 см
Пример 2. Найти значение выражения 4: 5
Сколько пятёрок в четвёрке? Нисколько. Записываем в частном 0 и ставим запятую:
Умножаем 0 на 5, получаем 0. Записываем ноль под четвёркой. Сразу же вычитаем этот ноль из делимого:
Теперь начнём дробить (делить) четвёрку на 5 частей. Для этого справа от 4 дописываем ноль и делим 40 на 5, получаем 8. Записываем восьмёрку в частном.
Завершаем пример, умножив 8 на 5, и получив 40:
Получили ответ 0,8. Значит значение выражения 4: 5 равно 0,8
Пример 3. Найти значение выражения 5: 125
Сколько чисел 125 в пятёрке? Нисколько. Записываем 0 в частном и ставим запятую:
Умножаем 0 на 5, получаем 0. Записываем 0 под пятёркой. Сразу же вычитаем из пятёрки 0
Теперь начнём дробить (делить) пятёрку на 125 частей. Для этого справа от этой пятёрки запишем ноль:
Делим 50 на 125. Сколько чисел 125 в числе 50? Нисколько. Значит в частном опять записываем 0
Значит в частном опять записываем 0
Умножаем 0 на 125, получаем 0. Записываем этот ноль под 50. Сразу же вычитаем 0 из 50
Теперь делим число 50 на 125 частей. Для этого справа от 50 запишем ещё один ноль:
Делим 500 на 125. Сколько чисел 125 в числе 500. В числе 500 четыре числа 125. Записываем четвёрку в частном:
Завершаем пример, умножив 4 на 125, и получив 500
Получили ответ 0,04. Значит значение выражения 5: 125 равно 0,04
Деление чисел без остатка
Итак, поставим в частном после единицы запятую, тем самым указывая, что деление целых частей закончилось и мы приступаем к дробной части:
Допишем ноль к остатку 4
Теперь делим 40 на 5, получаем 8. Записываем восьмёрку в частном:
40−40=0. Получили 0 в остатке. Значит деление на этом полностью завершено. При делении 9 на 5 получается десятичная дробь 1,8:
9: 5 = 1,8
Пример 2 . Разделить 84 на 5 без остатка
Сначала разделим 84 на 5 как обычно с остатком:
Получили в частном 16 и еще 4 в остатке. Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0
Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0
Теперь делим 40 на 5, получаем 8. Записываем восьмерку в частном после запятой:
и завершаем пример, проверив есть ли еще остаток:
Деление десятичной дроби на обычное число
Десятичная дробь, как мы знаем состоит из целой и дробной части. При делении десятичной дроби на обычное число в первую очередь нужно:
- разделить целую часть десятичной дроби на это число;
- после того, как целая часть будет разделена, нужно в частном сразу же поставить запятую и продолжить вычисление, как в обычном делении.
Например, разделим 4,8 на 2
Запишем этот пример уголком:
Теперь разделим целую часть на 2. Четыре разделить на два будет два. Записываем двойку в частном и сразу же ставим запятую:
Теперь умножаем частное на делитель и смотрим есть ли остаток от деления:
4−4=0. Остаток равен нулю. Ноль пока не записываем, поскольку решение не завершено. Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2
Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2
8: 2 = 4. Записываем четвёрку в частном и сразу умножаем её на делитель:
Получили ответ 2,4. Значение выражения 4,8: 2 равно 2,4
Пример 2. Найти значение выражения 8,43: 3
Делим 8 на 3, получаем 2. Сразу же ставим запятую после двойки:
Теперь умножаем частное на делитель 2 × 3 = 6. Записываем шестёрку под восьмёркой и находим остаток:
Делим 24 на 3, получаем 8. Записываем восьмёрку в частном. Сразу же умножаем её на делитель, чтобы найти остаток от деления:
24−24=0. Остаток равен нулю. Ноль пока не записываем. Сносим последнюю тройку из делимого и делим на 3, получим 1. Сразу же умножаем 1 на 3, чтобы завершить этот пример:
Получили ответ 2,81. Значит значение выражения 8,43: 3 равно 2,81
Деление десятичной дроби на десятичную дробь
Чтобы разделить десятичную дробь на десятичную дробь, надо в делимом и в делителе перенести запятую вправо на столько же цифр, сколько их после запятой в делителе, и затем выполнить деление на обычное число.
Например, разделим 5,95 на 1,7
Запишем уголком данное выражение
Теперь в делимом и в делителе перенесём запятую вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит мы должны в делимом и в делителе перенести запятую вправо на одну цифру. Переносим:
После перенесения запятой вправо на одну цифру десятичная дробь 5,95 обратилась в дробь 59,5. А десятичная дробь 1,7 после перенесения запятой вправо на одну цифру обратилась в обычное число 17. А как делить десятичную дробь на обычное число мы уже знаем. Дальнейшее вычисление не составляет особого труда:
Запятая переносится вправо с целью облегчить деление. Это допускается по причине того, что при умножении или делении делимого и делителя на одно и то же число, частное не меняется. Что это значит?
Это одна из интересных особенностей деления. Его называют свойством частного. Рассмотрим выражение 9: 3 = 3. Если в этом выражении делимое и делитель умножить или разделить на одно и то же число, то частное 3 не изменится.
Давайте умножим делимое и делитель на 2, и посмотрим, что из этого получится:
(9 × 2 ) : (3 × 2 ) = 18: 6 = 3
Как видно из примера, частное не поменялось.
Тоже самое происходит, когда мы переносим запятую в делимом и в делителе. В предыдущем примере, где мы делили 5,91 на 1,7 мы перенесли в делимом и делителе запятую на одну цифру вправо. После переноса запятой, дробь 5,91 преобразовалась в дробь 59,1 а дробь 1,7 преобразовалась в обычное число 17.
На самом деле внутри этого процесса происходило умножение на 10. Вот как это выглядело:
5,91 × 10 = 59,1
Поэтому от количества цифр после запятой в делителе зависит то, на что будет умножено делимое и делитель. Другими словами, от количества цифр после запятой в делителе будет зависеть то, на сколько цифр в делимом и в делителе запятая будет перенесена вправо.
Деление десятичной дроби на 10, 100, 1000
Деление десятичной дроби на 10, 100, или 1000 осуществляется таким же образом, как и . Например, разделим 2,1 на 10. Решим этот пример уголком:
Например, разделим 2,1 на 10. Решим этот пример уголком:
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится влево на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 2,1: 10. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 2,1 нужно перенести запятую влево на одну цифру. Переносим запятую влево на одну цифру и видим, что там больше не осталось цифр. В этом случае перед цифрой дописываем ещё один ноль. В итоге получаем 0,21
Попробуем разделить 2,1 на 100. В числе 100 два нуля. Значит в делимом 2,1 надо перенести запятую влево на две цифры:
2,1: 100 = 0,021
Попробуем разделить 2,1 на 1000. В числе 1000 три нуля. Значит в делимом 2,1 надо перенести запятую влево на три цифры:
2,1: 1000 = 0,0021
Деление десятичной дроби на 0,1, 0,01 и 0,001
Деление десятичной дроби на 0,1, 0,01, и 0,001 осуществляется таким же образом, как и . В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
Например, разделим 6,3 на 0,1. В первую очередь перенесём запятые в делимом и в делителе вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит переносим запятые в делимом и в делителе вправо на одну цифру.
После перенесения запятой вправо на одну цифру, десятичная дробь 6,3 превращается в обычное число 63, а десятичная дробь 0,1 после перенесения запятой вправо на одну цифру превращается в единицу. А разделить 63 на 1 очень просто:
Значит значение выражения 6,3: 0,1 равно 63
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится вправо на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 6,3: 0,1. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 6,3 нужно перенести запятую вправо на одну цифру. Переносим запятую вправо на одну цифру и получаем 63
Переносим запятую вправо на одну цифру и получаем 63
Попробуем разделить 6,3 на 0,01. В делителе 0,01 два нуля. Значит в делимом 6,3 надо перенести запятую вправо на две цифры. Но в делимом после запятой только одна цифра. В этом случае в конце нужно дописать ещё один ноль. В результате получим 630
Попробуем разделить 6,3 на 0,001. В делителе 0,001 три нуля. Значит в делимом 6,3 надо перенести запятую вправо на три цифры:
6,3: 0,001 = 6300
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Математический-Калькулятор-Онлайн v.1.0
Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.
Решение:
Как работать с математическим калькулятором
| Клавиша | Обозначение | Пояснение |
|---|---|---|
| 5 | цифры 0-9 | Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/- Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/- |
| . | точка (запятая) | Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5 |
| + | знак плюс | Сложение чисел (целые, десятичные дроби) |
| — | знак минус | Вычитание чисел (целые, десятичные дроби) |
| ÷ | знак деления | Деление чисел (целые, десятичные дроби) |
| х | знак умножения | Умножение чисел (целые, десятичные дроби) |
| √ | корень | Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2 |
| x 2 | возведение в квадрат | Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16 При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16 |
| 1 / x | дробь | Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число |
| % | процент | Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%» |
| ( | открытая скобка | Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10 |
| ) | закрытая скобка | Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки |
| ± | плюс минус | Меняет знак на противоположный |
| = | равно | Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат. |
| ← | удаление символа | Удаляет последний символ |
| С | сброс | Кнопка сброса. Полностью сбрасывает калькулятор в положение «0» |
Алгоритм работы онлайн-калькулятора на примерах
Сложение.
Сложение целых натуральных чисел { 5 + 7 = 12 }
Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }
Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }
Вычитание.
Вычитание целых натуральных чисел { 7 — 5 = 2 }
Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }
Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }
Умножение.
Произведение целых натуральных чисел { 3 * 7 = 21 }
Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }
Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }
Деление.

Деление целых натуральных чисел { 27 / 3 = 9 }
Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }
Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }
Извлечение корня из числа.
Извлечение корня из целого числа { корень(9) = 3 }
Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }
Извлечение корня из суммы чисел { корень(56 + 25) = 9 }
Извлечение корня из разницы чисел { корень (32 – 7) = 5 }
Возведение числа в квадрат.
Возведение в квадрат целого числа { (3) 2 = 9 }
Возведение в квадрат десятичных дробей { (2,2) 2 = 4,84 }
Перевод в десятичные дроби.
Вычисление процентов от числа
Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }
Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }
18% от числа 140 это { 140 * 0,18 = 25,2 }
Калькулятор сложения дробей
Создано Wojciech Sas, кандидатом наук
Отредактировано Bogna Szyk и Jack Bowater
Последнее обновление: 29 ноября 2021 г.
- Как складывать дроби?
- Сложение дробей с разными знаменателями
- Сложение и вычитание дробей
- Сложение дробей на практике — как пользоваться калькулятором сложения дробей?
Этот калькулятор сложения дробей поможет вам оценить сумма до пяти дробей в мгновение ока. Если вы хотите преобразовать дробь в проценты, этот калькулятор может помочь. В приведенной ниже статье вы узнаете не только о том, как складывать дроби, но и о том, как работать с вычитанием. Вы боретесь с , добавляя дроби с разными знаменателями ? Читайте дальше, чтобы никогда больше не сталкиваться с этой проблемой! После того, как вы закончите здесь, сложение фракций больше никогда не будет ужасом!
Ознакомьтесь с другими нашими полезными инструментами:
- Калькулятор соотношения
- Калькулятор эквивалентных дробей.
Как складывать дроби?
Дробь — это число, образованное из отношения двух чисел ( A и B ).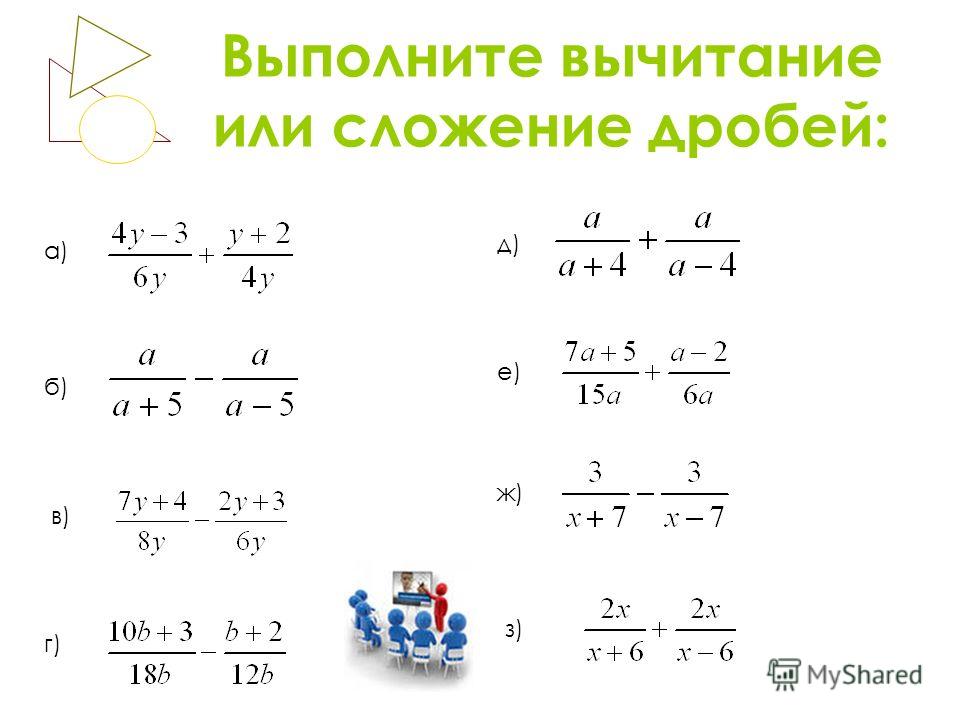 Эти числа обычно представляют собой целые числа (целые числа), так что:
Эти числа обычно представляют собой целые числа (целые числа), так что:
дробь = A / B .
Оказывается можно любую десятичную дробь преобразовать. В результате вы можете складывать столько десятичных знаков, сколько хотите, рассматривая их как дроби. Всякий раз, когда мы хотим сложить две дроби с общим знаменателем, скажем, 2 / 7 и 3 / 7 , нам необходимо Добавить числители, в то время как конфессия остается таким же :
2 /4444444 9004 9004. 3 2 /44444444 9004 9004. 3 . 7 = (2+3) / 7 = 5 / 7 .
Но как сложить дроби с разными знаменателями ?
Сложение дробей с разными знаменателями
Когда числа имеют разные знаменатели, сложение дробей немного сложнее, так как вы не можете просто складывать числители, как раньше. Хитрость заключается в использовании общий знаменатель . Давайте посмотрим, как это работает. Let's say we want to add
Хитрость заключается в использовании общий знаменатель . Давайте посмотрим, как это работает. Let's say we want to add 1 / 2 and 1 / 3 :
-
1 / 2 + 1 / 3 = … - Найдите общий знаменатель. Для этого мы можем оценить наименьшее общее кратное (НОК)
2и3.НОК(2,3) = 6 - Разложите каждую дробь так, чтобы знаменатель был этой НОК, в данном случае
6:1 / 2 = 3 / 6,1 / 3 = 2 / 6= 2 / 6 10101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101 - Поскольку мы знаем, как складывать дроби с одинаковым знаменателем, вы можете просто сложить эти дроби как обычно:
… = 3 / 6 + 2 / 6 = 5 / 9016 54 6
Есть и другие эквивалентные дроби для этого результата, например, 10 / 12 , 15 / 18 , и это лишь некоторые из них. Однако удобно представить результат в его простейшей форме .
Однако удобно представить результат в его простейшей форме .
Сложение и вычитание дробей
Теперь мы знаем, как работает сложение дробей, даже при сложении дробей с разными знаменателями - круто! Но как насчет вычитания? Это тоже просто?
Вы также можете использовать этот калькулятор сложения дробей для вычитания дробей. Нам просто нужно помнить, что вычитание дроби аналогично сложению . Например, что такое 3 / 9 - 2 / 8 ?
- Изменить вычитание на добавление:
3 / - 2 / 8 = 3 / 9 + ( -2 / ) + ( -2 / ) + ( -2 / ) + ( -2 / 8 ) + ( -2 / 8 ) + ( -2 / 8 ) + ( -2 / 8 )- Чтобы сделать вашу жизнь проще, максимально упростите дроби .
 Найдите наибольший общий делитель для каждой пары числителей и знаменателей:
Найдите наибольший общий делитель для каждой пары числителей и знаменателей: GCF(3,9) = 3,GCF(2,8) = 2- Перепишите выражение как:
1 / 3 + ( -1 / 4 )- Остальное как стандартное дополнение:
- Найдите общий знаменатель:
LCM(3,4) = 12- Разложите дроби и сложите их:
4 / 12 + ( -3 / 12 ) = 1 / 12- То же, что:
1 / 3 - 1 / 4 = 1 / 12 - Чтобы сделать вашу жизнь проще, максимально упростите дроби .
Кроме того, в нашем калькуляторе нет разницы между -1 / 4 или 1 / -4 - наш калькулятор сложения дробей будет обрабатывать эти выражения одинаково!
Сложение дробей на практике - как пользоваться калькулятором сложения дробей?
Представьте себе историю - вы на вечеринке с друзьями. И вот он – голод! Что еще хуже, вы только что поняли, что в холодильнике ничего не осталось.
И вот он – голод! Что еще хуже, вы только что поняли, что в холодильнике ничего не осталось.
Решение простое - вы собираетесь заказать пиццу, или две, или даже больше. Вы должны решить! Суть в том, что ваша любимая пиццерия продает пиццу целиком, но у вас есть инновационный метод, позволяющий разрезать пиццу на 6, 8 или 12 кусочков. Каждый хочет определенную долю пиццы: пятеро из вас хотят 4 пиццы из 6 частей, четверо из вас предпочитают 3 пиццы из 8 частей, а оставшиеся трое будут довольны 6 из 12 частей. Главный вопрос: Сколько пицц мы должны заказать?
Вы всегда можете оценить это вручную, но почему бы вам не попробовать наш калькулятор сложения дробей и сэкономить ваше время! Введите следующие значения:
-
5*4и6для первого числа -
4*3и8для второго номера -
3*6и12для третьего
Результат: 19 / 3 или 6 1 / 3 , как смешанный номер. Это значит, что шести пицц будет мало, так что лучше закажите семь!
Это значит, что шести пицц будет мало, так что лучше закажите семь!
Кроме того, вы можете выбрать пошаговое решение , чтобы увидеть все расчеты с пояснениями. Приглашаем всех прочитать ее, наслаждаясь вкусной едой!
Wojciech Sas, PhD кандидат
Значения (можно ввести до 5 дробей)
Они в
1 st дробь
Numerator (n₁)
Знаменатель (D₁)
2 ND Фракция
Numerator (n₂)
DENMINATOR (D₂)
Покажите шаг по шагу решению?
Ознакомьтесь с 17 похожими калькуляторами дробей 🍕
Сравнение дробейДесятичная дробьДеление дробей… Еще 14
Вычитание дробей онлайн, мы покажем вам, как это делается
Вам нужно вычесть дроби ? Con Nuestra calculadora онлайн puedes hacer Esta Operation de Forma Automática introduciendo el valor de una fracción. Para ello, simplemente tienes que usar el símbolo "/" para especificar el valor del numerador y denominador.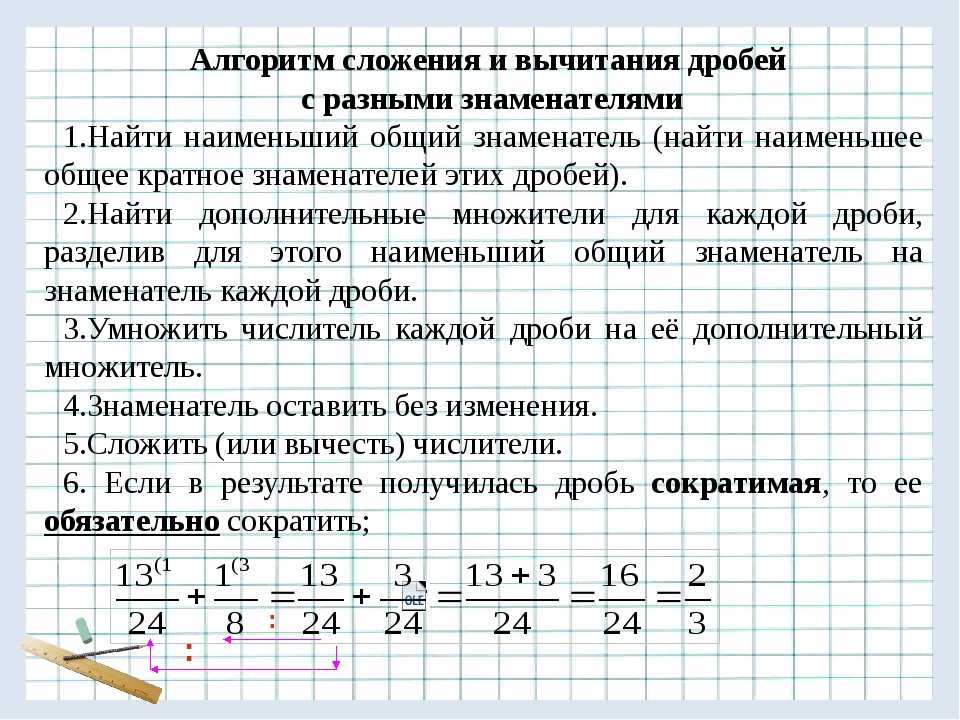 Por ejemplo, un medio se enscribe de la forma 1/2.
Por ejemplo, un medio se enscribe de la forma 1/2.
Каждое поле также поддерживает возможность работы со смешанными фракциями , es decir, fracciones con números enteros. Por ejemplo, puedes escribir una operation como 2 2/3 - 4 5/3, que sería algo como lo siguiente (2+2/3)-(4+5/3).
В обоих случаях вы получите вычитание двух дробей в неприводимом формате для решения любой математической задачи.
Разделы статьи
- Как вычитать дроби с одинаковым знаменателем
- Как вычитать дроби с разными знаменателями
- Онлайн-калькулятор дробей
Как вычитать дроби с одинаковыми знаменателями
Для вычитать дроби с одинаковыми знаменателями то же самое и вычесть числители, сохраняя их первоначальный порядок.
В примере, который мы предлагаем на картинке, вы видите три дроби со знаменателем 6, которые мы должны вычесть. Что мы делаем, так это сохраняем шестерку в качестве общего знаменателя и переходим к девятке. 0019 вычитание числителей дает дробь 3/6, которая не является несократимой.
0019 вычитание числителей дает дробь 3/6, которая не является несократимой.
Если мы хотим еще больше упростить, мы можем разделить числитель и знаменатель на 3 (общий множитель обоих), что даст 1/2. Если бы не было общего множителя, его нельзя было бы еще больше упростить, но это то, что вы можете проверить с помощью нашего калькулятора несократимых дробей.
Как вычитать дроби с разными знаменателями
Если мы хотим вычесть дроби с другим знаменателем Если вы не уверены, вам придется сделать еще несколько вычислений. В любом случае, процесс, который необходимо выполнить, состоит из следующих шагов:
- Поиск общего знаменателя для дробей, участвующих в вычитании, чего можно достичь путем поиска наименьшего общего кратного.
- Получив наименьшее общее кратное знаменателей, подставляем его в знаменатели соответствующих дробей.
- Теперь мы должны заменить числитель каждой дроби на его эквивалент .
 Это состоит в делении полученного знаменателя на исходный знаменатель. Полученное значение нужно умножить на исходный числитель и таким образом мы получим новый числитель дроби. В конце этого шага у нас будет новая дробь, эквивалентная исходной, следовательно, они стоят одинаково.
Это состоит в делении полученного знаменателя на исходный знаменатель. Полученное значение нужно умножить на исходный числитель и таким образом мы получим новый числитель дроби. В конце этого шага у нас будет новая дробь, эквивалентная исходной, следовательно, они стоят одинаково.
В предложенном примере мы видим, что в знаменателе у нас числа 4, 3 и 5. находим наименьшее общее кратное этих значений, в результате приходим к числу 60. Это означает, что три эквивалентные дроби будут иметь это значение в знаменателе.
Теперь нам нужно найти эквивалентных числителей Для этого применим процедуру, описанную в третьем пункте:
- Применим деление конечного знаменателя на начальный знаменатель: 60 / 3 = 20
- Умножаем результат на значение исходного числителя: 20 х 6 = 120
- Подставляем в числитель, чтобы получить результирующую дробь. В конце концов, мы перейдем от 6/3 к 120/60.
Это нужно повторить со всеми дробями, участвующими в операции, и когда все они имеют общий знаменатель, нам просто нужно вычесть числители. Не имеет значения, если у нас останется отрицательный числитель, это вполне верный результат.
Не имеет значения, если у нас останется отрицательный числитель, это вполне верный результат.
В предложенном примере мы видим, что полученную дробь можно упростить еще немного. Если мы войдем в калькулятор несократимых дробей и введем ее значение, то увидим, что -126/60 эквивалентно -21/10. Всегда удобно максимально упростить конечный результат.
Онлайн-калькулятор дробей
Если вам нужно продолжить операции с дробями, и это не вычитание, у нас есть калькулятор для вас, который позволит вам выполнять числовые преобразования или вычислять сложение, умножение, деление и другие операции с числителями и знаменателями.
Nacho
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace. Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
- Калькулятор несократимых дробей
- Калькулятор дробей
- Калькулятор сумм дробей
- Десятичная дробь
- Деление дробей онлайн
- Преобразование дроби в десятичную
- Преобразование дроби в проценты
- Равнозначные дроби
- Умножение дробей онлайн
- Преобразование процентов в дроби
- Вычитание дробей
Калькулятор сложения нескольких дробей
Сумма = `1051/70`
GENERATE WORK
сообщить об этом объявлении0019 Калькулятор сложения кратных дробей использует две или более правильных или неправильных дробей и вычисляет их сумму. Это онлайн-инструмент алгебры для нахождения суммы в простейшей форме двух или более правильных или неправильных дробей.
Необходимо выполнить следующие шаги:
- Введите в поле две или более дроби.
 Знаменатели этих дробей должны быть отличны от нуля.
Знаменатели этих дробей должны быть отличны от нуля. - Нажмите кнопку " GENERATE WORK ", чтобы произвести вычисления;
- Калькулятор сложения нескольких дробей даст сумму двух или более чисел, представленных в виде дробей.
Ввод: Две или более дроби;
Результат: Простейшая дробь.
Правило сложения кратных дробей: Сумма $n$ дробей определяется по следующей формуле {a_1}{b_1}+\frac{a_2}{b_1}+\ldots+\frac{a_n}{b_1}=\frac{a_1+a_2+\ldots a_n}{b_1},\quad \mbox{for}\; b_1\ne0$$
- Если знаменатели разные:
$$\begin{align} &\frac{a_1}{b_1}+\frac{a_2}{b_2}+\ldots+\frac{a_n}{b_n}= \frac {a_1\times \frac{LCM(b_1,b_2,\ldots,b_n)}{b_1}+a_2\times\frac{LCM(b_1,b_2,\ldots,b_n)}{b_2}+\ldots+a_n\ times\frac{LCM(b_1,b_2,\ldots,b_n)}{b_n}}{LCM(b_1,b_2,\ldots,b_n)}, \\& {for}\;b_1,b_2\ldots, b_n\ ne0\end{выравнивание}$$
где $LCM(b_1,b_2\ldots,b_n)$ — наименьшее общее кратное $b_1,b_2\ldots,b_n$.
Как найти сумму нескольких похожих и отличных дробей?
Сумма двух чисел не зависит от их порядка. Другими словами, оно удовлетворяет свойству коммутативности. Сумма чисел не зависит от того, как сгруппированы числа. Это свойство называется ассоциативным свойством. Когда мы имеем дело с дробями, есть два типа сложения:
- Когда все дроби подобны дробям
Когда знаменатели дробей равны, то их сумма будет суммой числителей над общим знаменателем. При необходимости результат может быть упрощен. Это можно выразить алгебраически: $$\frac{a_1}{b_1}+\frac{a_2}{b_1}+\ldots+\frac{a_n}{b_1}=\frac{a_1+a_2+\ldots a_n}{b_1},\quad \mbox{ за}\;b_1\ne0$$
- При несовпадении некоторых дробей
При несовпадении знаменателей дробей для сложения двух и более таких дробей необходимо выполнить следующие действия:
- Найти НОК знаменателей;
- Переписать дроби над НОК;
- Добавить новые числители;
- Результатом является сумма числителей НОК;
- При необходимости упростите результат.

Этот метод можно выразить алгебраически: $$\begin{align} &\frac{a_1}{b_1}+\frac{a_2}{b_2}+\ldots+\frac{a_n}{b_n}= \frac{a_1\times \frac{LCM(b_1, b_2,\ldots,b_n)}{b_1}+a_2\times\frac{LCM(b_1,b_2,\ldots,b_n)}{b_2}+\ldots+a_n\times\frac{LCM(b_1,b_2,\ ldots,b_n)}{b_n}}{LCM(b_1,b_2,\ldots,b_n)}\end{align}$$ для $b_1,b_2\ldots, b_n\ne0.$
Если $LCM(b_1,b_2,\ldots,b_n)=b_1\times b_2\times\ldots\times b_n$, то предыдущая формула принимает вид
$$\begin{align} &\frac{a_1}{ b_1}+\frac{a_2}{b_2}+\ldots+\frac{a_n}{b_n}= \frac{a_1\times b_2\times\ldots\times b_n+a_2\times b_1\times\ldots\times b_n+\ ldots+a_n\times b_1\times b_2\times\ldots\times b_{n-1}}{b_1\times b_2\times\ldots\times b_n} \end{align}$$ для $b_1,b_2\ldots, b_n\ne0.$
Например, найдем сумму для $\frac 27, \frac 64, \frac 85$ и $\frac 87$. Поскольку $LCM(7,4,5,7)=140$, то
\начать{выравнивать}
\frac 27+\frac 64+ \frac 85+\frac 87 & = \frac{2\times 20}{140}+\frac{6\times 35}{140}+\frac{8\times 28}{ 140}+\frac{8\times 20}{140}\\
& = \frac{40}{140}+\frac{210}{140}+\frac{224}{140}+\frac{160}{140}\\
& = \фракция{634}{140}
\end{выравнивание}
Чтобы записать сумму в простейшей форме, найдите GCF числителя и знаменателя
сумма. Поскольку $GCF(634,140)=2$, окончательный результат будет
$$\frac{634\div2}{140\div2}=\frac{317}{70}$$
Обратите внимание, что часть дроби может быть отрицательной дробью. Аналогичное рассмотрение может быть применено к сложению двух или более смешанных чисел или двух или более алгебраических дробей. Чтобы сложить два или более смешанных числа, преобразуйте смешанные числа в соответствующие неправильные дроби и примените описанную выше процедуру.
Поскольку $GCF(634,140)=2$, окончательный результат будет
$$\frac{634\div2}{140\div2}=\frac{317}{70}$$
Обратите внимание, что часть дроби может быть отрицательной дробью. Аналогичное рассмотрение может быть применено к сложению двух или более смешанных чисел или двух или более алгебраических дробей. Чтобы сложить два или более смешанных числа, преобразуйте смешанные числа в соответствующие неправильные дроби и примените описанную выше процедуру.
Работа сложения нескольких дробей с шагами показывает полный пошаговый расчет для нахождения суммы четырех дробей $\frac 27, \frac 64, \frac 85$ и $\frac 87$ с использованием правила сложения нескольких дробей . Для любых других дробей просто введите две или более правильных или неправильных дробей и нажмите кнопку «СОЗДАТЬ РАБОТУ». Учащиеся начальной школы могут использовать этот калькулятор сложения кратных одинаковых и непохожих дробей для выполнения работы, проверки результатов сложения двух или более чисел, полученных вручную, или эффективного выполнения домашних заданий.



 При этом любую неправильную дробь можно преобразовать в сумму натурального числа с правильным выражением.
При этом любую неправильную дробь можно преобразовать в сумму натурального числа с правильным выражением. Чтобы его усвоить и разобраться, следует знать алгоритм действий и принцип нахождения общего знаменателя. Он основан на главном свойстве дроби.
Чтобы его усвоить и разобраться, следует знать алгоритм действий и принцип нахождения общего знаменателя. Он основан на главном свойстве дроби.


 Найдите наибольший общий делитель для каждой пары числителей и знаменателей:
Найдите наибольший общий делитель для каждой пары числителей и знаменателей:  Это состоит в делении полученного знаменателя на исходный знаменатель. Полученное значение нужно умножить на исходный числитель и таким образом мы получим новый числитель дроби. В конце этого шага у нас будет новая дробь, эквивалентная исходной, следовательно, они стоят одинаково.
Это состоит в делении полученного знаменателя на исходный знаменатель. Полученное значение нужно умножить на исходный числитель и таким образом мы получим новый числитель дроби. В конце этого шага у нас будет новая дробь, эквивалентная исходной, следовательно, они стоят одинаково. Знаменатели этих дробей должны быть отличны от нуля.
Знаменатели этих дробей должны быть отличны от нуля.