Сравнение десятичных чисел онлайн калькулятор больше меньше. Сравнение чисел
Продолжаем изучать рациональные числа. В данном уроке мы научимся сравнивать их.
Из предыдущих уроков мы узнали, что чем правее число располагается на координатной прямой, тем оно больше. И соответственно, чем левее располагается число на координатной прямой, тем оно меньше.
Например, если сравнивать числа 4 и 1, то можно сразу ответить, что 4 больше чем 1. Это вполне логичное утверждение и каждый с этим согласится.
В качестве доказательства можно привести координатную прямую. На ней видно, что четвёрка лежит правее единицы
Для этого случая есть и правило, которое при желании можно использовать. Выглядит оно следующим образом:
Из двух положительных чисел больше то число, модуль которого больше.
Чтобы ответить на вопрос какое число больше, а какое меньше, сначала нужно найти модули этих чисел, сравнить эти модули, а потом уже ответить на вопрос.
Например, сравним те же числа 4 и 1, применяя вышеприведенное правило
Находим модули чисел:
|4| = 4
|1| = 1
Сравниваем найденные модули:
4 > 1
Отвечаем на вопрос:
4 > 1
Для отрицательных чисел существует другое правило, выглядит оно следующим образом:
Из двух отрицательных чисел больше то число, модуль которого меньше.
Например, сравним числа −3 и −1
Находим модули чисел
|−3| = 3
|−1| = 1
Сравниваем найденные модули:
3 > 1
Отвечаем на вопрос:
−3
Нельзя путать модуль числа с самим числом. Частая ошибка многих новичков. К примеру, если модуль числа −3 больше, чем модуль числа −1, это не означает, что число −3 больше, чем число −1.
Число −3 меньше, чем число −1 . Это можно понять, если воспользоваться координатной прямой
Видно, что число −3 лежит левее, чем −1 . А мы знаем, что чем левее, тем меньше.
Если сравнивать отрицательное число с положительным, то ответ будет напрашиваться сам. Любое отрицательное число будет меньше любого положительного числа. Например, −4 меньше, чем 2
Видно, что −4 лежит левее, чем 2. А мы знаем, что «чем левее, тем меньше».
Здесь в первую очередь нужно смотреть на знаки чисел. Минус перед числом будет говорить о том, что число отрицательное. Если знак числа отсутствует, то число положительное, но вы можете записать его для наглядности. Напомним, что это знак плюса
Напомним, что это знак плюса
Мы рассмотрели в качестве примера целые числа, вида −4, −3 −1, 2. Сравнить такие числа, а также изобразить на координатной прямой не составляет особого труда.
Намного сложнее сравнивать другие виды чисел, такие как обыкновенные дроби, смешанные числа и десятичные дроби, некоторые из которых являются отрицательными. Здесь уже в основном придётся применять правила, потому что точно изобразить такие числа на координатной прямой не всегда возможно. В некоторых случаях, число надо будет , чтобы сделать его более простым для сравнения и восприятия.
Пример 1. Сравнить рациональные числа
Итак, требуется сравнить отрицательное число с положительным. Любое отрицательное число меньше любого положительного числа. Поэтому не теряя времени отвечаем, что меньше, чем
Пример 2.
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то, модуль которого меньше.
Находим модули чисел:
Сравниваем найденные модули:
Пример 3. Сравнить числа 2,34 и
Сравнить числа 2,34 и
Требуется сравнить положительное число с отрицательным. Любое положительное число больше любого отрицательного числа. Поэтому не теряя времени отвечаем, что 2,34 больше, чем
Пример 4. Сравнить рациональные числа и
Находим модули чисел:
Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно переведём в неправильные дроби и приведём к общему знаменателю
Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа
Пример 5.
Требуется сравнить ноль с отрицательным числом. Ноль больше любого отрицательного числа, поэтому не теряя времени отвечаем, что 0 больше, чем
Пример 6. Сравнить рациональные числа 0 и
Требуется сравнить ноль с положительным числом. Ноль меньше любого положительного числа, поэтому не теряя времени отвечаем, что 0 меньше, чем
Пример 7 . Сравнить рациональные числа 4,53 и 4,403
Сравнить рациональные числа 4,53 и 4,403
Требуется сравнить два положительных числа. Из двух положительных чисел больше то число, модуль которого больше.
Сделаем в обеих дробях количество цифр после запятой одинаковым. Для этого в дроби 4,53 припишем в конце один ноль
Находим модули чисел
Сравниваем найденные модули:
Согласно правилу, из двух положительных чисел больше то число, модуль которого больше. Значит рациональное число 4,53 больше, чем 4,403 потому что модуль числа 4,53 больше, чем модуль числа 4,403
Пример 8. Сравнить рациональные числа и
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше.
Находим модули чисел:
Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно переведём смешанное число в неправильную дробь, затем приведём обе дроби к общему знаменателю:
Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа
Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа
Сравнивать десятичные дроби намного проще, чем обыкновенные дроби и смешанные числа. В некоторых случаях, посмотрев на целую часть такой дроби, можно сразу ответить на вопрос какая дробь больше, а какая меньше.
Чтобы сделать это, нужно сравнить модули целых частей. Это позволит быстро ответить на вопрос в задаче. Ведь как известно, целые части в десятичных дробях имеют вес больший, чем дробные.
Пример 9. Сравнить рациональные числа 15,4 и 2,1256
Модуль целой части дроби 15,4 больше, чем модуль целой части дроби 2,1256
поэтому и дробь 15,4 больше, чем дробь 2,1256
15,4 > 2,1256
Другими словами, нам не пришлось тратить время на дописывание нулей дроби 15,4 и сравнивать получившиеся дроби, как обычные числа
154000 > 21256
Правила сравнения остаются всё теми же. В нашем случае мы сравнивали положительные числа.
Пример 10. Сравнить рациональные числа −15,2 и −0,152
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей
Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей
Видим, что модуль целой части дроби −15,2 больше, чем модуль целой части дроби −0,152.
А значит рациональное −0,152 больше, чем −15,2 потому что модуль целой части числа −0,152 меньше, чем модуль целой части числа −15,2
−0,152 > −15,2
Пример 11. Сравнить рациональные числа −3,4 и −3,7
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей. Но проблема в том, что модули целых чисел равны:
В этом случае придётся пользоваться старым методом: найти модули рациональных чисел и сравнить эти модули
Сравниваем найденные модули:
Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное −3,4 больше, чем −3,7 потому что модуль числа −3,4 меньше, чем модуль числа −3,7
−3,4 > −3,7
Пример 12. Сравнить рациональные числа 0,(3) и
Сравнить рациональные числа 0,(3) и
Требуется сравнить два положительных числа. Причем сравнить периодическую дробь с простой дробью.
Переведём периодическую дробь 0,(3) в обыкновенную дробь и сравним её с дробью . После перевода периодической дроби 0,(3) в обыкновенную, она обращается в дробь
Находим модули чисел:
Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно приведём к общему знаменателю:
Согласно правилу, из двух положительных чисел больше то число, модуль которого больше. Значит рациональное число больше, чем 0,(3) потому что модуль числа больше, чем модуль числа 0,(3)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Не только простые числа можно сравнивать, но и дроби тоже. Ведь дробь — это такое же число как, к примеру, и натуральные числа. Нужно знать только правила, по которым сравнивают дроби.
Сравнение дробей с одинаковыми знаменателями.
Если у двух дробей одинаковые знаменатели, то такие дроби сравнить просто.
Чтобы сравнить дроби с одинаковыми знаменателями, нужно сравнить их числители. Та дробь больше у которой больше числитель.
Рассмотрим пример:
Сравните дроби \(\frac{7}{26}\) и \(\frac{13}{26}\).
Знаменатели у обоих дробей одинаковые равны 26, поэтому сравниваем числители. Число 13 больше 7. Получаем:
\(\frac{7}{26}
Сравнение дробей с равными числителями.
Если у дроби одинаковые числители, то больше та дробь, у которой знаменатель меньше.
Понять это правило можно, если привести пример из жизни. У нас есть торт. К нам в гости могут прийти 5 или 11 гостей. Если придут 5 гостей, то мы разрежем торт на 5 равных кусков, а если придут 11 гостей, то разделим на 11 равных кусков. А теперь подумайте в каком случаем на одного гостя придется кусок торта большего размера? Конечно, когда придут 5 гостей, кусок торта будет больше.
Или еще пример. У нас есть 20 конфет. Мы можем поровну раздать конфеты 4 друзьям или поровну поделить конфеты между 10 друзьями. В каком случае у каждого друга будет конфет больше? Конечно, когда мы разделим только на 4 друзей, количество конфет у каждого друга будет больше. Проверим эту задачу математически.
Мы можем поровну раздать конфеты 4 друзьям или поровну поделить конфеты между 10 друзьями. В каком случае у каждого друга будет конфет больше? Конечно, когда мы разделим только на 4 друзей, количество конфет у каждого друга будет больше. Проверим эту задачу математически.
\(\frac{20}{4} > \frac{20}{10}\)
Если мы до решаем эти дроби, то получим числа \(\frac{20}{4} = 5\) и \(\frac{20}{10} = 2\). Получаем, что 5 > 2
В этом и заключается правило сравнения дробей с одинаковыми числителями.
Рассмотрим еще пример.
Сравните дроби с одинаковым числителем \(\frac{1}{17}\) и \(\frac{1}{15}\) .
Так как числители одинаковые, больше та дробь, где знаменатель меньше.
\(\frac{1}{17}
Сравнение дробей с разными знаменателями и числителями.
Чтобы сравнить дроби с разными знаменателями, необходимо дроби привести к , а потом сравнить числители.
Сравните дроби \(\frac{2}{3}\) и \(\frac{5}{7}\).
Сначала найдем общий знаменатель дробей. Он будет равен числу 21.
Он будет равен числу 21.
\(\begin{align}&\frac{2}{3} = \frac{2 \times 7}{3 \times 7} = \frac{14}{21}\\\\&\frac{5}{7} = \frac{5 \times 3}{7 \times 3} = \frac{15}{21}\\\\ \end{align}\)
Потом переходим к сравнению числителей. Правило сравнения дробей с одинаковыми знаменателями.
\(\begin{align}&\frac{14}{21}
Сравнение .
Неправильная дробь всегда больше правильной. Потому что неправильная дробь больше 1, а правильная дробь меньше 1.
Пример:
Сравните дроби \(\frac{11}{13}\) и \(\frac{8}{7}\).
Дробь \(\frac{8}{7}\) неправильная и она больше 1.
\(1
Дробь \(\frac{11}{13}\) правильная и она меньше 1. Сравниваем:
\(1 > \frac{11}{13}\)
Получаем, \(\frac{11}{13}
Вопросы по теме:
Как сравнить дроби с разными знаменателями?
Ответ: надо привести к общему знаменателю дроби и потом сравнить их числители.
Как сравнивать дроби?
Ответ: сначала нужно определиться к какой категории относятся дроби: у них есть общий знаменатель, у них есть общий числитель, у них нет общего знаменателя и числителя или у вас правильная и неправильная дробь. После классификации дробей применить соответствующее правило сравнения.
После классификации дробей применить соответствующее правило сравнения.
Что такое сравнение дробей с одинаковыми числителями?
Ответ: если у дробей одинаковые числители, та дробь больше у которой знаменатель меньше.
Пример №1:
Сравните дроби \(\frac{11}{12}\) и \(\frac{13}{16}\).
Решение:
Так как нет одинаковых числителей или знаменателей, применяем правило сравнения с разными знаменателями. Нужно найти общий знаменатель. Общий знаменатель будет равен 96. Приведем дроби к общему знаменателю. Первую дробь \(\frac{11}{12}\) умножим на дополнительный множитель 8, а вторую дробь \(\frac{13}{16}\) умножим на 6.
\(\begin{align}&\frac{11}{12} = \frac{11 \times 8}{12 \times 8} = \frac{88}{96}\\\\&\frac{13}{16} = \frac{13 \times 6}{16 \times 6} = \frac{78}{96}\\\\ \end{align}\)
Сравниваем дроби числителями, та дробь больше у которой числитель больше.
\(\begin{align}&\frac{88}{96} > \frac{78}{96}\\\\&\frac{11}{12} > \frac{13}{16}\\\\ \end{align}\)
Пример №2:
Сравните правильную дробь с единицей?
Решение:
Любая правильная дробь всегда меньше 1.
Задача №1:
Сын с отцом играли в футбол. Сын из 10 подходов в ворота попал 5 раз. А папа из 5 подходов попал в ворота 3 раза. Чей результат лучше?
Решение:
Сын попал из 10 возможных подходов 5 раз. Запишем в виде дроби \(\frac{5}{10} \).
Папа попал из 5 возможных подходов 3 раз. Запишем в виде дроби \(\frac{3}{5} \).
Сравним дроби. У нас разные числители и знаменатели, приведем к одному знаменателю. Общий знаменатель будет равен 10.
\(\begin{align}&\frac{3}{5} = \frac{3 \times 2}{5 \times 2} = \frac{6}{10}\\\\&\frac{5}{10}
Ответ: у папы результат лучше.
Продолжаем изучать дроби. Сегодня мы поговорим об их сравнении. Тема интересная и полезная. Она позволит новичку почувствовать себя учёным в белом халате.
Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.
Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются , такими как больше (>) или меньше (
Ученые-математики уже позаботились о готовых правилах, позволяющие сразу ответить на вопрос какая дробь больше, а какая меньше. Эти правила можно смело применять.
Эти правила можно смело применять.
Мы рассмотрим все эти правила и попробуем разобраться, почему происходит именно так.
Содержание урока
Сравнение дробей с одинаковыми знаменателямиДроби, которые нужно сравнить, попадаются разные. Самый удачный случай это когда у дробей одинаковые знаменатели, но разные числители. В этом случае применяют следующее правило:
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше. И соответственно меньше будет та дробь, у которой числитель меньше.
Например, сравним дроби и и ответим, какая из этих дробей больше. Здесь одинаковые знаменатели, но разные числители. У дроби числитель больше, чем у дроби . Значит дробь больше, чем . Так и отвечаем. Отвечать нужно с помощью значка больше (>)
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части. пиццы больше, чем пиццы:
Каждый согласится с тем, что первая пицца больше, чем вторая.
Следующий случай, в который мы можем попасть, это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.
Например, сравним дроби и . У этих дробей одинаковые числители. У дроби знаменатель меньше, чем у дроби . Значит дробь больше, чем дробь . Так и отвечаем:
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. пиццы больше, чем пиццы:
Каждый согласиться с тем, что первая пицца больше, чем вторая.
Сравнение дробей с разными числителями и разными знаменателями
Нередко случается так, что приходиться сравнивать дроби с разными числителями и разными знаменателями.
Например, сравнить дроби и . Чтобы ответить на вопрос, какая из этих дробей больше или меньше, нужно привести их к одинаковому (общему) знаменателю. Затем можно будет легко определить какая дробь больше или меньше.
Затем можно будет легко определить какая дробь больше или меньше.
Приведём дроби и к одинаковому (общему) знаменателю. Найдём (НОК) знаменателей обеих дробей. НОК знаменателей дробей и это число 6.
Теперь находим дополнительные множители для каждой дроби. Разделим НОК на знаменатель первой дроби . НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:
Теперь найдём второй дополнительный множитель. Разделим НОК на знаменатель второй дроби . НОК это число 6, а знаменатель второй дроби это число 3. Делим 6 на 3, получаем дополнительный множитель 2. Записываем его над второй дробью:
Умножим дроби на свои дополнительные множители:
Мы пришли к тому, что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:
Правило правилом, а мы попробуем разобраться почему больше, чем . Для этого выделим целую часть в дроби . В дроби ничего выделять не нужно, поскольку эта дробь уже правильная.
Для этого выделим целую часть в дроби . В дроби ничего выделять не нужно, поскольку эта дробь уже правильная.
После выделения целой части в дроби , получим следующее выражение:
Теперь можно легко понять, почему больше, чем . Давайте нарисуем эти дроби в виде пицц:
2 целые пиццы и пиццы, больше чем пиццы.
Вычитание смешанных чисел. Сложные случаи.Вычитая смешанные числа, иногда можно обнаружить, что всё идёт не так гладко, как хотелось бы. Часто случается так, что при решении какого-нибудь примера ответ получается не таким, каким он должен быть.
При вычитании чисел уменьшаемое должно быть больше вычитаемого. Только в этом случае будет получен нормальный ответ.
Например, 10−8=2
10 — уменьшаемое
8 — вычитаемое
2 — разность
Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.
А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5−7=−2
5 — уменьшаемое
7 — вычитаемое
−2 — разность
В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.
Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.
Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.
С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.
Например, решим пример .
Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая. больше чем
поэтому смело можем вернуться к примеру и решить его:
Теперь решим такой пример
Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:
В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.
Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения .
Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Чтобы сравнить такие дроби, нужно привести их к одинаковому (общему) знаменателю. Не будем подробно расписывать, как это сделать. Если испытываете затруднения, обязательно повторите .
После приведения дробей к одинаковому знаменателю, получаем следующее выражение:
Теперь нужно сравнить дроби и . Это дроби с одинаковыми знаменателями. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .
А это значит, что уменьшаемое больше, чем вычитаемое
А значит мы можем вернуться к нашему примеру и смело решить его:
Пример 3. Найти значение выражения
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю.
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше, и меньше та, у которой числитель меньше . На самом деле, ведь знаменатель показывает, на сколько частей разделили одну целую величину, а числитель показывает, сколько таких частей взяли.
Получается, что делили каждый целый круг на одно и то же число 5 , а брали разное количество частей: больше взяли — большая дробь и получилась.
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше, и меньше та, у которой знаменатель больше. Ну и, в самом деле, если мы один круг разделим на 8 частей, а другой на 5 частей и возьмем по одной части от каждого из кругов. Какая часть будет больше?
Конечно, от круга, поделенного на 5 частей! А теперь представьте, что делили не круги, а торты. Вы бы какой кусочек предпочли, точнее, какую долю: пятую или восьмую?
Вы бы какой кусочек предпочли, точнее, какую долю: пятую или восьмую?
Чтобы сравнить дроби с разными числителями и разными знаменателями, надо привести дроби к наименьшему общему знаменателю, а затем сравнивать дроби с одинаковыми знаменателями.
Примеры. Сравнить обыкновенные дроби:
Приведем эти дроби к наименьшему общему знаменателю. НОЗ(4; 6)=12. Находим дополнительные множители для каждой из дробей. Для 1-й дроби дополнительный множитель 3 (12: 4=3 ). Для 2-й дроби дополнительный множитель 2 (12: 6=2 ). Теперь сравниваем числители двух получившихся дробей с одинаковыми знаменателями. Так как числитель первой дроби меньше числителя второй дроби (9, то и сама первая дробь меньше второй дроби.
Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.
Произведем сравнение обыкновенной дроби с натуральным числом.
Yandex.RTB R-A-339285-1
Сравнение дробей с одинаковыми знаменателями
Когда производится сравнение дробей с одинаковыми знаменателями, мы работаем только с числителем, а значит, сравниваем доли числа. Если имеется дробь 3 7 , то она имеет 3 доли 1 7 , тогда дробь 8 7 имеет 8 таких долей. Иначе говоря, если знаменатель одинаковый, производится сравнение числителей этих дробей, то есть 3 7 и 8 7 сравниваются числа 3 и 8 .
Отсюда следует правило сравнения дробей с одинаковыми знаменателями:из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.
Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.
Пример 1
Произвести сравнение заданных дробей 65 126 и 87 126 .
Решение
Так как знаменатели дробей одинаковые, переходим к числителям. Из чисел 87 и 65 очевидно, что 65 меньше. Исходя из правила сравнения дробей с одинаковыми знаменателями имеем, что 87 126 больше 65 126 .
Исходя из правила сравнения дробей с одинаковыми знаменателями имеем, что 87 126 больше 65 126 .
Ответ: 87 126 > 65 126 .
Сравнение дробей с разными знаменателями
Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.
Если имеются дроби с разными знаменателями, для их сравнения необходимо:
- найти общий знаменатель;
- сравнить дроби.
Рассмотрим данные действия на примере.
Пример 2
Произвести сравнение дробей 5 12 и 9 16 .
Решение
В первую очередь необходимо привести дроби к общему знаменателю. Это делается таким образом: находится НОК, то есть наименьший общий делитель, 12 и 16 . Это число 48 . Необходимо надписать дополнительные множители к первой дроби 5 12 , это число находится из частного 48: 12 = 4 , для второй дроби 9 16 – 48: 16 = 3 . Запишем получившееся таким образом: 5 12 = 5 · 4 12 · 4 = 20 48 и 9 16 = 9 · 3 16 · 3 = 27 48 .
После сравнения дробей получаем, что 20 48
Ответ: 5 12
Имеется еще один способ сравнения дробей с разными знаменателями. Он выполняется без приведения к общему знаменателю. Рассмотрим на примере. Чтобы сравнить дроби a b и c d , приводим к общему знаменателю, тогда b · d , то есть произведение этих знаменателей. Тогда дополнительные множители для дробей будут являться знаменатели соседней дроби. Это запишется так a · d b · d и c · b d · b . Используя правило с одинаковыми знаменателями, имеем, что сравнение дробей свелось к сравнениям произведений a · d и c · b . Отсюда получаем правило сравнения дробей с разными знаменателями:если a · d > b · c , тогда a b > c d , но если a · d
Пример 3
Произвести сравнение дробей 5 18 и 23 86 .
Решение
Данный пример имеет a = 5 , b = 18 , c = 23 и d = 86 . Тогда необходимо вычислить a · d и b · c . Отсюда следует, что a · d = 5 · 86 = 430 и b · c = 18 · 23 = 414 . Но 430 > 414 , тогда заданная дробь 5 18 больше, чем 23 86 .
Ответ: 5 18 > 23 86 .
Сравнение дробей с одинаковыми числителями
Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.
Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.
Рассмотрим на примере.
Пример 4
Произвести сравнение дробей 54 19 и 54 31 .
Решение
Имеем, что числители одинаковые, значит, что дробь, имеющая знаменатель 19 больше дроби, которая имеет знаменатель 31 . Это понятно, исходя из правила.
Ответ: 54 19 > 54 31 .
Иначе можно рассмотреть на примере. Имеется две тарелки, на которых 1 2 пирога, анна другой 1 16 . Если съесть 1 2 пирога, то насытишься быстрей, нежели только 1 16 . Отсюда вывод, что наибольший знаменатель при одинаковых числителях является наименьшим при сравнении дробей.
Сравнение дроби с натуральным числом
Сравнение обыкновенной дроби с натуральным числом идет как и сравнение двух дробей с записью знаменателей в виде 1 . Для детального рассмотрения ниже приведем пример.
Пример 4
Необходимо выполнить сравнение 63 8 и 9 .
Решение
Необходимо представить число 9 в виде дроби 9 1 . Тогда имеем необходимость сравнения дробей 63 8 и 9 1 . Далее следует приведение к общему знаменателю путем нахождения дополнительных множителей. После этого видим, что нужно сравнить дроби с одинаковыми знаменателями 63 8 и 72 8 . Исходя из правила сравнения, 63
Ответ: 63 8
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Калькулятор дробей 6 класс математика
Калькулятор дробей 6 класс математика
Калькулятор дробей выполнит основные арифметические действия с дробями и смешанными числами.
Если целая часть заполнена, калькулятор приведет смешанное число в неправильную дробь и выполнит операцию.
Заполните поля калькулятора чтобы найти сумму, разность, произведение и отношение дробей.
Основные операции с дробями
Сложение и вычитание
Чтобы Сложить дроби с разными знаменателями необходимо: привести дробные части к наименьшему общему знаменателю; затем сложить их числители. Рассмотрим на примере как сложить две дроби с разными знаменателями.
Пример Сложить дроби И
.
Наименьшее общее кратное знаменателей (8 и 6) равно 24.
Для нахождения Разности дробей необходимо: привести дробные части к наименьшему общему знаменателю; затем выполнить вычитание числителей.
Пример Найти разность дробей И
.
Общее кратное знаменателей НОК(16, 20)=80. Для вычисления наименьшего общего кратного можно воспользоваться калькулятором. Калькулятор вычислит НОК автоматически.
Умножение и деление
Для умножения двух дробей нужно: перемножить их числители и знаменатели.
Пример Найти произведение дробей И
.
Чтобы разделить дробь на другую нужно: умножить первую дробь на дробь, обратную второй: .
Пример Разделить дробь На
.
Приведение к общему знаменателю
Чтобы совершать операции с дробями часто требуется привести дроби к общему знаменателю. Рассмотрим процесс приведения двух дробей и к наименьшему общему знаменателю :
Пример Сравнить дроби И
Для сравнения дробей приведем их к общему знаменателю и сравним их числители. Воспользуемся шагами описанными выше и найдем наименьшее общее кратное знаменателей дробей и далее преобразуем:
.
НОК(18, 4)=36, дополнительный множитель первой дроби, доп. множитель второй дроби.
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
.
Для умножения двух дробей нужно: перемножить их числители и знаменатели.
Пример Сравнить дроби и
Воспользуемся шагами описанными выше и найдем наименьшее общее кратное знаменателей дробей и далее преобразуем.
Calcs. su
21.06.2020 14:59:38
2020-06-21 14:59:38
Источники:
Https://calcs. su/html/calcs/math/fraction. html
Калькулятор дробей » /> » /> .keyword { color: red; }
Калькулятор дробей 6 класс математика
Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:
Поделить числитель дроби на её знаменатель Результат от деления будет являться целой частью Остаток отделения будет являться числителем
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.
Как перевести десятичную дробь в обыкновенную или смешанную
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
Записать дробь в виде десятичная дробь 1 Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом. Найти наибольший общий делитель и сократить дробь.
Найти наибольший общий делитель и сократить дробь.
Например, переведем 0.36 в обыкновенную дробь:
Записываем дробь в виде: 0.36 1 Умножаем на 10 два раза, получим 36 100 Сокращаем дробь 36 100 = 9 25
Как перевести дробь в проценты
Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.
Как перевести проценты в дробь
Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
Записать дробь в виде десятичная дробь 1 Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом. Найти наибольший общий делитель и сократить дробь.
Например, переведем 0.36 в обыкновенную дробь:
Записываем дробь в виде: 0.36 1 Умножаем на 10 два раза, получим 36 100 Сокращаем дробь 36 100 = 9 25
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо.
Calcus. ru
17.09.2018 11:28:19
2018-09-17 11:28:19
Источники:
Https://calcus. ru/kalkulyator-drobej
Решение дробей 6 класс калькулятор » /> » /> .keyword { color: red; }
Калькулятор дробей 6 класс математика
Данный Онлайн калькулятор дробей предназначен для Сложения, вычитания, деления и умножения между собой обыкновенных дробей. А так же дробей с целой частью и десятичных дробей.
Основные возможности:
Сложение, вычитание, деление и умножение дробей. Расчет дробей с подробнейшим решением. Расчет дробей со степенями, скобками и буквами. Сокращение дробей. Поддержка до трех дробей онлайн.
- Калькулятор Инструкция Теория История Сообщить о проблеме
На данном калькуляторе можно посчитать сложение вычитание деление или умножение дробей. (-2) +1. При сложении дробей состоящих только из чисел калькулятор вычисляет НОД и НОК. При расчете сразу трех дробей сначала выполняется операция умножение(деления), затем сложения(вычитания). Для изменения этого порядка поставьте галочку в поле «Большие скобки» и выберите нужный порядок расчета. В этом случае первой будет выполняться операция в больших скобках.
(-2) +1. При сложении дробей состоящих только из чисел калькулятор вычисляет НОД и НОК. При расчете сразу трех дробей сначала выполняется операция умножение(деления), затем сложения(вычитания). Для изменения этого порядка поставьте галочку в поле «Большие скобки» и выберите нужный порядок расчета. В этом случае первой будет выполняться операция в больших скобках.
Онлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей. Если дробь имеет вид «смешанной дроби», то также заполните поле, соответствующее целой части дроби. Если у дроби нет целой части, т. е. дробь имеет вид «простой дроби», то оставьте данное поле пустым. Затем нажмите кнопку «Вычислить».
Дробью в математике называется число, представляющее часть единицы или несколько её частей. Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления.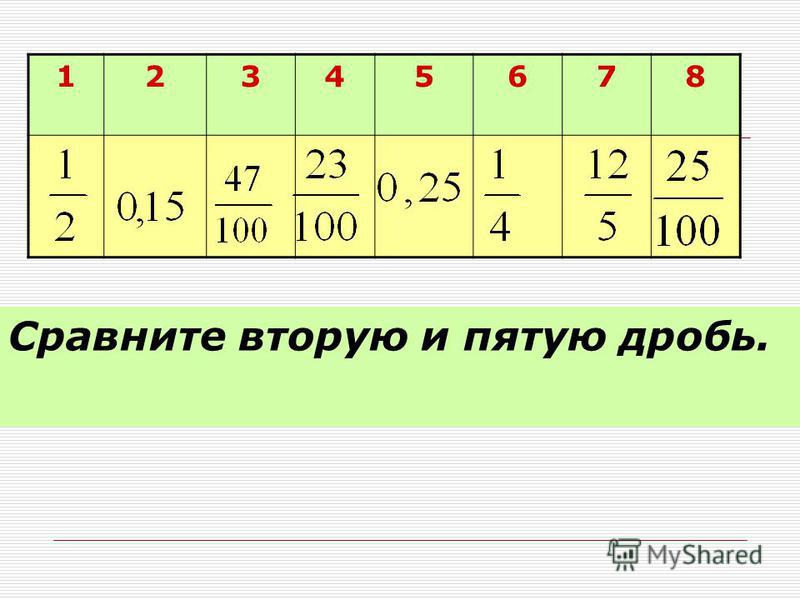 Число, располагающееся над чертой, называется Числителем. Число, располагающееся под чертой, называется Знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.
Число, располагающееся над чертой, называется Числителем. Число, располагающееся под чертой, называется Знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.
Дроби бывают Правильными и Неправильными. Правильной называется дробь, у которой числитель меньше знаменателя. Если у дроби числитель больше знаменателя, то такая дробь называется неправильной. Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть, называется Простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь (см. пример ниже).
Как работать с калькулятором обыкновенных дробей?
Калькулятор предназначен для решения Простых дробей и дробей с целыми числами (Смешанных). В будущем, планируется внедрение функции решения десятичных дробей, но в данный момент она отсутствует.
Для начала работы с дробным калькулятором необходимо понять Очень простой принцип ввода данных. Все целые числа вводятся с помощью больших кнопок, расположенных слева. Все числители вводятся с помощью маленьких белых кнопок, расположенных в правом верхнем блоке цифр. Все знаменатели, соответственно, вводятся путем нажатия на кнопки в правом нижнем углу. Данный способ ввода данных является в некотором роде инновационным, поскольку четко разграничивает целое, числитель и знаменатель, что облегчает вычисления, экономит время и делает взаимодействие с приложением более эффективным.
Допустим, вам требуется сложить квадратный корень из двух пятых и одну целую две девятых в шестой степени. Начните вводить пример с кнопки корня. После этого нажмите на цифру 2 в области числителя и на цифру пять в области знаменателя. Первое слагаемое готово. Теперь нажмите на знак «+» — это действие сложения. Далее введите целое число один на основной клавиатуре, потом число два в области числителя и девять в области знаменателя. », после чего на цифру шесть на основной клавиатуре. В результате, получится готовый пример:
», после чего на цифру шесть на основной клавиатуре. В результате, получится готовый пример:
Теперь нажмите на кнопку равно и получите Результат калькуляции. В примере выше проиллюстрирован практически весь арсенал возможностей калькулятора дробей. Точно таким же образом, вы можете осуществлять Умножение, деление и вычитание дробей, как простых, так и алгебраических, с одинаковыми и разными знаменателями, целыми числами и т. д. Также, калькулятор может вычислить проценты от дробей, что требуется не так часто, но тем не менее очень важно для решения многих актуальных задач.
Если вам требуется сделать положительное число отрицательным, то сначала введите число, а потом нажмите на кнопку «+/-». После этого число или дробь автоматически обернется в скобки с отрицательным значением или наоборот (в зависимости от изначального статуса числа). Если необходимо удалить число, числитель или знаменатель, то воспользуйтесь соответствующей стрелкой Backspace, которая есть в блоке и числителя и знаменателя. Стрелки работают одинаково и по очереди стирают числа или знаки, находящиеся на дисплее калькулятора.
Стрелки работают одинаково и по очереди стирают числа или знаки, находящиеся на дисплее калькулятора.
Управление калькулятором дробей с клавиатуры.
Использовать Калькулятор дробей онлайн можно не только с помощью компьютерной мыши, но и с помощью клавиатуры. Здесь логика очень проста:
Все целые числа вводятся как обычно, нажатиями на клавиши чисел. Все числители вводятся с добавлением клавиши CTRL (например, CTRL+1). Все знаменатели вводятся с добавлением клавиши ALT (например, ALT+2).
Действия умножения, деления, сложения и вычитания так же инициируются соответствующими кнопками клавиатуры, если они есть (обычно располагаются в правой части, в так называемой области Numpad). Удаление производится нажатием на клавишу Backspace. Действие очистки (красная кнопка «C») вызывается нажатием на клавишу «C». Квадратный корень – нажатием на соседнюю клавишу «V» . Удаление производится нажатием на клавишу Backspace.
Зачем нужен калькулятор дробей онлайн?
Калькулятор дробей онлайн предназначен для решения Обыкновенных и Смешанных дробей (с целыми числами). Решение дробей часто требуется школьникам и студентам, а также инженерам и аспирантам. Наш калькулятор предоставляет возможность производить с дробями следующие действия: Деление дробей, умножение дробей, сложение дробей и вычитание дробей. Также, калькулятор умеет работать с корнями и степенями, а еще с отрицательными числами, благодаря чему он многократно Превосходит аналогичные онлайн приложения.
Решение дробей часто требуется школьникам и студентам, а также инженерам и аспирантам. Наш калькулятор предоставляет возможность производить с дробями следующие действия: Деление дробей, умножение дробей, сложение дробей и вычитание дробей. Также, калькулятор умеет работать с корнями и степенями, а еще с отрицательными числами, благодаря чему он многократно Превосходит аналогичные онлайн приложения.
Калькулятор простых дробей онлайн поможет вам решить примеры с дробями и при этом вам не надо беспокоиться о том, как предварительно сократить дробь. Здесь это сделается Автоматически, т. к. приложение само вычисляет общий знаменатель и выдает вам готовый результат на экран.
В чем преимущества такого способа решения дробей?
Калькулятор Поддерживает работу со скобками, что позволяет решать дроби даже в сложных математических примерах. В частности, действия со скобками часто требуются при вычислении Алгебраических дробей или Отрицательных дробей, над которыми постоянно приходится корпеть всем школьникам средних классов. Дополнительно, вы можете использовать этот калькулятор для Сокращения дробей или решения дробей С разными знаменателями. Более того, в отличии от многих других бесплатных сервисов, данный калькулятор умеет работать с двумя, тремя, четырьмя и вообще с любым количеством дробей и чисел.
Дополнительно, вы можете использовать этот калькулятор для Сокращения дробей или решения дробей С разными знаменателями. Более того, в отличии от многих других бесплатных сервисов, данный калькулятор умеет работать с двумя, тремя, четырьмя и вообще с любым количеством дробей и чисел.
Калькулятор обыкновенных дробей Полностью бесплатный и не требует регистрации. Вы можете использовать его в любое время дня и ночи. Работать можно с помощью мыши или прямо с клавиатуры (это касается как чисел, так и действий). Мы постарались реализовать максимально Удобный интерфейс дробных вычислений, благодаря чему сложные математические калькуляции превратятся для вас в одно удовольствие! 🙂
Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части.
Car3g. ru
01.11.2018 23:51:16
2018-11-01 23:51:16
Источники:
Https://car3g. ru/info/reshenie-drobej-6-klass-kalkuljator/
Сравнить обыкновенные дроби онлайн.
 Сравнение дробей
Сравнение дробейВ повседневной жизни нам часто приходится сравнивать дробные величины. Чаще всего это не вызывает каких-либо трудностей. Действительно, всем понятно, что половина яблока больше, чем четверть. Но когда необходимо записать это в виде математического выражения, это может вызвать затруднения. Применяя следующие математические правила, вы легко можете справиться с этой задачей.
Как сравнивать дроби с одинаковыми знаменателями
Такие дроби сравнивать удобнее всего. В этом случае используйте правило:
Из двух дробей с одинаковыми знаменателями, но разными числителя, большей будет та, числитель которой больше, а меньшей – та, числитель которой меньше.
Например, сравнить дроби 3/8 и 5/8. Знаменатели в этом примере равны, следовательно, применяем это правило. 3
И действительно, если разрезать две пиццы на 8 долей, то 3/8 доли всегда меньше, чем 5/8.
Сравнение дробей с одинаковыми числителями и разными знаменателями
В этом случае сравнивают размеры долей-знаменателей. Следует применять правило:
Следует применять правило:
Если у двух дробей числители равны, то больше та дробь, знаменатель которой меньше.
Например, сравнить дроби 3/4 и 3/8. В этом примере числители равны, значит, используем второе правило. У дроби 3/4 знаменатель меньше, чем у дроби 3/8. Следовательно 3/4>3/8
И действительно, если вы съедите 3 куска пиццы, разделенной на 4 части, то будете более сыты, чем если бы съели 3 куска пиццы, разделенной на 8 частей.
Сравнение дробей с разными числителями и знаменателями
Применяем третье правило:
Сравнение дробей с разными знаменателями нужно привести к сравнению дробей с одинаковыми знаменателями. Для этого необходимо привести дроби к общему знаменателю и использовать первое правило.
Например, необходимо сравнить дроби и . Для определения большей дроби приведем эти две дроби к общему знаменателю:
- Теперь найдём второй дополнительный множитель: 6:3=2. Записываем его над второй дробью:
Математический-Калькулятор-Онлайн v. 1.0
1.0
Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.
Решение:
Как работать с математическим калькулятором
| Клавиша | Обозначение | Пояснение |
|---|---|---|
| 5 | цифры 0-9 | Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/- |
| . | точка (запятая) | Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5 |
| + | знак плюс | Сложение чисел (целые, десятичные дроби) |
| — | знак минус | Вычитание чисел (целые, десятичные дроби) |
| ÷ | знак деления | Деление чисел (целые, десятичные дроби) |
| х | знак умножения | Умножение чисел (целые, десятичные дроби) |
| √ | корень | Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2 При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2 |
| x 2 | возведение в квадрат | Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16 |
| 1 / x | дробь | Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число |
| % | процент | Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%» |
| ( | открытая скобка | Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10 |
| ) | закрытая скобка | Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки Обязательно наличие открытой скобки |
| ± | плюс минус | Меняет знак на противоположный |
| = | равно | Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат. |
| ← | удаление символа | Удаляет последний символ |
| С | сброс | Кнопка сброса. Полностью сбрасывает калькулятор в положение «0» |
Алгоритм работы онлайн-калькулятора на примерах
Сложение.
Сложение целых натуральных чисел { 5 + 7 = 12 }
Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }
Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }
Вычитание.
Вычитание целых натуральных чисел { 7 — 5 = 2 }
Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }
Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }
Умножение.

Произведение целых натуральных чисел { 3 * 7 = 21 }
Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }
Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }
Деление.
Деление целых натуральных чисел { 27 / 3 = 9 }
Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }
Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }
Извлечение корня из числа.
Извлечение корня из целого числа { корень(9) = 3 }
Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }
Извлечение корня из суммы чисел { корень(56 + 25) = 9 }
Извлечение корня из разницы чисел { корень (32 – 7) = 5 }
Возведение числа в квадрат.
Возведение в квадрат целого числа { (3) 2 = 9 }
Возведение в квадрат десятичных дробей { (2,2) 2 = 4,84 }
Перевод в десятичные дроби.
Вычисление процентов от числа
Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }
Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }
18% от числа 140 это { 140 * 0,18 = 25,2 }
Сравнить две дроби – значит определить, какая из дробей больше, какая меньше или установить, что дроби равны.
Сравнение дробей с одинаковыми числителями
При сравнении двух дробей, у которых одинаковые числители, больше будет та дробь, у которой знаменатель меньше.
Например, больше , так как количество взятых долей в обеих дробях одинаковое, но первая дробь содержит более крупные доли, чем вторая:
Сравнение дробей с одинаковыми знаменателями
При сравнении двух дробей, у которых одинаковые знаменатели, больше будет та дробь, у которой числитель больше.
Например, меньше , так как первая дробь содержит меньше взятых долей, чем вторая:
Сравнение дробей с разными знаменателями
Чтобы сравнить дроби, у которых разные числители и знаменатели, нужно привести их к общему знаменателю. После приведения дробей к общему знаменателю, их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.
Например, сравним две дроби: и . Приводим их к общему знаменателю:
Теперь сравниваем их:
так как , значит
Равенство дробей
Две обыкновенные дроби считаются равными, если равны их числители и знаменатели или, если они выражают одну и ту же часть единицы.
Сравнение дроби с натуральным числом
Правильная дробь меньше любого натурального числа.
Чтобы сравнить неправильную дробь с натуральным числом, нужно натуральное число представить в виде неправильной дроби, затем привести дроби к общему знаменателю. После приведения дробей к общему знаменателю, их сравнивают по правилу сравнения дробей с одинаковыми знаменателями.
Пример. Сравним неправильную дробь с числом 5.
1. Переводим натуральное число в неправильную дробь:
2. Приводим дроби к общему знаменателю:
3. Сравниваем:
так как , значит
Онлайн калькулятор сравнения дробей
Данный калькулятор поможет вам сравнить обыкновенные дроби. Просто введите две дроби и нажмите кнопку.
описание
Вам не нужно иметь навыки программирования для написания сложных сценариев или тратить время на классифицирование классифицированных программ — Excel или Word.
Как сравнить фракции
Теперь вы можете использовать готовые решения в повседневной работе.
Алгоритм поможет сразу отсортировать значения в алфавитном и обратном порядке, чтобы строить данные по количеству символов в слове или любому значению символа.
инструкции
Инструмент отлично справляется с добавленной стоимостью в столбце и отдельными словами, заданными запятой или пробелом.
Скопируйте данные, необходимые для сортировки в левом окне, укажите одну из четырех функций и нажмите кнопку Сортировать по .
По умолчанию он доступен Алфавитный порядок (A — R / 0 — 9) .
По выбору Обратный порядок (H — A / 9 — 0) , алгоритм сразу отображает матрицу в обратном направлении.
черты Значения на длину (от малого до большого) и Значения по длине (от более высокой до нижней) работайте по аналогичному принципу, но сортировка основана на количестве символов в строке.
Написать комментарий
Для меня важно знать, как работает служба и как ее можно улучшить. Написать комментарий по почте [email protected] или в нижней форме.
Как работать с калькулятором регулярных фракций?
Калькулятор предназначен для спасения простые фракции и фракции с целыми числами (смешанный ). Функция десятичных дробей запланирована в будущем, но в настоящее время она недоступна.
Чтобы начать работу с частичным калькулятором, вам нужно понять очень простой принцип ввод данных.
Все целые числа вводятся с помощью больших кнопок слева. Все счетчики вводятся с маленькими белыми кнопками, расположенными в верхней правой части цифр. Все символы вводятся нажатием кнопки в правом нижнем углу. Метод ввода данных является своего рода инновационным, поскольку он четко описывает весь числитель и знаменатель, который позволяет проводить расчеты, экономит время и позволяет более эффективно взаимодействовать с использованием.
Скажи это , вы должны добавить квадратный корень из двух пятых и один двадцать два на шестом шаге.
Начните вводить пример из корневой кнопки. Затем нажмите на номер 2 в области измерителя и номер пять в знаменателе. », а затем на номер шесть на главной клавиатуре.
», а затем на номер шесть на главной клавиатуре.
В результате мы получаем готовый пример:
в настоящее время Нажмите эквивалентную кнопку и перейдите стоимость результата .
В приведенном выше примере показан почти весь арсенал дробных калькуляторов. Вы можете сделать то же самое так же размножение, деление и вычитание фракций , так же просто, как алгебраические, с одинаковыми и разными знаменателями, целыми числами и т. д.
Калькулятор также может рассчитывать фракции из фракций, что не часто требуется, но тем не менее очень важно решить ряд неотложных проблем.
Чтобы получить положительное отрицательное число, сначала введите номер и нажмите кнопку «+/-».
После этого число или часть автоматически завертываются в скобки с отрицательным значением или наоборот (в зависимости от начального состояния номера). Чтобы удалить число, счетчик или знаменатель, используйте соответствующую стрелку возврат на одну позицию , который находится в блоке как числителя, так и знаменателя.
Стрелки работают одинаково, а затем удаляют номера или символы на экране компьютера.
Управляйте частичным калькулятором с клавиатуры.
Используйте его Калькулятор веб-фракций не только с компьютерной мышью, но и с клавиатурой.
Логика очень проста:
- Все вводится как обычно, нажимая цифровые клавиши.
- Все счетчики вводятся путем добавления клавиши CTRL (например, CTRL + 1).
- Все знаменатели вводятся путем добавления клавиши ALT (например, ALT + 2).
Меры умножения, деления, добавления и вычитания, а также запуска соответствующих клавиш на клавиатуре, если они есть (обычно расположены с правой стороны, так называемая область Numpad).
Удаление выполняется нажатием клавиши Backspace. Очистка (красная кнопка «C») запускается нажатием клавиши «C». Квадратный корень — нажатием соседней клавиши «V».
Удаление выполняется нажатием клавиши Backspace.
Зачем вам нужен онлайн-калькулятор?
Дробный калькулятор онлайн предназначен для обработки гладкий и смешанный дробей (с целым числом).
Решение фракций часто необходимо для студентов и студентов, а также для инженеров и выпускников. Наш калькулятор позволяет создавать следующие действия с частицами: расщепление фракций, умножение фракций, добавление фракций и вычитание фракций . Калькулятор также может работать с корнями и ставками, а также с отрицательными числами, что делает его несколько раз превышает аналогичные веб-приложения.
Простой калькулятор фракционной дроби онлайн поможет вам решить дела с фракциями, поэтому вам не нужно беспокоиться о том, как противодействовать фракции.
Он становится здесь автоматически , поскольку само приложение вычисляет общий знаменатель и, наконец, показывает конечный результат.
Каковы преимущества этого метода для решения фракций?
калькулятор поддерживает работу с скобками , что позволяет решать фракции, даже в сложных математических случаях. Кампании часто необходимы для скобок алгебраические дроби или отрицательные фракции , над которыми мы должны постоянно избегать всех учащихся средних школ.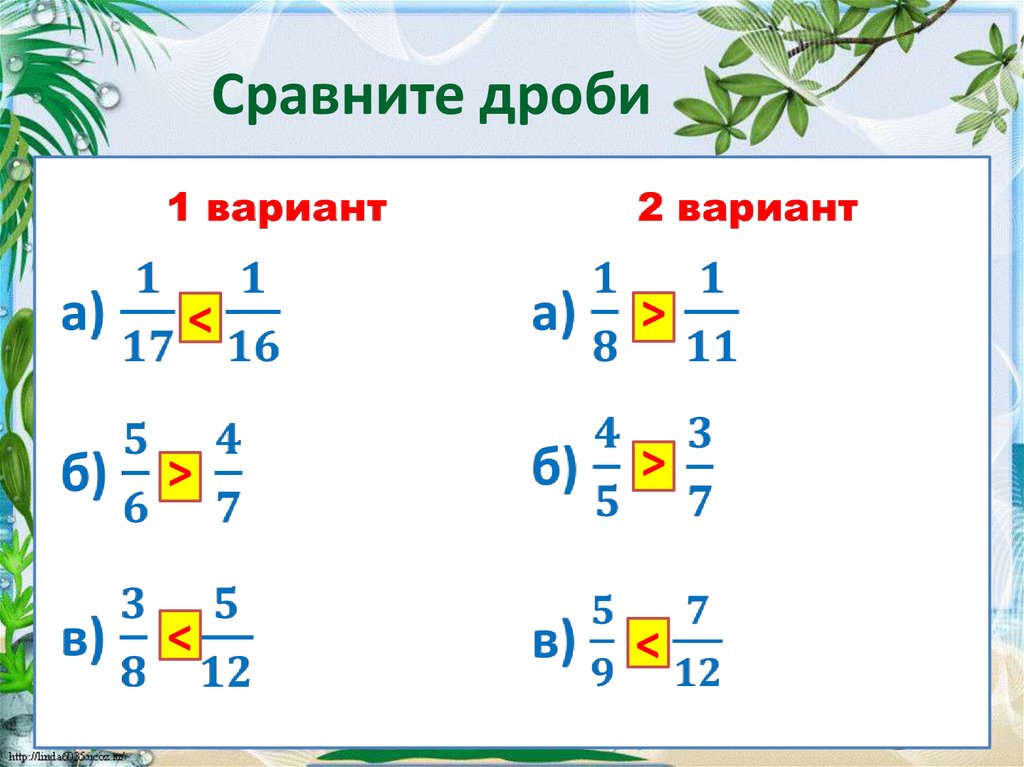
Калькулятор для сравнения фракций
Кроме того, вы можете использовать этот калькулятор сокращение фракций или дробные растворы с разными знаменателями . Кроме того, этот калькулятор, в отличие от многих других бесплатных сервисов, может работать с двумя, тремя, четырьмя и вообще с любым количеством дробей и чисел.
Калькулятор регулярных фракций абсолютно бесплатно и не требует регистрации.
Вы можете использовать его в любое время дня и ночи. Вы можете сделать это с помощью мыши или непосредственно с клавиатуры (это относится к числу и действиям). Мы попытались реализовать максимум удобный интерфейс частичные вычисления, которые делают сложные математические расчеты меняющимися в одно удовольствие!
Сравнение обыкновенных дробей
Удобный и простой онлайн-калькулятор фракций с точным решением вы можете:
- Складывайте, вычитайте, размножайте и размещайте фрагменты в Интернете,
- Получите частичное решение изображения и просто загрузите его.

Результат фракций будет здесь …
Наш калькулятор онлайн-калькуляторов имеет быстрый ввод .
Например, если вы хотите получить частичное решение , просто введите 1/2 + 2/7 в калькулятор и нажмите кнопку «Rescue Faction».
Калькулятор напишет вам детальное решение фракций и вопросы легко скопировать изображение .
Персонажи, используемые для записи в калькуляторе
Вы можете ввести пример решения с клавиатуры или с помощью кнопки.
Характеристики калькулятора веб-фракций
Калькулятор фракций может выполнять операции только с двумя простыми фракциями.
Они могут быть правильными (счетчик меньше знаменателя) или неверны (счетчик больше знаменателя). Числа в числителе и знаменателе не должны быть отрицательными и больше 999.
Наш онлайн-калькулятор принимает решения по фракциям и направляет ответ на правильный формат — уменьшает долю и, при необходимости, назначает всю часть.
Просто используйте свойства минус, чтобы сохранить отрицательные части. При умножении и делении отрицательных дробей знак плюс добавляет плюс. Это означает, что продукт и распределение отрицательных дробей идентичны произведению и распределению того же положительного. Если фракция отрицательная, если вы ее умножаете или делите, удалите минус и добавьте ее в ответ. При добавлении отрицательных фракций результат будет таким же, как добавление одинаковых положительных пропорций.
При умножении и делении отрицательных дробей знак плюс добавляет плюс. Это означает, что продукт и распределение отрицательных дробей идентичны произведению и распределению того же положительного. Если фракция отрицательная, если вы ее умножаете или делите, удалите минус и добавьте ее в ответ. При добавлении отрицательных фракций результат будет таким же, как добавление одинаковых положительных пропорций.
Если вы добавите одну отрицательную долю, то это то же самое, что и вычесть тот же самый положительный результат.
При вычитании отрицательных дробей результат будет таким же, как если бы они были изменены в местах и стали положительными.
Сравнение фракций
Это означает, что минус минус в этом случае дает плюс, и сумма не изменяется от суммы. Те же правила, которые мы используем при подсчете фракций, один из которых отрицателен.
Чтобы решить смешанные фракции (фракции, в которых размещена вся часть), просто заполните всю фракцию во фракцию.
Чтобы сделать это, умножьте всю часть на знаменатель и добавьте его в счетчик.
Если вы хотите сохранить 3 или более акций в Интернете, они должны быть приняты. Во-первых, подсчитайте первые две фракции, затем с полученным ответом определите следующую долю и так далее. Выполните операции на линии 2 фракций, и в конце вы получите правильный ответ.
Зачем принимать решения в калькуляторе
Решения в калькуляторе должны узнать, как сохранить дроби.
Калькулятор не имеет намерения решать фракции для вас.
Это не универсальный резак, это инструмент обучения. Это поможет вам понять решение, так что вы можете легко решить фракции самостоятельно. В дополнение к учебному калькулятору мы также рекомендуем изучить наши материалы: «Как разрешить фракции». Решение фракций. «
Если вы заметили какие-либо ошибки или неудобства при использовании калькулятора, пожалуйста, свяжитесь с нами в комментариях. Насколько это возможно, мы закончим калькулятор!
Онлайн калькулятор. Сравнение фракций.
Студент видит на экране несколько номеров с интересной цветовой схемой. Эти числа расположены в случайном порядке. Ребенок, который знает правильный порядок учетной записи, должен отредактировать от малого до большого. Проблема с упражнением заключается в том, что цифры, показанные на рисунке, не обязательно идут один за другим.
Эти числа расположены в случайном порядке. Ребенок, который знает правильный порядок учетной записи, должен отредактировать от малого до большого. Проблема с упражнением заключается в том, что цифры, показанные на рисунке, не обязательно идут один за другим.
Фактически, промежутки между ними могут быть важными. Но студент, который выполняет эту задачу, должен помнить, какой из чисел больше и меньше. Когда ребенок создает последовательность, он немедленно переходит на следующий уровень (если ответ правильный) или после просмотра правильной опции — если он совершает ошибку.
Это упражнение не только развивает логическое мышление, оно учит вас анализировать и готовить последовательные выводы из образа, но также помнить о правильной последовательности чисел при подсчете.
Порядок увеличения является естественным для многих партий, поэтому ребенок может легко обнаружить его.
Две неравные дроби подлежат дальнейшему сравнению для выяснения, какая дробь больше, а какая дробь меньше. Для сравнения двух дробей существует правило сравнения дробей, которое мы сформулируем ниже, а также разберем примеры применения этого правила при сравнении дробей с одинаковыми и разными знаменателями. В заключение покажем, как сравнить дроби с одинаковыми числителями, не приводя их к общему знаменателю, а также рассмотрим, как сравнить обыкновенную дробь с натуральным числом.
Для сравнения двух дробей существует правило сравнения дробей, которое мы сформулируем ниже, а также разберем примеры применения этого правила при сравнении дробей с одинаковыми и разными знаменателями. В заключение покажем, как сравнить дроби с одинаковыми числителями, не приводя их к общему знаменателю, а также рассмотрим, как сравнить обыкновенную дробь с натуральным числом.
Навигация по странице.
Сравнение дробей с одинаковыми знаменателями
Сравнение дробей с одинаковыми знаменателями по сути является сравнением количества одинаковых долей. К примеру, обыкновенная дробь 3/7 определяет 3 доли 1/7 , а дробь 8/7 соответствует 8 долям 1/7 , поэтому сравнение дробей с одинаковыми знаменателями 3/7 и 8/7 сводится к сравнению чисел 3 и 8 , то есть, к сравнению числителей.
Из этих соображений вытекает правило сравнения дробей с одинаковыми знаменателями : из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше, и меньше та дробь, числитель которой меньше.
Озвученное правило объясняет, как сравнить дроби с одинаковыми знаменателями. Рассмотрим пример применения правила сравнения дробей с одинаковыми знаменателями.
Пример.
Какая дробь больше: 65/126 или 87/126 ?
Решение.
Знаменатели сравниваемых обыкновенных дробей равны, а числитель 87 дроби 87/126 больше числителя 65 дроби 65/126 (при необходимости смотрите сравнение натуральных чисел). Поэтому, согласно правилу сравнения дробей с одинаковыми знаменателями, дробь 87/126 больше дроби 65/126 .
Ответ:
Сравнение дробей с разными знаменателями
Сравнение дробей с разными знаменателями можно свести к сравнению дробей с одинаковыми знаменателями. Для этого лишь нужно сравниваемые обыкновенные дроби привести к общему знаменателю .
Итак, чтобы сравнить две дроби с разными знаменателями, нужно
- привести дроби к общему знаменателю;
- сравнить полученные дроби с одинаковыми знаменателями.
Разберем решение примера.
Пример.
Сравните дробь 5/12 с дробью 9/16 .
Решение.
Сначала приведем данные дроби с разными знаменателями к общему знаменателю (смотрите правило и примеры приведения дробей к общему знаменателю). В качестве общего знаменателя возьмем наименьший общий знаменатель, равный НОК(12, 16)=48 . Тогда дополнительным множителем дроби 5/12 будет число 48:12=4 , а дополнительным множителем дроби 9/16 будет число 48:16=3 . Получаем и .
Сравнив полученные дроби, имеем . Следовательно, дробь 5/12 меньше, чем дробь 9/16 . На этом сравнение дробей с разными знаменателями завершено.
Ответ:
Получим еще один способ сравнения дробей с разными знаменателями, который позволит выполнять сравнение дробей без их приведения к общему знаменателю и всех сложностей, связанных с этим процессом.
Для сравнения дробей a/b
и c/d
, их можно привести к общему знаменателю b·d
, равному произведению знаменателей сравниваемых дробей. В этом случае дополнительными множителями дробей a/b
и c/d
являются числа d
и b
соответственно, а исходные дроби приводятся к дробям и с общим знаменателем b·d
.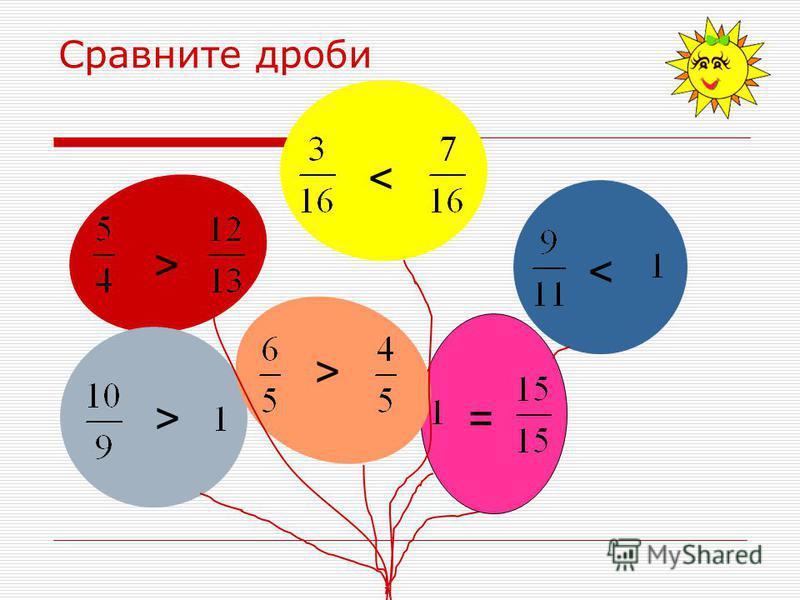 Вспомнив правило сравнения дробей с одинаковыми знаменателями, заключаем, что сравнение исходных дробей a/b
и c/d
свелось к сравнению произведений a·d
и c·b
.
Вспомнив правило сравнения дробей с одинаковыми знаменателями, заключаем, что сравнение исходных дробей a/b
и c/d
свелось к сравнению произведений a·d
и c·b
.
Отсюда вытекает следующее правило сравнения дробей с разными знаменателями : если a·d>b·c , то , а если a·d
Рассмотрим сравнение дробей с разными знаменателями этим способом.
Пример.
Сравните обыкновенные дроби 5/18 и 23/86 .
Решение.
В этом примере a=5 , b=18 , c=23 и d=86 . Вычислим произведения a·d и b·c . Имеем a·d=5·86=430 и b·c=18·23=414 . Так как 430>414 , то дробь 5/18 больше, чем дробь 23/86 .
Ответ:
Сравнение дробей с одинаковыми числителями
Дроби с одинаковыми числителями и разными знаменателями, несомненно, можно сравнивать с помощью правил, разобранных в предыдущем пункте. Однако, результат сравнения таких дробей легко получить, сравнив знаменатели этих дробей.
Существует такое правило сравнения дробей с одинаковыми числителями : из двух дробей с одинаковыми числителями больше та, у которой меньше знаменатель, и меньше та дробь, знаменатель которой больше.
Рассмотрим решение примера.
Пример.
Сравните дроби 54/19 и 54/31 .
Решение.
Так как числители сравниваемых дробей равны, а знаменатель 19 дроби 54/19 меньше знаменателя 31 дроби 54/31 , то 54/19 больше 54/31 .
Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.
Yandex.RTB R-A-339285-1
Сравнение дробей с одинаковыми знаменателями
Когда производится сравнение дробей с одинаковыми знаменателями, мы работаем только с числителем, а значит, сравниваем доли числа. Если имеется дробь 3 7 , то она имеет 3 доли 1 7 , тогда дробь 8 7 имеет 8 таких долей. Иначе говоря, если знаменатель одинаковый, производится сравнение числителей этих дробей, то есть 3 7 и 8 7 сравниваются числа 3 и 8 .
Отсюда следует правило сравнения дробей с одинаковыми знаменателями:из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.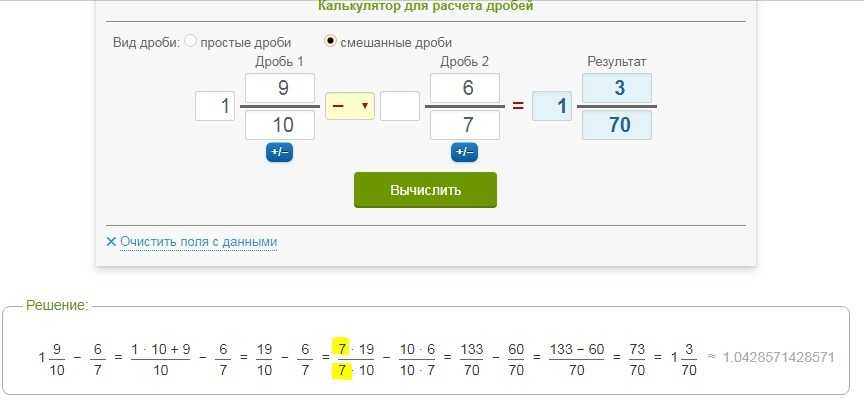
Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.
Пример 1
Произвести сравнение заданных дробей 65 126 и 87 126 .
Решение
Так как знаменатели дробей одинаковые, переходим к числителям. Из чисел 87 и 65 очевидно, что 65 меньше. Исходя из правила сравнения дробей с одинаковыми знаменателями имеем, что 87 126 больше 65 126 .
Ответ: 87 126 > 65 126 .
Сравнение дробей с разными знаменателями
Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.
Если имеются дроби с разными знаменателями, для их сравнения необходимо:
- найти общий знаменатель;
- сравнить дроби.
Рассмотрим данные действия на примере.
Пример 2
Произвести сравнение дробей 5 12 и 9 16 .
Решение
В первую очередь необходимо привести дроби к общему знаменателю. Это делается таким образом: находится НОК, то есть наименьший общий делитель, 12 и 16 . Это число 48 . Необходимо надписать дополнительные множители к первой дроби 5 12 , это число находится из частного 48: 12 = 4 , для второй дроби 9 16 – 48: 16 = 3 . Запишем получившееся таким образом: 5 12 = 5 · 4 12 · 4 = 20 48 и 9 16 = 9 · 3 16 · 3 = 27 48 .
Это делается таким образом: находится НОК, то есть наименьший общий делитель, 12 и 16 . Это число 48 . Необходимо надписать дополнительные множители к первой дроби 5 12 , это число находится из частного 48: 12 = 4 , для второй дроби 9 16 – 48: 16 = 3 . Запишем получившееся таким образом: 5 12 = 5 · 4 12 · 4 = 20 48 и 9 16 = 9 · 3 16 · 3 = 27 48 .
После сравнения дробей получаем, что 20 48
Ответ: 5 12
Имеется еще один способ сравнения дробей с разными знаменателями. Он выполняется без приведения к общему знаменателю. Рассмотрим на примере. Чтобы сравнить дроби a b и c d , приводим к общему знаменателю, тогда b · d , то есть произведение этих знаменателей. Тогда дополнительные множители для дробей будут являться знаменатели соседней дроби. Это запишется так a · d b · d и c · b d · b . Используя правило с одинаковыми знаменателями, имеем, что сравнение дробей свелось к сравнениям произведений a · d и c · b . Отсюда получаем правило сравнения дробей с разными знаменателями:если a · d > b · c , тогда a b > c d , но если a · d
Пример 3
Произвести сравнение дробей 5 18 и 23 86 .
Решение
Данный пример имеет a = 5 , b = 18 , c = 23 и d = 86 . Тогда необходимо вычислить a · d и b · c . Отсюда следует, что a · d = 5 · 86 = 430 и b · c = 18 · 23 = 414 . Но 430 > 414 , тогда заданная дробь 5 18 больше, чем 23 86 .
Ответ: 5 18 > 23 86 .
Сравнение дробей с одинаковыми числителями
Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.
Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.
Рассмотрим на примере.
Пример 4
Произвести сравнение дробей 54 19 и 54 31 .
Решение
Имеем, что числители одинаковые, значит, что дробь, имеющая знаменатель 19 больше дроби, которая имеет знаменатель 31 . Это понятно, исходя из правила.
Ответ: 54 19 > 54 31 .
Иначе можно рассмотреть на примере. Имеется две тарелки, на которых 1 2 пирога, анна другой 1 16 . Если съесть 1 2 пирога, то насытишься быстрей, нежели только 1 16 . Отсюда вывод, что наибольший знаменатель при одинаковых числителях является наименьшим при сравнении дробей.
Сравнение дроби с натуральным числом
Сравнение обыкновенной дроби с натуральным числом идет как и сравнение двух дробей с записью знаменателей в виде 1 . Для детального рассмотрения ниже приведем пример.
Пример 4
Необходимо выполнить сравнение 63 8 и 9 .
Решение
Необходимо представить число 9 в виде дроби 9 1 . Тогда имеем необходимость сравнения дробей 63 8 и 9 1 . Далее следует приведение к общему знаменателю путем нахождения дополнительных множителей. После этого видим, что нужно сравнить дроби с одинаковыми знаменателями 63 8 и 72 8 . Исходя из правила сравнения, 63
Ответ: 63 8
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Сравнение десятичных дробей — как правильно? правила и примеры
Понятие десятичной дроби
Прежде чем мы расскажем, как сравнивать десятичные дроби, вспомним основные определения, виды дробей и разницу между ними.
Дробь — это число в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Ее записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,1
- 2,53
- 9,932
Конечная десятичная дробь — это когда количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если знаменатель обыкновенной дроби равен 10, 100,1000 и т. д.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если знаменатель обыкновенной дроби равен 10, 100,1000 и т.
 д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Правило сравнения десятичных дробей
Чтобы сравнить две десятичные дроби, сначала нужно сравнить их целые части. Если целые части равны, продолжаем искать первый несовпадающий разряд. Большей будет та дробь, у которой соответствующий разряд больше.
Вот так с первой строчки раскрыли тему сравнения десятичных дробей 😜 Но это еще не все — едем дальше.
Алгоритм сравнения десятичных дробей
|
Применим правило на практике. Сравним десятичные дроби: 15,7 и 15,719.
Как решаем:
- Допишем в первой десятичной дроби нужное количество нулей, чтобы уравнять количество знаков справа от запятой: 15,700 и 15,719.
- Сравним десятичные дроби слева направо.
Целую часть с целой частью: 15 = 15. Целые части равны.
Десятые с десятыми: 7 = 7. Десятые также равны.
Сотые с сотыми: 0 < 1. Так как сотые второй десятичной дроби больше, значит и сама дробь больше: 15,700 < 15,719.
Ответ: 15,7 < 15,719.
Еще один способ сравнения десятичных дробей:
Чтобы сравнить две десятичные дроби, нужно уравнять количество знаков после запятой (приписать к одной из них справа нули), затем отбросить запятую, и сравнить два натуральных числа. |
Сравним 3,656 и 3,48.
Как решаем:
- Уравниваем количество знаков справа после запятой: 3,656 и 3,480.
- Отбросим запятые: 3656 и 3480.
- Сравним полученные числа: 3656 > 3480.
Ответ: 3,656 > 3,48.
Запоминаем!
Меньшая десятичная дробь лежит на координатном луче левее большей, а большая — правее меньшей.
Например, 0,3 < 0,4 < 0,5, поэтому точка A (0,3) лежит левее точки B (0,4), а точка C (0,5) лежит правее точки B (0,4).
Калькулятор дробей
Базовый калькулятор
Порядок/сортировка дробей
Используйте целые числа, десятичные дроби, дроби, смешанные числа или проценты
через запятую
В порядке возрастания от наименьшего к наибольшему
По убыванию от наибольшего к наименьшему
Ответ:
Порядок от наименьшего к наибольшему
-1/8 < 0,33 < 3/8 < 75% < 1 5/8
7
7 Рабочий0003Используя заданные входы:
3/8
1 5/8
75%
0. 33
33
-1/8
Переписать эти входные данные:
3/8
1 5/5/5/5/5/5/5/5/5/5/5/5/5/5/ 8
75%
0,33
-1/8
0,375
1,625
0,75
0,33
-0,125
Сортировка этой таблицы по десятичным значениям в соответствии с наименьшим от величайшего:
-110003
. 8
0,33
3/8
75%
1 5/8
-0.125
<
0.33
<
0.375
<
0.75
<
1,625
Следовательно, отсортированные входные данные в порядке от наименьшего к наибольшему:0003
Как этот калькулятор может быть лучше?
Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.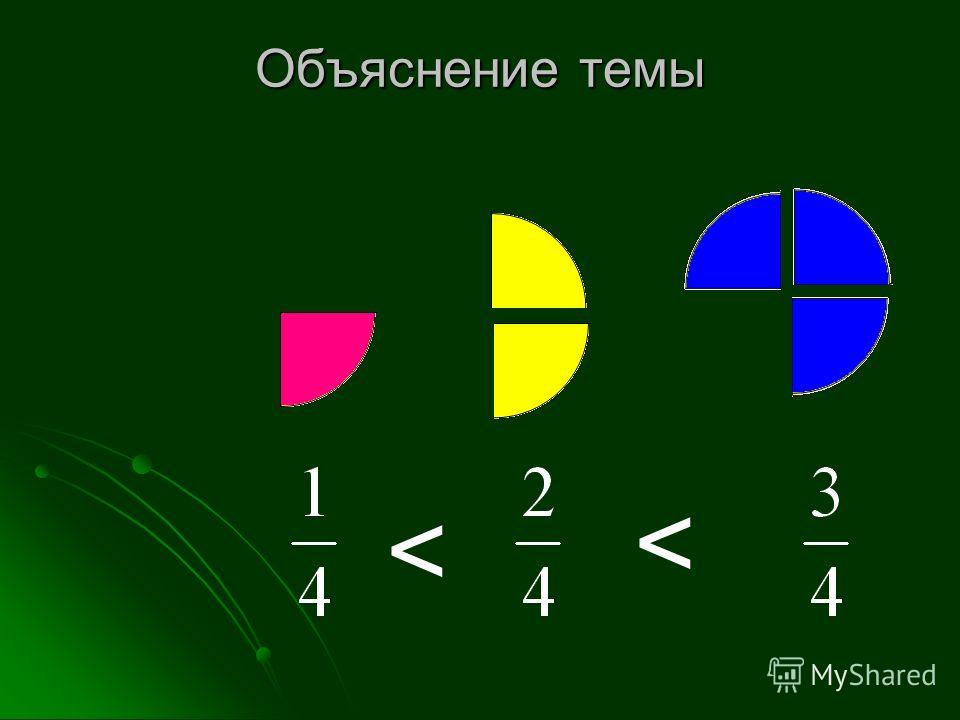
Получить виджет для этого калькулятора
© Calculator Soup
Поделитесь этим калькулятором и страницей
Калькулятор Использование
Сравнивайте и упорядочивайте дроби, целые числа, смешанные числа и десятичные дроби в порядке возрастания или убывания. Расположите дроби от наименьшего к наибольшему или от наибольшего к наименьшему.
Как упорядочивать дроби, целые числа и смешанные числа
Чтобы сравнивать и упорядочивать дроби, мы должны сначала преобразовать все целые числа, смешанные числа (смешанные дроби) и дроби в значения, которые мы можем сравнивать. Мы делаем это, сначала преобразовывая все термины в дроби, находя наименьший общий знаменатель (LCD), а затем переписывая каждый член как эквивалентную дробь с LCD. Затем мы сравниваем числители каждой дроби и располагаем их в правильном порядке от меньшего к большему или от большего к меньшему.
Действия по сравнению и упорядочению дробей, целых и смешанных чисел
- Преобразование целых и смешанных чисел в неправильные дроби
- Найдите наименьший общий знаменатель ЖК всех дробей
- Преобразуйте дроби в эквивалентные дроби, используя ЖК-дисплей
- Упорядочить новые дроби по числителю
- Сопоставьте исходные входные данные с упорядоченными дробями, чтобы увидеть окончательный порядок
Пример использования исходных данных этого калькулятора по умолчанию
Ввод: 2, 3/4, 9/12, 3 5/8, -12/16 в порядке от наименьшего к наибольшему
- Преобразование целых и смешанных чисел в неправильные дроби
• 3/4, 9/12 и -12/16 — правильные дроби, поэтому мы можем использовать их так, как они написаны.
• 2 в виде дроби равно 2/1.
• Преобразуйте 3 5/8 в неправильную дробь. Умножьте целое число 3 на знаменатель 8, чтобы получить 24. Добавьте 24 к числителю 5, чтобы получить 29/8.
Итак, 3 5/8 = 29/8.
• Все входные данные представлены в виде дробей: 2/1, 3/4, 9/12, 29/8, -12/16. - Найдите наименьший общий знаменатель: LCD 1, 4, 8, 12, 16 это 48
- Перепишите входные дроби как эквивалентные дроби, используя ЖК-дисплей
• 2, 3/4, 9/12, 3 5/8, -12/16 становятся:
• 96/48, 36/48, 36/48, 174/48, -36/48 - Упорядочить эти дроби от наименьшего до наибольшего числителя
• -36/48 < 36/48 = 36/48 < 96/48 < 174/48 - Разместите исходные дроби в том же порядке, что и их эквиваленты.

• -12/16 < 3/4 = 9/12 < 2 < 3 5/8
Связанные калькуляторы
Чтобы определить, какая дробь больше, а какая меньше, см. Калькулятор сравнения дробей.
Чтобы складывать, вычитать, умножать и делить дроби, см. Калькулятор дробей.
Сложение, вычитание, умножение и деление смешанных чисел и дробей см. Калькулятор смешанных чисел.
Чтобы упростить дробь до минимума, см. Калькулятор упрощенных дробей.
Подписаться на CalculatorSoup:
Калькулятор сравнения дробей — Solumaths
Сравнение дробей, интерактивный расчет
Сводка :
Калькулятор позволяет сравнивать две дроби с указанием шагов вычислений.
compare_fractions онлайн
Описание :
Функция compare_fractions позволяет сравнивать дроби с указанием шагов для достижения результата.
Для сравнения дробей между собой калькулятор использует следующие методы и правила.
Дроби с одинаковыми числителями
К сравнивают две дроби с одинаковыми числителями, сравнивая знаменатели, наибольшая дробь та, у которой знаменатель наименьший.
Чтобы сравнить две дроби с одним и тем же числителем, например: «4/5» и «4/9», введите сравните_фракции (4/5; 4/9) .
Дроби сравниваем с одинаковым знаменателем
К сравниваем две дроби с одинаковым знаменателем, сравниваем числители, наибольшая дробь та, у которой самый большой числитель.
Чтобы сравнить две дроби с одинаковым знаменателем, например: «3/4» и «7/4», введите
сравните_фракции (3/4; 7/4)
.
Сравнение дробей
К сравнение дробей , когда числители разные и знаменатели тоже разные, калькулятор приводит дроби к одному и тому же знаменателю, а затем сравнивает числители.
Чтобы сравнить 2 дроби с разными числителями и разными знаменателями, например, следующие: «19/11» и «13/7», введите compare_fractions(19/11;13/7) .
Викторины и игры на сравнение дробей
Сайт также предлагает викторины и игры на дроби и их сравнения , которые позволяют практиковать дробный счет.
Синтаксис:
сравнение_фракций (доля1; дробь2), где дробь1 и дробь 2 — сравниваемые дроби, результат возвращается в виде равенства или неравенства.
Примеры:
- compare_fractions(`4/5;3/7`) возвращает: `4/5>3/7`
- compare_fractions(`0,5;4/7`) возвращает: `0,5
Расчет онлайн с помощью compare_fractions (сравните две дроби)
См. также
также
Список связанных калькуляторов:
- Расчет биномиальных коэффициентов : binomial_coefficient.
 Калькулятор биномиального коэффициента, который позволяет вычислить биномиальный коэффициент из двух целых чисел.
Калькулятор биномиального коэффициента, который позволяет вычислить биномиальный коэффициент из двух целых чисел. - Сравните две дроби : compare_fractions. Калькулятор позволяет сравнивать две дроби, указывая шаги вычислений.
- Калькулятор разложения на частичные дроби: partial_fraction_decomposition. Калькулятор позволяет разбить рациональную дробь на простые элементы.
- Калькулятор простой факторизации: prime_factorization. Функция prime_factorization используется для онлайн-расчета разложения целого числа на простые множители.
- Знаменатель дроби : знаменатель. Функция знаменателя позволяет вычислить знаменатель дроби.
- Калькулятор дробей: дробь. Калькулятор дробей, который позволяет шаг за шагом выполнять все виды расчетов дробей.
- Числитель дроби: числитель. Функция числителя позволяет вычислить числитель дроби.
- Расчет НОД онлайн: НОД. Калькулятор НОД, который использует алгоритм Евклида для определения шагов вычисления НОД.

- Калькулятор процентов: проценты. Этот процентный калькулятор преобразует дроби или числа в проценты.
- Наименьшее общее кратное: lcm. Калькулятор LCM для расчета наименьшего общего кратного (НОК).
Список связанных упражнений:
- Сравнить две дроби : Цель этого упражнения — сравнить две дроби, выбрав соответствующий оператор сравнения из предложенного списка.
- Сравнение дробей : Цель этого решенного упражнения состоит в том, чтобы сравнить две дроби, используя правильный оператор.
Напоминания о курсах, калькуляторы, упражнения и игры: Дроби
Калькулятор сравнения дробей. В отличие от объяснения знаменателей
Создано Ханной Памула, докторантом
Отзыв от Dominik Czernia, PhD и Jack Bowater
Последнее обновление: 06 апреля 2022 г.
- Как сравнивать дроби?
- Сравнение дробей с одинаковым знаменателем
- Сравнение дробей с одинаковым числителем
- Сравнение дробей с разными знаменателями
- Как сравнивать дроби — смешанные дроби и другие случаи
- Пример: как пользоваться калькулятором сравнения дробей?
Используйте этот калькулятор сравнения дробей, когда вам трудно сравнивать дроби — будь то простые дроби, неправильные дроби, смешанные числа или даже целые числа . У ваших дробей не обязательно должен быть один и тот же знаменатель; инструмент отлично работает даже при сравнении дробей с разными знаменателями . Хотите узнать правила сравнения дробей? Не смотрите дальше! 🔍
Мы подробно объясним, как сравнивать дроби с работает тот же знаменатель , как и при сравнении дробей с тот же числитель .
Как сравнивать дроби?
Для сравнения дробей можно использовать два популярных метода:
- Десятичный метод — при котором каждую дробь преобразуют в десятичную.
 Это легко, когда у вас есть простой карманный калькулятор🖩 или наш преобразователь дроби в десятичную, поэтому мы не будем здесь вдаваться в подробности; и
Это легко, когда у вас есть простой карманный калькулятор🖩 или наш преобразователь дроби в десятичную, поэтому мы не будем здесь вдаваться в подробности; и - Метод с тем же знаменателем — который мы подробно опишем ниже, так как велика вероятность, что вы ищете именно этот метод 😉
Итак, в методе одного и того же знаменателя может встречаться несколько случаев:
- Сравнение дробей с одинаковым знаменателем — это, конечно, самый простой случай 😀
- Сравнение дробей с одинаковым числителем — тоже не хитрая задача 🙂
- Сравнение дробей с разными знаменателями — может быть наиболее проблематичным, так как вам нужно найти общий знаменатель или наименьший общий знаменатель. Тем не менее, это все еще кусок пирога, поверьте нам! 🍰
В следующих параграфах мы подробно описываем, как сравнивать дроби в каждом из этих случаев. Прокрутите вниз и найдите примеры из реальной жизни — битва за каждый кусочек пиццы.
Сравнение дробей с одинаковым знаменателем
Сравнение дробей с одинаковым знаменателем — самый простой вариант. Если две ваши дроби имеют одинаковый знаменатель (нижнее число), , то большая дробь будет той, у которой больше числитель (верхнее число). Так, например:
4 / 5 > 3 / 5 , так как 4 больше 3; и
3 / 7 < 6 / 7 , потому что 3 меньше 6.
. Подумайте об этом. , каждый срез имеет одинаковый размер. У кого больше ломтиков, у Майкла 3 ломтика или у Эмили 2 ломтика? Предположим, что мы разрезаем каждую пиццу на 8 равных частей: ³/₈ > ²/₈ .
Конечно, это Майкл! Три кусочка 🍕🍕🍕 определенно больше, чем два кусочка 🍕🍕, верно?
Сравнение дробей с одинаковыми числителями
Итак, что произойдет, если две дроби имеют одинаковый числитель? Тогда большая дробь — это дробь с меньшим знаменателем , например.
4 / 5 > 4 / 7
3 / 11 < 3 / 8
Возвращаясь к аналогии с пиццей:
Итак, она сказала всем, что в следующий раз все берут одинаковое количество ломтиков, но ее хитрый план состоял в том, что ломтики не равны по размеру😈. Одну пиццу она разрезала на 8 ломтиков и дала Майклу 3 ломтика, а другую пиццу она разрезала на 4 ломтика и взяла 3 ломтика себе. У кого больше пиццы? Ответ: 3 / 8 < 3 / 4 |
.
Сравнение дробей с разными знаменателями
3 / 8 и 1 / 6 ? Есть два способа сделать знаменатель одинаковым:- Метод общего знаменателя , при котором вы умножаете верхнюю и нижнюю часть дроби на знаменатель другой дроби:
3 / 8?1 / 6
3 / 8 ⋅ 6 / 6?1 / 6 ⋅ 8 / 8
18 / 48>8 / 48
- Метод наименьшего общего знаменателя (LCD) , где вы находите LCM знаменателей, а затем эквивалентные дроби обеих дробей с LCM в качестве знаменателя
3 / 8?1 / 6
НОК(8,6) = 24
9 / 24>4 / 24
Методы очень похожи, и вы можете использовать любой из них.
Вернемся к нашей истории с пиццей:
Майкл немного обиделся на нечестную игру Эмили. В следующий раз, когда они встретились, он прямо спросил Эмили, что ей больше нравится — 3 ломтика из 8 или 1 ломтик из 3? Путем быстрых расчетов в голове она выбрала первый вариант. Был ли это хороший выбор? 3 / 8 ? 1 / 3 9 / 24 > 8 / 24 |
Yes, it was! Разница в этом случае не такая большая, но чем больше пиццы, тем лучше! 😋
Как сравнивать дроби — смешанные дроби и другие случаи
В предыдущих параграфах мы описали случаи, когда вы сравниваете простые дроби.
Но что произойдет, если вы захотите сравнить, например. смешанные дроби или неправильные дроби? Наверняка вы можете воспользоваться нашим замечательным калькулятором сравнения дробей , он справится с такими задачами 😎 Но не волнуйтесь, мы объясним и здесь:
- Сравнение смешанных чисел
При сравнении двух смешанных дробей иногда сразу знаешь, какое смешанное число больше — если целая часть больше, то и смешанное число будет больше:
2 1 / 3 > 1 3 / 4
3 2 / 7 ? 3 1 / 4
3 8 / 28 > 3 7 / 28
- Comparing with improper fractions
Сравнение двух неправильных дробей работает точно так же, как если бы они были простыми дробями!
Если вы хотите сравнить смешанные дроби с неправильными — сделайте дроби однотипными:
- Преобразуйте неправильную дробь в смешанное число; или
- Преобразовать смешанное число в неправильную дробь.

Итак, универсальное решение:
- Найдите общий знаменатель ваших дробей. Если одна из дробей является смешанным числом, преобразуйте ее в неправильную дробь.
- Преобразуйте дроби так, чтобы они имели общий знаменатель.
- Сравните верхние числа — дробь с большим числителем является большей дробью 🎉
Пример: как пользоваться калькулятором сравнения дробей?
Мы почти уверены, что вы молодой, умный человек, и вы узнали, как работает калькулятор сравнения дробей, просто играя с ним. Но чтобы все было предельно ясно💎, мы покажем вам, как использовать наш инструмент шаг за шагом.
Возьмем более сложный случай — сравним дроби с разными знаменателями. Кроме того, одна дробь является смешанным числом, а другая — неправильной дробью: 1 5 / 6 и 20 / 11 .
- Выберите форму дроби .
 Поскольку одна из наших дробей является смешанным числом, выберите этот вариант.
Поскольку одна из наших дробей является смешанным числом, выберите этот вариант. - Введите первую дробь . В нашем примере целое число равно 1, числитель равен 5, а знаменатель равен 6.
- Введите вторую дробь . Мы оставим поле « целое число » пустым, поместим 20 в числителе и 11 в знаменателе.
- Тадаа!✨ Калькулятор сравнения дробей показывает результат :
1 5 / 6 больше 20 / 11 !
Более того, это показывает причину этого результата :
- Преобразует смешанное число в неправильную дробь: 1 5 / 6 = 11 / 6 ; и
- Отображает эквивалентные дроби с одинаковым знаменателем: 121 / 66 > 120 / 66
Разве это не удивительно? 😍
Hanna Pamuła, PhD candidate
Fraction form
1 st fraction
Whole number (W₁)
Numerator (n₁)
Denominator (d₁)
2 ND Фракция
Целое число (W₂)
Числование (n₂)
Знаменатель (D₂)
Результат
Проверьте 17 аналогичных фракций 🍕
Добавление фракций. Калькулятор сравнения дробей
Калькулятор сравнения дробей
Файл cookie
Уведомление
| 0 | ||||
| АС | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Калькулятор сравнения дробей поможет вам сравнить положительные и отрицательные дроби и даст вам подробное решение.
Фракция 1 Фракция 2 Пример сравнения дробей| Сравним дроби 4 | 3 |
| 7 |
| и 5 | 12 |
| 16 |
1.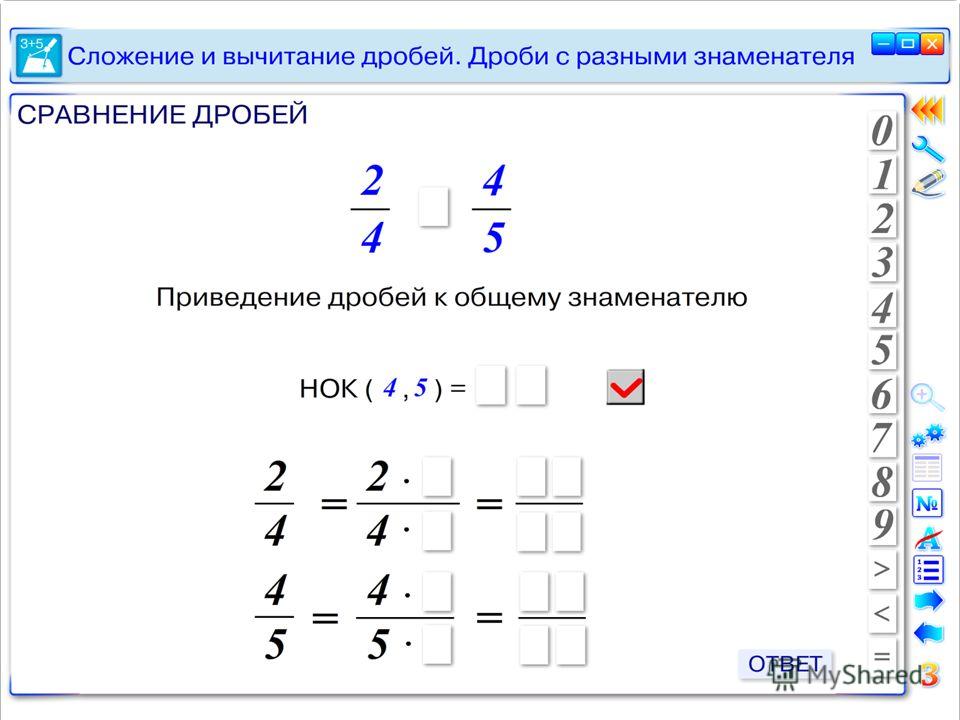 ) Преобразовать смешанную дробь ) Преобразовать смешанную дробь | |
| на неправильный: | |
| 4 | 3 | = |
| 7 |
| (4 · 7) + 3 | = | |
| 7 |
| 2.) Преобразовать смешанную дробь | |
| 5 | 12 |
| 16 |
| на неправильный: | |
| 5 | 12 | = |
| 16 |
| (5 · 16) + 12 | = | |
| 16 |
3. ) Сделаем знаменатели дробей одинаковыми, для этого умножим числитель первой дроби на знаменатель второй дроби, а числитель второй дроби на знаменатель первой. Новый общий знаменатель будет произведением знаменателей первой и второй дробей. ) Сделаем знаменатели дробей одинаковыми, для этого умножим числитель первой дроби на знаменатель второй дроби, а числитель второй дроби на знаменатель первой. Новый общий знаменатель будет произведением знаменателей первой и второй дробей. | |
| = | 31 ⋅ 16 |
| 7 ⋅ 16 |
| = | 496 |
| 112 |
| = | 92 ⋅ 7 |
| 7 ⋅ 16 |
| = | 644 |
| 112 |
4. ) Из двух дробей с одинаковым знаменателем больше та, у которой больше числитель. ) Из двух дробей с одинаковым знаменателем больше та, у которой больше числитель. |
| 496 | |
| 112 |
| < | 644 |
| 112 |
| < 5 | 12 |
| 16 |
| You may also find the following calculators helpful |
| Fraction Calculators |
| Simplifying Fractions Calculator |
| Improper to Mixed Fraction Calculator |
| Mixed Fraction to Improper Calculator |
| Fractions Калькулятор с пошаговым решением |
Возведение дроби в степень. Онлайн калькулятор. Онлайн калькулятор. |
| Decimal to Fraction Calculator |
| Fraction to Decimal Calculator |
| Compare Fractions Calculator |
| Common Denominator Calculator |
| Trigonometers Calculators |
| Sine Calculator |
| Cosine Calculator |
| Калькулятор тангенса |
| Калькулятор котангенса |
| Secant Calculator |
| Cosecant Calculator |
| Arcsine Calculator |
| Arccosine Calculator |
| Arctangent Calculator |
| Arccotangent Calculator |
| Arcsecant Calculator |
| Arccosecant Calculator |
| Калькуляторы систем счисления |
| Калькулятор римских чисел |
| Римские цифры От 1 до 3999 |
| Калькулятор систем счисления |
Двоичный калькулятор.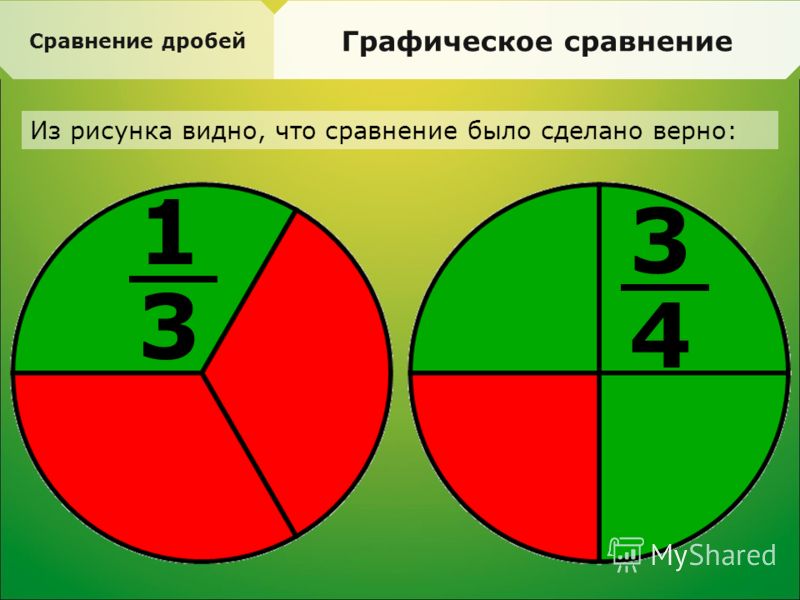 Сложение, вычитание, умножение и деление двоичных чисел. Сложение, вычитание, умножение и деление двоичных чисел. |
| Калькуляторы (теория чисел) |
| Кальденс |
| Кальденс.0488 |
| Калькулятор Gcd и Lcm с использованием алгоритма Евклида |
| Калькулятор Gcd и Lcm для любого количества чисел |
| Разбивка числа на его разрядное значение | Разделить на avido. Онлайн-калькулятор с шагами |
| Калькулятор процентов с шагами |
| Калькулятор преобразования научной записи в десятичную |
| Конвертер научной записи |
| Factorial Calculator With Steps |
| Logarithm Calculator |
| Quadratic Equations Calculator With Steps |
| Remainder Calculator |
| Root Calculator |
| Decimal Period Calculator |
| Big Number Calculator |
| Калькулятор округления чисел |
| Калькулятор свойств корней и показателей |
| Complex Number Calculator |
| Area Calculators |
| Area of a Square Calculator |
| Area of a Rectangle Calculator |
| Combinatorics Calculators |
| Permutations of N Elements Calculator |
| Комбинации N элементов с помощью M-калькулятора |
| Перестановки N элементов с помощью M-калькулятора |
| Математические тренажеры |
| Addition Math Trainer |
| Subtraction Math Trainer |
| Multiplication Math Trainer |
| Division Math Trainer |
| Multiplication Table Math Trainer |
| Online Preschool Counting Trainer |
| Online Preschool Тренажер внимательности |
Онлайн-тренажер по математике сложения, вычитания, умножения. Найдите правильный ответ. Найдите правильный ответ. |
| Online Numeric Expression Trainer |
| Linear Algebra and Analytical Geometers Calculators |
| Matrix Addition and Subtraction Calculator |
| Matrix Multiplication Calculator |
| Matrix Transpose Calculator |
| Matrix Determinant Calculator |
| Калькулятор обратной матрицы |
| Длина сегмента линии. Онлайн-калькулятор расстояния между точками. |
| Калькулятор векторных координат по двум точкам |
| Калькулятор векторного модуля (длины) |
| Калькулятор векторного сложения и вычитания |
| Калькулятор векторного произведения точек. Используя длину векторов и косинус угла между векторами. |
| Калькулятор векторного скалярного произведения. Используя векторные координаты. |
Калькулятор векторного произведения. Используя векторные координаты. Используя векторные координаты. |
| Vector Triple Product Calculator |
| Vector Multiplication by Number Calculator |
| Angle Between Vectors Calculator |
| Vector Collinearity Check Calculator |
| Vector Coplanarity Calculator |
| Converters |
| Length Преобразователь |
| Преобразователь скорости |
| Преобразователь ускорения |
| Physics Calculators |
Mechanics |
| Speed Time Distance Calculator |
| Acceleration Speed Distance Calculator |
| Displacement Time Calculator |
| Time Calculator |
| Newton’s Second Law Calculator |
| Калькулятор гравитационной силы |
| Калькулятор импульса |
| Калькулятор импульса |
| Object Weight Calculator |
Optics |
| Light Reflection and Refraction Calculator |
Electricity and Magnetism |
| Ohm’s Law Calculator |
| Coulomb’s Law Calculator |
| Калькулятор напряженности электрического поля |
| Калькулятор точечного электрического заряда Q |
| Force Acting on Charge Calculator |
| Distance From Charge Calculator |
| Potential Charge Energy Calculator |
| Electric Field Potential Calculator |
| Conductor and Sphere Capacitance Calculator |
Capacitors |
| Калькулятор емкости пластинчатых, цилиндрических и сферических конденсаторов |
| Electric Field Strength in Parallel Plate, Cylindrical and Spherical Capacitors Calculator |
| Voltage (Potential Difference) of Parallel Plate, Cylindrical and Spherical Capacitors Calculator |
| Distance Between Plates in Parallel Plate Capacitor Calculator |
| Plate Калькулятор площади в конденсаторе с параллельными пластинами |
| Калькулятор запасенной энергии в заряженном конденсаторе |
| Калькулятор энергии, накопленной в параллельных пластинчатых, цилиндрических и сферических заряженных конденсаторах |
| Калькулятор объемной плотности энергии параллельных пластинчатых, цилиндрических и сферических конденсаторов |
| Астрономические калькуляторы |
| Вес объекта на других планетах |
| Гравитационное ускорение на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор случайных чисел |
| Генератор паролей |
Калькулятор эквивалентных дробей с шагами
Калькулятор эквивалентных дробей
| Числитель: |
| Знаменатель: |
| Эквивалентные дроби для 1/3: |
Важно: 13 выглядит как дробь, но на самом деле это неправильная дробь. Существует бесконечное количество эквивалентных дробей до 13. Чтобы найти эквивалентную дробь до 13, или любой другой дроби, нужно просто умножить (или разделить, если дробь еще не уменьшена) оба числителя а знаменатель данной дроби на любое ненулевое натуральное число. Например: Умножив исходную дробь на 2, получим: 1 × 2 3 × 2 = 26 Вот полный список эквивалентных дробей до 13.13, 26, 39, 412, 515, 618, 721, 824, 927, 1030, 1133, 1236, 1339, 1442, 1545, 1648, 18541, 1741 , 1957, 2060… Подробнее о том, как найти эквивалентные дроби для 1/3 или любой другой дроби, читайте ниже на этой странице. Более простой список для копирования и вставки: 1/3, 2/6, 3/9, 4/12, 5/15, 6/18, 7/21, 8/24, 27 сентября, 10/30, 11/33, 12/36, 13/39, 14/42, 15/45, 16/48, 17/51, 18/54, 19/57, 20/60… |
Этот калькулятор эквивалентных дробей шаг за шагом покажет вам эквивалентные дроби для любой введенной вами дроби.
См. ниже пошаговое решение, как найти эквивалентные дроби.
Как найти эквивалентные дроби?
Две дроби эквивалентны, если они обе равны при записи в наименьшем выражении. Дробь 26 равна 13 при сокращении до наименьших членов. Чтобы найти равнозначные дроби, нужно просто умножить числитель и знаменатель той сокращенной дроби (13) на одно и то же натуральное число, т. е. умножить на 2, 3, 4, 5, 6…
Важно: 13 выглядит как дробь, но на самом деле это неправильная дробь.
- 26 эквивалентно 13, потому что 1 × 23 × 2 = 26
- 39 эквивалентно 13, потому что 1 × 33 × 3 = 39 = 412
- 515 эквивалентно 13, потому что 1 × 53 × 5 = 515
- и т. д. …
получить одно и то же значение, показывающее, что они эквивалентны. Если данная дробь не приводится к наименьшему члену, вы можете найти другие эквивалентные дроби, разделив числитель и знаменатель на одно и то же число.
Что такое эквивалентная дробь? Как узнать, равны ли две дроби?
Нахождение эквивалентных дробей может быть легким, если вы используете это правило:
Определение эквивалентных дробей: две дроби ab и cd эквивалентны, только если произведение (умножение) числителя (a) первой дроби и знаменателя (d ) другой дроби равно произведению знаменателя (b) первой дроби на числитель (c) другой дроби.
Другими словами, если вы перемножите (ab и cd) равенство останется, т. е. a.d = b.c. Итак, вот несколько примеров:
- 26 эквивалентно 13, потому что 2 × 3 = 6 × 1 = 6
- 39 эквивалентно 13, потому что 3 × 3 = 9 × 1 = 9
- 410222 эквивалентно 13, потому что 4 × 3 = 12 × 1 = 12
Таблица/таблица эквивалентных дробей
Эта таблица/таблица эквивалентных дробей содержит общепринятые практические дроби. Вы можете легко конвертировать дроби в десятичные, а также из долей дюймов в миллиметры.
| 1 / 64 | 1 / 32 | 1 / 16 | 1 / 8 | 1 / 4 | 1 / 2 | Десятичный | мм | |
|---|---|---|---|---|---|---|---|---|
| 1 / 64 | 0,015625 | 0,397 | ||||||
| 2 / 64 | 1 / 32 | 0,03125 | 0,794 | |||||
| 3 / 64 | 0,046875 | 1,191 | ||||||
| 4 / 64 | 2 / 32 | 1 / 16 | 0,0625 | 1,588 | ||||
| 5 / 64 | 0,078125 | 1,984 | ||||||
| 6 / 64 | 3 / 32 | 0,09375 | 2,381 | |||||
| 7 / 64 | 0,109375 | 2,778 | ||||||
| 8 / 64 | 4 / 32 | 2 / 16 | 1 / 8 | 0,125 | 3,175 | |||
| 9 / 64 | 0,140625 | 3,572 | ||||||
| 10 / 64 | 5 / 32 | 0,15625 | 3,969 | |||||
| 11 / 64 | 0,171875 | 4,366 | ||||||
| 12 / 64 | 6 / 32 | 3 / 16 | 0,1875 | 4,763 | ||||
| 13 / 64 | 0,203125 | 5,159 | ||||||
| 14 / 64 | 7 / 32 | 0,21875 | 5,556 | |||||
| 15 / 64 | 0,234375 | 5,953 | ||||||
| 16 / 64 | 8 / 32 | 4 / 16 | 2 / 8 | 1 / 4 | 0,25 | 6,35 | ||
| 17 / 64 | 0,265625 | 6,747 | ||||||
| 18 / 64 | 9 / 32 | 0,28125 | 7,144 | |||||
| 19 / 64 | 0,296875 | 7,541 | ||||||
| 20 / 64 | 10 / 32 | 5 / 16 | 0,3125 | 7,938 | ||||
| 21 / 64 | 0,328125 | 8,334 | ||||||
| 22 / 64 | 11 / 32 | 0,34375 | 8. 731 731 | |||||
| 23 / 64 | 0,359375 | 9,128 | ||||||
| 24 / 64 | 12 / 32 | 6 / 16 | 3 / 8 | 0,375 | 9,525 | |||
| 25 / 64 | 0,3 | 9,922 | ||||||
| 26 / 64 | 13 / 32 | 0,40625 | 10.319 | |||||
| 27 / 64 | 0,421875 | 10,716 | ||||||
| 28 / 64 | 14 / 32 | 7 / 16 | 0,4375 | 11. 113 113 | ||||
| 29 / 64 | 0,453125 | 11.509 | ||||||
| 30 / 64 | 15 / 32 | 0,46875 | 11.906 | |||||
| 31 / 64 | 0,484375 | 12.303 | ||||||
| 32 / 64 | 16 / 32 | 8 / 16 | 4 / 8 | 2 / 4 | 1 / 2 | 0,5 | 12,7 | |
| 33 / 64 | 0,515625 | 13.097 | ||||||
| 34 / 64 | 17 / 32 | 0,53125 | 13. 494 494 | |||||
| 35 / 64 | 0,546875 | 13.891 | ||||||
| 36 / 64 | 18 / 32 | 9 / 16 | 0,5625 | 14,288 | ||||
| 37 / 64 | 0,578125 | 14,684 | ||||||
| 38 / 64 | 19 / 32 | 0,59375 | 15.081 | |||||
| 39 / 64 | 0,609375 | 15.478 | ||||||
| 40 / 64 | 20 / 32 | 10 / 16 | 5 / 8 | 0,625 | 15. 875 875 | |||
| 41 / 64 | 0,640625 | 16.272 | ||||||
| 42 / 64 | 21 / 32 | 0,65625 | 16,669 | |||||
| 43 / 64 | 0,671875 | 17.066 | ||||||
| 44 / 64 | 22 / 32 | 11 / 16 | 0,6875 | 17.463 | ||||
| 45 / 64 | 0,703125 | 17.859 | ||||||
| 46 / 64 | 23 / 32 | 0,71875 | 18.256 | |||||
| 47 / 64 | 0,734375 | 18. 653 653 | ||||||
| 48 / 64 | 24 / 32 | 12 / 16 | 6 / 8 | 3 / 4 | 0,75 | 19.05 | ||
| 49 / 64 | 0,765625 | 19.447 | ||||||
| 50 / 64 | 25 / 32 | 0,78125 | 19.844 | |||||
| 51 / 64 | 0,796875 | 20.241 | ||||||
| 52 / 64 | 26 / 32 | 13 / 16 | 0,8125 | 20,638 | ||||
| 53 / 64 | 0,828125 | 21. 034 034 | ||||||
| 54 / 64 | 27 / 32 | 0,84375 | 21.431 | |||||
| 55 / 64 | 0,859375 | 21.828 | ||||||
| 56 / 64 | 28 / 32 | 14 / 16 | 7 / 8 | 0,875 | 22,225 | |||
| 57 / 64 | 0,8 | 22,622 | ||||||
| 58 / 64 | 29 / 32 | 0, | 23.019 | |||||
| 59 / 64 | 0, | 5 | 23.416 | |||||
| 60 / 64 | 30 / 32 | 15 / 16 | 0,9375 | 23. 813 813 | ||||
| 61 / 64 | 0,953125 | 24.209 | ||||||
| 62 / 64 | 31 / 32 | 0,96875 | 24.606 | |||||
| 63 / 64 | 0,984375 | 25.003 | ||||||
| 64 / 64 | 32 / 32 | 16 / 16 | 8 / 8 | 4 / 4 | 2 / 2 | 1 | 25,4 |
Артикул:
- [1] Как найти эквивалентные дроби
Equivalent Fractions - Samples
- Equivalent fractions of 4/95
- Equivalent fractions of 1/61
- Equivalent fractions of 43/29
- Equivalent fractions of 7/2
- Equivalent fractions of 28/14
- Эквивалентные дроби числа 38/35
- Эквивалентные дроби числа 13/76
- Эквивалентные дроби числа 1/11
- Эквивалентные дроби числа 43/87
- эквивалентные фракции 12/33
- эквивалентные фракции 18/60
- эквивалентные фракции 35/28 эквивалентные фракции 26/34
- из 2/93 787 из 2 36/34
- из 0147.

Отказ от ответственности
Несмотря на то, что мы прилагаем все усилия для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы не несут ответственности за какие-либо ошибки или упущения. Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.
Сравнение дробей
Иногда нам нужно сравнить две дроби, чтобы определить, какая из них больше или меньше.
Существует два основных способа сравнения дробей: с использованием десятичных знаков или с использованием того же знаменателя .
Десятичный метод сравнения дробей
Преобразуйте каждую дробь в десятичные, а затем сравните десятичные дроби.
Пример: что больше:
3 8 или же 5 12 ?Преобразуйте каждую дробь в десятичную.
Мы можем использовать калькулятор (3÷8 и 5÷12) или метод преобразования дробей в десятичные.
Во всяком случае, вот ответы, которые я получаю:
3 8 = 0,375 и 5 12 = 0,4166...
Итак, 5 12 больше.
Метод того же знаменателя
Знаменатель — это нижнее число в дроби.
Показывает, на сколько равных частей делится предмет
Когда две дроби имеют одинаковый знаменатель , их легко сравнивать:
Пример:
4 9 меньше чем 5 9 (потому что 4 меньше 5)| меньше | ||
| 4 9 | 5 9 |
Но когда знаменатели не совпадают, нам нужно сделать их одинаковыми (используя эквивалентные дроби).
Пример: Что больше:
3 8 или же 5 12 ?Посмотрите на это:
- Когда мы умножаем 8 × 3, мы получаем 24,
- и когда мы умножаем 12 × 2 мы также получаем 24,
давайте попробуем так ( важно: то, что мы делаем внизу, мы должны делать и наверху ):
| и |
| ||||||||||||||||||||||||||||||||||
Теперь мы можем видеть, что 9 24 меньше, чем 10 24 (потому что 9 меньше 10).
так 5 12 больше дробная часть.
| меньше | ||
| 3 8 | 5 12 |
Уравнивание знаменателей
Есть два основных способа сделать знаменатель одинаковым:
- Метод общего знаменателя или
- Метод наименьшего общего знаменателя
Они оба работают, используйте тот, который вам больше нравится!
Пример: Что больше:
5 6 или же 11 15 ?Используя метод общего знаменателя, мы умножаем каждую дробь на знаменатель другой:
| и |
| ||||||||||||||||||||||||||||||||||
Мы видим, что 75 90 это большая часть (потому что 75 больше, чем 66)
поэтому 5 6 больше
дробная часть.


 д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000. д.
д.


 Калькулятор биномиального коэффициента, который позволяет вычислить биномиальный коэффициент из двух целых чисел.
Калькулятор биномиального коэффициента, который позволяет вычислить биномиальный коэффициент из двух целых чисел.
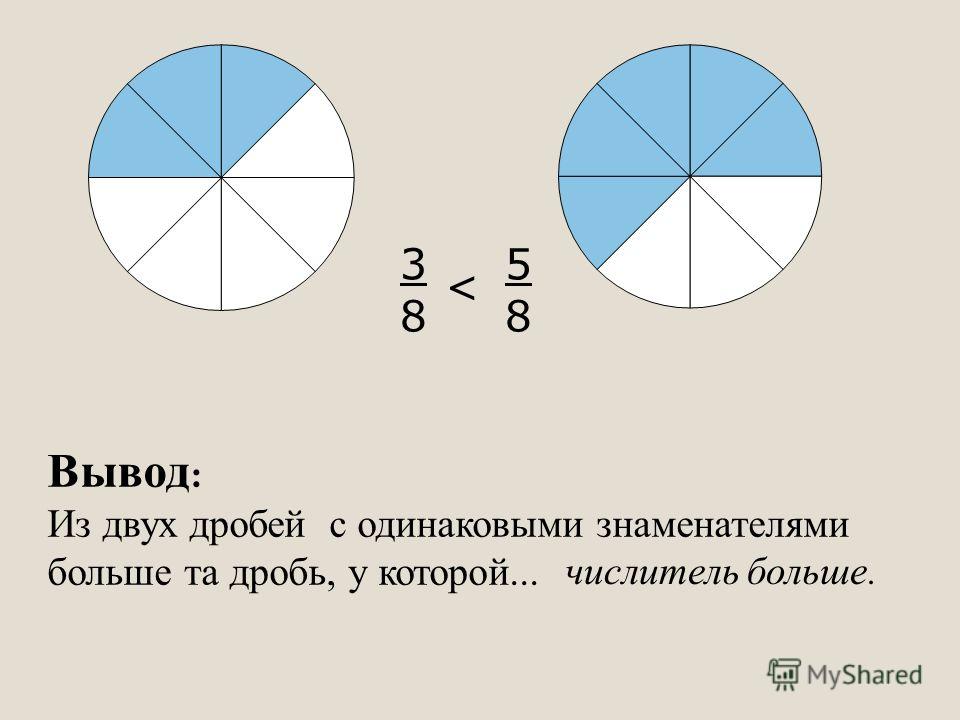 Это легко, когда у вас есть простой карманный калькулятор🖩 или наш преобразователь дроби в десятичную, поэтому мы не будем здесь вдаваться в подробности; и
Это легко, когда у вас есть простой карманный калькулятор🖩 или наш преобразователь дроби в десятичную, поэтому мы не будем здесь вдаваться в подробности; и
 Поскольку одна из наших дробей является смешанным числом, выберите этот вариант.
Поскольку одна из наших дробей является смешанным числом, выберите этот вариант.
