Пределы с тригонометрическими функциями: Как решать пределы с тригонометрическими функциями, примеры

Содержание

Примеры решения пределов тригонометрических функций с ответами

Алгоритм решения пределов тригонометрических функций

Теорема

Для тригонометрических функций существует много разных пределов, но как правило, все они вычисляются, опираясь на первый замечательный предел и его следствия.

Первый замечательный предел выглядит следующим образом:

Следствия первого замечательного предела

Главным следствием первого замечательного предела считают:

Также следствиями являются:

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Примеры решения пределов тригонометрических функций

Пример 1

Задание

Найти предел функции:

Решение

Заменим значение х на число, к которому стремится функция:

Так как мы пришли на неопределённость вида 0/0, преобразуем синус так, чтобы он стал вида первого замечательного предела:

Мы знаем, что первый замечательный предел равен единице, следовательно

Таким образом найдём предел функции:

Пример 2

Задание

Найти предел функции:

Решение

При замене х на число, к которому он стремится, снова получаем неопределённость

Данную задачу можно решить, применив правило Лопиталя.

Найдём производные числителя и знаменателя функции и решим задачу:

Пример 3

Задание

Найти предел функции:

Решение

При подстановке нуля получим неопределённость типа 0/0:

Воспользуемся свойством

Преобразуем функцию и упростим её:

Вынесем константу ½ за лимит и, пользуюсь свойством первого замечательного предела, найдём передел данной функции:

Пример 4

Задание

Найти предел функции:

Решение

Если заменить x на число, придём к неопределённости 0/0:

Для решения данного примера применим правило Лопиталя и заменим х на число в производных:

Пример 5

Задание

Вычислить предел функции:

Решение

Для решения данного примера воспользуемся свойством разности косинусов:

и получим

Вынесем минус за лимит, дабы не потерять и продолжим решение. Для решения задачи приведём функцию к виду первого замечательного предела. Для этого нужно разделить дробь на множители и добавить в знаменатель коэффициент, равный коэффициенту в числителе. А потом упростим выражение:

Снова вынесем константы за лимит и получим вид первого замечательного предела, с помощью которого приходим к искомому решению:

Пример 6

Задание

Вычислить предел функции:

Решение

При подстановке х снова получаем неопределённость

Значит будем искать передел путём приведения к виду первого замечательного предела.

Представим тангенс в виде частного синуса х и косинуса х

Приведём к общему знаменателю и разделим выражение на множители следующим образом:

Мы видим первый замечательный предел, а значит, можем упростить до:

Далее снова приведём числитель к общему знаменателю:

Вновь разделим на множители и подставим значение х во второй косинус:

Таким образом нам остаётся разобраться с первым числителем. Поменяем местами 1 и косинус и вынесем минус за лимит.

Далее воспользуемся формулой понижения степени и найдём решение:

Пример 7

Задание

Вычислить предел функции:

Решение

При простом вычислении получаем неопределённость

Следовательно, будем вычислять предел, опираясь на правило первого замечательного предела. Приведём тангенс к виду частного синуса и косинуса:

Разделим пример на множители.

Приведём синусы к виду первого замечательного предела и получим ответ:

Пример 8

Задание

Найти предел функции:

Решение

При подставлении числа на место х приходим к неопределённости типа 0/0:

Преобразуем tg, приведем выражение к общему знаменателю cos x, вынесем общий множитель – sin x за скобку:

Используя следствие из первого замечательного предела, преобразим выражение и избавимся от тангенса.

Затем вновь приведем функцию к следствию первого замечательного предела и найдем ответ:

Пример 9

Задание

Найти предел функции:

Решение

При подстановке числа видим неопределённость.

Следовательно, искать предел будем, опираясь на правило первого замечательного предела. Для этого заменим переменную, которая будет стремиться к нулю:

Подставим в функцию:

Опираясь на свойства тригонометрии, заменим тангенс.

Зная, что предел косинуса нуля = 1, преобразуем пример и приведём к виду первого замечательного предела.

Найдём ответ.

Пример 10

Задание

Вычислить предел функции:

Решение

Здесь так же получим неопределённость:

Значит, введём новую переменную t:

Подставим получившиеся значения в пример и найдём предел:

Средняя оценка 4.

5 / 5. Количество оценок: 2

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

23183

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

Пределы, содержащие тригонометрические функции

При вычислении пределов, содержащих тригонометрические функции, как правило, приходится обращаться к таблице эквивалентностей, предварительно преобразовав выражение с помощью тригонометрических формул.

Пример 2.20. Вычислить.

Решение.

Пример 2.21. Вычислить.

Решение. Вычислить этот предел в 2.4 не удалось. Рассмотрим другой путь рассуждений. С помощью преобразований перейдем в числителе от разности бесконечно малых к произведению бесконечно малых и заменим эквивалентными в произведении.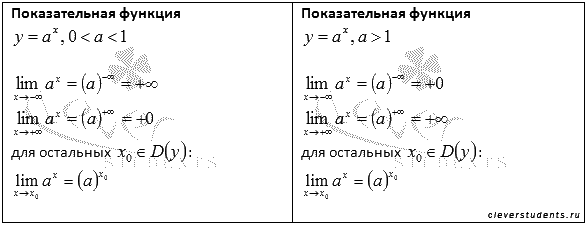

В некоторых случаях применение тригонометрических преобразований позволяет раскрыть неопределенность, не обращаясь к таблице эквивалентностей.

Пример 2.22. Вычислить.

Решение. Так каки, то имеем неопределенность. Имеет смысл преобразовать знаменатель по формуле, а потом разложить знаменатель на множители как разность квадратов. После сокращения общего множителя в числителе и знаменателе, неопределенность уйдет:

Пример 2.23. Вычислить.

Решение. Известно, что. Выражение, стоящее под знаком предела, дает неопределенностьпри. Уничтожить неопределенность только посредством преобразований, как это было сделано примере 2.22, не удастся. Сделаем замену переменной так, чтобы новая переменная стремилась к нулю. Положим,при, а. Далее воспользуемся формулой приведения:

Замечание. Пределтакже вычисляется путем замены переменной:и последующим применением формул приведения. Однако было бы ошибкой сразу прибегнуть к таблице эквивалентностей:. Дело в том, что аргументы данных функций –ине являются бесконечно малыми при.

Пределы выражений, содержащих показательную, логарифмическую и степенную функции

Пример 2.24. Вычислить.

Решение. Так как, то выражение, стоящее под знаком предела, придает неопределенность. Воспользуемся свойствами показательной функции:и преобразуем числитель дроби следующим образом:. Тогда

Пример 2.25. Вычислить.

Решение. В скобках воспользуемся свойством логарифмической функции:и выделим в аргументе логарифма единицу:Легко видеть, что, а выражениепри. По таблице эквивалентностей имеем:при,=

Пример 2.26. Вычислить.

Решение.Поскольку по определению логарифма, надо раскрыть неопределенность. Введем новую переменную, так чтобы она стремилась к нулю и сделаем замену в пределе:

Пример 2.27. Вычислить.

Решение. Применим к степенным выражениям соотношение и сделаем в пределе заменус целью воспользоваться эквивалентностьюпри. Тогда=

Предел показательно-степенной функции

Напомним, что функция , основание и показатель степени которой являются функциями, зависящими от переменной, называется показательно-степенной. Пользуясь тождествоми свойством логарифмической функции, представим показательно-степенную функцию в виде. В силу непрерывности показательной функции по формуле (2.6) получаем:

. (2.10)

Таким образом, нахождение исходного предела сводится к нахождению предела . Показательно-степенные выражения в пределе могут порождать три типа неопределенности:,,. Для раскрытия неопределенностиможно использовать второй замечательный предел.

Правила вычисления :

1. Если функции иимеют приконечные пределы, то справедливо соотношение

. (2.11)

2. Во всех остальных случаях рекомендуется перейти к основанию по формуле (2.10), вычислить предели воспользоваться свойствами показательной функции.

Пример 2.28. Вычислить.

Решение. Так как основание и показатель степени имеют приконечные пределы:,, то по формуле (2.10) получаем:

Пример 2.29. Вычислить.

Решение.Согласно формуле (2.7). Пользуясь свойствами показательной функции с основанием, большим единицы:и, окончательно получаем:

и.

Пример 2.30. Вычислить.

Решение.Найдем пределы основания и показателя степени при:

Однако поведение показательной функции на бесконечности существенно зависит от знака бесконечно удаленной точки. Для показательной функции с основанием, меньшим единицы, имеем:и. Проанализируем поведение функциипри. Еслистремится к 1 справа, т. е. оставаясь все время больше 1, то разностьстремится к нулю, также оставаясь положительной. Следовательно,. При стремлениик 1 слевабудет меньше 1, а разностьстремится к нулю, оставаясь отрицательной. В этом случае. Тогда предел исходной показательно-степенной функции будет зависеть от того, с какой стороныприближается к 1:

и.

Пример 2.31. Вычислить.

Решение. Неопределенностьможно раскрыть, не прибегая к формуле (2.10), а пользуясь вторым замечательным пределом. Воспользуемся свойством показательной функциии преобразуем выражение, стоящее под знаком предела, следующим образом:

По второму замечательному пределу (2.9) имеем:

Кроме того, . Тогда по формуле (2.11) окончательно получаем:

Список литературы

1. Письменный Д. Т. Конспект лекций по высшей математике: В 2 ч. М.: Айрис Пресс, 2006. Ч. 1.

2. Комплексные числа и многочлены: Методические указания к решению задач / Сост.: М. Н. Абрамова, Е. А. Толкачева, А. И. Куприянов. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2007.

Содержание

1. ПРЕДЕЛ ФУНКЦИИ 4

1. 1. Окрестность точки 4

1.2. Предел функции в точке. Непрерывность функции в точке 5

1.3. Предел функции на бесконечности 6

1.4. Бесконечно большая и бесконечно малая функции 7

1.5. Односторонние пределы 8

1.6. Элементарные функции 9

2. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ 12

2.1. Правила предельного перехода 12

2.2. Предел дробно-рациональной функции 16

2.3. Предел функций, содержащих иррациональные выражения 20

2.4. Замечательные пределы. Эквивалентные бесконечно малые функции 23

2.5. Пределы, содержащие тригонометрические функции 27

2.6. Пределы выражений, содержащих показательную, логарифмическую и степенную функции 30

2.7. Предел показательно-степенной функции 31

Редактор И. Г. Скачек

__________________________________________________________________

Подписано в печать Формат 6084 1/16. Бумага офсетная.

Печать офсетная. Печ. л. 2.0.

Гарнитура «Times». Тираж 250 экз. Заказ

__________________________________________________________________

Издательство СПбГЭТУ «ЛЭТИ»

Непосредственное вычисление пределов, таблица пределов функций

Определение непрерывности функции в точке и передела функции на бесконечности и на использовании свойств предела непрерывной функции способствует непосредственному вычислению пределов.

Определение 1

Значение предела в точке непрерывности определено значением функции в этой точке.

При опоре на свойства основные элементарные функции имеют предел в любой точке из области определения, вычисляется как значение соответствующей функции в этих точках.

Пример 1

Произвести вычисление предела функции limx→5arctg35·x

Решение

Функция арктангенса отличается непрерывностью на всей своей области определения. Отсюда получим, что в точке x0=5 функция является непрерывной. Из определения имеем, что для нахождения предела является значением этой же функции. Тогда необходимо произвести подстановку. Получим, что

limx→5arctg35·x=arctg35·5=arctg3=π3

Ответ: π3.

Для вычисления односторонних пределов необходимо использовать значения точек границ предела. У акрксинуса и акрккосинуса имеются такие значения x0=-1 или x0=1.

При x→+∞ или x→-∞ вычисляются пределы функции, заданные на бесконечностях.

Для упрощения выражений применяют свойства пределов:

Определение 2

limx→x0(k·f(x))=k·limx→x0f(x), k является коэффициентом.
limx→x0(f(x)·g(x))=limx→x0f(x)·limx→x0g(x), применяемое при получении неопределенности предела.
limx→x0(f(g(x)))=flimx→x0gx,используемое для непрерывных функций, где знак функции и предельного перехода можно менять местами.

Для того, чтобы научиться вычислять переделы, необходимо знать и разбираться в основных элементарных функциях. Ниже приведена таблица, в которой имеются переделы этих функций с приведенными разъяснениями и подробным решением. Для вычисления необходимо основываться на определении предела функции в точке и на бесконечности.

Таблица пределов функции

Для упрощения и решения пределов используется данная таблица основных пределов.

Функция корень n-ой степени

y=xn, где n=2, 4, 6 …

limx→∞xn=+∞n=+∞

Для любых x0 из опрелеления

limx→x0xn=x0n

Функция корень n-ой степени

y=xn, где n=3, 5, 7 …

limx→∞xn=+∞n=+∞limx→∞xn=-∞n=-∞

limx→x0xn=x0n

Степенная функция y=xa , a>0

Для любого положительного числа a
limx→∞xa=+∞a=+∞
Если a=2, 4, 6 …, то
limx→∞xa=-∞a=+∞
Если a=1, 3, 5, …, то
limx→∞xa=-∞a=-∞
Для любых x0, из области определния
limx→x0xa=(x0)a

Степенная функция y=xa, a<0

Для любого отрицательного числа a
limx→∞xa=(+∞)a=+0limx→0+0=(0+0)a=+∞
Если a=-2, -4, -4, . .., то
limx→∞xa=-∞a=+0limx→0-0xa=(0-0)a=+∞
Если a=-1, -3, -5, …, то
limx→∞xa=-∞a=-0limx→0-0xa=(0-0)a=-∞
Для любых x0 из области определения
limx→x0xa=(x0)a

Показательная функия

y=ax, 0<a<1

limx→∞ax=a-∞=+∞limx→∞ax=a+∞=+0

Для любых x0 из области опреления limx→x0ax=ax0

Показательная функия

y=ax, a>1limx→∞ax=a-∞=+0limx→x0ax=a+∞=+∞

Для любых знвчений x0 из област опредения limx→x0ax=ax0

Логарифмическая функция

y=loga(x), 0<a<1

limx→0+0logax=loga(0+0)=+∞limx→∞logax=loga(+∞)=-∞

Для любых x0 из области опрелеленияlimx→x0logax=logax0

Логарифмическая функция

y=loga(x), a>1

limx→0+0logax=loga(0+0)=-∞limx→∞logax=loga(+∞)=+∞

Для любых x0 из области опрелеления

limx→x0logax=logax0

Тригонометрические функции

Синус
limx→∞ sin x не существует
Для любых x0 из области опрелеления
limx→x0sin x=sin x0
Тангненсlimx→π2-0+π·ktg x=tgπ2-0+π·k=+∞limx→π2+0+π·ktg x=tgπ2+0+π·k=-∞

limx→∞tg x не существует

Для любых x0 из области опрелеления

limx→x0tg x=tg x0

Тригонометрические функции

Косинус
limx→∞cos x не существует
Для любых x0 из области опрелеления
limx→x0cos x=cos x0
Котангенсlimx→-0+π·kctg x=ctg(-0+π·k)=-∞limx→+0+π·kctg x=ctg(+0+π·k)=+∞

limx→∞ctg x не существует

Для любых x0 из области опрелеления
limx→x0сtg x=сtg x0

Обратные тригонометрические функции

Арксинус
limx→-1+0arcsin x=-π2limx→1-0arcsin x=π2

Для любых x0 из области опрелеления

limx→x0arcsin x=arcsin x0

Арккосинус
limx→-1+0arccos (x)=πlimx→1-0arccos (x)=0

Для любых x0 из области опрелеления

limx→x0arccis x=arccos x0

Обратные тригонометрические функции

Арктангес
limx→-∞ arctg (x)=-π2limx→+∞ arctg (x)=π2

Для любых x0 из области опрелеления

limx→x0arctg x=arctg x0

Арккотангенс
limx→-∞arcctg (x)=πlimx→+∞arcctg (x)=0

Для любых x0 из области опрелеления

limx→x0arcctg x=arcctg x0

Пример 2

Произвести вычисление предела limx→1×3+3x-1×5+3.

Решение

Для решения необходимо подставить значение х=1. Получаем, что

limx→1×3+3x-1×5+3=13+3·1-115+3=34=32

Ответ: limx→1×3+3x-1×5+3=32

Пример 3

Произвести вычисление предела функции limx→0(x2+2,5)1×2

Решение

Для того, чтобы раскрыть предел, необходимо подставить значение х, к которому стремится предел функции. В данном случае нужно произвести подстановку х=0. Подставляем числовое значение и получаем:

x2+2.5x=0=02+2.5=2.5

Предел записывается в виде limx→0(x2+2.5)1×2=limx→02.51×2. Далее необходимо заняться значением показателя. Он является степенной функцией 1×2=x-2. В таблице пределов, предоставленной выше, имеем, что limx→0+01×2=limx→0+0x-2=+∞ и limx→0+01×2=limx→0+0x-2=+∞, значит, имеем право записать как limx→01×2=limx→0x-2=+∞

Теперь вычислим предел. Получит вид limx→0(x2+2.5)1×2=limx→02.51×2=2.5+∞

По таблице пределов с показательными функциями, имеющими основание больше 1 получаем, что

limx→0(x2+2. 5)1×2=limx→02.51×22.5+∞=+∞

Ответ: limx→0(x2+2.5)1×2=+∞

Когда задан более сложный предел, то при помощи таблицы не всегда получится получать целое или конкретное значение. Чаще получаются разные виды неопределенностей, для разрешения которых необходимо применять правила.

Рассмотрим графическое разъяснение приведенной выше таблицы пределов основных элементарных функций.

Предел константы

Из рисунка видно, что функция у=С имеет предел на бесконечности. Такой же предел при аргументе, который стремится к х0. Он равняется числу C.

Предел функции корень n-ой степени

Четные показатели корня применимы для limx→+∞xn=+∞n=+∞, а нечетные, равные больше, чем значение 1, – для limx→+∞xn=+∞n=+∞, limx→-∞xn=-∞n=-∞. Область определения может принимать абсолютно любое значение х предела заданной функции корня n-ой степени, равного значению функции в заданной точке.

Предел степенной функции

Необходимо разделить все степенные функции по группам, где имеются одинаковые значения пределов, исходя из показателя степени.

Когда a является положительным числом, тогда limx→+∞xa=+∞a=+∞ и limx→-∞xa=-∞a=-∞. Когда x принимает любое значение, тогда предел степенной функции равняется значению функции в точке. Иначе это записывается как limx→∞xa=(∞)a=∞.

Когда a является положительным четным числом, тогда получаем limx→+∞xa=(+∞)a=+∞ и limx→-∞xa=(-∞)a=+∞, причем x из данной области определения является пределом степенной функции и равняется значением функции в этой точке. Предел имеет вид limx→∞xa=∞a=+∞.

Когда a имеет другие значения, тогда limx→+∞xa=(+∞)a=+∞, а область определения x способствует определению предела функции в заданной точке.

Когда a имеет значение отрицательных чисел, тогда получаем limx→+∞xa=+∞a=+0, limx→-∞xa=(-∞)a=-0, limx→0-0xa=(0-0)a=-∞,limx→0+0xa=0+0a=+∞, а значения x может быть любым из заданной области определения и равняется функции в заданной точке. Получаем, что limx→∞xa=∞a=0 иlimx→0xa=0a=∞.

Когда a является отрицательным четным числом, тогда получаем limx→+∞xa=(+∞)a=+0, limx→-∞xa=-∞a=+0, limx→0-0(0-0)a=+∞, limx→0+0xa=(0+0)a=+∞, а любое значение x на области определения дает результат предела степенной функции равным значению функции в точке. Запишем как limx→∞xa=(∞)a=+0 и limx→0xa=(0)a=+∞.

Когда значение a имеет другие действительные отрицательные числа, тогда получим limx→+∞xa=+∞a=+0 и limx→0+0xa=0+0a=+∞, когда x принимает любое значение из своей области определения, тогда предел степенной функции равняется значению функции в этой точке.

Предел показательной функции

Когда 0<a<1, имеем, что limx→-∞ax=a-∞=+∞, limx→+∞ax=(a)+∞=+∞, любое значение x из области определения дает пределу показательной функции значению функции в точке.

Когда a>1, тогда limx→-∞ax=(a)-∞=+0, limx→+∞ax=(a)+∞=+∞, а любое значение x из области определения дает предел функции равный значению этой функции в точке.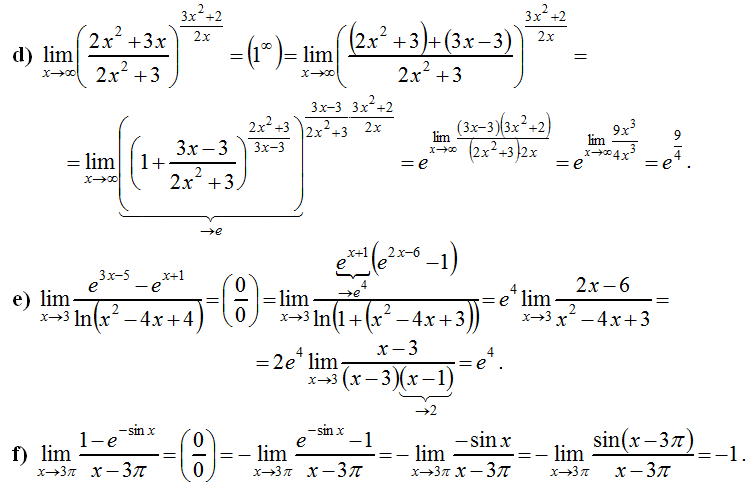

Предел логарифмической функции

Когда имеем 0<a<1, тогда limx→0+0logax=loga(0+0)=+∞, limx→+∞logax=loga(+∞)=-∞ , для всех остальных значений x из заданной области определения предел показательной функции равняется значению заданной функции в точках.

Когда a>1, получаем limx→0+0logax=loga(0+0)=-∞, limx→+∞logax=loga(+∞)=+∞,остальные значения x в заданной области определения дают решение предела показательной функции равному ее значению в точках.

Предел тригонометрических функций

Предел бесконечности не существует для таких функций как y=sin x, y=cos x. Любое значение x, входящее в область определения, равняется значению функции в точке.

Функция тангенса имеет предел вида limx→π2-0+π·ktg(x)=+∞, limx→π2+π·ktg(x)=∞ или limx→π2+π·ktg(x)=∞, тогда остальные значения x, принадлежащие области определения тангенса, равняется значению функции в этих точках.

Для функции y=ctg x получаем limx→-0+π·kctg(x)=-∞, limx→+0+π·kctg(x)=+∞ или limx→π·kctg (x)=∞, тогда остальные значения x, принадлежащие области определения, дают предел котангенса, равный значению функции в этих точках.

Предел обратных тригонометрических функций

Функция арксинус имеет предел вида limx→-1+0arcsin(x)=-π2 и limx→1-0arcsin (x)=π2, остальные значения x из области определения равняются значению функции в заданной точке.

Функция арккосинус имеет предел вида limx→-1+0arccos(x)=π и limx→1-0arccos(x)=0, когда остальные значения x, принадлежащие области определения, имеют предел арккосинуса, равного значению функции в этой точке.

Функция арктангенс имеет предел вида limx→-∞arctg(x)=-π2 и limx→+∞arctg(x)=π2, причем другие значения x, входящие в область определения, равняется значению функции в имеющихся точках.

Функция котангенса имеет предел вида limx→-∞arcctg(x)=π и limx→+∞arctg(x)=0, где x принимает любое значение из своей заданной области определения, где получаем предел арккотангенса, равного значению функции в имеющихся точках.

Все имеющееся значения пределов применяются в решении для нахождения предела любой из элементарных функций.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Что такое тригонометрические границы? (с решенными упражнениями) / математика | Thpanorama

тригонометрические пределы они являются пределами функций, так что эти функции образованы тригонометрическими функциями..

Есть два определения, которые должны быть известны, чтобы понять, как выполняется вычисление тригонометрического предела..

Эти определения:

— Предел функции «f», когда «x» стремится к «b»: он состоит в вычислении значения, к которому f (x) приближается, когда «x» приближается к «b», не достигая «b».

— Тригонометрические функции: тригонометрическими функциями являются функции синуса, косинуса и тангенса, обозначаемые как sin (x), cos (x) и tan (x) соответственно.

Другие тригонометрические функции получены из трех функций, упомянутых выше.

Пределы функций

Для пояснения понятия предела функции перейдем к показу нескольких примеров с простыми функциями. 0.

Эти выражения называются неопределенными, поскольку они являются математически выражениями, не имеющими смысла..

Кроме того, в зависимости от функций, входящих в исходный предел, результат, полученный при решении неопределенностей, может быть разным в каждом случае..

Примеры простых тригонометрических ограничений

Чтобы решить границы, всегда очень полезно знать графики задействованных функций. Ниже приведены графики функций синуса, косинуса и тангенса.

Некоторые примеры простых тригонометрических ограничений:

— Рассчитайте предел греха (х), когда «х» стремится к «0».

При просмотре графика вы можете видеть, что если «x» приближается к «0» (как слева, так и справа), то график синуса также приближается к «0». Следовательно, предел sin (x), когда «x» стремится к «0», равен «0»..

— Вычислить предел cos (x), когда «x» стремится к «0».

Наблюдая за косинус-графом, можно видеть, что когда «х» близок к «0», то косинус-граф близок к «1». Это подразумевает, что предел cos (x), когда «x» стремится к «0», равен «1».

Предел может существовать (быть числом), как в предыдущих примерах, но может также случиться, что он не существует, как показано в следующем примере.

— Предел tan (x), когда «x» стремится к «Π / 2» слева, равен «+ ∞», как видно на графике. С другой стороны, предел tan (x), когда «x» стремится к «-Π / 2» справа, равен «-∞».

Тождества тригонометрических границ

Два очень полезных тождества при расчете тригонометрических пределов:

— Предел «sin (x) / x», когда «x» стремится к «0», равен «1».

— Предел «(1-cos (x)) / x», когда «x» стремится к «0», равен «0».

Эти идентичности используются очень часто, когда у вас есть какая-то неопределенность.

Решенные упражнения

Решите следующие ограничения, используя идентификаторы, описанные выше.

— Вычислить предел «f (x) = sin (3x) / x», когда «x» стремится к «0».

Если функция «f» оценена в «0», будет получено определение типа 0/0. Поэтому мы должны попытаться разрешить эту неопределенность, используя описанные тождества.

Единственная разница между этим пределом и идентичностью — это число 3, которое появляется в функции синуса. Чтобы применить тождество, функцию «f (x)» необходимо переписать следующим образом: «3 * (sin (3x) / 3x)». Теперь и аргумент синуса и знаменатель равны.

Поэтому, когда «x» стремится к «0», использование идентификатора приводит к «3 * 1 = 3». Следовательно, предел f (x), когда «x» стремится к «0», равен «3».

— Вычислить предел «g (x) = 1 / x — cos (x) / x», когда «x» стремится к «0».

Когда «x = 0» подставляется в g (x), получается неопределенность типа ∞-∞. Для ее решения вычитаются дроби, что дает результат «(1-cos (x)) / x».

Теперь при применении второго тригонометрического тождества мы имеем предел g (x), когда «x» стремится к «0», равно 0.

— Рассчитайте предел «h (x) = 4tan (5x) / 5x», когда «x» стремится к «0».

Опять же, если вы оцените h (x) в «0», вы получите определение типа 0/0.

Перезапись tan (5x) как sin (5x) / cos (5x) приводит к тому, что h (x) = (sin (5x) / 5x) * (4 / cos (x)).

Использование предела 4 / cos (x), когда «x» стремится к «0», равно «4/1 = 4», и получается первая тригонометрическая идентичность, что предел h (x), когда «x» стремится «0» равно «1 * 4 = 4».

наблюдение

Тригонометрические пределы не всегда легко решить. В этой статье были показаны только основные примеры.

ссылки

Флеминг В. и Варберг Д. Э. (1989). Предварительная математика. Прентис Холл ПТР.
Флеминг В. и Варберг Д. Э. (1989). Предварительная математика: подход к решению проблем (2, иллюстрированный ред.). Мичиган: Прентис Хол.
Флеминг В. и Варберг Д. (1991). Алгебра и тригонометрия с аналитической геометрией. Пирсон Образование.
Ларсон Р. (2010). тригонометрия и алгебра (8 изд.). Cengage Learning.
Лил, Дж. М. и Вилория, Н. Дж. (2005). Плоская аналитическая геометрия. Мерида — Венесуэла: От редакции Venezolana C. A.
Перес, C. D. (2006). тригонометрия и алгебра. Пирсон Образование.
Перселл, Э.Дж., Варберг Д., Ригдон С.Э. (2007). расчет (Девятое издание). Прентис Холл.
Saenz, J. (2005). Дифференциальное исчисление с ранними трансцендентными функциями для науки и техники (Второе издание ред.). гипотенуза.
Скотт, С. А. (2009). Декартова плоская геометрия, часть: аналитические коники (1907) (перепечатка ред.). Источник Молнии.
Салливан, М. (1997). тригонометрия и алгебра. Пирсон Образование.

Первый и второй замечательный предел

Найти замечательные пределы трудно не только многим студентам первого, второго курса обучения которые изучают теорию пределов, но и некоторым преподавателям.

Формула первого замечательного предела

Следствия первого замечательного предела запишем формулами
1. 2. 3. 4. Но сами по себе общие формулы замечательных пределов никому на экзамене или тесте не помогают. Суть в том что реальные задания построены так что к записанным выше формулам нужно еще прийти. И большинство студентов, которые пропускают пары, заочно изучают этот курс или имеют преподавателей, которые сами не всегда понимают о чем объясняют, не могут вычислить самых элементарных примеров на замечательные пределы. Из формул первого замечательного предела видим, что с их помощью можно исследовать неопределенности типа ноль разделить на ноль для выражений с тригонометрическими функциями. Рассмотрим сначала ряд примеров на первый замечательный пределу, а потом изучим второй замечательный предел.

Пример 1. Найти предел функции sin(7*x)/(5*x)
Решение: Как видите функция под пределом близка к первому замечательному пределу, но сам предел функции точно не равен единице. В такого рода заданиях на пределы следует в знаменателе выделить переменную с таким же коэффициентом, который содержится при переменной под синусом. В данном случае следует разделить и умножить на 7

Некоторым такая детализация покажется лишней, но большинству студентов которым трудно даются пределы поможет лучше понять правила и усвоить теоретический материал. 2
Решение: При проверке подстановкой получим неопределенность 0/0 . Многим неизвестно, как свести такой пример до 1 замечательного предела. Здесь следует использовать тригонометрическую формулу

При этом предел преобразится к понятному виду

Нам удалось свести функцию к квадрату замечательного предела.

Пример 4. Найти предел
Решение: При подстановке получим знакомую особенность 0/0 . Однако переменная стремится к Pi , а не к нулю. Поэтому для применения первого замечательного предела выполним такую замену переменной х , чтобы новая переменная направлялась к нулю. Для этого знаменатель обозначим за новую переменную Pi-x=y

Таким образом использовав тригонометрическую формулу, которая приведена в предыдущем задании, пример сведен к 1 замечательному пределу.

Пример 5. Вычислить предел
Решение: Сначала неясно как упростить пределы. Но раз есть пример, значит должен быть и ответ. То что переменная направляется к единице дает при подстановке особенность вида ноль умножить на бесконечность, поэтому тангенс нужно заменить по формуле

После этого получим нужную неопределенность 0/0. Далее выполняем замену переменных в пределе, и используем периодичность котангенса

Последние замены позволяют использовать следствие 1 замечательного предела.

Второй замечательный предел равен экспоненте

Это классика к которой в реальных задачах на пределы не всегда легко прийти.
В вычислениях Вам понадобятся пределы — следствия второго замечательного предела:
1. 2. 3. 4.
Благодаря второму замечательному пределу и его последствиям можно исследовать неопределенности типа ноль разделить на ноль, единица в степени бесконечность, и бесконечность разделить на бесконечность, да еще и в таком же степени

Начнем для ознакомления с простых примеров.

Пример 6. Найти предел функции
Решение: Напрямую применить 2 замечательный пределу не получится. Сначала следует превратить показатель, чтобы он имел вид обратный к слагаемому в скобках

Это и есть техника сведения к 2 замечательному пределу и по сути — вывода 2 формулы следствия предела. (x-2)
Решение: Имеем особенность типа 1 в степени бесконечность. Если не верите, можете везде вместо «икс» подставить бесконечность и убедиться в этом. Для возведения под правило поделим в скобках числитель на знаменатель, для этого предварительно выполним манипуляции

Подставим выражение в предел и превратим к 2 замечательному пределу

Предел равен экспоненте в 10 степени. Константы, которые являются слагаемыми при переменной как в скобках так и степени никакой «погоды» не вносят — об этом следует помнить. А если Вас спросят преподаватели — «Почему не превращаете показатель?» (Для этого примера в x-3 ), то скажите что «Когда переменная стремится к бесконечности то к ней хоть добавляй 100 хоть отнимай 1000, а предел останется такой как и был!».
Есть и второй способ вычислять пределы такого типа. О нем расскажем в следующем задании.

Пример 9. Найти предел
Решение: Теперь вынесем переменную в числителе и знаменателе и превратим оду особенность на другую. Для получения конечного значения используем формулу следствия 2 замечательного предела

Пример 10. Найти предел функции
Решение: Заданный предел найти под силу не каждому. Для возведения под 2 предел представим, что sin (3x) это переменная, а нужно превратить показатель

Далее показатель запишем как степень в степени

В скобках описаны промежуточные рассуждения. В результате использования первого и второго замечательного предела получили экспоненту в кубе.

Пример 11. Вычислить предел функции sin(2*x)/ln(3*x+1)
Решение: Имеем неопределенность вида 0/0. Кроме этого видим, что функцию следует превращать к использованию обеих замечательных пределов. Выполним предыдущие математические преобразования

Далее без труда предел примет значение

Вот так свободно Вы будете чувствовать себя на контрольных работах, тестах, модулях если научитесь быстро расписывать функции и сводить под первый или второй замечательный предел. Если заучить приведенные методики нахождения пределов Вам трудно, то всегда можете заказать контрольную работу на пределы у нас.
Для этого заполните форму, укажите данные и вложите файл с примерами. Мы помогли многим студентам — сможем помочь и Вам!

Замечательных пределов существует несколько, но самыми известными являются первый и второй замечательные пределы. Замечательность этих пределов состоит в том, что они имеют широкое применение и с их помощью можно найти и другие пределы, встречающиеся в многочисленных задачах. Этим мы и будем заниматься в практической части данного урока. Для решения задач путём приведения к первому или второму замечательному пределу не нужно раскрывать содержащиеся в них неопределённости, поскольку значения этих пределов уже давно вывели великие математики.

Первым замечательным пределом называется предел отношения синуса бесконечно малой дуги к той же дуге, выраженной в радианной мере:

Переходим к решению задач на первый замечательный предел. Заметим: если под знаком предела находится тригонометрическая функция, это почти верный признак того, что это выражение можно привести к первому замечательнному пределу.

Пример 1. Найти предел .

Решение. Подстановка вместо x нуля приводит к неопределённости:

В знаменателе — синус, следовательно, выражение можно привести к первому замечательному пределу. Начинаем преобразования:

В знаменателе — синус трёх икс, а в числителе всего лишь один икс, значит, нужно получить три икс и в числителе. Для чего? Чтобы представить 3x = a и получить выражение .

И приходим к разновидности первого замечательного предела:

потому что неважно, какая буква (переменная) в этой формуле стоит вместо икса.

Умножаем икс на три и тут же делим:

В соответствии с замеченным первым замечательным пределом производим замену дробного выражения:

Теперь можем окончательно решить данный предел:

Пример 2. Найти предел .

Решение. Непосредственная подстановка вновь приводит к неопределённости «нуль делить на нуль»:

Чтобы получить первый замечательный предел, нужно, чтобы икс под знаком синуса в числителе и просто икс в знаменателе были с одним и тем же коэффициентом. Пусть этот коэффициент будет равен 2. Для этого представим нынешний коэффициент при иксе как и далее, производя действия с дробями, получаем:

Пример 3. Найти предел .

Решение. При подстановке вновь получаем неопределённость «нуль делить на нуль»:

Наверное, вам уже понятно, что из исходного выражения можно получить первый замечательный предел, умноженный на первый замечательный предел. Для этого раскладываем квадраты икса в числителе и синуса в знаменателе на одинаковые множители, а чтобы получить у иксов и у синуса одинаковые коэффициенты, иксы в числителе делим на 3 и тут же умножаем на 3. Получаем:

Пример 4. Найти предел .

Решение. Вновь получаем неопределённость «нуль делить на нуль»:

Можем получить отношение двух первых замечательных пределов. Делим и числитель, и знаменатель на икс. Затем, чтобы коэффициенты при синусах и при иксах совпадали, верхний икс умножаем на 2 и тут же делим на 2, а нижний икс умножаем на 3 и тут же делим на 3. Получаем:

Пример 5. Найти предел .

Решение. И вновь неопределённость «нуль делить на нуль»:

Помним из тригонометрии, что тангенс — это отношение синуса к косинусу, а косинус нуля равен единице. Производим преобразования и получаем:

Пример 6. Найти предел .

Решение. Тригонометрическая функция под знаком предела вновь наталкивает на мысль о применении первого замечательного предела. Представляем его как отношение синуса к косинусу.

Первым замечательным пределом именуют следующее равенство:

\begin{equation}\lim_{\alpha\to{0}}\frac{\sin\alpha}{\alpha}=1 \end{equation}

Так как при $\alpha\to{0}$ имеем $\sin\alpha\to{0}$, то говорят, что первый замечательный предел раскрывает неопределённость вида $\frac{0}{0}$. Вообще говоря, в формуле (1) вместо переменной $\alpha$ под знаком синуса и в знаменателе может быть расположено любое выражение, — лишь бы выполнялись два условия:

Выражения под знаком синуса и в знаменателе одновременно стремятся к нулю, т.е. присутствует неопределенность вида $\frac{0}{0}$.
Выражения под знаком синуса и в знаменателе совпадают.

Часто используются также следствия из первого замечательного предела:

\begin{equation} \lim_{\alpha\to{0}}\frac{\tg\alpha}{\alpha}=1 \end{equation} \begin{equation} \lim_{\alpha\to{0}}\frac{\arcsin\alpha}{\alpha}=1 \end{equation} \begin{equation} \lim_{\alpha\to{0}}\frac{\arctg\alpha}{\alpha}=1 \end{equation}

На данной странице решены одиннадцать примеров. Пример №1 посвящен доказательству формул (2)-(4). Примеры №2, №3, №4 и №5 содержат решения с подробными комментариями. Примеры №6-10 содержат решения практически без комментариев, ибо подробные пояснения были даны в предыдущих примерах. При решении используются некоторые тригонометрические формулы, которые можно найти .

Замечу, что наличие тригонометрических функций вкупе с неопределённостью $\frac {0} {0}$ ещё не означает обязательное применение первого замечательного предела. Иногда бывает достаточно простых тригонометрических преобразований, — например, см. .

Пример №1

Доказать, что $\lim_{\alpha\to{0}}\frac{\tg\alpha}{\alpha}=1$, $\lim_{\alpha\to{0}}\frac{\arcsin\alpha}{\alpha}=1$, $\lim_{\alpha\to{0}}\frac{\arctg\alpha}{\alpha}=1$.

а) Так как $\tg\alpha=\frac{\sin\alpha}{\cos\alpha}$, то:

$$ \lim_{\alpha\to{0}}\frac{\tg{\alpha}}{\alpha}=\left|\frac{0}{0}\right| =\lim_{\alpha\to{0}}\frac{\sin{\alpha}}{\alpha\cos{\alpha}} $$

Так как $\lim_{\alpha\to{0}}\cos{0}=1$ и $\lim_{\alpha\to{0}}\frac{\sin\alpha}{\alpha}=1$, то:

$$ \lim_{\alpha\to{0}}\frac{\sin{\alpha}}{\alpha\cos{\alpha}} =\frac{\displaystyle\lim_{\alpha\to{0}}\frac{\sin{\alpha}}{\alpha}}{\displaystyle\lim_{\alpha\to{0}}\cos{\alpha}} =\frac{1}{1} =1. $$

б) Сделаем замену $\alpha=\sin{y}$. Поскольку $\sin{0}=0$, то из условия $\alpha\to{0}$ имеем $y\to{0}$. Кроме того, существует окрестность нуля, в которой $\arcsin\alpha=\arcsin(\sin{y})=y$, поэтому:

$$ \lim_{\alpha\to{0}}\frac{\arcsin\alpha}{\alpha}=\left|\frac{0}{0}\right| =\lim_{y\to{0}}\frac{y}{\sin{y}} =\lim_{y\to{0}}\frac{1}{\frac{\sin{y}}{y}} =\frac{1}{\displaystyle\lim_{y\to{0}}\frac{\sin{y}}{y}} =\frac{1}{1} =1. $$

Равенство $\lim_{\alpha\to{0}}\frac{\arcsin\alpha}{\alpha}=1$ доказано.

в) Сделаем замену $\alpha=\tg{y}$. Поскольку $\tg{0}=0$, то условия $\alpha\to{0}$ и $y\to{0}$ эквивалентны. Кроме того, существует окрестность нуля, в которой $\arctg\alpha=\arctg\tg{y})=y$, поэтому, опираясь на результаты пункта а), будем иметь:

$$ \lim_{\alpha\to{0}}\frac{\arctg\alpha}{\alpha}=\left|\frac{0}{0}\right| =\lim_{y\to{0}}\frac{y}{\tg{y}} =\lim_{y\to{0}}\frac{1}{\frac{\tg{y}}{y}} =\frac{1}{\displaystyle\lim_{y\to{0}}\frac{\tg{y}}{y}} =\frac{1}{1} =1. $$

Равенство $\lim_{\alpha\to{0}}\frac{\arctg\alpha}{\alpha}=1$ доказано.

Равенства а), б), в) часто используются наряду с первым замечательным пределом. 2-4}{x+7}}=1$.

Пример №3

Найти $\lim_{x\to{0}}\frac{\sin{9x}}{x}$.

Так как $\lim_{x\to{0}}\sin{9x}=0$ и $\lim_{x\to{0}}x=0$, то мы имеем дело с неопределенностью вида $\frac{0}{0}$, т.е. выполнено. Однако выражения под знаком синуса и в знаменателе не совпадают. Здесь требуется подогнать выражение в знаменателе под нужную форму. Нам необходимо, чтобы в знаменателе расположилось выражение $9x$, — тогда станет истинным. По сути, нам не хватает множителя $9$ в знаменателе, который не так уж сложно ввести, — просто домножить выражение в знаменателе на $9$. Естественно, что для компенсации домножения на $9$ придётся тут же на $9$ и разделить:

$$ \lim_{x\to{0}}\frac{\sin{9x}}{x}=\left|\frac{0}{0}\right| =\lim_{x\to{0}}\frac{\sin{9x}}{9x\cdot\frac{1}{9}} =9\lim_{x\to{0}}\frac{\sin{9x}}{9x} $$

Теперь выражения в знаменателе и под знаком синуса совпали. Оба условия для предела $\lim_{x\to{0}}\frac{\sin{9x}}{9x}$ выполнены. Следовательно, $\lim_{x\to{0}}\frac{\sin{9x}}{9x}=1$. А это значит, что:

$$ 9\lim_{x\to{0}}\frac{\sin{9x}}{9x}=9\cdot{1}=9. $$

Ответ : $\lim_{x\to{0}}\frac{\sin{9x}}{x}=9$.

Пример №4

Найти $\lim_{x\to{0}}\frac{\sin{5x}}{\tg{8x}}$.

Так как $\lim_{x\to{0}}\sin{5x}=0$ и $\lim_{x\to{0}}\tg{8x}=0$, то здесь мы имеем дело с неопределенностью вида $\frac{0}{0}$. Однако форма первого замечательного предела нарушена. Числитель, содержащий $\sin{5x}$, требует наличия в знаменателе $5x$. В этой ситуации проще всего разделить числитель на $5x$, — и тут же на $5x$ домножить. Кроме того, проделаем аналогичную операцию и со знаменателем, домножив и разделив $\tg{8x}$ на $8x$:

$$\lim_{x\to{0}}\frac{\sin{5x}}{\tg{8x}}=\left|\frac{0}{0}\right| =\lim_{x\to{0}}\frac{\frac{\sin{5x}}{5x}\cdot{5x}}{\frac{\tg{8x}}{8x}\cdot{8x}}$$

Сокращая на $x$ и вынося константу $\frac{5}{8}$ за знак предела, получим:

$$ \lim_{x\to{0}}\frac{\frac{\sin{5x}}{5x}\cdot{5x}}{\frac{\tg{8x}}{8x}\cdot{8x}} =\frac{5}{8}\cdot\lim_{x\to{0}}\frac{\frac{\sin{5x}}{5x}}{\frac{\tg{8x}}{8x}} $$

Обратите внимание, что $\lim_{x\to{0}}\frac{\sin{5x}}{5x}$ полностью удовлетворяет требованиям для первого замечательного предела. 3}=\frac{1}{2}$.

Пример №9

Найти предел $\lim_{x\to{3}}\frac{1-\cos(x-3)}{(x-3)\tg\frac{x-3}{2}}$.

Так как $\lim_{x\to{3}}(1-\cos(x-3))=0$ и $\lim_{x\to{3}}(x-3)\tg\frac{x-3}{2}=0$, то наличествует неопределенность вида $\frac{0}{0}$. Перед тем, как переходить к её раскрытию, удобно сделать замену переменной таким образом, чтобы новая переменная устремилась к нулю (обратите внимание, что в формулах переменная $\alpha \to 0$). Проще всего ввести переменную $t=x-3$. Однако ради удобства дальнейших преобразований (эту выгоду можно заметить по ходу приведённого ниже решения) стоит сделать такую замену: $t=\frac{x-3}{2}$. Отмечу, что обе замены применимы в данном случае, просто вторая замена позволит поменьше работать с дробями. Так как $x\to{3}$, то $t\to{0}$.

$$ \lim_{x\to{3}}\frac{1-\cos(x-3)}{(x-3)\tg\frac{x-3}{2}}=\left|\frac{0}{0}\right| =\left|\begin{aligned}&t=\frac{x-3}{2};\\&t\to{0}\end{aligned}\right| =\lim_{t\to{0}}\frac{1-\cos{2t}}{2t\cdot\tg{t}} =\lim_{t\to{0}}\frac{2\sin^2t}{2t\cdot\tg{t}} =\lim_{t\to{0}}\frac{\sin^2t}{t\cdot\tg{t}}=\\ =\lim_{t\to{0}}\frac{\sin^2t}{t\cdot\frac{\sin{t}}{\cos{t}}} =\lim_{t\to{0}}\frac{\sin{t}\cos{t}}{t} =\lim_{t\to{0}}\left(\frac{\sin{t}}{t}\cdot\cos{t}\right) =\lim_{t\to{0}}\frac{\sin{t}}{t}\cdot\lim_{t\to{0}}\cos{t} =1\cdot{1} =1. 2x} =\lim_{x\to\frac{\pi}{2}}\frac{1-\sin{x}}{(1-\sin{x})(1+\sin{x})} =\lim_{x\to\frac{\pi}{2}}\frac{1}{1+\sin{x}} =\frac{1}{1+1} =\frac{1}{2}. $$

Аналогичный способ решения есть и в решебнике Демидовича (№475) . Что же касается второго предела, то как и в предыдущих примерах этого раздела, мы имеем неопределённость вида $\frac{0}{0}$. Отчего она возникает? Она возникает потому, что $\tg\frac{2\pi}{3}=-\sqrt{3}$ и $2\cos\frac{2\pi}{3}=-1$. Используем эти значения с целью преобразования выражений в числителе и в знаменателе. Цель наших действий: записать сумму в числителе и знаменателе в виде произведения. Кстати сказать, зачастую в пределах аналогичного вида удобна замена переменной, сделанная с таким расчётом, чтобы новая переменная устремилась к нулю (см., например, примеры №9 или №10 на этой странице). Однако в данном примере в замене смысла нет, хотя при желании замену переменной $t=x-\frac{2\pi}{3}$ несложно осуществить.

$$ \lim_{x\to\frac{2\pi}{3}}\frac{\tg{x}+\sqrt{3}}{2\cos{x}+1} =\lim_{x\to\frac{2\pi}{3}}\frac{\tg{x}+\sqrt{3}}{2\cdot\left(\cos{x}+\frac{1}{2}\right)} =\lim_{x\to\frac{2\pi}{3}}\frac{\tg{x}-\tg\frac{2\pi}{3}}{2\cdot\left(\cos{x}-\cos\frac{2\pi}{3}\right)}=\\ =\lim_{x\to\frac{2\pi}{3}}\frac{\frac{\sin\left(x-\frac{2\pi}{3}\right)}{\cos{x}\cos\frac{2\pi}{3}}}{-4\sin\frac{x+\frac{2\pi}{3}}{2}\sin\frac{x-\frac{2\pi}{3}}{2}} =\lim_{x\to\frac{2\pi}{3}}\frac{\sin\left(x-\frac{2\pi}{3}\right)}{-4\sin\frac{x+\frac{2\pi}{3}}{2}\sin\frac{x-\frac{2\pi}{3}}{2}\cos{x}\cos\frac{2\pi}{3}}=\\ =\lim_{x\to\frac{2\pi}{3}}\frac{2\sin\frac{x-\frac{2\pi}{3}}{2}\cos\frac{x-\frac{2\pi}{3}}{2}}{-4\sin\frac{x+\frac{2\pi}{3}}{2}\sin\frac{x-\frac{2\pi}{3}}{2}\cos{x}\cos\frac{2\pi}{3}} =\lim_{x\to\frac{2\pi}{3}}\frac{\cos\frac{x-\frac{2\pi}{3}}{2}}{-2\sin\frac{x+\frac{2\pi}{3}}{2}\cos{x}\cos\frac{2\pi}{3}}=\\ =\frac{1}{-2\cdot\frac{\sqrt{3}}{2}\cdot\left(-\frac{1}{2}\right)\cdot\left(-\frac{1}{2}\right)} =-\frac{4}{\sqrt{3}}. 2x}=\frac{1}{2}$, $\lim_{x\to\frac{2\pi}{3}}\frac{\tg{x}+\sqrt{3}}{2\cos{x}+1}=-\frac{4}{\sqrt{3}}$.

Доказательство:

Докажем вначале теорему для случая последовательности

По формуле бинома Ньютона:

Полагая получим

Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число убывает, поэтому величины возрастают. Поэтому последовательность возрастающая, при этом (2)*Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство

Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2: Сумму в скобке найдём по формуле суммы членов геометрической прогрессии: Поэтому (3)*

Итак, последовательность ограничена сверху, при этом выполняются неравенства (2) и (3): Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквой e. Т.е.

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что . Рассмотрим два случая:

1. Пусть Каждое значение x заключено между двумя положительными целыми числами: ,где — это целая часть x. => =>

Если ,то Поэтому, согласно пределу Имеем

По признаку (о пределе промежуточной функции) существования пределов

2. Пусть . Сделаем подстановку − x = t, тогда

Из двух этих случаев вытекает, что для вещественного x.

Следствия:

9 .) Сравнение бесконечно малых. Теорема о замене бесконечно малых на эквивалентные в пределе и теорема о главной части бесконечно малых.

Пусть функции a(x ) и b(x ) – б.м. при x ® x 0 .

ОПРЕДЕЛЕНИЯ.

1) a(x ) называется бесконечно малой более высокого порядка чем b(x ) если

Записывают: a(x ) = o(b(x )) .

2) a(x ) и b(x ) называются бесконечно малыми одного порядка , если

где С Îℝ и C ¹ 0 .

Записывают: a(x ) = O (b(x )) .

3) a(x ) и b(x ) называются эквивалентными , если

Записывают: a(x ) ~ b(x ).

4) a(x ) называется бесконечно малой порядка k относи-
тельно бесконечно малой b(x ), если бесконечно малые a(x ) и (b(x )) k имеют один порядок, т.е. если

где С Îℝ и C ¹ 0 .

ТЕОРЕМА 6 (о замене бесконечно малых на эквивалентные).

Пусть a(x ), b(x ), a 1 (x ), b 1 (x ) – б.м. при x ® x 0 . Если a(x ) ~ a 1 (x ), b(x ) ~ b 1 (x ),

то

Доказательство: Пусть a(x ) ~ a 1 (x ), b(x ) ~ b 1 (x ), тогда

ТЕОРЕМА 7 (о главной части бесконечно малой).

Пусть a(x ) и b(x ) – б.м. при x ® x 0 , причем b(x ) – б.м. более высокого порядка чем a(x ).

= , a так как b(x )– более высокого порядка чем a(x ) ,то , т.е. из ясно, что a(x ) + b(x ) ~ a(x )

10) Непрерывность функции в точке(на языке пределов эпсилон-дельта,геометрическое) Односторонняя непрерывность. Непрерывность на интервале, на отрезке. Свойства непрерывных функций.

1. Основные определения

Пусть f (x ) определена в некоторой окрестности точки x 0 .

ОПРЕДЕЛЕНИЕ 1. Функция f (x ) называется непрерывной в точке x 0 если справедливо равенство

Замечания .

1) В силу теоремы 5 §3 равенство (1) можно записать в виде

Условие (2) – определение непрерывности функции в точке на языке односторонних пределов .

2) Равенство (1) можно также записать в виде:

Говорят: «если функция непрерывна в точке x 0 , то знак предела и функцию можно поменять местами».

ОПРЕДЕЛЕНИЕ 2 (на языке e-d).

Функция f (x ) называется непрерывной в точке x 0 если «e>0 $d>0 такое , что

если x ÎU(x 0 , d) (т.е. | x – x 0 |

то f (x )ÎU(f (x 0), e) (т.е. | f (x ) – f (x 0) |

Пусть x , x 0 Î D (f ) (x 0 – фиксированная, x – произвольная)

Обозначим: Dx = x – x 0 – приращение аргумента

Df (x 0) = f (x ) – f (x 0) – приращение функции в точкеx 0

ОПРЕДЕЛЕНИЕ 3 (геометрическое).

Функция f (x ) называетсянепрерывной в точке x 0 если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции , т. е.

Пусть функция f (x ) определена на промежутке [x 0 ; x 0 + d) (на промежутке (x 0 – d; x 0 ]).

ОПРЕДЕЛЕНИЕ. Функция f (x ) называется непрерывной в точке x 0 справа (слева ), если справедливо равенство

Очевидно, что f (x ) непрерывна в точке x 0 Û f (x ) непрерывна в точке x 0 справа и слева.

ОПРЕДЕЛЕНИЕ. Функция f (x ) называется непрерывной на интервал е (a ; b ) если она непрерывна в каждой точке этого интервала .

Функция f (x ) называется непрерывной на отрезке [a ; b ] если она непрерывна на интервале (a ; b ) и имеет одностороннюю непрерывность в граничных точках (т.е. непрерывна в точке a справа, в точке b – слева).

11) Точки разрыва, их классификация

ОПРЕДЕЛЕНИЕ.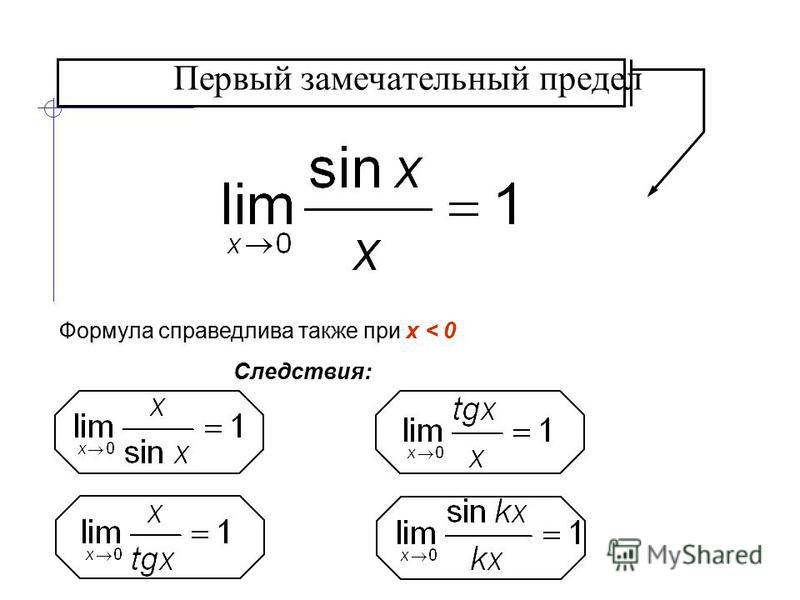 Если функция f (x ) определена в некоторой окрестности точки x 0 , но не является непрерывной в этой точке, то f (x ) называют разрывной в точке x 0 , а саму точку x 0 называют точкой разрыва функции f (x ) .

Замечания .

1) f (x ) может быть определена в неполной окрестности точки x 0 .

Тогда рассматривают соответствующую одностороннюю непрерывность функции.

2) Из определения Þ точка x 0 является точкой разрыва функции f (x ) в двух случаях:

а) U(x 0 , d)ÎD (f ) , но для f (x ) не выполняется равенство

б) U * (x 0 , d)ÎD (f ) .

Для элементарных функций возможен только случай б).

Пусть x 0 – точка разрыва функции f (x ) .

ОПРЕДЕЛЕНИЕ. Точка x 0 называется точкой разрыва I рода если функция f (x ) имеет в этой точке конечные пределы слева и справа .

Если при этом эти пределы равны, то точка x 0 называется точкой устранимого разрыва , в противном случае – точкой скачка .

ОПРЕДЕЛЕНИЕ. Точка x 0 называется точкой разрыва II рода если хотя бы один из односторонних пределов функции f (x ) в этой точке равен ¥ или не существует .

12) Свойства функций, непрерывных на отрезке (теоремы Вейерштрасса(без док-ва) и Коши

Теорема Вейерштрасса

Пусть функция f(x) непрерывна на отрезке , тогда

1)f(x)ограничена на

2)f(x) принимает на промежутке своё наименьшее и наибольшее значение

Определение : Значение функции m=fзовется наименьшим, если m≤f(x) для любого x€ D(f).

Значение функции m=fзовется наибольшим, если m≥f(x) для любого x€ D(f).

Наименьшее\наибольшее значение функция может принимать в нескольких точках отрезка.

f(x 3)=f(x 4)=max

Теорема Коши.

Пусть функция f(x) непрерывна на отрезке и х – число, заключенное между f(a) и f(b),тогда существует хотя бы одна точка х 0 € такая, что f(x 0)= g

Примеры решения второго замечательного предела со степенями. Замечательные пределы

Формула первого замечательного предела

Пример 1. Найти предел функции sin(7*x)/(5*x)
Решение: Как видите функция под пределом близка к первому замечательному пределу, но сам предел функции точно не равен единице. В такого рода заданиях на пределы следует в знаменателе выделить переменную с таким же коэффициентом, который содержится при переменной под синусом. В данном случае следует разделить и умножить на 7

Некоторым такая детализация покажется лишней, но большинству студентов которым трудно даются пределы поможет лучше понять правила и усвоить теоретический материал.
Также, если есть обратный вид функции — это также первый замечательный предел. А все потому, что замечательный предел равен единице

Это же правило касается и следствий 1 замечательного предела. Поэтому если Вас спросят «Чему равен первый замечательный предел?» Вы без колебаний должны ответить, что это — единица.

Пример 2. 2
Решение: При проверке подстановкой получим неопределенность 0/0 . Многим неизвестно, как свести такой пример до 1 замечательного предела. Здесь следует использовать тригонометрическую формулу

При этом предел преобразится к понятному виду

Нам удалось свести функцию к квадрату замечательного предела.

Второй замечательный предел равен экспоненте

Пример 1. Найти предел .

Решение. Подстановка вместо x нуля приводит к неопределённости:

И приходим к разновидности первого замечательного предела:

потому что неважно, какая буква (переменная) в этой формуле стоит вместо икса.

Умножаем икс на три и тут же делим:

В соответствии с замеченным первым замечательным пределом производим замену дробного выражения:

Теперь можем окончательно решить данный предел:

Пример 2. Найти предел .

Решение. Непосредственная подстановка вновь приводит к неопределённости «нуль делить на нуль»:

Пример 3. Найти предел .

Решение. При подстановке вновь получаем неопределённость «нуль делить на нуль»:

Пример 4. Найти предел .

Решение. Вновь получаем неопределённость «нуль делить на нуль»:

. {3x} = 1 $$

Разберем случаи, когда задача похожа на второй замечательный предел, но решается без него.

В статье: «Второй замечательный предел: примеры решений» была разобрана формула, её следствия и приведены частые типы задач по этой теме.

Термин «замечательный предел» широко используется в учебниках и методических пособиях для обозначения важных тождеств, которые помогают существенно упростить работу по нахождению пределов.

Но чтобы суметь привести свой предел к замечательному, нужно к нему хорошенько приглядеться, ведь они встречаются не в прямом виде, а часто в виде следствий, снабженные дополнительными слагаемыми и множителями. Впрочем, сначала теория, потом примеры, и все у вас получится!

Первый замечательный предел

Понравилось? Добавьте в закладки

Первый замечательный предел записывается так (неопределенность вида $0/0$):

$$ \lim\limits_{x\to 0}\frac{\sin x}{x}=1. $$

Следствия из первого замечательного предела

$$ \lim\limits_{x\to 0}\frac{x}{\sin x}=1. 2/2}=1. $$

Примеры решений: 1 замечательный предел

Пример 1. Вычислить предел $$\lim\limits_{x\to 0}\frac{\sin 3x}{8x}.$$

Решение. Первый шаг всегда одинаковый — подставляем предельное значение $x=0$ в функцию и получаем:

$$\left[ \frac{\sin 0}{0} \right] = \left[\frac{0}{0}\right].$$

Получили неопределенность вида $\left[\frac{0}{0}\right]$, которую следует раскрыть. Если посмотреть внимательно, исходный предел очень похож на первый замечательный, но не совпадает с ним. Наша задача — довести до похожести. Преобразуем так — смотрим на выражение под синусом, делаем такое же в знаменателе (условно говоря, умножили и поделили на $3x$), дальше сокращаем и упрощаем:

$$ \lim\limits_{x\to 0}\frac{\sin 3x}{8x} = \lim\limits_{x\to 0}\frac{\sin 3x}{3x}\frac{3x}{8x}=\lim\limits_{x\to 0}\frac{\sin (3x)}{3x}\frac{3}{8}=\frac{3}{8}. $$

Выше как раз и получился первый замечательный предел: $$ \lim\limits_{x\to 0}\frac{\sin (3x)}{3x} = \lim\limits_{y\to 0}\frac{\sin (y)}{y}=1, \text{ сделали условную замену } y=3x. {2}. $$

Доказательство:

Докажем вначале теорему для случая последовательности

По формуле бинома Ньютона:

Полагая получим

1. Пусть Каждое значение x заключено между двумя положительными целыми числами: ,где — это целая часть x. => =>

Если ,то Поэтому, согласно пределу Имеем

По признаку (о пределе промежуточной функции) существования пределов

2. Пусть . Сделаем подстановку − x = t, тогда

Из двух этих случаев вытекает, что для вещественного x.

Следствия:

Пусть функции a(x ) и b(x ) – б.м. при x ® x 0 .

ОПРЕДЕЛЕНИЯ.

1) a(x ) называется бесконечно малой более высокого порядка чем b(x ) если

Записывают: a(x ) = o(b(x )) .

2) a(x ) и b(x ) называются бесконечно малыми одного порядка , если

где С Îℝ и C ¹ 0 .

Записывают: a(x ) = O (b(x )) .

3) a(x ) и b(x ) называются эквивалентными , если

Записывают: a(x ) ~ b(x ).

где С Îℝ и C ¹ 0 .

ТЕОРЕМА 6 (о замене бесконечно малых на эквивалентные).

Пусть a(x ), b(x ), a 1 (x ), b 1 (x ) – б.м. при x ® x 0 . Если a(x ) ~ a 1 (x ), b(x ) ~ b 1 (x ),

то

Доказательство: Пусть a(x ) ~ a 1 (x ), b(x ) ~ b 1 (x ), тогда

ТЕОРЕМА 7 (о главной части бесконечно малой).

Пусть a(x ) и b(x ) – б.м. при x ® x 0 , причем b(x ) – б.м. более высокого порядка чем a(x ).

= , a так как b(x )– более высокого порядка чем a(x ) ,то , т.е. из ясно, что a(x ) + b(x ) ~ a(x )

1. Основные определения

Пусть f (x ) определена в некоторой окрестности точки x 0 .

ОПРЕДЕЛЕНИЕ 1. Функция f (x ) называется непрерывной в точке x 0 если справедливо равенство

Замечания .

1) В силу теоремы 5 §3 равенство (1) можно записать в виде

Условие (2) – определение непрерывности функции в точке на языке односторонних пределов .

2) Равенство (1) можно также записать в виде:

Говорят: «если функция непрерывна в точке x 0 , то знак предела и функцию можно поменять местами».

ОПРЕДЕЛЕНИЕ 2 (на языке e-d).

Функция f (x ) называется непрерывной в точке x 0 если «e>0 $d>0 такое , что

если x ÎU(x 0 , d) (т.е. | x – x 0 |

то f (x )ÎU(f (x 0), e) (т.е. | f (x ) – f (x 0) |

Пусть x , x 0 Î D (f ) (x 0 – фиксированная, x – произвольная)

Обозначим: Dx = x – x 0 – приращение аргумента

Df (x 0) = f (x ) – f (x 0) – приращение функции в точкеx 0

ОПРЕДЕЛЕНИЕ 3 (геометрическое).

Пусть функция f (x ) определена на промежутке [x 0 ; x 0 + d) (на промежутке (x 0 – d; x 0 ]).

Очевидно, что f (x ) непрерывна в точке x 0 Û f (x ) непрерывна в точке x 0 справа и слева.

11) Точки разрыва, их классификация

Замечания .

1) f (x ) может быть определена в неполной окрестности точки x 0 .

Тогда рассматривают соответствующую одностороннюю непрерывность функции.

2) Из определения Þ точка x 0 является точкой разрыва функции f (x ) в двух случаях:

а) U(x 0 , d)ÎD (f ) , но для f (x ) не выполняется равенство

б) U * (x 0 , d)ÎD (f ) .

Для элементарных функций возможен только случай б).

Пусть x 0 – точка разрыва функции f (x ) .

12) Свойства функций, непрерывных на отрезке (теоремы Вейерштрасса(без док-ва) и Коши

Теорема Вейерштрасса

Пусть функция f(x) непрерывна на отрезке , тогда

1)f(x)ограничена на

2)f(x) принимает на промежутке своё наименьшее и наибольшее значение

Определение : Значение функции m=fзовется наименьшим, если m≤f(x) для любого x€ D(f).

Значение функции m=fзовется наибольшим, если m≥f(x) для любого x€ D(f).

Наименьшее\наибольшее значение функция может принимать в нескольких точках отрезка.

f(x 3)=f(x 4)=max

Теорема Коши.

Объяснение урока: Пределы тригонометрических функций

В этом объяснителе мы узнаем, как вычислять пределы тригонометрических функций.

Пределы — полезный инструмент, помогающий нам понять форму функции вокруг значения; это один из фундаментальных строительных блоков исчисления. Мы можем найти предел любой тригонометрической функции, используя прямую замену.

Определение: оценка предела тригонометрических функций

Если 𝑎 находится в области определения тригонометрической функции, то мы можем вычислить ее предел в 𝑎 прямой подстановкой. В частности, для любого 𝑎∈ℝ

limsinsin→𝑥=𝑎,
limcoscos→𝑥=𝑎.

Для любого 𝑎 в области tan𝑥,

limtantan→𝑥=𝑎.

Эти результаты позволяют оценить предел многих тригонометрических выражений. Однако есть примеры, которые мы не можем оценить. Например, рассмотрим limsin→𝑥𝑥, где 𝑥 измеряется в радианах. Если мы попытаемся вычислить этот предел с помощью прямой подстановки, sin00=00, мы обнаружим неопределенную форму, а это означает, что нам нужно вычислить этот предел другим способом. Один из способов сделать это — нарисовать график 𝑦=𝑥𝑥sin.

На схеме видно, что по мере того, как значения 𝑥 приближаются к 0 с любой стороны, выходы функции приближаются к 1. Следовательно, схема показывает, что limsin→𝑥𝑥=1. Мы также можем увидеть это, построив таблицу.

𝑥	−0.1	−0.01	−0.001	→	0	←	0.001	0.01	0.1
sin𝑥𝑥	0.99833	0.99998	0.99999	→		←	0,99999	0,99998	0,99833

Еще раз, таблица предполагает, что по цене 𝑥 𝑥 𝑥 𝑥 𝑥 𝑥 𝑥 𝑥 𝑥 𝑥. отметив, что мы можем показать аналогичный результат, когда 𝑥 измеряется в градусах; однако при определении пределов мы почти всегда используем радианы. Итак, если не оговорено иное, будем считать, что предел любой тригонометрической функции включает в себя углы, измеряемые в радианах. Это дает нам следующий результат.

Теорема: предел тригонометрического выражения

Если 𝑥 измеряется в радианах, то limsin→𝑥𝑥=1.

Мы можем использовать этот результат, чтобы показать еще более общий результат. Пусть 𝑎∈ℝ−{0}. Подставляем 𝜃=𝑎𝑥 в предельный результат limsin→𝜃𝜃=1. Обратите внимание, что при 𝜃→0 и 𝑎𝑥→0, и 𝑥→0. Это дает нам 1 = 𝜃𝜃 = 𝑎𝑥𝑎𝑥.limsinlimsin→→

. Вынесение множителя 1𝑎 за пределы этого предела и перестановка дает нам limsin→𝑎𝑥𝑥=𝑎.

Стоит отметить, что этот результат справедлив и при 𝑎=0. Мы можем резюмировать это следующим образом.

Теорема: предел тригонометрического выражения

Если 𝑥 измеряется в радианах и 𝑎∈ℝ, то limsin→𝑎𝑥𝑥=𝑎.

Давайте рассмотрим пример использования этого результата для вычисления предела тригонометрического выражения.

Пример 1. Нахождение пределов с использованием тригонометрических функций

Оценить лимсинсин→𝑥.

Ответ

Поскольку этот предел включает частное тригонометрических функций, мы можем попытаться вычислить этот предел прямой подстановкой sin0=00.

Это дает нам неопределенную форму, что означает, что мы не можем оценить этот предел прямой подстановкой. Вместо этого мы будем использовать тот факт, что если 𝑥 измеряется в радианах, а 𝑎 является вещественной константой, то limsin→𝑎𝑥𝑥=𝑎. Хотя в вопросе не говорится, что 𝑥 измеряется в радианах, при определении пределов мы почти всегда работаем в радианах, поэтому мы будем исходить из этого для вопроса. Мы можем переписать предел следующим образом:

Предполагая, что оба предела существуют, мы можем записать это как произведение двух пределов: .

Возьмем обратное значение второго предела, используя правило степени для пределов, чтобы получить ×𝑥, если предел существует и не равен нулю. Затем мы можем оценить оба этих предела, используя наш предельный результат, limsin→𝑎𝑥𝑥=𝑎.

В первом пределе 𝑎=1, а во втором 𝑎=12. Следовательно, limsinlimsin→→𝑥𝑥×𝑥=1×12=2.

Есть еще два полезных предельных результата, связанных с тригонометрическими функциями, которые мы можем найти, исследуя их график или используя таблицу. Рассмотрим следующие наброски tan𝑥𝑥 и 1−𝑥𝑥cos, где 𝑥 измеряется в радианах.

На первой диаграмме мы видим, что по мере того, как значения 𝑥 приближаются к 0, выходы приближаются к 1. Итак, набросок предполагает limtan→𝑥𝑥=1. Точно так же на второй диаграмме, когда значения 𝑥 приближаются к 0, мы видим, что выходы приближаются к 0. Таким образом, набросок предполагает, что limcos→1−𝑥𝑥=0. Это дает нам следующие результаты.

Теорема: предел тригонометрического выражения.

Как и в случае с предельным результатом, включающим синус, мы можем использовать подстановку, чтобы найти предельный результат, где аргумент является постоянным кратным. Если 𝑎∈ℝ, используя 𝜃=𝑎𝑥, мы имеем 1=𝜃𝜃=𝑎𝑥𝑎𝑥.limtanlimtan→→

Удаление постоянного множителя 1𝑎 и перестановка дает limtan→𝑎𝑥𝑥=.

Аналогично, если 𝑎∈ℝ, используя 𝜃=𝑎𝑥, мы имеем 0=1−𝜃𝜃=1−𝑎𝑥𝑎𝑥.limcoslimcos→→

𝑎𝑥𝑥=0.

Мы можем подытожить это следующим образом.

Теорема: предел тригонометрического выражения.

Давайте рассмотрим пример того, как мы можем применить эти предельные результаты для вычисления предела тригонометрического выражения.

Пример 2. Нахождение пределов с использованием тригонометрических функций

Определить limcos→9−97𝑥3𝑥.

Ответ

Поскольку этот предел включает тригонометрическую функцию, мы можем попытаться вычислить этот предел путем прямой подстановки: 9−9(7×0)3(0)=00.cos

Это дает нам неопределенную форму, что означает, что мы не можем вычислить этот предел прямой подстановкой. Вместо этого мы будем использовать тот факт, что если 𝑥 измеряется в радианах и 𝑎∈ℝ, то limcos→1−𝑎𝑥𝑥=0.

Чтобы применить этот результат, мы упростим наш предел следующим образом: 1−7𝑥)𝑥=3×0=0.

Следовательно, limcos→9−97𝑥3𝑥=0.

В нашем следующем примере мы будем использовать предельный результат, включающий функции тангенса и синуса, для вычисления предела тригонометрической функции.

Пример 3. Нахождение пределов с использованием тригонометрических функций

Найти лимсинтан→7𝑥+33𝑥8𝑥.

Ответ

Поскольку это предел тригонометрического и алгебраического выражения, мы можем попытаться вычислить этот предел прямой подстановкой: sintan(7(0))+3(3(0))8(0) =00.

Поскольку это неопределенная форма, мы не можем определить значение этого предела из прямой подстановки. Вместо этого мы перепишем этот предел в терминах пределов, которые мы можем оценить. А именно, для любой реальной постоянной 𝑎 и 𝑥, измеряемой в радианах, limtanandlimsin→→𝑎𝑥𝑥=𝑎𝑎𝑥𝑥=𝑎.

Мы можем переписать предел в вопросе следующим образом:  → 7𝑥+33𝑥8𝑥 = 7𝑥8𝑥+33𝑥8𝑥 = 7𝑥8𝑥+33𝑥8𝑥 = 187𝑥𝑥+383𝑥𝑥 = 18хать7𝑥𝑥+383𝑥𝑥.

Мы можем оценить каждый из этих пределов отдельно. Во-первых, напомним, что если 𝑥 измеряется в радианах и константа 𝑎∈ℝ, то limsin→𝑎𝑥𝑥=𝑎. Используя этот результат, мы имеем limsin→7𝑥𝑥=7.

Далее напомним, что если 𝑥 измеряется в радианах и 𝑎∈ℝ, то limtan→𝑎𝑥𝑥=𝑎.

Следовательно, лимтан→3𝑥𝑥=3.

Подстановка значений этих пределов в уравнение дает нам 7)+38(3)=498+278=768=192.

Следовательно, лимсинтан→7𝑥+33𝑥8𝑥=192.

В нашем следующем примере мы объединим тригонометрическое тождество с предельными результатами тригонометрических функций для вычисления предела.

Пример 4. Нахождение пределов с использованием тригонометрических функций

Найти limsin→2−2𝑥4𝑥−2𝜋.

Ответ

Так как это предел тригонометрического и алгебраического выражения, мы можем попытаться вычислить этот предел прямой подстановкой: 2−24−2𝜋=00.sin является неопределенной формой, мы не можем определить значение этого предела из прямой подстановки. Вместо этого мы перепишем этот предел в терминах пределов, которые мы можем оценить. Перепишем предел следующим образом: 𝑥−.

Чтобы оценить этот предел, мы будем использовать замену 𝜃=𝑥−𝜋2. Когда 𝑥 приближается к 𝜋2, 𝜃 приближается к 0. Это дает нам limsinlimsin→→1−𝑥2𝑥−=1−𝜃+2𝜃.

Напомним, что sincos𝜃+𝜋2≡𝜃. Мы можем использовать это, чтобы переписать предел следующим образом:

Наконец, напомним, что limcos→1−𝑎𝑥𝑥=0.

Следовательно, 121−𝜃𝜃=12×0=0.limcos→

Следовательно, limsin→2−2𝑥4𝑥−2𝜋=0.

В нашем последнем примере мы будем использовать эти предельные результаты для оценки предела обратного тригонометрического выражения.

Пример 5. Нахождение пределов с использованием тригонометрических функций

Найти limcotcsc→6𝑥4𝑥8𝑥.

Ответ

Поскольку это предел тригонометрического и алгебраического выражения, мы можем попытаться вычислить этот предел прямой подстановкой. Однако 0 не находится в области определения этой функции. Вместо этого мы переписаем предел, сначала используя обратные тригонометрические идентичности: limcotcsclimlimsintan →  →  → 6𝑥4𝑥8𝑥 = 6𝑥 = 6𝑥8𝑥4𝑥.tansin

Затем мы можем переписать это с точки зрения предельных результатов. Если 𝑥 измеряется в радианах и 𝑎∈ℝ, limsinlimtan→→𝑎𝑥𝑥=𝑎,𝑎𝑥𝑥=𝑎.

Таким образом, у нас есть Limsintanlimsintanlimtanlimsinlimtanlimsinlimtanlimsinlimtanlimsin →  →  →  →  → →  → →  → → 6𝑥4𝑥4𝑥 = 6𝑥8𝑥𝑥4𝑥 = 6𝑥4𝑥8𝑥𝑥 = 6𝑥4𝑥8𝑥𝑥 = 6𝑥4𝑥8𝑥𝑥 = 64𝑥𝑥8𝑥𝑥.

Применяя предельные результаты, заключаем, что 6𝑥4𝑥8𝑥=3.

Давайте закончим повторением некоторых важных моментов из этого объяснения.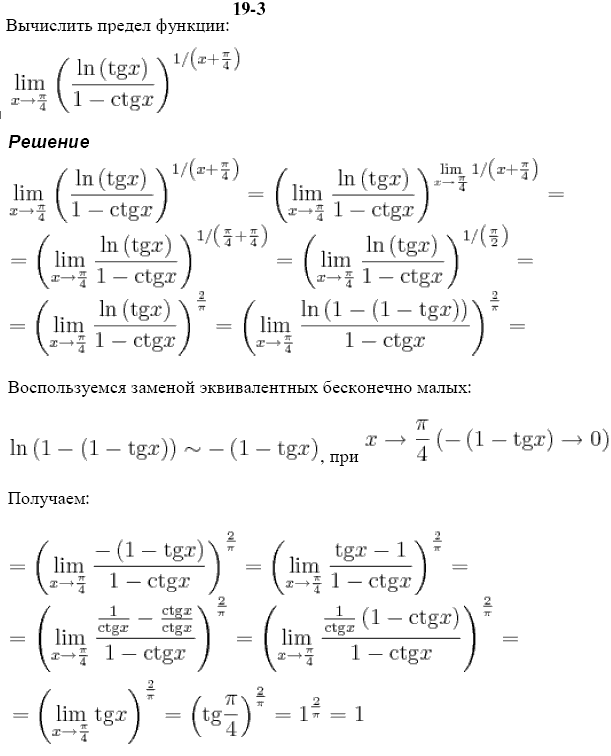

Ключевые моменты

Мы можем вычислить предел любой тригонометрической функции в точке 𝑥=𝑎 прямой подстановкой, если a находится в ее области определения.
Если 𝑥 измеряется в радианах, мы имеем следующие тригонометрические предельные результаты:

Если 𝑥 измеряется в радианах и 𝑎∈ℝ, мы имеем следующий тригонометрический предел Результаты:

Limsin → 𝑎𝑥𝑥 = 𝑎,
Limtan → 𝑎𝑥𝑥 𝑎,
Limcos → →1 −𝑎𝑥𝑥=0.

Мы можем использовать эти результаты для оценки предела тригонометрических функций.

Пределы тригонометрических функций — свойства, методы и примеры

Поскольку тригонометрические функции также подлежат оценке их предела и производной (вы узнаете об этом больше на уроках исчисления), мы должны понимать их пределы.

Это означает, что мы можем наблюдать за поведением различных тригонометрических функций по мере их приближения к различным значениям с помощью формул и свойств, используемых при оценке пределов тригонометрических функций.

Пределы тригонометрических функций, как и пределы любых функций, будут возвращать значение функции по мере приближения к определенному значению $\boldsymbol{x}$.

В этой статье мы сосредоточимся на пределах тригонометрических функций и, в частности, узнаем следующее:

Пределы основных тригонометрических функций.
Два важных предела тригонометрических функций.
Изучение способов получения пределов более сложных тригонометрических функций.

Мы также будем применять то, что узнали на наших уроках по тригонометрии, а также на наших предыдущих уроках по ограничениям, поэтому убедитесь, что ваши заметки всегда под рукой при прочтении этой статьи.

Мы можем оценить пределы тригонометрических функций, используя их различные свойства, которые мы можем наблюдать по их графикам и алгебраическим выражениям. В этом разделе мы установим следующее:

Предел всех шести тригонометрических функций, когда $x$ приближается к $a$, где $a$ находится в области определения функции.
Предел всех шести тригонометрических функций при $x$ приближается к $\pm \infty$.
Предел $\dfrac{\sin x}{x}$ и $\dfrac{1 – \cos x}{x}$ при приближении $x$ к $0$.

Давайте посмотрим на графики $y = \sin x$ и $y = \cos x$, как показано ниже.

Мы можем видеть, что пока $a$ находится в пределах области определения каждой функции, предел $y = \sin x$ и $y = \cos x$, когда $x$ приближается к $a$, может быть оценен с помощью метод замещения.

Это также относится к четырем оставшимся тригонометрическим функциям — имейте в виду, что $a$ должен принадлежать заданной области определения функции. Это означает, что когда $x = a$ является, например, вертикальной асимптотой $y = \tan x$, метод неприменим.

Пределы тригонометрических функций в виде $\boldsymbol{x \rightarrow a}$

Сведем эти пределы в таблицу:

$\boldsymbol{\lim_{x \rightarrow a} f(x) }$
$\lim_{x \rightarrow a} \sin x = \sin a$	$\lim_{x \rightarrow a} \csc x = \csc a$
$\lim_{ x \rightarrow a} \cos x = \cos a$	$\lim_{x \rightarrow a} \sec x = \sec a$
$\lim_{x \rightarrow a} \tan x = \ загар $	$\lim_{x \rightarrow a} \cot x = \cot a$

Как видно из графиков $y = \sin x$ и $y = \cos x$, функции приближаются к разным значениям от $-1$ до $1$. Другими словами, функция колеблется между значениями, поэтому мы не сможем найти предел $y = \sin x$ и $y = \cos x$ при $x \pm \infty$.

Этот аргумент применим и к остальным тригонометрическим функциям.

Пределы тригонометрических функций как $\boldsymbol{x \rightarrow \pm \infty}$

$\boldsymbol{\lim_{x \rightarrow \pm \infty} f(x)}$
\begin{align}\ lim_{x \rightarrow \pm \infty} \sin x\\ \lim_{x \rightarrow \pm \infty} \csc x \end{aligned}	Пределы не существуют для всех шести тригонометрических функций.
\begin{aligned}\lim_{x \rightarrow \pm \infty} \cos x\\ \lim_{x \rightarrow \pm \infty} \sec x \end{align}
\begin{aligned}\lim_{x \rightarrow \pm \infty} \tan x\\ \lim_{x \rightarrow \pm \infty} \cot x \end{aligned}

Это наиболее фундаментальные предельные свойства тригонометрических функций. Давайте продолжим и углубимся в более сложные выражения и посмотрим, как выглядит их поведение, когда $x$ приближается к разным значениям.

Вывод других пределов тригонометрических функций

Теорема сжатия играет важную роль в выводе пределов тригонометрических функций, поэтому не забудьте просмотреть свои заметки или статью по ссылке, чтобы быстро освежить в памяти.

Мы также будем использовать предельные законы и алгебраические методы для оценки пределов в этом разделе, поэтому не забудьте просмотреть и эти темы.

Используя темы высшей математики и теорему сжатия, мы можем доказать, что $\lim_{x \rightarrow 0} \dfrac{\sin x}{x} = 1$. Это одно из наиболее часто используемых свойств при нахождении пределов сложных тригонометрических выражений, поэтому обязательно запишите это свойство.

Теперь давайте используем $\lim_{x \rightarrow 0} \dfrac{\sin x}{x} = 1$, чтобы показать, что $\lim_{x \rightarrow 0} \dfrac{1 – \cos x}{ х} = 0$.

$\begin{aligned} \lim_{x \rightarrow 0} \dfrac{1 – \cos x}{x} &= \dfrac{1 – \cos 0}{0}\\&= \dfrac{1 – 1}{0}\\&= \color{red} \dfrac{0}{0}\end{aligned}$

Мы видим, что мы не сможем вычислить $\lim_{x \rightarrow 0} \dfrac{1 – \cos x}{x} = 0$ методом подстановки.

Вместо этого давайте поработаем с $\dfrac{1 – \cos x}{x}$, умножив его числитель и знаменатель на $ 1 + \cos x$.

$\begin{aligned} \lim_{x \rightarrow 0} \dfrac{1 – \cos x}{x}&= \lim_{x \rightarrow 0} \dfrac{1 – \cos x}{x} \cdot \dfrac{\color{blue}1 + \cos x}{\color{blue}1 + \cos x}\\&=\lim_{x \rightarrow 0} \dfrac{(1 — \cos{x }){(\color{blue}1 + \cos x)}}{x{(\color{blue}1 + \cos x)}}\end{aligned}$ 92 x}{x(1 + \cos x)}&=\lim_{x \rightarrow 0} \left( \dfrac{\sin{x}}{x} \cdot \dfrac{\sin{x}}{ 1+ \cos x} \right )\end{aligned}$

Мы можем применить закон произведения, $\lim_{x \rightarrow a} [f(x) \cdot g(x)] = \lim_{x \rightarrow a} f(x) \cdot \lim_{x \rightarrow a} g(x)$. Используйте $\lim_{x \rightarrow 0} \dfrac{\sin x}{x} = 1} и метод подстановки для оценки предела.

$\begin{align}\lim_{x \rightarrow 0} \left( \dfrac{\sin{x}}{x} \cdot \dfrac{\sin{x}}{1+ \cos x} \ right )&=\lim_{x \rightarrow 0} \dfrac{\sin{x}}{x} \cdot \lim_{x \rightarrow 0}\dfrac{\sin{x}}{1+ \cos x} \\&= 1 \cdot \lim_{x \rightarrow 0}\dfrac{\sin{0}}{1+ \cos 0}\\&= 1 \cdot \dfrac{0}{2}\\&= 0\end{выровнено}$

Таким образом, мы только что получили важное предельное свойство тригонометрических функций: $\lim_{x \rightarrow 0} \dfrac{1 – \cos x}{x} = 0$.

У нас есть еще два важных свойства, которые мы только что узнали из этого раздела:

$\lim_{x \rightarrow 0} \dfrac{\sin x}{x} = 1$
$\lim_{x \rightarrow 0} \dfrac{1 – \cos x}{x} = 0$.

Используя пределы наших шести тригонометрических функций, два специальных предела, которые мы только что изучили, и наши знания в области алгебраических и тригонометрических вычислений, мы сможем находить пределы сложных тригонометрических выражений.

Почему бы нам не проверить это и не применить то, что мы только что узнали, оценивая другие тригонометрические функции, показанные в следующих примерах?

Пример 1

Оцените значение следующего, если ограничения существуют.

а. $\lim_{x \rightarrow 0} \dfrac{\sin 6x}{6x}$
б. $\lim_{x \rightarrow 0} \dfrac{\sin 2x}{x}$
c. $\lim_{x \rightarrow 0} \dfrac{\sin 7x}{\sin 9x}$

Решение

Судя по форме трех тригонометрических выражений, можно предположить, что мы могли использовать $\ lim_{x \rightarrow 0} \dfrac{\sin x}{x} = 1$. Задача состоит в том, чтобы переписать три выражения в виде $\dfrac{\sin x}{x}$.

Начиная с $\lim_{x \rightarrow 0} \dfrac{\sin 6x}{6x}$, мы можем принять $u$ равным $6x$.

Когда $x \rightarrow 0$, $6x$ также приближается к $0$. Это также означает, что $u \rightarrow 0$.

Переписав выражение через $u$ и используя свойство $\lim_{x \rightarrow 0} \dfrac{\sin x}{x} = 1$, получим следующее:

$\begin{ выровнено} \lim_{x \rightarrow 0} \dfrac{\sin 6x}{6x} &= \lim_{u \rightarrow 0} \dfrac{\sin u}{u}\\&=1\end{выровнено} $

а. Это означает, что $\lim_{x \rightarrow 0} \dfrac{\sin 6x}{6x} = 1$.

Почему бы нам не применить аналогичный процесс для второй функции?

Если $u = 2x$ и $x \rightarrow 0$, имеем следующее:

$2x $ и, следовательно, $u$ также будет приближаться к $0$
Деление обеих частей $u = 2x$ на $2$ приведет к $\dfrac{u}{2} = x$

. Переписав выражение нашего данного, мы теперь можем оценить его предел, когда $x$ приближается к $0$, как показано ниже.

$\begin{align} \lim_{x \rightarrow 0} \dfrac{\sin 2x}{x} &= \lim_{u \rightarrow 0} \dfrac{\sin u}{\dfrac{u}{ 2}}\\&=\lim_{u \rightarrow 0} \dfrac{\sin u}{\dfrac{1}{2}u}\\&= 2\lim_{u \rightarrow 0} \dfrac{\ sin u}{u}\\&=2 \cdot 1\\&=2\end{выровнено}$

б. Следовательно, $\lim_{x \rightarrow 0} \dfrac{\sin 2x}{x} = 2$.

Третий немного сложнее, так как нам нужно алгебраически манипулировать выражением, поэтому мы можем применить формулу предела, которую мы уже знаем: $\lim_{x \rightarrow 0} \dfrac{\sin x}{ х} = 1$.

Начнем с того, что перепишем $\dfrac{\sin 7x}{\sin 9x}$ как произведение $\dfrac{\sin 7x}{x}$ и $\dfrac{x}{\sin 9x}$.

$\begin{align} \lim_{x \rightarrow 0} \dfrac{\sin 7x}{\sin 9x} &= \lim_{x \rightarrow 0} \left( \dfrac{\sin 7x}{x } \cdot \dfrac{x}{\sin 9{-1} \end{aligned}$

В таблице ниже показано, как $\lim_{x \rightarrow 0}\dfrac{\sin 7x}{x}$ и $\lim_{x \rightarrow 0}\dfrac{ \sin 7x}{x}$ можно вычислить, переписав $m$ как $7x$, а $n$ как $9x$.

$\boldsymbol{\lim_{x \rightarrow 0}\dfrac{\sin 7x}{x}}$	$\boldsymbol{\lim_{x \rightarrow 0}\dfrac{\sin 9x} {x}}$
$\begin{aligned} m &= 7x\\ \dfrac{m}{7}&= x \end{align}$	$\begin{aligned} n &= 9x\\ \dfrac{n}{9}&= x \end{aligned}$
Поскольку $x \rightarrow 0$, $7x \rightarrow 0$ и, следовательно, $m \rightarrow 0$.	Поскольку $x \rightarrow 0$, $9x \rightarrow 0$ и, следовательно, $n \rightarrow 0$.
$ \begin{aligned} \lim_{x \rightarrow 0} \dfrac{\sin 7x}{x}&=\lim_{m \rightarrow 0} \dfrac{\sin m}{\dfrac{m }{7}}\\&= 7 \cdot \lim_{m \rightarrow 0} \dfrac{\sin m}{m} \\&= 7 \cdot 1\\&= 7\end{align}$	$\begin{align} \lim_{x \rightarrow 0} \dfrac{\sin 7x}{x}&=\lim_{n \rightarrow 0} \dfrac{\sin n}{\dfrac{n}{9}}\\&= 9 \cdot \lim_{n \rightarrow 0} \dfrac{\sin n}{n} \\&= 9 \cdot 1\\&= 9\end{aligned}$

Мы использовали подход, аналогичный предыдущему пункту, для оценки двух пределов. Поскольку теперь у нас есть $\boldsymbol{\lim_{x \rightarrow 0}\dfrac{\sin 7x}{x} = 7}$ и $\boldsymbol{\lim_{x \rightarrow 0}\dfrac{\sin 9x} {x} = 9}$, мы можем подставить эти выражения в нашу основную задачу, $\lim_{x \rightarrow 0} \dfrac{\sin 7x}{x}\cdot \left(\lim_{x \rightarrow 0} \dfrac{\sin 9{-1}\\&= 7 \cdot \dfrac{1}{9}\\&= \dfrac{7}{9} \end{aligned}$

c. Это означает, что $\lim_{x \rightarrow 0} \dfrac{\sin 7x}{\sin 9x} = \dfrac{7}{9}$.

Пример 2

Оцените предел $\dfrac{\sec x -1}{x}$, когда $x$ приближается к $0$.

Решение

Замена не применима к этой задаче, поэтому мы должны использовать свойство, которое мы уже знаем. Самое близкое, что у нас может быть, это $\lim_{x \rightarrow 0} \dfrac{1 – \cos x}{x} = 0$, поскольку $\sec x$ и $\cos x$ являются отрицательными обратными величинами друг к другу.

Перепишем $\sec x$ как $\dfrac{1}{\cos x}$. Умножьте числитель и знаменатель нового выражения на $\cos x$ и посмотрим, что получится.

$\begin{align}\lim_{x \rightarrow 0}\dfrac{\sec x -1}{x} &=\lim_{x \rightarrow 0} \dfrac{\dfrac{1}{\cos x } – 1}{x}\\&=\lim_{x \rightarrow 0} \dfrac{\dfrac{1}{\cos x} – 1}{x} \cdot \dfrac{\color{blue} \cos x}{\color{blue} \cos x}\\&=\lim_{x \rightarrow 0} \dfrac{\dfrac{1}{\cos x} \cdot {\color{blue} \cos x} – 1\cdot {\color{blue} \cos x}}{x\cdot{\color{blue} \cos x}}\\&= \lim_{x \rightarrow 0}\dfrac{1-\cos x} {x\cos x}\end{выровнено}$

Мы можем переписать $\dfrac{1-\cos x}{x\cos x}$ как произведение двух множителей: $\dfrac{1-\cos x}{x}$ и $\dfrac{1} {\ соз х} $.

Применим закон произведения, $\lim_{x \rightarrow 0} [f(x) \cdot g(x)] = \lim_{x \rightarrow 0} f(x) \cdot \lim_{x \ стрелка вправо 0} g(x)$, чтобы переписать выражение.
Теперь мы можем использовать $\lim_{x \rightarrow 0} \dfrac{1 – \cos x}{x} = 0$ для первого фактора и использовать метод подстановки для второго фактора.

$\begin{aligned}\lim_{x \rightarrow 0}\dfrac{1-\cos x}{x\cos x}&= \lim_{x \rightarrow 0}\left(\dfrac{1- \cos x}{x} \cdot \dfrac{1}{\cos x}\right)\\&= \lim_{x \rightarrow 0} \dfrac{1-\cos x}{x}\cdot \lim_ {x \rightarrow 0} \dfrac{1}{\cos x}\\&=0 \cdot \dfrac{1}{\cos 0}\\&=0 \cdot 1\\&= 0\end{выровнено }$

Отсюда имеем $\dfrac{\sec x -1}{x} = 0$.

Пример 3

Оцените предел $\dfrac{2 – 2\tan x}{\cos x – \sin x}$, когда $x$ приближается к $\dfrac{\pi}{4} $.

Решение

Давайте сначала посмотрим, можно ли сразу подставить $x = \dfrac{\pi}{4}$, чтобы найти предел выражения.

$\begin{aligned}\lim_{x \rightarrow \frac{\pi}{4}} \dfrac{2 – 2\tan x}{\cos x – \sin x} &= \dfrac{2 – 2\tan \dfrac{\pi}{4}}{\cos \dfrac{\pi}{4} — \sin \dfrac{\pi}{4}}\\&= \dfrac{2 — 2(1) )}{\dfrac{\sqrt{2}}{2} – \dfrac{\sqrt{2}}{2}}\\&= \color{red} \dfrac{0}{0}\end{aligned }$

Это подтверждает, что нам придется проявить творческий подход, чтобы найти предел данной функции, поскольку он приближается к $\dfrac{\pi}{4}$.

Напомним, что $\tan{x} = \dfrac{\sin x}{\cos x}$, поэтому мы можем переписать числитель через $\sin x$ и $\cos x$. Получив новое выражение, умножьте и числитель, и знаменатель на $\cos x$.

$\begin{aligned}\lim_{x \rightarrow \frac{\pi}{4}} \dfrac{2 – 2\tan x}{\cos x – \sin x} &= \lim_{x \ стрелка вправо \frac{\pi}{4}} \dfrac{2 — 2 \cdot\dfrac{\sin x}{\cos x}}{\cos x — \sin x}\\&=\lim_{x \ стрелка вправо \frac{\pi}{4}} \dfrac{2 — 2 \cdot\dfrac{\sin x}{\cos x}}{\cos x — \sin x} \cdot \dfrac{\color{blue }\cos x}{\color{blue} \cos x}\\&=\lim_{x \rightarrow \frac{\pi}{4}} \dfrac{2 \cdot {\color{blue} \cos x } — 2 \cdot\dfrac{\sin x}{\cos x} \cdot {\color{blue} \cos x}}{(\cos x — \sin x)\cdot{\color{blue} \cos x}}\\&=\lim_{x \rightarrow \frac{\pi}{4}} \dfrac{2\cos x – 2\sin x}{\cos x(\cos x -\sin x)} \end{выровнено}$

Мы можем вынести $2$ из числителя и сократить общий множитель, общий для числителя и знаменателя.

$\begin{aligned}\lim_{x \rightarrow \frac{\pi}{4}} \dfrac{2\cos x – 2\sin x}{\cos x(\cos x -\sin x) } &= \lim_{x \rightarrow \frac{\pi}{4}} \dfrac{2(\cos x – \sin x)}{\cos x(\cos x -\sin x)}\\& =\lim_{x \rightarrow \frac{\pi}{4}} \dfrac{2\cancel{(\cos x – \sin x)}}{\cos x\cancel{(\cos x -\sin x )}}\\&= \lim_{x \rightarrow \frac{\pi}{4}} \dfrac{2}{\cos x} \end{aligned}$

Значение $\cos \dfrac{\pi}{4}$ равно $\dfrac{\sqrt{2}}{2}$, поэтому на этот раз знаменатель не будет равен нулю, когда мы используем замену метод.

$\begin{align} \lim_{x \rightarrow \frac{\pi}{4}} \dfrac{2}{\cos x}&= \dfrac{2}{\cos \dfrac{\pi} {4}}\\&= \dfrac{2}{\dfrac{\sqrt{2}}{2}}\\&= \dfrac{4 \cdot 2}{\sqrt{2}}\\&= \dfrac{8}{\sqrt{2}} \cdot \dfrac{\sqrt{2}}{\sqrt{2}}\\&= 4\sqrt{2}\end{aligned}$

Это означает что $\lim_{x \rightarrow \frac{\pi}{4}} \dfrac{2 – 2\tan x}{\cos x – \sin x} = 4\sqrt{2}$.

Этот пример также показывает, что некоторые пределы тригонометрических функций не потребуют от нас использования двух важных свойств: $\lim_{x \rightarrow 0} \dfrac{\sin x}{x} = 1$ и $\lim_{ х \rightarrow 0} \dfrac{1 – \cos x}{x} = 0$.

Вместо этого нам придется полагаться на фундаментальные свойства тригонометрических функций и их пределы.

Исчисление I — Доказательство пределов срабатывания

Уведомление для мобильных устройств

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

В этом разделе мы собираемся предоставить доказательство двух пределов, которые используются при выводе производной синуса и косинуса в разделе «Производные триггерных функций» главы «Производные».

Это доказательство этого предела использует теорему сжатия. Однако подготовка вещей для использования теоремы сжатия может быть довольно сложным геометрическим аргументом, которому может быть трудно следовать, поэтому мы постараемся сделать это довольно медленно.

Начнем с предположения, что $0 \le \theta \le \frac{\pi }{2}$. Поскольку мы доказываем предел, который имеет $\theta \to 0$, можно предположить, что $\theta $ не слишком велико ( , т.е. $\theta \le \frac{\pi }{2 }$). Кроме того, предполагая, что $\theta $ положительна, мы на самом деле собираемся сначала доказать, что указанный выше предел верен, если это правый предел. Как вы увидите, если мы сможем это доказать, доказательство предела будет легким.

Итак, теперь, когда мы позаботились о нашем предположении относительно $\theta $, давайте начнем с единичной окружности, описанной восьмиугольником с небольшим срезом, отмеченным, как показано ниже.

Точки $A$ и $C$ являются серединами соответствующих сторон восьмиугольника и фактически касаются окружности в этой точке. Назовем точку, где встречаются эти две стороны, $B$.

Из этого рисунка видно, что длина окружности меньше длины восьмиугольника. Это также означает, что если мы посмотрим на выделенный выше срез фигуры, то длина части окружности, входящей в срез, должна быть меньше длины части восьмиугольника, входящего в срез.

Поскольку мы собираемся выполнять большую часть нашей работы только над частью фигуры, давайте выделим ее и посмотрим только на нее. Вот набросок только среза.

Теперь обозначим часть круга как ${\mathop{\mbox{дуга}}\nolimits} AC$, а длины двух частей восьмиугольника, показанные как $\left| {AB} \right |$ и $\left| {BC} \right|$. Тогда по наблюдениям о длинах, которые мы сделали выше, мы должны иметь

\[\begin{equation}{\mathop{\mbox{дуга}}\nolimits} AC < \left| {АВ} \право| + \влево| {BC} \right|\label{eq:eq1}\end{equation}\]

Затем удлините линии $AB$ и $OC$, как показано ниже, и назовите точку их пересечения $D$. Треугольник, образованный теперь $AOD$, является прямоугольным треугольником. Все это показано на рисунке ниже.

Треугольник $BCD$ прямоугольный с гипотенузой $BD$, поэтому мы знаем $\left| {BC} \right| < \left| {BD} \right|$. Также обратите внимание, что $\left| {AB} \right| + \left| {BD} \right| = \left| {AD} \right|$. Если мы используем эти два факта в $\eqref{eq:eq1}$, мы получим

\[\begin{align}{\mathop{\mbox{дуга}}\nolimits} AC & < \left| {АВ} \право| + \влево| {БК} \право| \номер \\ & < \left| {АВ} \право| + \влево| {БД} \право| \номер\\ & = \влево| {AD} \право| \label{eq:eq2}\end{align}\]

Далее, как уже отмечалось, треугольник $AOD$ является прямоугольным, поэтому мы можем использовать небольшую тригонометрию прямоугольного треугольника, чтобы записать $\left| {AD} \right| = \left| {AO} \right |\танг\тета$. Также обратите внимание, что $\left| {AO} \right| = 1$, поскольку это не что иное, как радиус единичного круга. Использование этой информации в $\eqref{eq:eq2}$ дает

\[\begin{align}{\mathop{\mbox{дуга}}\nolimits} AC & < \left| {AD} \право| \номер\\ & < \слева| {AO} \right|\tan \theta \nonumber\\ & = \tan \theta \label{eq:eq3} \end{align}\]

Следующее, что нам нужно вспомнить, это то, что длина части круга равна радиусу круга, умноженному на угол (в радианах!), очерчивающий часть круга, которую мы пытаемся измерить. . Для нашей части это означает, что

\[{\mathop{\mbox{дуга}}\nolimits} AC = \left| {AO} \right|\theta = \theta \]

Прежде чем продолжить, небольшое примечание. Студенты часто спрашивают, почему мы всегда используем радианы на уроках исчисления. Вот почему! Формула длины части окружности, использованная выше, предполагала, что угол выражен в радианах. Формула для углов в градусах другая, и если бы мы использовали ее, то получили бы другой ответ. Итак, не забывайте всегда использовать радианы.

Итак, помещая это в $\eqref{eq:eq3}$, мы видим, что

\[\ theta = {\mathop{\mbox{arc}}\nolimits} AC <\tan \theta = \frac{{\sin\theta}}{{\cos\theta}}\]

или, если немного переставить, получим

\[\begin{equation}\cos\theta <\frac{{\sin\theta}}{\theta}\label{eq:eq4}\end{equation}\]

Через некоторое время мы вернемся к $\eqref{eq:eq4}$. Давайте теперь добавим еще пару строк на наш рисунок выше. Соединим $A$ и $C$ линией и опустим прямую вниз от $C$ до пересечения с $AO$ под прямым углом, и назовем точку пересечения \(E\ ). Все это показано на рисунке ниже.

Итак, первое, на что следует обратить внимание, это то, что

\[\begin{уравнение}\left| {СЕ} \право| <\слева| {АС} \право| < {\ mathop{\ mbox {дуга}} \ nolimits} AC \ label {eq: eq5} \ end {equation} \]

Также обратите внимание, что треугольник $EOC$ является прямоугольным треугольником с гипотенузой $\left| {CO} \right| = 1$. Используя триггер прямоугольного треугольника, мы можем увидеть, что

\[\слева| {СЕ} \право| = \ влево | {CO} \right|\sin \theta = \sin \theta \]

Подставив это в $\eqref{eq:eq5}$ и вспомнив, что ${\mathop{\mbox{arc}}\nolimits} AC = \theta $, мы получим,

\[\sin\theta=\left| {СЕ} \право| < {\ mathop{\ mbox {дуга}} \ nolimits} AC = \ тета \]

и немного переписав получаем,

\[\begin{equation}\frac{{\sin\theta}}{\theta} < 1 \label{eq:eq6} \end{equation}\]

Итак, мы почти закончили. Соединяя $\eqref{eq:eq4}$ и $\eqref{eq:eq6}$, мы видим, что

\[\ соз \ тета < \ гидроразрыва {{\ грех \ тета}} {\ тета} < 1 \]

при условии $0 \le \theta \le \frac{\pi }{2}$. Отметим также, что

\[\ mathop {\lim}\limits_{\theta\to 0} \cos\theta = 1\hspace{0,75in}\mathop {\lim}\limits_{\theta\to 0} 1 = 1\] 9+ }} \ frac {{\ sin \ theta}} {\ theta} = 1 \]

Итак, мы знаем, что предел верен, если мы работаем только с правым пределом. Однако мы знаем, что $\sin\theta$ — нечетная функция, поэтому

\[\frac{{\sin \left( { — \theta} \right)}}{{ — \theta}} = \frac{{ — \sin \theta}}{{ — \theta}} = \frac {{\ грех \ тета}} {\ тета} \]

Другими словами, если мы приближаемся к нулю слева ( 9- }} \frac{{\sin\theta}}{\theta} = 1\]

Теперь мы показали, что два односторонних предела одинаковы, поэтому мы также должны иметь

\[\ mathop {\lim}\limits_{\theta\to 0} \frac{{\sin\theta}}{\theta} = 1\]

Это было довольно длинное доказательство, и если вы не очень хорошо разбираетесь в геометрических аргументах, оно может быть пугающим и запутанным. Хорошо, второй предел очень просто доказать, если вы уже доказали первый предел. 92}\theta}}{{\theta\left({\cos\theta+1}\right)}}\\ & = \mathop {\lim}\limits_{\theta\to 0} \frac{{\ грех \ тета} {\ тета} \ гидроразрыв {{ — \ грех \ тета}} {{\ соз \ тета + 1}} \\ & = \ mathop {\ lim} \ limits _ {\ тета \ до 0} \ frac{{\sin\theta}}{\theta}\,\,\,\mathop {\lim}\limits_{\theta\to 0} \frac{{ — \sin\theta}}{{\cos\ тета + 1}}\конец{выравнивание*}\]

На этом этапе, поскольку мы только что доказали первый предел, а второй можно использовать напрямую, мы почти закончили. Все, что нам нужно сделать, это принять ограничения.

\[\ mathop {\ lim} \ limits _ {\ theta \ to 0} \ frac {{\ cos \ theta — 1}} {\ theta} = \ mathop {\ lim} \ limits _ {\ theta \ to 0} \ frac{{\sin\theta}}{\theta}\,\,\,\mathop {\lim}\limits_{\theta\to 0} \frac{{ — \sin\theta}}{{\cos\ тета + 1}} = \влево( 1 \вправо)\влево( 0 \вправо) = 0\]

6.

1.3 Пределы тригонометрических функций

Исчисление одной действительной переменной автора Pheng Kim Ving

Глава 6. Тригонометрические функции и их обратные значения Раздел 6.1.3. Пределы тригонометрических функций

6.1.3
Пределы О тригонометрических функциях

Возврат К содержанию
Перейти к проблемам и решениям

1. Бесконечные пределы

Следующие бесконечные пределы могут легко представить на рис. 1.1.

Конечно, эти пределы можно доказать. используя определения функций через синус и косинус функции. Для
пример:

Перейти Проблемы и решения Вернуться к началу страницы

2. Без ограничений в бесконечности

Перейти Проблемы и решения Вернуться к началу страницы

3. Основной предел

Теорема 3.

Пусть x будет углом измеряется в радианах. Тогда:

Доказательство
Предположим x — маленькое и позитивное. Ссылаться на Рис. 3.1. Наглядно:

(площадь треугольника ОПУ ) < (площадь кругового сектора OPA ) < (площадь треугольника ОЗА ).

Теперь предположим, что x мало и отрицательный. Пусть т = х > 0. Затем, используя тождество sin ( x ) = sin x получаем:

EOP

Необходимость измерения в радианах

измеряется в радианах, чтобы получить тот факт, что значение площади
круговой сектор OPA составляет (1/2) x . Что произойдет, если x не в радианах? Давайте сделаем некоторые числовые расчеты, как показано в
Рис. 3.3, чтобы увидеть, что произойдет, если x измеряется в градусах.

ОК. Что произойдет, если x не в радианах? это уравнение [3.1] больше не действует. Следовательно, условие теоремы 3.1, что
угол x измеряется в радианах, действительно необходимое для заключения, уравнение [3.1], чтобы быть действительным.

Обратите внимание, что тригонометрические тождества, такие как sin ² x + cos ² x = 1 или sin ( х + и ) = грех x , потому что и + потому что x sin y не требуется
что угол x выражен в радианах. Для таких идентичности, единицей измерения для x может быть градус, а также радиан.
Для их установления не требовалось, чтобы они были в каком-то конкретном подразделении.

Это А Основной предел

Предел в уравнении [3.1] классифицируется как фундаментальный тригонометрический предел. Причина в том, что это, ну, фундаментальный, или базовый,
в развитии исчисления тригонометрических функций. Как мы увидим, производные тригонометрических функций,
среди прочего, получаются при использовании этого предела.

Примечание 3.1

Перейти к проблемам и решениям Вернуться к началу Страница

4. Фундаментальный предел, применяемый к синусу функций

Example 4.1

Find:

Solution 1

EOS

Решение 2

EOS

Общий случай

В общем случае мы можем использовать это правило:

Используя это правило, аргумент греха и знаменатель должен быть той же функцией. В приведенном выше утверждении правила
аргумент sin и знаменатель функции ф ( х ).

Evaluate:

Solution

EOS

Example 4.3

Find:

Solution

EOS

Перейти к проблемам и решениям Вернуться к началу Страница

5. Предел частных, включающих косинус

Итак:

Примечания 5.1

i. Так как мы используйте уравнение [3. 1], чтобы вывести уравнение [5.1], угол х в уравнении. [5.1] должны измеряться в радианах, чтобы
уравнение, чтобы быть действительным.

Вернуться к началу страницы

Проблемы и решения

1. Найти каждое из следующих пределов, если он существует.

Решение

Наверх

из следующих пределов, если он существует.

Решение

не существует.

Вернуться наверх

3. Найти каждый из следующих пределов, если он существует.

Решение

Возврат к вершине страницы

9098 4. 99999999999999999999. 9999999999999. 99999999999. 9999999999. из следующих пределов, если он существует.

Решение

Возврат в верхнюю часть страницы

5. Найти каждый из следующих пределов, если он существует. Решение К содержанию

Пределы тригонометрических функций | Класс 11 Математика

Как известно, существует шесть тригонометрических функций. Предел каждой функции, стремящейся к точке, можно вычислить в соответствии с непрерывностью функции, учитывая ее область определения и область значений. На графике каждой функции мы можем наблюдать, что предел каждой функции в одной и той же точке различен.

Синусоидальная функция

Функция f(x) = sin(x) является непрерывной функцией во всей своей области определения, причем область определения состоит из всех действительных чисел. Диапазон этой функции составляет [-1, 1], как показано на графике ниже:

Таким образом, если предел функции синуса вычисляется для любого заданного действительного числа, он всегда определен и лежит между [-1, 1].

f(x) = sin(x)
lim _x→a f(x) = lim _x→a sin(x)
= sin (a), где A является реальным числом

Пример 1: Найдите LIM _{x → π/2} SIN (x)

Решение:

. ) определяется при π/2
Следовательно,
LIM _{x → π/2} SIN (x) = SIN (π/2) = 1

Пример 2: Найдите LIM _{x → π} SIN (SIN ( x)

Решение:

Как мы знаем, sin(x) определяется при π
Следовательно,
LIM _{x → π} sin (x) = sin (π) = 0

Косинусная функция

Функция f (x) = cos (x) является непрерывной функцией по всему домену , область определения которого состоит из всех действительных чисел.

Диапазон этой функции равен [-1, 1], как показано на графике ниже:

Таким образом, если предел функции косинуса вычисляется для любого заданного действительного числа, он всегда определен и лежит между [ -1, 1].

f(x) = cos(x)
lim _x→a f(x) = lim _x→a cos(x)
= cos(a), где a0 — действительное число Решение: lim _x→π/2 cos(x) = cos(π/2) = 0

Пример 2: Найдите LIM _{x → π} COS (x)

Решение:

as We Know Cos (x). _x→π cos(x) = cos(π) = -1

Функция тангенса

Функция f(x) = tan(x) определена для всех действительных чисел, за исключением значений, где cos(x) равно равным 0, то есть значениям π/2 + πn для всех целых чисел n. Таким образом, его областью определения являются все действительные числа, кроме π/2 + πn, n 6 Z.

Диапазон этой функции: (-∞, +c).

Итак, если предел касательной функции вычисляется в своей области определения, он всегда определен и лежит между (-∞, +∞).

f(x) = tan(x)
lim _x→a f(x) = lim _x→a tan(x)
= tan(a), где a принадлежит вещественному номеру. кроме π/2 + πn, n € Z

Пример 1. Найти lim _x→π/2 tan(x)

Решение:

Как мы видим на графике, tan(x) стремится к +∞ при x→-π/2 и к -∞ при x→+π/2
Итак, правый и левый пределы этого функции в π/2 не совпадают
Следовательно,
lim _x→π/2 tan(x) = не определено

Решение:

Поскольку мы знаем, что tan(x) непрерывен и определен в точке π
Следовательно,
lim _x→π tan(x) = tan(π) = 0

Функция Cosec

Функция f(x) = cosec(x) определена для всех действительных чисел, кроме значений, где sin(x) равен 0, т. е. есть значения πn для всех целых чисел n. Таким образом, ее областью определения являются все действительные числа, кроме πn, n € Z.

Диапазон значений этой функции равен (-∞,-1] U [1,+∞).

Итак, если предел функции косинуса вычисляется в своей области определения, то он всегда определен и лежит между ее диапазоном.

f(x) = cosec(x)
lim _x→a f(x) = lim _x→a cosec(x)
= cosec(a), где a принадлежит вещественному номеру. except for πn , n € Z

Example 1: Find lim _x→ _π _cosec(x)

Solution:

As we know sin(x) равен 0 при x→ π
Итак, 1/sin(x), т. е. cosec(x) при π нельзя определить
Следовательно,
Lim _{x →} _π COSEC (x) = не определено

Пример 2: найдите LIM _{x →}

. _/2 cosec(x)

Solution:

As we know tan(x) is continuous and defined at π /2
Therefore,
lim _x→ _π _/2 cosec(x) = cosec( π /2) = 1

Функция секанса

Функция f(x) = sec(x) определена для всех действительных чисел, кроме значений, где cos( x) равно 0, то есть значениям π/2 + πn для всех целых чисел n. Таким образом, ее областью определения являются все действительные числа, кроме π/2 + πn, n € Z.

Диапазон значений этой функции равен (-∞, -1] U [1, +∞)

Итак, если предел сек. функция вычисляется в своей области, которую она всегда определяет, и лежит между ее диапазоном. 9где принадлежит реальному нет. except for π/2 + πn, n € Z

Example 1: Find lim _x→ _π _/2 sec(x)

Solution:

Как мы знаем, cos(x) равен 0, поскольку x→ π /2
Таким образом, 1/cos(x), т. е. sec(x) при π /2, не может быть определено defined

Example 2: Find lim _x→ _π sec(x)

Solution:

As we know tan(x) is continuous and defined at π
Следовательно,
lim _x→ _π cosec(x) = sec( π ) = -1

Функция Cot

Функция f(x) = cot(x) определена для всех вещественных чисел, за исключением значений, где tan( x) равно 0, то есть значения πn для всех целых чисел n. Таким образом, ее областью определения являются все действительные числа, кроме πn, n € Z.

Диапазон значений этой функции равен (-∞, +∞)

Итак, если предел функции ctg вычисляется в ее области определения, она всегда определена и лежит между его диапазоном.

f(x) = кроватка(х)
lim _x→a f(x) = lim _x→a кроватка(x)
к реальному нет. кроме для πn, n € Z

Пример 1. Найти lim _x→π cot(x)

Итак, 1/tan(x), т. е. cot(x) в точке π не может быть определена

Следовательно,

limx→π cot(x) = Не определено

Пример 2. Найти lim _x→π/2 cot(x)

Решение:

Как известно, cot(x) непрерывен и определено в π/2
Следовательно,
lim _x→π/2 cot(x) = cot(π/2) = 0

Теорема сэндвича (теорема сжатия)

Теорема используется для вычисления предел тех функций, предел которых нельзя легко вычислить, например (sin x/x at x = 0).

Функция g(x) сжата или зажата между двумя функциями h(x) и g(x) таким образом, что f (x) ≤ g(x) ≤ h(x ) .

График при таких условиях можно увидеть следующим образом:

Мы можем сказать, что h(x) — это верхний предел g(x), а f(x) — его нижний предел в точке a, как это может быть наблюдается на графике выше:

if,
lim _x→a h(x) = L и lim _x→a f(x) = L,
, где a — это точка , в которой рассчитывается предел, а L — значение предела
Тогда
lim = _x3

Пример 1: Дано: g(x) = x2sin(1/x), Найти: lim _x→0 g(x)

Решение:

Мы знаем,
3 — 1 sin(1/x) ≤ 1 в своей области определения
Умножение на x2,
-x2 ≤ x2sin(1/x) ≤ x2
Тогда пусть f(x) = -x2 и h(x) = x2
f(x) ≤ g(x) ≤ h(x)
Используя сэндвич теорема,
As lim _x→a h(x) = lim _x→a f(x) = L
Следовательно,
lim _x→a g(x) = L
lim _x→0 f(x) = lim _x→0 -x2 = 0 и
lim _x→0 h(x) = lim _x→0 x2 = 0
Следовательно,
2 lim 2 х→0 г(х) = 0

Пример 2: Дано: g(x) = cos(x)/x, Найти: lim _x→∞ g(x)

Решение:

Мы знаем,
-1≤
cos(x)≤ 1 в своей области определения
Деление на x,
-1/x ≤ cos(x)/x ≤ 1/x
Тогда пусть f(x) = -1/x и h(x) = 1/x
f(x) ≤ g(x) ≤ h(x)

Используя теорему сэндвича,
As lim _{x→a 5 ) = L}
Следовательно,
lim _x→a g(x) = L
lim _x→∞ f(x) = lim _x→∞ -1/x→ 0 и 2lim x→
∞ H (x) = LIM _{x → ∞} 1/x = 0
Следовательно,
Lim _{x → ∞} G (x) = 0

Расчет ограничений из тригонарических функций
810

Рассчитанный Представлено несколько примеров нахождения пределов тригонометрических функций с подробными решениями и упражнениями с ответами.
Примеры с решениями
Пример 1
Найдите предел
lim _x→0 (1 — cos x) / x
Решение примера 1:
Умножим числитель и знаменатель (1 — cos x) / x на (1 + cos x) и запишем
lim _x→0 (1 — cos x) / x
= lim _x→0 [ (1 — cos x) / x ] *[ (1 + cos x) / (1 + cos x) ]
Числитель становится 1 — cos ² x = sin ² х, следовательно
lim _x→0 (1 — cos x) / x
= lim _x→0 [ (sin ² x) / x ] *[ 1/ (1 + cos x) ]
Предел может быть записан
lim _x→0 (1 — cos x) / x
= lim _x→0 [ (sin x) / x ] * lim _x→0 [ sin x / (1 + cos x) ] = (1)(0/2) = 0
Мы воспользовались теоремой: lim _x→0 [ (sin x) / x ] = 1
Пример 2
Найдите предел lim _x→0 sin 4 x / 4 x
Решение примера 2:
Пусть t = 4x. Когда x приближается к 0, t = 4x приближается к 0, так что
lim _x→0 sin 4 x / 4 x = lim _t→0 sin t / t
Теперь воспользуемся теоремой: lim _t→0 sin t / t = 1, чтобы найти предел
Найти предел lim _x→0 sin 4 x / 4 x = lim _t→0 sin t / t = 1
Пример 3
Найдите предел lim _x→0 sin 6 x / 5 x
Решение примера 3:
Пусть t = 6 x или x = t / 6. Когда x приближается к 0, t = 6 x приближается к 0, так что
lim _x→0 sin 6 x/5 x = lim _t→0 sin t/(5 t/6)
= lim _t→0 (6 / 5) sin t / t
= (6 / 5) lim _t→0 sin t / t
= (6/5) * 1 = 6/5
Пример 4
Найдите предел lim _x→-3 sin (x + 3) / (x ² +7x + 12)
Решение примера 4:
Если применить теорему о пределе частного двух функций, то получим неопределенный вид 0/0. Нужно найти другой путь. Для x = -3 знаменатель равен нулю и, следовательно, может быть разложен на множители, следовательно
lim _x→-3 sin (x + 3) / (x ² +7x + 12)
= lim _x→-3 sin (x + 3) / (x + 3)(x + 4)
Пусть t = x + 3 или x = t — 3. Когда x приближается к -3, t приближается к 0.
lim _x→-3 sin (x + 3) / (x ² +7x + 12)
= lim _x→-3 sin (x + 3) / (x + 3)(x + 4)
= lim _t→0 sin t / [ t (t + 1) ]
Применим теперь теорему о пределе произведения двух функций.
= lim _t→0 sin t / t * lim _t→0 1 / (t + 1)
= (1)*(1) = 1
Пример 5
Найдите предел lim _x→0 sin | х | / Икс
Решение примера 5:
Мы найдем предел при приближении x к 0 слева и при приближении x к 0 справа. Для х < 0, | х | = - х
lim _{x→0 ^—} sin | х | / Икс
= lim _{x→0 ^—} sin (- x ) / x
= — lim _{x→0 ^—} sin ( x ) / x
= -1
Для х > 0, | х | = х
lim
_{x→0 ⁺} sin | х | / Икс
= lim _{x→0 ⁺} sin x / x
= 1
Два предела слева и справа различны, поэтому указанный выше предел не существует.
lim _x→0 sin | х | /х не существует
Пример 6
Найдите предел lim _x→0 x / tan x
Решение примера 6:
Сначала используем тригонометрическое тождество tan x = sin x / cos x
= -1
lim _x→0 x / tan x
= lim _x→0 x / (sin x / cos x)
= lim _x→0 x cos x / sin x
= lim _x→0 cos x / (sin x / x)
Воспользуемся теперь теоремой о пределе частного.
= [ lim _x→0 cos x ] / [ lim _x→0 sin x / x ] = 1 / 1 = 1
Пример 7
Найдите предел lim _x→0 x csc x
Решение примера 7:
Сначала используем тригонометрическое тождество csc x = 1 / sin x
lim _x→0 x csc x
= lim _x→0 x / sin x
= lim _x→0 1 / (sin x / x)
Используется предел частного.
No related posts.
Навигация по записям
Предыдущая статьяОнлайн калькулятор сравнение дробей: Сравнения дробей онлайн.
Следующая статьяКотангенс четная или нечетная: HTTP 404 Resource not found
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Найти:
Рубрики
Геометрия
Математика
Физика
Химия
Школьная жизнь
Разное
© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»
Карта сайта