Электронный справочник по математике для школьников тригонометрия свойства тригонометрических функций знаки период четность нечетность синуса косинуса тангенса котангенса
| Справочник по математике | Тригонометрия |
Содержание
| Знаки тригонометрических функций |
| Периодичность тригонометрических функций |
| Четность тригонометрических функций |
Знаки тригонометрических функций
Знаки чисел
sin α , cos α , tg α , ctg α
определяются тем, в каком квадранте (четверти) координатной плоскости Oxy лежит луч OM (рисунки 1, 2, 3, 4).
| Рис.1. Знак sin α | Рис.2. Знак cos α |
| Рис.3. Знак tg α | Рис.4. Знак ctg α |
| Рис.1. Знак sin α |
| Рис.2. Знак cos α |
| Рис.3. Знак tg α |
| Рис.4. Знак ctg α |
Периодичность тригонометрических функций. Полупериодичность синуса и косинуса
Рассмотрим рисунок 5.
Рис.5
Если луч OM1, изображенный на рисунке 5, повернуть по ходу или против хода часов на полный угол (360 градусов или 2π радиан), то он совместится с самим собой. Следовательно, справедливы формулы:
sin (α° + 360°) = sin α°, cos (α° + 360°) = cos α°,
sin (α° – 360°) = sin α°, cos (α° – 360°) = cos α°,
а также формулы:
sin (α + 2π) = sin α , cos (α + 2π) = cos α ,
sin (α – 2π) = sin α, cos (α – 2π) = cos α .
Поворачивая луч OM1 на полный угол по ходу или против хода часов n раз ( 360n градусов или 2nπ радиан), получаем следующие формулы:
Таким образом, в случае, когда углы измеряются в градусах, периодами синуса и косинуса являются углы 360° n, .
В случае, когда углы измеряются в радианах, периодами синуса и косинуса являются числа 2nπ, .
В случае, когда углы измеряются в градусах, наименьшим положительным периодом синуса и косинуса является угол 360°.
В случае, когда углы измеряются в радианах, наименьшим положительным периодом синуса и косинуса является число 2π .
Теперь рассмотрим рисунок 6.
Рис.6
Если луч OM1, изображенный на рисунке 6, повернуть по ходу или против хода часов на развернутый угол (180 градусов или π радиан), то он совместится с лучом OM2 . Следовательно, справедливы формулы:
Следовательно, справедливы формулы:
sin (α° + 180°) = – sin α°, cos (α° + 180°) = – cos α°,
sin (α° – 180°) = – sin α°, cos (α° – 180°) = – cos α°,
а также формулы:
sin (α + π) = – sin α , cos (α + π) = – cos α ,
sin (α – π) = – sin α, cos (α – π) = – cos α.
Полученные формулы описывают свойство полупериодичности синуса и косинуса.
Таким образом, в случае, когда углы измеряются в градусах, угол 180° является полупериодом синуса и косинуса.
В случае, когда углы измеряются в радианах, полупериодом синуса и косинуса является число π.
СЛЕДСТВИЕ. Поскольку
то справедливы формулы:
Таким образом, в случае, когда углы измеряются в градусах, периодами тангенса и котангенса являются углы 180° n,
В случае, когда углы измеряются в радианах, периодами тангенса и котангенса являются числа nπ, .
В случае, когда углы измеряются в градусах, наименьшим положительным периодом тангенса и котангенса является угол 180°.
В случае, когда углы измеряются в радианах, наименьшим положительным периодом тангенса и котангенса являются число π.
Четность тригонометрических функций
Рассмотрим рисунок 7.
Рис.7
На этом рисунке
Следовательно, справедливы формулы:
sin ( – α ) = – sin α , cos ( – α ) = cos α ,
откуда вытекают формулы:
tg ( – α ) = – tg α , ctg ( – α ) = – ctg α .
Таким образом, косинус – четная функция, а синус, тангенс и котангенс – нечетные функции.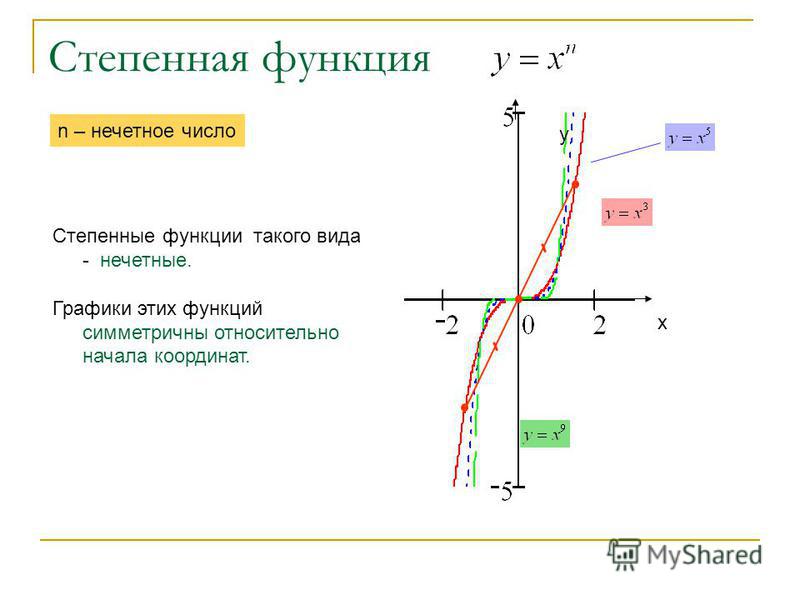
Конспект урока по математике по теме: «Четные и нечетные функции». | План-конспект урока на тему:
Четные и нечетные функции
Тип урока: комбинированный.
Технологии:
1) Здоровьесберегающая образовательная технология
2) Технология уровневой дифференциации
Цели урока: формирования у обучающихся представлений о четной и нечетной функции, закрепить эти понятия в ходе выполнения упражнений, способствовать развитию понятия о свойстве графиков четных и нечетных функций, навыков построения графиков функций; развитие алгоритмической культуры учащихся; воспитание добросовестного отношения у учащихся к учебному труду.
Оборудование: разноуровневые карточки-задания.
Ход урока
1. Актуализация знаний.
1) что мы называем числовой функцией?
(Числовой функцией с областью определения D называется соответствие, при котором каждому числу х из множества D сопоставляется по некоторому правилу число y, зависящее от х.)
2) что такое область определения функции?
( Все допустимые значения х)
3) что такое область значения функции?
( Все допустимые значения у)
4) Найдите область определения функции:
а) у=1/ х (D(f):x≠0)
б) у = (D(f) = (−∞;−2) υ (2;∞))
5) найдите область значения функции:
а) у = cos х (E(f): [-1;1])
6) начертите график функции у = соs х и у = sin x
(два человека у доски)
2. Изучение нового материала.
Изучение нового материала.
Посмотрите внимательно на доску, перед вами графики функций косинуса и синуса. Что у них общего и что их отличает?
( Общее у них область определения и область значения функций, отличает их симметрия относительно 0)
Рассмотрим у = соs х
Если у=0, =+2Пn, nєΖ
=+2Пn, nєΖ
То есть значение функции в т. = и т.= равно.
Другими словами f(-x)=f(x), такую функцию называют чётная.
Запишем определение:
Функция f называется четной, если для любого х из её области определения f(-x)=f(x).
Теперь рассмотрим у = sin x
Мы видим, что f(-x)=-f(x), такую функцию называют нечетной.
Запишем определение:
Функция f называется нечетной, если для любого х из её области определения f(-x)=-f(x).
Из тригонометрических функций только косинус является четной функцией, а синус, тангенс и котангенс являются нечетными.
Как вы видите:
-График четной функции симметричен относительно оси ординат (оси ОУ).
-График нечетной функции симметричен относительно начала координат.
Примеры:
1. Рассмотрим функцию f(x)=, выясним четная она или нечетная?
1)D(f):(−∞;∞),область определения симметрична относительно нуля.
2) f(-x)==, f(-x)= f(x), f- четная.
2. Рассмотрим функцию f(x)=, выясним четная она или нечетная?
1)D(f):(−∞;∞),область определения симметрична относительно нуля.
2) f(-x)==, f(-x)= -f(x), f-нечетная.
3. Следующая функция f(x)=+
1)D(f):(−∞;∞),область определения симметрична относительно нуля.
2) f(-x)==, f(-x)≠ -f(x), f(-x)≠ f(x),f-ни четная ни нечетная, т.е. функция общего вида.
3. Физминутка.
Закройте глаза и представьте перед собой большой белый экран. Необходимо мысленно раскрасить этот экран поочерёдно любым цветом: например, сначала жёлтым, потом оранжевым, зелёным, синим, но закончить раскрашивание нужно самым любимым цветом.
Отдохнули, теперь продолжаем.
4. Решение задач на закрепление темы.
1. № 57(а, б) вместе у доски разбираем.
2. №59(а, б) вместе у доски разбираем.
3.Прежде чем делать следующий номер, давайте вспомним как расположен график четной функции? А нечетной?
(график четной функции симметричен относительно оси ОУ)
(график нечетной функции симметричен относительно начала координат)
№ 61
5. Самостоятельная работа: разноуровневые карточки-задания.
Слабые учащиеся при выполнении задания № 1 получают карточку инструкцию.
Сильные учащиеся, выполнившие задания карточки, получают дополнительную карточку.
6. Подведение итогов урока, выставление оценок.
7. Домашнее задание: № 58, № 60.
Используемая литература
1. Колмогоров А.Н. Алгебра и начала анализа: Учебник для 10 –11 кл. общеобразоват. учреждений. М.: Просвещение, 2010. – 384с.: ил
Электронные образовательные ресурсы
- http://ru.wikipedia.org/wiki
- http://festival.1september.ru
Приложение.
КАРТОЧКА-ИНСТРУКЦИЯ К РЕШЕНИЮ ПРИМЕРОВ НА ПРОВЕРКУ ЧЕТНОСТИ И НЕЧЕТНОСТИ ФУНКЦИИ
Рассмотрим числовую функцию f(x)=3×2-5×4.
Для того чтобы выяснить четная или нечетная функция необходимо:
— найти область определения функции D(f) (значения для x) и показать, что эта область симметрична относительно 0.
— найти f(-x) и если:
f(-x)= f(x), то функция четная, а если f(-x)=-f(x), то функция нечетная.
РЕШЕНИЕ.
Так как в функцию f(x) в качества x можно подставить любое число, то D(f)=R и данное множество симметрично относительно 0.
Найдем f(-x), т.е. вместо x подставляем -x: f(-x)=3(-x)2-5(-x)4=3×2-5×4= f(x).
Таким образом, функция f(x)=3×2-5×4 является четной.
карточка №1.
Докажите, что функция f(x)=4х3+7х является нечетной.
Приведите пример четной функции.
карточка №2.
Докажите, что функция f(x)=16х6 — 3х4 является четной.
Приведите пример нечетной функции.
карточка №3.
- назовите номер графика четной функции;
- назовите номер графика нечетной функции;
- назовите номер графика функции, которая не является четной и не является нечетной;
Карточка №4.
Задание № 1: Проверьте, является ли четной или нечетной функция, заданная формулой:
1) g(х) = (Sinх)2 + 5х6
2) f(х) = 2х3 + 8x
3) k(х) = 5х2 + 3х + 5
Задание № 2: Дан фрагмент графика функции g(х), которая определена на [-10; 10]. Достройте график, если функция g(х):
— четная;
— нечетная.
Задание № 3. Периодическая функция y=f(x) с периодом, равным 3, определена на множестве всех действительных чисел. Известно, что f(2)=5, f(0)=-2. Найдите значение выражения 3f(8)-5f(-3).
Карточка №5.
Задание 1. Выяснить является ли функция четной или нечетной.
1) f(x)=x3+2Sinx+ctgx 2) f(x)=-3×2+2Cosx+3xSinx
Задание 2. Найдите значение функции y(x)=(3f(x)-f(-x))/(2g(x)-g(-x)) в точке x0, если известно, что функцияy=f(x) — четная, функция y=g(x) — нечетная, f(x0)=-3, g(x0)=2.
Задание 3. Функция y=f(x) определена на всей числовой прямой и является четной периодической функцией с периодом, равным 8. На отрезке [0;4] функция y=f(x) задана равенством f(x)=-x2+4x-1. Определите количество нулей функции y=f(x)на отрезке [-6;4].
Определите количество нулей функции y=f(x)на отрезке [-6;4].
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Тригонометрические тождества.
Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
.
Это соотношение называется основным тригонометрическим тождеством.
Если это уравнение поделить на квадрат косинуса и синуса соответственно имеем далее: и
Из определений тангенса и котангенса имеем, что .
Формулами приведения называются формулы следующего вида:
Здесь – любая тригонометрическая функция, – соответствующая ей кофункция (то есть косинус для синуса, синус для косинуса, тангенс для котангенса, котангенс для тангенса, секанс для косеканса и косеканс для секанса), n – целое число. Перед полученной функцией ставится тот знак, который имеет исходная функция в заданной координатной четверти при условии, что угол α острый, например:
.
Правила преобразования:
1) Если аргумент содержит где – нечетное натуральное число , то функция меняется на «конфункцию», т.е. синус на косинус, тангенс на котангенс и наоборот. Если – четное натуральное число , то название функции не изменяется.
2) Определяем знак («+» или «–») значения первоначальной функции. Преобразованное выражение сохраняет знак своего родителя.
Формулы сложения
Значения тригонометрических функций суммы и разности двух углов:
Формулы для кратных углов
Формулы двойного угла:
Формулы половинного угла:
Произведения
Формулы для произведений функций двух углов:
Суммы
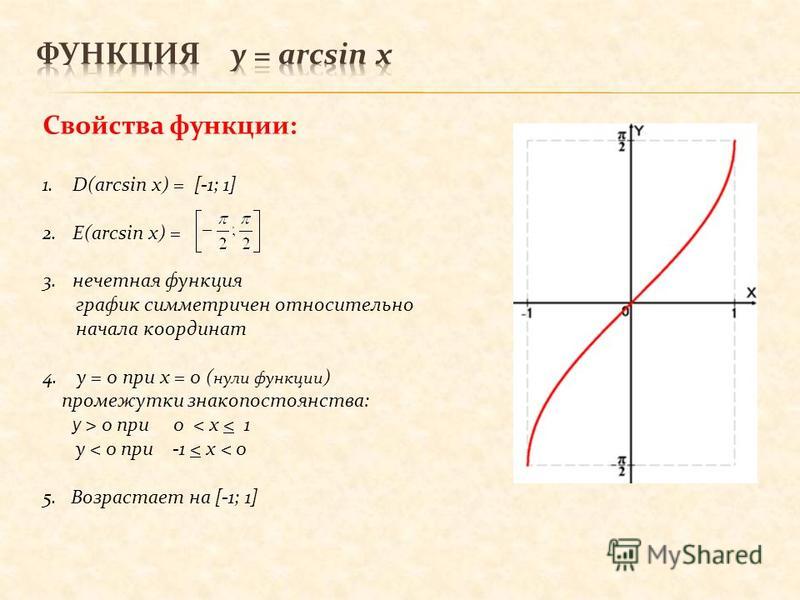
Обратные тригонометрические функции и их свойства. Арксинус, арккосинус, арктангенс, арккотангенс.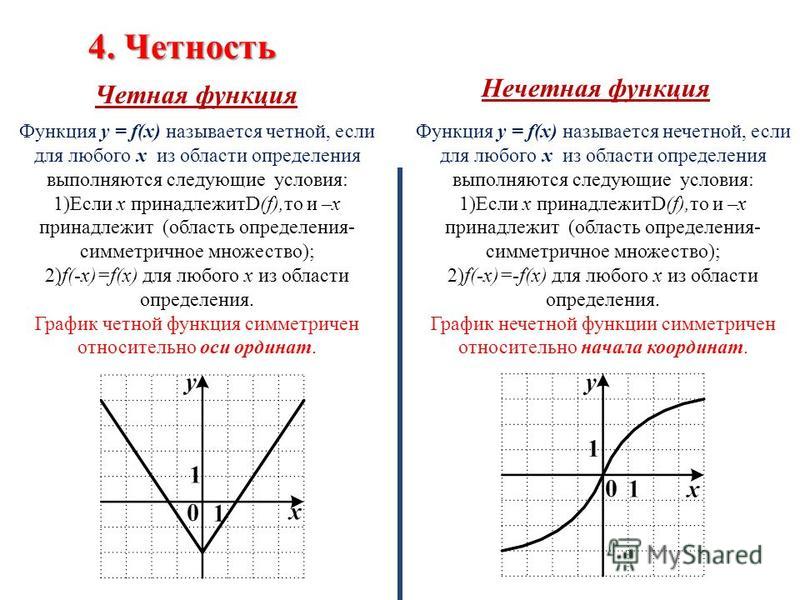
Функция
1.
2.
3.
4. функция нечетная, то есть
5. при ;
6. при ;
7. при ;
8. при ;
9. при .
Функция
1. ;
2.
3.
4. функция ни четная, ни нечетная, причем
5. при ;
6. при ;
7. при ;
8. при .
Функция
1.
2.
3.
4. функция нечетная, то есть
5. при ;
6. при ;
7. при ;
8. график функции имеет 2 асимптоты:
Функция
1.
2.
3.
4. функция ни четная, ни нечетная, причем
5. ни при каких ;
6. при ;
7. график функции имеет 2 асимптоты:
Тема 2.2 Обратные тригонометрические функции. Тригонометрические уравнения и неравенства
Простейшие тригонометрические уравнения. Решения тригонометрических уравнений. Простейшие тригонометрические неравенства. Арксинус, арккосинус, арктангенс, арккотангенс числа.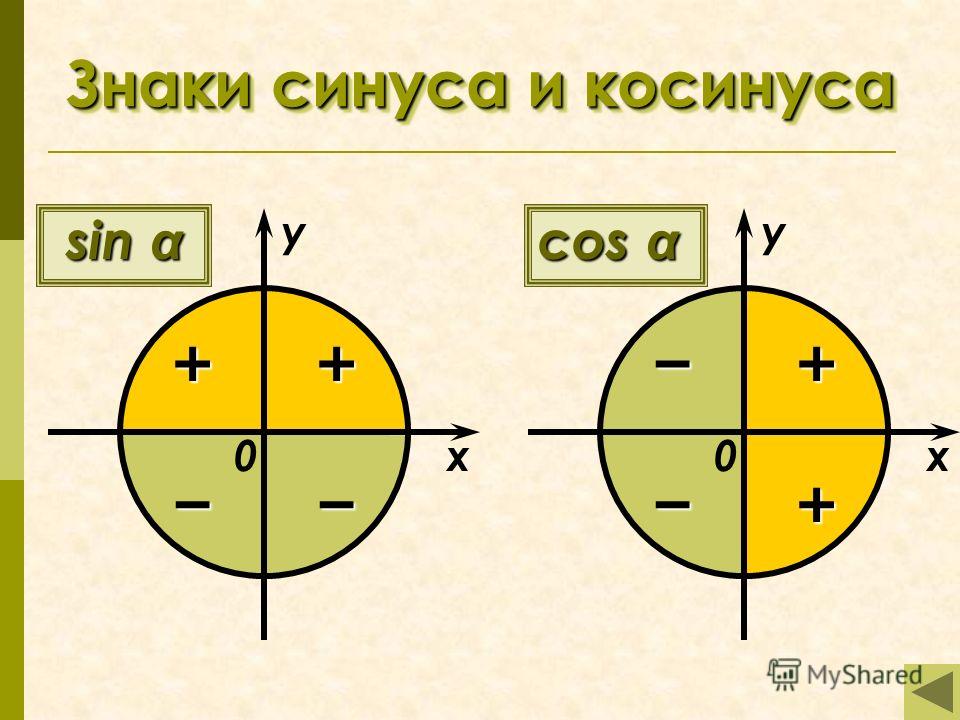
Тригонометрические уравнения
Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим.
Простейшие тригонометрические уравнения.
любое целое число;
любое целое число;
любое целое число;
здесь нет решений;
— любое целое число.
любое целое число;
любое целое число;
любое целое число;
здесь нет решений
— любое целое число.
– любое целое число;
— любое целое число.
— любое целое число;
— любое целое число.
Методы решения тригонометрических уравнений
Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида и решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения тригонометрических уравнений.
1. Алгебраический метод. Этот метод нам хорошо известен из алгебры ( метод замены переменной и подстановки ).
Этот метод нам хорошо известен из алгебры ( метод замены переменной и подстановки ).
Пример.Решить уравнение:
Решение. Используя формулы приведения, имеем: Делаем замену: тогда Находим корни: откуда следует два случая:
1)
2)
2. Разложение на множители. Этот метод рассмотрим на примерах.
Пример. Решить уравнение: .
Решение. Перенесём все члены уравнения влево: ,
преобразуем и разложим на множители выражение в левой части уравнения:
1)
2)
Пример. Решить уравнение: .
Решение. ,
2)
Пример. Решить уравнение:
Решение.
,
,
,
3.Приведение к однородному уравнению. Уравнение называется однородным относительно и , если все его члены одной и той же степени относительно и одного и того же угла. Чтобы решить однородное уравнение, надо:
Чтобы решить однородное уравнение, надо:
а) перенести все его члены в левую часть;
б) вынести все общие множители за скобки;
в) приравнять все множители и скобки нулю;
г) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на ( или ) в старшей степени;
д) решить полученное алгебраическое уравнение относительно .
Пример. Решить уравнение: .
Решение.
, отсюда ,
корни этого уравнения: отсюда
1)
2) .
4. Переход к половинному углу. Рассмотрим этот метод на примере:
Пример. Решить уравнение: .
Решение.
. . . . . . . . . .
5. Введение вспомогательного угла. Рассмотрим уравнение вида:
Где – коэффициенты; – неизвестное. Разделим обе части этого уравнения на :
.
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль (абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1. Тогда можно обозначить их соответственно как и (здесь — так называемый вспомогательный угол ), и наше уравнение принимает вид:
Тогда можно обозначить их соответственно как и (здесь — так называемый вспомогательный угол ), и наше уравнение принимает вид:
или и его решение: , где . Заметим, что введенные обозначения и взаимно заменяемы.
Пример. Решить уравнение: .
Решение. Здесь , поэтому делим обе части на
,
отсюда
6. Преобразование произведения в сумму. Здесь используются соответствующие формулы.
Пример. Решить уравнение: .
Решение. Преобразуем левую часть в сумму:
8. Универсальная подстановка. Рассмотрим этот метод на примере.
Пример.Решить уравнение:
Решение. Здесь возможны два случая:
1) , тогда
, . Делаем замену: , тогда , корни этого уравнения: :
а)
б)
2) , тогда .
Таким образом, решение даёт только первый случай
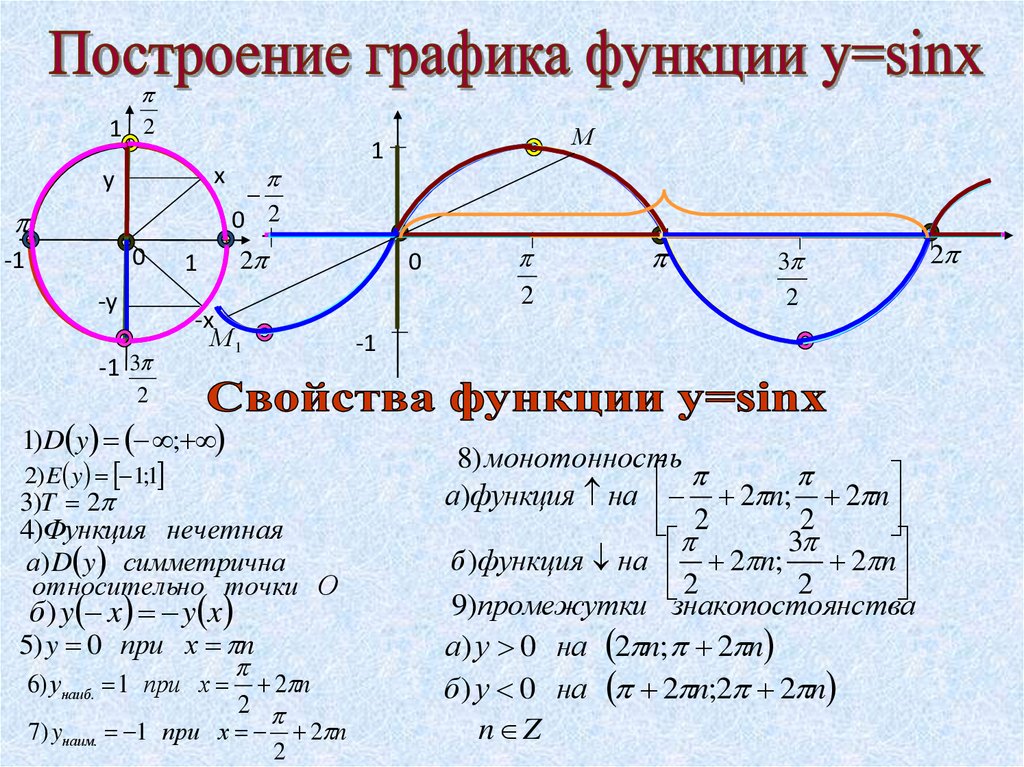
1. Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол . С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений. 2. К тригонометрическим функциям относятся следующие 6 функций: синус , косинус , тангенс ,котангенс , секанс и косеканс . Для каждой из указанных функций существует обратная тригонометрическая функция. 3. Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга . На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α. 4. Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r: 5. Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r: 6. Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x: 7. Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y: 8. Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y): 9. Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y): 10. 11. График функции синус 12. График функции косинус 13. 14. График функции котангенс 15. График функции секанс | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Интегрирование тригонометрических функции
Для интегрирования рациональных функций видаR(sin x, cos x) применяют подстановку , которая называется универсальной тригонометрической подстановкой. Тогда . Универсальная тригонометрическая подстановка часто приводит к большим вычислениям. Поэтому, по возможности, пользуются следующими подстановками.
- Если R(-sin(x),cosx) = -R(sin(x),cosx), то делают замену cos(x)=t и тогда sin(x)dx = -dt.

- При R(sin(x),-cosx) = — R(sin(x),cosx), полагают sin(x)=t при этом cos(x)dx=dt
- В случае R(-sin(x),-cosx) = R(sin(x),cosx) делают замену tg(x)=t, при которой x=arctg(t), , или замену ctg(x)=t, если это удобнее.
Интегрирование функций рационально зависящих от тригонометрических функций
1. Интегралы вида∫sinnxdx, ∫cosnxdx, n>0
a) Если n нечётное, то одну степень sinx (либо cosx) следует внести под знак дифференциала, а от оставшейся чётной степени следует перейти к противоположной функции.
б) Если n чётное, то пользуемся формулами понижения степени
2sin2x=1-cos2x, 2cos2x=1+cos2x.
2. Интегралы вида
∫tgnxdx, ∫ctgnxdx, где n – целое.
Необходимо использовать формулы
3. Интегралы вида ∫sinnx·cosmx dx
а) Пусть m и n разной чётности. Применяем подстановку t=sin x, если n — нечётное либо t=cos x, если m – нечётное.
б) Если m и n чётные, то пользуемся формулами понижения степени
2sin2x=1-cos2x, 2cos2x=1+cos2x.
4. Интегралы вида
Если числа m и n одинаковой чётности, то используем подстановку t=tg x. Часто бывает удобным применить приём тригонометрической единицы.
5.
∫sin(nx)·cos(mx)dx, ∫cos(mx)·cos(nx)dx, ∫sin(mx)·sin(nx)dx
Воспользуемся формулами преобразования произведения тригонометрических функций в их сумму:
- sin α·cos β = ½(sin(α+β)+sin(α-β))
- cos α·cos β = ½(cos(α+β)+cos(α-β))
- sin α·sin β = ½(cos(α-β)-cos(α+β))
- Решение онлайн
- Видеоинструкция
С помощью данного онлайн-калькулятора можно вычислять интегралы по частям. Решение сохраняется в формате Word.
Решение сохраняется в формате Word.
Также рекомендуется ознакомиться с возможностью нахождения интегралов онлайн.
Примеры
1. Вычислить интеграл ∫cos4x·sin3xdx.
Делаем замену cos(x)=t. Тогда ∫cos4x·sin3xdx =
2. Вычислить интеграл .
Делая замену sin x=t, получаем
3. Найти интеграл .
Делаем замену tg(x)=t. Подставляя, получаем
Заметим, что замена ctg(x)=t здесь удобнее, так как тогда , и поэтому
Интегрирование выражений вида R(sinx, cosx)
Пример №1. Вычислить интегралы:
Решение.
а) Интегрирование выражений вида R(sinx, cosx), где R — рациональная функция от sin x и cos x, преобразуются в интегралы от рациональных функций с помощью универсальной тригонометрической подстановки tg(x/2) = t.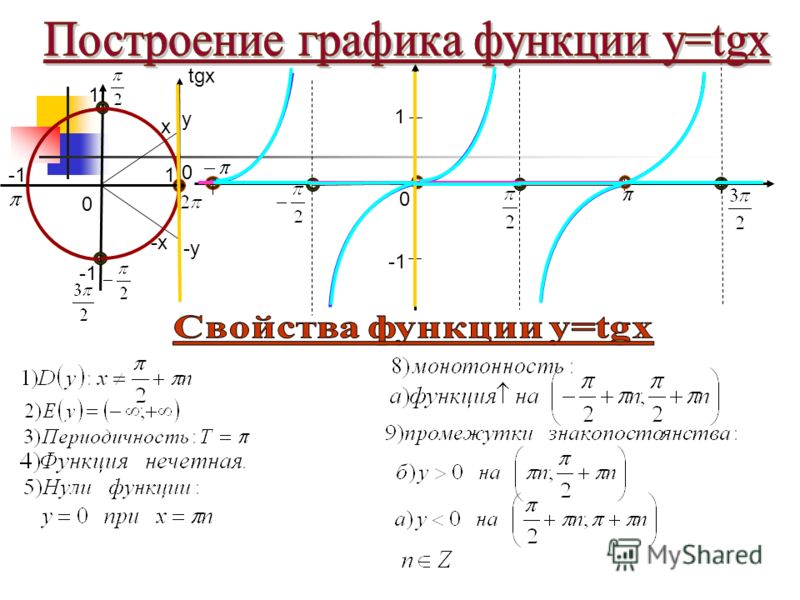
Тогда имеем
Универсальная тригонометрическая подстановка дает возможность перейти от интеграла вида
∫R(sinx, cosx) dx к интегралу от дробно-рациональной функции, но часто такая замена ведет к громоздким выражениям. При определенных условиях эффективными оказываются более простые подстановки:
- Если выполняется равенство
R(-sin x, cos x) = -R(sin x, cos x)dx, то применяется подстановка cos x = t. - Если выполняется равенство
R(sin x, -cos x) = -R(sin x, cos x)dx, то подстановка sin x = t. - Если выполняется равенство
R(-sin x, -cos x) = R(sin x, cos x)dx, то подстановка tgx = t или ctg x = t.
В данном случае для нахождения интеграла
применим универсальную тригонометрическую подстановку tg(x/2) = t.
Тогда
=
илиТак как дробь правильная, то, представляем в виде суммы интегралов:
Возвращась к исходной переменной будем иметь
b) Во втором примере рассмотрим важный частный случай, когда общее выражение ∫R(sinx, cosx) dx имеет вид ∫sinmx·cosnxdx. В этом частном случае, если m нечетно, следует применить подстановку cos x = t. Если нечетно n, следует применить подстановку sin x = t. Если оба показателя тип — четные неотрицательные числа (в частности, одно из них может быть равным нулю), то выполняют замену по известным тригонометрическим формулам:
В этом частном случае, если m нечетно, следует применить подстановку cos x = t. Если нечетно n, следует применить подстановку sin x = t. Если оба показателя тип — четные неотрицательные числа (в частности, одно из них может быть равным нулю), то выполняют замену по известным тригонометрическим формулам:
В данном случае
7.4: Другие тригонометрические функции
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1517
- OpenStax
- OpenStax
Цели обучения
- Найдите точные значения тригонометрических функций секанса, косеканса, тангенса и котангенса \(\frac{\pi}{3}\), \(\frac{\pi}{4}\) и \( \ гидроразрыва {\ пи} {6} \).

- Используйте опорные углы для вычисления секанса, тангенса и котангенса тригонометрических функций.
- Использовать свойства четных и нечетных тригонометрических функций.
- Распознавать и использовать фундаментальные тождества.
- Вычисление тригонометрических функций с помощью калькулятора.
Пандус для инвалидных колясок, соответствующий стандартам Закона об американцах-инвалидах, должен образовывать с землей угол, касательная которого равна \(\frac{1}{12}\) или меньше, независимо от его длины. Тангенс представляет собой отношение, поэтому это означает, что на каждый 1 дюйм подъема рампа должна иметь 12 дюймов пробега. Тригонометрические функции позволяют нам задавать формы и пропорции объектов независимо от точных размеров. Мы уже определили функции синуса и косинуса угла. Хотя синус и косинус являются наиболее часто используемыми тригонометрическими функциями, есть еще четыре. Вместе они составляют набор из шести тригонометрических функций. В этом разделе мы исследуем остальные функции.
В этом разделе мы исследуем остальные функции.
Нахождение точных значений тригонометрических функций секанс, косеканс, тангенс и котангенс \(t\), как показано на рисунке \(\PageIndex{1}\). Как и в случае с синусом и косинусом, мы можем использовать координаты \((x,y)\) для нахождения других функций.
Рисунок \(\PageIndex{1}\) Первая функция, которую мы определим, это тангенс. Тангенс угла есть отношение y -значение x -значение соответствующей точки на единичной окружности. На рисунке \(\PageIndex{1}\) тангенс угла \(t\) равен \(\frac{y}{x},x≠0 \). Поскольку значение y равно синусу \(t\), а значение x равно косинусу \(t\), тангенс угла \(t\) также может быть определяется как \( \frac{ \sin t}{ \cos t}, \cos t≠0.\) Касательная функция обозначается аббревиатурой \( \tan.\) Остальные три функции могут быть выражены как обратные функции мы уже определили.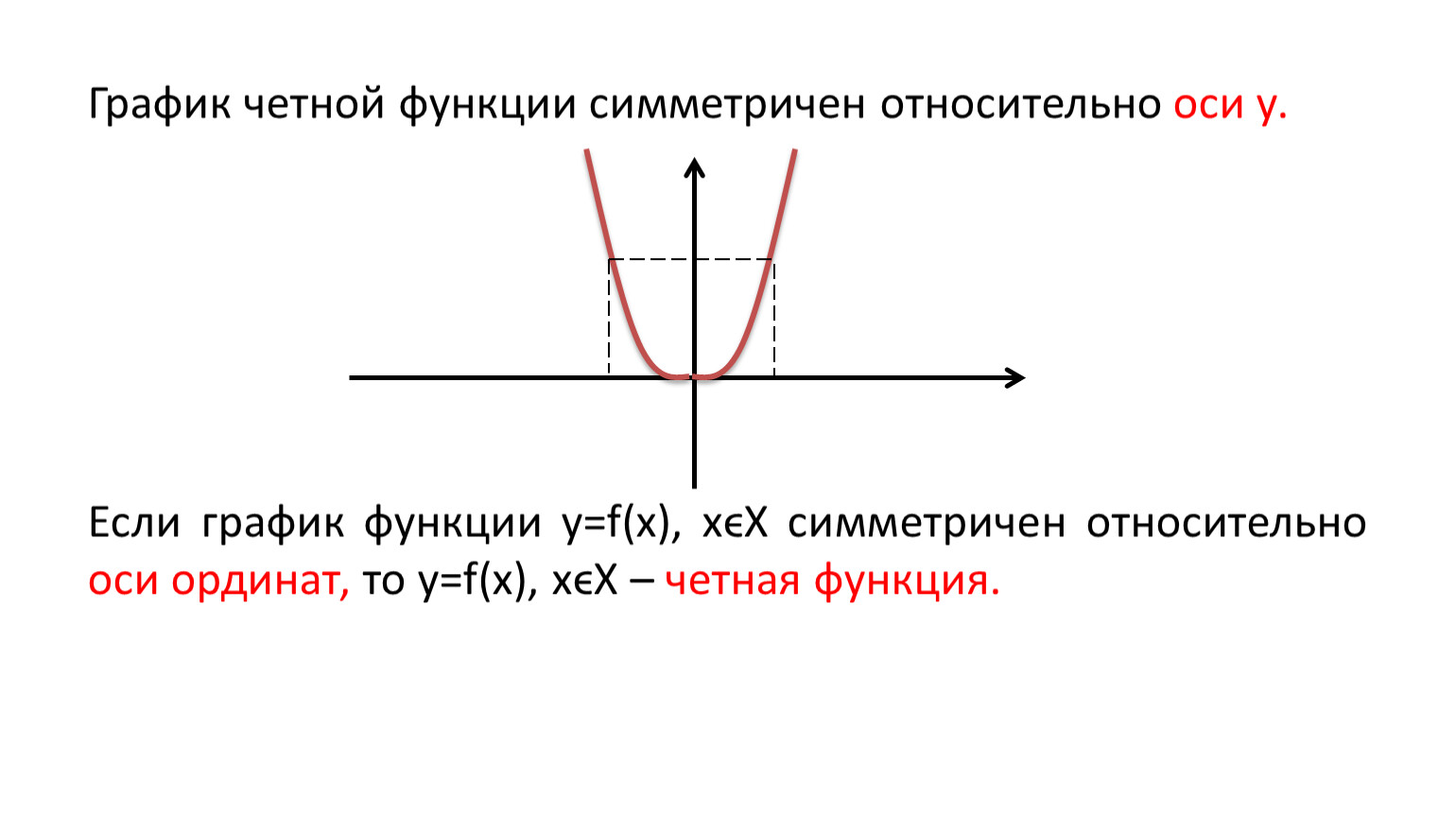
- Функция секанса является обратной функцией косинуса. На рисунке \(\PageIndex{1}\) секанс угла \(t\) равен \(\frac{1}{\cos t} = \frac{1}{x},x≠0\ ). Функция секущей обозначается как \(\sec\).
- Функция котангенса является обратной величиной функции тангенса. На рисунке \(\PageIndex{1}\) котангенс угла \(t\) равен \( \frac{ \cos t}{ \sin t}= \frac{x}{y}, y≠ 0.\) Функция котангенса обозначается как \( \cot.\)
- Функция косеканса является обратной функцией синуса. На рисунке \(\PageIndex{1}\) косеканс угла \(t\) равен \(\frac{1}{\sin t}= \frac{1}{y},y≠0. \) Функция косеканса обозначается как \(\csc.\)
ФУНКЦИИ ТАНГЕНСА, СЕКАНСАНТА, КОСЕКАНСА И КОТАНГЕНСА
Если \(t\) является действительным числом и \((x,y)\) является точкой, где конечная сторона угла \(t\) радиан пересекает единичный круг, тогда
\[\begin{align} \tan t &= \frac{y}{x},x≠0 \\ \sec t & =\frac{1}{x},x≠ 0 \\ \csc t &=\frac{1}{y},y≠0 \\ \cot t &= \frac{x}{y},y≠0 \end{align}\]
Пример \(\PageIndex{1}\): нахождение тригонометрических функций из точки на единичной окружности
Точка \((−\frac{\sqrt{3}}{2},\frac{1}{ 2})\) находится на единичной окружности, как показано на рисунке \(\PageIndex{2}\). Найдите \(\sin t, \cos t, \tan t, \sec t, \csc t,\) и \( \cot t\).
Найдите \(\sin t, \cos t, \tan t, \sec t, \csc t,\) и \( \cot t\).
Решение
Поскольку нам известны координаты \((x,y)\) точки на единичной окружности, обозначенной углом \(t\), мы можем использовать эти координаты, чтобы найти шесть функций:
\[\begin{align*} \sin t &=y=\dfrac{1}{2} \\ \cos t &=x= -\dfrac{\sqrt{3}}{2} \\ \ tan t &= \dfrac{y}{x}= \dfrac{\frac{1}{2}}{−\frac{\sqrt{3}}{2}}=\dfrac{1}{2}( −\dfrac{2}{\sqrt{3}})=-\dfrac{1}{\sqrt{3}}=-\dfrac{\sqrt{3}}{3} \\ \sec t &= \ dfrac{1}{x}=\dfrac{1}{-\frac{\sqrt{3}}{2}}=-\dfrac{2}{\sqrt{3}}=-\dfrac{2\sqrt {3}}{3} \\ \csc t &= \dfrac{1}{y}=\dfrac{1}{\frac{1}{2}}=2 \\ \cot t &= \dfrac{ x}{y}=\dfrac{−\frac{\sqrt{3}}{2}}{\frac{1}{2}}=-\dfrac{\sqrt{3}}{2}(\dfrac {2}{1})=-\sqrt{3} \end{align*}\]
Упражнение \(\PageIndex{1}\):
Точка \((\frac{\sqrt{2}}{2},−\frac{\sqrt{2}}{2})\) равна на единичном круге, как показано на рисунке \(\PageIndex{3}\). Найдите \(\sin t, \cos t, \tan t, \sec t, \csc t,\) и \( \cot t\).
Решение
\( \sin t=−\frac{\sqrt{2}}{2}, \cos t= \frac{\sqrt{2}} {2}, \tan t=-1, \sec t=\sqrt{2}, \csc t=-\sqrt{2}, \cot t=-1\)
Пример \(\PageIndex{2} \): Нахождение тригонометрических функций угла
Найдите \( \sin t, \cos t, \tan t, \sec t, \csc t, \) и \( \cot t\), когда \(t=\frac{π}{6}\) .
Решение
Ранее мы использовали свойства равносторонних треугольников, чтобы показать, что \( \sin \frac{π}{6}=\frac{1}{2}\) и \( \cos \frac{ π}{6}=\frac{\sqrt{3}}{2} \). Мы можем использовать эти значения и определения тангенса, секанса, косеканса и котангенса как функции синуса и косинуса, чтобы найти остальные значения функции.
\[ \begin{align*} \tan \dfrac{π}{6} & = \dfrac{ \sin \frac{π}{6}}{\cos \frac{π}{6}} \\ & = \ dfrac {\ frac {1} {2} {\ frac {\ sqrt {3}} {2}} = \ dfrac {1} {\ sqrt {3}} = \ dfrac {\ sqrt {3} }{3} \\ \sec \dfrac{π}{6} &= \dfrac{1}{\cos \frac{π}{6}} \\ & = \dfrac{1}{\frac{\sqrt {3}}{2}} = \dfrac{2}{\sqrt{3}}= \dfrac{2\sqrt{3}}{3} \\ \csc \dfrac{π}{6} &= \ dfrac{1}{ \sin \frac{π}{6}}= \dfrac{1}{\frac{1}{2}}=2 \\ \cot \dfrac{π}{6} & = \dfrac {\ cos \ frac {π} {6}} {\ sin \ frac {π} {6}} \\ & = \ dfrac {\ frac {\ sqrt {3}} {2}} {\ frac {1} {2}} =\sqrt{3} \end{align*}\]
Упражнение \(\PageIndex{2}\):
Найдите \( \sin t, \cos t, \tan t, \sec t, \csc t,\) и \( \cot t\), когда \ (t=\frac{π}{3}. \)
\)
Решение
\(\begin{align} \sin \frac{π}{3} & = \frac{\sqrt{3}}{ 2} \\ \cos \frac{π}{3} &=\frac{1}{2} \\ \tan \frac{π}{3} &= \sqrt{3} \\ \sec \frac{ π}{3} &= 2 \\ \csc \frac{π}{3} &= \frac{2\sqrt{3}}{3} \\ \cot \frac{π}{3} &= \ frac{\sqrt{3}}{3} \end{align}\)
Поскольку мы знаем значения синуса и косинуса для общих углов первого квадранта, мы можем найти и другие значения функции для этих углов, установив x x равно косинусу, а y y равно синусу, а затем с использованием определений тангенса, секанса, косеканса и котангенса. Результаты показаны в таблице \(\PageIndex{1}\).
| Уголок | \(0\) | \(\frac{π}{6}, \text{или } 30°\) | \(\frac{π}{4}, \text{или } 45°\) | \(\frac{π}{3},\text{ или }60°\) | \(\frac{π}{2},\text{ или }90°\) |
|---|---|---|---|---|---|
| Косинус | 1 | \(\ гидроразрыва {\ sqrt {3}} {2} \) | \(\ гидроразрыва {\ sqrt {2}} {2} \) | \(\ гидроразрыва{1}{2}\) | 0 |
| Синус | 0 | \(\ гидроразрыва{1}{2}\) | \(\ гидроразрыва {\ sqrt {2}} {2} \) | \(\ гидроразрыва {\ sqrt {3}} {2} \) | 1 |
| Касательная | 0 | \(\ гидроразрыва {\ sqrt {3}} {3} \) | 1 | \(\sqrt{3}\) | Не определено |
| Секущая | 1 | \(\frac{2\sqrt{3}}{3}\) | \(\sqrt{2}\) | 2 | Не определено |
| Косеканс | Не определено | 2 | \(\sqrt{2}\) | \(\frac{2\sqrt{3}}{3}\) | 1 |
| Котангенс | Не определено | \(\sqrt{3}\) | 1 | \(\ гидроразрыва {\ sqrt {3}} {3} \) | 0 |
Использование опорных углов для вычисления тангенса, секанса, косеканса и котангенса
Мы можем вычислять тригонометрические функции углов вне первого квадранта, используя опорные углы, как мы уже делали с функциями синуса и косинуса.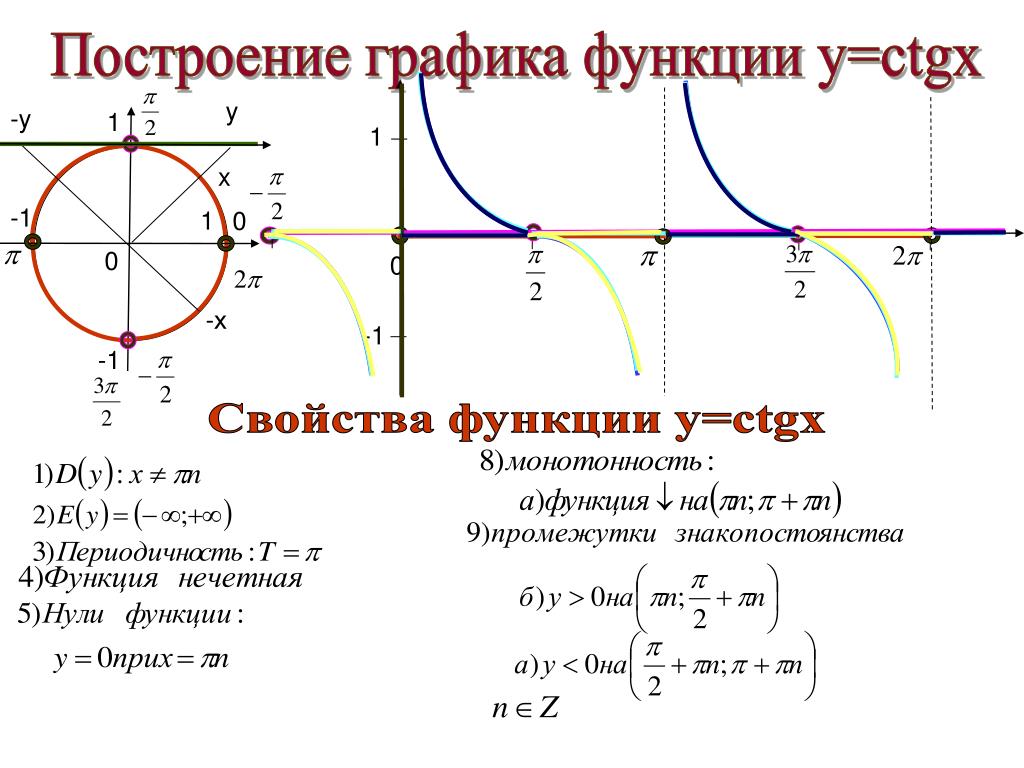 Процедура та же: Найдите опорный угол образован конечной стороной данного угла с горизонтальной осью. Значения тригонометрической функции для исходного угла будут такими же, как и для эталонного угла, за исключением положительного или отрицательного знака, который определяется значениями x и y в исходном квадранте. На рисунке \(\PageIndex{4}\) показано, какие функции в каком квадранте положительны.
Процедура та же: Найдите опорный угол образован конечной стороной данного угла с горизонтальной осью. Значения тригонометрической функции для исходного угла будут такими же, как и для эталонного угла, за исключением положительного или отрицательного знака, который определяется значениями x и y в исходном квадранте. На рисунке \(\PageIndex{4}\) показано, какие функции в каком квадранте положительны.
Чтобы помочь нам вспомнить, какие из шести тригонометрических функций положительны в каждом квадранте, мы можем использовать мнемоническую фразу «Умный класс триггеров». Каждое из четырех слов во фразе соответствует одному из четырех квадрантов, начиная с квадранта I и вращаясь против часовой стрелки. В квадранте I, то есть « A », a Все шесть тригонометрических функций положительны. В квадранте II, « S рынок», только s ine и его обратная функция, косеканс, положительны. В квадранте III « T установка» только t тангенс и его обратная функция, котангенс, положительны. Наконец, в квадранте IV, « C девушка», только c озин и его обратная функция, секанс, положительны.
В квадранте III « T установка» только t тангенс и его обратная функция, котангенс, положительны. Наконец, в квадранте IV, « C девушка», только c озин и его обратная функция, секанс, положительны.
HOWTO: Учитывая угол не в первом квадранте, используйте опорные углы, чтобы найти все шесть тригонометрических функций
- Измерьте угол, образованный конечной стороной данного угла и горизонталью ось. Это опорный угол.
- Оценить функцию по эталонному углу.
- Обратите внимание на квадрант, в котором находится конечная сторона исходного угла. На основе квадранта определите, является ли выход положительным или отрицательным.
Пример \(\PageIndex{3}\): использование опорных углов для нахождения тригонометрических функций
Использование опорных углов для нахождения всех шести тригонометрических функций \(−\frac{5π}{6}\).
Решение
Угол между конечной стороной этого угла и осью x равен \(\frac{π}{6}\), так что это опорный угол. Поскольку \(-\frac{5π}{6}\) находится в третьем квадранте, где и \(x\), и \(y\) отрицательны, косинус, синус, секанс и косеканс будут отрицательными, а тангенс и котангенс будет положительным.
\[ \begin{align} \cos (-\dfrac{5π}{6}) &=-\dfrac{\sqrt{3}}{2}, \sin (-\dfrac{5π}{6} )=-\dfrac{1}{2}, \tan (-\dfrac{5π}{6}) = \dfrac{\sqrt{3}}{3} \\ \sec (-\dfrac{5π}{ 6}) &=-\dfrac{2\sqrt{3}}{3}, \csc (-\dfrac{5π}{6})=-2, \cot (-\dfrac{5π}{6}) =\sqrt{3} \end{align} \]
Упражнение \(\PageIndex{3}\)
Используйте опорные углы, чтобы найти все шесть тригонометрических функций \(−\frac{7π}{4}\) .
Решение
\( \sin (−\frac{7π}{4})= \frac{\sqrt{2}}{2}, \cos(\frac{−7π}{4})= \frac{\sqrt{2}}{2}, \tan (\frac{−7π}{4})=1,\) 93\) — нечетная функция.
Мы можем проверить, является ли тригонометрическая функция четной или нечетной, нарисовав единичную окружность с положительным и отрицательным углами, как показано на рисунке \(\PageIndex{7}\). Синус положительного угла равен \(y\). Синус отрицательного угла равен − y . Таким образом, синусоидальная функция является нечетной функцией. Таким образом мы можем проверить каждую из шести тригонометрических функций. Результаты показаны в таблице \(\PageIndex{2}\).
Синус положительного угла равен \(y\). Синус отрицательного угла равен − y . Таким образом, синусоидальная функция является нечетной функцией. Таким образом мы можем проверить каждую из шести тригонометрических функций. Результаты показаны в таблице \(\PageIndex{2}\).
| \(\begin{align} \sin t &=y \\ \sin (-t) &=-y \\ \sin t &≠sin(-t) \end{align}\) | \( \begin{align} \cos t &=x \\ \cos (−t)=x \\ \cos t &= \cos (-t) \end{align}\) | \(\begin{align} \tan (t) &= \frac{y}{x} \\ \tan (-t) &=-\frac{y}{x} \\ \tan t &≠ \ загар (−t) \end{align}\) |
| \(\begin{align} \sec t &= \frac{1}{x} \\ \sec (−t) &= \frac{1}{x} \\ \sec t &= \sec (−t) \end{align}\) | \( \begin{align} \csc t &= \frac{1}{y} \\ \csc (-t) &= \frac{1}{-y} \\ \csc t &≠ \csc ( −t) \end{align}\) | \( \begin{align} \cot t &= \frac{x}{y} \\ \cot (−t) &= \frac{x}{−y} \\ \cot t & ≠ \cot ( −t) \end{align}\) |
ЧЕТНЫЕ И НЕЧЕТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
- Четная функция — это функция, в которой \(f(−x)=f(x)\).

- Нечетная функция — это функция, в которой \(f(−x)=−f(x)\).
Косинус и секанс четные:
\[ \begin{align} \cos (−t) &= \cos t \\ \sec (-t) &= \sec t \end{align}\]
Синус, тангенс, косеканс и котангенс нечетны:
\[\begin{align} \sin (-t) &=- \sin t \\ \tan (-t) &=-\tan t \\ \csc (-t) &=-\csc t \\ \cot (-t) &=-\cot t \end{align}\]
Пример \(\PageIndex{4}\): использование четных и нечетных свойств Тригонометрические функции
Если секанс угла t равен 2, чему равна секанс \(−t\)?
Решение
Секанс — четная функция. Сеанс угла равен секансу противоположного ему угла. Таким образом, если секанс угла t равен 2, то секанс угла \(−t\) также равен 2.
Упражнение \(\PageIndex{4}\):
Если котангенс угла \(t\) равно \(\sqrt{3}\), чему равен котангенс \(−t?\)
Решение
\(-\sqrt{3}\)
Распознавание и использование фундаментальных тождеств
Мы исследовали ряд свойств тригонометрических функций. Теперь мы можем пойти дальше и вывести некоторые фундаментальные тождества. Идентичности — это утверждения, истинные для всех значений входных данных, для которых они определены. Обычно тождества можно вывести из уже известных нам определений и отношений. Например, тождество Пифагора, которое мы узнали ранее, было получено из теоремы Пифагора и определений синуса и косинуса.
Теперь мы можем пойти дальше и вывести некоторые фундаментальные тождества. Идентичности — это утверждения, истинные для всех значений входных данных, для которых они определены. Обычно тождества можно вывести из уже известных нам определений и отношений. Например, тождество Пифагора, которое мы узнали ранее, было получено из теоремы Пифагора и определений синуса и косинуса.
ОСНОВНЫЕ Тождества
Мы можем вывести некоторые полезные тождества из шести тригонометрических функций. Остальные четыре тригонометрические функции можно связать обратно с функциями синуса и косинуса, используя следующие основные соотношения:
\[ \tan t= \dfrac{ \sin t}{ \cos t} \]
\[ \sec t= \dfrac{1}{\cos t}\]
\[ \csc t= \dfrac{1}{\sin t}\]
\[ \cot t= \dfrac{1}{ \tan t} = \dfrac{ \cos t}{ \sin t} \]
Пример \(\PageIndex{5}\): использование тождеств для вычисления тригонометрических функций
- Учитывая \( \sin (45°)= \frac{\sqrt{2}}{2}, \cos (45°)= \frac{\sqrt{2}}{2}\), оценить \ ( \загар(45°).
 \)
\) - Учитывая \( \sin (\frac{5π}{6})= \frac{1}{2}, \cos(\frac{5π}{6})=-\frac{\sqrt{3}}{ 2},\) оценивают \(\sec (\frac{5π}{6})\).
Решение
Поскольку мы знаем значения синуса и косинуса для этих углов, мы можем использовать тождества для вычисления других функций.
- \[ \begin{align*} \tan(45°) &=\dfrac{ \sin(45°)}{ \cos (45°)} \\ &= \dfrac{\frac{\sqrt{ 2}}{2}}{\frac{\sqrt{2}}{2}} \\ & =1 \end{align*} \]
- \[\begin{align*} \sec (\dfrac{5π}{6}) &= \dfrac{1}{ \cos (\frac{5π}{6})} \\ &= \dfrac{1 }{−\frac{\sqrt{3}}{2}} \\ &= \dfrac{−2\sqrt{3}}{1} \\ &=\dfrac{−2}{\sqrt{3} } \\ &=-\dfrac{2\sqrt{3}}{3} \end{align*}\]
Упражнение \(\PageIndex{5}\)
Вычислить \(\csc (\frac{7π}{6}).\)
Решение
\(−2\)
Пример \( \PageIndex{6}\): использование тождеств для упрощения тригонометрических выражений
Упростить \(\frac{ \sec t}{ \tan t}. \)
\)
Решение
Мы можем упростить это, переписав обе функции в терминах синуса и косинуса.
\[\begin{array}{lll} \dfrac{\sec t}{\tan t} & =\dfrac{1 / \cos t}{\sin t / \cos t} & \text{Чтобы разделить функции умножаем на обратную.} \\ \text{} &= \dfrac{1}{\cos t} \dfrac{ \cos t}{\sin t} & \text{Разделите косинусы.} \\ \text{} & =\dfrac{1}{\sin t} & \text{Упростите и используйте идентификатор.} \\ \text{} & = \csc t \end{array}\]
Показав, что \(\frac{ \sec t}{ \tan t}\) можно упростить до \( \csc t\), мы фактически установили новое тождество.
\[ \dfrac{ \sec t}{ \tan t}= \csc t \nonumber \]
Упражнение \(\PageIndex{6}\)
Упрощение \(( \tan t)( \cos t ).\)
Решение
\( \sin t \)
Альтернативные формы пифагорейской идентичности
Мы можем использовать эти фундаментальные тождества для получения альтернативных форм пифагорейской идентичности 92 t &= \dfrac{25}{169} \\ \sin t &=±\sqrt{\dfrac{25}{169}} \\ \sin t &=±\dfrac{\sqrt{25}}{ \sqrt{169}} \\ \sin t &=± \dfrac{5}{13} \end{align} \]
Знак синуса зависит от y -значений в квадранте, где угол расположен. Поскольку угол находится в квадранте IV, где y -значения отрицательны, его синус отрицателен, \(-\frac{5}{13}\).
Поскольку угол находится в квадранте IV, где y -значения отрицательны, его синус отрицателен, \(-\frac{5}{13}\).
Остальные функции можно вычислить, используя тождества, связывающие их с синусом и косинусом.
\[ \begin{align} \tan t &= \dfrac{\sin t}{\cos t}=\dfrac{−\frac{5}{13}}{\frac{12}{13}} =−\dfrac{5}{12} \\ \sec t &= \dfrac{1}{ \cos t}=\dfrac{1}{\frac{12}{13}}=\dfrac{13}{ 12} \\ \csc t &= \dfrac{1}{\sin t}=\dfrac{1}{-\frac{5}{13}} =-\dfrac{13}{5} \\ \cot t &= \dfrac{1}{ \tan t}=\dfrac{1}{-\frac{5}{12}}=-\dfrac{12}{5} \end{align} \]
Упражнение \(\PageIndex{7}\):
Если \( \sec (t)=− \frac{17}{8}\) и \(0 Решение \( \cos t=-\frac{8}{17}, \sin t=\frac{15}{17}, \tan t=-\frac{15}{8}\ ) \( \csc t= \frac{17}{15}, \cot t=-\frac{8}{15} \) Как мы обсуждали в начале главы, функция, которая повторяет свои значения в регулярные интервалы известны как периодическая функция . Другие функции также могут быть периодическими. Например, длина месяцев повторяется каждые четыре года. Если x x представляет продолжительность времени, измеренную в годах, и \(f(x)\) представляет количество дней в феврале, тогда \(f(x+4)=f(x)\). Этот шаблон повторяется снова и снова во времени. Другими словами, каждые четыре года в феврале гарантированно будет такое же количество дней, как и четыре года назад. Положительное число 4 является наименьшим положительным числом, удовлетворяющим этому условию, и называется периодом. А период — это кратчайший интервал, за который функция завершает один полный цикл — в этом примере период равен 4 и представляет собой время, которое требуется нам, чтобы убедиться, что в феврале одинаковое количество дней. ПЕРИОД ФУНКЦИИ Период \(P\) повторяющейся функции f f — это число, представляющее интервал, такой что \(f(x+P)=f(x)\) для любого значения \ (Икс\). Период функций косинуса, синуса, секанса и косеканса равен \(2π\). Период функций тангенса и котангенса равен \(π\). Пример \(\PageIndex{8}\): нахождение значений тригонометрических функций Найдите значения шести тригонометрических функций угла \(t\) на основе рисунка \(\PageIndex{9}\) . Решение \[\begin{align*} \sin t &= y=-\dfrac{\sqrt{3}}{2} \\ \cos t &=x =-\dfrac{1}{2} \\ \tan t &= \dfrac{ \sin t}{\cos t}=\dfrac{-\frac{\sqrt{3}}{2} }{−\frac{1}{2}}= \sqrt{3} \\ \sec t &= \dfrac{1}{\cos t} = \dfrac{1}{-\frac{1}{2 }}=−2 \\ \csc t &= \dfrac{1}{\sin t}= \dfrac{1}{-\frac{\sqrt{3}}{2}}=-\dfrac{2\ sqrt{3}}{3} \\ \cot t &= \dfrac{1}{\tan t}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3 } \end{выравнивание*}\] Упражнение \(\PageIndex{8}\) Найдите значения шести тригонометрических функций угла \(t\) на основе рисунка \(\PageIndex{10}\) . Решение \(\begin{align} \sin t &=−1, \cos t=0, \tan t= \text{Undefined} \\ \\sec t &= \text{Undefined}, \csc t=−1, \cot t=0 \end{align}\) Пример \(\PageIndex{9}\): нахождение значения тригонометрических функций Если \( \sin(t)=-\frac{\sqrt{3}}{2}\) и \( \cos (t)=\frac{1}{2}\), найдите \( \ сек (t),\csc (t),\tan (t), \cot (t).\) Решение \[ \begin{align} \sec t &= \dfrac{1}{ \cos t}= \dfrac{1}{\frac{1}{2}}=2 \\ \ csc t &= \dfrac{1}{\sin t}= \dfrac{1}{-\frac{\sqrt{3}}{2}}-\dfrac{2\sqrt{3}}{3} \ \ \ tan t &= \ dfrac {\ sin t} {\ cos t} = \ dfrac {− \ frac {\ sqrt {3}} {2}} {\ frac {1} {2}} = − \ sqrt {3} \\ \cot t &= \dfrac{1}{\tan t}= \dfrac{1}{-\sqrt{3}}=-\dfrac{\sqrt{3}}{3} \end {align}\] Упражнение \(\PageIndex{9}\): Если \(\sin (t)= \frac{\sqrt{2}}{2}\) и \(\cos (t )=\frac{\sqrt{2}}{2},\) найти \(\sec (t), \csc (t),\tan (t),\) и \(\cot (t)\) . Решение \( \sec t= \sqrt{2},\csc t=\sqrt{2}, \tan t=1, \cot t=1\) Мы научились вычислять шесть тригонометрических функций для обычных углов первого квадранта и использовать их в качестве справочных углов для углов в других квадрантах. Чтобы оценить тригонометрические функции других углов, мы используем научный или графический калькулятор или компьютерную программу. Если калькулятор имеет режим градусов и режим радиан, убедитесь, что выбран правильный режим, прежде чем выполнять вычисления. Вычисление функции тангенса с помощью научного калькулятора, в отличие от графического калькулятора или системы компьютерной алгебры, похоже на вычисление синуса или косинуса: введите значение и нажмите клавишу TAN. Для взаимных функций может не быть специальных клавиш с надписью CSC, SEC или COT. В этом случае функция должна оцениваться как обратная величина синуса, косинуса или тангенса. Если нам нужно работать с градусами, а наш калькулятор или программное обеспечение не имеет режима градусов, мы можем ввести градусы, умноженные на коэффициент преобразования \(\frac{π}{180}\), чтобы преобразовать градусы в радианы. Чтобы найти секанс \(30°\), мы могли бы нажать \[\mathrm{(для \; a \; научный \; калькулятор):\dfrac{1}{30×\frac{π}{180}}COS}\] или \[ \mathrm {(для \; a \; построения графика \; калькулятора): \dfrac{1}{cos(\frac{30π}{180})} }\] как: Имея угол в радианах, используйте научную калькулятор для нахождения косеканса как: Для измерения угла в радианах используйте графическую утилиту/калькулятор, чтобы найти косеканс Пример \(\PageIndex{10}\): вычисление косеканса с использованием технологии Вычислите косеканс \(\frac{5π}{7}\). Решение Для научного калькулятора введите следующую информацию: \[ \mathrm{1 / ( 5 × π / 7 ) SIN =}\] \[ \mathrm{ \csc (\dfrac {5π}{7})≈1,279} \] Упражнение \(\PageIndex{10}\): Вычислите котангенс числа \(−\frac{π}{8}\). \(≈−2,414\) средства массовой информации Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с другими тригонометрическими функциями. Тригонометрические функции являются периодическими. Для четырех тригонометрических функций, синуса, косинуса, косеканса и секанса, оборот одного круга или \(2π\) приведет к тем же самым результатам для этих функций. А для тангенса и котангенса только половина оборота даст одинаковые результаты.
Тригонометрические функции являются периодическими. Для четырех тригонометрических функций, синуса, косинуса, косеканса и секанса, оборот одного круга или \(2π\) приведет к тем же самым результатам для этих функций. А для тангенса и котангенса только половина оборота даст одинаковые результаты.


Вычисление тригонометрических функций с помощью калькулятора

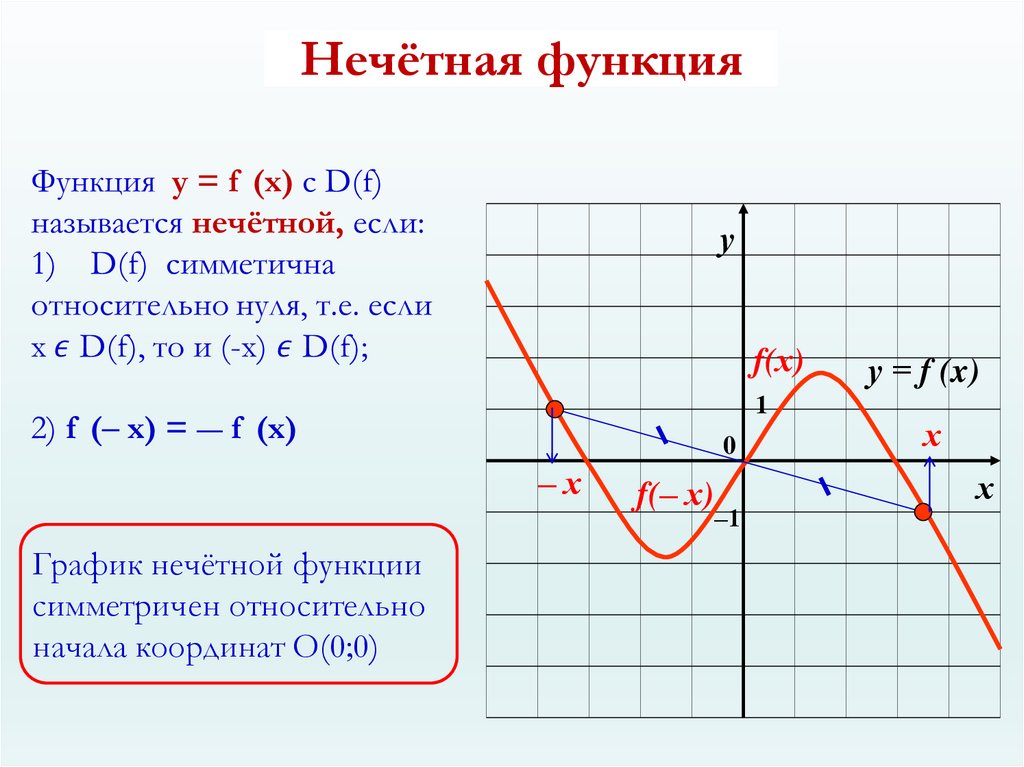
Ключевые уравнения
.»>
Касательная функция \( \tan t= \frac{ \sin t}{\cos t}\) Функция секанса \( \sec t= \frac{1}{ \cos t}\) Функция косеканса \( \csc t= \frac{1}{\sin t}\) Функция котангенса \( \cot t= \frac{1}{\tan t}= \frac{\cos t}{\sin t}\)
Ключевые понятия
- Тангенс угла представляет собой отношение значения y к значению x соответствующей точки на единичной окружности.
- Секанс, котангенс и косеканс являются обратными значениями других функций. Секанс является обратной величиной функции косинуса, котангенс является обратной величиной функции тангенса, а косеканс является обратной величиной функции синуса.
- Шесть тригонометрических функций можно найти из точки на единичной окружности.
 См. Пример.
См. Пример. - Тригонометрические функции также можно найти под углом. См. Пример.
- Тригонометрические функции углов вне первого квадранта могут быть определены с помощью эталонных углов. См. Пример.
- Функция называется четной, если \(f(-x)=f(x)\), и нечетной, если \(f(-x)=-f(x)\).
- Косинус и секанс четны; синус, тангенс, косеканс и котангенс нечетны.
- Четные и нечетные свойства можно использовать для вычисления тригонометрических функций. См. Пример.
- Тождество Пифагора позволяет найти косинус из синуса или синус из косинуса.
- Тождества можно использовать для вычисления тригонометрических функций. См. пример и пример.
- Фундаментальные тождества, такие как Пифагорейское тождество, можно алгебраически манипулировать для создания новых тождеств. См. Пример.
- Тригонометрические функции повторяются через равные промежутки времени.
- Период \(P\) повторяющейся функции f f — это наименьший интервал, такой что \(f(x+P)=f(x)\) для любого значения \(x\).

- Значения тригонометрических функций специальных углов можно найти с помощью математического анализа.
- Чтобы вычислить тригонометрические функции других углов, мы можем использовать калькулятор или компьютерную программу. См. Пример.
Глоссарий
- косеканс
- обратная функция синуса: на единичной окружности, \( \csc t=\frac{1}{y},y≠0\)
- котангенс
- обратная функция касательной: на единичной окружности, \( \cot t= \frac{x}{y},y≠0\)
- личности
- утверждений, истинных для всех значений входных данных, для которых они определены
- период
- наименьший интервал \(P\) повторяющейся функции \(f\) такой, что \(f(x+P)=f(x)\)
- секанс
- обратная функция косинуса: на единичной окружности, \( \sec t= \frac{1}{x},x≠0 \)
- тангенс
- частное синуса и косинуса: на единичной окружности, \( \tan t= \frac{y}{x},x≠0\)
Эта страница под названием 7. 4: Другие тригонометрические функции распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
4: Другие тригонометрические функции распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Теги
- косеканс
- котангенс
- тождеств
- период
- секанс
- источник@https://openstax.
 org/details/books/precalculus
org/details/books/precalculus - тангенс
Преобразование графика котангенса — концепция
Котангенс — это функция, обратная триггеру функции тангенса, и может быть определена как cot(theta)=cos(theta)/sin(theta). Это нечетная функция, означающая раскладушка (-тета) = — раскладушка (тета), и она обладает тем свойством, что раскладушка (тета + пи) = раскладушка (тета). Поскольку синус является знаменателем, а функция не определена, когда sin(theta)=0, график котангенса имеет вертикальные асимптоты при всех целых числах, кратных пи, когда sin(theta)=0.
косинус синус котангенс четные и нечетные функции период добавления пи-идентификаций вертикальные асимптоты
Я хочу поговорить о преобразованиях графика котангенса, но сначала давайте рассмотрим кое-что о котангенсе. у равно котангенс тета помните, что котангенс такой же, как косинус тета над синусом тета это важное тождество, и нам нужно будет выяснить несколько фактов о котангенсе, например, котангенс четный или нечетный? Ну, мы можем использовать тот факт, что косинус четный, а синус нечетный. Котангенс отрицательного тета будет равен косинусу отрицательного тета по синусу отрицательного тета. Косинус отрицательного тета равен косинусу тета, а синус отрицательного тета равен отрицательному синусу тета, и, таким образом, это равняется отрицательному котангенс тета, теперь у нас есть функция кивка котангенса. Таким образом, противоположные входы дают противоположные результаты, это важно знать. Затем я хочу узнать, что происходит, когда я добавляю число пи, теперь я знаю, что это равно косинусу числа тета плюс число пи и синусу числа числа тета плюс число пи.
у равно котангенс тета помните, что котангенс такой же, как косинус тета над синусом тета это важное тождество, и нам нужно будет выяснить несколько фактов о котангенсе, например, котангенс четный или нечетный? Ну, мы можем использовать тот факт, что косинус четный, а синус нечетный. Котангенс отрицательного тета будет равен косинусу отрицательного тета по синусу отрицательного тета. Косинус отрицательного тета равен косинусу тета, а синус отрицательного тета равен отрицательному синусу тета, и, таким образом, это равняется отрицательному котангенс тета, теперь у нас есть функция кивка котангенса. Таким образом, противоположные входы дают противоположные результаты, это важно знать. Затем я хочу узнать, что происходит, когда я добавляю число пи, теперь я знаю, что это равно косинусу числа тета плюс число пи и синусу числа числа тета плюс число пи.
Теперь оба косинуса и синуса свойства, что если вы добавите пи к входу, вы получите противоположный результат. Таким образом, это может быть минус косинус тета по сравнению с минус синус тета. Теперь минусы сократятся, и вы просто получите котангенс тета. Поэтому, если вы добавите число пи, вы получите точно такой же вывод, это означает, что котангенс периодичен с периодом пи, поэтому нам нужно это знать. Хорошо, давайте начнем составлять таблицу значений котангенса; давайте начнем с 0, теперь котангенс равен косинусу относительно синуса, синус 0 равен 0. Таким образом, котангенс будет неопределенным при 0, как насчет, скажем, пи больше 4, косинус и синус оба имеют значение корень 2 больше 2. Итак, это будет 1, корень 2 больше 2 больше корня 2 больше 2, 1 корень пи больше 2. Косинус числа пи больше 2 равен 0, синус корня пи 2 равен 1, поэтому мы получаем 0 больше 1, что равно 0,
Теперь минусы сократятся, и вы просто получите котангенс тета. Поэтому, если вы добавите число пи, вы получите точно такой же вывод, это означает, что котангенс периодичен с периодом пи, поэтому нам нужно это знать. Хорошо, давайте начнем составлять таблицу значений котангенса; давайте начнем с 0, теперь котангенс равен косинусу относительно синуса, синус 0 равен 0. Таким образом, котангенс будет неопределенным при 0, как насчет, скажем, пи больше 4, косинус и синус оба имеют значение корень 2 больше 2. Итак, это будет 1, корень 2 больше 2 больше корня 2 больше 2, 1 корень пи больше 2. Косинус числа пи больше 2 равен 0, синус корня пи 2 равен 1, поэтому мы получаем 0 больше 1, что равно 0,
Теперь позвольте мне работать в обратном направлении, позвольте мне дать нам немного места здесь, котангенс тета. Я вернусь к отрицательному числу пи больше 4, потому что функция узла котангенса, котангенс отрицательного числа пи больше 4 будет противоположен котангенсу числа пи больше 4 4. Таким образом, мы получим отрицательную 1 здесь также потому, что у него есть период пи, если я добавлю к этому число пи, что даст мне 3 пи на 4, я получу тот же результат. И я действительно могу использовать периодичность, чтобы получить остальную часть вывода, если я добавлю к этому пи, до 0 я получу пи. Я получаю тот же вывод undefined, на самом деле это один полный период функции котангенса. Итак, я могу начать строить графики, позвольте мне начать с построения вертикальных асимптот, там будет вертикальная асимптота для x=0 и для x=pi. Итак, один из них здесь, а другой здесь, что происходит между ними?
И я действительно могу использовать периодичность, чтобы получить остальную часть вывода, если я добавлю к этому пи, до 0 я получу пи. Я получаю тот же вывод undefined, на самом деле это один полный период функции котангенса. Итак, я могу начать строить графики, позвольте мне начать с построения вертикальных асимптот, там будет вертикальная асимптота для x=0 и для x=pi. Итак, один из них здесь, а другой здесь, что происходит между ними?
При пи больше 2 мы получаем 0, это пи больше 2, при пи больше 4 мы получаем 1 и при 3 пи больше 4 мы получаем отрицательную 1. Теперь вспомните форму тангенса, котангенс имеет очень похожую форму, он получил это вид изогнутой формы и, конечно, имеет асимптотическое поведение. Итак, это грубая форма графика котангенса. Теперь, если вы хотите нарисовать больше, помните, что это один период, все, что вам нужно сделать, это продублировать этот период. Я могу взять все это и сдвинуть вправо, а при сдвиге вправо все сдвигается вправо, включая асимптоту. Так, например, когда я сдвигаю это вправо, эта асимптота также сдвигается вправо. Итак, я получаю еще один при x = 2 pi, и я также могу сместиться влево, эта асимптота, сдвинутая влево, дает мне x, равное отрицательному pi. Итак, позвольте мне сдвинуть каждую из этих точек вправо, эта точка, сдвинутая вправо, дает мне точку на 3 пи больше 2, эту здесь, эту я поставлю здесь, и мы просто используем периодичность в этой точке.
Так, например, когда я сдвигаю это вправо, эта асимптота также сдвигается вправо. Итак, я получаю еще один при x = 2 pi, и я также могу сместиться влево, эта асимптота, сдвинутая влево, дает мне x, равное отрицательному pi. Итак, позвольте мне сдвинуть каждую из этих точек вправо, эта точка, сдвинутая вправо, дает мне точку на 3 пи больше 2, эту здесь, эту я поставлю здесь, и мы просто используем периодичность в этой точке.
Я сдвину это влево Я получаю точку здесь, здесь, здесь и это 3 периода функции котангенса. Итак, вы заметите, что на самом деле было очень легко разработать ключевые точки для этой функции, все, что мне нужно было сделать, это помнить, что котангенс равен косинусу относительно синуса, и это позволило мне найти нули функции, а также где функция была неопределенной. Очень легко узнать, что котангенс числа пи на 4 равен 1, потому что косинус и синус оба являются корнем 2 на 2. Я также использовал тот факт, что котангенс был нечетным, чтобы получить это значение, а затем я использовал периодичность и превратил это значение в значение в 3 pi больше 4. И это все, что вам нужно: 0, pi больше 4, pi больше 2, 3 pi больше 4 и pi, и как только вы получите полный период, используйте периодичность, чтобы расширить график в обоих направлениях.
И это все, что вам нужно: 0, pi больше 4, pi больше 2, 3 pi больше 4 и pi, и как только вы получите полный период, используйте периодичность, чтобы расширить график в обоих направлениях.
Кофункция и нечетно-четные тождества
Горячая математикаКофункциональные тождества
грех ( π 2 − Икс ) знак равно потому что ( Икс ) потому что ( π 2 − Икс ) знак равно грех ( Икс ) загар ( π 2 − Икс ) знак равно детская кроватка ( Икс ) csc ( π 2 − Икс ) знак равно сек ( Икс ) сек ( π 2 − Икс ) знак равно csc ( Икс ) детская кроватка ( π 2 − Икс ) знак равно загар ( Икс )
Пример:
Найдите значение
детская кроватка
(
60
°
)
.
Используйте кофункциональную идентичность загар ( 90 ° − θ ) знак равно детская кроватка ( θ ) переписать задачу.
детская кроватка ( 60 ° ) знак равно загар ( 90 ° − 60 ° ) знак равно загар ( 30 ° ) знак равно 3 3
Четно-нечетные тождества
потому что
(
Икс
)
является четной функцией,
грех
(
Икс
)
является нечетной функцией, поскольку
тригонометрические функции
для реальных переменных.
грех ( − Икс ) знак равно − грех ( Икс ) потому что ( − Икс ) знак равно потому что ( Икс ) загар ( − Икс ) знак равно − загар ( Икс ) csc ( − Икс ) знак равно − csc ( Икс ) сек ( − Икс ) знак равно − сек ( Икс ) детская кроватка ( − Икс ) знак равно − детская кроватка ( Икс )
Пример:
Если
потому что
(
α
)
знак равно
1
2
, определять
потому что
(
−
α
)
а также
сек
(
−
α
)
.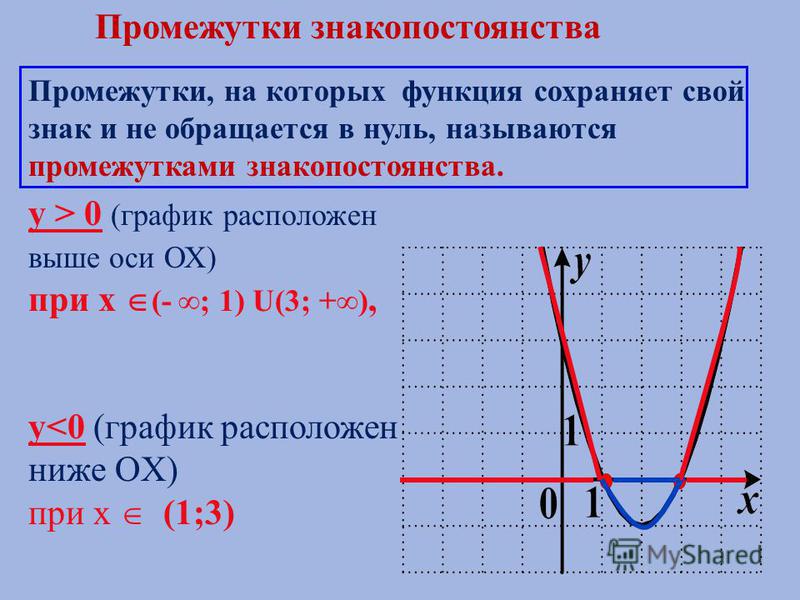
потому что ( − α ) знак равно потому что ( α ) знак равно 1 2
сек ( α ) знак равно 1 потому что ( α ) знак равно 1 ( 1 2 ) знак равно 2
сек ( − α ) знак равно сек ( α ) знак равно 2
Тригонометрические четно-нечетные функции | Brilliant Math & Science Wiki
Хеманг Агарвал, Мэй Ли, Йонас Менци, а также
способствовал
Содержимое
- Тригонометрические четные и нечетные функции
- Приложения и примеры
- Смотрите также
Функции косинуса и синуса удовлетворяют следующим свойствам:
cos(−θ)=cosθsin(−θ)=−sinθ.
\begin{выровнено} \cos(-\тета) &= \cos\тета\\ \sin(-\theta) &= -\sin \theta. \end{align}cos(-θ)sin(-θ)=cosθ=-sinθ.
Доказательство:
Из определения косинуса и синуса в единичной окружности,x=cosθ и y=sinθ.x= \cos \theta \quad \text{ и } \quad y= \sin \theta. х=cosθ и y=sinθ.
Мы видим, что как для θ\thetaθ, так и для −θ-\theta−θ xxx остается одним и тем же. Таким образом, cosθ=cos(−θ)\cos\theta=\cos (-\theta)cosθ=cos(−θ).
Точно так же мы можем видеть, что yyy в двух случаях являются аддитивными обратными значениями друг друга. Таким образом, sin(−θ)=−sinθ\sin (-\theta)=-\sin\thetasin(−θ)=−sinθ. □_\квадрат□
Теперь, когда у нас есть приведенные выше тождества, мы можем доказать несколько других тождеств, как показано в следующем примере:
Докажите личности
tan(−θ)=−tanθcot(−θ)=−cotθcsc(−θ)=−cscθsec(−θ)=secθ.
\begin{выровнено} \загар(-\тета) &= -\загар \тета\\ \кроватка(-\тета) &= -\кроватка \тета\\ \csc(-\тета) &= -\csc \тета\\ \сек(-\тета) &= \сек \тета. \end{align}tan(-θ)cot(-θ)csc(-θ)sec(-θ)=-tanθ=-cotθ=-cscθ=secθ.
У нас есть
тангенс(-θ)=sin(-θ)cos(-θ)=-sinθcosθ=-тангенсθcot(-θ)=1тангенс(-θ)=1-тангенсθ =−cotθcsc(−θ)=1sin(−θ)=1−sinθ=−cscθsec(−θ)=1cos(−θ)=1cosθ=secθ. □\begin{выровнено} \ tan (- \ theta) & = \ frac {\ sin (- \ theta)} {\ cos (- \ theta)} = \ frac {- \ sin \ theta} {\ cos \ theta} = — \ tan \ тета\\ \cot(-\theta) &=\frac{1}{\tan(-\theta)}=\frac{1}{-\tan \theta}=-\cot \theta\\ \csc(-\theta) &=\frac{1}{\sin (-\theta)}=\frac{1}{-\sin \theta}=-\csc \theta\\ \sec(-\theta) &=\frac{1}{\cos(-\theta)}=\frac{1}{\cos \theta}=\sec \theta. \ _\площадь \end{align}tan(-θ)cot(-θ)csc(-θ)sec(-θ)=cos(-θ)sin(-θ)=cosθ-sinθ=-tanθ=tan(- θ)1=-tanθ1=-cotθ=sin(-θ)1=-sinθ1=-cscθ=cos(-θ)1=cosθ1=secθ. □ 9\круг} \\ &= \frac{\sqrt{3}}{2} + 2 \\ &= \frac{\sqrt{3} + 4}{2}.
\ _\площадь \end{выравнивание} cos(−30∘)+sec(−60∘)=cos30∘+sec60∘=23+cos60∘1=23+2=23+4. □
Упростите tanx×cot(−x). \tan x \times \cot(-x). Танкс×кот(-х).
Из тригонометрических четно-нечетных функций имеем
tanx×cot(−x)=tanx×(−cotx)=tanx×(−1tanx)=−1. □ \begin{выровнено} \tan x \times \cot(-x) &= \tan x \times (-\cot x ) \\ &= \tan x \times \left(-\frac{1}{\tan x}\right) \\ &= -1. \ _\площадь \end{выровнено} tanx×cot(-x)=tanx×(-cotx)=tanx×(-tanx1)=-1. □
ParallelAngleBisector
Прямоугольник ABCDABCDABCD вписан в окружность ООО радиусом 1 на приведенной выше схеме. Пусть θ\thetaθ будет углом, образованным AO‾\overline {AO}AO и осью xxx. Тогда какая вершина имеет
2sin(−θ2)cos(−θ2) 2\sin\left(-\frac{\theta}{2}\right)\cos\left(-\frac{\theta}{2}\right) 2sin(−2θ)cos(−2θ)
в качестве yyy-координаты?
Обратите внимание, что выражение можно переписать следующим образом:
2sin(−θ2)cos(−θ2)=−2sinθ2cosθ2(поскольку sin(−x)=−sinx,cos(−x)=cosx)=−sinθ .
(поскольку sin2θ=2sinxcosx) \begin{выровнено} 2\sin\left(-\frac{\theta}{2}\right)\cos\left(-\frac{\theta}{2}\right) &= -2 \sin \frac{\theta}{ 2} \cos \frac{\theta}{2} &&\quad \big(\text{since} \sin (-x) = -\sin x, \cos(-x) = \cos x\big) \ \ &= -\sin\тета. &&\quad (\text{так как} \sin 2\theta = 2\sin x \cos x) \end{выровнено} 2sin(-2θ)cos(-2θ)=-2sin2θcos2θ=-sinθ.(поскольку sin(-x)=-sinx,cos(-x)=cosx)( поскольку sin2θ=2sinxcosx)
Также обратите внимание, что координата yyy точки AAA равна sinθ \sin \thetasinθ, а точки AAA и CCC симметричны относительно начала координат. Тогда yyy-координата точки CCC должна быть равна −sinθ.-\sin\theta.−sinθ.
Следовательно, наш ответ — вершина C.C.C. □ _\квадрат □
Процитировать как: Тригонометрические четно-нечетные функции. Brilliant.org . Извлекаются из https://brilliant.org/wiki/trigonometric-even-odd-functions/
Четные и нечетные тождества – объяснение и примеры
Четные и нечетные тождества для тригонометрических функций включают использование четности или нечетности тригонометрической функции для нахождения тригонометрических значений отрицательных углов.
В частности, синус, тангенс, косеканс и котангенс являются нечетными функциями. Функции косинуса и секанса четны.
Как и все тригонометрические тождества, четные и нечетные тождества играют важную роль в физических науках и технике.
Прежде чем продолжить работу с этим разделом, просмотрите четные и нечетные функции и идентификаторы триггеров.
В этом разделе рассматриваются:
- Нечетные тождества
- Четные тождества
- Как определить, является ли функция синуса нечетной или четной?
Нечетные тождества
Нечетные тождества — это тригонометрические тождества, возникающие из-за того, что данная тригонометрическая функция является нечетной функцией.
Напомним, что нечетной функцией называется функция $f(x)$ такая, что $f(-x) = -f(x)$. То есть соответствующие положительные и отрицательные входы имеют выходы с одинаковым абсолютным значением. Однако знаки этих выходов будут разными.
Однако знаки этих выходов будут разными.
Отражение нечетной функции по оси $x$, а затем по оси $y$ (или наоборот) отображает функцию в саму себя. То есть нечетные функции симметричны относительно начала координат.
В тригонометрии функции синуса, косеканса, тангенса и котангенса нечетны. Этот факт дает четыре нечетных тождества:
- $sin(-x) = -sin(x)$
- $csc(-x) = -csc(x)$
- $tan(-x) = -tan(x)$
- $cot (-x) = -cot(x)$
Обратные триггерные функции арксинус и арктангенс также нечетны. Следовательно, есть также два нечетных тождества с обратным триггером:
- $arcsin(-x) = -arcsin(x)$
- $arctan(-x) = -arctan(x)$
Четный Тождества
Четный тождества в тригонометрии — это тождества, вытекающие из того факта, что данная тригонометрическая функция четна.
Напомним, что четная функция — это функция $f$ такая, что $f(-x) = f(x)$.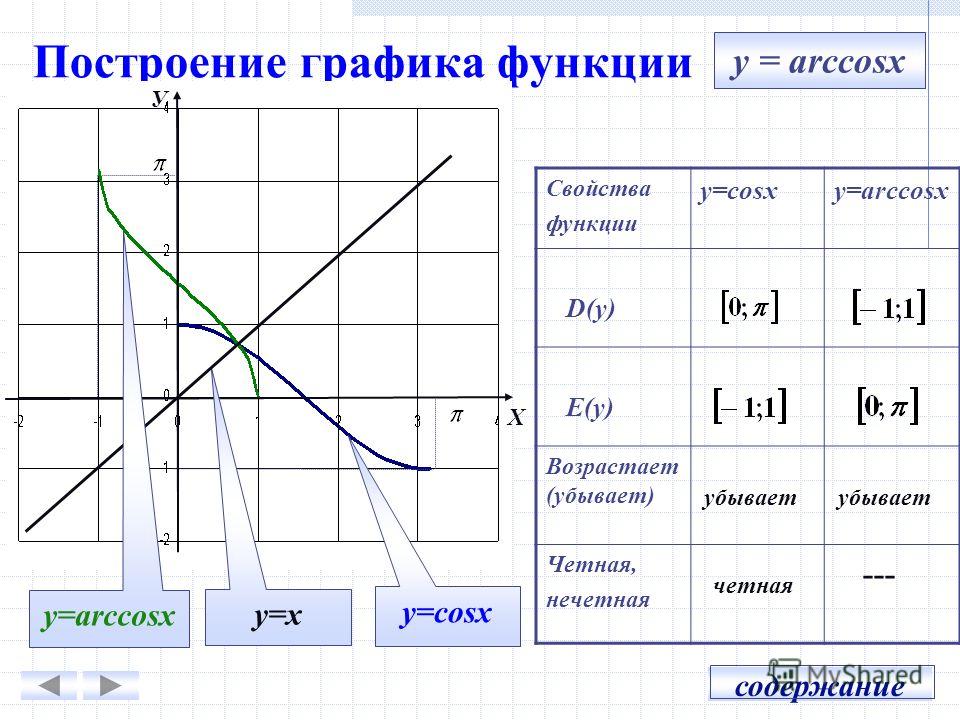 То есть соответствующие положительные и отрицательные входы имеют одинаковый выход. Такие функции симметричны относительно оси y, и их отражение по оси y сопоставляет их самим себе.
То есть соответствующие положительные и отрицательные входы имеют одинаковый выход. Такие функции симметричны относительно оси y, и их отражение по оси y сопоставляет их самим себе.
Есть две функции триггера по четным числам: косинус и секанс. Таким образом, имеются два тригонометрических четных тождества:
- $cos(-x) = cos(x)$
- $sec(-x) = sec(-x)$
Нет четных обратных триггерных функций.
Как определить, является ли синусоидальная функция четной или нечетной?
Можно определить, является ли триггерная функция четной или нечетной, алгебраически или графически.
Сделать это графически проще. Если ось Y является линией симметрии функции, то она четная. Если функция симметрична относительно начала координат (поворачивая ее на 180 градусов или отражая по обеим осям), то она нечетна.
Алгебраически нужно доказать, что для любого $x$ $f(-x) = f(x)$ для четной функции и что $f(-x) = -f(x)$ для функция должна быть нечетной.
Алгебраические доказательства четности и нечетности
С тригонометрическими функциями это делается путем рассмотрения основных определений синуса и косинуса в контексте единичного круга.
Напомним, что отрицательный угол на единичной окружности измеряется по часовой стрелке, а положительный угол измеряется против часовой стрелки.
В единичной окружности синус угла равен высоте прямоугольного треугольника, образованного конечным радиусом и осью x. На рисунке синус угла $BAD$ равен $DI$. Отрицательный угол, соответствующий $BAD$, измеряется по часовой стрелке, поэтому он равен $BAE$. На рисунке синус этого угла равен $IE$.
Так как $DI$ простирается вверх от оси x, его длина положительна. Поскольку $IE$ продолжается вниз, его длина отрицательна. Но их величины будут одинаковыми.
Аналогично, синус $BAF$ равен $FH$, а синус $BAG$, соответствующего отрицательного угла, равен $HG$. Эти две линии также имеют одинаковую величину, но разные синусы.
Следовательно, синусы двух углов с одинаковой величиной, но измеренных в противоположном направлении, будут иметь одинаковую величину, но разные знаки. Следовательно, синус нечетный.
Обратите внимание, однако, что косинусы (горизонтальная линия прямоугольного треугольника угла) находятся на одной стороне оси x. Для $BAD$ и $BAE$ это $AI$. Для $BAF$ и $BAG это $AH$. Следовательно, косинус не меняется в зависимости от знака угла. Таким образом, косинус четный.
Нечетность или четность других триггерных функций следует из нечетности или четности синуса и косинуса.
Четные и нечетные преобразования
Обратите внимание, что преобразования функции могут влиять на то, являются ли они четными или нечетными.
В частности, сдвиги по горизонтали и вертикали могут сделать нечетную функцию четной, а четную — нечетной. Например, $cos(x-\frac{\pi}{2})$ отображает косинус в синус. Следовательно, $cos(x-\frac{\pi}{2})$ нечетно.
Преобразования также могут сделать так, чтобы функция не была ни нечетной, ни четной. Преобразование $sin(x)-1$ является примером.
Преобразование $sin(x)-1$ является примером.
Примеры
В этом разделе рассматриваются распространенные примеры задач на четные и нечетные тождества триггеров и их пошаговые решения.
Пример 1
Используйте четность и нечетность синуса и косинуса, чтобы доказать, что функция тангенса нечетна.
Решение
Требуется показать, что тангенс нечетен. То есть, что:
$tan(-x) = -tanx$.
Напомним, что $tanx = \frac{sinx}{cosx}$. Следовательно:
$tan(-x) = \frac{sin(-x)}{cos(-x)}$.
Поскольку синус нечетный, а косинус четный, это упрощается до:
$tan(-x) = \frac{-sinx}{cosx} = -\frac{sinx}{cosx} = -tanx$.
Пример 2
Является ли функция $y=sinx-1$ четной, нечетной или ни одной?
Решение
Простой способ проверить, является ли функция четной, нечетной или ни той, ни другой, состоит в том, чтобы найти значение функции для отрицательного угла и положительного угла с одинаковой величиной. В этом случае используйте углы $\frac{\pi}{2}$ и $-\frac{\pi}{2}$.
В этом случае используйте углы $\frac{\pi}{2}$ и $-\frac{\pi}{2}$.
При $\frac{\pi}{2}$ синус равен $1$. Следовательно, $sinx-1 = 0$.
При $-\frac{\pi}{2}$ синус равен $-1$. Следовательно, $sinx-1 = -2$.
Следовательно, эта функция не является ни нечетной, ни четной.
Обратите внимание, однако, что этот метод может дать подсказку о том, является ли функция четной или нечетной, но не доказать это. Например, $sin(\pi) = 0 = sin(-\pi)$. В этих двух точках функция $sinx-1$ равна $1$, но эта функция нечетна.
Пример 3
Найдите синус $\frac{\pi}{4}$ и $-\frac{\pi}{4}$.
Решение
Напомним, что синус $\frac{\pi}{4}$ равен $\frac{\sqrt{2}}{2}$. Кроме того, поскольку синус нечетен, $sin(-x) = -sinx$. Следовательно, $sin(-\frac{\pi}{4}) = -sin(\frac{\pi}{4})$.
Таким образом, $sin(-\frac{\pi}{4}) = -\frac{\sqrt{2}}{2}$.
Пример 4
Найдите секанс $-\frac{\pi}{6}$.
Решение
Напомним, что функция секанса является обратной функцией косинуса.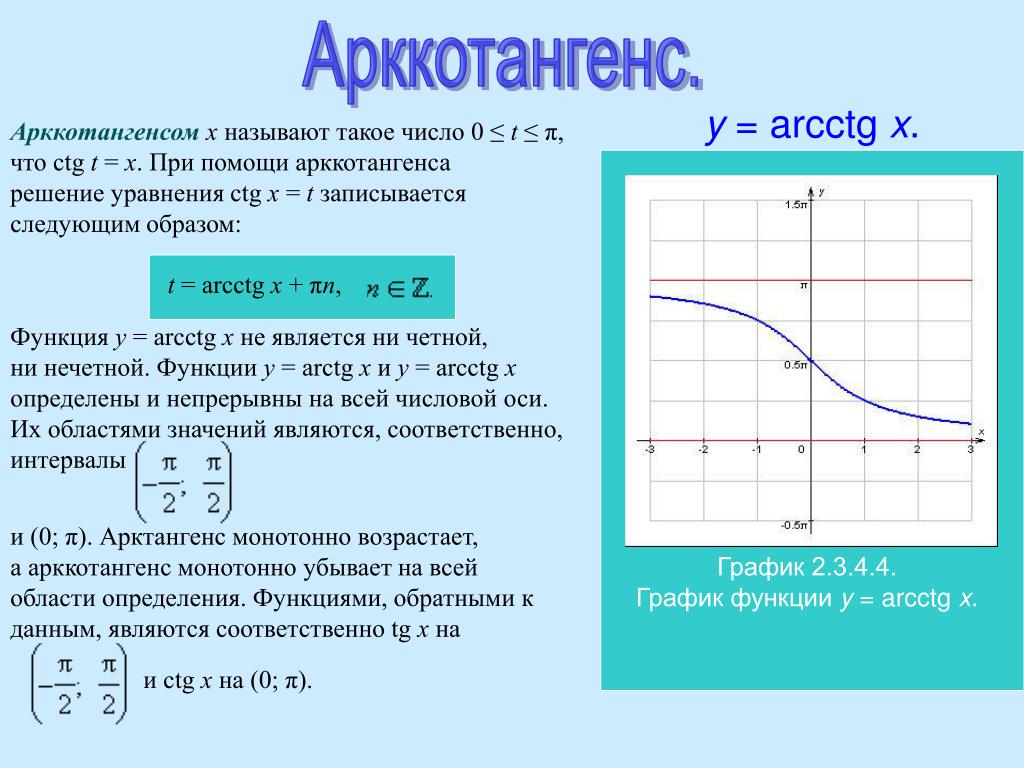 То есть $secx=\frac{1}{cosx}$. Как и косинус, он четный.
То есть $secx=\frac{1}{cosx}$. Как и косинус, он четный.
Следовательно:
$sec(-\frac{\pi}{6}) = sec(\frac{\pi}{6})$.
Поскольку секанс угла $\frac{\pi}{6}$ в радианах равен $\frac{1}{\frac{\sqrt{3}}{2}} = \frac{2\sqrt{3 }}{3}$, секанс угла $-\frac{\pi}{6}$ также равен $\frac{2\sqrt{3}}{3}$.
Пример 5
Используйте тот факт, что косинус четен, чтобы доказать, что $cos(x-y) = cos(y-x)$.
Решение
Для начала обратите внимание, что $y-x = -(x-y)$.
Следовательно, $cos(y-x) = cos(-(x-y))$. Однако, поскольку косинус четный, $cos(-(xy)) = cos(xy)$. Следовательно, $cos(y-x) = cos(x-y)$ для любых углов $x$ и $y$.
Общие базовые стандарты: CCSS.Math.Content.HSF-TF.A.4
- Дом /
- Общие основные стандарты /
- Математика
Стандарты
- О
- Средняя школа: номер и количество
- Средняя школа: Алгебра
- Средняя школа: Функции
- О
- Функции интерпретации
- Функции построения
- Линейные, квадратичные и экспоненциальные модели
- Тригонометрические функции
- Средняя школа: моделирование
- Средняя школа: геометрия
- Старшая школа: статистика и вероятность
- 8 класс
- 7 класс
- 6 класс
- 5 класс
- 4 класс
- 3 класс
- 2 класс
- 1 класс
- Детский сад
Тригонометрические функции HSF-TF.
 A.4
A.4- Стандарт
- Примеры заданий
- Выровненные ресурсы
4. Используйте единичный круг для объяснения симметрии (нечетной и четной) и периодичности тригонометрических функций.
Учащиеся должны уметь определять симметрию тригонометрических функций. Они также должны знать, что когда мы говорим «симметрия», мы не имеем в виду зеркала и палиндромы.
Сравнивая значения тригонометрических функций в квадрантах I и IV, учащиеся могут определить, является ли функция нечетной или четной . Однако для этого они должны сначала действительно знать, что такое четные и нечетные функции.
Учащиеся должны знать, что косинус и секанс являются функциями и даже и симметричны относительно оси y . Мы знаем, что это верно из-за тождеств отрицательных углов для косинуса и секанса.
cos(- θ ) = cos θ
сек(- θ ) = сек θ
Как и ожидалось, остальные функции (синус, косеканс, тангенс и котангенс) являются нечетными функциями и симметричны относительно начала координат. Они также имеют отрицательные угловые тождества.
Они также имеют отрицательные угловые тождества.
SIN (- θ ) = -SIN θ
CSC (- θ ) = -CSC θ
TAN (- θ ) = -TAN θ
77777 (. ) = -кроватка θ
Учащиеся могут спутать эти тождества со всеми учащимися, изучающими математику (ASTC). Напомните им, что эти тождества применимы к углам, а ASTC — к квадрантам. В любом случае, они оба по-прежнему применяются!
Вы также можете воспользоваться этой возможностью, чтобы поговорить об этих функциях как о линиях на единичной окружности. Это не обязательно, но учащимся может быть полезно увидеть тригонометрические функции, представленные таким образом, чтобы они могли лучше понять отношения этих функций и сделать прогнозы (о том, что может произойти с функцией тангенса, когда θ = π ⁄ 2 , например).
Студенты также должны знать, что шесть тригонометрических функций являются периодическими функциями. В частности, периоды синуса, косеканса, косинуса и секанса равны 2π, а периоды тангенса и котангенса равны π. Чтобы понять почему, переместите θ от 0 до 2π на единичной окружности и проверьте, как меняется каждая функция.
В частности, периоды синуса, косеканса, косинуса и секанса равны 2π, а периоды тангенса и котангенса равны π. Чтобы понять почему, переместите θ от 0 до 2π на единичной окружности и проверьте, как меняется каждая функция.
После каждой точки функция повторяется, что означает, что sin( θ + 2π) = sin θ . То же самое относится к пяти другим тригонометрическим функциям и их соответствующим периодам. Такова природа периодичности.
Ссылки
Рабочий лист F-TF.4Ответы F-TF.4
Совмещенные ресурсы
- ACT Math 4.5 Тригонометрия
- ACT Math 5.1 Тригонометрия
Видео
- ПРЕДЫДУЩИЙ СТАНДАРТ
- СЛЕДУЮЩИЙ СТАНДАРТ
Дополнительные стандарты от старшей школы: Функции — тригонометрические функции
- HSF-TF.A.1
- HSF-TF.A.3
- HSF-TF.B.6
- HSF-TF.


 Шпаргалки. Детский сад, Школа. / / Понятие функции. Основные свойства функций. Область определения и значения. Четность и нечетность. Периодичность, нули функции, промежутки знакопостоянства, монотонность (возрастание, убывание), экстремумы (максимумы, минимумы), асимптоты
Шпаргалки. Детский сад, Школа. / / Понятие функции. Основные свойства функций. Область определения и значения. Четность и нечетность. Периодичность, нули функции, промежутки знакопостоянства, монотонность (возрастание, убывание), экстремумы (максимумы, минимумы), асимптоты Четность и нечетность
Четность и нечетность

 Свойства синуса, косинуса, тангенса и котангенса ЕГЭ на 4? А не лопнешь от счастья?
Свойства синуса, косинуса, тангенса и котангенса ЕГЭ на 4? А не лопнешь от счастья? 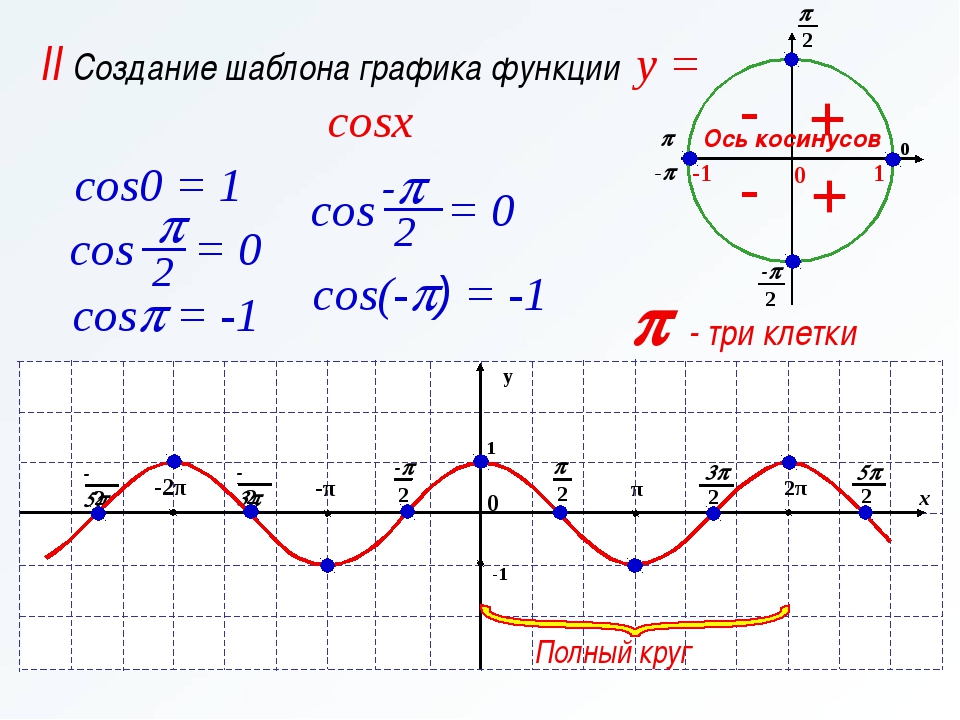 Это простые понятия. И ничем эта тема не сложнее других. Просто нужно с самого начала чётко уяснить ответы на эти самые вопросы. Это очень важно. Если уяснили – тригонометрия вам понравится. Итак,
Это простые понятия. И ничем эта тема не сложнее других. Просто нужно с самого начала чётко уяснить ответы на эти самые вопросы. Это очень важно. Если уяснили – тригонометрия вам понравится. Итак,
 Отношения других соответствующих сторон также не изменятся . Можно как угодно менять длины сторон в прямоугольном треугольнике, увеличивать, уменьшать, не меняя угла х – отношения соответствующих сторон не изменятся . Можно проверить, а можно поверить древним людям на слово.
Отношения других соответствующих сторон также не изменятся . Можно как угодно менять длины сторон в прямоугольном треугольнике, увеличивать, уменьшать, не меняя угла х – отношения соответствующих сторон не изменятся . Можно проверить, а можно поверить древним людям на слово. Синус, косинус, тангенс и котангенс – это некоторые числа. Безразмерные. Просто числа. Для каждого угла – свои.
Синус, косинус, тангенс и котангенс – это некоторые числа. Безразмерные. Просто числа. Для каждого угла – свои.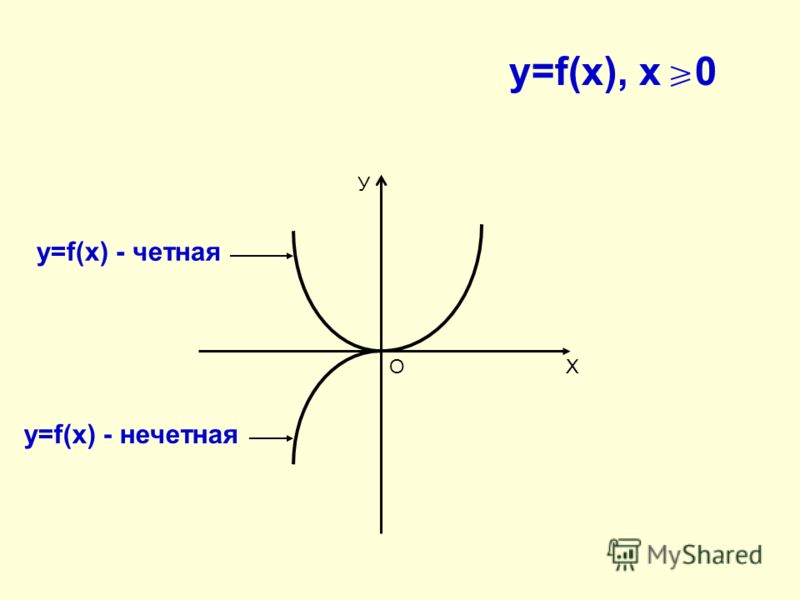 .. При чём здесь угол?
.. При чём здесь угол? 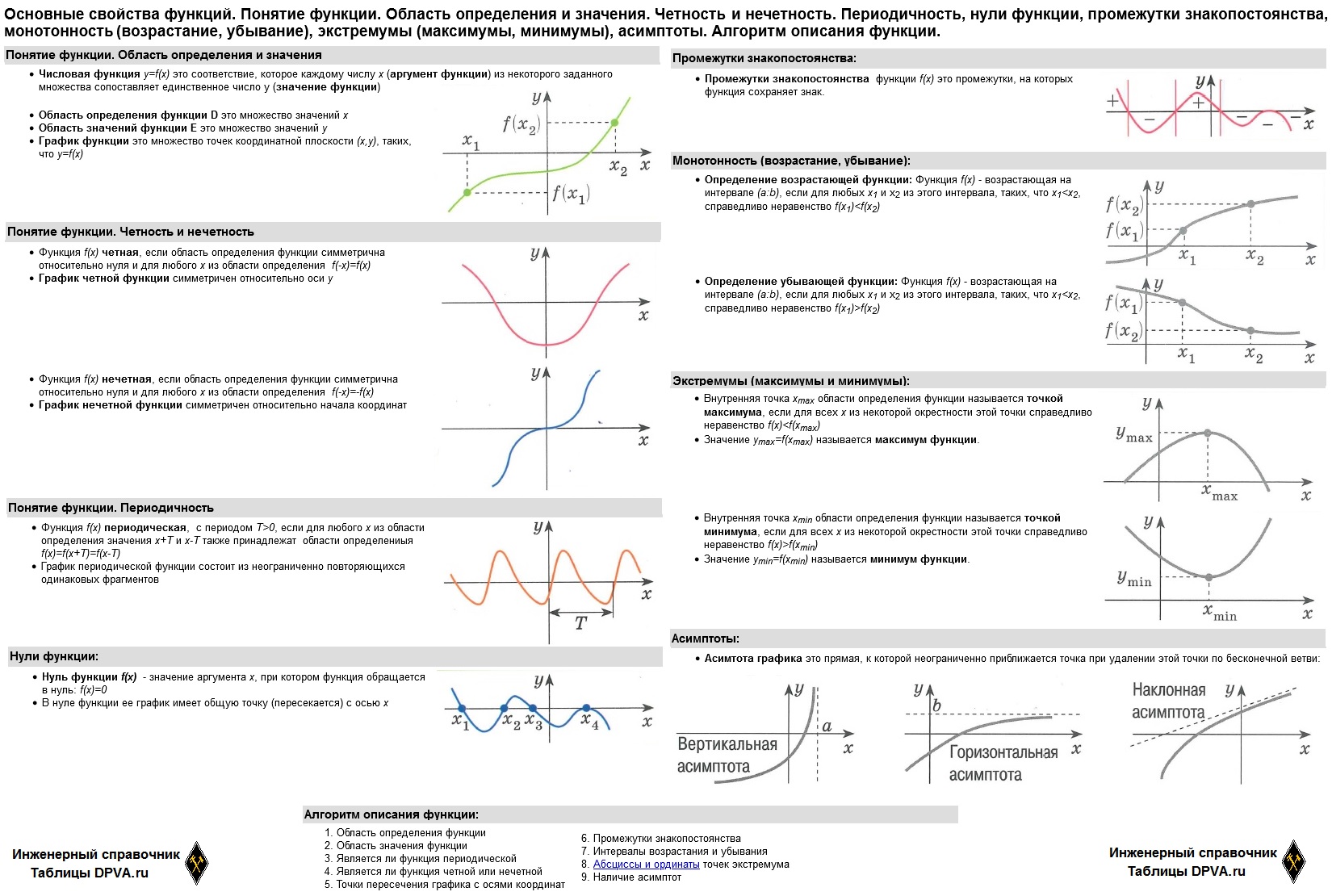 Таблицы Брадиса называются. Они очень давно составлены. Когда ещё не было ни калькуляторов, ни компьютеров…
Таблицы Брадиса называются. Они очень давно составлены. Когда ещё не было ни калькуляторов, ни компьютеров… Просто пишем, по определению косинуса (отношение прилежащего катета к гипотенузе):
Просто пишем, по определению косинуса (отношение прилежащего катета к гипотенузе): А у таких углов все тригонометрические функции — и синус, и косинус, и тангенс с котангенсом — положительные. Т.е. отрицательный ответ мы здесь просто отбрасываем. Имеем право.
А у таких углов все тригонометрические функции — и синус, и косинус, и тангенс с котангенсом — положительные. Т.е. отрицательный ответ мы здесь просто отбрасываем. Имеем право. Иногда требуется знать и таблицу синусов косинусов тангенсов и котангенсов.
Иногда требуется знать и таблицу синусов косинусов тангенсов и котангенсов. Найти значение выражения:
Найти значение выражения: 
 ..
.. 
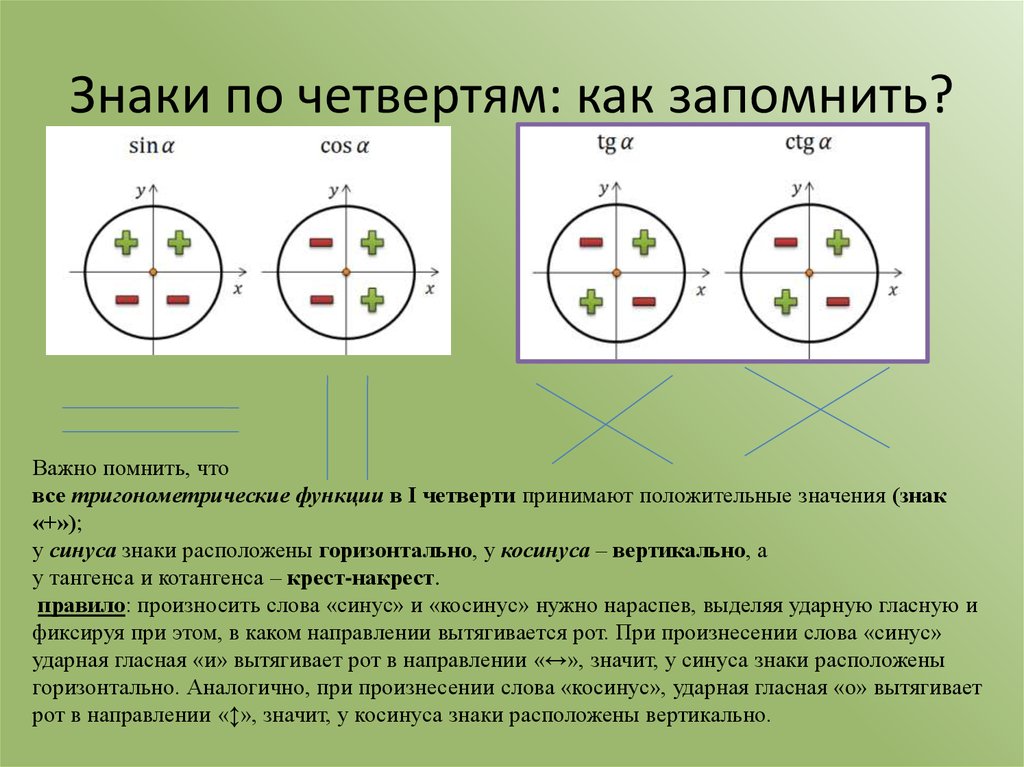 В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:
В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:  График функции тангенс
График функции тангенс  Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
 Данная окружность имеет центр в начале координат на координатной плоскости. Для определения заданных функций будем использовать радиус-вектор ОР , который начинается в центре окружности, а точка Р является точкой окружности. Данный радиус-вектор образует угол альфа с осью ОХ . Так как окружность имеет радиус, равный единице, то ОР = R = 1 .
Данная окружность имеет центр в начале координат на координатной плоскости. Для определения заданных функций будем использовать радиус-вектор ОР , который начинается в центре окружности, а точка Р является точкой окружности. Данный радиус-вектор образует угол альфа с осью ОХ . Так как окружность имеет радиус, равный единице, то ОР = R = 1 .
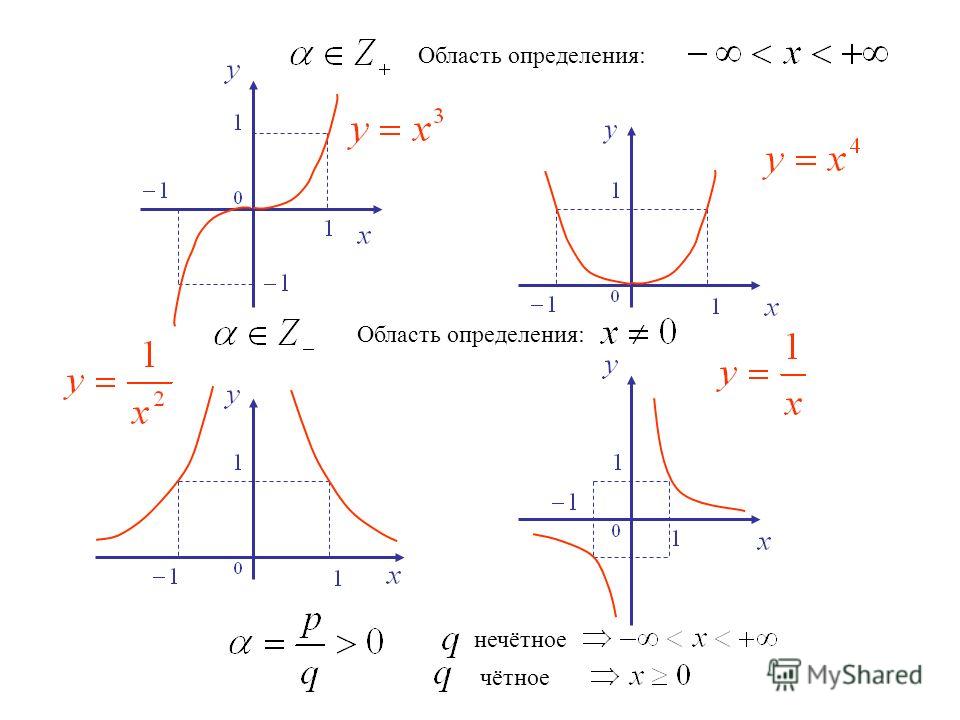



 \)
\) См. Пример.
См. Пример.
 org/details/books/precalculus
org/details/books/precalculus \begin{выровнено}
\cos(-\тета) &= \cos\тета\\
\sin(-\theta) &= -\sin \theta.
\end{align}cos(-θ)sin(-θ)=cosθ=-sinθ.
\begin{выровнено}
\cos(-\тета) &= \cos\тета\\
\sin(-\theta) &= -\sin \theta.
\end{align}cos(-θ)sin(-θ)=cosθ=-sinθ. \begin{выровнено}
\загар(-\тета) &= -\загар \тета\\
\кроватка(-\тета) &= -\кроватка \тета\\
\csc(-\тета) &= -\csc \тета\\
\сек(-\тета) &= \сек \тета.
\end{align}tan(-θ)cot(-θ)csc(-θ)sec(-θ)=-tanθ=-cotθ=-cscθ=secθ.
\begin{выровнено}
\загар(-\тета) &= -\загар \тета\\
\кроватка(-\тета) &= -\кроватка \тета\\
\csc(-\тета) &= -\csc \тета\\
\сек(-\тета) &= \сек \тета.
\end{align}tan(-θ)cot(-θ)csc(-θ)sec(-θ)=-tanθ=-cotθ=-cscθ=secθ. \ _\площадь
\end{выравнивание} cos(−30∘)+sec(−60∘)=cos30∘+sec60∘=23+cos60∘1=23+2=23+4. □
\ _\площадь
\end{выравнивание} cos(−30∘)+sec(−60∘)=cos30∘+sec60∘=23+cos60∘1=23+2=23+4. □ (поскольку sin2θ=2sinxcosx) \begin{выровнено}
2\sin\left(-\frac{\theta}{2}\right)\cos\left(-\frac{\theta}{2}\right) &= -2 \sin \frac{\theta}{ 2} \cos \frac{\theta}{2} &&\quad \big(\text{since} \sin (-x) = -\sin x, \cos(-x) = \cos x\big) \ \
&= -\sin\тета. &&\quad (\text{так как} \sin 2\theta = 2\sin x \cos x)
\end{выровнено} 2sin(-2θ)cos(-2θ)=-2sin2θcos2θ=-sinθ.(поскольку sin(-x)=-sinx,cos(-x)=cosx)( поскольку sin2θ=2sinxcosx)
(поскольку sin2θ=2sinxcosx) \begin{выровнено}
2\sin\left(-\frac{\theta}{2}\right)\cos\left(-\frac{\theta}{2}\right) &= -2 \sin \frac{\theta}{ 2} \cos \frac{\theta}{2} &&\quad \big(\text{since} \sin (-x) = -\sin x, \cos(-x) = \cos x\big) \ \
&= -\sin\тета. &&\quad (\text{так как} \sin 2\theta = 2\sin x \cos x)
\end{выровнено} 2sin(-2θ)cos(-2θ)=-2sin2θcos2θ=-sinθ.(поскольку sin(-x)=-sinx,cos(-x)=cosx)( поскольку sin2θ=2sinxcosx)