График функции. — Алгебра — 7 класс
7 класс.
График функции.
Для того, чтобы ввести понятие графического задания функции, определим сначала, что есть график функции.
Графиком функции называется множество точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. (Напомним, что абсцисса – это координата х, ордината – координата у).
Поскольку, по определению функции, каждому значению аргумента соответствует только одно значение функции, то для графика соблюдается такое же правило: каждой абсциссе графика соответствует только одно значение ординаты.
Например,
На графиках показано, что абсциссе соответствует только одно значение ; абсциссе – только одно значение . И так далее.
Итак, теперь рассмотрим графический способ задания функции.
Например, дан график функции .
По графику функции можно узнать значение функции по выбранным значениям аргумента. Пусть . Находим на оси Ох координату, равную 1 и из этой точки проводим перпендикуляр до пересечения с графиком. Из точки пересечения проводим перпендикуляр к оси Оу и находим . Аналогично, при таким же способом находим . При . Точно также мы можем найти значение функции при любом выбранном значении аргумента.
При всей наглядности графического способа, у него есть существенные недостатки. На этом же графике видно, что если мы захотим выбрать не целое значение аргумента, а, например, , то точно найти это число на координатной оси проблематично, как также найти соответствующее значение . Значит, главным недостатком этого способа является сложность получения точных значений.
Рассмотрим теперь табличный способ задания функции и определим его преимущества и недостатки.
Этот способ задания функции чаще всего используется в практических целях, например, при замерах температуры наружного воздуха через определённые промежутки времени. Эта функция будет отображать зависимость температуры от времени .
ч | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
10 | 10 | 9,5 | 9 | 8,5 | 8 | 8,5 | 8,5 | 9 | 9 | 10 | 11 | 11,5 |
Однако, при таком задании функции, область определения всегда ограничена. Здесь мы можем судить об изменении температуры только при изменении времени от 0 часов до 12 часов. Тем более, что невозможно точно сказать, какая была температура, например, в .
Здесь мы можем судить об изменении температуры только при изменении времени от 0 часов до 12 часов. Тем более, что невозможно точно сказать, какая была температура, например, в .
Преимущество табличного способа в том, что не нужно ничего находить и считать, всё наглядно отображено в таблице.
А недостатком, конечно, является невозможность определить промежуточные значения функции.
Таким образом, самый точный способ задания функции – это аналитический, т.е. с помощью формулы.
Разберёмся теперь, как построить график функции, которая задана с помощью формулы.
Например, построить график функции , если с шагом 1.
Решение. Условие означает, что выбирать значения х можно только от до , а шаг, равный 1 означает, что эти значения должны отличаться на 1. Другими словами, будем выбирать следующие значения х: . Каждое из этих значений подставляем в формулу вместо х и считаем, чему равен у.
Каждое из этих значений подставляем в формулу вместо х и считаем, чему равен у.
Для удобства занесём эти значения в таблицу:
х | -2 | -1 | 0 | 1 | 2 |
у | 11 | 4 | 1 | 2 | 7 |
Теперь строим координатную плоскость, отмечаем на ней точки с координатами: , а затем плавно соединяем эти точки.
Таким образом, мы получили график функции при .
Если значения аргумента не заданы, то мы их выбираем самостоятельно, причём эти значения должны принадлежать области определения функции, захватывать положительные и отрицательные числа и шаг должен быть не слишком большой.
На рисунке изображён график некоторой функции.
Пользуясь графиком, найдите:
значение , если
значения , которым соответствует
значения аргумента, при которых значение функции равно нулю.
На рисунке изображён график некоторой функции.
Пользуясь графиком, найдите:
значение , если
значения , которым соответствует
значения аргумента, при которых значение функции равно нулю.

На рисунке изображён график функции.
Пользуясь графиком, найдите:
значение , если
значения , которым соответствует
значения аргумента, при которых значение функции равно нулю.
Функция задана формулой , где .
Составьте таблицу значений функции с шагом 1.
Постройте график функции, используя составленную таблицу.
Используя график, найдите, при каких значениях аргумента значения функции отрицательны.
Функция задана формулой , где .
Составьте таблицу значений функции с шагом 1.
Постройте график функции, используя составленную таблицу.
Используя график, найдите, при каких значениях аргумента значения функции положительны.

Функция задана формулой , где .
Составьте таблицу значений функции с шагом 1.
Постройте график функции, используя составленную таблицу.
Используя график, найдите, при каких значениях аргумента значения функции отрицательны.
Принадлежат ли графику функции, заданной формулой , точки ; ?
Принадлежат ли графику функции, заданной формулой , точки ; ?
Принадлежат ли графику функции, заданной формулой , точки ; ?
Найдите координаты точки пересечения графика функции с осью ординат.
Укажите координаты точек пересечения графика функции с осью абсцисс.
Найдите координаты точек пересечения графика функции с осями координат.
Выясните, пересекает ли график функции оси координат.
 Ответ объясните.
Ответ объясните.Найдите координаты точки пересечения графика функции с осью ординат.
Укажите координаты точек пересечения графика функции с осью абсцисс.
Найдите координаты точек пересечения графика функции с осями координат.
Выясните, пересекает ли график функции оси координат. Ответ объясните.
Какие из точек принадлежат графику функции ?
Какие из точек принадлежат графику функции ?
Найдите координаты точки пересечения графика функции , если , с осью ординат.
Укажите координаты точек пересечения графика функции с осью абсцисс.
Найдите координаты точек пересечения графика функции с осями координат.
Выясните, пересекает ли график функции оси координат.
 Ответ объясните.
Ответ объясните.Найдите координаты точки пересечения графика функции , если , с осью ординат.
Укажите координаты точек пересечения графика функции с осью абсцисс.
Найдите координаты точек пересечения графика функции с осями координат.
Выясните, пересекает ли график функции оси координат. Ответ объясните.
На отрезке задана функция .
Используя этот график, найдите:
нули этой функции;
число решений уравнения в зависимости от ;
наибольшее и наименьшее значение функции на отрезке ;
промежутки, на которых значения функции положительны и отрицательны.
На отрезке задана функция .
Используя этот график, найдите:
нули этой функции;
число решений уравнения в зависимости от ;
наибольшее и наименьшее значение функции на отрезке ;
промежутки, на которых значения функции положительны и отрицательны.

На отрезке задана функция .
Используя этот график, найдите:
все решения уравнения ;
число решений уравнения в зависимости от ;
наибольшее и наименьшее значение функции на отрезке ;
промежутки, на которых и .
На отрезке задана функция .
Используя этот график, найдите:
все решения уравнения ;
число решений уравнения в зависимости от ;
наибольшее и наименьшее значение функции на отрезке ;
промежутки, на которых и .
Постройте график функции
Какие из точек принадлежат графику этой функции?
Постройте график функции
Какие из точек принадлежат графику этой функции?
Постройте график функции
Укажите область определения и область значений данной функции.
Постройте график функции
Укажите область определения и область значений данной функции.
Найдите область определения функции , где , и постройте её график.
Найдите область определения функции , где , и постройте её график.
Найдите область определения функции , где , и постройте её график.
Найдите область определения функции , где , и постройте её график.
Постройте графики функций , если
Заполните таблицу значений для функции и постройте её график.
График функции – ломаная , где
.
Постройте график этой функции.
С помощью графика найдите .

Определите, при каких значениях х значение равно .
Назовите целые значения х, при которых принимает положительные значения; отрицательные значения.
График функции – ломаная , где
.
Постройте график этой функции.
С помощью графика найдите .
Определите, при каких значениях х значение равно .
Назовите целые значения х, при которых принимает положительные значения; отрицательные значения.
На рисунке изображён график движения туристов по холмистой местности. На оси абсцисс откладывается время движения от момента выхода из палаточного лагеря, на оси ординат – пройденное расстояние.
По графику определите:
сколько километров прошли туристы до второго привала?
сколько времени длился первый привал?
на каком расстоянии от лагеря были туристы в 2 ч 30 мин.
 ?
?за сколько времени прошли туристы первые два километра?
сколько всего километров прошли туристы?
сколько времени шли туристы от первого до второго привала?
сколько километров прошли туристы за промежуток времени от 1,5 часов до 3,5 часов (считая от начала движения)?
4
График линейной функции | ЮКлэва
Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое линейная функция.
Начнем с небольшой проверки:
- Как выглядит линейная функция в общем виде (формула)?
- Почему она называется линейной?
- Как влияет коэффициент при \( \displaystyle x\) на график линейной функции?
Если хоть один вопрос вызвал затруднения, прочти тему «Линейная функция».
Приступим к покорению линий и графиков!
Рассмотрим пример для функции \( y=2x+1\):
Проще всего найти функцию, если аргумент: \( x=0:y\left( 0 \right)=2\cdot 0+1=1\).
Итак, первая точка имеет координаты \( \left( 0;1 \right)\).
Теперь возьмем любое другое число в качестве \( x\), например, \( x=1:y\left( 1 \right)=2\cdot 1+1=3\).
Вторая точка имеет координаты \( \left( 1;3 \right)\).
Угловой коэффициент \( \displaystyle k\) – это тангенс угла наклона прямой.
Для его нахождения выберем две точки \( \displaystyle A\) и \( \displaystyle B\) на графике и построим прямоугольный треугольник с гипотенузой \( \displaystyle AB\)
\( \displaystyle k=tg\alpha =\frac{BC}{AC}=\frac{2}{1}=2\)
Построение графика линейной функции
Итак, ты уже умеешь обращаться с линейной функцией, анализировать ее график и строить его по точкам.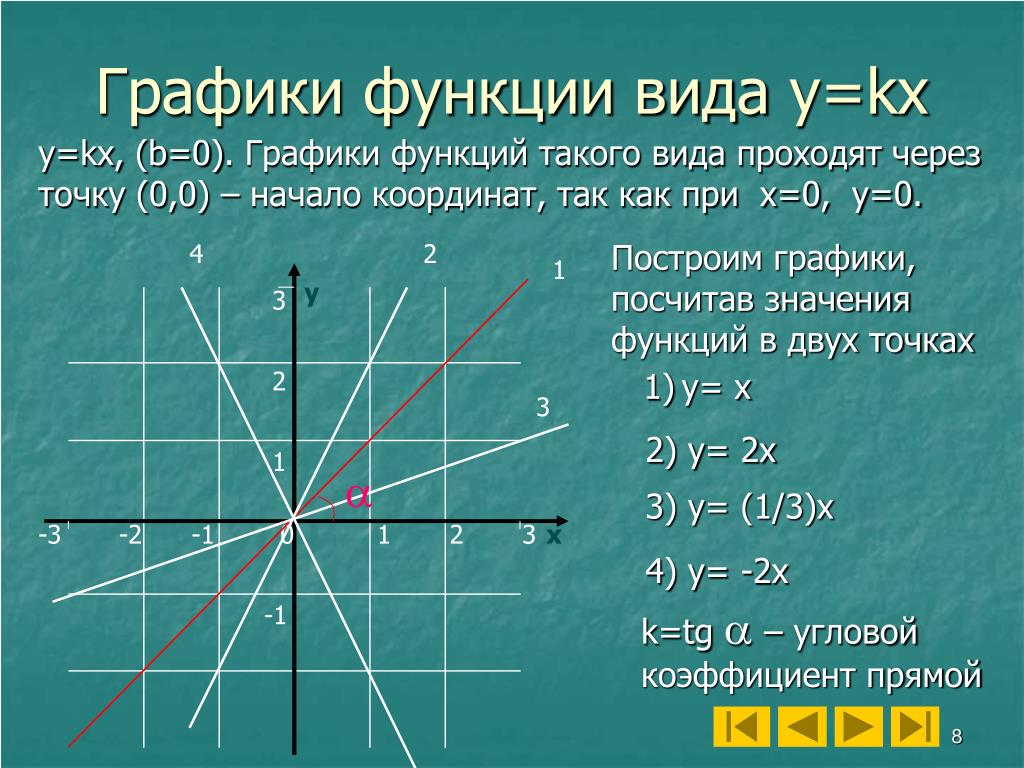 Кстати, сколько нужно точек, чтобы построить график линейной функции?
Кстати, сколько нужно точек, чтобы построить график линейной функции?
Скажу сразу, эта тема настолько простая, что много нового ты здесь не выучишь. Но ты научишься не теряться во всяких нестандартных ситуациях.
Итак, дамы и господа, линейная функция:
\( \displaystyle y=kx+b\)
Построение графика линейной функции: ты берешь два каких-либо икса, (например, \( \displaystyle 0\) и \( \displaystyle 1\)), подставляешь их в формулу, находишь соответствующие игреки.
Затем отмечаешь эти две точки на координатной плоскости, прикладываешь линейку, и график готов. Просто и быстро, и ничего выдумывать не надо.
Но бывает, что функция задана по-другому, например, неявно. Сейчас разберем, как быстро справляться с такими ситуациями.
Пример неявно заданной линейной функции
Постройте график уравнения \( \displaystyle 2y+3x=6\).
Ну а что тут сложного? Чтобы произвести построение графика линейной функции выражаем y и строим по точкам.
Это да, но можно сделать
Выясним, в какой точке эта прямая будет пересекать ось \( \displaystyle Ox\).
Что характерно для этой точке? Правильно, \( \displaystyle y=0\). Так и пишем:
\( \displaystyle 2\cdot 0+3x=6\text{ }\Rightarrow \text{ }x=2\)
А теперь проделаем то же самое с другой осью: в какой точке график пересекает ось \( \displaystyle Oy\)?
\( \displaystyle x=0\text{ }\Rightarrow \text{ }2y+3\cdot 0=6\text{ }\Rightarrow \text{ }y=3\)
Бум! Вот и они – две точки графика. Осталось только приложить линейку:
Согласись, это было быстро и просто!
А теперь сам:
\( \displaystyle 4x-5y=3\)
Ладно, а как еще можно задать функцию?
Ну, например словесно:
Прямая проходит через точку \( \displaystyle A\left( 2;3 \right)\), а ее угловой коэффициент равен \( \displaystyle 0,75\).
Ну что же, вспоминаем: что такое угловой коэффициент?
Пример №2
Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку \( A\left( 3;1 \right)\) и параллельной прямой \( y=-1,5x+1\).
Строить график прямой \( y=-1,5x+1\) нельзя.
О, это что-то новенькое. Про параллельность прямых мы еще не учили.
Но как обычно, все просто. Нарисуем несколько параллельных прямых на координатной плоскости:
Что у них общего? Вообще, какие параметры важны для графиков? Конечно же, коэффициенты \( k\) и \( b\).
И сразу становится ясно: раз \( k\) отвечает за наклон, а наклон у них одинаковый (это же параллельные прямые, а ось \( Ox\) – секущая), значит, у них одинаковый коэффициент \( k\)!
Вернемся к задаче. Напомню условие:
Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку \( A\left( 3;1 \right)\) и параллельной прямой \( y=-1,5x+1\).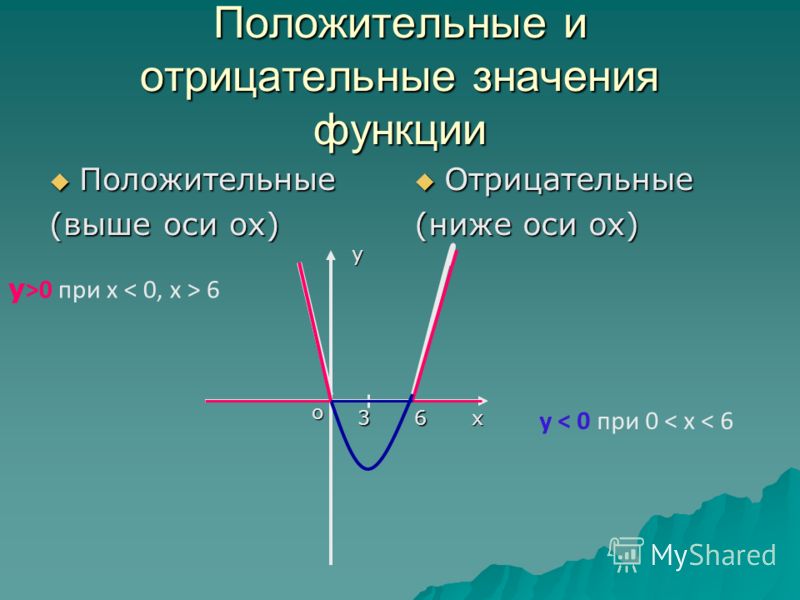 {2}}-1}{x+1}=\frac{\left( x-1 \right)\left( x+1 \right)}{x+1}=x-1\)
{2}}-1}{x+1}=\frac{\left( x-1 \right)\left( x+1 \right)}{x+1}=x-1\)
Вот и все!
А, нет, не все… еще ведь ОДЗ: на ноль делить нельзя, бла бла бла…
Ладно, ничего сложного здесь нет: \( x+1\ne 0\text{ }\Rightarrow \text{ }x\ne -1\).
Это и есть все отличие от обычной прямой: просто надо будет выколоть из графика одну точку: \( y=x-5\).
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
Элементарные функции и их графики (ЕГЭ 18. Задача с параметром)
Задачи с параметром из ЕГЭ зачастую предполагают исследование функций или хотя бы знание их свойств.
Чтобы научиться исследовать функции, для начала лучше всего научиться строить их графики.
На этом уроке мы рассмотрим основные элементарные функции, научимся строить их графики и узнаем, как на них влияют разные параметры (коэффициенты в функциях).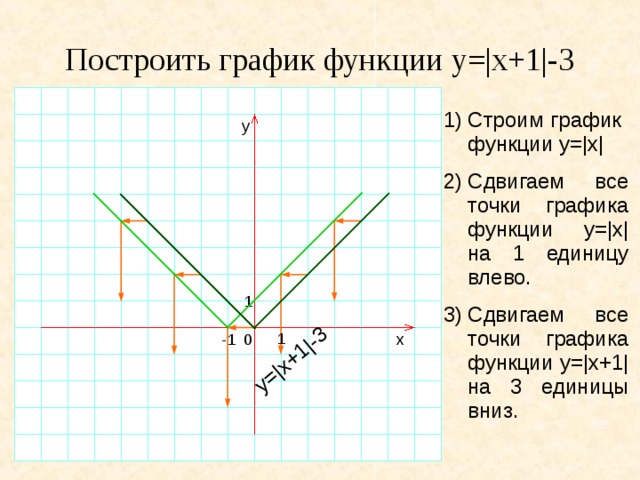
Мы рассмотрим:
- степенную функцию (линейную, квадратичную, обратную зависимость, корни),
- тригонометрические и обратные тригонометрические,
- показательную и
- логарифмическую функции.
Преобразования графиков функций (ЕГЭ 18. Задачи с параметром)
Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль?
Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?
Можно! И на этом уроке мы научимся производить такие трансформации.
Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.
Постройте и прочитайте график функции
Reshak.ru – сборник решебников для учеников старших классов. Здесь можно найти решебники, ГДЗ, переводы текстов по школьной программе. Практически весь материал, собранный на сайте – сделанный для людей. Все решебники выполнены качественно, с приятной навигацией. Вы сможете скачать гдз, решебник английского, улучшить ваши школьные оценки, повысить знания, получить намного больше свободного времени.
Практически весь материал, собранный на сайте – сделанный для людей. Все решебники выполнены качественно, с приятной навигацией. Вы сможете скачать гдз, решебник английского, улучшить ваши школьные оценки, повысить знания, получить намного больше свободного времени.
Главная задача сайта: помогать школьникам в решении домашнего задания. Кроме того, весь материал гдз совершенствуется, добавляются новые сборники решений.
Информация
© adminreshak.ru
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Ребята, мы с вами построили много графиков функций, например, параболы, гиперболы, графики тригонометрических функций и другие. Давайте вспомним, как мы это делали. Мы выбирали точки на оси абсцисс, высчитывали значения ординат нашей функций и плавно соединяли наши ординаты на координатной плоскости. То есть, мы строили график по точкам.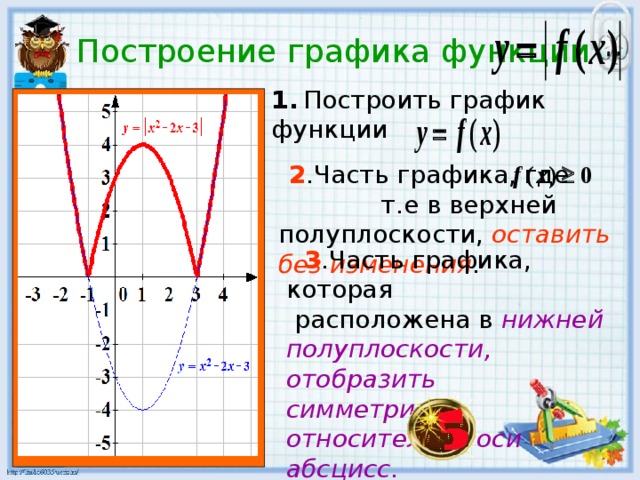 При построении многих графиков, точки нужно выбирать обдуманно. Теперь давайте обобщим наши знания и напишем общие правила построения графиков функций.
При построении многих графиков, точки нужно выбирать обдуманно. Теперь давайте обобщим наши знания и напишем общие правила построения графиков функций.
Что же такое график функции?
График функции – это множество точек, абсциссы которых являются значениями из области определения, а ординаты – значениями функции y= f(x). График любой функций строят по точкам. Но если мы точно не знаем, какой будет вид у графика, то точки надо выбирать обдуманно. Ребята, какие важные точки есть у функций?
Давайте, вспомним их:
а) Стационарные и критические точки. Такие точки мы научились находить при вычислении экстремумов функций. Это точки, в которой производная либо равна нулю, либо не существует.
б) Точки экстремума. Точки максимума и минимума функций. Точки, возле которых определяется характер монотонности.
в) Точки пересечения графика с осью абсцисс и осью ординат. Значения, в которых функция y= f(x)= 0 – точки пересечения с осью абсцисс.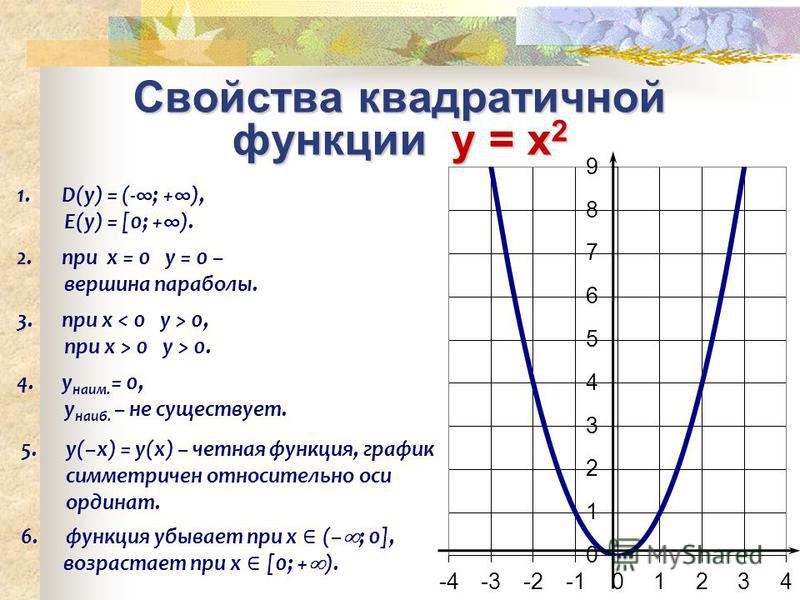 А если вычислить f(0) – то эта точка пересечения с осью ординат.
А если вычислить f(0) – то эта точка пересечения с осью ординат.
г) Точки разрыва функций. Эти точки ищутся для не непрерывных функций.
Правило построения графиков функций
Ребята, давайте запишем основные правила построения графиков функций:
- Если функция y= f(x) непрерывна на всей числовой прямой, то надо найти стационарные и критические точки, точки экстремума, промежутки монотонности, точки пересечения графика с осями координат и при необходимости выбрать еще несколько контрольных точек, в которых следует подсчитать значение нашей функции.
- Если функция y= f(x) определена не на всей числовой прямой, то начинать следует с нахождения области определения функции, с указания точек ее разрыва.
- Полезно исследовать функцию на чётность, поскольку графики четной или нечетной функций обладают симметрией (соответственно относительно оси y или относительно начала координат), и, следовательно, можно сначала построить только ветвь графика при x ≥ 0, а затем дорисовать симметричную ветвь.

- Если то прямая y= b является горизонтальной асимптотой нашего графика функции. Асимптота – это некоторой ориентир для нашей функции. Это то, к чему стремится график функции в точке, но не достигает этого значения.
- Если f(x)=$frac$; и при x= a знаменатель обращается в нуль, а числитель отличен от нуля, то x= a – это вертикальная асимптота.
Несколько правил, упрощающих построение графиков функций:
а) График функции y= f(x) + a получается из графика функции y= f(x) (график y= f(x) заранее известен), путем параллельного переноса графика y= f(x) на а единиц вверх, если а > 0; и на а единиц вниз, если а 2 , б) y= x 2 + 2, в) y= x 2 – 3.
Графики наших функций получается из графика функции y=x 2 , путем его параллельного переноса: б) на две единицы вверх, в) на три единицы вниз.
Графики наших функций:
б) График функции y= f(x + a) получается из графика функции y= f(x) (график y= f(x) заранее известен). Используем параллельный перенос графика y= f(x) на а единиц влево, если а > 0, и на а единиц вправо, если а 2 , б) y= (x + 1) 2 .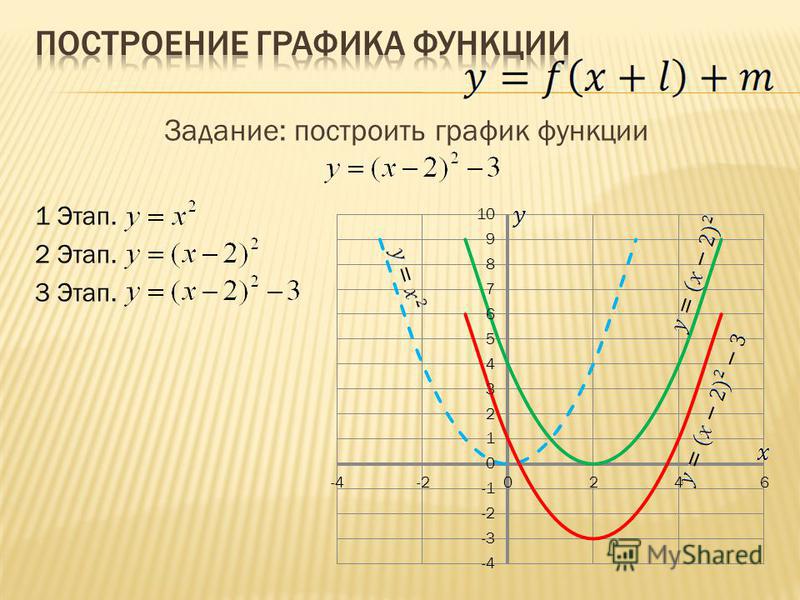
Графики наших функций получается из графика функции y= x 2 , путем его параллельного переноса: б) на две единицы вправо, в) на одну единицу влево.
Графики наших функций:
в) Для построения графика функции y= f(-x), следует построить график функции y= f(x) и отразить его относительно оси ординат. Полученный график является графиком функции y= f(-x).
Для примера построим два графика: a) y= x 3 , б) y= (-x) 3 .
Графики нашей функций получается из графика функции y=x 3 , путем отражения относительно оси ординат.
3 » title=»График функции относительно оси ординат» />
г) Для построения графика функции y= -f(x) следует построить график функции y=f(x) и отразить его относительно оси абсцисс.
Для примера построим два графика: a) y= cos(x), б) y=-cos(x). Графики нашей функций получается из графика функции y= cos(x), путем отражения относительно оси абсцисс.
Ребята, теперь давайте построим графики функций, вид которых заранее не известен. Будем использовать правила, которые мы определили в начале.
Будем использовать правила, которые мы определили в начале.
Примеры на построение
I. Построить график функции: y= 2x 2 + 4x – 5.
Решение:
1) Область определения: D(y)= (-∞; +∞).
2) Найдем стационарные точки:
y’= 4x + 4,
4x + 4 = 0,
x= -1.
3) Определим вид стационарной точки и характер монотонности:
Точка x= -1 – точка минимума. Найдем значение функции в точке x= -1
y(-1)= 2(-1) 2 + 4(-1) – 5= -7.
Итак, наша функция убывает на промежутке =(-∞;-1), x= -1 – точка минимума, функция возрастает на промежутке (-1; +∞).
Вычислим значения функции в паре точек:
Построим график функции:
II. Построить график функции: y= 5x 3 – 3x 5 .
Решение:
1) Область определения: D(y)= (-∞;+∞).
2) Найдем стационарные точки:
y’= 15x 2 – 15x 4 ,
y’= 15x 2 (1 – x 2 )= 15x 2 (1 – x)(1 + x),
15x 2 (1 – x)(1 + x)= 0,
x= 0; ±1.
3) Определим вид стационарной точки и характер монотонности:
Точка x= -1 – точка минимума.
Точка x= 0 – точка перегиба, функция в этой точки так же возрастает, но вогнутость меняется в другую сторону.
Точка x= 1 – точка максимума.
Найдем значение функции в точке x= -1: y(-1)= 5(-1) 3 – 3(-1) 5 = -2.
Найдем значение функции в точке x= 0: y(0)= 5(0) 3 – 3(0) 5 = 0.
Найдем значение функции в точке x= 1: y(1)= 5(1) 3 – 3 (1) 5 = 2
5) Исследуем функцию на четность: y(-x)= 5(-x 3 ) – 3(-x 5 )= -5x 3 + 3 5 = -y(x)
По определению функция нечетная, и график симметричен относительно начало координат.
Итак, функция нечетная.
Наша функция убывает на промежутке равном (-∞;-1).
x= -1 – точка минимума. Функция возрастает на (-1;1).
x= 0 – точка перегиба.
x= 1 – точка максимума. Функция возрастает на (1;+∞).
Вычислим значения функции в паре точек:
Построим график функции:
III. Построить график функции: y=$frac$.
Решение:
1) Область определения: D(y)= (-∞;-2)U(-2;2)U(2;+∞).
По определению функция четная.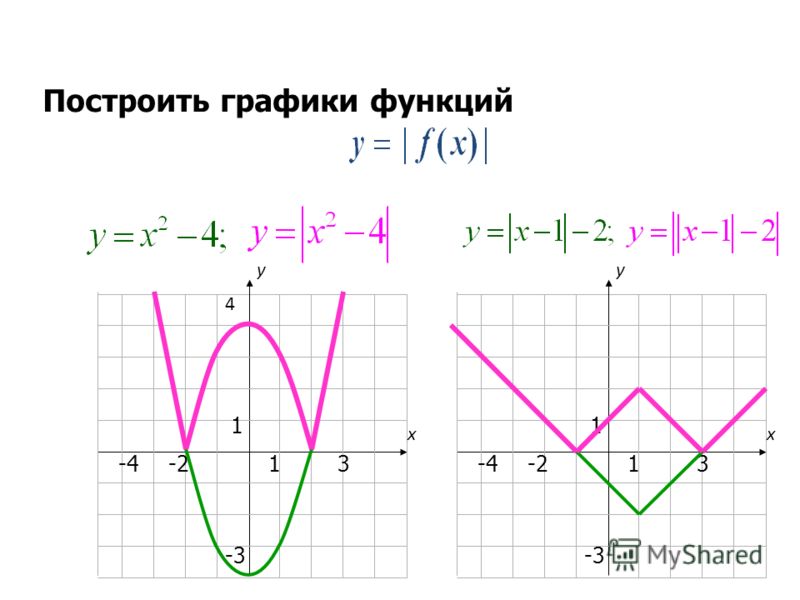 Значит, график функции симметричен относительно оси ординат, можно сначала построить график функции для x ≥ 0. 3) Прямая x= 2 – вертикальная асимптота, т.к. знаменатель нашей функции в этой точке обращается в нуль.
Значит, график функции симметричен относительно оси ординат, можно сначала построить график функции для x ≥ 0. 3) Прямая x= 2 – вертикальная асимптота, т.к. знаменатель нашей функции в этой точке обращается в нуль.
Найдем горизонтальную асимптоту:
Прямая y= 1 – горизонтальная асимптота.
4) Найдем стационарные и критические точки: Критических точек у нашей функции нет, т.к. производная определена всюду на области определения нашей функции.
5) Определим вид стационарной точки и характер монотонности: Точка x= 0 – точка максимума.
Итак, наша функция четная. Она возрастает на промежутке равном (-∞;0), x= 0 – точка максимума. Функция убывает на (0;+∞).
Прямая x= 2 – вертикальная асимптота. Прямая y= 1 – горизонтальная асимптота.
Вычислим значения функции в паре точек:
Т.к. функция четная построим сначала график для x ≥ 0.
0 » />
Используя свойство четных функций, отразим график функции относительно оси ординат.
Задачи на построение графиков функций для самостоятельного решения
1) Построить график функции: $y= (-x)^2 + 4x – 7$.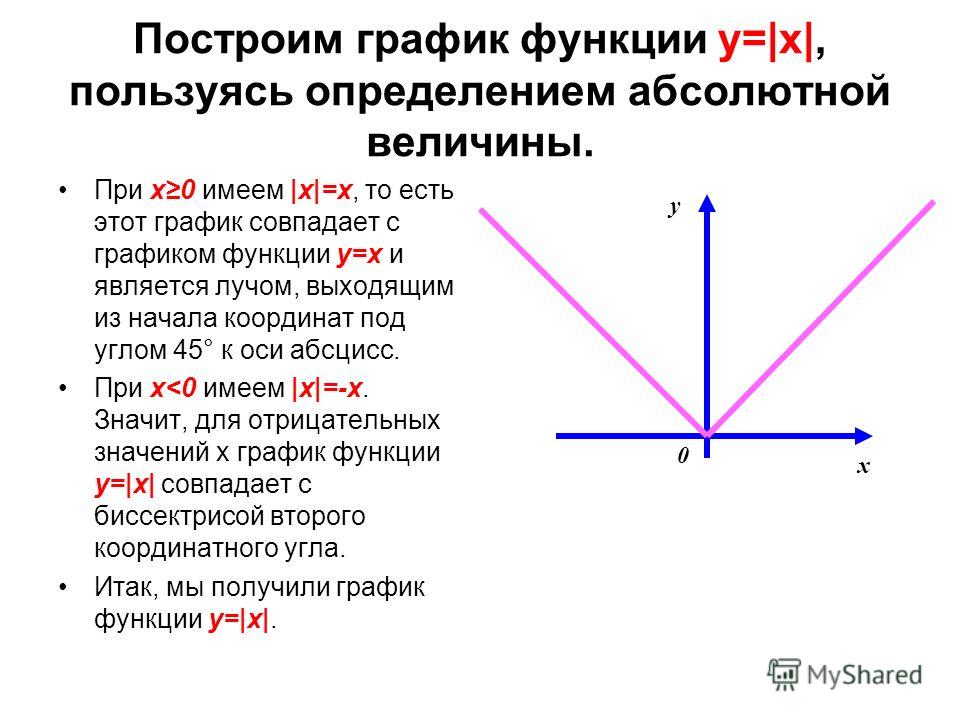 2/16=1)
2/16=1)
С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.
Построение графиков онлайн весьма полезный способ графически отобразить то, что не в силах передать словами.
Информация – это будущее электронного маркетинга, при этом правильно преподнесенные зрительные образы являются мощным инструментом для привлечения целевой аудитории.
Тут на помощь приходит инфографика, позволяющая в простой и выразительной форме преподносить различного рода информацию.
Однако построение инфографических изображений требует определенного аналитического мышления и богатства фантазии.
Спешим вас обрадовать – в интернете достаточно ресурсов, предоставляющих построение графиков онлайн.
Yotx.ru
Замечательный русскоязычный сервис, осуществляющий построение графиков онлайн по точкам (по значениям) и графиков функций (обычных и параметрических).
Этот сайт обладает интуитивно понятным интерфейсом и легок в использовании. Не требует регистрации, что существенно экономит время пользователя.
Позволяет быстро сохранять готовые графики на компьютере, а также генерирует код для размещения на блоге или сайте.
На Yotx.ru есть учебник и примеры графиков, которые были созданы пользователями.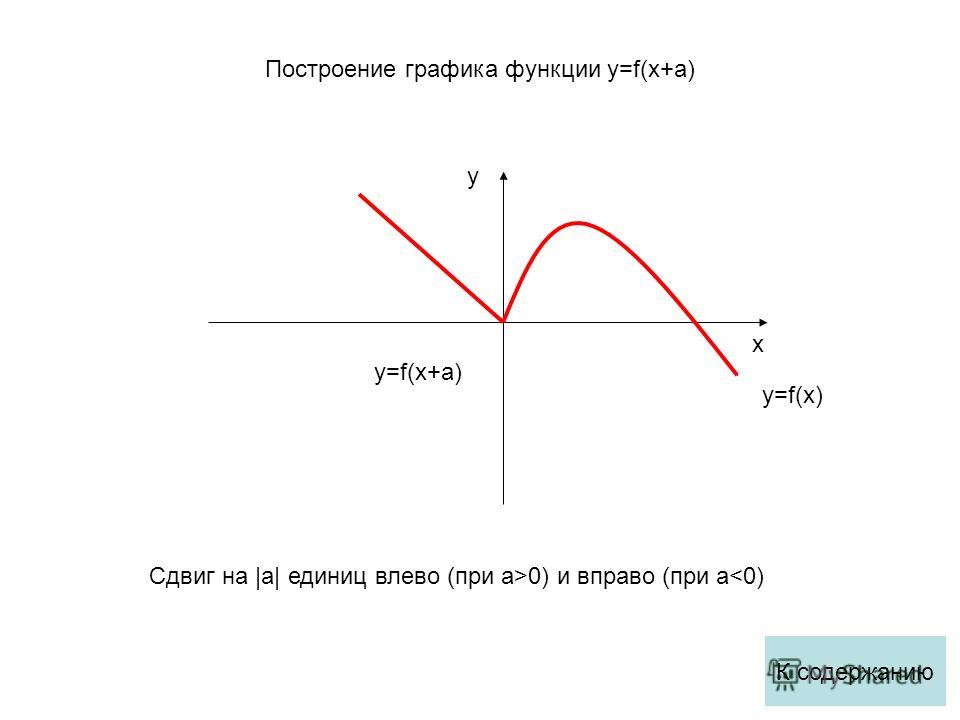
Возможно, для людей, углубленно изучающих математику или физику, этого сервиса будет мало (например, нельзя построить график в полярных координатах, так как на сервисе нет логарифмической шкалы), но для выполнения самых простых лабораторных работ вполне достаточно.
Преимуществом сервиса является то, что он не заставляет как многие другие программы, искать полученный результат по всей двумерной плоскости.
Размер графика и интервалы по осям координат автоматически генерируются так, чтобы график оказался удобным для просматривания.
Одновременно на одной плоскости есть возможность построить несколько графиков.
Дополнительно на сайте можно использовать калькулятор матриц, с помощью которого легко производить различные действия и преобразования.
ChartGo
Англоязычный сервис для разработки многофункциональных и разноцветных гистограмм, линейных графиков, круговых диаграмм.
Для обучения пользователям представляется подробное руководство и деморолики.
ChartGo будет полезен для тех, кто нуждается в регулярно. Среди подобных ресурсов отличается простотой «Create a graph online quickly».
Построение графиков онлайн осуществляется по таблице.
В начале работы необходимо выбрать одну из разновидностей диаграмм.
Приложение обеспечивает пользователям ряд простых вариантов настройки построения графиков различных функций в двумерных и трехмерных координатах.
Можно выбрать одну из разновидностей диаграмм и переключаться между 2D и 3D.
Настройки размера обеспечивают максимальный контроль между вертикальной и горизонтальной ориентацией.
Пользователи могут настраивать свои диаграммы с уникальным названием, а также присваивать названия для X и Y элементов.
Для построения графиков онлайн xyz в разделе «Example» доступно множество макетов, которые можно изменять на свое усмотрение.
Обратите внимание! В ChartGo в одной прямоугольной системе может быть построено множество графиков.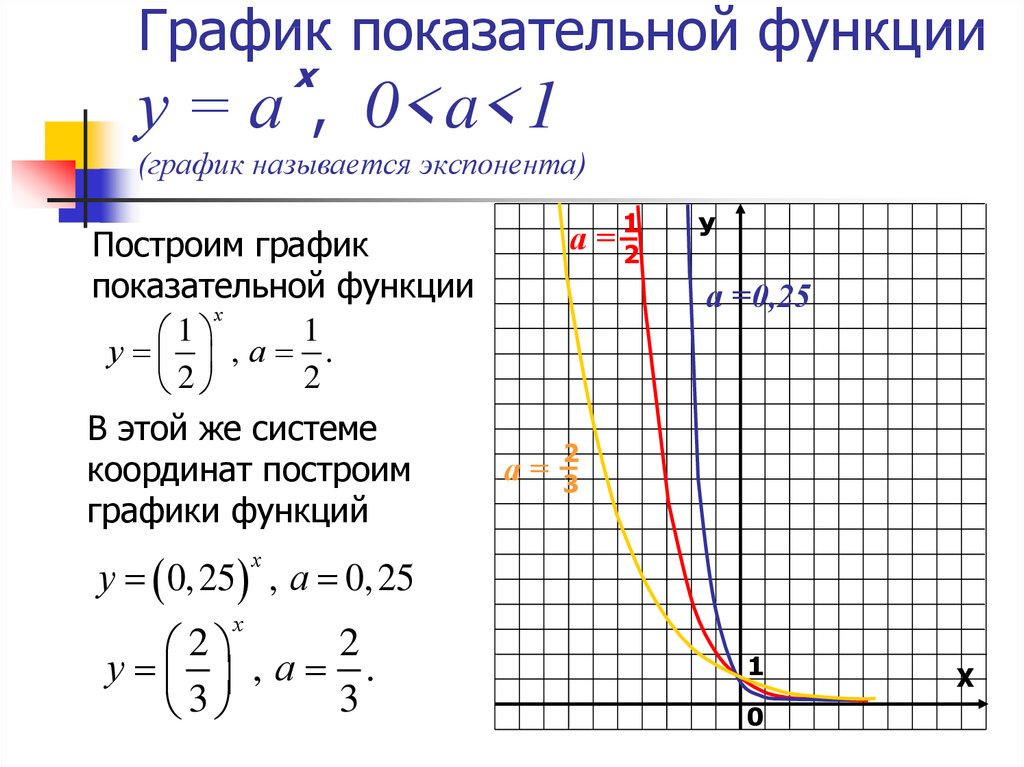 При этом каждый график составлен с помощью точек и линий. Функции действительного переменного (аналитические) задаются пользователем в параметрическом виде.
При этом каждый график составлен с помощью точек и линий. Функции действительного переменного (аналитические) задаются пользователем в параметрическом виде.
Разработан и дополнительный функционал, который включает мониторинг и вывод координат на плоскости или в трехмерной системе, импорт и экспорт числовых данных в определенных форматах.
Программа имеет гибко настраиваемый интерфейс.
После создания диаграммы, пользователь может воспользоваться функцией печати результата и сохранения графика в виде статичного рисунка.
OnlineCharts.ru
Еще одно отличное приложение для эффектного представления информации вы можете найти на сайте OnlineCharts.ru, где можно построить график функции онлайн бесплатно.
Сервис способен работать с множеством видов диаграмм, включая линейные, пузырьковые, круговые, столбчатые и радиальные.
Система обладает очень простым и наглядным интерфейсом. Все доступные функции разделены вкладками в виде горизонтального меню.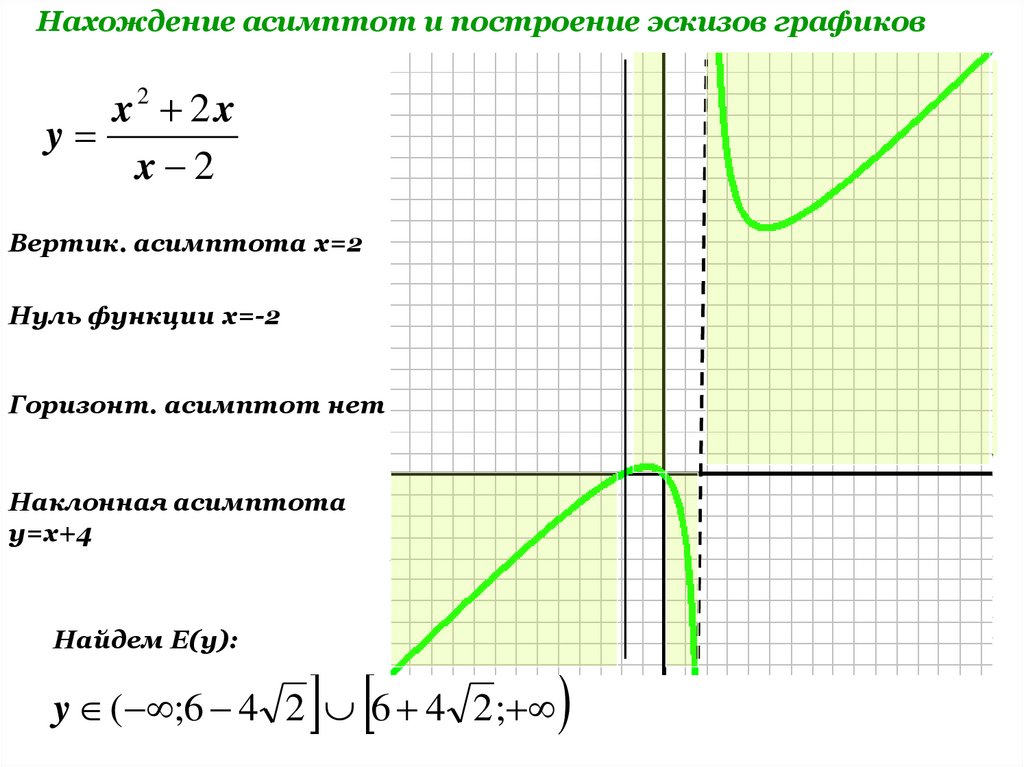
Чтобы начать работу необходимо выбрать тип диаграммы, которую вы хотите построить.
После этого можно настроить некоторые дополнительные параметры внешнего вида, в зависимости от выбранного типа графика.
Во вкладке «Добавить данные» пользователю предлагается задать количество строк и если необходимо количество групп.
Также можно определить цвет.
Обратите внимание! Вкладка «Подписи и шрифты» предлагает задать свойства подписей (нужно ли их выводить вообще, если да, то каким цветом и размером шрифта). Также предоставляется возможность выбора типа шрифта и его размера для основного текста диаграммы.
Все предельно просто.
Aiportal.ru
Самый простой и наименее функциональный из всех, представленных здесь онлайн-сервисов. Создать трехмерный график онлайн на этом сайте не удастся.
Он предназначен для построения графиков сложных функций в системе координат на определенном интервале значений.
Для удобства пользователей сервис предоставляет справочные данные по синтаксису различных математических операций , а также по перечню поддерживаемых функций и константных значений. 3$.
3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.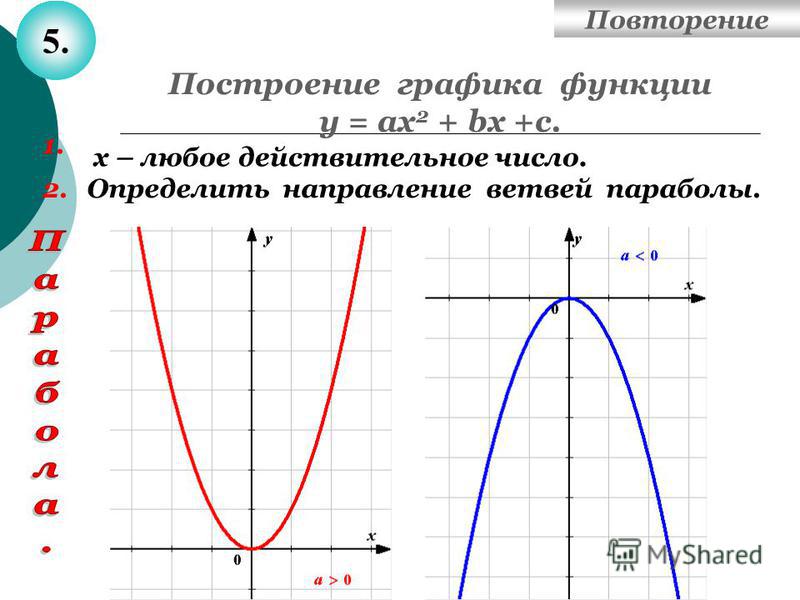
На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака «=».
- Нажмите кнопку «Построить график» .
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить» .
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:» .
- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.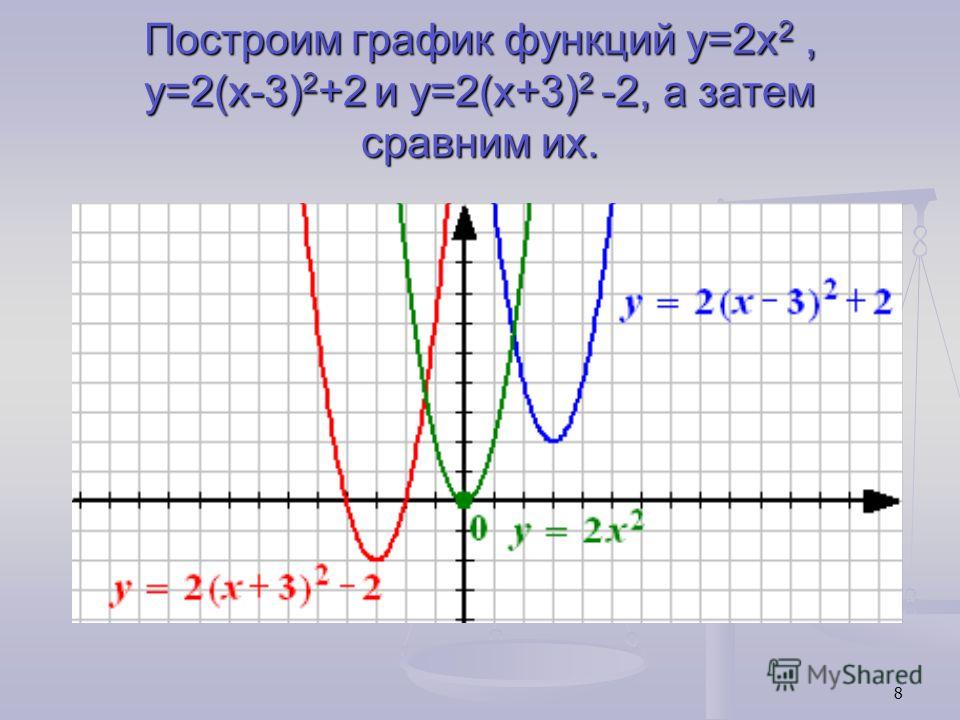
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений.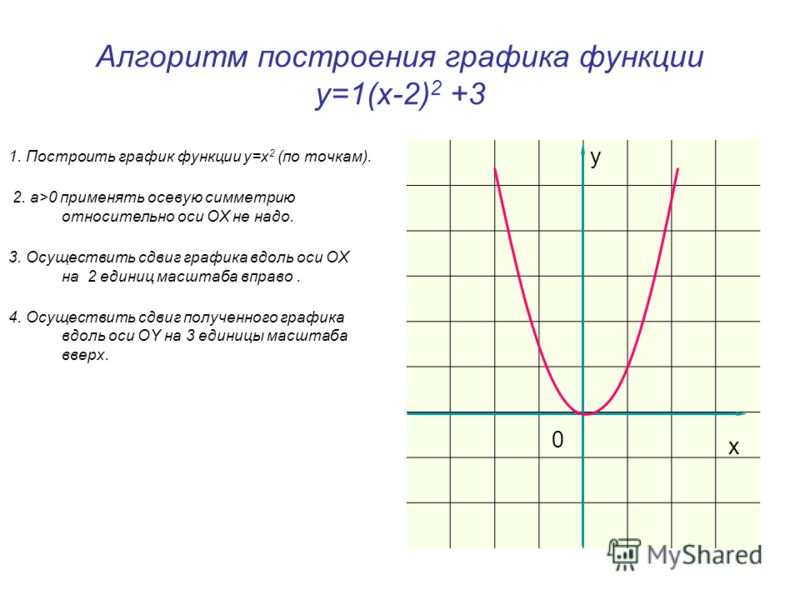 Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости).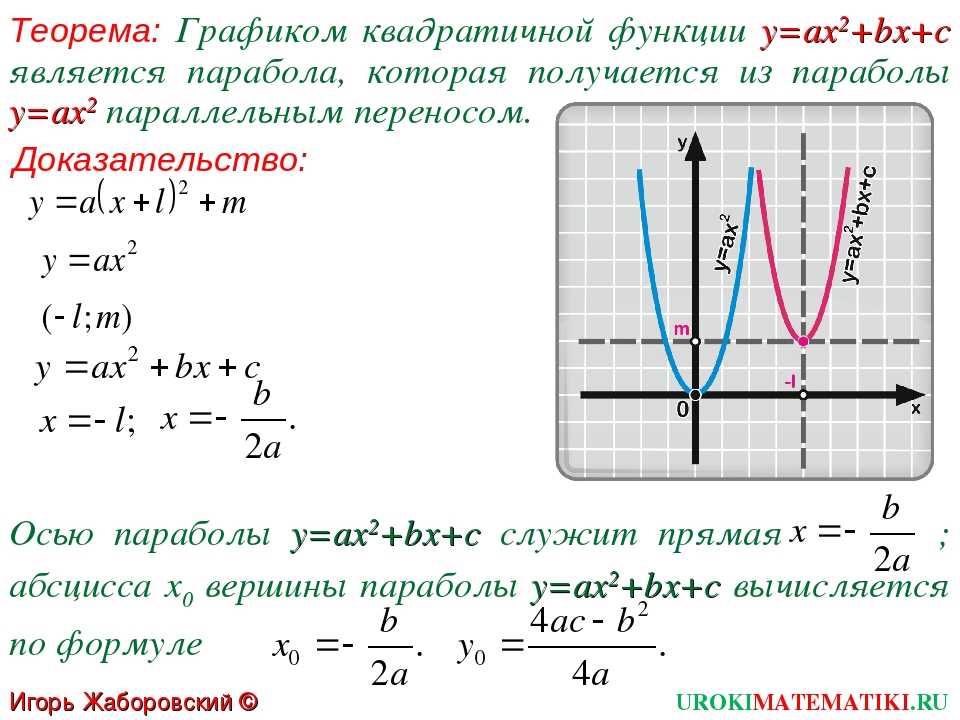 В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция

Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.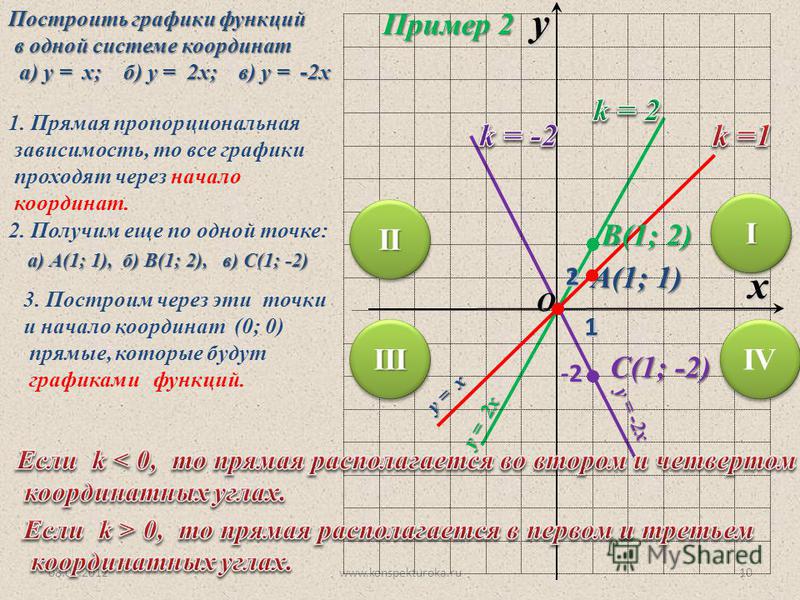
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т.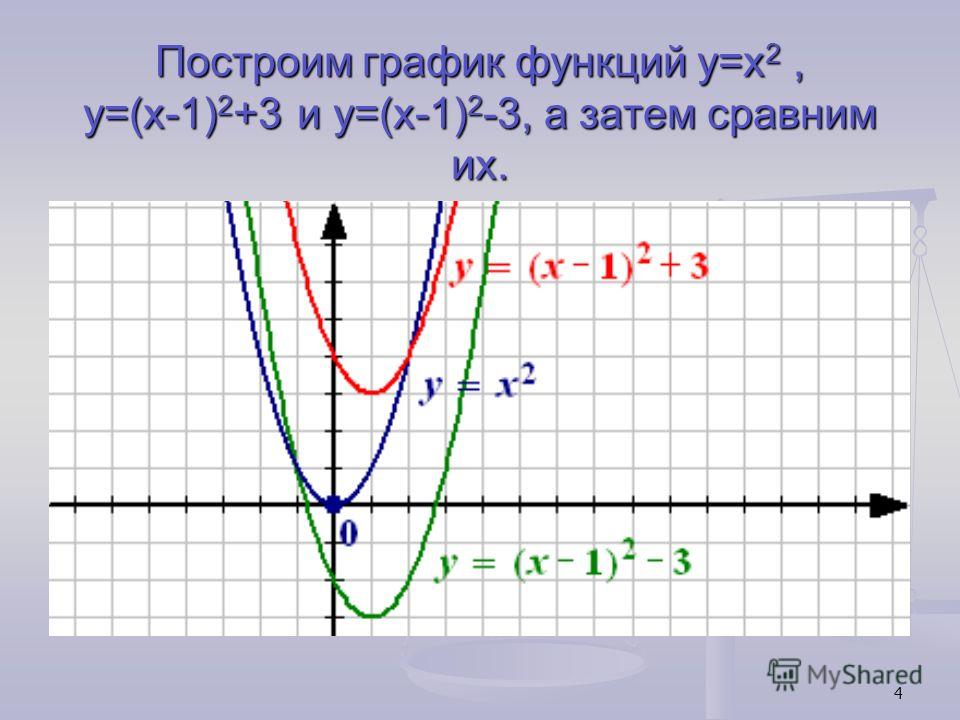 е. часть графика функции
е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).
Пример 2. Построить график функции у = |х|.
Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
Пример 3 . Построить график функции y = |x 2 — 2x|.
Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x).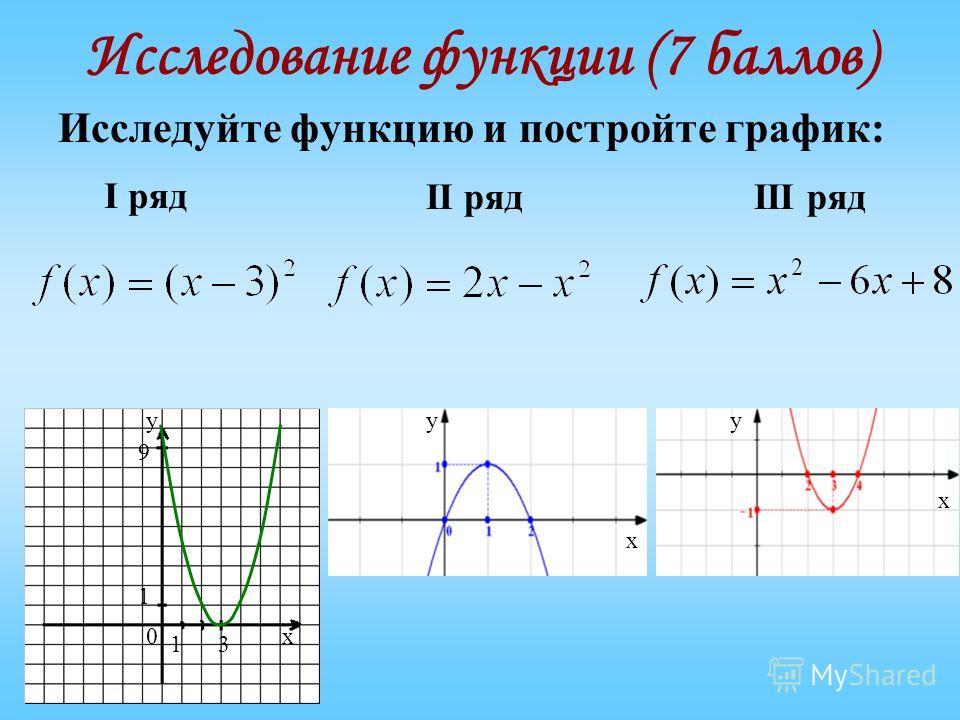 если заданы графики функций y = f(x) и y = g(x) .
если заданы графики функций y = f(x) и y = g(x) .
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .
При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.
График функции, построение графика, урок по алгебре за 10 класс, презентация
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:Построение графиков функций (PDF)
Ребята, мы с вами построили много графиков функций, например, параболы, гиперболы, графики тригонометрических функций и другие. Давайте вспомним, как мы это делали. Мы выбирали точки на оси абсцисс, высчитывали значения ординат нашей функций и плавно соединяли наши ординаты на координатной плоскости. То есть, мы строили график по точкам. При построении многих графиков, точки нужно выбирать обдуманно. Теперь давайте обобщим наши знания и напишем общие правила построения графиков функций.
Что же такое график функции?
График функции – это множество точек, абсциссы которых являются значениями из области определения, а ординаты — значениями функции y= f(x). График любой функций строят по точкам. Но если мы точно не знаем, какой будет вид у графика, то точки надо выбирать обдуманно. Ребята, какие важные точки есть у функций?
Давайте, вспомним их:
а) Стационарные и критические точки.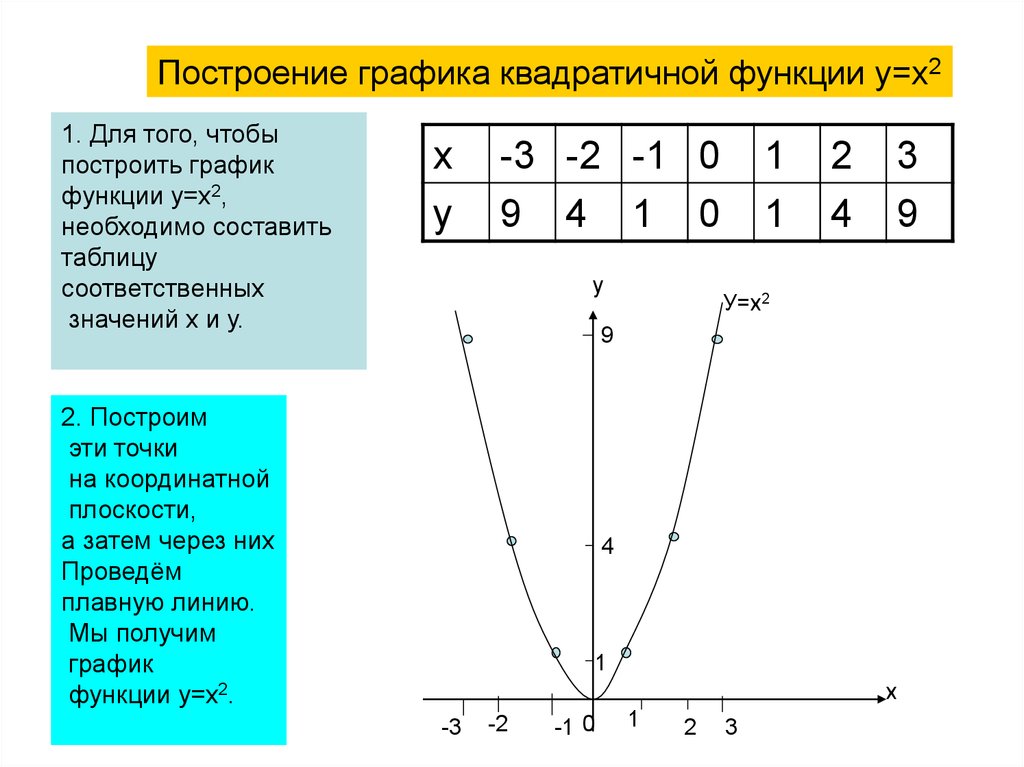 Такие точки мы научились находить при вычислении экстремумов функций. Это точки, в которой производная либо равна нулю, либо не существует.
Такие точки мы научились находить при вычислении экстремумов функций. Это точки, в которой производная либо равна нулю, либо не существует.б) Точки экстремума. Точки максимума и минимума функций. Точки, возле которых определяется характер монотонности.
в) Точки пересечения графика с осью абсцисс и осью ординат. Значения, в которых функция y= f(x)= 0 – точки пересечения с осью абсцисс. А если вычислить f(0) – то эта точка пересечения с осью ординат.
г) Точки разрыва функций. Эти точки ищутся для не непрерывных функций.
Правило построения графиков функций
Ребята, давайте запишем основные правила построения графиков функций:
- Если функция y= f(x) непрерывна на всей числовой прямой, то надо найти стационарные и критические точки, точки экстремума, промежутки монотонности, точки пересечения графика с осями координат и при необходимости выбрать еще несколько контрольных точек, в которых следует подсчитать значение нашей функции.

- Если функция y= f(x) определена не на всей числовой прямой, то начинать следует с нахождения области определения функции, с указания точек ее разрыва.
- Полезно исследовать функцию на чётность, поскольку графики четной или нечетной функций обладают симметрией (соответственно относительно оси y или относительно начала координат), и, следовательно, можно сначала построить только ветвь графика при x ≥ 0, а затем дорисовать симметричную ветвь.
- Если то прямая y= b является горизонтальной асимптотой нашего графика функции. Асимптота — это некоторой ориентир для нашей функции. Это то, к чему стремится график функции в точке, но не достигает этого значения.
- Если f(x)=$\frac{p(x)}{q(x)}$; и при x= a знаменатель обращается в нуль, а числитель отличен от нуля, то x= a — это вертикальная асимптота.
Несколько правил, упрощающих построение графиков функций:
а) График функции y= f(x) + a получается из графика функции y= f(x) (график y= f(x) заранее известен), путем параллельного переноса графика y= f(x) на а единиц вверх, если а > 0; и на а единиц вниз, если аДля примера построим три графика: а) y= x2, б) y= x2 + 2, в) y= x2 — 3.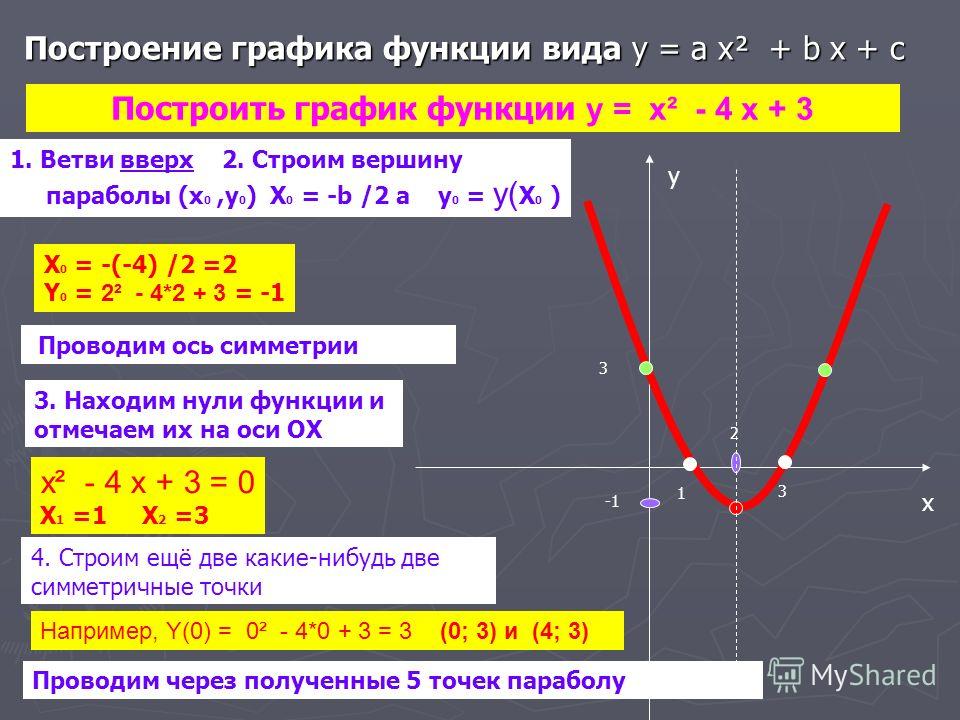
Графики наших функций:
б) График функции y= f(x + a) получается из графика функции y= f(x) (график y= f(x) заранее известен). Используем параллельный перенос графика y= f(x) на а единиц влево, если а > 0, и на а единиц вправо, если а
Для примера построим три графика: а) y= (x — 2)2, б) y= (x + 1)2.
Графики наших функций получается из графика функции y= x2, путем его параллельного переноса: б) на две единицы вправо, в) на одну единицу влево.
Графики наших функций:
в) Для построения графика функции y= f(-x), следует построить график функции y= f(x) и отразить его относительно оси ординат. Полученный график является графиком функции y= f(-x).
Для примера построим два графика: a) y= x3, б) y= (-x)3.
Графики нашей функций получается из графика функции y=x3, путем отражения относительно оси ординат.
г) Для построения графика функции y= -f(x) следует построить график функции y=f(x) и отразить его относительно оси абсцисс.
Для примера построим два графика: a) y= cos(x), б) y=-cos(x). Графики нашей функций получается из графика функции y= cos(x), путем отражения относительно оси абсцисс.
Ребята, теперь давайте построим графики функций, вид которых заранее не известен. Будем использовать правила, которые мы определили в начале.
Примеры на построение
I. Построить график функции: y= 2x2 + 4x — 5.
Решение:
1) Область определения: D(y)= (-∞; +∞).
2) Найдем стационарные точки:
y’= 4x + 4,
4x + 4 = 0,
x= -1.
3) Определим вид стационарной точки и характер монотонности:
Точка x= -1 – точка минимума. Найдем значение функции в точке x= -1
y(-1)= 2(-1)2 + 4(-1) — 5= -7.
Итак, наша функция убывает на промежутке =(-∞;-1), x= -1 – точка минимума, функция возрастает на промежутке (-1; +∞).
Вычислим значения функции в паре точек:
Построим график функции:
II. Построить график функции: y= 5x3 — 3x5.
Построить график функции: y= 5x3 — 3x5.
Решение:
1) Область определения: D(y)= (-∞;+∞).
2) Найдем стационарные точки:
y’= 15x2 — 15x4,
y’= 15x2(1 — x2)= 15x2(1 — x)(1 + x),
15x2(1 — x)(1 + x)= 0,
x= 0; ±1.
3) Определим вид стационарной точки и характер монотонности:
Точка x= -1 – точка минимума.
Точка x= 0 – точка перегиба, функция в этой точки так же возрастает, но вогнутость меняется в другую сторону.
Точка x= 1 – точка максимума.
Найдем значение функции в точке x= -1: y(-1)= 5(-1)3 — 3(-1)5= -2.
Найдем значение функции в точке x= 0: y(0)= 5(0)3 — 3(0)5= 0.
Найдем значение функции в точке x= 1: y(1)= 5(1)3 — 3 (1)5= 2
По определению функция нечетная, и график симметричен относительно начало координат.
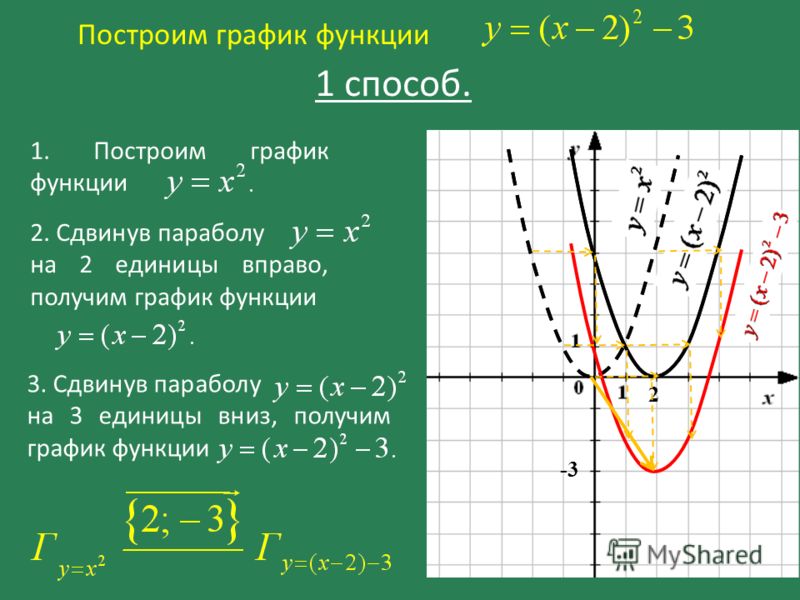 2-4}$= y(x) По определению функция четная. Значит, график функции симметричен относительно оси ординат, можно сначала построить график функции для x ≥ 0.
3) Прямая x= 2 – вертикальная асимптота, т.к. знаменатель нашей функции в этой точке обращается в нуль.
2-4}$= y(x) По определению функция четная. Значит, график функции симметричен относительно оси ординат, можно сначала построить график функции для x ≥ 0.
3) Прямая x= 2 – вертикальная асимптота, т.к. знаменатель нашей функции в этой точке обращается в нуль.Найдем горизонтальную асимптоту:
Прямая y= 1 – горизонтальная асимптота.
4) Найдем стационарные и критические точки: Критических точек у нашей функции нет, т.к. производная определена всюду на области определения нашей функции.5) Определим вид стационарной точки и характер монотонности: Точка x= 0 – точка максимума.
Итак, наша функция четная. Она возрастает на промежутке равном (-∞;0), x= 0 – точка максимума. Функция убывает на (0;+∞).
Прямая x= 2 – вертикальная асимптота. Прямая y= 1 – горизонтальная асимптота.
Вычислим значения функции в паре точек:
Т.к. функция четная построим сначала график для x ≥ 0.
Используя свойство четных функций, отразим график функции относительно оси ординат. 2, что значит автоматическое возведение указанной ячейки в квадрат.
2, что значит автоматическое возведение указанной ячейки в квадрат.
 Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel.
 Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25. - Создайте сразу два столбца — X и Y, куда будете записывать данные.
- Запишите самостоятельно первые два или три значения с указанным шагом.
- Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
- Перейдите к столбцу Y и объявите функцию
=SIN(, а в качестве числа укажите первое значение X. - Сама функция автоматически высчитает синус заданного числа.
- Растяните столбец точно так же, как это было показано ранее.
- Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
- Выделите столбец с Y и перейдите на вкладку «Вставка».
- Создайте стандартный график, развернув выпадающее меню.
- График функции от y=sin(x) успешно построен и отображается правильно.
 Редактируйте его название и отображаемые шаги для простоты понимания.
Редактируйте его название и отображаемые шаги для простоты понимания.
Мы рады, что смогли помочь Вам в решении проблемы. Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Содержание
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
Построение графика линейной функции в Excel
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.
Установка шага значений аргумента функцииДалее строим таблицу значений линейной функции:
- В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
- Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
- Выделяем эти ячейки.
- Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.
Автозаполнение значений аргумента функцииДалее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Запись расчётной формулы для значений функцииВнимание! Запись формулы начинается со знака равно(=).
Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.
Копирование формулыПостроение графика функции
Выделяем прямоугольный диапазон ячеек A5:J6.
Выделение таблицы функцииПереходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
Построение диаграммы типа “График”График линейной функцииПосле построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
Теперь можно ввести новые значения постоянных k и b для изменения графика.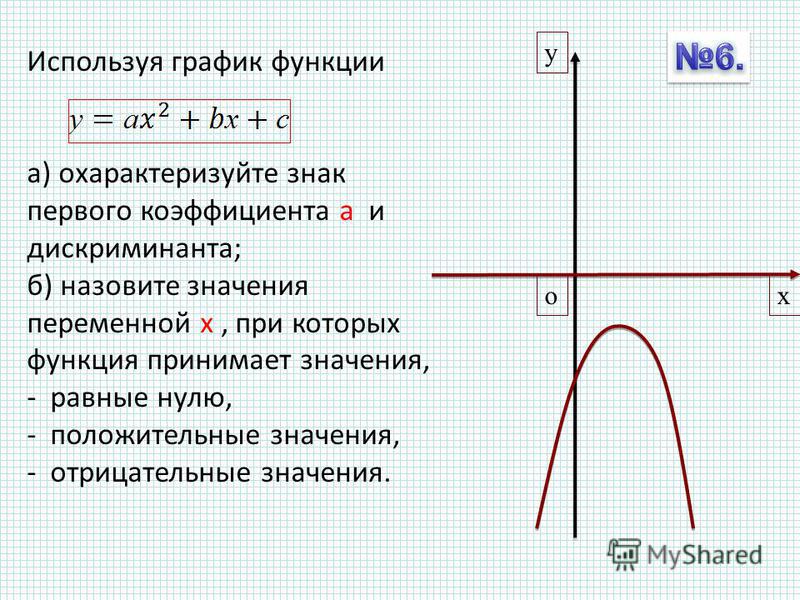 И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы – Оси – Дополнительные параметры оси..
И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы – Оси – Дополнительные параметры оси..
В правой части окна появиться боковая панель настроек Формат оси.
Редактирование параметров координатной оси- Кликните на раскрывающийся список Параметры оси.
- Выберите Вертикальная ось (значений).
- Кликните зеленый значок диаграммы.
- Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.
 И главную единицу измерения – значение 1.
И главную единицу измерения – значение 1. - Повторите тоже для горизонтальной оси.
Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
Квадратичная функция y=ax
2+bx+cВыполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
График квадратичной функцииКубическая парабола y=ax
3Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
График кубической параболыГипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже).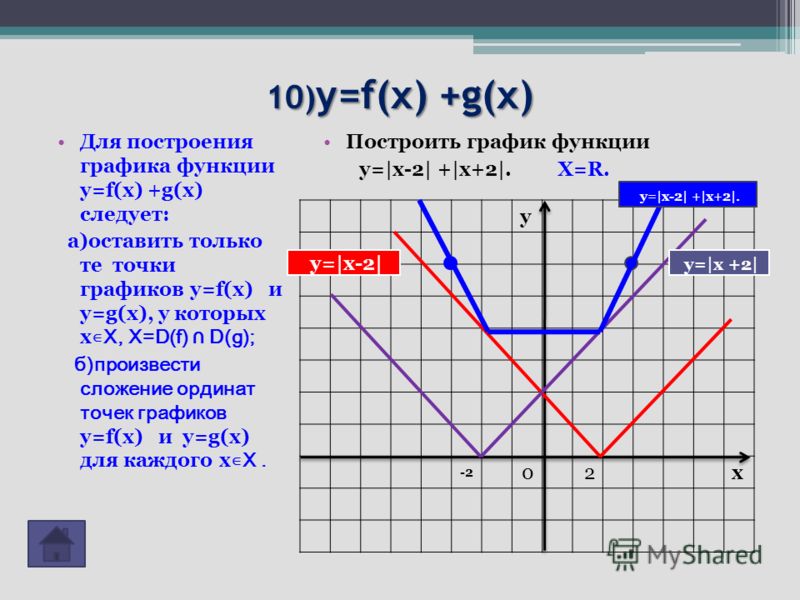 Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Получаем результат
График гиперболыПостроение тригонометрических функций sin(x) и cos(x)
Таблица значений функции sin(x)Запись расчетной формулы функции sin(x) в ExcelВ нашем примере =$B$3*SIN($D$3*B6).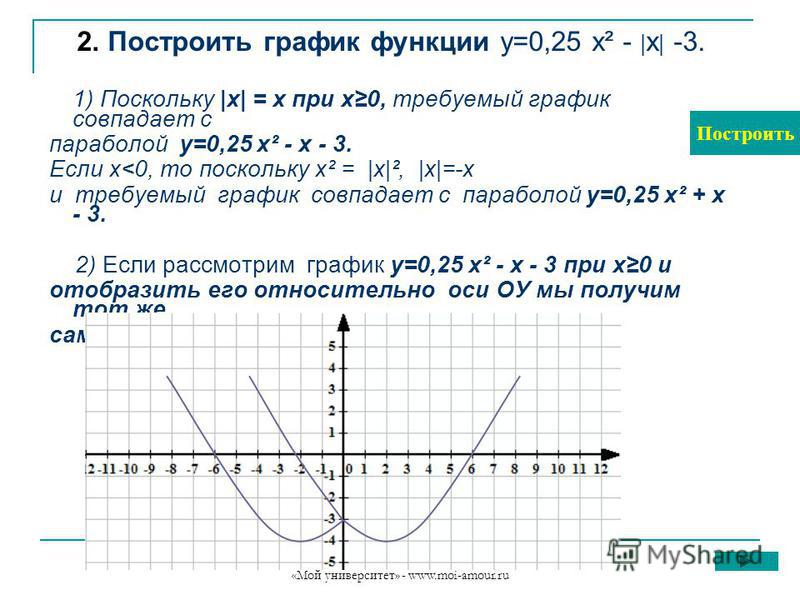 Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице. После заполнения таблицы приступаем к построению графика.
Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице. После заполнения таблицы приступаем к построению графика.
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
Построение диаграммы Точечная с гладкими кривымиВ итоге получим диаграмму.
График sin(x) после вставки диаграммыТеперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
Настройка сетки при построении графикаТеперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
Произведем настройки здесь.
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
Настройка формата горизонтальной оси Х графика функцииТеперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5. Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
PS: Интересные факты про логотипы известных компаний
Дорогой читатель! Вы посмотрели статью до конца. Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.
Построим в MS EXCEL график функции, заданный системой уравнений. Эта задача часто встречается в лабораторных работах и почему-то является “камнем преткновения” для многих учащихся.
Пусть дана система уравнений
Требуется на отрезке [-1; 4] построить график функции f(x). Параметры a = 5 и b = 2 необходимо задать в отдельных ячейках.
Решение (1 ряд данных)
Чтобы построить график функции в MS EXCEL можно использовать диаграмму типа График или Точечная.
СОВЕТ: О построении диаграмм см. статью Основы построения диаграмм в MS EXCEL. О различии диаграмм Точечная и График см. статью График vs Точечная диаграмма в MS EXCEL.
Создадим таблицу с исходными данными для x от -1 до 4, включая граничные значения (см. файл примера, лист Ряд1 ):
Шаг по х выберем равным 0,2, чтобы график содержал более 20 точек.
Чтобы построить диаграмму типа Точечная:
- выделите любую ячейку таблицы;
- во вкладке Вставка в группе Диаграммы выберите диаграмму Точечная с прямыми отрезками и маркерами.
Чтобы построить диаграмму типа График:
- выделите любую столбец f(x) вместе с заголовком;
- во вкладке Вставка в группе Диаграммы выберите диаграмму График маркерами.
У обеих диаграмм один общий недостаток — обе части графика соединены линией (в диапазоне х от 1 до 1,2). Из этого можно сделать ошибочный вывод, что, например, для х=1,1 значение функции равно около -15. Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график используя 2 ряда данных.
Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график используя 2 ряда данных.
Решение (2 ряда данных)
Создадим другую таблицу с исходными данными в файле примера, лист График :
Второй и третий столбец таблицы будут использоваться для построения 2-х рядов данных. Первый столбец — для подписей по оси х. Для значений x>1 будет построен второй график (в степени 3/2), для остальных — парабола. Значения #Н/Д (нет данных) использованы для удобства — в качестве исходных данных для ряда можно брать значения из целого столбца. В противном случае пришлось бы указывать диапазоны соответствующих ячеек при построении диаграммы. При изменении шага по х — это вызвало бы необходимость перестроения диаграммы.
У такой диаграммы имеется недостаток — в диапазоне х от 1 до 1,2 на диаграмме теперь нет вообще значений. Чтобы избежать этого недостатка — построим диаграмму типа Точечная с 3-мя рядами данных.
Решение (3 ряда данных)
Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График .
файл примера, лист График .
Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).
Цели и задачи.
- Развитие приемов умственной деятельности, формирование и развитие функционального мышления учащихся, развитие познавательных потребностей учащихся, создание условий для приобретения опыта работы учащихся в среде ИКТ.
- Достижение сознательного усвоения учебного материала учащимися, работа над повышением грамотности устной речи, правильного использования компьютерных терминов.
- Научить применять возможности MS Excel в повседневной жизни, в познавательной деятельности.
- Закрепить навыки создания таблиц и диаграмм.
- Научить решать систему уравнений графическим методом, исследовать график функции.

Читайте также: Need for speed underground 3 2019
Оборудование урока: компьютеры, мультимедиа проектор.
Программное обеспечение: Windows XP, пакет программ MS Office 2003.
Тема нашего урока тесно связана с математикой разделы “Графики функций” и “Решение систем уравнений”. Поэтому нам понадобятся ранее полученные навыки. Но мы постараемся упростить нашу задачу с помощью применения современных вычислительных средств.
Запишите в тетради тему урока и укажите дату.
Назовите мне кого из класса сегодня нет.
Давайте вспомним, что такое уравнение, и как его можно решить графически.
Назовите, пожалуйста, что в математике называют уравнением, решением уравнения и системой уравнений.
(Учащиеся приводят определения)
Уравнение – это математическое выражение, содержащее неизвестную величину (переменную) и 0 с правой стороны от знака =.
Система уравнений – несколько связанных уравнений, имеющих одинаковые обозначения неизвестных величин (переменных).
Решением уравнения – называют такое значение неизвестной величины, при подстановке которого левая часть выражения принимает значение 0. И мы получаем верное равенство.
Но, с другой стороны, подобное выражение можно представить как функцию с зависимой и независимой величинами. Если мы слева от знака = поставим Y, а справа заданное выражение. Y – зависимая величина, Х – независимая величина. В этом случае Решением уравнения является точка пересечения графика функции с осью ОХ.
Для решения уравнения графическим методом необходимо рассчитать значения функции в ключевых точках с координатой Х (Х меняется в диапазоне допустимых значений), нанести эти точки на систему координат, построить график функции и определить координаты точки пересечения графика с осью ОХ.
Это достаточно сложная задача. Нужно достаточно много вычислений и аккуратное построение графика функции. Также мы заранее не можем сказать, из какого диапазона чисел необходимо брать значения Х.
Но эту задачу может взять на себя ЭВМ.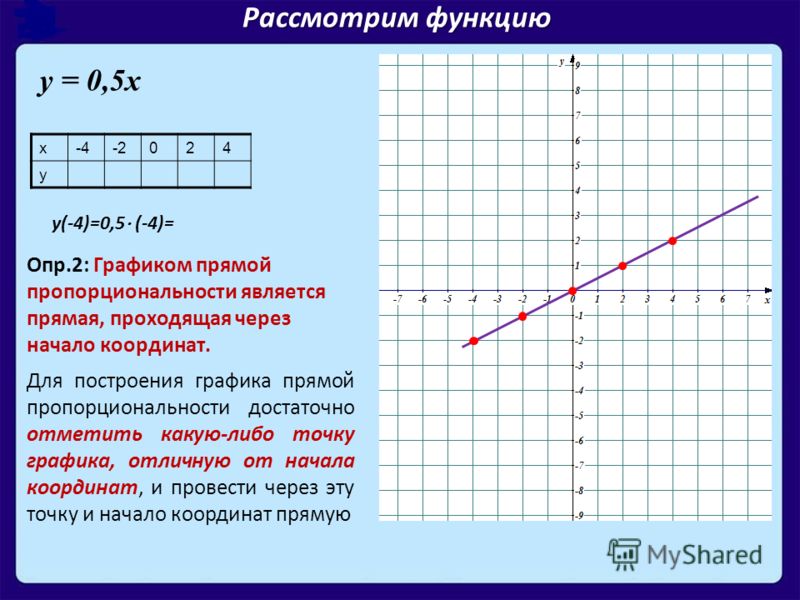
Мы воспользуемся возможностями программы MS Excel.
Основная часть
Давайте разобьемся на 2 группы. Сильные ученики, которые уже хорошо владеют средствами MS Excel, попытаются самостоятельно разработать таблицу. А остальные ребята будут вместе со мной последовательно выполнять действия.
Сильные ученики пересаживаются за дальние компьютеры и самостоятельно разрабатывают таблицу для решения системы уравнений. Они должны получить примерно такую картинку на экране.
С остальными мы работаем в режиме “Делай как Я”. Я демонстрирую действия на экране проектора и комментирую, вы стараетесь выполнять эти действия у себя на ЭВМ.
И так. Мы запустили программу MS Excel.
Мы хотим разработать таблицу для решения системы уравнений:
Читайте также: Сетевой провод для принтера
Нам необходимо задать диапазон изменения величины Х и рассчитать соответствующее значение Y.
Сформируем начальные данные.
В ячейку A1 запишем – нач Х =. В ячейку D1 запишем – шаг Х =.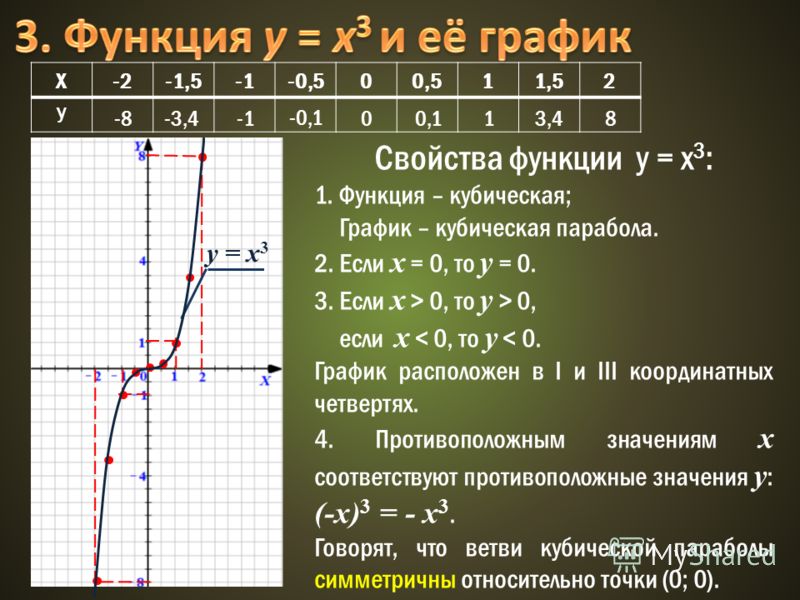 В ячейках B1, E1 их соответствующие значения – (-2,5) и 0,15.
В ячейках B1, E1 их соответствующие значения – (-2,5) и 0,15.
В ячейках C4, F4 запишем общий вид наших уравнений. В строке 5 сформируем заголовки будущих таблиц значений заданных функций.
Теперь в столбиках B, E мы должны сформировать значения для величины Х. А в столбиках C, E значения величин Y. У нас должна получиться вот такая картинка. Столбики со значением величины X мы должны сформировать так, чтобы было удобно менять начальное его значение и шаг X, которые мы создали в заголовке.
Формулы, которые нам нужно ввести приведены на рисунке.
Заметьте, что большинство формул повторяются, и их можно ввести методом копирования.
Заполните, пожалуйста, в каждой таблице 20-25 строчек.
Символ $ в формуле обозначает, что данный адрес ячейки является абсолютным и он не будет изменяться при копировании формулы.
Проверьте, чтобы ваши расчётные данные совпадали с рисунком 2.
Нам осталось красиво оформить таблицы. Для этого нужно указать, какие границы отображать в ячейках расположения расчётных таблиц.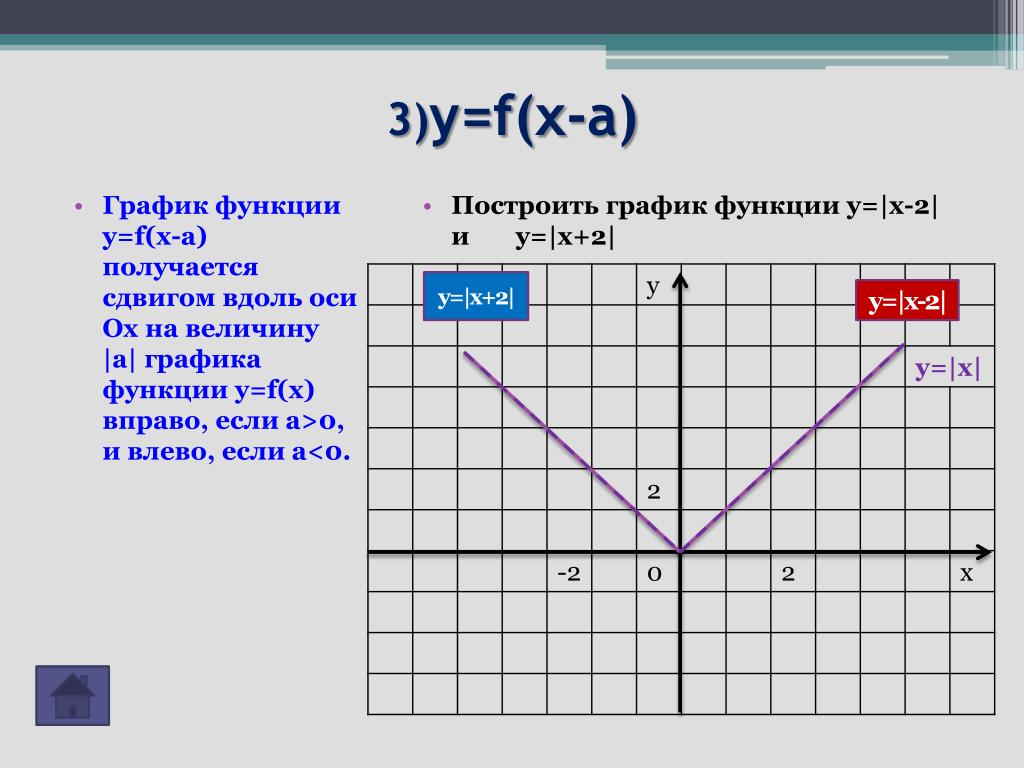 Выделите их указателем мышки и задайте режим “Все границы”.
Выделите их указателем мышки и задайте режим “Все границы”.
Теперь нам необходимо построить графики заданных функций. Для этого воспользуемся инструментом “Диаграммы”.
Выберем тип диаграммы Точечная-Сглаженная и на следующем экране укажем необходимые нам диапазоны данных, как указано на рисунке. Незабудем указать название для каждого графика. Легенду расположим снизу. А саму диаграмму “На текущем листе”, поместив её справа от расчётных таблиц.
Если вы всё сделали правильно, то у вас на экране должна получиться вот такая картинка.
У кого не получилось, давайте вместе разберёмся в ошибках и добъёмся требуемого результата.
Теперь изменяя значения в ячейках B1, D1 можно смещать графики функций вдоль оси ОХ и изменять их масштаб.
Мы видим, что одно из решений нашей системы уравнений равно -1,5.
Изменяя начальное значение Х, найдите на графике второе решение системы уравнений.
Сколько у вас получилось?
Великолепно.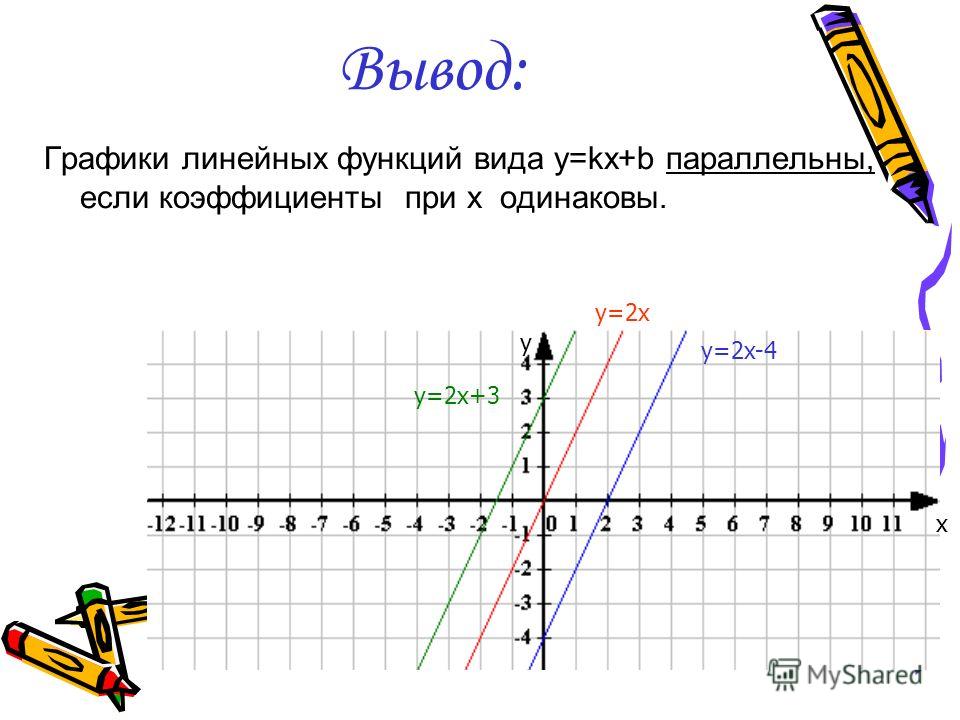 У нас получилось. Мы легко решили такую сложную систему уравнений.
У нас получилось. Мы легко решили такую сложную систему уравнений.
Но можно немного изменить нашу таблицу и усовершенствовать для решения множества подобных систем уравнений или для исследования графиков заданных функций.
Для этого нужно внести изменения в таблицу и расчётные формулы.
Можно сделать следующим образом, как показано на рисунке. Формулы в ячейках показаны на следующем рисунке.
Самостоятельно внесите все необходимые изменения.
Попробуйте изменять коофициенты A, B, C, D и посмотрите, как меняется форма и положение графиков соответствующих формул.
Заключительный этап урока
Ребята, как вы думаете, что удобней самостоятельно строить график функции на бумаге или поручить эту задачу ЭВМ?
Читайте также: Как отметить друзей на фейсбуке
А что легче для вас?
Конечно же, на данном этапе вам удобней самостоятельно на бумаге построить график функции. Но в конце урока мы получили универсальную таблицу, которая позволяет решать множество подобных заданий.
Мы ещё раз убедились, что компьютер это мощный инструмент, который позволяет не только приятно проводить время за играми, но и решать серьёзные задачи.
Надеюсь, что вам понравилось сегодняшняя работа. И вы Довольны достигнутыми результатами.
Корнями уравнения являются значения точек пересечения графика функции с осью абсцисс. Решением системы уравнений являются точки пересечения графиков функций. Такой метод нахождения корней называется графическим.
При помощи табличного процессора можно решать уравнения и системы уравнений. Для графического решения подойдут средства построения диаграмм.
Рассмотрим конкретный пример.
Найти решение следующей системы уравнений:
Ответ записать с точностью до 0,1.
Преобразуем данную систему:
1. Для оценки решений воспользуемся диаграммой, на которой отобразим графики обеих функций. Для этого, на рабочем листе MS Excel создадим таблицу со следующими значениями (рисунок 1):
· 1 строка – строка заголовков;
· столбец А: заполняем ячейки А2:А22 числами от -10 до 10 с шагом 1;
· при заполнении столбца В в ячейку В2 заносим формулу =А2*А2, которую затем копируем до ячейки В22;
Рисунок 1 – Таблица с данными для приблизительного поиска решений
· при заполнении столбца С в ячейку С2 заносим формулу =2*А2+4,копируем ее до ячейки С22.
С помощью мастера диаграмм выберем тип диаграммы График и построим диаграмму первоначальной оценки решений (рисунок 2).
Рисунок 2 – Диаграмма первоначальной оценки решения
На рисунке 2 вы можете увидеть координаты точек пересечения графиков – решения системы. Однако, пока мы получили только приближенные значения решений.
Для уточнения значения решений построим графики в интервалах от -2 до 0, где находится первое решение, и от 2 до 4, где находится второе решение с шагом, 0,1 (рисунок 3).
Рисунок 3 – Таблицы с данными для уточнения решений
2. Составляем новую таблицу для — 2 ≤ x ≤ 0. Строим точечную диаграмму для получения первого решения (рисунок 4).
Рисунок 4 – Поиск первого решения
3. Составляем новую таблицу для 2 ≤ x ≤ 4.Строим точечную диаграмму для получения второго решения (рисунок 5).
Рисунок 5 – Поиск второго решения
Решением нашей системы будут координаты точек пересечения графиков: x1= -1,25; y1= 1,5; x2= 3,2; y2= 10,8.
Графическое решение системы уравнений является приближенным.
Приложение 7
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10074 — | 7514 — или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
очень нужно
Опубликовано вкл 24.02.2014 – 12:42 Автор: Белкин Алексей
Цель работы – показать алгоритм построение графиков функций в Excel, принцип построения линий высших порядков в полярной системе координат с помощью формул перехода от декартовых координат к полярным координатам.
Использование компьютерных программ для построения графиков функций, изучение их свойств и закономерностей, дает возможность рассмотреть большое количество примеров с минимальными усилиями. Данная работа предназначена в помощь учителям при изучении функции, а также ученикам с целью заинтересовать их математикой, информатикой, показав возможности использования информационных технологий на уроках математики.
Данная работа предназначена в помощь учителям при изучении функции, а также ученикам с целью заинтересовать их математикой, информатикой, показав возможности использования информационных технологий на уроках математики.
Скачать:
| Вложение | Размер |
|---|---|
| rabota_belkin_aleksey_s_titul.doc | 936 КБ |
Предварительный просмотр:
«Районная научно-практическая конференция
«От исследования – к научному поиску»
Учреждение: МБОУ «Многопрофильная гимназия г. Лагани»
Секция: Естественно-научная
Тема работы:
«Построение и исследование графиков
функций при помощи электронных
Таблиц Excel.»
Автор работы: Белкин Алексей Васильевич,
ученик 10 класса МБОУ «Многопрофильная гимназия г. Лагани»
Научный руководитель: Никифоров Евгений Алексеевич,
учитель математики МБОУ «Многопрофильная гимназия г. Лагани»
г. Лагань – 2013
ОГЛАВЛЕНИЕ
Введение | 2 |
Microsoft Excel. | 3-5 |
1.2. Полярная система координат | 5-6 |
1.3. Инструкция по построению кривых в полярных координатах с помощью программы Microsoft Excel | 6-10 |
1.4. Построение кусочно-заданной функции на примере построения эскиза национального орнамента | 11-12 |
Заключение | 13 – 14 |
Список литературы | 15 |
ВВЕДЕНИЕ
Актуальность работы. При изучении, темы преобразования графиков функций возникла необходимость построения графиков элементарных функций и уравнений выше второй степени. Для изучения свойств этих функций Microsoft Excel предлагает широкие возможности, которые в школьных учебниках по информатике не оговариваются.
Вопрос (мотивация): Как построить график с изменяющимся параметром, для дальнейшего его изучения?
Проблема: необходимо найти удобный (сравнительно простой, наглядный, доступный) способ построения графиков элементарных функций и уравнений степеней выше второй с двумя переменными.
Гипотеза: для решения поставленной проблемы, возможно использовать инструменты прикладной программы Microsoft Excel, а для построения графиков уравнений высших порядков ввести новые переменные, или новую систему координат, или и то и другое одновременно.
Поэтому, объект нашего исследования – прикладная программа Microsoft Excel, ее возможности для построений графиков функций и исследования их.
Исходя из этого, предметом нашего исследования стали уравнения элементарных функций и кривых высших порядков.
Цель работы – показать алгоритм построение графиков функций в Excel, принцип построения линий высших порядков в полярной системе координат с помощью формул перехода от декартовых координат к полярным координатам. Результаты исследования: в процессе работы я:
- Научился строить графики функций, с дальнейшей возможностью изучения их свойств
- изучил переход от декартовой системы координат к полярной и обратно;
- исследовал изменения вида графиков функций и кривых, в зависимости от параметров входящих в её уравнение;
- познакомились с некоторыми замечательными кривыми известных математиков.

Планы и перспективы: продолжить изучение плоских кривых.
- Инструкция по построению кривых с помощью программы
Microsoft Excel.
Пусть задана функция y= f(x), где х – независимая переменная , а y – переменная зависящая от х.
Для начала нам необходимо задать значения независимой переменной с заданным шагом (шаг лучше выбрать дробным значением). Чем меньше шаг вычисления независимой переменной тем точнее построенный график.
Задаем формулу по которой определяется зависимая переменная. Вычисляем для каждого значения независимой переменной ее соответствующее значение функции.
По построенным данным строим график функции.
Следовательно, математическая модель у нас уже есть. Рассмотрим пример построения уравнения графика и ее исследования
. Рассмотрим в качестве примера тригонометрическую функцию
ГЛАВА ТРЕТЬЯ, в которой Пух и Пятачок отправились на охоту и чуть-чуть не поймали Буку
Самодельный телефон
«Течет река Волга»
Философские стихи Кристины Россетти
Как нарисовать портрет?
Excel – наиболее популярная программа для работы с электронными таблицами. В программе Excel очень удобно выполнять экономико-статистические и другие расчеты, а также формировать разнообразные таблицы и отчеты.
В программе Excel очень удобно выполнять экономико-статистические и другие расчеты, а также формировать разнообразные таблицы и отчеты.
Одной из наиболее типичных задач, при работе с программой Excel, является построение графика. Благодаря инструментам Excel создать график довольно просто. В данной статье мы рассмотрим эту задачу и расскажем о том, как построить график в Excel.
Шаг № 1. Подготовка данных для графика.
Для того чтобы построить график в Excel нам нужны исходные данные. У вас будут свои исходные данные, а мы рассмотрим процесс создания графиков на примере вот такой простой таблицы с информацией об урожае.
Шаг № 2. Выделяем данные, которые будут использоваться для построения графика в Excel.
Для того чтобы при создании графика программа Excel могла сразу получить нужные данные, вам необходимо выделить область в которой они находятся.
Шаг № 3. Переходим на вкладку «Вставка»
Не снимая выделения, с необходимой нам области, переходим на вкладку «Вставка».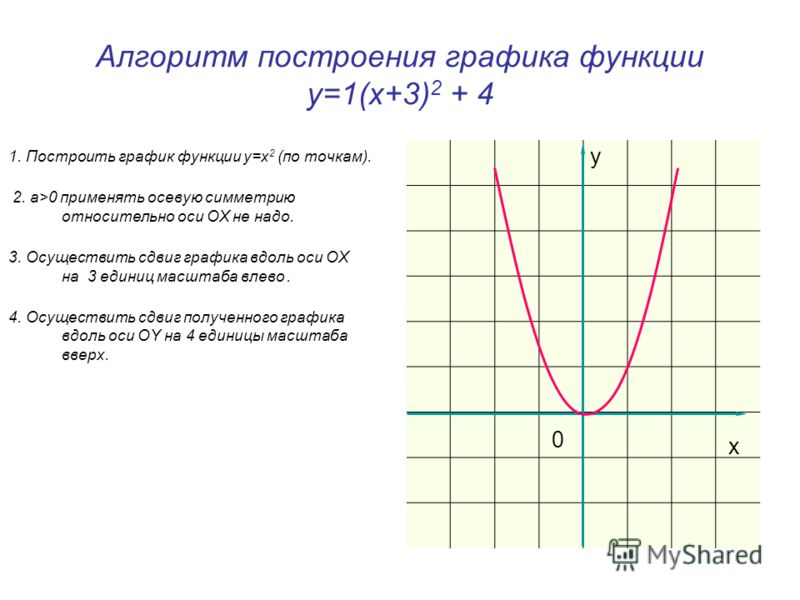
Шаг № 4. Создаем график с помощью соответствующей кнопки.
На вкладке «Вставка» найдите кнопку «График». Нажмите на данную кнопку и в выпадающем меню выберите один из вариантов оформления графика. Позже вы сможете поменять оформление.
Шаг № 5. Настройка созданного графика.
После того как вы создали график, на листе Excel должно появится небольшое плавающее окно с графиком. Вы можете переместить данное окно в любое удобное для вас место.
Шаг № 6. Настройка параметров построенного графика.
После построения графика программа Excel позволяет настроить практически все его параметры. Например, если вы неверно указали область с данными, то можно воспользоваться функцией «Выбрать данные». Данная функция позволяет изменить область, данные с которой используются для создания графика.
Для этого выделите ваш график и откройте вкладку «Конструктор». На данной вкладке находится кнопка «Выбрать данные».
Нажмите на эту кнопку и выделите правильную область и нажмите на кнопку «OK».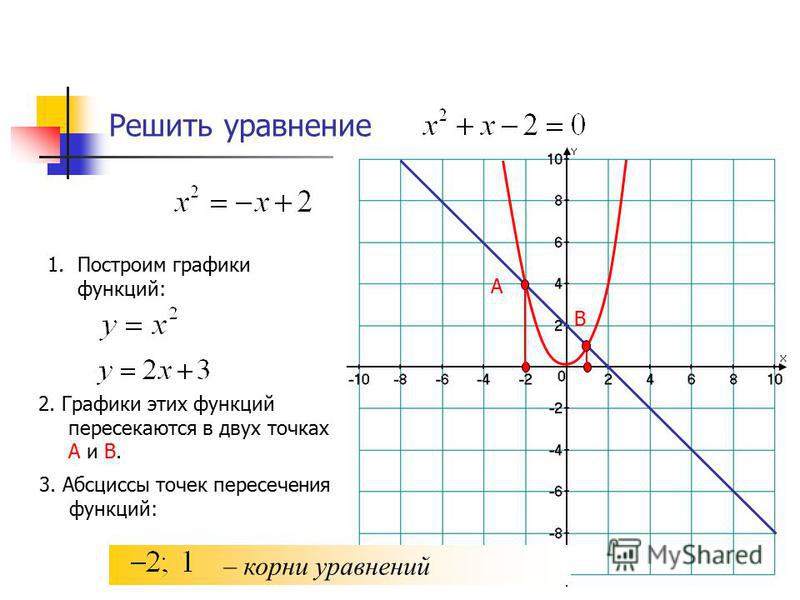
После этого программа Excel перестроит график с использованием новых данных. Кроме этого на вкладках «Конструктор», «Макет» и «Формат» вы найдете множество настроек, которые изменяют внешний вид графика. Это позволит создать график, который будет вписываться по стилю в ваш документ.
Как в excel построить график
4. График функции
График функции представляет собой набор всех точек, координаты которых ( x , y ) удовлетворяют функции `y = f(x)`. Это означает, что для каждого значения x существует соответствующее значение y , которое получается при подстановке в выражение для `f(x)`.
Так как нет ограничений на возможное количество точек для графика функции, мы сначала будем следовать этой процедуре:
- Выберите несколько значений x (не менее 5)
- Получите соответствующие значения функции и занесите их в таблицу
- Нанесите эти точки на график, соединив их плавной кривой
Тем не менее, вам рекомендуется изучить общие формы некоторых общих кривых (таких как прямая линия,
парабола, тригонометрические и экспоненциальные кривые, с которыми вы столкнетесь в следующих главах).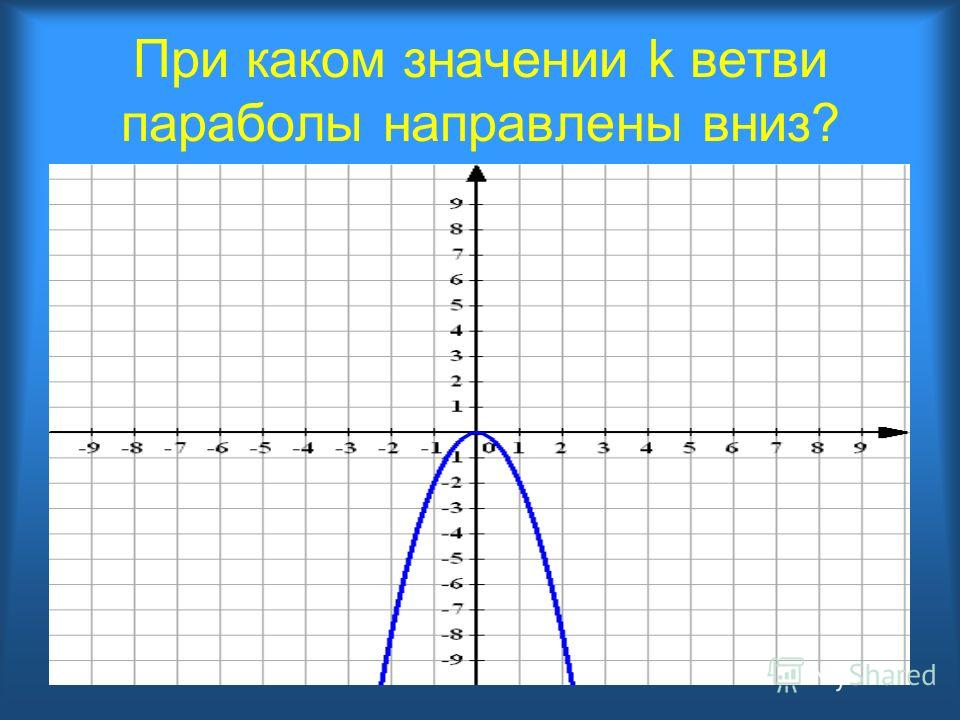 Это намного проще, чем рисовать точки, и полезнее на потом!
Это намного проще, чем рисовать точки, и полезнее на потом!
Пример 1
Нужна миллиметровка?
Значок миллиметровкиСкачать миллиметровку
Человек ростом `2 м« бросает мяч прямо вверх, и его высота в момент времени t (через с ) определяется выражением ч = 2 + 9 т — 4,9 т 2 м.
График функции.
Ответить
Мы начинаем с `t = 0`, так как отрицательные значения времени здесь нет практического смысла.
Мы выбираем значения с интервалом `0,5` секунды (если бы мы использовали интервалы `t = 1\ «s», мы бы не увидели достаточно деталей на графике).
| т | 0 | 0,5 | 1 | 1,5 | 2 |
| ч | 2 | 5,3 | 6.1 | 4,5 | 0,4 |
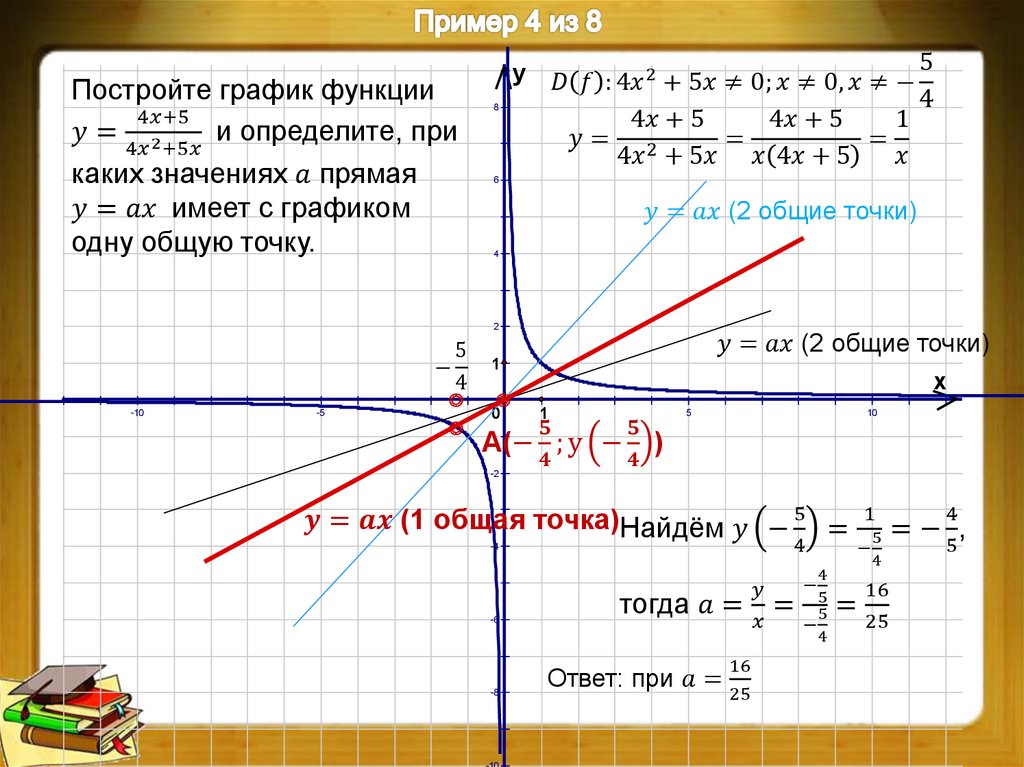 511.521234567-1Открыть изображение на новой странице
511.521234567-1Открыть изображение на новой страницеГрафик снаряда (парабола).
Эта форма называется параболой и является в приложениях математики.
ПРИМЕЧАНИЕ:
(1) Этот график представляет собой высоту в зависимости от времени. Мяч пошел прямо вверх, а не вперед. (На нашем графике может показаться, что мяч двигался не только вверх, но и в направлении x , но это не так.)
(2) Мы могли бы написать функцию в этом примере с ч ( т ), а не просто ч . Следующие 2 уравнения означают одно и то же.
ч = 2 + 9 т − 4,9 т 2
ч ( т ) = 2 + 9 т − 4.9 т 2
Пример 2
Скорость (в м/с) мяча в примере 1 в момент времени t (в s ) дано по
v = 9 − 9,8 т
Нарисуйте график v — t .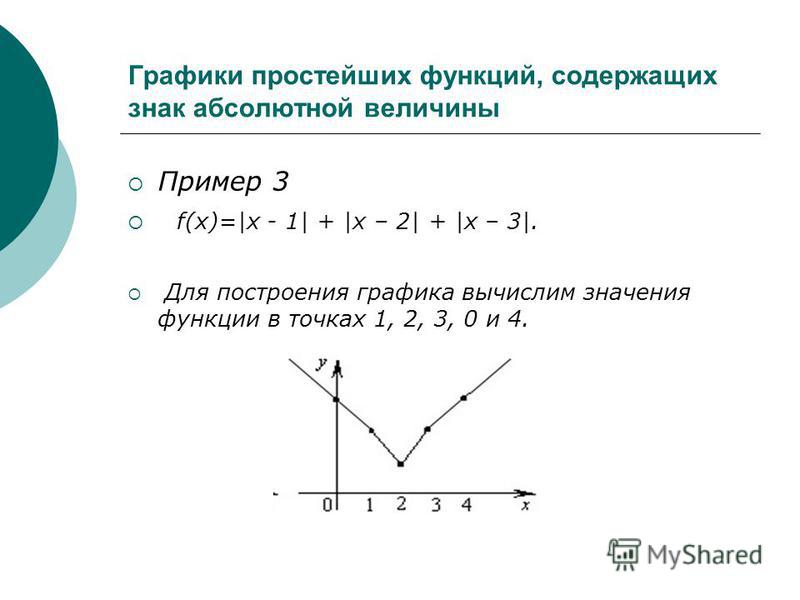 Что это
скорость в момент удара мяча о землю?
Что это
скорость в момент удара мяча о землю?
Ответить
Это прямая линия, так как она представлена в виде
y = m x + c
Подробнее о прямой линии.
Поскольку мы узнали, что это прямая линия, нам нужно только построить 2 точки и присоединяйтесь к ним. Но мы находим 3 точки, просто чтобы убедиться, что у нас правильная линия.
| т | 0 | 1 | 2 |
| v | 9 | -0,8 | -10,6 |
График `v` против `t` — прямая линия.
Наш график начинается с `t = 0` (поскольку отрицательные значения времени в этом примере не имеют значения).
В течение первых `0,918\ «с»` мяч движется вверх (положительная скорость, то есть синяя линия находится выше t -ось), но тормозит.
После этого мяч падает на землю и становится быстрее (участок, где синяя линия находится ниже оси t ).
Мяч упал на землю примерно через `t = 2,04\ «с»` (мы можем см. это из примера 1). Скорость , когда удар мяча о землю на графике, который мы только что нарисовали, составляет около `-11\ «м/с»`. На этом график останавливается.
Наш график предполагает, что мяч приземляется на песок и не отскакивает.
Обычно, как мы сделали здесь, мы берем скорость от до направление должно быть положительным.
Пример 3
Постройте график функции y = x − x 2 .
Ответить
(a) Определите значения y- для типичного набора значений x и запишите их в таблицу.
| х | −2 | −1 | 0 92`, парабола. Обратите внимание, что кривая выходит за пределы, показанные на графике. Пример 4График функции `y=1+1/x` Ответить (a) Примечание: y не определено для `x = 0` из-за деление на `0` Следовательно, `x = 0` не находится в домене (b) Составьте таблицу значений:
(c) Мы знаем, что около `x = 0` произойдет что-то странное (поскольку граф там не определен). Итак, мы проверяем, что происходит в некоторых типичных точках между `x = -1` и `x = 1`: , когда `x = −0,5,` `y = 1 + 1/(−0,5) = 1 − 2 = −1` , когда `x = 0,5, \ y = 1 + 1/(0,5) = 1 + 2 = 3` (d) По мере приближения значения x к `0` точки приближаются к и -ось, хотя они ее не трогают. (Чтобы убедиться в этом, нарисуйте точки, где `x = 0,4`, `x = 0,3`, `x = 0,2`, `x = 0,1` и даже `x = 0,01`.) 12345-1-2 -3-4-512345-1-2-3-4xyОткрыть изображение на новой страницеГрафик `y=1+1/x`, гипербола. Это прерывистая функция. На этой кривой есть еще одна асимптота: `y = 1`, отмеченная пунктирной линией. Обратите внимание, что кривая не проходит через это значение. Пример 5График функции `y=sqrt(x+1)` Ответить (a) Примечание: y не определено для значений x меньше чем `-1`. (Попробуйте что-нибудь в своем калькуляторе, например `x = −4`.) (b) Мы определяем некоторые значения x и соответствующие значения y и записываем их в таблицу:
(c) Рисуем наш график следующим образом. График `y=sqrt(x+1)`. Это полупарабола. Пример 6Электрическая мощность P (в ваттах), отдаваемая батареи в зависимости от сопротивления R (в омах) составляет: 92` График зависимости мощности от сопротивления. Ответить (a) Отрицательные значения для R не имеют физического значение, поэтому P не отображается для отрицательных значений Р. (б) Составьте таблицу значений:
Так как `y = 0`, когда `x = 0` и `x = 1`, мы исследуем, что происходит между этими 2 x -значениями: Когда `x = 1/2, y = -1/ 8.` Вот наш график: 12-11234-1-2xyОткрыть изображение на новой страницеQ2. `y=sqrt(x)` Ответить Мы можем извлечь квадратный корень только из положительного числа, поэтому `x ≥ 0`. Квадратный корень числа может быть только положительным, поэтому `y ≥ 0`. Этот график на самом деле представляет собой половину параболы с горизонтальной осью. 123412xyОткрыть изображение на новой страницеГрафик `y=sqrt(x)`, полупарабола. Конический бак для воды Q3. Начертите эскизный график высоты воды в конусе против времени. Ответить Нам нужно смоделировать высоту в момент времени t на основе того, что мы знаем о конусах. Мы также должны предположить несколько вещей. (Мы упрощаем себе жизнь по мере продвижения вперед. Нам разрешено это делать, поскольку нам просто нужно придумать базовый график высоты воды в момент времени t ). Интуитивно мы ожидаем, что высота воды сначала будет медленно уменьшаться, а затем падать быстрее ближе к концу. объем конуса 9(1″/»3)`. R Графика — Рисование❮ Предыдущая Далее ❯ График Функция Функция принимает параметры для указания точек на диаграмме. Параметр 1 указывает точки на оси x . Параметр 2 указывает точки на оси Y . В самом простом случае вы можете использовать функцию plot() для построения графика двух чисел относительно друг друга: ПримерНарисуйте одну точку на диаграмме в позиции (1) и позиции (3): plot(1, 3) Результат: Попробуйте сами » Чтобы нарисовать больше точек, используйте векторы : ПримерНарисуйте две точки на диаграмме, одну в позиции (1, 3) и одну в позиции (8, 10): plot(c(1, 8), c(3, 10)) Результат: Попробуйте сами » Несколько точекВы можете нанести столько точек, сколько хотите, просто убедитесь, что у вас одинаковое количество точек по обеим осям: Примерplot(c(1, 2, 3, 4, 5), c(3, 7, 8, 9, 12)) Результат: Попробуйте сами » Для лучшей организации, когда у вас много значений, лучше использовать переменные: Пример x <- c(1, 2, 3, 4, 5) plot(x, y) Результат: Попробуйте сами » Последовательности точек Если вы хотите рисовать точки последовательно, на обеих осях x и Y-ось , используйте ПримерГрафик (1:10) Результат: Попробуйте его самостоятельно » Нарисуйте линию. Примерplot(1:10, type="l") Результат: Попробуйте сами » Метки графика Функция Примерplot(1:10, main="Мой график", xlab="Ось X", ylab="Ось Y") Результат: Попробуйте О себе » Внешний вид графикаСуществует множество других параметров, которые можно использовать для изменения внешнего вида точек. Цвета Используйте Примерplot(1:10, col="red") Результат: Попробуйте сами » Размер Используйте Примерplot(1:10, cex=2) Результат: Попробуйте сами » Форма точки Используйте Примерplot(1:10, pch=25, cex=2) Результат: Попробуйте сами » Значения параметра ❮ Предыдущая Следующий ❯ NEW Мы только что запустили Узнать ВЫБОР ЦВЕТАКОД ИГРЫИграть в игру Top TutorialsУчебное пособие по HTMLУчебное пособие по CSS Учебное пособие по JavaScript Учебное пособие Учебное пособие по SQL Учебное пособие по Python Учебное пособие по W3. 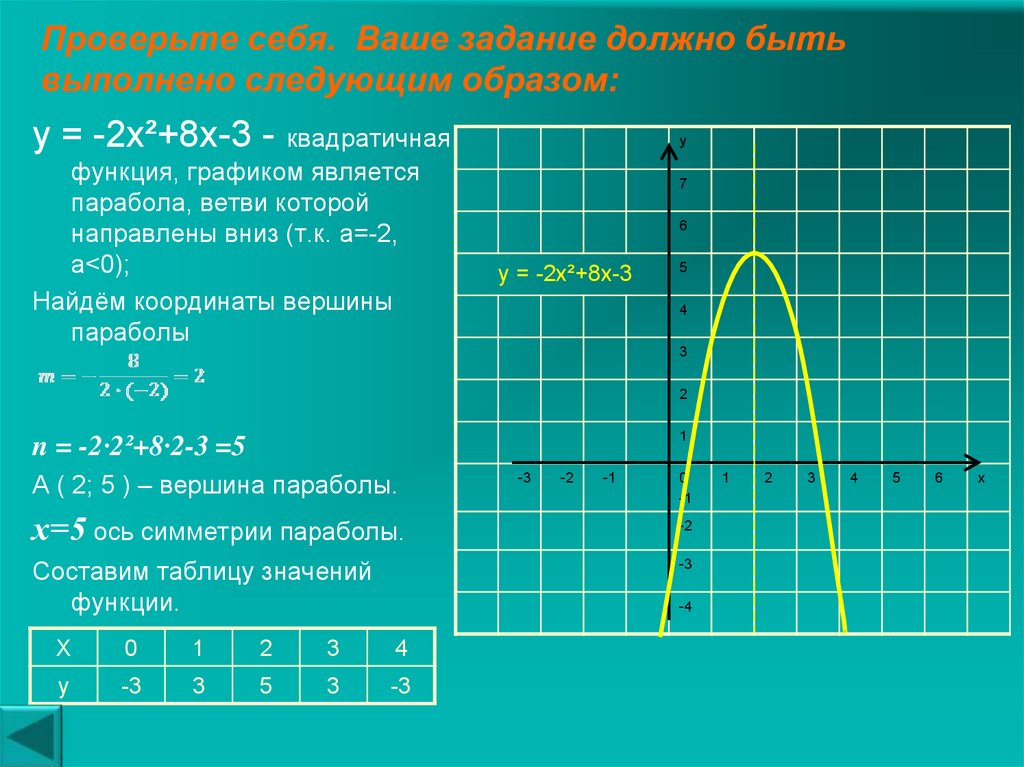 CSS CSS Учебное пособие по Bootstrap Учебное пособие по PHP Учебное пособие по Java Учебное пособие по C++ Учебное пособие по jQuery 9088
Справочник по HTML Основные примерыПримеры HTMLПримеры CSS Примеры JavaScript Примеры инструкций Примеры SQL Примеры Python Примеры W3.CSS Примеры Bootstrap Примеры PHP Примеры Java Примеры XML Примеры jQuery ФОРУМ | О W3Schools оптимизирован для обучения и обучения. Примеры могут быть упрощены для улучшения чтения и обучения.
Учебники, ссылки и примеры постоянно пересматриваются, чтобы избежать ошибок, но мы не можем гарантировать полную правильность всего содержания. Copyright 1999-2022 Refsnes Data. Все права защищены. Постоянная функция — определение, график, характеристики, примерыПостоянная функция используется для представления величины, которая остается постоянной с течением времени, и считается самой простой из всех типов вещественных функций. Постоянные функции — это линейные функции, графики которых представляют собой горизонтальные линии на плоскости. Максимальные оценки, которые можно получить на экзамене, можно рассматривать как один из реальных примеров постоянных функций. Постоянная функция имеет одинаковый выход даже при разных входных значениях. В этой статье давайте узнаем о постоянных функциях, их определении и графиках с решенными примерами.
Что такое постоянная функция?Постоянная функция — это функция, имеющая одинаковый диапазон для разных значений домена. Графически постоянная функция представляет собой прямую линию, параллельную оси x. Область определения функции — это значение x, представленное на оси x, а диапазон функции — это y или f(x), которые отмечены относительно оси y. Любую функцию можно рассматривать как постоянную, если она имеет вид y = k , где k — константа, а k — любое действительное число. Это также записывается как f(x) = k . Здесь нужно отметить, что значение f(x) всегда будет равно «k» и не зависит от значения x. Вот несколько примеров постоянных функций:
Одна из интересных вещей, связанных с постоянной функцией, заключается в том, что мы можем ввести любое действительное число, которое захотим для x, и мы можем мгновенно узнать значение функции в этом x без использования каких-либо вычислений. Как найти постоянную функцию?В этом разделе мы научимся различать постоянную функцию и функцию, которая не является постоянной функцией. Чтобы узнать, является ли функция постоянной функцией, сделайте следующее:
(i) Рассмотрим линейную функцию y = x + 2. Можем ли мы в этом примере получить разные выходные данные, изменяя входные значения? Ответ положительный, потому что:
Поскольку мы получаем разные результаты, изменяя входные значения, это НЕ постоянная функция. (ii) Рассмотрим функцию y = 3. Здесь мы можем заметить, что независимо от нашего значения x или ввода, y всегда будет 3.
Поскольку мы не можем получить разные результаты, изменяя входные значения, это постоянная функция. Графики постоянных функций Вам может быть интересно, как постоянная функция будет выглядеть на координатной плоскости.
Ниже приведен график постоянной функции f(x) = 3. Итак, график f(x) = 3 представляет собой горизонтальную линию, поскольку координаты y всех точек одинаковы (как 3). Следовательно, графики всех постоянных функций представляют собой горизонтальные линии. Характеристики постоянной функции Все постоянные функции пересекают вертикальную ось в соответствии со значением их константы и не пересекают горизонтальную ось, так как параллельны ей. Кроме того, постоянные функции непрерывны, поскольку они представляют собой горизонтальные линии, которые непрерывно продолжаются с обеих сторон без каких-либо разрывов. Наклон постоянной функцииПостоянная функция — это линейная функция, общий формат которой y = mx + k, где m и k — константы. Таким образом, постоянная функция f(x) = k (или) y = k может быть записана как y = 0x + k. Сравнивая это уравнение с формой пересечения наклона y = mx+b, мы получаем, что его наклон равен m = 0. Таким образом, наклон постоянной функции равен 0. Область и диапазон постоянной функцииПостоянная функция является линейной функцией, диапазон которой содержит только один элемент независимо от количества элементов области определения. Поскольку постоянная функция определена для всех действительных значений x:
Производные постоянной функцииПостоянная функция является самой простой из всех функций, поэтому ее производную легче вычислить. Мы можем использовать прямую замену, чтобы найти производную постоянной функции. Правило дифференцирования постоянной функции f(x) таково: d/dx (c) = 0, Из приведенного выше дифференцирования видно, что производная постоянной функции равна нулю. Кроме того, производная считается наклоном касательной функции в любой заданной точке, и мы уже знаем, что наклон постоянной функции всегда равен 0. Давайте рассмотрим пример, чтобы понять постоянные функции и их соответствующие производная. Постоянная функция y = -1 и ее производная y' = 0. Предел постоянной функцииСогласно свойствам пределов предел постоянной функции равен той же константе. Например, если функция y = 7, то предел этой функции равен 7. Это можно представить как: lim ₓ → ₐ C = C. Постоянные функции в реальном мире Есть так много мест, где постоянные функции находят свое применение в реальной жизни.
Важные примечания о постоянной функции: Вот несколько пунктов, которые следует помнить при изучении постоянной функции
☛ Связанные темы: Ознакомьтесь со следующими страницами, посвященными постоянным функциям
Часто задаваемые вопросы о постоянной функцииЧто такое постоянная функция в алгебре?Постоянная функция — это функция, имеющая одно и то же значение диапазона для разных значений домена. Графически постоянная функция представляет собой горизонтальную линию, которая является прямой линией, параллельной оси x. Что такое уравнение постоянной функции? Уравнение постоянной функции имеет вид f(x) = k, где k — константа и любое действительное число. Как узнать, постоянна ли функция?Функция является постоянной функцией, если:
Является ли постоянная функция линейной?Да, постоянная функция является линейной функцией, поскольку графики постоянной и линейной функций представляют собой прямые линии на плоскости. Таким образом, постоянная функция всегда линейна, в частности, это всегда горизонтальная линия. Является ли постоянная функция непрерывной?Да, постоянная функция всегда непрерывна, так как ее график представляет собой горизонтальную линию, и мы можем нарисовать ее, не отрывая ручки/карандаша. Может ли постоянная функция быть Onto?Да, постоянная функция f(x) = k может быть онто-функцией только тогда, когда ее кодовая область совпадает с ее диапазоном (то есть {k}). Что такое степень постоянной функции? Степень постоянной функции равна нулю, так как константа k может быть записана как f(x) = kx 0 . Является ли постоянная функция сюръективной?Нет, постоянная функция не является сюръективной, поскольку она не является однозначной. Константная функция — это функция, выходное значение которой остается неизменным для каждого переданного ей входного значения. Следовательно, постоянная функция не является сюръективной. Он может быть сюръективным, только если кодовый домен равен диапазону, то есть {k}. Является ли постоянная функция инъективной?Нет, постоянная функция не является инъективной. Константная функция — это функция, в которой выходное значение одинаково для каждого переданного ей входного значения. Поскольку инъективная функция никогда не отображает два разных входных значения в одно и то же выходное значение. Следовательно, постоянная функция не может рассматриваться как инъективная. Постоянная функция инъективна только тогда, когда область определения имеет только один элемент. Что такое производная постоянной функции?Производная любой постоянной функции считается равной нулю (dk/dx = 0) Что такое интеграл постоянной функции? Интеграл постоянной функции по переменной представляет собой константу, умноженную на переменную. Нарисуйте функцию в виде непрерывной кривой — geom_function • ggplot2 Источник: Вычисляет и рисует функцию в виде непрерывной кривой. Это позволяет легко наложить функцию поверх существующего графика. Функция называется с сеткой равномерно расположенных значений вдоль оси x, и результаты рисуется (по умолчанию) линией. Использованиеgeom_function( отображение = NULL, данные = NULL, стат = "функция", позиция = "личность", ..., на.рм = ЛОЖЬ, show.legend = нет данных, inherit.aes = ИСТИНА ) stat_function( отображение = NULL, данные = NULL, геом = "функция", позиция = "личность", ..., весело, хлим = НУЛЬ, п = 101, аргументы = список(), на.рм = ЛОЖЬ, show. Аргументы
Эстетика
Узнайте больше о настройке эстетики в Вычисляемые переменные
См. также Примеры# geom_function() полезен для наложения функций set.seed(1492) ggplot(data.frame(x = rnorm(100)), aes(x)) + геометрическая_плотность() + geom_function(весело = dnorm, цвет = "красный") # Чтобы построить функции без данных, укажите диапазон оси x база <- ggplot() + xlim(-5, 5) base + geom_function(fun = dnorm) base + geom_function(fun = dnorm, args = list(mean = 2, sd = .5)) # Базовая механика оценивает функцию в дискретных точках # и соединим точки линиями base + stat_function(fun = dnorm, geom = "точка") base + stat_function(fun = dnorm, geom = "точка", n = 20) base + geom_function(fun = dnorm, n = 20) # Две функции на одном графике база + geom_function(aes(color = "normal"), fun = dnorm) + geom_function (aes (color = "t, df = 1"), fun = dt, args = list (df = 1)) # Использование пользовательской анонимной функции base + geom_function(fun = function(x) 0. Создание пользовательских функций построения графиков с помощью matplotlib | Матиас КальдериниTLDR: определите свои собственные функции, которые включают построение графиков по определенным осям, используя следующий синтаксис: def custom_plot(x, y, ax=None, **plt_kwargs): Репозиторий исходного кода можно найти по этой ссылке. В предыдущем посте я показал вам, как лучше организовать свои фигуры. Поскольку основное внимание в этом посте уделялось общей структуре и представлению общей фигуры, сами графики были довольно простыми в том смысле, что они использовали только одну предопределенную функцию matplotlib, такую как Здесь я покажу вам, как создавать свои собственные функции построения графиков, которые можно легко использовать, вызывая их на ваших организованных графиках примерно следующим образом: fig, axes = plt. Вместе с хорошей организацией подграфиков это поможет вам максимизировать ваши статические графики на matplotlib (предвосхищая последующее руководство по динамическим графикам… может быть…) и используйте информацию из разных графиков, чтобы поделиться всеобъемлющей историей ваших данных. Первый шаг к созданию серии пользовательских графиков на фигуре — это возможность подключить отдельный пользовательский график к отдельным осям. Первым шагом является передача осей, по которым мы хотим построить график, в нашу пользовательскую функцию. Это можно сделать просто так: def custom_plot(x, y, ax=None, **plt_kwargs): Так что же я там делал? Первой важной частью здесь является аргумент Почему if ax is None: мы видим, что если объект осей не был указан в Давайте проверим это, сначала построив график без указания осей, а затем указав определенные оси: # Без указания осей (по умолчанию None -> gca()) # Предоставление осей Пока все хорошо; мы можем создать функцию для построения данных, и мы можем подключить ее к определенным осям нашего графика (она даже позаботится о себе, если оси не были предоставлены). А как насчет Если вы не привыкли работать с В качестве отступления, если вы действительно раньше не видели этот тип звездочек, использование одинарных звездочек def no_kwargs_plot(x, y, ax=None): Нет ошибок, нет проблем… Однако, что, если вы хотите сделать линию толще? Обычно в def no_kwargs_plot(x, y, ax=None, linewidth=1): Это решит проблему. Но как насчет всех других возможных аргументов в .plot() . Записывать их все в нашу функцию вместе со значениями по умолчанию было бы очень долго и не очень практично: def no_kwargs_plot(x, y, ax=None, linewidth=1, other=1,. Вот где использование нотации Например, если бы мы использовали нашу функцию построения графика как def print_kwargs_only(x, y, ax=None, **plt_kwargs): Таким образом, использование Ранее я упоминал, что Таким образом, не зная, сколько и какие настройки графика будут использоваться, мы можем передать их все той части нашей функции, которая будет выполнять построение графика. Мы можем увидеть это снова, используя нашу исходную функцию plt. Это позаботится об основном синтаксисе. С этим вы уже сможете начать создавать еще несколько интересных сюжетов. Однако прежде чем приступить к делу, нам нужно позаботиться об одной потенциальной проблеме, с которой вы можете столкнуться при использовании Ответ заключается в том, что « Чем здесь отличается и как его использовать?Сначала посмотрим на список возможных входов.Теперь вместо Если вы следовали моему объяснению до Использование их позже с двойной звездочкой ничем не отличается от оригинального Давайте посмотрим, как это использовать: plot_params = {'linewidth': 2, 'c': 'g', 'linestyle':'--'} Итак, когда дело доходит до создания пользовательских функций, из которых вы можете строить графики, предыдущего раздела должно быть достаточно для того, чтобы вы немного повеселились со статическими участки. В следующем разделе я просто приведу пример графика с использованием пользовательской функции, надеюсь, он вдохновит вас на создание собственных графиков. Представьте, что вы хотите посмотреть, как размер выборки из данной случайной величины влияет на оценку лежащего в ее основе распределения вероятностей. Предположим, у нас есть непрерывная случайная величина X, которая нормально распределена со средним значением μ (мю) и стандартным отклонением σ (сигма) (, т. Мы хотели бы знать, как на оценку плотности ядра scipy (kde) влияет размер нашей случайной выборки (сколько раз мы случайным образом выбираем из нашего нормального распределения), сравнивая ее с оценкой основного истинного распределения плотности вероятности (pdf) . Мы сделаем это, построив сами образцы, их kde и лежащую в их основе PDF для различных значений N. def , kde_kwargs={}, ax=None): Давайте разберем функцию шаг за шагом: Во-первых, входные данные. Здесь вместо того, чтобы запрашивать массивы данных, мы будем создавать наши собственные данные из генератора случайных чисел Гаусса. Поэтому нам нужно запросить соответствующие статистические параметры μ и σ (среднее значение и стандартное отклонение соответственно для гауссовых распределений). Нам также нужно задать количество отбираемых образцов N. На самом деле мы будем перебирать различные значения N позже, чтобы увидеть влияние размера выборки на оценку. Идея состоит в том, чтобы отображать выборки в виде точек рассеяния, а pdf и kde — в виде обычных линейных графиков. Таким образом, мы предоставим в качестве входных данных словарь для соответствующих параметров построения графика (ширина линии, размер маркера и т. д.). Наконец, мы зададим оси фигуры, на которой мы хотим построить все три вещи. Первая часть функции просто сгенерирует случайную гауссову выборку размера N из предоставленных статистических параметров. Вторая часть кода создаст пары x-y линейного графика, соответствующие PDF нормального распределения, заданного μ и σ. Мы ограничиваем диапазон PDF до ± 5 стандартных отклонений, поскольку все, что дальше по обеим сторонам, в любом случае будет довольно маленьким. Третья часть кода сначала вычисляет kde нашего образца, а затем применяет его к тому же диапазону значений по оси x, что и наш PDF-файл. Наконец, в четвертой части кода мы просто отображаем в виде точечной диаграммы все выборочные значения по оси x (на высоте 0), а pdf и kde — в виде линейных графиков. Все три, с соответствующими аргументами ключевого слова построения графика. # Параметры выборки Вот и все! Надеюсь, вы научились добавлять возможности построения графиков в свои функции, правильно передавая соответствующие оси и аргументы ключевых слов. Это должно помочь вам иметь все более модульный код для быстрого изучения и визуализации ваших данных. Первоначально опубликовано по адресу https://maticalderini.github.io 28 апреля 2020 г. APC Средняя скорость изменения функцииМотивирующие вопросы
Имея функцию, моделирующую определенное явление, естественно задать такие вопросы, как «как функция изменяется на заданном интервале» или «на каком интервале функция изменяется быстрее?» Концепция средней скорости изменения позволяет нам сделать эти вопросы более математически точными. Для функции \(s\), сообщающей о местонахождении движущегося объекта на прямом пути в момент времени \(t\text{,}\), мы определяем среднюю скорость изменения \(s\) на интервале \ ([a,b]\) будет количеством 92\) вместе с точками \((1.5,s(1.5))\) и \((2.5, s(2.5))\text{.}\) Сделайте копию графика по осям на рисунке 1.3. 1, обозначая ключевые точки, а также шкалу осей. Какова область применения модели? Диапазон? Почему? Рисунок 1.3.1. Оси для построения функции положения.Вручную найдите уравнение прямой, проходящей через точки \((1.5,s(1.5))\) и \((2.5, s(2.5))\text{.}\) Напишите прямую в сформируйте \(y = mt + b\) и постройте линию в Desmos , а также по осям выше. Какова геометрическая интерпретация значения \(AV_{[1.5,2.5]}\) в свете вашей работы над предыдущими вопросами? Как изменятся ваши ответы на предыдущие вопросы, если вместо этого мы рассмотрим интервал \([0,25, 0,75]\text{?}\) \([0,5, 1,5]\text{?}\) \([1, 3]\текст{?}\) Подраздел 1. 3.1 Определение и интерпретация средней скорости изменения функции 3.1 Определение и интерпретация средней скорости изменения функцииВ контексте функции, которая измеряет высоту или положение движущегося объекта в данный момент времени, значение средней скорости изменения функции на заданном интервале равно средняя скорость движущегося объекта, потому что это отношение изменения положения к изменению во времени . Например, в предварительном просмотре 1.3.1 единицами измерения \(AV_{[1.5,2.5]} = -32\) являются «футы в секунду», поскольку единицы измерения в числителе — «футы», а в знаменателе — «секунды». ». Более того, \(-32\) численно совпадает с наклоном линии, соединяющей две соответствующие точки на графике функции положения, как показано на рисунке 1.3.2. Тот факт, что средняя скорость изменения в этом примере отрицательна, указывает на то, что мяч падает. Рисунок 1.3.2. Средняя скорость изменения \(s\) на \([1.5,2.5]\) для функции в предварительном просмотре 1.3.1. Рисунок 1.3.3. Средняя скорость изменения абстрактной функции \(f\) на интервале \([a,b]\text{.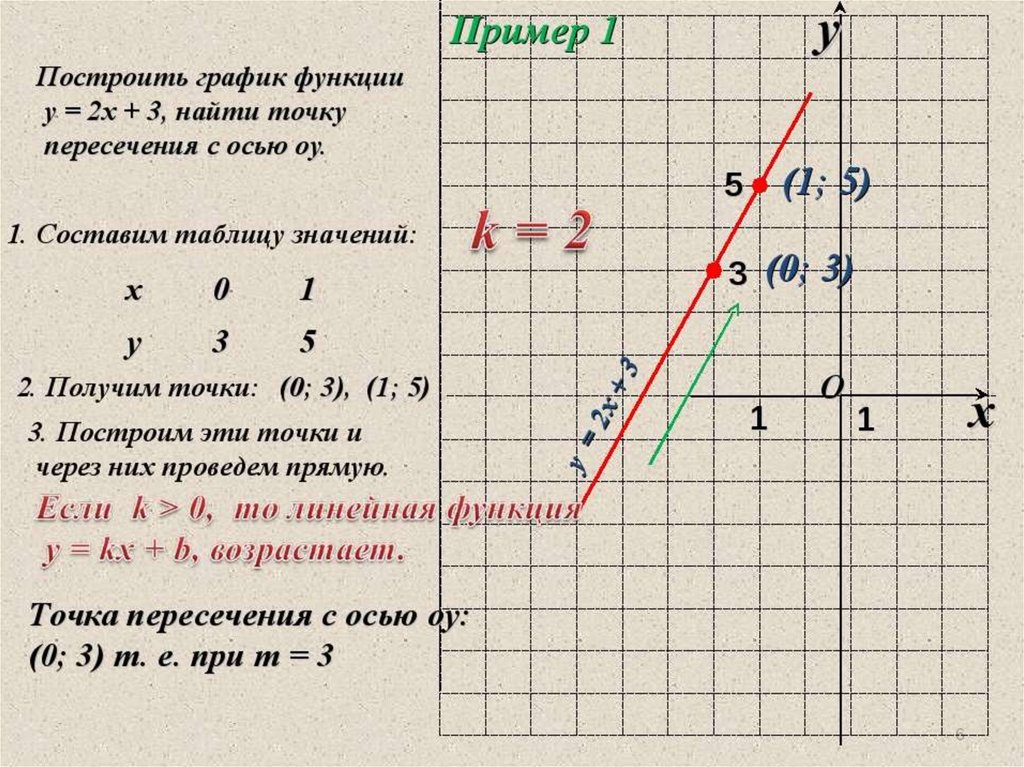 }\) }\)В то время как средняя скорость изменения функции положения говорит нам о средней скорости движущегося объекта, в других контекстах средняя скорость изменения функции может быть определена аналогичным образом и имеет соответствующую интерпретацию. Дадим следующее формальное определение. Определение 1.3.4.Для функции \(f\), определенной на интервале \([a,b]\text{,}\) средняя скорость изменения \(f\) на \([a,b]\) это количество \begin{уравнение*} AV_{[a,b]} = \frac{f(b) - f(a)}{b-a}\text{.} \end{equation*} В любой ситуации единицы средней скорости изменения помогают нам интерпретировать ее значение, и эти единицы всегда являются «единицами выпуска на единицу затрат». При этом средняя скорость изменения \(f\) на \([a,b]\) всегда соответствует наклону прямой между точками \((a,f(a))\) и \(( b,f(b))\text{,}\), как показано на рисунке 1.3.3. Мероприятие 1.3.2. Согласно переписи населения США, население округов Кент и Оттава в Мичигане, где находится GVSU 1 с 1960 по 2010 год, измеренное с интервалом \(10\) лет, приведено в следующих таблицах.
Пусть \(K(Y)\) представляет население округа Кент в году \(Y\), а \(W(Y)\) - население округа Оттава в году Y.
Средняя скорость изменения функции на интервале дает нам отличный способ описать, как функция ведет себя в среднем. Например, если мы вычислим \(AV_{[1970,2000]}\) для округа Кент мы находим, что \begin{уравнение*} AV_{[1970,2000]} = \frac{574,336 - 411,044}{30} = 5443,07\text{,} \end{уравнение*} , который говорит нам, что в среднем за год с 1970 по 2000 год население графства Кент увеличилось примерно на \(5443\) человек. Другими словами, мы могли бы также сказать, что с 1970 по 2000 год округ Кент рос в среднем на \(5443\) человек в год. \begin{уравнение*} AV_{[1990,2000]} = \frac{574,336 - 500,631}{10} = 7370,5\text{,} \end{уравнение*} мы можем не только сказать, что население округа Кент увеличилось примерно на \(7370\) в среднем за год между 1990 и 2000 годами, но также и то, что население росло быстрее с 1990 по 2000 год, чем с 1970 по 2000 год. Наконец, мы можем даже использовать среднюю скорость изменения функции для предсказания будущего поведения. Поскольку население менялось в среднем на \(7370,5\) человек в год с 192\text{,}\) мы вычислили, что \(AV_{[1.5,2.5]} = -32\text{,}\), что указывает на то, что на интервале \([1.5,2.5]\text{,}\ ) высота теннисного мяча уменьшается со средней скоростью \(32\) футов в секунду. Точно так же для населения округа Кент, поскольку \(AV_{[1990,2000]} = 7370,5\text{,}\), мы знаем, что на интервале \([1990,2000]\) население увеличивается со скоростью средний показатель \(7370,5\) человек в год. Мы даем следующие формальные определения, чтобы прояснить, что значит говорить, что функция возрастает или убывает. Определение 1.3.7.Пусть \(f\) — функция, определенная на интервале \((a,b)\) (то есть на множестве всех \(x\), для которых \(a \lt x \lt b\) ). Мы говорим, что \(f\) возрастает на \((a,b)\) при условии, что функция всегда возрастает при движении слева направо. То есть для любых \(x\) и \(y\) в \((a,b)\text{,}\) если \(x \lt y\text{,}\), то \(f( х) \lt f(y)\text{.}\) Точно так же мы говорим, что \(f\) убывает на \((a,b)\) при условии, что функция всегда падает при движении слева направо. То есть для любых \(x\) и \(y\) в \((a,b)\text{,}\) если \(x \lt y\text{,}\), то \(f( х) \gt f(y)\text{.}\) Если мы вычисляем среднюю скорость изменения функции на интервале, мы можем решить, увеличивается функция или уменьшается в среднем на интервале, но требуется больше работы 2 , чтобы решить, возрастает ли функция или уменьшение всегда на интервале. Мероприятие 1.3.3.Давайте рассмотрим две разные функции и посмотрим, как разные вычисления их средней скорости изменения говорят нам об их соответствующем поведении. Графики \(q\) и \(h\) показаны на рисунках 1.3.8 и 1.3.9.t\text{.}\) Вычислить \(AV_{[-1,1]}\text{,}\) \(AV_{[1,3]}\text{,}\) и \(AV_{[ 3,5]}\text{.}\) Что ваши вычисления говорят вам о поведении функции \(h\) на \([-1,5]\text{?}\) На графиках на рисунках 1.3.8 и 1.3.9 начертите отрезки линий, соответствующие наклоны которых представляют собой средние скорости изменения, вычисленные вами в (a) и (b). Рисунок 1.3.8. График \(q\) из части (а).Рис. 1.3.9. График \(h\) из части (b).Верно или неверно: Поскольку \(AV_{[0,3]} = 1\text{,}\), функция \(q\) возрастает на интервале \((0,3)\text{.} \) Обоснуйте свое решение. Приведите пример функции, которая имеет одинаковую среднюю скорость изменения независимо от выбранного вами интервала. Вы можете представить свой пример в виде таблицы, графика или формулы; независимо от вашего выбора, напишите предложение, чтобы объяснить. Полезно иметь возможность связать информацию о средней скорости изменения функции и ее график. Например, если мы определили, что \(AV_{[-3,2]} = 1,75\) для некоторой функции \(f\text{,}\), это говорит нам о том, что в среднем функция возрастает между точками \(x = -3\) и \(x = 2\) и делает это со средней скоростью \(1,75\) единиц по вертикали на каждую единицу по горизонтали. Более того, мы даже можем определить, что разница между \(f(2)\) и \(f(-3)\) равна \begin{уравнение*} f(2)-f(-3) = 1,75 \cdot 5 = 8,75 \end{уравнение*} , так как \(\frac{f(2)-f(-3)}{2-(-3)} = 1,75\text{.}\) Мероприятие 1.3.4.Нарисуйте не менее двух различных возможных графиков, удовлетворяющих критериям функции, указанным в каждой части. Сделайте ваши графики как можно более разными. Если граф не может удовлетворять критериям, объясните, почему.
Подраздел 1.3.3 Резюме
Упражнения 1.3.4 Упражнения1.Пусть \(P_1\) и \(P_2\) - население (в сотнях) городов 1 и 2 соответственно. В таблице ниже показаны данные для этих двух популяций за пять разных лет.
Найдите среднюю скорость изменения каждой совокупности за каждый из интервалов времени, указанных ниже. (a) С 1980 по 1987 год средняя скорость изменения населения города 1 составляла сто человек в год, а средняя скорость изменения населения города 2 составляла сто человек в год. (b) С 1987 по 1999 год средняя скорость изменения населения города 1 составляла сто человек в год, а средняя скорость изменения населения города 2 составляла сто человек в год. (c) С 1980 по 1999 год средняя скорость изменения населения города 1 составляла сто человек в год, а средняя скорость изменения населения города 2 составляла сто человек в год. 92 +7\) между каждой из пар точек ниже. (a) Между \((3, 34)\) и \((5, 82)\) ответ = (b) Между \((c, k)\) и \ ((q, t)\) ответ = (c) Между \((x,\ f(x))\) и \((x+h,\ f(x+h))\ ) ответ = 4.В 2005 году в вашей коллекции 45 компакт-дисков. В 2008 году у вас 130 компакт-дисков. В 2012 году у вас 50 дисков. Какова средняя скорость изменения размера вашей коллекции компакт-дисков между: (а) 2005 и 2008? (б) 2008 и 2012? (с) 2005 и 2012? 5. На основании приведенных ниже графиков \(f(x)\) и \(g(x)\) ответьте на следующие вопросы. а) Какова средняя скорость изменения \(f(x)\) на интервале \(\ 2,2 \leq x \leq 6,1 \\) ? b) Какова средняя скорость изменения \(g(x)\) на интервале \(\ 2,2 \leq x \leq 6,1 \\) ? 6.График ниже показывает пройденное расстояние \(D\) (в милях) как функцию времени, \(t\) (в часах). (Нажмите на график, чтобы увеличить его.) а) Для каждого интервала найдите значения \(\Delta D\) и \(\Delta t\) между указанным началом и конец времен. Внесите свои ответы в соответствующие столбцы таблицы ниже.
б) На основании ваших результатов из (а) следует, что средняя скорость изменения \(D\) постоянна, она не зависит от того, какой интервал времени вы выберете. \(\frac{ \Delta D }{ \Delta t} =\) c) Какое из приведенных ниже утверждений ПРАВИЛЬНО объясняет значение вашего ответа на часть (b)? Выберите ВСЕ подходящие варианты (могут применяться несколько вариантов).
|

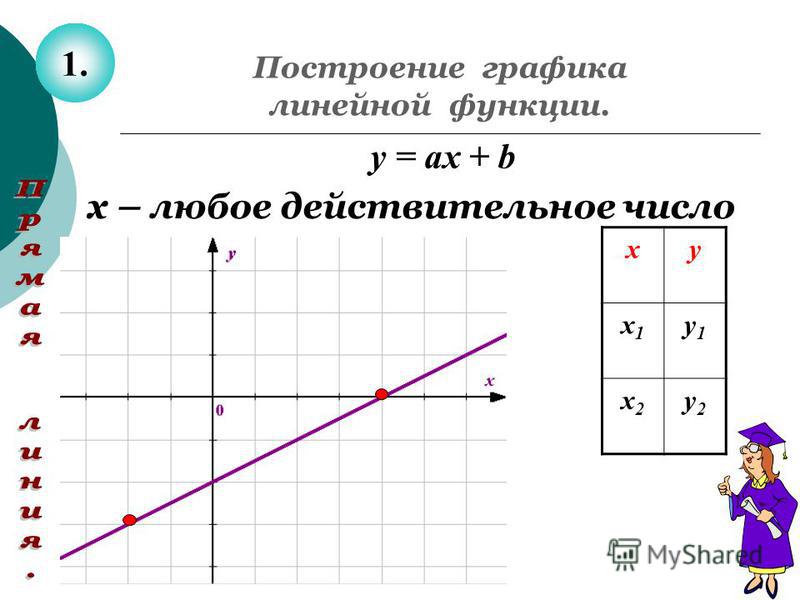
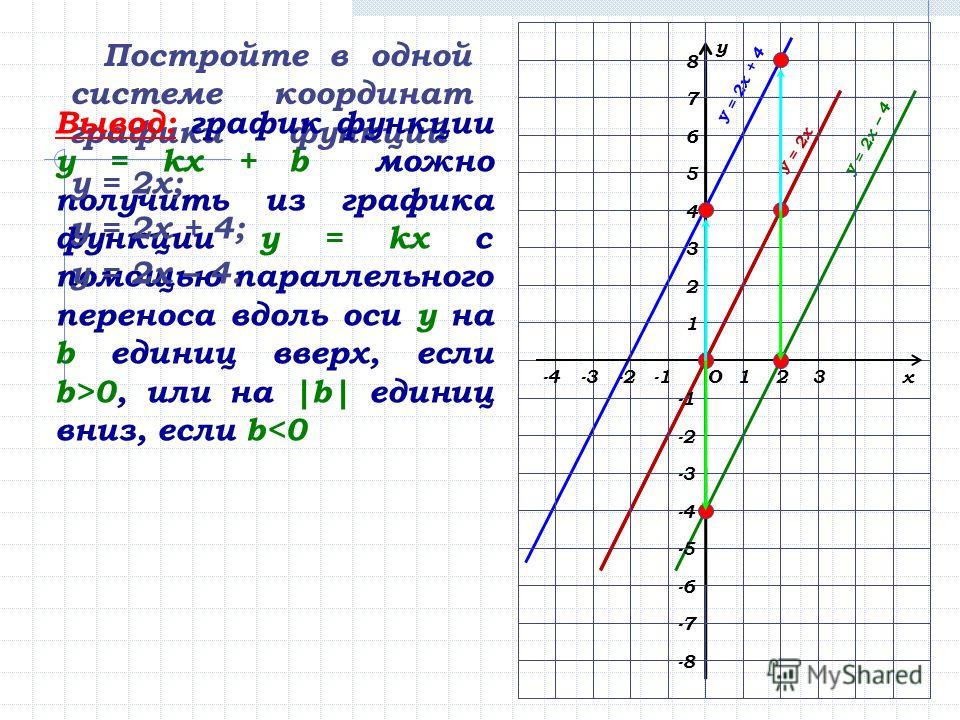
 Ответ объясните.
Ответ объясните.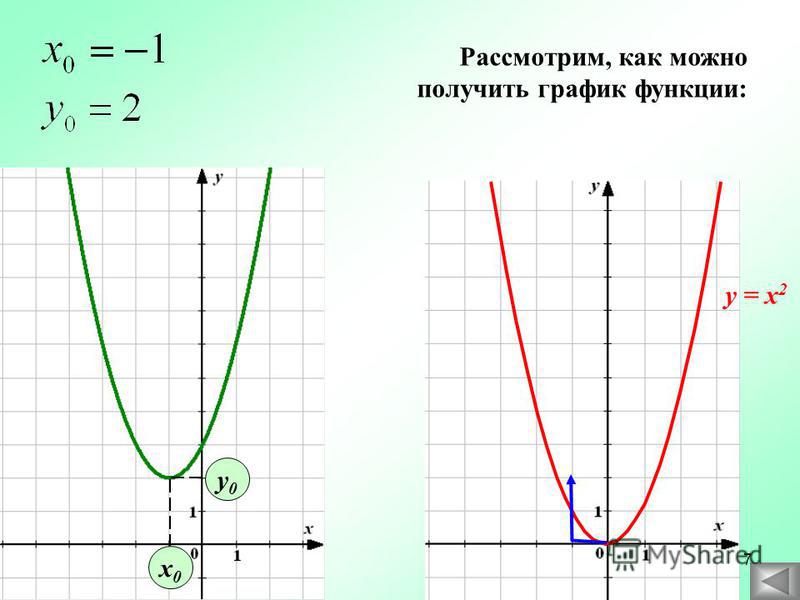 Ответ объясните.
Ответ объясните.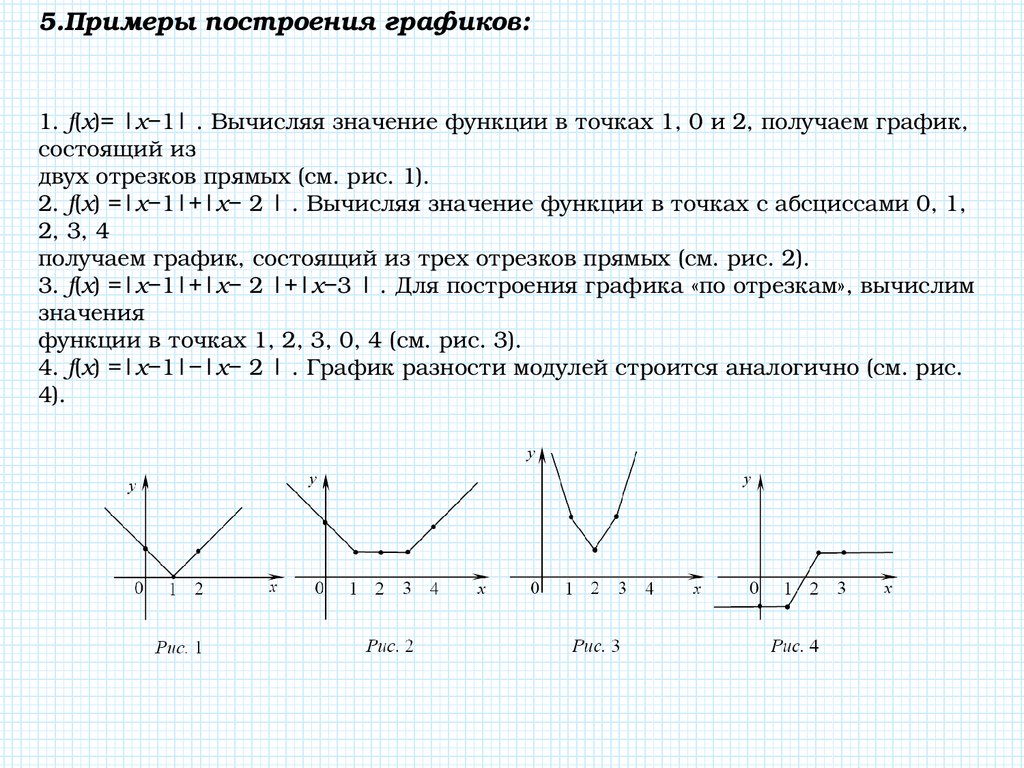
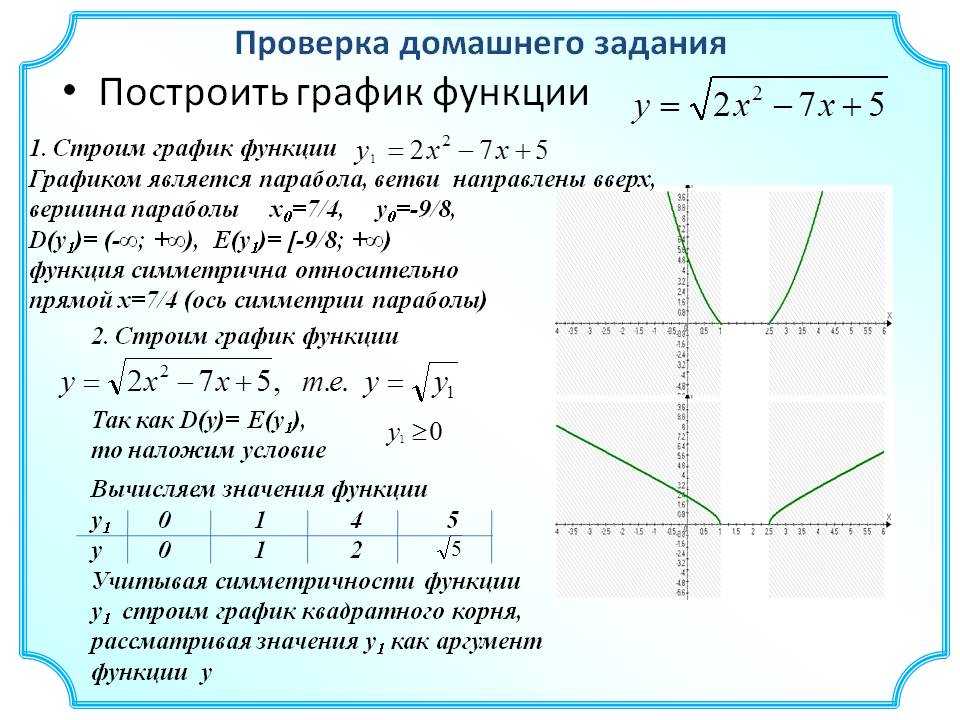
 ?
?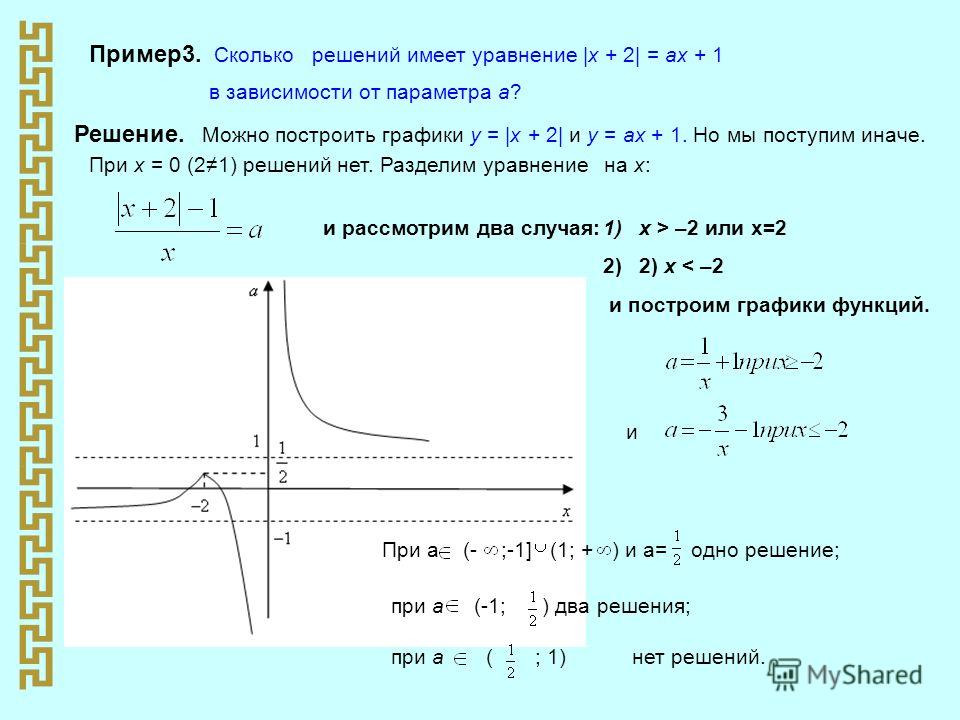
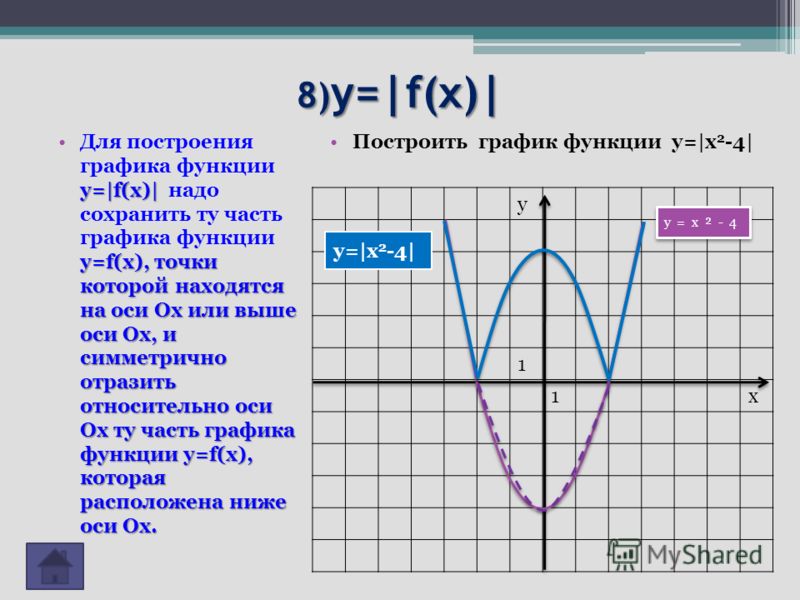
 Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.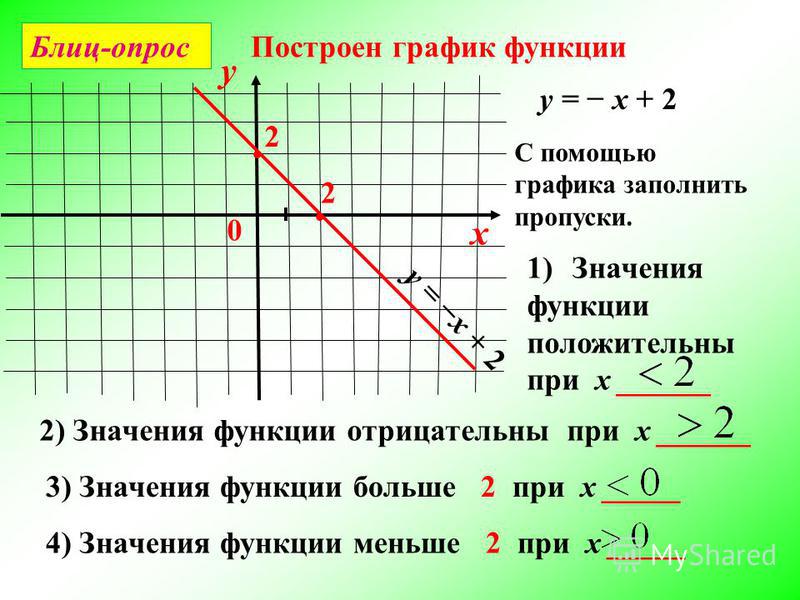 Редактируйте его название и отображаемые шаги для простоты понимания.
Редактируйте его название и отображаемые шаги для простоты понимания.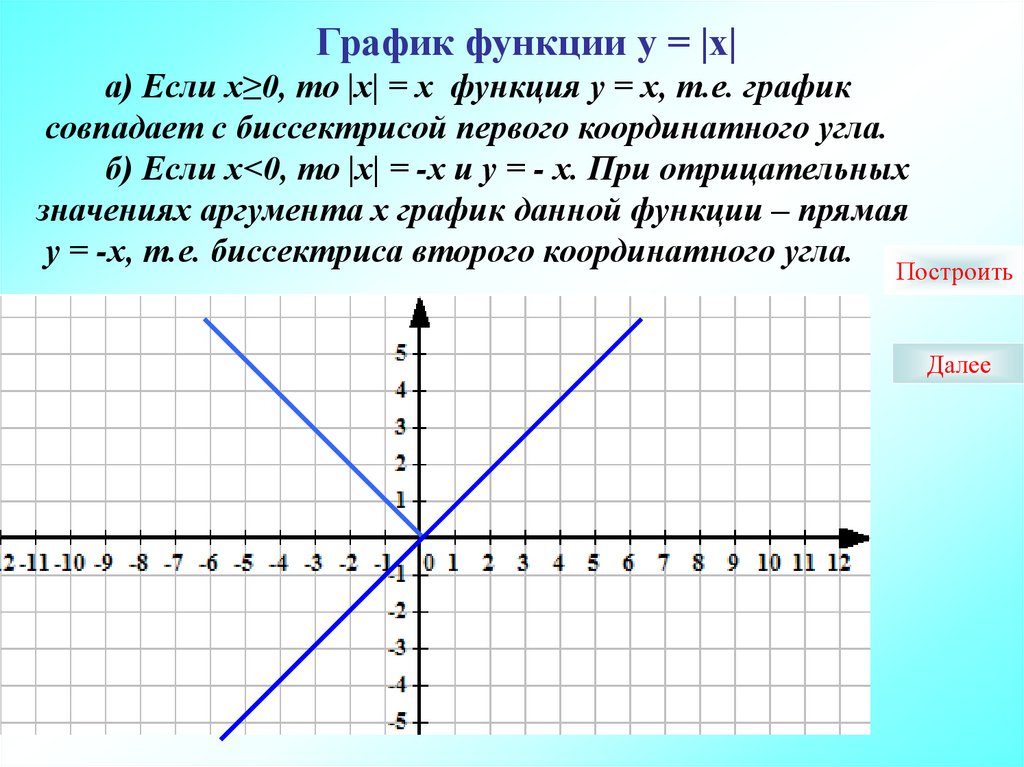 Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.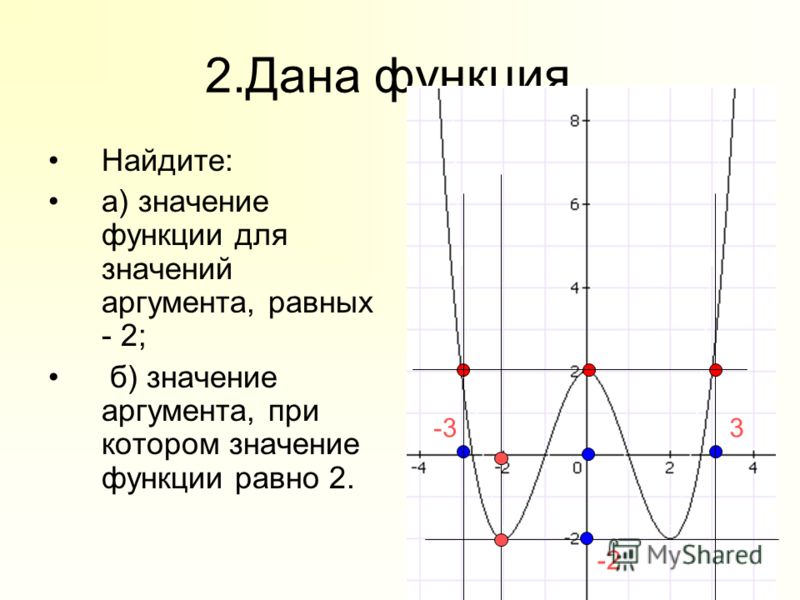 И главную единицу измерения – значение 1.
И главную единицу измерения – значение 1.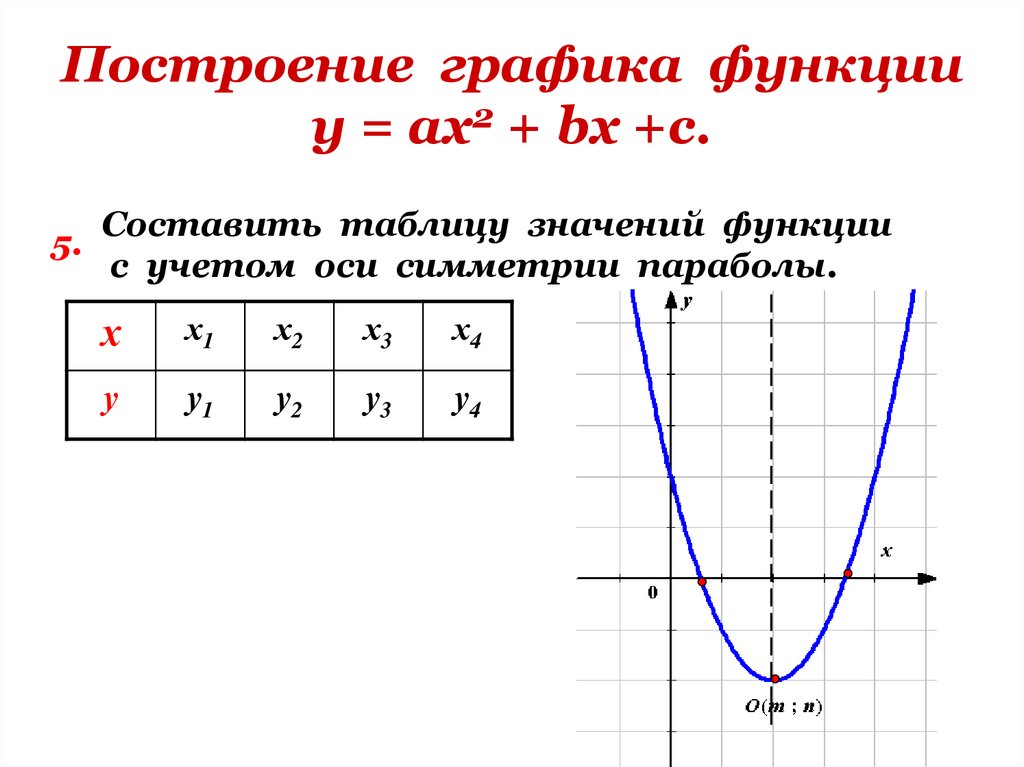
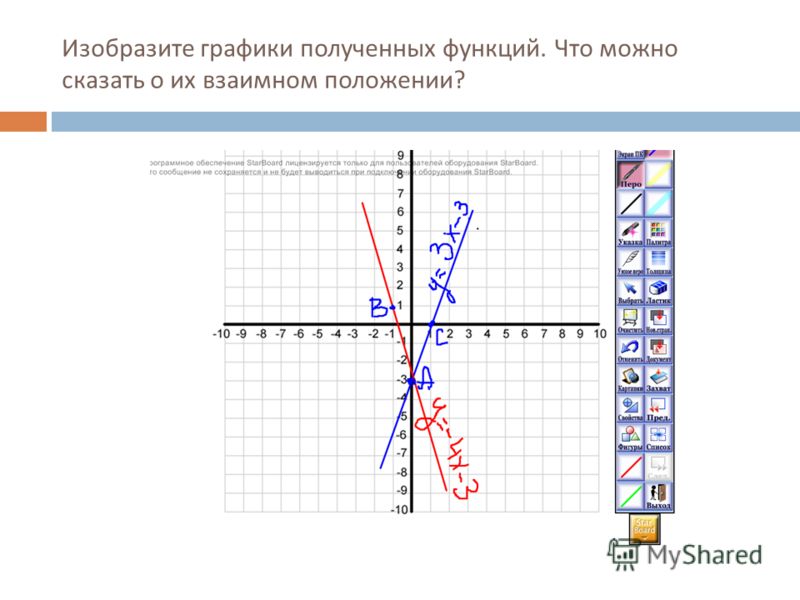
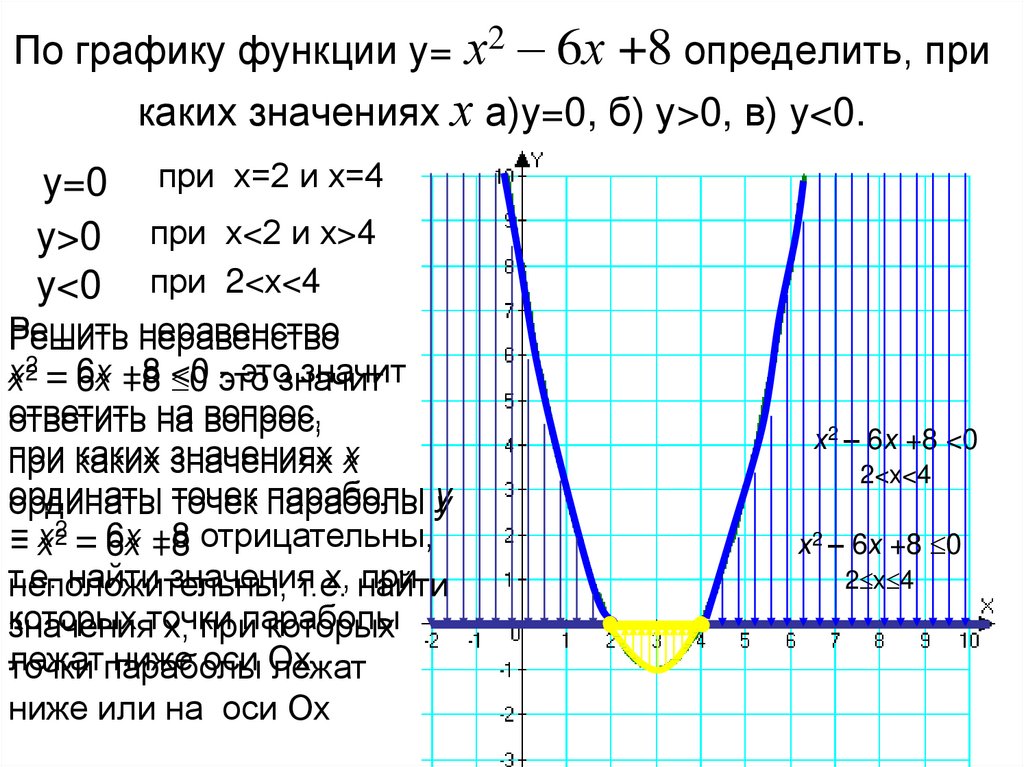
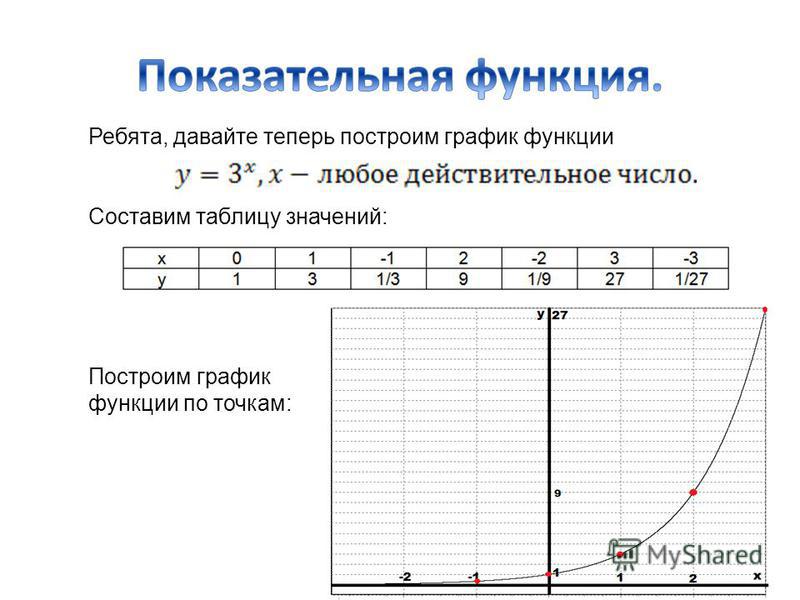
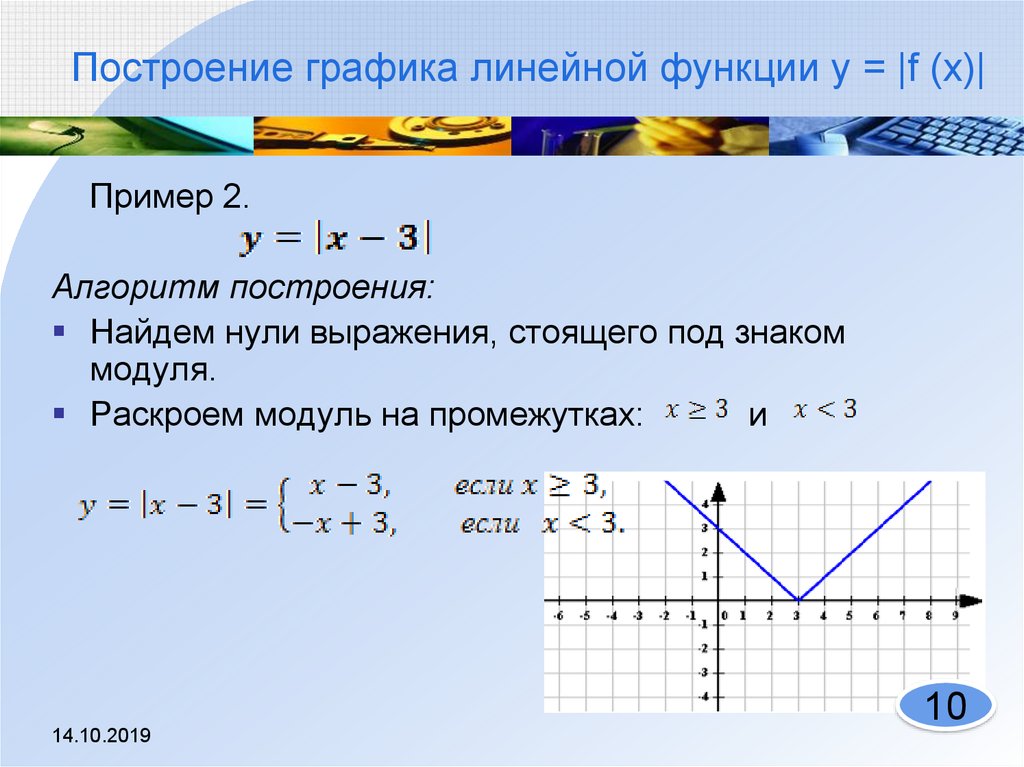 Это всего лишь общий вопрос, и нет никаких практических ограничений ни для значений x , ни для y .
Это всего лишь общий вопрос, и нет никаких практических ограничений ни для значений x , ни для y .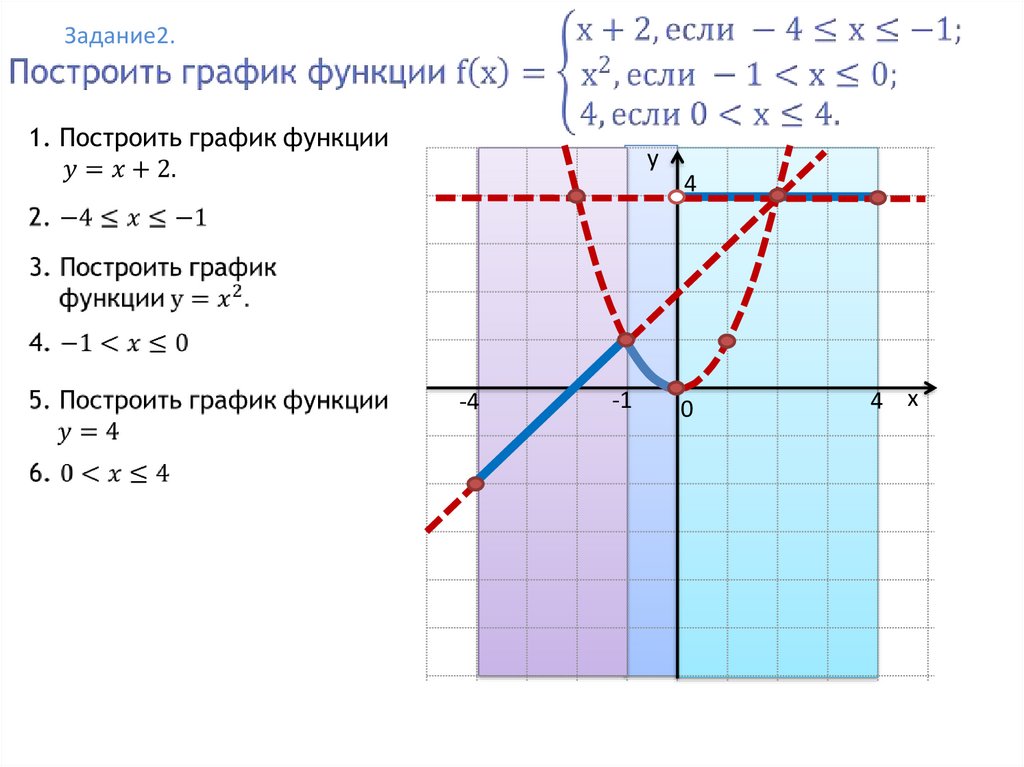 Ось и называется асимптота кривой.
Ось и называется асимптота кривой.

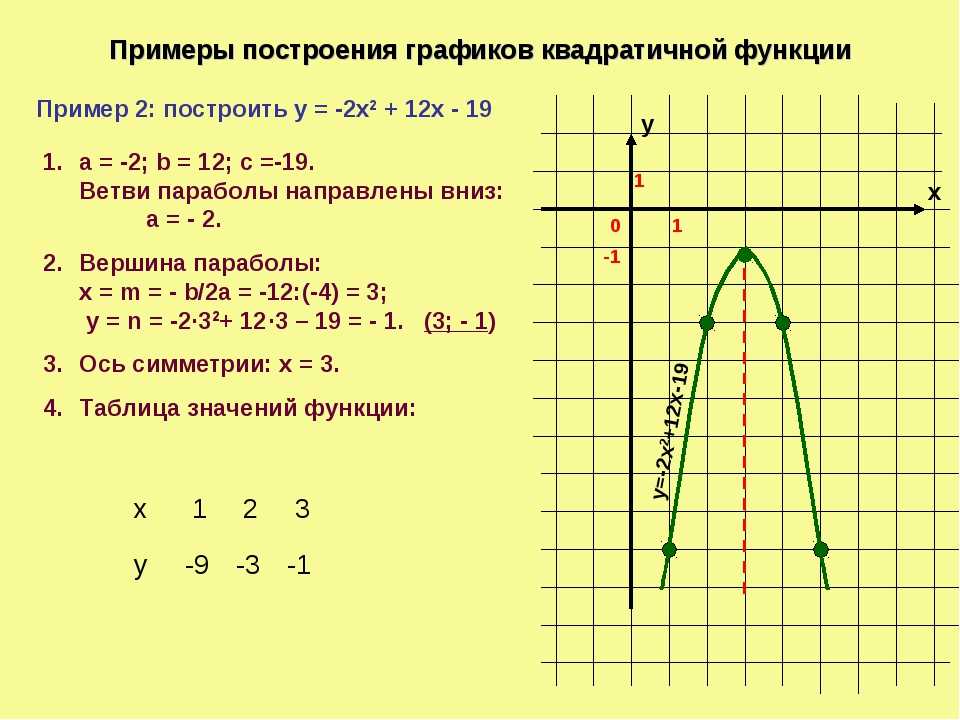 ( Заявка ) Вода вытекает из бака в форме перевернутого конуса (т.е. вода вытекает
через острый конец конуса и самую широкую часть
конус вверху). Объем воды уменьшается на
постоянная ставка.
( Заявка ) Вода вытекает из бака в форме перевернутого конуса (т.е. вода вытекает
через острый конец конуса и самую широкую часть
конус вверху). Объем воды уменьшается на
постоянная ставка.
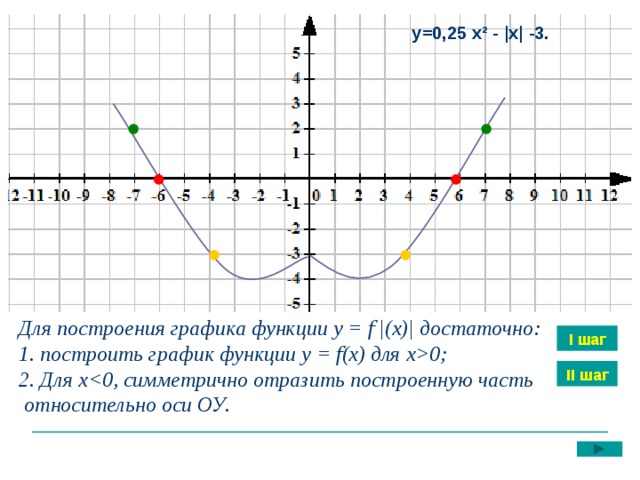 Функция также принимает параметр типа
Функция также принимает параметр типа  Используя W3Schools, вы соглашаетесь прочитать и принять наши условия использования,
куки-файлы и политика конфиденциальности.
Используя W3Schools, вы соглашаетесь прочитать и принять наши условия использования,
куки-файлы и политика конфиденциальности.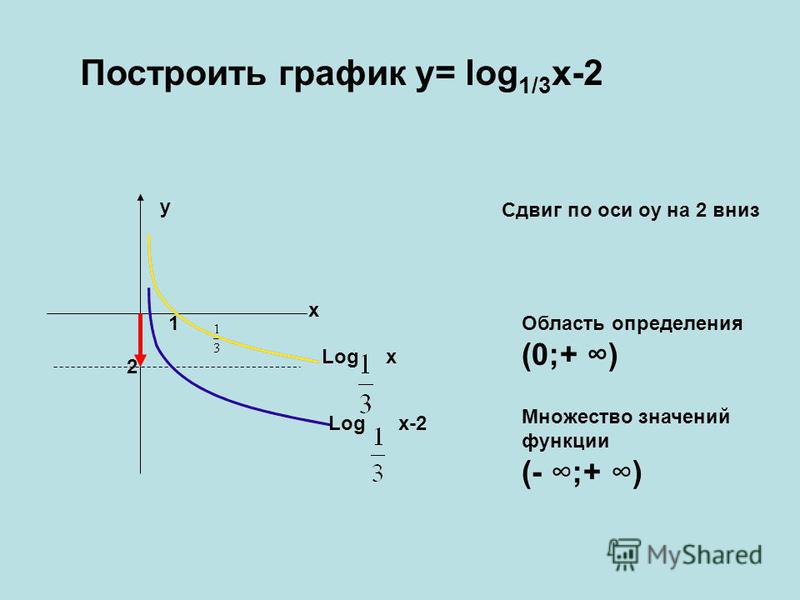
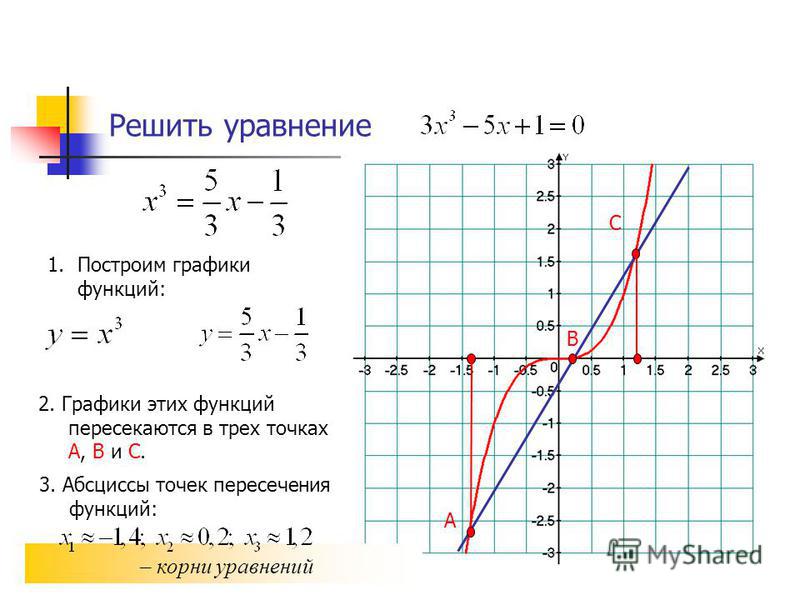 В общем, мы можем определить постоянную функцию как функцию, которая всегда имеет одно и то же постоянное значение, независимо от входного значения.
В общем, мы можем определить постоянную функцию как функцию, которая всегда имеет одно и то же постоянное значение, независимо от входного значения.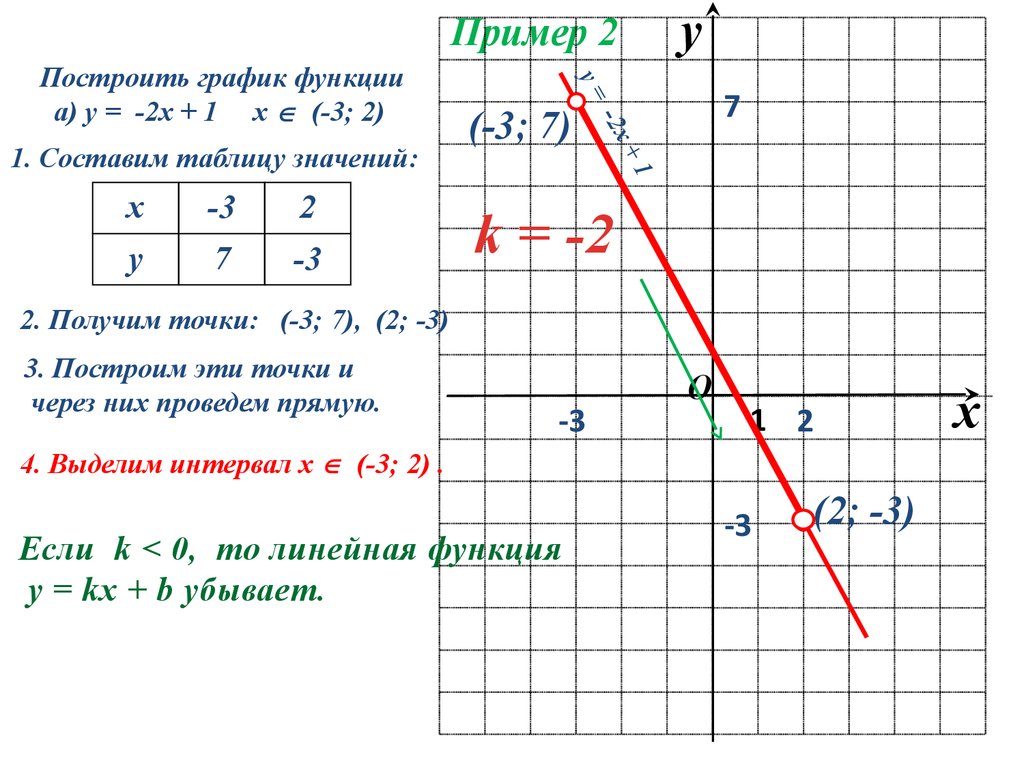 Если это возможно, то это не постоянная функция
Если это возможно, то это не постоянная функция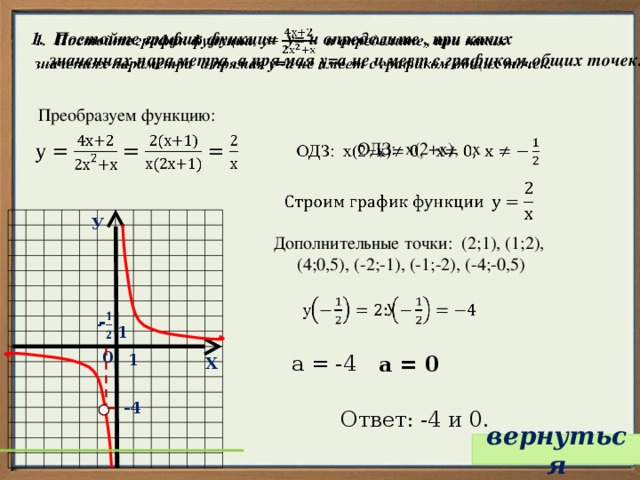 Если вы когда-нибудь видели горизонтальную линию на графике, то вы видели график постоянной функции. Константная функция относится к функции с действительным знаком без переменной в ее определении. Рассмотрим постоянную функцию f(x) = 3, где f: R → R.
Если вы когда-нибудь видели горизонтальную линию на графике, то вы видели график постоянной функции. Константная функция относится к функции с действительным знаком без переменной в ее определении. Рассмотрим постоянную функцию f(x) = 3, где f: R → R.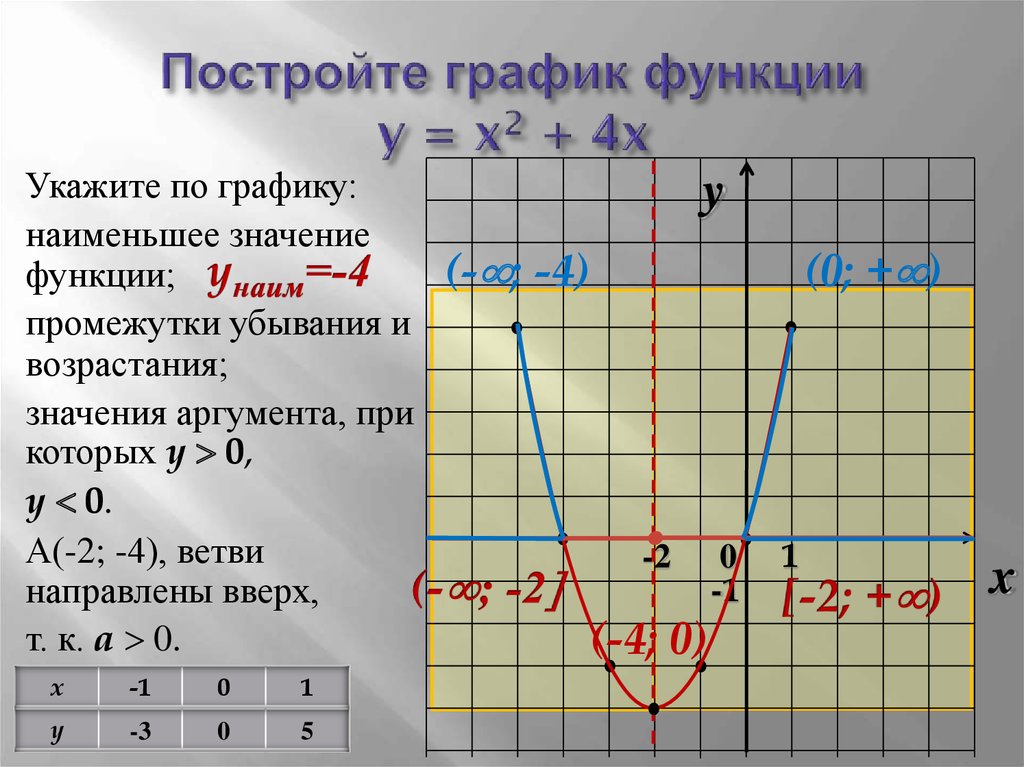 Вот некоторые из важных характеристик постоянной функции:
Вот некоторые из важных характеристик постоянной функции: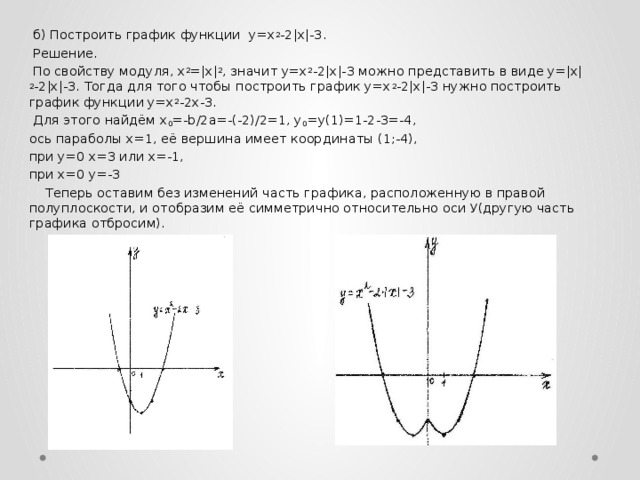 Диапазон = {к}
Диапазон = {к} Здесь постоянные функции используются для моделирования ситуаций, когда один параметр является постоянным и не зависит от других независимых параметров. Вот несколько примеров постоянных функций в реальном мире:
Здесь постоянные функции используются для моделирования ситуаций, когда один параметр является постоянным и не зависит от других независимых параметров. Вот несколько примеров постоянных функций в реальном мире: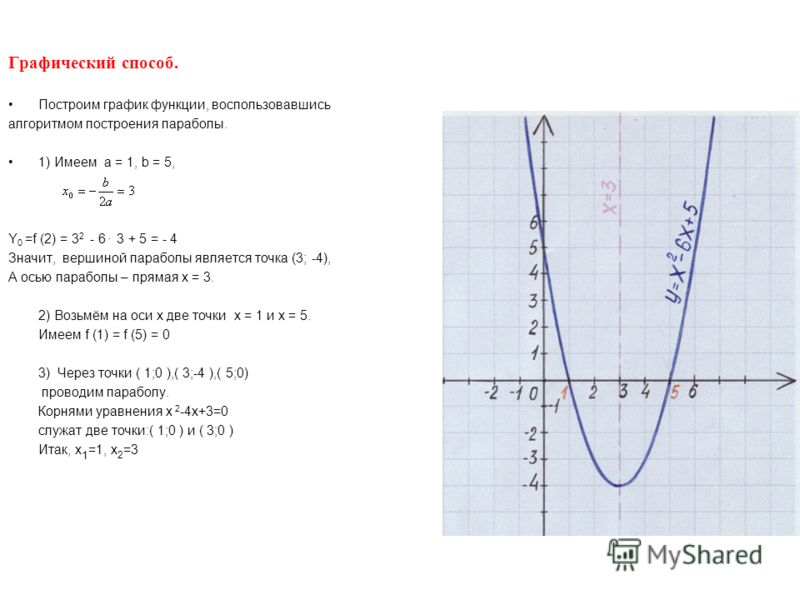
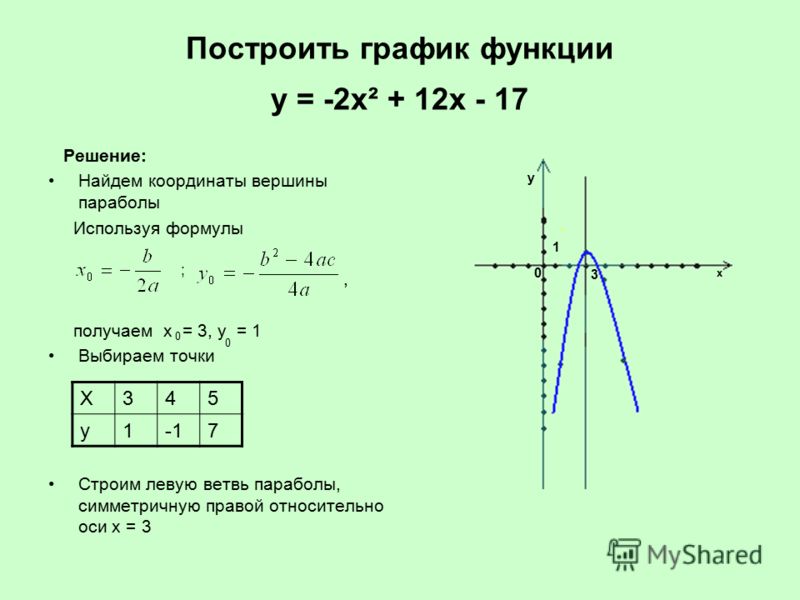 Пример постоянной функции: f(x) = 4.
Пример постоянной функции: f(x) = 4.
 т. е. ∫ k dx = kx + C, где C — постоянная интегрирования.
т. е. ∫ k dx = kx + C, где C — постоянная интегрирования. legend = нет данных,
inherit.aes = ИСТИНА
)
legend = нет данных,
inherit.aes = ИСТИНА
) 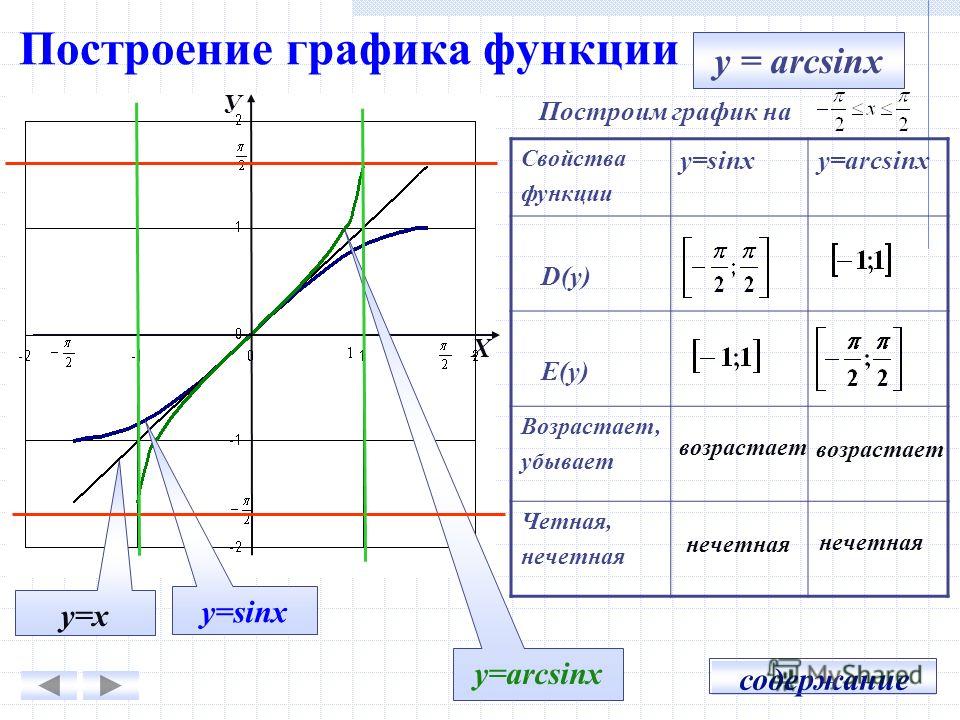 Они также могут быть параметрами
к паре геом/стат.
Они также могут быть параметрами
к паре геом/стат.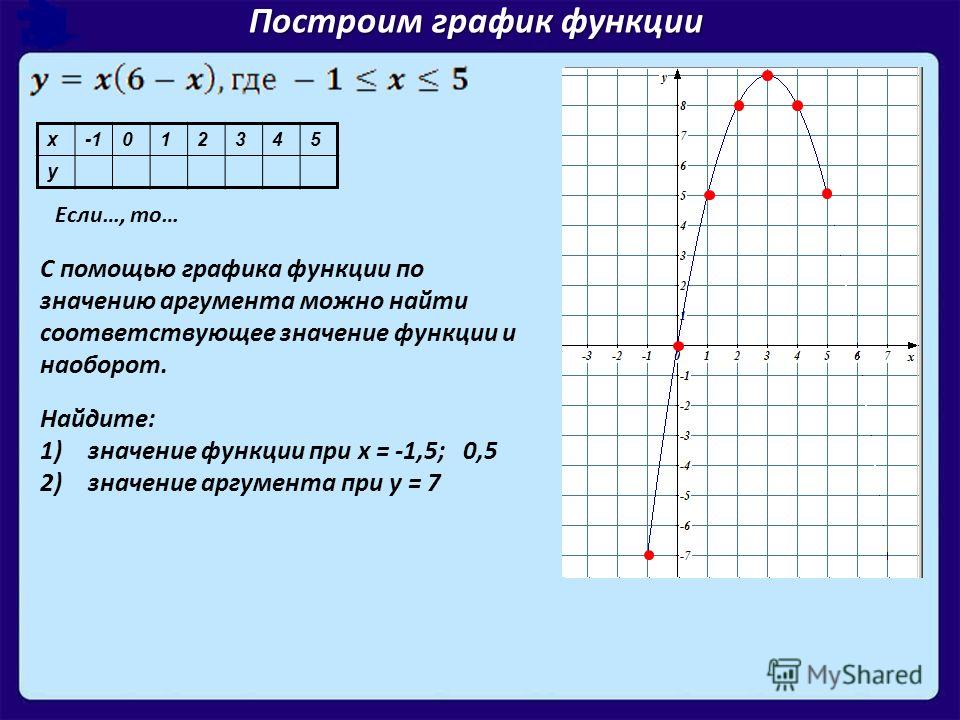 Либо 1) анонимная функция в базе, либо
синтаксис формулы rlang (см.
Либо 1) анонимная функция в базе, либо
синтаксис формулы rlang (см. 
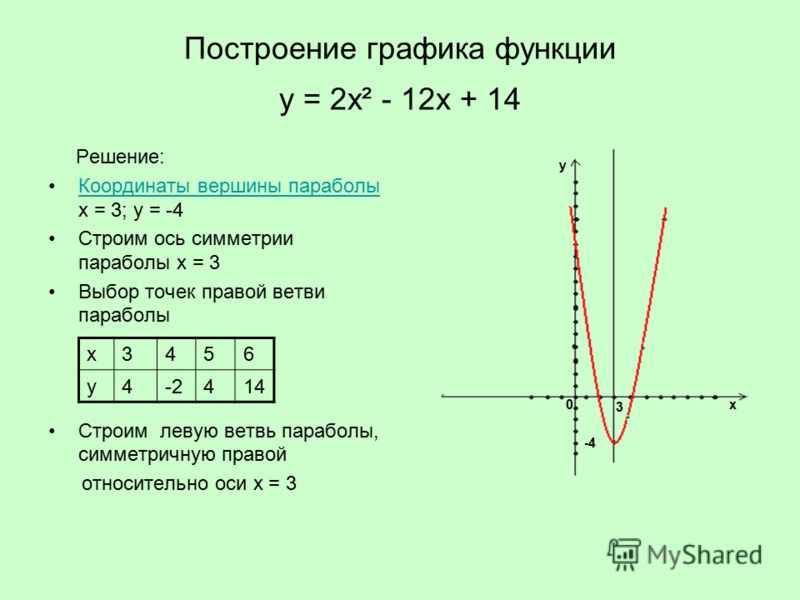 5*exp(-abs(x)))
base + geom_function(fun = ~ 0.5*exp(-abs(.x)))
# Использование пользовательской именованной функции
f <- function(x) 0.5*exp(-abs(x))
база + geom_function (веселье = f)
5*exp(-abs(x)))
base + geom_function(fun = ~ 0.5*exp(-abs(.x)))
# Использование пользовательской именованной функции
f <- function(x) 0.5*exp(-abs(x))
база + geom_function (веселье = f)
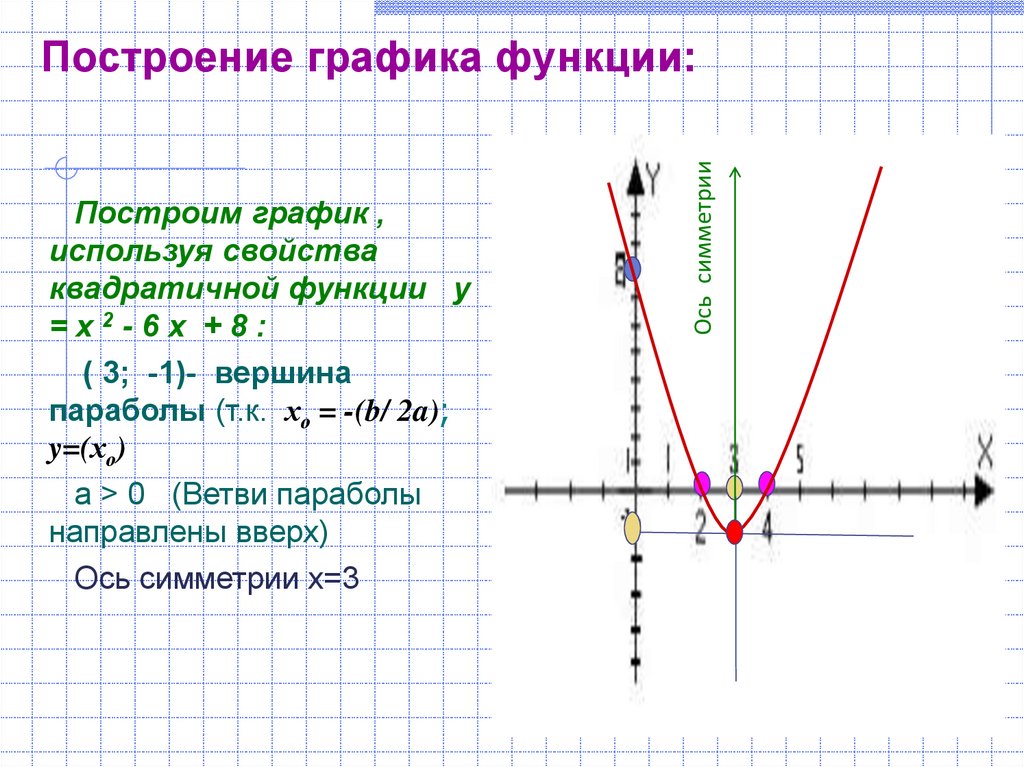 Мы увидели, как можно аккуратно отображать различные графики с помощью подграфиков, как добавлять свободно плавающие оси и как легко создавать мозаичную организацию осей с помощью GridSpec.
Мы увидели, как можно аккуратно отображать различные графики с помощью подграфиков, как добавлять свободно плавающие оси и как легко создавать мозаичную организацию осей с помощью GridSpec. subplots(number_of_subplots)
subplots(number_of_subplots) 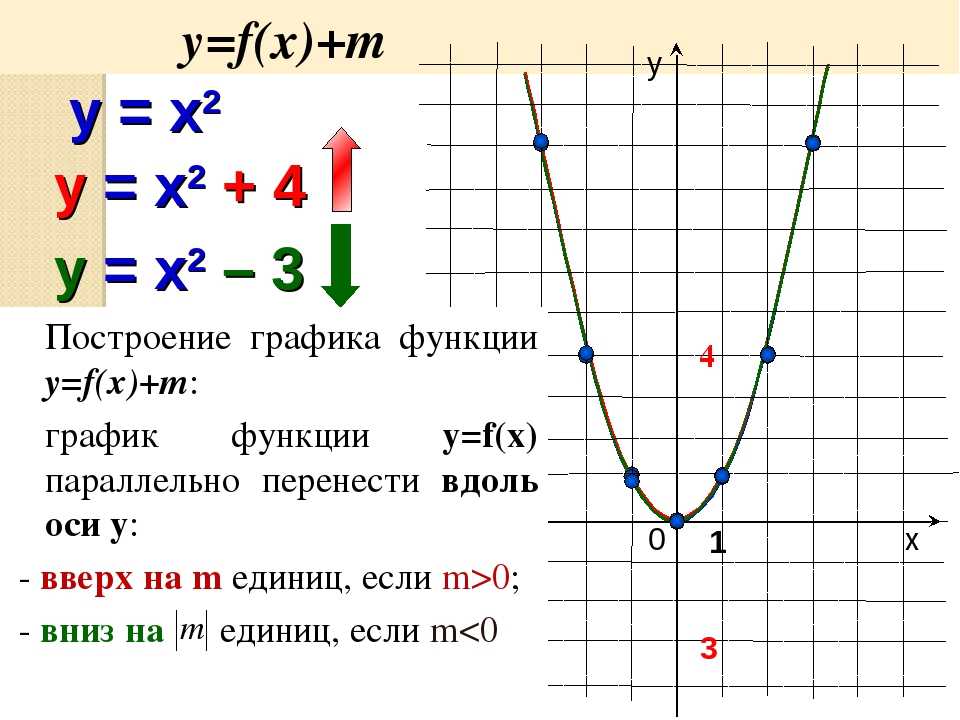 По сути,
По сути, 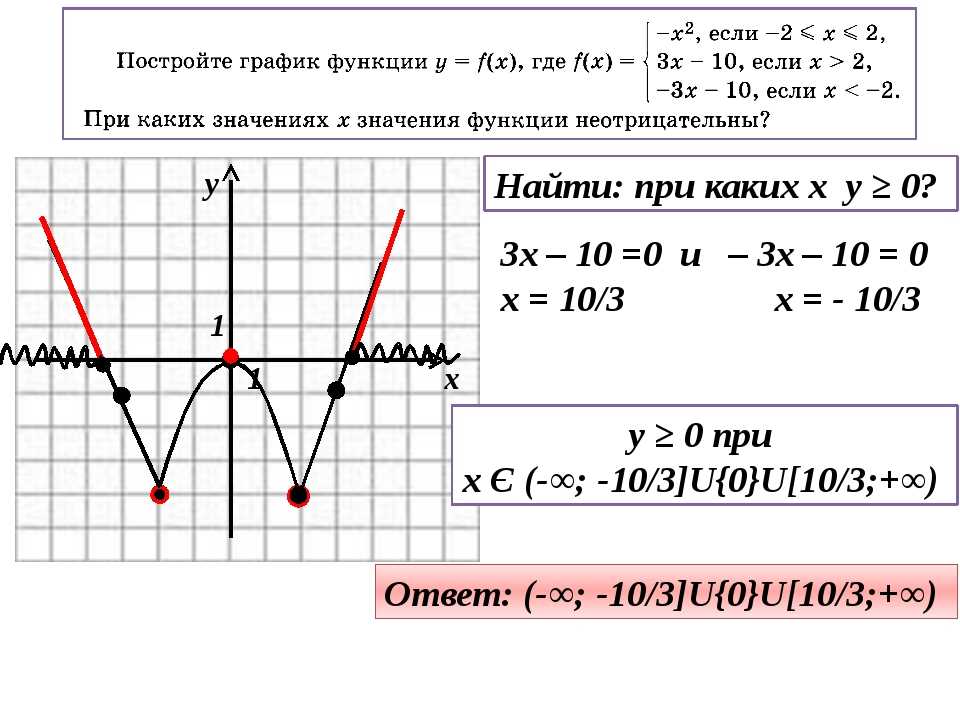
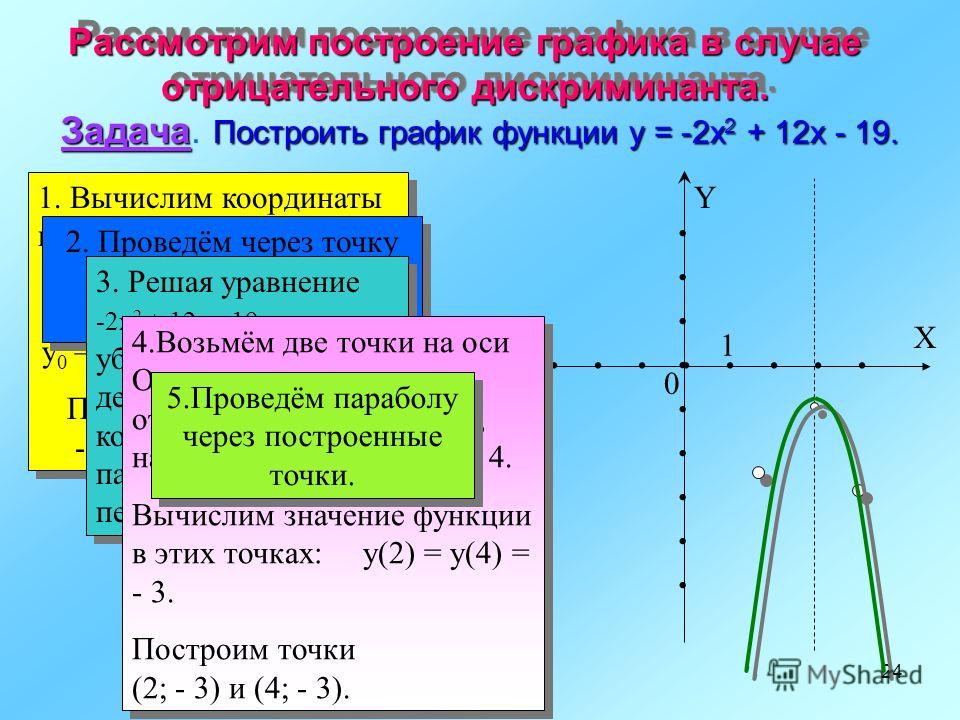 show()
show() 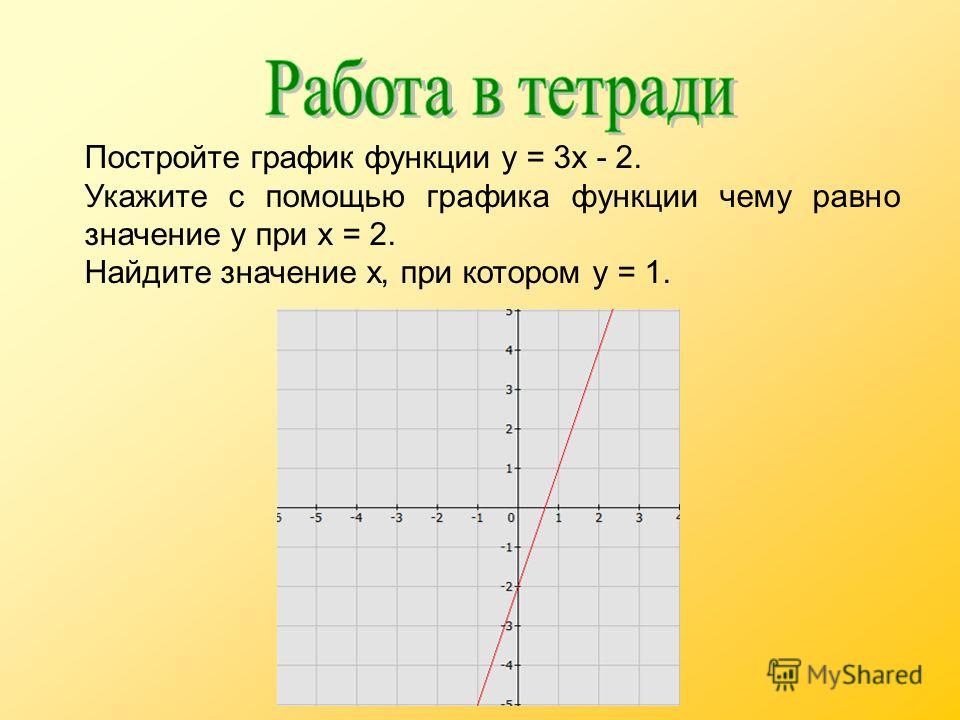 ... может быть...). Во всяком случае, вернемся к нашему примеру с
... может быть...). Во всяком случае, вернемся к нашему примеру с 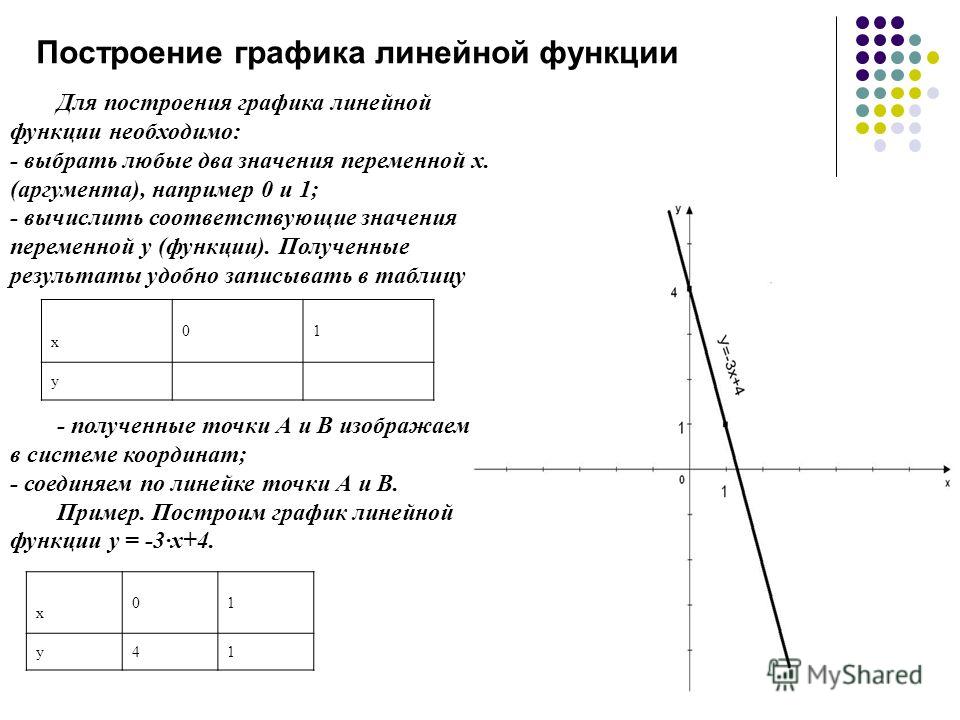 ..):
..):  Но как же используется этот словарь дополнительных аргументов ключевых слов?
Но как же используется этот словарь дополнительных аргументов ключевых слов?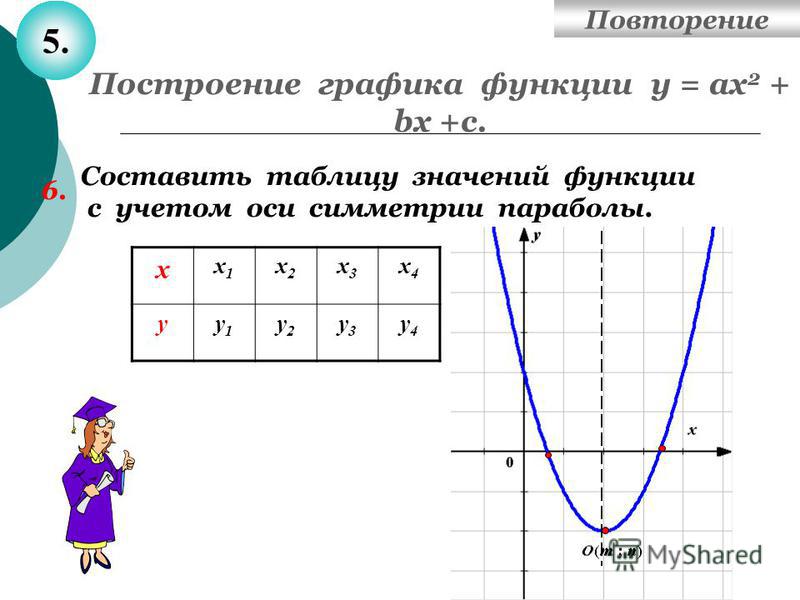 figure(figsize=(10, 5))
figure(figsize=(10, 5)) 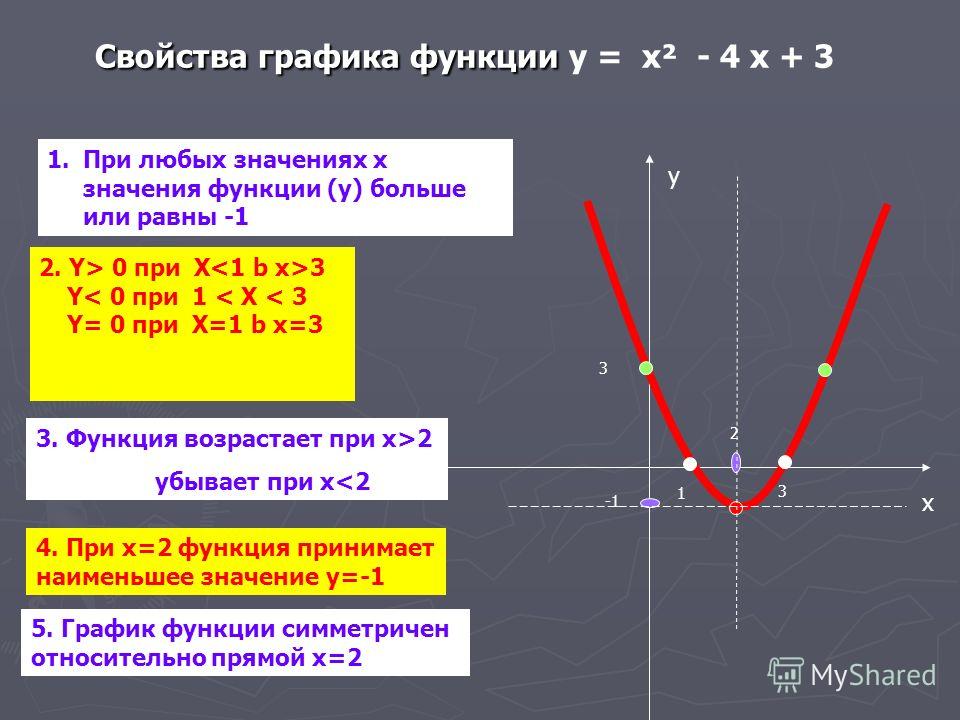 gca()
gca()  Мы используем пустые словари в качестве значений по умолчанию, потому что, если бы вы не предоставили словарь настроек, мы столкнулись бы с проблемами при попытке распаковать их (или их отсутствие) с помощью
Мы используем пустые словари в качестве значений по умолчанию, потому что, если бы вы не предоставили словарь настроек, мы столкнулись бы с проблемами при попытке распаковать их (или их отсутствие) с помощью 
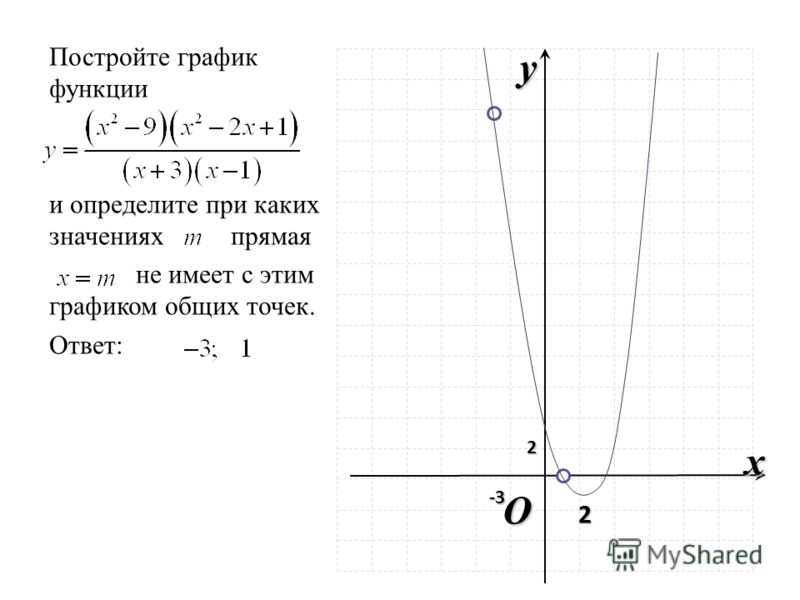 gca()
gca() 
 subplots(6, figsize= (15, 20))
subplots(6, figsize= (15, 20)) 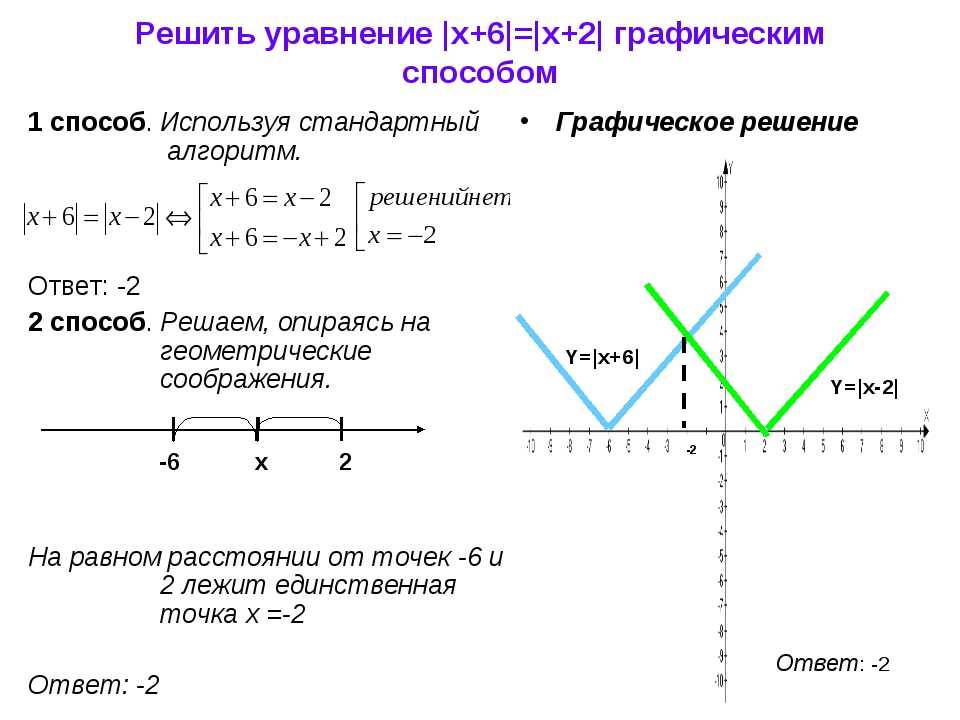 Первоначально мы сосредоточимся на средней скорости изменения объекта, движущегося по прямолинейному пути.
Первоначально мы сосредоточимся на средней скорости изменения объекта, движущегося по прямолинейному пути.
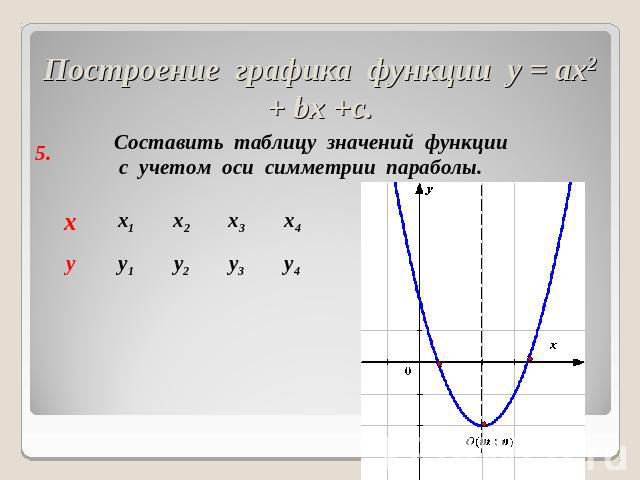 }\) Ваше предложение должно начинаться примерно так: «В среднем году в период с 1990 по 2010 год население округа Оттава составляло \(\ldots\)»
}\) Ваше предложение должно начинаться примерно так: «В среднем году в период с 1990 по 2010 год население округа Оттава составляло \(\ldots\)» Эти идеи также дают возможность проводить сравнения во времени. С
Эти идеи также дают возможность проводить сравнения во времени. С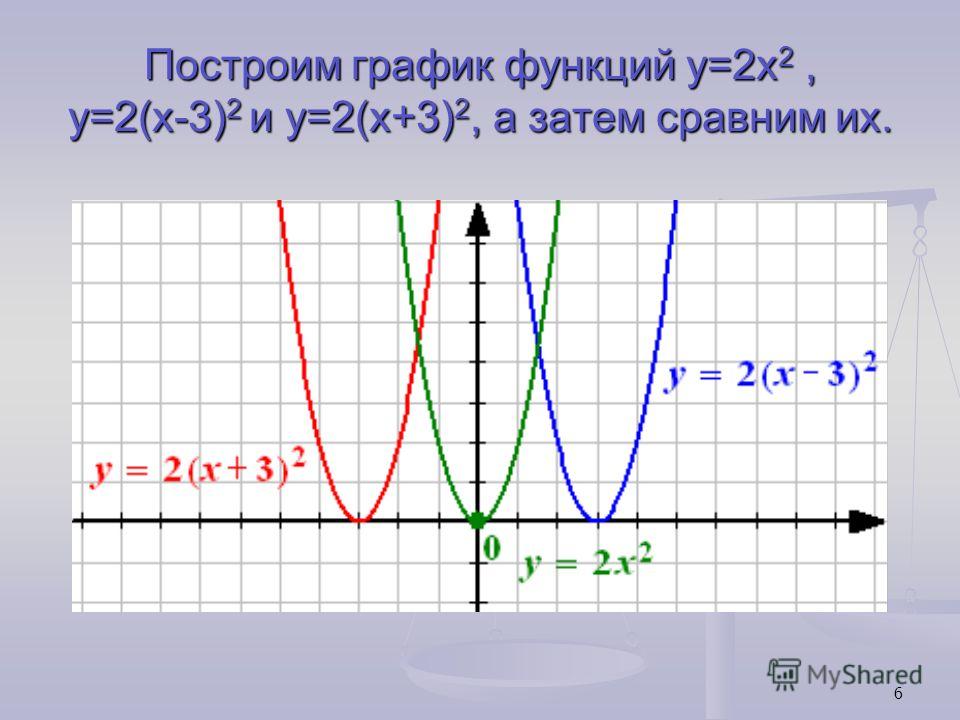

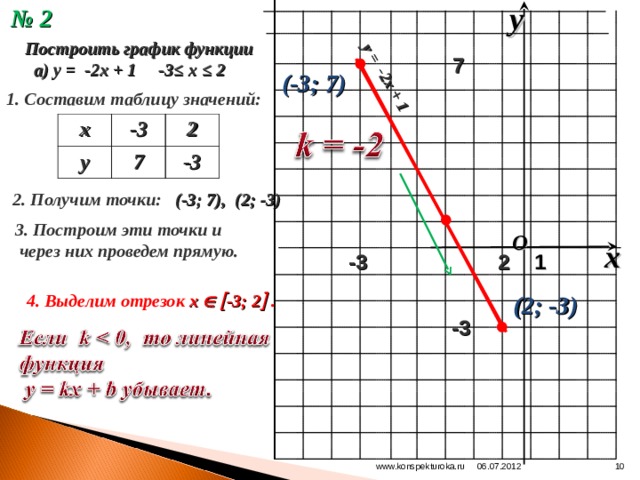
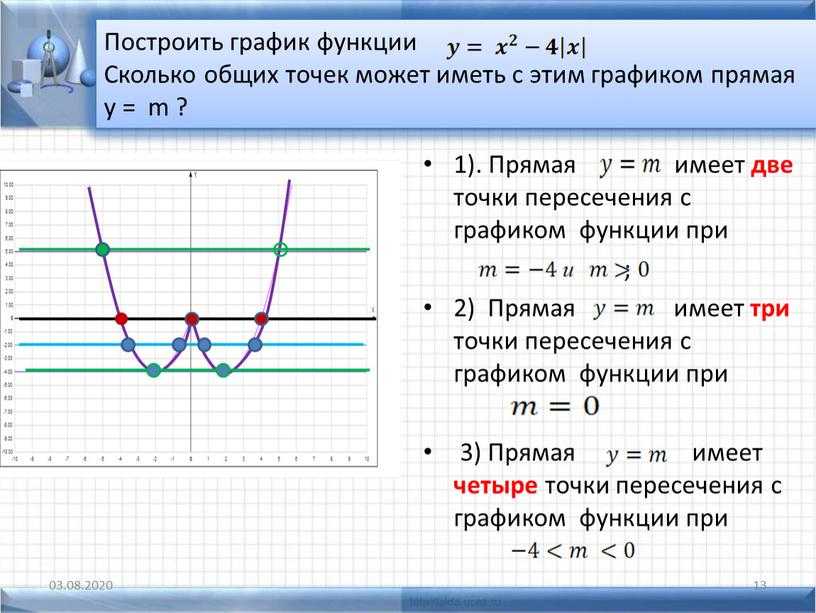 }\)
}\) В прикладных настройках единицами \(AV_{[a,b]}\) являются «единицы вывода на единицу ввода».
В прикладных настройках единицами \(AV_{[a,b]}\) являются «единицы вывода на единицу ввода».
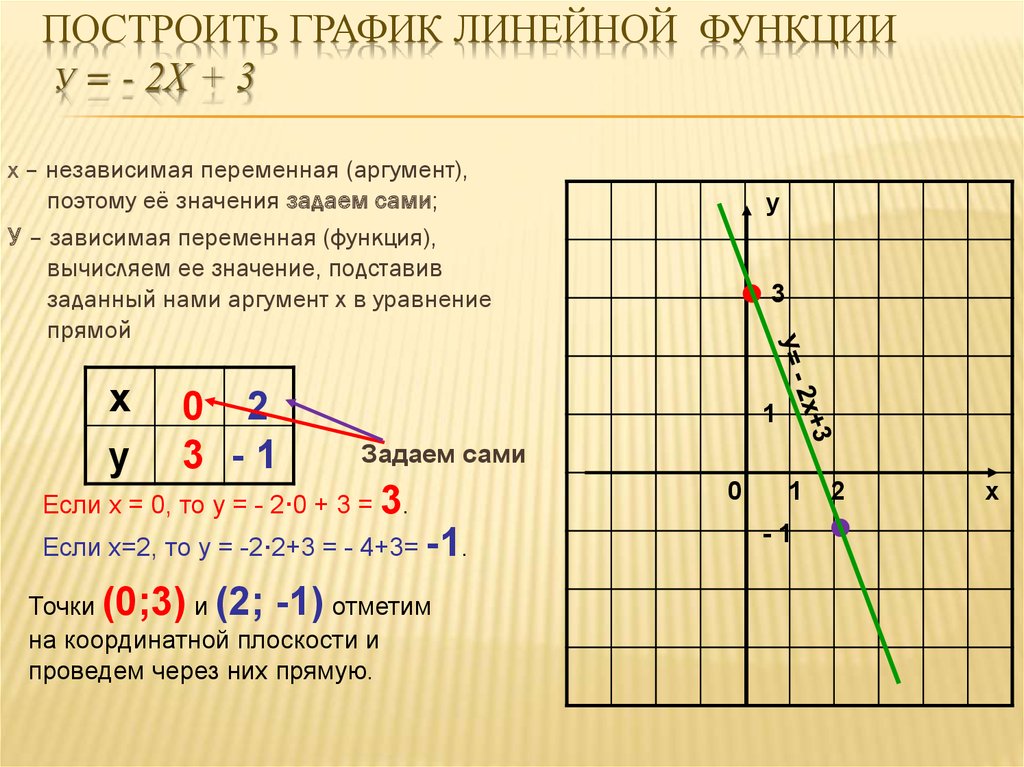 Вы не должны аппроксимировать ни один из ваших ответов.
Вы не должны аппроксимировать ни один из ваших ответов. Какова постоянная скорость изменения \(D\text{?}\)
Какова постоянная скорость изменения \(D\text{?}\)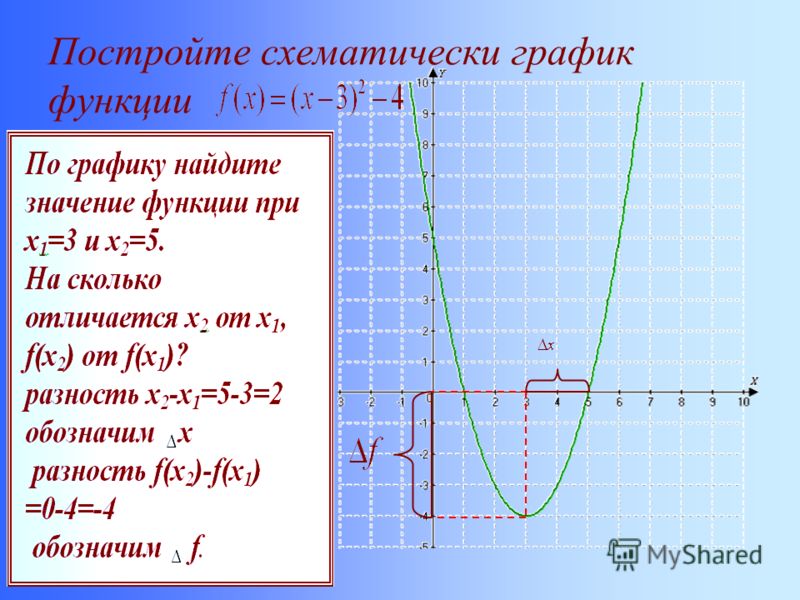 Введите соответствующую букву отрезка рядом с соответствующей формулой. Ясно, что не все буквы будут использоваться.
Введите соответствующую букву отрезка рядом с соответствующей формулой. Ясно, что не все буквы будут использоваться.
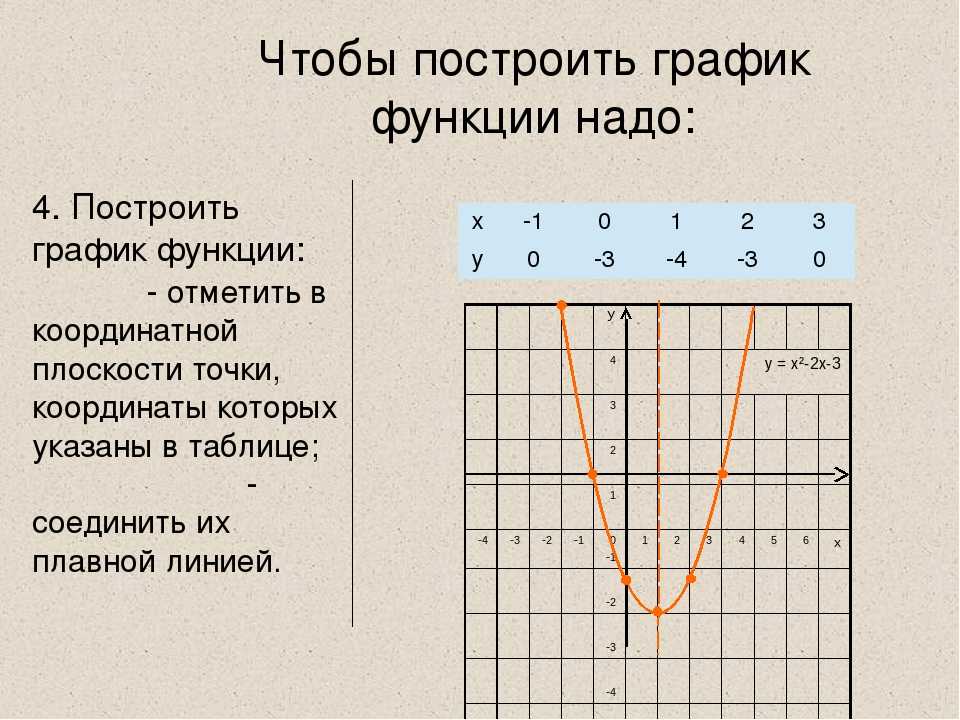 00\)
00\)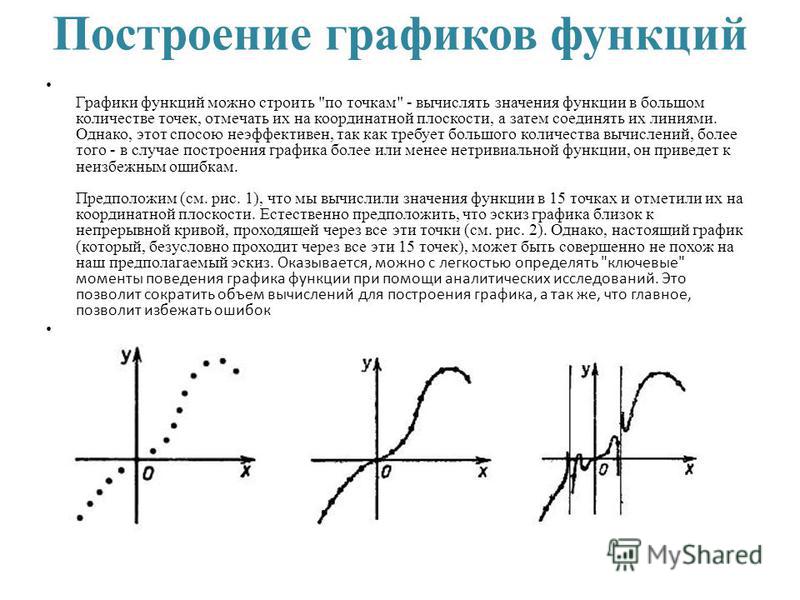 3.11. Функция положения автомобиля измеряется в тысячах футов. Например, точка \((2,4)\) на графике указывает на то, что за 2 минуты автомобиль проехал 4000 футов.
3.11. Функция положения автомобиля измеряется в тысячах футов. Например, точка \((2,4)\) на графике указывает на то, что за 2 минуты автомобиль проехал 4000 футов.