| 1 | Найти число возможных исходов | 7 выбор 3 | |
| 2 | Найти число возможных исходов | 8 выбор 3 | |
| 3 | Найти число возможных исходов | 5 выбор 2 | |
| 4 | Найти число возможных исходов | 4 выбор 2 | |
| 5 | Найти число возможных исходов | 8 выбор 4 | |
| 6 | Найти число возможных исходов | 10 выбор 3 | |
| 7 | Найти число возможных исходов | 7 выбор 4 | |
| 8 | Найти число возможных исходов | 6 выбор 3 | |
| 9 | Найти число возможных исходов | 9 выбор 3 | |
| 10 | Найти число возможных исходов | 3 выбор 2 | |
| 11 | Найти число возможных исходов | 6 выбор 4 | |
| 12 | Найти число возможных исходов | 5 выбор 4 | |
| 13 | Найти число возможных исходов | 7 перестановка 3 | |
| 14 | Найти число возможных исходов | 7 выбор 2 | |
| 15 | Найти число возможных исходов | 10 выбор 5 | |
| 16 | Найти число возможных исходов | 10 выбор 6 | |
| 17 | Найти число возможных исходов | 13 выбор 5 | |
| 18 | Найти число возможных исходов | 3 выбор 3 | |
| 19 | Найти число возможных исходов | 4 выбор 1 | |
| 20 | Найти число возможных исходов | 4 выбор 4 | |
| 21 | Найти число возможных исходов | ||
| 22 | Найти число возможных исходов | 6 перестановка 3 | |
| 23 | Найти число возможных исходов | 8 выбор 5 | |
| 24 | Найти число возможных исходов | 9 перестановка 4 | |
| 25 | Найти число возможных исходов | 13 выбор 3 | |
| 26 | Найти число возможных исходов | 12 выбор 2 | |
| 27 | Найти число возможных исходов | 12 выбор 4 | |
| 28 | Найти число возможных исходов | 12 выбор 3 | |
| 29 | Найти число возможных исходов | 9 выбор 5 | |
| 30 | Найти число возможных исходов | 9 выбор 2 | |
| 31 | Найти число возможных исходов | 7 выбор 5 | |
| 32 | Найти число возможных исходов | 6 перестановка 6 | |
| 33 | Найти число возможных исходов | 8 перестановка 5 | |
| 34 | Найти число возможных исходов | 8 перестановка 3 | |
| 35 | Найти число возможных исходов | 7 перестановка 5 | |
| 36 | Найти число возможных исходов | 52 выбор 5 | |
| 37 | Найти число возможных исходов | 5 перестановка 3 | |
| 38 | Найти число возможных исходов | 12 выбор 5 | |
| 39 | Найти число возможных исходов | 3 выбор 1 | |
| 40 | Найти число возможных исходов | 11 выбор 5 | |
| 41 | Найти число возможных исходов | 10 выбор 2 | |
| 42 | Найти число возможных исходов | 15 выбор 3 | |
| 43 | Найти число возможных исходов | 52 выбор 4 | |
| 44 | Найти число возможных исходов | 9 выбор 4 | |
| 45 | Найти число возможных исходов | 9 перестановка 3 | |
| 46 | Найти число возможных исходов | 7 перестановка 4 | |
| 47 | Найти число возможных исходов | 7 перестановка 2 | |
| 48 | Найти число возможных исходов | ||
| 49 | Найти число возможных исходов | 11 выбор 2 | |
| 50 | Найти число возможных исходов | 11 выбор 3 | |
| 51 | Найти число возможных исходов | 10 перестановка 5 | |
| 52 | Найти число возможных исходов | 5 выбор 5 | |
| 53 | Найти число возможных исходов | 6 выбор 1 | |
| 54 | Найти число возможных исходов | 8 перестановка 4 | |
| 55 | Найти число возможных исходов | 8 выбор 6 | |
| 56 | Найти число возможных исходов | 13 выбор 4 | |
| 57 | Вычислить | e | |
| 58 | Найти уравнение, перпендикулярное прямой | -7x-5y=7 | |
| 59 | Найти число возможных исходов | 13 выбор 2 | |
| 60 | Найти число возможных исходов | 10 перестановка 2 | |
| 61 | Найти число возможных исходов | 10 перестановка 3 | |
| 62 | Найти число возможных исходов | 10 выбор 7 | |
| 63 | Найти число возможных исходов | 20 выбор 4 | |
| 64 | Найти число возможных исходов | 6 перестановка 4 | |
| 65 | Найти число возможных исходов | 5 перестановка 4 | |
| 66 | Найти число возможных исходов | 6 выбор 5 | |
| 67 | Найти число возможных исходов | 52 выбор 3 | |
| 68 | Найти число возможных исходов | 4 выбор 0 | |
| 69 | Найти число возможных исходов | 9 перестановка 7 | |
| 70 | Найти число возможных исходов | 6 выбор 2 | |
| 71 | Найти число возможных исходов | 5 перестановка 5 | |
| 72 | Найти число возможных исходов | 5 перестановка 2 | |
| 73 | Найти число возможных исходов | 6 выбор 6 | |
| 74 | Найти число возможных исходов | 7 выбор 6 | |
| 75 | Найти число возможных исходов | 8 перестановка 6 | |
| 76 | Найти число возможных исходов | 7 перестановка 7 | |
| 77 | Найти число возможных исходов | 9 перестановка 5 | |
| 78 | Найти число возможных исходов | 2 перестановка 2 | |
| 79 | Найти число возможных исходов | 10 выбор 8 | |
| 80 | Найти число возможных исходов | 12 выбор 7 | |
| 81 | Найти число возможных исходов | 15 выбор 5 | |
| 82 | Найти обратный элемент | [[1,0,1],[2,-2,-1],[3,0,0]] | |
| 83 | Определить область значений | 1/4x-7 | |
| 84 | Найти число возможных исходов | 10 перестановка 7 | |
| 85 | Найти число возможных исходов | 12 выбор 6 | |
| 86 | Найти число возможных исходов | 2 выбор 1 | |
| 87 | Найти число возможных исходов | 30 выбор 3 | |
| 88 | Найти число возможных исходов | 9 выбор 6 | |
| 89 | Найти число возможных исходов | 8 перестановка 2 | |
| 90 | Найти число возможных исходов | 7 выбор 1 | |
| 91 | Найти число возможных исходов | 6 перестановка 2 | |
| 92 | Найти число возможных исходов | 4 перестановка 2 | |
| 93 | Найти число возможных исходов | 4 перестановка 3 | |
| 94 | Найти число возможных исходов | 3 перестановка 3 | |
| 95 | Найти число возможных исходов | 46 выбор 6 | |
| 96 | Найти число возможных исходов | 5 перестановка 1 | |
| 97 | Найти число возможных исходов | 52 выбор 7 | |
| 98 | Найти число возможных исходов | 52 перестановка 5 | |
| 99 | Найти число возможных исходов | 9 выбор 1 | |
| 100 | Найти число возможных исходов | 9 перестановка 6 |
Наибольший общий делитель.
 Взаимно простые числа. 6 класс
Взаимно простые числа. 6 классНаибольший общий делитель.
Взаимно простые числа
1
Решите уравнения, записывая только ответы.
3
д
84 : л = 14;
84 : т = 7;
84 : е = 21;
84 : л = 4;
84 : ь = 3;
84 : д = 28;
84 : е = 6;
84 : и = 12;
4
е
6
л
л=6
т = 12
е=4
л = 21
ь = 28
д=3
е = 14
и=7
7 12 14 21 28
и т е л ь
Расположите ответы в порядке возрастания.
Назовите, какое слово получилось. Дайте определение
делителя натурального числа.
2
3
875
175
35
7
1
5
5
5
7
Назовите наибольший делитель, отличный
от самого числа. Как его найти?
4
2376
1188
594
297
99
33
11
1
2
2
2
2
3
3
11
Назовите наибольший делитель, отличный
от самого числа. Как его найти?
5
5625
1875
625
125
25
5
1
3
3
5
5
5
5
Назовите наибольший делитель, отличный
от самого числа. Как его найти?
Как его найти?
6
Для каждой пары чисел: 18 и 9; 10 и 7; 15 и 20; 14 и 35; 48 и 36;
Найдите все делители каждого числа.
Подчеркните их общие делители.
Выделите их наибольший общий делитель.
18: 1, 2, 3, 6, 9,18. 14:
35:
9: 1, 3, 9.
15:
10: 1, 10.
20:
7: 1, 7.
48:
36:
1, 2, 7, 14.
1, 5, 7, 35.
1, 3, 5, 15.
1, 2, 4, 5, 10, 20.
1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
1, 2, 3, 4, 6, 9,12, 18, 36.
7
наибольшее натуральное число, на которое
делятся без остатка числа а и b, называют
наибольшим общим делителем этих чисел.
Обозначают: НОД (48; 36) = 12
Запишем НОД для чисел
НОД (18; 9) = 9,
НОД (15; 20) = 5,
НОД (10; 7) = 1,
НОД (14; 35) = 7,
НОД (48; 36) = 12.
Этот способ удобен, когда количество делителей,
хотя бы у одного из чисел, невелико (способ 1).
8
Способ 2.
1. Разложите числа на простые множители.
2. Выпишите общие простые множители.
3. Найдите произведение полученных простых
множителей.
24 2
60 2
12 2
30 2
6 2
15 3
3 3
55
1
1
24 = 2 ∙ 2 ∙ 2 ∙ 3;
60 = 2 ∙ 2 ∙ 3 ∙ 5
НОД(24;60) = 2 ∙ 2 ∙ 3 = 12.
9
50 2
25 5
5 5
1
50 = 2 ∙ 5 ∙ 5;
175 5
35 5
77
1
175 = 5 ∙ 5 ∙ 7
НОД(50;175) = 5 ∙ 5= 25
10
675 3
225 3
75 3
25 5
5 5
1
675 = 3 ∙ 3 ∙ 3 ∙ 5 ∙ 5;
875 5
175 5
35 5
77
1
875 = 5 ∙ 5 ∙ 5 ∙ 7
НОД(675;875) = 5 ∙ 5= 25
11
7920 2
3960 2
1980 2
990 2
495 3
165 3
55 5
11 11
1
594 2
297 3
99 3
33 3
11 11
1
7920 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3 ∙ 5 ∙ 11
594 = 2 ∙ 3 ∙ 3 ∙ 3 ∙ 11
НОД(7920;594) = 2 ∙ 3 ∙ 3 ∙ 11 = 198
12
Чтобы найти наибольший общий делитель
нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) из множителей, входящих в каждое разложение
подчеркнуть общие множители;
3) найти произведение подчеркнутых множителей.
Если все данные числа делятся на одно из них, то
это число и является наибольшим общим
делителем данных чисел.
13
В одной корзине 32 яблока, в другой корзине 40 груш. Какое наибольшее
количество одинаковых наборов можно составить, используя эти фрукты.
Найти
наибольшее
число,
на
Что нужно
сделать, чтобы
ответить
на вопрос
задачи?
которое делятся
числа
32 и 40, то
есть найти их наибольший общий
делитель.
40 груш
32 яблока
НОД (32; 40) = 8.
Ответ: 8 наборов.
14
Для каждой пары чисел: 35 и 88; 25 и 9; 5 и 3; 7 и 8;
Найдите все делители каждого числа.
Подчеркните их общие делители.
Выделите их наибольший общий делитель.
35: 1, 5, 7, 35
88: 1, 2, 4, 8, 11, 22, 44, 88
НОД (35; 88) = 1.
25: 1, 5, 25
9: 1, 3, 9
НОД (25; 9) = 1;
5: 1, 5
3: 1, 3
НОД( 5; 3) = 1;
7: 1, 7
8: 1, 8
НОД (7; 8) = 1.
15
НОД (35; 88) = 1
НОД( 5; 3) = 1
НОД (25; 9) = 1
НОД (7; 8) = 1
16
Древние греки придумали замечательный способ,
позволяющий искать наибольший общий делитель двух
натуральных чисел без разложения на множители. Он носил
Он носил
название «Алгоритма Евклида».
Он заключается в том, что наибольшим общим
делителем двух натуральных чисел является последний,
отличный от нуля, остаток при последовательном делении
чисел.
Положим, требуется найти НОД (455; 312), Тогда
455 : 312 = 1 (ост. 143), получаем 455 = 312 ∙ 1 + 143
312 : 143 = 2 (ост. 26),
312 = 143 ∙ 2 + 26
143 : 26 = 5 (ост. 13),
143 =26 ∙ 5 + 13
26: 13 = 2 (ост. 0),
26 = 13 ∙ 2
Последний делитель или последний, отличный от нуля
остаток 13 будет искомым НОД (455; 312) = 13.
17
Ребята получили на новогодней елке одинаковые подарки.
Во всех подарках вместе было 123 апельсина и 82 яблока.
Сколько ребят присутствовало на елке? Сколько апельсинов
и сколько яблок было в каждом подарке?
82 яблока
123 апельсина
Сколько ребят -?
Сколько яблок — ?
Сколько апельсинов -?
апельсинов
и яблок
Как Количество
узнать,НОД
сколько
ребят
Найти
чисел
123 было
и 82. на елке?
на елке?
должно делиться на одно и то же
наибольшее число.
НОД (123; 82) = 41, значит, 41 человек.
123 : 41 = 3 (ап.)
82 : 41 = 2 (ябл.)
Ответ: ребят 41, апельсинов 3, яблок 2.
18
Найдите наибольший общий делитель числителя и
знаменателя дробей.
20
30
13
26
8
24
24
60
15
35
8
9
19
Для поездки за город работникам завода было выделено несколько автобусов, с
одинаковым числом мест в каждом автобусе. 424 человека поехали в лес, а 477
человек — на озеро. Все места в автобусах были заняты, и ни одного человека не
осталось без места. Сколько автобусов было выделено и сколько пассажиров было
в каждом автобусе?
Найти НОД чисел
424 и 477. 424 2
НОД (424; 477) = 53,
212 2
значит, 53 пассажира в
106 2
одном автобусе.
53 53
424 : 53 = 8 (авт.) — в лес.
1
477 3
159 3
53 53
1
477 : 53 = 9 (авт.) — на озеро.
8 + 9 = 17 (авт.)
Ответ: 17 автобусов, 53 пассажира в каждом.
20
Какое число называют общим делителем данных
натуральных чисел?
Какое число называют наибольшим общим делителем
двух натуральных чисел?
Какие числа называют взаимно простыми?
Как найти наибольший общий делитель нескольких
натуральных чисел?
Если числа взаимно простые, то какому числу равен их
наибольший общий делитель?
Верно ли: «Если числа простые, то они взаимно
простые»? Ответ обоснуйте.
21
Найдите наименьшее общее кратное » задачи
НОД и НОК »
Найдите наименьшее общее кратное чисел 1)15и30 2)8и35 3)10и16
Решение: 15 = 3 * 5 30 = 2 * 3 * 5
НОК (15 и 30) = 2 * 3 * 5 = 30 — наименьшее общее кратное
8 = 2 * 2 * 2 35 = 5 * 7
НОК (8 и 35) = 8 * 35 = 280 — наименьшее общее кратное
Числа 8 и 35 — взаимно простые, так как у них нет общих делителей, кроме единицы
10 = 2 * 5 16 = 2 * 2 * 2 * 2
НОК (10 и 16) = 2 * 2 * 2 * 2 * 5 = 80 — наименьшее общее кратное1) НОК числа 15 и 30 (30), 2) 8 и 35 (280), 3) 10и16 (80)
1.
 2*91/7=9*13=117 что и требовалось доказать а делится на b
2*91/7=9*13=117 что и требовалось доказать а делится на b- 1. Разложите на простые множители число 105. 2.Найдите наибольший общий делитель чисел 770 и 231 3.Найдите наименьшее общее кратное чисел 70 30 4.Найдите наибольший общий делитель и наименьшее кратное чисел 6 и 24
Решение: 1)105=3*5*72)770=2*5*7*11
231=3*7*11
Откуда получаем наибольший общий делитель 7*11=77
3)70=2*5*7
30=5*2*3
Откуда НОК равен 2*5*3*7=210
4)6=2*3
24=2*2*2*3
Откуда НОК=2*3*2*2=24 и НОД=2*3=6
1. Разложите на простые множители число 105
105=3·5·7
2. Найдите наибольший общий делитель чисел 770 и 231
Разложим данные числа на простые множители
770=2·5·7·11
231=3·7·11
Отсюда получаем наибольший общий делитель (НОД) 7·11=77
3.
 Найдите наименьшее общее кратное чисел 70 и 30
Найдите наименьшее общее кратное чисел 70 и 30Разложим данные числа на простые множители
70=2·5·7
30=2·3·5
Отсюда получаем наименьшее общее кратное (НОК) 2·3·5·7=210
4. Найдите наибольший общий делитель и наименьшее кратное чисел 6 и 24
Разложим данные числа на простые множители
6=2·3
24=2·2·2·3
Отсюда получаем наибольший общий делитель (НОД) 2·3=6
и наименьшее общее кратное (НОК) 2·2·2·3=24
Помогите с заданием №3(г, д, е). Содержание задания: Найдите Нок (35,70), Нок(24,48), Нок(56,112). и с номером №2(г, д, е) Содержание задания: найдите Нок(35,20), Нок(16,12), Нок (56,63). если сможете сделайте и это задание: являются ли данные числа взимно простыми? Найдите наименьшее общее кратное этих чисел. а)12 и 25 б)17 и 59 в)55 и 42 г)50 и 51 д)11 и 48 е)39 и 50.
Решение: Помогите с заданием №3(г, д, е). Содержание задания: Найдите Нок (35,70), Нок(24,48), Нок(56,112). и с номером №2(г, д, е) Содержание задания: найдите Нок(35,20), Нок(16,12), Нок (56,63).
и с номером №2(г, д, е) Содержание задания: найдите Нок(35,20), Нок(16,12), Нок (56,63).
Найдите наименьшее общее кратное этих чисел.
а) нок(12, 25)=нок(2*2*3, 5*5)=2*2*3*5*5=300. Взаимно простые
б) нок(17, 59)=17*59=1003 взаимно простые
в) нок(55, 42)=нок(5*11, 2*3*7)=2*3*5*7*11=2310. Взаимно простые
г) нок(50, 51)=50*51=2*3*5*5*17=2550 взаимно простые
д) нок(11, 48)=2*2*2*2*3*11=528 взаимно простые
е) нок(39, 50)=2*3*5*5*13=1950 взаимно простыеНайдите наименьшее общее кратное чисел пр помощи разложения на множители: а) 24 и 72 б) 15 и 31 в)252 и 378 г) 60, 130 и 195.
Решение: В б получаеться 155 а на остальные не знаюНаименьшее общее кратное (НОК) — это наименьшее число, на которое делятся данные числа. Для его нахождения разложим их на простые множители и составим НОК, чтобы ВСЕ множители КАЖДОГО числа имелись в этом наборе. (НОК — это произведение таких множителей). Если НОК найдено правильно, оно делится на все данные числа без остатка.

а). 24 = 2*2*2*3; 72 = 2*2*2*3*3; НОК(24;72) = 2*2*2*3*3 = 72; 72:24=3; 72:72=1
б). 15 = 3*5; 31 = 1*31; НОК(15;31) = 3*5*31 = 465; 465:15 =31; 465:31=15
в). 252 = 2*2*3*3*7; 378 = 2*3*3*3*7; НОК (252;378) = 2*2*3*3*3*7 = 756; 756:252=3; 756:378=2
г). 60 = 2*2*3*5; 130 = 2*5*13; 195 =3*5*13;
НОК(60;130;195) = 2*2*3*5*13 = 780;
780:60=13; 780:130 = 6; 780:195=4
Найдите наименьшее общее кратное чисел под буквой а 18 45 под буквой B 30 40 под буквой B 210 и 350
Решение: А)18 І 2 45 І 3
9 І 3 15 І 3
3 І 3 5 І 5
1 І 1І
НОК(18,45)=2*3²*5=90
б)30 І 2 40 І 2
15 І 3 20 І 2
5 І 5 10 І 2
1 І 5 І 5
1 І
НОК(30,40)=2³*3*5=120
в) 210 І 2 350 І 2
105 І 3 175 І 5
35 І 5 35 І 5
7 І 7 7 І 7
1 І 1 І
НОК(210,350)=2*3*5²*7=1050Найдите наименьшее общее кратное ( подробно ) 168, 231, 60.

Решение: Разложим числа на простые множители. Сначала запишем разложение на множители самого большого число, затем остальные числа. Подчеркнем в разложении меньших чисел множители, которые не вошли в разложение наибольшего числа.231 = 3 · 7 · 11168 = 2 · 2 · 2 · 3 · 760 = 2 · 2 · 3 · 5Чтобы определить НОК, необходимо недостающие множители (эти множители подчеркнуты) добавить к множителям большего числа и перемножить их: НОК (168; 231; 60) = 3 · 7 · 11 · 2 · 2 · 2 · 5 = 9240Наиме́ньшее о́бщее кра́тное (НОК) двух целых чисел А и В есть наименьшее натуральное число, которое делится на А и В без остатка.
В данном случае три числа.
Раскладываем числа 168, 231 и 60 на простые множители.
168 = 3*7*2*2*2
231 = 3*7*11
60 = 3*5*2*2
Возьмем разложение большего числа 231 и умножаем на недостающие множители из разложения чисел 168 и 60, т. е. на числа 5 и три «двойки».
НОК(60; 168; 231) = 3*7*11*5*2*2*2= 231*5*8=9240.
Ответ: НОК(60; 168; 231)=9240.
Найдите наименьшее общее кратное чисел:
a)2 и 9
б)12 и 18
в)53 и 63
г)336 и 132
д)31, 62 и 98
е)98, 86 и 196
Решение: Чтобы найти НОК чисел нужно:
1) разложить числа на простые множители
2) выписать все простые числа, которые входят хотя бы в одно из полученных выражений
3) каждое из простых чисел взять с наибольшим из показателей степени, с которыми оно входит в разложения чисел
т. е.
а) у двойки один простой множитель (2), значит 2=2
у девятки два простых множителя (3,3), значит 9=3*3
НОК (9;2)=2*3(во второй степени)=18
наименьший общий делитель 2 и 9 это число 18
б) 12=2*2*3=2(во второй степени) *3
18=2*3*3=2*3(во второй степени)
НОК(12;18)=2(2)*3(2)=36
в)53=53 (т. к. оно само является простым числом)
63=3*3*7=3(2)*7
нок(63;53)= 53*3(2)*7=3339
г)336=2*2*2*2*3*7=2(4)*3*7
132=2*2*3*11=2(2)*3*11
нок(336;132)=2(4)*3*7*11=3696
д)31=31
62=2*31
98=2*7*7=2*7(2)
нок(31;62;98)=31*2*7(2)=868
е)98=2*7(2)
86=2*43
196=2*2*2*7*7=2(3)*7(2)
нок(98;86;196)=2(3)*7(2)*43=4816Найдите наименьшее общее кратное чисел а)18 и 27 б)7875 и 4725
Решение: 18 = 2 * 3 * 3 27 = 3 * 3 * 3
НОК (18 и 27) = 2 * 3 * 3 * 3 = 54 — наименьшее общее кратное
54 : 18 = 3 54 : 27 = 2
7 875 = 3 * 3 * 5 * 5 * 5 * 7 4 725 = 3 * 3 * 3 * 5 * 5 * 7
НОК (7 875 и 4 725) = 3 * 3 * 3 * 5 * 5 * 5 * 7 = 23 625 — наименьшее общее кратное
23 625 : 7 875 = 3 23 625 : 4 725 = 5а) 18|2
9|3
3|3
1
18 = 2*3*3 = 2*3²
27|3
9|3
3|3
1
27 = 3*3*3 = 3³
2*3³ = 54
НОК (18;27) = 54
б) 7875|3
2625|3
875|5
175|5
35|5
7|7
1
7875 = 3*3*5*5*5*7 = 3²*5³*7
4725|3
1575|3
525|3
175|5
35|5
7|7
1
4725 = 3*3*3*5*5*7 = 3³*5²*7
3³*5³*7 = 23625
НОК (7875;4725) = 23625Найдите наименьшее общее кратное чисел A и B если а равно 504 б равно 540
Решение: простые множители первого числа: 2 ; 2 ; 2 ; 3 ; 3 ; 7 ;
простые множители второго числа: 2 ; 2 ; 3 ; 3 ; 3 ; 5 ;
Общие множители: 1; 2 ; 2 ; 3 ; 3 ;
НОК будет равен = 7560Решение в приложении.

НОД(540, 504)=2²·3²=4*9=36
НОК(540, 504)=2³·3³·5·7=2520
111213 14 15 > >>
Мерзляк 6 класс — § 5. Наибольший общий делитель
- Ответы к учебнику для 6 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Какое число называют наибольшим общим делителем двух чисел?
Наибольший общий делитель двух чисел (НОД) — это наибольшее число, на которое нацело делятся оба этих числа.
2. Как можно найти НОД двух натуральных чисел, используя их разложения на простые множители?
Чтобы найти наибольший общий делитель (НОД) надо:
- Разложить оба числа на простые множители и записать их в виде произведения степеней.
- Определить степени, основания которых являются одинаковыми в обоих произведениях.
- Выбрать из каждой пары степеней с одинаковыми основаниями степень с меньшим показателем.
- Перемножить выбранные степени.
Полученное число и будет НОД двух данных чисел.
Например найдём наибольший общий множитель для чисел 18 и 24, используя данное правило:
1. Разложим оба числа на простые множители и записать их в виде произведения степеней.
2. Определим степени, основания которых являются одинаковыми в обоих произведениях (соответствующие одинаковые основания степеней подчёркнуты линиями зелёного и фиолетового цвета).
3. Выберем из каждой пары степеней с одинаковыми основаниями степень с меньшим показателем.
4. Перемножить выбранные степени.
Значит набольший общий делитель чисел 18 и 24 равен 6.
Ответ: НОД (18, 24) = 6
3. Какие числа называют взаимно простыми?
Взаимно простые — это числа, у которых наибольший общий делитель равен 1.
4. Чему равен наибольший общий делитель двух чисел, одно из которых кратно другому?
Если одно из чисел кратно другому, то наибольшим общим делителем будет меньшее из этих чисел.
Решаем устно
1. Какие из чисел 1, 2, 3, 4, 5, 6, 10, 11, 14, 15, 17, 31, 32, 33 являются простыми, а какие — составными?
Простые числа:
1, 2, 3, 5, 11, 17, 31.
Составные числа:
4, 6, 10, 14, 15, 32, 33.
2. Назовите все простые значения х, при которых будет верным неравенство 40 < х < 50.
41, 43, 47, 49.
3. Назовите все составные значения у, при которых будет верным неравенство 15 < у < 25.
19, 18, 20, 21, 22, 24.
4. Какие одинаковые цифры надо поставить вместо звёздочек, чтобы было верным равенство 2,* + 4,* = 7,6?
Надо поставить цифры 8, так как 2,8 + 4,8 = 7,6.
5. Является ли данное разложение на множители разложением на простые множители:
1) 120 = 2 • 3 • 4 • 5
Нет, так как разложение на простые множители записывается в виде степеней, основаниями у которых являются простые числа, а число 4 — составное число.
2) 567 = 7 • 9
Нет, так как разложение на простые множители записывается в виде степеней, основаниями у которых являются простые числа, а число 9 — составное число.
3) 180 = 3 • 6 • 10
Нет, так как разложение на простые множители записывается в виде степеней, основаниями у которых являются простые числа, а числа 6 и 10 — составные.
6. Сколько всего делителей у числа а, если а = 3 • 5 • 19?
Делителями числа являются все возможные произведения его простых делителей, а также единицы:
- 1
- 3
- 3 • 5
- 3 • 19
- 3 • 5 • 19
- 5
- 5 • 19 = 95
Ответ: у этого числа всего 7 делителей.
Упражнения
138. Найдите наибольший общий делитель чисел:
139. Найдите наибольший общий делитель чисел:
140. Найдите наибольший общий делитель чисел а и b:
1) а = 2 • 2 • 3 • 5 • 7 • 19 и b = 2 • 3 • 3 • 7 • 11 • 13;
НОД(a, b) = 2 • 3 • 7 = 42
2) и
НОД(a, b) = 2² • 3² • 11² • 19 = 4 • 9 • 121 • 19 = 82 764
141. Найдите наибольший общий делитель чисел:
Найдите наибольший общий делитель чисел:
142. Найдите наибольший общий делитель чисел:
143. Среди данных пар чисел выберите пары взаимно простых чисел. Для пар чисел, не являющихся взаимно простыми, укажите наибольший общий делитель.
144. Составьте все пары взаимно простых чисел из чисел 12, 14, 33, 25.
Разложим числа на простые множители:
Взаимно простыми называются числа, у которых наибольший общий множитель равен 1. Значит взаимно простыми будут следующие пары чисел:
- 12 и 25;
- 14 и 33;
- 14 и 25;
- 33 и 25.
145. Составьте все пары взаимно простых чисел из чисел 15, 16, 21, 77.
Разложим числа на простые множители:
Взаимно простыми называются числа, у которых наибольший общий множитель равен 1. Значит взаимно простыми будут следующие пары чисел:
- 15 и 16;
- 15 и 77;
- 16 и 21;
- 16 и 77.

146. Запишите все правильные дроби со знаменателем 15, у которых числитель и знаменатель — взаимно простые числа.
147. Запишите все неправильные дроби с числителем 16, у которых числитель и знаменатель — взаимно простые числа.
148. Докажите, что:
1) числа 364 и 495 — взаимно простые
Числа 364 и 495 не имеют общих множителей, больших 1.
2) числа 380 и 399 не являются взаимно простыми
Числа 380 и 399 имеют общий множитель больший, чем 1. Это число 19. Значит они не являются взаимно простыми числами.
149. Докажите, что:
1) числа 945 и 572 — взаимно простые
Числа 945 и 572 не имеют общих множителей, больших 1.
2) числа 1 095 и 738 не являются взаимно простыми
Числа 1 095 и 738 имеют общий множитель больший, чем 1. Это число 3. Значит они не являются взаимно простыми числами.
150. Используя цифры 2, 3, 4, запишите все возможные двузначные числа (цифры в каждом двузначном числе должны быть различными). Из полученных чисел выпишите пары взаимно простых чисел.
Из цифр 2, 3, 4 можно записать двузначные числа (если цифры ы каждом различны):
- 23, 24,
- 32, 34,
- 42, 43.
Из них взаимно простыми будут пары чисел:
- 23 и 24;
- 23 и 32;
- 23 и 34;
- 23 и 42;
- 23 и 43;
- 43 и 24;
- 43 и 32;
- 43 и 34;
- 43 и 42.
Так как 223 и 43 — простые числа, а остальные числа чётные — значит между собой не могут быть взаимно простыми.
151. Напишите три нары составных чисел такие, что в парах числа являются взаимно простыми.
Например, такими числами могут быть:
- 16 и 25;
- 80 и 81;
- 28 и 333.
152. Между учениками 6 класса поделили поровну 155 тетрадей и 62 ручки. Сколько в этом классе учеников?
Разложим числа 155 и 62 на простые множители:
Наибольший общий делитель для этих чисел равен 31: НОД (155, 62) = 31.
Значит в классе 31 ученик.
Ответ: 31 ученик.
153. На автомобили погрузили 96 контейнеров с картофелем и 64 контейнера с капустой. Сколько было автомобилей, если известно, что их не меньше 20 и на всех автомобилях было одинаковое количество контейнеров с картофелем и одинаковое количество контейнеров с капустой?
1) Найдём все общие делители для чисел 96 и 64:
2) Значит общими делителями для чисел 96 и 64 могут быть числа:
- 2¹ = 2
- 2² = 2 • 2 = 4
- 2³ = 2 • 2 • 2 = 8
- = 2 • 2 • 2 • 2 = 16
- = 2 • 2 • 2 • 2 • 2 = 32
3) Из чисел 2, 4, 8, 16 и 32 только число 32 > 20. Значит всего могло быть только 32 автомобиля.
Ответ: 32 автомобиля.
154. Между школьными библиотеками разделили 92 толковых и 138 орфографических словарей русского языка. Сколько было школ, если известно, что их не менее 25 и все школы получили одинаковые комплекты, состоящие из словарей двух видов?
1) Найдём все общие делители для чисел 92 и 138:
2) Значит общими делителями для чисел 92 и 138 могут быть числа:
- 2
- 23
- 2 • 23 = 46
3) Из чисел 2, 23 и 46 только число 46 > 25. Значит всего могло быть только 46 школ.
Значит всего могло быть только 46 школ.
Ответ: 46 школ.
155. Для новогодних подарков приобрели 96 шоколадок, 72 апельсина и 84 банана. Какое наибольшее количество одинаковых подарков можно из них составить, если необходимо использовать все продукты? Сколько в отдельности шоколадок, апельсинов и бананов будет в каждом подарке?
1) Найдём наибольший общий делитель (НОД) для чисел 96, 72 и 84:
Значит наибольшее количество подарков, которые можно сформировать из всех продуктов, будет 12 штук.
2) Посчитаем, сколько шоколадок, апельсинов и бананов будет в каждом подарке:
- 96 : 12 = 8 (шт.) — шоколадок будет в каждом подарке.
- 72 : 12 = 6 (шт.) — апельсинов будет в каждом подарке.
- 84 : 12 = 7 (шт.) — бананов будет в каждом подарке.
Ответ: Всего получиться 12 подарков, в каждом подарке будет по: 8 шоколадок, 6 апельсинов и 7 бананов.
156. Из 156 жёлтых, 234 белых и 390 красных роз составляли букеты. Какое наибольшее количество одинаковых букетов можно составить, если необходимо использовать все цветы?
Какое наибольшее количество одинаковых букетов можно составить, если необходимо использовать все цветы?
Найдём наибольший общий делитель (НОД) для чисел 156, 234 и 390:
Значит наибольшее количество букетов, которые можно составить, если необходимо использовать все цветы — 78 штук.
Ответ: 78 букетов.
Упражнения для повторения
157. Используя цифры 2, 5 и 9 (цифры не могут повторяться), запишите трехзначное число, которое:
1) кратно 2
952 или 892 — чтобы число было кратно 2, на конце должна быть чётная цифра.
2) кратно 5
295 или 925 — чтобы число было кратно 5, а конце должна быть цифра 5 или 0, но среди заданных цифр нуля нет.
Можно ли с помощью этих цифр записать число, кратное 3
Чтобы число делилось на 3 надо, чтобы сумма его цифр делилась на 3.
2 + 5 + 9 = 7 + 9 = 16 — не делится на 3, значит ни одно трёхзначное число, составленное из этих цифр, не будет делится на 3.
158. Какую цифру можно поставить вместо звёздочки в записи 1*8, чтобы полученное число делилось нацело на 18?
Чтобы число делилось на 18 надо, чтобы число было чётным и сумма его цифр делилась на 9. Проверим последовательно все возможные варианты цифр на месте звёздочки:
- если вместо звёздочки поставить 0, то получим чётное число 108, а 1 + 8 = 9 делится на 9 — значит на месте звёздочки может быть цифра 0;
- если вместо звёздочки поставить 1, то получим чётное число 118, а 1 + 1 + 8 = 10 не делится на 9 — значит на месте звёздочки не может быть цифра 1;
- если вместо звёздочки поставить 2, то получим чётное число 128, а 1 + 2 + 8 = 11 не делится на 9 — значит на месте звёздочки не может быть цифра 2;
- если вместо звёздочки поставить 3, то получим чётное число 138, а 1 + 3 + 8 = 12 не делится на 9 — значит на месте звёздочки не может быть цифра 3;
- если вместо звёздочки поставить 4, то получим чётное число 148, а 1 + 4 + 8 = 13 не делится на 9 — значит на месте звёздочки не может быть цифра 4;
- если вместо звёздочки поставить 5, то получим чётное число 158, а 1 + 5 + 8 = 14 не делится на 9 — значит на месте звёздочки не может быть цифра 5;
- если вместо звёздочки поставить 6, то получим чётное число 168, а 1 + 6 + 8 = 15 не делится на 9 — значит на месте звёздочки не может быть цифра 6;
- если вместо звёздочки поставить 7, то получим чётное число 178, а 1 + 7 + 8 = 16 не делится на 9 — значит на месте звёздочки не может быть цифра 7;
- если вместо звёздочки поставить 8, то получим чётное число 188, а 1 + 8+ 8 = 17 не делится на 9 — значит на месте звёздочки не может быть цифра 8;
- если вместо звёздочки поставить 9, то получим чётное число 198, а 1 + 9 + 8 = 18 делится на 9 — значит на месте звёздочки может быть цифра 9.

Ответ: вместо звездочки можно поставить цифру 0 или 9.
159. Запишите число 19 в виде суммы трёх простых чисел.
19 = 3 + 5 + 11
160. Если к некоторому двузначному числу справа дописать нуль, то данное число увеличится на 432. Найдите это число.
Пусть х — искомое двузначное число, тогда 10х — число, которое получиться из искомого, если справа к нему дописать нуль. Мы знаем, что 10х на 432 больше, чем х. Можем составить уравнение:
Значит искомое число равно 48.
Ответ: 48.
161. Найдите числа, которых недостаёт в цепочке вычислений:
Составим уравнения и решим их:
Ответ: a = 0,05; b = 0,34; c = 0,04.
Составим уравнения и решим их:
Ответ: a = 1,5; x = 0,4; y = 0,05.
Задача от мудрой совы
162. Барон Мюнхгаузен рассказывал, что он разрезал арбуз на четыре части, а после того, как его съели, осталось пять корок. Может ли такое быть, если корки не ломать?
Может ли такое быть, если корки не ломать?
Да, это возможно. Для того, чтобы разрезать арбуз на 4 части, а потом получить 5 корок, надо:
- вырезать сердцевину арбуза, например в виде цилиндра (на рисунке обозначено красными линиями), чтобы после того, как этот кусок будет съеден, осталось 2 корки — верхняя и нижняя;
- разрезать оставшуюся часть арбуза ещё на 3 части (на рисунке линии разрезов обозначены синим).
Итого получиться:
- 4 куска — 1 центральный и 3 боковых
- 5 корок — верхняя, нижняя и 3 боковых.
Ответ: да, это возможно.
- Ответы к учебнику для 6 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Как перевести к общему знаменателю. Приведение дроби к наименьшему общему знаменателю: правило, примеры решений
Схема приведения к общему знаменателю
- Нужно определить, какое будет наименьшее общее кратное для знаменателей дробей.
 Если Вы имеете дело со смешанным или целым числом, то его нужно сначала превратить в дробь, а уже потом определять наименьшее общее кратное. Чтобы целое число превратить в дробь, нужно в числителе записать само это число, а в знаменателе — единицу. Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5.
Если Вы имеете дело со смешанным или целым числом, то его нужно сначала превратить в дробь, а уже потом определять наименьшее общее кратное. Чтобы целое число превратить в дробь, нужно в числителе записать само это число, а в знаменателе — единицу. Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5. - После этого необходимо найти дополнительный множитель, который определяется делением НОЗ на знаменатель каждой дроби.
- Последний шаг — умножение дроби на дополнительный множитель.
Важно запомнить, что приведение к общему знаменателю нужно не только для сложения или вычитания. Для сравнения нескольких дробей с разными знаменателями также необходимо сначала привести каждую из них к общему знаменателю.
Приведение дробей к общему знаменателю
Для того чтобы понять, как привести к общему знаменателю дробь, необходимо разобраться в некоторых свойствах дробей. Так, важным свойством, используемым для приведения к НОЗ, является равенство дробей. Другими словами, если числитель и знаменатель дроби умножается на число, то в результате получает дробь, равная предыдущей. В качестве примера приведём следующий пример. Для того чтобы привести дроби 5/9 и 5/6 к наименьшему общему знаменателю, нужно выполнить следующие действия:
Так, важным свойством, используемым для приведения к НОЗ, является равенство дробей. Другими словами, если числитель и знаменатель дроби умножается на число, то в результате получает дробь, равная предыдущей. В качестве примера приведём следующий пример. Для того чтобы привести дроби 5/9 и 5/6 к наименьшему общему знаменателю, нужно выполнить следующие действия:
- Сначала находим наименьшее общее кратное знаменателей. В данном случае для чисел 9 и 6 НОК будет равно 18.
- Определяем дополнительные множители для каждой из дробей. Делается это следующим образом. Делим НОК на знаменатель каждой из дробей, в результате получаем 18: 9 = 2, а 18: 6 = 3. Эти числа и будут дополнительными множителями.
- Приводим две дроби к НОЗ. Умножая дробь на число, нужно умножить и числитель, и знаменатель. Дробь 5/9 можно умножить на дополнительный множитель 2, в результате чего получится дробь, равная данной, — 10/18. То же самое делаем со второй дробью: 5/6 умножаем на 3, в результате чего получаем 15/18.

Как видим из представленного выше примера, обе дроби были приведены к наименьшему общему знаменателю. Чтобы окончательно разобраться в том, как найти общий знаменатель, необходимо освоить еще одно свойство дробей. Оно заключается в том, что числитель и знаменатель дроби можно сократить на одно и то же число, которое называется общим делителем. Например, дробь 12/30 можно сократить до 2/5, если разделить ее на общий делитель — число 6.
Как приводить дроби к общему знаменателю
Если у обыкновенных дробей одинаковые знаменатели, то говорят, что эти дроби приведены к общему знаменателю .
Пример 1
Например, дроби $\frac{3}{18}$ и $\frac{20}{18}$ имеют одинаковые знаменатели. Говорят, что они имеют общий знаменатель $18$. Дроби $\frac{1}{29}$, $\frac{7}{29}$ и $\frac{100}{29}$ имеют также одинаковые знаменатели. Говорят, что они имеют общий знаменатель $29$.
Если у дробей знаменатели не одинаковые, то их можно свести к общему знаменателю. Для этого необходимо умножить их числители и знаменатели на определенные дополнительные множители.
Пример 2
Как привести две дроби $\frac{6}{11}$ и $\frac{2}{7}$ к общему знаменателю.
Решение.
Умножим дроби $\frac{6}{11}$ и $\frac{2}{7}$ на дополнительные множители $7$ и $11$ соответственно и приведем их к общему знаменателю $77$:
$\frac{6\cdot 7}{11\cdot 7}=\frac{42}{77}$
$\frac{2\cdot 11}{7\cdot 11}=\frac{22}{77}$
Таким образом, приведением дробей к общему знаменателю называют умножение числителя и знаменателя данных дробей на дополнительные множители, которые в результате позволяют получить дроби с одинаковыми знаменателями.
Общий знаменатель
Определение 1
Любое положительное общее кратное всех знаменателей некоторого набора дробей называют общим знаменателем .
Другими словами, общий знаменатель заданных обыкновенных дробей – любое натуральное число, которое можно разделить на все знаменатели заданных дробей.
Из определения вытекает бесконечное множество общих знаменателей данного набора дробей.
Пример 3
Найти общие знаменатели дробей $\frac{3}{7}$ и $\frac{2}{13}$.
Решение .
Данные дроби имеют знаменатели, равные $7$ и $13$ соответственно. Положительные общие кратные чисел $2$ и $5$ равны $91, 182, 273, 364$ и т.д.
Любое из этих чисел можно использовать в качестве общего знаменателя дробей $\frac{3}{7}$ и $\frac{2}{13}$.
Пример 4
Определить, можно ли дроби $\frac{1}{2}$, $\frac{16}{7}$ и $\frac{11}{9}$ привести к общему знаменателю $252$.
Решение.
Чтобы определить, как привести дробь к общему знаменателю $252$, необходимо проверить является ли число $252$ общим кратным знаменателей $2, 7$ и $9$. Для этого разделим число $252$ на каждый из знаменателей:
$\frac{252}{2}=126,$ $\frac{252}{7}=36$, $\frac{252}{9}=28$.
Число $252$ делится нацело на все знаменатели, т.е. является общим кратным чисел $2, 7$ и $9$. Значит, данные дроби $\frac{1}{2}$, $\frac{16}{7}$ и $\frac{11}{9}$ можно свести к общему знаменателю $252$.
Ответ: можно.
Наименьший общий знаменатель
Определение 2
Среди всех общих знаменателей заданных дробей можно выделить наименьшее натуральное число, которое называют наименьшим общим знаменателем .
Т.к. НОК – наименьший положительный общий делитель данного набора чисел, то НОК знаменателей заданных дробей является наименьшим общим знаменателем данных дробей.
Следовательно, чтобы найти наименьший общий знаменатель дробей, нужно найти НОК знаменателей этих дробей.
Пример 5
Заданы дроби $\frac{4}{15}$ и $\frac{37}{18}$. Найти их наименьший общий знаменатель.
Решение .
Знаменатели данных дробей равны $15$ и $18$. Найдем наименьший общий знаменатель как НОК чисел $15$ и $18$. Используем для этого разложение чисел на простые множители:
$15=3\cdot 5$, $18=2\cdot 3\cdot 3$
$НОК(15, 18)=2\cdot 3\cdot 3\cdot 5=90$.
Ответ: $90$.
Правило приведения дробей к наименьшему общему знаменателю
Чаще всего при решении задач алгебры, геометрии, физики и т. п. принято обыкновенные дроби приводить к наименьшему общему знаменателю, а не к любому общему знаменателю.
п. принято обыкновенные дроби приводить к наименьшему общему знаменателю, а не к любому общему знаменателю.
Алгоритм :
- С помощью НОК знаменателей заданных дробей найти наименьший общий знаменатель.
- 2.Вычислить дополнительный множитель для заданных дробей. Для этого найденный наименьший общий знаменатель необходимо разделить на знаменатель каждой дроби. Полученное число и будет дополнительным множителем данной дроби.
- Умножить на найденный дополнительный множитель числитель и знаменатель каждой дроби.
Пример 6
Найти наименьший общий знаменатель дробей $\frac{4}{16}$ и $\frac{3}{22}$ и привести к нему обе дроби.
Решение.
Воспользуемся алгоритмом приведения дробей к наименьшему общему знаменателю.
Вычислим наименьшее общее кратное чисел $16$ и $22$:
Разложим знаменатели на простые множители: $16=2\cdot 2\cdot 2\cdot 2$, $22=2\cdot 11$.
$НОК(16, 22)=2\cdot 2\cdot 2\cdot 2\cdot 11=176$.
Вычислим дополнительные множители для каждой дроби:
$176\div 16=11$ – для дроби $\frac{4}{16}$;
$176\div 22=8$ – для дроби $\frac{3}{22}$.
Умножим числители и знаменатели дробей $\frac{4}{16}$ и $\frac{3}{22}$ на дополнительные множители $11$ и $8$ соответственно. Получим:
$\frac{4}{16}=\frac{4\cdot 11}{16\cdot 11}=\frac{44}{176}$
$\frac{3}{22}=\frac{3\cdot 8}{22\cdot 8}=\frac{24}{176}$
Обе дроби приведены к наименьшему общему знаменателю $176$.
Ответ: $\frac{4}{16}=\frac{44}{176}$, $\frac{3}{22}=\frac{24}{176}$.
Иногда для того, чтобы находить наименьший общий знаменатель, нужно провести ряд трудоемких вычислений, что может не оправдывать цель решения задачи. В таком случае можно воспользоваться наиболее простым способ – свести дроби к общему знаменателю, который представляет собой произведение знаменателей данных дробей.
Приведение дробей к общему знаменателю
Дроби И имеют одинаковые знаменатели. Говорят, что они имеют общий знаменатель 25. Дроби и имеют разные знаменатели, но их можно привести к общему знаменателю с помощью основного свойства дробей. Для этого найдем число, которое делится на 8 и на 3, например, 24. Приведем дроби к знаменателю 24, для этого умножим числитель и знаменатель дроби на дополнительный множитель 3. Дополнительный множитель обычно пишут слева над числителем:
Приведем дроби к знаменателю 24, для этого умножим числитель и знаменатель дроби на дополнительный множитель 3. Дополнительный множитель обычно пишут слева над числителем:
Умножим числитель и знаменатель дроби на дополнительный множитель 8:
Приведем дроби и к общему знаменателю. Чаще всего дроби приводят к наименьшему общему знаменателю, который является наименьшим общим кратным знаменателей данных дробей. Так как НОК (8, 12) = 24, то дроби можно привести к знаменателю 24. Найдем дополнительные множители дробей: 24:8 = 3, 24:12 = 2. Тогда
К общему знаменателю можно приводить несколько дробей.
Пример. Приведем дроби к общему знаменателю. Так как 25 = 5 2 , 10 = 2 5, 6 = 2 3, то НОК (25, 10, 6) = 2 3 5 2 = 150.
Найдем дополнительные множители дробей и приведем их к знаменателю 150:
Сравнение дробей
На рис. 4.7 изображен отрезок АВ длины 1. Он разделен на 7 равных частей. Отрезок АС имеет длину , а отрезок AD имеет длину .
Длина отрезка AD больше длины отрезка AС т. е. дробь больше дроби
е. дробь больше дроби
Из двух дробей с общим знаменателем больше та, у которой числитель больше, т. е.
Например, или
Чтобы сравнить любые две дроби, их приводят к общему знаменателю, а затем применяют правило сравнения дробей с общим знаменателем.
Пример. Сравнить дроби
Решение. НОК (8, 14) = 56. Тогда Так как 21 > 20, то
Если первая дробь меньше второй, а вторая меньше третьей, то первая меньше третьей.
Доказательство. Пусть даны три дроби. Приведем их к общему знаменателю. Пусть после этого они будут иметь вид Так как первая дробь меньше
второй, то r
Дробь называется правильной , если ее числитель меньше знаменателя.
Дробь называется неправильной , если ее числитель больше знаменателя или равен ему.
Например, дроби-правильные, а дроби -неправильные.
Правильная дробь меньше 1, а неправильная дробь больше или равна 1.
На этом уроке мы рассмотрим приведение дробей к общему знаменателю и решим задачи по этой теме. Дадим определение понятию общего знаменателя и дополнительного множителя, вспомним о взаимно простых числах. Дадим определение понятию наименьший общий знаменатель (НОЗ) и решим ряд задач на его нахождение.
Дадим определение понятию общего знаменателя и дополнительного множителя, вспомним о взаимно простых числах. Дадим определение понятию наименьший общий знаменатель (НОЗ) и решим ряд задач на его нахождение.
Тема: Сложение и вычитание дробей с разными знаменателями
Урок: Приведение дробей к общему знаменателю
Повторение. Основное свойство дроби.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Например, числитель и знаменатель дроби можно разделить на 2. Получим дробь . Эту операцию называют сокращением дроби. Можно выполнить и обратное преобразование, умножив числитель и знаменатель дроби на 2. В этом случае говорят, что мы привели дробь к новому знаменателю. Число 2 называют дополнительным множителем.
Вывод. Дробь можно привести к любому знаменателю кратному знаменателю данной дроби. Для того чтобы привести дробь к новому знаменателю, ее числитель и знаменатель умножают на дополнительный множитель.
1. Приведите дробь к знаменателю 35.
Число 35 кратно 7, то есть 35 делится на 7 без остатка. Значит, это преобразование возможно. Найдем дополнительный множитель. Для этого разделим 35 на 7. Получим 5. Умножим на 5 числитель и знаменатель исходной дроби.
2. Приведите дробь к знаменателю 18.
Найдем дополнительный множитель. Для этого разделим новый знаменатель на исходный. Получим 3. Умножим на 3 числитель и знаменатель данной дроби.
3. Приведите дробь к знаменателю 60.
Разделив 60 на 15, получим дополнительный множитель. Он равен 4. Умножим числитель и знаменатель на 4.
4. Приведите дробь к знаменателю 24
В несложных случаях приведение к новому знаменателю выполняют в уме. Принято только указывать дополнительный множитель за скобочкой чуть правее и выше исходной дроби.
Дробь можно привести к знаменателю 15 и дробь можно привести к знаменателю 15. У дробей и общий знаменатель 15.
Общим знаменателем дробей может быть любое общее кратное их знаменателей. Для простоты дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Для простоты дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Пример. Привести к наименьшему общему знаменателю дроби и .
Сначала найдем наименьшее общее кратное знаменателей данных дробей. Это число 12. Найдем дополнительный множитель для первой и для второй дроби. Для этого 12 разделим на 4 и на 6. Три — это дополнительный множитель для первой дроби, а два — для второй. Приведем дроби к знаменателю 12.
Мы привели дроби и к общему знаменателю, то есть мы нашли равные им дроби, у которых один и тот же знаменатель.
Правило. Чтобы привести дроби к наименьшему общему знаменателю, надо
Во-первых, найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
Во-вторых, разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель.
В-третьих, умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
а) Привести к общему знаменателю дроби и .
Наименьший общий знаменатель равен 12. Дополнительный множитель для первой дроби — 4, для второй — 3. Приводим дроби к знаменателю 24.
б) Привести к общему знаменателю дроби и .
Наименьший общий знаменатель равен 45. Разделив 45 на 9 на 15, получим, соответственно, 5 и 3. Приводим дроби к знаменателю 45.
в) Привести к общему знаменателю дроби и .
Общий знаменатель — 24. Дополнительные множители, соответственно, — 2 и 3.
Иногда бывает трудно подобрать устно наименьшее общее кратное для знаменателей данных дробей. Тогда общий знаменатель и дополнительные множители находят с помощью разложения на простые множители.
Привести к общему знаменателю дроби и .
Разложим числа 60 и 168 на простые множители. Выпишем разложение числа 60 и добавим недостающие множители 2 и 7 из второго разложения. Умножим 60 на 14 и получим общий знаменатель 840. Дополнительный множитель для первой дроби — это 14. Дополнительный множитель для второй дроби — 5. Приведем дроби к общему знаменателю 840.
Дополнительный множитель для второй дроби — 5. Приведем дроби к общему знаменателю 840.
Список литературы
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. — М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс. — ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О. и др. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.
Можно скачать книги, указанные в п.1.2. данного урока.
Домашнее задание
Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. — М.: Мнемозина, 2012. (ссылка см. 1.2)
Домашнее задание: №297, №298, №300.
Другие задания: №270, №290
В данной статье рассказывается, как привести дроби к общему знаменателю и как найти наименьший общий знаменатель. Приведены определения, дано правило приведения дробей к общему знаменателю и рассмотрены практические примеры.
Что такое приведение дроби к общему знаменателю?
Обыкновенные дроби состоят из числителя — верхней части, и знаменателя — нижней части. Если дроби имеют одинаковый знаменатель, говорят, что они приведены к общему знаменателю. Например, дроби 11 14 , 17 14 , 9 14 имеют одинаковый знаменатель 14 . Другими словами, они приведены к общему знаменателю.
Если же дроби имеют разные знаменатели, то их всегда можно привести к общему знаменателю при помощи нехитрых действий. Чтобы сделать это, нужно числитель и знаменатель умножить на определенные дополнительные множители.
Очевидно, что дроби 4 5 и 3 4 не приведены к общему знаменателю. Чтобы это сделать, нужно с использованием дополнительных множителей 5 и 4 привести их к знаменателю 20. Как именно сделать это? Умножим числитель и знаменатель дроби 4 5 на 4 , а числитель и знаменатель дроби 3 4 умножим на 5 . Вместо дробей 4 5 и 3 4 получим соответственно 16 20 и 15 20 .
Как именно сделать это? Умножим числитель и знаменатель дроби 4 5 на 4 , а числитель и знаменатель дроби 3 4 умножим на 5 . Вместо дробей 4 5 и 3 4 получим соответственно 16 20 и 15 20 .
Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю — это умножение числителей и знаменателей дробей на такие множители, что в результате получаются идентичные дроби с одинаковым знаменателем.
Общий знаменатель: определение, примеры
Что такое общий знаменатель?
Общий знаменатель
Общий знаменатель дробей — это любое положительное число, которое является общим кратным всех данных дробей.
Другими словами, общим знаменателем какого-то набора дробей будет такое натуральное число, которое без остатка делится на все знаменатели этих дробей.
Ряд натуральных чисел бесконечен, и поэтому, согласно определению, каждый набор обыкновенных дробей имеет бесконечное множество общих знаменателей. Иначе говоря, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.
Общий знаменатель для нескольких дробей легко найти, пользуясь определением. Пусть есть дроби 1 6 и 3 5 . Общим знаменателем дробей будет любое положительное общее кратное для чисел 6 и 5 . Такими положительными общими кратными являются числа 30, 60, 90, 120, 150, 180, 210 и так далее.
Рассмотрим пример.
Пример 1. Общий знаменатель
Можно ди дроби 1 3 , 21 6 , 5 12 привести к общему знаменателю, который равен 150 ?
Чтобы выяснить, так ли это, нужно проверить, является ли 150 общим кратным для знаменателей дробей, то есть для чисел 3 , 6 , 12 . Другими словами, число 150 должно без остатка делиться на 3 , 6 , 12 . Проверим:
150 ÷ 3 = 50 , 150 ÷ 6 = 25 , 150 ÷ 12 = 12 , 5
Значит, 150 не является общим знаменателем указанных дробей.
Наименьший общий знаменатель
Наименьшее натуральное число из множества общих знаменателей какого-то набора дробей называется наименьшим общим знаменателем.
Наименьший общий знаменатель
Наименьший общий знаменатель дробей — это наименьшее число среди всех общих знаменателей этих дробей.
Наименьший общий делитель данного набора чисел — это наименьшее общее кратное (НОК). НОК всех знаменателей дробей является наименьшим общим знаменателем этих дробей.
Как найти наименьший общий знаменатель? Его нахождение сводится к нахождению наименьшего общего кратного дробей. Обратимся к примеру:
Пример 2. Найти наименьший общий знаменатель
Нужно найти наименьший общий знаменатель для дробей 1 10 и 127 28 .
Ищем НОК чисел 10 и 28 . Разложим их на простые множители и получим:
10 = 2 · 5 28 = 2 · 2 · 7 Н О К (15 , 28) = 2 · 2 · 5 · 7 = 140
Как привести дроби к наименьшему общему знаменателю
Существует правило, которое объясняет, как привести дроби к общему знаменателю. Правило состоит из трех пунктов.
Правило приведения дробей к общему знаменателю
- Найти наименьший общий знаменатель дробей.
- Для каждой дроби найти дополнительный множитель. Чтобы найти множитель нужно наименьший общий знаменатель разделить на знаменатель каждой дроби.

- Умножить числитель и знаменатель на найденный дополнительный множитель.
Рассмотрим применение этого правила на конкретном примере.
Пример 3. Приведение дробей к общему знаменателю
Есть дроби 3 14 и 5 18 . Приведем их к наименьшему общему знаменателю.
По правилу, сначала найдем НОК знаменателей дробей.
14 = 2 · 7 18 = 2 · 3 · 3 Н О К (14 , 18) = 2 · 3 · 3 · 7 = 126
Вычисляем дополнительные множители для каждой дроби. Для 3 14 дополнительный множитель находится как 126 ÷ 14 = 9 , а для дроби 5 18 дополнительный множитель будет равен 126 ÷ 18 = 7 .
Умножаем числитель и знаменатель дробей на дополнительные множители и получаем:
3 · 9 14 · 9 = 27 126 , 5 · 7 18 · 7 = 35 126 .
Приведение нескольких дробей к наименьшему общему знаменателю
По рассмотренному правилу к общему знаменателю можно приводить не только пары дробей, но и большее их количество.
Приведем еще один пример.
Пример 4. Приведение дробей к общему знаменателю
Привести дроби 3 2 , 5 6 , 3 8 и 17 18 к наименьшему общему знаменателю.
Вычислим НОК знаменателей. Находим НОК трех и большего количества чисел:
Н О К (2 , 6) = 6 Н О К (6 , 8) = 24 Н О К (24 , 18) = 72 Н О К (2 , 6 , 8 , 18) = 72
Для 3 2 дополнительный множитель равен 72 ÷ 2 = 36 , для 5 6 дополнительный множитель равен 72 ÷ 6 = 12 , для 3 8 дополнительный множитель равен 72 ÷ 8 = 9 , наконец, для 17 18 дополнительный множитель равен 72 ÷ 18 = 4 .
Умножаем дроби на дополнительные множители и переходим к наименьшему общему знаменателю:
3 2 · 36 = 108 72 5 6 · 12 = 60 72 3 8 · 9 = 27 72 17 18 · 4 = 68 72
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
как найти для двух чисел, основные определения и примеры нахождения
Математика
12.11.21
12 мин.
При решении задач по математике в начальных классах иногда требуется найти наибольший общий делитель, или сокращенно — НОД. Однако не все учащиеся знают правильный алгоритм этой операции, а также путают ее с НОК (наименьшим общим кратным). Чтобы не совершать таких ошибок, специалисты-математики разработали универсальные алгоритмы отличия и нахождения искомых значений.
Чтобы не совершать таких ошибок, специалисты-математики разработали универсальные алгоритмы отличия и нахождения искомых значений.
Оглавление:
- Признаки делимости
- Разложение на простые элементы
- Нахождение НОД
- Определение НОК
При решении задач по математике в начальных классах иногда требуется найти наибольший общий делитель, или сокращенно — НОД. Однако не все учащиеся знают правильный алгоритм этой операции, а также путают ее с НОК (наименьшим общим кратным). Чтобы не совершать таких ошибок, специалисты-математики разработали универсальные алгоритмы отличия и нахождения искомых значений.
Общие сведения
Специалисты перед обучением рекомендуют составить список базовых знаний, необходимых для нахождения наибольшего общего делителя и наименьшего общего кратного. Он состоит из таких элементов:
- Определения величин.

- Признаки делимости чисел.
- Разложение на простые элементы или множители.
- Алгоритмы или методики нахождения.
НОД — максимальное значение величины, на которую делятся 2 или большее количество чисел. НОК — параметр, характеризующий наименьшее общее делимое. Чтобы понять разницу между этими терминами, нужно разобрать операцию деления двух чисел.
Первый элемент — делимое, т. е. оно делится на определенный элемент (делитель). Результатом является частное. Математики называют последнее частным двух или более значений. Далее нужно разобрать признаки делимости.
Признаки делимости
В математике существуют 2 понятия: цифры и числа. Главное отличие — при комбинации цифр получаются числа. Кроме того, каждое значение состоит из разрядов (единиц, десятков, сотен, тысяч). Последние читаются слева направо, т. е. 657 состоит из единиц (7), десятков (5) и сотен (6). Если объединить их, получится искомая величина. Операция имеет такой вид: 7+50+600=657.
Если объединить их, получится искомая величина. Операция имеет такой вид: 7+50+600=657.
Признаками делимости называются критерии, на основании которых число можно разделить на искомое значение без остатка. К ним относятся следующие правила:
- R (любое действительное число).
- Последняя цифра — четная, т. е. 24/2 — делится, т. к. 4 — четное.
- Сумма цифр, составляющих число, возможно разделить на 3. Пример: 36/3={3+6=9/3=9}=12.
- Последние 2 цифры можно разделить на 4, т. е. 844/4={44/4=11}=211.
- Последний разряд эквивалентен одному из двух значений (0 или 5), 810/5={0}=162.
- Для числа 6 одновременно выполняются второй и третий пункт. Пример: 96/6={6-четное} и {9+6=15/3=15}=16.
- 7: расчет по формуле [a*b*c*d+e]/7, где e — разряд единиц, а все остальные (слева направо) — десятки, сотни, тысячи и десятки тысяч. Правило справедливо и для величин с разным количеством разрядов. Пример: 861/7={(8*6+1)/7=49/7=7}=123.

- Деление на 8 осуществляется по второму и четвертому признакам одновременно, т. е. 184/8={4 — четное} и {84/4=21}=23.
- Сумму разрядов можно разделить на 9. Пример: 108/9={1+0+8=9/9=1}=12.
- Последняя цифра эквивалентна 0, т. е. 140/10={0}=14.
- 2 разряда равны между собой (11, 22, 33 и т. д. ) или величина, образованная разрядами сотен и десятков без единиц, делится на 11 (121={(12−1)/11=1}).
Однако признаков делимости недостаточно для перехода к соответствующим алгоритмам. Следующий этап — разложение числа на простые элементы натурального типа.
Разложение на простые элементы
Простые множители — числа, которые делятся только на единицу или на эквивалентную величину, т. е. 7/1 и 7/7. Разложение величины на простые элементы — найти совокупность чисел, произведение которых и будет составлять искомое значение. Например, 30=3*5*2. Для выполнения этой операции математики разработали специальный алгоритм:
- Написать значение.

- Определить по признакам делимости первый множитель.
- Выполнить операцию деления.
- Подобрать второй множитель для величины, полученной в 3 пункте.
- Реализовать пункты со 2 по 4 включительно.
Однако для понимания принципа работы алгоритма, нужно выполнить разложение на простые значения на практике. Например, для 176 реализация методики имеет следующий вид:
- 176.
- 2: 176/2=88.
- 11: 88/11=8.
- 2: 8/2=4.
- 2: 4/2=2.
- 2: 2/2=1.
Следовательно, 176=2*11*2*2*2. Однако результат можно записать в более упорядоченной форме: 176=11*2*2*2*2*2. Далее следует перейти к алгоритмам, посредством которых можно вычислить НОК и НОД.
Нахождение НОД
Найти НОД двух чисел можно следующими способами: разложением на простые множители или посредством алгоритма Евклида. Первый имеет такой вид:
- Раскладываются первое и второе значения на простые множители.

- Выбираются общие множители и перемножаются между собой.
Для реализации методики на практике нужно разобрать нахождение НОД 86 и 92. Она имеет такой вид:
- 92: 92/2=46/2=23, т. е. 92=23*2*2.
- 86: 86/2=43*2.
- НОД: 2.
Наиболее простой является методика Евклида для нахождения НОД. Она позволяет быстро найти искомое значение и имеет такой вид:
- Разделить большее значение на меньшее (записать отдельно целую часть и остаток).
- Если есть остаток, искомое большое число нужно на него разделить.
- Выполнять пункты алгоритма, пока остаток не будет равным 0. Результат — это и есть НОД.
Чтобы понять смысл, нужно применить ее к числам 92 и 86. Это выглядит следующим образом:
- 92/86=1{6}.
- 86/6=14{2}.
- 14/2=7{0}.
- НОД=2, т. к. в третьем пункте нет остатка от деления.
Далее нужно рассмотреть методику нахождения НОК, чтобы окончательно понять отличие от НОД.
Определение НОК
НОК находится также посредством разложения на множители, но алгоритм существенно отличается от НОД. Он имеет следующий вид:
- Разложить величины на множители.
- Взять наименьшее и дополнить его недостающими элементами.
- Вычислить искомое значение НОК.
Чтобы понять принцип работы алгоритма, его нужно реализовать на практике. Для числовых значений 18 и 12 он имеет такой вид:
- 18=3*3*2.
- 12=2*2*3.
- НОК=12*3=36.
Следовательно, наименьшим общим кратным двух чисел является 36. Искомую величину нужно находить в алгебре для приведения обыкновенных дробей к общему знаменателю при выполнении арифметических операций сложения и вычитания. Следует отметить, что операцию можно выполнять не только для двух, но и для трех чисел. При этом алгоритм существенно усложняется.
Примеры решения
Одной из сложных задач является следующая: найти наибольший общий делитель чисел 32, 66 и 84. Для решения можно воспользоваться одним из способов. Оптимальным из них является разложение на множители:
- 32=2*2*2*2*2.
- 66=11*3*2.
- 84=2*3*2*2*2*2.
- НОД=2.
По методике Евклида решать не рекомендуется, т. к. это усложнит вычисления. Основной принцип физико-математических дисциплин — оптимизация расчетов, т. е. нужно искать способ с наименьшим количеством преобразований и расчетов.
В следующей задаче требуется осуществить поиск НОД для 66, 121, 77 и 110. В этом случае также рекомендуется разложить на простые множители все 4 числа. Поиск решения выполняется по такой методике:
- 66=11*3*2.
- 121=11*11.
- 77=11*7.
- 110=11*5*2.
- НОД=11.
Если рассмотреть 2 этих примера, можно сделать вывод, что считать НОД довольно просто. Далее нужно найти НОК для 22 и 32. Это осуществляется по такой методике:
Это осуществляется по такой методике:
- 22=11*2.
- 32=8*4=2*2*2*2*2.
- НОК=11*2*2*2*2*2=22*16=352.
Еще одним типом задачи является одновременное нахождение НОД и НОК для чисел 45, 85, 94 и 96. Решение имеет следующий вид:
- 45=5*3*3.
- 85=17*5.
- 94=2*47.
- 96=2*2*3*2*2*2.
- НОД=1 (нет общих множителей, кроме единицы).
- НОК=5*3*3*17*2*47*2*2*2*2*2=1150560.
В математике встречаются более сложные задачи. Одна из них имеет такую формулировку: НОД двух чисел эквивалентен 9, первое число равно 90 и больше второго. Необходимо найти второе ближайшее целое значение. Решается задание по такому алгоритму:
- 90=9*10.
- 81=9*9.
- НОД=9.
Задача решается методом подбора, поскольку по условию ближайшая целая величина эквивалентна 81.
Таким образом, нахождение НОД является довольно простой операцией, если следовать алгоритму и иметь базовые знания.
Наибольший общий делитель чисел 11 и 17
Существует много методов, которые мы можем применить для вычисления НОД чисел 11 и 17.
В нашем первом методе мы найдем разложение чисел 11 и 17 на простые множители.
Во втором методе мы создадим список всех множителей чисел 11 и 17.
Это числа, на которые числа 11 и 17 делятся без остатка.
Когда они у нас есть, все, что нам нужно сделать, это найти тот, который является самым большим общим числом из 2 списков.
Теперь давайте рассмотрим каждый метод и рассчитаем GCF чисел 11 и 17.
- Факторизация простых чисел
- Список факторов
- Алгоритм Евклида
- Двоичный алгоритм наибольшего общего делителя
Метод 1 — Факторизация простых чисел
При использовании метода факторизации простых чисел все, что нам нужно сделать, это найти общие простые делители чисел 11 и 17, а затем умножить их. Очень просто:
Очень просто:
Шаг 1: Давайте создадим список всех простых множителей 11 и 17:
Простые делители числа 11:
Как вы можете видеть ниже, простые делители числа 11 равны 11 .
Давайте проиллюстрируем простую факторизацию 11 в экспоненциальной форме:
11 = 11 1
Простые множители 17:
Как вы можете видеть ниже, простые множители 17 равны 17 .
Давайте проиллюстрируем простую факторизацию 17 в экспоненциальной форме:
17 = 17 1
Шаг 2: Запишите список всех общих простых делителей чисел 11 и 17:
Как видно из приведенных выше блоков, общие простые делители чисел 11 и 17 равны 1 . .
Шаг 3: Все, что нам нужно сделать сейчас, это перемножить эти общие простые множители:
Найти произведение всех общих простых множителей путем их умножения:
1 1 = 1
Готово!
Согласно нашим расчетам выше, Наибольший общий делитель чисел 11 и 17 равен 1
Метод 2.
 Список делителей
Список делителейС помощью этого простого метода нам нужно найти все делители чисел 11 и 17, Факторы — это числа, которые делят другое число без остатка и просто определяют общие, а затем выбирают, какое из них больше.
Шаг 1: Создайте список всех чисел, которые делят 11 и 17 без остатка:
Список факторов, которые делят 11 без остатка:
1 и 11 .
Список факторов, которые делят 17 без остатка:
1 и 17 .
Шаг 2: Определите наибольшее общее число из двух приведенных выше списков:
Как вы можете видеть в списках множителей сверху, для чисел 11 и 17 мы выделили число 1 , а это значит, что мы нашли Наибольший Общий Делитель, или GCF.
Согласно нашим расчетам выше, Наибольший общий делитель чисел 11 и 17 равен 1
Метод 3 — алгоритм Евклида
Алгоритм Евклида говорит, что если число k является GCM 11 и 17,
тогда число k также является НОД остатка от деления чисел 11 и 17.
Мы выполняем эту процедуру до тех пор, пока напоминание не станет равным 0.
Наибольший общий делитель — это последнее ненулевое число.
Шаг 1: Рассортируйте числа в порядке возрастания:
11, 17
Шаг 2
Выньте из набора меньшее число как делитель: 11
Оставшийся набор: 17
Найдите напоминание о делении между числом и делителем
17 мод 11 = 6
Соберите делитель и все остатки и отсортируйте их в порядке возрастания. Удалите все дубликаты и 0. Наш набор:
6, 11
Повторяйте процесс, пока в наборе не останется только одно число.
Выньте из набора меньшее число как делитель: 6
Оставшийся набор: 11
Найдите напоминание о делении между числом и делителем
11 мод 6 = 5
Соберите делитель и все остатки и отсортируйте их в порядке возрастания. Удалите все дубликаты и 0. Наш набор:
5, 6
Повторяйте процесс, пока в наборе не останется только одно число.
Выньте из набора меньшее число как делитель: 5
Оставшийся набор: 6
Найдите напоминание о делении числа на делитель
6 мод 5 = 1
Соберите делитель и все остатки и отсортируйте их в порядке возрастания. Удалите все дубликаты и 0. Наш набор:
1, 5
Повторяйте процесс, пока в наборе не останется только одно число.
Выньте из набора наименьшее из делителей: 1
Оставшийся набор: 5
Найти напоминание о делении числа на делитель
5 мод 1 = 0
Соберите делитель и все остатки и отсортируйте их в порядке возрастания. Удалите все дубликаты и 0. Наш набор:
1
Шаг 3: Возьмите оставшееся число из нашего набора как алгоритм Штейна или двоичный алгоритм Евклида, представляет собой алгоритм, который вычисляет наибольший общий делитель двух неотрицательных целых чисел. Алгоритм Штейна использует более простые арифметические операции, чем обычный алгоритм Евклида; он заменяет деление арифметическими сдвигами, сравнениями и вычитанием.

Хотя алгоритм в его современной форме был впервые опубликован израильским физиком и программистом Йозефом Штайном в 1967 году, он мог быть известен во II веке до н. э. в древнем Китае.
Шаг 1: Отсортируйте числа и установите начальный GCF равным 1
Список: 11, 17
Шаг 2: Выберите первое число, 11.
Вычтите 11 из оставшихся значений и разделите результат на 2.
Удалить дубликаты и отсортировать:
(17-11)/2 = 3
Полученный список: 3, 11
Шаг 3: Выберите первое число, 3.
Вычтите 3 из оставшихся значений и разделите результат на 2.
Удалите дубликаты и отсортируйте:
(11-3)/2 = 4
Полученный список: 3, 4
Шаг 4: Разделите все оставшиеся четные значения на 2, удалите дубликаты и отсортируйте.
Повторите процесс, если в списке есть четные номера:
4/2 = 2
Результирующий список: 2, 3
2/2 = 1
Полученный список: 1, 3
Шаг 5: Выберите первое число, 1.
Вычтите 1 из оставшихся значений и разделите результат на 2.
Удалите дубликаты и отсортируйте:
(3-1)/2 = 1
Получившийся список: 1
Шаг 6: Остается только одно число, 1.
Умножьте его на ваш текущий GCF:
GCF = 1*1 = 1
Наибольший общий делитель 11 и 17 равен 1
Другие наибольшие общие делители 11
GCF 11 и 15
GCF 11 и 16
GCF 11 и 17
GCF 11 и 18
GCF 11 и 19
GCF 11 и 20
GCF 11 и 21
GCF 11 и 22
GCF 11 и 23
GCF 11 и 24
Другие наибольшие общие факторы 17
GCF 17 и 21
GCF 17 и 22
GCF 17 и 23
GCF 17 и 24
GCF 17 и 25
GCF 17 и 26
GCF 17 и 27
GCF 17 и 28
GCF 17 и 29
GCF 17 и 30
Калькулятор GCF – наибольший общий множитель (калькулятор HCF/GCD)
Примечание. GCF, GCD и HCF – это одни и те же термины, используемые для обозначения одной и той же концепции.
Калькулятор/поиск GCF вычисляет наибольший (самый высокий) общий делитель заданных чисел, используя:
- Метод списка факторов
- Метод простой факторизации
- Метод деления
- Евклидов алгоритм
- Двоичный алгоритм (Стейна)
- Перевернутое деление
Помимо HCF, он также вычисляет наименьшее общее кратное (НОК) для заданных чисел.
В следующих разделах мы обсудим методы, используемые калькулятором НОД для нахождения НОД, определение НОД, как рассчитать НОД без использования калькулятора НОД, а также несколько примеров, объясняющих, как найти наибольший общий множитель.
Что такое GCF?
Наибольший общий делитель (GCF) набора чисел — это наибольший делитель, общий для всех чисел. Он широко известен как наивысший общий фактор (HCF).
Например, 8, 12, и 16 имеют два общих фактора, которые составляют 2 и 4. . Лучшие 4. . из 8, 12, и 16 это 4.
. Лучшие 4. . из 8, 12, и 16 это 4.
Как рассчитать GCF?
Если вы уже здесь, вы можете узнать, как найти GCF . GCF можно рассчитать несколькими методами. Ниже вы можете найти различные способы расчета GCF/HCF.
1. Метод факторизации
Пример: Найдите GCF 12 и 16 , используя метод факторизации.
Решение:
Метод факторизации или списка множителей использует множители заданных чисел для нахождения наибольшего общего множителя.
Шаг 1: Перечислите все множители данных чисел.
Шаг 2: Найдите наибольший общий множитель.
Обратитесь к изображению ниже для получения дополнительной информации.
2.
 Метод деления
Метод деленияПример: Найдите GCF 30 и 42 методом пошагового деления .
Решение:
Шаг 1: Разделите наибольшее число на наименьшее.
Шаг 2: Возьмите делитель из предыдущего шага и разделите его на остаток, полученный на предыдущем шаге.
Шаг 3: Повторяйте шаги 2 и , пока остаток не станет равным нулю. Последний делитель будет наибольшим (наибольшим) общим множителем.
Используйте средство поиска HCF, указанное выше, чтобы проверить результат ручных вычислений. Обратитесь к изображению ниже для иллюстрации метода шага деления.
3. ПРАВДА ФАНТАЗИЦИЯ
Пример: Найдите GCF 24 и 36 с использованием метода основной факторизации .
Решение:
Шаг 1: Сделайте множители заданных чисел с помощью дерева множителей, как показано на рисунке ниже.
Шаг 2: Выделите или обведите общие делители данных чисел.
Шаг 3: Умножьте все общие множители, чтобы получить GCF. Если есть только один общий множитель, то нет необходимости умножать.
Калькулятор наибольшего общего делителя (знаменателя) перечисляет все шаги вычисления. Это не просто инструмент расчета. Его также можно использовать для изучения методов вычисления наибольшего общего множителя.
Таблица наибольшего общего делителя.
| GCF of 2 and 4 is | 2 |
| GCF of 2 and 5 is | 1 |
| GCF of 3 and 4 is | 1 |
| GCF of 5 and 25 is | 5 |
| GCF of 4 and 5 is | 1 |
| GCF of 16 and 24 is | 8 |
| GCF of 5 and 7 is | 1 |
| GCF of 15 and 20 это | 20 |
| GCF of 8 and 12 | 4 |
| GCF of 8,9 and 25 is | 1 |
| HCF of 2 and 3 is | 1 |
| HCF of 4 and 8 is | 4 |
| GCF of 3,4 and 6 is | 1 |
| HCF of 3 and 5 is | 1 |
| HCF of 680,510 and 340 is | 4 |
| HCF of 2 и 8 это | 2 |
| HCF of 18 and 48 is | 6 |
| HCF of 12 and 48 is | 12 |
| GCF of 30 and 42 is | 6 |
- Stapel, E.
 , 2020. LCM и GCF | Пурпурная математика.
, 2020. LCM и GCF | Пурпурная математика. - Mathforum.org. 2020.
- Analyzemath.com. 2020. Найдите наибольший общий делитель (GCF) в математике.
- Эстела, М., 2020. Нахождение наибольшего общего делителя с использованием метода списка — Чилимат. 93-8
9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92 Все множители чисел 1-100
Ниже приведен список или таблица всех множителей чисел, начиная с 1 до 100 .
 Вы можете использовать этот ресурс, чтобы быстро найти все множители первых ста (100) элементов набора счетных чисел.
Вы можете использовать этот ресурс, чтобы быстро найти все множители первых ста (100) элементов набора счетных чисел.ИНДЕКС ВСЕХ МНОЖИТЕЛЕЙ ЧИСЕЛ ОТ 1 ДО 1000
Если вы обнаружите какие-либо ошибки или опечатки в отношении факторов чисел ниже, пожалуйста, напишите мне по адресу [email protected], чтобы я мог их немедленно исправить. Благодарю вас!
Если вам нужно повторить, как найти все делители числа, пожалуйста, ознакомьтесь с моим уроком «Нахождение всех делителей числа».
Коэффициент 1: 1
Факторы 2: 1, 2
Факторы 3: 1, 3
Факторы 4: 1, 2, 4
Факторы 4: 1, 2, 4
Факторы 4: 1, 2, 4
Факторы 4: 1, 2, 4
5: 1, 5Коэффициенты 6: 1, 2, 3, 6
Коэффициенты 7: 1, 7
Коэффициенты 8: 1, 2, 4, 8
Факторы 9: 1, 3, 9
Факторы 10: 1, 2, 5, 10
Факторы 11: 1, 11
Множители 12: 1, 2, 3, 4, 6, 12
Множители 13: 1, 13
Множители 14: 1, 2, 7, 14
9008: Множители 9008 1, 3, 5, 15Коэффициенты 16: 1, 2, 4, 8, 16
Коэффициенты 17: 1, 17
Факторы 18: 1, 2, 3, 6, 9, 18
Факторы 19: 1, 19
Коэффициенты 20: 1, 2, 4, 5, 20
10, 20 9008 Множители 21: 1, 3, 7, 21
Множители 22: 1, 2, 11, 22
Множители 23: 1, 23
Множители 3, 4, 6, 8, 12, 24
Коэффициенты 25: 1, 5, 25
Коэффициенты 26: 1, 2, 13, 26
Коэффициенты 1, 3, 9, 27
Коэффициенты 28: 1, 2, 4, 7, 14, 28
Коэффициенты 29: 1, 29
9008: множители 0 30 3, 5, 6, 10, 15, 30.
 , 3, 11, 33
, 3, 11, 33Множители 34: 1, 2, 17, 34
Множители 35: 1, 5, 7, 35
Множители 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Коэффициенты 37: 1, 37
Коэффициенты 38: 1, 2, 19, 38
2 : 1, 3, 13, 39Факторы 40: 1, 2, 4, 5, 8, 10, 20, 40
Факторы 41: 1, 41
2: 1, 2, 3, 6, 7, 14, 21, 42Коэффициенты 43: 1, 43
Коэффициенты 44: 1, 2, 4, 11, 22, 44
Факторы 45: 1, 3, 5, 9, 15, 45Факторы 46: 1, 2, 23, 46
Факторы 47: 1, 47
3 908 4 Факторы 908 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Коэффициенты 49: 1, 7, 49
Коэффициенты 50: 1, 2, 5, 10, 25 , 50
Коэффициенты 51: 1, 3, 17, 51
Коэффициенты 52: 1, 2, 4, 13, 26, 52
Коэффициенты 583: 1, 2, 4, 13, 26, 520003
Коэффициенты 54: 1, 2, 3, 6, 9, 18, 27, 54
Коэффициенты 55: 1, 5, 11, 55
Коэффициенты 58: 1, 2, 086 4, 7, 8, 14, 28, 56.
 , 59
, 59Коэффициенты 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Коэффициенты 61: 1, 61
2 : 1, 2, 31, 62Коэффициенты 63: 1, 3, 7, 9, 21, 63
Коэффициенты 64: 1, 2, 4, 8, 16, 32, 3
Коэффициенты 65: 1, 5, 13, 65
Коэффициенты 66: 1, 2, 3, 6, 11, 22, 33, 66 Множители 68: 1, 2, 4, 17, 34, 68
Множители 69: 1, 3, 23, 69
Множители 70: 1, 2, 5, 7, 10, 14 , 35, 70
Коэффициенты 71: 1, 71
Коэффициенты 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Коэффициенты 9 1, 73
Коэффициенты 74: 1, 2, 37, 74
Коэффициенты 75: 1, 3, 5, 15, 25, 75
Коэффициенты 86: 1, , 19, 38, 76
Коэффициенты 77: 1, 7, 11, 77
Коэффициенты 78: 1, 2, 3, 6, 13, 26, 39, 78 Коэффициенты
2:
1, 79Факторы 80: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
Коэффициенты 81: 1, 3, 9, 90, 0 81
Коэффициенты 82: 1, 2, 41, 82
Коэффициенты 83: 1, 83
Коэффициенты 84: 1, 2, 3, 4, 6, 14, 12 , 28, 42, 84
Множители 85: 1, 5, 17, 85
Множители 86: 1, 2, 43, 86
9, 3087 Множители 87: 1, 2, 43, 86 87
Коэффициенты 88: 1, 2, 4, 8, 11, 22, 44, 88
Коэффициенты 89: 1, 89 6, 9, 10, 15, 18, 30, 45, 90.

Факторы 93: 1, 3, 31, 93
Факторы 94: 1, 2, 47, 94
Факторы 95: 1, 5, 19, 95
Факторы 1, 5, 19, 95
.6: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96Коэффициенты 97: 1, 97
Коэффициенты 98: 1, 2, 7 , 14, 49, 98
Коэффициенты 99: 1, 3, 9, 11, 33, 99
Коэффициенты 100: 1, 2, 4, 5, 10, 20, 25, 50, 100
Вас также может заинтересовать:
Нахождение всех делителей числа методом радуги
Числа, кратные 1-100
Наибольший общий делитель. Наименьшее общее кратное. Полный курс арифметики
Навыки
в н
А Р И Т М Е Т И КСодержание | Главная | Введение
Урок 33
Наибольший общий делитель
Наименьшее общее кратное
Теперь мы узнаем, как найти наибольший общий делитель и наименьшее общее кратное двух чисел из их простых факторизаций.
 (Мы видели, как найти LCM непосредственно в Уроке 23.)
(Мы видели, как найти LCM непосредственно в Уроке 23.)Во-первых, давайте посмотрим, как найти все делители числа из его простых множителей.
Мы говорим, что одно число является делителем секунды, когда второе является его кратным. 4 является делителем 36, потому что 36 кратно 4. Мы можем видеть, что в простых множителях 36:
36 = 2 × 2 × 3 × 3.
Помимо порядка, 36 = 9 × 4.
4 является делителем 36. (И 9 тоже.)
Все делители числа можно найти из его простых множителей.
Пример 1. Вот простая факторизация числа 60:
.60 = 2 × 2 × 3 × 5.
Беря эти простые числа по одному, затем по два, затем по три и так далее, мы можем построить все делители числа 60.
По отдельности: 2, 3, 5 и 1.
Не забудьте 1. Хотя 1 не простое число, 1 является делителем любого числа.
Два одновременно: 2 × 2, 2 × 3, 2 × 5, 3 × 5.
То есть: 4, 6, 10, 15.

Три одновременно: 2 × 2 × 3, 2 × 2 × 5, 2 × 3 × 5.
То есть: 12, 20, 30.
Все четыре: 2 × 2 × 3 × 5 = 60.
Это все делители числа 60. 60 кратно каждому из них.
Задача 1. Напишите разложение числа 180 на простые множители. Затем постройте все его делители.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!180 = 2 × 2 × 3 × 3 × 5.
По отдельности: 2, 3, 5 и 1.
Два за раз: 2 × 2, 2 × 3, 2 × 5, 3 × 3, 3 × 5.
Три одновременно: 2 × 2 × 3, 2 × 2 × 5, 2 × 3 × 3, 2 × 3 × 5,
3 × 3 × 5.Четыре сразу: 2 × 2 × 3 × 3, 2 × 2 × 3 × 5, 2 × 3 × 3 × 5.
Все пять: 2 × 2 × 3 × 3 × 5
Эти номера:
1 2 3 5 4 6 10 9 15 12 20 18 30 45 36 60 90 180
Задача 2.
 Некоторое число не делится на 3. Поэтому почему оно не делится на 12?
Некоторое число не делится на 3. Поэтому почему оно не делится на 12?Поскольку 12 = 2 × 2 × 3, то любое число, которое делится на 12, то есть кратно 12, должно иметь 3 в качестве простого делителя.
Наибольший общий делитель
Вот все делители 12:
1, 2, 3, 4, 6, 12.
Вот все делители 20:
1, 2, 4, 5, 10, 20.
Какие числа являются общими делителями 12 и 20?
1, 2, 4.
Какое число является их наибольшим общим делителем?
4.
Задача 3. Какое число является наибольшим общим делителем каждой пары?
а) 6, 9. 3 б) 8, 12. 4 в) 16, 40. 8 г) 7, 14. 7 д) 4, 20.  4
4е) 6, 42. 6 ж) 5, 11. 1 ч) 6, 35. 1 и) 1, 12. 1 Задача 4. Какие простые делители являются общими для этих двух чисел?
2 × 2 × 2 × 5 и 2 × 5 × 5
2 × 5
2 × 5 — это их наибольший общий делитель.
Ибо мы можем построить делители числа из его простых множителей. Из простых чисел каждого числа можно составить делитель 2 × 5.
Наибольший общий делитель двух чисел — это наибольшее произведение простых чисел, которые являются общими для этих двух чисел.
Задача 5. Найти наибольший общий делитель каждой пары.
а) 3 × 11 и 11 × 13. 11 б) 5 × 7 × 7 и 5 × 5 × 7.  5 × 7
5 × 7c) 2 × 3 × 7 и 5 × 7 × 7 × 11. 7
d) 2 × 2 × 2 × 3 × 5 × 5 и 2 × 3 × 3 × 5 × 5 × 5 × 7.
2 × 3 × 5 × 5
У них одна двойка, одна тройка и две пятерки.
д) 3 × 7 и 11 × 29. 1
Эти числа не имеют простых чисел. Но 1 — это общий делитель каждой пары чисел. В данном случае это их единственный и наибольший общий делитель.
е) 5 × 5 и 5 × 5 × 5 × 5 × 5. 5 × 5
Задача 6. Найдите наибольший общий делитель каждой пары.
а) 45 и 75. 15 б) 42 и 63. 21 в) 30 и 77. 1 Задача 7.
а) Каков наибольший общий делитель чисел 12 и 35? 1
1 — общий делитель каждой пары чисел. Но когда 1 является их единственным и, следовательно, их наибольшим общим делителем, мы говорим, что эти числа взаимно просты.
 Итак, 12 и 35 не простые числа, а 9.2081 относительно простых.
Итак, 12 и 35 не простые числа, а 9.2081 относительно простых.b) Запишите простые факторизации чисел 12 и 35.
12 = 2 × 2 × 3, 35 = 5 × 7,
c) Какие основные факторы у них общие? Никто.
Вот как распознать, когда два числа взаимно просты.
Задача 8. Какие из этих пар взаимно просты?
а) 6 и 35. Да. б) 6 и 21. № в) 8 и 27. Да. г) 13 и 91. № д) 9 и 20. Да. е) 1 и 16. Да. Наименьшее общее кратное
Мы видели примеры того, что мы подразумеваем под наименьшим общим кратным, в Уроке 23. Мы также видели способ его найти.
Задача 9.
 Какое число является наименьшим общим кратным каждой пары?
Какое число является наименьшим общим кратным каждой пары?а) 9 и 12. 36 б) 6 и 8. 24 в) 10 и 12. 60 г) 3 и 15. 15 д) 4 и 24. 24 е) 11 и 55. 55. ж) 2 и 3. 6 ч) 5 и 8. 40 и) 8 и 9. 72 Задача 10. Назовите наименьшее общее кратное (НОК) каждой пары. Затем назовите их наибольший общий делитель (НОД).
а) 12 и 16. НЦМ = 48. НОД = 4,
б) 15 и 20. НЦМ = 60. НОД = 5.
c) 13 и 39. НЦМ = 39. НОД = 13.
г) 5 и 8.
 НЦМ = 40. НОД = 1.
НЦМ = 40. НОД = 1.д) 20 и 24. НЦМ = 120. НОД = 4.
Задача 11. Какое число является наименьшим общим кратным 6, 8 и 10? 120
Теперь мы увидим, как найти НОК, записав простые факторизации.
Пример 2. Вот простые факторизации 24 и 20.
24 = 2 × 2 × 2 × 3, 20 = 2 × 2 × 5,
Теперь каждое кратное этих чисел будет иметь свою собственную разложение на простые множители. Факторизация числа, кратного 24, будет содержать все простые числа 24, а число, кратное 20, будет содержать все простые числа 20. обычное число, кратное , будет содержать все простые числа каждого из них. Их наименьшее общее кратное будет наименьшим произведением, которое содержит все простые числа каждого числа.
Вот он:
НОК = 2 × 2 × 2 × 3 × 5.
Мы взяли наибольшее каждого простого числа из двух чисел: три двойки из 24, одна 3 из 24 и одна 5 из 20. 2 × 3 и
2 × 2 × 5.
Чтобы вычислить это число, порядок факторов не имеет значения. (Урок 9.) Поэтому давайте воспользуемся преимуществом 2 × 5 = 10. Мы сгруппируем факторы следующим образом:
(2 × 5) × (2 × 2 × 3) = 10 × 12 = 120.
Задача 12. Постройте наименьшее общее кратное следующих чисел.
а) 2 × 3 и 3 × 5. НОК = 2 × 3 × 5 = 30.
б) 3 × 3 × 5 и 3 × 5 × 5. НОК = 3 × 3 × 5 × 5 = 225,
c) 2 × 3 × 5 × 5. и 2 × 2 × 2 × 5 × 7.
c) НОК = 2 × 2 × 2 × 3 × 5 × 5 × 7 = 4200.
d) 2 × 2 и 2 × 2 × 2. LCM = 2 × 2 × 2 = 8,
д) 7 и 11. НОК = 7 × 11 = 77,
f) 2 × 3 и 5 × 7. LCM = 2 × 3 × 5 × 7 = 210,
г) 2 × 5, 7 × 11 и 5 × 11. НОК = 2 × 5 × 7 × 11 = 770,
Задача 13. Найдите наименьшее общее кратное каждой пары.
а) 21 и 33. 3 × 7 × 11 = 231,
б) 65 и 39. 195 в) 54 и 75.  1350
1350г) 6 и 77. 462 д) 17 и 33. 561 Задача 14. Найдите наименьшее общее кратное числа
.а) 6, 8 и 10. 2 × 2 × 2 × 3 × 5 = 120. Сравните задачу 11.
б) 14, 35 и 55. 770.
Задача 15. 15 и какие другие числа имеют наименьшее общее кратное 60?
60 = 2 × 2 × 3 × 5. Поскольку 15 = 3 × 5, то каждое из остальных чисел должно иметь 2 × 2. Вот эти числа:
.2 × 2 = 4,
2 × 2 × 3 = 12,
2 × 2 × 5 = 20,
2 × 2 × 3 × 5 = 60,
Введение | Главная | Содержание
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: teacher@themathpage.
 com
comПримеры наибольшего общего делителя (НОД)
В математике наибольшим общим делителем двух или более чисел является наибольшее положительное целое число x, которое делит оба заданных числа. Наибольший общий фактор дополнительно упоминается как GCF. В этом Наибольшее можно заменить на Высшее, а множитель можно заменить на Делитель. Таким образом, GCF также известен как HCF (самый высокий общий делитель), наибольший общий делитель (GCD) и наибольший общий делитель (HCD).
На этой странице для лучшего понимания мы будем предоставлять различные вопросы с кратким объяснением здесь. В этой статье мы рассмотрели различные вопросы о наибольшем общем факторе (GCF) для улучшения их навыков, а также для лучшей практики. GCF чаще всего используется с дробями, которые широко используются в повседневной жизни.
См. также:
- Наибольший общий делитель
- Примеры старшего общего делителя
- Рабочий лист по HCF и LCM
Примеры нахождения наибольшего общего делителя (НОД)
Задача 1:
Найдите НОД чисел 72 и 81.
Решение:
Учитывая значения 72 и 81. .
Итак, делители числа 72 равны 1, 2, 3, 4, 6, 8, 9, 12, 18.
Делители числа 81 равны 1, 3, 9, 27.
Итак, общие делители числа 72, 81 равны 1, 3, 9.
Далее запишите, что наибольший общий делитель среди них равен 9.
Таким образом, наибольший общий делитель данных чисел равен 9.Задача 2:
Каков наибольший общий делитель (НОД) чисел 11, 121, 143?Решение:
Как указано в вопросе, значения равны 11, 121, 143.
Теперь найдем наибольший общий множитель. Итак, сначала напишите общие факторы.
Делители числа 11 равны 1, 11
Делители числа 121 равны 1, 11
Делители числа 143 равны 1, 11,
Общие делители числа 11, 121, 143 равны 1, 11.
Следовательно, наибольший общий делитель среди них 11,Задача 3:
Запишем наибольший множитель чисел 15 и 35.Решение:
Учитывая значения,
Сначала мы должны перечислить множители 15 и 35, а затем найти общие множители .
Теперь запишите, что делители числа 15 равны 1, 3, 5 и 15.
Делители числа 35 равны 1, 5, 7.
Общие делители чисел 15 и 35 равны 1, 5.
Среди этих чисел 5 наибольшее (наибольшее) число.
Таким образом, GCF 15 и 35 равен 5. Это записывается как GCF(15, 35) = 5,Задача 4:
Чему равен GCF числа 26, 62?Решение:
Учитывая значения 26 и 62.
Теперь напишите множители.
Делители числа 26 равны 1, 2, 13.
Делители числа 62 равны 1, 2.
Итак, общие делители равны 1, 2.
Среди них Наибольший (наибольший) делитель равен 2.
Следовательно, Наибольший общий делитель чисел 26 и 62 равен 2.Задача 5:
Найдите GCF (наибольший общий делитель) чисел 48, 148 и 36, используя разложение на простые множители.Решение:
Учитывая, что значения для нахождения GCF равны 48, 148 и 36.
Используя простую факторизацию, теперь запишите множители.
Итак, делители числа 48 равны 2 x 2 x 2 x 6.
Делители числа 148 равны 2 x 2 x 37.
Делители числа 36 равны 2 x 2 x 3 x 3.
Общие делители равны 2 x 2 = 4
Таким образом, GCF заданных чисел равен 4.Практикуйтесь в математике онлайн с неограниченным количеством вопросов, представленных в листах заданий по математике 5-го класса, и быстро станьте расцветающим математиком.
Задача 6:
Каков наибольший общий делитель числа 45 120?Решение:
Учитывая значения 45, 120.
Теперь мы должны записать делители 45 равны 1, 3, 5, 9, 15.
Делители 120 равны 1, 2, 3, 4 , 5, 6, 8, 10, 12, 15.
Следовательно, общие делители чисел 45 и 120 равны 1, 3, 5 и 15.
Следовательно, наибольший общий делитель (НОД) или НОД заданных чисел равен 15.Задача 7:
Напишите наибольшие общие делители чисел 77, 99, 121?Решение:
Даны значения 77, 99 и 121.
Сначала запишите общий множитель.
Множители числа 77 равны 1, 7 и 11.
Множители числа 99 равны 1, 3, 11.
Множители числа 121 равны 1, 11
Следовательно, общие делители равны 1, 11.
Итак, наибольшее Общий делитель (GCF) 77, 99 и 121 равен 11.Задача 8:
Две трубы длиной 32 м и 36 м. Трубы разрезаются на куски одинаковой длины. Найдите максимальную длину трубы каждого куска.Решение:
Как указано в вопросе,
Длина двух труб 32м и 36м.
GCF – необходимая длина каждого отрезка трубы.
32 = 2 x 16
36 = 2 x 28
Общий наибольший множитель равен 2.
Следовательно, требуемая максимальная длина трубы для каждого отрезка составляет 2 м.Задача 9:
Найдите наибольший общий делитель (НОД) чисел 128 и 96.Решение:
Учитывая значения,
Используя метод простой факторизации,
Множители числа 128 равны 2 x 2 x 2 x 2 x 2 x 2 x 2
Множители числа 96 равны 2 x 2 x 2 x 2 x 2 x 3
Теперь напишите общие делители GCF (128, 96) = 2 x 2 x 2 x 2 x 2 = 32.
Таким образом, GCF равен 32.(OR)
Согласно алгоритму деления Евклида,
128 = 96 x 1 + 32
96 = 32 x 3 + 0
Следовательно , наибольший общий делитель (НОД) чисел 128 и 96 равен 32.Задача 10:
Чему равен НОД чисел 19 и 17?Решение:
Учитывая значения,
Сначала мы должны перечислить делители чисел 19 и 17, а затем найти общие делители.
Делители числа 19 равны 1 и 19.
Делители числа 17 равны 1 и 17.
Общие делители числа семь и 17 равны 1.
Среди этих чисел 1 является наибольшим (самым большим) числом.
Таким образом, GCF чисел 19 и 17 равен 1. Это записывается как GCF(19, 17) = 1.
Часто задаваемые вопросы по примерам GCF
1. Напишите разницу между HCF и GCF?
HCF и GCF одинаковы. Нет никакой разницы между HCF и GCD. Наибольший общий множитель (GCF), Наибольший общий показатель (GCM) и Наибольший общий делитель похожи.


 2*91/7=9*13=117 что и требовалось доказать а делится на b
2*91/7=9*13=117 что и требовалось доказать а делится на b Найдите наименьшее общее кратное чисел 70 и 30
Найдите наименьшее общее кратное чисел 70 и 30 и с номером №2(г, д, е) Содержание задания: найдите Нок(35,20), Нок(16,12), Нок (56,63).
и с номером №2(г, д, е) Содержание задания: найдите Нок(35,20), Нок(16,12), Нок (56,63). 






 Если Вы имеете дело со смешанным или целым числом, то его нужно сначала превратить в дробь, а уже потом определять наименьшее общее кратное. Чтобы целое число превратить в дробь, нужно в числителе записать само это число, а в знаменателе — единицу. Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5.
Если Вы имеете дело со смешанным или целым числом, то его нужно сначала превратить в дробь, а уже потом определять наименьшее общее кратное. Чтобы целое число превратить в дробь, нужно в числителе записать само это число, а в знаменателе — единицу. Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5.






 , 2020. LCM и GCF | Пурпурная математика.
, 2020. LCM и GCF | Пурпурная математика. Вы можете использовать этот ресурс, чтобы быстро найти все множители первых ста (100) элементов набора счетных чисел.
Вы можете использовать этот ресурс, чтобы быстро найти все множители первых ста (100) элементов набора счетных чисел. , 3, 11, 33
, 3, 11, 33 , 59
, 59
 (Мы видели, как найти LCM непосредственно в Уроке 23.)
(Мы видели, как найти LCM непосредственно в Уроке 23.)
 Некоторое число не делится на 3. Поэтому почему оно не делится на 12?
Некоторое число не делится на 3. Поэтому почему оно не делится на 12? 4
4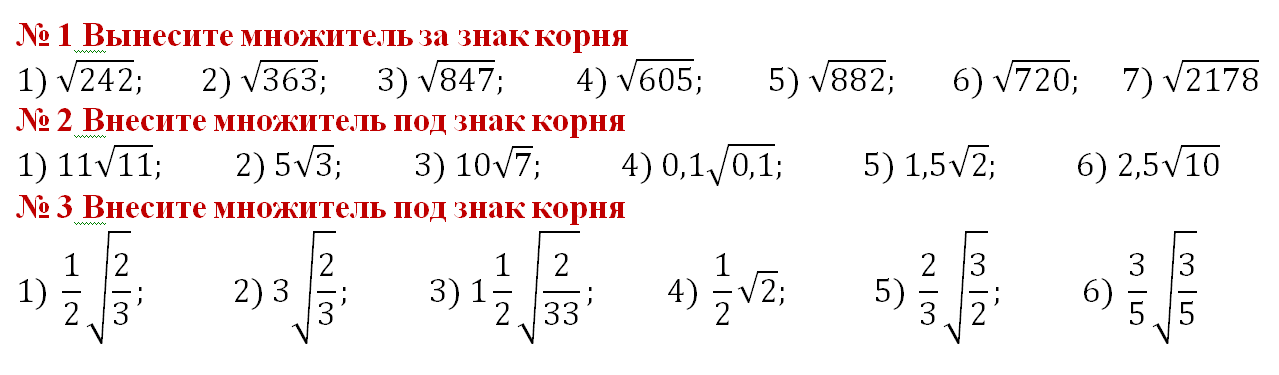 5 × 7
5 × 7 Итак, 12 и 35 не простые числа, а 9.2081 относительно простых.
Итак, 12 и 35 не простые числа, а 9.2081 относительно простых. Какое число является наименьшим общим кратным каждой пары?
Какое число является наименьшим общим кратным каждой пары? НЦМ = 40. НОД = 1.
НЦМ = 40. НОД = 1.
 1350
1350 com
com




