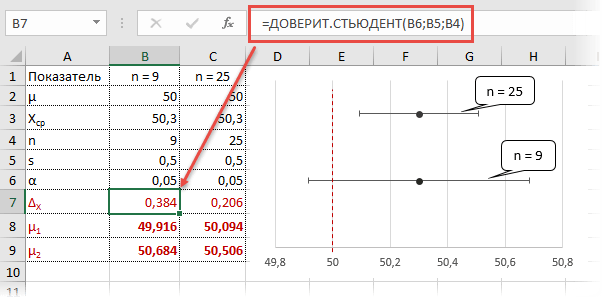
Онлайн расчет критерия Т-Стьюдента для независимых выборок
Онлайн калькулятор параметрического критерия Т-Стьюдента для независимых выборок позволяет получить расчет сразу на сайте. Итоговое описание состоит из таблиц, графиков и текстовых выводов. Его можно сказать в формате Word, а таблицы в Excel.
Шаг 1. Введите название исследуемых шкал
Шаг 1.1. Вы можете внести несколько названий шкал для исследования критерия Т-Стьюдента
Шаг 2. Внесите название ПЕРВОГО замера, количество человек в ней и нажмите на кнопку «Внести данные»
Шаг 2.1. Появится таблица с пустыми ячейками
Шаг 2.2. Внесите исходные данные группы
Вы можете внести данные для расчета критерия Т-Стьюдента поочередно вручную или скопировать их из вашего Excel файла.
Шаг 3. Внесите название ВТОРОГО замера, количество человек в ней и нажмите на кнопку «Внести данные»
Шаг 3.1. Появится таблица с пустыми ячейками
Шаг 3.2. Внесите исходные данные группы
Вы можете внести данные поочередно вручную или скопировать их из вашего Excel файла.
Шаг 4. Проверяем исходные данные
Именно по ним будет осуществляться онлайн расчет всех показателей критерия Стьюдента. В случае необходимости можно вернуться на предыдущие шаги и изменить данные.
Шаг 5. Краткий отчет
Для незарегистрированных пользователей доступен только краткий отчет-таблица в которой указано — эмпирическое значение критерия и уровень значимости.
Если вы разбираетесь в статистике, этих данных хватит вам, чтобы сделать вывод о наличии/отсутствии различий между замерами.
Шаг 5.1. Регистрация / Авторизация
Для того, чтобы получить более полный отчет с информацией о средних значениях с указание различий нужно зарегистрироваться в сервисе.
Вы можете зарегистрироваться используя свою почту или профиль ВКонтакте.
Шаг 6. Обычный отчет
После регистрации вам станет доступен более полный отчет в котором содержится информация о:
- средних значениях в каждом замере
- эмпирическое значении критерия
- уровне значимости критерия
- звездочкой в таблице указаны шкалы, по которым есть различия (в нашем примере это «Интеллект» и «Физическая агрессия», «Косвенная агрессия»).

Также вы можете скачать итоговую таблицу в формате Excel.
Вы также можете получить подробный отчет в котором будут графики и нужные текстовые описания, для этого нужно оплатить работу сервиса.
Шаг 7. Полный статистический отчет
После оплаты, в течении суток, вы сможете неограниченное количество раз запускать калькулятор и получать итоговые расчеты.
В полном отчете доступно:
- названия шкал,
- средние значения по каждой шкале,
- эмпирические значения критерия,
- уровень значимости с отметкой о наличии различий,
- описание различий,
- описание выраженности значений в каждой группе,
- графики «ящики-усы»
- возможность скачать результаты одним файлом Word c указанием всех таблиц, графиков и описаний
В случае, если результаты расчетов вас не устроят, мы гарантируем, что бесплатно внесем все необходимые правки в вашу работу.
t критерий
Вы искали t критерий? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и t критерий стьюдента, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «t критерий».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как t критерий,t критерий стьюдента,t критерий стьюдента онлайн калькулятор,t критерий стьюдента формула,t критерия стьюдента,t статистика,t статистика стьюдента,t статистика это,t тест,автоматический расчет критерия стьюдента,в каких случаях требуется знание коэффициента стьюдента,для чего используется коэффициент стьюдента,достоверность различий по t критерию стьюдента,как рассчитать коэффициент стьюдента,как рассчитать критерий стьюдента,коефіцієнт стьюдента,коэффициент стьюдента как рассчитать,коэффициент стьюдента формула,коэффициент стьюдента это,коэффициента стьюдента формула,критерий t стьюдента,критерий стьюдента,критерий стьюдента для зависимых выборок,критерий стьюдента для независимых выборок,критерий стьюдента как рассчитать,критерий стьюдента онлайн,критерий стьюдента применяется для,критерий стьюдента формула,критерий стьюдента это,критерий т,критерий т стьюдента,критерий т стьюдента онлайн,критерия t стьюдента,метод стьюдента,метод стьюдента формула,онлайн критерий стьюдента,онлайн критерий т стьюдента,онлайн расчет критерия стьюдента,расчет критерия стьюдента онлайн,статистика стьюдента,статистика т,стьюдент,стьюдент онлайн расчет,стьюдента,стьюдента формула,т критерий,т критерий стьюдента,т критерий стьюдента автоматический расчет,т критерий стьюдента онлайн,т статистика,тест стьюдента,формула t критерий стьюдента,формула коэффициент стьюдента,формула коэффициента стьюдента,формула критерий стьюдента,формула метод стьюдента,формула стьюдента,что показывает коэффициент стьюдента.
Решить задачу t критерий вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Калькулятор испытаний T
Общая путаница с тестом
t Помимо количества вариантов испытаний t , испытания t часто путают и с совершенно разными методиками. Вот как держать их все прямо.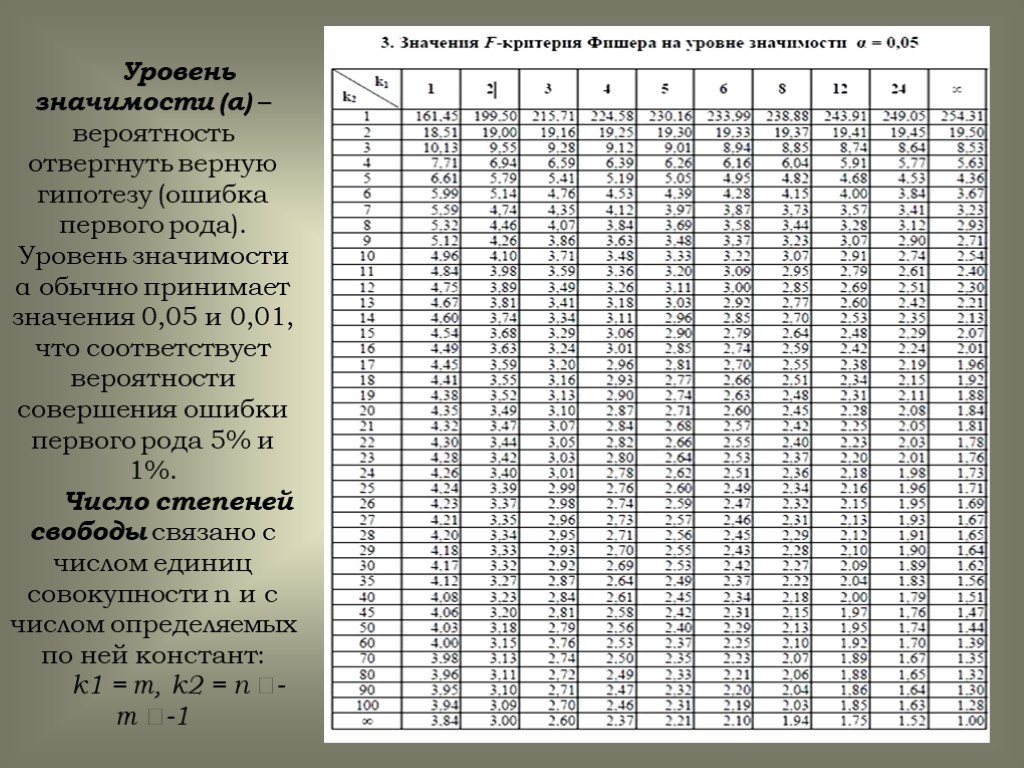
Корреляция и регрессия используются для измерения того, насколько два фактора движутся вместе. Хотя тесты t являются частью регрессионного анализа, они сосредоточены только на одном факторе путем сравнения средних значений в разных выборках.
Дисперсионный анализ используется для сравнения средних значений по трем или более общим группам. Напротив, тесты t сравнивают средние значения ровно между двумя группами.
Наконец, таблицы непредвиденных обстоятельств сравнивают количество наблюдений внутри групп, а не рассчитанное среднее значение. Поскольку тесты t сравнивают средние значения непрерывной переменной между группами, таблицы непредвиденных обстоятельств используют такие методы, как хи-квадрат вместо тестов t .
Предположения
т испытаний Поскольку существует несколько версий тестов t , важно проверить предположения, чтобы выяснить, какая из них лучше всего подходит для вашего проекта.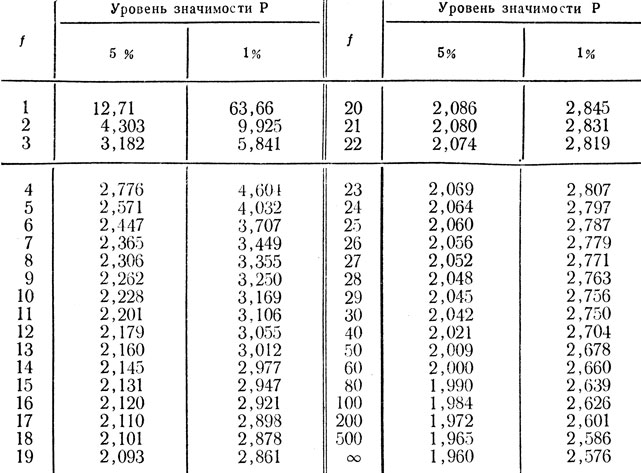 Вот наши контрольные списки анализа для непарных тестов t и парных тестов t , которые являются двумя наиболее распространенными. В них (и в окончательном руководстве по тестам t ) подробно описаны основные предположения, лежащие в основе любого теста
Вот наши контрольные списки анализа для непарных тестов t и парных тестов t , которые являются двумя наиболее распространенными. В них (и в окончательном руководстве по тестам t ) подробно описаны основные предположения, лежащие в основе любого теста
- Ровно две группы
- Образец обычно распределяется
- Независимые наблюдения
- Неравная или равная дисперсия?
- Парные или непарные данные?
Интерпретация результатов
Три разных варианта тестов t имеют несколько разные интерпретации, но все они зависят от проверки гипотез и значений P. Вам нужно выбрать порог значимости для вашего значения P (часто 0,05) перед выполнением теста.
Хотя значения P можно легко неправильно истолковать, они являются наиболее часто используемым методом для оценки наличия доказательств различия между выборкой собранных данных и нулевой гипотезой. После того, как вы выполнили правильный тест t , посмотрите на полученное значение P. Если результат теста меньше вашего порога, у вас есть достаточно доказательств, чтобы сделать вывод о том, что данные значительно отличаются.
Если результат теста меньше вашего порога, у вас есть достаточно доказательств, чтобы сделать вывод о том, что данные значительно отличаются.
Если результат теста больше или равен вашему порогу, вы не можете сделать вывод о наличии разницы. Тем не менее, вы также не можете сделать вывод, что не было окончательно никакой разницы. Возможно, набор данных с большим количеством наблюдений привел бы к другому выводу.
В зависимости от теста, который вы запускаете, вы можете увидеть другие статистические данные, которые использовались для расчета значения P, включая среднюю разницу, t-статистику, степени свободы и стандартную ошибку. Доверительный интервал и обзор вашего набора данных также приведены на странице результатов.
График
t испытаний Этот калькулятор не предоставляет диаграмму или график тестов t , однако построение графиков является важной частью анализа, поскольку оно может помочь объяснить результаты 9 тестов.0003 t проверьте и выделите любые потенциальные выбросы.
Prism создан для индивидуальной графики и диаграмм качества публикации. Для тестов t мы рекомендуем просто наносить на график сами точки данных и среднее значение или оценочный график. Еще один популярный подход — использование сюжета для скрипки, как в Prism.
За дополнительной информацией
Наше окончательное руководство по тестам t включает примеры, ссылки и интуитивно понятные объяснения по этому вопросу. Это просто лучшее место для начала, если вы ищете больше о тестах t !
Если вам понравился этот калькулятор, вам понравится использовать Prism для анализа. Воспользуйтесь бесплатной 30-дневной пробной версией, чтобы сделать больше с вашими данными, например:
- Четкое руководство по выбору правильного теста t и подробные сводки результатов
- Пользовательские, качество публикации t тестовая графика, скрипичные сюжеты и многое другое
- Дополнительные варианты тестов t , включая проверку нормальности, а также вложенные и множественные тесты t
- Альтернативы непараметрическим тестам, такие как Вилкоксон, Манн-Уитни и Колмогоров-Смирнов.

Посмотрите наше видео о том, как выполнить т тест в Призме, для примера от начала до конца!
Помните, что эта страница предназначена только для двух образцов тестов t . Если у вас есть только один образец, вам нужно использовать этот калькулятор.
Мы рекомендуем:
Руководство: Полное руководство по тестам t
Видео: Как выполнить тест t с двумя образцами
Видео: Как выполнить
Видео: Множественные тесты t — парные и непарные
Prism Academy: освойте ключевые концепции статистики и визуализации данных
Полное руководство по T-тестам
Полное руководство по t-тестам
Стьюдентный тест — это один из простейших статистических методов, который используется для оценки наличия статистической разницы между средними значениями двух разных выборок. Критерий Стьюдента особенно полезен, когда у вас есть небольшое количество выборочных наблюдений (менее 30 или около того) и вы хотите сделать выводы о большей совокупности.
Характеристики данных определяют соответствующий тип t-теста. Все t-тесты используются как самостоятельные анализы для очень простых экспериментов и исследовательских вопросов, а также для выполнения отдельных тестов в рамках более сложных статистических моделей, таких как линейная регрессия. В этом руководстве мы изложим все, что вам нужно знать о t-тестах, в том числе предоставим простой рабочий процесс, чтобы определить, какой t-тест подходит для ваших конкретных данных или вам лучше подходит другая модель.
Что такое t-тест?
Стьюдентный тест — это статистический метод, используемый для количественной оценки разницы между средним значением (средним значением) переменной из двух выборок (наборов данных). Переменная должна быть числовой. Некоторыми примерами являются рост, валовой доход и количество веса, потерянного на определенной диете.
Ат-тест показывает, является ли наблюдаемая вами разница «неожиданной» на основе ожидаемой разницы. Они используют t-распределения для оценки ожидаемой изменчивости. Когда у вас есть выборка разумного размера (более 30 или около того наблюдений), t-критерий все еще можно использовать, но вместо него можно использовать другие тесты, использующие нормальное распределение (z-критерий).
Когда у вас есть выборка разумного размера (более 30 или около того наблюдений), t-критерий все еще можно использовать, но вместо него можно использовать другие тесты, использующие нормальное распределение (z-критерий).
Иногда t-тесты называют t-тестами Стьюдента, что является просто отсылкой к их необычной истории.
Свое название он получил потому, что пивовар из пивоварни Гиннесс, Уильям Госсет , опубликовал о методе под псевдонимом «Студент». Он хотел получить информацию из очень маленьких образцов (часто 3-5), потому что требовалось много усилий, чтобы заварить каждый бочонок для своих образцов.
Когда следует использовать t-тест?
Т-тест целесообразно использовать, когда вы собрали небольшую случайную выборку из некоторой статистической «популяции» и хотите сравнить среднее значение из вашей выборки с другим значением. Значение для сравнения может быть фиксированным значением (например, 10) или средним значением второго образца.
Например, если интересующей вас переменной является средний рост шестиклассников в вашем регионе, вы можете измерить рост 25 или 30 случайно выбранных шестиклассников. С помощью t-теста можно ответить на такие вопросы, как «Средний рост больше четырех футов?»
С помощью t-теста можно ответить на такие вопросы, как «Средний рост больше четырех футов?»
Как работает t-тест?
Основываясь на вашем эксперименте, t-тесты делают достаточно предположений о вашем эксперименте, чтобы вычислить ожидаемую изменчивость, а затем они используют это, чтобы определить, являются ли наблюдаемые данные статистически значимыми. Для этого t-тесты полагаются на предполагаемую «нулевую гипотезу». В приведенном выше примере нулевая гипотеза состоит в том, что средний рост меньше или равен четырем футам.
Допустим, мы измеряем рост 5 случайно выбранных шестиклассников, и средний рост составляет пять футов. Означает ли это, что «истинный» средний рост всех шестиклассников превышает четыре фута, или мы случайно оказались выше среднего роста учеников?
Чтобы оценить это, нам нужно распределение, которое показывает все возможные средние значения, полученные из выборки из пяти человек в популяции, где истинное среднее равно четырем. Это может показаться невозможным, поэтому существуют особые предположения, которые необходимо сделать для выполнения t-теста.
При таких предположениях все, что необходимо для определения «выборочного распределения среднего», — это размер выборки (в данном случае 5 учащихся) и стандартное отклонение данных (скажем, 1 фут).
Этого достаточно, чтобы построить график распределения среднего значения, а именно:
Обратите внимание на вертикальную линию x = 5, которая была нашим средним значением для выборки. Мы (используем программное обеспечение) вычисляем площадь справа от вертикальной линии, что дает нам значение P (0,09в таком случае). Обратите внимание, что, поскольку наш исследовательский вопрос заключался в том, является ли средний студент на больше, чем на четыре фута, распределение сосредоточено на четырех. Поскольку нас интересует только то, является ли среднее значение больше четырех футов, в данном случае мы используем односторонний тест .
Используя стандартный уровень достоверности 0,05 в этом примере, мы не имеем доказательств того, что истинный средний рост шестиклассников выше 4 футов.
Каковы предположения для t-тестов?
- Одна интересующая переменная : Это не корреляция или регрессия, когда вас интересует взаимосвязь между несколькими переменными. С помощью t-теста у вас могут быть разные выборки, но все они измеряют одну и ту же переменную (например, рост).
- Числовые данные: Вы имеете дело со списком измерений, которые можно усреднить. Это означает, что вы не просто подсчитываете появление в различных категориях (например, цвет глаз или политическая принадлежность).
- Две группы или меньше: Если у вас более двух выборок данных, t-тест является неправильным методом. Скорее всего, вам нужно попробовать ANOVA.
- Случайная выборка : Вам нужна случайная выборка из вашей статистической «целевой совокупности», чтобы сделать достоверные выводы о большей совокупности. Если ваше население настолько мало, что вы можете все измерить, то у вас есть «перепись» и вам не нужна статистика.
 Это потому, что вам не нужно оценивать истину, поскольку вы измерили истину без изменчивости.
Это потому, что вам не нужно оценивать истину, поскольку вы измерили истину без изменчивости. - Нормально распределенный : Чем меньше размер вашей выборки, тем важнее, чтобы ваши данные исходили из нормального гауссового распределения. Если у вас есть основания полагать, что ваши данные не распределены нормально, рассмотрите альтернативы непараметрического t-теста . В этом нет необходимости для больших выборок (обычно 25 или 30, если только данные не сильно искажены). Причина в том, что в этом случае применяется центральная предельная теорема, которая говорит, что даже если распределение ваших данных не является нормальным, распределение среднего значения ваших данных является нормальным, поэтому вы можете использовать z-критерий, а не t-критерий.
Как узнать, какой t-тест использовать?
Существует множество типов t-тестов на выбор, но вам не обязательно разбираться во всех деталях каждого варианта.
Вам просто нужно ответить на несколько вопросов, которые помогут вам выбрать правильный t-тест. С этой целью мы составили этот рабочий процесс, чтобы вы могли определить, какой тест подходит для ваших данных.
С этой целью мы составили этот рабочий процесс, чтобы вы могли определить, какой тест подходит для ваших данных.
У вас есть один или два образца?
Вы сравниваете средние значения двух разных образцов или сравниваете среднее значение одного образца с фиксированным значением? Пример исследовательского вопроса: «Средний рост моей выборки учащихся шестого класса больше четырех футов?»
Если у вас есть только одна выборка данных, вы можете щелкнуть здесь, чтобы перейти к примеру одновыборочного t-критерия , в противном случае ваш следующий шаг – спросить:
Совпадают ли наблюдения в двух выборках или связаны ли они способ?
Это могут быть измерения одних и тех же испытуемых до и после, или, возможно, ваше исследование разделило «пары» испытуемых (технически разные, но имеющие общие интересующие характеристики) на две выборки. В обоих случаях измеряется одна и та же переменная.
Если это так, вы смотрите на некую пару образцов t test . Связанный раздел поможет вам выбрать, какой именно из этого семейства лучше всего подходит для вас, будь то разница (наиболее распространенная) или соотношение.
Связанный раздел поможет вам выбрать, какой именно из этого семейства лучше всего подходит для вас, будь то разница (наиболее распространенная) или соотношение.
Если вы не уверены, что спаривание правильное, задайте себе другой вопрос:
Вы сравниваете разные наблюдения в каждой из двух выборок?
Если ответ положительный, то у вас t-тест непарных или независимых выборок. Две выборки должны измерять одну и ту же переменную (например, рост), но представлять собой выборки из двух разных групп (например, команды А и команды Б).
Цель состоит в том, чтобы сравнить средства, чтобы увидеть, существенно ли различаются группы. Например, «Средний рост команды А больше, чем у команды Б?» В отличие от парных, единственная связь между группами в этом случае заключается в том, что мы измеряли одну и ту же переменную для обеих. Существует две версии t-тестов для непарных выборок (объединенные и необъединенные) в зависимости от того, принимаете ли вы одну и ту же дисперсию для каждой выборки.
Вы проводили один и тот же эксперимент несколько раз на одном и том же объекте/единице наблюдения?
Если да, то у вас есть вложенный t-критерий (если только у вас больше двух групп выборок). Это более сложная концепция для понимания. Например, если вы измеряете, насколько хорошо удобрение А работает по сравнению с удобрением Б. Допустим, у вас есть 12 горшков для выращивания растений (по 6 горшков для каждого удобрения), и вы выращиваете по 3 растения в каждом горшке.
В этом случае у вас есть 6 единиц наблюдения для каждого удобрения, по 3 подвыборки из каждого горшка. Вы хотели бы проанализировать это с помощью вложенного t-теста 9.0154 . «Вложенным» фактором в данном случае являются горшки. Важно отметить, что нас не интересует оценка изменчивости внутри каждого горшка, мы просто хотим принять ее во внимание.
У вас может возникнуть соблазн провести тест непарных образцов здесь, но это предполагает, что у вас есть 6*3 = 18 повторений для каждого удобрения. Однако три повтора в каждом горшке связаны между собой, и t-тест непарных образцов не будет учитывать это.
Однако три повтора в каждом горшке связаны между собой, и t-тест непарных образцов не будет учитывать это.
Что, если ни один из них не похож на мой эксперимент?
Если вы не видите свой исследовательский вопрос выше, обратите внимание, что t-тесты — это очень простые статистические инструменты. Многие эксперименты требуют более сложных методов для оценки различий. Если интересующая переменная представляет собой пропорцию (например, 10 из 100 произведенных продуктов были бракованными), то вы должны использовать z-тесты. Если вы проводите измерения до и после и проходите более одного лечения (например, контрольная диета или лечебная диета), вам нужен дисперсионный анализ.
Как выполнить t-тест с помощью программного обеспечения?
Если вам интересно, как провести t-тест, проще всего воспользоваться статистическим программным обеспечением, таким как Prism или онлайн-калькулятором t-теста .
Если вы используете программное обеспечение, все, что вам нужно знать, это то, какой t-тест подходит ( используйте рабочий процесс здесь ) и понимать, как интерпретировать вывод. Для этого вам также потребуется:
Для этого вам также потребуется:
- Определить, является ли ваш тест односторонним или двусторонним
- Выбрать уровень значимости
Мой тест односторонний или двусторонний?
Будет ли у вас односторонний или двусторонний тест, зависит от вашей исследовательской гипотезы. Выбор подходящего теста очень важен и требует честности от исследователя. Это связано с тем, что у вас больше «мощности» с односторонними тестами, а это означает, что вы можете легче обнаружить статистически значимую разницу. Если вы не записали свою исследовательскую гипотезу как однонаправленную перед проведением эксперимента, вам следует использовать двусторонний тест.
Двусторонние тесты
Двусторонние тесты являются наиболее распространенными, и они применимы, когда ваш исследовательский вопрос просто спрашивает: «Есть ли разница?»
Односторонние тесты
В отличие от односторонних тестов, где исследовательские вопросы являются направленными, что означает, что либо вопрос звучит так: « больше, чем », либо вопрос таков: « меньше, чем ». ». Эти тесты могут обнаружить разницу только в одном направлении.
». Эти тесты могут обнаружить разницу только в одном направлении.
Выбор уровня значимости
Все t-тесты оценивают, отличается ли среднее значение совокупности от какого-либо другого значения, и со всеми оценками связана некоторая изменчивость, или то, что статистики называют «ошибкой». Прежде чем анализировать ваши данные, вы хотите выбрать уровень значимости, обычно обозначаемый греческой буквой альфа, 𝛼. Научный стандарт устанавливает альфа равным 0,05.
Альфа 0,05 приводит к 95% доверительным интервалам и определяет пороговое значение, когда значения P считаются статистически значимыми.
Один выборочный t-тест
Если у вас есть только один образец списка чисел, вы выполняете одновыборочный t-тест. Все, что вам нужно сделать, это сравнить среднее из этой группы с некоторым известным значением, чтобы проверить, есть ли доказательства того, что оно значительно отличается от этого стандарта. Используйте для этого наш бесплатный одновыборочный калькулятор t-критерия .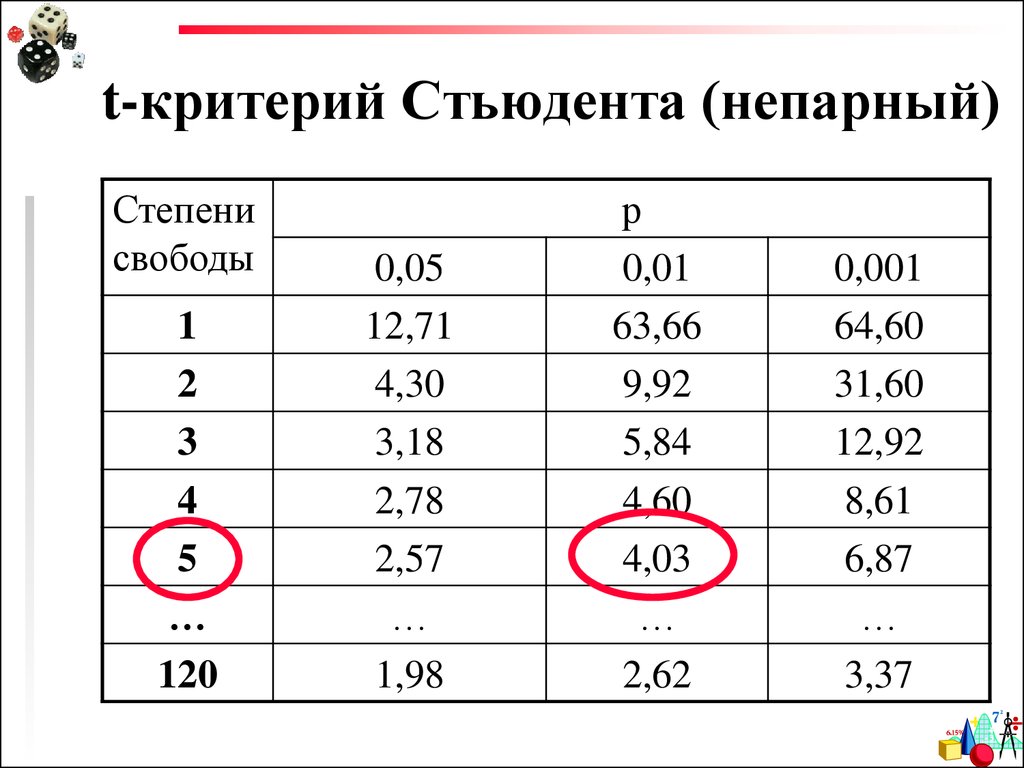
Один из тестовых примеров исследовательского вопроса: «Выше ли средний пятиклассник четырех футов?»
Это простейшая версия t-критерия, имеющая множество применений при проверке гипотез. Иногда «известное значение» называют «нулевым значением». Хотя нулевое значение в t-тестах часто равно 0, это может быть любое значение. Название происходит от значения, которое точно представляет нулевую гипотезу, где нет существенной разницы.
Каждый раз, когда вы знаете точное число, с которым вы пытаетесь сравнить свою выборку данных, это может сработать. И конечно же: она может быть как одно-, так и двусторонней.
Формула t-критерия для одной выборки
Статистическое программное обеспечение справится с этим за вас, но если вам нужны подробности, формула для t-критерия для одной выборки: тестируются против
В одновыборочном t-критерии вычисление степеней свободы простое: на одну меньше, чем количество объектов в вашем наборе данных (вы увидите, что это записано как n-1 ).
Пример t-критерия для одной выборки
Для нашего примера в Prism у нас есть набор данных из 12 значений из эксперимента с пометкой «% контроля». Возможно, это высота образца растений, обработанных новым удобрением. Значение 100 соответствует стандартной контрольной высоте. Аналогичным образом, 123 представляет собой растение, высота которого на 123 % выше контрольной (то есть на 23 % больше).
Мы проведем двусторонний одновыборочный t-критерий, чтобы увидеть, становятся ли растения в среднем короче или выше при использовании удобрения. Мы будем использовать порог значимости 0,05. Вот вывод:
Вы можете видеть в выводе, что фактическое среднее значение выборки было 111. Достаточно ли это отличается от отраслевого стандарта (100), чтобы сделать вывод о наличии статистической разницы?
Быстрый ответ: да, есть убедительные доказательства того, что высота растений с удобрением превышает отраслевой стандарт (p = 0,015). Преимущество использования программного обеспечения заключается в том, что оно выполняет некоторые из более сложных шагов за вас. В этом случае он вычисляет статистику вашего теста (t = 2,88), определяет соответствующие степени свободы (11) и выводит значение P.
В этом случае он вычисляет статистику вашего теста (t = 2,88), определяет соответствующие степени свободы (11) и выводит значение P.
Более информативным, чем значение P, является доверительный интервал разницы, который составляет от 2,49 до 18,7. Доверительный интервал говорит нам, что, основываясь на наших данных, мы уверены, что истинная разница между нашей выборкой и базовым значением 100 находится где-то между 2,49 и 18,7. Пока разница статистически значима, интервал не будет содержать нуля.
Вы можете следовать этим советам для интерпретации собственного одновыборочного теста.
Построение графика одновыборочного t-критерия
Для некоторых методов (например, регрессии) построение графика данных является очень полезной частью анализа. Для t-тестов создание диаграммы ваших данных по-прежнему полезно для выявления каких-либо странных закономерностей или выбросов, но небольшой размер выборки означает, что вы, возможно, уже знакомы со всеми странными вещами в ваших данных.
Здесь у нас есть простой график точек данных, возможно, с отметкой для среднего. Мы сделали это в качестве примера, но правда в том, что график обычно более нагляден для t-тестов с двумя выборками, чем для одной выборки.
Двухвыборочные t-тесты
Существует несколько видов двухвыборочных t-тестов, причем две основные категории — это парные и непарные (независимые) выборки.
Стьюдентный критерий для парных выборок
В t-критерии для парных выборок, также называемом t-тестом для зависимых выборок, используются две выборки данных, и каждое наблюдение в одной выборке «сопоставляется» с наблюдением во второй выборке. Наиболее распространенным примером является измерение каждого субъекта до и после лечения. Пример парного t-теста для исследования: «Есть ли статистическая разница между средним количеством эритроцитов до и после лечения?»
Наличие двух близкородственных образцов упрощает анализ. Статистическое программное обеспечение, такое как этот калькулятор парного t-критерия , просто возьмет разницу между двумя значениями, а затем сравнит эту разницу с 0.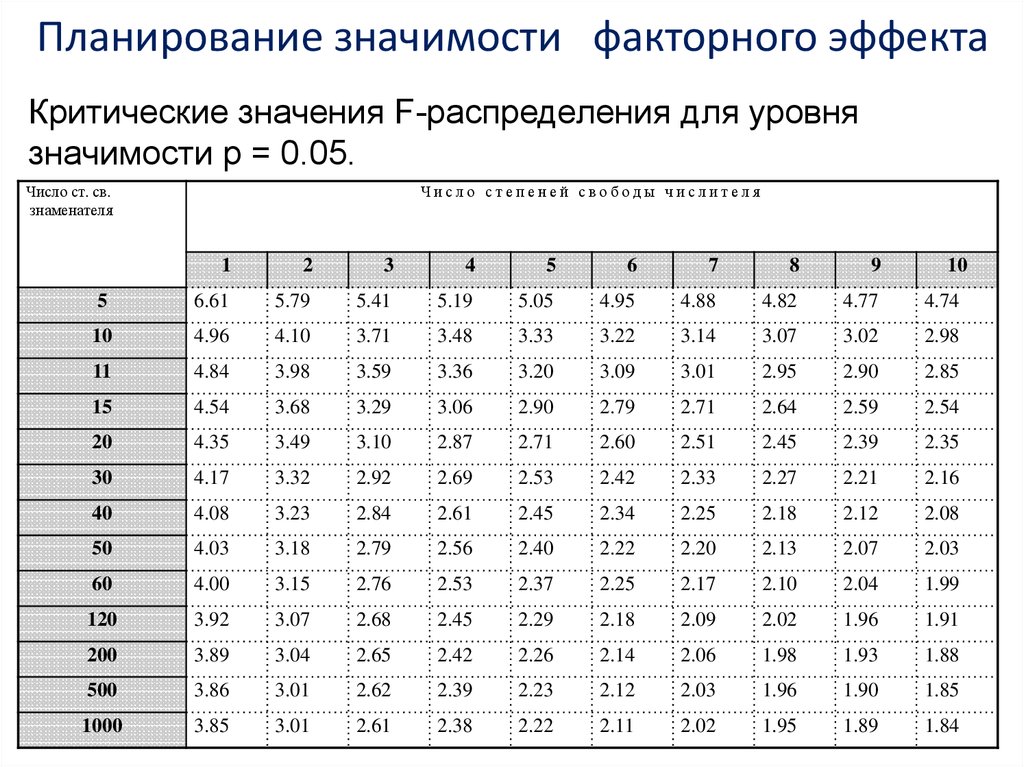
В некоторых (редких) ситуациях определение разницы между парами нарушает предположения t-тест, потому что средняя разница изменяется в зависимости от размера значения «до» (например, разница между «до» и «после» больше, когда для начала было больше). В этом случае вместо использования теста разницы используйте соотношение значений до и после, которое называется 9.0153 коэффициент t тестирует .
Формула парного t-критерия
Формула для парных выборок t-критерия:
- Md: Средняя разница между выборками
- sd: Стандартное отклонение различий свободы такие же, как прежде. Если вы готовитесь к экзамену, вы можете помнить, что степени свободы по-прежнему равны n-1 (не n-2), потому что мы преобразовываем данные в один столбец различий, а не рассматриваем две группы по отдельности.
Также обратите внимание, что нулевое значение здесь равно просто 0. Нет реальной причины включать «минус 0» в уравнение, кроме как для иллюстрации того, что мы все еще проводим проверку гипотезы.
 После того, как вы берете разницу между двумя средними значениями, вы сравниваете эту разницу с 0.
После того, как вы берете разницу между двумя средними значениями, вы сравниваете эту разницу с 0.Пример
Для нашего примера данных у нас есть пять испытуемых, и у каждого было проведено два измерения: до («контроль») и после лечение («лечение»). Если мы установим альфа = 0,05 и проведем двусторонний тест, мы увидим статистически значимую разницу между обработанной и контрольной группой (p = 0,0160, t = 4,01, df = 4). Нам 95% уверены, что истинная средняя разница между обработанной и контрольной группой составляет от 0,449 до 2,47.
График парного t-критерия
Значимый результат значения P свидетельствует о том, что лечение оказало некоторый эффект, и мы также можем посмотреть на это графически. Линии, соединяющие наблюдения, могут помочь нам определить закономерность, если она существует. В этом случае линии показывают, что все наблюдения увеличились после лечения. Хотя не все графики такие простые, здесь они очень хорошо согласуются с результатами t-теста.

Оценочный график Prism еще более полезен, поскольку он показывает как данные (как показано выше), так и доверительный интервал для разницы между средними значениями. Вы можете легко увидеть свидетельство значимости, поскольку доверительный интервал справа не содержит нуля.
Вот еще несколько советов по построению графиков для парных t-тестов .
Непарные выборки t-критерий
Непарные выборки t-критерий, также называемый независимыми выборками t-критерий, подходит, когда у вас есть две группы выборок, которые не коррелируют друг с другом. Фармацевтический пример — это тестирование лечебной группы по сравнению с контрольной группой, состоящей из разных субъектов. Сравните это с парной выборкой, которая может записывать одних и тех же субъектов до и после лечения.
При использовании непарных t-тестов, в дополнение к выбору уровня значимости и одно- или двустороннего теста, вам необходимо определить, следует ли предполагать, что дисперсии между группами одинаковы или нет.
 Если вы предполагаете равные дисперсии, то вы можете «объединить» расчет стандартной ошибки между двумя выборками. В противном случае стандартным выбором является t-критерий Уэлча, который корректирует неравные дисперсии. Этот выбор влияет на расчет статистики теста и мощность теста, которая представляет собой чувствительность теста к обнаружению статистической значимости.
Если вы предполагаете равные дисперсии, то вы можете «объединить» расчет стандартной ошибки между двумя выборками. В противном случае стандартным выбором является t-критерий Уэлча, который корректирует неравные дисперсии. Этот выбор влияет на расчет статистики теста и мощность теста, которая представляет собой чувствительность теста к обнаружению статистической значимости.Перед проведением эксперимента лучше выбрать, будете ли вы использовать объединенную или не объединенную (Уэлча) стандартную ошибку, потому что общеизвестно, что стандартный статистический тест проблематичен. Подробнее о неравных дисперсиях см. здесь .
Пока вы используете статистическое программное обеспечение, такое как этот калькулятор t-критерия для двух выборок , так же легко вычислить статистику теста независимо от того, предполагаете ли вы, что дисперсии ваших двух выборок одинаковы. Однако, если вы делаете это вручную, вычисления усложняются из-за неравных отклонений.
Формула t-критерия для непарных (независимых) выборок
Общая формула t-критерия для двух выборок:
- M1 и M2: два сравниваемых значения, по одному из каждого набора данных две выборки (рассчитанные с использованием объединенной или не объединенной стандартной ошибки)
Вычисление знаменателя (стандартной ошибки) может быть сложным, как и степени свободы.
 Если группы не сбалансированы (одинаковое количество наблюдений в каждой), вам нужно будет учитывать и то, и другое при определении n для теста в целом.
Если группы не сбалансированы (одинаковое количество наблюдений в каждой), вам нужно будет учитывать и то, и другое при определении n для теста в целом.Пример
В качестве примера для этого семейства мы проводим t-тест парных выборок, предполагая равные дисперсии (объединенные). Основываясь на нашей исследовательской гипотезе, мы проведем двусторонний тест и используем альфа = 0,05 для нашего уровня значимости. Наши выборки были несбалансированными, с двумя выборками по 6 и 5 наблюдений соответственно.
Значение P (p = 0,261, t = 1,20, df = 9) выше нашего порога 0,05. Мы не нашли достаточных доказательств, чтобы предположить существенную разницу. Вы можете видеть, что доверительный интервал разницы средних значений равен -9.от 0,58 до 31,2.
Обратите внимание, что результат F-теста показывает, что дисперсии двух групп существенно не отличаются друг от друга.
Построение графика t-теста для непарных выборок
Для t-теста для непарных выборок построение графика данных может быстро помочь вам получить представление о двух группах и о том, насколько они похожи или различны.
 Как и в парном примере, это помогает подтвердить доказательства (или их отсутствие), обнаруженные при выполнении самого t-теста.
Как и в парном примере, это помогает подтвердить доказательства (или их отсутствие), обнаруженные при выполнении самого t-теста.Ниже вы можете видеть, что наблюдаемое среднее значение для женщин выше, чем для мужчин. Но из-за изменчивости данных мы не можем сказать, действительно ли средства различаются или разница случайна.
Непараметрические альтернативы для t-критерия
Если ваши данные получены из нормального распределения (или чего-то достаточно близкого к нормальному распределению), то t-критерий действителен. Если это предположение нарушается, вы можете использовать непараметрические альтернативы.
Т-тесты оценивают, отличается ли среднее значение от другого значения, тогда как непараметрические альтернативы сравнивают либо медиану, либо ранг. Хорошо известно, что медианы гораздо более устойчивы к выбросам, чем среднее значение.
Недостатком непараметрических тестов является то, что они не обладают такой большой статистической мощностью, а это означает, что требуется большая разница, чтобы определить, является ли она статистически значимой.

Критерий знакового ранга Уилкоксона
Критерий знакового ранга Вилкоксона является непараметрическим родственником одновыборочного t-критерия. Это сравнивает выборочную медиану с гипотетическим медианным значением. Иногда его даже ошибочно называют t-критерием Уилкоксона (хотя он вычисляет статистику «W»).
А если у вас есть две связанные выборки, вам следует вместо этого использовать тест на соответствие пар Уилкоксона . Две версии Уилкоксона различны, а версия с согласованными парами предназначена специально для сравнения средней разницы для парных выборок.
Критерии Манна-Уитни и Колмогорова-Смирнова
Для непарных (независимых) выборок имеется множественных вариантов для непараметрического тестирования. Манн-Уитни более популярен и сравнивает средние ранги (порядок значений от наименьшего к наибольшему) двух выборок. Манна-Уитни часто неверно представляют как сравнение медиан, но это не всегда так. Колмогоров-Смирнов проверяет, различаются ли общие распределения между двумя выборками.

Дополнительные часто задаваемые вопросы по t-тесту
Какова формула t-теста?
Точная формула зависит от того, какой тип t-теста вы используете, хотя существует базовая структура, общая для всех t-тестов. Вся статистика t-теста будет иметь вид:
- t : Статистика t-теста, которую вы вычисляете для своего теста Среднее : стандартная ошибка среднего , также называемое стандартным отклонением среднего значения, которое учитывает дисперсию и размер вашего набора данных
Точная формула для любого t-критерия может немного отличаться, особенно расчет стандартной ошибки. Имеет значение не только то, сравниваются ли один или два образца, но и взаимосвязь между образцами.
Что такое t-распределение?
Стьюдентное распределение похоже на нормальное распределение. Это колоколообразная кривая, но по сравнению с нормальной у нее более толстые хвосты, а это означает, что экстремумы наблюдаются чаще. Т-распределения идентифицируются по количеству степеней свободы.
 Чем выше число, тем ближе t-распределение к нормальному распределению. Примерно после 30 степеней свободы t и стандартная нормаль практически совпадают.
Чем выше число, тем ближе t-распределение к нормальному распределению. Примерно после 30 степеней свободы t и стандартная нормаль практически совпадают.t-распределение по степеням свободы
Что такое степени свободы?
Степени свободы — это мера того, насколько велик ваш набор данных. Это не совсем количество наблюдений, потому что они также учитывают количество параметров (например, среднее значение, дисперсию), которые вы оценили.
В чем разница между парными и непарными t-тестами?
Как парные, так и непарные t-критерии включают две выборочные группы данных. При парном t-тесте значения в каждой группе связаны (обычно это значения до и после, измеренные на одном и том же испытуемом). Напротив, с непарными t-тестами наблюдаемые значения не связаны между группами. Например, непарный или независимый t-критерий сравнивает средний рост детей в школе A и в школе B.
Когда следует использовать z-тест, а не t-тест?
Z-тесты, которые сравнивают данные с использованием нормального распределения, а не t-распределения, в основном используются для двух ситуаций.
 Во-первых, когда вы оцениваете пропорции (количество отказов на конвейере). Во-вторых, когда размер вашей выборки достаточно велик (обычно около 30), вы можете использовать нормальное приближение для оценки средних значений.
Во-первых, когда вы оцениваете пропорции (количество отказов на конвейере). Во-вторых, когда размер вашей выборки достаточно велик (обычно около 30), вы можете использовать нормальное приближение для оценки средних значений.Когда следует использовать дисперсионный анализ вместо t-критерия?
Используйте ANOVA, если у вас есть более двух групповых средних для сравнения.
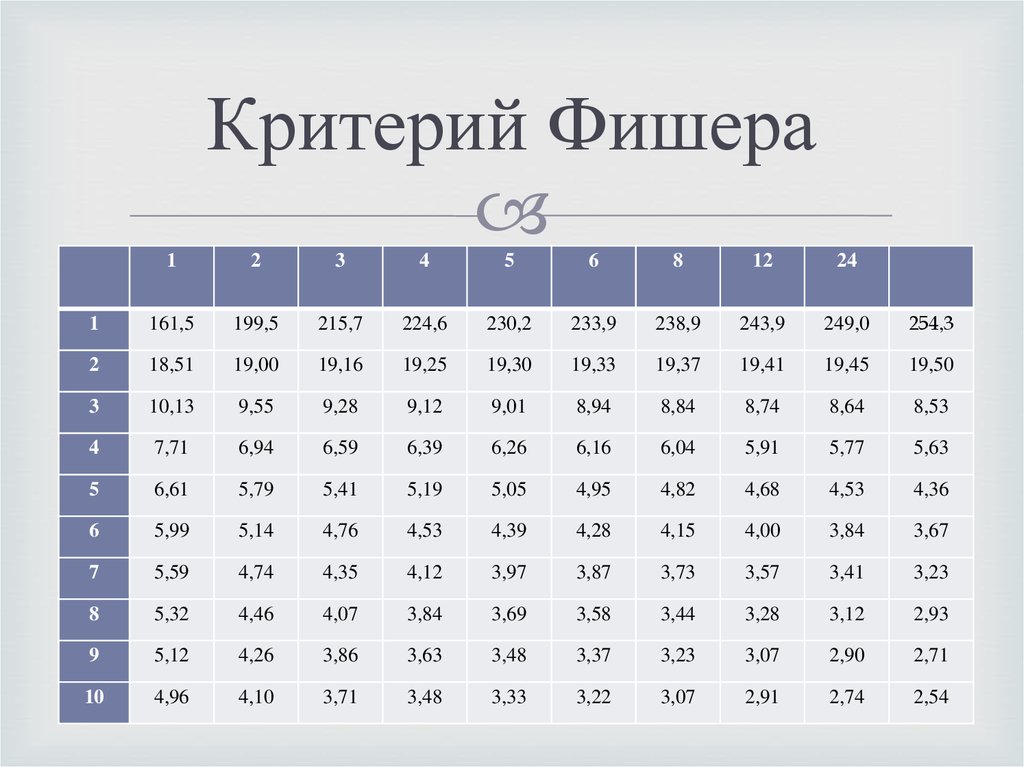
В чем разница между критерием Стьюдента и критерием хи-квадрат?
Критерий хи-квадрат используется для оценки таблиц непредвиденных обстоятельств , в которых записывается подсчет количества субъектов, попадающих в определенные категории (например, грузовик, внедорожник, автомобиль). t-тесты сравнивают средние значения интересующей переменной (например, роста, веса).
Что такое Р-значения?
P-значения — это вероятность того, что вы получите данные, такие же или более экстремальные, чем наблюдаемые данные, при условии, что нулевая гипотеза верна. Это полный рот, и их много проблем с P-значениями, о которых нужно знать.

Что такое критические значения t-теста?
Критические значения — это классическая форма (они не используются напрямую в современных вычислениях) для определения того, является ли статистический тест значимым или нет. Исторически вы могли рассчитать статистику теста на основе своих данных, а затем использовать t-таблицу для поиска порогового значения (критического значения), которое представляло «значимый» результат. Затем вы сравните наблюдаемую статистику с критическим значением.
Как рассчитать степени свободы для моего t-критерия?
В большинстве случаев степени свободы представляют собой количество имеющихся у вас наблюдений минус количество параметров, которые вы пытаетесь оценить. Расчет не всегда прост и аппроксимируется для некоторых t-тестов.
Статистическое программное обеспечение вычисляет степени свободы автоматически как часть анализа, поэтому их более подробное понимание не требуется, разве что для удовлетворения любого любопытства.



 Это потому, что вам не нужно оценивать истину, поскольку вы измерили истину без изменчивости.
Это потому, что вам не нужно оценивать истину, поскольку вы измерили истину без изменчивости.  После того, как вы берете разницу между двумя средними значениями, вы сравниваете эту разницу с 0.
После того, как вы берете разницу между двумя средними значениями, вы сравниваете эту разницу с 0.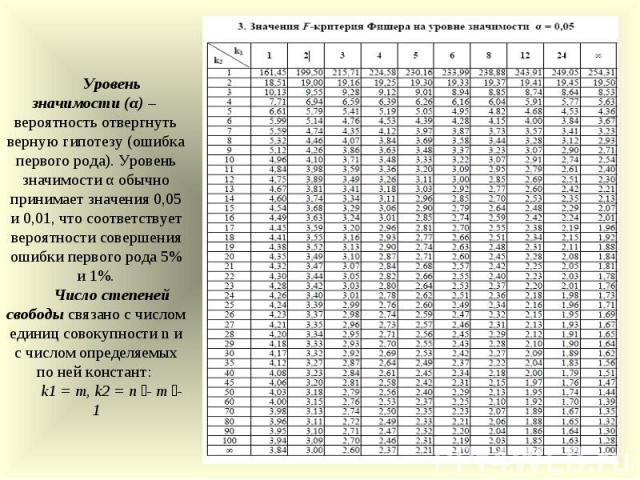
 Если вы предполагаете равные дисперсии, то вы можете «объединить» расчет стандартной ошибки между двумя выборками. В противном случае стандартным выбором является t-критерий Уэлча, который корректирует неравные дисперсии. Этот выбор влияет на расчет статистики теста и мощность теста, которая представляет собой чувствительность теста к обнаружению статистической значимости.
Если вы предполагаете равные дисперсии, то вы можете «объединить» расчет стандартной ошибки между двумя выборками. В противном случае стандартным выбором является t-критерий Уэлча, который корректирует неравные дисперсии. Этот выбор влияет на расчет статистики теста и мощность теста, которая представляет собой чувствительность теста к обнаружению статистической значимости.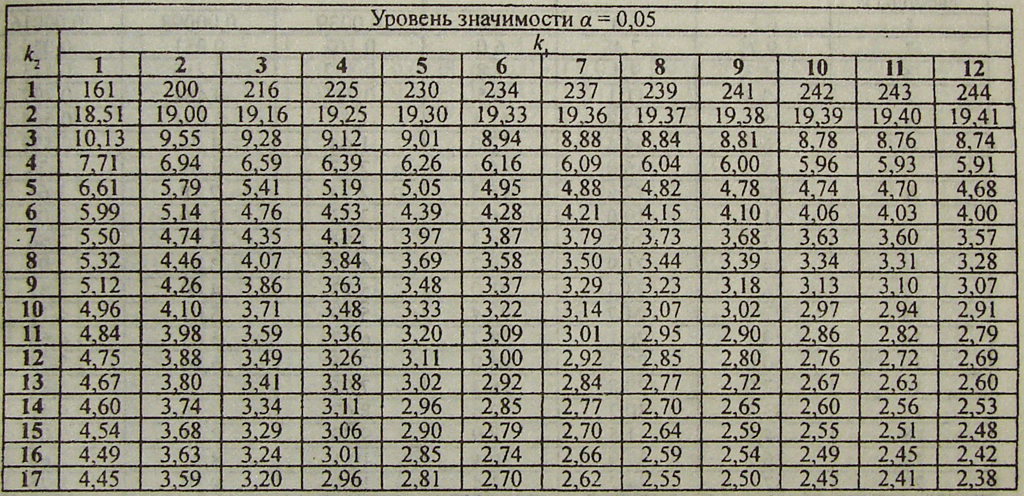 Если группы не сбалансированы (одинаковое количество наблюдений в каждой), вам нужно будет учитывать и то, и другое при определении n для теста в целом.
Если группы не сбалансированы (одинаковое количество наблюдений в каждой), вам нужно будет учитывать и то, и другое при определении n для теста в целом. Как и в парном примере, это помогает подтвердить доказательства (или их отсутствие), обнаруженные при выполнении самого t-теста.
Как и в парном примере, это помогает подтвердить доказательства (или их отсутствие), обнаруженные при выполнении самого t-теста.

 Чем выше число, тем ближе t-распределение к нормальному распределению. Примерно после 30 степеней свободы t и стандартная нормаль практически совпадают.
Чем выше число, тем ближе t-распределение к нормальному распределению. Примерно после 30 степеней свободы t и стандартная нормаль практически совпадают. Во-первых, когда вы оцениваете пропорции (количество отказов на конвейере). Во-вторых, когда размер вашей выборки достаточно велик (обычно около 30), вы можете использовать нормальное приближение для оценки средних значений.
Во-первых, когда вы оцениваете пропорции (количество отказов на конвейере). Во-вторых, когда размер вашей выборки достаточно велик (обычно около 30), вы можете использовать нормальное приближение для оценки средних значений.
