Математика — страница 5
Сейчас читают:
- Как оформлять реферат правильно — образец
- Оформление курсовой работы по ГОСТу: образец
- Как оформить титульный лист реферата?
- Оформление рисунков в дипломе (примеры)
- Правила оформления приложений в курсовой работе
- Оформление списка литературы по ГОСТу 2020, 2021 образец
- Оформление диплома в 2022 году
- Оформление курсовой работы по госту 2020, 2021
Не успеваете написать работу?
Заполните форму и узнайте стоимость
Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертацияКонтактные данные — строго конфиденциальны!
Указывайте телефон без ошибок! — потребуется для входа в личный кабинет.
* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности
Подтверждение
Ваша заявка принята.
Ей присвоен номер 0000.
Просьба при ответах не изменять тему письма и присвоенный заявке номер.
В ближайшее время мы свяжемся с Вами.
Ошибка оформления заказа
Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам.
Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.
Математика
12.11.21
11 мин.
Формулы площади прямоугольного треугольника через катеты
При решении задач по геометрии очень часто возникает необходимость вычислить площадь прямоугольного треугольника через катеты. В интернете можно найти много информации на эту тему, но не всегда она соответствует действительности, поскольку некоторые авторы не являются экспертами в физико-математическом направлении.
Читать полностью
Математика
12.11.21
11 мин.
Свойства рациональных дробей и примеры решения задач
На уроках алгебры в 8 классе рассматриваются рациональные дроби и их свойства. Тема является очень важной, поскольку приобретаются навыки упрощения тождеств, решения уравнений, анализа функций, а также выполнения других операций. Математики рекомендуют перед практикой разобрать теорию и основные алгоритмы исследования выражений этого типа. Общие сведения Рациональная дробь — разновидность рационального выражения, числитель и знаменатель которой…
Читать полностью
Математика
12.11.21
10 мин.
Примеры пересечения множеств в 8 и 3 классе
Математика тесно связана с различными дисциплинами, одной из которых является информатика.
В последней применяются массивы, состоящие из чисел, букв и слов. Чтобы научиться работать с этим типом данных, необходимо разобрать объединение и пересечение множеств, примеры которых разбираются на уроках по алгебре в 8 классе средних образовательных школах. Однако для начала нужно изучить теорию.
Общие сведения
Множеством (массивом)…
Математика
12.11.21
12 мин.
Формула вычисления объёма и площади прямоугольника
Форма объекта и его линейные размеры определяют один из важных с геометрической точки зрения параметров — объём. Формула для прямоугольника, позволяющая его вычислить, довольно проста и основана на знании стороны и высоты. Но при решении не всегда известны значения рёбер фигуры, поэтому приходится использовать свойства параллелограмма, а именно — способы нахождения площади. Общие сведения По своей сути…
Читать полностью
Математика
12.
11.21
13 мин.
Алгоритм, примеры сложения и вычитания смешанных чисел
Одни и те же значения в математике можно записать различными выражениями. Использование той или иной записи зависит от конкретного примера. Довольно часто приходится иметь дело со смешанными числами. Их сложение и вычитание опирается на правила простейших арифметических действий с обыкновенными дробями, имеющими одинаковые знаменатели. Другими словами, целую часть в выражении представляют в виде дроби и выполняют необходимое действие.
Читать полностью
Математика
12.11.21
10 мин.
Вариация — понятие, относительные и абсолютные показатели, способы их расчета
Этот термин ведёт своё происхождение от латинского слова «varito». Оно переводится как «изменение» или «различие».
Вариация — это количественная мера изменения определённых данных, которая помогает исследовать её случайные изменения.
Для их анализа применяют различные статистические методы.
О них будет более подробно рассказано в этой статье.
Онлайн-калькулятор показателей вариации
Показатели вариации в статистике
Статистика…
Читать полностью
Математика
12.11.21
9 мин.
Арифметическая (алгебраическая) прогрессия — определение, примеры нахождения с решением
Часто, при решении задач, связанных с наблюдениями и присвоением значения определенному событию за определенный промежуток времени, получается ряд чисел, который именуется арифметической прогрессией.
Одна из главных отличительных особенностей — такая математическая модель имеет закономерность, по которой можно вычислить любой неизвестный член, что упрощает прогнозирование при вычислении физических ситуаций.
Примерами повседневного использования могут являться наблюдение за температурой воздуха, прогнозирование расходов с занесением результатов в таблицу и др.
Читать полностью
Математика
12.11.21
13 мин.
Паскаль (Pascal) — основы программирования для начинающих
Пожалуй, нет ни одного современного человека, кто бы не знал язык Паскаль (основы программирования). И это не удивительно! Еще в учебнике по информатике для школьников расписаны самые основные понятия этой уникальной программы. Сейчас, в век информационных технологий, каждый может провести для себя обучение по самоучителю онлайн (пройдя курсы «Изучение языков программирования с нуля»; «Паскаль для чайников» и другие). История изучаемого языка не так проста: Паскаль претерпел множество изменений, прежде чем…
Читать полностью
Математика
12.11.21
9 мин.
Степень — свойства, правила, действия и формулы
Одной из главных характеристик в алгебре, да и во всей математике является степень.
Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.
В данной статье рассмотрим самые важные вопросы, касающиеся этого определения. А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.
Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем…
Читать полностью
Математика
12.11.21
10 мин.
Комбинаторика — основные понятия и формулы с примерами
Комбинаторика — раздел математики. Основные понятия и формулы комбинаторики как науки применяются во всех сферах жизни.
Неудивительно, что она включена в программу 11 класса, а также во вступительные испытания во многих ВУЗах РФ. Ее основы лежат в прикладном искусстве многих сфер деятельности человека.
Ее история насчитывает более 6 веков. Первые комбинаторные задачи появились в трудах философов и математиков Средневековья.
Читать полностью
Математика
12.11.21
8 мин.
Парабола — свойства и график квадратичной функции
Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже. Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика. Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа. Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание.…
Читать полностью
Математика
12.11.21
13 мин.
Клавиатура компьютера — назначение и описание клавиш
В статье будут рассматриваться современная раскладка клавиатуры компьютера и её назначение, будет дано описание клавиш и фото.
Клавиатура прошла ряд видоизменений с 1984 года до нашего времени. Она приобретала дополнительные элементы, чтобы сделать работу за компьютером проще для начинающих и комфортнее для профессионалов.
Любому пользователю теперь доступна комплектация под его творческие амбиции.
Компьютерная клавиатура — фото, описание и устройство
На размер клавиатуры влияет число дублирующих клавиш. К примеру, для…
Читать полностью
Математика
12.11.21
5 мин.
Площадь поверхности цилиндра — формула расчета
Как вычислить площадь поверхности цилиндра — тема данной статьи. В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.
Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями.
Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его…
Читать полностью
Математика
12.11.21
13 мин.
Объём и площадь поверхности правильной четырёхугольной призмы
В школьной программе по курсу стереометрии изучение объёмных фигур обычно начинается с простого геометрического тела — многогранника призмы. Роль её оснований выполняют 2 равных многоугольника, лежащих в параллельных плоскостях. Частным случаем является правильная четырёхугольная призма. Её основами являются 2 одинаковых правильных четырёхугольника, к которым перпендикулярны боковые стороны, имеющие форму параллелограммов (или прямоугольников, если призма не наклонная). Как…
Читать полностью
Математика
12.11.21
9 мин.
Формулы сокращённого умножения (ФСУ): таблица и применение
Одной из первых тем, изучаемых в курсе алгебры, являются формулы сокращённого умножения.
В 7 классе они применяются в самых простых ситуациях, где требуется распознать в выражении одну из формул и выполнить разложение многочлена на множители или, наоборот, быстро возвести сумму или разность в квадрат или куб. В дальнейшем ФСУ используют для быстрого решения неравенств и уравнений и даже для вычисления…
Читать полностью
Математика
12.11.21
8 мин.
Что такое трапеция: свойства четырёхугольника, теоремы и формулы
В курсе геометрии за 8-й класс подразумевается изучение свойств и признаков выпуклых четырёхугольников. К ним относятся параллелограммы, частными случаями которых являются квадраты, прямоугольники и ромбы, и трапеции. И если решение задач на различные вариации параллелограмма чаще всего не вызывает сильных затруднений, то разобраться, какой четырёхугольник называется трапецией, несколько сложнее. Определение и виды В отличие от других четырёхугольников, изучаемых в школьной…
Читать полностью
Математические трюки для быстрого счёта читать онлайн Ингве Фогт (Страница 2)
Правило 1
Первое правило на удивление простое.
Порядок чисел при умножении роли не играет:
…
a × b = b × a
Если буквы вам не по душе, могу продемонстрировать то же самое на простейшем цифровом примере.
3 × 7 даст тот же результат, что 7 × 3. Итак, то, в каком порядке перемножать числа, совершенно не важно.
Правило 2
Второе правило тоже манна небесная для тех, кто пребывает в заблуждении и считает математику сложной.
Порядок чисел при сложении роли не играет.
…
a + b = b + a
И вот вам пример: 2 + 3 дадут в результате то же число, что и 3 + 2.
Правило 3
Квадрат определенного числа выглядит следующим образом: a × a = a2.
Обратите внимание на крошечную цифру 2 над последней «а» — читая эту книгу, вы успеете близко с ней познакомиться. Математики называют такие цифры степенями.
Вот еще пример: 3 × 3 можно обозначить как 32.
Разумеется, отрицательные числа тоже можно возводить в квадрат:
…
(‒a) × (‒a) = (‒a)2 = a2
Например: (‒3) × (‒3) соответствует (‒3)2.
А вот это невероятно красиво:
(‒3)2 дает тот же результат, что и 32.
Правило 4
На квадратные корни тоже приятно посмотреть:
Это означает, что если извлечь квадратный корень из возведенного в квадрат числа, то это же число и получится.
На языке цифр это выглядит вот так:
Правило 5
Когда надо умножать отрицательные числа, многие впадают в ступор. Если вас это тоже касается, то быстрому счету вам придется учиться долго.
Одно из важнейших правил звучит так: минус на минус дает плюс.
…
(‒x) × (‒y) = x × y
Примеры:
.
..
(‒2) × (‒3) = 2 × 3 = 6
(‒4) × (‒5) = 4 × 5 = 20
А вот если минус умножить на плюс, то получится, наоборот, минус:
…
(‒x) × y = ‒(x × y)
Примеры:
…
(‒2) × 3 = ‒(2 × 3) = ‒6
4 × (‒5) = ‒(4 × 5) = ‒20
Запомним это — минус на минус и минус на плюс, и тогда все минусы математики превратятся для вас в плюсы!
Правило 6
Если хотите понять доказательства приведенных в этой книге методов, придется научиться разлагать числовые выражения на множители и раскрывать скобки:
…
a(b + c) = ab + ac
(a + c)(b + d) = ab + ad + cb + cd
Вот и все — больше про разложение на множители знать нам ничего не понадобится.
Правило 7
Некоторые методы быстрого счета в этой книге основаны на трех видах квадратичных тождеств, которые включены в стандартную школьную программу. Все они — особые случаи правила 6:
…
(a + c)(b + d) = ab + ad + cb + cd
Квадратичное тождество первого типа:
…
(a + b)2 = a2 + 2ab + b2
Квадратичное тождество второго типа:
…
(a ‒ b)2 = a2 ‒ 2ab + b2
Квадратичное тождество третьего типа:
…
(a + b)(a ‒ b) = a2 ‒ b2
С этими семью правилами в готовальне у вас есть все шансы стать чемпионами быстрого счета. Ну что ж, пора отправляться завоевывать мир! Удачи и успехов!
3
Ходячий калькулятор
Чемпион мира по быстрому счету
В начальной школе я терпеть не мог спорт, зато мечтал стать чемпионом мира по решению в уме всяких математических примеров.
Поэтому мне казалось ужасно несправедливым, что школьные спортсмены то и дело выступали на разных соревнованиях, ведь соревнований по математике просто не существовало. Сейчас-то я понимаю, что мое мнение о собственных математических способностях было необоснованно завышенным, я жил в мечтах: хотя считал я и правда довольно быстро, а числа так просто обожал, моих способностей не хватало, если числа в примерах были больше приведенных в таблице умножения. Впрочем, об этом никто не догадывался. Слухи о моих феноменальных математических способностях разлетались со скоростью света и с действительностью ничего общего не имели. Никогда не забуду, как мама одного из моих одноклассников на глазах у всего класса погладила меня по голове и выразила свое восхищение: еще бы, ведь я умею в уме перемножать многозначные числа. Мне тогда было девять лет. А еще мама моего одноклассника слышала, будто я умею и миллионы перемножать. Все это было неправдой, но стеснительность помешала мне опровергнуть слухи.
Я смотрел на эту женщину и вспоминал, как однажды, будучи первоклашкой, возвращался из школы домой и был пойман шестиклассниками, которые потребовали сделать за них домашку по математике. Они крепко держали меня (впрочем, особых усилий от них не требовалось — я был самым мелким во всей школе) и, пока я не решил все задачки, не отпускали.
Задачки у них оказались очень простыми. В одной я нарочно допустил ошибку — хотел проверить, заметят ли они, но они, к моей великой радости, ничего не заподозрили. Легенда о моем таланте вдребезги разлетелась в шестом классе, когда отец отвел меня к университетскому профессору, предварительно рассказав ему о моих невероятных успехах. Профессор дал мне несколько примеров и выглядел довольно-таки разочарованным, когда я ошибся в первом же из них. Именно в тот момент я понял, что лучше всего считаю в спокойной обстановке и наилучшее впечатление произвожу на тех, кто сам с математикой не дружит.
В уме быстрее всех в мире считает американец по имени Скотт Фленсбург, и для него обстановка никакого значения не имеет.
Его часто приглашают на знаменитые ток-шоу, а звезда американских телеэкранов Реджис Филбин назвал Фленсбурга живым калькулятором. Скотт Фленсбург посчитает в голове быстрее, чем мы успеем посчитать на калькуляторе. 27 апреля 2000 г. он попал в Книгу рекордов Гиннесса, потому что за 15 секунд наибольшее количество раз прибавил случайно выбранное двузначное число. Ему досталось число 38, и за это ничтожно короткое время он успел прибавить его 36 раз и выдать ответы: 38, 76, 114, 152, 190, 228 и так далее до 1368. Это означает, что одной секунды ему хватало, чтобы прибавить число 38 два раза. Мягко говоря, потрясающе. Попробуйте сами! Так быстро считать еще никому не удавалось!
Как сказал, демонстрируя по телевизору свой рекорд, он сам, «встроенный в мозг калькулятор — это щедрый подарок, вот только слова мешают». Дело в том, что считает Фленсбург быстрее, чем успевает произнести ответ, хотя говорит тоже не медленно. Это несоответствие скорости работы мозга темпу речи можно сравнить с супербыстрым компьютером, подключенным к постоянно зависающему принтеру.
С такой же скоростью Скотт Фленсбург умножает и делит числа. Мы еще и калькулятор не успеем включить, а он уже извлечет квадратный и кубический корень и с той же скоростью выдаст ответ, даже если в нем имеются дроби. «Я не атлет, я матлет», — повторяет он словно мантру. Если имена великих спортсменов — Златана, Роналду и Болта — знакомы каждому, то матлеты не известны никому. А ведь как чудесно было бы узнать о них в детстве!
Конец ознакомительного фрагмента
Калькулятор и решатель тригонометрических тождеств
Получите подробные решения ваших математических задач с помощью нашего пошагового калькулятора
Доказательство тригонометрических тождеств . Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. Проверьте все наши онлайн-калькуляторы здесь!1
2
3
4
5
6
7
8
A
B
C
0006 DF
G
M
N
U
V
W
x
Y
Z
.
(◻)
+
—
×
◻/◻
/
÷
◻ 2
◻ ◻
√◻
√
◻ √ ◻
◻ √
∞
e
π
ln
log
log ◻
LIM
D/DX
D □ x
∫
∫ ◻
| ◻ |
θ
=
>
<
>=
<=
sin
cos
tan
cot
sec
csc
asin
acos
atan
acot
асек
акск
Sinh
COSH
TANH
COOTH
SECH
CSCH
ASINH
ACOSH
ATANH
ACOTH
ASECH
ACSCH
669
ASECH
666
ASECH
9
9
Пример
Решенные проблемы
Сложные задачи
1
Решенный пример доказательства тригонометрических тождеств
$\frac{1}{\cos\left(x\right)}-\frac{\cos\left(x\right)}{1+\sin\left(x \right)}=\tan\left(x\right)$
2
Наименьшее общее кратное (НОК) суммы алгебраических дробей состоит из произведения общих множителей с наибольшим показателем степени и необычных множителей
$L.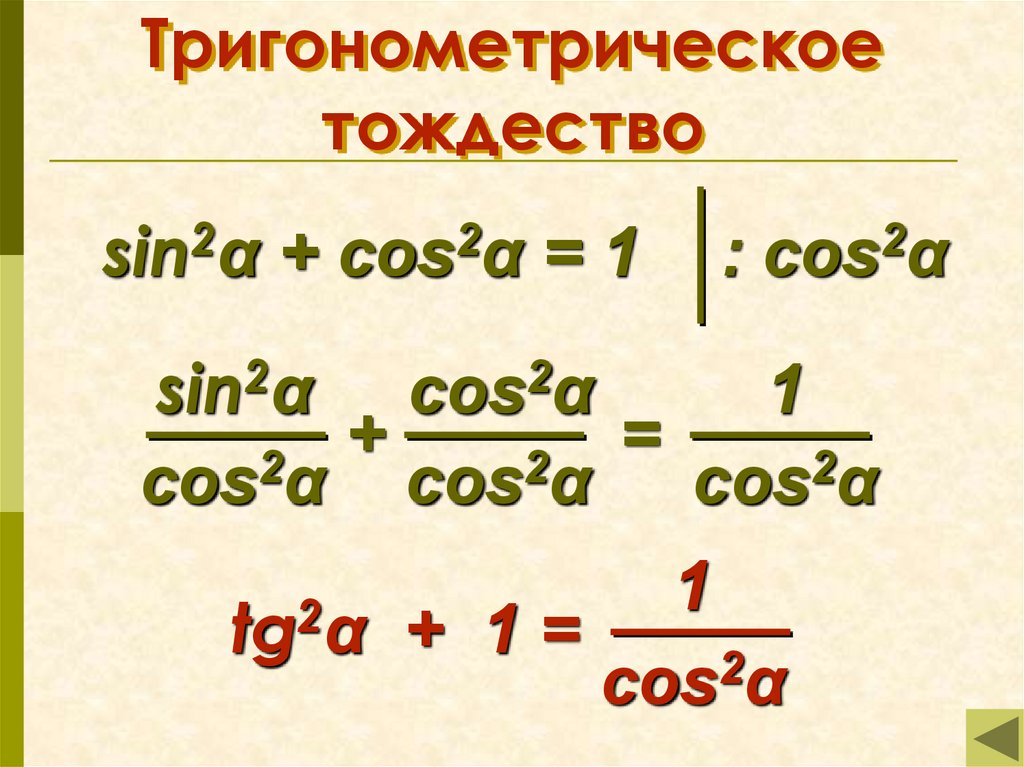
C.M.=\cos\left(x\right)\left(1 +\sin\left(x\right)\right)$
3
Получили наименьшее общее кратное, поместим НОК в знаменатель каждой дроби и в числитель каждой дроби прибавим множители, которые нам нужны для завершения 92+\sin\left(x\right)$ по НОД: $\sin\left(x\right)$
$\frac{\sin\left(x\right)\left(\sin\left( x\right)+1\right)}{\cos\left(x\right)\left(1+\sin\left(x\right)\right)}=\tan\left(x\right)$
7
Упростите дробь $\frac{\sin\left(x\right)\left(\sin\left(x\right)+1\right)}{\cos\left(x\right)\left(1) +\sin\left(x\right)\right)}$ на $\sin\left(x\right)+1$
$\frac{\sin\left(x\right)}{\cos\left (х\справа)}=\загар\слева(х\справа)$
8
Примените тригонометрическое тождество: $\frac{\sin\left(x\right)}{\cos\left(x\right)}$$=\tan\left(x\right)$
$\tan \влево(х\вправо)=\загар\влево(х\вправо)$
9
Поскольку обе стороны равенства равны, мы доказали тождество
верно
Окончательный ответ
правда
Борьба с математикой?
Доступ к подробным пошаговым решениям тысяч проблем, число которых растет с каждым днем!
Калькулятор и решатель тригонометрических тождеств
Получите подробные решения ваших математических задач с помощью нашего пошагового калькулятора тригонометрических тождеств
.