Онлайн калькулятор упрощение логических выражений: Математическая логика · oнлайн с подробным объяснением

Основные законы электроники для начинающих. Последовательное и параллельное соединение. Соединение резисторов. Как с помощью трех резисторов (1К) получить сборки с шестью различными сопротивлениями (0.33К, 0.5К, 0.66К, 1К, 1.5К, 2К, 3К). Как с помощью резисторов трех номиналов получить необходимый ряд сопротивлений. Соединение конденсаторов. Закон Ома.

Алгебра логики, разработанная Джорджем Булем (булева алгебра) — основа всех современных компьютеров и цифровых устройств. Знание базовых элементов алгебры логики необходимо для создания BEAM-роботов на логических цепях. Алгебра логики оперирует всего двумя значениями — логической истиной и логической ложью.

Операция логического отрицания. Инверсия. Обозначение инверсии в логических формулах и выражениях. Инвертор — базовый кирпичик BEAM-робототехники. Для чего используют инверторы.

Операция логического умножения (конъюнкции) в алгебре логики. Обозначение логического умножения в формулах. Свойства логического умножения. Логическое умножение логической переменной на логическую константу.

Логическая операция сложения (дизъюнкция) в логической алгебре.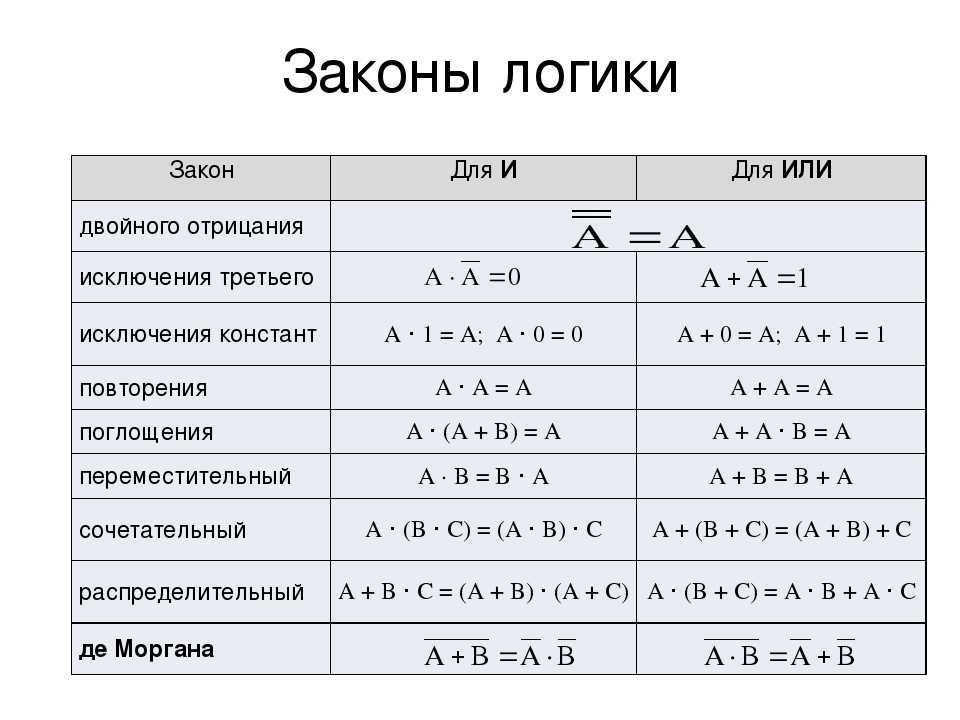 Как обозначается дизъюнкция в логических выражениях. Свойства логического сложения. Логичекое сложение переменной и логической константы. Таблица истинности для операции логического сложения.

Основные законы алгебры логики. Законы де Моргана. Следствия законов логической алгебры.

Логические элементы, реализующие базовые логические операции. Логический элемент НЕ (инвертор). Логический элемент И (умножение). Логический элемент ИЛИ (сложение). Обозначение логических элементов на логических и электронных схемах. Стандарты DIN и ANSI в обозначениях логических элементов. Комбинированыые логические элементы. Логический базис. Как получить с помощью комбинированных элементов одного вида все другие логические элементы.

Калькулятор булевой алгебры — онлайн-упрощение булевых логических выражений

Поиск инструмента

Калькулятор логических выражений

Инструмент/калькулятор для упрощения или минимизации логических выражений (булева алгебра), содержащих логические выражения с И, ИЛИ, НЕ, XOR.

Результаты

Калькулятор логических выражений — dCode

Метки: Символьные вычисления, Электроника

Поделиться

dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Упрощение логических выражений

См. также: Таблица истинности — Решатель уравнений — Двоичный код

Ответы на вопросы (FAQ)

Что такое логическое выражение? (Определение)

A Логическое выражение (или Логическое выражение) — это математическое выражение, использующее Булева алгебра , которая использует логические значения (0 или 1, истина или ложь) в качестве переменных и имеет логические значения в качестве результата/упрощения. Выражение может содержать такие операторы, как конъюнкция (И), дизъюнкция (ИЛИ) и отрицание (НЕ).

Как упростить/минимизировать логическое выражение?

Для упрощения булевых уравнений можно использовать различные методы: помимо классического развития через ассоциативность, коммутативность, дистрибутивность и т. д., таблицы истинности или диаграммы Венна обеспечивают хороший обзор выражений.

Пример: Исходное выражение (LaTeX) $$ \overline{a \land b \land (c \lor \bar{d})} \lor \bar{b} $$

dCode допускает несколько синтаксисов:

Алгебраическая запись

Пример: !(ab(c+!d))+!b с неявным умножением ab = a AND b и ! (восклицательный знак) для строки : логический НЕ .

Логические/компьютерные обозначения

Пример: !(a&&b&&(c||!d))||!b с двойным символом и (амперсанд) для И и двойным символом | (прямая, вертикальная черта) для логического ИЛИ .

Буквенное обозначение

Пример: НЕ (a И b И (c ИЛИ НЕ d)) ИЛИ НЕ b

Для одного и того же выражения может быть несколько минимальных представлений, dCode предоставляет решение и выводит алгебраическое обозначение.

Некоторые обозначения неоднозначны, избегайте функционального обозначения ‘XOR(a,b)’ для записи a XOR b , также избегайте суффикса штрих/апостроф перед `a’ и предпочтите !a .

Что такое методы упрощения булевой алгебры?

Булева алгебра обладает многими свойствами (булевыми законами):

1 — Элемент тождества: $0$ нейтрален для логического ИЛИ, тогда как $1$ нейтрален для логического И

$$a + 0 = a \\a . 1 = a $$

2 — Поглощение: $1$ поглощает для логического ИЛИ, а $0$ поглощает для логического И

$$ a + 1 = 1 \\ a.0 = 0 $$

3 — Идемпотентность: многократное применение одной и той же операции не меняет значение

$$ a + a = a + a + \cdots + а = а \ а . а = а . а . \cdots . a = a $$

4 — Инволюция или двойное дополнение: противоположность противоположности $ a $ est $ a $

$$ a = \overline{\overline{a}} = !(!a) $$

5 — Дополнительность по противоречию: $ a $ AND $ \text{not}(a) $ невозможно, поэтому ложно и равно $ 0 $

$$ а . \overline{a} = 0 $$

6 — Дополнительность по исключенному третьему: $ a $ OR $ \text{not}(a) $ всегда истинно, поэтому $ 1 $

$$ a + \overline{ a} = 1 $$

7 — Закон ассоциативности: скобки между одинаковыми операторами бесполезны

$$ a.(b.c) = (a.b).c = a.b.c \\ a+(b+c) = (a+b) +c = a+b+c $$

8 — Закон коммуникативности: порядок не имеет значения

$$ a.b = b. a \\ a+b = b+a $$

9 — Закон распределения: И распределено над ИЛИ, но также ИЛИ распределяется по И

$$ a.(b+c) = a.b + a.c \\ a+(b.c) = (a+b).(a+c) $$

10 — Законы Де Моргана (подробнее см. ниже)

$$ \overline{a+b} = \overline{a}.\overline{b} \\ \overline{a.b} = \overline{a}+\overline{b} $$

11 — Другие упрощения комбинации указанных выше

$$ a.(a+b) = a \\ a+(a.b) = a \\ (a.b) + (a.!b) = a \\ (a+b).(a+ !b) = a \\ a + (!a.b) = a + b \\ a.(!a + b) = a.b \\ a.b + \overline{a}.c = a.b + \overline{a}.c + b.c $$

Как показать/продемонстрировать, что 2 логических выражения равны?

Метод 1: упростите их , пока не получите то же самое написание в булевой алгебре .

Метод 2: путем вычисления их таблицы истинности , которая должна быть идентичной.

Что такое закон де Моргана?

Законы де Моргана часто используются для перезаписи логических выражений. Обычно они формулируются так: не (а и б) = (не а) или (не б) и не (а или б) = (не а) и (не б) . Вот эквивалентные логические записи:

$$ \overline{(a \land b)} \leftrightarrow (\overline{a}) \lor (\overline{b}) \iff \overline{AB} = \overline{a} + \overline{b } $$

$$ \overline{(a \lor b)} ​​\leftrightarrow (\overline{a}) \land (\overline{b}) \iff \overline{a+b} = \overline{a} . \overline{b} $$

Что такое дизъюнктивная или конъюнктивная нормальная форма?

В логике можно использовать разные форматы для обеспечения лучшей читабельности или удобства использования.

Нормальная дизъюнктивная форма (DNF) использует сумму произведений (SOP):

Пример: (a&&c)||b

Нормальная конъюнктивная форма (CNF) или форма предложения использует произведение сумм (POS):

Пример: (a+b).(b). +c)

Как показать пошаговые расчеты?

Шаги расчета, какими их может себе представить человек, для решателя не существуют. Выполняемые операции являются бинарными побитовыми и не соответствуют выполняемым при разрешении с помощью карандаша и бумаги.

Исходный код

dCode сохраняет право собственности на исходный код «Калькулятора логических выражений». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Калькулятор логических выражений», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Булевых выражений». Функции калькулятора (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, script или доступ к API для «Калькулятора логических выражений» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!

Cite dCode

Копирование и вставка страницы «Калькулятор логических выражений» или любых его результатов разрешено, если вы цитируете dCode!
Цитировать как источник (библиографию):
Калькулятор логических выражений на dCode.fr [онлайн-сайт], получено 08 февраля 2023 г., https://www.dcode.fr/boolean-expressions-calculator

Сводка

• Упрощение логических выражений
• Что такое логическое выражение? (Определение)
• Как упростить/уменьшить логическое выражение?
• Что такое методы упрощения булевой алгебры?
• Как показать/продемонстрировать, что 2 логических выражения равны?
• Что такое закон де Моргана?
• Что такое дизъюнктивная или конъюнктивная нормальная форма?
• Как показать пошаговые расчеты?

Похожие страницы

• Таблица истинности
• Решатель уравнений
• Двойной логический
• Булевы Minterms и Maxterms
• Binary Code
• Math Expression Simplifier
• Remove Parentheses
• DCODE’S TOOLS LIST

Support

• Paypal
• Patreon
• More

Forum/Help

Keywords

bool,boole,boolean ,выражение,алгебра,логика,логическое,упростить,упрощение,и,или,не,исключающее ИЛИ,амперсанд,труба,восклицательный знак,морган

Ссылки

▲

Калькулятор булевой алгебры 9(B v C)

Поддерживаемые операции: И , ИЛИ , НЕ , XOR , ПОДРАЗУМЕВАЕТ , ПРЕДОСТАВЛЯЕТСЯ И ЭКВИВ .

Операции и константы нечувствительны к регистру.

Переменные чувствительны к регистру, могут быть длиннее одного символа, могут содержать только буквенно-цифровые символы символов, цифр и символа подчеркивания и не может начинаться с цифры.

Операции

Операции выполняются в порядке приоритета, от большего к меньшему. Операции с одинаковым приоритетом выполняются слева направо. Чтобы сначала выполнить конкретную операцию, заключите ее в скобки ( ) .

Эксплуатация	Псевдонимы	Вычисляется как true , если	Вычисляется как false , если	Приоритет 9& · *	оба A и B являются истинными .	одно или оба являются ложными .	средний
А ЭКВИВ В	⇔ ≡ ↔ =	оба A и B являются истинными ; или оба ложные .	один правда а другой ложь .	средний
A ПОДРАЗУМЕВАЕТ B	⇒ → ⊂ <	A — это false ; или A равно true и B равно true .	A равно true и B равно false .	средний
А ПРЕДОСТАВЛЯЕТСЯ B	⇐ ← ⊃ >	A это true и B это true ; или B равно false .	A равно false и B равно true .	средний
А ИЛИ В	∨ v + ∥ |	A - это true ; B это правда ; или оба true .	оба являются ложными .	самый низкий
А Исключающее ИЛИ Б	⊻ ⊕	A равно true и B равно false ; или A равно false и B равно true .	оба являются истинными или оба ложными .	самый низкий

Константы

Константа	Псевдонимы	Описание
ИСТИНА	1 Т ⊤ правда	Всегда оценивается как true . No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт