Найти координаты середины отрезка — онлайн калькулятор
Середина отрезка — это точка, принадлежащая этому отрезку и находящаяся на равном расстоянии от его концов. Координаты середины отрезка, который имеет концы A(xa,ya) и B(xb,yb), рассчитывается по формулам:
xc=xa+xb2,
yc=xb+yb2.
Чтобы найти середину отрезка по координатам онлайн:
- введите данные координат точек A и B в соответствующие поля;
- для получения решения нажмите на кнопку «Рассчитать».
Как найти середину отрезка с помощью онлайн-калькулятора
Рассмотрим пример, наглядно демонстрирующий работу с онлайн-калькулятором. Найдем середину произвольного отрезка, начальная и конечная точки которого имеют координаты (1;4) и (3;0). Для этого:
- Выберем размерность (2 или 3). Калькулятор позволяет задать отрезок соответственно на плоскости, или в пространстве. В нашем конкретном примере выберем плоскость (2):
- Введем в пустые поля координаты начальной и конечной точек отрезка:
- После ввода координат остается нажать «Рассчитать» и получить ответ с решением:
Материалы, которые помогут вам лучше разобраться в теме:
- Нахождение координат середины отрезка: примеры, решения
- Расстояние от точки до точки: формулы, примеры, решения
- Деление отрезка в заданном соотношении: координаты точки
- Прямая на плоскости – необходимые сведения
- Прямая в пространстве – необходимые сведения
- Прямоугольная система координат на плоскости и в пространстве
Ответ:
Решение
Ответ:
- list» :key=»`error-${eIdx}`» v-html=»e»/>
Похожие калькуляторы:
- Длина отрезка. Расстояние между точками
- Каноническое уравнение прямой проходящей через две точки
- Параметрическое Уравнение прямой проходящей через две точки
- Расстояние от точки до прямой на плоскости
- Уравнение плоскости (координаты трех точек)
- Уравнение плоскости (координаты вектора нормали и точки)
- Точка пересечения прямых (с угловыми коэффициентами)
- Расстояние от точки до прямой в пространстве
- Расстояние от точки до плоскости
- Расстояние между плоскостями
- Угол между плоскостями
- Угол между прямой и плоскостью
Найти координаты середины отрезка онлайн
С помощью сервиса Zaochnik школьники и студенты могут находить середину отрезка онлайн. Эта возможность сокращает время на подготовку к занятиям. Самостоятельно полученный ответ легко сверить с решением на сайте. Подробные вычисления в случае нестыковки помогут выявить и исправить неточности.
Эта возможность сокращает время на подготовку к занятиям. Самостоятельно полученный ответ легко сверить с решением на сайте. Подробные вычисления в случае нестыковки помогут выявить и исправить неточности.
Расчет середины отрезка по координатам онлайн имеет ряд преимуществ:
- нет надобности искать необходимую формулу для вычислений – она уже заложена в программе;
- набор действий выполняется за один раз и подробно отображается в решении;
- исключены неточности в вычислениях, которые возникают при расчетах на бумаге;
- сервис не ограничивает число запросов на расчет от пользователя;
- за использование калькулятора не требуется платить.
Если у вас возникли вопросы при самостоятельном изучении этой или других тем, напишите консультанту. Наш специалист оперативно предложит вам выгодные условия сотрудничества по решению задач.
Понравился калькулятор? Поделись с друзьями!
Найти координаты середины отрезка онлайн.
 Координаты середины отрезка. Формулы координат середины отрезка
Координаты середины отрезка. Формулы координат середины отрезкаНачальные геометрические сведения
Понятие отрезка, как и понятие точки, прямой, луча и угла, относится к начальным геометрическим сведениям. С перечисленных понятий начинается изучение геометрии.
Под «начальными сведениями» обычно понимают нечто элементарное и простое. В понимании, возможно, это так и есть. Тем не менее, такие простые понятия часто встречаются и оказываются необходимыми не только в нашей повседневной жизни, но и в производстве, строительстве и прочих сферах нашей жизнедеятельности.
Начнём с определений.
Определение 1
Отрезок — часть прямой, ограниченная двумя точками (концами).
Если концы отрезка являются точками $A$ и $B$, то образованный отрезок записывают как $AB$ или $BA$. Такому отрезку принадлежат точки $A$ и $B$, а также все точки прямой, лежащие между этими точками.
Определение 2
Середина отрезка — точка отрезка, которая делит его пополам на два равных отрезка.
Если это точка $C$, то $AC=CB$.
Измерение отрезка происходит сравнением с определённым отрезком, принятым за единицу измерения. Чаще всего используют сантиметр. Если в заданном отрезке сантиметр укладывается ровно четыре раза, то это означает, что длина данного отрезка равна $4$ см.
Введём простое наблюдение. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих отрезков.
Формула нахождения координаты середины отрезка
Формула нахождения координаты середины отрезка относится к курсу аналитической геометрии на плоскости.
Дадим определение координатам.
Определение 3
Координаты — это определённые (или упорядоченные) числа, которые показывают положение точки на плоскости, на поверхности или в пространстве.
В нашем случае, координаты отмечаются на плоскости, определённой координатными осями.
Рисунок 3. Координатная плоскость. Автор24 — интернет-биржа студенческих работ
Опишем рисунок. На плоскости выбрана точка, называемая началом координат. Её обозначают буквой $O$. Через начало координат проведены две прямые (координатные оси), пересекающиеся под прямым углом, причём одна из них строго горизонтальная, а другая — вертикальная. Такое положение считается обычным. Горизонтальная прямая называется осью абсцисс и обозначается $OX$, вертикальная — осью ординат $OY$.
Её обозначают буквой $O$. Через начало координат проведены две прямые (координатные оси), пересекающиеся под прямым углом, причём одна из них строго горизонтальная, а другая — вертикальная. Такое положение считается обычным. Горизонтальная прямая называется осью абсцисс и обозначается $OX$, вертикальная — осью ординат $OY$.
Таким образом, оси определяют плоскость $XOY$.
Координаты точек в такой системе определяются двумя числами.
Существуют разные формулы (уравнения), определяющие те или иные координаты. Обычно в курсе аналитической геометрии изучают разные формулы прямых, углов, длины отрезка и прочие.
Перейдём сразу к формуле координаты середины отрезка.
Определение 4
Если координаты точки $E(x,y)$ — это середина отрезка $M_1M_2$, то:
Рисунок 4. Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ
Практическая часть
Примеры из школьного курса геометрии достаточно просты. Рассмотрим несколько основных.
Для лучшего понимания, рассмотрим для начала элементарный наглядный пример.
Пример 1
Имеем рисунок:
На рисунке отрезки $AC, CD, DE, EB$ равны.
- Серединой каких отрезков является точка $D$?
- Какая точка является серединой отрезка $DB$?
- точка $D$ является серединой отрезков $AB$ и $CE$;
- точка $E$.
Рассмотрим другой простой пример, в котором нужно вычислить длину.
Пример 2
Точка $B$ — середина отрезка $AC$. $AB = 9$ см. Какая длина $AC$?
Так как т. $B$ делит $AC$ пополам, то $AB = BC= 9$ см. Значит, $AC = 9+9=18$ см.
Ответ: 18 см.
Прочие подобные примеры обычно идентичны и ориентированы на умение сопоставлять значения длин и их представление с алгебраическими действиями. Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром.
Не составляет никакого труда. Для их расчета существует простое выражение, которое легко запомнить. Например, если координаты концов какого-либо отрезка соответственно равняются (х1; у1) и (х2; у2) соответственно, то координаты его середины рассчитываются как среднее арифметическое этих координат, то есть:
Вот и вся сложность.
Рассмотрим расчет координат центра одного из отрезков на конкретном примере, как Вы и просили.
Задача.
Найти координаты некоей точки М, если она является серединой (центром) отрезка КР, концов которого имеют такие координаты: (—3; 7) и (13; 21) соответственно.
Решение.
Используем рассмотренную выше формулу:
Ответ . М (5; 14).
С помощью данной формулы можно также найти не только координаты середины какого-либо отрезка, но и его концов. Рассмотрим пример.
Задача.
Даны координаты двух точек (7; 19) и (8; 27). Найти координаты одного из концов отрезка, если предыдущие две точки являются его концом и серединой.
Решение.
Обозначим концы отрезка К и Р, а его середину S. Перепишем формулу с учетом новых названий:
Подставим известные координаты и вычислим отдельные координаты:
После кропотливого труда я вдруг заметил, что размеры веб страниц достаточно велики, и если так пойдёт дальше, то можно тихо мирно озвереть =) Поэтому предлагаю вашему вниманию небольшое эссе, посвященное очень распространённой геометрической задаче – о делении отрезка в данном отношении , и, как частный случай, о делении отрезка пополам .
Данная задача по тем или иным причинам не вписалась в другие уроки, но зато сейчас есть прекрасная возможность рассмотреть её подробно и неторопливо. Приятная новость состоит в том, что мы немного отдохнём от векторов и сконцентрируем внимание на точках и отрезках.
Формулы деления отрезка в данном отношении Понятие деления отрезка в данном отношенииНередко обещанного вовсе ждать не приходится, сразу рассмотрим пару точек и, очевидное невероятное – отрезок :
Рассматриваемая задача справедлива, как для отрезков плоскости, так и для отрезков пространства. То есть, демонстрационный отрезок можно как угодно разместить на плоскости или в пространстве. Для удобства объяснений я нарисовал его горизонтально.
То есть, демонстрационный отрезок можно как угодно разместить на плоскости или в пространстве. Для удобства объяснений я нарисовал его горизонтально.
Что будем делать с данным отрезком? На этот раз пилить. Кто-то пилит бюджет, кто-то пилит супруга, кто-то пилит дрова, а мы начнём пилить отрезок на две части. Отрезок делится на две части с помощью некоторой точки , которая, понятно, расположена прямо на нём:
В данном примере точка делит отрезок ТАКИМ образом, что отрезок в два раза короче отрезка . ЕЩЁ можно сказать, что точка делит отрезок в отношении («один к двум»), считая от вершины .
На сухом математическом языке этот факт записывают следующим образом: , или чаще в виде привычной пропорции: . Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном случае: .
Пропорцию несложно составить и в другом порядке: – сия запись означает, что отрезок в два раза длиннее отрезка , но какого-то принципиального значения для решения задач это не имеет.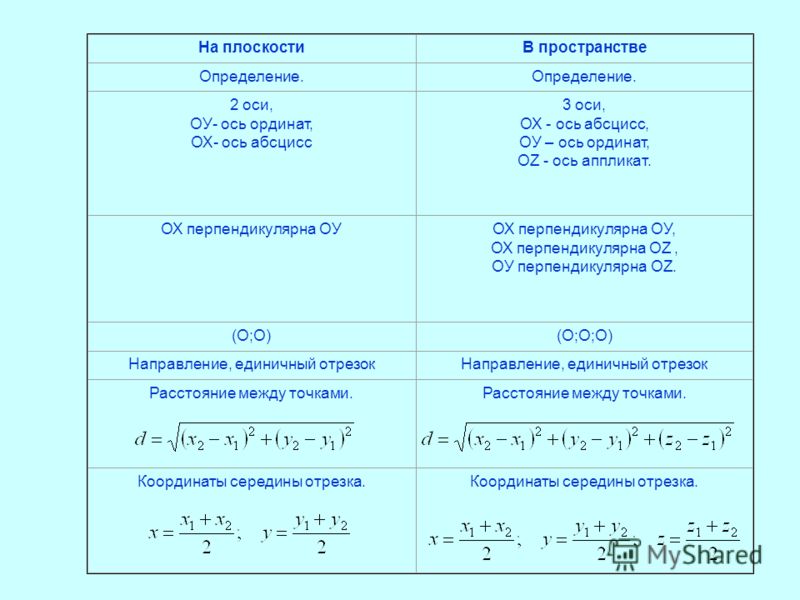 Можно так, а можно так.
Можно так, а можно так.
Разумеется, отрезок легко разделить в каком-нибудь другом отношении, и в качестве закрепления понятия второй пример:
Здесь справедливо соотношение: . Если составить пропорцию наоборот, тогда получаем: .
После того, как мы разобрались, что значит разделить отрезок в данном отношении, перейдём к рассмотрению практических задач.
Если известны две точки плоскости , то координаты точки , которая делит отрезок в отношении , выражаются формулами:
Откуда взялись данные формулы? В курсе аналитической геометрии эти формулы строго выводятся с помощью векторов (куда ж без них? =)). Кроме того, они справедливы не только для декартовой системы координат, но и для произвольной аффинной системы координат (см. урок Линейная (не) зависимость векторов. Базис векторов ). Такая вот универсальная задача.
Пример 1
Найти координаты точки , делящей отрезок в отношении , если известны точки
Решение : В данной задаче .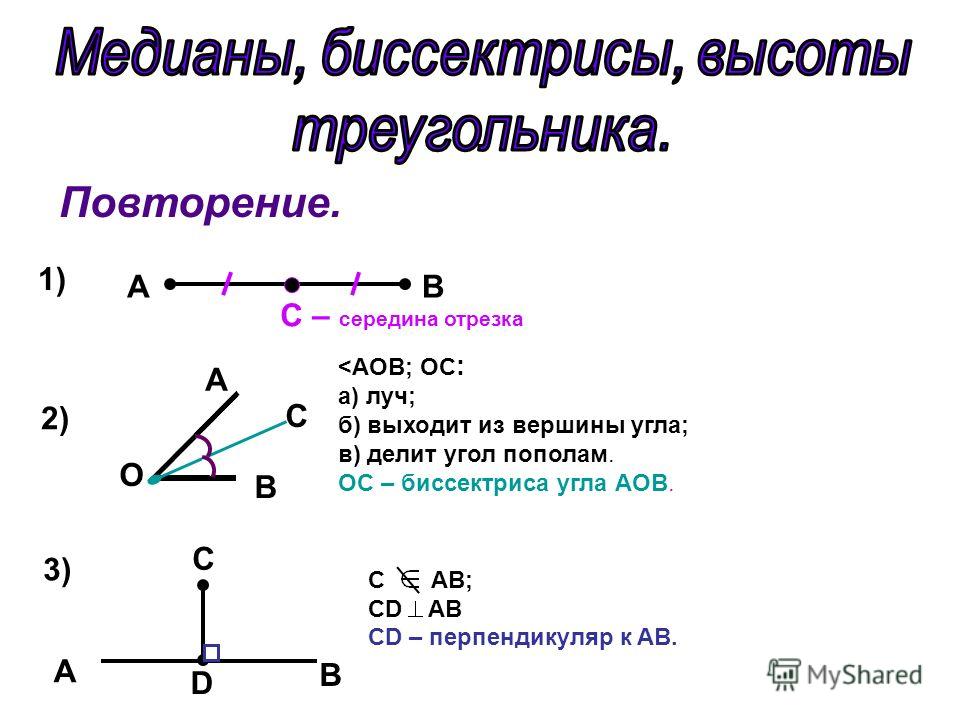 По формулам деления отрезка в данном отношении, найдём точку :
По формулам деления отрезка в данном отношении, найдём точку :
Ответ :
Обратите внимание на технику вычислений: сначала нужно отдельно вычислить числитель и отдельно знаменатель. В результате часто (но далеко не всегда) получается трёх- или четырёхэтажная дробь. После этого избавляемся от многоэтажности дроби и проводим окончательные упрощения.
В задаче не требуется строить чертежа, но его всегда полезно выполнить на черновике:
Действительно, соотношение выполняется, то есть отрезок в три раза короче отрезка . Если пропорция не очевидна, то отрезки всегда можно тупо измерить обычной линейкой.
Равноценен второй способ решения : в нём отсчёт начинается с точки и справедливым является отношение: (человеческими словами, отрезок в три раза длиннее отрезка ). По формулам деления отрезка в данном отношении:
Ответ :
Заметьте, что в формулах необходимо переместить координаты точки на первое место, поскольку маленький триллер начинался именно с неё.
Также видно, что второй способ рациональнее ввиду более простых вычислений. Но всё-таки данную задачу чаще решают в «традиционном» порядке. Например, если по условию дан отрезок , то предполагается, что вы составите пропорцию , если дан отрезок , то «негласно» подразумевается пропорция .
А 2-ой способ я привёл по той причине, что частенько условие задачи пытаются намеренно подзапутать. Именно поэтому очень важно выполнять черновой чертёж чтобы, во-первых, правильно проанализировать условие, а, во-вторых, в целях проверки. Обидно допускать ошибки в такой простой задаче.
Пример 2
Даны точки . Найти:
а) точку , делящую отрезок в отношении ;
б) точку , делящую отрезок в отношении .
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Иногда встречаются задачи, где неизвестен один из концов отрезка:
Пример 3
Точка принадлежит отрезку . Известно, что отрезок в два раза длиннее отрезка . Найти точку , если .
Решение : Из условия следует, что точка делит отрезок в отношении , считая от вершины , то есть, справедлива пропорция: . По формулам деления отрезка в данном отношении:
Сейчас нам неизвестны координаты точки : , но это не является особой проблемой, так как их легко выразить из вышеприведённых формул. В общем виде выражать ничего не стОит, гораздо проще подставить конкретные числа и аккуратно разобраться с вычислениями:
Ответ :
Для проверки можно взять концы отрезка и, пользуясь формулами в прямом порядке, убедиться, что при соотношении действительно получится точка . И, конечно же, конечно же, не лишним будет чертёж. А чтобы окончательно убедить вас в пользе клетчатой тетради, простого карандаша да линейки, предлагаю хитрую задачу для самостоятельного решения:
Пример 4
Точка . Отрезок в полтора раза короче отрезка . Найти точку , если известны координат точек .
Решение в конце урока. Оно, кстати, не единственное, если пойдёте отличным от образца путём, то это не будет ошибкой, главное, чтобы совпали ответы.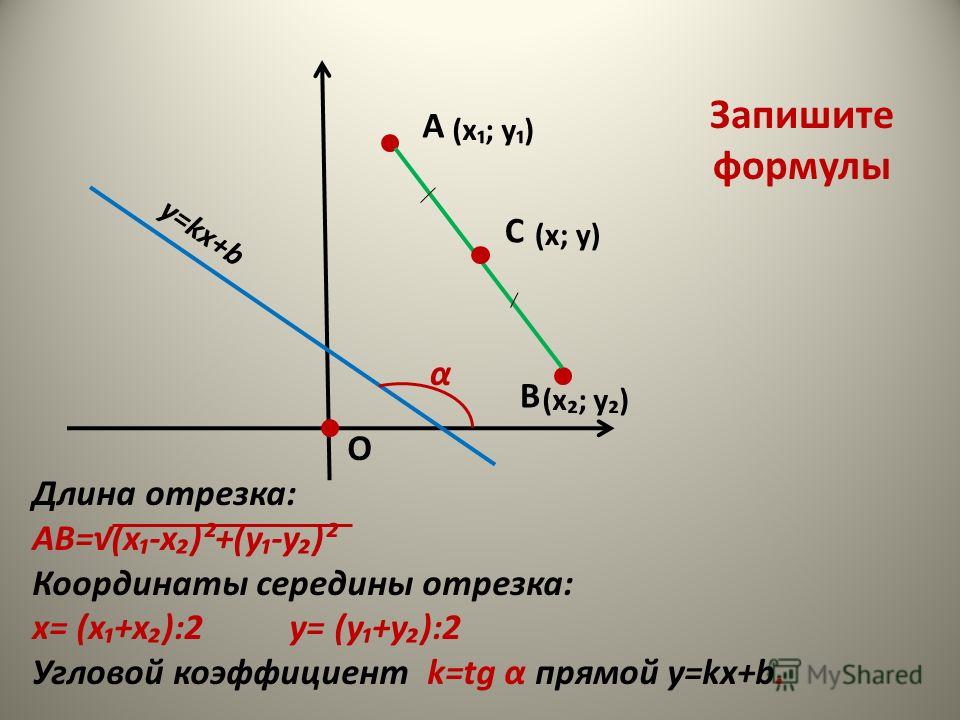
Для пространственных отрезков всё будет точно так же, только добавится ещё одна координата.
Если известны две точки пространства , то координаты точки , которая делит отрезок в отношении , выражаются формулами:
.
Пример 5
Даны точки . Найти координаты точки , принадлежащей отрезку , если известно, что .
Решение : Из условия следует отношение: . Данный пример взят из реальной контрольной работы, и его автор позволил себе небольшую шалость (вдруг кто споткнётся) – пропорцию в условии рациональнее было записать так: .
По формулам координат середины отрезка:
Ответ :
Трёхмерные чертежи в целях проверки выполнять значительно сложнее. Однако всегда можно сделать схематический рисунок, чтобы разобраться хотя бы в условии – какие отрезки необходимо соотносить.
Что касается дробей в ответе, не удивляйтесь, обычное дело. Много раз говорил, но повторюсь: в высшей математике принято орудовать обыкновенными правильными и неправильными дробями.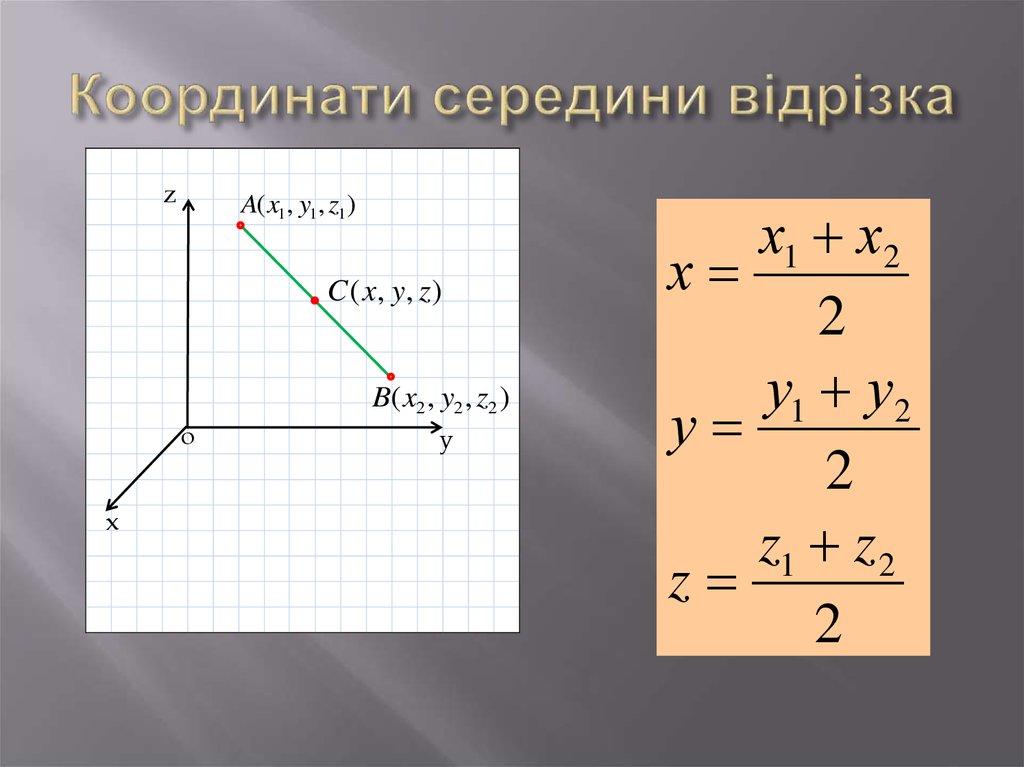 Ответ в виде пойдёт, но вариант с неправильными дробями более стандартен.
Ответ в виде пойдёт, но вариант с неправильными дробями более стандартен.
Разминочная задача для самостоятельного решения:
Пример 6
Даны точки . Найти координаты точки , если известно, что она делит отрезок в отношении .
Решение и ответ в конце урока. Если трудно сориентироваться в пропорциях, выполните схематический чертёж.
В самостоятельных и контрольных работах рассмотренные примеры встречаются как сами по себе, так и составной частью более крупных задач. В этом смысле типична задача нахождения центра тяжести треугольника.
Разновидность задания, где неизвестен один из концов отрезка, разбирать не вижу особого смысла, так как всё будет похоже на плоский случай, разве что вычислений чуть больше. Лучше вспомним годы школьные:
Формулы координат середины отрезкаДаже неподготовленные читатели могут помнить, как разделить отрезок пополам. Задача деления отрезка на две равные части – это частный случай деления отрезка в данном отношении. Двуручная пила работает самым демократичным образом, и каждому соседу за партой достаётся по одинаковой палке:
Двуручная пила работает самым демократичным образом, и каждому соседу за партой достаётся по одинаковой палке:
В этот торжественный час стучат барабаны, приветствуя знаменательную пропорцию . И общие формулы чудесным образом преображаются в нечто знакомое и простое:
Удобным моментом является тот факт, что координаты концов отрезка можно безболезненно переставить:
В общих формулах такой роскошный номер, как понимаете, не проходит. Да и здесь в нём нет особой надобности, так, приятная мелочь.
Для пространственного случая справедлива очевидная аналогия. Если даны концы отрезка , то координаты его середины выражаются формулами:
Пример 7
Параллелограмм задан координатами своих вершин . Найти точку пересечения его диагоналей.
Решение : Желающие могут выполнить чертёж. Граффити особенно рекомендую тем, кто капитально забыл школьный курс геометрии.
По известному свойству, диагонали параллелограмма своей точкой пересечения делятся пополам, поэтому задачу можно решить двумя способами.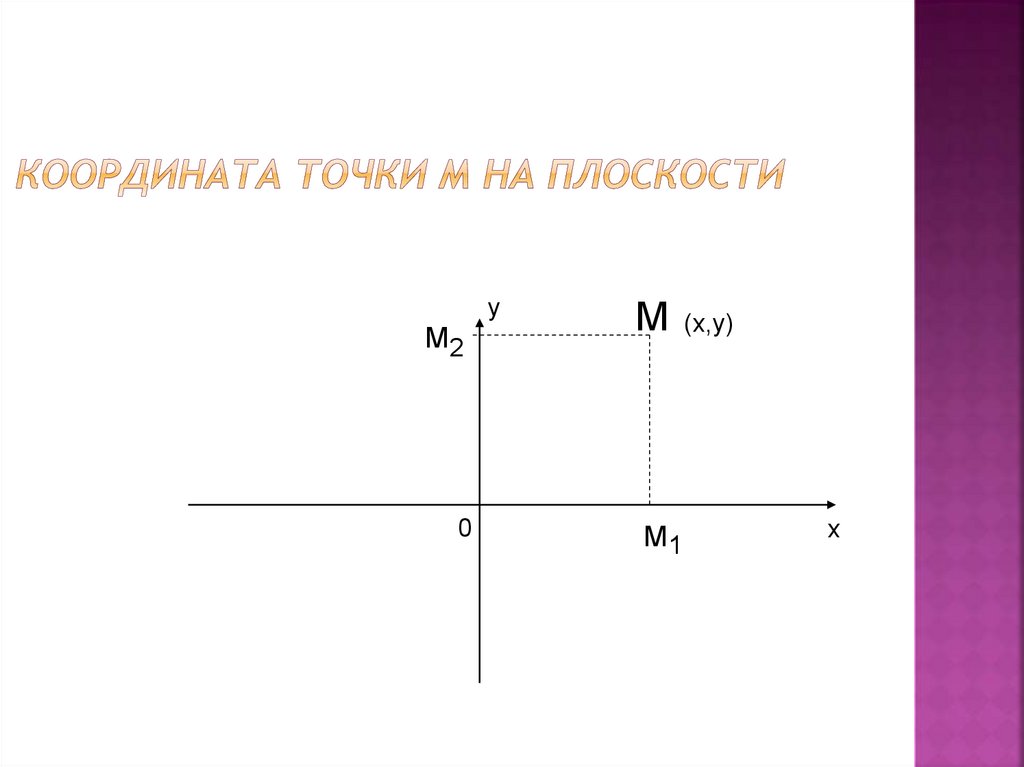
Способ первый : Рассмотрим противоположные вершины . По формулам деления отрезка пополам найдём середину диагонали :
Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.
Итак, пусть отрезок задан своими концами — точками A = (x a ; y a ; z a) и B = (x b ; y b ; z b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:
Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.
· Задача . Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A 1 B 1 . Найдите координаты этой точки.
Решение . Поскольку точка K — середина отрезка A 1 B 1 , ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A 1 = (0; 0; 1) и B 1 = (1; 0; 1). Теперь найдем координаты точки K:
Запишем координаты концов: A 1 = (0; 0; 1) и B 1 = (1; 0; 1). Теперь найдем координаты точки K:
Ответ : K = (0,5; 0; 1)
· Задача . Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A 1 B 1 C 1 D 1 .
Решение . Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A 1 L = C 1 L, т.е. точка L — это середина отрезка A 1 C 1 . Но A 1 = (0; 0; 1), C 1 = (1; 1; 1), поэтому имеем:
Ответ : L = (0,5; 0,5; 1)
Простейшие задачи аналитической геометрии.
Действия с векторами в координатах
Задания, которые будут рассмотрены, крайне желательно научиться решать на полном автомате, а формулы запомнить наизусть , даже специально не запоминать, сами запомнятся =) Это весьма важно, поскольку на простейших элементарных примерах базируются другие задачи аналитической геометрии, и будет досадно тратить дополнительное время на поедание пешек. Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.
Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.
Изложение материала пойдет параллельным курсом – и для плоскости, и для пространства. По той причине, что все формулы… сами увидите.
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Определение 1
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y .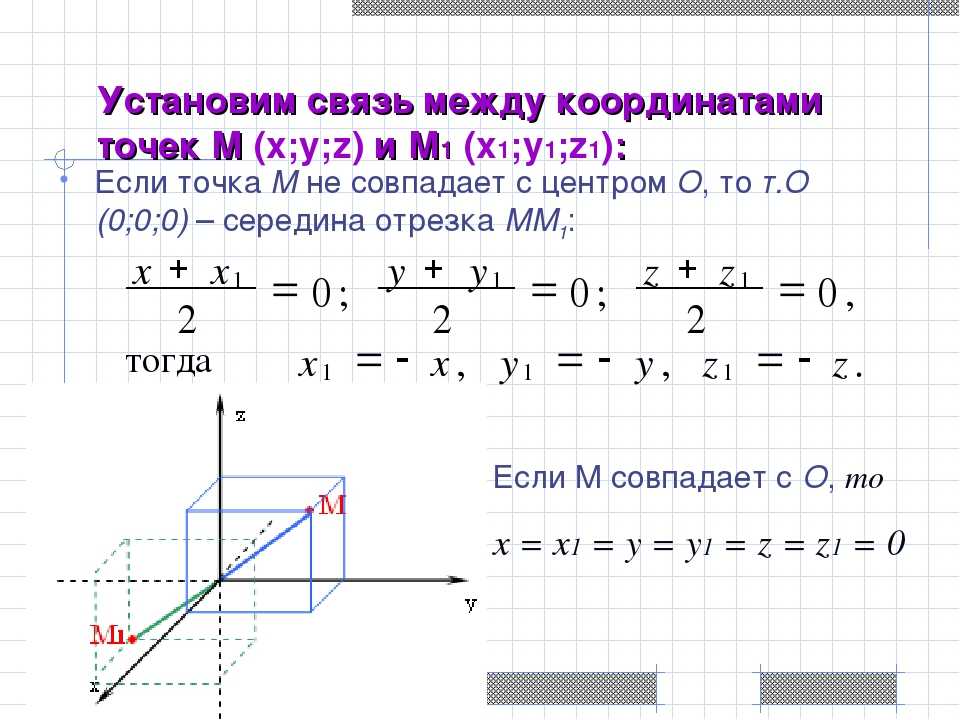 И тогда, опираясь на полученную ранее формулу, получим:
И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т. е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Пример 1
Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ : координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ: 58
Пример 3
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ: координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Формула нахождения координаты середины отрезка
Начальные геометрические сведения
Понятие отрезка, как и понятие точки, прямой, луча и угла, относится к начальным геометрическим сведениям. С перечисленных понятий начинается изучение геометрии.
С перечисленных понятий начинается изучение геометрии.
Под «начальными сведениями» обычно понимают нечто элементарное и простое. В понимании, возможно, это так и есть. Тем не менее, такие простые понятия часто встречаются и оказываются необходимыми не только в нашей повседневной жизни, но и в производстве, строительстве и прочих сферах нашей жизнедеятельности.
Начнём с определений.
Определение 1
Отрезок — часть прямой, ограниченная двумя точками (концами).
Если концы отрезка являются точками $A$ и $B$, то образованный отрезок записывают как $AB$ или $BA$. Такому отрезку принадлежат точки $A$ и $B$, а также все точки прямой, лежащие между этими точками.
Рисунок 1. Отрезок. Автор24 — интернет-биржа студенческих работ
Определение 2
Середина отрезка — точка отрезка, которая делит его пополам на два равных отрезка.
Если это точка $C$, то $AC=CB$.
Рисунок 2. Середина отрезка. Автор24 — интернет-биржа студенческих работ
Измерение отрезка происходит сравнением с определённым отрезком, принятым за единицу измерения. Чаще всего используют сантиметр. Если в заданном отрезке сантиметр укладывается ровно четыре раза, то это означает, что длина данного отрезка равна $4$ см.
Чаще всего используют сантиметр. Если в заданном отрезке сантиметр укладывается ровно четыре раза, то это означает, что длина данного отрезка равна $4$ см.
Введём простое наблюдение. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих отрезков.
Формула нахождения координаты середины отрезка
Формула нахождения координаты середины отрезка относится к курсу аналитической геометрии на плоскости.
Дадим определение координатам.
Определение 3
Координаты — это определённые (или упорядоченные) числа, которые показывают положение точки на плоскости, на поверхности или в пространстве.
В нашем случае, координаты отмечаются на плоскости, определённой координатными осями.
Рисунок 3. Координатная плоскость. Автор24 — интернет-биржа студенческих работ
Опишем рисунок. На плоскости выбрана точка, называемая началом координат. Её обозначают буквой $O$. Через начало координат проведены две прямые (координатные оси), пересекающиеся под прямым углом, причём одна из них строго горизонтальная, а другая — вертикальная. Такое положение считается обычным. Горизонтальная прямая называется осью абсцисс и обозначается $OX$, вертикальная — осью ординат $OY$.
Такое положение считается обычным. Горизонтальная прямая называется осью абсцисс и обозначается $OX$, вертикальная — осью ординат $OY$.
Таким образом, оси определяют плоскость $XOY$.
Координаты точек в такой системе определяются двумя числами.
Существуют разные формулы (уравнения), определяющие те или иные координаты. Обычно в курсе аналитической геометрии изучают разные формулы прямых, углов, длины отрезка и прочие.
Перейдём сразу к формуле координаты середины отрезка.
Определение 4
Если координаты точки $E(x,y)$ — это середина отрезка $M_1M_2$, то:
Рисунок 4. Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ
Практическая часть
Примеры из школьного курса геометрии достаточно просты. Рассмотрим несколько основных.
Для лучшего понимания, рассмотрим для начала элементарный наглядный пример.
Пример 1
Имеем рисунок:
Рисунок 5.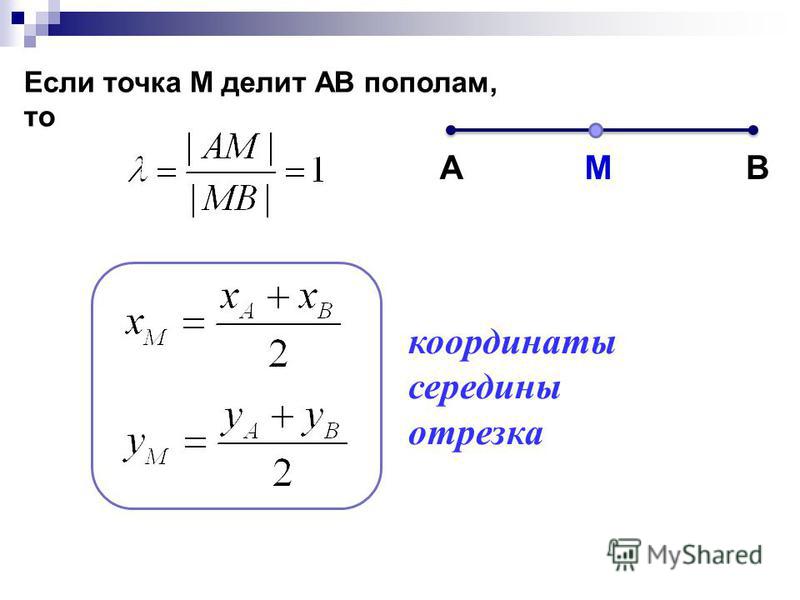 Отрезки на плоскости. Автор24 — интернет-биржа студенческих работ
Отрезки на плоскости. Автор24 — интернет-биржа студенческих работ
На рисунке отрезки $AC, CD, DE, EB$ равны.
- Серединой каких отрезков является точка $D$?
- Какая точка является серединой отрезка $DB$?
Ответы:
- точка $D$ является серединой отрезков $AB$ и $CE$;
- точка $E$.
Рассмотрим другой простой пример, в котором нужно вычислить длину.
Пример 2
Точка $B$ — середина отрезка $AC$. $AB = 9$ см. Какая длина $AC$?
Так как т. $B$ делит $AC$ пополам, то $AB = BC= 9$ см. Значит, $AC = 9+9=18$ см.
Ответ: 18 см.
Прочие подобные примеры обычно идентичны и ориентированы на умение сопоставлять значения длин и их представление с алгебраическими действиями. Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.
Приведём пример, демонстрирующий такой случай.
Пример 3
Точка $B$ — середина отрезка $AC$. $AC = 8,4$ см. Какая длина $AB$?
Так как т. $B$ делит $AC$ пополам, то $AB = \frac{8,4}{2}$ см. Значит, $AB = 4,2$ см.
Ответ: 4,2 см.
Если в очередной задаче возникают трудности с пониманием её решения (например, нетипичные случаи с несколькими отрезками, образующими углами и прочими усложнениями), то лучше рассмотреть задачу, сделав по её условию рисунок. Наглядность способствует лучшему пониманию и более скорому нахождению решения.
Теперь решим задачи по аналитической геометрии.
Пример 4
Даны точки $T_1(7,11)$ и $T_2(1,23)$. Требуется найти координаты середины отрезка $T_1T_2$.
Абсцисса середины отрезка: $x=\frac{7+1}{2}=4$. Ордината: $y=\frac{11+23}{2}=17$.
Ответ: $(4,17)$.
Пример 5
Даны точки $T(6,-1)$ и $S(-4,-8)$. Точка $S$ — середина $TK$. Найти координаты $K$.
Подставим значения и получим уравнения:
$-4=\frac{6+x_2}{2}, -8=\frac{-1+y_2}{2}. $
$
Найдём координаты:
$-2=6+x_2, -4=-1+y_2; x_2=-8, y_2=-3$.
Ответ: $K(-8,-3)$.
Обучение математике • блог онлайн-школы Skysmart 🏫
Задачи на пропорции
Математика
85671
Область допустимых значений функции
Математика
86112
Деление в столбик
Математика
424706
Свойства степеней. Действия со степенями
Математика
281686
Как находить проценты от числа
Математика
259624
Как найти дискриминант квадратного уравнения
Математика
378716
Раскрытие скобок
Математика
85081
Как найти площадь фигуры
Математика
149849
Правильное округление чисел
Математика
164882
Осевая и центральная симметрия
Математика
156432
Наибольший общий делитель (НОД), свойства и формулы
Математика
165336
Неполные квадратные уравнения
Математика
139179
Равнобедренный треугольник: свойства, признаки и формулы
Математика
265742
Обыкновенные дроби
Математика
176640
Разложение чисел на простые множители
Математика
8493
Вычитание дробей
Математика
99669
Натуральные числа
Математика
302504
Длина окружности
Математика
309149
Умножение десятичных дробей
Математика
117843
Масштаб в математике
Математика
77391
Вектор
Математика
523
Площадь прямоугольного треугольника
Математика
396270
Вычитание столбиком
Математика
39667
Действительные числа
Математика
73065
Как найти площадь прямоугольника
Математика
294504
Модуль числа
Математика
245449
Как найти координаты точки?
Математика
62978
Объем параллелепипеда
Математика
220777
Квадратичная функция. Построение параболы
Построение параболы
Математика
280354
Область определения функции
Математика
266832
Как умножать в столбик
Математика
158839
Как перевести дробь в десятичную и наоборот
Математика
230819
Как найти периметр фигуры
Математика
165008
График линейной функции, его свойства и формулы
Математика
298254
Как найти периметр прямоугольника
Математика
154587
Как найти периметр треугольника
Математика
183306
Как решать систему неравенств
Математика
27538
Что такое угол? Виды углов
Математика
76130
Сложение и вычитание степеней
Математика
204842
Равенство и неравенство. Знаки: больше, меньше, равно
Знаки: больше, меньше, равно
Математика
864464
Параллелограмм: свойства и признаки
Математика
233121
Прямая и обратная пропорциональность
Математика
142825
Время, скорость, расстояние
Математика
272250
Параллельность прямых
Математика
27901
Разряды и классы чисел
Математика
251740
Зачем нужна математика
Математика
34107
Сложение и вычитание десятичных дробей
Математика
31801
Десятичные дроби
Математика
255157
Решение простых линейных уравнений
Математика
305312
Как найти площадь треугольника
Математика
711672
Отрицательная степень
Математика
167687
Как найти периметр квадрата
Математика
63078
Порядок действий в математике
Математика
307509
Компланарность векторов
Математика
915
Что такое функция?
Математика
80811
Все формулы приведения
Математика
18775
Коллинеарность векторов
Математика
9628
Логарифмы
Математика
45696
Площадь круга: как найти, формулы
Математика
347529
Построение графиков функций
Математика
307923
Касательная к окружности
Математика
88905
Метод интервалов, решение неравенств
Математика
165256
Как решать задачи с процентами
Математика
326674
Как перевести периодическую дробь
Математика
110905
Как хорошо сдать ОГЭ по математике
Математика
19893
Что такое гипербола
Математика
60460
Вынесение общего множителя за скобки
Математика
52885
Деление чисел с остатком
Математика
86177
Деление дробей: теория и практика
Математика
133077
Как найти диаметр окружности
Математика
234202
Таблица производных функций
Математика
90914
Разложение многочлена способом группировки
Математика
39718
Сложение дробей: теория и практика
Математика
118115
Прямоугольный параллелепипед. Что это такое?
Что это такое?
Математика
163838
Что такое аксиома, теорема и доказательство теоремы
Математика
63931
Деление десятичных дробей
Математика
138818
Основные геометрические фигуры
Математика
157809
Иррациональные числа
Математика
51133
Как умножать отрицательные числа
Математика
30486
Сравнение десятичных дробей
Математика
24994
Как сокращать алгебраические дроби?
Математика
86495
Теория графов. Основные понятия и виды графов
Математика
106768
Умножение дробей: теория и практика
Математика
210506
Признаки равенства треугольников
Математика
308607
Как определить площадь квадрата
Математика
204441
Какие числа называются целыми
Математика
86725
Сумма разрядных слагаемых
Математика
72799
Факториал
Математика
139502
Центральные и вписанные углы
Математика
123085
Теория вероятностей, формулы и примеры
Математика
372722
Теорема косинусов и синусов
Математика
137512
Как решать систему уравнений
Математика
158045
Сокращенное умножение: правила, формулы
Математика
301602
Теорема Виета для квадратного уравнения
Математика
483575
Признаки делимости чисел
Математика
69213
Взаимно простые числа
Математика
38174
Числовые и буквенные выражения
Математика
43599
Сокращение обыкновенных дробей
Математика
109179
Векторное произведение векторов
Математика
78078
Таблица степеней
Математика
79339
Как решать квадратные уравнения
Математика
376922
Что такое рациональные числа?
Математика
126878
Теорема Пифагора
Математика
348737
Решение линейных неравенств
Математика
75411
Возрастание и убывание функции
Математика
8182
Сравнение дробей: как правильно
Математика
126480
Показательные уравнения
Математика
68933
Что такое квадратный корень
Математика
158252
Решение уравнений с дробями
Математика
366200
Арифметическая прогрессия: свойства и формулы
Математика
235916
Четные и нечетные числа
Математика
171680
Таблица умножения: поможем выучить легко и быстро
Математика
107751
Умножение многочлена на многочлен
Математика
24071
Сложение чисел с разными знаками
Математика
35726
Многочлен стандартного вида
Математика
40835
Свойства умножения и деления
Математика
45051
Единичная окружность
Математика
16180
Сложение и вычитание смешанных чисел
Математика
70470
Свойства сложения и вычитания
Математика
45249
Расстояние от точки до прямой
Математика
7632
Показательные неравенства
Математика
43334
Простая формула, чтобы подсчитать среднее арифметическое
Математика
129971
Плоскость
Математика
1585
Задачи на нахождение процента
Математика
23533
Основное тригонометрическое тождество
Математика
74089
Сколько стоят занятия с репетитором
Математика
8015
Как найти радиус окружности
Математика
161462
Уравнение касательной к графику функции
Математика
8877
Основы геометрии
Математика
76199
Законы математики
Математика
33472
Округление десятичных дробей
Математика
41388
Простые и составные числа
Математика
54123
Скалярное произведение векторов
Математика
192350
Перпендикулярные прямые
Математика
839
Как найти среднюю линию треугольника?
Математика
107779
Теорема синусов
Математика
84430
Умножение и деление степеней
Математика
126926
Что такое пропорция
Математика
53345
Формула длины вектора
Математика
2526
Прямоугольная система координат. Ось абсцисс и ординат
Ось абсцисс и ординат
Математика
68664
Противоположные числа
Математика
16386
Координаты середины отрезка
Математика
1027
Угол между прямой и плоскостью
Математика
55
Деление числа на произведение
Математика
7137
Теоремы, которые точно пригодятся на ЕГЭ
Математика
245
Развертка прямоугольного параллелепипеда
Математика
22438
Взаимно обратные числа
Математика
31888
Аналитическая геометрия.
Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.
№1 Составить уравнение прямой, которая проходит через точку М(-3,2) и параллельна прямой
Решение.
Уравнение прямой будем искать по формуле
Так как у параллельных прямых угловые коэффициенты равны k1=k2 , то
Подставим угловой коэффициент и точку М(-3,2) в уравнение (1)
Искомое уравнение прямой
Ответ:
№2 Через точку М(2,5) провести прямую так, чтобы ее отрезок, заключенный между осями координат, делится в этой точке пополам.
Решение.
Пусть данная прямая пересекает ось ОY в точке А(0,а), ось ОХ в точке В(b,0). Координаты середины отрезка АВ (это точка М) равны
Получим
Составим уравнение прямой АВ с помощью формулы
Ответ:
№3 Составить уравнение сторон треугольника, зная одну из его вершин А(-1,3) и уравнения двух высот
Р ешение. Выполним рисунок
Пусть высота ВН1 имеет уравнение
а высота СН2 задается уравнением
Так как известны уравнения высот, то известны координаты нормальных векторов этих высот n1(3; – 4)- нормальный вектор высоты ВН1 и n2(5; 2) — нормальный вектор высоты СН2. Так как стороны треугольника АС и АВ должны быть перпендикулярными этим высотам то для вывода уравнения этих сторон воспользуемся формой уравнения прямой, проходящей через данную точку А(-1,3) в данном направлении:
Так как стороны треугольника АС и АВ должны быть перпендикулярными этим высотам то для вывода уравнения этих сторон воспользуемся формой уравнения прямой, проходящей через данную точку А(-1,3) в данном направлении:
Координаты точки В найдем как точку пересечения прямой АВ и высоты ВН1. Для этого составим систему уравнений
Координаты точки В(4,5)
Координаты точки С найдем как точку пересечения прямой АС и высоты СН2. Для этого составим систему уравнений
Координаты точки С(2,-1)
Уравнение стороны ВС построим, воспользовавшись формой уравнения прямой, проходящей через две заданные точки В(4,5) и С(2,-1)
Уравнение стороны АС, где А(-1,3) и С(2,-1), имеет вид
Уравнение стороны АВ, где А(-1,3) и В(4,5), имеет вид
Ответ: уравнение АВ , уравнение АС ,
уравнение ВС
№4 Найти фокальный радиус точки М параболы, если абсцисса этой точки равна7.
Решение.
Фокальный радиус точки параболы найдем по формуле
, где х – абсцисса точки М, р – параметр параболы
По условию х=7.
Определим параметр р. Так как каноническое уравнение параболы имеет вид , то
Тогда фокальный радиус равен
Ответ: 12
№5 Определить вид кривой, найти ее оси, фокусы, уравнения директрис, построить эту кривую
Решение.
Для приведения уравнения кривой второго порядка к каноническому виду применим метод выделения полного квадрата.
Сгруппируем слагаемые, содержащие текущие координаты. Коэффициенты при и вынесем за скобки:
Выделим полный квадрат:
Разделим обе части равенства на 2:
Запишем полученное уравнение в каноническом виде:
Данная кривая – эллипс с центром в точке (-1/2, 0).
Найдем ее оси. Большая полуось равна , малая полуось равна .
Фокусы эллипса находятся в точках и , где
Тогда
и
Директрисами эллипса называются прямые, определяемые уравнениями
, где
Директрисы равны
Построим данную кривую
Ответ: ,, , , ,
№6 Назвать и построить кривую
Решение.
Для приведения уравнения кривой второго порядка к каноническому виду применим метод выделения полного квадрата.
Сгруппируем слагаемые, содержащие текущие координаты. Коэффициенты при и вынесем за скобки:
Выделим полный квадрат:
Данная кривая есть гипербола с центром в точке (3,-2), с фокусами на оси ординат.
Построим данную кривую.
Ответ: — гиперола
№7 Определить вид и параметры поверхности, построить ее методом сечений
Решение.
Данная поверхность – однополостный гиперболоид с центром в точке (-2,0,1), параметры , вытянутый вдоль оси ОХ.
Исследуем поверхность методом параллельных сечений.
Будем пересекать поверхность горизонтальными плоскостями .
Подставим в уравнение. Получим
При любом таком сечении получаются гиперболы с фокусами на оси ординат , полуосями , центр в точке (-2,0,0)
Подставим в уравнение. Получим
При любом таком сечении получаются эллипсы с фокусами на оси ординат , полуосями , центр в точке (0,0,1)
Подставим в уравнение. Получим
Получим
При любом таком сечении получаются гиперболы с фокусами на оси OZ , полуосями , центр в точке (-2,0,1)
Координатные плоскости являются плоскостями симметрии. Поверхность изображена на рисунке
№8 Назвать и построить поверхности
а)
б)
Решение.
а)
Данная поверхность представляет собой параболический цилиндр, с центром в точке (0,0,1), вытянутый вдоль оси OY.
б)
Данная поверхность представляет собой эллиптический параболоид, с центром в точке (1,0,0), вытянутый вдоль оси OZ.
Как найти координаты точки зная длину отрезка
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1, а на ось Х длина проекции равна x2-x1. Применим теорему Пифагора: |AB|² = (y2 – y1)² + (x2 – x1)². В данном случае |AB| является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5). Применяя теорему Пифагора, получаем: |AB|² = (2 – 1)² + (5 – 3)² = 1 + 4 = 5. А это значит, что длина нашего отрезка равна 5:1/2.
А это значит, что длина нашего отрезка равна 5:1/2.
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1.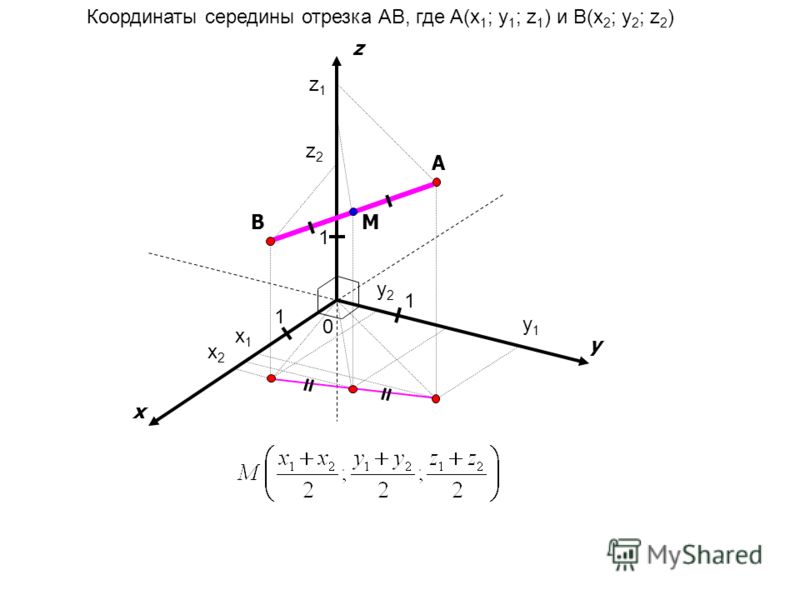
Рассчитаем длину отрезка А, для этого найдем квадратный корень:
Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1, то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61.
Этот онлайн калькулятор рассчитывает длину отрезка и координаты середины отрезка (средней точки) по декартовым координатам концов отрезка. Отрезок и средняя точка отображаются на графике, также на графике показан графический способ нахождения середины отрезка.
Эта страница существует благодаря следующим персонам
Timur
- Статья : Расчет длины отрезка и координат середины отрезка по двум точкам – Автор, Переводчик en – ru
- Калькулятор : Расчет длины отрезка и координат середины отрезка по двум точкам – Автор, Переводчик en – ru
Этот онлайн калькулятор рассчитывает длину отрезка и координаты середины отрезка по введенным декартовым координатам двух точек – концов отрезка.
Формула вычисления расстояния между двумя точками и это формула длины гипотенузы прямоугольного треугольника . Координаты середины отрезка – среднее арифметическое координат точек .
Отрезок и средняя точка отображаются на графике. Также среднюю точку можно найти построением. Для этого на графике надо построить две дуги с центрами на концах отрезка и с радиусом равным длине отрезка. Затем надо построить прямую линию между точками пересечения дуг. Эта линия пересечет исходный отрезок в середине.
Отрезком обозначают ограниченный двумя точками участок прямой. Точки – концы отрезка.
Общеизвестный факт, что каждая точка А плоскости имеет свои координаты (х, у).
В данном примере вектор AB задан координатами (х2— х1, y2— y1). Квадрат длины вектора будет равен сумме квадратов его координат. Следовательно, расстояние d между точками А и В, или, что то же самое, длина вектора АВ, вычисляется согласно формуле:
Эта формула длины отрезка предоставляет возможность рассчитывать расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек
Вышеуказанную формулу длины отрезка можно доказать и другим способом. В системе координат заданы координаты крайних точек отрезка координатами его концов(х1y1) и (х2,у2).
В системе координат заданы координаты крайних точек отрезка координатами его концов(х1y1) и (х2,у2).
Прочертим прямые лини через эти точки перпендикулярно к осям координат, в результате имеем прямоугольный треугольник. Первоначальный отрезок является гипотенузой образовавшегося треугольника. Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.
Установим длину этих проекций.
На ось у длина проекции равна y2 – y1, а на ось х длина проекции равна х2 – х1. На основании теоремы Пифагора видим, что |AB|² = (y2 – y1)² + (x2 – x1)².
В рассмотренном случае |AB| выступает длиной отрезка.
Вычислим длину отрезка АВ, для этого извлечем квадратный корень. Результатом является все та же формула длины отрезков по известным координатам конца и начала.
Результатом является все та же формула длины отрезков по известным координатам конца и начала.
Midpoint Calculator
Использование калькулятора
Середина отрезка — это точка, которая находится посередине между двумя точками. Средняя точка находится на одинаковом расстоянии от каждой конечной точки.
Используйте этот калькулятор, чтобы вычислить среднюю точку, расстояние между двумя точками или найти конечную точку, зная среднюю и другую конечные точки.
Решения для расчета средней и конечной точек
Введите две точки, используя числа, дроби, смешанные числа или десятичные дроби. Калькулятор средней точки показывает работу, которую нужно найти:
- Средняя точка между двумя заданными точками
- Конечная точка задана одной конечной точкой и средней точкой
- Расстояние между двумя конечными точками
Калькулятор также предоставляет ссылку на Калькулятор уклона, который решит и продемонстрирует работу по нахождению уклона, уравнениям линии и точкам пересечения x и y для заданных двух точек.
Как вычислить середину
Вы можете найти середину отрезка по двум конечным точкам (x 1 , у 1 ) и (х 2 , у 2 ). Добавьте каждую координату x и разделите на 2, чтобы найти x средней точки. Добавьте каждую координату y и разделите на 2, чтобы найти y средней точки.
Вычислите среднюю точку (x M , y M ), используя формулу средней точки:
\( (x_{M}, y_{M}) = \left(\dfrac {x_{1} + x_ {2}} {2} , \dfrac {y_{1} + y_{2}} {2}\right) \)
Важно отметить, что середина — это средняя точка на линии сегмент . Истинная линия в геометрии бесконечно длинна в обоих направлениях. Но отрезок прямой имеет 2 конечные точки, поэтому можно вычислить среднюю точку. Луч имеет один конец и бесконечно длинный в другом направлении.
Пример: найти середину
Допустим, вы знаете две точки на отрезке, и их координаты (6, 3) и (12, 7). Найдите середину по формуле средней точки.
Найдите середину по формуле средней точки.
\( (x_{M}, y_{M}) = \left(\dfrac {x_{1} + x_{2}} {2} , \dfrac {y_{1} + y_{2}} { 2}\справа) \)
- Сначала добавьте координаты x и разделите на 2. Это даст вам координату x средней точки, x M
- Во-вторых, добавьте координаты y и разделите на 2. Это даст вам координату y средней точки, y М
- Возьмите каждый результат, чтобы получить среднюю точку. В этом примере средняя точка (9, 5).

\(x_{M} = \dfrac {x_{1} + x_{2}} {2} \)
\(x_{M} = \dfrac {6 + 12} {2} \)
\(x_{M} = \dfrac {18} {2} \)
\( х_{М} = {9} \)
\(y_{M} = \dfrac {y_{1} + y_{2}} {2} \)
\(y_{M} = \dfrac {3 + 7} {2} \)
\(y_{M} = \dfrac {10} {2} \)
\(у_{М} = {5} \)
Как рассчитать расстояние между двумя точками
Если вы знаете конечные точки отрезка, вы можете использовать их для расчета расстояния между двумя точками. Здесь вы на самом деле находите длину отрезка. Используйте формулу для расстояния между 2 точками: 92} \)
\(d = \sqrt {36 + 64} \)
\(d = \sqrt {100} \)
\(d = 10\)
Подобно этому калькулятору средней точки, наш Калькулятор двухмерного расстояния. Расстояние между 2 точками в 3 измерениях с координатами (x, y, z) см. 3-х мерный калькулятор расстояний.
Как вычислить конечную точку
Если вы знаете конечную точку и середину отрезка, вы можете вычислить отсутствующую конечную точку. Начните с формулы средней точки сверху и определите координаты неизвестной конечной точки.
Начните с формулы средней точки сверху и определите координаты неизвестной конечной точки.
- Сначала возьмем формулу средней точки:
- И разбить его, чтобы у вас были отдельные уравнения для координат x и y средней точки
- Переставьте каждое уравнение так, чтобы вы решали x 2 и y 2
\( x_{2} = 2x_{M} — x_{1} \)
\(у_{2} = 2у_{М} — у_{1} \)
- Поскольку вы знаете середину, вставьте ее координаты вместо x M и y M в каждом уравнении
- Вставьте координаты вашей известной конечной точки в значения для x 1 и г 1
- Наконец, решите каждое уравнение, чтобы найти x 2 и y 2 , которые будут координатами вашей отсутствующей конечной точки
\((x_{M}, y_{M}) = \left(\dfrac {x_{1} + x_{2}} {2}, \dfrac {y_{1} + y_{2}} {2 }\справа) \)
\(x_{M} = \dfrac {x_{1} + x_{2}} {2} \)
\(y_{M} = \dfrac {y_{1} + y_{2}} {2} \)
Пример: найти конечную точку
Используя приведенные выше шаги, давайте найдем конечную точку отрезка, где мы знаем, что одна конечная точка (6, -4), а средняя точка (1, 7). Конечная точка – это (x 1 , y 1 ) координата. Середина – это (x M , y M ) координата.
Конечная точка – это (x 1 , y 1 ) координата. Середина – это (x M , y M ) координата.
- Сначала возьмем формулу средней точки:
- И переставьте уравнения так, чтобы вы решали x2 и y2
- Вставьте координаты вашей средней точки (1, 7) вместо x M и y M в каждом уравнении
- Вставьте координаты вашей известной конечной точки (6, -4) в значения для x 1 и у 1
- Решите каждое уравнение, чтобы найти x 2 и y 2 .

- Ваша отсутствующая конечная точка (x 2 , y 2 ) равно (-4, 18)
\((x_{M}, y_{M}) = \left(\dfrac {x_{1} + x_{2}} {2}, \dfrac {y_{1} + y_{2}} {2 }\справа) \)
\( х_{2} = 2х_{М} — х_{1} \)
\(у_{2} = 2у_{М} — у_{1} \)
\( х_{2} = 2(1) — х_{1} \)
\(у_{2} = 2(7) — у_{1} \)
\( х_{2} = 2(1) — 6 \)
\(у_{2} = 2(7) — (-4) \)
\( х_{2} = 2 — 6 \)
\(х_{2} = -4 \)
\( у_{2} = 14 + 4 \)
\( у_{2} = 18 \)
Калькулятор средней точки
Средняя точка (x M , y M ) = (4, 5)
GENERATE WORK
сообщить об этом объявлении
GENERATE WORK
Работа со средней точкой с шагами
Калькулятор средней точки использует координаты двух точек `A(x_A,y_A)` и `B(x_B,y_B)` в двумерной декартовой координатной плоскости и находит точка на полпути между двумя заданными точками `A` и `B` на отрезке прямой. Это онлайн-инструмент геометрии, требующий 2 конечных точек в двумерной декартовой координатной плоскости. Это альтернативный метод нахождения середины отрезка без циркуля и линейки.
Это альтернативный метод нахождения середины отрезка без циркуля и линейки.
Необходимо выполнить следующие шаги:
- Введите в поле координаты (`x_A`,`y_A`) и (`x_B`,`y_B`) двух точек A и B. Эти значения должны быть действительными числами или параметрами;
- Нажмите кнопку » GENERATE WORK «, чтобы выполнить вычисление;
- Калькулятор средней точки выдаст координаты средней точки `M (x_M , y_M )` сегмента линии `overline{AB}`.
Ввод: Две упорядоченные пары действительных чисел. Обратите внимание, что некоторые координаты могут быть переменными
Вывод: Упорядоченная пара действительных чисел или переменных.
Формула средней точки:
Если у нас есть координаты двух точек `A(x_A,y_A)` и `B(x_B,y_B)`, то определяется середина отрезка линии `overline{AB}` по формуле
`M(x_M,y_M)\equiv M(\frac{x_A + x_B}{2}, \frac{y_A + y_B}{2})`
Что такое середина?
Как мы знаем, отрезок линии над линией{AB} – это часть прямой, которая ограничена двумя различными точками A и B, которые называются конечными точками отрезка линии над линией{AB}. `. Точка `M` является серединой отрезка `overline{AB}`, если она является элементом отрезка и делит его на два конгруэнтных отрезка `overline{AM}\congoverline{MB}`. Каждый отрезок между серединой M и конечной точкой имеет равные
длина. Часто говорят, что точка M делит пополам отрезок `overline{AB}`. Другими словами, середина — это центр или середина отрезка. Любой отрезок имеет уникальную середину. Итак, мы можем найти середину любого отрезка на координатной плоскости, используя формулу mipoint.
`. Точка `M` является серединой отрезка `overline{AB}`, если она является элементом отрезка и делит его на два конгруэнтных отрезка `overline{AM}\congoverline{MB}`. Каждый отрезок между серединой M и конечной точкой имеет равные
длина. Часто говорят, что точка M делит пополам отрезок `overline{AB}`. Другими словами, середина — это центр или середина отрезка. Любой отрезок имеет уникальную середину. Итак, мы можем найти середину любого отрезка на координатной плоскости, используя формулу mipoint.
Как рассчитать среднюю точку?
Координата x средней точки M отрезка `overline{AB}` представляет собой среднее арифметическое x-координат конечных точек отрезка `overline{AB}`. Точно так же y-координата середины M отрезка `overline{AB}` является средним арифметическим y-координат конечных точек отрезка `overline{AB}`.
Работа с шагами показывает полный пошаговый расчет того, как найти координаты центральной точки отрезка, имеющего 2 конечные точки A с координатами (5,8) и B с координатами (3,2). Для любых других комбинаций конечных точек просто укажите координаты 2 конечных точек и нажмите кнопку «СОЗДАТЬ РАБОТУ». Учащиеся начальной школы могут использовать этот калькулятор средней точки для создания работы, проверки результатов или эффективного решения домашних заданий.
Для любых других комбинаций конечных точек просто укажите координаты 2 конечных точек и нажмите кнопку «СОЗДАТЬ РАБОТУ». Учащиеся начальной школы могут использовать этот калькулятор средней точки для создания работы, проверки результатов или эффективного решения домашних заданий.
| Midpoint between 2 Points | |
|---|---|
| (x A , y A ) and (x B , y B ) | Midpoint |
| (2, 4) и (4, 4) | (3, 4) |
| (0, 2) и (2, 8) | (1, 5) | (-5, 6) |
| (3, -5) и (7, 9) | (5, 2) |
| (1, 0) и (5, 4) | (3, 2) |
| (-7, 5) и (7, 3) | (0, 2) 4) |
| (4, 7) и (2, 9) | (3, 8) |
| (1, 0) и (5, 4) | (3, 2) |
| (5, 4) | |
| (3, 12) и (9, 15) | (6, 13,5) |
| (6, 5) и (9, 2) | (7,5, 3,5) |
| (1, 7) и (1, 23) | (1, 15) |
| (2, 7) и (6, 3) | (4, 5) |
| (6, 7) и (4, 3) | (5, 5) |
| (1, 7) и (3, 3) | (2, 5) |
| (1, 7) и (3, 2) | (2, 4,5) |
| (8, 5) и (3, 7) | (5,5, 6) |
| (9, 8) и (3, 5) | 906,5 ( )|
| (-1, -6) и (4, 5) | (1,5, -0,5) |
| (-3, -1) и (4, -5) | (0,5, -3) |
| (-4, 4) и (-2, 2) | (-3, 3) ) |
| (-4, 5) и (-6, 7) | (-5, 6) |
| (-4, 9) и (1, -6) | (-1,5, 1,5) ) |
| (-5, -7) и (2, -4) | (-1,5, -5,5) |
| (-7, 1) и (3, -5) | (-2 , -2) |
Реальные задачи с использованием средней точки
Поскольку упорядоченная пара чисел представляет координаты точки на двумерной декартовой плоскости, калькулятор средней точки чаще всего используется в аналитической геометрии.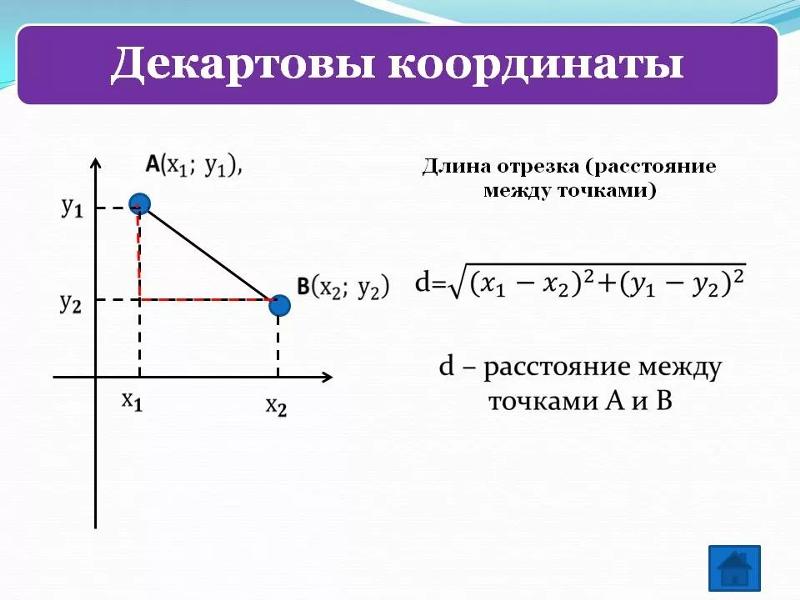 o)`, а Париж расположен в `(48,9o)`, которые обозначают северную широту и западную долготу. Если Белград и Париж являются конечными точками отрезка, соединяющего эти города, найти широту и долготу середины этого отрезка.
o)`, а Париж расположен в `(48,9o)`, которые обозначают северную широту и западную долготу. Если Белград и Париж являются конечными точками отрезка, соединяющего эти города, найти широту и долготу середины этого отрезка.
Практическое задание 2:
Найдите координаты середины `M` `\overline{PQ}`.
Калькулятор средней точки, формула, пошаговое вычисление, реальные приложения и практические задачи были бы очень полезны для учащихся начальной школы (образование K-12), чтобы узнать, что такое середина отрезка прямой в геометрии, как ее найти и где это может быть применимо в реальных задачах.
Midpoint Calculator + Online Solver With Free Steps
| Midpoint Calculator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Как найти длину отрезка с конечными точками Чтобы найти длину отрезка, вы добавляете квадрат разности x к квадрату разности y и вычисляете квадратный корень результата.
Таким образом, учитывая конечные точки (-3, 3) и (5, 3), вы должны найти расстояние следующим образом: 1 = 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| х 2 = 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| y 2 = 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Distance Formula Solution | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d | = | √ | (x 2 — x 1 ) 2 + (Y 2 — Y 1 ) 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| D | = | √ | (5 — -3) | . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| д | = | √ | (8) 2 + (0) 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| d | = | √ | 64 + 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| d | = | √ | 64 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| D | = | . сегмент с конечными точками (фактические результаты из Калькулятора расстояний и средних точек на этой странице). сегмент с конечными точками (фактические результаты из Калькулятора расстояний и средних точек на этой странице).Пример №1: (0, 4) и (5, 6)Найдите середину и длину линии, образованной координатами конечной точки (0, 4) и (5, 6).
На основании приведенных выше вычислений средняя точка линии, образованной координатами конечной точки (0, 4) и (5, 6), равна (2,5, 5), а расстояние между ними конечные точки 5. Пример #2: (-4, -9) и (3, 5)Найдите середину и длину линии, образованной координатами конечной точки (-4, -9) и (3, 5).
На основании приведенных выше расчетов середина линии, образованной координатами конечной точки (-4, -9) и (3, 5), равна (-0,5, -2), а расстояние между двумя конечными точками равно 15,65247584249. Пример №3: (-3, 7) и (5, -9)Найдите середину и длину линии, образованной координатами конечной точки (-3, 7) и (5, -9).
Исходя из приведенных выше расчетов, середина линии, образованной координатами конечной точки (-3, 7) и (1, -1), равна (-3, 7) и (1,-9) ), а расстояние между двумя конечными точками равно 17,88854381999832. Вернуться к калькуляторуВернуться к калькуляторуВернуться к калькулятору средней точкиВернуться к калькулятору средней точки 767 практических тестов Вопрос дня Карточки Учитесь по концепции ← Предыдущая 1 2 Следующая → ACT Math Help » Алгебра » Координатная плоскость » Линии » Формула середины » Как найти середину отрезка Какова координата точки, которая находится посередине между (-2, -4) и (6, 4)? Возможные ответы: (0,2) (2,0) (2,2) (3,1) Правильный Ответ: 9000 .0005 (2,0) Объяснение: Формула средней точки: Сообщить об ошибке Какова середина MN между точками M(2, 6) и N (8, 4)? Возможные ответы: (3, 1) (2, 1) (3, 5) (5, 2) (5, 5) Правильный Ответ: Правильный ответ: . (5, 5) Объяснение: Формула средней точки равна . Сложите значения x вместе и разделите их на 2, и сделайте то же самое для значений y. x: (2 + 8) / 2 = 10 / 2 = 5 y: (6 + 4) / 2 = 10 / 2 = 5 Середина MN равна (5,5). Сообщить об ошибке В стандартной координатной плоскости какова середина отрезка, проходящего из точки (3, 5) в точку (7, 9)? Возможные ответы: (7, 5) (10,14) (5, 7) (–2, –2) (7,6) 05 9 Правильный ответ (5, 7) Объяснение: Формула средней точки . Простой способ запомнить это состоит в том, что для нахождения средней точки просто нужно найти среднее значение двух координат x и среднее значение двух координат y. В этом случае две координаты x равны 3 и 7, а две координаты y равны 5 и 9. Сообщить об ошибке Найти середину отрезка с концами (–1, 4) и (3, 6). Возможные ответы: (5, 1) (1, 5) (3, 2) (4, 5) Правильный ответ: (1, 5) Объяснение: Формула для средней точки = (x 1 + x 2 )/2, (y 1 + y 2 )/2. (4 + 6)/2 или (1, 5) в качестве средней точки. Сообщить об ошибке В стандартной координатной плоскости x, y каковы координаты середины линии, конечные точки которой (–6, 4) и (4, –6)? Возможные ответы: 1, 1 –1, –1 –1, 1 –1, 1 / 2 1, –1 11. –1, –1 Пояснение: Для решения этой задачи воспользуемся формулой средней точки. Находим среднее значение координат x и y. (–6 + 4)/2, (4 + –6)/2 = –1, –1 Сообщить об ошибке Какова середина прямой с точками и ? Возможные ответы: Правильный ответ: Объяснение: Метод A: Чтобы найти середину, начертите числовую прямую, содержащую точки и . Затем рассчитайте расстояние между двумя точками. В этом случае расстояние между и равно . Разделив расстояние между двумя точками на 2, вы установите расстояние от одной точки до средней точки. Поскольку середина находится на расстоянии 12 от любого конца, средняя точка равна 5,9.0005 Метод B: , чтобы найти среднюю точку, используйте формулу средней точки: Сообщите о ошибке Janice и Mark работают в городе с Neat -Gridded Streets. Если Дженис работает на пересечении 33 rd Street и 7 Avenue, а Марк работает в 15 th Street и 5 th Avenue, сколько кварталов каждый из них проедет на обед, если они встретятся на перекрестке точно между обоими офисами? Возможные ответы: Правильный ответ: Объяснение: Переводя пересечения в точки на графике, Дженис работает в (33,7), а Марк работает в (15,5). Сообщить об ошибке Какая точка на прямой с действительными числами находится посередине между и ? Возможные ответы: Правильный ответ: Объяснение: На числовой прямой это единицы от . Найдем середину этого расстояния, разделив его на 2. Чтобы найти середину, мы прибавляем это значение к меньшему числу или вычитаем его из большего числа. Среднее значение будет . Сообщить об ошибке Какая средняя точка между и ? Возможные ответы: Правильный ответ: Объяснение: Используя формулу средней точки, Получаем: Что становится: что становится Сообщить об ошибке Что такое середина отрезка с концами и ? Возможные ответы: Правильный ответ: Объяснение: Середину линии можно найти с помощью формулы средней точки, которая определяется как: Таким образом, когда мы подставляем наши значения, мы получаем среднюю точку Сообщить об ошибке 5 0 Предыдущий 1 2 Далее → Уведомление об авторских правах 14 Диагностические тесты
767 практических тестов
Вопрос дня
Карточки
Learn by Concept Средняя точка относится к точке, которая находится посередине линии, соединяющей две точки. Формула средней точки используется для нахождения средней точки между двумя точками, координаты которых нам известны. Формула средней точки также используется для нахождения координат конечной точки, если известны координаты другой конечной точки и средней точки. В координатной плоскости, если провести линию, соединяющую две точки (4, 2) и (8, 6), то координаты середины линии, соединяющей эти две точки, равны ({4 + 8}/2, {2 + 6}/2) = (12/2, 8/2) = (6, 4). Давайте узнаем больше о формуле средней точки и различных методах нахождения середины линии. Средняя точка — это точка, лежащая между двумя точками и находящаяся посередине линии, соединяющей эти две точки. Если провести линию, соединяющую две точки, то средней точкой будет точка в середине линии, равноудаленная от двух точек. Для любых двух точек, скажем A и C, средней точкой является точка B, расположенная посередине между точками A и C. Следовательно, чтобы вычислить среднюю точку, мы можем просто измерить длину отрезка и разделить ее на 2. Обратите внимание, что точка B равноудалена от A и C. Середина существует только для отрезка. Линия или луч не могут иметь середины, потому что линия неопределенна в обоих направлениях, а луч имеет только один конец и поэтому может быть продолжен. Формула средней точки Формула средней точки определяется для точек на осях координат. Формула средней точки в математикеДаны две точки A (x) 1 , (y) 1 и B (x) 2 , (y) 2 , средняя точка между A и B определяется как , M(x) 3 , (y) 3 = [(x) 1 + (x) 2 ]/2, [(y) 1 + (y) 5 22 ]/2, где M — середина между A и B, а (x) 3 , (y) 3 — ее координаты. Давайте посмотрим на этот пример и найдем середину двух точек на одномерной оси. Предположим, у нас есть две точки, 5 и 9, на числовой прямой. Середина будет вычисляться как: (5 + 9)/2 = 14/2 = 7. Таким образом, 7 является серединой 5 и 9. Таким образом, формула для средней точки имеет вид пример, чтобы увидеть применение формулы средней точки. Пример: Используя формулу средней точки, найдите среднюю точку между точками X(5, 3) и Y(7, 8). Решение: Пусть M будет серединой между X и Y. M = ((5 + 7)/2, (3 + 8)/2) = (6, 11/2) Следовательно, координаты середины между X и Y равны (6, 11/2). Как найти середину? Далее, на основе точек и значений их координат используются следующие два метода для нахождения середины линии, соединяющей две точки. Метод 1: Если отрезок прямой вертикальный или горизонтальный, то, разделив длину на 2 и считая это значение от любой из конечных точек, мы получим середину отрезка прямой. Посмотрите на рисунок, показанный ниже. Координаты точек A и B равны (-3, 2) и (1, 2) соответственно. Длина горизонтальной линии \(\overline{AB}\) равна 4 единицам. Половина этой длины составляет 2 единицы. Перемещение на 2 единицы из точки (-3, 2) даст (-1, 2). Итак, (-1, 2) — это середина \(\overline{AB}\). Метод 2: Другой способ найти среднюю точку — использовать формулу средней точки. Координаты точек A и B равны (-3, -3) и (1, 4) соответственно. Используя формулу средней точки, мы имеем: ({-3 + 1}/2, {-3 + 4}/2) = (-2/2, 1/2) = (-1,1/2). Метод 3: Один из способов найти середину прямой, заданной на плоскости, — это построение. Мы можем использовать конструкцию циркуля и линейки, чтобы сначала построить линзу, используя дуги окружности одинакового (и достаточно большого) радиуса с центрами в двух конечных точках, а затем соединив вершины линзы (две точки, где дуги пересекаются). Вот пример определения координат конечной точки по средней точке и координатам другой конечной точки. Пример: Середина R между точками P и Q имеет координаты (4, 6). Если координаты Q равны (8, 10), то каковы координаты точки P? Решите его, используя формулу средней точки. Решение: Р = (м, н) R = ((m + 8)/2, (n + 10)/2) = (4, 6) Решение для n, Следовательно, координаты P равны (0, 2). Важные примечания по средней точке: Следующие точки являются важными свойствами средних точек.
Формула средней точки включает вычисления отдельно для x-координаты точек и y-координаты точек. Кроме того, вычисления точек между двумя заданными точками также включают в себя аналогичные вычисления координаты x и координаты y заданных точек. Следующие две формулы тесно связаны с формулой средней точки.
Центроид треугольника Формула Точка пересечения медиан треугольника называется центром треугольника. Медиана — это линия, соединяющая вершину с серединой противоположной стороны треугольника. Центроид делит медиану треугольника в отношении 2:1. Для треугольника с вершинами (x) 1 , (y) 1 , (x) 2 , (y) 2 , (x) 3 , (y) 3 формула для нахождения координат центра тяжести треугольника выглядит следующим образом. Формула сеченияФормула сечения помогает найти координаты любой точки, которая находится на линии, соединяющей две точки. Далее, отношение, в котором точка разделила линию, соединяющую две заданные точки, необходимо, чтобы узнать координаты точки. Точка может располагаться между точками или в любом месте за точками, но на одной линии. Формула сечения для нахождения координат точки, которая делит линию, соединяющую точки (x) 1 , (у) 1 и (х) 2 , (у) 2 в соотношении m:n выглядит следующим образом. Знак плюс используется в формуле для нахождения координат точки, которая делит точки внутри, а знак минус используется, если точка делится снаружи. ☛ Связанные темы: Ознакомьтесь с еще несколькими интересными статьями, которые содержат дополнительные концептуальные идеи, вращающиеся вокруг формулы средней точки.
Часто задаваемые вопросы о Midpoint FormulaЧто такое формула средней точки в координатной геометрии? Формула средней точки в координатной геометрии определяется как формула для нахождения центральной точки прямой с использованием координат ее концов. Что означает середина?Средняя точка определяется как точка, которая находится в середине линии, соединяющей две точки. Это точка, которая равноудалена от обеих конечных точек и, таким образом, делит отрезок пополам. Как использовать формулу средней точки?Формула средней точки очень проста, когда дело доходит до ее применения.
☛ Также проверьте: Вы можете попробовать этот калькулятор средней точки, чтобы проверить результат, полученный для средней точки отрезка линии — Калькулятор средней точки Что такое формула средней точки в Word? Для середины линии, соединяющей две точки, координаты которых заданы, формула середины точки словесно может быть описана как половина суммы x-координат двух точек и половина суммы y-координат две точки. Почему важна формула средней точки?Формула средней точки имеет различные применения в реальной жизни, например, для целей строительства и т. д. Она имеет важное значение в геометрии, например,
Может ли середина быть дробью?Да, среднее значение также может быть дробным. Это в основном зависит от числового значения двух точек. Средняя точка представляет собой сумму числового значения двух точек, деленную на 2. Для таких точек, как -4 и 5 на числовой прямой, средняя точка равна +1/2. Как рассчитать среднюю точку? Середину можно найти по формуле [(x) 1 + (x) 2 ]/2, [(y) 1 + (y) 2 ]/2. Здесь (x) 1 , (y) 1 и (x) 2 , (y) 2 — координаты двух точек, а середина — точка, лежащая на равном расстоянии между этими двумя точками. Может ли середина быть нулем?Средняя точка может быть нулевой. Это зависит от значения двух точек. Для двух точек на числовой прямой в точках со значениями -4 и 4 середина равна 0. А для двух точек, таких как (-2, 5) и (2, -5), середина равна (0 , 0). Что такое середина линии?Середина линии — это точка, равноудаленная от концов линии и в середине линии. Если конечные точки линии (x) 1 , (y) 1 и (x) 2 , (y) 2 , то формула для средней точки линии будет {[(x ) 1 + (x) 2 ]/2, [(y) 1 + (y) 2 ]/2} Что такое середина кривой?Середина кривой — это середина наибольшей хорды, которую можно провести для кривой. Середина окружности — это середина ее наибольшей хорды, которая является диаметром окружности. Что такое середина треугольника? Середина треугольника является центром тяжести треугольника. Центроид – это точка пересечения медиан треугольника. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


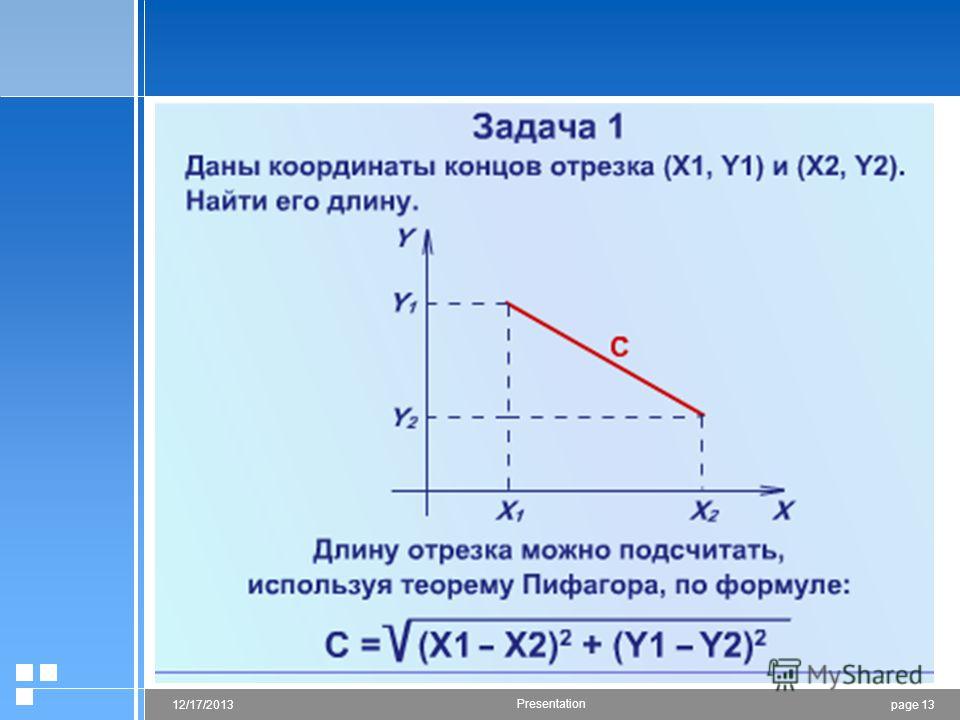
 Когда имеется много чисел и вам нужно определить среднюю точку , вам пригодится калькулятор средней точки.
Когда имеется много чисел и вам нужно определить среднюю точку , вам пригодится калькулятор средней точки.









 5
5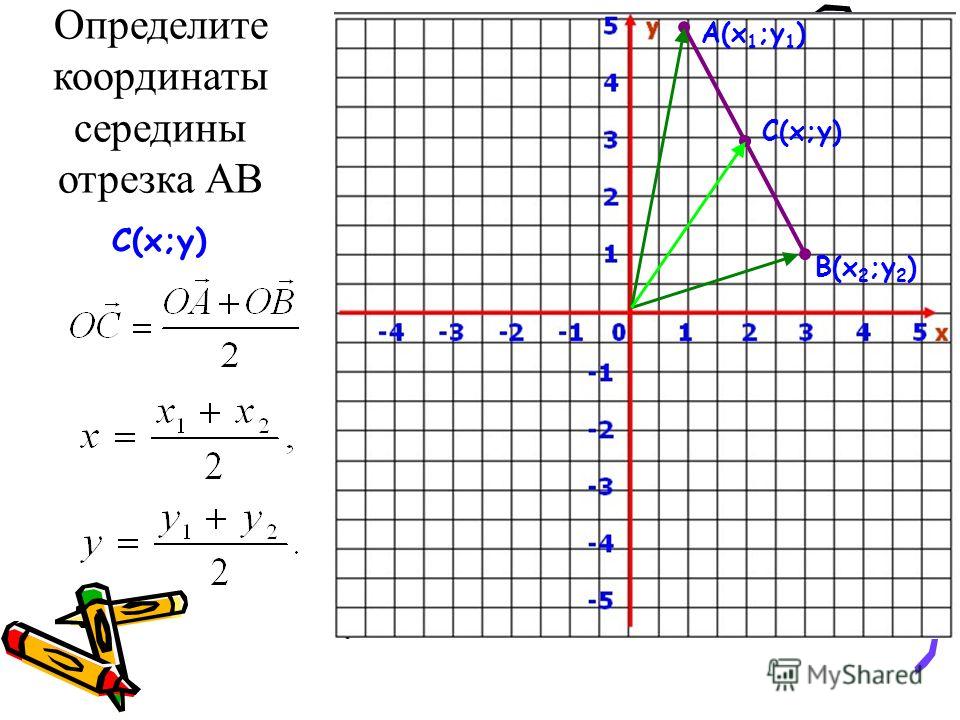 385164807134504.
385164807134504. 5
5 8529.
8529.

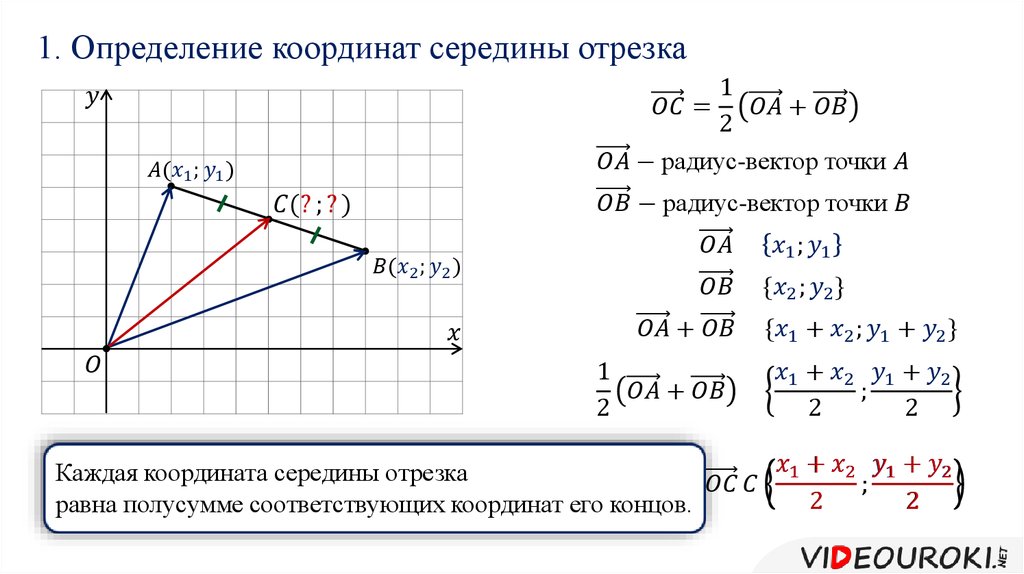 Если мы подставим эти значения в формулу средней точки, мы получим (3 + 7/2), (5 + 9) /2, что равно (5, 7). Если вы получили (–2, –2), возможно, вы вычли свои координаты x и y вместо сложения. Если вы получили (10,14), возможно, вы забыли разделить свои координаты x и y на 2. Если вы получили (6,6), возможно, вы нашли среднее значение x 1 и y 2 и x 2 и y 1 вместо того, чтобы хранить вместе координаты x и координаты y. Если вы получили (7, 5), возможно, вы поменяли местами координаты x и y.
Если мы подставим эти значения в формулу средней точки, мы получим (3 + 7/2), (5 + 9) /2, что равно (5, 7). Если вы получили (–2, –2), возможно, вы вычли свои координаты x и y вместо сложения. Если вы получили (10,14), возможно, вы забыли разделить свои координаты x и y на 2. Если вы получили (6,6), возможно, вы нашли среднее значение x 1 и y 2 и x 2 и y 1 вместо того, чтобы хранить вместе координаты x и координаты y. Если вы получили (7, 5), возможно, вы поменяли местами координаты x и y. Подставляя две координаты x и две координаты y от конечных точек, мы получаем (–1 + 3)/2.
Подставляя две координаты x и две координаты y от конечных точек, мы получаем (–1 + 3)/2.
 Середина этих двух точек находится путем взятия среднего значения координат x и среднего значения координат y, что дает ((33+15)/2, (5+7)/2) или (24, 6) . Путешествие в одном направлении за раз, количество блоков от любого офиса до 24 -я -я улица — 9, а количество кварталов до 6 -го — 1, всего 10 кварталов.
Середина этих двух точек находится путем взятия среднего значения координат x и среднего значения координат y, что дает ((33+15)/2, (5+7)/2) или (24, 6) . Путешествие в одном направлении за раз, количество блоков от любого офиса до 24 -я -я улица — 9, а количество кварталов до 6 -го — 1, всего 10 кварталов. Две опорные точки являются конечными точками линии, а средняя точка лежит между двумя точками. Середина делит линию, соединяющую эти две точки, на две равные половины. Кроме того, если провести линию, делящую пополам линию, соединяющую эти две точки, линия проходит через середину.
Две опорные точки являются конечными точками линии, а средняя точка лежит между двумя точками. Середина делит линию, соединяющую эти две точки, на две равные половины. Кроме того, если провести линию, делящую пополам линию, соединяющую эти две точки, линия проходит через середину.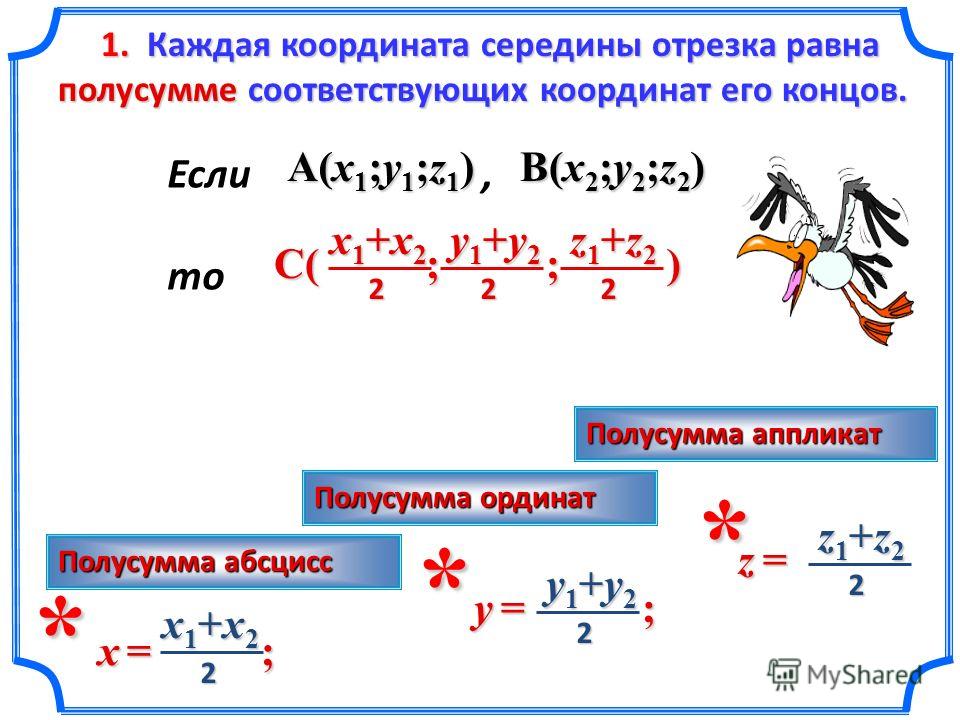
 Пусть (x) 1 , (y) 1 и (x) 2 , (y) 2 — концы отрезка. Средняя точка равна половине суммы x-координат двух точек и половине суммы y-координат двух точек. Формула средней точки для вычисления середины отрезка, соединяющего эти точки, может быть представлена как
Пусть (x) 1 , (y) 1 и (x) 2 , (y) 2 — концы отрезка. Средняя точка равна половине суммы x-координат двух точек и половине суммы y-координат двух точек. Формула средней точки для вычисления середины отрезка, соединяющего эти точки, может быть представлена как , (х) 1 , (у) 1 и (х) 2 , (у) 2 . Для любого линейного отрезка средняя точка находится посередине между двумя его конечными точками. Выражение для координаты x средней точки равно [(x) 1 + (x) 2 ]/2, что является средним значением координат x. Точно так же выражение для координаты y имеет вид [(y) 1 + (y) 2 ]/2, что является средним значением координаты y.
, (х) 1 , (у) 1 и (х) 2 , (у) 2 . Для любого линейного отрезка средняя точка находится посередине между двумя его конечными точками. Выражение для координаты x средней точки равно [(x) 1 + (x) 2 ]/2, что является средним значением координат x. Точно так же выражение для координаты y имеет вид [(y) 1 + (y) 2 ]/2, что является средним значением координаты y.
 Точка пересечения линии, соединяющей бугры и отрезок, является серединой отрезка.
Точка пересечения линии, соединяющей бугры и отрезок, является серединой отрезка.
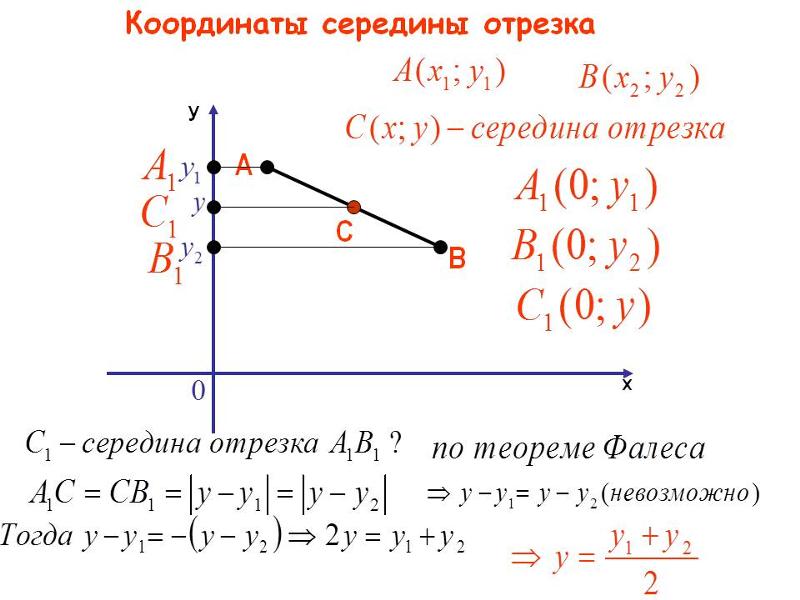
 Формула средней точки используется для нахождения половины пути, то есть точки, которая делит прямую на две равные части.
Формула средней точки используется для нахождения половины пути, то есть точки, которая делит прямую на две равные части.

