Периметр и площадь. Периметр и площадь прямоугольника Нахождение периметра
Наверняка каждый из нас учил в школе такую важную составляющую геометрии, как периметр. Нахождение периметра просто необходимо для решения множества задач. О том, как найти периметр, расскажет наша статья.
Стоит помнить, что периметр любой фигуры это почти всегда сумма ее сторон. Давайте рассмотрим несколько разных геометрических фигур.
- Прямоугольник — это такой четырехугольник, у которого параллельные стороны равны попарно между собой. Если одна сторона X, а другая Y, то мы получим такую формулу для нахождения периметра этой фигуры:
P = 2(X+Y) = X+Y+X+Y = 2X+2Y.
Пример решения задачи:
Допустим, что сторона X = 5 см, сторона Y = 10 см. Значит, подставив эти значения в нашу формулу, мы получим — P = 2*5 см + 2* 10см = 30 см.
- Трапеция — это четырехугольник, у которого две противоположные стороны параллельны, но не равны между собой. Периметр трапеции — это сумма всех четырех её сторон:
P = X+Y+Z+W, где X, Y, Z, W — стороны фигуры.

Пример решения задачи:
Допустим, что сторона X = 5 см, сторона Y = 10 см, сторона Z = 8 см, сторона W = 20 см. Значит, подставив эти значения в нашу формулу, мы получим — P = 5 см + 10 см + 8 см + 20 см = 43 см.
- Периметр круга (длину окружности) можно вычислить по формуле:
P = 2rπ = dπ, где r — это радиус круга, d — диаметр круга.
Пример решения задачи:
Допустим, что радиус r нашего круга равен 5 см, тогда диаметр d будет равен 2*5 см = 10 см. Известно, что π = 3,14. Значит, подставив эти значения в нашу формулу, мы получим — P = 2*5 см*3,14 = 31,4 см.
- Если Вам необходимо найти периметр треугольника, то Вы можете столкнуться с рядом проблем при этом, поскольку треугольники могут иметь очень разные формы. Например, есть острый, тупой, равнобедренный, прямоугольный или равносторонний треугольники. Хотя формула для всех видов треугольников такая:
P = X+Y+Z, где X, Y, Z — стороны фигуры.
Проблема в том, что при решении многих задач на нахождение периметра этой фигуры Вам не всегда будут известны длины всех сторон. Например, вместо информации о длине одной из сторон Вы можете иметь градус угла или длину высоты конкретного треугольника. Это существенно осложнит задачу, но не сделает ее решение нереальным. О том, как найти периметр треугольника, какой формы бы он не был можно прочитать » «.
Например, вместо информации о длине одной из сторон Вы можете иметь градус угла или длину высоты конкретного треугольника. Это существенно осложнит задачу, но не сделает ее решение нереальным. О том, как найти периметр треугольника, какой формы бы он не был можно прочитать » «. - Периметр такой фигуры, как ромб находят также как и периметр квадрата, ведь ромб — это параллелограмм, который имеет равные стороны. Узнать, как найти периметр квадрата можно прочитав статью на нашем сайте » «.
Теперь Вы знаете, как найти сторону периметра той геометрической фигуры, какой Вам нужно!
На этом занятии мы познакомимся с новым понятием — периметр прямоугольника. Мы сформулируем определение этого понятия, выведем формулу для его вычисления. Также повторим сочетательный закон сложения и распределительный закон умножения.
На данном уроке мы познакомимся с периметром прямоугольника и его вычислением.
Рассмотрим следующую геометрическую фигуру (рис. 1):
Рис. 1. Прямоугольник
1. Прямоугольник
Данная фигура — прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.
Прямоугольник — это четырехугольник, у которого четыре прямых угла и стороны попарно равны.
Что в нашей жизни может иметь прямоугольную форму? Например, книга, крышка стола или земельный участок.
Рассмотрим следующую задачу:
Задача 1 (рис. 2)
Вокруг земельного участка строителям понадобилось поставить забор. Ширина этого участка — 5 метров, длина — 10 метров. Забор какой длины получится у строителей?
Рис. 2. Иллюстрация к задаче 1
Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон. У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2.
Найдем значение выражения (5+10)·2. Сначала выполняем действие в скобках: 5+10=15. А затем повторяем число 15 два раза: 15·2=30.
Ответ: 30 метров.
Периметр прямоугольника — сумма длин всех его сторон. Формула для подсчета периметра прямоугольника : , здесь a — длина прямоугольника, а b — ширина прямоугольника. Сумма длины и ширины называется
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 7 см и 3 см: (7+3)·2=20 (см).
Периметр любой фигуры измеряется в линейных единицах.
На данном уроке мы познакомились с периметром прямоугольника и формулой его вычисления.
Произведение числа и суммы чисел равно сумме произведений данного числа и каждого из слагаемых.
Если периметр — это сумма длин всех сторон фигуры, то полупериметр — сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).
Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).
Список литературы
- Александрова Э.И. Математика. 2 класс. — М.: Дрофа, 2004.
- Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. — М.: Астрель, 2006.
- Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. — М.: Просвещение, 2012.
- Festival.1september.ru ().
- Nsportal.ru ().
- Math-prosto.ru ().
Домашнее задание
- Найти периметр прямоугольника, у которого длина 13 метров, а ширина — 7 метров.
- Найти полупериметр прямоугольника, если его длина — 8 см, а ширина — 4 см.
- Найти периметр прямоугольника, если его полупериметр — 21 дм.
Не многие формулы из курса школьной математики мы применяем в повседневной жизни. Однако, есть такие уравнения, которые имеют применение, если не на регулярной основе, то время от времени. Одна из таких формул — вычисление периметра фигуры.
Что такое периметр?
Периметром называют суммарную длину всех сторон геометрической фигуры. Для его обозначения используется буква латинского алфавита «Р». Проще говоря, чтобы найти периметр, необходимо измерить длины всех сторон геометрической фигуры и сложить полученные значения. Длина вычисляется обычным измерительным прибором, таким как линейка, рулетка, сантиметровая лента и прочее.
Единицей измерения соответственно являются сантиметры, метры, миллиметры и другие меры длины. Длина стороны многоугольника вычисляется путем прикладывания измерительного прибора от одной вершины к другой. Начало шкалы деления прибора должно совпадать с одной из вершин. Второе числовое значение, на которое попадает другая вершина и является длиной стороны многоугольника. Таким же образом необходимо измерить все длины сторон фигуры и полученные значения сложить. Единицей измерения периметра является та же самая единица, которая используется для измерения стороны фигуры.
Прямоугольником следует называть геометрическую фигуру, которая состоит из четырех сторон разной длины и три угла у которой прямые. При построении такой фигуры на плоскости получается так, что стороны у нее будут попарно равны, но не равны все между собой. Что такое периметр прямоугольника? Это также суммарная длина всех длин фигуры. Но так как у прямоугольника по две стороны имеют одинаковое значение, то в вычислении периметра можно дважды сложить длины двух смежных сторон. Единицей измерения периметра прямоугольника также являются общепринятые единицы измерения.
При построении такой фигуры на плоскости получается так, что стороны у нее будут попарно равны, но не равны все между собой. Что такое периметр прямоугольника? Это также суммарная длина всех длин фигуры. Но так как у прямоугольника по две стороны имеют одинаковое значение, то в вычислении периметра можно дважды сложить длины двух смежных сторон. Единицей измерения периметра прямоугольника также являются общепринятые единицы измерения.
Треугольником следует называть геометрическую фигуру, имеющую три угла (как разного значения, так и одинакового) и состоящую из отрезков, образованных от точек пересечения лучей, образующих углы. Треугольник имеет три стороны и три угла. В нем могут быть из трех равны две стороны. Такой треугольник следует считать равнобедренным. Бывают такие фигуры, в которых равны все три стороны между собой. Принято такие треугольники называть равносторонними.
Что такое периметр треугольника? Его вычисление можно провести по аналогии с периметром четырехугольника. Равен периметр треугольника суммарной длине длин его сторон. Вычисление периметра треугольника, в котором две стороны равны — равнобедренного — упрощается умножением одной длины равных сторон на два. К полученному значению необходимо прибавить значение длины третьей стороны. Вычисление периметра треугольника с равными сторонами можно свести к простому вычислению произведения одной длины стороны треугольника на три.
Равен периметр треугольника суммарной длине длин его сторон. Вычисление периметра треугольника, в котором две стороны равны — равнобедренного — упрощается умножением одной длины равных сторон на два. К полученному значению необходимо прибавить значение длины третьей стороны. Вычисление периметра треугольника с равными сторонами можно свести к простому вычислению произведения одной длины стороны треугольника на три.
Прикладное значение периметра
Вычисление периметра в повседневной жизни применяется во многих сферах, но чаще всего при выполнении строительных, геодезических, топографических, архитектурных, планировочных работах. Но перечисленным сферы применения вычисления периметра, конечно же, не ограничиваются.
Например, при выполнении геодезических и топографических работ очень часто возникает необходимость посчитать периметр границ определенного участка. Но на практике участки редко имеют правильную форму. Поэтому вычисление длины периметра происходит по формуле расчета суммы длин всех сторон участка.
Необходимость вычисления периметра участка очень часто обусловлена тем, что необходимо знать, какое количество материала потребуется для установки ограждений. Даже простой приусадебный участок нуждается в измерении периметра для того, чтобы грамотно обнести его забором.
Измерительные приборы на местности
Для вычисления периметра на местности невозможно использование простой ученической линейки. Поэтому специалисты используют специальные приборы. Конечно, самый простой и доступный вариант — это измерение длины границы участка шагами. Размер шага взрослого человека составляет примерно один метр. Иногда один метр и двадцать сантиметров. Но этот способ очень неточный и дает большую погрешность в измерении. Он подходит в том случае, если нет необходимости точного вычисления длины границы, а есть потребность просто прикинуть примерную длину.
Для более точного вычисления длины сторон участка и, соответственно, периметра, существуют специальные приборы. В первую очередь, можно воспользоваться специальной металлической рулеткой или обычным проводом.
Также существуют специальные измерительные устройства, такие как дальномеры. Приборы бывают оптические, лазерные, световые, ультразвуковые. Следует помнить, что чем дальше дальномер способен измерять расстояние, тем выше у него погрешность. Такие приборы используются в геодезических и топографических съемках.
Прямоугольник обладает многими отличительными особенностями, исходя из которых, выработаны правила вычисления его различных числовых характеристик. Итак, прямоугольник:
Плоская геометрическая фигура;
Четырехугольник;
Фигура, у которой противоположные стороны равны и параллельны, все углы прямые.
Периметр – это общая длина всех сторон фигуры.
Вычисление периметра прямоугольника — довольно простая задача.
Все, что вам нужно знать, это ширину и длину прямоугольника. Поскольку прямоугольник имеет две равные длины и две равные ширины, измеряется только одна сторона.
Периметр прямоугольника равен удвоенной сумме 2-х его сторон длины и ширины.
P = (a + b) 2, где a — длина прямоугольника, b — ширина прямоугольника.
Так же периметр прямоугольника можно найти при помощи суммы всех сторон.
P= a+a+b+b, где а– длина прямоугольника, b – ширина прямоугольника.
Периметр квадрата — это длина стороны квадрата, умноженная на 4.
P = a 4, где a — длина стороны квадрата.
Дополнение: Нахождение найти площади и периметра прямоугольников
В программе обучения за 3 класс предусмотрено изучение многоугольников и их особенностей. Для того чтобы понять, как найти периметр прямоугольника и площадь, разберемся, что подразумевается под этими понятиями.
Основные понятия
Нахождение периметра и площади требует знания некоторых терминов. К ним относятся:
- Прямой угол. Образуется из 2 лучей, имеющих общее начало в виде точки. При знакомстве с фигурами (3 класс) прямой угол определяют с помощью угольника.
- Прямоугольник. Это четырехугольник, все углы которого являются прямыми. Его стороны называют длиной и шириной.
 Как известно, противоположные стороны этой фигуры равны.
Как известно, противоположные стороны этой фигуры равны. - Квадрат. Является четырехугольником, все стороны которого равны.
При знакомстве с многоугольниками их вершины могут называться АВСД. В математике принято именовать точки на чертежах буквами латинского алфавита. В названии многоугольника перечисляют все вершины без пропусков, например, треугольник ABC.
Вычисление периметра
Периметр многоугольника — это сумма длин всех его сторон. Эта величина обозначается латинской буквой P. Уровень знаний для предложенных примеров — 3 класс.
Задача №1: «Начертите прямоугольник 3 см шириной и 4 см длиной с вершинами ABCD. Найдите периметр прямоугольника ABCD».
Формула будет выглядеть так: P=AB+BC+CD+AD либо P=AB×2+BC×2.
Ответ: P=3+4+3+4=14 (см) либо P=3×2 + 4×2=14 (см).
Задача №2: «Как найти периметр прямоугольного треугольника ABC, если значения сторон равны 5, 4 и 3 см?».
Ответ: P=5+4+3=12 (см).
Задача №3: «Найдите периметр прямоугольника, одна сторона которого равна 7 см, а другая на 2 см длиннее».
Ответ: P=7+9+7+9=32 (см).
Задача №4: «Соревнования по плаванию проходили в бассейне, периметр которого составляет 120 м. Сколько метров проплыл участник соревнований, если ширина бассейна 10 м?».
В данной задаче стоит вопрос, как найти длину бассейна. Для решения найдите длины сторон прямоугольника. Ширина известна. Сумма длин двух неизвестных сторон должна составить 100 м. 120-10×2=100. Чтобы узнать расстояние, которое преодолел пловец, нужно разделить полученный результат на 2. 100:2=50.
Ответ: 50 (м).
Вычисление площади
Более сложной величиной является площадь фигуры. Для ее измерения используют мерки. Эталоном среди мерок являются квадраты.
Площадь квадрата со стороной 1 см равна 1 см². Квадратный дециметр обозначен как дм², а квадратный метр — м².
Области применения единиц измерения могут быть такими:
- В см² измеряют маленькие предметы, например фотографии, обложки учебников, листы бумаги.
- В дм² можно измерить географическую карту, оконное стекло, картину.

- Для измерения пола, квартиры, земельного участка используют м².
Если начертить прямоугольник 3 см длиной и 1 см шириной и разбить на квадраты со стороной 1 см, то в нем поместится 3 квадрата, а значит, его площадь составит 3 см². Если прямоугольник разбит на квадраты, найдем периметр прямоугольника также без затруднений. В данном случае он равен 8 см.
Другой способ посчитать количество квадратов, вмещающихся в фигуру, — это использование палетки. Начертим на кальке квадрат площадью 1 дм², что составляет 100 см². Поместим кальку на фигуру и посчитаем число квадратных сантиметров в одном ряду. После этого выясним количество рядов, а затем перемножим значения. Значит, площадь прямоугольника — это произведение его длины и ширины.
Способы сравнения площадей:
- На глаз. Иногда достаточно просто взглянуть на предметы, поскольку в некоторых случаях и невооруженным глазом видно, что одна фигура занимает больше места, как, например, учебник, лежащий на столе рядом с пеналом.

- Наложение. Если фигуры совпадают при наложении, их площади равны. Если же одна из них полностью помещается внутри второй, то ее площадь меньше. Места, занимаемые тетрадным листом и страницей из учебника, можно сравнить, наложив их друг на друга.
- По количеству мерок. Фигуры при наложении могут и не совпадать, однако иметь одинаковую площадь. Сравнить в этом случае можно, подсчитав количество квадратов, на которые разбита фигура.
- Числа. Сравниваются численные значения, измеренные одной и той же меркой, например, в м².
Пример №1: «Швея сшила детское одеяло из квадратных разноцветных лоскутков. Один лоскуток длиной 1 дм, в ряду по 5 штук. Сколько дециметров ленты понадобится швее для обработки краев одеяла, если известна площадь 50 дм²?».
Чтобы решить задачу, нужно ответить на вопрос, как найти длину прямоугольника. Далее найдем периметр прямоугольника, составленного из квадратов. Из задачи ясно, что ширина одеяла — 5 дм, вычисляем длину, разделив 50 на 5, и получаем 10 дм. Теперь найдите периметр прямоугольника со сторонами 5 и 10. P=5+5+10+10=30.
Теперь найдите периметр прямоугольника со сторонами 5 и 10. P=5+5+10+10=30.
Ответ: 30 (м).
Пример №2: «На раскопках обнаружен участок, где могут находиться древние сокровища. Сколько территории придется исследовать ученым, если известен периметр 18 м и ширина прямоугольника 3 м?».
Определим длину участка, проделав 2 действия. 18-3×2=12. 12:2=6. Искомая территория будет также равна 18 м² (6×3=18).
Ответ: 18 (м²).
Таким образом, зная формулы, вычислить площадь и периметр не составит труда, а приведенные выше примеры помогут попрактиковаться в решении математических задач.
Содержимое:
Вычисление периметра прямоугольника — довольно простая задача. Все, что вам нужно знать, это ширину и длину прямоугольника. Если эти величины не даны, вам необходимо найти их. Эта статья расскажет, как это сделать.
Шаги
1 Стандартный метод
- 1 Формула для вычисления периметра. Основная формула для вычисления периметра прямоугольника: P = 2 * (l + w) .

- Запомните: периметр – это общая длина всех сторон фигуры.
- В этой формуле P — «периметр», l — длина прямоугольника, w — ширина прямоугольника.
- У длины всегда большее значение, чем у ширины.
- Поскольку прямоугольник имеет две равные длины и две равные ширины, измеряется только одна сторона l (длина) и одна сторона w (ширина) (хотя у прямоугольника четыре стороны).
- Вы также можете записать формулу в виде: P = l + l + w + w
- 2 Найдите длину и ширину. В обычной математической задаче длина и ширина прямоугольника, как правило, даны. Если вы ищите периметр прямоугольника в реальной жизни, используйте линейку или рулетку, чтобы найти длину и ширину.
- Если вы вычисляете периметр прямоугольника в реальной жизни, используйте рулетку или мерную ленту, чтобы найти длину и ширину нужного участка. Если работы проводятся на открытом воздухе, измерьте все стороны, чтобы убедиться, что параллельные стороны действительно совпадают.

- Например: l = 14 см, w = 8 см
- Если вы вычисляете периметр прямоугольника в реальной жизни, используйте рулетку или мерную ленту, чтобы найти длину и ширину нужного участка. Если работы проводятся на открытом воздухе, измерьте все стороны, чтобы убедиться, что параллельные стороны действительно совпадают.
- 3 Сложите длину и ширину. Подставьте значения в формулу и сложите их.
- Обратите внимание, что в соответствии с порядком операций, математические выражения в скобках решаются в первую очередь.
- Например: P = 2 * (l + w) = 2 * (14 + 8) = 2 * (22)
- 4 Умножьте эту сумму на два (согласно формуле).
- Обратите внимание, что умножив сумму на два, вы учли две другие стороны прямоугольника. Складывая ширину и длину, вы складываете только две стороны фигуры. Поскольку две другие стороны прямоугольника равны двум сложенным, сумма просто умножается на два и таким образом находится общая сумма всех четырех сторон.
- Полученное число будет периметром прямоугольника.
- Например: P = 2 * (l + w) = 2 * (14 + 8) = 2 * (22) = 44 см
- 5 Альтернативный метод: сложите l + l + w + w . Вместо сложения двух сторон и умножения их на два, можно просто сложить все четыре стороны и найти периметр прямоугольника.

- Если вам тяжело дается понятие периметра, то данный метод как раз для вас.
- Например: P = l + l + w + w = 14 + 14 + 8 + 8 = 44 см
2 Вычисление периметра через площадь и одну сторону
- 1 Формула для площади прямоугольника. Если вам дана площадь прямоугольника, вы должны знать формулу для ее вычисления, чтобы найти недостающую информацию для вычисления периметра.
- Запомните: площадь фигуры — это значение общего пространства, которое ограничено сторонами фигуры.
- Формула для вычисления площади прямоугольника: A = l * w
- Формула для вычисления периметра прямоугольника: P = 2 * (l + w)
- В приведенных выше формулах А — «площадь», P — «периметр»,l — длина прямоугольника, w — ширина прямоугольника.
- 2 Разделите площадь на данную в задаче сторону, чтобы найти другую сторону.
- Так как для вычисления площади вам нужно умножить длину на ширину, то разделив площадь на ширину, вы получите длину.
 Аналогично, деление площади на длину даст вам ширину.
Аналогично, деление площади на длину даст вам ширину. - Например: A = 112 см2, l = 14 см
- A = l * w
- 112 = 14 * w
- 112/14 = w
- 8 = w
- Так как для вычисления площади вам нужно умножить длину на ширину, то разделив площадь на ширину, вы получите длину.
- 3 Добавьте длину и ширину. Теперь, когда у вас есть значения длины и ширины, их можно подставить в формулу для вычисления периметра прямоугольника.
- Первым делом нужно сложить длину и ширину, поскольку данная часть уравнения заключена в скобки.
- Согласно порядку вычислений, первым выполняется действие, приведенное в скобках.
- 4 Умножьте сумму длины и ширины на два. После того как вы сложили длину и ширину прямоугольника, можно найти периметр, умножив полученное число на два. Это необходимо для добавления оставшихся двух сторон прямоугольника.
- Противоположные стороны прямоугольника равны, именно поэтому сумму длины и ширины нужно умножить на два.
- Одинакова как длина противоположных сторон, так и ширина.
- Например: Р = 2 * (14 + 8) = 2 * (22) = 44 см
3 Периметр прямоугольной фигуры
- 1 Запишите основную формулу для определения периметра.
 Периметр – это общая длина всех сторон фигуры.
Периметр – это общая длина всех сторон фигуры.- Прямоугольник имеет четыре стороны. Стороны, образующие длину, равны друг другу и стороны, образующие ширину, равны друг другу. Таким образом, периметр является суммой этих четырех сторон.
- Прямоугольная фигура. Рассмотрим фигуру формы «L». Такая фигура может быть разбита на два прямоугольника. Однако, при вычислении периметра фигуры такое разбиение на два прямоугольника не учитывается. Периметр рассматриваемой фигуры: , где S – стороны фигуры (смотрите рисунок).
- Каждая “s” – это отдельная сторона сложного прямоугольника.
- 2 В обычной математической задаче стороны фигуры, как правило, даны. Если вы ищите периметр прямоугольной фигуры в реальной жизни, используйте линейку или рулетку, чтобы найти ее стороны.
- Для объяснения введем следующие обозначения: L, W, l1, l2, w1, w2 . Прописные L и W l и w
- Таким образом, формула Р = S1 + S2 + S3 + S4 + S5 + S6 записывается в виде: (обе формулы, по сути, одинаковы, но используют разные переменные).

- Переменные “w” и “l” просто заменяют числа.
- Пример: L = 14 см, W = 10 см, l1 = 5 см, l2 = 9 см, w1 = 4 см, w2 = 6 см.
- Обратите внимание, что l1 +l2 =L . Аналогично, w 1 + w2 =W .
- 3 Сложите стороны.
- 48 см
4 Периметр прямоугольной фигуры (известны только некоторые стороны)
- 1 Проанализируйте данные вам значения сторон. Вы можете найти периметр прямоугольной фигуры, если вам даны по крайней мере одна полная длина или полная ширина и, по крайней мере, три неполные ширины и длины.
- Для «L»-образной прямоугольной фигуры используется формула P = L + W + l1 + l2 + w1 + w2
- В приведенной выше формуле: P – это периметр, прописные L и W обозначают полную длину и ширину фигуры. Строчные l и w обозначают неполную длину и ширину фигуры.
- Пример: L = 14 см, l1 = 5 см, w1 = 4 см, w2 = 6 см; Требуется найти: W, l2.

- 2 Используя данные значения сторон, найдите неизвестные стороны. Учтите, что l1 +l2 =L . Аналогично, w 1 + w2 =W .
- Например: L = l1 + l2; W = w1 + w2
- L = l1 + l2
- 14 = 5 + l2
- 14 – 5 = l2
- 9 = l2
- W = w1 + w2
- W = 4 + 6
- W = 10
- Например: L = l1 + l2; W = w1 + w2
- 3 Сложите стороны. Подставьте значения в формулу и вычислите периметр прямоугольной фигуры.
- P = L + W + l1 + l2 + w1 + w2 = 14 + 10 + 5 + 9 + 4 + 6 = 48 см
Что вам понадобится
- Карандаш
- Бумага
- Калькулятор (опционально)
- Линейка или рулетка (опционально)
Задачи на нахождение периметра и площади для 4 класса с ответами » Kupuk.net
Для решения задач на нахождения периметра и площади прямоугольников и квадратов необходимо освоить следующие основные формулы:
a — длина
b — ширина
P — периметр
S — площадь
Формулы площади и периметра для квадрата
P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата
Формулы площади и периметра для прямоугольника
P = a + b + a + b; P = 2a + 2b;
P = (a + b) · 2 — периметр прямоугольника
S = a · b — площадь прямоугольника
Примеры решения задач разной сложности на нахождение периметра и площади
Задача 1
Каков периметр треугольника ABC?
Ответ: периметр треугольника равен 125 см.
Задача 2
Красный треугольник является равносторонним со стороной 23 сантиметров. Чему равен его периметр?
Ответ: Все три стороны равностороннего треугольника равны. Таким образом, его периметр равен 23 · 3 = 69 см.
Задача 3
Равнобедренный треугольник имеет периметр 37 сантиметров, а его основание имеет длину 9 сантиметров. Каждая из двух других сторон будет иметь длину _____ см.?
Ответ: Равнобедренный треугольник имеет две равные стороны. Сумма равных сторон будет 37 — 9 = 28 см. Значит, каждая из них будет равна 28 : 2 = 14 см.
Задача 4
У Тимы есть сад в форме квадрата со стороной 9 метров. Какова длина забора, который опоясывает сад?
Ответ: Все стороны квадрата равны. Длина забора P равна длине стороны умноженной на 4. P = 4 · 9 = 36 метров.
Задача 5
В прямоугольнике ABCD красная сторона составляет 18 см, а синяя сторона 12 см. Чему равен периметр прямоугольника?
Ответ: Периметр прямоугольника равен 60 см.
Задача 6
Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?
Ответ: Площадь прямоугольника 56 м².
Задача 7
Площадь витрины квадратной формы 64м². Узнай ее периметр.
Ответ: Периметр витрины равен 32 м.
Задача 8
Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.
Ответ: Площадь прямоугольника равна 630 см².
Задача 9
Парк имеет форму прямоугольника с длиной 24 метра и шириной 18 метров. Если на его сторонах надо посадить деревья с отступом в 2 метра друг от друга, то сколько нужно деревьев?
Ответ: 42 дерева.
Задача 10
Каков периметр синей фигуры?
Ответ: Здесь есть два квадрата, у которых есть общая часть стороны. Так как сторона квадрата равна 10 см и часть стороны равна 8 см, то общая часть 2 см, а оставшаяся часть второго квадрата равна 8 см.
Периметр равен 10 + 10 + 8 + 10 + 10 + 10 + 8 + 10 = 76 см.
Задача 11
Два прямоугольных участка имеют одинаковую площадь. Длина первого — 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?
Ответ: Длина второго участка 40 м.
Задача 12
Найди периметр квадрата со стороной 8 см.
Ответ: Периметр квадрата 32 см.
Задача 13
Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.
Решение:
6 · 4 = 24 (см) -находим периметр квадрата
3 + 3 = 6 (см) -сумма ширины прямоугольника
24 — 6 = 18 (см)- сумма двух длин прямоугольника
18 : 2 = 9 (см)
Ответ: Длина прямоугольника 9 см.
Задача 14
Длина бассейна прямоугольной формы 15 м. Найди периметр бассейна, если его площадь 120 м2.
Решение:
120:15=8 (м)- ширина бассейна
(8+15)·2= 46 (м)
Ответ: Периметр бассейна 46 метров
Задача 15
Периметр квадрата 8 см. Из трех таких квадратов сложили прямоугольник. Найди периметр получившегося прямоугольника.
Из трех таких квадратов сложили прямоугольник. Найди периметр получившегося прямоугольника.
Решение:
8:4=2 (см)- сторона квадрата
2+2+2+2+2+2+2+2=16(см)
Ответ: Периметр прямоугольника 16 см.
Задача 16
Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см. На сколько см² он ошибся?
Решение:
5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 — 45 = 3 (см²)
Ответ: Ученик ошибся на 3 см²
Задача 17
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.
Решение:
4·2=8 (дм) -длина окна
8·4=32 (дм²)
Ответ: Площадь окна 32 дм²
Задача 18
Один прямоугольный участок имеет длину 36 м, а ширину 20 м. Найдите ширину другого участка с такой же площадью, если его длина на 6 м меньше длины первого участка.
Ответ: Ширина другого участка 24 м.
Задача 19
У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?
Ответ: Площадь квадрата больше на 4 см.
Задача 20
Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
Ответ: Площадь квадрата 36 см², периметр квадрата 24 см.
Задача 21
У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
Ответ: Площадь прямоугольника 35 м², периметр прямоугольника 24 см.
Задача 22
Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?
Решение:
1) 8 ∙ 8 = 64 (площадь клумбы)
2) 64 : 16 = 4(1/16 клумбы)
3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
4) 64 – 28 = 36
Ответ: Незабудками засажено 36 м².
Задача 23
Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?
Чему равна его площадь, если периметр составляет 18 см?
Решение:
1) 6 ∙ 2 = 12
2) 18 – 12 = 6
3) 6 : 2 = 3 (ширина прямоугольника)
4) 3 ∙ 6 = 18
Ответ: Площадь прямоугольника 18 м².
Задача 24
Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?
Решение:
1) 4800 : 60 = 80 (длина стола)
2) 60 ∙ 2 = 120 см
3) 80 ∙ 2 = 160 см
4) 120 + 160 = 280 см
Ответ: Периметр стола 280 см.
Задача 25
Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?
Решение:
1) 5 ∙ 2 = 10
2) 40 – 10 = 30
3) 30 : 2 = 15 (другая сторона прямоугольника)
4) 5 ∙ 15 = 75
Ответ: Площадь прямоугольника 75 см².
Задача 26
Площадь квадрата 49 кВ дм. Узнайте его периметр.
Решение:
1) 49 : 7 = 7 (сторона квадрата)
2) 7 ∙ 4 = 28 (периметр квадрата)
Ответ: Периметр квадрата равен 28 дм.
Задача 27
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.
Решение:
1) 4 ∙ 2 = 8 (длина окна)
2) 4 ∙ 8 = 32
Ответ: Площадь окна равна 32 м².
Задача 28
Длина участка земли 54 м. ширина — 48 м. 5/9 площади засажено картофелем. Остальная часть участка – капустой. Какая площадь засажена капустой?
Решение:
1) 54 ∙ 48 = 2592 (площадь участка земли)
2) 2592 : 9 = 288 (1/9 площади)
3) 288 ∙ 5 = 1440 (5/9 площади)
4) 2592 – 1440 = 1152
Ответ: Капустой засадили 1152 м².
Задача 29
Найди периметр квадрата со стороной 16 см.
Ответ: Периметр квадрата 64 см.
Задача 30
Найди длину прямоугольника с помощью уравнения, если его ширина 7 см, а периметр равен 40 см.
Решение:
P = (a + b) · 2 — периметр прямоугольника
или
(a + b) · 2 = P,
где a — длина = ?, b — ширина = 7 см, P — периметр = 40 см.
Составим уравнение:
(а + 7) · 2 = 40
2а + 14 = 40
2а = 40 — 14
2а = 26
а = 26 : 2
а = 13
Ответ: Длина прямоугольника 13 см.
Задача 31
Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.
Ответ: Ширина прямоугольника 5 см.
Задача 32
Периметр квадрата 24 см. Найди его площадь.
Решение:
24 : 4 = 6 (см)
6 · 6 = 36 (см²)
Ответ: Площадь квадрата 36 см².
Задача 33
Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.
Ответ: Площадь прямоугольника 56 см².
Задача 34
Площадь прямоугольника 40 см². Ширина его 4 см. Чему равен периметр прямоугольника?
Решение:
40 : 4 = 10 (см)
(10 + 4) · 2 = 28 (см)
Ответ: Периметр прямоугольника 28 см.
Задача 35
Ребро куба равно 2 сантиметров. Найти площадь всех граней куба.
Решение:
Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.
У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).
Если S = a · a — площадь квадрата, тогда
S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6
2 · 2 · 6 = 24 (см²)
Ответ: Площадь всех граней куба равна 24 см².
Задача 36
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Ответ: Площадь получившейся фигуры равна 44.
Задача 37
Площадь одной клетки равна 1см.
- Найдите площадь фигуры, изображённой на рисунке A.
- Найдите площадь фигуры, изображённой на рисунке B.
- Найдите площадь фигуры, изображённой на рисунке C.
- Найдите площадь фигуры, изображённой на рисунке D.
- Найдите площадь фигуры, изображённой на рисунке E.
Ответ: Площадь фигуры A 18,5 см², площадь фигуры B 20,5 см², площадь фигуры C 30,5 см², площадь фигуры A 18,5 см², площадь фигуры E 12 см².
Задача 38
Найдите площади и периметры фигурок. Сделайте вывод.
Ответ: Пусть каждая из сторон клетки равна 1 см, тогда применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²
Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура A имеет четыре стороны, тогда 1 + 4 + 1 + 4 = 10 см — периметр фигуры.
Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура B имеет четыре стороны, тогда 2 + 2 + 2 + 2 = 8 см — периметр фигуры.
Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура C имеет шесть сторон, тогда 3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.
Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура D имеет восемь сторон, тогда 1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.
Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура E имеет восемь сторон, тогда 1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.
Вывод: Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат. У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат.
Задача 39
Квадрат в данной фигуре имеет периметр 24 см. Синий треугольник — периметр 15 см. Каков периметр красной фигуры?
Ответ: Периметр красной фигуры равен 27 см.
Задача 40
Периметр каждого из зеленых квадратов 12 см. Каков периметр большого квадрата?
Ответ: Периметр равен 36 см.
Задача 41
Площадь прямоугольника 72 см2. Какова длина и ширина прямоугольника, если ширина в 2 раза меньше, чем его длина?
Ответ: Длина прямоугольника равна 12 см. а ширина — 6 см.
Задача 42
Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см.
Ответ: Периметр прямоугольника равен 24 см.
Задача 43
Периметр красного квадрата равен 16см. Красные треугольники равносторонние. Каково расстояние проползет улитка по пути ABCDFGHA?
Ответ: Расстояние пройденное улиткой будет равно 28 см.
Задача 44
В зале длиной 12 м и шириной 8 м надо покрыть пол квадратными плитками. Сколько потребуется плиток, если площадь каждой плитки 4 дм2?
Ответ: 2400 плиток.
Задача 45
Каков периметр зеленой зоны, если ширина синей зоны равна 3 метра?
Ответ: Периметр зеленой зоны равен 100 метров.
Что периметр и его находить. Периметр и площадь прямоугольника. Измерительные приборы на местности
Урок и презентация на тему: «Периметр и площадь прямоугольника»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»
Что такое прямоугольник и квадрат
Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.
Читается так: четырёхугольник ABCD; квадрат EFGH.
Что такое периметр прямоугольника? Формула расчета периметра
Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.Периметр обозначается латинской буквой P .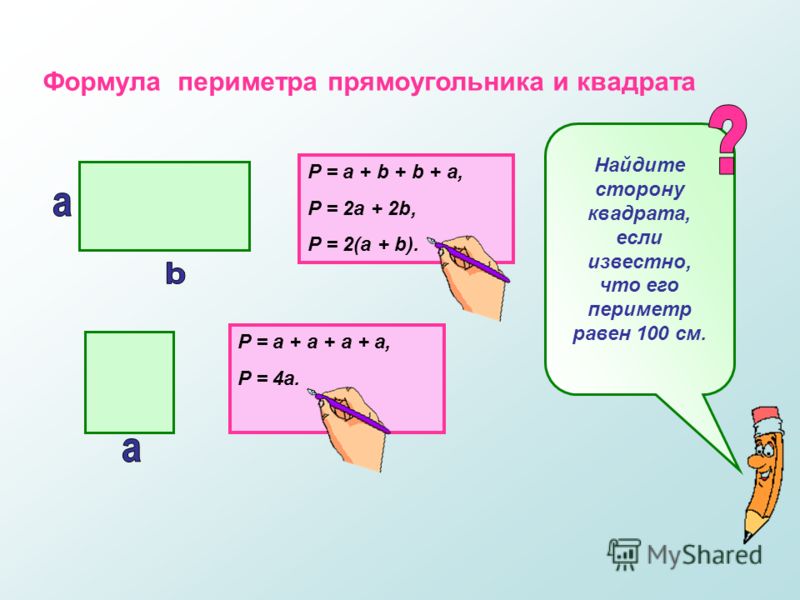 Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.
Запишем формулу периметра четырехугольника ABCD:
P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .
Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:
P ABCD = 2 * (AB + BС)
P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: P ABCD = 16 см.
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.P ABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:
P ABCD = 4 * AB
Пример.

Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.
Решение.
1. Нарисуем квадрат ABCD с исходными данными.
2. Вспомним формулу расчета периметра квадрата:
P ABCD = 4 * AB
3. Подставим в формулу наши данные:
P ABCD = 4 * 6 см = 24 см
Ответ: P ABCD = 24 см.
Задачи на нахождение периметра прямоугольника
1. Измерь ширину и длину прямоугольников. Определи их периметр.
2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.
3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.
2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)В вычислениях обозначается латинской буквой S .
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.
S AKMO = AK * KM
Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .
Ответ: 14 см 2 .
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя.Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
S AВСО = AB * BC = AB * AB
Пример.
Определи площадь квадрата AKMO со стороной 8 см.
S AKMО = AK * KM = 8 см * 8 см = 64 см 2
Ответ: 64 см 2 .
Задачи на нахождение площади прямоугольника и квадрата
1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
Прямоугольник обладает многими отличительными особенностями, исходя из которых, выработаны правила вычисления его различных числовых характеристик. Итак, прямоугольник:
Плоская геометрическая фигура;
Четырехугольник;
Фигура, у которой противоположные стороны равны и параллельны, все углы прямые.
Периметр – это общая длина всех сторон фигуры.
Вычисление периметра прямоугольника — довольно простая задача.
Все, что вам нужно знать, это ширину и длину прямоугольника. Поскольку прямоугольник имеет две равные длины и две равные ширины, измеряется только одна сторона.
Поскольку прямоугольник имеет две равные длины и две равные ширины, измеряется только одна сторона.
Периметр прямоугольника равен удвоенной сумме 2-х его сторон длины и ширины.
P = (a + b) 2, где a — длина прямоугольника, b — ширина прямоугольника.
Так же периметр прямоугольника можно найти при помощи суммы всех сторон.
P= a+a+b+b, где а– длина прямоугольника, b – ширина прямоугольника.
Периметр квадрата — это длина стороны квадрата, умноженная на 4.
P = a 4, где a — длина стороны квадрата.
Дополнение: Нахождение найти площади и периметра прямоугольников
В программе обучения за 3 класс предусмотрено изучение многоугольников и их особенностей. Для того чтобы понять, как найти периметр прямоугольника и площадь, разберемся, что подразумевается под этими понятиями.
Основные понятия
Нахождение периметра и площади требует знания некоторых терминов. К ним относятся:
- Прямой угол. Образуется из 2 лучей, имеющих общее начало в виде точки.
 При знакомстве с фигурами (3 класс) прямой угол определяют с помощью угольника.
При знакомстве с фигурами (3 класс) прямой угол определяют с помощью угольника. - Прямоугольник. Это четырехугольник, все углы которого являются прямыми. Его стороны называют длиной и шириной. Как известно, противоположные стороны этой фигуры равны.
- Квадрат. Является четырехугольником, все стороны которого равны.
При знакомстве с многоугольниками их вершины могут называться АВСД. В математике принято именовать точки на чертежах буквами латинского алфавита. В названии многоугольника перечисляют все вершины без пропусков, например, треугольник ABC.
Вычисление периметра
Периметр многоугольника — это сумма длин всех его сторон. Эта величина обозначается латинской буквой P. Уровень знаний для предложенных примеров — 3 класс.
Задача №1: «Начертите прямоугольник 3 см шириной и 4 см длиной с вершинами ABCD. Найдите периметр прямоугольника ABCD».
Формула будет выглядеть так: P=AB+BC+CD+AD либо P=AB×2+BC×2.
Ответ: P=3+4+3+4=14 (см) либо P=3×2 + 4×2=14 (см).
Задача №2: «Как найти периметр прямоугольного треугольника ABC, если значения сторон равны 5, 4 и 3 см?».
Ответ: P=5+4+3=12 (см).
Задача №3: «Найдите периметр прямоугольника, одна сторона которого равна 7 см, а другая на 2 см длиннее».
Ответ: P=7+9+7+9=32 (см).
Задача №4: «Соревнования по плаванию проходили в бассейне, периметр которого составляет 120 м. Сколько метров проплыл участник соревнований, если ширина бассейна 10 м?».
В данной задаче стоит вопрос, как найти длину бассейна. Для решения найдите длины сторон прямоугольника. Ширина известна. Сумма длин двух неизвестных сторон должна составить 100 м. 120-10×2=100. Чтобы узнать расстояние, которое преодолел пловец, нужно разделить полученный результат на 2. 100:2=50.
Ответ: 50 (м).
Вычисление площади
Более сложной величиной является площадь фигуры. Для ее измерения используют мерки. Эталоном среди мерок являются квадраты.
Площадь квадрата со стороной 1 см равна 1 см². Квадратный дециметр обозначен как дм², а квадратный метр — м².
Квадратный дециметр обозначен как дм², а квадратный метр — м².
Области применения единиц измерения могут быть такими:
- В см² измеряют маленькие предметы, например фотографии, обложки учебников, листы бумаги.
- В дм² можно измерить географическую карту, оконное стекло, картину.
- Для измерения пола, квартиры, земельного участка используют м².
Если начертить прямоугольник 3 см длиной и 1 см шириной и разбить на квадраты со стороной 1 см, то в нем поместится 3 квадрата, а значит, его площадь составит 3 см². Если прямоугольник разбит на квадраты, найдем периметр прямоугольника также без затруднений. В данном случае он равен 8 см.
Другой способ посчитать количество квадратов, вмещающихся в фигуру, — это использование палетки. Начертим на кальке квадрат площадью 1 дм², что составляет 100 см². Поместим кальку на фигуру и посчитаем число квадратных сантиметров в одном ряду. После этого выясним количество рядов, а затем перемножим значения. Значит, площадь прямоугольника — это произведение его длины и ширины.
Способы сравнения площадей:
- На глаз. Иногда достаточно просто взглянуть на предметы, поскольку в некоторых случаях и невооруженным глазом видно, что одна фигура занимает больше места, как, например, учебник, лежащий на столе рядом с пеналом.
- Наложение. Если фигуры совпадают при наложении, их площади равны. Если же одна из них полностью помещается внутри второй, то ее площадь меньше. Места, занимаемые тетрадным листом и страницей из учебника, можно сравнить, наложив их друг на друга.
- По количеству мерок. Фигуры при наложении могут и не совпадать, однако иметь одинаковую площадь. Сравнить в этом случае можно, подсчитав количество квадратов, на которые разбита фигура.
- Числа. Сравниваются численные значения, измеренные одной и той же меркой, например, в м².
Пример №1: «Швея сшила детское одеяло из квадратных разноцветных лоскутков. Один лоскуток длиной 1 дм, в ряду по 5 штук. Сколько дециметров ленты понадобится швее для обработки краев одеяла, если известна площадь 50 дм²?».
Чтобы решить задачу, нужно ответить на вопрос, как найти длину прямоугольника. Далее найдем периметр прямоугольника, составленного из квадратов. Из задачи ясно, что ширина одеяла — 5 дм, вычисляем длину, разделив 50 на 5, и получаем 10 дм. Теперь найдите периметр прямоугольника со сторонами 5 и 10. P=5+5+10+10=30.
Ответ: 30 (м).
Пример №2: «На раскопках обнаружен участок, где могут находиться древние сокровища. Сколько территории придется исследовать ученым, если известен периметр 18 м и ширина прямоугольника 3 м?».
Определим длину участка, проделав 2 действия. 18-3×2=12. 12:2=6. Искомая территория будет также равна 18 м² (6×3=18).
Ответ: 18 (м²).
Таким образом, зная формулы, вычислить площадь и периметр не составит труда, а приведенные выше примеры помогут попрактиковаться в решении математических задач.
На этом занятии мы познакомимся с новым понятием — периметр прямоугольника. Мы сформулируем определение этого понятия, выведем формулу для его вычисления. Также повторим сочетательный закон сложения и распределительный закон умножения.
Также повторим сочетательный закон сложения и распределительный закон умножения.
На данном уроке мы познакомимся с периметром прямоугольника и его вычислением.
Рассмотрим следующую геометрическую фигуру (рис. 1):
Рис. 1. Прямоугольник
Данная фигура — прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.
Прямоугольник — это четырехугольник, у которого четыре прямых угла и стороны попарно равны.
Что в нашей жизни может иметь прямоугольную форму? Например, книга, крышка стола или земельный участок.
Рассмотрим следующую задачу:
Задача 1 (рис. 2)
Вокруг земельного участка строителям понадобилось поставить забор. Ширина этого участка — 5 метров, длина — 10 метров. Забор какой длины получится у строителей?
Рис. 2. Иллюстрация к задаче 1
Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон. У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
Найдем значение выражения (5+10)·2. Сначала выполняем действие в скобках: 5+10=15. А затем повторяем число 15 два раза: 15·2=30.
Ответ: 30 метров.
Периметр прямоугольника — сумма длин всех его сторон. Формула для подсчета периметра прямоугольника : , здесь a — длина прямоугольника, а b — ширина прямоугольника. Сумма длины и ширины называется полупериметром . Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 7 см и 3 см: (7+3)·2=20 (см).
Периметр любой фигуры измеряется в линейных единицах.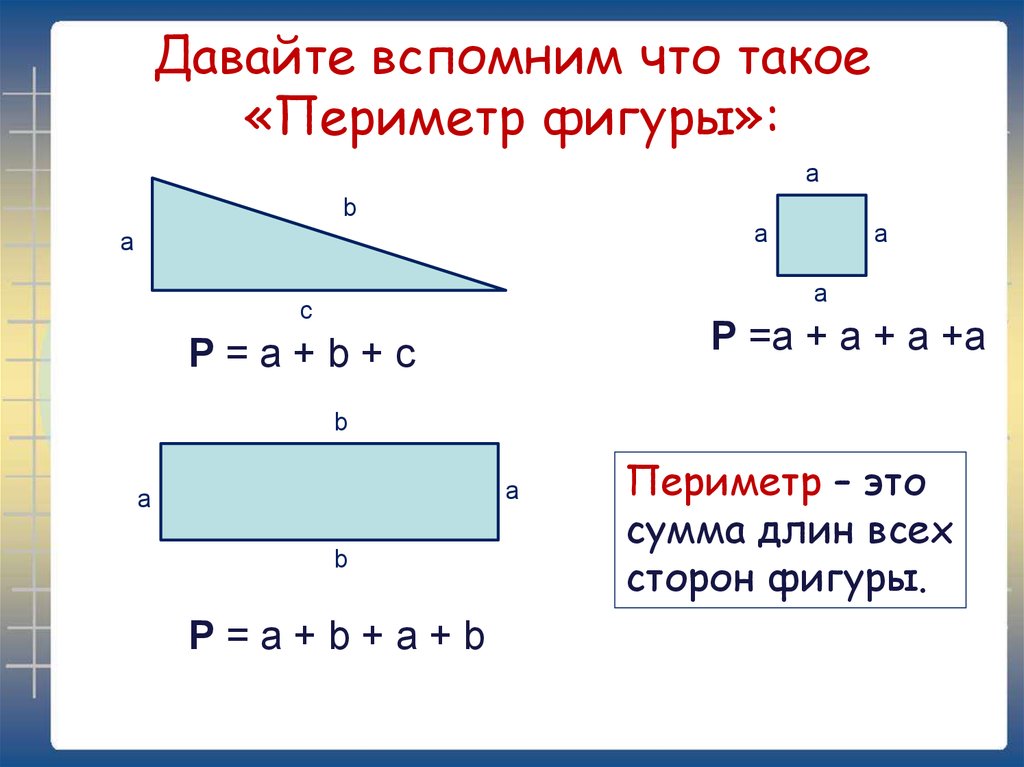
На данном уроке мы познакомились с периметром прямоугольника и формулой его вычисления.
Произведение числа и суммы чисел равно сумме произведений данного числа и каждого из слагаемых.
Если периметр — это сумма длин всех сторон фигуры, то полупериметр — сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).
Список литературы
- Александрова Э.И. Математика. 2 класс. — М.: Дрофа, 2004.
- Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. — М.: Астрель, 2006.
- Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. — М.: Просвещение, 2012.
- Festival.1september.ru ().
- Nsportal.ru ().
- Math-prosto.ru ().
Домашнее задание
- Найти периметр прямоугольника, у которого длина 13 метров, а ширина — 7 метров.
- Найти полупериметр прямоугольника, если его длина — 8 см, а ширина — 4 см.

- Найти периметр прямоугольника, если его полупериметр — 21 дм.
В следующих тестовых заданиях требуется найти периметр фигуры, изображенной на рисунке.
Найти периметр фигуры можно разными способами. Можно преобразовать исходную фигуру таким образом, чтобы периметр новой фигуры можно было бы легко вычислить (например, перейти к прямоугольнику).
Другой вариант решения — искать периметр фигуры непосредственно (как сумму длин всех её сторон). Но в этом случае нельзя полагаться только на рисунок, а находить длины отрезков, исходя из данных задачи.
Хочу предупредить: в одном из заданий среди предложенных вариантов ответов я не нашла того, который получился у меня.
C) .
Перенесем стороны маленьких прямоугольников с внутренней области во внешнюю. В результате большой прямоугольник замкнулся. Формула для нахождения периметра прямоугольника
В данном случае, a=9a, b=3a+a=4a. Таким образом, P=2(9a+4a)=26a. К периметру большого прямоугольника прибавляем сумму длин четырех отрезков, каждый из которых равен 3a.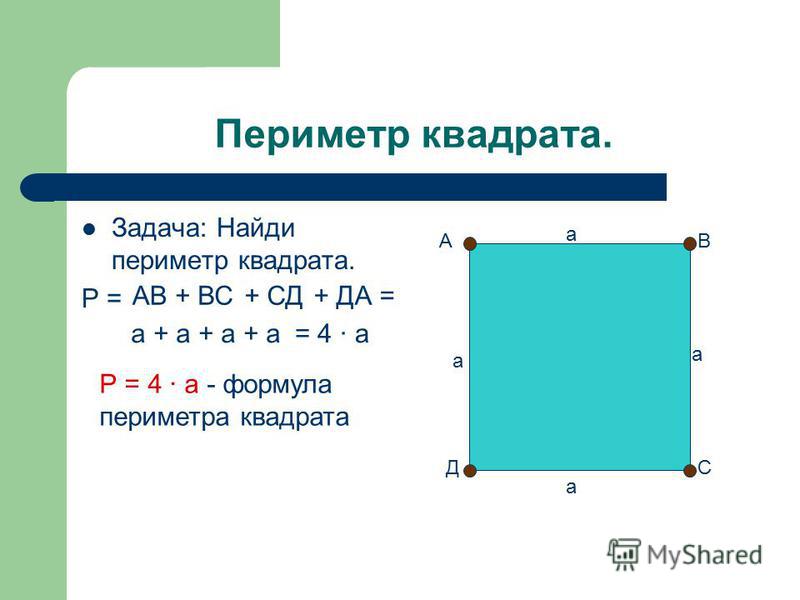 В итоге, P=26a+4∙3a=38a .
В итоге, P=26a+4∙3a=38a .
C) .
После переноса внутренних сторон маленьких прямоугольников во внешнюю область, получаем большой прямоугольник, периметр которого равен P=2(10x+6x)=32x, и четыре отрезка, два — диной по x, два — по 2x.
Итого, P=32x+2∙2x+2∙x=38x .
?) .
Перенесем 6 горизонтальных «ступенек» из внутренней части во внешнюю. Периметр полученного большого прямоугольника равен P=2(6y+8y)=28y. Осталось найти сумму длин отрезков внутри прямоугольника 4y+6∙y=10y. Таким образом, периметр фигуры равен P=28y+10y=38y .
D) .
Перенесем вертикальные отрезки из внутренней области фигуры влево, во внешнюю область. Чтобы получить большой прямоугольник, перенесём одни из отрезков длиной 4x в нижний левый угол.
Периметр исходной фигуры найдём как сумму периметра этого большого прямоугольника и длин оставшихся внутри трёх отрезков P=2(10x+8x)+6x+4x+2x=48x .
E) .
Перенеся внутренние стороны маленьких прямоугольников во внешнюю область, получим большой квадрат. Его периметр равен P=4∙10x=40x. Чтобы получить периметр исходной фигуры, нужно у периметру квадрата прибавить сумму длин восьми отрезков, каждый длиной 3x. Итого, P=40x+8∙3x=64x .
B) .
Перенесём все горизонтальные «ступеньки» и вертикальные верхние отрезки во внешнюю область. Периметр полученного прямоугольника равен P=2(7y+4y)=22y. Чтобы найти периметр исходной фигуры, нужно к периметру прямоугольника прибавить сумму длин четырех отрезков, каждый длиной y: P=22y+4∙y=26y .
D) .
Перенесем из внутренней области во внешнюю все горизонтальные линии и передвинем две вертикальные внешние линии в левом и правом углах, соответственно, на z левее и правее. В результате получим большой прямоугольник, периметр которого равен P=2(11z+3z)=28z.
Периметр исходной фигуры равен сумме периметра большого прямоугольника и длин шести отрезков по z: P=28z+6∙z=34z .
B) .
Решение полностью аналогично решению предыдущего примера. После преобразования фигуры находим периметр большого прямоугольника:
P=2(5z+3z)=16z. К периметру прямоугольника прибавляем сумму длин оставшихся шести отрезков, каждый из которых равен z: P=16z+6∙z=22z .
Геометрия, если не ошибаюсь, в мое время изучалась с пятого класса и периметр был и есть одним из ключевых понятий. Итак, периметр — это сумма длин всех сторон (обозначается латинской литерой P) . Вообще, трактуют данный термин по разному, например,
- общая длина границы фигуры,
- длина всех ее сторон,
- сумма длин ее граней,
- длина ограничивающей фигуру линии,
- сумма всех длин сторон многоугольника
Для различных фигур существуют свои формулы определения периметра. Чтобы понять сам смысл, предлагаю самостоятельно вывести несколько несложных формул:
Чтобы понять сам смысл, предлагаю самостоятельно вывести несколько несложных формул:
- для квадрата,
- для прямоугольника,
- для параллелограмма,
- для куба,
- для параллелепипеда
Периметр квадрата
Для примера возьмем самое простое — периметр квадрата.
Все стороны квадрата равны. Пусть одна сторона носит название «a» (также, как и остальные три), тогда
P = a + a + a + a
или более компактная запись
Периметр прямоугольника
Усложним задачу и возьмем прямоугольник. В данном случае уже нельзя сказать, что все стороны равны, поэтому пусть длины сторон прямоугольника будут равны a и b.
Тогда формула будет иметь следующий вид:
P = a + b + a + b
Периметр параллелограмма
Аналогичная ситуация будет и с параллелограммом (см. периметр прямоугольника)
Периметр куба
Что же делать, если мы имеем дело с объемной фигурой? Например, возьмем куб. Куб имеет 12 сторон и все они равны. Соответственно, периметр куба можно вычислить следующим образом:
Соответственно, периметр куба можно вычислить следующим образом:
Периметр параллелепипеда
Ну, и для закрепления материала вычислим периметр параллелепипеда. Тут необходимо немного поразмышлять. Давайте делать это вместе. Как мы знаем, прямоугольный параллелепипед представляет собой фигуру, сторонами которой являются прямоугольники. У каждого параллелепипеда есть два основания. Возьмем одно из оснований и посмотрим на его стороны — они имеют длину a и b. Соответственно, периметр основания есть P = 2a + 2b. Тогда периметр двух оснований есть
(2a + 2b) * 2 = 4a + 4b
Но ведь у нас есть еще и сторона «c». Значит формула для вычисления периметра параллелепипеда будет иметь следующий вид:
P = 4a + 4b + 4c
Как видно из примеров выше, всё, что необходимо сделать для определения периметра фигуры — найти длину каждой из сторон, а затем их сложить.
В заключение хочется отметить, что не всякая фигура имеет периметр. К примеру, у шара периметра нет.
Как найти площадь квадрата окружности?
Содержание
- — Как найти площадь квадрата?
- — Как вычислить площадь квадрата и его диагональ?
- — Как найти площадь и периметр у квадрата?
- — Что такое площадь квадрата и как её найти?
- — Как найти площадь квадрата в 4 классе?
- — Как найти площадь квадрата в 3 классе?
- — Как найти площадь квадрата по диаметру?
- — Как найти длину диагонали прямоугольника Если есть площадь и периметр?
- — Как найти площадь ромба по диагонали?
- — Как найти площадь и периметр параллелограмма?
- — Как найти площадь треугольника если известны все его стороны?
- — Как найти формулу периметра квадрата?
- — Как найти площадь фигуры?
- — Как найти квадрат прямоугольника?
- — Как найти диагональ в квадрате?
S = 4 * r2, где r — это радиус вписанной окружности.
Как найти площадь квадрата?
Формулы для вычисления площади квадрата
- Площадь квадрата равна квадрату длины его стороны. S = a2
- Площадь квадрата равна половине квадрата длины его диагонали. S = d2
Как вычислить площадь квадрата и его диагональ?
Диагонали квадрата равны между собой и используются в формуле площади квадрата через диагональ. То есть площадь квадрата равна квадрату длины диагонали поделенному на два. Учитывая, что стороны фигуры равны, можно рассчитать длину диагонали из формулы площади прямоугольного треугольника или по теореме Пифагора.
Как найти площадь и периметр у квадрата?
Периметр квадрата равен сумме длин всех его сторон. Площадь квадрата равна произведению длин двух его сторон.
Что такое площадь квадрата и как её найти?
Формула вычисления площади
- По длине стороны: Площадь квадрата (S) равняется квадрату длины его стороны:
- По по длине диагонали Площадь квадрата равняется половине квадрата длины его диагонали:
Как найти площадь квадрата в 4 классе?
Для вычисления площади квадрата нужно умножить его длину на саму себя.
Как найти площадь квадрата в 3 классе?
Площадь квадрата равна квадрату его стороны. Периметр квадрата равен сумме его четырех сторон.
Как найти площадь квадрата по диаметру?
Если нам дана диагональ
Возводим ее в квадрат и делим на два. S = d2 : 2, где где d — диагональ.
Как найти длину диагонали прямоугольника Если есть площадь и периметр?
Площадь прямоугольника равна произведению длины стороны a на длину стороны b. Периметр прямоугольника равен удвоенной сумме сторон a и b. Диагональ прямоугольника равна квадратному корню из суммы квадратов сторон a и b.
Как найти площадь ромба по диагонали?
Ромб — это четырёхугольник, у которого все стороны равны. Ромб с прямыми углами называется квадратом. Площадь ромба равна половине произведения его диагоналей: S = (AC · BD) / 2.
Ромб с прямыми углами называется квадратом. Площадь ромба равна половине произведения его диагоналей: S = (AC · BD) / 2.
Как найти площадь и периметр параллелограмма?
1) Периметр параллелограмма равен удвоенной сумме 2-х его смежных сторон (a, b).
- P — периметр параллелограмма
- a — длина 1-ой стороны параллелограмма
- b — длина 2-ой стороны параллелограмма
Как найти площадь треугольника если известны все его стороны?
Формула Герона для вычисления площади треугольника.
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
Как найти формулу периметра квадрата?
1) Периметр квадрата равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у квадрат длины всех сторон равны). 2) Периметр квадрата равен произведению длины его диагонали на два корня из двух.
Как найти площадь фигуры?
Узнать площадь фигуры помогут следующие формулы:
- S = a * b, где a, b — ширина и высота прямоугольника.
- S = a * √(d2 — а2), где а — известная сторона, d — диагональ. Диагональ — это отрезок, который соединяет противоположные стороны фигуры. …
- S = 0,5 ∗ d2 ∗ 𝑠𝑖𝑛(𝑎), где d — диагональ.
23 июл. 2020 г.
Как найти квадрат прямоугольника?
Общая формула: S = a2, где S — площадь квадрата, а a — его сторона. Чтобы узнать площадь прямоугольника, надо взять его длину и ширину (в одинаковых единицах измерения) и найти их произведение (площадь должна быть выражена в соответствующих единицах измерения).
Как найти диагональ в квадрате?
Диагональ квадрата равна стороне квадрата, умноженной на корень из двух.
Интересные материалы:
Сколько можно хранить салаты с майонезом?
Сколько можно хранить сардельки в морозилке?
Сколько можно хранить селедку домашнего посола?
Сколько можно хранить смесь в бутылочке при комнатной температуре?
Сколько можно хранить соленую кету?
Сколько можно хранить соленую селедку без рассола?
Сколько можно хранить соленые грибы в морозилке?
Сколько можно хранить сосиски в открытой упаковке?
Сколько можно хранить сосиску в морозилке?
Сколько можно хранить соус песто в холодильнике?
Как найти периметр квадрата, если известна его площадь. Периметр, площадь и объём Как найти периметр квадрата, если дан радиус описанной окружности
Урок и презентация на тему: «Периметр и площадь прямоугольника»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»
Что такое прямоугольник и квадрат
Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.
Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.
Читается так: четырёхугольник ABCD; квадрат EFGH.
Что такое периметр прямоугольника? Формула расчета периметра
Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.
Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.
Запишем формулу периметра четырехугольника ABCD:
P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Пример.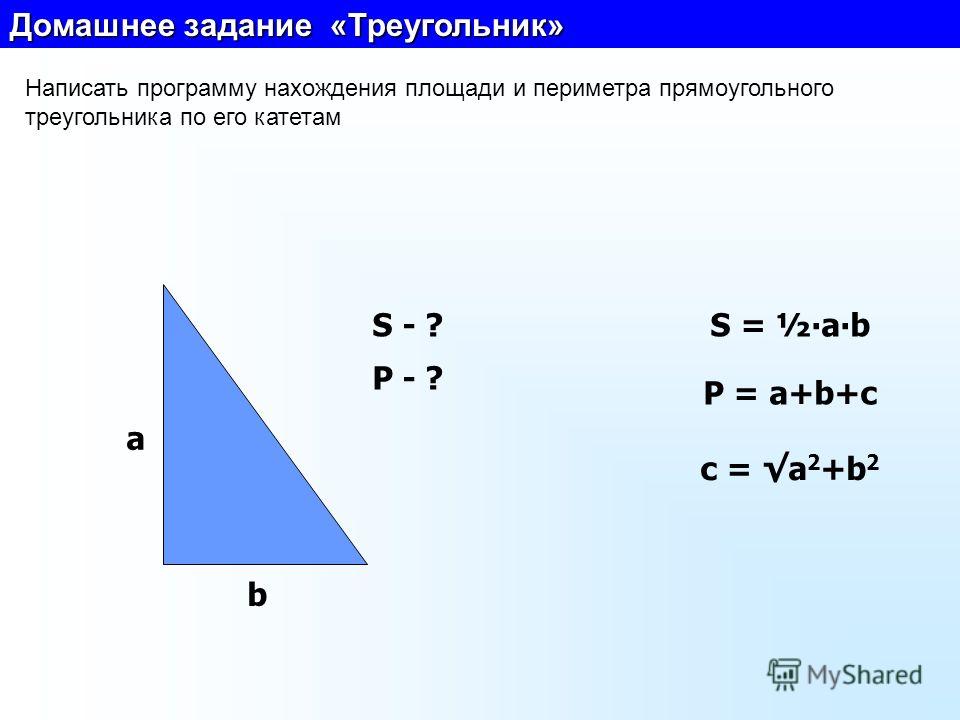
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .
Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:
P ABCD = 2 * (AB + BС)
P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: P ABCD = 16 см.
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.
P ABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:
P ABCD = 4 * AB
Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.
Решение.
1. Нарисуем квадрат ABCD с исходными данными.
2. Вспомним формулу расчета периметра квадрата:
P ABCD = 4 * AB
3. Подставим в формулу наши данные:
Подставим в формулу наши данные:
P ABCD = 4 * 6 см = 24 см
Ответ: P ABCD = 24 см.
Задачи на нахождение периметра прямоугольника
1. Измерь ширину и длину прямоугольников. Определи их периметр.
2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.
3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.
2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры.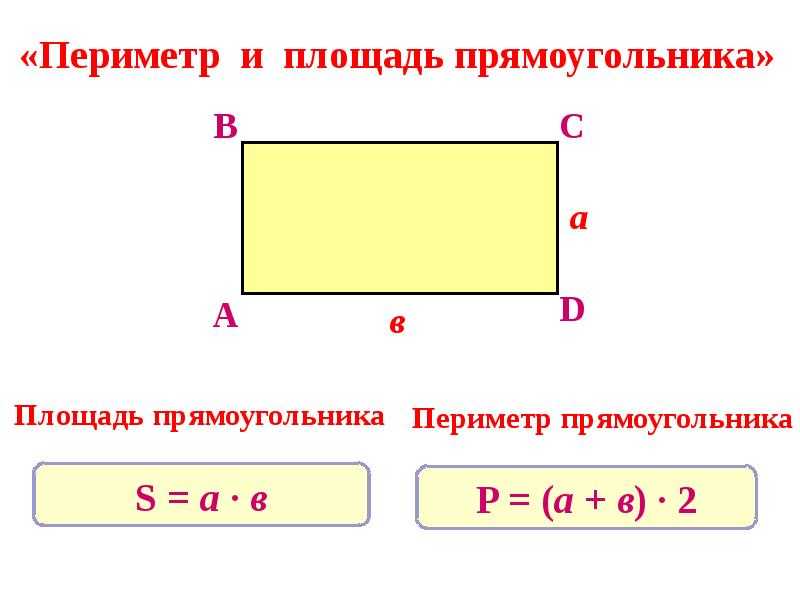 Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S .
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.
S AKMO = AK * KM
Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .
Ответ: 14 см 2 .
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя.
Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
S AВСО = AB * BC = AB * AB
Пример.
Определи площадь квадрата AKMO со стороной 8 см.
S AKMО = AK * KM = 8 см * 8 см = 64 см 2
Ответ: 64 см 2 .
Задачи на нахождение площади прямоугольника и квадрата
1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
Отношение между радиусом окружности и длиной стороны квадрата. Расстояние от центра описанной окружности до вершины вписанного в нее квадрата равно радиусу окружности. Чтобы найти сторону квадрата s , необходимо диагональю разделить квадрат на 2 прямоугольных треугольника. Каждый из этих треугольников будет иметь равные стороны a и b и общую гипотенузу с , равную удвоенному радиусу описанной окружности (2r ).
Воспользуйтесь теоремой Пифагора, чтобы найти сторону квадрата. Теорема Пифагора гласит, что в любом прямоугольном треугольнике с катетами а и b и гипотенузой с : a 2 + b 2 = c 2 . Так как в нашем случае а = b (не забывайте, что мы рассматриваем квадрат!), и мы знаем, что с = 2r , то мы можем переписать и упростить это уравнение:
Теорема Пифагора гласит, что в любом прямоугольном треугольнике с катетами а и b и гипотенузой с : a 2 + b 2 = c 2 . Так как в нашем случае а = b (не забывайте, что мы рассматриваем квадрат!), и мы знаем, что с = 2r , то мы можем переписать и упростить это уравнение:
- a 2 + a 2 = (2r) 2 «»; теперь упростим это уравнение:
- 2a 2 = 4(r) 2 ; теперь разделим обе стороны уравнения на 2:
- (a 2) = 2(r) 2 ; теперь извлечем квадратный корень из обеих сторон уравнения:
- a = √(2r) . Таким образом, s = √(2r) .
Умножьте найденную сторону квадрата на 4, чтобы найти его периметр. В этом случае периметр квадрата: P = 4√(2r) . Эту формулу можно переписать так: Р = 4√2 * 4√r = 5,657r , где r – радиус описанной окружности.
Пример. Рассмотрим квадрат, вписанный в окружность радиусом 10. Это означает, что диагональ квадрата равна 2 * 10 = 20. Используя теорему Пифагора, мы получим: 2(a 2) = 20 2 , то есть 2a 2 = 400. Теперь разделим обе стороны уравнения на 2 и получим: a 2 = 200. Теперь извлечем квадратный корень из обеих сторон уравнения и получим: а = 14,142 . Умножим это значение на 4 и вычислим периметр квадрата: P = 56,57 .
Используя теорему Пифагора, мы получим: 2(a 2) = 20 2 , то есть 2a 2 = 400. Теперь разделим обе стороны уравнения на 2 и получим: a 2 = 200. Теперь извлечем квадратный корень из обеих сторон уравнения и получим: а = 14,142 . Умножим это значение на 4 и вычислим периметр квадрата: P = 56,57 .
- Обратите внимание, что вы могли бы получить тот же результат, просто умножив радиус (10) на 5,657: 10 * 5,567 = 56,57 ; но такой метод трудно запомнить, поэтому лучше пользоваться процессом вычисления, описанным выше.
Квадрат — это геометрическая фигура, представляющая собой четырехугольник все углы и стороны которого равны. Его также можно назвать прямоугольником , смежные стороны которого равны, или ромбом , у которого все углы равны 90º . Благодаря абсолютной симметрии найти площадь или периметр квадрата очень легко.
Инструкция:
- Во-первых, определим, что периметром называется сумма длин всех сторон плоской геометрической фигуры, которая измеряется теми же величинами, что и длина.
 Вычислить периметр квадрата можно двумя способами.
Вычислить периметр квадрата можно двумя способами.
Через длину стороны и диагонали
- Поскольку периметр квадрата определяется суммой длин всех его сторон, а стороны у данной фигуры равны, то высчитать значение данной величины можно умножив длину одной стороны на число «4 ». Соответственно формулы будут выглядеть следующим образом: P = а + а + а + а или Р = а * 4 , где Р – это периметр квадрата и а – длина стороны .
- Кроме этого, в зависимости от условия задачи, периметр квадрата можно высчитать путем умножения длины его диагонали на два корня из двух: Р = 2√2 * d , где Р – это периметр квадрата и d — его диагональ .
- Некоторые задачи требуют найти периметр квадрата , зная его площадь . Сделать это также не составит труда. Площадь данной фигуры равна длине его стороны, возведенной в квадрат: S = а 2 , где S – площадь квадрата и а – длина его стороны .
 Либо же площадь равна квадратному значению длины его диагонали, разделенному на два: S = d 2 /2 , где S – все та же площадь и d – диагональ квадрата .
Либо же площадь равна квадратному значению длины его диагонали, разделенному на два: S = d 2 /2 , где S – все та же площадь и d – диагональ квадрата . - Зная формулы и значение площади, не трудно найти длину стороны или длину диагонали, а затем вернуться к формулам вычисления периметра и высчитать его значение.
Через радиус вписанной и описанной окружности
- Наконец, немаловажно понимать и как найти периметр квадрата , если известен радиус окружности описанной вокруг него (или, напротив, в него вписанной). Вписанная в данную геометрическую фигуру окружность касается середины каждой стороны, и ее радиус равен половине любой стороны: R в = ½ а , где R в – радиус вписанной окружности и а – сторона квадрата .
- Описанная окружность проходит через все вершины квадрата и ее радиус равен половине длины диагонали: R о = ½ d , где R о – это радиус описанной вокруг квадрата окружности и d – его диагональ .

- Потому в первом случае периметр будет вычисляться по формуле: Р = 8 R в , а во втором: P = 4 х √2 х R о .
С помощью сайтов и интернет-калькулятора
- Если вы вдруг по какой-то причине забыли формулы, то освежить знания поможет интернет. Зайдите в браузер, откройте страницу поисковика и в окне вбейте соответствующий запрос, например: «периметр квадрата формула ». Система выдаст огромное число сайтов справочного характера, которые помогут вам в данном вопросе, а также позволят справиться с решением задач, касающихся других геометрических фигур.
- Кроме этого, если у вас нет желания разбираться в формулах и считать значения самостоятельно, то можно воспользоваться услугами интернет-калькуляторов . В качестве примера можно привести сайт. Раздел «Формулы периметра геометрических фигур » содержит теоретическую информацию, подкрепленную наглядными иллюстрациями. Если же перейти по ссылке «онлайн калькулятор », которая находится в окне каждой фигуры, то перед вами откроется страница для расчетов.

- Выберите в окне снизу, на основании чего вы собираетесь высчитать периметр квадрата (сторона или диагональ), а затем введите имеющиеся данные. Система выдаст результат , руководствуясь установленными формулами.
- Кроме этого, на сайте вы найдете и много другой информации, способной облегчить работу с математическими задачами . При желании можно поискать и более удобные или познавательные справочные сайты.
- Если же вы не можете разобраться с самим ходом решения задачи, то здесь можно обратиться за помощью к людям, которые хорошо владеют методикой решения математических упражнений. Их всегда можно найти на соответствующих форумах , например, или.
Периметр двумерной фигуры – это общая длина ее границы, равная сумме длин сторон фигуры. Квадрат – это фигура с четырьмя сторонами одинаковой длины, которые пересекаются под углом 90°. Так как в квадрате все стороны имеют одинаковую длину, то вычислить его периметр очень легко. Эта статья расскажет вам, как вычислить периметр квадрата по одной данной стороне, по данной площади и по данному радиусу окружности, описанной вокруг квадрата.
Эта статья расскажет вам, как вычислить периметр квадрата по одной данной стороне, по данной площади и по данному радиусу окружности, описанной вокруг квадрата.
Периметр — это числовой показатель, который находится по формуле 4х, где х – длина стороны геометрической фигуры, а 4 – количество сторон фигуры. Рассмотрим несколько способов данного расчета.
1-й способ: Вычисление периметра по данной стороне
Если известны размеры площади, в таком случае от заданной величины возможно найти периметр квадрата. Для этого потребуется извлечь корень квадратный, так мы найдем длину стороны, и вычислить итоговое значение по приведенной формуле. Если требуется найти периметр квадрата по диагональной линии, потребуется воспользоваться таблицей Пифагора.
Геометрическая фигура диагональю поделена на равнобедренные треугольники с прямым углом, и если диагональ известна, то значение сторон геометрической фигуры необходимо рассчитать с помощью формулы, где квадрат z (диагонали) равен удвоенному квадрату стороны u. В итоге имеем такое значение: u равна корню квадратному, который был извлечен из половины квадрата гипотенузы. Далее следует помножить итоговое значение в 4 раза и получить периметр геометрической фигуры, т. е. квадрата.
В итоге имеем такое значение: u равна корню квадратному, который был извлечен из половины квадрата гипотенузы. Далее следует помножить итоговое значение в 4 раза и получить периметр геометрической фигуры, т. е. квадрата.
2-й способ: Вычисление периметра по данной площади
Формула для вычисления площади квадрата. Площадь любого прямоугольника (а квадрат – это частный случай прямоугольника) равна произведению его длины на его ширину. Поскольку длина и ширина квадрата равны, то его площадь вычисляется по формуле: A = s*s = s2, где s – длина стороны квадрата.
Извлеките квадратный корень из значения площади, чтобы найти сторону квадрата. Для этого в большинстве случаев воспользуйтесь калькулятором (введите значение площади и нажмите клавишу «√»). Вы также можете вычислить квадратный корень вручную.
Если площадь квадрата равна 20, то его сторона равна: s = √20 = 4,472.
Если площадь квадрата равна 25, то s = √25 = 5.
Умножьте найденную сторону на 4, чтобы найти периметр. Вычисленное значение стороны подставьте в формулу для нахождения периметра: P = 4s. Вы найдете периметр квадрата.
Вычисленное значение стороны подставьте в формулу для нахождения периметра: P = 4s. Вы найдете периметр квадрата.
В нашем первом примере: P = 4 * 4,472 = 17,888.
Периметр квадрата, площадь которого равна 25, а сторона равна 5, равен Р = 4 * 5 = 20.
3-й способ:Вычисление периметра по данному радиусу окружности, описанной вокруг квадрата
Вписанный квадрат – это квадрат, вершины которого лежат на окружности.
Отношение между радиусом окружности и длиной стороны квадрата. Расстояние от центра описанной окружности до вершины вписанного в нее квадрата равно радиусу окружности. Чтобы найти сторону квадрата s, необходимо диагональю разделить квадрат на 2 прямоугольных треугольника. Каждый из этих треугольников будет иметь равные стороны a и b и общую гипотенузу с, равную удвоенному радиусу описанной окружности (2r).
Воспользуйтесь теоремой Пифагора, чтобы найти сторону квадрата. Теорема Пифагора гласит, что в любом прямоугольном треугольнике с катетами а и b и гипотенузой с: a2 + b2 = c2. Так как в нашем случае а = b (не забывайте, что мы рассматриваем квадрат!), и мы знаем, что с = 2r, то мы можем переписать и упростить это уравнение:
Так как в нашем случае а = b (не забывайте, что мы рассматриваем квадрат!), и мы знаем, что с = 2r, то мы можем переписать и упростить это уравнение:
a2 + a2 = (2r)2″‘; теперь упростим это уравнение:
2a2 = 4(r)2; теперь разделим обе стороны уравнения на 2:
(a2) = 2(r)2; теперь извлечем квадратный корень из обеих сторон уравнения:
a = √(2r). Таким образом, s = √(2r).
Умножьте найденную сторону квадрата на 4, чтобы найти его периметр. В этом случае периметр квадрата: P = 4√(2r). Эту формулу можно переписать так: Р = 4√2 * 4√r = 5,657r, где r – радиус описанной окружности.
Пример. Рассмотрим квадрат, вписанный в окружность радиусом 10. Это означает, что диагональ квадрата равна 2 * 10 = 20. Используя теорему Пифагора, мы получим: 2(a2) = 202, то есть 2a2 = 400. Теперь разделим обе стороны уравнения на 2 и получим: a2 = 200. Теперь извлечем квадратный корень из обеих сторон уравнения и получим: а = 14,142. Умножим это значение на 4 и вычислим периметр квадрата: P = 56,57.
Обратите внимание, что вы могли бы получить тот же результат, просто умножив радиус (10) на 5,657: 10 * 5,567 = 56,57; но такой метод трудно запомнить, поэтому лучше пользоваться процессом вычисления, описанным выше.
Квадрат представляет собой положительный четырехугольник (либо ромб), в котором все углы являются прямыми, а стороны равны между собой. Как и у всякого другого верного многоугольника, у квадрата дозволено высчитать периметр и площадь. Если площадь квадрата теснее знаменита, то обнаружить его стороны, а после этого и периметр не составит труда.
Инструкция
1. Площадь квадрата находится по формуле:S = a?Это обозначает, что для того, дабы вычислить площадь квадрата , надобно умножить длины 2-х его сторон друг на друга. Как следствие, если знать площадь квадрата , то при извлечении корня из данного значения дозволено узнать длину стороны квадрата .Пример: площадь квадрата 36 см?, дабы узнать сторону данного квадрата , нужно извлечь квадратный корень из значения площади. Таким образом, длина стороны данного квадрата 6 см
Таким образом, длина стороны данного квадрата 6 см
2. Для нахождения периметр а квадрата нужно сложить длины всех его сторон. С подмогой формулы это дозволено выразить так:P = a+a+a+a.Если извлечь корень из значения площади квадрата , а после этого сложить получившуюся величину 4 раза, то дозволено обнаружить периметр квадрата .
3. Пример: Дан квадрат с площадью 49 см?. Требуется обнаружить его периметр .Решение:Вначале нужно извлечь корень площади квадрата : ?49 = 7 смЗатем, вычислив длину стороны квадрата , дозволено вычислить и периметр : 7+7+7+7 = 28 смОтвет: периметр квадрата площадью 49 см? составляет 28 см
Зачастую в геометрических задачах требуется обнаружить длину стороны квадрата, если вестимы другие его параметры – такие, как площадь, диагональ либо периметр.
Вам понадобится
- Калькулятор
Инструкция
1. Если вестима площадь квадрата, то для того, дабы обнаружить сторону квадрата, нужно извлечь квадратный корень из числового значения площади (потому что площадь квадрата равняется квадрату его стороны):a=?S, гдеa – длина стороны квадрата;S – площадь квадрата.Единицей измерения стороны квадрата будет являться линейная единица измерения длины, соответствующая единице измерения площади. Скажем, если площадь квадрата дана в сантиметрах квадратных, то длина его стороны получится примитивно в сантиметрах.Пример:Площадь квадрата составляет 9 квадратных метров.Обнаружить длину стороны квадрата.Решение:a=?9=3Ответ:Сторона квадрата равняется 3 метрам.
Если вестима площадь квадрата, то для того, дабы обнаружить сторону квадрата, нужно извлечь квадратный корень из числового значения площади (потому что площадь квадрата равняется квадрату его стороны):a=?S, гдеa – длина стороны квадрата;S – площадь квадрата.Единицей измерения стороны квадрата будет являться линейная единица измерения длины, соответствующая единице измерения площади. Скажем, если площадь квадрата дана в сантиметрах квадратных, то длина его стороны получится примитивно в сантиметрах.Пример:Площадь квадрата составляет 9 квадратных метров.Обнаружить длину стороны квадрата.Решение:a=?9=3Ответ:Сторона квадрата равняется 3 метрам.
2. В том случае, когда знаменит периметр квадрата, для определения длины стороны необходимо числовое значение периметра поделить на четыре (потому что квадрат имеет четыре стороны идентичной длины):a=P/4, где:a – длина стороны квадрата;P – периметр квадрата.Единицей измерения стороны квадрата будет являться та же самая линейная единица измерения длины как и у периметра. 2), где:a – длина стороны квадрата;d – длина диагонали квадрата.Единицей измерения стороны квадрата будет являться единица измерения длины та же самая, что и у диагонали. Скажем, если диагональ квадрата измерена в сантиметрах, то и длина его стороны получится в сантиметрах.Пример:Диагональ квадрата равняется 10 метров.Обнаружить длину стороны квадрата.Решение:a=10/?2, либо примерно: 7,071Ответ:Длина стороны квадрата равняется 10/?2, либо приблизительно 1,071 метра.
2), где:a – длина стороны квадрата;d – длина диагонали квадрата.Единицей измерения стороны квадрата будет являться единица измерения длины та же самая, что и у диагонали. Скажем, если диагональ квадрата измерена в сантиметрах, то и длина его стороны получится в сантиметрах.Пример:Диагональ квадрата равняется 10 метров.Обнаружить длину стороны квадрата.Решение:a=10/?2, либо примерно: 7,071Ответ:Длина стороны квадрата равняется 10/?2, либо приблизительно 1,071 метра.
Квадрат – прекрасная и простая плоская геометрическая фигура. Это прямоугольник с равными сторонами. Как же обнаружить периметр квадрата , если знаменита длина его стороны?
Инструкция
1. Раньше каждого, стоит припомнить, что периметр есть ни что иное как сумма длин сторон геометрической фигуры. Рассматриваемый нами квадрат имеет четыре стороны. Больше того, по определению квадрата , все эти стороны равны между собой.Из этих предпосылок вытекает простая формула для нахождения периметр а квадрата – периметр квадрата равен длине стороны квадрата , умноженной на четыре:Р = 4а, где а – длина стороны квадрата .
Видео по теме
Периметром называют всеобщую длину границы фигуры почаще каждого на плоскости. Квадрат — положительный четырехугольник либо ромб, у которого все углы прямые, либо параллелограмм, у которого все стороны и углы равны.
Вам понадобится
- Знания по геометрии.
Инструкция
1. Периметр квадрата равен сумме длин его сторон. Потому что квадрат, по своей сути, есть четырехугольник, то и сторон у него четыре, а значит периметр равен сумме длин четырех сторон либо P = a+b+c+d.
2. Квадрат, как видно из определения, верная геометрическая фигура, а это значит, что все его стороны равны. Значит a=b=c=d. Следственно P = a+a+a+a либо P = 4*a.
3. Пускай сторона квадрата равна 4, то есть a=3. Тогда периметр либо длина квадрата , по полученной формуле, будет равен P = 4*3 либо P=12. Число 12 и будет являться длиной либо, что одно и тоже, периметром квадрата .
Видео по теме
Обратите внимание!
Периметр квадрата величина неизменно правильная, как и любая иная длина.
Полезный совет
Аналогичным образом дозволено обнаружить и периметр ромба, потому что квадрат является частным случаем ромба с прямыми углами.
Периметр характеризует длину замкнутого силуэта. Как и площадь, он может быть обнаружен по иным величинам, приведенным в условии задачи. Задачи на нахождении периметра крайне зачастую встречаются в школьном курсе математики.
Инструкция
1. Зная периметр и сторону фигуры, дозволено обнаружить иную ее сторону, а также площадь. Сам же периметр, в свою очередь, может быть обнаружен по нескольким заданным сторонам либо по углу и сторонам, в зависимости от условий задачи. Также в ряде случаев его выражают через площадь. Особенно примитивно находится периметр прямоугольника. Начертите прямоугольник с одной из сторон, равной а, и диагональю, равной d. Зная эти две величины, обнаружьте по теореме Пифагора иную его сторону, которая является шириной прямоугольника. Обнаружив ширину прямоугольника, вычислите его периметр дальнейшим образом: p=2(a+b). Эта формула объективна для всех прямоугольников, от того что у всякого из них четыре стороны.
Обнаружив ширину прямоугольника, вычислите его периметр дальнейшим образом: p=2(a+b). Эта формула объективна для всех прямоугольников, от того что у всякого из них четыре стороны.
2. Обратите внимание на тот факт, что периметр треугольника в большинстве задач находят при наличии информации правда бы об одном его угле. Впрочем, имеются и задачи, в которых все стороны треугольник знамениты, и тогда периметр может быть вычислен простым суммированием, без применения тригонометрических вычислений: p=a+b+c, где a, b и c – стороны. Но такие задачи встречаются в учебниках редко, от того что метод их решения явствен. Больше трудные задачи по нахождению периметра треугольника решайте поэтапно. Скажем, начертите равнобедренный треугольник, у которого знамениты основание и угол при нем. Для того дабы обнаружить его периметр, сначала обнаружьте стороны a и b дальнейшим образом: b=c/2cos?. От того что a=b (треугольник равнобедренный), сделайте дальнейший итог: a=b=c/2cos?.
3. Периметр многоугольника вычисляйте аналогичным образом, складывая длины всех его сторон: p=a+b+c+d+e+f и так дальше. Если многоугольник положительный и вписан в окружность либо описан около нее, вычислите длину одной из его сторон, а после этого умножьте на их число. Скажем, дабы обнаружить стороны шестиугольника, вписанного в окружность, действуйте дальнейшим образом: a=R, где a – сторона шестиугольника, равная радиусу описанной окружности. Соответственно, если шестиугольник верный, то его периметр равен: p=6a=6R. Если окружность вписана в шестиугольник, то сторона последнего равна: a=2r?3/3. Соответственно, периметр такой фигуры обнаружьте дальнейшим образом: p=12r?3/3.
Если многоугольник положительный и вписан в окружность либо описан около нее, вычислите длину одной из его сторон, а после этого умножьте на их число. Скажем, дабы обнаружить стороны шестиугольника, вписанного в окружность, действуйте дальнейшим образом: a=R, где a – сторона шестиугольника, равная радиусу описанной окружности. Соответственно, если шестиугольник верный, то его периметр равен: p=6a=6R. Если окружность вписана в шестиугольник, то сторона последнего равна: a=2r?3/3. Соответственно, периметр такой фигуры обнаружьте дальнейшим образом: p=12r?3/3.
Хоть слово «периметр» и случилось от греческого обозначения окружности, им принято называть суммарную длину границ всякий плоской геометрической фигуры, включая квадрат. Вычисление этого параметра, как водится, трудности не представляет и может быть осуществлено несколькими методами, в зависимости от знаменитых начальных данных.
Инструкция
1. Если вестима длина стороны квадрата (t), то для нахождения его периметра (p) примитивно увеличьте эту величину в четыре раза: p=4*t.
2. Если длина стороны незнакома, но в условиях задачи дана длина диагонали (c), то этого довольно для вычисления длины сторон, а следственно и периметра (p) многоугольника. Используйте теорему Пифагора, которая заявляет, что квадрат длины длинной стороны прямоугольного треугольника (гипотенузы) равен сумме квадратов длин коротких сторон (катетов). В прямоугольном треугольнике, составленном из 2-х смежных сторон квадрата и соединяющего их крайние точки отрезка, гипотенуза совпадает с диагональю четырехугольника. Из этого вытекает, что длина стороны квадрата равна отношению длины диагонали к квадратному корню из двойки. Используйте это выражение в формуле для вычисления периметра из предыдущего шага: p=4*c/?2.
3. Если дана лишь площадь (S) ограниченного периметром квадрата участка плоскости, то и этого будет довольно, дабы определить длину одной стороны. Потому что площадь всякого прямоугольника равна произведению длин его смежных сторон, то для нахождения периметра (p) извлеките квадратный корень из площади, а итог увеличьте в четыре раза: p=4*?S.
4. Если знаменит радиус описанной вблизи квадрата окружности (R), то для нахождения периметра многоугольника (p) умножьте его на восемь и поделите полученный итог на квадратный корень из двойки: p=8*R/?2.
5. Если окружность, радиус которой вестим, вписана в квадрат, то вычисляйте его периметр (p) простым умножением радиуса (r) на восьмерку: P=8*r.
6. Если рассматриваемый квадрат в условиях задачи описан координатами своих вершин, то для вычисления периметра вам потребуются данные лишь о 2-х вершинах, принадлежащих к одной из сторон фигуры. Определите длину этой стороны, исходя из все той-же теоремы Пифагора для треугольника, составленного из нее самой и ее проекций на оси координат, а полученный итог увеличьте в четыре раза. Потому что длины проекций на координатные оси равны модулю разностей соответствующих координат 2-х точек (X?;Y? и X?;Y?), то формулу дозволено записать так: p=4*?((X?-X?)?+(Y?-Y?)?).
Периметром в всеобщем случае называют длину линии, которая ограничивает замкнутую фигуру. Для многоугольников периметром является сумма всех длин сторон. Эту величину дозволено измерить, а для многих фигур и легко рассчитать, если вестимы длины соответствующих элементов.
Для многоугольников периметром является сумма всех длин сторон. Эту величину дозволено измерить, а для многих фигур и легко рассчитать, если вестимы длины соответствующих элементов.
Вам понадобится
- – линейка либо рулетка;
- – крепкая нить;
- – роликовый дальномер.
Инструкция
1. Дабы измерить периметр произвольного многоугольника, измерьте при помощи линейки либо иным измерительным прибором все его стороны, а после этого обнаружьте их сумму. Если дан четырехугольник со сторонами 5, 3, 7 и 4 см, которые измерены линейкой, обнаружьте периметр, сложив их совместно Р=5+3+7+4=19 см.
2. Если же фигура произвольная и включает в себя не только прямые линии, то измерьте ее периметр традиционной веревкой либо ниткой. Для этого расположите ее так, дабы она верно повторяла все линии, ограничивающие фигуру, и сделайте на ней отметку, если дозволено, примитивно обрежьте ее дабы избежать путаницы. После этого при помощи рулетки либо линейки, измерьте длину нитки, она и будет равна периметру данной фигуры. Непременно следите за тем, дабы нить максимально верно повторяла линию для большей точности итога.
Непременно следите за тем, дабы нить максимально верно повторяла линию для большей точности итога.
3. Периметр трудной геометрической фигуры измеряйте роликовым дальномером (курвиметром). Для этого не линии намечается точка, в которую устанавливается ролик дальномера и прокатывается по ней, до возвращения в начальную точку. Дистанция, измеренная роликовым дальномером, и будет равна периметру фигуры.
4. Периметр некоторых геометрических фигур вычисляйте. Скажем, дабы обнаружить периметр всякого положительного многоугольника (выпуклого многоугольника, стороны которого равны), длину стороны умножьте на число углов либо сторон (они равны). Дабы обнаружить периметр верного треугольника со стороной 4 см умножьте это число на 3 (Р=4?3=12 см).
5. Дабы обнаружить периметр произвольного треугольника, сложите длины всех его сторон. Если не даны все стороны, а есть углы между ними, обнаружьте их по теореме синуса либо косинуса. Если знамениты две стороны прямоугольного треугольника, третью обнаружьте по теореме Пифагора и обнаружьте их сумму. Скажем, если знаменито, что катеты прямоугольного треугольника равны 3 и 4 см, то гипотенуза будет равна?(3?+4?)=5 см. Тогда периметр Р=3+4+5=12 см.
Скажем, если знаменито, что катеты прямоугольного треугольника равны 3 и 4 см, то гипотенуза будет равна?(3?+4?)=5 см. Тогда периметр Р=3+4+5=12 см.
6. Дабы обнаружить периметр круга, обнаружьте длину окружности, которая его ограничивает. Для этого ее радиус r умножьте на число??3,14 и число 2 (P=L=2???r). Если знаменит диаметр, рассматривайте, что он равен двум радиусам.
Периметром многоугольника называют замкнутую ломаную линию, составленную из всех его сторон. Нахождение длины этого параметра сводится к суммированию длин сторон. Если все отрезки, образующие периметр такой двухмерной геометрической фигуры, имеют идентичные размеры, многоугольник именуется верным. В этом случае вычисление периметра гораздо упрощается.
Инструкция
1. В самом простом случае, когда вестимы длина стороны (а) верного многоугольника и число вершин (n) в нем, для вычисления длины периметра (Р) примитивно перемножьте эти две величины: Р = а*n. Скажем, длина периметра верного шестиугольника со стороной в 15 см должна быть равна 15*6=90 см.
Скажем, длина периметра верного шестиугольника со стороной в 15 см должна быть равна 15*6=90 см.
2. Вычислить периметр такого многоугольника по вестимому радиусу (R) описанной около него окружности тоже допустимо. Для этого придется вначале выразить длину стороны с применением радиуса и числа вершин (n), а после этого умножить полученную величину на число сторон. Дабы рассчитать длину стороны умножьте радиус на синус числа Пи, поделенного на число вершин, а итог удвойте: R*sin(?/n)*2. Если вам комфортнее вычислять тригонометрическую функцию в градусах, замените число Пи на 180°: R*sin(180°/n)*2. Периметр вычислите умножением полученной величины на число вершин: Р = R*sin(?/n)*2*n = R*sin(180°/n)*2*n. Скажем, если шестиугольник вписан в круг с радиусом 50 см, его периметр будет иметь длину 50*sin(180°/6)*2*6 = 50*0,5*12 = 300 см.
3. Схожим методом дозволено посчитать периметр, не зная длины стороны положительного многоугольника , если он описан около окружности с знаменитым радиусом (r). В этом случае формула для вычисления размера стороны фигуры будет отличаться от предыдущей лишь задействованной тригонометрической функцией. Замените в формуле синус на тангенс, дабы получить такое выражение: r*tg(?/n)*2. Либо для расчетов в градусах: r*tg(180°/n)*2. Для вычисления периметра увеличьте полученную величину в число раз, равное числу вершин многоугольника : Р = r*tg(?/n)*2*n = r*tg(180°/n)*2*n. Скажем, периметр восьмиугольника, описанного вблизи круга с радиусом в 40 см, будет примерно равен 40*tg(180°/8)*2*8 ? 40*0,414*16 = 264,96 см.
В этом случае формула для вычисления размера стороны фигуры будет отличаться от предыдущей лишь задействованной тригонометрической функцией. Замените в формуле синус на тангенс, дабы получить такое выражение: r*tg(?/n)*2. Либо для расчетов в градусах: r*tg(180°/n)*2. Для вычисления периметра увеличьте полученную величину в число раз, равное числу вершин многоугольника : Р = r*tg(?/n)*2*n = r*tg(180°/n)*2*n. Скажем, периметр восьмиугольника, описанного вблизи круга с радиусом в 40 см, будет примерно равен 40*tg(180°/8)*2*8 ? 40*0,414*16 = 264,96 см.
Квадрат представляет собой геометрическую фигуру, состоящую из четырех сторон идентичной длины и четырех прямых углов, всякий из которых равен 90°. Определение площади либо периметра четырехугольника, причем всякого, требуется не только при решении задач по геометрии, но и в повседневной жизни. Эти знания могут стать пригодными, скажем, во время ремонта при расчете необходимого числа материалов – покрытий для пола, стен либо потолка, а также для разбивки газонов и грядок и т. д.
д.
Инструкция
1. Для определения площади квадрата умножьте величину длины на величину ширины. Потому что в квадрате длина и ширина идентичны, то значение одной стороны довольно построить в квадрат. Таким образом, площадь квадрата равна длине его стороны, возведенной в квадрат. Единицей измерения площади могут быть квадратные миллиметры, сантиметры, дециметры, метры, километры.Дабы определить площадь квадрата, дозволено воспользоваться формулойS = aa, где S – площадь квадрата,а – сторона квадрата.
2. Пример № 1. Комната имеет форму квадрата. Сколько ламината (в кв.м) понадобится для того, дабы всецело покрыть пол, если длина одной стороны комнаты составляет 5 метров.Запишите формулу: S = aa. Подставьте в нее указанные в условии данные.Потому что а = 5 м, следственно, площадь будет равнаS (комнаты) = 5х5= 25 кв.м, значит, и S (ламината) = 25 кв.м.
3. Периметр представляет собой всеобщую длину границы фигуры. В квадрате периметр – это длина всех четырех, причем идентичных, сторон. То есть, периметр квадрата представляет собой сумму всех его четырех сторон. Дабы вычислить периметр квадрата, довольно знать длину одной его стороны. Измеряется периметр в миллиметрах, сантиметрах, дециметрах, метрах, километрах.Для определения периметра имеется формула:P = a + а + а + а илиP = 4a, гдеР – периметр,а – длина стороны.
То есть, периметр квадрата представляет собой сумму всех его четырех сторон. Дабы вычислить периметр квадрата, довольно знать длину одной его стороны. Измеряется периметр в миллиметрах, сантиметрах, дециметрах, метрах, километрах.Для определения периметра имеется формула:P = a + а + а + а илиP = 4a, гдеР – периметр,а – длина стороны.
4. Пример № 2. Для отделочных работ помещения в форме квадрата требуются потолочные плинтуса. Вычислите всеобщую длину (периметр) плинтусов, если величина одной стороны комнаты равна 6 метров. Запишите формулу P = 4a.Подставьте в нее указанные в условии данные:Р (комнаты) = 4 х 6 = 24 метра.Следственно, длина потолочных плинтусов тоже будет равна 24 метров.
Видео по теме
Обратите внимание!
Для квадрата объективны следующие определения:Квадрат – это прямоугольник, тот, что владеет равными между собой сторонами.Квадрат – это специальная разновидность ромба, у которого весь из углов равен 90 градусам.Являясь положительным четырехугольником, вокруг квадрата дозволено описать либо вписать окружность. Радиус вписанной в квадрат окружность дозволено обнаружить по формуле:R = t/2, где t – сторона квадрата.Если же окружность описана вокруг него, то ее радиус находится так:R = (?2*t)/2Исходя из данных формул, дозволено вывести новые для нахождения периметра квадрата:P = 8*R, где R – радиус вписанной окружности;P = 4*?2*R, где R – радиус описанной окружности.Квадрат является уникальной геометрической фигурой, от того что он безусловно симметричен, самостоятельно от того, как и где провести ось симметрии.
Радиус вписанной в квадрат окружность дозволено обнаружить по формуле:R = t/2, где t – сторона квадрата.Если же окружность описана вокруг него, то ее радиус находится так:R = (?2*t)/2Исходя из данных формул, дозволено вывести новые для нахождения периметра квадрата:P = 8*R, где R – радиус вписанной окружности;P = 4*?2*R, где R – радиус описанной окружности.Квадрат является уникальной геометрической фигурой, от того что он безусловно симметричен, самостоятельно от того, как и где провести ось симметрии.
Задачи на нахождение периметра и площади для 4 класса с ответами
Для решения задач на нахождения периметра и площади прямоугольников и квадратов необходимо освоить следующие основные формулы:
a — длина
b — ширина
P — периметр
S — площадь
Формулы площади и периметра для квадрата
P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата
Формулы площади и периметра для прямоугольника
P = a + b + a + b; P = 2a + 2b;
P = (a + b) · 2 — периметр прямоугольника
S = a · b — площадь прямоугольника
Примеры решения задач разной сложности на нахождение периметра и площади
Задача 1
Каков периметр треугольника ABC?
Ответ: периметр треугольника равен 125 см.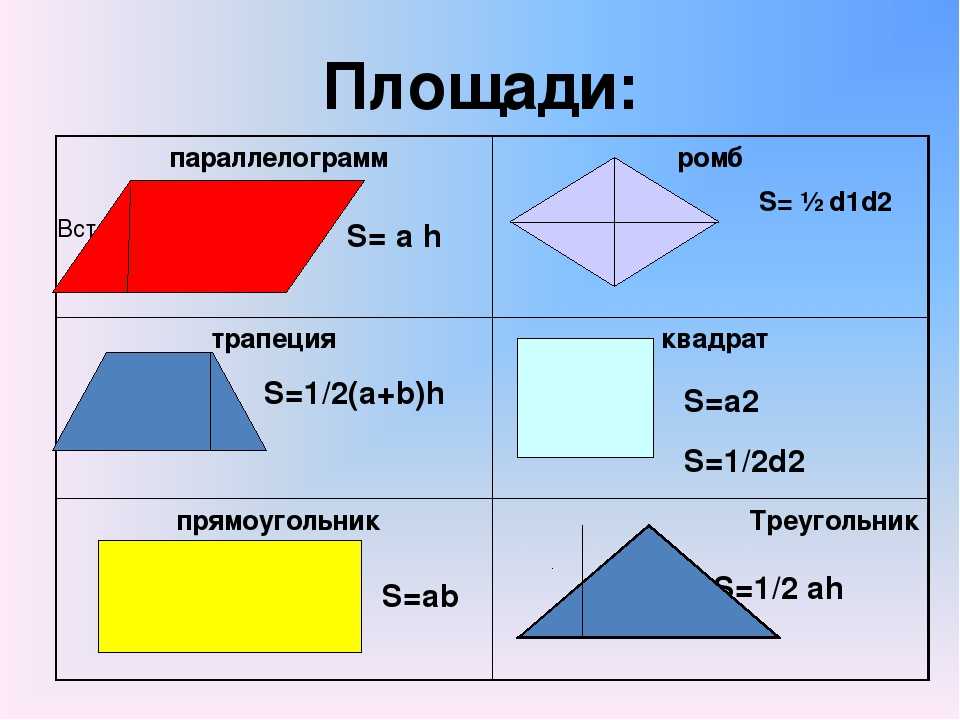
Задача 2
Красный треугольник является равносторонним со стороной 23 сантиметров. Чему равен его периметр?
Ответ: Все три стороны равностороннего треугольника равны. Таким образом, его периметр равен 23 · 3 = 69 см.
Задача 3
Равнобедренный треугольник имеет периметр 37 сантиметров, а его основание имеет длину 9 сантиметров. Каждая из двух других сторон будет иметь длину _____ см.?
Ответ: Равнобедренный треугольник имеет две равные стороны. Сумма равных сторон будет 37 — 9 = 28 см. Значит, каждая из них будет равна 28 : 2 = 14 см.
Задача 4
У Тимы есть сад в форме квадрата со стороной 9 метров. Какова длина забора, который опоясывает сад?
Ответ: Все стороны квадрата равны. Длина забора P равна длине стороны умноженной на 4. P = 4 · 9 = 36 метров.
Задача 5
В прямоугольнике ABCD красная сторона составляет 18 см, а синяя сторона 12 см. Чему равен периметр прямоугольника?
Ответ: Периметр прямоугольника равен 60 см.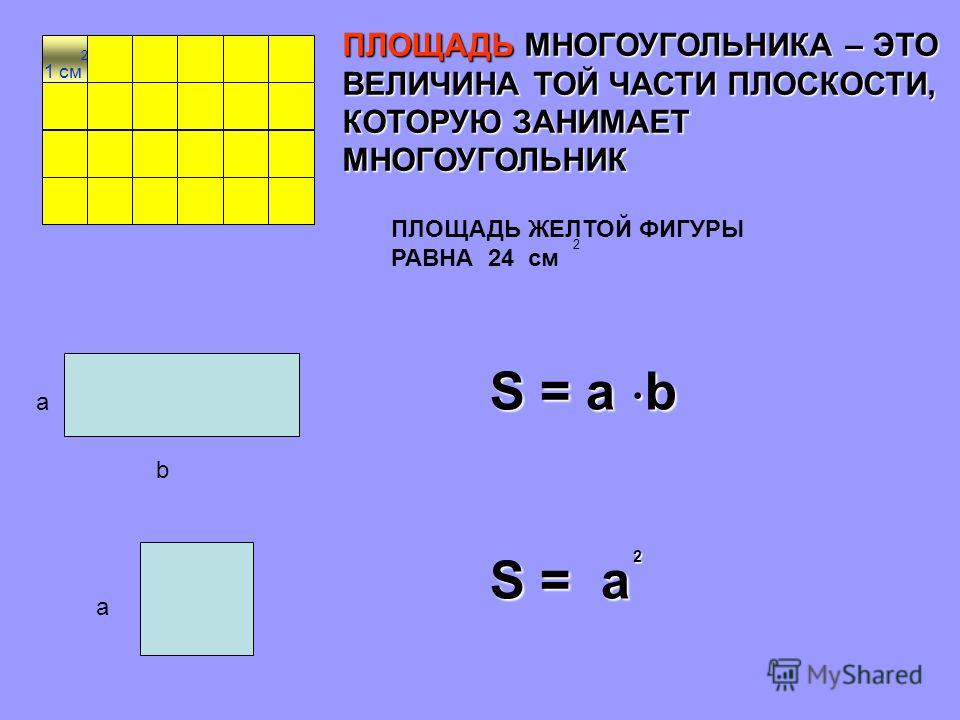
Задача 6
Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?
Ответ: Площадь прямоугольника 56 м².
Задача 7
Площадь витрины квадратной формы 64м². Узнай ее периметр.
Ответ: Периметр витрины равен 32 м.
Задача 8
Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.
Ответ: Площадь прямоугольника равна 630 см².
Задача 9
Парк имеет форму прямоугольника с длиной 24 метра и шириной 18 метров. Если на его сторонах надо посадить деревья с отступом в 2 метра друг от друга, то сколько нужно деревьев?
Ответ: 42 дерева.
Задача 10
Каков периметр синей фигуры?
Ответ: Здесь есть два квадрата, у которых есть общая часть стороны. Так как сторона квадрата равна 10 см и часть стороны равна 8 см, то общая часть 2 см, а оставшаяся часть второго квадрата равна 8 см.
Периметр равен 10 + 10 + 8 + 10 + 10 + 10 + 8 + 10 = 76 см.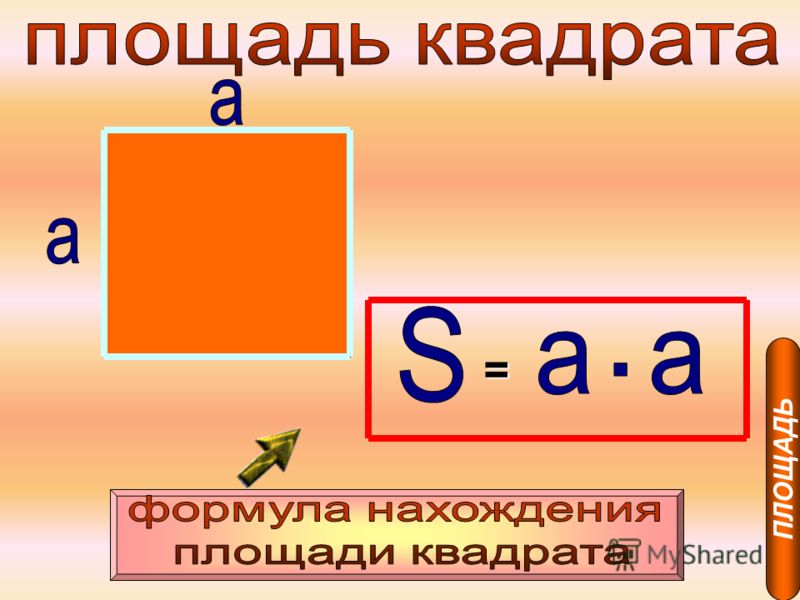
Задача 11
Два прямоугольных участка имеют одинаковую площадь. Длина первого — 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?
Ответ: Длина второго участка 40 м.
Задача 12
Найди периметр квадрата со стороной 8 см.
Ответ: Периметр квадрата 32 см.
Задача 13
Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.
Решение:
6 · 4 = 24 (см) -находим периметр квадрата
3 + 3 = 6 (см) -сумма ширины прямоугольника
24 — 6 = 18 (см)- сумма двух длин прямоугольника
18 : 2 = 9 (см)
Ответ: Длина прямоугольника 9 см.
Задача 14
Длина бассейна прямоугольной формы 15 м. Найди периметр бассейна, если его площадь 120 м2.
Решение:
120:15=8 (м)- ширина бассейна
(8+15)·2= 46 (м)
Ответ: Периметр бассейна 46 метров
Задача 15
Периметр квадрата 8 см. Из трех таких квадратов сложили прямоугольник. Найди периметр получившегося прямоугольника.
Из трех таких квадратов сложили прямоугольник. Найди периметр получившегося прямоугольника.
Решение:
8:4=2 (см)- сторона квадрата
2+2+2+2+2+2+2+2=16(см)
Ответ: Периметр прямоугольника 16 см.
Задача 16
Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см. На сколько см² он ошибся?
Решение:
5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 — 45 = 3 (см²)
Ответ: Ученик ошибся на 3 см²
Задача 17
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.
Решение:
4·2=8 (дм) -длина окна
8·4=32 (дм²)
Ответ: Площадь окна 32 дм²
Задача 18
Один прямоугольный участок имеет длину 36 м, а ширину 20 м. Найдите ширину другого участка с такой же площадью, если его длина на 6 м меньше длины первого участка.
Ответ: Ширина другого участка 24 м.
Задача 19
У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?
Ответ: Площадь квадрата больше на 4 см.
Задача 20
Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
Ответ: Площадь квадрата 36 см², периметр квадрата 24 см.
Задача 21
У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
Ответ: Площадь прямоугольника 35 м², периметр прямоугольника 24 см.
Задача 22
Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?
Решение:
1) 8 ∙ 8 = 64 (площадь клумбы)
2) 64 : 16 = 4(1/16 клумбы)
3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
4) 64 – 28 = 36
Ответ: Незабудками засажено 36 м².
Задача 23
Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?
Чему равна его площадь, если периметр составляет 18 см?
Решение:
1) 6 ∙ 2 = 12
2) 18 – 12 = 6
3) 6 : 2 = 3 (ширина прямоугольника)
4) 3 ∙ 6 = 18
Ответ: Площадь прямоугольника 18 м².
Задача 24
Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?
Решение:
1) 4800 : 60 = 80 (длина стола)
2) 60 ∙ 2 = 120 см
3) 80 ∙ 2 = 160 см
4) 120 + 160 = 280 см
Ответ: Периметр стола 280 см.
Задача 25
Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?
Решение:
1) 5 ∙ 2 = 10
2) 40 – 10 = 30
3) 30 : 2 = 15 (другая сторона прямоугольника)
4) 5 ∙ 15 = 75
Ответ: Площадь прямоугольника 75 см².
Задача 26
Площадь квадрата 49 кВ дм. Узнайте его периметр.
Решение:
1) 49 : 7 = 7 (сторона квадрата)
2) 7 ∙ 4 = 28 (периметр квадрата)
Ответ: Периметр квадрата равен 28 дм.
Задача 27
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.
Решение:
1) 4 ∙ 2 = 8 (длина окна)
2) 4 ∙ 8 = 32
Ответ: Площадь окна равна 32 м².
Задача 28
Длина участка земли 54 м. ширина — 48 м. 5/9 площади засажено картофелем. Остальная часть участка – капустой. Какая площадь засажена капустой?
Решение:
1) 54 ∙ 48 = 2592 (площадь участка земли)
2) 2592 : 9 = 288 (1/9 площади)
3) 288 ∙ 5 = 1440 (5/9 площади)
4) 2592 – 1440 = 1152
Ответ: Капустой засадили 1152 м².
Задача 29
Найди периметр квадрата со стороной 16 см.
Ответ: Периметр квадрата 64 см.
Задача 30
Найди длину прямоугольника с помощью уравнения, если его ширина 7 см, а периметр равен 40 см.
Решение:
P = (a + b) · 2 — периметр прямоугольника
или
(a + b) · 2 = P,
где a — длина = ?, b — ширина = 7 см, P — периметр = 40 см.
Составим уравнение:
(а + 7) · 2 = 40
2а + 14 = 40
2а = 40 — 14
2а = 26
а = 26 : 2
а = 13
Ответ: Длина прямоугольника 13 см.
Задача 31
Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.
Ответ: Ширина прямоугольника 5 см.
Задача 32
Периметр квадрата 24 см. Найди его площадь.
Решение:
24 : 4 = 6 (см)
6 · 6 = 36 (см²)
Ответ: Площадь квадрата 36 см².
Задача 33
Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.
Ответ: Площадь прямоугольника 56 см².
Задача 34
Площадь прямоугольника 40 см². Ширина его 4 см. Чему равен периметр прямоугольника?
Решение:
40 : 4 = 10 (см)
(10 + 4) · 2 = 28 (см)
Ответ: Периметр прямоугольника 28 см.
Задача 35
Ребро куба равно 2 сантиметров. Найти площадь всех граней куба.
Решение:
Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.
У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).
Если S = a · a — площадь квадрата, тогда
S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6
2 · 2 · 6 = 24 (см²)
Ответ: Площадь всех граней куба равна 24 см².
Задача 36
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Ответ: Площадь получившейся фигуры равна 44.
Задача 37
Площадь одной клетки равна 1см.
- Найдите площадь фигуры, изображённой на рисунке A.
- Найдите площадь фигуры, изображённой на рисунке B.
- Найдите площадь фигуры, изображённой на рисунке C.
- Найдите площадь фигуры, изображённой на рисунке D.
- Найдите площадь фигуры, изображённой на рисунке E.
Ответ: Площадь фигуры A 18,5 см², площадь фигуры B 20,5 см², площадь фигуры C 30,5 см², площадь фигуры A 18,5 см², площадь фигуры E 12 см².
Задача 38
Найдите площади и периметры фигурок. Сделайте вывод.
Ответ: Пусть каждая из сторон клетки равна 1 см, тогда применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²
Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура A имеет четыре стороны, тогда 1 + 4 + 1 + 4 = 10 см — периметр фигуры.
Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура B имеет четыре стороны, тогда 2 + 2 + 2 + 2 = 8 см — периметр фигуры.
Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура C имеет шесть сторон, тогда 3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.
Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура D имеет восемь сторон, тогда 1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.
Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура E имеет восемь сторон, тогда 1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.
Вывод: Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат. У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат.
Задача 39
Квадрат в данной фигуре имеет периметр 24 см. Синий треугольник — периметр 15 см. Каков периметр красной фигуры?
Ответ: Периметр красной фигуры равен 27 см.
Задача 40
Периметр каждого из зеленых квадратов 12 см. Каков периметр большого квадрата?
Ответ: Периметр равен 36 см.
Задача 41
Площадь прямоугольника 72 см2. Какова длина и ширина прямоугольника, если ширина в 2 раза меньше, чем его длина?
Ответ: Длина прямоугольника равна 12 см. а ширина — 6 см.
Задача 42
Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см.
Ответ: Периметр прямоугольника равен 24 см.
Задача 43
Периметр красного квадрата равен 16см. Красные треугольники равносторонние. Каково расстояние проползет улитка по пути ABCDFGHA?
Ответ: Расстояние пройденное улиткой будет равно 28 см.
Задача 44
В зале длиной 12 м и шириной 8 м надо покрыть пол квадратными плитками. Сколько потребуется плиток, если площадь каждой плитки 4 дм2?
Ответ: 2400 плиток.
Задача 45
Каков периметр зеленой зоны, если ширина синей зоны равна 3 метра?
Ответ: Периметр зеленой зоны равен 100 метров.
Предыдущая
МатематикаЗадачи на кратное сравнение 3 класс
Следующая
МатематикаЗадачи на движение для 4 класса — формулы и примеры решений
открытых учебников | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий. Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без торговой марки)
Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Практический вопрос по площади и периметру всех фигур
Площадь и периметр — это измеряемые параметры, относящиеся к различным двумерным фигурам, таким как треугольники, прямоугольники, квадраты, параллелограммы и т. д. называется площадью этой конкретной фигуры. Другими словами, площадь фигуры — это мера, связанная с частью плоскости, заключенной в фигуре. Единицей площади является квадрат, например, квадратный метр, квадратный сантиметр и т. д.
Например, если длина (l) прямоугольника равна 10 см, а ширина (b) равна 5 см, то площадь прямоугольника
= 1xb = 10×5 = 50 кв. смПериметр:-
Длина границы вокруг любой замкнутой плоскости называется периметром. Таким образом, сумма сторон плоской формы является периметром этой конкретной формы.
Единица измерения периметра такая же, как единица измерения сторон данной формы, например, метр, сантиметр и т.
д.
Например, если стороны треугольника равны 2 см, 8 см и 4 см соответственно, то 12 см, 14 см, 18 см, тогда
Периметр треугольника = 12 см + 14 см + 18 см = 44 cmDifferent shapes:-
1. Triangle
2. Square
3. Circle
4. Regular polygonFormulas of Area and perimeter of different shapes:-
1. Triangle :Ниже показаны различные типы треугольников –
i) Равносторонний треугольник:
Все углы этого треугольника равны 60° и все его стороны равны. Если сторона равна a, то
Площадь = √3a²/4
Периметр = 3aii) Равнобедренный треугольник:
Две стороны равны. Пусть каждая из равных сторон равна a, а третья сторона равна b, тогда
Площадь = [b√(4a² – b²)] / 4
Периметр = a + a + b = 2a + biii) Неравномерность Треугольник:
У него три неравные стороны.
Пусть стороны будут a, b и c, тогда
Площадь = √[s(s-a)(s-b)(s-c) [ формула Герона]
Где s = (a+b+c)/2
Периметр = a + b + civ) Прямоугольный треугольник :
Площадь = 1/2 × Основание × Высота
Периметр = a + b + c2. Четырехугольник:-
Различные типы четырехугольника показаны ниже У квадрата равны четыре стороны. Пусть сторона равна a, тогда
Площадь = сторона² = a²
Периметр = 4 × сторона = 4aII) Параллелограмма:
Площадь = основание × высота
Периметр = 2 (длина + ширина)III) прямоугольник:
Область = длина × территория
Perimeter = 2 (длина + балл). iv) Трапеция:
Четыре стороны: a, b, c и d.
Площадь = 1/2 (сумма параллельных сторон) × высота
Периметр = a + b + c + dv) Ромб:
Стороны равны a, диагонали равны d1 и d2
Площадь = 1/2 × d1 × d2
Периметр = 4a3.
Окружность:-
Если радиус окружности равен r, то
Площадь = πr²
Периметр = 2πr4 9003 900 Многоугольник:-
Стороны многоугольника равны a, тогдаПлощадь = 5a² × √3/4
Периметр n-стороннего многоугольника = n × сторонаЗадачи, связанные с площадью и периметром:-
1 .Вопрос
Найдите периметр треугольника со сторонами равными 5 см, 9см и 10 см.
A) 24 см
B) 12 см
C) 16 см
D) 18 см
E) 30 смОтвет:- A
Sol.
Требуемый периметр = Сумма сторон = (5 + 9 + 10) см = 24 см2. Вопрос
Периметр равностороннего треугольника равен 75 см. Найдите его площадь.
A) 225√3/4 см²
B) 110√3/4 см²
C) 625√3/4 см²
D) 729√3/4 см²
E) Ни один из этихОтвет:- C
Сол. При этом периметр равностороннего треугольника равен 75 см.
Пусть сторона будет «a»
Мы знаем,
3a = 75
a = 25
Требуемая площадь = (√3 × 25²)/4 = 625√3/4 кв.см.3. Вопрос
Периметр квадрата 48 см. Найдите его сторону и площадь.
A) 12, 144
B) 16, 144
C) 20, 200
D) 15, 125
E) Ни один из этихОтвет:- A
Sol.
Пусть его сторона = а
Согласно вопросу,
4а = 48
а = 12 см
Сторона = 12 см
Площадь = сторона² = 12² = 144 см²4. Вопрос
Если длина и ширина прямоугольного дома равны 25 м и 10 м, то найти его площадь и периметр.
A) 250, 70
B) 200, 50
C) 150, 40
D) 250, 25
E) ни один из этихОтвет:- A
Sol.
Площадь = длина × ширина = 25×10 = 250 м²
Периметр = 2(длина + ширина) = 2(25+10) = 70 м5. Вопрос
Если площадь основания и площадь параллелограмма равны 10 см и 250 кв.
см, то найдите его высоту.
A) 15 см
B) 18 см
C) 22 см
D) 25 см
E) 30 смОтвет:- D
Sol .
Площадь = Основание × Высота
Высота = Площадь/ Основание = 250/10 = 25 см6. Вопрос
Если площадь и высота прямоугольного треугольника равны 42 см² и 14 см. затем найти его основу.
A) 8 см
B) 6 см
C) 9 см
D) 12 см
E) 15 смОтвет:- B
Sol.
Мы знаем,
Площадь прямоугольного треугольника,
Площадь = 1/2 × Основание × Высота
=> 42 = 1/2 × Основание × 14
Основание = 6 см.7. Вопрос
Колесо совершает 200 оборотов, преодолевая расстояние 44 км. Найдите радиус колеса.
A) 30 м
B) 35 м
C) 25 м
D) 40 м
E) 50 мОтвет:- B
Сол.
Расстояние, пройденное за 1 оборот
= общее расстояние/полный оборот
= 44 × 1000/200 = 220 м 7/22
r = 35 м
Таким образом, радиус колеса = 35 мМетод 2:
Применяя логику, согласно которой в 22/7 7 должно быть кратным одному из заданных вариантов.
Здесь 35 — это вариант.
8. Вопрос
Если длину прямоугольника увеличить на 10%, а ширину прямоугольника уменьшить на 5%, то найти процентное изменение площади.
A) Увеличение на 4,5 %
B) Увеличение 5 %
C) Уменьшение 4 %
D) Уменьшение 5 %
E) Ничего из перечисленногоОтвет:-A
Sol.
Пусть, длина =a и ширина = b
Требуемое изменение в %
= (a + b + ab/100)%
= [10 – 5 – (10×5)/100] %
= 4,5 %
Таким образом, площадь увеличилась на 4,5 %.Метод 2:
110/100 × 95/100
= 1045/1000
= 1045-1000/1000 × 100
= 4,5%
9. Вопрос
Что процент из его площадь увеличится, если стороны квадрата увеличить на 22%?
A) 24,80 %
B) 30,65 %
C) 35,60 %
D) 48,84 %
E) 50,74 %= [ 22+22+ (22×22)/100]%
= (44 + 4,84)%
= 48,84 %10.
Вопрос
Радиус кольца (в виде окружности) равен 28 см. . Затем кольцо формуется в форме квадрата. Найдите площадь образовавшегося квадрата?
A. 2000 cm²
B. 1936 cm²
C. 2200 cm²
D. 1152 cm²
E. 1576 cm²
Answer: B
Explanation:
Radius of the ring ( круг) (р) = 28 см.
Длина кольца (окружность/периметр) = 2πr=2π(28)=176 см
Пусть сторона квадрата равна «а» см.
Периметр квадрата (4a) = длина окружности = 176 см
или, 4a = 176 см
или, a = 44 см
Площадь квадрата = a² = 44² = 1936 см²
Таким образом, площадь квадрата 1936 см².
11. Вопрос
Ширина прямоугольного парка составляет 50% его длины. Если периметр поля равен 900 м, то площадь парка:
A. 65 000 м²
B. 62 000 м²
C. 45 000 м²
D. 68 500 м²
E. Ни один из этихОтвет: (C).

Пояснение:
Пусть длина прямоугольного парка равна х м.
∴ ширина = 50% от x = x/2
Периметр прямоугольного парка = 900
или, 2(длина + ширина) = 900
или, 2(x+x/2)=900
или, 3x/2 = 450
или, x = 300
∴ Длина = 300 м
Ширина = 300/2 = 150 м
∴ Площадь = длина * Ширина = 300 × 150 = 45000 м²12. Вопрос
Диагональ квадратного парка составляет 20 м. Какова площадь парка?
A. 200 м²
B. 500 м²
C. 450 м²
D. 60 м²Ответ: A
Объяснение:
Площадь квадрата = 1/2 × 910 ² (диагональ) /2 × 20 × 20 = 200 м²13. Вопрос
В школе есть прямоугольная площадка. Если его периметр и длина равны 120 м и 45 м соответственно, найдите:
(i) ширина
(ii) площадь.A) 15 м, 675 м²
B) 25 м, 575 м²
C) 15 м, 225 м²
D) 30 м, 300 м²
E) Ничего из этогоОтвет:- A 9 9 :
(i) Периметр прямоугольной площадки = 120 м
Теперь
2(l + b) = 120
l + b = 60
45 + b = 60
b = 60 – 45 = 15 м
Итак, ширина = 15 м.
(ii) Площадь прямоугольной площадки = l × b = 45 м × 15 м = 675 м²
Итак, требуемая площадь = 675 м²14. Вопрос
Проволока длиной 88 см сначала сгибается в круг, а затем в квадрат. У кого будет больше площадь?
A) круг > квадрат
B) квадрат > круг
C) квадрат = круг
D) ничего из этого
Ответ: — A
Сторона квадрата = 88 ÷ 4 см = 22 см
Площадь квадрата = (Сторона)2 = (22)² см² = 484 см²
Длина окружности = 88 см
2πr = 88
r = 88× 1/2×7/22 = 14 см
Площадь круга = πr² = 22/7 × 14² = 616 см²
Так как 616 см² > 484 см²Итак, круг имеет больше площади.
Площадь и периметр треугольника
В этой статье вы узнаете, как вычислить площадь и периметр треугольника.
Слово площадь относится к области, которая находится внутри границы геометрической фигуры или плоского объекта. Обычно мы используем квадратные единицы для изображения площади объекта.
Стандартной единицей площади является метр в квадрате (. Мы можем найти площади всех геометрических фигур, таких как круги, квадраты, прямоугольники, треугольники и т. д. Для этой цели у нас есть специальные формулы. В следующих нескольких разделах мы обсудим, как для вычисления площадей различных типов треугольников.
Площадь треугольника
Площадь треугольника определяется следующим образом:
Общая площадь, заключенная между тремя сторонами треугольника, известна как площадь этого треугольника треугольник равен половине произведения основания и высоты треугольника. Математически формулу площади треугольника можно записать так:
Площадь =
Это означает, что для вычисления площади треугольника мы должны знать основание и высоту треугольника. Следует иметь в виду, что основание и высота треугольника перпендикулярны друг другу. Иногда высота треугольника неизвестна. Чтобы найти площадь такого треугольника, нам нужно сначала узнать высоту.
В этих ситуациях мы используем разные формулы для вычисления площадей треугольника. Все эти сценарии обсуждаются ниже с примерами.
Лучшие репетиторы по математике
Поехали
Площадь треугольника, когда известна высота
В этом разделе мы увидим, как вычислить площадь треугольника с известной высотой.
Найдите площадь следующего треугольника:
В приведенном выше треугольнике даны высота и основание треугольника, поэтому воспользуемся общей формулой для нахождения площади треугольника.
Площадь =
Площадь =
Площадь =
Площадь равностороннего треугольника (высота неизвестна)
Все стороны равностороннего треугольника равны. Формула для расчета площади равностороннего треугольника приведена ниже:
Площадь =
Например, рассмотрим равносторонний треугольник, ниже которого измерена одна сторона:
Мы подставим 8 в приведенную выше формулу для расчета площадь равностороннего треугольника:
Площадь =
Площадь =
Площадь =
Площадь равнобедренного треугольника с известными сторонами
Равнобедренный треугольник — это треугольник, у которого длины двух сторон равны.
Возможна ситуация, когда стороны равнобедренного треугольника известны, а высота неизвестна. В этой ситуации мы можем использовать следующую формулу для вычисления площади треугольника:
Площадь =
В приведенном выше треугольнике длины двух сторон равны, следовательно, это равнобедренный треугольник. Нам неизвестна высота треугольника, поэтому воспользуемся приведенной выше формулой для вычисления его площади.
Площадь =
Площадь =
Площадь =
Мы знаем, что запомнить все приведенные выше формулы для равносторонних или равнобедренных сторон может быть сложно. Когда стороны известны, а высота неизвестна, вы можете просто использовать формулу Герона, которая обсуждается ниже, для вычисления площади треугольника. Это верно для всех типов треугольников, будь то равнобедренные, равнобедренные, прямоугольные или прямоугольные.
Формула Герона для вычисления площади, когда известны только стороны
Мы также можем использовать формулу Герона для вычисления площади треугольника, когда известны длины трех сторон.
Чтобы использовать эту формулу, мы должны знать периметр треугольника, который относится к расстоянию вокруг треугольника и вычисляется путем суммирования длин всех трех сторон треугольника. Используйте следующие шаги для вычисления площади по формуле Герона:
- На первом этапе процесса найдите полупериметр треугольника, просуммировав три стороны и разделив число на 2. Полупериметр — это просто половина периметр треугольника.
- На втором этапе примените значение, полученное на первом этапе треугольника, к основной формуле, известной как формула Герона.
Формула Герона для вычисления площади треугольника приведена ниже:
Площадь =
Здесь s — полупериметр, а a, b и c — стороны треугольника.
Рассмотрим следующий пример:
Найдите площадь следующего треугольника:
Стороны a, b и c равны 12 см, 9см и 8 см. Сначала мы вычислим полупериметр, подставив эти значения в приведенную ниже формулу:
Полупериметр =
Полупериметр =
Полупериметр =
Теперь мы подставим это значение полупериметра в приведенную ниже формулу на Найдите площадь:
Площадь =
Площадь =
Площадь =
Рассмотрим другой пример ниже
Найдите площадь следующего треугольника:
Значения сторон a, b и c равны 18 см, 15 см и 9 см.
Сначала мы вычислим полупериметр, подставив эти значения в приведенную ниже формулу:
Полупериметр =
Полупериметр =
Полупериметр =
Теперь мы подставим это значение полупериметра в приведенную ниже формулу на Найдите площадь:
Площадь =
Площадь =
Площадь =
Площадь =
Периметр треугольника
Периметр любой двумерной фигуры относится к расстоянию вокруг фигуры. Мы можем вычислить периметр любой замкнутой фигуры, просто просуммировав длины всех трех сторон. В этом разделе вы узнаете, как вычислить периметр различных типов треугольников, когда известна их длина.
Формула
Формула для нахождения периметра треугольника приведена ниже:
Периметр = сумма трех сторон
Стандартной единицей измерения периметра является метр или сантиметр.
The following table shows the formula for computing the sides of three types of triangle:
Equilateral Triangle Isosceles Triangle Scalene Triangle
- Отсюда видно, что периметр равностороннего треугольника в 3 раза больше его длины
- Периметр равнобедренного треугольника равен сумме удвоенных длин равных сторон и основания
- Периметр разностороннего треугольника равен сумме длин всех трех сторон треугольника
Рассмотрим следующее треугольник, длины трех сторон которого даны:
Длины сторон 12 см 9 см и 8 см соответственно.
Чтобы рассчитать периметр, подставьте эти значения в формулу ниже:
Периметр = a + b + c
= 12 + 9 + 8 = 29 см
геометрия — Как соотнести площади круга, квадрата, прямоугольника и треугольника, если они имеют одинаковый периметр??
Я думаю, вы исходите из ошибочного и чрезмерно упрощенного представления о том, что периметр фигуры дает больше информации, чем при определении площади фигуры.
Теоретически, вам нужно знать каждые деталей кривой формы — не только длину/периметр, но и каждые поворотов и углов поворота.
Конечно, если форма имеет общий образец или формулу, то, вероятно, можно определить большую часть этой информации по относительно небольшому объему данных. Например, если вы знаете, что фигура представляет собой многоугольник, достаточно знать длины всех сторон и размеры всех углов. И если вы знаете все углы, кроме одного, вы можете определить этот окончательный угол, и если вы знаете все углы и все стороны, кроме одной, вы можете определить конечную сторону.
Но вообще нужно знать лот больше только по общему периметру и количеству сторон.
Но опять же, если вы знаете больше информации о форме, вы часто можете получить больше информации. Если, например, вы знаете, что это равносторонний $n$-угольник, и вы знаете, что его периметр равен $P$, вы знаете, что все стороны равны $P/n$. (Однако, если $n > 3$, вы не знаете углов, поэтому вы не знаете и площадь.) Если вы знаете, что это равноугольный $n$-угольник, вы знаете полный угол, а также для каждого угла. Если вы знаете, что это прямоугольник, то вы знаете, что все углы прямые, и это параллелограмм, поэтому все, что вам нужно для площади, это две стороны (ширина и высота). Если вы знаете периметр, вам нужна только одна сторона, и вы можете определить другую сторону.
Итак, ваш вопрос.
Периметр = $P$.
Треугольник: Со сторонами $a,b,c: a+b+c = P$ и углами $A,B,C: A+B+C = 180$. Угол $A$ лежит против угла $a$, угол $B$ лежит против угла $b$, а угол $C$ лежит против угла c$.
У нас недостаточно информации. Если бы у нас было две стороны, мы могли бы получить третью из периметра, а затем использовать тригонометрические тождества для получения углов. Или, если бы у нас было два угла, мы могли бы получить третий, а затем мы могли бы получить триггерные пропорциональные длины, а из периметра мы могли бы получить стороны. Или, если у нас есть одна сторона и один угол, используя триггер и ограничение периметра, мы можем сделать все остальное. 92 \frac{\sqrt{3}}4$.
Четырехугольник:
Если вы не знаете, прямоугольник это или параллеграмм, то формулы вообще нет. Но вы можете знать, что если стороны равны $a,b,c,d$, а углы равны $A,B,C,D$ (заглавные напротив строчных букв), вы знаете: $a + b + c + d = P $ и $A+B+C+D= 360$. И вы можете рассчитать площадь, «разрезав» ее на два треугольника, вычислив их площадь и сложив их.
Прямоугольник:
Вы знаете, что углы прямые и что это параллелограмм, поэтому $a = c$ и $b = d$, поэтому $2a + 2b = P$ и $b = \frac {P- 2a} 2$, поэтому площадь равна $a*b = a*\frac{P — 2a}2 = \frac P{2a} — a^2$.
92}{16}$
Стоит обратить внимание на площадь правильного $n$-угольника.
Правильный $n$-угольник имеет равные $n$ сторон, поэтому $s = \frac Pn$.
И правильный $n$-угольник имеет $n$ углов. Эти углы в сумме составляют $({n-2})*180$, потому что мы можем разрезать $n$-угольник на $n-2$ треугольников, каждый из углов которых равен $180$. Таким образом, каждый угол $n$-угольника равен $\theta = \frac{n-2}n * 180$.
Мы можем разрезать $n$-угольник на части равнобедренного треугольника. Каждый равнобедренный тройной срез имеет основание длины $s = \frac Pn$. Угол основания равен $\frac {\theta}2 = \frac{n-2}n*92$
Формулы периметра и площади для двумерных геометрических фигур
На этой странице приведены формулы Периметра и площади для двумерных геометрических фигур , таких как квадрат, прямоугольник, ромб, параллелограмм, трапеция или трапеция, треугольник, прямоугольный треугольник, эллипс, окружность, сектор окружности, сегмент окружности и т.
д.
Содержание
- 1 Формулы для двумерных геометрических фигур
- 1.1 Квадрат
- 1.2 Прямоугольник
- 1.3 Ромб
- 1.4 Параллелограмм
- 1.5 Трапеция (трапеция)
- 1.6 Треугольник
- 1.6.1 Формулы для равносторонних треугольников
900.2- 1.6.3 Формулы для прямоугольного треугольника и формулы для длины треугольника, если заданы одна сторона и угол Дуга и сектор окружности
- 1,7,3 Сегмент круга и периметра сегмента
- 1,7,4 Площадь кругового кольца
- 1,8 Эллипс
квадрат
Сторон
Площадь квадрата = A = сторона 2 = a 2 = (1/2) d 2
Длина диагонали = d =
Прямоугольник
Периметр прямоугольника = 2 × (длина + ширина) = 2 (a + b)
Площадь прямоугольника = длина × ширина = ab4 9 из 000 диагональ ( d ) = √ (a 2 + b 2 )
Ромб
Для ромба все стороны равны = a, высота по вертикали = d & h2, h3 также являются диагоналями AB | округ Колумбия, AD || BC
Периметр ромба = 4a
Area of the Rhombus = ad = (1/2) d1 d2
Parallelogram
Area of parallelogram = base × height = a x h
Perimeter of parallelogram = 2 × (сторона1 + сторона2) = 2 (a + b)
Трапеция (трапеция)
В трапеции две стороны параллельны,
3 Площадь
3
Периметр трапеции или трапеции =
Треугольник
Формулы для треугольника
Площадь треугольника = (1/2) x Основание x Высота =
Полуметр = 2003Площадь треугольника
Радиус вписанного треугольника = Площадь /S
Формулы для равностороннего треугольника 2Радиус окружности равностороннего треугольника = =
Площадь окружности равностороннего треугольника =
Радиус вписанной окружности равностороннего треугольника = = a / (2 √3) 3 Формулы для 92 Прямоугольный треугольник и формула для длины треугольника, заданного одной стороной и углом
На приведенном выше рисунке ABC представляет собой прямоугольный треугольник x = длина смежной стороны, y = длина гипотенузы и h = высота треугольника.
Закон Пифагора –
Площадь прямоугольного треугольника =
Sin β = h / y ⇒ h = y Sin β
Cos β = x / y ⇒ x = y Cos β
β h / Tan x ⇒ h = x Tan βCosine Law
c 2 = a 2 + b 2 – 2 ab Cos γ
b 2 = a 2 + c 2 – 2 ac Cos β
a 2 = b2 + c 2 – 2 bc Cos α
Закон синуса
Площадь треугольника
Круг
Формулы для области и окружности круга
Область круга (A) = π x (radius) 2 = π R 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 2. = ( π/4 ) D 2 = 0,7854 x D 2
Диаметр круга (D) =
Длина окружности ( C ) = 2 π x Радиус = 2 π r = 2 π r D
Площадь круга =( 1/2) x длина окружности x радиус = (1/2) x C x r
Формула для дуги и сектора окружностиДлина дуги окружности ( l ) =
Площадь сектора (малого) =
Если угол θ в радианах означает один радиан = 180/π , тогда
Площадь сектора =
Угол сектора круга θ =
Сегмент круга и периметр сегмента
Площадь сегмента =
Периметр сегмент =
Дуга Длина сегмента окружности = l = 0,01745 x r x θ
Длина хорды окружности = =
Площадь круглого кольца
Площадь круглого кольца = = ( π/4) ( D 2 – d 2 ) = 0,7854 (D 5 – 2 d 2 )
Площадь круглого кольца = π (R 2 – r 2 )
Эллипс
D = диаметр верхней полуоси
Площадь эллипса = = 0,7854 x D x d
D = 2 x радиус = 2 м, D = 2 x радиус = 2 N
Периметр эллипса (формула — 1) ≈
Периметр ollipse (формала – — 2) ≈
Обе формулы дают приблизительные значения, но формула- 2 дает лучшее приближение, которое получено индийским математиком Рамануджан
Связанные статьи:
.
Конверсии. Оборудование. Расчет чертежей
Онлайн-калькулятор для определения объема жидкости для вертикально установленного цилиндра с секционированной частью.
Сахарная промышленность Процесс Процесс Процесс Расчет мощности
Площадь прямоугольной калькуляции
Длина (A)
Ширина (B)
Площадь (A)
Периметр (P)
Диагонал (D)
Перейти к площади прямоугольника
Перейти к вычислению площади прямоугольника
Перейти к периметру прямоугольника
Перейти к вычислению периметра прямоугольника
Перейти к вычислению диагонали прямоугольника
Перейти к вычислению диагонали прямоугольника
Перейти к применению этих вычислений в реальной жизни для вычисления площади прямоугольника
Если вам нужно найти площадь и периметр прямоугольника, этот калькулятор является удобным инструментом, который вам понадобится.
Просто введя длину и ширину, этот калькулятор почти мгновенно найдет периметр (P) и площадь (A).
Если вас интересуют калькуляторы для различных других форм, вы можете посмотреть другие наши удобные калькуляторы. Но вы можете остаться здесь и узнать больше о нахождении площади прямоугольника.
Прямоугольник имеет четыре угла по 90 градусов. Если длины всех сторон одинаковы, то прямоугольник также является квадратом. Длины сторон будут указаны как a или b , или вы можете использовать l и w для «длины» и «ширины». Диагональ, идущая от одной вершины к противоположной, делящей прямоугольник на два квадрата, называется диагональю и обозначается как 9.1635 д .
Вот основные формулы, используемые калькулятором.
Площадь(A) = a(b)
Периметр (расстояние вокруг внешней стороны прямоугольника) = a + a + b + b или 2 a + 2 b и обозначается как (P)
Диагональ равна d ² = a ² + b ², что является теоремой Пифагора (см.
наш калькулятор теоремы Пифагора).
Пример расчета площади прямоугольника:
Предположим, что длина a = 6 дюймов, а ширина b = 4 дюйма
A = a * b , поэтому A = 6(4) = 24 дюйма²
0 те же размеры, мы можем вычислить периметр.
Периметр равен 2 a + 2 b , поэтому в этом примере периметр
P = 2(6) + 2(4) = 20 дюймов
Чтобы найти диагональ, используя те же размеры:
г ² = 6² + 4² = 36 + 16 = 52
Извлеките квадратный корень из обеих сторон, а диагональ d будет приблизительно равна 7,2 дюйма
Эти примеры иллюстрируют, как вычислить площадь, периметр и диагональ прямоугольника вручную, но если вы предпочитаете использовать калькулятор для получения более быстрых результатов или просто проверить свою работу, тогда не стесняйтесь делать это. Отличительной особенностью калькулятора является то, что вы можете найти либо длину, либо ширину, если знаете периметр и длину одной из сторон.
. Мы можем получить площадь прямоугольника, следуя этой формуле: A = L * W
A — площадь, L — длина, W — ширина.
Пример 1Вычислите площадь прямоугольника, имеющего длину 7 сантиметров и ширину 5 сантиметров.
Формула:A = L * W
Ответ:A = 35. Длина ( L ). 3. 35.1635 Вт ). При умножении вы получите 35 в качестве вашей площади.
Периметр прямоугольникаПосмотрите на изображение ниже, человек ходит вокруг коробки. Путь, который он проходит от начальной точки и обратно, является периметром. Зная длину и ширину прямоугольника, мы можем теперь получить периметр прямоугольника. Обе противоположные стороны прямоугольника конгруэнтны, что означает, что сложив эти стороны, мы можем вычислить периметр.
Вычисление периметра прямоугольникаТеперь, сложив все стороны прямоугольника, мы можем получить периметр.
Вот уравнение для получения периметра прямоугольника:
P = L + W + L + W
Поскольку мы знаем, что обе противоположные стороны прямоугольника идентичны, мы можем упростить уравнение, используя это уравнение :
P = 2L + 2W
Пример 1Найдите периметр прямоугольника, длина которого 12 сантиметров, а ширина 7 сантиметров.
Формула:P = L + W + L + W или
P = 2L + 2W
. 12 + 7 илиP = 2(12) + 2(7)
Ответ будет P = 38. Прибавив 12 ( L ) + 7 ( W ) + 35 ( 916L ) + 7 ( W ) , вы получите 38. Умножив длину ( L ) и ширину ( W ) на 2, затем сложив частное, вы получите тот же ответ.
Диагональ прямоугольникаЕсли присмотреться, прямоугольник представляет собой комбинацию двух прямых углов.
{2}}\) \(D = \sqrt{34}\)
D = 5,83
Реальные приложения для получения площади прямоугольникаМолодожены хотят положить плитку на пол в главной спальне. Комната имеет длину 20 футов и ширину 30 футов. Плитка, которую они выбрали, имеет длину 24 дюйма и ширину 36 дюймов. Решите, сколько плиток нужно, чтобы заполнить главную спальню.
Советы:
1. Найдите площадь, занимаемую главной спальней.
2. Вычислите площадь плитки
3. Выберите единицу измерения. В этом примере будут использоваться ноги.
Solution:A = L * W
A = 20 ft x 30 ft
A = 600 ft²
Tip:
Прежде чем мы получим площадь каждой плитки, переведем футы в дюймы
Пример преобразования:
1 foot = 12 inches
2 feet = 24 inches
3 feet = 36 inches
Area of 1 tile = L × W
Area of 1 tile = 2 × 3
Площадь 1 плитки = 6 футов²
Это означает, что каждая плитка имеет площадь 6 футов² и должна покрывать площадь комнаты, которая составляет 600 футов².

 Например, вместо информации о длине одной из сторон Вы можете иметь градус угла или длину высоты конкретного треугольника. Это существенно осложнит задачу, но не сделает ее решение нереальным. О том, как найти периметр треугольника, какой формы бы он не был можно прочитать » «.
Например, вместо информации о длине одной из сторон Вы можете иметь градус угла или длину высоты конкретного треугольника. Это существенно осложнит задачу, но не сделает ее решение нереальным. О том, как найти периметр треугольника, какой формы бы он не был можно прочитать » «. Как известно, противоположные стороны этой фигуры равны.
Как известно, противоположные стороны этой фигуры равны.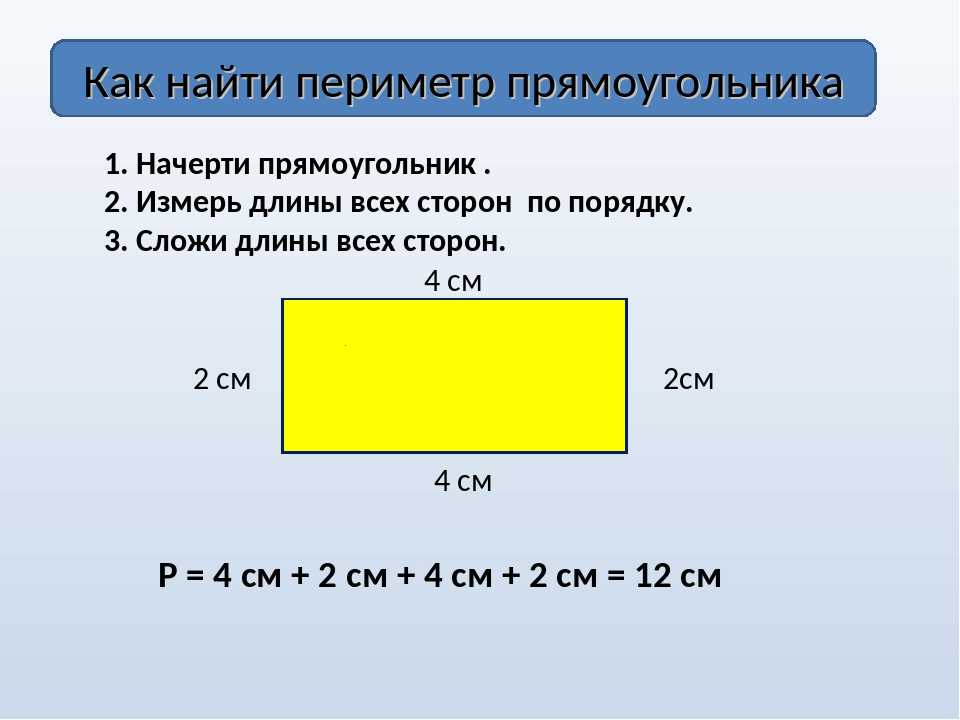
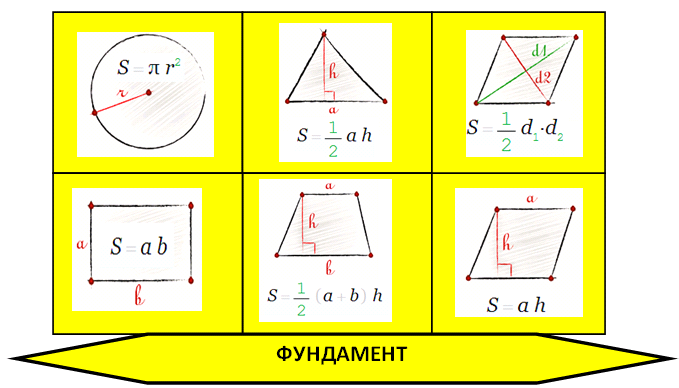
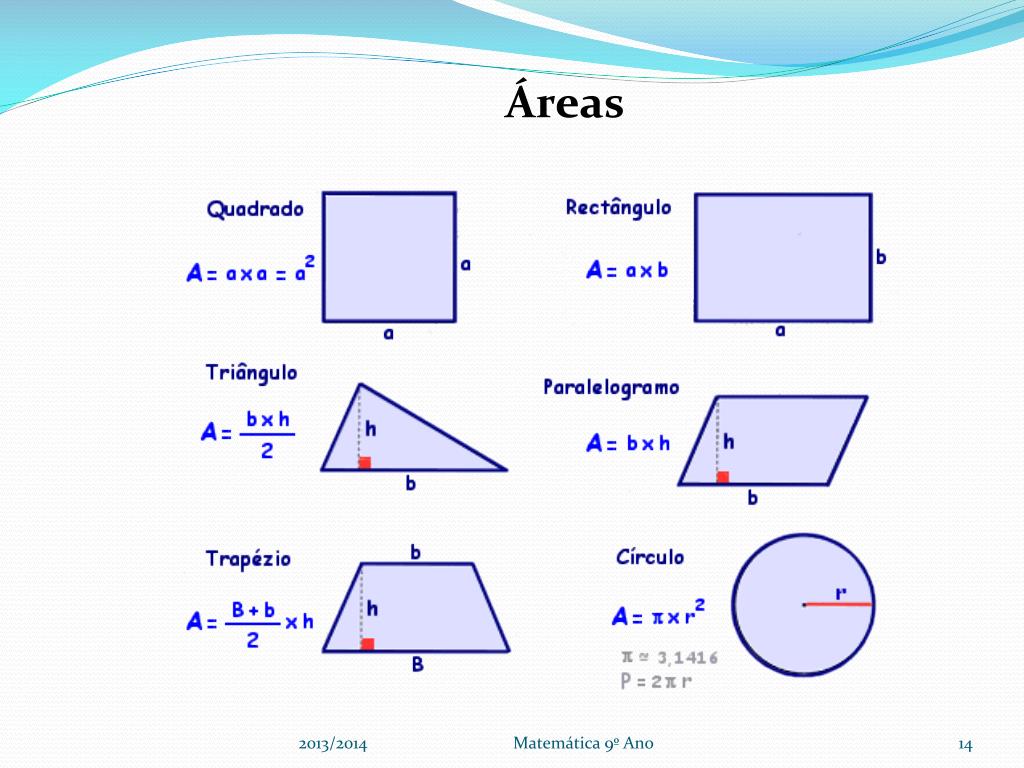


 Аналогично, деление площади на длину даст вам ширину.
Аналогично, деление площади на длину даст вам ширину. Периметр – это общая длина всех сторон фигуры.
Периметр – это общая длина всех сторон фигуры.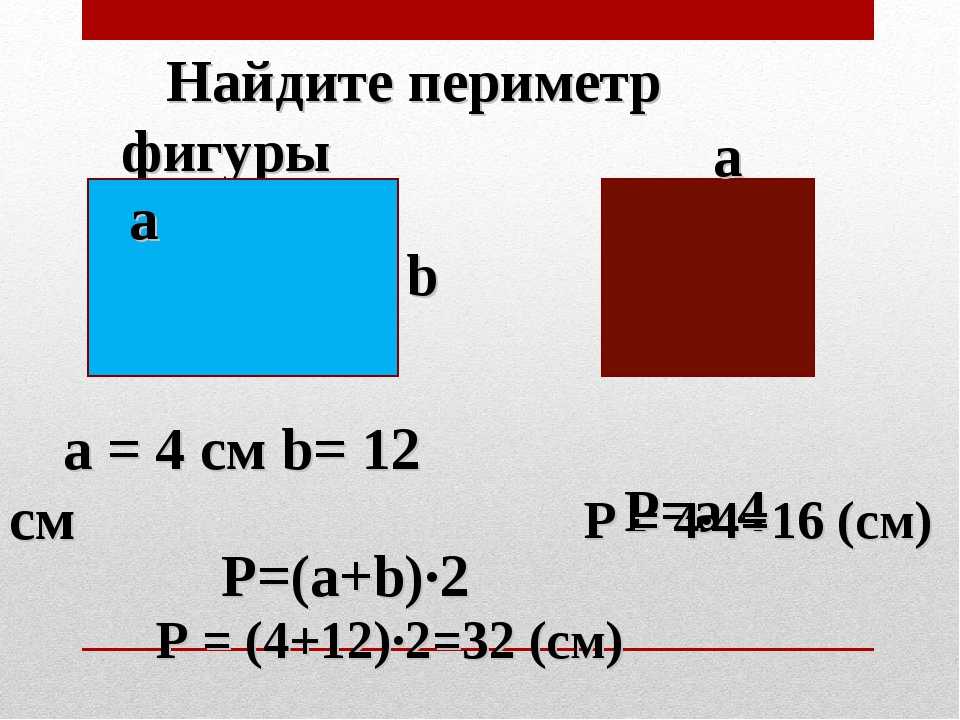


 Вычислить периметр квадрата можно двумя способами.
Вычислить периметр квадрата можно двумя способами.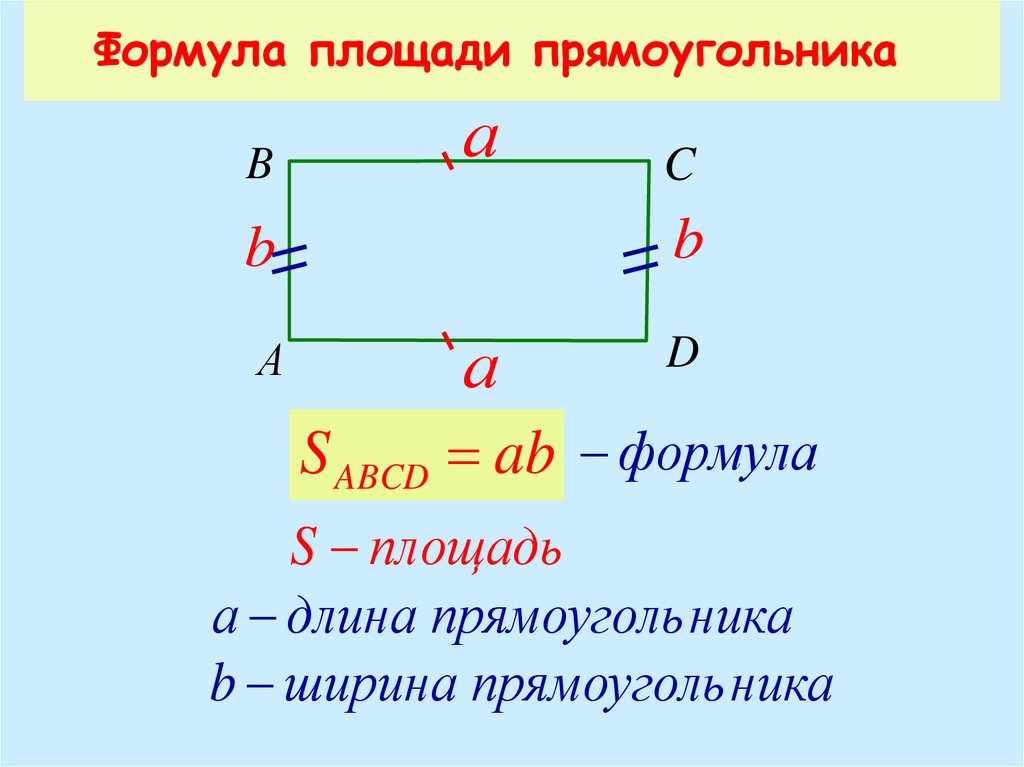 Либо же площадь равна квадратному значению длины его диагонали, разделенному на два: S = d 2 /2 , где S – все та же площадь и d – диагональ квадрата .
Либо же площадь равна квадратному значению длины его диагонали, разделенному на два: S = d 2 /2 , где S – все та же площадь и d – диагональ квадрата .

 д.
д. Пусть стороны будут a, b и c, тогда
Пусть стороны будут a, b и c, тогда Окружность:-
Окружность:- 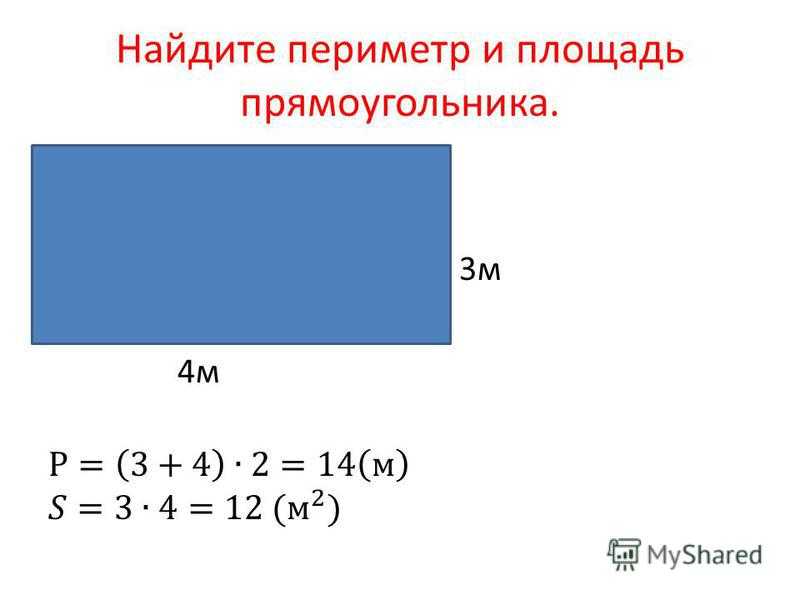
 см, то найдите его высоту.
см, то найдите его высоту. Здесь 35 — это вариант.
Здесь 35 — это вариант.  Вопрос
Вопрос 

 Стандартной единицей площади является метр в квадрате (. Мы можем найти площади всех геометрических фигур, таких как круги, квадраты, прямоугольники, треугольники и т. д. Для этой цели у нас есть специальные формулы. В следующих нескольких разделах мы обсудим, как для вычисления площадей различных типов треугольников.
Стандартной единицей площади является метр в квадрате (. Мы можем найти площади всех геометрических фигур, таких как круги, квадраты, прямоугольники, треугольники и т. д. Для этой цели у нас есть специальные формулы. В следующих нескольких разделах мы обсудим, как для вычисления площадей различных типов треугольников. В этих ситуациях мы используем разные формулы для вычисления площадей треугольника. Все эти сценарии обсуждаются ниже с примерами.
В этих ситуациях мы используем разные формулы для вычисления площадей треугольника. Все эти сценарии обсуждаются ниже с примерами. Возможна ситуация, когда стороны равнобедренного треугольника известны, а высота неизвестна. В этой ситуации мы можем использовать следующую формулу для вычисления площади треугольника:
Возможна ситуация, когда стороны равнобедренного треугольника известны, а высота неизвестна. В этой ситуации мы можем использовать следующую формулу для вычисления площади треугольника: Чтобы использовать эту формулу, мы должны знать периметр треугольника, который относится к расстоянию вокруг треугольника и вычисляется путем суммирования длин всех трех сторон треугольника. Используйте следующие шаги для вычисления площади по формуле Герона:
Чтобы использовать эту формулу, мы должны знать периметр треугольника, который относится к расстоянию вокруг треугольника и вычисляется путем суммирования длин всех трех сторон треугольника. Используйте следующие шаги для вычисления площади по формуле Герона: Сначала мы вычислим полупериметр, подставив эти значения в приведенную ниже формулу:
Сначала мы вычислим полупериметр, подставив эти значения в приведенную ниже формулу: Чтобы рассчитать периметр, подставьте эти значения в формулу ниже:
Чтобы рассчитать периметр, подставьте эти значения в формулу ниже:

 92}{16}$
92}{16}$ д.
д. 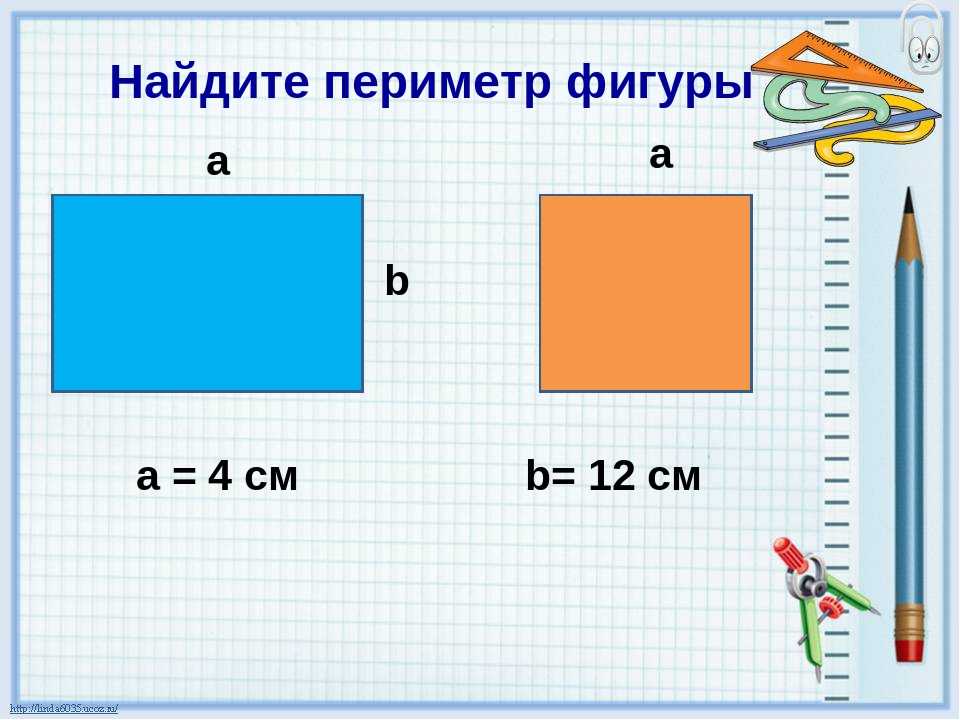
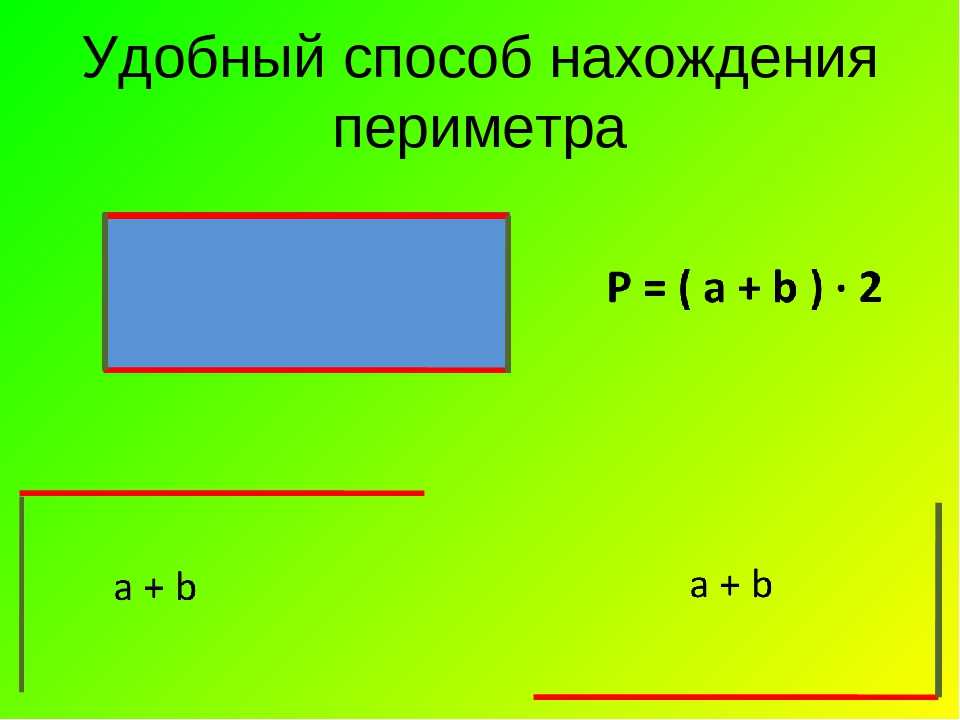 Конверсии. Оборудование. Расчет чертежей
Конверсии. Оборудование. Расчет чертежей
 наш калькулятор теоремы Пифагора).
наш калькулятор теоремы Пифагора).
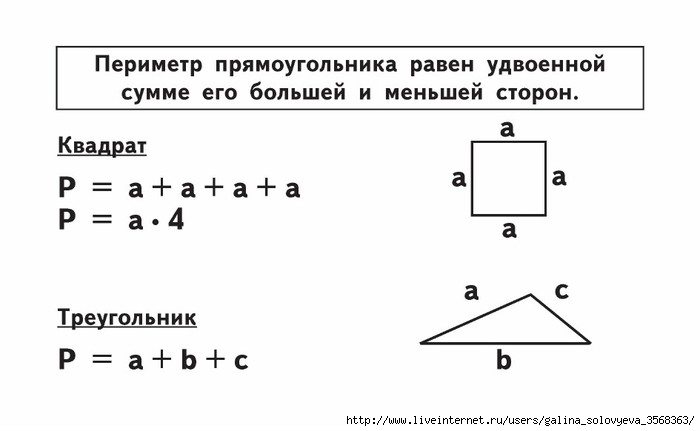 Вот уравнение для получения периметра прямоугольника:
Вот уравнение для получения периметра прямоугольника: {2}}\)
\(D = \sqrt{34}\)
{2}}\)
\(D = \sqrt{34}\)