Наибольшее и наименьшее значение функций
12. Наибольшее и наименьшее значение функций
Исследование степенных и иррациональных функций
просмотреть (55 шт.)
Исследование частных просмотреть (11 шт.)
Исследование произведений просмотреть (29 шт.)
Исследование показательных и логарифмических
функций просмотреть (23 шт.)
Исследование тригонометрических функций
просмотреть (28 шт.)
Исследование функций без помощи производной
просмотреть (16 шт.)
функция возрастает
Предположим, что функция f
не имеет на отрезке [а; b] критических
точек.
наибольшее
значение
наименьшее
значение
Тогда она возрастает (рис. 1) или
убывает (рис. 2) на этом отрезке.
a
b
функция убывает
наибольшее
значение
наименьшее
значение
a
b
Значит,
наибольшее и наименьшее значения
функции f на отрезке [а; b] — это
значения в концах а и b.
Примеры
Пусть теперь функция f имеет на
отрезке [а; b] конечное число
критических точек.
наибольшее
значение
наименьшее
значение
a c
b
наибольшее
значение
наибольшее
значение
наименьшее
значение
наименьшее
значение
a c
n b
Наибольшее и наименьшее
значения функция f может
принимать в критических точках
функции или в точках а и b.
Чтобы найти наибольшее и
наименьшее значения функции,
имеющей на отрезке конечное
число критических точек, нужно
вычислить значения функции во
всех критических точках и на
концах отрезка, а затем из
полученных чисел выбрать
наибольшее и наименьшее.
Вывод :
Если поведение функции
постоянно внутри отрезка, то
своего наибольшего и
наименьшего значения она
достигает в концах отрезка
Если поведение функции внутри отрезка
не постоянно, то функция может
достигать своего наибольшего и
наименьшего значения либо в концах
отрезка, либо в точках экстремума
1.
Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4]
Значения функции в
концах отрезка.
1) y(0) = 0
y(4) = 43– 27 4 = – 44
3
-3
Найдем критические
точки, которые
принадлежат
заданному отрезку.
2) y / = 3×2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
y(3) = 33– 27 3 = –54
Выбрать наименьшее из
полученных значений.
x = 3 [0; 4]
x = –3 [0; 4]
№12
— 5 4
3
10 х
х
Выполнение этапов решения можно изменить, как вам удобно.
Этапы
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
3. Вычислить
значения функции в
критических точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее или
наибольшее
Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3×2 – 27
3
-3
2) y / = 3×2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
x = 3 [0; 4]
x = –3 [0; 4]
3) y(0) = 0
y(4) = 43– 27 4 = – 44
y(3) = 33– 27 3 = –54
№12
— 5 4
3
10 х
х
Предположим, что функция f
имеет на отрезке [а; b] одну точку
экстремума.
наименьшее
значение
a
b
Если это точка минимума, то в этой
точке функция будет принимать
наименьшее значение.
наибольшее
значение
Если это точка максимума, то в этой
точке функция будет принимать
наибольшее значение.
a
b
Другой способ решения
Этапы
1. Найти f /(x)
2. Найти критические
точки, взять те,
которые
принадлежат
данному отрезку.
3. Вычислить
значения функции в
критических точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее и
наибольшее
Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3×2 – 27
3
-3
2) y / = 3×2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
y\
y
+
0
-3
–
+
3
min
4
x
3)
y(3) = 33– 27 3 = –54
№ 12
— 5 4
3
10 х
х
Наименьшее
значение функция
будет принимать в
точке минимума.
Можно сэкономить
на вычислениях
значений функции в
концах отрезка.
Этот способ будет удобно
вспомнить, когда вычисления значений функции в
концах отрезка будет сложным.
2. Найдите наибольшее значение функции y = x3 – 3x + 4
на отрезке [– 2; 0]
Значения функции в
концах отрезка.
1) y(0) = 4
y(-2) = (-2)3– 3 (-2) +4 = 2
1
-1
Найдем критические
точки, которые
принадлежат
заданному отрезку.
2) y / = 3×2 – 3 = 3(x2 – 1) = 3(x – 1)(x + 1)
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
y(-1) = (-1)3– 3 (-1) + 4 = 6
Выбрать наибольшее из
полученных значений.
x = 1 [-2; 0]
x = –1 [-2; 0]
№ 12
6
3
10 х
х
3. Найдите наименьшее значение функции y = x3 – 2×2 + x +3
на отрезке [ 1; 4 ]
Значения функции в
концах отрезка.
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
1) y(1) = 1 – 2 + 1 + 3 = 3
y(4) = 43– 2 42 + 4 + 3 = 39
2) y / = 3×2 – 4x + 1= 3(x – 1)(x – 1 )
3
3×2 – 4x + 1 = 0
D=16–4*3*1=4
4+2
x1=
= 1 [1; 4]
6
4-2
1
= [1; 4]
x2=
6
3
y(1) = 3
№ 12
3
3
10 х
х
x3
9x 7
4. Найдите наибольшее значение функции y
3
на отрезке [ -3; 3 ]
3
( 3)
Значения функции в
у ( 3)
9( 3) 7 9 27 7 11
концах отрезка.
3
33
у (3) 9 3 7 9 27 7 25
3
2
Найдем критические
3
х
точки, которые
у/
9 х 2 9 ( х 3)( х 3)
3
принадлежат
заданному отрезку.
x = 3 [-3; 3]
x = –3 [-3; 3]
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наибольшее из
полученных значений.
y(-3) = 11
y(-3) = -25
В 11
1 1
3
10 х
х
5. Найдите наибольшее значение функции
на отрезке [ 1; 9 ]
Значения функции в
концах отрезка.
3
2
3
2
3
2
y x 3x 1
у(1) 1 3 1 1 1 3 1 1
3
2 2
у (9) 9 3 9 1 (3 ) 27 1
27 27 1 1
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
3
х 3 0
3
3
/
у х 3
х 3 2
2
2
3 х 6 0
1
2
х 2
х 4 [1; 9]
3
2
3
2 2
у (4) 4 3 4 1 (2 ) 12 1
8 12 1 3
Выбрать наибольшее из
полученных значений.
№ 12
1
3
10 х
х
2
6. Найдите наименьшее значение функции y x х 3 x 1
3
на отрезке [ 1; 9 ]
Значения функции в
концах отрезка.
3
2
3
2
y x 2 31x 1
х 21 3
x 1 1 1
у(1) 1 3y
1 x1
3
2 2
у (9) 9 3 9 13 (3 ) 27 1
y х 2 3x 1
27 27 1 1
Найдем критические
точки, которые
принадлежат
заданному отрезку.
1
Запишем функцию
3 в удобном
х 3 виде
0 2
для дифференцирования
3 2
3
/
у х 3
х 3 2
2
2
3 х 6 0
х 2
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
х 4 [1; 9]
3
2
3
2 2
у (4) 4 3 4 1 (2 ) 12 1
8 12 1 3
№ 12
— 3
3
10 х
х
х 2 25
7. Найдите наименьшее значение функции y
х
на отрезке [-10; 1 ]
1
D(y): x = 0
y x 25
х
Значения функции в
1
2
концах отрезка.
х
25
у ( 10) 10 25
10 2,5 12,5
y
10
/
х
х
1
1
у (1) 1 25 26
2
1
х
y х 25
х
2
1
25
х
25
х
Найдем критические
у / 1 Запишем
25 функцию
1
в
2
2 удобном
2
точки, которые
х
хвиде
х
для
дифференцирования
принадлежат
( х 5)( х 5)
x = 5 [-10; 1]
заданному отрезку.
х2
x = –5 [-10; 1]
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
x = 0 D(y)
1
у ( 5) 5 25
5 5 10
5
№ 12
— 1 2 , 5
3
10 х
х
х 2 25
7. Найдите наименьшее значение функции y
Найдите наименьшее значение функции y
х
на отрезке [-10; 1 ]
D(y): x = 0
Значения функции в
концах отрезка.
Можно решить задание,
применив формулу:
u u / v uv/
v2
v
/
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
№ 12
— 1 2 , 5
3
10 х
х
36
y х
х
8. Найдите наибольшее значение функции
на отрезке [ 1; 9 ]
1
Значения функции в
концах отрезка.
/
1
1
2
х
х
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наибольшее из
полученных значений.
D(y): x = 0
y x 36
х
1
у (1) Запишем
1 36 функцию
37
в удобном
1
для дифференцирования
виде
1
у (9) 9 36 9 4 13
9
36 х 2 36
1
/
у 1 36 2 1 2
2
х
х
х
( х 6)( х 6)
x = 6 [ 1; 9]
х2
x = –6 [ 1; 9]
x = 0 D(y)
1
у (6) 6 36 6 6 12
6
№ 12
3 7
3
10 х
х
9. Найдите наибольшее значение функции y 8 х e
Найдите наибольшее значение функции y 8 х e
на отрезке [ 3; 10 ]
1). Первое число меньше 1, т.к.
Значения функции
знаменатель
e4 > 5.в
у (3) (8 3)e 4
концах
отрезка.
2).
Второе
число – отрицательноe.
3). Значит, наибольшее число 1.
3
uv u/ v uv/
x 7
5
4
e
у(10) (8 10)e 2e3
/
Найдем критические
точки, которые
принадлежат
заданному отрезку.
у / (8 х) / e x 7 (8 х)(e x 7 ) /
e x 7 (8 х)e x 7 e x 7 ( 1 8 х)
e
x 7
7
(7 х )
x = 7 [ 3; 10]
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наибольшее из
полученных значений.
1
у(7) (8 7)e7 7 1e0 1
№ 12
1
3
10 х
х
10. Найдите наименьшее значение функции y х 8 х 8 e
на отрезке [ 1; 7 ]
2
2 х
у(1) (1 8 8)e 1 e
Значения функции в
концах отрезка.
1
uv u v uv у(7) (49 56 8)e e5
Найдем критические у / ( х 2 8 х 8) / e 2 х ( х 2 8 х 8)( e 2 х ) /
/
/
точки, которые
принадлежат
заданному отрезку.
5
/
(2 х 8)e 2 х ( х 2 8 х 8)e 2 х ( 1)
e 2 х (2 х 8 х 2 8 х 8) e 2 х ( х 2 10 х 16)
e
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
2 х
( х 10 х 16) e
2
x = 2 [ 1; 7]
x = 8 [ 1; 7]
2 х
8
( х 8)( х 2)
Наименьшее число – 4, т.к.
первые два положительные.
1
у(2) (4 16 8)e0 4
№12
— 4
2
3
10 х
х
lnx
/
1
x
11. Найдите наибольшее значение функции
y = ln(x+5)5 – 5x на отрезке [-4,5; 0]
1
5
5 x 20
у 5
5
5
х 5
х 5
х 5
y = 5ln(x+5) – 5x
Запишем
функцию
5( x 4) в удобном
2. Найти
x=
-4 [-4,5; 0]
для дифференцирования
виде
х 5
критические точки,
1. Найти f /(x)
взять те, которые
принадлежат
данному отрезку.
3. Вычислить значения
функции в критических
точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее или
наибольшее.
/
y\
y
–
-4,5+ +
-5
-4
max
0
x
0
у ( 4) ln 15 5 ( 4)
0 20 20
№12
2 0
3
10 х
х
Наибольшее
значение функция
будет принимать в
точке максимума.
Можно сэкономить
на вычислениях
значений функции в
концах отрезка.
12. Найдите наибольшее значение функции
1 5
y = ln(11x) – 11x + 9 на отрезке [
; ]
22 22
lnx 1x
/
1
1
1
/
у
(11х) 11
11 11 11
11х
11х
х
1 11x
1
1 5
[ 22 ; 22 ]
x=
11
х
/
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
1
22
y\
y
5
22
–
+
x
1
11
max
0
1
у ln 1 1 9 0 1 9 8
11
№ 12
8
3
10 х
х
Наибольшее
значение функция
будет принимать в
точке максимума.
Можно сэкономить на
вычислениях
значений функции в
концах отрезка.
lnx
/
1. Найти f
/(x)
13. Найдите наименьшее значение функции
5 7
y = 2х2 – 5x + lnx – 3 на отрезке [
; ]
6 6
1
x
1
4( х 1)( х )
2
1
4
х
5
х
1
4
у / 4х 5
х
х
х
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
x=1
y\
y
5
6
–
7
6
+
x
1
min
0
у 1 2 5 ln 1 3 2 8 6
№12
— 6
3
10 х
х
[
5
6
; 76 ]
Наименьшее
значение функция
будет принимать в
точке минимума.
Можно сэкономить на
вычислениях
значений функции в
концах отрезка.
cosx – sinx
/
14. Найдите наибольшее значение функции
3
; 0
y = 7cosx +16x – 2 на отрезке
2
у 7 sin х 16
/
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
0
7 sin х 16 0
16
sin х
7
т.к. sin х [ 1;1]
Функция на всей области
определения возрастает.
Нетрудно догадаться,
что у / > 0.
Тогда наибольшее
значение функция будет
иметь в правом конце
отрезка, т.е. в точке х=0.
3
3
3
у
7 cos
16
2 24 2
2
2
2
у 0 7 cos 0 16 0 2 7 2 5
№ 12
5
3
10 х
х
Если вы не догадались,
то вычислите значения
функции в каждом конце
отрезка и выберите
наибольшее.
sinx cosx
15. Найдите наибольшее значение функции
/
y = 10sinx –
у 10 cos х
/
1. Найти f
/(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
10 cos х
36
36
36
5
; 0
x + 7 на отрезке
6
Критических точек нет.
Тогда наибольшее
значение функция будет
принимать в одном из
концов отрезка.
36
cos х
10
т.к. cos х [ 1;1]
Можно было и раньше
догадаться, что
наибольшее значение
будет именно в левом
конце отрезка!
Как?
1
5
5 36 5
у
10 sin
7 10 30 7 32
2
6
6 6
Синус –нечетная функция
0
Формула приведения
5
5
1
у 0 sin
10 sin
7 7 № sin
0 0
sin
sin
12 3 2
6
6
6
3
10 х
х
6
2
cosx – sinx
16. Найдите наименьшее значение функции
Найдите наименьшее значение функции
/
у / 5 sin x 6
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
3
у
2
y = 5cosx – 6x + 4 на отрезке
5 sin x 6 0
6
sin х
5
т.к. sin х [ 1;1]
0
3
5 cos
2
3
6
2
у 0 5 cos 0 0 4 9
№ 12
9
3
10 х
Функция на всей области
определения убывает.
Нетрудно догадаться, что
у / < 0.
Тогда наименьшее
значение функция будет
иметь в правом конце
отрезка, т.е. в точке х=0.
4 9 4
1
х
3
2 ; 0
Если вы не догадались,
то вычислите значения
функции в каждом конце
отрезка и выберите
наименьшее.
17. Найдите наибольшее значение функции
y = 12cosx + 6 3 x – 2 3 + 6 на отрезке 0 ;
2
1. Найти f /(x)
у / 12 sin x 6 3
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
12 sin x 6 3 0
3
sin х
2
х ( 1)
n
3
3
n
Но нам не нужны ВСЕ
у 12 cos 6 3 2 3 6
12
стационарные
точки.
3
3
3
Необходимо сделать выбор тех
значений, которые попадут в
заданный отрезок
у 12 cos 6 3 2 3 6 6 3 0 ;
2
2
2
у 0 12 cos 0 6 3 0 2 3 6 18 2 3
№ 12
1 2
3
10 х
х
2
17. Найдите наибольшее значение функции
y = 12cosx + 6 3 x – 2 3 + 6 на отрезке 0 ;
2
1. Найти f /(x)
у / 12 sin x 6 3
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
12 sin x 6 3 0
y\
y
0
3
sin х
2
+
3
–
max
2
x
3
Убедимся, что данная точка
является точкой максимума на
заданном промежутке.
Значит, наибольшее значение
функция достигает именно в этой
точке.
Тогда значения функции в концах
отрезка можно не считать.
у 12 cos 6 3 2 3 6 12
3
3
3
№ 12
1 2
3
10 х
х
18. Найдите наименьшее значение функции
7 3
14 3
7 3
y = 11 +
–
х–
cosx на отрезке 0 ;
2
18
3
3
1. Найти f /(x)
Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
y\
y
0
–
7 3 14 3
у
sin x
6
3
3
7 3 14 3
sin x 0
3
3
Можно убедиться, что данная
1
n
точка
является
точкой
х ( 1)
минимума
n
sin x
на заданном промежутке.
6
2
/
+
6 min
2
x
Значит, наименьшее значение
функция
достигает
именно в этой
Но нам не
нужны ВСЕ
точке.
стационарные точки.
Тогда
значения
функции
в концах
Необходимо
сделать
выбор
тех
отрезка
можно
не считать.
значений,
которые
попадут в
заданный отрезок
7 3 7 3 14 3
у 11
cos 11 7 4
18
18
3
6
6
№ 12
4
0 ; 2
3
10 х
х
tgx
/
19. Найдите наименьшее значение функции
1
cos2x y = 4tgx – 4x – + 5 на отрезке 4 ; 4
1. Найти f /(x)
2. Найти
Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
1
у 4
4
2
cos x
/
4
0
4
4 0
2
cos x
cos 2 x 1
Нам не нужны ВСЕ
у 4 5 1
4
у 4 5 9 2
4
у 0 0 0 5 5
4
стационарные точки.
Необходимо сделать выбор тех
значений, которые попадут в
3. Вычислим
значения функции
заданный
отрезок
в критических точках
;
и на концах отрезка.
4 4
4. Из вычисленных значений
сделаем выбор наименьшего.
№ 12
1
3
10 х
х
tgx
/
20. Найдите наибольшее значение функции
1
2
cos x y = 3tgx – 3x + 5 на отрезке 4 ; 0
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
1
у 3
3
2
cos x
/
0
3
3 0
2
cos x
cos 2 x 1
4
Нам не нужны ВСЕ
3. Вычислим значения функции в критическихстационарные
точках и на концах
точки.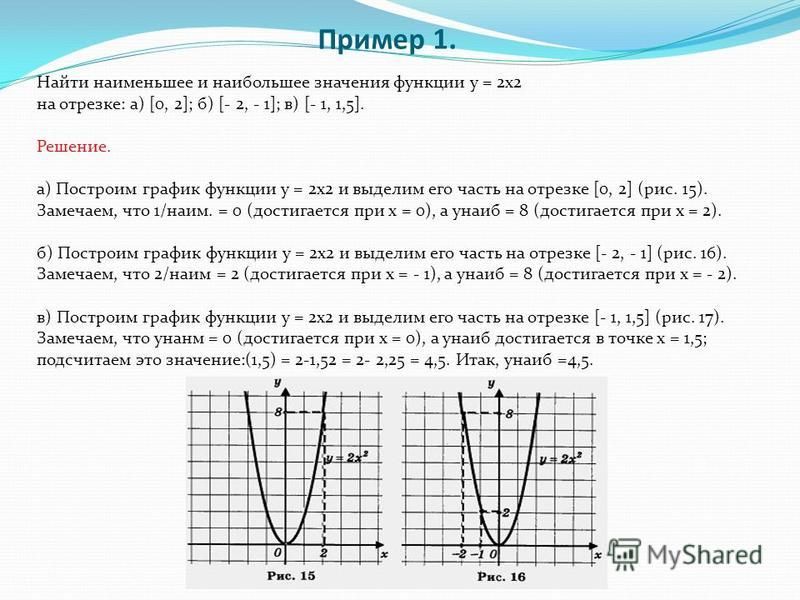 отрезка.
отрезка.
Необходимо сделать выбор тех
4. Из вычисленных значений сделаем выбор наибольшего.
значений, которые попадут в
-1
заданный отрезок
3 4 ; 0 3
у 3tg 3 5 3
5 2
4
4
4 0 4 4
у 0 3tg0 0 5 5
№12
5
3
10 х
х
Нахождение точек
минимума (min)
и максимума (max)
функции
Алгоритм нахождения точек
экстремума:
1.Найти производную функции.
2.Решить уравнение f ´(х)=0, и найти тем самым
стационарные точки.
3.Методом интервалов установить промежутки
знакопостоянства производной.
4.Если при переходе через точку х0:
— производная не меняет знак, то х0 – точка перегиба;
— производная меняет знак с «+» на «-», то х0 точка
максимума;
— производная меняет знак с «-» на «+», то х0 точка
минимума.
№1 Найдите точку максимума функции
y x 48x 17
3
y 3x 48
2
1.
y ‘ ( x) 0 3x 2 48 0
2
Решение.
3( x 2 16) 0 : 3
( x 2 16) 0
( x 4)( x 4) 0 ( x 4) 0 или ( x 4) 0 x 4 или x 4
3.
4.
xmax 4
№12
—
4
3
10 х
х
Наибольшее и наименьшее значение функции на отрезке
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Начнем с того, что на практике наибольший интерес применение производной представляет для нахождения наибольшего и наименьшего значений заданной функции.
При этом наибольшее и наименьшее значения заданной функции, как правило, разыскивается на некотором интервале, который является или всей областью определения заданной функции или ее некоторой частью. Различают несколько видов рассматриваемых интервалов:
- отрезок $[a;b]$;
- открытый интервал: $(a;b),(a;b],[a;b)$;
- бесконечный промежуток $(-\infty ;a),(-\infty ;a],(a;+\infty ),[a;+\infty ),(-\infty ;+\infty )$.

Функция $y=f(x)$, определенная и непрерывная на некотором отрезке, достигает на данном отрезке своих наибольшего и наименьшего значений.
Определение 1
Наибольшее значение заданной функции $y=f(x)$ на некотором промежутке $X$ — это такое значение функции, для которого выполняется неравенство $\forall x\in X,x\ne x_{0} :\, \, f(x)\le f(x_{0} )$. Обозначается следующим образом: $\mathop{\max }\limits_{x\in X} y=f(x_{0} )$.
Определение 2
Наименьшее значение заданной функции $y=f(x)$ на некотором промежутке $X$ — это такое значение функции, для которого выполняется неравенство $\forall x\in X,x\ne x_{0} :\, \, f(x)\ge f(x_{0} )$. Обозначается следующим образом: $\mathop{\min }\limits_{x\in X} y=f(x_{0} )$.
Другими словами:
- наибольшее значение заданной функции $y=f(x)$ — это самое большое значение, принимаемое на рассматриваемом интервале при $x=x_{0} $;
- наименьшее значение заданной функции $y=f(x)$ — это самое маленькое значение, принимаемое на рассматриваемом интервале при $x=x_{0} $.
 {2} +4=16+4=20\]
{2} +4=16+4=20\]- Вывод:
Наибольшее значение заданной функции на отрезке $[-1;2]$: $y(2)=20$.
Наименьшее значение заданной функции на отрезке $[-1;2]$: $y(0)=y(-1)=4$.
Алгоритм нахождения наибольшего и наименьшего значения заданной функции на некотором открытом или бесконечном интервале:
- нахождение области определения заданной функции, проверка, является ли в рассматриваемый интервал подмножеством области определения;
- нахождение критических точек, содержащихся в рассматриваемом интервале;
- нахождение стационарных точек, содержащихся в рассматриваемом интервале;
- вычисление значений заданной функции в стационарных точках и в критических точках.
- выбор наибольшего и наименьшего значений среди вычисленных.
Примечание 1
Вычисление значений заданной функции на концах интервала зависит от вида рассматриваемого интервала.
 Если рассматриваемый интервал имеет вид:
Если рассматриваемый интервал имеет вид:$[a;b)$, то вычисляются значение заданной функции в точке $x=a$ и односторонний предел $\mathop{\lim }\limits_{x\to b-0} f(x)$; $(a;b]$, то вычисляются значение заданной функции в точке $x=b$ и односторонний предел $\mathop{\lim }\limits_{x\to a+0} f(x)$; $(a;b)$, то вычисляются односторонние пределы $\mathop{\lim }\limits_{x\to a+0} f(x)$ и $\mathop{\lim }\limits_{x\to b-0} f(x)$; $[a;+\infty )$, то вычисляются значение заданной функции в точке $x=a$ и предел $\mathop{\lim }\limits_{x\to +\infty } f(x)$; $(a;+\infty )$, то вычисляются односторонний предел $\mathop{\lim }\limits_{x\to a+0} f(x)$ и предел $\mathop{\lim }\limits_{x\to +\infty } f(x)$; $(-\infty ;b]$, то вычисляются значение заданной функции в точке $x=b$ и предел $\mathop{\lim }\limits_{x\to -\infty } f(x)$; $(-\infty ;b)$, то вычисляются односторонний предел $\mathop{\lim }\limits_{x\to b-0} f(x)$ и предел $\mathop{\lim }\limits_{x\to -\infty } f(x)$; $(-\infty ;+\infty )$, то вычисляются пределы $\mathop{\lim }\limits_{x\to +\infty } f(x)$ и $\mathop{\lim }\limits_{x\to -\infty } f(x)$.
{2} } $.
Производная не существует в точке $x=2$ (критическая точка).
- нахождение стационарных точек, содержащихся в рассматриваемом интервале;
Производная не обращается в ноль, следовательно, стационарных точек нет.
- вычисление значений заданной функции в стационарных точках и в критических точках.
Нет вычислений, так как точки отсутствуют.
- вычисление значений заданной функции на концах интервала;
\[y(3)=\frac{4}{3-2} =\frac{4}{1} =4\] \[\mathop{\lim }\limits_{x\to +\infty } \frac{4}{x-2} =\mathop{\lim }\limits_{x\to +\infty } \frac{4/x}{1-2/x} =\frac{0}{1-0} =0\]
- выбор наибольшего и наименьшего значений среди вычисленных.
Наибольшее значение заданной функции на интервале $[3;+\infty )$: $y(3)=4$.
Наименьшее значение заданной функции на интервале $[3;+\infty )$: $y(+\infty )=0$.
Пример 5
Найти наименьшее и наибольшее значения заданной функции: $y=e^{x} $ на интервале $(-\infty ;+\infty )$.
 {+\infty } } =\frac{1}{+\infty } =0\]
{+\infty } } =\frac{1}{+\infty } =0\]- выбор наибольшего и наименьшего значений среди вычисленных.
Наименьшее значение заданной функции на интервале $(-\infty ;+\infty )$: $y(-\infty )=0$.
Наибольшего значения нет.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 17.02.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Наибольшее и наименьшее значение функции (22 слайда)
Слайд 1
Наибольшее и наименьшее значение функции
Открытый банк заданий по математике http://mathege. ru:8080/or/ege/Main.action
ru:8080/or/ege/Main.action Слайд 2
a
b
a
b
Предположим, что функция f не имеет на отрезке [а; b] критических точек. Тогда она возрастает (рис. 1) или убывает (рис. 2) на этом отрезке. Значит, наибольшее и наименьшее значения функции f на отрезке [а; b] — это значения в концах а и b.
функция возрастает
функция убываетСлайд 3
a
b
a
b
Пусть теперь функция f имеет на отрезке [а; b] конечное число критических точек. Наибольшее и наименьшее значения функция f может принимать в критических точках функции или в точках а и b. Чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.
ПримерыСлайд 4
Этапы
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
3. Вычислить значения функции в критических точках и на концах отрезка.
4. Из вычисленных значений выбрать наименьшее или наибольшее
Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4]
1) y / = 3×2 – 27
2) y / = 3×2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
3) y(0) = 0
1.Слайд 5
Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4]
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наименьшее из полученных значений.
1) y(0) = 0
2) y / = 3×2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
Значения функции в критических точках, которые принадлежат заданному отрезку.
Выполнение этапов решения можно изменить, как вам удобно.Слайд 6
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наибольшее из полученных значений.
1) y(0) = 4
2) y / = 3×2 – 3 = 3(x2 – 1) = 3(x – 1)(x + 1)
Значения функции в критических точках, которые принадлежат заданному отрезку.
Найдите наибольшее значение функции y = x3 – 3x + 4 на отрезке [– 2; 0]
2.Слайд 7
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наименьшее из полученных значений.
1) y(1) = 1 – 2 + 1 + 3 = 3
y(4) = 43– 2 42 + 4 + 3 = 39
2) y / = 3×2 – 4x + 1=
y(1) = 3
Значения функции в критических точках, которые принадлежат заданному отрезку.
Найдите наименьшее значение функции y = x3 – 2×2 + x +3 на отрезке [ 1; 4 ]
3.
3×2 – 4x + 1 = 0
D=16–4*3*1=4Слайд 8
Найдите наибольшее значение функции на отрезке [ -3; 3 ]
4.
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наибольшее из полученных значений.
y(-3) = 11
Значения функции в критических точках, которые принадлежат заданному отрезку.
y(-3) = -25Слайд 9
Найдите наибольшее значение функции на отрезке [ 1; 9 ]
5.
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наибольшее из полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.Слайд 10
Найдите наименьшее значение функции на отрезке [ 1; 9 ]
6.
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наименьшее из полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.Слайд 11
Найдите наименьшее значение функции на отрезке [-10; 1 ]
7.
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наименьшее из полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.Слайд 12
Найдите наименьшее значение функции на отрезке [-10; 1 ]
7.
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наименьшее из полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.
Слайд 13
Найдите наибольшее значение функции на отрезке [ 1; 9 ]
8.
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наибольшее из полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.
Запишем функцию в удобном для дифференцирования видеСлайд 14
Найдите наибольшее значение функции y = 7cosx +16x – 2 на отрезке
9.
Функция на всей области определения возрастает. Нетрудно догадаться, что у / > 0. Тогда наибольшее значение функция будет иметь в правом конце отрезка, т.е. в точке х=0.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
Если вы не догадались, то вычислите значения функции в каждом конце отрезка и выберите наибольшее.
0Слайд 15
Критических точек нет. Тогда наибольшее значение функция будет принимать в одном из концов отрезка.

Можно было и раньше догадаться, что наибольшее значение будет именно в левом конце отрезка! Как?
Найдите наибольшее значение функции y = 10sinx – x + 7 на отрезке
10.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
0Слайд 16
Функция на всей области определения убывает. Нетрудно догадаться, что у / Найдите наименьшее значение функции y = 5cosx – 6x + 4 на отрезке
16.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
1
0
Если вы не догадались, то вычислите значения функции в каждом конце отрезка и выберите наименьшее.Слайд 17
Найдите наибольшее значение функции y = 12cosx + 6 x – 2 + 6 на отрезке
11.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.Слайд 18
Найдите наибольшее значение функции y = 12cosx + 6 x – 2 + 6 на отрезке
12.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
Убедимся, что данная точка является точкой максимума на заданном промежутке. Значит, наибольшее значение функция достигает именно в этой точке. Тогда значения функции в концах отрезка можно не считать.
Можно рассуждать иначе
maxСлайд 19
Найдите наименьшее значение функции y = 11 + – х – cosx на отрезке
13.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
Можно убедиться, что данная точка является точкой минимума на заданном промежутке. Значит, наименьшее значение функция достигает именно в этой точке. Тогда значения функции в концах отрезка можно не считать.
minСлайд 20
Найдите наименьшее значение функции y = 4tgx – 4x – + 5 на отрезке
14.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
0Слайд 21
Найдите наибольшее значение функции y = 3tgx – 3x + 5 на отрезке
15.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
0
-1
0Слайд 22
При использовании материалов сайта необходимо сделать ссылку на сайт http://le-savchen.ucoz.ru
Максимум функции Калькулятор
Поиск инструмента
Поиск инструмента в dCode по ключевым словам:
Просмотр полного списка инструментов dCodeМаксимум функции
Инструмент для определения максимального значения функции: максимальное значение, которое может принимать функция. Это глобальный максимум, а не локальный максимум.
Результаты
Максимум функции — dCode
Теги: Функции
Поделиться
dCode и другие
dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !Калькулятор максимума
Калькулятор минимума
⮞ Перейти к: Минимум функции
Ответы на вопросы (FAQ)
Каково определение максимума функции?
Для любой функции $f$, определенной на интервале $I$, взяв $m$ вещественное число этого интервала, если $f(x) 92 $, определенной над $ \mathbb{R} $, функция достигает своего максимума в $ x=0 $, $ f(x=0) = 0 $ и $ f(x)
максимум функции всегда определяется с интервалом, может быть локальным (между 2-мя значениями) или глобальным: над областью определения функции.

Как вычислить максимум функции?
максимума функции обнаруживаются, когда производная становится равной нулю и меняет знак (переходит через 0 с положительной стороны на отрицательную). 9- $. Тогда глобальный экстремум функции равен $1$ при $x=0$.
Как рассчитать локальный максимум на интервале?
Добавьте одно или несколько ограничений, указывающих условия для каждой переменной.
Пример: Найти максимум $ \cos{x} $ для $ -\pi
Указать dCode несколько уравнений с оператором && (логическое И) для разделения уравнений
Что такое экстремум?
Экстремум — это название, данное экстремальному значению функции, значению, которое может быть максимальным ( максимум функции ) или минимум (минимум функции).
Что такое мажоранта функции?
Мажоранта — это любое значение, большее или равное максимальному значению, достигнутому функцией.

Каков максимум постоянной функции?
Постоянная функция $f(x)=c$ является прямой и всегда равна $c$, поэтому ее максимум $c$ достигается при любом значении $x$
Каков максимум аффинной функции ?
Аффинная функция $ f (x) = ax + b $ — это прямая, которая всегда имеет максимум $ +\infty $ 92 + bx + c $ then
— Если $ a
— Если $ a > 0 $, максимум $ f $ равен $ +\infty $, когда $ x $ стремится к $ +\infty $ исходный код. За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Максимальная функция», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Максимальная функций» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанных на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т.
 д.) и все данные загрузка, сценарий или доступ к API для «Максимальной функции» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
д.) и все данные загрузка, сценарий или доступ к API для «Максимальной функции» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.Цитировать dCode
Копирование и вставка страницы «Максимум функции» или любых ее результатов разрешено, если вы цитируете dCode!
Цитировать как источник (библиографию):
Максимум функции на dCode.fr [онлайн-сайт], получено 07 октября 2022 г., https://www.dcode.fr/maximum-functionСводка
- Калькулятор максимума
- Калькулятор минимума
- Каково определение максимума функции?
- Как вычислить максимум функции?
- Как рассчитать локальный максимум на интервале?
- Что такое экстремум?
- Что такое мажоранта функции?
- Каков максимум постоянной функции?
- Каков максимум аффинной функции?
- Каков максимум полиномиальной функции 2-й степени?
Похожие страницы
- Минимум функции
- Производная
- Экстремум функции
- Stationary Point of a Function
- Period of a Function
- Reciprocal Function
- Newton Interpolating Polynomial
- DCODE’S TOOLS LIST
Support
- Paypal
- Patreon
- More
Forum/Help
Ключевые слова
максимум,максимум,функция,производная,калькулятор,минимум,экстремум,найти
Ссылки
▲
Локальный максимум и минимум, нахождение локального максимума и минимума
LearnPracticeDownload
Локальные максимум и минимум — это точки функций, которые дают максимальный и минимальный диапазон.
 Локальные максимумы и локальные минимумы можно вычислить, найдя производную функции. Тест первой производной и тест второй производной являются двумя важными методами нахождения локального максимума и локального минимума.
Локальные максимумы и локальные минимумы можно вычислить, найдя производную функции. Тест первой производной и тест второй производной являются двумя важными методами нахождения локального максимума и локального минимума.Давайте узнаем больше о том, как найти локальный максимум и минимум, как найти локальный максимум и минимум, а также о примерах локального максимума и минимума.
1. Что такое локальный максимум и минимум? 2. Методы поиска локального максимума и минимума 3. Важные условия для местного максимума и минимума 4. Примеры локальных максимумов и минимумов 5. Практические вопросы 6. Часто задаваемые вопросы о локальном максимуме и минимуме Что такое локальный максимум и минимум?
Локальные максимумы и минимумы — это входные значения, для которых функция выдает максимальное и минимальное выходные значения соответственно.
 Функциональное уравнение или графики недостаточно полезны для нахождения точек локальных максимумов и локальных минимумов. Производная функции очень полезна при нахождении локального максимума и локального минимума функции.
Функциональное уравнение или графики недостаточно полезны для нахождения точек локальных максимумов и локальных минимумов. Производная функции очень полезна при нахождении локального максимума и локального минимума функции.Рассмотрим функцию f(x). Входное значение \(x_1\), для которого \(f(x_1)\) > 0, называется локальным максимумом, а \(f(x_1)\) — локальным максимальным значением, а входное значение \( x_1\), для которых \(f(x_2)\) < 0, называется локальным минимумом, а \(f(x_2)\) - локальным минимальным значением. Локальный максимум и минимум рассчитываются только для определенного интервала и не применяются ко всему диапазону функции.
методов поиска локального максимума и минимума
Локальный максимум и минимум можно определить, взяв производную от заданной функции. Проверка первой производной и проверка второй производной полезны для нахождения локального максимума и минимума. Давайте разберемся подробнее в каждом из этих тестов.
Проверка первой производной
Проверка первой производной помогает найти поворотные точки, в которых выход функции имеет максимальное или минимальное значение.
 Для теста первой производной. определим функцию f(x) на открытом интервале I. Пусть функция f(x) непрерывна в критической точке c интервала I. Здесь мы имеем следующие условия для отождествления локального максимума и минимума от первой производной тест.
Для теста первой производной. определим функцию f(x) на открытом интервале I. Пусть функция f(x) непрерывна в критической точке c интервала I. Здесь мы имеем следующие условия для отождествления локального максимума и минимума от первой производной тест.- Если f ′(x) меняет знак с положительного на отрицательный по мере увеличения x через c, т. е. если f ′(x) > 0 в каждой точке, достаточно близкой к c и слева от нее, и f ′(x) < 0 в каждой точке, достаточно близкой и правее от c, то c является точкой локальных максимумов.
- Если f ′(x) меняет знак с отрицательного на положительный по мере увеличения x через c, т. е. если f ′(x) < 0 в каждой точке, достаточно близкой к c и слева от нее, и f ′(x) > 0 в каждой точке, достаточно близкой и правее от c, то c является точкой локального минимума.
- Если f ′(x) существенно не меняется при увеличении x через c, то c не является ни точкой локальных максимумов, ни точкой локальных минимумов. Фактически такая точка называется точкой перегиба.

Следующие шаги помогут выполнить тест первой производной и найти предельные точки.
- Найдите первую производную заданной функции и найдите предельные точки, приравняв выражение первой производной к нулю.
- Найдите по одной точке на соседней левой стороне и соседней правой стороне предельной точки и подставьте эти соседние точки в функции первой производной.
- Если для соседней точки слева производная функции положительна, а для соседней точки справа отрицательна, то предельной точкой являются локальные максимумы.
- Если производная функции отрицательна для соседней точки слева, а положительна для соседней точки справа, то предельной точкой являются локальные минимумы.
Проверка второй производной
Проверка второй производной — это систематический метод нахождения абсолютного максимума и абсолютного минимума значения функции с действительным знаком, заданной на замкнутом или ограниченном интервале. Здесь мы рассматриваем дважды дифференцируемую функцию f(x), определенную на отрезке I, и точку x=k, принадлежащую этому отрезку (I).
 Здесь у нас есть следующие условия для определения локального максимума и минимума из теста второй производной.
Здесь у нас есть следующие условия для определения локального максимума и минимума из теста второй производной.- x = k, является точкой локальных максимумов, если f'(k) = 0 и f»(k) < 0. Точка при x = k является локальным максимумом, а f(k) называется локальное максимальное значение f(x).
- x = k является точкой локальных минимумов, если f'(k) = 0 и f»(k) >0 . Точка при x = k является локальным минимумом, а f(k) называется локальным минимальным значением f(x).
- Тест не пройден, если f'(k) = 0 и f»(k) = 0. А точка x = k называется точкой перегиба.
Следующая последовательность шагов облегчает проверку второй производной, чтобы найти локальные максимумы и локальные минимумы функции с действительным знаком.
- Найти первую производную f'(x) функции f(x) и приравнять первую производную к нулю f'(x) = 0, к предельным точкам \(x_1, x_2\).
- Найдите вторую производную функции f»(x) и подставьте предельные точки во вторую производную\(f»(x_1), f»(x_2)\).
 .
. - Если вторая производная больше нуля\(f»(x_1) > 0\), то предельная точка \((x_1)\) является локальным минимумом.
- Если вторая производная меньше нуля \(f»(x_2)<0\), то предельной точкой \((x_2)\) являются локальные максимумы.
Важные условия для местного максимума и минимума
Следующие важные термины полезны для лучшего понимания локальных максимумов и минимумов.
- Максимум: Максимальное входное значение x, при котором функция f(x) имеет максимальный выход, называется максимумом функции. Обычно он определяется в пределах интервала и также называется локальным максимумом.
- Абсолютный максимум: Абсолютный максимум — это точка x во всем диапазоне функции f(x), в которой она имеет максимальное значение. Абсолютный максимум также иногда называют глобальным максимумом.
- Минимум: Минимальное входное значение x, при котором функция f(x) имеет минимальный выход, называется минимумом функции.
 Обычно он определяется в пределах интервала и также называется локальным минимумом.
Обычно он определяется в пределах интервала и также называется локальным минимумом. - Абсолютный минимум: Абсолютный минимум — это точка x во всем диапазоне функции f(x), в которой она имеет минимальное значение. Абсолютный минимум также иногда называют глобальным минимумом.
- Точка инверсии: Значение x в области определения f(x), которая не является ни локальным максимумом, ни локальным минимумом, называется точкой инверсии. Точки в непосредственной близости слева и справа от точки инверсии имеют нулевой наклон.
- Максимальное значение: Выход, полученный функцией f(x) при подстановке значения точки локального максимума вместо x, называется максимальным значением функции. Это максимальное значение функции во всем диапазоне функции.
- Минимальное значение: Выход, полученный функцией f(x) при подстановке значения точки локального минимума вместо x, называется минимальным значением функции.
 Это минимальное значение функции во всем диапазоне функции.
Это минимальное значение функции во всем диапазоне функции. - Теорема об экстремальном значении: Для функции f, заданной на отрезке [a, b] и непрерывной на этом отрезке, существуют точки c, d на интервале [a, b], в которых эта функция f достигает максимального и минимального значения. ф(с) > ф(х) > ф(д).
Связанные темы
Следующие темы помогают лучше понять локальный максимум и минимум.
- Производная формула
- Дифференциация
- Теорема о среднем значении
- Теорема Ролля
- Формула дифференциальных уравнений
- Применение деривативов
Примеры локального максимума и минимума
Пример 1: Найдите локальные максимумы и локальные минимумы функции f(x) = 2x 3 + 3x 2 — 12x + 5, используя критерий первой производной.
Решение:
Данная функция есть f(x) = 2x 3 + 3x 2 — 12x + 5
f'(x) = 6x 2 6′ 9003 + (х) = 0; 6x 2 — 6x — 12 = 0, 6(x 2 + x — 2) = 0, 6(x — 1)(x + 2) = 0
Следовательно, предельные точки x = 1 и x = -2.

Возьмем точки в непосредственной близости от x = 1. Это точки {0, 2}.
f'(0) = 6(0 2 + 0 — 2) = 6(-2) = -12 и f'(2) = 6(2 2 + 2 — 2) = 6( 4) = +24
Производная функции отрицательна слева от x = 1 и положительна справа. Следовательно, x = 1 — локальные минимумы.
Теперь возьмем точки в непосредственной близости от x = -2. Очки равны {-3, -1}.
f'(-3) = 6((-3) 2 + (-3) — 2) = 6(4) = +24 и f'(-1) = 6((-1) 2 + (-1) -2) = 6(-2) = -12
Производная функции положительна слева от x = -2 и отрицательна справа. Следовательно, x = -2 — локальные максимумы.
Следовательно, локальные максимумы равны -2, а локальные минимумы -1.
Пример 2: Найти локальные максимумы и локальные минимумы функции f(x) = x 3 — 6x 2 +9x + 15. с использованием теста второй производной.
Решение:
Данной функцией является f(x) = x 3 — 6x 2 +9x + 15.

f'(x) = 3x 2 + 90×70 — 12 Пусть us найти нули выражения. f'(x) = 0.
f'(x) = 3(x 2 — 4x + 3)
x 2 — 4x + 3 = 0 или (x — 1)(x — 3) =0.
Здесь х = 1, а х = 3
f»(x) = 6x — 12
f»(1) = 6(1) — 12 = 6 — 12 = -6., f» (1) < 0, а x = 1 — максимумы.
f»(3) = 6(3) — 12 = 18 — 12 = 6, f»(3) > 0, x = 3 — минимумы.
Следовательно, при использовании теста второй производной локальные максимумы равны 1 с максимальным значением f(1) = 19, а локальные минимумы равны 3 с минимальным значением f(3) = 15
перейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по локальному максимуму и минимуму
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о локальном максимуме и минимуме
Как найти локальный минимум и максимум?
Локальный минимум и максимум можно найти, продифференцировав функцию и найдя точки поворота, в которых наклон равен нулю.
 Далее эти поворотные точки можно проверить разными методами, чтобы найти локальный максимум и минимум. Тест первой производной или тест второй производной помогает найти локальный минимум и максимум.
Далее эти поворотные точки можно проверить разными методами, чтобы найти локальный максимум и минимум. Тест первой производной или тест второй производной помогает найти локальный минимум и максимум.В чем разница между локальными максимумами и абсолютными максимумами?
Локальный максимум — это точка внутри интервала, в которой функция имеет максимальное значение. Абсолютные максимумы также называются глобальными максимумами и представляют собой точку во всей области определения данной функции, которая дает максимальное значение функции.
Каково использование локальных максимумов и минимумов?
Локальный максимум и минимум можно использовать для поиска оптимального решения реальной проблемной ситуации, выраженного в виде уравнения. Входные значения, для которых эти выражения имеют максимальный или минимальный результат, могут быть вычислены из локального максимума и минимума.
Математические листы и
Визуальная учебная программаНайти минимальное и максимальное значение в массиве
Сложность: Среда
.
 A[] размера n вам нужно найти максимальный и минимальный элемент, присутствующий в массиве. Ваш алгоритм должен делать минимальное количество сравнений.
A[] размера n вам нужно найти максимальный и минимальный элемент, присутствующий в массиве. Ваш алгоритм должен делать минимальное количество сравнений.Например:
Ввод: A[] = {4, 2, 0, 8, 20, 9, 2}
Вывод: Максимум: 20, Минимум: 0
Ввод: A[] = {-8, -3, -10, -32, -1}
Вывод: Максимум: -1, Минимум: -32
Возможные дополнительные вопросы, которые можно задать интервьюеру: —
- Обязательно ли элементы массива положительны? ( Ответ: Нет, они могут быть положительными, отрицательными или нулевыми)
- Отсортирован ли элемент массива? (Ответ: Нет, они могут быть в любом порядке)
- Может ли массив содержать дубликаты? ( Ответ: Конечно, это возможно.)
Примечание к проблеме: — Интервьюер не будет судить о вашем алгоритме для этого вопроса на основе временной сложности, поскольку все решения имеют временную сложность O(n). Узким местом в этой задаче является количество сравнений, которое требуется вашему алгоритму для определения максимального и минимального элемента.
Решения Вам нужно максимально уменьшить количество сравнений.
Вам нужно максимально уменьшить количество сравнений.- Линейный поиск: увеличение цикла на 1
- Разделяй и властвуй: метод турнира
- Сравнение в парах: увеличение цикла на 2
1. Линейный поиск: увеличение цикла на 1
Мы инициализируем как минимальный, так и максимальный элемент к первому элементу, а затем пройтись по массиву, сравнивая каждый элемент и при необходимости обновляя минимум и максимум.
Псевдокод
int[] getMinMax(int A[], int n) { интервал макс = А [0] интервал мин = А [0] для ( я = 1 до n-1 ) { если (А[i] > макс) макс = А [я] иначе, если ( A[i] < min ) мин = А [я] } // По соглашению пусть ans[0] = максимум и ans[1] = минимум int ans[2] = {макс, мин} возврат ответа }Анализ сложности
На каждом этапе цикла мы делаем 2 сравнения в худшем случае.
 Общее количество сравнений (в худшем случае) = 2*(n-1) = 2n - 2
Общее количество сравнений (в худшем случае) = 2*(n-1) = 2n - 2Временная сложность = O(n), пространственная сложность = O(1)
В лучшем случае всего n-1 сравнений были сделаны. ( Как? )
Критические идеи!
- Мы инициализировали максимум и минимум первым элементом массива - почему?
- Какими будут входные данные в лучшем и худшем случае?
- Как мы можем уменьшить количество сравнений, сделанных здесь?
2. Разделяй и властвуй: метод турнира
Еще один способ сделать это — следовать стратегии разделяй и властвуй. Как и при сортировке слиянием, мы можем разделить массив на две равные части и рекурсивно найти максимум и минимум этих частей. После этого сравните максимум и минимум этих частей, чтобы получить максимум и минимум всего массива.
Шаги решения
- Напишите рекурсивную функцию, принимающую массив и его начальный и конечный индексы в качестве параметров
- Базовые случаи будут
- Если размер массива равен 1, верните элемент как максимальный и минимальный
- Если размер массива равен 2, сравнить два элемента и вернуть максимум и минимум
3.
 Рекурсивная часть равна
Рекурсивная часть равна- Рекурсивно вычислить и сохранить максимум и минимум для левой и правой частей
- Определить максимальное и минимальное значения путем 2 сравнений
4. Вернуть максимальное и минимальное значения.
Псевдокод
int[] findMinMax(int A[], int start, int end) { инт макс; инт мин; если (начало == конец) { макс = А [начало] мин = А [начало] } иначе если (начало + 1 == конец) { если ( А [начало] < А [конец] ) { макс = А[конец] мин = А [начало] } еще { макс = А [начало] мин = А[конец] } } еще { int mid = начало + (конец - начало)/2 int left[] = findMinMax(A, начало, середина) int right[] = findMinMax(A, середина+1, конец) если ( слева [0] > справа [0] ) макс = слева [0] еще макс = справа [0] если ( слева [1] < справа [1] ) мин = слева[1] еще мин = справа[1] } // По соглашению, мы принимаем ans[0] как максимум, а ans[1] как минимум int ans[2] = {макс, мин} возврат ответа }Анализ сложности
Для подсчета количества сравнений, поскольку это рекурсивная функция, определим рекуррентное соотношение:
T(n) = 2 T(n/2) + 2 Т(2) = 1 Т(1) = 0 Мы можем решить это рекуррентное отношение с помощью основного метода/метода рекурсивного дерева.
 если n является степенью числа 2
T(n) = 3n/2 - 2
если n является степенью числа 2
T(n) = 3n/2 - 2 Временная сложность = O(n) и пространственная сложность = O(logn) (для стека рекурсивных вызовов)
Если n является степенью 2, алгоритму требуется ровно 3n/2 –2 сравнения, чтобы найти минимум и максимум. Если это не степень 2, потребуется еще несколько (незначительно).
Критические мысли!
- Как анализировать рекурсию с помощью теоремы мастера и метода дерева рекурсии?
- Как получается, что пространственная сложность равна O(logn)?
- Почему 2 базовых варианта? Что, если мы удалим базовый вариант с размером массива 2?
- Почему при вычислении середины массива предпочтение отдается середине = начало + (конец - начало)/2, а не (начало + конец)/2?
- Можно ли еще уменьшить количество сравнений?
В этом подходе мы выбираем элементы массива парами и обновляем минимальное и максимальное значения.
 Если размер массива нечетный, мы инициализируем первый элемент как min и max, а если он четный, мы сравниваем первые два элемента и соответственно инициализируем min и max.
Если размер массива нечетный, мы инициализируем первый элемент как min и max, а если он четный, мы сравниваем первые два элемента и соответственно инициализируем min и max.Этапы решения
- Создайте максимальную и минимальную переменные.
- Проверить размер массива
- Если нечетно, инициализировать min и max первым элементом
- Если четное, сравните элементы и установите min с меньшим значением, а max с большим значением. элемент большего размера с максимальным значением, при необходимости обновите максимальное значение.
- Сравните меньший элемент с минимумом, при необходимости обновите минимум.
5. Возврат макс. и мин.
Псевдокод
int[] findMinMax(int A[], int n) { инт макс, мин в я если (n нечетно) { макс = А[0] мин = А[0] я = 1 } еще { если (А[0] < А[1]) { макс = А[1] мин = А[0] } еще { макс = А[0] мин = А[1] } я = 2 } в то время как ( я < п ) { если (А[я] < А[я+1]) { если (А[i] < мин) мин = А [я] если (А[i+1] > макс. )
макс = А[я+1]
}
еще
{
если (А[i] > макс)
макс = А [я]
если (А[i+1] < мин)
мин = А[я+1]
}
я = я + 2
}
// По соглашению, мы принимаем ans[0] как максимум, а ans[1] как минимум
int ans[2] = {макс, мин}
возврат ответа
}
)
макс = А[я+1]
}
еще
{
если (А[i] > макс)
макс = А [я]
если (А[i+1] < мин)
мин = А[я+1]
}
я = я + 2
}
// По соглашению, мы принимаем ans[0] как максимум, а ans[1] как минимум
int ans[2] = {макс, мин}
возврат ответа
} Анализ сложности
Временная сложность — O(n), пространственная сложность — O(1).
Для каждой пары всего три сравнения, первое среди элементов пары, а два других с минимальным и максимальным значениями.
Общее количество сравнений:-
- Если n нечетное, 3 * (n-1) / 2
- Если n четное, 1 + 3*(n-2)/2 = 3n/2-2
Критические идеи!
- Почему min и max инициализируются по-разному для массивов четного и нечетного размера?
- Почему увеличение цикла на 2 помогает уменьшить общее количество сравнений?
- Есть ли другой способ решить эту проблему? Считать.



 {2} +4=16+4=20\]
{2} +4=16+4=20\] Если рассматриваемый интервал имеет вид:
Если рассматриваемый интервал имеет вид:
 {+\infty } } =\frac{1}{+\infty } =0\]
{+\infty } } =\frac{1}{+\infty } =0\] ru:8080/or/ege/Main.action
ru:8080/or/ege/Main.action 








 д.) и все данные загрузка, сценарий или доступ к API для «Максимальной функции» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
д.) и все данные загрузка, сценарий или доступ к API для «Максимальной функции» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!  Локальные максимумы и локальные минимумы можно вычислить, найдя производную функции. Тест первой производной и тест второй производной являются двумя важными методами нахождения локального максимума и локального минимума.
Локальные максимумы и локальные минимумы можно вычислить, найдя производную функции. Тест первой производной и тест второй производной являются двумя важными методами нахождения локального максимума и локального минимума. Функциональное уравнение или графики недостаточно полезны для нахождения точек локальных максимумов и локальных минимумов. Производная функции очень полезна при нахождении локального максимума и локального минимума функции.
Функциональное уравнение или графики недостаточно полезны для нахождения точек локальных максимумов и локальных минимумов. Производная функции очень полезна при нахождении локального максимума и локального минимума функции. Для теста первой производной. определим функцию f(x) на открытом интервале I. Пусть функция f(x) непрерывна в критической точке c интервала I. Здесь мы имеем следующие условия для отождествления локального максимума и минимума от первой производной тест.
Для теста первой производной. определим функцию f(x) на открытом интервале I. Пусть функция f(x) непрерывна в критической точке c интервала I. Здесь мы имеем следующие условия для отождествления локального максимума и минимума от первой производной тест.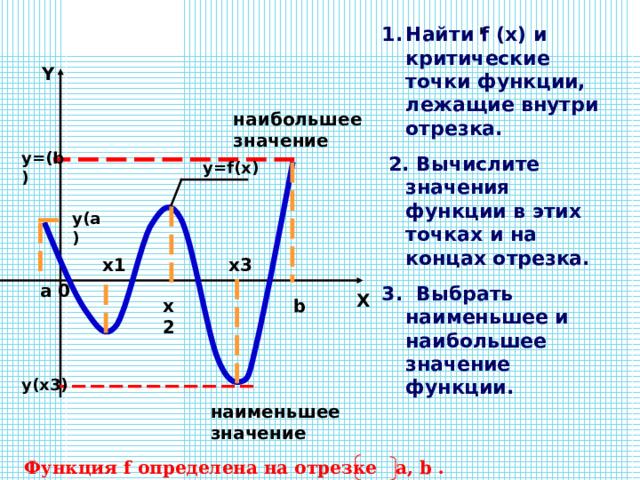
 Здесь у нас есть следующие условия для определения локального максимума и минимума из теста второй производной.
Здесь у нас есть следующие условия для определения локального максимума и минимума из теста второй производной. .
. Обычно он определяется в пределах интервала и также называется локальным минимумом.
Обычно он определяется в пределах интервала и также называется локальным минимумом. Это минимальное значение функции во всем диапазоне функции.
Это минимальное значение функции во всем диапазоне функции.
 Далее эти поворотные точки можно проверить разными методами, чтобы найти локальный максимум и минимум. Тест первой производной или тест второй производной помогает найти локальный минимум и максимум.
Далее эти поворотные точки можно проверить разными методами, чтобы найти локальный максимум и минимум. Тест первой производной или тест второй производной помогает найти локальный минимум и максимум. A[] размера n вам нужно найти максимальный и минимальный элемент, присутствующий в массиве. Ваш алгоритм должен делать минимальное количество сравнений.
A[] размера n вам нужно найти максимальный и минимальный элемент, присутствующий в массиве. Ваш алгоритм должен делать минимальное количество сравнений. Вам нужно максимально уменьшить количество сравнений.
Вам нужно максимально уменьшить количество сравнений. Общее количество сравнений (в худшем случае) = 2*(n-1) = 2n - 2
Общее количество сравнений (в худшем случае) = 2*(n-1) = 2n - 2 Рекурсивная часть равна
Рекурсивная часть равна если n является степенью числа 2
T(n) = 3n/2 - 2
если n является степенью числа 2
T(n) = 3n/2 - 2  Если размер массива нечетный, мы инициализируем первый элемент как min и max, а если он четный, мы сравниваем первые два элемента и соответственно инициализируем min и max.
Если размер массива нечетный, мы инициализируем первый элемент как min и max, а если он четный, мы сравниваем первые два элемента и соответственно инициализируем min и max. )
макс = А[я+1]
}
еще
{
если (А[i] > макс)
макс = А [я]
если (А[i+1] < мин)
мин = А[я+1]
}
я = я + 2
}
// По соглашению, мы принимаем ans[0] как максимум, а ans[1] как минимум
int ans[2] = {макс, мин}
возврат ответа
}
)
макс = А[я+1]
}
еще
{
если (А[i] > макс)
макс = А [я]
если (А[i+1] < мин)
мин = А[я+1]
}
я = я + 2
}
// По соглашению, мы принимаем ans[0] как максимум, а ans[1] как минимум
int ans[2] = {макс, мин}
возврат ответа
} 