Онлайн найти аргумент комплексного числа: Комплексные числа онлайн

Решение высшей математики онлайн

‹— Назад

Рассмотрим на плоскости декартову прямоугольную систему координат . Каждому комплексному числу можно сопоставить точку с координатами , и наоборот, каждой точке с координатами можно сопоставить комплексное число . Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплекные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью.

        Пример 17.3   Изобразим на комплексной плоскости числа , , , , :

Рис.17.1.Изображение комплексных чисел точками плоскости

        

Однако чаще комплексные числа изображают в виде вектора с началом в точке , а именно, комплексное число изображается радиус-вектором точки с координатами . В этом случае изображение комплексных чисел из предыдущего примера будет таким:

Рис.17.2.Изображение комплексных чисел векторами

Отметим, что изображением суммы двух комплексных чисел , является вектор, равный сумме векторов, изображающих числа и . Иными словами, при сложении комплексных чисел складываются и векторы, их изображающие (рис. 17.3).

Рис.17.3.Изображение суммы комплексных чисел

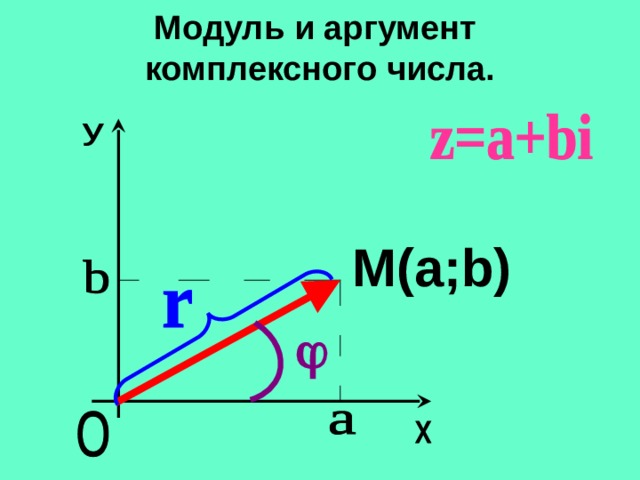
Пусть комплексное число изображается радиус-вектором. Тогда длина этого вектора называется модулем числа и обозначается . Из рисунка 17.4 очевидно, что

(17.6)

Рис.17.4.Модуль и аргумент

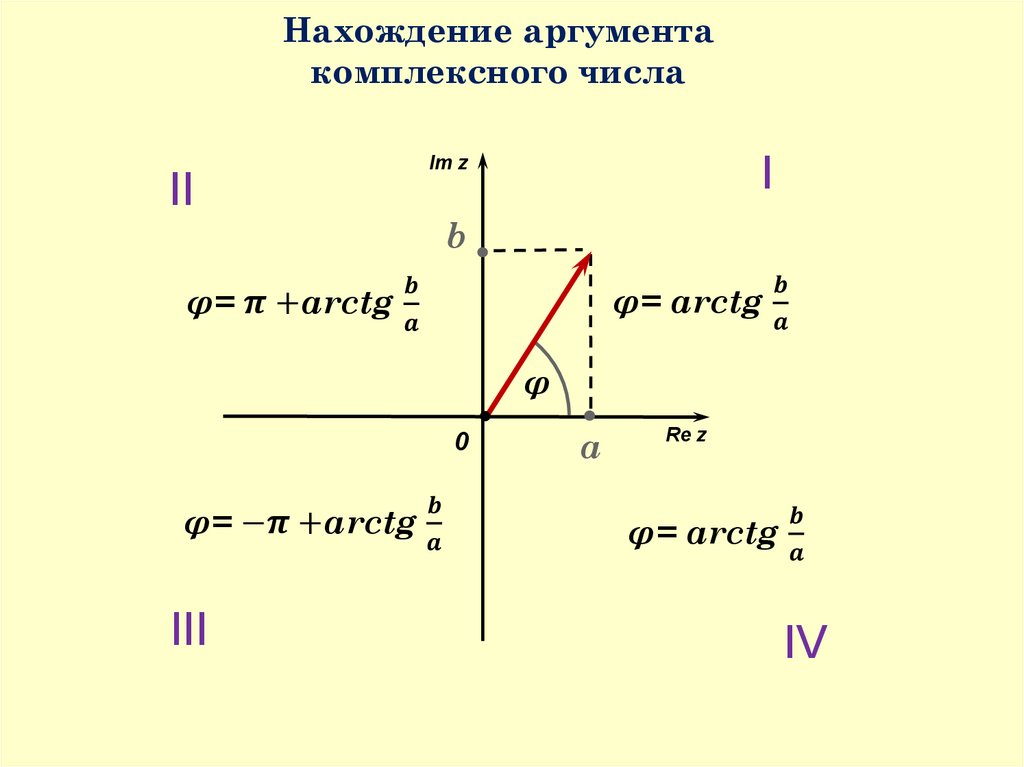
Угол, образованный радиус-вектором числа с осью , называется аргументом числа и обозначается . Аргумент числа определяется не однозначно, а с точностью до числа, кратного . Однако, обычно аргумент указывают в диапазоне от 0 до или в диапазоне от до . Кроме того у числа аргумент не определен.

На рис. 17.4 равен углу . Из того же рисунка очевидно, что

С помощью этого соотношения можно находить аргумент комплексного числа:

или

(17.7)

причем первая формула действует, если изображение числа находится в первой или четвертой четверти, а вторая, если — во второй или третьей. Если , то комплексное число изображается вектором на оси и его аргумент равен или .

Получим еще одну полезную формулу. Пусть . Тогда ,

С учетом формулы (17.6) получим

или

        Пример 17. 4   Найдите модуль и аргумент комплексных чисел: , , , , .

Решение. Запишем числа со строгим указанием действительной и мнимой части:

Тогда по формулам (17.6) и (17.7) находим:

В последнем случае можно вычислить с помощью калькулятора и записать .         

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Комплексные числа Python — complex и операции с ними

Комплексное число — это любое число в форме a + bj , где a и b — действительные числа, а j*j = -1.

В Python есть несколько способов создать такое комплексное число.

• Мы можем напрямую использовать синтаксис a + bj для создания комплексного числа.

>>> a = 4 + 3j
>>> print(a)
(4+3j)
>>> print(type(a))
<class 'complex'>

• Мы также можем использовать complex класс для создания комплексного числа

>>> a = complex(4, 3)
>>> print(type(a))
<class 'complex'>
>>> print(a)
(4+3j)

Реальные и мнимые части в комплексном числе

Каждое комплексное число ( a + bj ) имеет действительную часть (

a ) и мнимую часть ( b ).

Чтобы получить действительную часть, используйте number.real , а для получения мнимой части используйте number.imag .

>>> a
(4+3j)
>>> a. real
4.0
>>> a.imag
3.0

Сопряжение комплексного числа

Сопряжение комплексного числа a + bj определяется как a - bj . Мы также можем использовать number.conjugate() для получения конъюгата.

>>> a
(4 + 3j)
>>> a.conjugate()
(4-3j)

Арифметические операции

Подобно действительным числам, комплексные числа также можно складывать, вычитать, умножать и делить. Давайте посмотрим, как мы могли бы это сделать в Python.

a = 1 + 2j
b = 2 + 4j
print('Addition =', a + b)
print('Subtraction =', a - b)
print('Multiplication =', a * b)
print('Division =', a / b)

Выход:

Addition = (3+6j)
Subtraction = (-1-2j)
Multiplication = (-6+8j)
Division = (2+0j)

ПРИМЕЧАНИЕ. В отличие от действительных чисел, мы не можем сравнивать два комплексных числа. Мы можем сравнивать только их действительную и мнимую части по отдельности, поскольку это действительные числа. Приведенный ниже фрагмент доказывает это.

>>> a
(4+3j)
>>> b
(4+6j)
>>> a < b
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: '<' not supported between instances of 'complex' and 'complex'

Фаза (аргумент)

Мы можем представить комплексное число как вектор, состоящий из двух компонентов на плоскости, состоящей из

real и imaginary осей. Следовательно, две составляющие вектора — это действительная и мнимая части.

Угол между вектором и действительной осью определяется как argument или phase комплексного числа.

Формально это определяется как:

фаза (число) = arctan (мнимая_часть / действительная_часть)

где функция arctan является обратной математической функцией tan.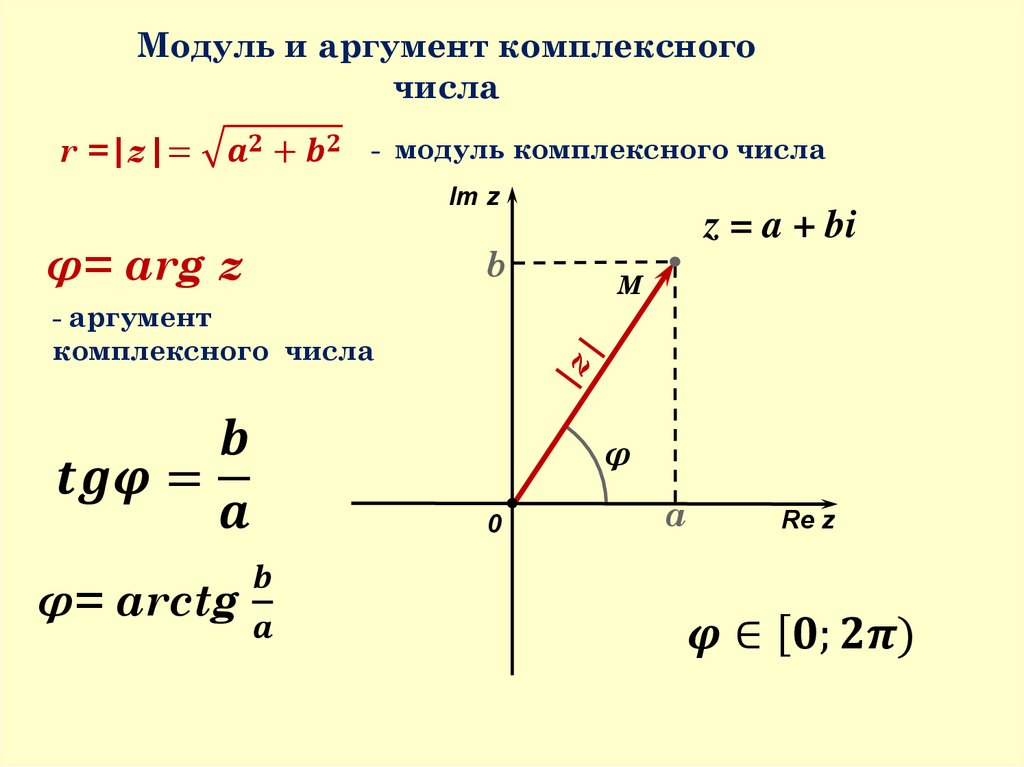

В Python мы можем получить фазу комплексного числа, используя модуль cmath для комплексных чисел. Мы также можем использовать функцию math.arctan и получить фазу из ее математического определения.

import cmath
import math

num = 4 + 3j

# Using cmath module
p = cmath.phase(num)
print('cmath Module:', p)

# Using math module
p = math.atan(num.imag/num.real)
print('Math Module:', p)

Вывод:

cmath Module: 0.6435011087932844
Math Module: 0.6435011087932844

Обратите внимание, что эта функция возвращает фазовый угол в radians , поэтому, если нам нужно преобразовать в degrees , мы можем использовать другую библиотеку, например numpy .

import cmath
import numpy as np

num = 4 + 3j

# Using cmath module
p = cmath. phase(num)
print('cmath Module in Radians:', p)
print('Phase in Degrees:', np.degrees(p))

Вывод:

cmath Module in Radians: 0.6435011087932844
Phase in Degrees: 36.86989764584402

Прямоугольные и полярные координаты

Комплексное число может быть записано в формате прямоугольных или полярных координат с помощью cmath.rect() и cmath.polar() .

>>> import cmath
>>> a = 3 + 4j
>>> polar_coordinates = cmath.polar(a)
>>> print(polar_coordinates)
(5.0, 0.9272952180016122)

>>> modulus = abs(a)
>>> phase = cmath.phase(a)
>>> rect_coordinates = cmath.rect(modulus, phase)
>>> print(rect_coordinates)
(3.0000000000000004+3.9999999999999996j)

Константы в модуле cmath

В модуле cmath есть специальные константы. Некоторые из них перечислены ниже.

print('π =', cmath.pi)
print('e =', cmath.e)
print('tau =', cmath.tau)
print('Positive infinity =', cmath.inf)
print('Positive Complex infinity =', cmath.infj)
print('NaN =', cmath.nan)
print('NaN Complex =', cmath.nanj)

Вывод:

π = 3.141592653589793
e = 2.718281828459045
tau = 6.283185307179586
Positive infinity = inf
Positive Complex infinity = infj
NaN = nan
NaN Complex = nanj

Тригонометрические функции

Тригонометрические функции для комплексного числа также доступны в модуле cmath .

import cmath

a = 3 + 4j

print('Sine:', cmath.sin(a))
print('Cosine:', cmath.cos(a))
print('Tangent:', cmath.tan(a))

print('ArcSin:', cmath.asin(a))
print('ArcCosine:', cmath.acos(a))
print('ArcTan:', cmath. atan(a))

Вывод:

  

  
Sine: (3.853738037919377-27.016813258003936j)
Cosine: (-27.034945603074224-3.8511533348117775j)
Tangent: (-0.0001873462046294784+0.999355987381473j)
ArcSin: (0.6339838656391766+2.305509031243477j)
ArcCosine: (0.9368124611557198-2.305509031243477j)
ArcTan: (1.4483069952314644+0.15899719167999918j)

Гиперболические функции

Подобно тригонометрическим функциям, гиперболические функции для комплексного числа также доступны в модуле cmath .

import cmath

a = 3 + 4j

print('Hyperbolic Sine:', cmath.sinh(a))
print('Hyperbolic Cosine:', cmath.cosh(a))
print('Hyperbolic Tangent:', cmath.tanh(a))

print('Inverse Hyperbolic Sine:', cmath.asinh(a))
print('Inverse Hyperbolic Cosine:', cmath.acosh(a))
print('Inverse Hyperbolic Tangent:', cmath.atanh(a))

Вывод:

Hyperbolic Sine: (-6.
  c = (-13.128783081462158-15.200784463067954j)
log2(c) = (2.321928094887362+1.3378042124509761j)
log10(c) = (0.6989700043360187+0.4027191962733731j)
sqrt(c) = (2+1j)

Другие

Есть несколько разных функций, чтобы проверить, является ли комплексное число конечным, бесконечным или nan . Также есть функция проверки близости двух комплексных чисел.

>>> print(cmath.isfinite(2 + 2j))
True

>>> print(cmath.isfinite(cmath.inf + 2j))
False

>>> print(cmath.isinf(2 + 2j))
False

>>> print(cmath.isinf(cmath.inf + 2j))
True

>>> print(cmath.isinf(cmath.nan + 2j))
False

>>> print(cmath.isnan(2 + 2j))
False

>>> print(cmath.isnan(cmath.inf + 2j))
False

>>> print(cmath.isnan(cmath.nan + 2j))
True

>>> print(cmath.isclose(2+2j, 2.  01+1.9j, rel_tol=0.05))
True

>>> print(cmath.isclose(2+2j, 2.01+1.9j, abs_tol=0.005))
False

тригонометрия — Нахождение аргумента комплексного числа без калькулятора

Задать вопрос

спросил 7 лет, 11 месяцев назад

Изменено 7 лет, 11 месяцев назад

Просмотрено 3к раз

$\begingroup$ 9n$$

Моя идея состояла в том, чтобы вычислить аргумент и абсолютное значение, а затем использовать полярное представление.

Но я думаю, что идея не в том, чтобы использовать калькулятор. Так что я застрял на $$ \arctan \sqrt{3}$$

Если я воспользуюсь калькулятором, чтобы найти это значение, я легко решу это упражнение.

Как рассчитать $ \arctan \sqrt{3}$ без использования калькулятора? Это возможное?

Редактировать

Если возможно, любой общий метод наиболее ценен, так как я уже застрял в следующем упражнении, где я пытаюсь найти аргумент $-3+i$. 92} = 1$$ $$\sin\theta = \frac{y}{r} \ \ , \ \ \cos\theta = \frac{x}{r}$$ $$\sin\theta = \frac{\sqrt{3}}{2} \ \ , \ \ \cos\theta = \frac{1}{2}$$ Здесь и $\sin\theta$, и $\cos\theta$ находятся в 1-м квадранте, поэтому $$\тета = \frac{\pi}{3}$$ $$\operatorname{Arg} z = \frac{\pi}{3}$$

$\endgroup$

тригонометрия — Нахождение аргумента комплексного числа и преобразование в полярную форму

спросил 92}$), что оставило бы меня с $z = 5(\cos\theta+i\sin\theta)$, я просто не уверен, как здесь вывести $\theta$.

В учебнике говорится о двух вещах: $\theta = \arg(z)$ и $\tan\theta = b/a$, не знаю, как это поможет.

• тригонометрия
• комплексные числа

$\endgroup$

1

$\begingroup$

Подсказка: независимо от $|z|$ вы получите $\tan(\theta)=\frac{4}{3}$. Итак, взяв обратное значение, вы получите $\theta$ в радианах.

$\endgroup$

$\begingroup$

В вашем учебнике сказано, что если $z = a+ bi$, то $\tan \theta = \frac{b}{a}$, так что $$\theta = \arctan \frac{b}{a}$$

В вашем случае это $\theta = \arctan \frac{4}{3}$ для $z = 3+ 4i$. Хотя, на самом деле, условность аргумента делает это не таким простым. Статья в Википедии хорошо объясняет вычисление аргумента.

$\endgroup$

$\begingroup$

Это правда, что $\tan\theta=\frac{b}{a}$, но вы должны быть осторожны, потому что $\tan\theta=\tan(\theta+\pi)$. Если $a$ и $b$ оба отрицательны, $\arctan(b/a)$ не даст вам правильного ответа, вы должны сделать $\arctan(b/a)+\pi$ (поскольку $b/ а=(-б)/(-а)$). Вы также должны быть осторожны, если один из $a$ или $b$ отрицателен.

$\endgroup$

$\begingroup$

Для первого квадранта комплексной плоскости мы знаем, что аргумент определяется как: 9{-1}(\frac{b}{a})$

$\endgroup$

$\begingroup$

Вопрос: Пусть $z=a+ib.$ Почему в общем случае верна следующая формула , а не ? $$\mathrm{Arg}(z)=\arctan\left(\frac ba\right)$$

Ответ: Предположим, что $b<0.$

Тогда $Z \text{ лежит в квадранте } 2\;\text{or}\;3.$

Итак, $\;\mathrm{Arg}(z)>\frac{\pi}2\quad\text{or}\quad\mathrm{Arg}( z)<-\frac{\pi}2.$ 92}}\right) \text{ if } b<0.