()
| |
Список функций
| Имя | Описание | |
|---|---|---|
log2(x)
|
логарифм по основанию 2 от x | |
lg(x) или log10(x)
|
логарифм по основанию 10 от x | |
log(x;b)
|
логарифм x по основанию b log(x;3) | |
ln(x)
|
натуральный логарифм (логарифм по основанию e (2. x x
|
экспонента от х (e в степени x) |
sqrt(x)
|
квадратный корень из x | |
sign(x)
|
функция знака: -1 если x<0, 1 если x>0 и 0 если x=0 | |
| Тригонометрические функции | ||
sin(x)
|
синус х | |
cos(x)
|
косинус х | |
tg(x) или
tan(x)
|
тангенс х | |
ctg(x) или
cot(x)
| котангенс х | |
arcsin(x) или
asin(x)
|
арксинус х | |
arccos(x) или
acos(x)
|
арккосинус х | |
arctg(x) или
atan(x)
|
арктангенс х | |
arcctg(x) или
acot(x)
|
арккотангенс х | |
sinh(x) или
sh(x)
|
гиперболический синус х | |
cosh(x) или
ch(x)
|
гиперболический косинус х | |
tanh(x)
th(x)
|
гиперболический тангенс х | |
coth(x) или
cth(x)
| гиперболический котангенс х | |
asinh(x)
|
гиперболический арксинус х | |
acosh(x)
|
гиперболический арккосинус х | |
atanh(x)
|
гиперболический арктангенс х | |
acoth(x)
|
гиперболический арккотангенс х | |
Встроенные константы
| Имя | Описание |
|---|---|
pi
|
Пи = 3,14.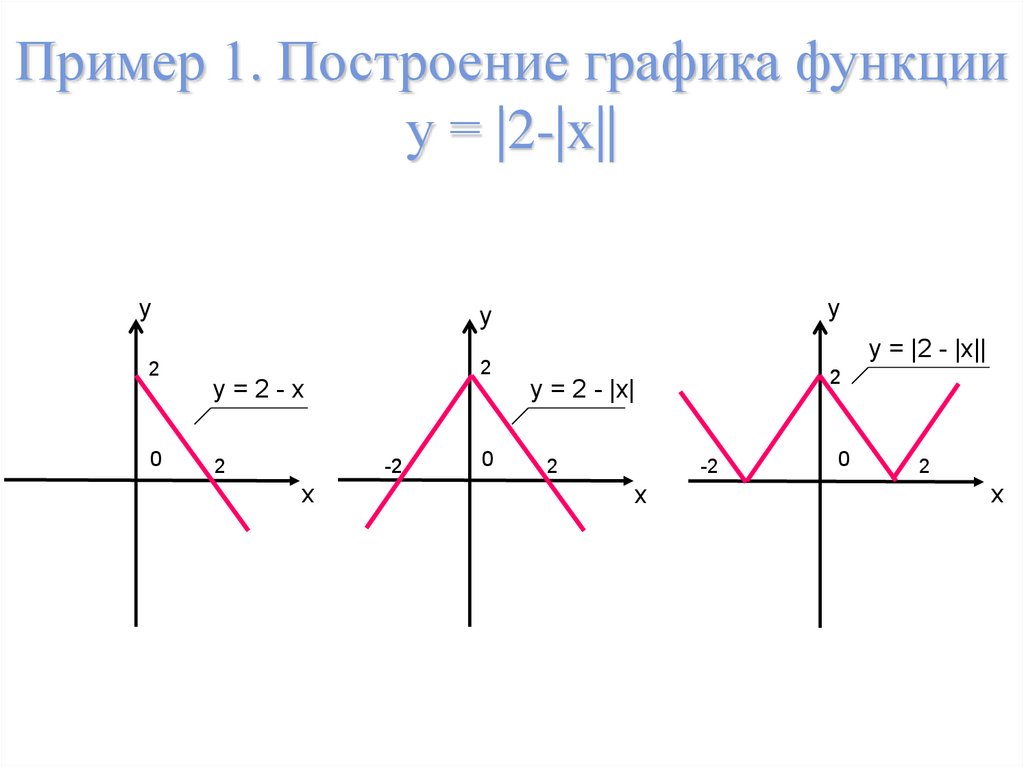 .. ..
|
e
|
e = 2,71828… число Эйлера |
График функции 1 ч. Строим график функций онлайн
Интернет
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция.
На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака «=».
- Нажмите кнопку «Построить график» .
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком.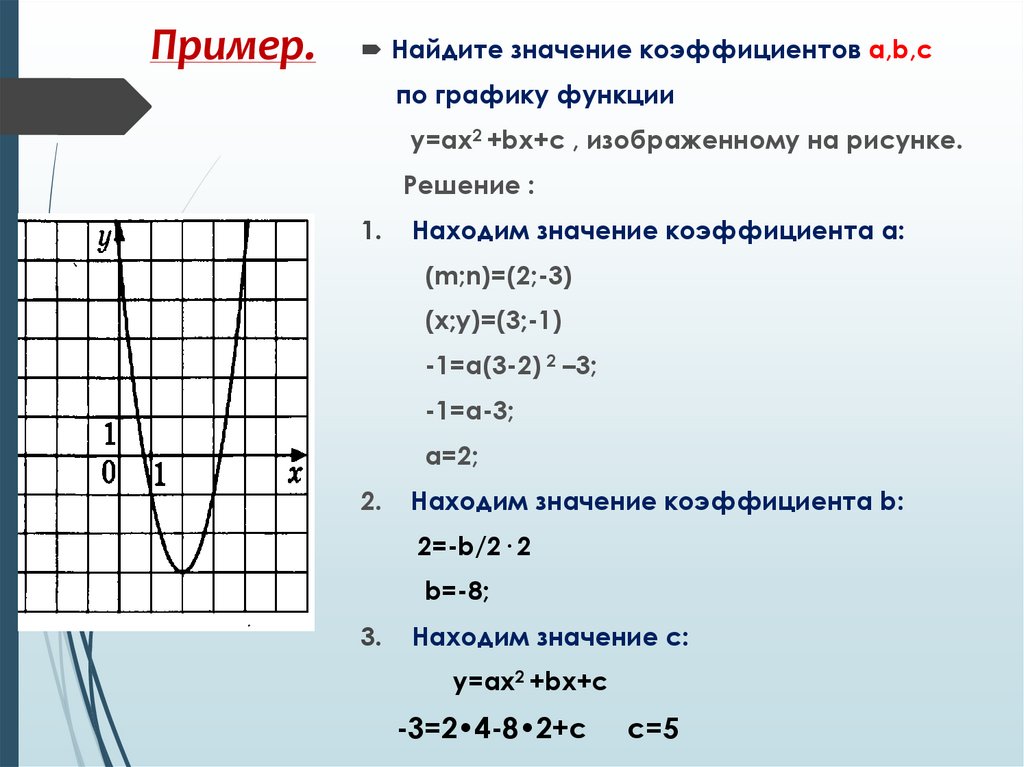 Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить» .
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:» .
- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.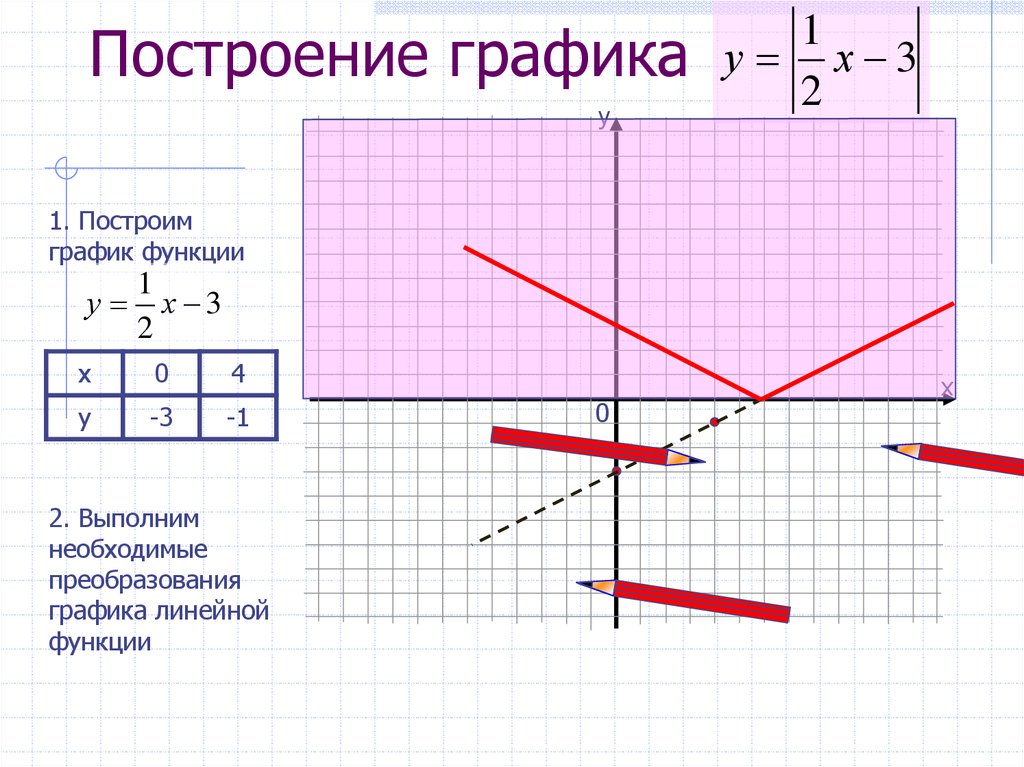
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x).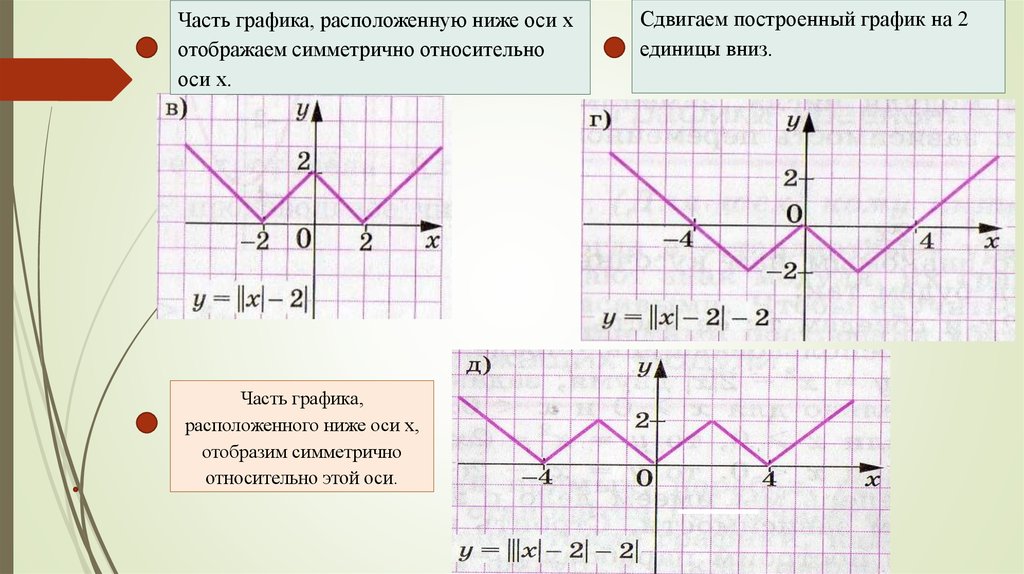 Значит, графики таких функций симметричны относительно оси 0y.
Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
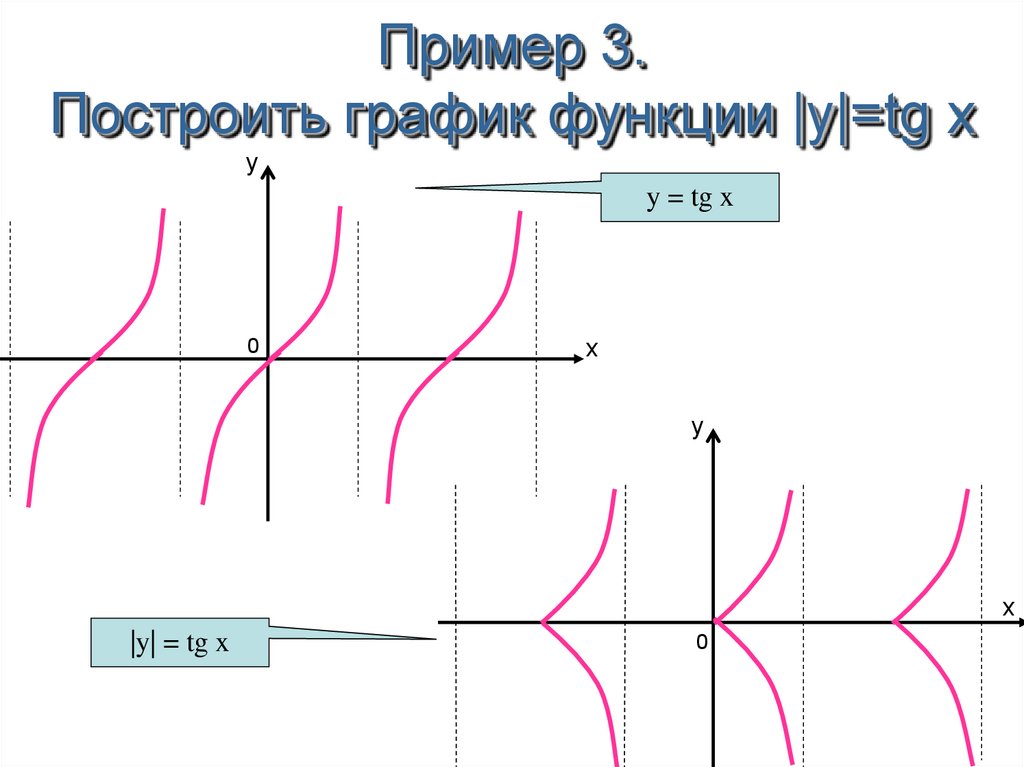
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
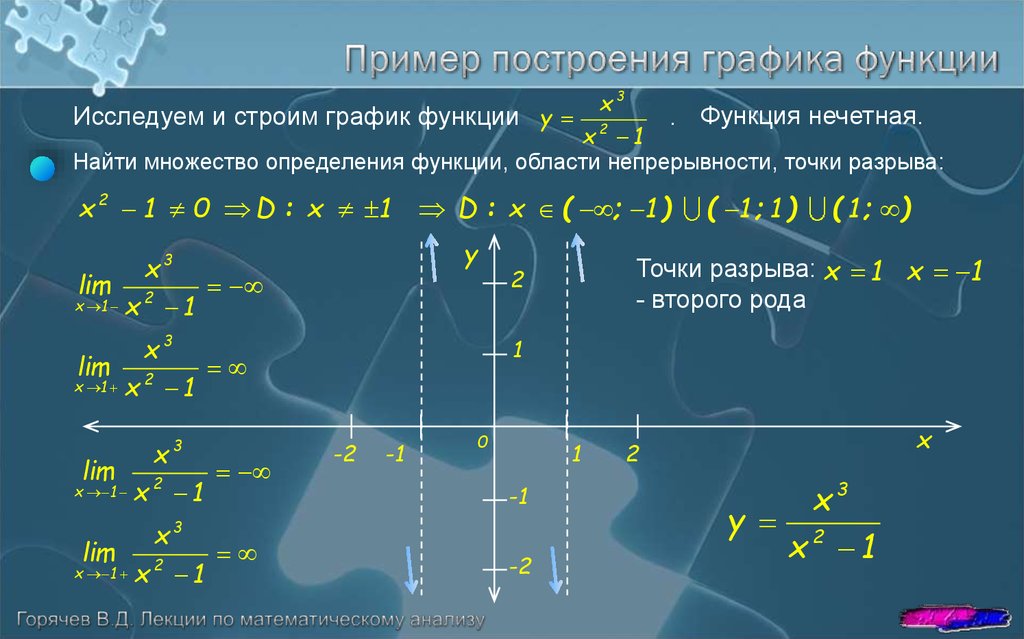
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11) .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus.ru
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
- Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.

Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
Как построить график функции?
Графические функции — это способ создания кривой, представляющей функцию на координатной плоскости. Если функция представлена графиком, то каждая точка на кривой удовлетворяет уравнению функции. График функции часто является полезным методом представления отношения моделей функций, и попытка манипулировать математическим выражением для функции может пролить свет на свойства функции. Многие существенные явления можно моделировать, используя функции, представленные в виде выражений.
Шаги для построения графика функции
При построении графика функции мы предпринимаем следующие шаги:
Найдите область определения и диапазон функции и держите их в уме при построении кривой.
Найдите и начертите точки пересечения x и y.
Определите, есть ли отверстия.
Найдите асимптоты по вертикали, горизонтали и наклону и нарисуйте пунктирные линии, чтобы разбить график по этим линиям и убедиться, что график их не касается.
Создайте таблицу значений, взяв несколько случайных значений x (по обе стороны от точки пересечения x и по обе стороны от вертикальной асимптоты) и вычислив соответствующие значения y.
Нанесите точки из таблицы и соедините их, используя асимптоты, домен и диапазон.

Построение графика базовой функции
График базовой функции
Основная концепция построения графиков функций
Если возможно, определите форму. Если это линейная функция вида f(x) = ax+b, ее график представляет собой линию; если это квадратичная функция вида . Его график представляет собой параболу.
нахождение на нем некоторых точек путем подстановки некоторых случайных значений x и нахождение соответствующих значений y путем подстановки каждого значения в функцию
Например,
В этом разделе представлены семь основных функций, которые будут использоваться на протяжении всего курса. Точки построения используются для построения графика каждой функции. Имейте в виду, что f(x)=y, поэтому f(x) и y могут использоваться взаимозаменяемо.
Постоянная функция — это любая функция вида f(x)=c, где c может быть любым действительным числом. Постоянные функции линейны и имеют вид f(x)=0x+c. Из этой формы ясно, что наклон равен 0, а точка пересечения с осью y равна (0, c). c получается путем вычисления любого значения x, например, x=2.
Постоянные функции линейны и имеют вид f(x)=0x+c. Из этой формы ясно, что наклон равен 0, а точка пересечения с осью y равна (0, c). c получается путем вычисления любого значения x, например, x=2.
График постоянной функции представляет собой горизонтальную линию. Домен состоит из всех действительных чисел R, а диапазон состоит из одного значения c.
Идентификация функций с помощью графиков
Мы будем использовать два теста для идентификации функций с помощью графиков. Если горизонтальная линия пересекает кривую более одного раза в какой-то точке, кривая не имеет обратной функции. Короче говоря, если у вас есть кривая, тест вертикальной линии определяет, является ли она функцией, а тест горизонтальной линии определяет, является ли функция, обратная этой кривой.
Тест вертикальной линии
Тест вертикальной линии можно использовать для определения того, представляет ли график функцию. Вертикальная линия соединяет все точки с одинаковым значением x. Значение y точки на графике, где вертикальная линия пересекает его, представляет выход для этого входного значения x. Если какая-либо вертикальная линия пересекает график более одного раза, график не определяет функцию, поскольку это значение x имеет более одного выхода. Для каждого входного значения функция выдает только одно выходное значение.
Значение y точки на графике, где вертикальная линия пересекает его, представляет выход для этого входного значения x. Если какая-либо вертикальная линия пересекает график более одного раза, график не определяет функцию, поскольку это значение x имеет более одного выхода. Для каждого входного значения функция выдает только одно выходное значение.
Если, с другой стороны, вертикальная линия пересекает график более одного раза, это указывает на то, что одно значение x связано с более чем одним значением y. Это условие приводит к тому, что отношение «дисквалифицируется» или не рассматривается как функция.
Тест горизонтальной линии
После того, как мы определили, что график определяет функцию, мы можем использовать тест горизонтальной линии, чтобы увидеть, является ли она однозначной функцией. Проведите горизонтальные линии поперек графика. Горизонтальная линия соединяет все точки с одинаковым значением y. Вход для этого выходного значения y является значением x точки, где вертикальная линия пересекает функцию. Если какая-либо горизонтальная линия пересекает график более одного раза, график не представляет функцию, поскольку это значение y имеет более одного входа.
Если какая-либо горизонтальная линия пересекает график более одного раза, график не представляет функцию, поскольку это значение y имеет более одного входа.
Использование теста горизонтальной линии
Для x R графики f(x) = x 2 + 1 и f(x) = 2x – 1 показаны ниже.
Заключение
В этой статье мы делаем вывод, что процесс рисования графика соответствующей функции известен как графическое отображение функций. График функции чрезвычайно полезен. Мы можем не всегда знать выражение для функции, но мы знаем некоторые ее значения, возможно, из эксперимента. График может дать нам хорошее представление о том, какую функцию можно использовать для решения задачи. А для идентификации функций с помощью графиков мы выполним тест вертикальной линии, который определяет, является ли кривая функцией, а тест горизонтальной линии определяет, является ли обратная кривая функцией.
Создание графика с помощью словаря в Python
Предварительное условие — графики
Чтобы нарисовать график с использованием встроенных библиотек — построение графика в Python
В этой статье мы увидим, как реализовать график в Python с использованием словарной структуры данных в Python.
Ключи используемого словаря — это узлы нашего графа, а соответствующие значения — это списки с каждым из узлов, которые соединяются ребром.
Этот простой граф имеет шесть узлов (a–f) и пять дуг:
а -> в б -> в б -> е с -> а с -> б с -> г с -> е г -> с е -> с e -> b
Это может быть представлено следующей структурой данных Python. Это словарь, ключами которого являются узлы графа. Для каждого ключа соответствующим значением является список, содержащий узлы, соединенные прямой дугой с этим узлом.
график = { "а" : ["с"],
«б» : [«в», «е»],
"с": ["а", "б", "г", "е"],
"Округ Колумбия"],
«е» : [«с», «б»],
"ф": []
} Графическое представление приведенного выше примера:
defaultdict: Обычно словарь Python выдает KeyError, если вы пытаетесь получить элемент с ключом, которого в данный момент нет в словаре. defaultdict позволяет, если ключ не найден в словаре, вместо выдачи KeyError создается новая запись. Тип этой новой записи задается аргументом defaultdict.
Тип этой новой записи задается аргументом defaultdict.
Функция Python для создания графика:
# определение функции
def generate_edges (график):
края = []
# для каждого узла в графе
для узла в графе:
# для каждого соседнего узла одного узла
для соседа в графе [узел]:
# если ребро существует, то добавить
ребра.append((узел, сосед))
ребра возврата Рекомендуется: сначала попробуйте свой подход на {IDE} , прежде чем переходить к решению.
Implementation:
Python3
|
Output
[('а', 'с'), ('б', 'с'), ('б', 'д'), ('с', 'г'),
('с', 'е'), ('с', 'а'), ('с', 'б'), ('е', 'б'),
('e', 'c'), ('d', 'c')] Поскольку мы взяли пример с неориентированным графом, то у нас дважды выводится одно и то же ребро, скажем, как ('a','c') и («в», «а»). Мы можем преодолеть это с помощью ориентированного графа.
Мы можем преодолеть это с помощью ориентированного графа.
Ниже приведены еще несколько программ на графах на питоне:
Чтобы сгенерировать путь от одного узла к другому :
Используя словарь Python, мы можем найти путь от одного узла к другому в графе. Идея аналогична DFS в графах.
В функции изначально путь представляет собой пустой список. В начале, если начальный узел совпадает с конечным узлом, функция вернет путь. В противном случае код идет вперед и обращается ко всем значениям начального узла и ищет путь, используя рекурсию.
Python3
|
Output
['d', 'a', 'c']
Программа для генерации всех возможных путей от одного узла к другому. :
:
В обсуждаемой выше программе мы сгенерировали первый возможный путь. Теперь давайте сгенерируем все возможные пути от начального узла к конечному узлу. Основное функционирование работает так же, как функционирование приведенного выше кода. Место, где возникает разница, заключается в том, что вместо мгновенного возврата первого пути он сохраняет этот путь в списке с именем «пути» в примере, приведенном ниже. Наконец, после перебора всех возможных путей он возвращает список путей. Если пути от начального узла к конечному узлу нет, возвращается None.
Implementation:
Python3
'E' ], 9000 36' ], ' ' |
9097 9. 'г', 'а', 'в']] Программа для создания кратчайшего пути. : Чтобы добраться до кратчайшего из всех путей, мы используем немного другой подход, как показано ниже. При этом, когда мы получаем путь от начального узла к конечному узлу, мы сравниваем длину пути с переменной с именем как кратчайший, которая инициализируется значением «Нет». Если длина сгенерированного пути меньше длины кратчайшего, если кратчайший не равен None, вновь сгенерированный путь устанавливается как значение кратчайшего. Implementation: Вывод Эта статья предоставлена Shivam Pradhan (anuj_charm) и Rishabh Bansal . Опять же, если пути нет, возвращается None
Опять же, если пути нет, возвращается None Python3
graph = { 'a' :[ 'c' ], 'b' :[ 'd' ], 'c' :[ 'e' ], 'd' :[ а , 'd' ], 'e' :[ 'b' , 'c' ] } def find_shortest_path(graph, start, end, path = []): path = path + [start] if start = = end: return path shortest = None for node in График [Start]: IF Узел Не в Путь: 0138 newpath = find_shortest_path(graph, node, end, path) if newpath: if not shortest or len (новый путь) < len (кратчайший): кратчайший = новый путь0003 return shortest print (find_shortest_path(graph, 'd' , 'c' )) ['d', 'a', 'c']

 append(v)
append(v) 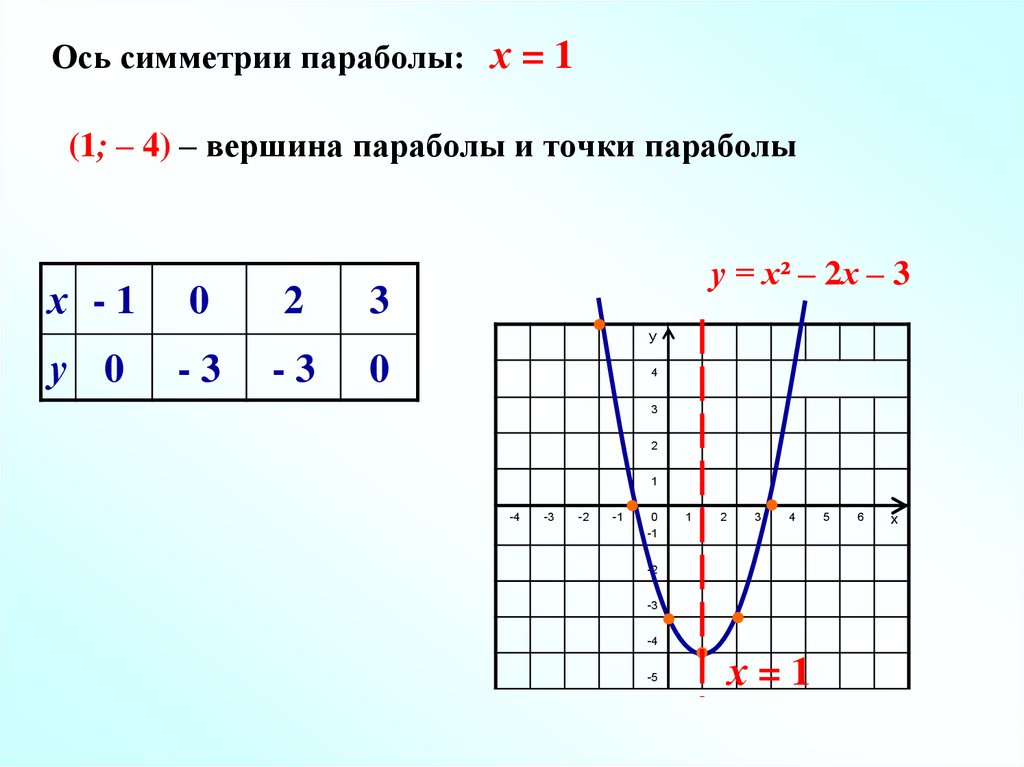 append((node, neighbour))
append((node, neighbour)) 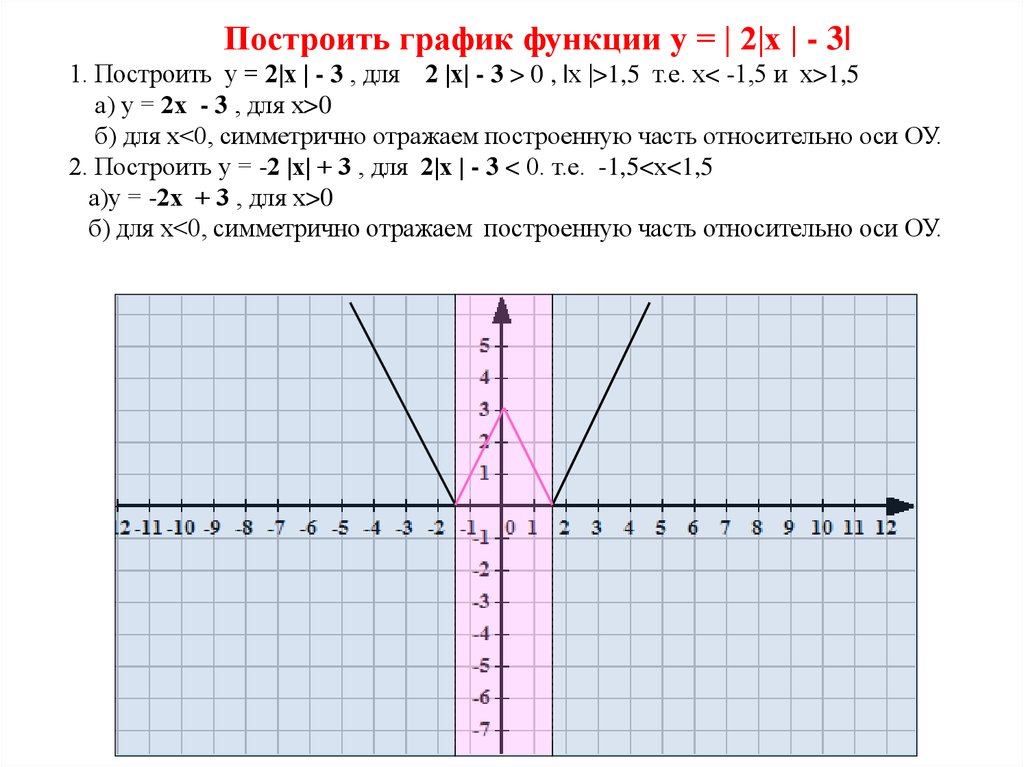 0137 ],
0137 ], 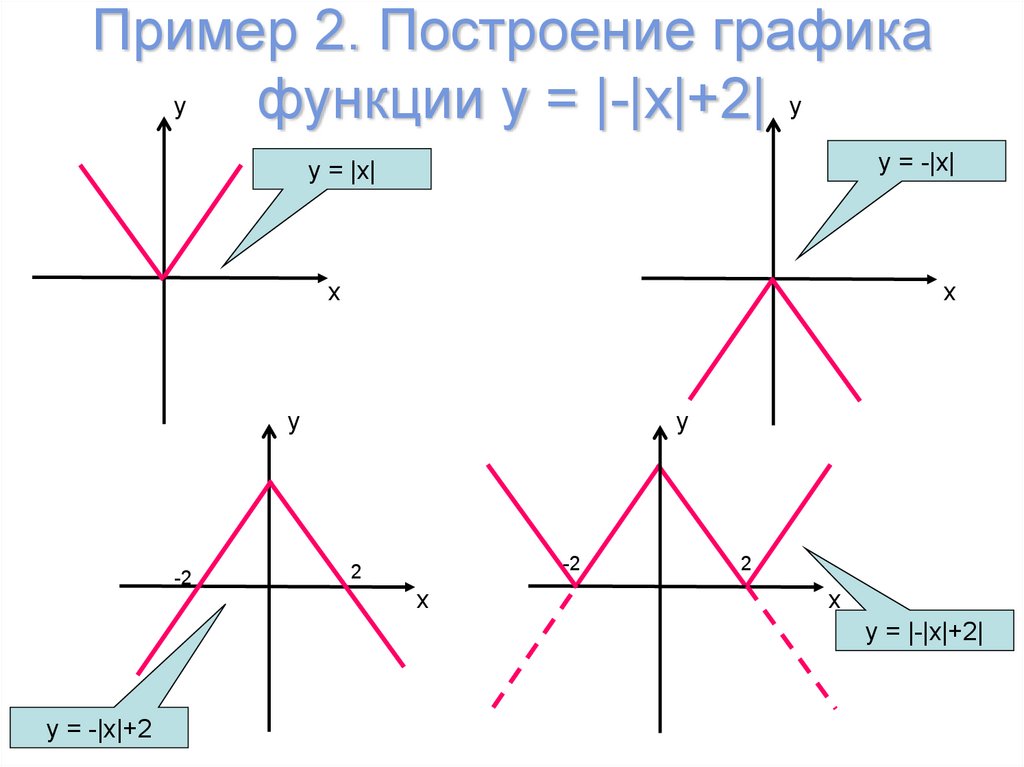 0138
0138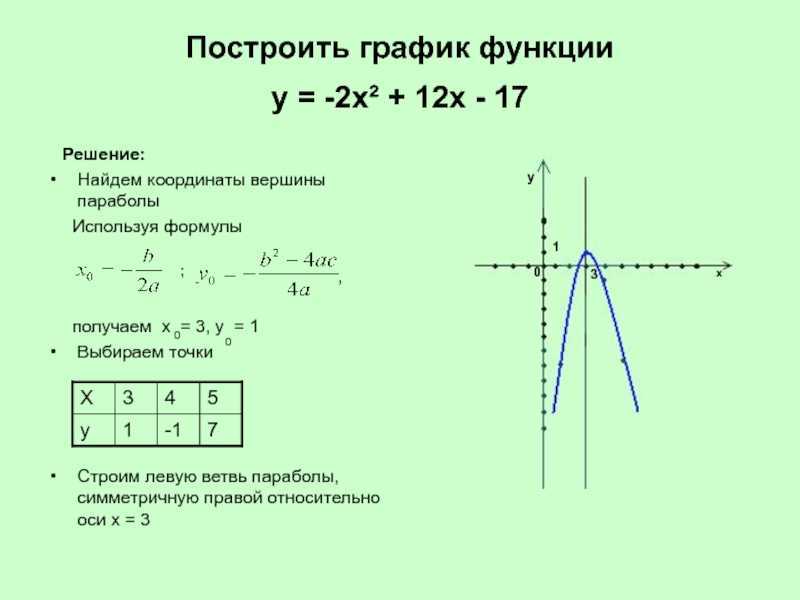
 append(newpath)
append(newpath)