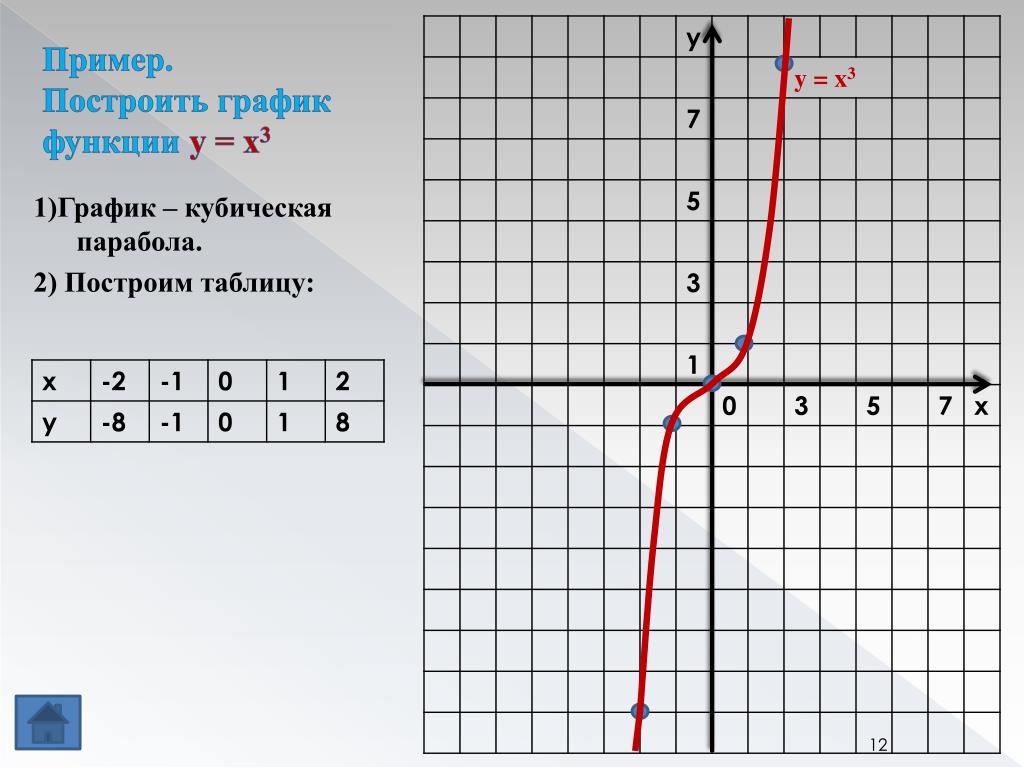
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x).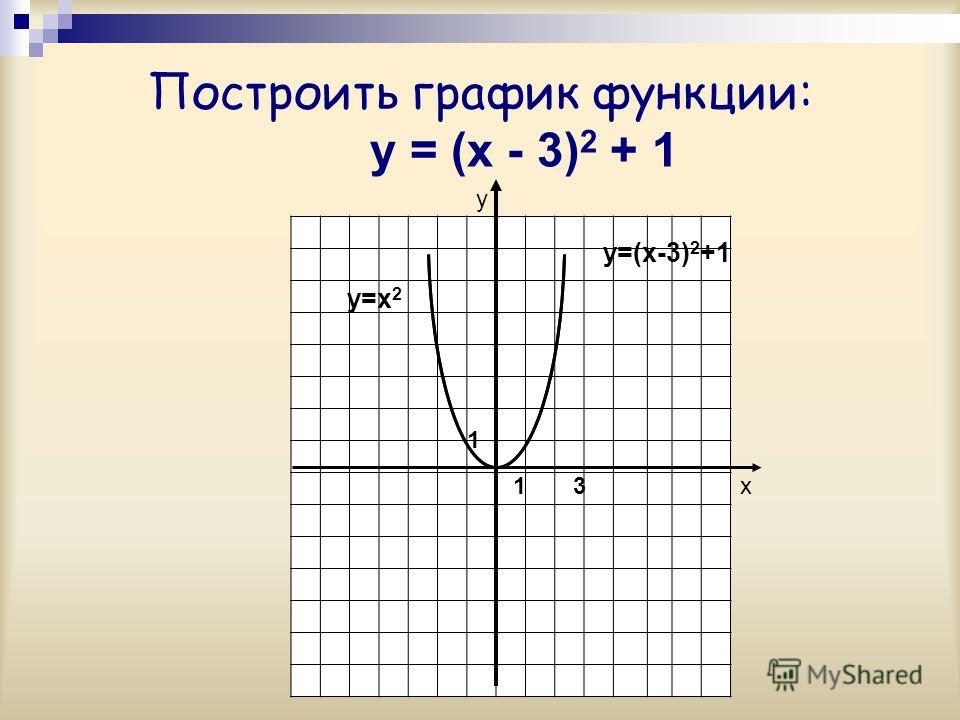
Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11) .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Разберем как строить график с модулем.
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞).
На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=— (x-3)-(— (x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.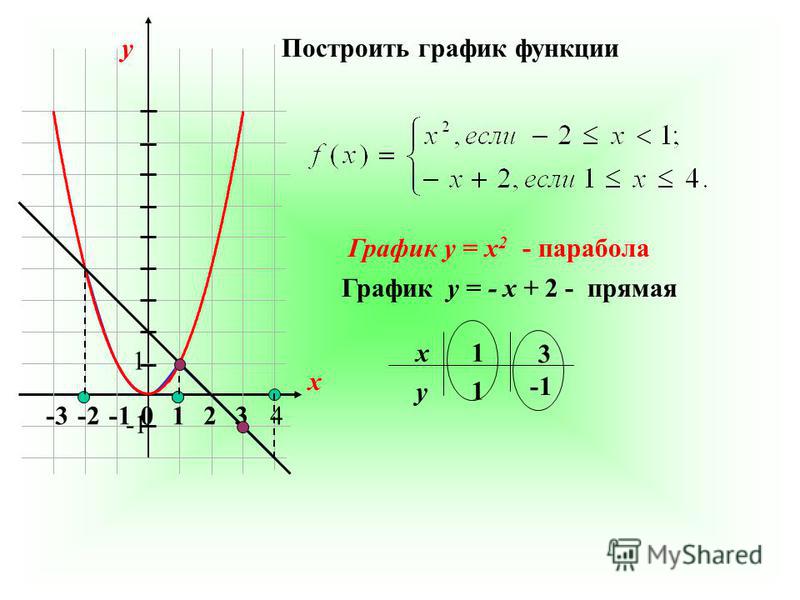
y=— (x-3)-(+ (x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+ (x-3)-(+ (x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.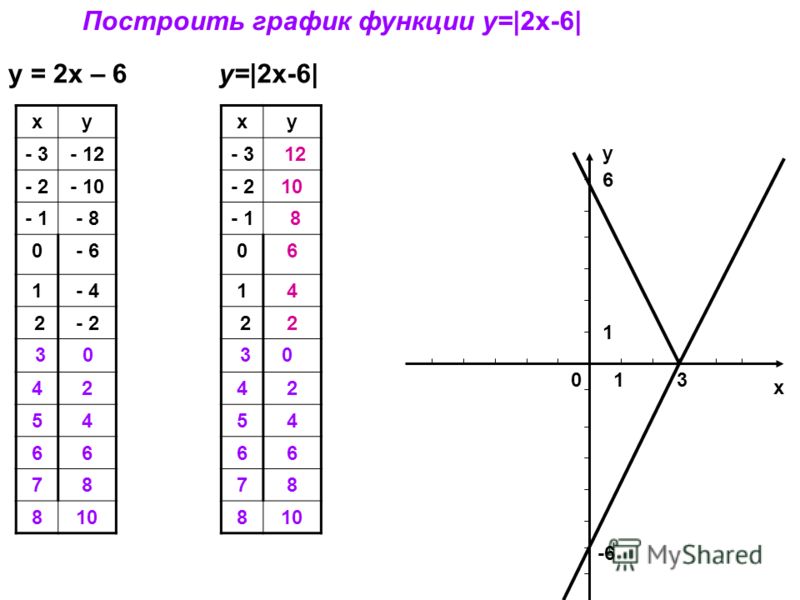
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.
Ответ: при k принадлежащей интервалу (-∞;-2)U и возрастает на промежутке }
Какая точка является решением Y 3x − 1? – Обзоры Вики
Ответ: Решения y = 3x — 1 равны (1, 2) и (0, -1) Мы подставим координату x и координату y в уравнение y = 3x — 1, чтобы проверить, являются ли данные точки решением уравнения.
Отсюда, каковы точки пересечения линии y =- 3x 1? Координаты x и y являются значениями точек на линии y = 3x – 1.) 2) Определите m (наклон) и b (отрезок y). Наклон равен 3, что также можно записать как 3/1. Чай y-перехват равен -1.
3×1 решено? Это одна из самых печально известных нерешенных загадок в мире. Премии предлагались за ее решение более сорока лет, но никто полностью и успешно не решил ее [5]. Задача 3X+1 была численно проверена для большого диапазона значений n.
Является ли y 3x 1 пропорциональным отношением? Определите, показывает ли уравнение y = 3x пропорциональную зависимость.
Объяснять. Да уравнение пропорциональное потому что отношения равны.
Является ли y 3x 1 линейной функцией?
Каков наклон прямой, параллельной прямой y 3x 1? y = -3x+1 имеет наклон -3. Поскольку параллельные линии имеют одинаковые наклоны, новая линия также будет иметь наклон -3.
Как найти точку пересечения Y 1 3x? Объедините 13 1 3 и xx. Перепишите в форме пересечения наклона. Используя форму пересечения наклона, y-пересечение равно 0 .
Почему 3×1 невозможно?
Умножьте на 3 и прибавьте 1. От полученного четного числа разделите наибольшую степень числа 2, чтобы получить новое нечетное число T(x). Если вы продолжите повторять эту операцию, достигнете ли вы в конце концов 1, независимо от того, с какого нечетного числа вы начали? Проще говоря, эта проблема остается нерешенным.
Также возможно ли 3×1? Гипотеза 3x+1 утверждает, что, начиная с любого положительного целого числа n, повторная итерация этой функции в конечном итоге дает значение 1. Гипотезу 3x+1 легко сформулировать, но, по-видимому, ее трудно решить.
Кто изобрел 3х1?
Каково бы ни было ее точное происхождение, проблема 3x + 1 определенно была известна математическому сообществу к началу 1950-х годов; был обнаружен в 1952 г. B. Туэйтс [69].
Как построить график y 3×5?
Как Y 2x 3 выглядит на графике?
Как найти пропорциональную зависимость на графике? Если график зависимости это линия или луч, проходящий через начало координат, то оно пропорционально.
Если это линия или луч, не проходящий через начало координат, то он не пропорционален. Кроме того, если оно нелинейно, то оно и не пропорционально.
Как найти пропорциональные отношения? Вы можете сказать, показывает ли таблица пропорциональные отношения путем вычисления отношения каждой пары значений. Если все эти отношения одинаковы, в таблице показано пропорциональное соотношение.
Как найти прямо пропорциональные?
Уравнение прямой пропорциональности y = kx, где x и y — заданные величины, а k — любое постоянное значение. Некоторые примеры уравнений прямой пропорциональности: y=3x, m=10n, 10p=q и т. д.
Какой тип функции y 3x 1? Форма y = mx + b, как записывается y = 3x + 1, называется форма наклона-перехвата, и является распространенным способом записи уравнений прямой линии. Это потому, что «m» — это уравнение, называемое наклоном линии. Наклон y = 3x + 1 равен 3. «b» — это точка пересечения y, значение y, когда x = 0.
Какое уравнение параллельно 3X1?
Уравнение прямой, проходящей через (0,0), имеет вид Y=мХ.
где m — наклон линии. Теперь эта линия параллельна линии Y=3X-1; поэтому m=3. Следовательно, уравнение линии Y=3X .
Что из следующего перпендикулярно y 3X 1? Наклон линии y = 3x + 1 равен 3. Таким образом, любая перпендикулярная к ней линия должна иметь наклон {(-1)/3} = (-1/3). Годы: -1/3.
Каков наклон линии, перпендикулярной Y 1?
Линия y=−1 имеет наклон 0, поэтому любая линия, перпендикулярная ей, будет иметь неопределенный уклон.
Каков градиент графика с уравнением y 1 3x? Наклон 1/3 а точка пересечения по оси y равна 0, так что эта линия пересекает начало координат.
Каков наклон y 1/3 1?
Используя форму пересечения наклона, наклон равен 0 .
3-8Как построить график y=-1/3x+1 ?
Цитата страницы Начать эссе значок-вопрос Спросите репетитораНачать бесплатную пробную версию
Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяСсылайтесь на эту страницу следующим образом:
«Как построить график y=-1/3x+1?» eNotes Editorial , 1 февраля 2013 г.
, https://www.enotes.com/homework-help/how-do-show-y-1-3x-1-graph-382716.
По состоянию на 1 января 2023 г.
`y=-1/3x +1` является линейным уравнением. Следовательно, его график представляет собой прямую.
Кроме того, данное уравнение находится в форме пересечения с наклоном y=mx+b, где m — это наклон, а b — это пересечение с осью y.
Итак, наклон линии равен «-1/3», а ее точка пересечения по оси Y равна (0,1).
Чтобы построить график, начните с точки (0,1). Затем используйте наклон для определения других точек.
Поскольку наклон отрицательный, одна точка находится на 1 единицу вниз и на 3 единицы вправо от точки пересечения с осью y. Это точка (3, 0). Отсюда снова переместитесь на 1 единицу вниз и на 3 единицы вправо. Тогда другой точкой будет (6, -1).
Кроме того, точки выше точки пересечения с осью y можно определить, переместив их на 1 единицу вверх и на 3 единицы влево. Итак, одна из точек равна (-3, 2). Повторяя шаги, другая точка (-6, 3).
Теперь, когда известны некоторые точки y=-1/3x+1, соединим их. И продлите линию на обоих концах.
Следовательно, график `y=-1/3x+1`:
Утверждено редакцией eNotes
Математика
Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
14 Ответы воспитателя
Математика
Последний ответ опубликован 09 октября 2017 г. в 00:54:39
Добавьте 1 плюс 2 плюс 3 плюс 4. . . вплоть до 100.
3 Ответы воспитателя
Математика
Последний ответ опубликован 3 октября 2011 г.