Онлайн расчет длины дуги: Онлайн калькулятор: Калькулятор длины дуги

Содержание

Онлайн-калькулятор для расчета длины дуги кругового сектора

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

В публикации представлены онлайн-калькуляторы и формулы, с помощью которых можно рассчитать длину дуги кругового сектора через радиус окружности и центральный угол сектора (в градусах или радианах).

Расчет длины дуги сектора
- Через радиус круга и угол сектора в градусах
- Через радиус круга и угол сектора в радианах

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина с учетом указанных данных.

Напомним, дуга кругового сектора – это участок между двумя точками, лежащими на линии окружности и полученными в результате пересечения этой окружности двумя радиусами, образовавшими сектор круга.

На рисунке ниже дуга сектора AOB – это часть окружности между точками A и B.

Через радиус круга и угол сектора в градусах

Примечание: число π, используемое в калькуляторе, округлено до 3,1415926536.

Формула расчета

Через радиус круга и угол сектора в радианах

Формула расчета

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Расчёт полукруглой теплицы — онлайн калькулятор

Укажите необходимый масштаб чертежей.

Заполните параметры теплицы в миллиметрах:

X – Ширина теплицы выбирается исходя из бюджета, наличия свободного места для размещения на участке, а также Ваших пожеланий и целей. Стандартная ширина теплиц заводского изготовления находится в пределах 1800-6000 мм. Оптимальное значение X для комфортной работы в теплице не меньше 2400 мм. Такой размер позволяет оборудовать в теплице проход шириной 600 мм (что оптимально), поставить стеллажи с рассадой или оборудовать грядки по обе стороны до 900 мм (сложно ухаживать за растениями дотягиваясь дальше указанного расстояния).

Z – Длина парника, может быть любой, если позволяют размеры участка. При выборе значения Z следует учитывать стандартные размеры материала, который будет применяться для остекления. Например, если используется полиэтиленовая пленка значение длины Z должно быть кратным 1000 мм, а если поликарбонат – кратным 2100 мм.

Один из решающих аспектов, влияющих на выбор ширины и длины теплицы, это ширина покрытия. Стандартная ширина листа поликарбоната 2100 мм это максимально допустимая ширина, при которой не происходит провисание под собственным весом, при условии обеспечении упора краями материала на каркас. Теплица, покрытая материалом максимальной ширины более светлая, поскольку в таком случае используется меньше стоек. Однако при определении оптимального количества стоек каркаса также следует учитывать климатические особенности Вашего региона (снеговые и ветровые нагрузки).

Y – Высота теплицы выбирается исходя из удобства работы в ней (определяющим фактором является рост работника). Значение Y влияет на длину дуги каркаса (больше высота – длиннее дуга и большее количество материала необходимо для остекления). Оптимальная высота теплицы 2000 – 2200 мм.

При выборе основных параметров теплицы следует учитывать рекомендации СП 107.13330.2012 «Теплицы и парники» (актуализированная редакция СНиП 2.10.04-85).

A – Количество вертикальных секций на фасаде теплицы, следует выбирать с учетом геометрических размеров материала для обшивки.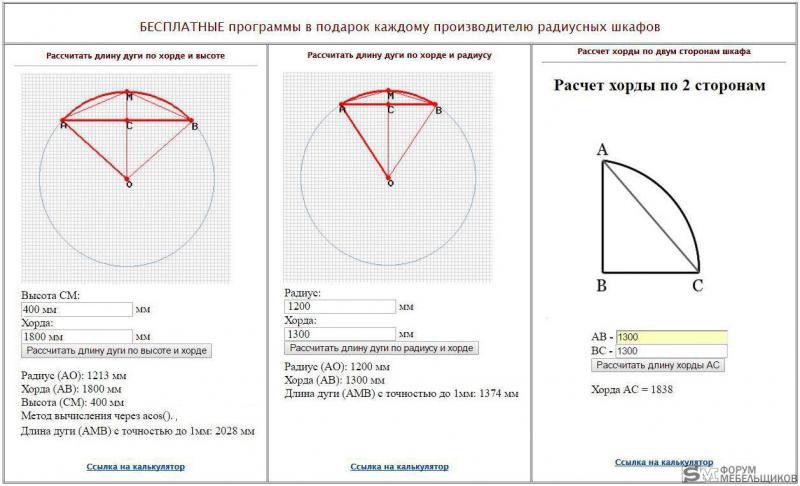

E – Число вертикальных сегментов стен, зависит от размеров используемого для обшивки материала и длины парника. Например, для шести метровой теплицы остекленной поликарбонатом стандартной ширины, значение E следует принимать не меньше 3.

D – Количество ячеек в вертикальном сегменте принимается с учетом свойств материала остекления и прочности каркаса. Если используется поликарбонат, достаточно значения D=3 (поскольку в конструкции он согнут и напряжен, то хорошо воспринимает нагрузки на растяжение-сжатие), для парниковой пленки следует принимать значение D больше чтобы исключить провисание.

У Вас есть возможность подобрать оптимальные размеры секций и ячеек изменяя их количество, при этом размеры будут отображены на чертежах теплицы.

Нажмите «Рассчитать»

Калькулятор поможет посчитать площадь, объем и периметр полукруглой теплицы. А также площади крыши, боковых стен и фасадов и полную площадь остекления, что необходимо для закупки материала обшивки в нужном количестве. Кроме того вы узнаете длину дуг теплицы (их количество) и длину материалов для изготовления каркаса. Использование данного онлайн калькулятора позволит Вам достаточно точно рассчитать материалы для изготовления арочной теплицы своими руками и оценить финансовые вложения в ее постройку. Также будет произведен расчет длины и дуги арки теплицы.

Важно: при использовании поликарбоната для остекления теплицы его следует сгибать поперек ребер жесткости.

Калькулятор разницы в процентах — Онлайн калькулятор разницы в процентах

Калькулятор разницы в процентах — это онлайн-инструмент, который помогает рассчитать процентную разницу любых двух чисел. Абсолютная величина отношения разности двух чисел к их среднему, выраженная в процентах, называется процентной разницей.

Что такое калькулятор процентной разницы?

Калькулятор процентной разницы поможет вам рассчитать относительную разницу между двумя числами и выразить результат в процентах. Процентная разница используется для представления относительного изменения двух величин в виде процентов. Чтобы использовать Калькулятор процентной разницы введите значения в поля ввода.

Калькулятор процентной разницы

Как пользоваться калькулятором процентной разницы?

Пожалуйста, следуйте инструкциям ниже, чтобы найти процентную разницу с помощью калькулятора процентной разницы:

Шаг 1 : Используйте онлайн-калькулятор процентной разницы Cuemath.
Шаг 2: Введите начальное значение и конечное значение в поля ввода.
Шаг 3 : Нажмите « Вычислить », чтобы найти разницу в процентах.
Шаг 4 : Нажмите « Сброс », чтобы очистить поля и ввести новые значения.

Как работает калькулятор процентной разницы?

Предположим, что заданы начальное и конечное значения величины. Затем шаги для расчета процентной разницы следующие:

Вычтите конечное значение из начального значения.

Взять среднее из двух значений. Среднее значение можно рассчитать как сумму наблюдений, деленную на общее количество наблюдений.
Разделите разницу, полученную на шаге 1, на среднее значение, полученное на шаге 2.
Затем мы берем абсолютное значение числа, полученного на шаге 3. Получение абсолютного значения числа подразумевает, что мы удаляем отрицательный знак числа. Таким образом, абсолютное значение всегда будет положительной величиной. Абсолютное значение величины, скажем, x, представляется как |x|.
Значение, полученное на шаге 4, затем умножается на 100, чтобы получить результат в процентах.

Формула для процентной разницы приведена ниже:

Процентная разница = \(\left | \frac{Начальное значение — Конечное значение}{\frac{Начальное значение + Конечное значение}{2}} \right |\times 100\)

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы.

С Cuemath находите решения простыми и легкими шагами.

Записаться на бесплатный пробный урок

Решенные примеры на калькуляторе процентной разницы

Пример 1:

Найдите процентную разницу, если заданы значения 100 и 200. Проверьте это с помощью онлайн-калькулятора процентной разницы.

Решение:

Дано: Начальное значение (a) = 100, конечное значение (b) = 200

Разница в процентах = |Разница / Среднее| × 100%

= |(a − b) / ((a + b)/2)| × 100%

= |(100 — 200) / ((100 + 200)/2)| × 100%

= |-100/150| × 100%

= |-0,666| × 100%

= 0,666 × 100%

= 66,666%

Таким образом, процентная разница двух значений = 66,666%.

Пример 2:

Найдите процентную разницу, если заданы значения 300 и 148. Проверьте ее с помощью онлайн-калькулятора процентной разницы.

Решение:

Дано: Начальное значение (a) = 300, конечное значение (b) = 148

Разница в процентах = |Разница / Среднее| × 100%

= |(a − b) / ((a + b)/2)| × 100%

= |(300 — 148) / ((300 + 148)/2)| × 100%

= |152 / 224| × 100%

= 0,678 × 100%

= 67,8%

Таким образом, процентная разница между двумя значениями = 67,8%

Точно так же вы можете попробовать калькулятор процентной разницы, чтобы найти процентную разницу для следующих значений.

Начальное значение = 80, конечное значение = 280
Начальное значение = 220, Конечное значение = 120

☛ Статьи по теме:

Разница в процентах
Абсолютное значение

☛ Математические калькуляторы:

Калькулятор кубических футов – онлайн-калькулятор кубических футов

Калькулятор кубических футов — это онлайн-инструмент, который вычисляет объем прямоугольного параллелепипеда и выполняет преобразование единиц измерения для представления объема в кубических футах. Объем прямоугольного параллелепипеда можно вычислить, умножив длину, ширину и высоту.

Что такое калькулятор кубических футов?

Калькулятор кубических футов используется для вычисления объема прямоугольного параллелепипеда и выражения его в кубических футах. Кубоид представляет собой трехмерную твердую фигуру, ограниченную 6 четырехугольными гранями. Чтобы использовать калькулятор кубических футов , введите значения в поля ввода и выберите единицу измерения из раскрывающегося списка.

Калькулятор кубических футов

Как пользоваться калькулятором кубических футов?

Выполните перечисленные ниже действия, чтобы найти объем прямоугольного параллелепипеда и преобразовать его единицы с помощью онлайн-калькулятора кубических футов.

Шаг 1 : Перейдите к онлайн-калькулятору кубических футов Cuemath.
Шаг 2 : Введите значения в поля ввода и выберите единицу измерения из раскрывающегося меню.
Шаг 3 : Нажмите « Рассчитать », чтобы вычислить объем, выполнить преобразование единиц измерения и отобразить его в кубических футах.
Шаг 4 : Нажмите « Сброс », чтобы очистить поля и ввести новые значения.

Как работает калькулятор кубических футов?

Объем большинства трехмерных объектов можно рассчитать, умножив площадь основания на его высоту. Предположим, у нас есть прямоугольный параллелепипед с длиной (l), шириной (b) и высотой (h). Формула объема дается как:

Объем прямоугольного параллелепипеда = l × b × h.

Здесь площадь основания (прямоугольной формы) определяется как l × b.

Следующие коэффициенты пересчета используются для преобразования соответствующих единиц в кубические футы.

длина (футы) × ширина (футы) × высота (футы) = кубические футы
длина (дюймы) × ширина (дюймы) × высота (дюймы) ÷ 1728 = кубические футы
длина (ярды) × ширина (ярды) × высота (ярды) × 27 = кубические футы
длина (см) × ширина (см) × высота (см) ÷ 28316,846 = кубический фут
длина (метры) × ширина (метры) × высота (метры) × 35,315 = кубические футы

Чтобы преобразовать единицы измерения из одних в другие, нам потребуется использовать унитарный метод. В зависимости от типа преобразования нам придется либо умножать, либо делить объем на заданные коэффициенты преобразования.