Экономия на строительстве бака
|
|
|
||||||||||||||||||||||||||||
Рассчитайте силу в вашем гидравлическом цилиндре простым способом
Продукты Категория
Гидравлические цилиндры
Гидравлические насосы и силовые агрегаты
Инструменты для болтового соединения
Инструменты для обслуживания фланцев
Гидравлический и механический съемник
Оборудование для испытания свай под нагрузкой
Гидравлический пресс
В гидравлических системах сила является важнейшим элементом управления потоком жидкостей и газов. В этой статье мы обсудим, как рассчитать силу, действующую на гидравлический цилиндр.
В этой статье мы обсудим, как рассчитать силу, действующую на гидравлический цилиндр.
Во-первых, нам нужно знать размеры поршня и цилиндра. Во-вторых, нам нужно знать рабочее давление гидроцилиндра. Силу, действующую на гидравлический цилиндр, можно рассчитать по следующей формуле: F = P x A, где F — сила, P — давление жидкости в цилиндре, а A — рабочая площадь поршня. Это уравнение можно использовать для расчета сил в любой гидравлической системе.
Например, эффективная площадь цилиндра двустороннего действия составляет 0.145 м² при нажиме и 0.048 м² при втягивании, номинальное рабочее давление 70 МПа.
Толкающая сила должна составлять F(толкание)=70 МПаX0.145 м²=10.15 тонны, а тяговое усилие должно составлять F(тяга)=70 МПаX0.048 м²=3.3 тонны.
Похожие сообщения
Как работает гидравлический насос?
Гидравлический насос — это машина, которая использует силу жидкости для перемещения объектов. Первые насосы были изобретены в семнадцатом веке, и они в основном использовались для орошения. Однако со временем гидравлические насосы стали использоваться для множества других целей, включая добычу полезных ископаемых, производство и перемещение объектов. Как работает гидравлический насос? Гидравлический насос — это машина, которая использует давление жидкости для перемещения предметов. Он работает, используя узел поршня и цилиндра, чтобы проталкивать и вытягивать жидкость через серию трубок. Сила движения жидкости по трубкам создает механическую силу, которую можно использовать для совершения работы. Существует два основных типа гидравлических насосов: поршневые и импеллерные. Поршневой насос имеет поршень, который движется вперед и назад внутри цилиндра. Сила, создаваемая этим движением, используется для проталкивания или вытягивания жидкости через систему. Рабочее колесо представляет собой вращающийся цилиндр, и его можно использовать как поршневой насос или как аэратор. Основными компонентами гидравлического насоса являются поршни, цилиндры, клапаны и трубы. Все они связаны вместе, чтобы создать систему, которая может перемещать жидкости.
Однако со временем гидравлические насосы стали использоваться для множества других целей, включая добычу полезных ископаемых, производство и перемещение объектов. Как работает гидравлический насос? Гидравлический насос — это машина, которая использует давление жидкости для перемещения предметов. Он работает, используя узел поршня и цилиндра, чтобы проталкивать и вытягивать жидкость через серию трубок. Сила движения жидкости по трубкам создает механическую силу, которую можно использовать для совершения работы. Существует два основных типа гидравлических насосов: поршневые и импеллерные. Поршневой насос имеет поршень, который движется вперед и назад внутри цилиндра. Сила, создаваемая этим движением, используется для проталкивания или вытягивания жидкости через систему. Рабочее колесо представляет собой вращающийся цилиндр, и его можно использовать как поршневой насос или как аэратор. Основными компонентами гидравлического насоса являются поршни, цилиндры, клапаны и трубы. Все они связаны вместе, чтобы создать систему, которая может перемещать жидкости. Поршень
Поршень
Испытание на нагрузку сваи 2700 тонн
Блок питания для испытаний на нагрузку свай RIVERLAKE ZJ9 представляет собой управляемую ПЛК систему испытаний на нагрузку свай, которая может контролировать, отображать, записывать и загружать давление цилиндров в реальном времени, тоннаж выходной силы в реальном времени, давление мощности в реальном времени. пакет, время испытания под нагрузкой в режиме реального времени. В этом проекте наша электростанция ZJ9 работала с 9 единицами гидравлических цилиндров двойного действия HCRL30012 с контргайкой для создания макс. общая выходная сила 2700 тонн. Помимо вышеперечисленных функций, мы можем даже встроить тензодатчик Bluetooth и датчики с циферблатным датчиком Bluetooth в наше оборудование для загрузки свай, чтобы отображать и записывать данные о нагрузке в реальном времени от тензодатчиков и данные о смещении сваи в реальном времени от циферблат.
Как правильно выбрать гидравлический динамометрический ключ для вашей работы
Что такое гидравлический динамометрический ключ? Гидравлический динамометрический ключ — это инструмент, используемый для приложения крутящего момента к соединению или болту. Он использует силу гидравлической жидкости для вращения рукоятки ключа и приложения давления к болту или соединению. Динамометрические ключи полезны при установке или снятии деталей в труднодоступных местах, а также их можно использовать для общего ремонта. Типы гидравлических динамометрических ключей Сегодня на рынке представлено множество типов гидравлических динамометрических ключей. Некоторые из наиболее распространенных типов включают динамометрические ключи с низким профилем, квадратным хвостовиком и циферблатом. Каждый тип имеет свои уникальные преимущества, которые могут быть полезны в определенных ситуациях. Низкопрофильные динамометрические ключи часто считаются наиболее компактным вариантом. Они также, как правило, являются наименее дорогим вариантом, что делает их хорошим выбором, если вам нужен гаечный ключ только для случайного использования. У них более короткие ручки и меньшие головки, что делает их идеальными для узких мест или областей с ограниченным пространством. Динамометрические ключи с квадратным хвостовиком аналогичны низкопрофильным динамометрическим ключам с точки зрения их размера и возможностей.
Он использует силу гидравлической жидкости для вращения рукоятки ключа и приложения давления к болту или соединению. Динамометрические ключи полезны при установке или снятии деталей в труднодоступных местах, а также их можно использовать для общего ремонта. Типы гидравлических динамометрических ключей Сегодня на рынке представлено множество типов гидравлических динамометрических ключей. Некоторые из наиболее распространенных типов включают динамометрические ключи с низким профилем, квадратным хвостовиком и циферблатом. Каждый тип имеет свои уникальные преимущества, которые могут быть полезны в определенных ситуациях. Низкопрофильные динамометрические ключи часто считаются наиболее компактным вариантом. Они также, как правило, являются наименее дорогим вариантом, что делает их хорошим выбором, если вам нужен гаечный ключ только для случайного использования. У них более короткие ручки и меньшие головки, что делает их идеальными для узких мест или областей с ограниченным пространством. Динамометрические ключи с квадратным хвостовиком аналогичны низкопрофильным динамометрическим ключам с точки зрения их размера и возможностей. Однако у них более широкие головки и более длинные ручки, что облегчает их использование при работе с большими болтами или шурупами.
Однако у них более широкие головки и более длинные ручки, что облегчает их использование при работе с большими болтами или шурупами.
Утечки в гидроцилиндрах (и как их исправить)
Что такое гидроцилиндр и как он работает? Гидравлический цилиндр представляет собой механический привод, предназначенный для передачи гидростатической силы в одном направлении. Обычно используется в строительном оборудовании, гражданском строительстве и машинах, предназначенных для производственного процесса. В гидравлическом цилиндре используется любая форма гидравлической жидкости, обычно масло, которая толкается вперед и назад поршнем в каждую сторону цилиндра. Это позволяет работать линейному движению, заставляя такие машины, как бульдозеры и тракторы, выполнять движения, такие как разрушение зданий или подъем тяжестей, которые не могут быть выполнены с помощью человеческой силы. Гидравлические цилиндры состоят из поршневого штока, поршневого уплотнения и двух отдельных частей, соединенных вместе болтами и гайками для создания силы гидравлической жидкости внутри трубки цилиндра.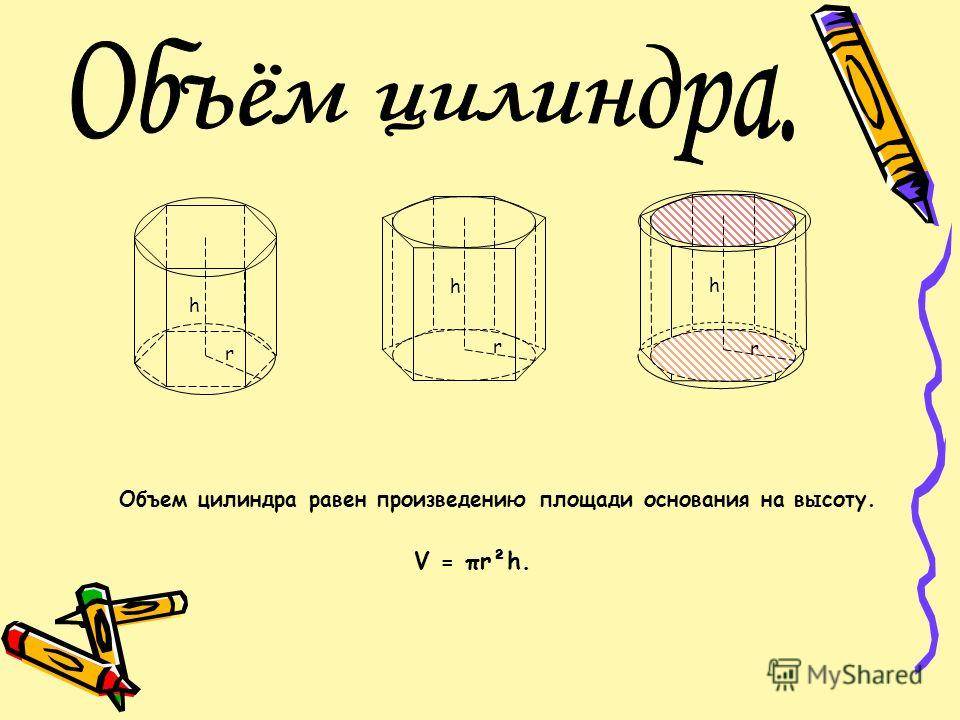 Гидравлический цилиндр оказывает огромное усилие, от нескольких килограммов до нескольких тысяч тонн! Независимо от линейного движения, которое вам нужно автоматизировать, гидроцилиндр хорошего качества является идеальным решением для любого производства, сельского хозяйства, гражданского строительства или потребностей компании по автоматизации. Что вызывает течь гидравлических цилиндров? Общей проблемой для инженерных и производственных компаний, работающих с высокими нагрузками, является разработка способов минимизации утечек из их гидравлических цилиндров. Утечки в
Гидравлический цилиндр оказывает огромное усилие, от нескольких килограммов до нескольких тысяч тонн! Независимо от линейного движения, которое вам нужно автоматизировать, гидроцилиндр хорошего качества является идеальным решением для любого производства, сельского хозяйства, гражданского строительства или потребностей компании по автоматизации. Что вызывает течь гидравлических цилиндров? Общей проблемой для инженерных и производственных компаний, работающих с высокими нагрузками, является разработка способов минимизации утечек из их гидравлических цилиндров. Утечки в
Пневматический цилиндр — сила, развиваемая в зависимости от давления
Цилиндр одностороннего действия
Сила, создаваемая пневматическим цилиндром одностороннего действия, может быть выражена как
/ 4 (1)
, где
F = Сила Exerted (N)
P = давление датчика (N/ M 2 , PA)
A = площадь полнопроходного сечения (м 2 )
d = диаметр полнопроходного поршня (м)
Калькулятор цилиндра одностороннего действия — выходной ход
Диаметр 904 Рассчитать усилие с известным давлением и давлением 904 (кПа) (1 бар = 100 кПа)
Диаметр цилиндра (мм)
- Сделать ярлык для этого калькулятора на главном экране?
Расчет необходимого диаметра с известными силой и давлением
Force (N)
Pressure (kPa)
Calculate required Pressure with known Force and Diameter
Force (N)
Diameter (mm)
Example — Single Acting Piston
Сила, создаваемая пневматическим цилиндром одностороннего действия с 1 бар (10 5 Н/м 2 ) и полным диаметром 100 мм (0,1 м) , может быть рассчитана как
F = p π d 2 / 4
= (10 5 N/m 2 ) π (0.
1 m) 2 / 4
= 785 N
= 0.785 kN
Air Cylinder — Pressure/Force Diagram
SI-units
Imperial Units
Double Acting Cylinder
The force exerted by double acting pneumatic cylinder on outstroke can be expressed as (1). Сила, действующая на внутренний гребок, может быть выражена как
F = P π (D 1 2 — D 2 2 ) / 4 (2)
, где
D 1 = Full Piston Boter Boter Boreton Boter Boteron Boreton. )
d 2 = диаметр штока поршня (м)
Калькулятор цилиндров двойного действия — ход на входе
Расчет силы по известным давлению и диаметру
Давление (кПа)0011
Cylinder Diameter (mm)
Piston Rod Diameter (mm)
Calculate required Diameter with known Force and Pressure
Calculate required Pressure with known Force and Diameter
Example — Double Acting Piston
The усилие от пневматического цилиндра одностороннего действия с 1 бар (10 5 Н/м 2 ) , полным диаметром 100 мм (0,1 м) и диаметром штока 10 mm (0. 01 m) can be calculated as
01 m) can be calculated as
F = p π (d 1 2 — d 2 2) / 4
= (10 5 N / M 2 ) π [(0,1 м) 2 — (0,01 м) 2
] / 4 = 778 N
= 0,78 кв. по грузоподъемности — за счет штока и уменьшенной площади активного наддува 9{2} $ и т. д. Полную площадь поверхности цилиндра можно рассчитать, если вычислить площадь двух оснований и площадь криволинейной грани.
Давайте узнаем, как найти площадь поверхности цилиндра и его формулы.
Цилиндр – объемная трехмерная фигура
Цилиндр — это одна из основных трехмерных фигур в геометрии, которая имеет два параллельных круговых основания на некотором расстоянии. Два круглых основания соединены изогнутой поверхностью на фиксированном расстоянии от центра. Отрезок, соединяющий центры двух круговых оснований, является осью цилиндра. Расстояние между двумя круглыми основаниями называется высотой цилиндра.
Газовый баллон для сжиженного нефтяного газа является одним из реальных примеров баллонов.
Поскольку цилиндр имеет трехмерную форму, он обладает двумя основными свойствами: площадью поверхности и объемом. Общая площадь поверхности цилиндра равна сумме площади его криволинейной поверхности и площади двух круглых оснований. Пространство, занимаемое цилиндром в трех измерениях, называется его объемом.
Вот некоторые из важных свойств цилиндра:
- Основания цилиндра всегда конгруэнтны и параллельны друг другу.
- Если ось цилиндра находится под прямым углом к основанию, а основания находятся точно друг над другом, то он называется «Правильный цилиндр».
- Если одно из оснований цилиндра отображается боком, а ось не образует прямого угла с основаниями, то такой цилиндр называется «Наклонный цилиндр».
- Если основания круглые, то он называется прямым круговым цилиндром.
- Лучшей альтернативой круглому основанию цилиндра является эллипс.
Если основание цилиндра имеет эллиптическую форму, то он называется «эллиптическим цилиндром». - Если геометрическое место линии движется параллельно и на фиксированное расстояние от оси, получается круговой цилиндр.
- Цилиндр похож на призму, так как везде имеет одинаковое поперечное сечение.
Для простоты понимания правильный цилиндр или правильный круговой цилиндр рассматриваются для изучения различных свойств цилиндра.
СКАЧАТЬ БЕСПЛАТНО КАРТОЧКИ ПО МАТЕМАТИКЕ:
Красиво оформленные и пригодные для печати карточки, которые помогут вам запомнить все важные математические понятия и формулы.
Правый круговой цилиндр
Цилиндр, основания которого имеют круглую форму и параллельны друг другу, называется правильным круговым цилиндром. Это трехмерная форма. Ось цилиндра соединяет центр двух оснований цилиндра. Это наиболее распространенный тип цилиндров, используемых в повседневной жизни.
Он отличается от наклонного цилиндра тем, что не имеет параллельных оснований и напоминает наклонную конструкцию.
Детали правого кругового цилиндра
Три части правого круглого цилиндра:
- Верхнее круглое основание
- Изогнутая боковая поверхность
- Нижнее круглое основание
Свойства правого кругового цилиндра
Это свойства прямого кругового цилиндра.
- Линия, соединяющая центры окружности, называется осью.
- Когда мы вращаем прямоугольник вокруг одной стороны как оси вращения, образуется правильный цилиндр.
- Сечение, полученное при разрезании прямоугольного кругового цилиндра плоскостью, содержит два элемента, а параллели оси цилиндра представляют собой прямоугольник. 9{2}$ и т. д.). Есть два типа площади поверхности цилиндра
- Изогнутая поверхность
- Общая площадь поверхности
Изогнутая поверхность цилиндра
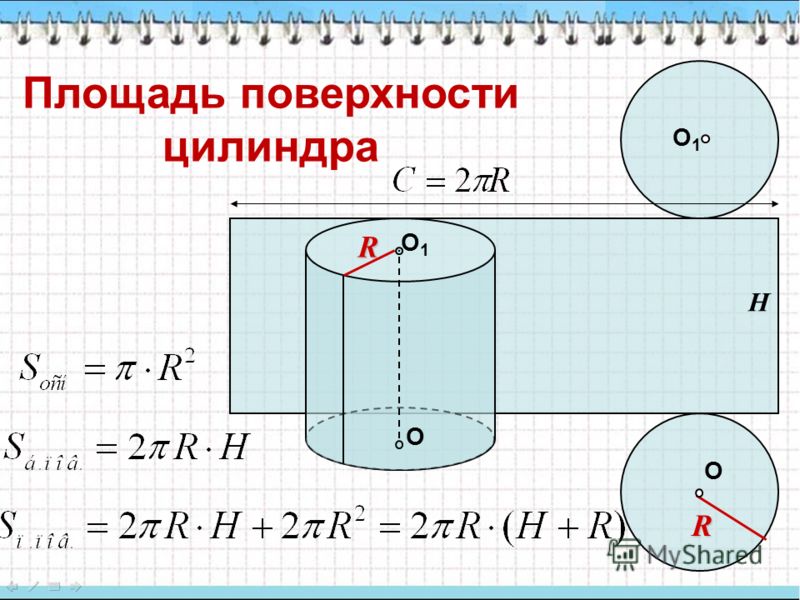
Площадь криволинейной поверхности цилиндра — это площадь поверхности, покрытая только его криволинейной поверхностью.
Формула для расчета площади криволинейной поверхности цилиндра: $2 \pi r h$, где $r$ — радиус основания цилиндра, $h$ — высота цилиндра, а $\pi$ — математическая константа. , и при расчете принимается $\frac {22}{7}$ или $3,14$.
Расчет площади криволинейной поверхности цилиндра Формула
Правильный круговой цилиндр можно рассматривать как $3D$ форму, образованную путем наложения ряда окружностей друг на друга.
Рассмотрим цилиндр с радиусом основания $r$ и высотой $h$, образованный кучей (или штабелем) высоты $h$, образованной окружностями радиуса $r$.
Площадь криволинейной поверхности этого цилиндра будет равна сумме длин окружностей всех этих окружностей.
Длина окружности радиуса $r$ равна $2\pi r$.
Следовательно, сумма длин всех окружностей будет равна $2 \pi r + 2 \pi r + 2 \pi r + … + \left( h \text{ times} \right) = 2 \pi r \times h = 2 \pi rh$.
Формула площади криволинейной поверхности цилиндра: $2 \pi rh$.
Знаменитые математические соревнования для детей
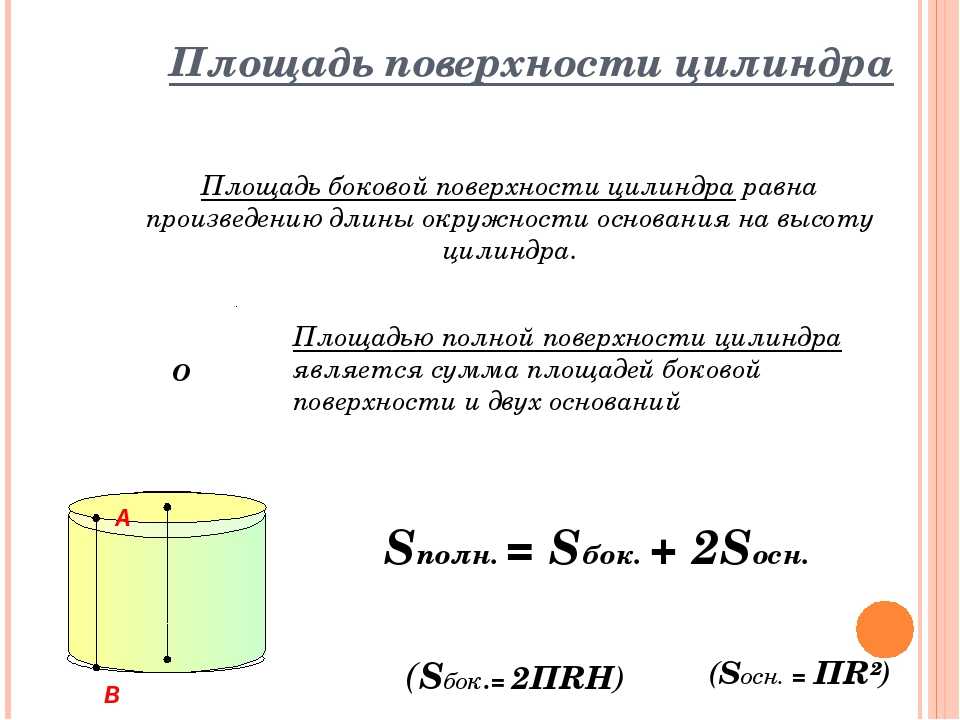
Общая площадь поверхности цилиндра
Общая площадь поверхности цилиндра получается путем сложения площади двух оснований и площади криволинейной поверхности. Таким образом, формула для полной площади поверхности цилиндра имеет вид: 9{2} + 2 \pi rh = 2 \pi r \left(r + h \right)$.
Формула полной площади поверхности цилиндра: $2 \pi r \left(r + h \right)$.
Примеры
Пример 1: Диаметр основания цилиндра составляет $12 см$, а высота $8 см$. Найдите площадь полной поверхности твердого цилиндра.
Диаметр основания цилиндра $d = 12 см$
Радиус основания цилиндра $r = \frac {d}{2} = \frac {12}{2} = 6 см$
Высота цилиндра $h = 8 см$ 9{2}$
Пример 2: Цилиндрический столб диаметром 50 см$ и высотой 7 м$.
Найдите стоимость покраски криволинейной поверхности столба из расчета ₹12$ за кв.м.
Диаметр цилиндрической стойки $d = 50 см$
Радиус цилиндрического столба $r = \frac {d}{2} = \frac {50}{2} = 25 см = 0,25 м$
Высота цилиндрического столба $h = 7 м$
Окрашиваемая площадь цилиндрической стойки равна площади боковой поверхности цилиндрической стойки. 9{2}$
Пусть высота цилиндра $h$
Площадь криволинейной поверхности цилиндра = $2 \pi rh$
Следовательно, $2 \times \frac {22}{7} \times 7 \times h = 110 =>44h = 110 => h = \frac {110}{44} = 2,5 см$
Пример 4: Сколько квадратных метров листового металла потребуется для изготовления закрытого цилиндрического резервуара высотой $1,8 м$ и диаметром основания $140 см$?
Диаметр цилиндрической емкости $d = 140 см$
Радиус цилиндрической емкости $r = \frac {d}{2} = \frac {140}{2} = 70 см = 0,7 м$ 9{2}$.
Заключение
Площадь поверхности 3D-формы (твердого объекта) — это мера общей площади, которую занимает поверхность объекта.
Существует два типа площадей поверхности в цилиндре: площадь криволинейной поверхности, вычисляемая по формуле $2 \pi rh$, и общая площадь поверхности, вычисляемая по формуле $2 \pi r \left(r + h \right)$, где $r$ и $h$ — радиус круглого основания и высота цилиндра соответственно.
Практические задачи
9{2}$. Если радиус цилиндра равен $7 футов$, найдите высоту цилиндра.
- Какой из следующих цилиндров имеет наибольшую площадь поверхности?
- Цилиндр радиусом $10 футов$ и высотой $20 футов$.
- Цилиндр радиусом $20 футов$ и высотой $10 футов$.
- Цилиндр диаметром $30 футов$ и высотой $20 футов$.
- Какова общая площадь поверхности цилиндра с радиусом $12$ дюймов и высотой $14$ дюймов? $\влево(\pi = 3,14\вправо)$.
- Цилиндр имеет общую площадь поверхности $484$ квадратных футов. Если высота цилиндра $4$ фута, каков радиус цилиндра? $\left( \pi = \frac {22}{7} \right)$
- Стоимость покраски цилиндрического контейнера составляет 6 долларов США за квадратный дюйм.
Сколько будет стоить покраска цилиндрических контейнеров стоимостью $10$ радиусом $10$ дюймов и высотой $20$ дюймов? Используйте $\pi = 3,14$
Рекомендуемое чтение
- Площадь поверхности куба (определение, формула и примеры)
- Площадь поверхности прямоугольного параллелепипеда (определение, формула и примеры)
- Площадь прямоугольника – определение, формула и примеры
- Площадь квадрата – определение, формула и примеры
- Площадь треугольника – формулы, методы и примеры
- Площадь круга – формула, вывод и примеры
- Площадь ромба – формулы, методы и примеры
- Площадь воздушного змея – формулы, методы и примеры
- Периметр многоугольника (с формулой и примерами)
- Периметр трапеции – определение, формула и примеры
- Периметр воздушного змея – определение, формула и примеры
- Периметр ромба – определение, формула и примеры
- Окружность (периметр) круга – определение, формула и примеры
- Периметр квадрата – определение, формула и примеры
- Периметр прямоугольника – определение, формула и примеры
- Периметр треугольника – определение, формула и примеры
- Что такое 2D-фигуры — имена, определения и свойства
Часто задаваемые вопросы
Как найти площадь поверхности цилиндра?
В цилиндре есть два типа площади поверхности.

а) Площадь криволинейной поверхности: Площадь криволинейной поверхности цилиндра — это площадь поверхности, покрытая только его криволинейной поверхностью. Формула для расчета площади криволинейной поверхности цилиндра: $2 \pi r h$.
б) Общая площадь поверхности: Общая площадь поверхности цилиндра получается путем сложения площади двух оснований и площади криволинейной поверхности. Формула для расчета общей площади поверхности цилиндра: $2 \pi r \left(r + h \right)$.где $r$ — радиус основания цилиндра, $h$ — высота цилиндра, а $\pi$ — математическая константа, принимается равной $\frac {22}{7}$ или $3.14 $ при расчете.
Какова формула площади поверхности цилиндра?
а) Формула для расчета площади криволинейной поверхности цилиндра: $2 \pi r h$.
б) Формула для расчета площади полной поверхности цилиндра: $2 \pi r \left(r + h \right)$.Что такое CSA и TSA баллона?
Цилиндр состоит из двух типов поверхностей: одна представляет собой криволинейную поверхность, а другая представляет собой круглое основание.


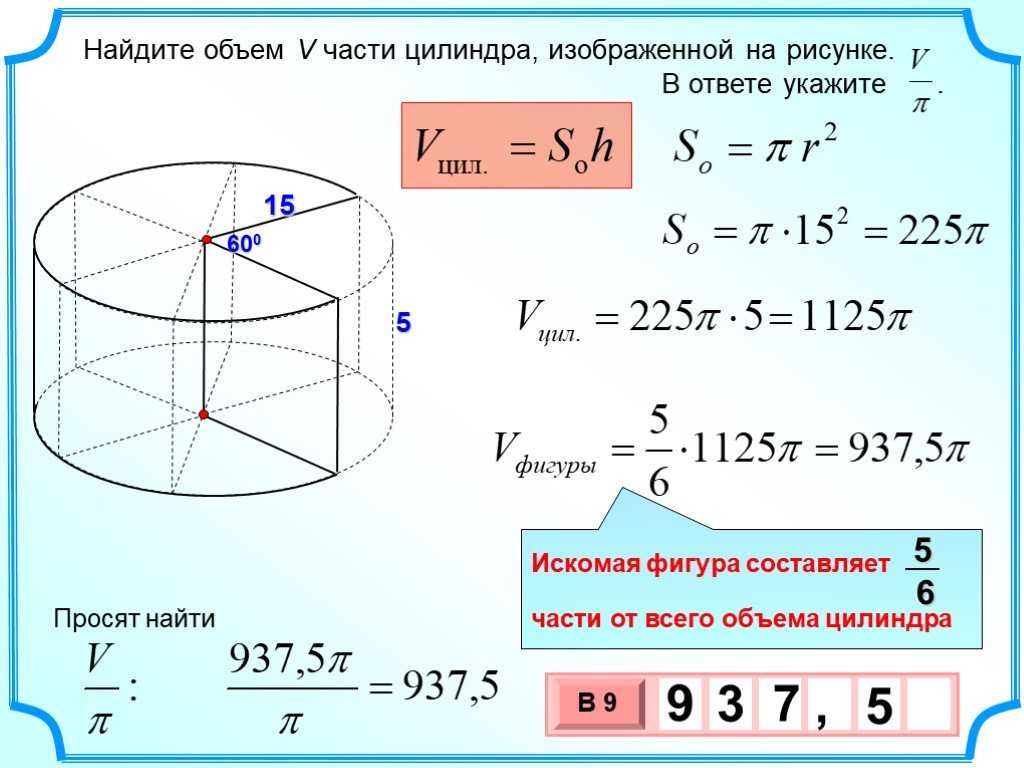
 Необходимо построить на даче бак в виде цилиндра, который бы вмещал 3 кубометра воды и условием что бы затраты на металл для бака были минимальны.
Необходимо построить на даче бак в виде цилиндра, который бы вмещал 3 кубометра воды и условием что бы затраты на металл для бака были минимальны.
 Просто считать по формуле
Просто считать по формуле 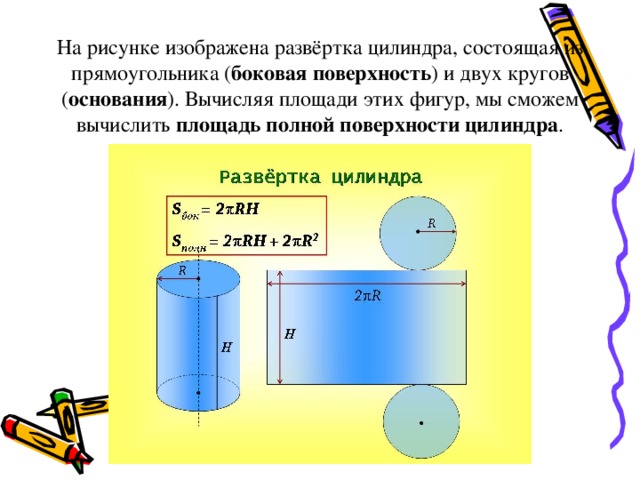 Настройка.
Настройка. 1 m) 2 / 4
1 m) 2 / 4 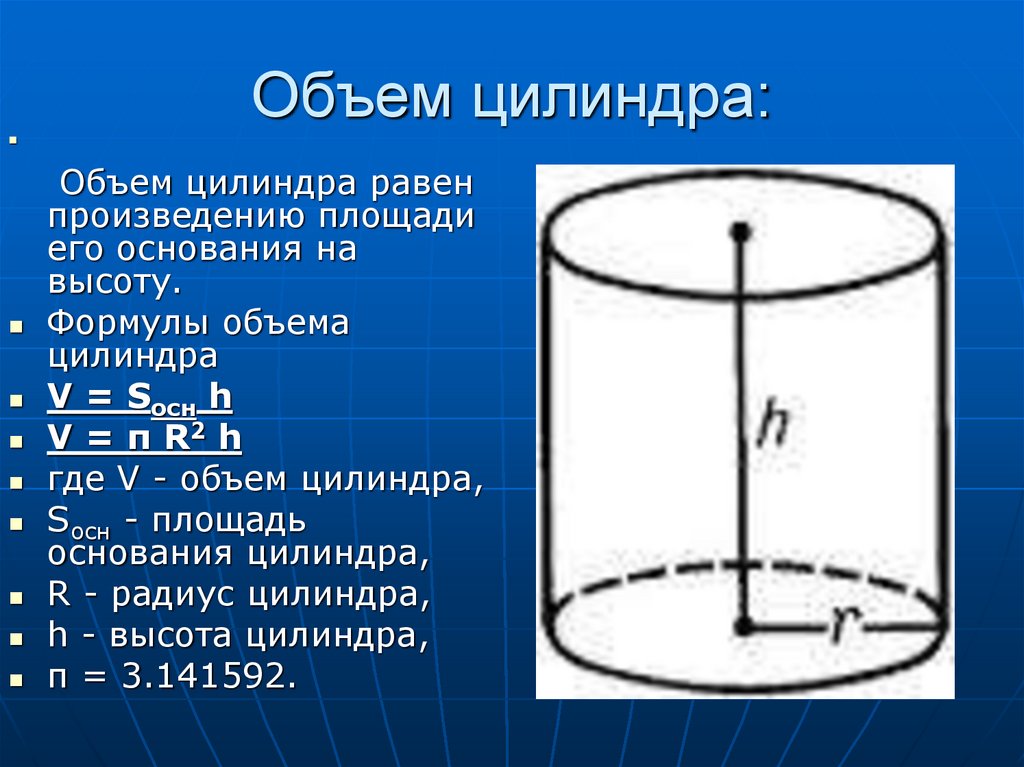 Газовый баллон для сжиженного нефтяного газа является одним из реальных примеров баллонов.
Газовый баллон для сжиженного нефтяного газа является одним из реальных примеров баллонов.
 Он отличается от наклонного цилиндра тем, что не имеет параллельных оснований и напоминает наклонную конструкцию.
Он отличается от наклонного цилиндра тем, что не имеет параллельных оснований и напоминает наклонную конструкцию. Формула для расчета площади криволинейной поверхности цилиндра: $2 \pi r h$, где $r$ — радиус основания цилиндра, $h$ — высота цилиндра, а $\pi$ — математическая константа. , и при расчете принимается $\frac {22}{7}$ или $3,14$.
Формула для расчета площади криволинейной поверхности цилиндра: $2 \pi r h$, где $r$ — радиус основания цилиндра, $h$ — высота цилиндра, а $\pi$ — математическая константа. , и при расчете принимается $\frac {22}{7}$ или $3,14$.
 Найдите стоимость покраски криволинейной поверхности столба из расчета ₹12$ за кв.м.
Найдите стоимость покраски криволинейной поверхности столба из расчета ₹12$ за кв.м. Существует два типа площадей поверхности в цилиндре: площадь криволинейной поверхности, вычисляемая по формуле $2 \pi rh$, и общая площадь поверхности, вычисляемая по формуле $2 \pi r \left(r + h \right)$, где $r$ и $h$ — радиус круглого основания и высота цилиндра соответственно.
Существует два типа площадей поверхности в цилиндре: площадь криволинейной поверхности, вычисляемая по формуле $2 \pi rh$, и общая площадь поверхности, вычисляемая по формуле $2 \pi r \left(r + h \right)$, где $r$ и $h$ — радиус круглого основания и высота цилиндра соответственно. Сколько будет стоить покраска цилиндрических контейнеров стоимостью $10$ радиусом $10$ дюймов и высотой $20$ дюймов? Используйте $\pi = 3,14$
Сколько будет стоить покраска цилиндрических контейнеров стоимостью $10$ радиусом $10$ дюймов и высотой $20$ дюймов? Используйте $\pi = 3,14$