Метод контурных токов онлайн | FaultAn.ru
В программе онлайн-расчёта электрических цепей появился расчёт по методу контурных токов.
Выбор метода расчёта осуществляется в спадающем списке. Для расчёта по методу контурных токов необходимо выбрать метод расчёта «МКТ». Используемая методика при расчёте по методу узловых потенциалов приведена здесь.
Пример схемы и расчёт:
Исходные данные и схема:
- E1:
- Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза, °: 0
- R1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- L1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- C1:
- Номер элемента: 1
- Сопротивление, Ом: 1
После нажатия кнопки «Расчёт» на исходной схеме появляется нумерация узлов и формируется решение:
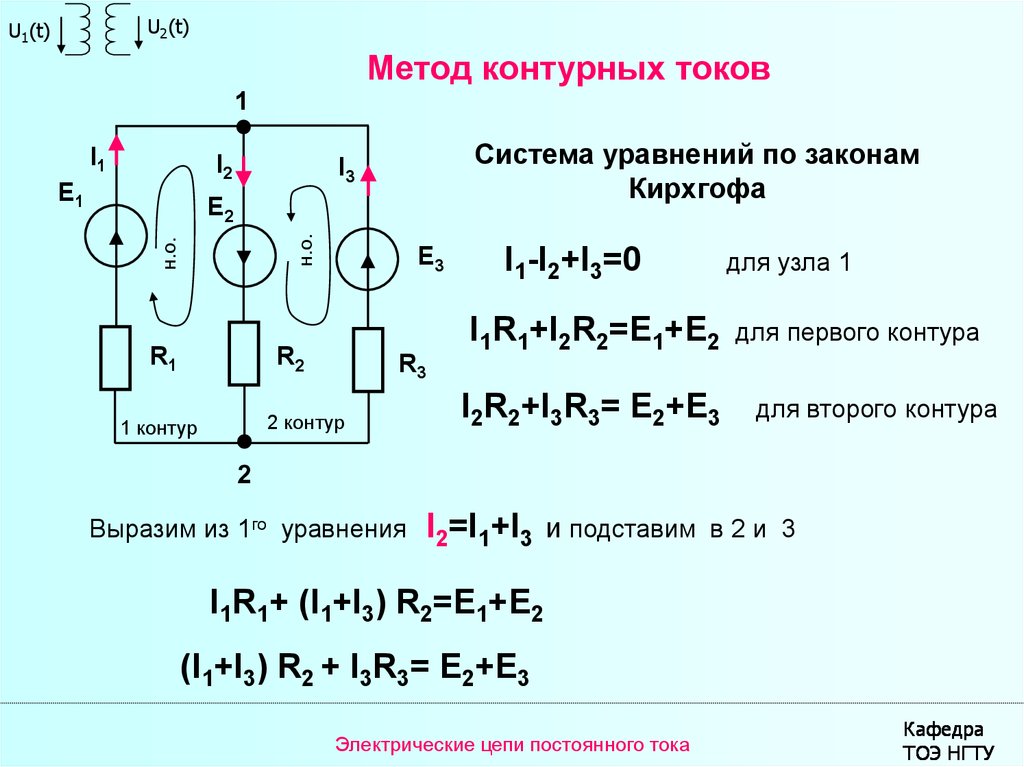
Рассчитаем схему по методу контурных токов.
В данной схеме: узлов − 2, ветвей − 3, независимых контуров − 2.
Количество уравнений, составляемых по методу контурных токов, равно $ N_\textrm{в}- N_\textrm{у} + 1 $, где $ N_\textrm{в} $ − число ветвей без источников тока, $ N_\textrm{у} $ − число узлов.
Для данной схемы количество уравнений, составляемых по методу контурных токов, равно 3 − 2 + 1 = 2.
Произвольно зададим направления обхода контуров и соответствующие контурные токи.
Принятые направления обхода контуров:
Контур №1 обходится через элементы $ \underline{E}_{1} $, $ R_{1} $, $ L_{1} $ в указанном порядке. Через эти элементы протекает контурный ток $ \underline{I}_{11} $.
Контур №2 обходится через элементы $ L_{1} $, $ C_{1} $ в указанном порядке. Через эти элементы протекает контурный ток $ \underline{I}_{22} $.
Составим уравнения по методу контурных токов.
Составим уравнение для контура №1:
$$ \underline{I}_{11} \cdot (R_{1}+jX_{L1})+\underline{I}_{22} \cdot jX_{L1}=\underline{E}_{1} $$
Составим уравнение для контура №2:
$$ \underline{I}_{22} \cdot (jX_{L1}- jX_{C1})+\underline{I}_{11} \cdot jX_{L1}=0 $$
Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми контурными токами.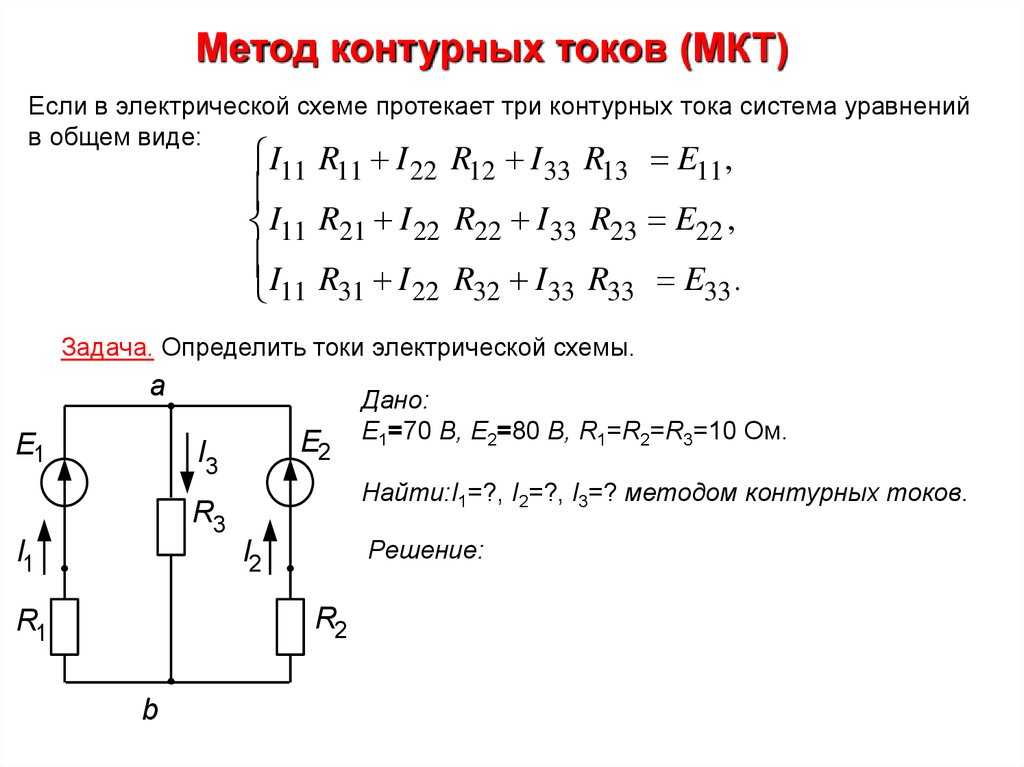
Система уравнений по методу контурных токов для исходной цепи выглядит следующим образом:
$$ \begin{cases}\underline{I}_{11} \cdot (R_{1}+jX_{L1})+\underline{I}_{22} \cdot jX_{L1} = \underline{E}_{1} \\ \underline{I}_{22} \cdot (jX_{L1}- jX_{C1})+\underline{I}_{11} \cdot jX_{L1} = 0 \\ \end{cases} $$
Подставим в полученную систему уравнений значения сопротивлений и источников и получим:
$$ \begin{cases}(1+1j)\cdot \underline{I}_{11}+ j \cdot \underline{I}_{22}=100 \\ j \cdot \underline{I}_{11}=0 \\ \end{cases} $$
Решим систему уравнений и получим искомые контурные токи:
$$ \underline{I}_{11} = 0\space\textrm{А} $$
$$ \underline{I}_{22} = -100j\space\textrm{А} $$
Произвольно зададим направления токов в ветвях.
Принятые направления токов:
Ток $ \underline{I}_{1} $ направлен от узла ‘2 у.’ к узлу ‘1 у.’ через элементы $ \underline{E}_{1} $, $ R_{1} $.
Ток $ \underline{I}_{2} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ L_{1} $.
Ток $ \underline{I}_{3} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ C_{1} $.
Рассчитаем токи в ветвях исходя из полученных контурных токов.
$$ \underline{I}_{1} =\underline{I}_{11}=0=0 $$ $$ \underline{I}_{2} =\underline{I}_{11}+\underline{I}_{22}=0+(-100j)=-100j $$ $$ \underline{I}_{3} =-\underline{I}_{22}=-(-100j)=100j $$
После завершения расчёта на экран также выводятся векторные диаграммы токов и напряжений.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вам потребуется только нарисовать схему в редакторе программы и задать численные значения элементов. 
1. Схема
Составим систему уравнений для двух контуров нашей цепи:
Анализ сетки (метод контурного тока)
Решение любой цепи с использованием метода или теоремы анализа сетки включает следующие шаги:
1. Для каждого замкнутого контура предполагается, что ток циркулирует по контуру. Ток в каждом контуре помечен изогнутой стрелкой и соответствующей меткой тока, например: I1, I2, I3…. . Направление тока во всех петлях делается одинаковым (либо по часовой стрелке, либо против часовой стрелки), как показано на рисунке ниже:
Анализ сетки
2. Затем вычисляется ток, протекающий через каждую ветвь. Если ветвь лежит только на одной сетке, то ток, протекающий через ветвь, является током, протекающим через сетку, а если ветвь является общей для двух сеток, то ток, протекающий через ветвь, представляет собой алгебраическую сумму токов, протекающих через ячейки на ветвь которой лежит, как показано на рисунке ниже:
Анализ сетки 3.
Затем в каждой сетке или цикле формируется уравнение с использованием KVL, как показано ниже:
вкл., Контур 1:
вкл., Контур 2:
вкл., Контур 3:
4. Затем решаются уравнения для определения токов сетки I1. I2, I3 и, в конечном счете, ток и падение напряжения в каждой ветви.
Суперсетка и зависимые источники:
Суперсетка — это сетка, в которой источник тока содержится между двумя сетками. Зависимые источники — это источник, который зависит от другого источника. Когда цепь или сетка содержит эти два особых случая, применение метода анализа сетки требует особого рассмотрения.
Чтобы применить метод анализа сетки в Super Mesh:
Мы должны создать одно уравнение для обеих соседних сеток, включающее источник тока, а источник тока должен быть связан с током сетки двух сеток. Например: В следующей суперсетке:
СуперсеткаУравнения для анализа сетки:
и ,
Чтобы применить метод анализа сетки в сетке, которая содержит зависимые источники:
источник, как будто это независимый источник, и тогда мы должны связать зависимый источник с другими токами сетки.
Например: В следующей сетке:
Уравнения для анализа сетки:
И ,
Метод анализа сетки в действии:
Давайте решим следующую схему, используя анализ сетки или метод контурного тока:
Анализ сетки 900 02Здесь ,
Уравнение для сетки с текущей сеткой I2:
Или,
Уравнение для комбинированной сетки I1 , I3 (поскольку это суперсетка):
Или,
И ,
Таким образом, решая эти уравнения, мы получаем:
Анализ электрической сети
Пример анализа сетки с решением
Здесь, в статье Пример анализа сетки с решением мы решили различные задачи, связанные с анализом сетки. При решении этих задач мы предполагаем, что у вас есть базовые знания о законе напряжения Кирхгофа и анализе сетки.
Пример: 1 Используя анализ сетки, определите ток через батарею 10 В для цепи, показанной на рис. 1 .
Решение: Сначала источник тока преобразуется в эквивалентный источник напряжения, а контурные токи именуются (рис. 2).
Применение КВЛ в петле-1,
или, …..(1)
и в петле-2,
9 0002или, …..(2)
Решение уравнений (1) & (2),
и
⸫ Ток батареи 10 В составляет 4,91A, который входит в аккумулятор через клемму -ve, как показано на рисунке.
Пример: 2 Определите узловые напряжения и ток через резисторы, используя метод сетки для сети, показанной на рисунке 3.
Решение: три петли (рис. 4).
Для петли-1,
или,
или, …..(i)
Для петли-2,
или,
или, …..(ii)
Решение уравнения (i) и ( ii),
;
⸫ Ток через резистор 5 Ом
Ток через резистор 2 Ом
Ток через резистор 6 Ом 9 0009
Ток через резистор 1 Ом
Кроме того,
напряжение в узле «a» = 0 В
напряжение в узле «b»
напряжение в узле «c»
напряжение в узле «d» = 12 В.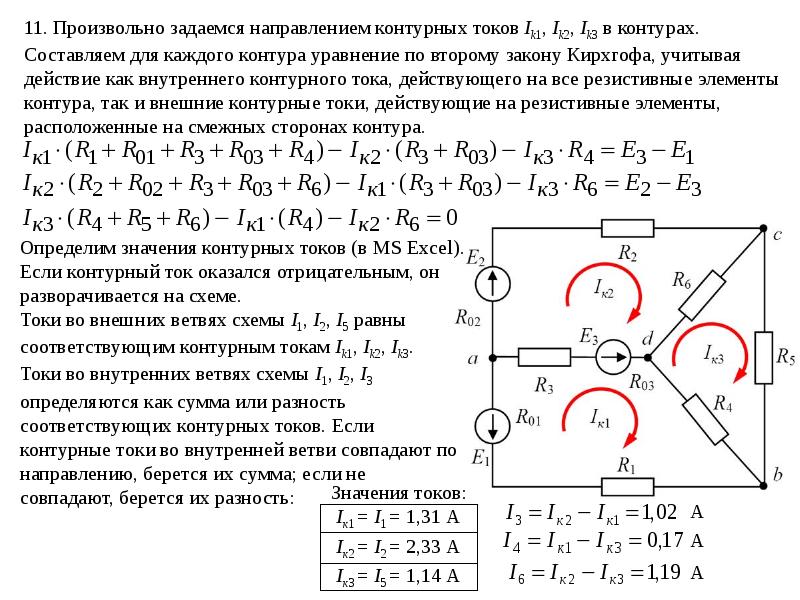
Пример: 3 На рисунке 5 получите уравнения сетки. Если e 1 = e 2 = e 3 = 1 В и все сопротивления равны друг другу, по 1 Ом каждое, каковы будут токи контура?
Решение:
Пусть контурные токи равны i 1 , я 2 , и я 3 .
Уравнения контура приведены ниже:
Для контура-1
или, …..(i)
Для контура-2
или, …..(ii)
Для петли- 3
или …..(iii)
очевидно, что
(скажем)
Таким образом, для петли-1,
⸫ i = 1A
Токи петли во всей петле s будет одинаковым и равным 1А для каждого контура.
Пример: 4 Какая мощность обеспечивается зависимым от источника источником на рисунке 6?
Решение:
В цикле bcde,
или, ….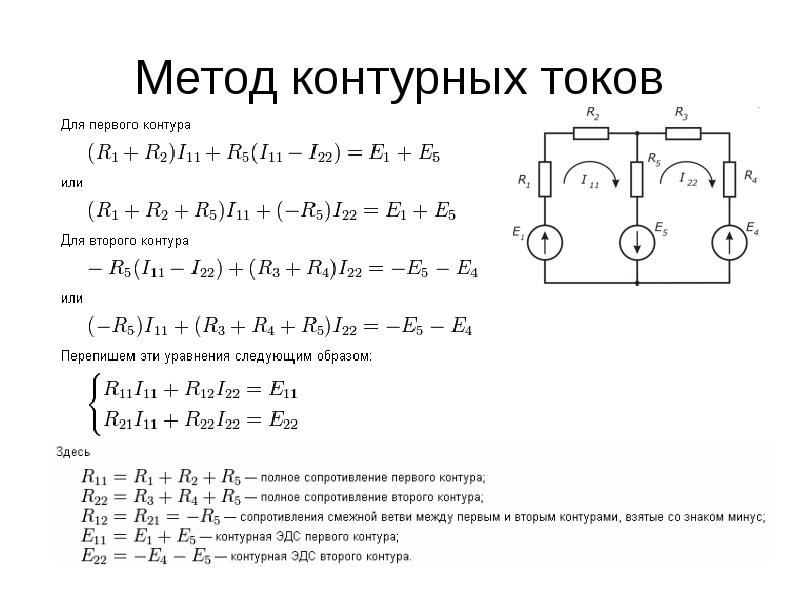
.(i)
Но …..(ii)
[Поскольку источник тока 1 А с силой тока 1 А через резистор 1 Ом]
Используя (ii),
или
[из (ii)]
Таким образом, мощность предоставленный зависимым источником:
=-84 Вт (поглощаемая мощность).
Пример: 5 Найдите v с помощью метода сетки так, чтобы ток через источник 5 В был равен нулю (рис. 7).
Решение:
В шлейфе-1,
или, …..(1)
В шлейфе-2,
9000 9
или,
или, …..(2)
В шлейфе-3,
или …..(3)
Однако, согласно вопросу,
i 1 = 0 [i 1 — ток через источник 5 В]
⸫ Три уравнения (1) , (2) и (3) становятся
…..(4)
….
.(5)
…..(6)
Из уравнений (4) и (6) получаем
…..(7)
Однако, из уравнений (5) и (6) 2 ⸫ Напряжение v должно быть 10В.
Пример: 6 Используя анализ сетки, найдите ток, протекающий через источник 50 В в сети, показанной на рисунке 8.
Решение:
Сначала источник тока переносится на источник напряжения, а схема перерисовывается на рис. 9. 2
или, …..( 1)
В контуре-2,
или, …..(2)
Решение уравнений (1) и (2),
i 2 = ток через источник 50 В = 5,48 А
Пример: 7 В схеме на рис. 10 найдите методом сетки.
Решение:
Пусть ток в петле abcd равен i 1 , а в петле befc — i 2 .
⸫ В цикле abcd,
….
.(1)
Пока, в цикле befc,
9 0002 …..(2)Решение (1) и (2),
…..(3)
Но, [с использованием (3)]
9 0087 Пример: 8 Используя анализ сетки, найдите величину источника, зависящего от тока (рис. 11), и ток через 2-омный резистор.
Решение:
Очевидно, что в цикле-1
i 1 = -2A
В контуре-3,
…..(1)
Однако,
Подставив эти значения в (1),
или,
или,
В контуре-2,
или,
или,
или,
или
или
⸫
Также
Значение зависимого источника
Таким образом, амплитуда зависимого источника = 1,45 В.
Величина фактического тока i, который, как выяснилось, направлен вверх по цепи, фактическая полярность зависимого источника противоположна показанной.
Ток через резистор 2 Ом составляет i 2 , т. е. 0,183 А, протекающий против часовой стрелки в петле-2.
Пример: 9 Найдите контурный ток i 1 , i 2 и i 3 в сети на рис. 12 методом сетки.
Решение:
В цикле 1 анализ сетки дает,
или, …..(1)
900 02 В контуре 2,[где v — предполагаемое напряжение в узле «x»]
или, …..(2)
Но с использованием KVL в цикле 3,
…..(3)
Используя значение v из (3) в (2),
или, …. .(4)
Кроме того, проверка контура 3 показывает, [уравнение (1)]
[уравнение (2)]
[уравнение ( 5)]
Решение этих уравнений
Какова мощность потерь на резисторе 10 Ом в сети, показанной на рисунке 13? Используйте метод сетки.