Сначала умножение или плюс: Порядок действий в Математике

alexxlab / / Разное

Содержание

Порядок выполнения математических действий | интернет проект BeginnerSchool.ru

Сегодня мы поговорим о порядке выполнения математических действий. Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.

Читаем выражение слева направо и выбираем порядок действий по приоритету. Сначала выполняем действия в скобках. Затем умножение и/или деление. Далее складываем и вычитаем.

Если скобки имеют несколько вложений, то есть если внутри скобок есть ещё скобки, то сначала выполняем действия во внутренних скобках. Для простоты понимания, выражение в скобках можно воспринимать как самостоятельное выражение, то есть как отдельный пример, который надо решить. Внутри скобок действия выполняются согласно тому же порядку: Действия в скобках, затем умножение/деление, затем сложение/вычитание.

Умножение и деление не имеет между собой приоритета и выполняются слева направо, также как и сложение с вычитанием.

Рассмотрим пример:

38 – (10 + 6) = 22;

Итак, вспомним о том, что сначала вычисляются выражения в скобках

1) в скобках: 10 + 6 = 16;

2) вычитание: 38 – 16 = 22.

Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.

10 ÷ 2 × 4 = 20;

Порядок выполнения действий:

1) слева направо, сначала деление: 10 ÷ 2 = 5;

2) умножение: 5 × 4 = 20;

10 + 4 – 3 = 11, т.е.:

1) 10 + 4 = 14;

2) 14 – 3 = 11.

Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.

18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7

Порядок выполнения действий:

1) 18 ÷ 2 = 9;

2) 2 × 3 = 6;

3) 12 ÷ 3 = 4;

4) 9 – 6 = 3; т. е. слева направо – результат первого действия минус результат второго;

5) 3 + 4 = 7; т.е. результат четвертого действия плюс результат третьего;

Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.

30 + 6 × (13 – 9) = 54, т.е.:

1) выражение в скобках: 13 – 9 = 4;

2) умножение: 6 × 4 = 24;

3) сложение: 30 + 24 = 54;

Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:

1)      действия, заключенные в скобках;

2)      умножение и деление;

3)      сложение и вычитание.

Понравилась статья — поделитесь с друзьями:

Оставляйте пожалуйста комментарии в форме ниже

Порядок действий в математике. Действия первой, второй ступеней в выражениях.

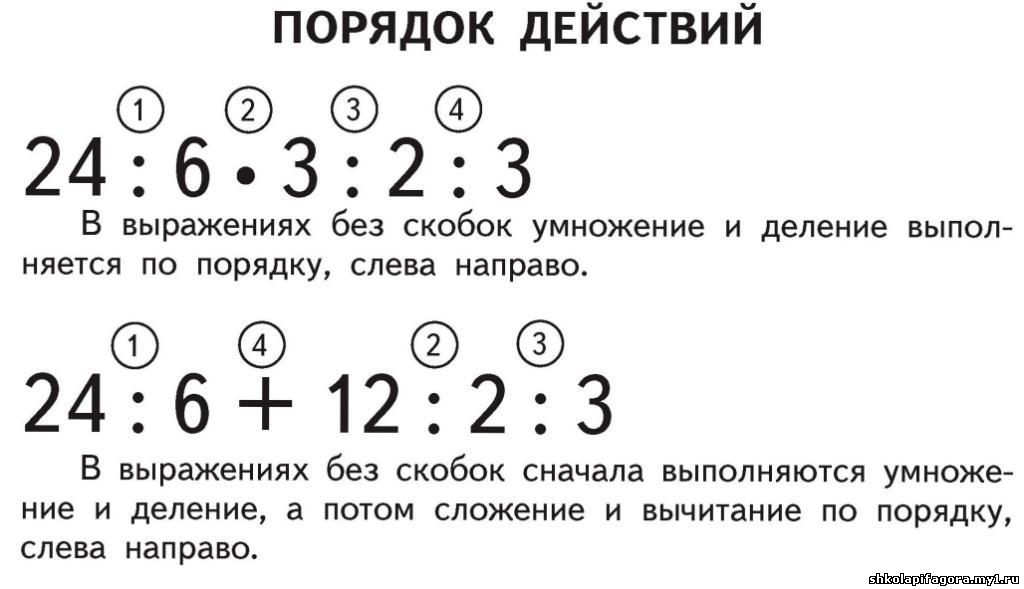Что первое умножение или деление

Действия первой и второй ступени с натуральными числами. Порядок действий

Мы уже рассмотрели арифметические действия сложения и вычитания. Эти действия называются действиями первой ступени. Умножение и деление принято считать действиями второй ступени. Если в математическом выражении есть несколько действий, включая действия и первой, и второй ступени, есть разные числа, соответственно результат зависит от порядка совершенных действий. Поэтому при решении примеров следует соблюдать правильный порядок действий.

Если в выражении нет скобок и присутствуют только действия второй ступени, то действия выполняются в том порядке, в котором они написаны, слева направо.

Например, 80 : 4 ⋅ 2 : 10 = 20 ⋅ 2 : 10 = 40 : 10 = 4

Если в выражении нет скобок и присутствуют только действия первой ступени, то действия выполняются в том порядке, в котором они написаны, слева направо.

Например, 56 + 10 – 25 + 30 = 66 – 25 + 30 = 41 + 30 = 71

Если в выражении нет скобок и случаются действия разных степеней, то сначала выполняют действия  второй ступени, а затем действия первой ступени. Напомним, умножение и деление считаются действиями второй ступени, сложение и вычитание – действиями первой ступени.

Например, 43 + 25 ⋅ 4 – 10. Сначала выполним умножение 25 ⋅ 4 = 100, 43 + 100 – 10 = 133.

Если в выражении есть скобки, сначала выполняем действия в скобках, а затем все остальные согласно порядку действий. Если в скобках записано выражение из нескольких действий первой и второй ступеней, то в скобках также сначала выполняем действия второй ступени.

То есть порядок действий в выражении будет следующим:

  1. действия в скобках
  2. умножение и деление,
  3. сложение и вычитание.

Действия в пределах одной ступени выполняются поочередно слева направо.

Сначала сложение или вычитание?

Сложение и вычитание являются действиями первой ступени, если нет скобок, то они выполняются поочередно слева направо.

Какое первое действие – умножение или деление?

И умножение, и деление – это действия второй степени, они «равноправны». Поэтому, если нет скобок, действия выполняются поочередно слева направо.

Сначала умножение или сложение?

Поскольку умножение является действием высшей степени, а сложение – действием низшей степени, если нет скобок, то сначала выполняем умножение.

Что сначала – деление или вычитание?

Поскольку деление является действием высшей степени, а вычитание – действием низшей степени, если нет скобок, сначала выполняем деление.

Алгоритм вычисления числового выражения

Перед вычислением числового выражения следует определить порядок действий и только после этого приступать к расчетам.

Рассмотрим выражение с несколькими действиями и скобками.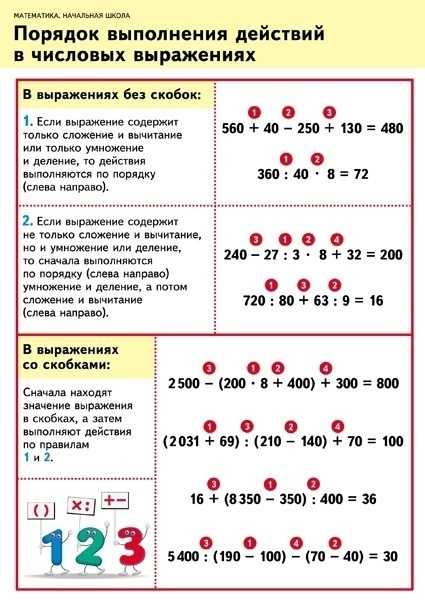

(53 – 42 : 7) ⋅ (22 ⋅ 2 +36 — 12) + 30

Первоочередность действий в данном выражении будет такой:

  • 42 разделить на 7 (42 : 7 = 6)
  • Из 53 вычесть результат первого действия: 53 – 6 = 47
  • Во вторых скобках сначала нужно выполнить умножение 22 на 2: 22 ⋅ 2 = 44
  • К результату умножения прибавляем 36: 44 + 36 = 80
  • Из полученной суммы вычитаем 12: 80 – 12 = 68
  • Умножим множители, которые являются результатами выполнения действий в первых и вторых скобках: 47 ⋅ 68 = 3196
  • К произведению прибавляем 30: 3196 + 30 = 3226

Ответ: (53 – 42 : 7) ⋅ (22 ⋅ 2 +36 -12) + 30 = 3226

Порядок действий с круглыми, квадратными и фигурными скобками

В математических выражениях встречаются не только круглые () скобки, но и квадратные —  [ ]  и фигурные  { }. Фигурные и квадратные скобки используют тогда, когда у скобки необходимо взять выражение в скобках. Порядок действий со скобками следующий: сначала выполняем действия внутри круглых скобок согласно правилам последовательности, второй этап – действия в квадратных скобках, третий этап – действия в фигурных скобках согласно правилам последовательности.

Рассмотрим выражение с круглыми и квадратными скобками

100 — 4 ⋅ [14 + 45 : (10 + 5)] + 6 ⋅ (30 + 4 ⋅ 5 + 10).

  1. Выполним действия в круглых скобках:

10 + 5 = 15

30 + 4 ⋅ 5 + 10 = 30 + 20 + 10 = 60

  1. Выполним действия в квадратных скобках: 14 + 45 : 15 = 17
  2. Выполним остальные действия: 100 – 4 ⋅ 17 + 6 ⋅ 60 = 100 – 68 + 360 = 32 + 360 = 392

Порядок операций — PEMDAS

Операции

«Операции» означают такие действия, как сложение, вычитание, умножение, деление, возведение в квадрат и т. д. Если это не число, то, вероятно, это операция.

Но когда вы видите что-то вроде…

7 + (6 × 5 2 + 3)

… какую часть нужно вычислить в первую очередь?

Начать слева и идти направо?
Или идти справа налево?

Предупреждение: Вычислите их в неправильном порядке, и вы можете получить неверный ответ!

Итак, люди давно договорились следовать правилам при расчетах, а они таковы:

Порядок действий

Сначала делайте что-то в скобках

  4 × (5 + 3) = 4 × 8 =

32

 
  4 × (5 + 3) = 20 + 3 =

23

 (неверно)

Экспоненты (степени, корни) перед умножением, делением, сложением или вычитанием

  5 × 2 2
=		 5 × 4 =

20

 
  5 × 2 2 = 10 2 =

100

 (неверно)

Умножьте или разделите перед сложением или вычитанием

  2 + 5 × 3 = 2 + 15 =

17

 
  2 + 5 × 3 = 7 × 3 =

21

 (неверно)

В противном случае просто идите слева направо

  30 ÷ 5 × 3 = 6 × 3 =

18

 
  30 ÷ 5 × 3 = 30 ÷ 15 =

2

 (неверно)

Как мне все это запомнить.

.. ? ПЕМДАС!

Р

P первый

Е

E экспоненты (т. е. степени и квадратные корни и т. д.)

МД

M умножение и D ivision (слева направо)

КАК

Добавление A и удаление S (слева направо)

Разделить и умножить ранги одинаково (и идти слева направо).

Прибавлять и вычитать ранги поровну (и идти слева направо)

Итак, сделайте так:

После того, как вы сделали «P» и «E», просто идите слева направо, выполняя любую «M» или «D», как вы их найдете.

Затем идите слева направо, выполняя любые «A» или «S», как вы их найдете.



Вы можете вспомнить, сказав: « P аренда E извините M y D ухо A unt S союзник».

Или … Пухлые эльфы могут потребовать перекусить
Попкорн Пончики каждый понедельник Всегда воскресенье
Пожалуйста, ешьте мамины вкусные яблочные штрудели
Люди повсюду принимают решения о суммах

Вы можете предпочесть GEMS ( G rouping, E xponents, M умножить или разделить, добавить или S вычесть).
В Великобритании говорят БОДМАС (скобки, порядок, деление, умножение, сложение, вычитание).
В Канаде говорят BEDMAS (скобки, экспоненты, деление, умножение, сложение, вычитание).
Все это означает одно и то же! Неважно, как вы это помните, главное, чтобы вы поняли это правильно.

Примеры

Пример: Как вычислить

3 + 6 × 2 ?

M умножение перед A дополнение:

Сначала 6 × 2 = 12 , затем 3 + 12 = 15


900 02 Пример: как вычислить (3 + 6) × 2 ?

P первые

первые (3 + 6) = 9 , тогда 9 × 2 = 18


Пример: Как вычислить

12 / 6 × 3 / 2 ?

M умножение и D ivision имеют одинаковый ранг, поэтому просто идите слева направо:

Сначала 12 / 6 = 2 , затем 2 × 3 = 6 , затем 6 / 2 = 3

Практический пример:

Пример: Сэм бросил мяч прямо вверх со скоростью 20 метров в секунду, какое расстояние он пролетел за 2 секунды?

Сэм использует специальную формулу, учитывающую влияние гравитации:

высота = скорость × время — (1/2) × 9,8 × время 2

Сэм вводит скорость 20 метров в секунду и время 2 секунд:

высота = 20 × 2 − (1/2) × 9,8 × 2 2

Теперь расчеты!

Начните с: 20 × 2 − (1/2) × 9,8 × 2 2

Сначала скобки: 20 × 2 − 0,5 × 9,8 × 2 2

Затем в степени0013 2 =4):20 × 2 − 0,5 × 9,8 × 4

Затем умножить: 40 − 19,6

Вычесть и ГОТОВО! 20,4

Мяч достигает 20,4 метра через 2 секунды

Экспоненты экспонентов .

..

Что насчет этого примера?

4 3 2

Экспоненты особенные: они идут сверху вниз (сначала сделайте экспоненту сверху). Итак, мы вычисляем так:

Начать с:   4 3 2
3 2 = 3×3:   4 9
4 9 = 4×4×4×4×4×4×4×4×4:   262144

Так 4 3 2 = 4 (3 2 ) , не (4 3 ) 2

 

 

И наконец, что насчет примера с самого начала?

Начните с: 7 + (6 × 5 2 + 3)

Скобки сначала, а затем Показатель степени :7 + (6 × 25 + 3)

Затем Умножьте :7 + (150 + 3 )

Затем Добавить :7 + (153)

Скобки завершено: 7 + 153

Последняя операция Добавить : 160

 

297, 1566, 1572, 298, 1568, 381, 1570, 3854, 3855, 383

Заказ математических операций, БОДМАС | SkillsYouNeed

Для расчета, который имеет только одну математическую операцию с двумя числами, это простой случай сложения, вычитания, умножения или деления, чтобы найти ответ.

А как быть, когда есть несколько номеров и разные операции? Может быть, вам нужно делить и умножать или складывать и делить. И что ты тогда делаешь?

К счастью, математика основана на логике. Как это часто бывает, есть несколько простых правил, которые помогут вам определить порядок выполнения вычислений. Они известны как «Порядок действий» .

Правила упорядочения в математике — BODMAS

BODMAS — полезная аббревиатура, указывающая порядок решения математических задач. Важно, чтобы вы следовали правилам BODMAS, потому что без них ваши ответы могут быть неверными.

Аббревиатура BODMAS означает: ракетки

  • B (части расчета в скобках всегда идут первыми).
  • O заказы (числа, включающие степени или квадратные корни).
  • D ivision.
  • M умножение.
  • Дополнение .
  • S вычитание.

BODMAS, BIDMAS или PEMDAS?

Часто можно встретить BIDMAS вместо БОДМАС. Они точно такие же. В BIDMAS «I» относится к индексам, которые аналогичны ордерам. Для получения дополнительной информации см. нашу страницу, посвященную специальным номерам и понятиям.

PEMDAS

PEMDAS обычно используется в США и работает так же, как BODMAS. Акроним PEMDAS:

P aretheses,

E xponents (степени и корни),

M умножение и D ivision, 90 009

Дополнение и исключение S .


Дальнейшее чтение из книги «Навыки, которые вам нужны»

«Навыки, которые вам нужны» Руководство по арифметике

Это руководство, состоящее из четырех частей, знакомит вас с основами счета от арифметики до алгебры, с промежуточными остановками на дроби, деци малас, геометрия и статистика.

Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.

Использование BODMAS

Скобки

Начните с чего-нибудь внутри скобок , двигаясь слева направо.

Приказы

Затем сделайте что-нибудь, связанное со степенью или квадратным корнем (они также известны как приказы ), снова работая слева направо, если их больше одного.

Деление и умножение

После того, как вы сделали какие-либо части вычислений с использованием скобок или степеней, следующим шагом будет деление 9.0563 и умножить на .

Умножение и деление имеют одинаковый ранг, поэтому вы работаете с суммой слева направо, выполняя каждую операцию в том порядке, в котором она указана.

См. наши страницы: Умножение и Деление , чтобы узнать больше.

Сложение и вычитание

Последним шагом является вычисление любого сложения или вычитания . Опять же, вычитание и сложение имеют одинаковый ранг, и вы просто работаете слева направо.

См. наши страницы: Сложение и Вычитание , чтобы узнать больше.

Собираем все вместе

Этот окончательный рабочий пример включает в себя все элементы BODMAS.

Тестовые вопросы BODMAS

Правила BODMAS легче всего понять после некоторой практики и примеров.

Попробуйте эти расчеты самостоятельно, а затем откройте окно (щелкните символ + слева), чтобы увидеть работу и ответы.

В этом расчете нет скобок или порядков.

  1. Умножение предшествует сложению, поэтому начните с 20 × 3 = 60.
  2. Расчет теперь выглядит как 3 + 60

Таким образом, ответ будет 63 .

  1. Начните со скобок. (3 + 2) = 5.
  2. Расчет теперь выглядит как 25 − 5 ÷ 5
  3. Деление предшествует вычитанию. 5 ÷ 5 = 1.
  4. Расчет теперь выглядит как 25 − 1
    5. .

Таким образом, ответ будет 24 .

  1. Начните со скобок. (1+10) = 11.
  2. Расчет теперь выглядит как 10 + 6 × 11
  3. Умножение предшествует сложению. 6 × 11 = 66,
  4. Расчет теперь выглядит как 10 + 66.

Таким образом, ответ будет 76 .

Когда нет такого знака, как в этом вычислении, оператор является умножением, таким же, как запись 5 × (3 + 2) + 5 2 .

  1. Сначала выполните вычисления внутри скобок: (3 + 2) = 5.
  2. Это дает вам 5 × 5 + 5 2 .
  3. Следующий шаг — заказы, в данном случае квадрат. 5 2 = 5 × 5 = 25. Теперь у вас есть 5 × 5 + 25.
  4. Деление и умножение предшествуют сложению и вычитанию, поэтому ваш следующий шаг 5 × 5 = 25. Теперь вычисление выглядит так: 25 + 25 = 50.

Ответ: 50 .

В этом есть все! Но не паникуйте. BODMAS по-прежнему применяется, и все, что вам нужно сделать, это отменить расчет.

  1. Начните со скобок. (105 + 206) = 311.
  2. Расчет теперь выглядит как 311 – 550 ÷ 5 2 + 10
  3. Далее приказы или силы. В данном случае это 5 2 = 25,
    4. .
  4. Расчет теперь выглядит как 311 – 550 ÷ 25 + 10
  5. Далее, деление и умножение. Умножения нет, а деление 550 ÷ 25 = 22.
  6. Теперь расчет выглядит так: 311 – 22 + 10.
  7. Хотя у вас осталось еще две операции, ранг сложения и вычитания одинаков, поэтому вы просто выполняете слева направо. 311 – 22 = 289 и 289 + 10 = 299.

Ответ: 299 .

Подобные проблемы часто циркулируют в социальных сетях с надписями вроде «90% людей понимают это неправильно». Просто следуйте правилам BODMAS, чтобы получить правильный ответ.

  1. Здесь нет скобок и порядков, поэтому начните с деления и умножения.
  2. 7 ÷ 7 = 1 и 7 × 7 = 49.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *