Статья «Графический метод решения задач» по математике для обучающихся 7-11 классов
Графический метод решения задач.
В школьной практике в последнее время один из ведущих способов решения задач связан с алгебраическим (аналитическим) методом их решения, что указывает на определённый разрыв между методами решения задач, применяемыми в науке, технике, повседневной жизни.
Устранение, где это возможно, указанного разрыва является одной из важнейших проблем усиления политехнической направленности школьного курса обучения. В большей степени эта проблема вызвана тем, что существующие учебные и методические пособия не уделяют должного внимания различным методам решения задач. Между тем реализация их даёт большие возможности для совершенствования обучения математике. Для обеспечения дальнейшего повышения
качества обучения недостаточно совершенствовать лишь вычислительные
методы математики, но необходимо также развивать и совершенствовать
геометрические и графические методы, составляющие основы конструктивного
мышления.
Графические методы и проецирование, как мне кажется, могут
успешно конкурировать и сочетаться с аналитическими , как отличающиеся большей наглядностью и простотой.
В своей практике я часто применяю этот метод для решения задач из разных тем и разделов алгебры и геометрии. В одной небольшой статье не представляется возможным сколь-нибудь обстоятельно раскрыть все аспекты. Для выявления определённых преимуществ графических методов перед аналитическими рассмотрю решения некоторых задач.
1. Решение текстовых задач с использованием координатного метода.
Как уже отмечалось выше, один из ведущих способов решения текстовых задач связан с использованием уравнений, первое знаком-ство с которыми начинается в начальной школе. Обучающиеся пя-тых- шестых классов, по существу, решают текстовые задачи только составлением уравнения по их условию. Считаю чрезмерное
увлечение этим способом не вполне оправданным.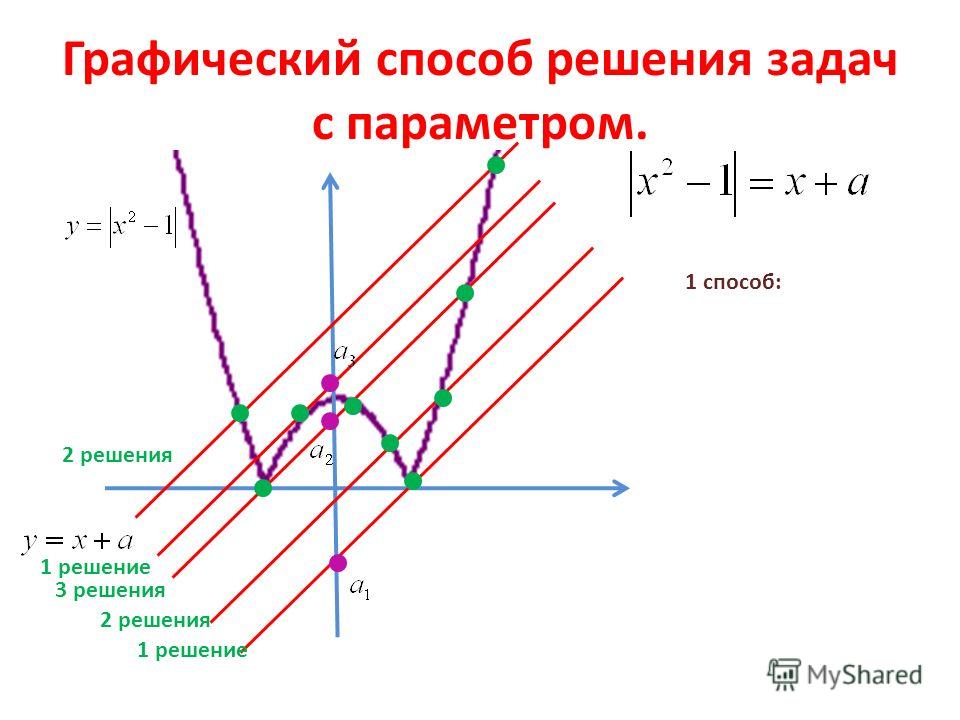
Некоторые задачи решаются проще арифметическим способом с использованием координатного луча. Замечу, что в процессе решения задач единичный отрезок явно не указывается, но подразумевается в каждой наглядной иллюстрации.
Задача 1. Турист часть пути прошёл пешком, часть проехал на вело-
сипеде, остальной путь проехал на машине. Пешком турист
преодолел путь, в четыре раза меньший, чем на велосипеде,
а на машине на 300 км. больший, чем пешком. Какой путь
турист прошёл пешком, если на машине он проехал на
60 км. больше, чем на велосипеде?
РЕШЕНИЕ:
1 способ 2 способ
Пусть х км.- путь туриста пешком. Изобразим схематически
Тогда 4х км.
— путь, проделанный движение туриста на раз-
на велосипеде, ( х + 300 )км., или ных участках его пути.
( 4х + 60 )км.- путь на машине. п:
Составим уравнение и решим его: в:
х + 300 = 4х + 60; м:
4х – х = 300 – 60; -60
3х = 240;
х = 240 : 3; + 300
х = 80. Покажем, какова разница в
километрах между ними.
Из чертежа явно видно, что
Турист прошёл пешком 80 км.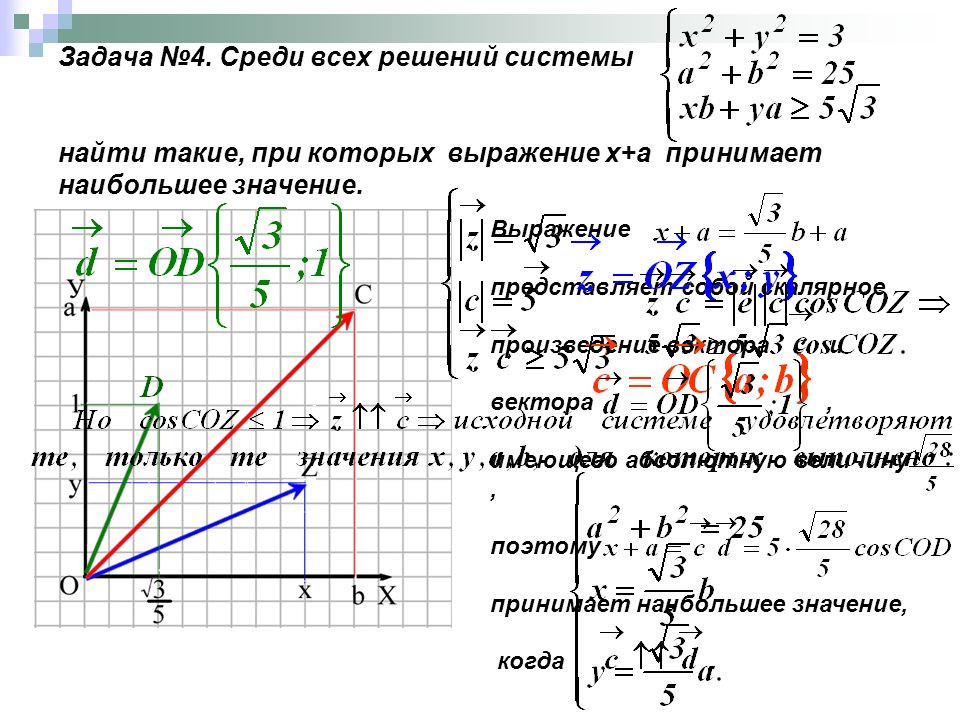
. в трёх частях
пути 240 км.,
значит в одной части 80 км.
Ответ: 80 км.
Рассмотрим ещё один пример:
Задача 2: Из деревни вышел пешеход, а через два часа вслед за ним
выехал велосипедист. Скорость велосипедиста 10 км/ч., а
скорость пешехода 5км/ч.. Через сколько времени после
своего выезда велосипедист догонит пешехода.
РЕШЕНИЕ:
Решим задачу графически.
|______|______|______|______|_______________
0 5 10 15 20
Ответ: встреча
произойдёт через два часа.
Ознакомление обучающихся с этим способом не потребует много времени, однако его применение поможет учителю в обучении решению задач.
Хочу отметить, что возможно и разумное сочетание рассмотренных способов, например, сначала изобразить наглядно условие задачи для лучшего его понимания, а после этого ввести х и составить уравнение по условию.
Использование координатного луча кроме непосредственной помощи в нахождении верного пути решения задачи формирует координатные представления обучающихся. Это, несомненно, станет дополнительной основой при дальнейшем изучении координатного метода.
2. Графики равномерного движения при решении текстовых задач.
Задача 2. Из двух населённых пунктов А и В одновременно навстречу
друг другу выходят два туриста. При встрече оказывается,
что турист, вышедший из А, прошёл на 2 км. больше, чем
турист, вышедший из В.
Продолжая движение с той же
скоростью, первый турист прибывает в В через 1 час 36мин.,
а второй в А – через 2 часа 30 мин.. Найдите расстояние АВ
и скорость каждого туриста.
Обычно при решении текстовых задач на движение для наглядности
пройденное расстояние изображают отрезком. Применение коорди-натной прямой для решения этой задачи вряд ли приведёт к его упро-щению. Этот недостаток можно устранить, применяя графическое представление движения, известное из курса физики.
Отмечу, что при решении задач на равномерное движение, если равны скорости, пройденные расстояния и промежутки времени, полезны соотношения:
s1/s2 = t1/t2 ;
v1/v2 = t1/t2 ;
s1/s2 = v1/v2 .
Кроме того, напомню, что тангенс угла наклона прямой х = x0 + vt к оси Оt численно равен скорости тела.
Вернёмся теперь к задаче.
РЕШЕНИЕ:
Построим график движения туристов.
По условию задачи РО – РК = 2
s КС = 1,6 и ОД = 2,5.
Из подобия треугольников
В К 1,6 С (ïВКР ≈ïДОР, ïСКР ≈ïАОР )
следует, что
Р ==, но ВК = АО,
Поэтому =, или АО= 2.
А О 2,5 Д t Далее, =, откуда
РК = 8 км.
V1= 5км/ч. и V2= 4 км/ч..
Как видим, использование графиков приводит к простому и красивому решению.
Задача 2: Теплоход от Горького до Астрахани идёт пятеро суток,
а от Астрахани до Горького идёт семеро суток. Сколько
дней будет плыть плот от Горького до Астрахани.
РЕШЕНИЕ:
Д Х
А
К
Г О В С Р
Скорость движения теплохода относительно плывущего плота одна
и та же как по
течению реки, так и против течения, поэтому если теплоход и плот выйдут из Г
одновременно, то теплоход, возвратясь из А, встретит плот через столько же
дней, сколько он потратил на путь из Г в А, следовательно, ГО = ОВ = 5.
Так как ОДВ подобен ВКС и ВКГ подобен РХГ, то
из соответственных соотношений получим, что ГР = 35.
Ответ: плот будет плыть 35 дней.
3. Графический метод решения стереометрических задач.
Аналогичным образом обстоят дела и при изучении стереометрии.
Обычно при решении стереометрических задач учителя знакомят
обучающихся только с аналитическими методами их решения, а
графические методы вновь остаются за рамками должного внимания.
Задача 3. Через вершину конуса, радиус основания которого R,про-
ведена плоскость под углом φ к его высоте. Найти площадь
полученного сечения, если образующая конуса составляет
с плоскостью основания угол α.
Для
аналитического решения задачи требуется выполнить много вычислений, что для
некоторых обучающихся трудно. Для предуп-реждения этих трудностей используем
графический метод решения задачи, сущность которого ученикам хорошо известна из
курса черчения.
1.Выполним эскиз фигуры в наглядном изображении.
2.Ясно, что в сечении получается треугольник, для вычисления
площади которого нужно найти длину отрезков MN и SK.
3.Располагаем фигуру так, чтобы плоскость треугольника SОА
была параллельна плоскости проекций V. Тогда основание
конуса будет параллельно плоскости проекций Н.
В этом случае отрезки OA, SK, SO и углы α и φ проецируют-
ся в натуральную величину на фронтальной плоскости проек-
ции.
4. Допустим, что R=10 мм., φ = 350 и α = 400.
5.Выберем масштаб 2:1.
6. Выполним построение на эпюре.
а) сначала строим равнобедренный треугольник s/a/b/ по основа-
нию 2R=40мм. и по углу α = 350 при основании, являющемся
фронтальной проекцией конуса.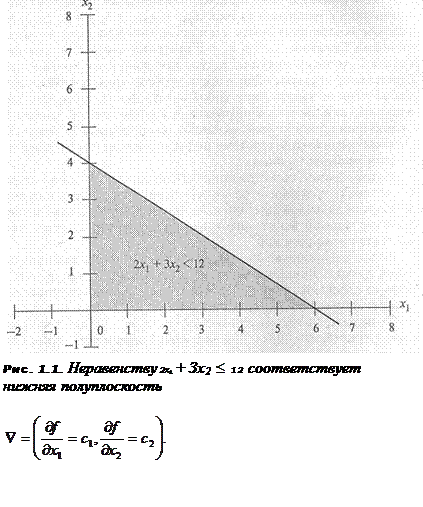
От точки s/ под углом φ=400
к высоте s/o/ треугольника s/a/b/ проводим s/k/ , являющийся
фронтальной проекцией сечения.
Основание сечения mn проецируется на этой плоскости натуральную величину. Чтобы найти натуральную величину высоты сечения,
выполним вращение его плоскости и приведём её к положению, параллельному горизонтальной плоскости проекций. С помощью линии связи строим отрезок s0k.
7. Измерив длину отрезков и зная масштаб М2:1, находим
mn=16,5мм. и s0k=9мм..
8. Находим площадь сечения: S ∆mns0 = mn·s0k = 74,25(мм2).
Применение этого метода, во-первых, помогает подготовить
обучающихся к работе на производстве, где часто решаются
аналогичные задачи данным методом. Во-вторых, облегчает
решение сложных
геометрических задач на комбинацию или на сечения.
Однако следует учитывать индивидуальные особенности ученика.
Алгебраические решения ближе тому, кто любит формулы и пре-образования; решения с использованием графиков привлекают тех, кто нуждается в содержательных образах.
Наконец, следует отметить, что приведённые в статье методы
решения задач развивают пространственное представление и конструктивно-графические способности, позволяют формировать у обучающихся правильное представление о роли чертежа в курсе математики. Кроме того, они являются прекрасным средством реализации межпредметных связей между алгеброй, геометрией и физикой; геометрией и черчением. При этом знания, полученные на уроках по разным предметам, объединяются, становятся более осознанными, действенными.
Понятно, что использование описанных методов требует оп-
ределённых навыков графического представления условий задачи.
Они могут быть сформированы совместными усилиями учителей
физики, черчения, математики.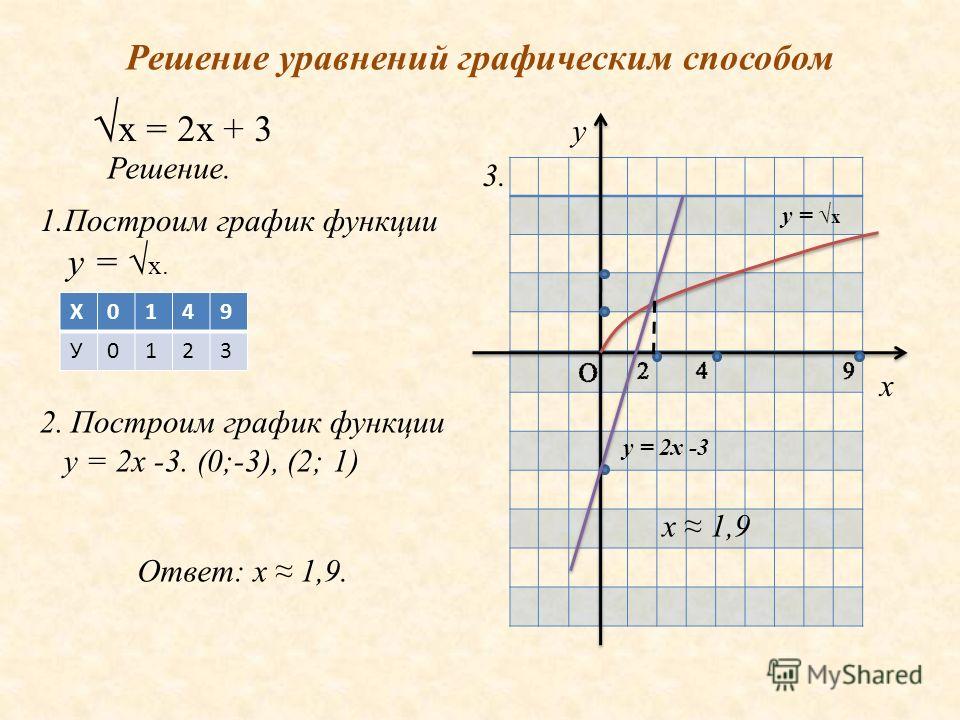
Уверена в одном, затраченные уси
лия быстро окупятся.
16. Графический метод решения задач линейного программирования
Графический метод характеризуется простотой и наглядностью, однако он недостаточно точен и применим только для задач с не более чем тремя переменными. Последнее обусловлено тем, что человек, живущий в трехмерном пространстве, практически не способен представить себе визуально пространство более высокого порядка.
Метод основан
на том, что каждое ограничение неравенство
отсекает в n-мерном пространстве n-мерную
полуплоскость (в данной курсовой работе
это – двухмерное пространство (плоскость)
и простая полуплоскость). Совокупность
этих полуплоскостей (если ограничения
совместны) образует n-мерный многогранник
допустимых решений. Оптимальное решение
достигается в одной из вершин многогранника.
Для определения этой вершины необходимо
построить поверхность уровня целевой
функции (в курсовом проекте – линию
уровня).
Затем следует перемещать эту
поверхность (линию) в направлении
градиента до крайней точки области
допустимых решений (ОДР).
Рассмотрим следующий простой пример решения задачи линейного программирования (ЗЛП) графическим методом.
Математическая модель:
2Х1+3Х2≤60;
3Х1+2Х2≤60;
4Х1+20Х2≤200;
Х1≥0; Х2≥0;
F=40Х1+30Х2→Мах.
Перейдем от неравенств к равенствам:
2Х1+3Х2=60;
3Х1+2Х2=60;
4Х1+20Х2=200.
Это уравнения прямых линий, которые могут быть легко построены по двум точкам:
для первого ограничения –
Х1=0; Х2=20;
Х2=0; Х1=30.
для второго ограничения –
Х1=0; Х2=30;
Х2=0; Х1=20.
для третьего ограничения –
Х1=0; Х2=10;
Х2=0; Х1=50.
Градиент целевой функции – это вектор, характеризующий направление и скорость изменения функции (в данном случае – целевой функции). Он определяется ее частными производными по каждой переменной:
Линия уровня
целевой функции перпендикулярна
градиенту.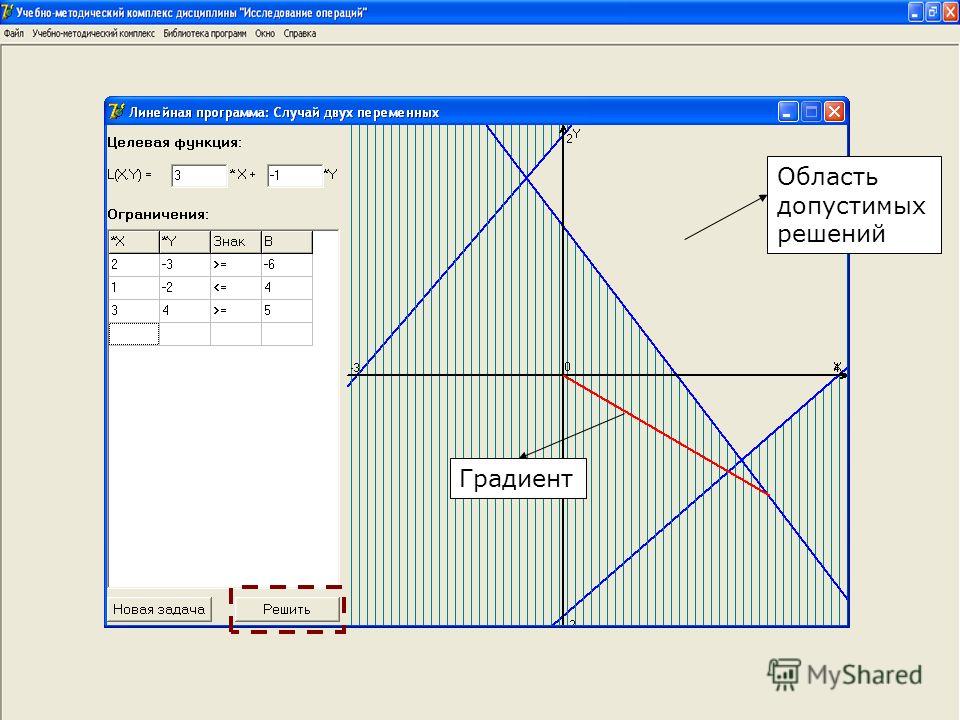
Графическое решение данной задачи приведено на рисунке 6.1.
Рис. 6.1. Графическое решение задачи
Область допустимых решений (ОДР) в данном случае образуется четырехугольником ОВСД. Ни одна точка внутри его или на его границе не противоречит ни одному из ограничений. Оптимальное решение находится в одной из вершин четырехугольника. Для нахождения оптимального решения перемещаем линию уровня целевой функции в направлении градиента до крайней точки ОДР. Такой точкой является точка С с координатами: Х1=16; Х2=8. Значение целевой функции F=40×16+30×8=880. Очевидно, что это решение не отличается высокой точностью, что характерно для графического метода. Из рисунка видно, что ресурсы второго и третьего видов использованы полностью, а ресурс первого вида оказался в избытке. Для количественной оценки этого избытка определим сначала расход данного ресурса: 2×16+3×8=56. Запас равен 60, тогда остаток составит 60–56=4.
Графический метод
Графическим
методом в основном решаются задачи с
малым числом переменных.
Он включает
следующие этапы:
1. Строится многогранник решений.
Геометрический смысл системы ограничений состоит в следующем: уравнение a11x1 + … + a1nxn = b1 представляет собой
гиперплоскость в n-мерном пространстве, неравенство же есть точки подпространства, лежащие по одну сторону от
гиперплоскости и образующие выпуклое множество. Следовательно, система ограничений (1.2) задачи линейного
программирования есть множество точек n-мерного пространства, причем это множество выпуклое и каждая точка является
решением системы неравенств.
2. Находятся вектор
и вершина многоугольника решений, на которой достигается max z.
Известно, что вектор-градиент функции z показывает направление наибольшего роста функции. Строится линия уровня c1x1
+…+ cnxn = h, проходящая через начало координат. Линия уровня обладает замечательным свойством: после подстановки
координат
любой ее точки в выражение целевой
функции z последняя принимает постоянное
значение.
Далее перемещаем
линию уровня в направлении вектора с до тех пор, пока не будет достигнута угловая вершина многоугольника решений либо
установлена неограниченность функции на множестве решений.
3. Определяются координаты угловой вершины, являющиеся оптимальным планом, и значение целевой функции в этой
точке. Замечание. При нахождении решения задачи линейного программирования графическим методом могут встретиться
случаи, изображенные на следующих рисунках.
На первом рисунке изображен случай, когда целевая функция принимает максимальное значение в единственной точке M.
Из второго рисунка видно, что максимальное значение целевая функция принимает в любой точке отрезка AB. На третьем рисунке изображен случай, когда целевая функция не ограничена сверху на множестве допустимых решений. Отметим, что нахождение минимального значения целевой функции отличается от нахождения ее максимального
значения
лишь тем, что линия уровня c1x1 +.
.. + cnxn = h
перемещается не в направлении вектора
с, а в противоположном направлении.
Графический метод решения задачи по линейному программированию и помощь с домашним заданием
Отличная помощь от графического метода решения задачи по задаче линейного программирования Помощь по задаче
Решение задач по линейному программированию может быть очень сложной темой для прорыва. Студенту трудно не только его основное значение, но и расчетное решение его задач. Но вы не можете просто изменить тему в целом. Что вы можете сделать, так это присоединиться к myhomeworkhelp.com и получить нашу команду графического метода решения задачи линейного программирования Помощь в выполнении домашних заданий, чтобы выполнить и выполнить все ваши задания без особых задержек.
Что такое линейное программирование?
Мы хорошо разбираемся в детализации предмета и поэтому можем заверить вас, что если вы обратитесь за помощью к нашей именитой команде, то вам больше не нужно будет думать о заданиях вашего предмета.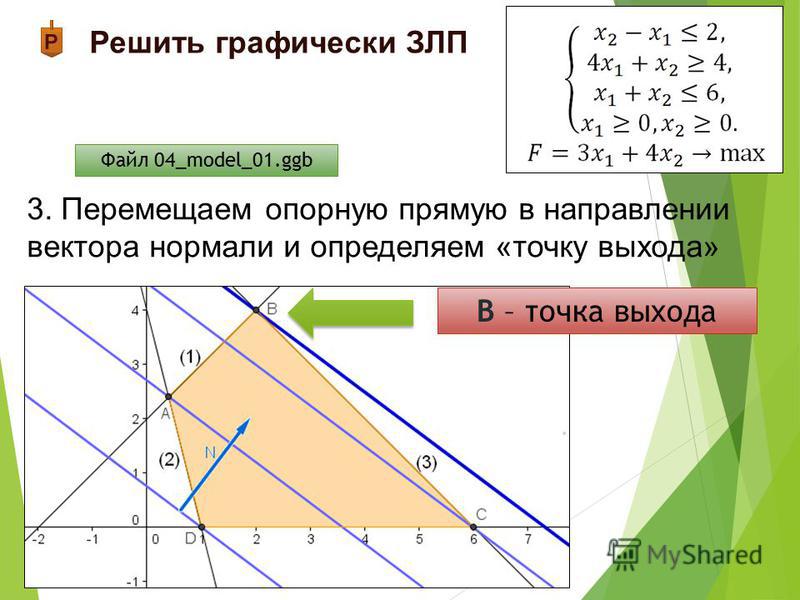
И это потому, что команда умеет предоставлять вам лучший контент. Они объяснили проблему линейного программирования следующим образом:
Линейное программирование — это часть матричной алгебры, которая используется для решения широкого класса задач в форме системы линейных уравнений. Это своего рода уравнение, в котором переменные величин стоят первыми по степени, а их график представляет собой прямую линию. Его функции классифицируются по функциям целей, которые могут либо максимизировать, либо минимизировать в зависимости от его предела. И пределы, и функции целей должны быть готовы либо к линейному неравенству, либо к равенству. Функции заключаются в том, чтобы максимизировать отдачу, и это также с минимальными затратами. Есть три предположения, сделанные для линейного программирования, в которых наша команда по графическому методу решения задачи назначения задачи линейного программирования имеет опыт, и они:
- Быть линейным:
Такие функции, как стоимость, технические потребности и цены, должны быть линейными.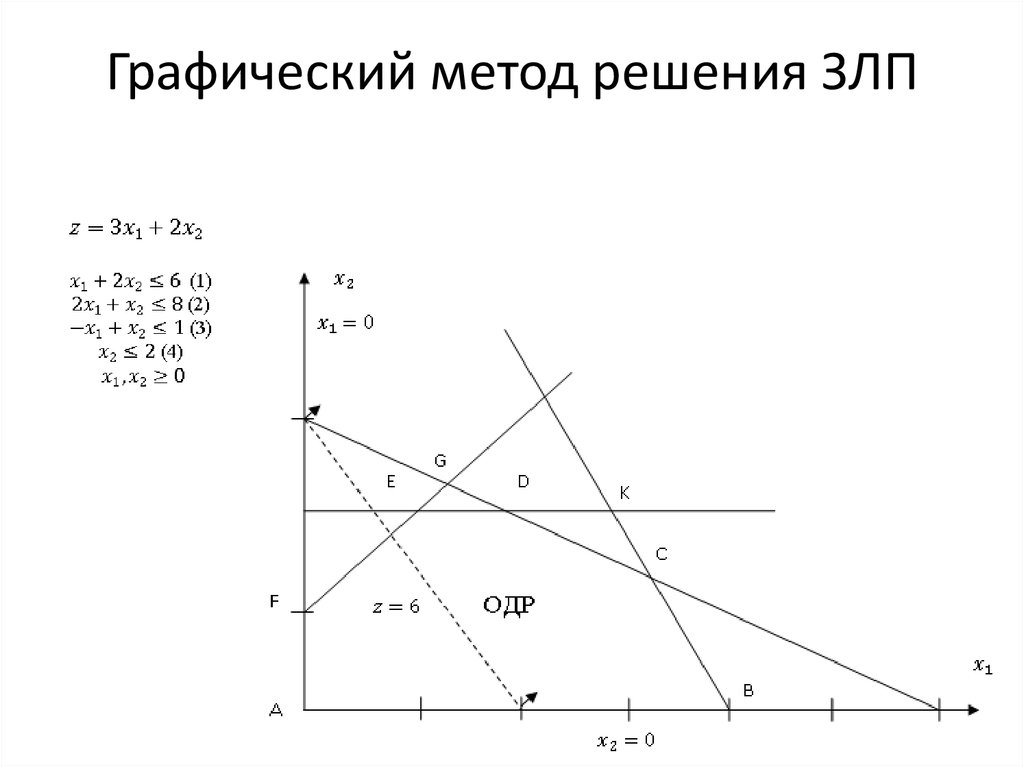
- Знание достоверности:
Твердо зная все параметры.
- Без минусов:
Значения переменных в решениях должны быть положительными.
Есть два способа решения задачи линейного программирования —
1. Графический метод
2. Симплексный метод
Графические методы имеют свои ограничения, так как они имеют две переменные и фиксированное количество пределов, так как могут быть только две переменные для оценки в графическом представлении. Таким образом, это ограничивает использование графического метода в реальном мире. Но мы заверяем вас, что члены нашей команды приложат все усилия, чтобы ваши задания были успешными, пока вы учитесь. Это потому что; мы только что создали эту команду графического метода решения проблемы линейного программирования с помощью домашней работы, чтобы они могли легко решить все ваши проблемы.
Причины выбрать нас:
Мы с гордостью можем сказать, что у нас есть наставники, обладающие опытом в самых разных областях.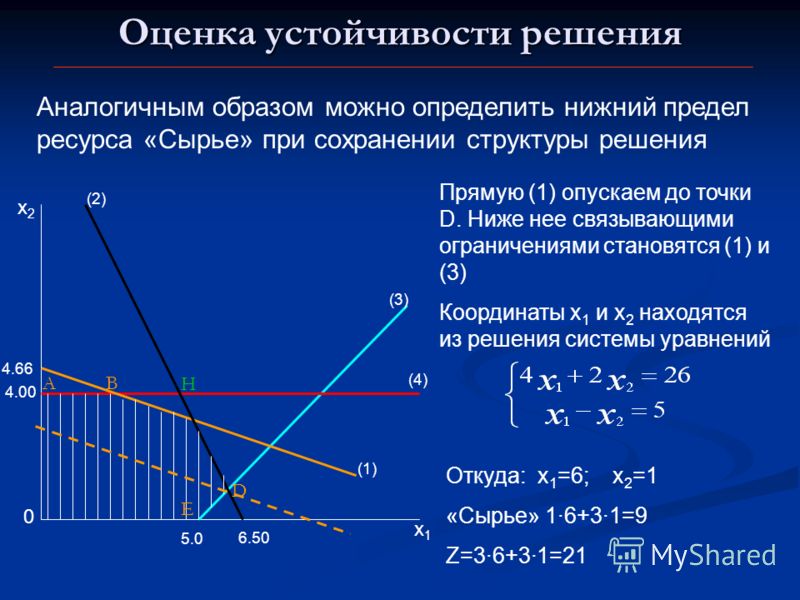
Мы не развлекаемся, просто заполняя страницы, чтобы закончить ваши задания. Мы знаем, как важно выполнить задание с подробной работой, которую также будет легко понять. Содержание работы тщательно проверяется нашими экспертами, чтобы избежать орфографических, грамматических и типографских ошибок. Наша команда онлайн 24×7, чтобы помочь вам разобраться в этой теме.
Поскольку наша работа будет на 100% оригинальной, не будет никакого плагиата, даже если нам придется воспользоваться онлайн-помощью для сбора какой-либо информации. Кроме того, стоимость наших услуг очень низкая по сравнению с другими онлайн-провайдерами. И мы строго верим в соблюдение наших сроков, поскольку это самая важная вещь, которую мы предоставляем, а также наша приверженность производительности.
Итак, что вас сдерживает? Присоединяйтесь к myhomeworkhelp.com как можно скорее, чтобы воспользоваться лучшим графическим методом решения справки по задаче линейного программирования.
Одновременные уравнения — узнайте и поймите их онлайн
Одновременные уравнения — это наборы уравнений с несколькими неизвестными значениями.
Их можно использовать для расчета того, что на самом деле представляет каждое неизвестное. Вы также можете увидеть, что они относятся к системам уравнений.
Пример графического отображения одновременных уравнений, transom.org
На приведенном выше графике показаны одновременные уравнения
1)
2)
две линии пересекаются. На самом деле это один из способов решения одновременных уравнений, но в этом руководстве мы покажем вам лучшие и более быстрые способы, так что читайте дальше!
Ознакомьтесь с нашим руководством по решению линейных уравнений, если вам нужно освежить знания о решении одного неизвестного, так как мы будем опираться на него.
Зачем нужны одновременные уравнения?
Если вы хотите решить уравнение только с одним неизвестным значением, процесс обычно очень прост. Однако все усложняется, когда вводятся дополнительные неизвестные.
Рассмотрим первое уравнение из предыдущего:
Вы можете попробовать разные числа и увидеть, что одним из возможных решений будет . Но на самом деле их бесконечных решений. Подумайте, что было бы, если бы x или y были дробями!
Нам нужно второе уравнение для определения единственного уникального решения.
Как решать одновременные уравнения?
Одновременные уравнения можно решать несколькими способами. Мы покажем вам два лучших способа, так как они быстрее, чем использование графика, как показано ранее. Каждый способ может быть проще в зависимости от вопроса, и вы можете обнаружить, что один из них кажется вам более естественным, поэтому обязательно попробуйте оба.
Решение методом исключения
Одним из способов решения одновременных уравнений является исключение . Вы можете использовать этот метод наиболее легко, когда неизвестное, которое вы хотите исключить, имеет один и тот же коэффициент в каждом уравнении, но мы покажем вам, как использовать его и в других случаях.
Вернемся к нашим исходным уравнениям:
Мы можем видеть, что если мы сложим каждую часть двух уравнений вместе, мы сможем легко исключить y. (Вы можете добавить или вычесть уравнения в зависимости от ситуации.) Давайте попробуем!
Остается одно уравнение:
Теперь мы можем подставить его в одно из исходных уравнений, чтобы найти у: путем подстановки этих значений в другое уравнение. Это очень важно, чтобы помочь вам обнаружить ошибки, которые вы, возможно, сделали.
Решить
Для начала вы можете вычесть каждую часть одного уравнения из другой, чтобы исключить x;
Теперь вы можете работать с ответами, чтобы сформировать новое уравнение для решения для y;
Теперь этот ответ можно подставить в одно из исходных уравнений для решения x;
Наконец, не забудьте проверить свои ответы, подставив их в одно из уравнений;
Решение методом исключения (разные коэффициенты)
Теперь рассмотрим новый пример:
1)
2)
В этом примере использование исключения не так просто, как раньше. Нам нужно каким-то образом изменить уравнения, чтобы сделать коэффициенты одинаковыми. Нам разрешено делать это до тех пор, пока мы выполняем одну и ту же операцию с обеих сторон уравнения.
Похоже, мы можем получить один и тот же коэффициент при у, умножив первое уравнение на 3, а второе на 2. Попробуем так:
1)
2)
заменим в нашем ответе x как прежде:
Проверка:
Решайте
, чтобы сделать это первое, что вам нужно сделать два из коэффициентов. уравнение на 2, что дает нам эти уравнения;
Теперь вы можете вычесть одно уравнение из другого, чтобы исключить y и найти x;
Теперь вы можете ввести x в одно из уравнений, чтобы найти y;
Не забывайте, что можно проверить свои ответы, подставив оба ответа в уравнение и убедившись, что оно работает;
Решение подстановкой
Есть еще один способ, которым мы могли бы подойти к первому набору уравнений: подстановка.
Вспомните, что в наших предыдущих примерах, как только мы нашли одно значение, мы можем подставить его обратно в уравнение, чтобы найти другое. Этот метод включает в себя ту же технику, но на другом этапе процесса.
1)
2)
Чтобы использовать метод подстановки, вы можете начать с подстановки уравнения 2 в y уравнения 1, чтобы помочь вам найти x;
Теперь вы можете подставить 4 в одно из уравнений, чтобы найти y;
1)
2)
В этом случае нам нужно изменить уравнение 2, чтобы получить его через y, это позволит нам подставить его в уравнение 1 и решить для x ;
3)
4)
Последний шаг остается прежним: мы просто используем это значение во втором уравнении, что дает нам y = 1, как и раньше. Тогда обязательно проверьте свой ответ!
Как решать одновременные уравнения с квадратным уравнением?
Для решения одновременных уравнений с квадратным уравнением мы используем метод подстановки, который применялся ранее.
1)
2)
На графике эти уравнения будут выглядеть так:
Рабочий пример, transom.org
Первое, что нам нужно сделать в этом случае, это изменить первое уравнение. Ключ в том, чтобы сделать их обоих равными y (т. е. равными одному и тому же), потому что это означает, что мы можем сделать их обоих равными друг другу.
3)
Теперь у нас есть квадратное уравнение , которое вы можете решить, используя предпочитаемый вами метод. В этом примере мы собираемся использовать факторизацию . (Если вам нужно попрактиковаться в этом, ознакомьтесь с нашей статьей о факторинге квадратных выражений!)
Как видите, у нас есть два возможных значения x. Это означает, что нам нужно подставить их обратно, чтобы найти две пары решений наших одновременных уравнений:
1) или 1)
Это дает нам пары
или
проверить:
2)
В этом примере у нас было два решения, но важно помнить, что их не обязательно должно быть два.
Может быть один или даже ни одного, точно так же, как когда вы решаете квадратное уравнение самостоятельно. Например, подумайте, сколько решений будет на графике, показанном ниже:
Пример графика, показывающего несколько решений, transom.org
Как вы формируете свои собственные одновременные уравнения?
Для составления собственных одновременных уравнений может потребоваться интерпретация текста. Некоторые вопросы более многословны и требуют некоторого размышления, чтобы построить уравнения, прежде чем решать их.
Али покупает 2 ириски и 3 жевательных резинки. Би покупает 3 ириски и 2 жевательных резинки. Сумма Али составляет 0,10 фунта стерлингов, а Беа платит 0,15 фунта стерлингов. Сколько стоят ириски и жевательные резинки?
Во-первых, нам нужно идентифицировать переменные. В данном случае это ириски и жевательные резинки. Мы видим, что 2 ириски и 3 жевательных резинки стоят 10 пенсов, а 3 ириски и 2 жевательных резинки стоят 15 пенсов.