Онлайн составить уравнение плоскости проходящей через 3 точки: Онлайн калькулятор. Уравнение плоскости

Уравнение плоскости, проходящей через три точки

Похожие презентации:

«Уравнение плоскости» (профильный уровень), урок №1, 11 класс

Уравнение поверхности F(x,y,z)=0

Плоскость и прямая в пространстве

Плоскость. Уравнение плоскости по точке и нормальному вектору

Уравнение плоскости

Расстояние между двумя точками. Середина отрезка. Координаты середины отрезка. Тема 4

Расположение плоскости, в зависимости от коэффициентов уравнения

Плоскость в пространстве

Аналитическая геометрия на плоскости

Плоскость. Уравнения плоскости

1. Уравнение плоскости, проходящей через три точки

Задачи ЕГЭ (С2)

2. Уравнение плоскости

Ах + Ву + Сz + D = 0,
где А, В, С, D – числовые
коэффициенты

3. Особые случаи уравнения:

D = 0, Ax+By+Cz = 0
плоскость проходит через начало координат.
А = 0; Ву + Cz +D = 0
плоскость параллельна оси Ох
В = 0; Ах + Cz +D = 0
плоскость параллельна оси Оу
C = 0, Ax+By+D = 0
плоскость параллельна оси Oz.

4. Особые случаи уравнения:

А = В = 0, Сz + D = 0
плоскость параллельна плоскости
Оху
А = С = 0, Ву + D = 0
плоскость параллельна плоскости
Охz
B = C = 0, Ax + D = 0
плоскость параллельна плоскости

5. Особые случаи уравнения:

C = D = 0, Ax +By = 0
плоскость проходит через ось Oz.
Уравнения координатных
плоскостей:
x = 0,
плоскость Оyz
y = 0, плоскость Оxz
z = 0, плоскость Оxy

6. Плоскость не проходит через начало координат, не параллельна координатным осям

7. Точки пересечения с осями координат

с осью Ох:
(-D/A; 0; 0)
с осью Оy:
(0; -D/B; 0)
с осью Оz:
(0; 0; -D/C)

8. Две плоскости

9. Алгоритм составления уравнения плоскости, проходящей через три точки

М(x¹, y¹, z¹),
N(x², y², z²),
K(x³, y³, z³)
Подставить координаты точек
в уравнение плоскости.
Получится система трех
уравнений с четырьмя
переменными.

10. Замечание

Если плоскость проходит через
начало координат, положить D
= 0,
если не проходит, то D = 1

11.

ЗадачаВ правильной четырехугольной
призме ABCDA¹B¹C¹D¹ со
стороной основания 12 и
высотой 21 на ребре АА¹ взята
точка М так,
АМ = 8, на
ребре ВВ¹ взята точка К так, что
В¹К равно 8. Написать
уравнение плоскости D¹МК.

13. Запишем координаты точек

М(0, 0, 13)
К(12, 0, 8)
D¹(0, 12, 0)

14. Подставим в систему уравнений

15. Найдем А, В, С

16. Уравнение плоскости

17. Умножим обе части уравнения на -156

Уравнение плоскости D¹МК
5x + 13y + 12z – 156 = 0

18. Задача 1

В правильной четырехугольной
призме ABCDA¹B¹C¹D¹ сторона
основания равна 2, и диагональ
боковой грани равна √10.
Написать уравнение плоскостей
АВ¹С и плоскости основания
призмы.

19. Задача 2

В правильной шестиугольной
призме ABCDEFA¹B¹C¹D¹E¹F¹
сторона основания равна 4, и
диагональ боковой грани равна
5.
Написать уравнение плоскостей
А¹В¹E и плоскости основания
призмы.

20. Плоскость проходит через начало координат

Плоскость параллельна оси
Ох

22. Плоскость параллельна плоскости Оху

23. Плоскость параллельна плоскости Охz

24. Плоскость Oxy

English     Русский Правила

Уравнение плоскости, проходящей через три точки

Пусть даны три точки ,и. Если точки не лежат на одной прямой, то через них всегда можно провести единственную плоскость. Обозначим (х, у, z) координаты произвольной точки М пространства и рассмотрим три вектора: ,,. ТочкаМ лежит на плоскости М₁М₂М₃

в том и только в том случае, когда перечисленные три вектора компланарны, а значит , т.е. определитель, составленный из их координат, равен нулю:

.

Пример V.5. Написать уравнение плоскости, проходящей через точки ,и.

Решение. Пусть – произвольная точка плоскости, тогда векторы,,компланарны, поэтому:

Вычисляя определитель по правилу треугольников, получим:или.

Теорема V.1. В пространстве всякая плоскость выражается уравнением первой степени ,.

Доказательство. В предыдущем пункте было установлено, что всякая плоскость может быть задана уравнением вида (V.4):

, .

Раскрыв скобки и обозначив , получим общее уравнение первой степени относительно

x, y, z: , эквивалентное уравнению (V.4). Поэтому оно определяет ту же плоскость, что и уравнение (V.4), и называется общим уравнением плоскости. Коэффициенты при переменных в этом уравнении сохраняют тот же геометрический смысл, что и в равенстве (V.4), то есть являются координатами нормального вектора плоскости. Так как нормальный вектор плоскости является ненулевым, то коэффициентыA, B и C не могут быть одновременно равны нулю. Итак, мы доказали, что всякая плоскость в определяется уравнением первой степени относительно переменных координат x, y, z.

Теорема V.2 (обратная). Всякое линейное уравнение с тремя переменными ,, определяет плоскость в пространстве , если хотя бы один из коэффициентов при переменных не равен нулю.

Доказательство. Пусть x₀, y₀, z₀ – какое-либо решение данного уравнения. Тогда , откуда. Подставляя в данное уравнение вместоD его значение и группируя члены, получим

.

Это уравнение плоскости, проходящей через точку и имеющей нормальный вектор. Следовательно, и равносильное ему уравнениеопределяет плоскость [перпендикуляр-ную вектору].

Пример V.6. Построить в прямоугольной системе координат плоскость, заданную уравнением .

Решение. Для построения плоскости необходимо и достаточно знать какие-либо три ее точки (не лежащие на одной прямой), например точки пересечения плоскости с осями координат. Полагая в заданном уравнении , получим. Следовательно, заданная плоскость пересекает ось

Oz в точке . Аналогично, приполучим, то есть точку; приполучим, то есть точку. По трем точкам,,строим заданную плоскость (рис.V.6).

Частные случаи общего уравнения плоскости. Рассмотрим особенности расположения плоскости в тех случаях, когда те или иные коэффициенты общего уравнения обращаются в нуль.

1. При уравнениеопределяет плоскость, проходящую через начало координат, так как координаты точкиудовлетворяют этому уравнению.

2. При уравнениеопределяет плоскость, параллельную осиОх, поскольку нормальный вектор этой плоскости перпендикулярен осиОх (его проекция на ось Ох равна нулю). Аналогично при плоскостьпараллельна осиОу, а при плоскостьпараллельна осиОz.

3. При уравнение определяет плоскость, проходящую через ось

Ох, поскольку она параллельна оси Ох () и проходит через начало координат (). Аналогично плоскость проходит через ось Оу, а плоскость – через ось Оz.

4. При уравнение определяет плоскость, параллельную координатной плоскости Оxу, поскольку она параллельна осям Oх () и Оу (). Аналогично, плоскость параллельна плоскости уОz, а плоскость – плоскости Оxz.

Рис. V.6

5. При уравнение(или ) определяет координатную плоскость Оxу, так как она параллельна плоскости Оxу () и проходит через начало координат (). Аналогично уравнениев пространстве определяет координатную плоскостьОxz, а уравнение – координатную плоскостьОyz.

Пример V.7. Составить уравнение плоскости P, проходящей через ось Оу и точку .

Решение. Уравнение плоскости, проходящей через ось Оу, имеет вид . Для определения коэффициентовA и C воспользуемся тем, что точка принадлежит плоскостиP. Поэтому ее координаты удовлетворяют написанному выше уравнению плоскости:  , откуда. Подставив найденное значениеA в уравнение , получим:, или.

Это и есть искомое уравнение.

исчисление — Найдите уравнение плоскости, зная, что она проходит через 3 точки

$\begingroup$

Мне нужно найти уравнение плоскости, проходящей через $(0, 0, 0), (4, 0, -2), (0, 8, -6)$.

Я сделал следующее:

Уравнение плоскости имеет вид $$ax+by+cz+d=0$$

Поскольку точки $(0, 0, 0), (4, 0 , -2), (0, 8, -6)$ — точки плоскости, имеем, что $$d=0 \\ 4a-2c=0 \Rightarrow a=\frac{c}{2} \\ 8b -6c=0 \Rightarrow b=\frac{3c}{4}$$

Итак, $$\frac{c}{2}x+\frac{3c}{4}y+cz=0 \Rightarrow \frac{1}{2}x+\frac{3}{4}y+z= 0$$

Верно??

Есть ли другой способ найти уравнение плоскости??

Может быть, с помощью векторного произведения??

• исчисление
• векторный анализ
• векторы
• перекрестное произведение

$\endgroup$

$\begingroup$

Подсказка : сначала найдите нормаль к плоскости: $N = \begin{pmatrix} 4 \\ 0 \\ -2 \end{pmatrix} \times \begin{pmatrix} 0 \\ 8 \\- 6 \end{pmatrix} = (a,b,c)$, то ваша плоскость:

$a(x-0)+b(y-0)+c(z-0) = 0$

$\endgroup$

1

$\begingroup$

Поскольку вы упомянули векторное произведение, давайте воспользуемся им.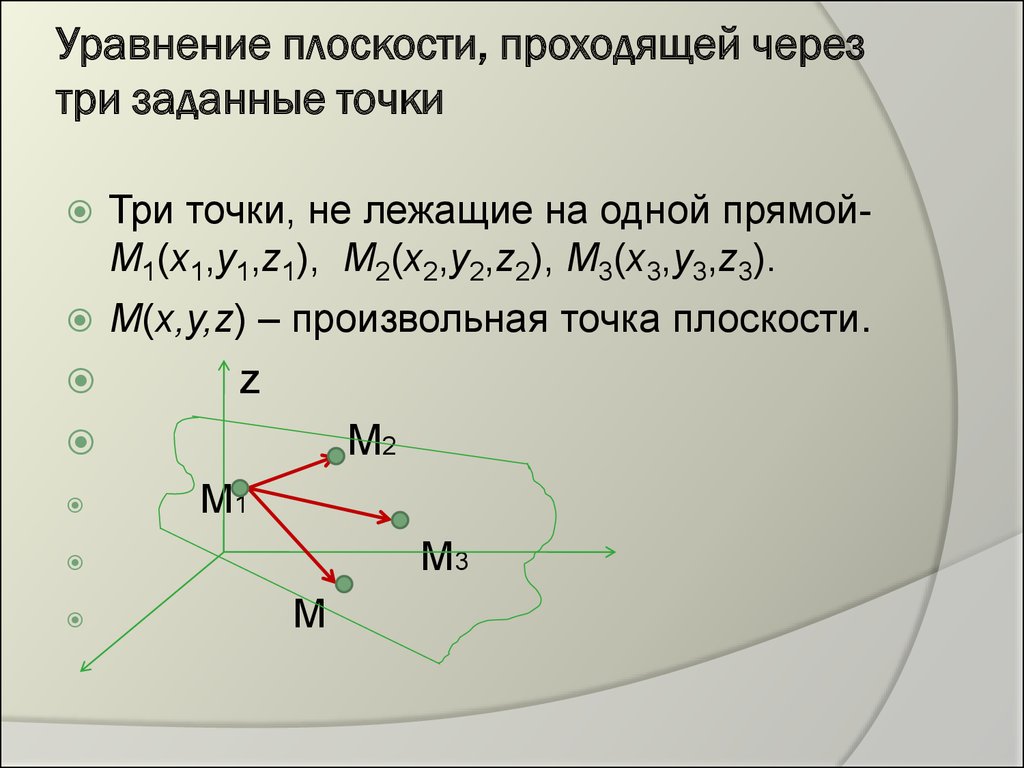

Если у вас есть плоскость $\Pi$ и $P,Q,R \in \Pi$, то векторы $Q-P$ и $R-P$ лежат в плоскости. Следовательно, $(Q-P)\times(R-P)$ нормальна к плоскости.

В вашем упражнении $(4,0,-2)$ и $(0,8,-6)$ лежат на одной плоскости. Тогда $(2,0,-1)$ и $(0,4,-3)$ тоже лежат в плоскости. Итак: $$\begin{vmatrix} {\bf i} & {\bf j} & {\bf k} \\ 2 & 0 &-1 \\ 0 & 4 & -3\end{vmatrix} = (4 ,6,8) $$нормальна к плоскости. Давайте вместо этого будем использовать $(2,3,4)$. Имеем, что плоскость $\Pi: 2x+3y+4z = 0$. (Я уже использую это ${\bf 0}\in \Pi \ подразумевает d = 0$).

$\endgroup$

$\begingroup$

Плоскость однозначно определяется точкой на плоскости и перпендикулярным вектором к самолету. Такой вектор называется нормальным к плоскости.

Дана точка $P_0 = (x_0, y_0, z_0)$ и нормаль $\vec n = (a, b, c)$ к плоскости, точка $P = (x, y, z)$ будет лежать на плоскости, если $\vec{P_0P}$ перпендикулярна $\vec n$, то есть

\begin{equation}\vec n \bullet \vec{P_0P}=0\end{equation}

Если вместо точки и нормали взять три неколлинеарных точек $P_1(x_1,y_1,z_1), P_2(x_2,y_2,z_2)$ и $P_3(x_3,y_3,z_3)$, формируем векторы $\vec{P_1P_2}$ и $\vec{P_1P_3} $.

Векторное произведение $\vec{P1P2}\times\vec{P1P3}$ является вектором, перпендикулярным обоим векторам $\vec{P_1P_2}$ и $\vec{P_1P_3}$ и, следовательно, перпендикулярным к самолету. Используйте одну из точек, полученный вектор из перекрестного произведения в приведенном выше уравнении получить уравнение плоскости.

Получаем, \begin{уравнение} \begin{vmatrix} x-x_1 & y-y_1 & z-z_1\\ x_2-x_1 и y_2-y_1 и z_2-z_1\\ x_3-x_1 и y_3-y_1 и z_3-z_1\\ \end{vmatrix} =0 \end{equation}

— уравнение плоскости , даны три точки. $2x+4z+3y = 0$

$\endgroup$

$\begingroup$

Немного геометрии и линейной алгебры.

Мы знаем, что площадь треугольника с тремя вершинами пропорциональна определителю:

\begin{vmatrix} х_1 и у_1 и z_1\\ х_2 и у_2 и z_2\\ х_3 и у_3 и z_3\\ \end{vmatrix}

Определитель равен нулю, если точки лежат на одной прямой.

Получается путем установки перекрестного произведения равным нулю. Теперь давайте подтянем нашу общую точку.

Пусть одна точка будет общей точкой P (x,y). Я оставляю вам возможность нарисовать простую разностную векторную диаграмму треугольника, где вектор P вычитается, а другой изменяется. Когда площадь равна нулю, векторные линии идут в одном направлении, оставляя нулевую замкнутую область, поэтому возникает ситуация, когда общая прямая теперь должна проходить через плоскость, определяемую тремя точками.

\начало{уравнение} \begin{vmatrix} x-x_1 & y-y_1 & z-z_1\\ x_2-x_1 и y_2-y_1 и z_2-z_1\\ x_3-x_1 и y_3-y_1 и z_3-z_1\\ \end{vmatrix} =0 \end{уравнение}

$\endgroup$

Найдите уравнение плоскости, проходящей через три точки A(0, 1, 2), B(3, 4, -1), C(2, 4, 2) в декартовой форме.

ИНСТИТУТ ААКАША-ТРЁХМЕРНАЯ ГЕОМЕТРИЯ — СЕКЦИЯ ЗАДАНИЯ — J

11 видео

РЕКЛАМА

Ab Padhai karo bina ads ke

Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!

Войти, если уже куплено

Обновлено: 27-06-2022

Текст Решение

Решение

Мы знаем, что уравнение плоскости, проходящей через три точки A, B, C в декартовой форме, равно
∣∣ ∣ ∣∣x−x1y−y1z−z1x2−x1y2−y1z2−z1x3−x2y3−y2z3−z2∣∣ ∣ ∣∣=0
здесь три точки: A(0, 1, 2), B(3, 4, -1) и C(2, 4, 2)
поэтому уравнение плоскости
∣∣ ∣ ∣∣x−0y−1z−23−04−1−1−22−34−42+1∣∣ ∣ ∣∣=0
∣∣ ∣ ∣∣xy−1z−233−3−103∣∣ ∣ ∣∣=0
9x+(1−y)(9−3)+3(z−2)=0
9x+6−6y+3z−6=0
9x−6y+3z=0
3x−2y+ z+0

Ответить

Пошаговое решение от экспертов, которое поможет вам в разрешении сомнений и получении отличных оценок на экзаменах.

---

Похожие видео

Найдите векторное уравнение плоскости, проходящей через три точки A(0, 0, 2), B(1, -1, 1), C(3, 4, 5) .

72793244

Найти векторное и декартово уравнение плоскости, проходящей через точки A(1, 1, -2), B(1,2,1) и C (2, -1,1).

96593400

Уравнение плоскости в векторной форме, проходящей через точки (1,0,1), (1, -1,1) и (4, -3,2) составляет

121601946

से गुजरनेवाले तल सदिश एवं एवं क क000 समीक समीकरणों को प्राप्त कीजिए
(1, 2, 3), (-2, 3, -1), (3, -1, -2)

152621608

निम्न तीन बिंदुओं से से से से से से से से गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज000 के सदिश एवं कार्तीय समीकरणों को प्राप्त कीजिए
(3, -2, 1), (5, 4, -1), (6, -5, 4)

152621609

Найдите уравнение плоскости, проходящей через точки (3, 4, 2), (2, -2, -1) и (7, 0, 1).

320225035

Найти декартово уравнение плоскости, проходящей через три неколлинеарные точки: (1, 1, 0) , (1, 2, 1) и (- 2, 2, — 1)

642720862

Найти декартово уравнение плоскости, проходящей через три неколлинеарные точки: (0, — 1, — 1) , (4, 5, 1) и (3, 9, 4)

642720863

Найти декартово уравнение плоскость, проходящая через три неколлинеарные точки: (0, — 1, 0) , (2, 1, — 1) и (1, 1, 1)

642720865

Найти уравнение Декарта плоскости, проходящей через три неколлинеарные точки: (2, 1, — 1), (6, 5, 0) и (2, — 1, — 5)

642720866

Найдите уравнение декартовой плоскости, проходящей через три неколлинеарные точки: (1, 3, 1), (2, 5, 7) и (4, 1, 5)

642720868

Найдите уравнения плоскостей которая проходит через три точки.