Ранг матрицы методом Гаусса | Мозган калькулятор онлайн
Для того что бы вычислить ранг матрицы можно применить метод окаймляющих миноров или метод Гаусса. Рассмотрим метод Гаусса или метод элементарных преобразований.
Рангом матрицы называют максимальный порядок её миноров, среди которых есть хотя бы один, не равный нулю.
Рангом системы строк (столбцов) называется максимальное количество линейно независимых строк (столбцов) этой системы.
Метод Гаусса использует элементарные преобразования, которые не изменяют ее ранг:
- Транспонирование.
- Перестановка местами строк или столбцов.
- Прибавление одной строки/столбца к другой строке/столбцу умноженного на ненулевое число.
- Умножение строки или столбца на ненулевое число.

С помощью данного метода нужно привести матрицу к ступенчатому виду и посчитать количество строк, в которых есть хоть один не нулевой элемент.
Пример
Рассмотрим данный метод на примере. Дана матрицы:
Для облегчения дальнейших расчетов поменяем местами строку №1 со строкой №2.
Сделаем элемент a3,1 равный нулю.
Из строки №3 вычтем строку №1, умноженную на 3/2.
Сделаем элемент a4,1 равный нулю.
Из строки №4 вычитаем строку №1, умноженную на 2.
Сделаем элемент a3,2 равный нулю.
Из строки №3 вычтем строку №2, умноженную на -1/4. Мы его получили разделив элимент a3,2 = -0.5 на элимент a2,2 = 2.
Сделаем элемент a4,2 равный нулю.
Из строки №4 вычтем строку №2, умноженную на -1/2.
Сделаем элемент a4,3 равный нулю.
Из строки №4 вычитаем строку №3, умноженную на 2.
В получившейся матрице одна строка содержит нулевые элементы, а три строки имеют не нулевые элементы. Ответ: Ранг=3.
Решение системы линейных уравнений методом Жордана-Гаусса (метод прямоугольников)
Решение системы линейных уравнений методом Жордана-Гаусса (метод прямоугольников)
Видеоурок: Метод Жордана-Гаусса (метод прямоугольников)
Пример из видеоурока в рукописном виде:
Пример 2.
Запишем систему в виде:
1 | -2 | 2 | -1 | -1 | 2 | 4 |
0 | -1 | 1 | 3 | -1 | 2 | -2 |
-2 | 4 | -4 | -2 | -2 | 1 | 1 |
-1 | 1 | 0 | -1 | 1 | 1 | -2 |
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника: НЭ = СЭ — (А*В)/РЭ, где РЭ — разрешающий элемент (1), А и В — элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
1 | -2 | 2 | -1 | -1 | 2 | 4 |
0 | -1 | 1 | 3 | -1 | 2 | -2 |
0 | 0 | 0 | -4 | -4 | 5 | 9 |
0 | -1 | 2 | -2 | 0 | 3 | 2 |
Разрешающий элемент равен (-1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
1 | 0 | -7 | 1 | -2 | 8 | |
0 | 1 | -1 | -3 | 1 | -2 | 2 |
0 | 0 | 0 | -4 | -4 | 5 | 9 |
0 | 0 | 1 | -5 | 1 | 1 | 4 |
Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
1 | 0 | 0 | -7 | 1 | -2 | |
0 | 1 | 0 | -8 | 2 | -1 | 6 |
0 | 0 | 1 | -5 | 1 | 1 | 4 |
0 | 0 | 0 | -4 | -4 | 5 | 9 |
Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
1 | 0 | 0 | 0 | 8 | -10.75 | -7.75 |
0 | 1 | 0 | 0 | 10 | -11 | -12 |
0 | 0 | 1 | 0 | 6 | -5. | -7.25 |
0 | 0 | 0 | 1 | 1 | -1.25 | -2.25 |
Теперь исходную систему можно записать как:
x1 = -7.75 — 8×5 — 10.75×6
x2 = -12 — 10×5 — 11×6
x3 = -7.25 — 6×5 — 5.25×6
x4 = -2.25 — x5 — 1.25×6
Необходимо переменные x5,x6 принять в качестве свободных переменных и через них выразить остальные переменные.
Приравняем переменные x5,x6 к 0
x1 = -7.75
x2 = -12
x3 = -7.25
x4 = -2.25
Среди базисных переменных есть отрицательные значения. Следовательно, данное решение не опорное.
Численные методы: решение систем линейных уравнений
В прикладных задачах часто возникает необходимость решать системы линейных уравнений.
Система линейных алгебраических уравнений с n неизвестными — это система уравнений вида
(1)
Слово система означает, что все уравнения рассматриваются как одно целое.
В общем случае у нас имеется m — уравнений, n — количество неизвестных. x1, x2,…, xn — неизвестные, которые следует определить.
В системе (1) – фиксированные коэффициенты, b1, b2, …, bm — свободные члены — предполагаются известными.
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Задача состоит в том, чтобы найти такие которые удовлетворяют всем уравнениям (1).
В частном случае мы имеем одно линейное уравнение:
Конечно, такое уравнение легко решить, если предположить, что коэффициент не равен 0, имеем: = .
Очевидно, в общем случае имеются 3 варианта решений: система имеет ни одного решения, имеет одно решение, более одного решения.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если нет ни одного решения.
Система линейных уравнений может быть представлена в матричной форме как:
или:
Ax = b
Здесь A — это матрица системы, x — столбец неизвестных, а b — столбец свободных членов.
Если к матрице A приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.
Рассмотрим, например, систему вида и поймем, как найти ее решение:
(2)
Предположим на минуту, что в первом уравнении y отсутствует, а во втором отсутствует x, тогда мы имели бы решение именно то решение, которое нам нужно.
Вопрос: как исходную систему привести к такому виду и можно ли это сделать.
Заметим, что с тождествами мы можем делать следующие вещи: домножать на одно и то же число, отличное от 0, складывать, вычитать и тд, это похоже с тем, что вы раскладываете монеты по своим карманам, не меняя общей суммы.
От этих операций тождество не меняется.
В системе (2) у нас два тождества, домножим второе тождество на 2 и вычтем из первого, получим:
(3)
Формально у нас есть еще старое тождество , но оно нам не понадобится (подумайте, почему).
Система (3) точно такая же, как система (2).
Из второго уравнения системы (3) сразу получим:
Никто не мешает нам подставить это значение в первое уравнение:
Отсюда сразу находим, что
Итак, путем простых действий мы нашли, что система (2) может быть представлена в виде:
Именно такие естественные соображения приводят к общему методу решения систем линейных уравнений, известному как метод исключения или метод Гаусса.
Метод Гаусса является одним из самых распространенных прямых методов решения систем линейных уравнений Ax = b:
Опишем этот метод в общем случае.
Вначале исходная система приводится к верхнетреугольному виду.
Это достигается следующей последовательностью преобразований (прямой ход).
Будем считать для удобства, что элемент aij исходной матрицы и компоненты вектора bi есть, соответственно, элементы aij (1) первого шага преобразованной матрицы A1 и преобразованного вектора b1:A = A1, b=b1.
Далее, на втором шаге прибавим к второй строке первую, умноженную на
Аналогично поступим со всеми оставшимися строками, т.е. прибавим к каждой i-ой строке i=2,3,…,N, первую, умноженную на коэффициент
При этом соответственно изменится и вектор b1.
Таким образом, 2 шаг.
Имеем систему уравнений A2x = b2:
где
3 шаг.
Прибавим к новой третьей строке новую вторую, умноженную на
То же самое сделаем с остальными строками 4,5,…,N, т.е. прибавим к i-ой строке вторую, умноженную на
При этом получим систему A3x = b3:
(k+1)-ый шаг:
Здесь
Поступая так и далее, на шаге N-1 получаем верхнетреугольную систему:
При этом, мы также получили матрицу C переводных коэффициентов, имеющую вид:
Решение полученной треугольной системы как легко видеть, имеет вид (обратный ход метода Гаусса):
Заметим, что при прямом ходе метода Гаусса может возникнуть ситуация, когда происходит деление на нуль, да и вообще, желательно не делить на малое число, чтобы не накапливалась ошибка.
Поэтому метод Гаусса обычно проводят с частичным выбором главного элемента, то есть после каждого шага (пусть это был k-й шаг) переставляют строки с номерами k,k+1,…,N таким образом, чтобы на месте kk оказался элемент наибольший из всех в k-ом столбце при m>k (при этом, естественно, переставляются и компоненты вектора b).
Можно для максимальной точности переставлять также и столбцы преобразуемой матрицы, чтобы на месте kk оказался максимальный элемент из всех с индексами больше, либо равными k.
Эта процедура называется методом Гаусса с выбором главного элемента. Она несколько повышает точность по сравнению с частичным выбором главного элемента, но весьма неудобна, в том числе для программирования, поскольку при перестановке строк компоненты искомого вектора x переставлять не надо, тогда как при перестановке столбцов надо переставлять и соответствующие компоненты вектора x.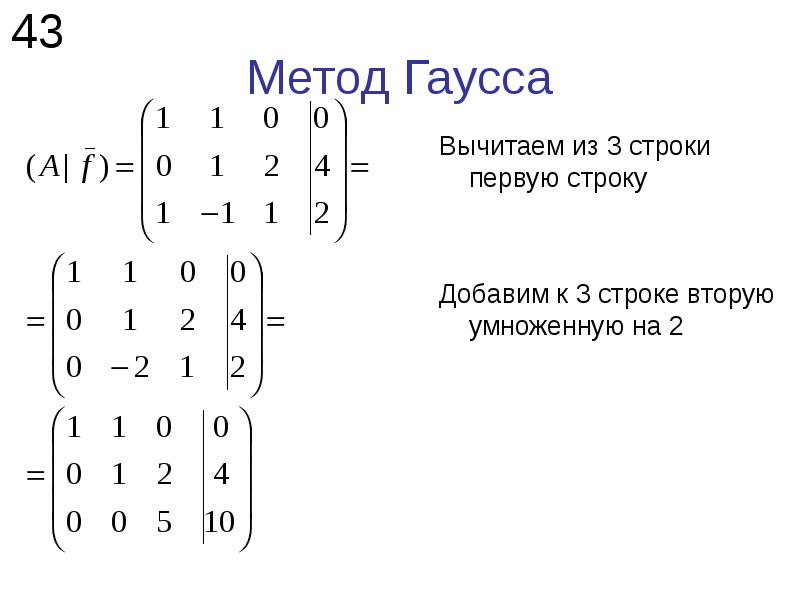
Опишем обратный ход метода Гаусса в несколько иной форме (треугольное разложение).
Введем матрицы Mk по правилу:
На каждом шаге метода Гаусса получается некоторая промежуточная матрица:
и вектор
Нетрудно видеть, что
Вопрос. Почему
Если производить также выбор главных элементов, то необходимо использовать оператор P перестановки индексов l и m, матричные элементы которого равны:
При применении оператора перестановки индексов к матрице слева, меняются местами строки матрицы и компоненты свободного вектора (PAx = Pb), если же его применить справа к матрице, то меняются местами ее столбцы и компоненты решения
Существует большой класс так называемых итерационных методов решения систем уравнений, аналогичных итерационным методам нахождения корней нелинейных уравнений.
Итерационные методы последовательно уточняют решение, отправляясь от начального приближения.
При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций.
Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений.
Идея состоит в том, чтобы найти неподвижную точку матричного уравнения
(5)
эквивалентного начальной системе линейных алгебраических уравнений.
При итерации в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:
.
Термин неподвижная точка становится ясен, если вы внимательно посмотрите на уравнение (5), по самому своему смыслу величина Х является неподвижной точкой.
Более подробное описание методов решения систем линейных уравнений можно найти в специальной литературе, наша задача дать обзор методов и основные идеи решения такого рода задач.
Обусловленность линейных систем, погрешность
При решении абстрактной задачи Ax = b, где A — оператор произвольной природы, важным моментом является корректность ее постановки.
Задача считается корректной, если решение существует и единственно и , кроме того, решение непрерывно зависит от данных (то есть, при также стремится к нулю).
Однако и непрерывная зависимость от входных данных может иметь свои нюансы.
Чем меньшее (большее) изменение решения вызывает вариация входных данных, тем более хорошо (плохо) обусловленной считается задача.
Понятие обусловленности является тем более существенным для численных методов, поскольку на практике входные данные известны, как правило, с некоторой погрешностью.
Кроме того, существуют ошибки округления, возникающие при вычислениях.
Таким образом, формально корректная задача, являясь плохо обусловленной, может оказаться разрешимой столь неточно, что в этом будет отсутствовать практический смысл.
Чем можно охарактеризовать количественно обусловленность для линейных систем?
Пусть A — квадратная NxN — матрица.
Рассмотрим задачу Ax = b.
Пусть также некоторая норма в пространстве RN
Норма оператора A определяется стандартно:
Обозначим y = Ax и введем число m по правилу:
Величина называется числом обусловленности.
Очевидно:
- если A — диагональная, то (Для какой нормы, или для всех вышеприведенных?). Чем меньше число обусловленности C(A), тем лучше обусловлена система. Действительно, пусть вариация правой части, а соответствующее изменение решения.
Тогда справедливо следующее неравенство:
Доказательство. Имеем:
Имеем:
Так как
то
Аналогично, поскольку
Объединяя два неравенства, окончательно получаем для оценки погрешности:
В начало
Содержание портала
Решение уравнений методом Гаусса | matematicus.ru
С помощью метода Гаусса можно решить любую систему линейных уравнений с различным числом уравнений и неизвестных переменных. И именно этим свойством этот метод превосходит матричный метод и метод Крамера.
Суть метода состоит в приведении системы линейных уравнений к ступенчатому (треугольному) виду за счет последовательного исключения неизвестных. Затем её решения с помощью обратной подстановки.
Допустимые преобразования матрицы:
- Перестановка местами двух строк или двух столбцов;
- Умножение строки на число, которое не равно 0;
- Прибавление одной строки к другой.

- Исключение или добавление нулевой строки
Допустим, дана система линейных алгебраических уравнений с четырьмя уравнениями и четырьмя неизвестными.
Составим расширенную матрицу СЛАУ:
Затем первое уравнение СЛАУ делим на a11. При этом a11≠0, если равно нуля, то переставляем две строки или два столбца местами так, чтобы избавится от нуля. После полученное уравнение умножаем на a21 и вычитаем из второго уравнения, дальше, умножаем на a31 и вычитаем из третьего уравнения и т.д.
Также поступаем и с оставшемся уравнениями, т.е. со вторым, третьем и четвёртым. В итоге должна получится матрица ступенчатого или треугольного вида.
Система уравнений примет вид
Такую систему элементарно решить обратным ходом, т.е. последовательным решением уравнений от нижнего к верхнему.
Рассмотрим наиболее подробно метод Гаусса при решении СЛАУ на практике.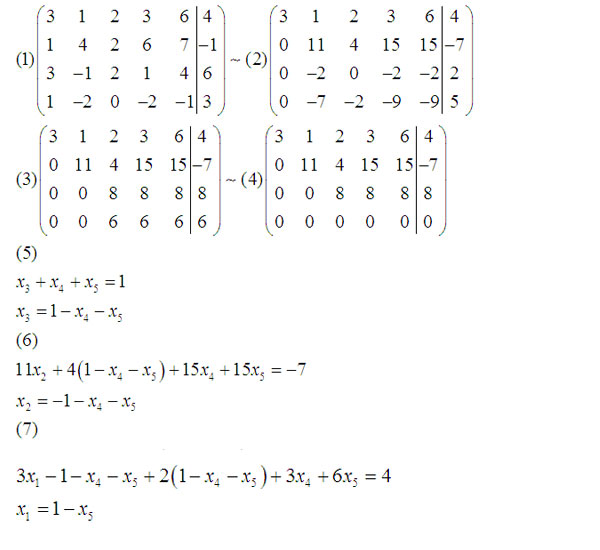
Пример 1
Решить методом Гаусса систему уравнений
Решение
Составим расширенную матрицу системы уравнений:
Первую строку разделим на a11, но так как в этой строке a11=0, то необходимо поменять строку у которой первый элемент не равен нулю. Выберем по модулю наибольшей элемент, это a41=2 Поэтому поменяем первую и четвёртую строки местами.
Получаем:
Первую строку разделим на a11=2. Получим матрицу:
Умножаем элементы первой строки на -1 и прибавляем к элементам второй строк. Получим матрицу:
Умножаем элементы первой строки на -1 и прибавляем к элементам третьей строки.
Четвёртую строку оставляем без изменений, так как её первый элемент равен нулю.
Теперь первый столбец не трогаем.
Начинаем повторять действия, которые применяли ранее.
Второе уравнение разделим на a22=-1/2, тогда
Умножаем элементы второй строки на -1/2 и прибавляем к элементам третьей строки.
Умножаем элементы второй строки на -1 и прибавляем к элементам четвёртой строки.
Первый и второй столбец не трогаем.
Третьей столбец разделим на 2.
Умножаем элементы третьей строки на -1 и прибавляем к элементам четвёртой строки.
Получаем ступенчатую систему алгебраических уравнений:
Отсюда, решая систему снизу вверх, получаем корни системы уравнений
Приведём простой пример краткой записи решения СЛАУ методом Гаусса
Пример 2
Решить систему линейных уравнений с тремя неизвестными методом Гаусса.
Решение
Составим расширенную матрицу системы линейных уравнений .
Следовательно, искомая система может быть представлена в ступенчатом виде:
Решая последовательно уравнение, получаем:
Ответ: z = 3; y = 2; x = 1
в чем суть, решение системы уравнений, примеры с объяснением
Благодаря великим ученым было открыто множество эффективных теорем для работы со сложными математическими задачами. Один из таких примеров — метод Гаусса.
Метод Гаусса — что это такое
Метод Гаусса представляет собой методику эквивалентного преобразования исходной системы линейных уравнений в систему, решаемую существенно проще, чем исходный вариант.
Метод Гаусса используют для решения систем линейных алгебраических формул. Такой способ обладает рядом важных преимуществ:
- Нет необходимости сравнивать уравнения для оценки совместимости.
- Решение систем равенств, в которых число определителей совпадает или не совпадает с количеством неизвестных переменных.

- Поиск решений для уравнений с нулевым определителем.
- Сравнительно небольшое количество вычислительных операций для получения результата.
Основные определения и обозначения
Матрицы: определение и свойства
Такие системы являются наиболее удобным способом представления данных, с которыми впоследствии производят манипуляции. Матрица имеет вид прямоугольника для удобства расчетов. При использовании метода Гаусса работа осуществляется с треугольными матрицами, при записи которых применяется прямоугольник с нулями на тех местах, где числа отсутствуют. Часто нули не записывают, а только подразумевают.
Важным параметром матрицы является размер:
- ширина — это количество строк, обозначают буквой m;
- длину выражают числом столбцов, записывают буквой n.

Размер матрицы будет записан в формате А m*n. В случае, когда m=n, матрица является квадратной, а m=n служит ее порядком. Номера строк и столбцов изменяются.
Определитель
Матрица обладает крайне важной характеристикой. Таким параметром является определитель. Данную величину рассчитывают с помощью диагонали. Для этого в матрице необходимо провести воображаемые диагональные линии. Затем следует найти произведение элементов, которые располагаются на этих диагоналях, а полученные значения суммировать таким образом:
- Если диагональ обладает наклоном в правую сторону, то знак «+».
- Для диагоналей, наклоненных влево, знак «–».
Рассчитать определитель представляется возможным лишь в случае работы с квадратной матрицей.
Если необходимо определить данный параметр для прямоугольной матрицы, то следует выполнить следующие манипуляции:
- из числа строк и числа столбцов выбрать наименьшее и обозначить его k;
- отметить в матрице произвольным образом k столбцов и k строк.

Элементы, которые расположены на пересечении отмеченных столбцов и строк, образуют новую квадратную матрицу. В случае, когда определитель является числом, не равным нулю, то данный параметр будет обозначен как базисный минор первоначальной прямоугольной матрицы. Перед решением систем уравнений методом Гаусса полезно рассчитать определитель. Если данная характеристика равна нулю, то матрица имеет бесконечное множество решений либо не имеет их вовсе. В таком случае потребуется определить ранг матрицы.
Классификация систем
Ранг матрицы является распространенным понятием. Он обозначает максимальный порядок ее определителя, который не равен нулю. По-другому можно сказать, что ранг матрицы представляет собой порядок базисного минора. Исходя из данного критерия, СЛАУ классифицируют на несколько типов. В совместных системах, которые состоят лишь из коэффициентов, ранг основной матрицы совпадает с рангом расширенной. Для подобных систем характерно одно или множество решений. По этой причине совместные системы подразделяют на следующие типы:
По этой причине совместные системы подразделяют на следующие типы:
- определенные, обладающие одним решением, в которых наблюдается равенство ранга матрицы и количество неизвестных;
- неопределенные;
- обладающие бесконечным числом решений с рангом матрицы, который меньше количества неизвестных.
В несовместных системах ранги, характеризующие основную и расширенную матрицы, отличаются. С помощью метода Гаусса в процессе решения можно прийти либо к однозначному доказательству несовместности системы, либо к решению общего вида для системы, обладающей бесконечным количеством решений.
Источник: asiaplustj.infoОсновные правила и разрешаемые преобразования при использовании метода Гаусса
Перед тем, как решать систему, необходимо ее упростить. На данном этапе выполняют элементарные преобразования, которые не влияют на конечный результат. Определенные манипуляции справедливы лишь в случае матриц, исходниками которых являются СЛАУ. Список элементарных преобразований:
Список элементарных преобразований:
- Перестановка строк. При перемене записей в системе местами ее решение не меняется. Можно менять место строк в матрице, учитывая столбец со свободными членами.
- Произведение всех элементов строк и некоторого коэффициента. Сокращаются большие числа в матрице, и исключаются нули. При этом множество решений сохраняется без изменений, а дальнейшие манипуляции существенно упрощаются. Важным условием является отличие от нуля коэффициента.
- Удаление строк, которые содержат пропорциональные коэффициенты. Данное преобразование следует из предыдущего пункта. При условии, что две или более строк в матрице обладают пропорциональными коэффициентами, то при произведении или делении одной из строк на коэффициент пропорциональности получают две или более абсолютно одинаковые строки. В этом случае лишние строки исключают, оставляя только одну.
- Удаление нулевой строки. Бывают случаи, когда в процессе манипуляций с уравнениями возникает строка, все элементы которой, в том числе свободный член, равны нулю.
 Нулевую строку допустимо исключать из матрицы.
Нулевую строку допустимо исключать из матрицы. - Суммирование элементов одной строки с элементами другой, умноженными на некоторый коэффициент, в соответствующих столбцах. Данное преобразование имеет наиболее важное значение из всех перечисленных.
Особенности использования метода Гаусса для решения СЛАУ
На первом этапе система уравнений записывается в определенном виде. Пример выглядит следующим образом:
Источник: wp.comКоэффициенты необходимо представить в виде таблицы. С правой стороны в отдельном столбце записаны свободные члены. Данный блок отделен для удобства решения. Матрицу со столбцом со свободными членами называют расширенной.
Источник: wp.comЗатем основная матрица с коэффициентами приводится к верхней треугольной форме. Данное действие является ключевым моментом при решении системы уравнений с помощью метода Гаусса. По итогам преобразований матрица должна приобрести такой вид, чтобы слева внизу находились одни нули:
Источник: wp. com
comПри записи новой матрицы в виде системы уравнений можно отметить, что последняя строка уже содержит значение одного из корней, которое в дальнейшем подставляется в уравнение выше для нахождения следующего корня и так далее. Подобное описание позволяет разобраться в методе Гаусса в общих чертах.
Обратный и прямой ход метода Гаусса
В первом случае необходимо представить запись расширенной матрицы системы. При выполнении обратного метода Гаусса далее в главную матрицу добавляют столбец со свободными членами.
Источник: wp.comСуть такого способа заключается в выполнении элементарных преобразований, по итогам которых данная матрица приводится к ступенчатому или треугольному виду. В этом случае над или под главной диагональю матрицы располагаются только нули.
Источник: wp.comВарианты дальнейших действий:
- перемена строк матрицы местами, при наличии одинаковых или пропорциональных строк их можно исключить, кроме одной;
- деление либо умножение строки на любое число, не равное нулю;
- удаление нулевых строк;
- добавление строки, умноженной на число, не равное нулю, к другой строке.

Имея преобразованную систему с одной неизвестной Xn, которая становится известной, можно выполнить поиск в обратном порядке остальных неизвестных с помощью подстановки известных х в уравнения системы, вплоть до первого. Данный способ называют обратным методом Гаусса.
Примеры решений с объяснением
Пример 1
Требуется решить с помощью метода Гаусса систему линейных уравнений, которая выглядит следующим образом:
Источник: wp.comРешение
Необходимо записать расширенную матрицу:
Источник: wp.comЗатем нужно выполнить преобразования. В результате матрица должна приобрести треугольный вид. Для этого следует умножить первую строку на (3) и умножить вторую строку на (-1). В результате суммирования второй и первой строк получается следующее:
Источник: wp.comДалее следует умножить третью строку на (-1). После добавления третьей строки ко второй получаем следующие преобразования:
Источник: wp. com
comПосле этого необходимо умножить первую строку на (6) и вторую строку на (13). Далее следует добавить вторую строку к первой:
Источник: wp.comПосле того, как система преобразована, остается вычислить неизвестные:
\(x_{3}=\frac{98}{49}=2\)
\(x_{2}=\frac{14-7x_{3}}{6}=\frac{14-7*2}{6}=0\)
\(x_{3}=\frac{-9+5x_{2}+6x_{3}}{3}=\frac{-9+5*0+6*2}{3}=1\)
Данный пример демонстрирует единственное решение системы.
Источник: supertics.comПример 2
Необходимо решить систему уравнений, которая выглядит следующим образом:
Источник: wp.comРешение
Необходимо составить матрицу:
Источник: wp.comСогласно методу Гаусса уравнение первой строки по итогам преобразований не меняется. Удобнее, когда левый верхний элемент матрицы обладает наименьшим значением. В таком случае первые элементы остальных строк после преобразований будут равны нулю. Таким образом, составленная матрица будет решаться проще, если на место первой строки поставить вторую:
вторая строка:
\(k = (-a_{21} /a_{11}) = (-3/1) = -3\)
\(a»_{21} = a_{21} + k×a_{11} = 3 + (-3)×1 = 0\)
\(a» _{22} = a_{22} + k×a _{12} = -1 + (-3)×2 = -7\)
\(a»_{ 23} = a_{23} + k×a_{13} = 1 + (-3)×4 = -11\)
b» 2 = b 2 + k×b 1 = 12 + (-3)×12 = -24
третья строка:
\(k = (-a_{31} /a_{11}) = (-5/1) = -5\)
\(a»_{31} = a_{31} + k×a_{11} = 5 + (-5)×1 = 0\)
\(a»_{32} = a_{32} + k×a_{12} = 1 + (-5)×2 = -9\)
\( a»_{33} = a_{33} + k×a_{13} = 2 + (-5)×4 = -18\)
\( b»_3 = b_3 + k×b_1 = 3 + (-5)×12 = -57\)
Матрица с промежуточными результатами манипуляций будет иметь следующий вид:
Источник: wp. com
comБлагодаря некоторым операциям можно придать матрице наиболее удобный вид. К примеру, вторую строку можно избавить от всех «минусов» путем умножения каждого элемента на «-1». Можно заметить, что для третьей строки характерны все элементы, кратные трем. В этом случае строка сокращается с помощью произведения каждого элемента на «-1/3». Минус позволит удалить отрицательные значения.
Источник: wp.comДалее следует приступить к манипуляциям со второй и третьей строками. Необходимо суммировать третью и вторую строки. Вторая строка при этом умножается на такой коэффициент, при котором элемент а 32 будет равен нулю.
\(k = (-a_{32} /a_{22}) = (-3/7) = -3/7\)
В случае, когда некоторые преобразования приводят в результате к получению не целого числа, следует оставить его в этом виде. Таким образом, вычисления будут более точными. Затем при получении ответов можно определиться с его дальнейшем округлением или переводом в другую форму записи.
\(a»_{32} = a_{32} + k×a_{22} = 3 + (-3/7)×7 = 3 + (-3) = 0\)
\(a»_{33} = a_{33} + k×a_{23} = 6 + (-3/7)×11 = -9/7\)
\(b»_3 = b_3 + k×b_2 = 19 + (-3/7)×24 = -61/7\)
Преобразованная матрица будет иметь следующий вид:
Матрица обладает ступенчатым видом. Дальнейшие преобразования с помощью метода Гаусса нецелесообразны. В этом случае можно удалить из третьей строки общий коэффициент «-1/7».
Дальнейшие преобразования с помощью метода Гаусса нецелесообразны. В этом случае можно удалить из третьей строки общий коэффициент «-1/7».
Затем необходимо представить запись матрицы в виде системы уравнений для вычисления корней.
x + 2y + 4z = 12 (1)
7y + 11z = 24 (2)
Найти корни можно обратным методом Гаусса. Уравнение (3) содержит значение z:
y = (24 — 11×(61/9))/7 = -65/9
С помощью первого уравнения можно определить х:
x = (12 — 4z — 2y)/1 = 12 — 4×(61/9) — 2×(-65/9) = -6/9 = -2/3
Подобная система является совместной и определенной, для которого характерно единственное решение. Ответ будет следующим:
x 1 = -2/3, y = -65/9, z = 61/9.
Метод Гаусса предполагает последовательное исключение неизвестных. Методика справедлива в случае решения квадратных систем линейных алгебраических уравнений. Несмотря на простоту метода, многие студенты сталкиваются с некоторыми трудностями в процессе поиска правильного решения. Это связано с наличием знаков «+» и «-». Поэтому для решения СЛАУ требуется проявить внимательность. А получить квалифицированную помощь можно на ресурсе Феникс.Хелп.
Это связано с наличием знаков «+» и «-». Поэтому для решения СЛАУ требуется проявить внимательность. А получить квалифицированную помощь можно на ресурсе Феникс.Хелп.
Метод Гаусса — определение с примерами решения
Содержание:
- Опишем метод Гаусса подробнее
- Примеры с решением
Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является метод Гаусса, состоящий в последовательном исключении неизвестных.
Пусть дана система уравнений (4.3)
Процесс решения по методу Гаусса состоит из двух этапов. На нервом этапе (прямой ход) система приводится к i ступенчатому (в частности, треугольному) виду.
Приведенная ниже система имеет ступенчатый вид
где
Коэффициенты называются главными элементами системы. На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Опишем метод Гаусса подробнееПрямой ход. Будем считать, что элемент (если то первым в системе запишем уравнение, в котором коэффициент при отличен от нуля). Преобразуем систему (4.3), исключив неизвестное во всех уравнениях, кроме первого (используя элементарные преобразования системы).
Для этого умножим обе части первого уравнения на и сложим почленно со вторым уравнением системы.
Затем умножим обе части первого уравнения на и сложим с третьим уравнением сиап стемы. Продолжая этот процесс, получим эквивалентную систему
Здесь
новые значения коэффициентов и правых частей, которые полу чаю юя после первого шага. Аналогичным образом, считая главным элементом исключим неизвестное из всех уравнений системы, кроме первого и второго, и так далее.
Продолжаем этот процесс, пока это возможно. Если в процессе приведения системы (4.3) к ступенчатому виду появятся нулевые уравнения, т. е. равенства вида их отбрасывают. Если же появится уравнение вида то это свидетельствует о несовместности системы. Второй этап {обратный ход) заключается в решении ступенчатой системы.
Ступенчатая система уравнений, вообще говоря, имеет бесчисленное множество решений. В последнем уравнении этой системы выражаем первое неизвестное через остальные неизвестные Затем подставляем значение в предпоследнее уравнение системы и выражаем затем находим Придавая свободным неизвестным произвольные значения, получим бесчисленное множество решений системы.
Возможно вам будут полезны данные страницы:
Замечания: 1. Если ступенчатая система оказывается треугольной, т. е. то исходная система имеет единственное решение. Из последнего уравнения находим хп, из предпоследнего уравнения далее поднимаясь по системе вверх, найдем все остальные неизвестные На практике удобнее работать не с системой (4.3), а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на ).
Примеры с решением
Пример 4.4.
Решить систему методом Гаусса:
Решение:
В результате элементарных преобразований над расширенной матрицей системы
исходная система свелась к ступенчатой:
Поэтому общее решение системы: Если положить, например, то найдем одно из частных решений этой системы
Пример 4.5.
Решить систему методом Гаусса:
Решение:
Произведем элементарные преобразования над строчками расширенной матрицы системы:
Полученная матрица соответствует системе
Осуществляя обратный ход, находим Рассмотрим решение системы (1.25) т линейных уравнений с п неизвестными. Заметим, что матрица коэффициентов системы не обязательно должна быть квадратной.
Предлагаемые методы решения систем линейных алгебраических уравнений сводятся к элементарным преобразованиям над уравнениями системы.
Преобразования Гаусса удобно проводить, осуществляя преобразования не самих уравнений, а строк матрицы их коэффициентов.
Рассмотрим матрицу
(1.33) называемую расширенной матрицей системы (1.25), так как в нее, кроме коэффициентов матрицы А системы (1.25), дополнительно включен столбец свободных членов В. Метод Гаусса (метод последовательного исключения неизвестных. Рассмотрим систему (1.25) в случае
Суть метода Гаусса заключается в том, что с помощью элементарных преобразований расширенная матрица системы (1.33) приводится к равносильной матрице ступенчатого вида по алгоритму поиска ранга матрицы (см. пример 1.13). Это и есть прямой ход метода Гаусса.
На основании полученной ступенчатой матрицы составляется новая система уравнений, равносильная исходной, из которой последовательно, начиная с последнего уравнения, находятся все неизвестные; это суть обратного хода метода Гаусса.
Пример 1.18.
Решить систему уравнений методом Гаусса:
Решение:
Расширенная матрица системы имеет вид
Используя элементарные преобразования (см. пример 1.14), сведем эту матрицу к ступенчатой, не забывая при этом, что теперь в строке уже не три, а четыре элемента.
Вспомнив, что до черты стоят коэффициенты системы уравнений, а после нее — столбец свободных членов, выпишем получившуюся систему уравнений:
Теперь применим обратный ход метода Гаусса. Из последнего 4 2 тл уравнения полученной системы найдем
Из второго уравнения найдем Аналогично найдем из первого уравнения, подставив в него уже наиденные два неизвестных
Получим решение системы
Предлагаем читателю убедиться, что найденные числа образуют решение данной системы. Расширенная матрица системы. Ступенчатая матрица. Метод Гаусса. Коэффициенты системы (1.1) удобно объединить в прямоугольную таблицу, называемую матрицей системы. Для матрицы принято обозначение:
Матрица содержит т горизонтальных рядов, называемых строками, и вертикальных рядов, называемых столбцами, числа называются ее элементами. Таким образом, первый индекс элемента — это номер строки (номер уравнения системы (1.1)), а второй индекс — номер столбца (или номер неизвестного коэффициентом при котором является уравнении системы (1.1)).
Например, матрица
квадратная матрица 3-го — единичная матрица 2-го порядка. Если к матрице А добавить столбец из свободных членов, то получим так называемую расширенную матрицу А* системы, содержащую всю информацию о системе:
Для системы из примера 1.1 матрицей системы является а расширенной матрицей этой системы является матрица На практике элементарным преобразованиям подвергают не саму систему, а ее расширенную матрицу.
Преобразованиям двух типов над системой (1.1) соответствуют два типа элементарных преобразований над строками матрицы 1-й тип — перестановка местами двух любых ее строк; 2-й тип — сложение соответствующих элементов двух любых строк, все элементы одной из которых предварительно умножены на одно и то же число.
Целью элементарных преобразований является приведение расширенной матрицы системы (1.1) к так называемой ступенчатой форме.
Определение 1.6. Матрица называется ступенчатой, если для нее выполняются следующие условия: 1) если какая-либо строка данной матрицы состоит из нулей, то и все последующие строки также состоят из нулей; 2) если — первый ненулевой элемент строки, а — первый ненулевой элемент строки,то Так, например, матрица
является ступенчатой.
Матрица из одной строки считается ступенчатой по определению. Теорема 1.2. Любую матрицу Л конечным числом элементарных преобразований первого и второго типов можно преобразовать в ступенчатую матрицу.
Пример 1.7.
Привести к ступенчатому виду матрицу
Решение:
Выполним следующие элементарные преобразования над матрицей
1) к элементам второй строки прибавим элементы первой строки и из элементов третьей строки вычтем элементы первой строки, в результате преобразуется к виду: — расширенная матрица системы.
2) переставим вторую и третью строки:
3) из третьей строки полученной матрицы вычтем вторую строку, умноженную на 3, получим:
На приведении расширенной матрицы системы (1.1) к ступенчатой матрице основан метод Гаусса, или метод последовательного исключения неизвестных. Система линейных уравнений с расширенной ступенчатой матрицей называется ступенчатой системой, по теореме 1.1 она будет равносильна соответствующей системе в форме (1.1). Приведение системы (1.1) к ступенчатой форме называется прямым ходом метода Гаусса.
Решение полученной ступенчатой системы называется обратным ходом метода Гаусса. Он может быть выполнен как в форме последовательного определения неизвестных, начиная с последнего уравнения ступенчатой системы, так и в форме преобразования матрицы к ступенчатой матрице специального вида.
Пример 1.8.
Решить методом Гаусса систему уравнений
Решение:
Прямой ход метода Гаусса. В примере 1.7 матрица при помощи элементарных преобразований приведена к ступенчатой матрице
Теперь матрице сопоставим систему, для которой она будет расширенной матрицей:
Обратный ход метода Гаусса. 1-й способ. Имеем: . 2-й способ.
Умножим последнюю строку матрицы на 1 /5, сложим со второй строкой, после чего к первой строке прибавим последнюю, умноженную на (-2), с целью получить нули в третьем столбце:
Напишем систему с расширенной матрицей
Ответ: система совместная и определенная, она имеет единственное решение:
Метод Гаусса — решение систем линейных уравнений, пример — смотреть онлайн видео урок бесплатно! Автор: alWEBra — Линейная алгебра
В этом видео уроке рассказывается о том, как использовать метод Гаусса при решении систем линейных уравнений, пример. Метод Гаусса является универсальным методом решения систем линейных уравнений. Он основан на последовательном исключении неизвестных. Здесь будет рассмотрен простейший случай, т.е. когда система имеет единственное решение. При решении, системе уравнений сопоставляется, так называемая, расширенная матрица, состоящая из коэффициентов при неизвестных и свободных членов. Суть Метода Гаусса заключается в том, что по определенным правилам выполняется преобразование этой матрицы к виду, в котором ниже главной диагонали располагаются только нули. Элементарные преобразования матрицы выполняются по таким правилам как перемена местами двух строк, умножение (деление) строки на число, добавление к строке другой строки, умножение на число и вычеркивание строки из нулей. После такого преобразования система уравнений легко решается. В качестве примера практического применения метода Гаусса, будет рассмотрено задание с решением системы линейных уравнений с тремя неизвестными. Видео урок «Метод Гаусса — решение систем линейных уравнений, пример» вы можете смотреть онлайн в любое время совершенно бесплатно. Удачи Вам!
- Автор: alWEBra
- Длительность: 5:32
- Дата: 22.11.2013
- Смотрели: 515
- Рейтинг: 5.0/1
Если у Вас есть качественные видео уроки, которых нет на нашем сайте, то Вы можете добавить их в нашу коллекцию. Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.
Решающих систем с исключением Гаусса — College Algebra
Цели обучения
В этом разделе вы:
- Напишите расширенную матрицу системы уравнений.
- Напишите систему уравнений из расширенной матрицы.
- Выполняет операции со строками в матрице.
- Решите систему линейных уравнений с помощью матриц.
Немецкий математик Карл Фридрих Гаусс (1777–1855).
Карл Фридрих Гаусс жил в конце 18 — начале 19 века, но до сих пор считается одним из самых плодовитых математиков в истории.Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика. Его открытия в области теории матриц изменили способ работы математиков за последние два столетия.
Мы впервые столкнулись с исключением Гаусса в системах линейных уравнений: две переменные. В этом разделе мы еще раз вернемся к этой технике решения систем, на этот раз с использованием матриц.
Написание расширенной матрицы системы уравнений
Матрица может служить средством представления и решения системы уравнений.Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы. Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства. Когда система написана в такой форме, мы называем ее расширенной матрицей.
Например, рассмотрим следующую систему уравнений.
Мы можем записать эту систему в виде расширенной матрицы:
Мы также можем написать матрицу, содержащую только коэффициенты.Это называется матрицей коэффициентов.
Система уравнений три на три, например
имеет матрицу коэффициентов
и представлена расширенной матрицей
Обратите внимание, что матрица написана так, что переменные выстраиваются в свои собственные столбцы: члены x идут в первый столбец, y -термы во втором столбце и z -термы в третьем столбце. Очень важно, чтобы каждое уравнение было написано в стандартной форме, чтобы переменные совпадали.Если в уравнении отсутствует член переменной, коэффициент равен 0.
Для данной системы уравнений напишите расширенную матрицу.
- Запишите коэффициенты членов x как числа в первом столбце.
- Запишите коэффициенты членов y в виде чисел во втором столбце.
- Если есть z -термин, запишите коэффициенты в виде чисел в третьем столбце.
- Нарисуйте вертикальную линию и напишите константы справа от нее.
Написание расширенной матрицы для системы уравнений
Напишите расширенную матрицу для данной системы уравнений.
Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.
Запишите расширенную матрицу данной системы уравнений.
Написание системы уравнений из расширенной матрицы
Мы можем использовать расширенные матрицы, чтобы помочь нам решать системы уравнений, потому что они упрощают операции, когда системы не обременены переменными.Однако важно понимать, как перемещаться между форматами, чтобы сделать поиск решений более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.
Напишите систему уравнений из расширенной матрицы.
Выполнение операций со строками в матрице
Теперь, когда мы можем писать системы уравнений в форме расширенной матрицы, мы рассмотрим различные операции со строками, которые могут выполняться с матрицей, такие как сложение, умножение на константу и перестановка строк.
Выполнение строковых операций над матрицей — это метод, который мы используем для решения системы уравнений. Чтобы решить систему уравнений, мы хотим преобразовать матрицу в форму строки-эшелона, в которой есть единицы вниз по главной диагонали от верхнего левого угла до нижнего правого угла и нули в каждой позиции ниже главной диагонали. как показано.
Мы используем операции со строками, соответствующие операциям с уравнениями, чтобы получить новую матрицу, эквивалентную строкам в более простой форме.Вот рекомендации по получению формы рядного эшелона.
- В любой ненулевой строке первым ненулевым числом является 1. Оно называется ведущим 1.
- Любые нулевые строки помещаются внизу матрицы.
- Любая ведущая 1 находится ниже и правее предыдущей ведущей 1.
- Любой столбец, в котором в начале стоит 1, имеет нули во всех остальных позициях в столбце.
Чтобы решить систему уравнений, мы можем выполнить следующие операции со строками, чтобы преобразовать матрицу коэффициентов в форму ряда строк и выполнить обратную подстановку, чтобы найти решение.
- Поменяйте местами ряды. (Обозначение 🙂
- Умножить строку на константу. (Обозначение 🙂
- Добавить произведение одной строки на константу к другой строке. (Замечание:
Каждая из строковых операций соответствует операциям, которые мы уже научились решать системы уравнений с тремя переменными. С помощью этих операций есть несколько ключевых ходов, которые быстро достигнут цели написания матрицы в виде эшелона строк. Чтобы получить матрицу в виде эшелона строк для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, так что строку 1 можно использовать для преобразования оставшихся строк.
Исключение по Гауссу
Метод исключения Гаусса относится к стратегии, используемой для получения матрицы в виде строки-эшелона. Цель состоит в том, чтобы записать матрицу с номером 1 в качестве записи по главной диагонали и иметь все нули внизу.
Первый шаг стратегии Гаусса включает получение 1 в качестве первой записи, так что строка 1 может использоваться для изменения строк ниже.
Учитывая расширенную матрицу, выполните операции со строками для получения формы «строка-эшелон».
- Первое уравнение должно иметь старший коэффициент 1. Поменяйте местами строки или умножьте на константу, если необходимо.
- Используйте операции со строками, чтобы получить нули в первом столбце под первой записью 1.
- Используйте операции со строками, чтобы получить 1 в строке 2, столбец 2.
- Используйте операции со строками, чтобы получить нули в нижнем столбце 2, под записью 1.
- Используйте операции со строками, чтобы получить 1 в строке 3, столбец 3.
- Продолжайте этот процесс для всех строк, пока в каждой записи по главной диагонали не будет 1, а внизу будут только нули.
- Если какие-либо строки содержат все нули, поместите их внизу.
Решите данную систему методом исключения Гаусса.
Решите данную систему методом исключения Гаусса.
Использование исключения Гаусса для решения системы уравнений
Используйте метод исключения Гаусса для решения данной системы уравнений.
Решение зависимой системы
Решите систему уравнений.
Выполнение операций со строками в расширенной матрице 3 × 3 для получения формы Row-Echelon
Выполняет строковые операции с заданной матрицей, чтобы получить форму строки-эшелона.
Запишите систему уравнений в виде ряда.
Решение системы линейных уравнений с использованием матриц
Мы видели, как написать систему уравнений с расширенной матрицей, а затем как использовать строковые операции и обратную подстановку для получения формы «строка-эшелон».Теперь мы перейдем на шаг дальше от строковой формы, чтобы решить систему линейных уравнений 3 на 3. Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.
Решение системы линейных уравнений с использованием матриц
Решите систему линейных уравнений с помощью матриц.
Решение зависимой системы линейных уравнений с использованием матриц
Решите следующую систему линейных уравнений, используя матрицы.
Решите систему, используя матрицы.
Можно ли решить любую систему линейных уравнений методом исключения Гаусса?
Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.
Дана система уравнений, решите с помощью матриц с помощью калькулятора.
- Сохранить расширенную матрицу как матричную переменную
- Используйте функцию ref ( в калькуляторе, вызывая каждую матричную переменную по мере необходимости.
Решение систем уравнений с матрицами с помощью калькулятора
Решите систему уравнений.
Применение матриц 2 × 2 к финансам
Кэролайн инвестирует в общей сложности 12 000 фунтов стерлингов в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая — 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 фунтов стерлингов. Сколько было вложено по каждой ставке?
Применение матриц 3 × 3 к финансам
Ava инвестирует в общей сложности 10 000 фунтов стерлингов в три счета, один из которых платит 5% годовых, другой — 8%, а третий — 9%.Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 евро. Сумма, вложенная под 9%, была вдвое больше суммы, инвестированной под 5%. Сколько было вложено по каждой ставке?
У нас есть система трех уравнений с тремя переменными. Пусть будет сумма, вложенная под 5%, пусть будет сумма, вложенная под 8%, пусть будет сумма, вложенная под 9%. Таким образом,
В качестве матрицы имеем
Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелон.
Третья строка сообщает usthus
Вторая строка говорит нам Подставляя, мы получаем
Первая строка говорит нам о замене и получаем
Ответ: 3000 евро вложены под 5%, 1000 евро вложены под 8% и 6000 евро инвестированы под 9%.
Небольшая обувная компания взяла ссуду в размере 1 500 000 фунтов стерлингов для расширения своих запасов. Часть денег была взята под 7%, часть — под 8%, часть — под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 евро. Используйте матрицы, чтобы найти сумму, заимствованную по каждой ставке.
? 150 000 при 7%, 750 000 фунтов стерлингов при 8%, 600 000 фунтов стерлингов при 10%
Ключевые концепции
- Расширенная матрица — это матрица, которая содержит коэффициенты и константы системы уравнений.См. (Рисунок).
- Матрица, дополненная постоянным столбцом, может быть представлена как исходная система уравнений. См. (Рисунок).
- Операции со строками включают в себя умножение строки на константу, добавление одной строки к другой строке и замену строк местами.
- Мы можем использовать метод исключения Гаусса для решения системы уравнений. См. (Рисунок), (Рисунок) и (Рисунок).
- Операции со строками выполняются над матрицами для получения формы «строка-эшелон». См. (Рисунок).
- Чтобы решить систему уравнений, запишите ее в форме расширенной матрицы.Выполните операции со строками, чтобы получить форму эшелона строк. Обратно-заменитель, чтобы найти решения. См. (Рисунок) и (Рисунок).
- Калькулятор можно использовать для решения систем уравнений с использованием матриц. См. (Рисунок).
- Многие реальные проблемы можно решить с помощью расширенных матриц. См. (Рисунок) и (Рисунок).
Упражнения по разделам
Словесный
Можно ли записать любую систему линейных уравнений в виде расширенной матрицы? Объясните, почему да или почему нет. Объясните, как написать эту расширенную матрицу.
Да. Для каждой строки коэффициенты переменных записываются поперек соответствующей строки и помещается вертикальная черта; затем константы помещаются справа от вертикальной полосы.
Можно ли записать любую матрицу в виде системы линейных уравнений? Объясните, почему да или почему нет. Объясните, как написать эту систему уравнений.
Есть только один правильный метод использования операций со строками в матрице? Попытайтесь объяснить две различные операции со строками, которые можно выполнить для расширенной матрицы
.Нет, существует множество правильных методов использования строковых операций над матрицей.Есть два возможных способа: (1) Поменять местами строки 1 и 2. Затем (2) Разделить строку 1 на 9.
Можно ли решить матрицу с нулевым элементом на диагонали? Объясните, почему да или почему нет. Что бы вы сделали, чтобы исправить ситуацию?
Может ли матрица с 0 элементами для всей строки иметь одно решение? Объясните, почему да или почему нет.
Нет. Матрица с 0 элементами для всей строки будет иметь либо ноль, либо бесконечно много решений.
Алгебраические
Для следующих упражнений напишите расширенную матрицу линейной системы.
Для следующих упражнений напишите линейную систему из расширенной матрицы.
Для следующих упражнений решите систему методом исключения Гаусса.
Расширения
Для следующих упражнений используйте метод исключения Гаусса для решения системы.
Реальные приложения
Для следующих упражнений настройте расширенную матрицу, описывающую ситуацию, и найдите желаемое решение.
Ежедневно в магазине кексов продается 5 000 кексов со вкусом шоколада и ванили. Если вкус шоколада в 3 раза популярнее, чем аромат ванили, сколько кексов продается в день?
В конкурирующем магазине кексов ежедневно продаются кексы на сумму 4520 фунтов стерлингов.Шоколадные кексы стоят 2,25 евро, а кексы из красного бархата — 1,75 евро. Если общее количество кексов, проданных в день, составляет 2200, сколько штук каждого вкуса продается каждый день?
860 красный бархат, 1340 шоколад
Вы вложили 10 000 евро в два счета: один с простой процентной ставкой 3%, а другой — с процентной ставкой 2,5%. Если ваша общая сумма процентов по истечении одного года составила 283,50 фунтов стерлингов, какая сумма была на каждом счете по истечении года?
Вы вложили 2300 евро на счет 1 и 2700 евро на счет 2.Если общая сумма процентов по истечении одного года составляет 254 евро, а на счете 2 процентная ставка в 1,5 раза выше, чем на счете 1, каковы процентные ставки? Предположим простые процентные ставки.
4% на счет 1, 6% на счет 2
Bikes’R’Us производит велосипеды по 250 фунтов стерлингов. Это стоит производителю 180 фунтов стерлингов за велосипед, плюс стартовый взнос в размере 3500 фунтов стерлингов. Через сколько проданных велосипедов производитель выйдет на уровень безубыточности?
Крупный магазин бытовой техники рассматривает возможность приобретения пылесосов у небольшого производителя.Магазин сможет приобрести пылесосы по цене 86 фунтов стерлингов каждый, с оплатой доставки в размере 9 200 фунтов стерлингов, независимо от того, сколько пылесосов продано. Если магазин должен начать получать прибыль после продажи 230 единиц, сколько они должны взимать за пылесосы?
Три самых популярных вкуса мороженого — это шоколад, клубника и ваниль, составляющие 83% вкусов, продаваемых в магазине мороженого. Если ваниль продается на 1% больше, чем в два раза больше клубники, а шоколад продается на 11% больше, чем ваниль, сколько в общем потреблении мороженого приходится на ароматы ванили, шоколада и клубники?
В магазине мороженого растет спрос на три вкуса.В прошлом году банановое, тыквенное и мороженое с каменистой дорогой составили 12% от общего объема продаж мороженого. В этом году на те же три вида мороженого пришлось 16,9% продаж мороженого. Продажи по каменистой дороге увеличились вдвое, продажи бананов увеличились на 50%, а продажи тыквы — на 20%. Если у мороженого по каменистой дороге было на один процент меньше продаж, чем у бананового, узнайте, какой процент продаж мороженого было произведено каждым отдельным мороженым в прошлом году.
Банан — 3%, тыква — 7%, а каменистая дорога — 2%
Пакет с ореховой смесью содержит кешью, фисташки и миндаль.Всего в сумке 1000 орехов, а миндаля на 100 меньше, чем фисташек. Кешью весит 3 г, фисташки — 4 г, миндаль — 5 г. Если мешок весит 3,7 кг, узнайте, сколько орехов каждого вида в нем.
Пакет с ореховой смесью содержит кешью, фисташки и миндаль. Изначально в сумке было 900 орехов. Было съедено 30% миндаля, 20% кешью и 10% фисташек, и теперь в сумке осталось 770 орехов. Первоначально кешью было на 100 штук больше, чем миндаля.Для начала выясните, сколько орехов каждого типа было в пакете.
100 миндальных орехов, 200 кешью, 600 фисташек
Глоссарий
- дополненная матрица
- матрица коэффициентов, примыкающая к столбцу констант, разделенному вертикальной линией в скобках матрицы
- матрица коэффициентов
- матрица, содержащая только коэффициенты из системы уравнений
- Исключение по Гауссу
- с использованием элементарных операций со строками для получения матрицы в виде строки-эшелона
- главная диагональ
- записей из левого верхнего угла по диагонали в правый нижний угол квадратной матрицы
- рядная форма
- после выполнения операций со строками матричная форма, которая содержит единицы по главной диагонали и нули в каждом пробеле ниже диагонали
- эквивалент ряда
- две матрицы и эквивалентны строкам, если одна может быть получена из другой путем выполнения основных операций со строками
- строковые операции
- : добавление одной строки к другой, умножение строки на константу, перестановка строк и т. Д. С целью получения формы «строка-эшелон»
Исключение по Гауссу
Тип 2.Умножьте строку на ненулевую константу.
Тип 3. Добавьте одну строку, кратную одной, в другую.
Цель этих операций — преобразовать — или уменьшить — исходную расширенную матрицу в одну из форм, где A ′ — верхний треугольник ( a ij ′ = 0 для i> j ), любые нулевые строки появляются внизу матрицы, и первая ненулевая запись в любой строке находится справа от первой ненулевой записи в любой более высокой строке; такая матрица, как говорят, имеет форму эшелон .Решения системы представлены более простой расширенной матрицей [ A ′ | b ′], можно найти путем осмотра нижних рядов и обратной подстановки в более высокие ряды. Поскольку элементарные операции со строками не меняют решений системы, векторы x , которые удовлетворяют более простой системе A ′ x = b ′, как раз те, которые удовлетворяют исходной системе, A x = b .
Пример 3 : Решите следующую систему с помощью исключения Гаусса:
Расширенная матрица, которая представляет эту систему:
Первая цель — получить нули под первой записью в первом столбце , что означает исключение первой переменной x из второго и третьего уравнений.Для этого выполняются следующие операции со строками:
Вторая цель — получить ноль под второй записью во втором столбце, что означает исключение второй переменной y из третьего уравнения. Один из способов добиться этого — добавить -1/5 второй строки к третьей строке. Однако, чтобы избежать дробей, есть еще один вариант: сначала поменять местами второй и третий ряды. Замена двух строк просто меняет местами уравнения, что явно не изменит решения системы:
Теперь прибавьте −5 раз вторую строку к третьей строке:
Поскольку матрица коэффициентов преобразована в эшелонированную форму, «прямая» часть исключения Гаусса завершена.Теперь остается использовать третью строку для оценки третьего неизвестного, затем выполнить обратную подстановку во вторую строку для оценки второго неизвестного и, наконец, выполнить обратную замену в первой строке для оценки первого неизвестного.
Третья строка финальной матрицы переводится в 10 z = 10, что дает z = 1. Обратная подстановка этого значения во вторую строку, которая представляет уравнение y — 3 z = — 1, дает y = 2.Обратная подстановка обоих этих значений в первую строку, которая представляет уравнение x — 2 y + z = 0, дает x = 3. Таким образом, решение этой системы: ( x, y, z ) = (3, 2, 1).
Пример 4 : Решите следующую систему с помощью исключения Гаусса:
Для этой системы расширенная матрица (вертикальная линия опущена) составляет
Сначала умножьте строку 1 на 1/2:
Теперь добавление −1 первой строки ко второй строке дает нули под первой записью в первом столбце:
Перестановка второй и третьей строк дает желаемую матрицу коэффициентов верхней треугольной формы:
В третьей строке теперь указано z = 4.Обратная подстановка этого значения во вторую строку дает y = 1, а обратная подстановка обоих этих значений в первую строку дает x = −2. Решение этой системы, следовательно, ( x, y, z ) = (−2, 1, 4).
Исключение Гаусса-Джордана . Исключение по Гауссу осуществляется путем выполнения элементарных операций со строками для получения нулей ниже диагонали матрицы коэффициентов, чтобы привести ее к эшелонированной форме. (Напомним, что матрица A ′ = [ a ij ′] имеет эшелонированную форму, когда a ij ′ = 0 для i> j , любые нулевые строки появляются внизу матрицы , и первая ненулевая запись в любой строке находится справа от первой ненулевой записи в любой более высокой строке.Как только это будет сделано, проверка нижней строки (строк) и обратная подстановка в верхние строки определяют значения неизвестных.
Однако можно сократить (или полностью исключить) вычисления, связанные с обратной подстановкой, выполнив дополнительные операции со строками для преобразования матрицы из эшелонированной формы в сокращенную форму эшелона. Матрица находится в форме сокращенного эшелона, когда, помимо того, что она находится в форме эшелона, каждый столбец, содержащий ненулевую запись (обычно равную 1), имеет нули не только под этой записью, но и над этой записью.Грубо говоря, исключение Гаусса работает сверху вниз, чтобы создать матрицу в форме эшелона, тогда как исключение Гаусса-Жордана продолжается с того места, где остановилось Гаусса, затем работая снизу вверх для создания матрицы в форме уменьшенного эшелона. Техника будет проиллюстрирована на следующем примере.
Пример 5 : Известно, что высота, y , подброшенного в воздух объекта задается квадратичной функцией от t (время) в форме y = at 2 + bt + c .Если объект находится на высоте y = 23/4 в момент времени t = 1/2, при y = 7 в момент времени t = 1, и при y = 2 при t = 2 , определите коэффициенты a, b и c .
Так как t = 1/2 дает y = 23/4
, в то время как два других условия, y ( t = 1) = 7 и y ( t = 2) = 2, дают следующие уравнения для a, b и c :
Следовательно, цель — решить систему
Расширенная матрица для этой системы сокращается следующим образом:
На этом прямая часть исключения Гаусса завершена, поскольку матрица коэффициентов приведена к эшелонированной форме.Однако, чтобы проиллюстрировать исключение Гаусса-Жордана, выполняются следующие дополнительные элементарные операции со строками:
Эта окончательная матрица сразу дает решение: a = −5, b = 10 и c = 2.
Пример 6 : Решите следующую систему с помощью исключения Гаусса:
Расширенная матрица для этой системы —
Кратные значения первой строки добавляются к другим строкам, чтобы получить нули под первой записью в первом столбце:
Затем −1 раз вторая строка добавляется к третьей строке:
В третьей строке теперь указано 0 x + 0 y + 0 z = 1, уравнение, которому не могут удовлетворять никакие значения x, y и z .Процесс останавливается: у этой системы нет решений.
Предыдущий пример показывает, как метод исключения по Гауссу обнаруживает противоречивую систему. Небольшое изменение этой системы (например, изменение постоянного члена «7» в третьем уравнении на «6») проиллюстрирует систему с бесконечным числом решений.
Пример 7 : Решите следующую систему с помощью исключения Гаусса:
Те же операции, которые применяются к расширенной матрице системы в примере 6, применяются к расширенной матрице для данной системы:
Здесь третья строка переводится в 0 x + 0 y + 0 z = 0, уравнение, которому удовлетворяют любые x, y и z .Поскольку здесь нет ограничений на неизвестные, на неизвестные не три условия, а только два (представленные двумя ненулевыми строками в окончательной расширенной матрице). Поскольку имеется 3 неизвестных, но только 2 константы, 3–2 = 1 неизвестных, скажем, z , произвольно; это называется свободной переменной . Пусть z = t , где t — любое действительное число. Обратная подстановка z = t во вторую строку (- y + 5 z = −6) дает
Обратная подстановка z = t и y = 6 + 5 t в первую строку ( x + y -3 z = 4) определяет x :
Следовательно, каждое решение системы имеет вид
, где t — любое действительное число.Существует бесконечно много решений, поскольку каждое действительное значение t дает отдельное конкретное решение. Например, выбор t = 1 дает ( x, y, z ) = (−4, 11, 1), а t = 3 дает ( x, y, z ) = (4, — 9, −3) и т. Д. Геометрически эта система представляет три плоскости в R 3 , которые пересекаются по линии, и (*) является параметрическим уравнением для этой линии.
Пример 7 дает иллюстрацию системы с бесконечным множеством решений, как возникает этот случай и как записывается решение.Каждая линейная система, имеющая бесконечно много решений, должна содержать хотя бы один произвольный параметр (свободная переменная). После того как расширенная матрица была приведена к эшелонированной форме, количество свободных переменных равно общему количеству неизвестных минус количество ненулевых строк:
Это согласуется с теоремой B выше, которая утверждает, что линейная система с меньшим количеством уравнений, чем неизвестных, если она согласована, имеет бесконечно много решений. Условие «меньше уравнений, чем неизвестных» означает, что количество строк в матрице коэффициентов меньше количества неизвестных.Следовательно, приведенное выше уравнение в рамке подразумевает, что должна быть хотя бы одна свободная переменная. Поскольку такая переменная по определению может принимать бесконечно много значений, система будет иметь бесконечно много решений.
Пример 8 : Найдите все решения для системы
Во-первых, обратите внимание, что есть четыре неизвестных, но только три уравнения. Следовательно, если система непротиворечива, гарантировано, что у нее будет бесконечно много решений, а это состояние характеризуется по крайней мере одним параметром в общем решении.После того, как соответствующая расширенная матрица построена, исключение Гаусса дает
Тот факт, что в эшелонированной форме расширенной матрицы остались только две ненулевые строки, означает, что 4-2 = 2 переменных свободны:
Следовательно, выбрав y и z в качестве свободных переменных, пусть y = t 1 и z = t 2 . Во второй строке сокращенной расширенной матрицы следует
, а первая строка дает
Таким образом, решения системы имеют вид
, где t 1 t 2 могут принимать любые реальные значения.
Пример 9 : Пусть b = ( b 1 , b 2 , b 3 ) T и пусть A будет матрицей
Для каких значений b 1 , b 2 и b 3 будет ли система A x = b согласованной?
Расширенная матрица для системы A x = b читает
, который гауссовский элиминатин сокращает следующим образом:
Нижняя строка теперь подразумевает, что b 1 + 3 b 2 + b 3 должен быть равен нулю, чтобы эта система была согласованной.Следовательно, в данной системе есть растворины (фактически бесконечно много) только для тех векторов-столбцов b = ( b 1 , b 2 , b 3 ) T , для которых b 1 + 3 b 2 + b 3 = 0,
Пример 10 : Решите следующую систему (сравните с Примером 12):
Такая система, как эта, где постоянный член в правой части каждого уравнения равен 0, называется гомогенной системой .В матричной форме он читается как A x = 0 . Поскольку каждая гомогенная система согласована — поскольку x = 0 всегда является решением — однородная система имеет либо ровно одно решение ( тривиальное решение , x = 0 ), либо бесконечно много. Сокращение строки матрицы коэффициентов для этой системы уже было выполнено в примере 12. Нет необходимости явно дополнять матрицу коэффициентов столбцом b = 0 , поскольку никакая элементарная операция со строкой не может повлиять на эти нули.То есть, если A ‘является эшелонированной формой A , то операции элементарной строки преобразуют [ A | 0 ] в [ A ′ | 0 ]. По результатам Примера 12,
Поскольку последняя строка снова подразумевает, что z можно принять как свободную переменную, пусть z = t , где t — любое действительное число. Обратная подстановка z = t во вторую строку (- y + 5 z = 0) дает
и обратная подстановка z = t и y = 5 t в первую строку ( x + y — 3 z = 0) определяет x :
Следовательно, каждое решение этой системы имеет вид ( x, y, z ) = (−2 t , 5 t, t ), где t — любое действительное число.Существует бесконечно много растворенных веществ, поскольку каждое действительное значение t дает уникальное частное решение.
Обратите внимание на разницу между набором решений для системы в Примере 12 и здесь. Хотя у обоих была одна и та же матрица коэффициентов A , система в примере 12 была неоднородной ( A x = b , где b ≠ 0 ), а здесь — соответствующая однородная система, A x = 0 .Помещая свои решения рядом,
общее решение для Ax = 0 : ( x, y, z ) = (−2 t , 5 t , t )
общее решение для Ax = b : ( x, y, z ) = (−2 t , 5 t , t ) + (−2, 6, 0)
иллюстрирует важный факт:Теорема C . Общие решения для согласованной неоднородной лиенарной системы, A x = b , равны общему решению соответствующей однородной системы, A x = 0 , плюс частное решение неоднородная система.То есть, если x = x h представляет собой общее решение A x = 0 , тогда x = x h + x представляет общее решение A x + b , где x — любое конкретное решение (согласованной) неоднородной системы A x = b .
[Техническое примечание: теорема C, которая касается линейной системы , имеет аналог в теории линейных дифференциальных уравнений .Пусть L — линейный дифференциальный оператор; то общее решение разрешимого неоднородного линейного дифференциального уравнения, L (y) = d (где d ≢ 0), равно общему решению соответствующего однородного уравнения, L (y) = 0 плюс частное решение неоднородного уравнения. То есть, если y = y h воспроизводит общее решение L (y) = 0, то y = y h + y представляет собой общее решение L (y ) = d , где y — любое частное решение (решаемого) неоднородного линейного уравнения L (y) = d .]
Пример 11 : Определить все решения системы
Запишите расширенную матрицу и выполните следующую последовательность операций:
Поскольку в этой конечной (эшелонированной) матрице остаются только 2 ненулевые строки, есть только 2 ограничения и, следовательно, 4-2 = 2 из неизвестных, скажем, y и z , являются свободными переменными. Пусть y = t 1 и z = t 2 .Обратная подстановка y = t 1 и z = t 2 во второй строке ( x — 3 y + 4 z = 1) дает
Наконец, обратная замена x = 1 + 3 t 1 — 4 2 , y = t 1 и z = t 2 в первую строка (2 w -2 x + y = −1) определяет w :
Следовательно, каждое решение этой системы имеет вид
, где t 1 и t 2 — любые действительные числа.Другой способ написать решение:
, где t 1 , t 2 ∈ R .
Пример 12 : Определите общее решение
, которая является однородной системой, соответствующей неоднородной в примере 11 выше.
Поскольку решение неоднородной системы в примере 11 равно
Теорема C означает, что решение соответствующей однородной системы (где t 1 , t 2 ∈ R ) получается из (*), просто отбрасывая конкретное решение, x = (1 / 2,1,0,0) неоднородной системы.
Пример 13 : Докажите теорему A: независимо от ее размера или количества неизвестных, содержащихся в ее уравнениях, линейная система не будет иметь решений, ровно одно решение или бесконечно много решений.
Доказательство . Пусть данная линейная система записана в матричной форме A x = b . Теорема действительно сводится к следующему: если A x = b имеет более одного решения, то на самом деле их бесконечно много.Чтобы установить это, пусть x 1 и x 2 будут двумя разными решениями A x = b . Теперь будет показано, что для любого реального значения t вектор x 1 + t ( x 1 — x 2 ) также является решением A x = b ; Поскольку t может принимать бесконечно много различных значений, из этого следует желаемый вывод.Поскольку A x 1 = b и A x 2 ,
Следовательно, x 1 + t ( x 1 — x 2 ) действительно является решением A x = b , и теорема доказана.
Обращение матрицы с использованием исключения Гаусса-Джордана
М. Борна
В этом разделе мы увидим, как работает метод исключения Гаусса-Жордана, на примерах.
Вы можете повторно загружать эту страницу сколько угодно раз и каждый раз получать новый набор чисел. Вы также можете выбрать матрицу другого размера (внизу страницы).
(Если вам сначала нужна дополнительная информация, вернитесь к «Введение в матрицы»).
Выберите размер матрицы, который вас интересует, и нажмите кнопку.
Матрица A:
Пример, сгенерированный случайным образом, показан ниже.
Телефонные пользователи
ПРИМЕЧАНИЕ: Если вы разговариваете по телефону, вы можете прокрутить любые широкие матрицы на этой странице вправо или влево, чтобы увидеть все выражение.
Пример (3 × 3)
Найдите матрицу, обратную матрице A , используя метод исключения Гаусса-Жордана.
| А = | 12 | 9 | 5 | ||
| 8 | 13 | 2 | |||
| 14 | 10 | 4 |
Наша процедура
Запишем матрицу A слева и матрицу идентичности I справа, разделенную пунктирной линией, как показано ниже.Результат называется расширенной матрицей .
Мы включили номера строк, чтобы было понятнее.
| 1 | 0 | 0 | Ряд [1] | |
| 0 | 1 | 0 | Ряд [2] | |
| 0 | 0 | 1 | Ряд [3] |
Затем мы выполняем несколько операций со строками над двумя матрицами, и наша цель — получить единичную матрицу на левом , например:
| ? | ? | ? | Ряд [1] | |
| ? | ? | ? | Ряд [2] | |
| ? | ? | ? | Ряд [3] |
(Технически мы сокращаем матрицу A до сокращенной формы эшелона строк , также называемой канонической формой строк ).
Результирующая матрица справа будет обратной матрицей от A .
Наша процедура операций со строками выглядит следующим образом:
- Получим «1» в верхнем левом углу, разделив первую строку
- Тогда мы получим «0» в оставшейся части первого столбца
- Тогда нам нужно получить «1» во второй строке, втором столбце
- Затем мы делаем все остальные записи во втором столбце «0».
Продолжаем так до тех пор, пока слева не останется единичная матрица.
Давайте теперь продолжим и найдем обратное.
Решение
Начнем с:
| 1 | 0 | 0 | Ряд [1] | |
| 0 | 1 | 0 | Ряд [2] | |
| 0 | 0 | 1 | Ряд [3] |
Новый ряд [1]
Разделите строку [1] на 12 (чтобы получить «1» в нужной позиции):
Это дает нам:
| 1 | 0.75 | 0,4167 | |
| 8 | 13 | 2 | |
| 14 | 10 | 4 |
| 0,0833 | 0 | 0 | Ряд [1] | |
| 0 | 1 | 0 | Ряд [2] | |
| 0 | 0 | 1 | Ряд [3] |
Новый ряд [2]
Ряд [2] — 8 × Ряд [1] (чтобы получить 0 в желаемой позиции):
8 — 8 × 1 = 0
13 — 8 × 0.75 = 7
2 — 8 × 0,4167 = -1,3333
0 — 8 × 0,0833 = -0,6667
1 — 8 × 0 = 1
0 — 8 × 0 = 0
Это дает нам новую строку [2]:
| 1 | 0,75 | 0,4167 | |
| 0 | 7 | -1,3333 | |
| 14 | 10 | 4 |
| 0,0833 | 0 | 0 | Ряд [1] | |
| -0.6667 | 1 | 0 | Ряд [2] | |
| 0 | 0 | 1 | Ряд [3] |
Новый ряд [3]
Ряд [3] — 14 × Ряд [1] (чтобы получить 0 в желаемой позиции):
14 — 14 × 1 = 0
10 — 14 × 0,75 = -0,5
4 — 14 × 0,4167 = -1,8333
0 — 14 × 0,0833 = -1,1667
0 — 14 × 0 = 0
1 — 14 × 0 = 1
Это дает нам новую строку [3]:
| 1 | 0.75 | 0,4167 | |
| 0 | 7 | -1,3333 | |
| 0 | -0,5 | -1,8333 |
| 0,0833 | 0 | 0 | Ряд [1] | |
| -0,6667 | 1 | 0 | Ряд [2] | |
| -1,1667 | 0 | 1 | Ряд [3] |
Новый ряд [2]
Разделите строку [2] на 7 (чтобы получить «1» в нужной позиции):
Это дает нам:
| 1 | 0.75 | 0,4167 | |
| 0 | 1 | -0,1905 | |
| 0 | -0,5 | -1,8333 |
| 0,0833 | 0 | 0 | Ряд [1] | |
| -0,0952 | 0,1429 | 0 | Ряд [2] | |
| -1,1667 | 0 | 1 | Ряд [3] |
Новый ряд [1]
Ряд [1] — 0.75 × Ряд [2] (чтобы получить 0 в желаемой позиции):
1 — 0,75 × 0 = 1
0,75 — 0,75 × 1 = 0
0,4167 — 0,75 × -0,1905 = 0,5595
0,0833 — 0,75 × -0,0952 = 0,1548
0 — 0,75 × 0,1429 = -0,1071
0 — 0,75 × 0 = 0
Это дает нам новую строку [1]:
| 1 | 0 | 0,5595 | |
| 0 | 1 | -0,1905 | |
| 0 | -0.5 | -1,8333 |
| 0,1548 | -0,1071 | 0 | Ряд [1] | |
| -0,0952 | 0,1429 | 0 | Ряд [2] | |
| -1,1667 | 0 | 1 | Ряд [3] |
Новый ряд [3]
Ряд [3] — -0,5 × Ряд [2] (чтобы получить 0 в желаемой позиции):
0 — -0.5 × 0 = 0
-0,5 — -0,5 × 1 = 0
-1,8333 — -0,5 × -0,1905 = -1,9286
-1,1667 — -0,5 × -0,0952 = -1,2143
0 — -0,5 × 0,1429 = 0,0714
1 — -0,5 × 0 = 1
Это дает нам новую строку [3]:
| 1 | 0 | 0,5595 | |
| 0 | 1 | -0,1905 | |
| 0 | 0 | -1,9286 |
| 0.1548 | -0,1071 | 0 | Ряд [1] | |
| -0,0952 | 0,1429 | 0 | Ряд [2] | |
| -1,2143 | 0,0714 | 1 | Ряд [3] |
Новый ряд [3]
Разделите строку [3] на -1,9286 (чтобы получить «1» в нужной позиции):
Это дает нам:
| 1 | 0 | 0.5595 | |
| 0 | 1 | -0,1905 | |
| 0 | 0 | 1 |
| 0,1548 | -0,1071 | 0 | Ряд [1] | |
| -0,0952 | 0,1429 | 0 | Ряд [2] | |
| 0,6296 | -0,037 | -0,5185 | Ряд [3] |
Новый ряд [1]
Ряд [1] — 0.5595 × Ряд [3] (чтобы получить 0 в желаемой позиции):
1 — 0,5595 × 0 = 1
0 — 0,5595 × 0 = 0
0,5595 — 0,5595 × 1 = 0
0,1548 — 0,5595 × 0,6296 = -0,1975
-0,1071 — 0,5595 × -0,037 = -0,0864
0 — 0,5595 × — 0,5185 = 0,2901
Это дает нам новую строку [1]:
| 1 | 0 | 0 | |
| 0 | 1 | -0,1905 | |
| 0 | 0 | 1 |
| -0.1975 | -0,0864 | 0,2901 | Ряд [1] | |
| -0,0952 | 0,1429 | 0 | Ряд [2] | |
| 0,6296 | -0,037 | -0,5185 | Ряд [3] |
Новый ряд [2]
Ряд [2] — -0,1905 × Ряд [3] (чтобы получить 0 в желаемой позиции):
0 — -0,1905 × 0 = 0
1 — -0,1905 × 0 = 1
-0.1905 — -0,1905 × 1 = 0
-0,0952 — -0,1905 × 0,6296 = 0,0247
0,1429 — -0,1905 × -0,037 = 0,1358
0 — -0,1905 × -0,5185 = -0,0988
Это дает нам новую строку [2]:
| -0,1975 | -0,0864 | 0,2901 | Ряд [1] | |
| 0,0247 | 0,1358 | -0,0988 | Ряд [2] | |
| 0,6296 | -0,037 | -0.5185 | Ряд [3] |
Мы достигли нашей цели по созданию матрицы идентичности слева. Таким образом, мы можем заключить, что обратная матрица A является правой частью расширенной матрицы:
| А -1 = | -0,1975 | -0,0864 | 0,2901 | ||
| 0,0247 | 0,1358 | -0,0988 | |||
| 0.6296 | -0,037 | -0,5185 |
Примечания
- Приведенное выше объяснение показывает все шаги. Человек обычно может пойти несколькими путями. Кроме того, иногда в правильной позиции уже есть «1» или «0», и в этих случаях нам не нужно ничего делать для этого шага.
- Всегда записывайте, что вы делаете на каждом этапе — очень легко заблудиться!
- Я показал результаты с точностью до 4 знаков после запятой, но с максимальной точностью использовалась повсюду.Имейте в виду, что небольшие ошибки округления будут накапливаться во всей задаче. Всегда используйте полную точность калькулятора! (Используйте всю память вашего калькулятора.)
- Очень иногда возникают странные результаты из-за внутреннего представления чисел компьютером. То есть он может хранить «1» как 0,999999999872.
Посмотреть еще?
Вы можете вернуться к началу страницы и выбрать другой пример.
ФормаRow Echelon Form и сокращенная Row Echelon Form
Содержание (Щелкните, чтобы перейти к этому разделу:
- Форма эшелона?
- Форма эшелона
- Форма пониженного эшелона
- Исключение по Гауссу
- Ранг матрицы
Что такое форма эшелона?
ФормаEchelon означает, что матрица находится в одном из двух состояний:
- Форма рядного эшелона.
- Уменьшенная форма рядного эшелона.
Это означает, что матрица удовлетворяет следующим трем требованиям:
- Первое число в строке (называемое ведущим коэффициентом) — 1. Примечание: некоторые авторы не требуют, чтобы ведущий коэффициент был равен 1; это могло быть любое число. Вы можете узнать у своего инструктора, какой версии этого правила они придерживаются).
- Каждая ведущая единица находится справа от первой.
- Любые ненулевые строки всегда находятся над строками со всеми нулями.
Следующие примеры представляют собой матрицы в эшелонированной форме:
Следующие примеры представляют собой , а не в эшелонированной форме:
Матрица A не имеет строк со всеми нулями ниже ненулевых строк.
Матрица B имеет 1 на 2 позиции в третьем ряду. Для формы эшелона строки он должен быть справа от ведущего коэффициента над ним. Другими словами, он должен быть на четвертой позиции вместо 3.
Матрица C имеет 2 в качестве ведущего коэффициента вместо 1.
Матрица D имеет -1 в качестве ведущего коэффициента вместо 1.
Другой способ думать о матрице в форме эшелона — это то, что матрица подверглась гауссовскому исключению, которое представляет собой серию операций со строками.
Уникальность и формы эшелона
Эшелонированная форма матрицы не уникальна, что означает, что при сокращении строк возможно бесконечное количество ответов. Уменьшенная форма эшелона строки находится на другом конце спектра; он уникален на , что означает, что сокращение строк в матрице даст один и тот же ответ независимо от того, как вы выполняете одни и те же операции со строками.
Вернуться к началу.
Что такое форма эшелона строк?
Матрица находится в форме эшелона строк, если она соответствует следующим требованиям:
- Первое ненулевое число слева («ведущий коэффициент») всегда находится справа от первого ненулевого числа в строке выше.
- Строки, состоящие из нулей, находятся внизу матрицы.
Форма рядного эшелона. «А» может представлять любое число.
Технически ведущий коэффициент может быть любым числом.Однако в большинстве учебников линейной алгебры утверждается, что ведущим коэффициентом должно быть число 1. Чтобы добавить путаницы, некоторые определения формы эшелона строк утверждают, что должны быть нули как выше , так и ниже ведущего коэффициента. Поэтому лучше всего следовать определению, данному в учебнике, которому вы следуете (или тому, что дал вам ваш профессор). Если вы не уверены (то есть сейчас воскресенье, у вас должна быть домашняя работа, и вы не можете связаться с профессором), безопаснее всего использовать 1 в качестве ведущего коэффициента в каждой строке.
Если ведущий коэффициент в каждой строке — это только ненулевое число в этом столбце, матрица называется уменьшенной эшелонированной строкой.
Матрица 3 × 5 в сокращенной форме эшелона строк.
Строковые эшелонированные формы обычно встречаются в линейной алгебре, когда вас иногда просят преобразовать матрицу в эту форму. Форма эшелона строк может помочь вам увидеть, что представляет собой матрица, а также является важным шагом к решению систем линейных уравнений.
Онлайн-калькулятор формы эшелона строк
Этот онлайн-калькулятор преобразует любую матрицу, и предоставляют операции со строками, которые помогут вам от шага к шагу. На следующем изображении (из калькулятора Old Dominion University Calculator показано, как матрица [01, 00, 59] приводится к форме эшелона строк с помощью двух простых операций со строками:
Back to Top.
Что такое форма сокращенного эшелона строк?
Уменьшенная форма эшелона строк — это тип матрицы, используемый для решения систем линейных уравнений.Форма пониженного ряда имеет четыре требования:
- Первое ненулевое число в первой строке (, ведущая запись ) — это число 1.
- Вторая строка также начинается с цифры 1, которая находится правее первой записи в первой строке. В каждом последующем ряду цифра 1 должна быть правее.
- Начальная запись в каждой строке должна быть единственным ненулевым числом в ее столбце.
- Любые ненулевые строки помещаются внизу матрицы.
Матрица 3 × 5 в сокращенной форме эшелона строк.
Преобразование матрицы в форму сокращенного эшелона строк
Любая матрица может быть преобразована в сокращенную форму эшелона строк с помощью метода, называемого исключением по Гауссу. Это особенно полезно для решения систем линейных уравнений. Большинство графических калькуляторов (например, TI-83) имеют функцию rref, которая преобразует матрицу в сокращенную форму эшелона строк. См. Эту статью на веб-сайте Университета штата Колорадо, где приведены инструкции по использованию TI-89 и TI-83 для расчета формы сокращенного эшелона строки.
Этот онлайн-калькулятор на веб-сайте Old Dominion University преобразует вводимую вами матрицу в сокращенную форму эшелона строк.
Для ручного расчета требуется знание элементарных операций со строками, а именно:
- Поменяйте местами одну строку с другой.
- Умножить одну строку на ненулевую константу.
- Заменить одну строку на: одну строку плюс константу, умноженную на другую строку.
Кроме того, недостаточно просто знать правила, вы должны уметь смотреть на матрицу и принимать логическое решение о том, какое правило вы собираетесь использовать и когда.Вы пытаетесь преобразовать матрицу в сокращенный ряд строк, поэтому вам также нужно будет обратиться к четырем требованиям, приведенным в начале этой статьи. Если вам нужно вручную преобразовать матрицу в сокращенную форму эшелона строк, рекомендуется использовать один из приведенных выше калькуляторов, чтобы проверить свою работу. Фактически, если вы используете онлайн-калькулятор ODU, он даже предоставит вам операции со строками. На изображении ниже показано преобразование калькулятором матрицы [204,923]:
Вернуться к началу.
Что такое метод исключения Гаусса?
Метод исключения Гаусса — это способ найти решение системы линейных уравнений.Основная идея состоит в том, что вы выполняете математическую операцию над строкой и продолжаете, пока не останется только одна переменная. Например, некоторые возможные операции со строками:
- Поменять местами любые два ряда
- Сложите две строки вместе.
- Умножить одну строку на ненулевую константу (например, 1/3, -1, 5)
Одновременно можно выполнять несколько операций со строками. Например, умножьте одну строку на константу, а затем добавьте результат к другой строке.
После этого цель состоит в том, чтобы получить матрицу в уменьшенной форме эшелона строк, где ведущий коэффициент, 1, в каждой строке находится справа от ведущего коэффициента в строке над ней.Другими словами, вам нужно получить 1 в верхнем левом углу матрицы. В следующей строке должен быть 0 в позиции 1 и 1 в позиции 2. Это дает вам решение системы линейных уравнений.
Пример исключения Гаусса
Решите следующую систему линейных уравнений методом исключения Гаусса:
- х + 5у = 7
- -2x — 7y = -5
Шаг 1: Преобразуйте уравнение в форму матрицы коэффициентов . Другими словами, просто возьмите коэффициент для чисел и забудьте пока о переменных:
Шаг 2. Превратите числа в нижней строке в положительные, прибавив 2 раза первую строку:
Шаг 3: Умножьте вторую строку на 1/3.Это дает вам второй ведущий 1:
Шаг 4: Умножьте строку 2 на -5, а затем добавьте это к строке 1:
Вот и все!
В первой строке у вас x = -8, а во второй строке y = 3. Обратите внимание, что x и y находятся в тех же положениях, что и при преобразовании уравнения на шаге 1, поэтому все, что вам нужно сделать, это прочтите решение:
Вернуться к началу.
Что такое ранг матрицы?
Ранг матрицы равен количеству линейно независимых строк.Линейно независимая строка — это строка, которая не является комбинацией других строк.
Следующая матрица имеет две линейно независимых строки (1 и 2). Однако, когда в смесь добавляется третья строка, вы можете видеть, что первая строка теперь равна сумме второй и третьей строк. Следовательно, ранг этой конкретной матрицы равен 2, так как имеется только две линейно независимых строки.
Ранг матрицы всегда будет на меньше, чем — количество ненулевых строк или количество столбцов в матрице.Если все строки в матрице линейно независимы, матрица имеет ранг , полный ранг строки . Для квадратной матрицы она имеет полный ранг только в том случае, если ее определитель не равен нулю.
Выяснить ранг матрицы, пытаясь определить на глаз, сколько строк или столбцов линейно независимы, может быть практически невозможно. Более простой (и, возможно, очевидный) способ — преобразовать в форму эшелона строк.
Как найти матрицу Рейтинг
Найти ранг матрицы просто, если вы знаете, как найти матрицу эшелона строк.Чтобы найти ранг любой матрицы:
- Найдите матрицу эшелонов строк.
- Подсчитайте количество ненулевых строк.
Преобразование матрицы в форму эшелона строк.
Вышеупомянутая матрица была преобразована в форму эшелона строк с двумя ненулевыми строками. Следовательно, ранг матрицы равен 2.
Вы также можете найти отличный инструмент для конвертации на сайте Old Dominion University.
Вернуться к началу.
Список литературы
Эверитт, Б.S .; Скрондал А. (2010), Кембриджский статистический словарь, Cambridge University Press.
Гоник Л. (1993). Мультяшный справочник по статистике. HarperPerennial.
Сирл, С. (2017). Матричная алгебра, полезная для статистики (серия Уайли по вероятности и статистике), 2-е издание. Вайли.
Нужна помощь с домашним заданием или контрольным вопросом? С помощью Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Обращение матрицы с использованием элементарных операций со строками (Гаусс-Джордан)
Также называется методом Гаусса-Жордана.
Это интересный способ найти обратную матрицу:
Поиграйте со строками (сложение, умножение или замена) пока мы не превратим Matrix A в Identity Matrix I
И, ТАКЖЕ внесение изменений в матрицу идентичности, она волшебным образом превращается в инверсию!
«Элементарные операции со строками» — это простые вещи, такие как добавление строк, умножение и замена местами… но давайте посмотрим на примере:
Пример: найти обратную букву «А»:
Мы начинаем с матрицы A и записываем ее с Матрицей идентичности I рядом с ней:
(это называется «Расширенная матрица»)
Матрица идентификации
«Матрица идентичности» является матричным эквивалентом числа «1»:
Матрица идентификации 3×3
- Это «квадрат» (в нем столько же строк, что и столбцов),
- Он имеет 1 с по диагонали и 0 с по всей остальной части.
- Его символ — заглавная буква I .
Теперь мы делаем все возможное, чтобы превратить «А» (Матрица слева) в Матрицу Идентичности. Цель состоит в том, чтобы матрица A имела 1 сек по диагонали и 0 сек в другом месте (матрица идентичности) … и правая сторона используется для поездки, с каждой выполняемой с ней операцией.
Но мы можем выполнять только эти «Элементарные операции со строками» :
- поменять местами строк
- умножить или разделить каждый элемент в строке на константу
- заменить строку на , прибавив к ней или вычтя из нее число, кратное другой строке
И мы должны сделать это для всей строки , вот так:
Начните с A рядом с I
Добавить строку 2 к строке 1,
, затем разделите строку 1 на 5,
Затем возьмите 2 раза первую строку и вычтите ее из второй строки,
Умножить вторую строку на -1/2,
Теперь поменяйте местами вторую и третью строки,
Наконец, вычтите третью строку из второй строки,
И готово!
И матрица преобразована в Матрицу идентификации…
… и в то же время идентификационная матрица превратилась в A -1
СДЕЛАНО! Как по волшебству, и так же весело, как решать любую головоломку.
И обратите внимание: не существует «правильного способа» сделать это, просто продолжайте играть, пока у нас не получится!
(Сравните этот ответ с тем, который мы получили на тему «Обращение матрицы» с использованием младших, сомножителей и адъюгата. Это то же самое? Какой метод вы предпочитаете?)
Большие матрицы
Мы можем сделать это с матрицами большего размера, например, попробуйте эту матрицу 4×4:
Начать как это:
Посмотри, сможешь ли ты сделать это сам (я бы начал с деления первой строки на 4, но ты делаешь это по-своему).
Вы можете проверить свой ответ с помощью калькулятора матрицы (используйте кнопку «inv (A)»).
Почему это работает
Мне нравится думать об этом так:
- когда мы превращаем «8» в «1» делением на 8,
- и проделайте то же самое с «1», оно превратится в «1/8»
И «1/8» является (мультипликативным) , обратным 8
Или, точнее говоря:
Общий эффект всех операций со строками такой же, как умножение на A -1
Итак, A становится I (потому что A -1 A = I )
And I становится A -1 (потому что A -1 I = A -1 )
Wolfram | Примеры альфа: матрицы
Свойства матрицы
Исследуйте различные свойства данной матрицы.
Вычислить свойства матрицы:
Другие примеры
Матричная арифметика
Сложение, вычитание и умножение векторов и матриц.
{{2, -1, 1}, {0, -2, 1}, {1, -2, 0}}.{x, y, z}Другие примеры
След
Вычислить след или сумму членов на главной диагонали матрицы.
Вычислить след матрицы:
Другие примеры
Детерминант
Вычислить определитель квадратной матрицы.
Вычислить определитель матрицы:
Другие примеры
Обратный
Обратить квадратную обратимую матрицу или найти псевдообратную неквадратную матрицу.
Вычислить обратную матрицу:
Другие примеры
Уменьшение строк
Привести матрицу к уменьшенной форме эшелона строк.
уменьшение строки {{2, 1, 0, -3}, {3, -1, 0, 1}, {1, 4, -2, -5}}Другие примеры
Собственные значения и собственные векторы
Вычислить собственную систему заданной матрицы.
Вычислить собственные значения матрицы:
Вычислить собственные векторы матрицы:
Вычислить характеристический полином матрицы:
Другие примеры
Другие матричные операции
Выполняет различные операции с матрицами, например сопряженное транспонирование.
Вычислите транспонирование матрицы:
Вычислить ранг матрицы:
Вычислить нулевое значение матрицы:
Вычислить адъюгат матрицы:
Другие примеры
Диагонализация
Найдите диагонализацию квадратной матрицы.
Другие примеры
Другие примеры
Матричные разложенияПреобразует матрицу в указанное разложение.
Вычислите LU-разложение квадратной матрицы:
Вычислите разложение по сингулярным числам:
Другие примеры
Другие примеры
Геометрические преобразованияНайдите матричные представления для геометрических преобразований.
Вычислите матрицу вращения 2 x 2:
Вычислите матрицу отражения 3 x 3:
Другие примеры
Типы матриц
Найдите информацию о различных типах матриц.
Определите, имеет ли матрица указанное свойство:
Получите информацию о типе матрицы:
Другие примеры
Алгебра — расширенные матрицы
Решите каждую из следующих систем уравнений.
a \ (\ begin {align *} 3x + y — 2z & = 2 \\ x — 2y + z & = 3 \\ 2x — y — 3z & = 3 \ end {align *} \) Показать решениеДавайте сначала запишем расширенную матрицу для этой системы.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} {\ color {Red} 3} & 1 & {- 2} & 2 \\ 1 & {- 2} & 1 & 3 \\ 2 & {- 1} & {- 3} & 3 \ end {array}} \ right] \]Как и в предыдущих примерах, мы помечаем красным цветом числа, которые мы хотим изменить на данном шаге.Первый шаг здесь — получить 1 в верхнем левом углу, и, опять же, у нас есть много способов сделать это. В этом случае мы заметим, что если мы поменяем местами первую и вторую строки, мы сможем получить 1 в этом месте с относительно небольшой работой.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} {\ color {Red} 3} & 1 & {- 2} & 2 \\ 1 & {- 2} & 1 & 3 \\ 2 & {- 1} & {- 3} & 3 \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_1} \ leftrightarrow {R_2}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ {\ color {Red} 3} & 1 & {- 2} & 2 \\ {\ color {Red} 2} & {- 1} & {- 3} & 3 \ end {array}} \ right] \]Следующий шаг — получить два числа под этой единицей равными нулю.Также обратите внимание, что это почти всегда требует выполнения операции третьей строки. Кроме того, мы можем сделать и то, и другое за один шаг следующим образом.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ {\ color {Red} 3} & 1 & {- 2} & 2 \\ {\ color {Red } 2} & {- 1} & {- 3} & 3 \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_2} — 3 {R_1} \ to {R_2 }} \\ {{R_3} — 2 {R_1} \ to {R_3}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & {\ color {Red} 7} & {- 5} & {- 7} \\ 0 & 3 & {- 5} & {- 3} \ end {array}} \ right] \]Далее мы хотим превратить 7 в 1.Мы можем сделать это, разделив вторую строку на 7.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & {\ color {Red} 7} & {- 5} & {- 7} \\ 0 & 3 & {- 5} & {- 3} \ end {array}} \ right] \ begin {array} {* {20} {c}} {\ frac {1} {7} {R_2}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & 1 & {- \ frac {5} {7}} & {- 1} \\ 0 & {\ color {Красный} 3} & {- 5} & {- 3} \ end {array}} \ right] \]Итак, здесь фигурирует дробь.Такое случается время от времени, так что не стоит сильно волноваться по этому поводу. Следующий шаг — заменить 3 под этой новой единицей на 0. Обратите внимание, что мы пока не будем беспокоиться о -2 над ней. Иногда так же легко превратить это в 0 на том же этапе. Однако в этом случае это, вероятно, так же легко сделать позже, как мы увидим.
Итак, используя операцию третьей строки, получаем
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & 1 & {- \ frac {5} {7}} & {- 1} \\ 0 & { \ color {Red} 3} & {- 5} & {- 3} \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_3} — 3 {R_2} \ в {R_3}} \\ \ в \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & 1 & {- \ frac {5} {7}} & { — 1} \\ 0 & 0 & {\ color {Red} — \ frac {{20}} {7}} & 0 \ end {array}} \ right] \]Далее нам нужно преобразовать число в правом нижнем углу в 1.Мы можем сделать это с помощью операции второй строки.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & 1 & {- \ frac {5} {7}} & {- 1} \\ 0 & 0 & { \ color {Red} — \ frac {{20}} {7}} & 0 \ end {array}} \ right] \ begin {array} {* {20} {c}} {- \ frac {7} {{ 20}} {R_3}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & {\ color {Red} 1} & 3 \\ 0 & 1 & {\ цвет {Красный} — \ frac {5} {7}} & {- 1} \\ 0 & 0 & 1 & 0 \ end {array}} \ right] \]Теперь нам нужны нули над этой новой единицей.Итак, использование операции третьей строки дважды, как показано ниже, сделает то, что нам нужно.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & {\ color {Red} 1} & 3 \\ 0 & 1 & {\ color {Red} — \ frac {5] } {7}} & {- 1} \\ 0 & 0 & 1 & 0 \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_2} + \ frac {5} {7} { R_3} \ to {R_2}} \\ {{R_1} — {R_3} \ to {R_1}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {\ цвет {Красный} — 2} & 0 & 3 \\ 0 & 1 & 0 & {- 1} \\ 0 & 0 & 1 & 0 \ end {array}} \ right] \]Обратите внимание, что в этом случае последний столбец не изменился на этом этапе.Это произошло только потому, что последняя запись в этом столбце была нулевой. В общем, этого не произойдет.
Последний шаг — преобразовать -2 над 1 во втором столбце в ноль. Это легко сделать с помощью операции третьего ряда.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {\ color {Red} — 2} & 0 & 3 \\ 0 & 1 & 0 & {- 1} \\ 0 & 0 & 1 & 0 \ end {array}} \ right ] \ begin {array} {* {20} {c}} {{R_1} + 2 {R_2} \ to {R_1}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & {- 1} \\ 0 & 0 & 1 & 0 \ end {array}} \ right] \]Итак, у нас есть расширенная матрица в окончательном виде и решение будет
\ [x = 1, \, \, \, y = — 1, \, \, \, z = 0 \]Это можно проверить, подставив их во все три уравнения и убедившись, что все они удовлетворяются.
b \ (\ begin {align *} 3x + y — 2z & = — 7 \\ 2x + 2y + z & = 9 \\ — x — y + 3z & = 6 \ end {align *} \) Показать решение
Опять же, первый шаг — записать расширенную матрицу.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} {\ color {Red} 3} & 1 & {- 2} & {- 7} \\ 2 & 2 & 1 & 9 \\ {- 1} & { — 1} & 3 и 6 \ end {array}} \ right] \]На этот раз мы не можем получить 1 в верхнем левом углу, просто поменяв местами строки.Мы могли бы поменять местами первую и последнюю строку, но это также потребовало бы другой операции, чтобы превратить -1 в 1. Хотя это несложно, это две операции. Обратите внимание, что мы можем использовать операцию третьей строки, чтобы получить 1 в этом месте следующим образом.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} {\ color {Red} 3} & 1 & {- 2} & {- 7} \\ 2 & 2 & 1 & 9 \\ {- 1} & { — 1} & 3 и 6 \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_1} — {R_2} \ to {R_1}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ {\ color {Red} 2} & 2 & 1 & 9 \\ {\ color {Red} — 1 } & {- 1} & 3 & 6 \ end {array}} \ right] \]Теперь мы можем использовать операцию третьей строки, чтобы превратить два красных числа в нули.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ {\ color {Red} 2} & 2 & 1 & 9 \\ { \ color {Red} — 1} & {- 1} & 3 & 6 \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_2} — 2 {R_1} \ to {R_2 }} \\ {{R_3} + {R_1} \ to {R_3}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3 } & {- 16} \\ 0 & {\ color {Red} 4} & 7 & {41} \\ 0 & {- 2} & 0 & {- 10} \ end {array}} \ right] \]Следующий шаг — получить 1 на месте, занимаемом красной 4.Мы могли бы сделать это, разделив всю строку на 4, но это добавило бы пару несколько неприятных дробей. Итак, вместо этого мы собираемся поменять местами вторую и третью строки. Причина этого станет очевидной достаточно скоро.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & {\ color {Red} 4} & 7 & {41 } \\ 0 & {- 2} & 0 & {- 10} \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_2} \ leftrightarrow {R_3}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & {\ color {Red} — 2} & 0 & {- 10 } \\ 0 и 4 и 7 и {41} \ end {array}} \ right] \]Теперь, если мы разделим вторую строку на -2, мы получим 1 в том месте, которое нам нужно.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & {\ color {Red} — 2} & 0 & { — 10} \\ 0 & 4 & 7 & {41} \ end {array}} \ right] \ begin {array} {* {20} {c}} {- \ frac {1} {2} {R_2}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & {\ color {Red} 4} & 7 & { 41} \ end {array}} \ right] \]Прежде чем перейти к следующему шагу, давайте заметим здесь пару вещей.Во-первых, нам удалось избежать дробей, что всегда хорошо, а во-вторых, эта строка готова. В конечном итоге нам понадобился бы ноль в этом третьем месте, и мы получили его бесплатно. Более того, это не изменится ни в одной из последующих операций. Это происходит не всегда, но если это произойдет, наша жизнь станет легче.
Теперь давайте воспользуемся операцией третьей строки, чтобы заменить красную 4 на ноль.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & {\ color {Red} 4} & 7 & {41} \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_3} — 4 {R_2} \ to {R_3}} \\ \ to \ end {массив } \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & {\ color {Red} 7} & {21} \ end {массив}} \ справа] \]Теперь мы можем разделить третью строку на 7, чтобы получить число в правом нижнем углу в единицу.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & {\ color {Red} 7} & {21} \ end {array}} \ right] \ begin {array} {* {20} {c}} {\ frac {1} {7} {R_3}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {\ color {Red} — 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end {array}} \ right] \]Затем мы можем использовать операцию третьей строки, чтобы заменить -3 на ноль.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {\ color {Red} — 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end { array}} \ right] \ begin {array} {* {20} {c}} {{R_1} + 3 {R_3} \ to {R _ {\ kern 1pt}}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {\ color {Red} — 1} & 0 & {- 7} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end {array}} \ right] \]Последний шаг — затем снова превратить -1 в 0, используя операцию третьей строки.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {\ color {Red} — 1} & 0 & {- 7} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end {array}} \ right ] \ begin {array} {* {20} {c}} {{R_1} + {R_2} \ to {R _ {\ kern 1pt}}} \\ \ to \ end {array} \ left [{\ begin { array} {rrr | r} 1 & 0 & 0 & {- 2} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end {array}} \ right] \]Тогда решение этой системы:
\ [x = — 2, \, \, \, y = 5, \, \, \, z = 3 \] .

 25
25

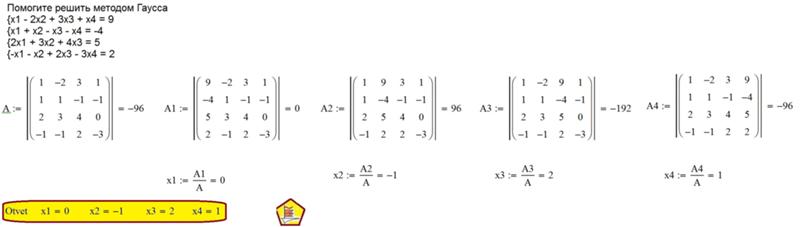


 Нулевую строку допустимо исключать из матрицы.
Нулевую строку допустимо исключать из матрицы.