Таблица пифагора до 15 – Таблица умножения | Формулы с примерами

Таблица умножения на 15

Большая таблица умножения чисел на 15 (пятнадцать) 

Множители	Произведение (Результат)
15 * 1 =	15
15 * 2 =	30
15 * 3 =	45
15 * 4 =	60
15 * 5 =	75
15 * 6 =	90
15 * 7 =	105
15 * 8 =	120
15 * 9 =	135
15 * 10 =	150
15 * 11 =	165
15 * 12 =	180
15 * 13 =	195
15 * 14 =	210
15 * 15 =	225
15 * 16 =	240
15 * 17 =	255
15 * 18 =	270
15 * 19 =	285
15 * 20 =	300
15 * 21 =	315
15 * 22 =	330
15 * 23 =	345
15 * 24 =	360
15 * 25 =	375
15 * 26 =	390
15 * 27 =	405
15 * 28 =	420
15 * 29 =	435
15 * 30 =	450
15 * 31 =	465
15 * 32 =	480
15 * 33 =	495
15 * 34 =	510
15 * 35 =	525
15 * 36 =	540
15 * 37 =	555
15 * 38 =	570
15 * 39 =	585
15 * 40 =	600
15 * 41 =	615
15 * 42 =	630
15 * 43 =	645
15 * 44 =	660
15 * 45 =	675
15 * 46 =	690
15 * 47 =	705
15 * 48 =	720
15 * 49 =	735
15 * 50 =	750
15 * 51 =	765
15 * 52 =	780
15 * 53 =	795
15 * 54 =	810
15 * 55 =	825
15 * 56 =	840
15 * 57 =	855
15 * 58 =	870
15 * 59 =	885
15 * 60 =	900
15 * 61 =	915
15 * 62 =	930
15 * 63 =	945
15 * 64 =	960
15 * 65 =	975
15 * 66 =	990
15 * 67 =	1005
15 * 68 =	1020
15 * 69 =	1035
15 * 70 =	1050
15 * 71 =	1065
15 * 72 =	1080
15 * 73 =	1095
15 * 74 =	1110
15 * 75 =	1125
15 * 76 =	1140
15 * 77 =	1155
15 * 78 =	1170
15 * 79 =	1185
15 * 80 =	1200
15 * 81 =	1215
15 * 82 =	1230
15 * 83 =	1245
15 * 84 =	1260
15 * 85 =	1275
15 * 86 =	1290
15 * 87 =	1305
15 * 88 =	1320
15 * 89 =	1335
15 * 90 =	1350
15 * 91 =	1365
15 * 92 =	1380
15 * 93 =	1395
15 * 94 =	1410
15 * 95 =	1425
15 * 96 =	1440
15 * 97 =	1455
15 * 98 =	1470
15 * 99 =	1485
15 * 100 =	1500
… * 101 =	…

---

Автор: Bill4iam

---

kvn201.com.ua

Как быстро и легко запомнить таблицу умножения

На первый взгляд таблица Пифагора большая и непонятная. Посмотришь на неё и разводишь руками – как это всё запомнить?!

Не надо паники!  Стоит для начала внимательно её рассмотреть. 

Ведь вся хитрость таблицы Пифагора в том, что на ней хорошо заметны закономерности!

Именно поэтому с ней таблицу умножения получается запомнить легко и быстро.

Вот их-то, в основном,  мы и будем запоминать.

А для начала нам эти закономерности надо найти.

Кстати, возможно уже сейчас вам захотелось

 

Распечатать таблицу Пифагора пустую и заполненную

 

Здесь вы найдёте заполненную таблицу, такую как  на картинках в этой статье.

Это таблица пустая большая

А это – две поменьше на один лист

Итак.

 

Как легко и быстро запомнить таблицу умножения

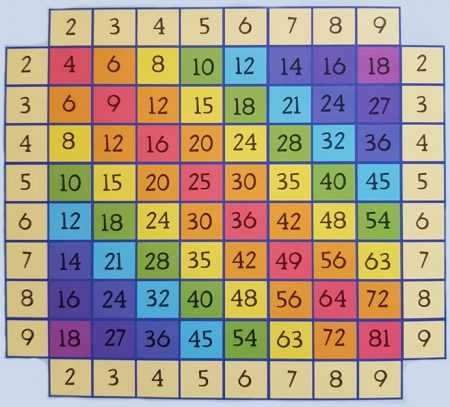
Таблица Пифагора детям

Смотрим внимательно. Что мы тут видим? Вообще-то, каждый из вас имеет полное право увидеть свои закономерности. От этого даже лучше запомнится.

Я же с вами здесь поделюсь тем, что заметили мы с дочкой Мариной.

Первое наблюдение, или минус полтаблицы

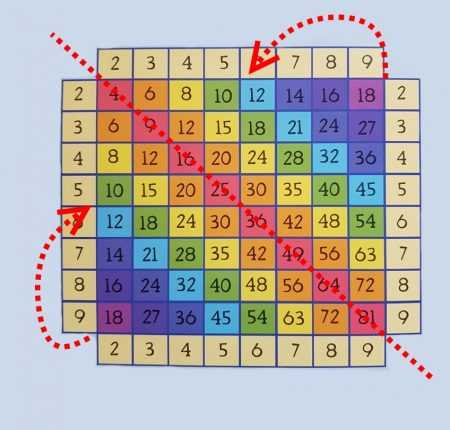
При внимательном рассмотрении, оказывается, что нижняя половинка таблички, если её сложить по малиновой диагонали, зеркально отражает верхнюю.

Почему так? Догадались? Верно – потому что

2 х 5 = 5 х 2

Ну а

8 х 7 = 7 х 8

А это означает, что нам надо выучить только половину таблицы. Уже в два раза легче!

Смотрим дальше

 

Умножение на два

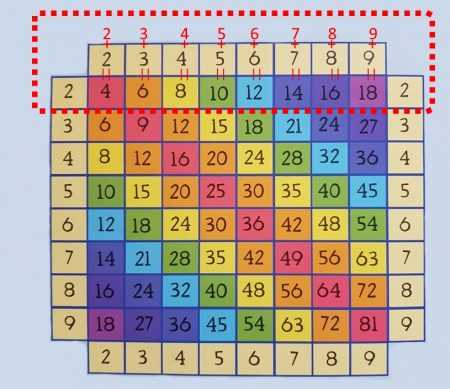
Что такое умножение на два?  Ну конечно – взять число два раза

2 х 2 = 2 + 2

8 х 8 = 8 + 8

Надеюсь прибавить в уме число к самому себе тут каждый сможет?

Повторите несколько раз в уме, сколько будет от 2 до 9 умножить на два.

Готово! Умножение на два мы выучили

 

 

Умножение на три и на четыре

Тут особо никаких секретов нет. Просто умножение на три это ещё раз прибавить к числу, умноженному на два его же.

То есть 2 х 3 = 4 + 2, а 6 х 3 = 12 + 6 и т.д.

 

Ну а для умножения на четыре – нужно сложить результат умножения на два сам с собой.

2 х 4 = 4 + 4, а 6 х 4 = 12 + 12

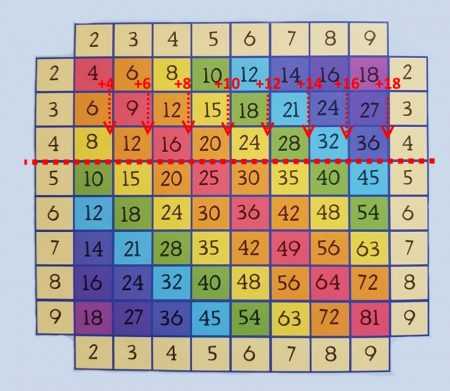
Одним словом – для умножения на три и четыре надо бы уметь быстро вспоминать умножение на два.

 

Здесь  я вам уже очень советую нарисовать много пустых таблиц Пифагора и постепенно их заполнять. Те ячейки, которые уже знаешь – как.

Умножение  на пять

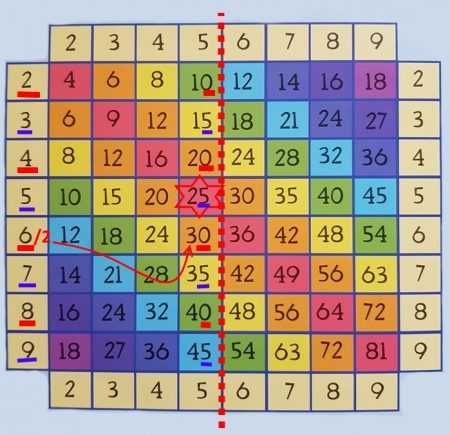
Переходим к умножению на пять. Почему на пять? Потому что про пять есть хитрость.

Итак. Посмотрите на столбик умножения на пять. Видите что  у нас там?

Да. У нас там или круглое число (то, что заканчивается на ноль), или с пятёркой на конце.  Каждое последующее число больше предыдущего на пять.

А теперь вот какой ещё мы с Мариной обнаружили фокус:

Если умножаем пять на чётное число – результат круглый. Если на нечётное – результат с пятёркой на конце.

Плюс ещё один секрет – для чётных чисел, чтобы получить первую цифру, нужно разделить число на два.

То есть:

Если нам нужно умножить 6 на 5. Что мы делаем:

Первое – шесть четное, значит на конце – нолик.

Второе – 6 разделить на два – 3. Значит вначале – три!

Значит,  6 на 5 будет 30!

Ну и, конечно же, запомните, что пятью пять – двадцать пять! Это же просто песня какая-то!

 

Теперь, когда мы уже знаем умножение на 2, 3, 4, и 5,  совершенно точно пора заполнить нашу табличку и посмотреть – сколько ещё осталось выучить?

Да! Заполняйте не только столбики 2,3, 4, 5, но и строчки 2, 3, 4, и 5.

Ну, что видите? Учить-то уже почти и нечего!

 

Умножение на девять

Тут есть какая-то хитрость с костяшками пальцев. Я её, увы, не помню.

Мы с умножением на 9 поступаем так:

Надеюсь, все тут знают, что 2 х 10 это 20, 3 х 10 это 30, а 8 х 10 это 80 ?

Отлично?

Так вот, умножение на девять, это ведь умножение на 10 минус число.

То есть:

2 х 9  это у нас 20 ­– 2 = 18

А

5 х 9 это – 50 – 5 = 45.

И не забывайте, что мы вообще-то с вами уже изучили умножение на два и на пять и на три.

 

Умножение на шесть, семь и восемь

Снова заполните все квадратики таблицы Пифагора. Те, что вам уже известны.

Видите сколько осталось?

А это можно и выучить, правда?

Впрочем, думаю, и здесь можно найти какие-то закономерности.

Например, если уж совсем не учится, можно вспомнить какие-то ближайшие выученные квадратики и добавлять к ним нужное число.

Например:

Возьмём умножение на шесть.

И тут у нас, кстати,  ещё  одна песенка: шестью шесть ­– тридцать шесть!  Запомнили?

Далее…

Вообще-то до пяти мы уже всё знаем. Ну, а если вдруг забыли, сколько будет 6 на 4?

Вспоминаем так: 6 х 5 = 30 (это ну очень легко вспомнить) . Значит, 6х4 это у нас – 30 – 6 = 24

Дальше у нас идёт… 6х6. «Шесть на шесть – тридцать шесть! Совершенно верно!»

Ага. Значит, 6 х 7 у нас… Это  будет 36 + 6 = 42!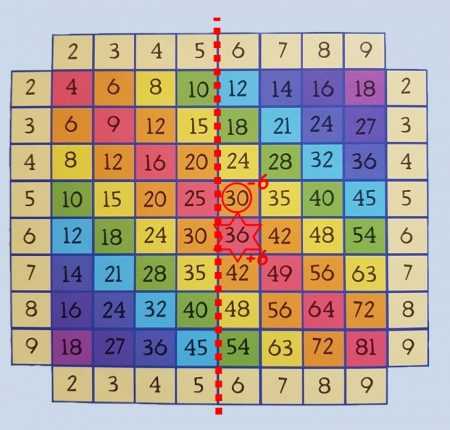

 

Вот  и закончились все наши секреты, которые мне удалось припомнить.

Легко вам и интересно выучить таблицу умножения!

Учите с нами, заходите почаще!

 

irinaroslova.ru

Альтернатива таблице Пифагора, которая поможет р

Помните, как всех нас заставляли в школе зазубривать таблицу умножения наизусть? От нас даже не требовалось особого понимания её свойств. Достаточно было лишь запомнить аккуратные столбцы примеров. Даже на тетрадках по математике чуть ли не в обязательном порядке изображалась такая таблица умножения. Вот как это выглядело поколение назад:

Да и сегодня практически ничего не изменилось.  И наши дети продолжают заучивать наизусть НЕПРАВИЛЬНУЮ таблицу умножения. Да-да, вы не ослышались! То, что изображено на школьных тетрадях —  НЕ таблица умножения.

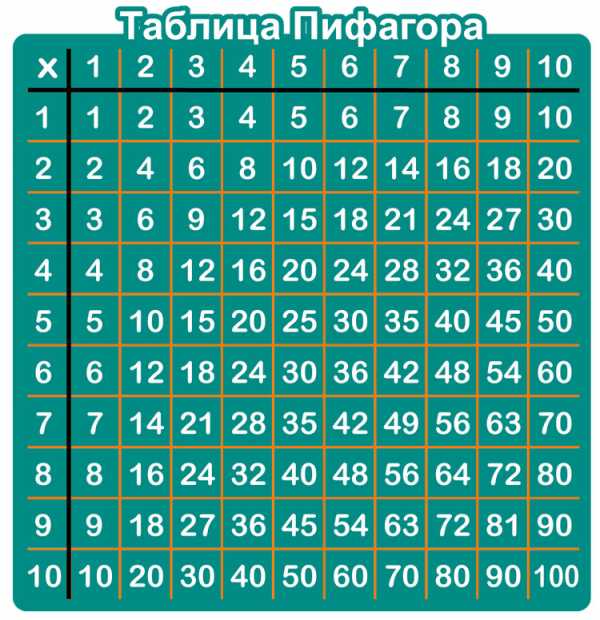
Настоящая таблица умножения выглядит вот так:

Во-первых, это действительно таблица. Во-вторых, она интересная! У неё даже есть своё особое название — «таблица Пифагора».  Для заучивания вы можете оставить в покое верхнюю и левую колонки можно не брать, запомнив только основной прямоугольник.

Вот три причины, по которым «таблица Пифагора» лучше общеизвестных столбиков:

1. В ней нет мусора и информационного шума в виде левой части примеров;

2. Над ней можно подумать. Кроме того, ребёнок автоматически будет искать в ней закономерности. И самостоятельно их находить. даже если он ещё не знает, что такое умножение;

3. Таблицу Пифагора можно повесить перед глазами ребёнка, и вскоре он совершенно незаметно для себя запомнит эти числа. Кстати, в «таблице» надо запоминать гораздо меньше, чем в «примерах».

Приведём простой пример использования таблицы Пифагора для развития математического мышления: числа, симметричные относительно диагонали — равны. Следовательно, от перестановки мест сомножителей произведение не меняется (то есть, умножение коммутативно).

Такая таблица запоминается лучше, эффективнее и интереснее, поскольку человеческий мозг ориентирован на поиск симметрии. Любая симметрия автоматически врезается нам в память. И когда ребенок учится умножать таким образом, он воспринимает этот процесс как своё достижение! А то, что человек придумал сам, запоминается навсегда, в отличие от того, что ему пришлось зазубрить или услышать от других.

В процессе запоминания таблицы Пифагора мозг не просто воспринимает сухую информацию в виде каких-то непонятных столбиков примеров, а думает и анализирует и постоянно тренируется.

Вот ещё один замечательный факт: если взять любое число и провести прямоугольник от начала таблицы до этого числа, то количество клеточек в прямоугольнике и будет равняться этому числу.

Таким образом, умножение обретает более глубинный смысл. Это уже не сокращенная запись нескольких одинаковых слагаемых, а правило из геометрии: площадь прямоугольника равна произведению сторон.

Ну а делить с такой таблицей вообще проще простого!!!

Распечатайте своему ребёнку такую таблицу умножения в дополнение к той, что он проходит в школе, и объясните, как ею пользоваться. Можно также выделить на такой таблице квадраты по диагонали.

Психологи утверждают, что развитие логического и аналитического мышления пригодится любому ребёнку. Подобно судоку или раскраскам для взрослых, таблица Пифагора является отличной тренировкой для мозга!

Источник: http://pyatimenutka.ru/

Революционный способ решения примеров на умножение. Почему я раньше о нем не знала?

5 гениальных математических лайфхаков

fabiosa.ru

Таблица умножения для детей: Распечатать. Как учить

Нередко родители сталкиваются с проблемой, когда ребенку задают выучить таблицу умножения. Все мы были когда-то детьми, тоже учили и как-то выучили. Конечно, проще выучить стихотворение на урок литературы, а здесь столько чисел и как всё запомнить? Ребенку «зубрежка» надоедает, становится скучной. Кроме этого у него может быть плохо развита способность запоминать отдельные не связанные между собой элементы, так называемая механическая память.

На сегодняшний день существует много различных методов заучивания таблицы умножения для детей. Их часто практикуют в школе, но даже к третьему классу, дети не понимают, что учат. Поэтому дожидаться, когда школьнику зададут на дом выучить таблицу умножения, не стоит.

Таблица умножения для детей: способы запоминания

Чтобы помочь ребенку быстро выучить таблицу умножения, нужно понимать сам процесс умножения.Для начала ребенок должен хорошо уметь считать и понимать, например, что к  2 яблокам прибавить ещё 2 яблока будет 4. Важно, чтобы малыш правильно произносил цифры и не путал их. Только тогда можно приступить к изучению таблицы Пифагора.

Таблица Пифагора для детей скачать и распечатать

К занятиям родители должны приготовить различные одинаковые предметы: кружочки, квадратики, яблоки, груши и др. Последние лучше вырезать из картона. Затруднений при умножении на единицу у ребенка возникнуть не должно. Начнем с умножения на 2. Для этого следует разложить, например, картонные яблоки или другие предметы 4 ряда по 2 единицы. Предложите ребенку посчитать количество рядов и предметов. Объясните, что если умножить 2 ряда на 2 предмета, будет 4; 4 ряда на 2 предмета будет 8 и т. д. Когда ребенок освоит умножение на два, переходите к умножению на три. Здесь уже сделайте 3 ряда по 3 предмета.

Скачать таблицу умножения на 2

Как выучить таблицу умножения в игровой форме

Другой быстрый способ, который поможет выучить таблицу умножения, это изучение в игровой форме. Этот метод следует применять тогда, когда ребенок «вызубрил» таблицу и имеет некоторые пробелы.  Данный игровой метод представляет собой игру в фанты. Необходимо сделать заготовку карточек, на которых написать умножения на различные числа.

Принцип игры следующий: ребенку предлагаете взять любую карточку, к примеру 5×7, при правильном ответе карточку кладет к себе, если ответ неверный карточка кладется вниз колоды. Путем повторения одних и тех же примеров,  ребенок их легко запомнит и усвоит.

Если в семье два школьника, то это будет отличным вариантом изучения таблицы умножения. При этом у ребенка задействована не только механическая, но и зрительная память.

Чтобы работала не только механическая, но и визуальная память, Скачайте таблицу умножения (плакат), распечатайте и повесьте  на видное место. Приобрести можно и специальные магнитики с цифрами на холодильник. Ребенку не будет скучно  учить  одному. Вы на кухне готовите ужин, а малыш учит таблицу, передвигая правильно магнитики. В помощь ребенку сейчас имеется большой выбор различных товаров. Поэтому у родителей не должно возникнуть трудностей, при выборе таблице умножения.

Таблица умножения в стихах

Следующий прием, который поможет ребенку выучить таблицу умножения, мнемонический. Суть его в том, что ребенок заучивает рифмованные слова или ассоциации.

Таблица умножения на 3 в стихах

Изучение таблицы умножения требует усидчивости и терпения от школьника, но некоторые способы запоминания таблицы умножения облегчат запоминание, и сделают его веселым и быстрым.

Например, вот так легко запомнить таблицу умножения на 9.

Распечатать таблицу умножения на 9

Эффективный способ запоминания умножения на 9

Скачать плакат «Таблица умножения»

Сохраните на компьютер и распечатайте таблицу умножения:

 

Полезные статьи:

КАК НАУЧИТЬ РЕБЕНКА БЫСТРО СЧИТАТЬ

ЦИФРЫ КАРТОЧКИ РАСПЕЧАТАТЬ

МЕТОДИКИ МАТЕМАТИЧЕСКОГО РАЗВИТИЯ ДОШКОЛЬНИКОВ

 

razvitiedetei.info

Таблица умножения — Кормление в стойлах они введут вместе с просвещением…

Вы же наверняка знаете, что я преподаю математику. А еще вы не раз слышали мнение, что уровень математического образования падает.

Вот, когда мои дети учились во втором классе, я отчетливо себе поняла, почему падает уровень математического образования в школе. Именно во втором классе при закладке самого фундамента математического образования возникает такая гигантская невосполнимая дыра, которую уже никакими костылями в виде калькуляторов не подопрешь.

А именно, главная проблема — в таблице умножения. Посмотрите на тетради в клетку, которые есть у ваших детей-школьников.
Я долго-долго ходила по магазинам в поисках тетрадей. И все равно, на всех — вот такая картина.

Есть тетради еще хуже (для старшеклассников) на которых таблицы умножения нет, а есть куча бессмысленных формул.
Ну, так чем же эта тетрадь плоха? Ничего не подозревающий родитель видит, что на тетради таблица умножения. Вроде, всю жизнь же на тетрадях была таблица умножения? Что не так-то?

А проблема как раз в том, что на тетради НЕ таблица умножения.

Таблица умножения, дорогие мои читатели, это вот: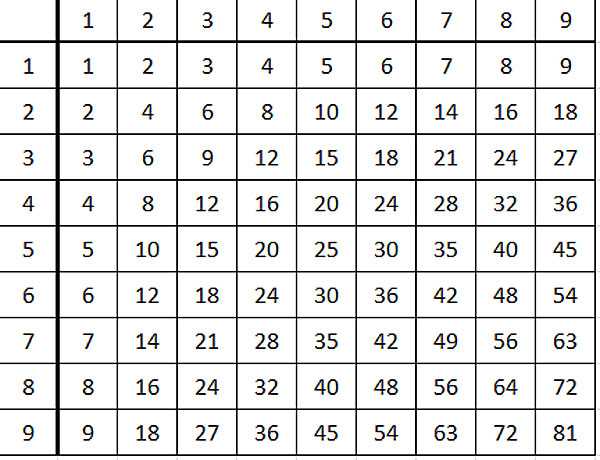

Иногда эту же таблицу даже называют красивым слово «таблица Пифагора». Верхнюю и левую колонки можно не брать, только основной прямоугольник.

Во-первых, это таблица. Во-вторых, она интересная!
Ни один ребенок в здравом уме не будет рассматривать выписанные столбиками примеры.
Ни один ребенок, как бы гениален он ни был, не сможет найти в выписанных примерах интересные фишки и закономерности.
Ну, и вообще, когда учитель говорит: «выучи таблицу умножения», а ребенок даже перед собой таблицы не видит — он сразу понимает, что математика — это такая наука, где обычные вещи названы как-то по-другому и надо много-много зубрить, а понять ничего невозможно. И вообще, надо делать «так, как сказано», а не «так, как есть смысл».

Чем же «таблица» лучше?
Во-первых, в ней нет мусора и информационного шума в виде левой части примеров.
Во-вторых, над ней можно подумать. Тут даже нигде не написано, что это умножение — просто таблица.
В-третьих, если она постоянно под рукой и ребенок на нее постоянно натыкается, он волей-неволей начинает запоминать эти числа. В частности, на вопрос «семью восемь» он никогда не ответит 55 — ведь числа 55 вообще в таблице нет и не было!
Запоминать столбики примеров способны только дети с аномальной памятью. В «таблице» надо запоминать гораздо меньше.

Кроме того, ребенок автоматом ищет закономерности. И сам самостоятельно их находит. Даже такие закономерности находят дети, еще не умеющие умножать.
Например: числа, симметричные относительно диагонали — равны. Понимаете, людской мозг просто настроен искать симметрию, и если ее находит и замечает — очень радуется. А что это означает? Это означает, что от перестановки мест сомножителей произведение не меняется (или что умножение коммутативно, говоря проще).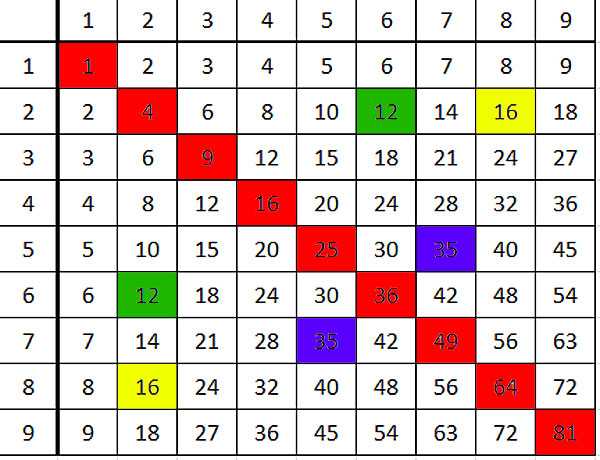

Понимаете, ребенок замечает это сам! А то, что человек придумал сам, он запомнит навсегда, в отличие от того, что он зазубрил или ему сказали.
Помните свой экзамен в вузе по математике? Вы же забыли все теоремы курса, кроме той, что вам досталась, и вам пришлось ее доказывать злобному преподу! Ну, это если вы не списывали, конечно. (Я утрирую, но почти всегда это близко к правде).

А потом ребенок видит, что можно не всю таблицу учить, а только половину. Если мы уже знаем строчку умножения на 3, то нам не надо запоминать «восемь на три», а достаточно вспомнить «три на восемь». Уже вдвое меньше работы.

А кроме того, очень важно, что ваш мозг не принимает сухую информацию в виде каких-то непонятных столбиков примеров, а думает и анализирует. Т.е. тренируется.

Кроме коммутативности умножения можно заметить, например, еще такой замечательный факт. Если ткнуть в любое число и провести прямоугольник от начала таблицы до этого числа, то количество клеточек в прямоугольнике — ваше число.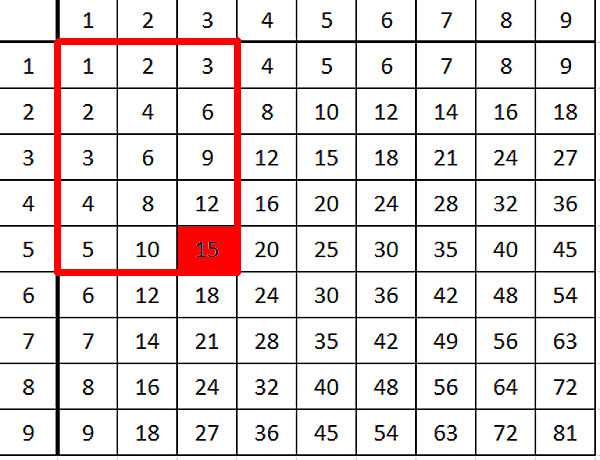

И тут умножение уже получает более глубинный смысл, чем просто сокращенная запись нескольких одинаковых слагаемых. Идет смысл и для геометрии — площадь прямоугольника равна произведению его сторон )

А вы не представляете, насколько проще делить с такой таблицей!!!

Короче, если ваш ребенок во втором классе, распечатайте ему вот такую, правильную, таблицу умножения. Повесьте на стену большую, чтобы он на нее поглядывал, когда делает уроки или сидит за компом. Или еще какой дурью страдает. И напечатайте и заламинируйте ему маленькую (или напишите на картоне). Пусть он ее в школу с собой таскает, и просто удобно под рукой держит. (не помешает на такой таблице выделить квадраты по диагонали, чтобы лучше видно)
У моих детей есть — вот такая. И им это реально помогло во втором классе и до сих пор очень сильно помогает на уроках математики.

Вот, честное слово, сразу средний балл по математике увеличится, а ребенок перестанет ныть, что математика тупая. А в придачу, в будущем вашему ребенку тоже будет проще. Он поймет, что надо шевелить мозгами, а не зубрить. И мало, что поймет, он еще и научится это делать.

И повторюсь: в примерах столбиками ничего плохого нет. И количество информации в них содержится такое же, как и в «таблице». Но и ничего хорошего в таких примерах тоже нет. Это — информационный мусор, из которого нужное еще не враз найдешь.

antonisakov.livejournal.com

Таблица умножения Пифагора.Тайны или реальность.

Структура таблицы умножения Пифагора

Впервые таблица Пифагора примерно в таком же виде, каком мы ее находим на обложках ученических тетрадей, появилось в сочинениях Никомаха (1-2 вв.).

Числа в каждой строке таблицы Пифагора образуют последовательность чисел составленных определенным образом.

Умножение натуральных чисел есть не что иное, как многократное прибавление к сумме одного и того же слагаемого.

Таблица Пифагора симметрична относительно диагонали, ведущей из левого верхнего угла в правый нижний. Данное свойство – геометрическая иллюстрация свойства умножения.

Цифры в первом столбце и последние цифры в девятом столбце повторяют друг друга, но идут в обратном порядке. Этим свойством обладают последние цифры второго и восьмого столбцов; третьего и седьмого, четвертого и шестого. Я сделал открытие: для произвольных двух цифр А и В последняя цифра произведения АВ равна последней цифре произведения (10-А)*(10-В), так как разность чисел АВ и (10-А)*(10-В) делится на 10. Рассмотрим некоторые факты: назовем квартетом четыре числа таблицы Пифагора расположенные в вершинах некоторого квадрата, а числа стоящие на диагонали таблицы – диагональными.

Оказывается, если стороны этого квадрата параллельны диагоналям таблицы Пифагора, то суммы диагональных чисел квартета равны. Если стороны квадрата параллельны сторонам таблицы, то равны произведения диагональных чисел квартета. Если при этом квадрат расположен симметрично главной диагонали таблицы Пифагора, то суммы всех чисел квартета – квадрат некоторого натурального числа.

Таблица умножения Пифагора¹

	2	3	4	5	6	7	8	9
2	4	6	8	10	12	14	16	18
3	6	9	12	15	18	21	24	27
4	8	12	16	20	24	28	32	36
5	10	15	20	25	30	35	40	45
6	12	18	24	30	36	42	48	54
7	14	21	28	35	42	49	56	63
8	16	24	32	40	48	56	64	72
9	18	27	36	45	54	63	72	81

Очень интересно составлена таблица умножения на 9 (см. таблицу 2), если внимательно посмотреть, то можно заметить закономерность:

9
18
27
36
45
54
63
72
81

Таблица № 2

Поэтому свою таблицу умножения Пифагор считал самым значительным открытием, так как в ней зашифрован закон гармонии развития числовой основы вселенной, как единой целой.

В российских школах традиционно доходят до 10*10. В Великобритании до 12*12, что связано, в том числе с единицами английской системе мер длины (1фут =12 дюймов) и денежного обращения (существовавшей до 1971 г.: 1 фут стерлингов=20 шиллингам, 1 шиллинг=12 пенсам).

Практическое применение таблицы умножения Пифагора

Мною было найдено в источниках одно из удивительных применений таблицы Пифагора – гадание, где нехитрые вычисления помогут раскрыть характер человека.

В современных интерпретациях Пифагора способы предсказания и расчета судьбы человека по дате его рождения присутствуют в таблице № 3, в которой в квадрате из 9 ячеек, расположены цифры, каждая из которых указывает на одно из определяющих качеств человека.

Таблица № 3

1111	2222	3333
4444	5555	6666
7777	8888	9999

Набор цифр даты рождения тестируемого человека даёт возможность заполнить таблицу и таким образом «прочитать» судьбоносные качества человека, дать ему представление о том, на что ему следует опираться в своей жизни.

Это – не так и уж мало, особенно для человека только – только входящего в жизнь.

Результаты практического применения

Для этого нужно узнать дату рождения и провести исследование.

О чём может рассказать дата моего рождения, используя квадрат Пифагора.

Начинаем складывать:

1. Цифры дня и месяца рождения: 2+1+0+1=4

2. Цифры года рождения: 1+9+9+5=24

3. Складываем получившиеся два числа: 4+24=28, получилось первое рабочее число-28

4. Складываем цифры первого рабочего числа: 2+8=10, получили второе рабочее число-10

5. Из первого рабочего числа отнимите удвоенную первую цифру дня рождения: 28-2*2=24, получили третье рабочее число-24

6. Для того, чтобы получилось следующее рабочее число, сложите цифры третьего числа 2+4=6, получили четвертое рабочее число-6

Получили два ряда цифр:

1ряд – дата рождения: 21.01.1995

2ряд – рабочие числа: 28,10,24,6

Подсчитайте общее количество цифр в двух рядах. В моём случае их 15. По словам Пифагора, человек приходит на землю 15 раз, а потом переходит жить в другое, более совершенное измерение.

Теперь нарисуйте квадрат 3 на 3 и разделите на 9 маленьких квадратиков.

В первый квадратик впишите все единицы из двух рядов, во второй двойки, в третий -тройки и так далее.

А теперь посмотрим, о чём рассказывают нам цифры.

Квадрат 1. Характер

1. эгоист

11- человек эгоистичный, но иногда может подумать о других

111- человек с положительным устойчивым характером

1111- характер очень волевой и сильный

11111- самодур и диктатор

111111 – жестокий человек, но для близких пойдет на всё. Крайне неприятен в общении.

Квадрат 2. Биоэнергия

Двоек нет. Биополе отсутствует. Канал открыт для активного поглощения энергии, таким людям нравятся старые вещи (коллекционеры). Они неплохо относятся к окружающим, но при этом пытаются поживиться за счёт других, «поглощая их биополе».

2 – биоэнергии хватает для жизни, но в данный момент её маловато, поэтому надо заниматься спортом. Эти люди сверхчувствительны к атмосферным перепадам.

22 – биоэнергии достаточно, такой человек способен лечить других людей.

222 – хороший экстрасенс.

2222- этих людей очень любит противоположный пол, но если присутствует и 666 то нужно быть осторожнее.

Квадрат 3. Организованность и способности к наукам

Нет троек — очень аккуратный и пунктуальный человек, который выделяется среди окружающих культурной речью и воспитанностью.

3 — у таких людей всё зависит от настроения. Они не любят беспорядок, но уборку проводят в зависимости от настроения (хочу делаю, хочу — нет).

33 – хорошие способности к точным наукам ( математике, физике, химии).

333 — способность к наукам. Аккуратные до занудства.

3333 — из них получаются хорошие ученые.

Квадрат 4. Здоровье

Нет четверок – у этого человека проблемы со здоровьем.

4 — здоровье нормальное, проблемы начинаются в преклонном возрасте.

44- очень здоровый человек, обладающий высокой сопротивляемостью болезням.

444 – то же что и 44, только ярче выражено.

Квадрат 5. Интуиция

Нет пятерок – человек родился с неоткрытым каналом интуиции. Он активен, старается что-то предпринять. Всегда обдумывает свои действия, но совершает много ошибок, таким людям приходится пробивать себе дорогу с огромным трудом

5 — канал открытый, эти люди делают меньше ошибок.

55 – сильно развитая интуиция ( могут быть следователями или юристами).

555 — ясновидящие, всё, что происходит вокруг им понятно, они знают, что делать.

5555 — таким людям подвластно время и пространство.

Квадрат 6

Нет шестерок – человек пришёл в этот мир, чтобы получить профессию, физический труд он не любит, но вынужден им заниматься.

6 — земной человек, думает об учебе, но без физической работы ему не обойтись.

66 — любит трудиться, хотя физическая работа для него только –хобби.

666 — тревожный знак, очень привлекательный, активный человек, однако требует от партнера больших денежных затрат.

6666 -этот человек много и тяжело работал.

Квадрат 7

Нет семерок-человек тяжёлой судьбы

7 — у этого человека есть неярко выраженный талант.

77 — знак очень талантливых людей. Они музыкальны, имеют художественный вкус, могут рисовать. В нем есть всё и хорошее и плохое.

777 — знак особый, эти люди столкнутся с серьёзными трудностями.

7777 — знак тревоги, люди будьте осторожны.

Квадрат 8. Ответственность

Нет восьмерок- человек легко берёт в долг, но не спешит отдавать.

8 — человек с развитым чувством ответственности.

88 -очень развито чувство ответственности. Этот человек всегда готов помочь другим.

888 — призван служить народу.

8888 — человек имеет парапсихологические способности, а так же имеет способности в области точных наук.

Квадрат 9. Ум

9 — такому человеку надо развивать свой ум.

99 — умная голова, но дана лентяю.

999 — умный, удачливый человек.

9999 — человек редкого ума, однако груб и немилосерден.

Проанализировав дату своего рождения, я получил следующую таблицу:

1ряд – дата рождения: 21.01.1995

2ряд – рабочие числа: 28,10,24,6

Вывод:

У меня характер очень волевой и сильный, присутствуют экстрасенсорные способности. Я очень аккуратный и пунктуальный человек, здоровье хорошее, о здоровье задумаюсь в старости, присутствует интуиция, земной человек, думаю об учебе, но без физической работы мне не обойтись, человек с развитым чувством ответственности, умная голова, но дана лентяю, хотя я с этим не согласен.

Мне было интересно узнать о своих родителях, используя данный квадрат.

Моя мама родилась 13.06.1967 года, а папа 29.09.1965 года. Я составил по описанной схеме два квадрата.

Начинаем складывать:

1. Цифры дня и месяца рождения: 1+3+6=10 / 2+9+9=20

2. Цифры года рождения: 1+9+6+7=23 / 1+9+6+5=21

3. Складываем получившиеся два числа: 10+23=33, получилось первое рабочее число-33 / 41

4. Складываем цифры первого рабочего числа: 3+3=6, получили второе рабочее число-6 / 5

5. Из первого рабочего числа отнимите удвоенную первую цифру дня рождения: 33-2*1=31, получили третье рабочее число-31 / 37

6. Для того чтобы получилось следующее рабочее число, сложите цифры третьего числа 3+1=4, получили четвертое рабочее число-4 /10

Получили два ряда цифр:

1ряд – дата рождения: 13.06.1967 / 29.09.1965

2ряд – рабочие числа:33, 6, 31, 4 / 41, 5, 37, 1

Подсчитайте общее количество цифр в двух рядах, в этом случае их 13. По словам Пифагора, человек приходит на землю 15 раз, значит, мама и папа прейдут на землю ещё 2 раза.

Мама Папа

Вывод:

Мама – это человек с положительным устойчивым характером. Такие как она могут стать хорошими учеными. Здоровье хорошее, проблемы начнутся в преклонном возрасте. Очень привлекательный, активный человек, однако требует от партнера больших денежных затрат. У обладательницы одной 9 преобладает неярко выраженный талант. Нет восьмерок — человек легко берёт в долг, но не спешит отдавать. Моя мама очень экономна, и не берет в долг. Нет пятерок – человек родился с неоткрытым каналом интуиции. Он активен, старается что-то предпринять. Всегда обдумывает свои действия, но совершает много ошибок, таким людям приходится пробивать себе дорогу с огромным трудом.

Папа – это человек с положительным устойчивым характером. Биоэнергии хватает для жизни, но в данный момент её маловато, поэтому надо заниматься спортом. Эти люди сверхчувствительны к атмосферным перепадам. У таких людей всё зависит от настроения. Они не любят беспорядок, но уборку проводят в зависимости от настроения (хочу делаю , хочу — нет). Здоровье хорошее, проблемы начнутся в преклонном возрасте. Сильно развитая интуиция (могут быть следователями или юристами). Земной человек, думает об учебе, о работе, но без физической работы ему не обойтись. Папа имеет три 9, что по таблице Пифагора означает, что он человек умный и удачливый.

Нет восьмерок- человек легко берёт в долг, но не спешит отдавать. Мой папа умный и удачливый человек.

Результаты тестирования

Очень интересно было узнать у своих одноклассников и учащихся нашей школы, о том знают ли они таблицу умножения Пифагора, как она была составлена, где она появилась впервые, можно ли её применить к магическому гаданию, и хотели бы вы узнать о своём характере и магическом влиянии звезд на вашу жизнь. Все эти вопросы² я задал учащимся пятых – одиннадцатых классов.

Мною был проведен социологический опрос с 6 -11 классы, который показал уровень знания истории математики, знания таблицы умножения.

Вот такие интересные результаты я получил³.

Вывод: Анализируя результаты опроса, большинство знает: таблицу умножения Пифагора, структуру по которой составлена таблица, биографию ученого, догадываются о практическом применении и хотят узнать о своём характере, но не знают о первом упоминании, о таблице умножения Пифагора в сочинениях Никомаха.

Заключение:

Я узнал много нового о жизни Пифагора, о его исследованиях, но для меня осталось загадкой, является ли Пифагор автором таблицы умножения, так как в литературных источниках, подтверждению этому факту не нашлось.

Мне стало понятно, что возникновение школы Пифагора оказала большое влияние на становление философии. Заслугой пифагорейцев было заложение основ развития математических, физических, астрономических и географических знаний, которые изучают в наше время в школах. В основе вещей лежит число, учил Пифагор, познать мир — значит познать управляющие им числа. Изучая числа, они разработали числовые отношения, и нашли их во всех науках — музыке, астрономии, математике, физике и так далее. Интересно было узнать, что в сферу интересов членов союза входили научные исследования – религиозные и философские изыскания, политическая деятельность. Пифагорейцы вели суровый образ жизни, превыше всего ценили самообладание, смелость и коллективную дисциплину, жили они вместе, у них было совместное имущество, и даже свои открытия они считали общим достоянием. Из этого я сделал вывод, что открытие «Таблицы умножения Пифагора», остается загадкой и автор её неизвестен. Деятельность же союза была окружена тайной, поэтому никаких текстов о ранних Пифагорейцах не осталось.

Мне стало ясно, что свою таблицу умножения Пифагор считал самым значительным открытием, так как в ней зашифрован закон гармонии развития числовой основы вселенной, как единой целой.

Мною было найдено в источниках одно из удивительных применений таблицы Пифагора – гадание. Я провел исследование и узнал, как влияют на меня числа, скрывающиеся в дате моего дня рождения, так же исследовал дату рождения моих родителей, используя квадрат Пифагора.

Я научился в поисковой системе сети Интернет находить нужную мне информацию.

Проведя опрос среди учащихся нашей школы, я сделал следующие выводы, чтобольшинство знает: таблицу умножения Пифагора, структуру по которой составлена таблица, биографию ученого, догадываются о практическом применении и хотят узнать о своём характере, но не знают о первом упоминании, о таблице умножения Пифагора в сочинениях Никомаха.

Теперь я могу рассказать по желанию любого человека, как влияет числа даты его рождения на его судьбу.

Данная работа поможет учащимся узнать много нового о жизни Пифагора, о применении таблицы умножения, об использовании таблицы в магических целях.

Учителя могут использовать биографию Пифагора на уроках математики, истории, МХК или воспользоваться списком литературы или адресами в Интернете.

Занимаясь исследованием данной темы и рассмотрев различные точки зрения, я сделал вывод, что цели, которые я ставил перед собой, я достиг. А работа, проведенная мной, является завершенной.

Приложение № 1

Анкета:

1. Знаете ли вы таблицу умножения Пифагора?

2. Знаете ли вы, как составлена таблица умножения?

3. Пифагор был древнегреческим ученым?

4. Впервые таблица умножения Пифагора появилась в сочинениях:

А) Никомаха

Б) Фалеса

В) Пифагора

Г) Архимеда

1. Знаете ли вы о практическом применении таблицы умножения Пифагора?

2. Как вы думаете можно ли применить таблицу умножения Пифагора к магическому гаданию?

3. Хотите ли вы узнать о своем характере, используя квадрат Пифагора?

Список литературы

1. Ямвлих, «О пифагоровой жизни».

2. Башмакова И. Г., Лапин А. И. «Пифагор» /Квант. — 1986. — № 1.

3. Бертран Рассел, «История западной философии».

4. А. А. Корнеев. «Два источника, две составные части таблицы Пифагора» /

5. Пифагореизм.

6. Неопифагореизм.

7. Теорема Пифагора.

8. Пифагоров строй.

9. Пифагоровы числа.

10. Пифагоровы штаны.

11. Пифагорейский пентакл.

12. Пифагор Регийский.

13. Пифагор (кратер) .

14. А.Б. Павлова «К проблеме о связи пифагореизма с Востоком»

15. Реале Дж., Антисери Д. Западная философия от истоков до наших дней. Античность. М., 1997.

16. Жмудь Л.Я. Пифагор и его школа. Л., 1990.

17. Целлер Э. Очерки истории греческой философии. СПб., 1996.

18. Шредер Л.Ю. Пифагор и индийцы // Журнал Министерства Народного Просвещения. 1888. №10-11.

19. Фрагменты ранних греческих философов. Ч. 1 / Под ред. И.Д. Рожанского. М., 1989.

20. Лукьянов А.Е. Становление философии на Востоке (Древний Китай и Индия). М., 1992.

21. Пифагорейские Золотые Стихи с комментарием философа Гиерокла: Пер. с древнегреч. И. Петер. М., 1996.

22. Алексей Корнеев. «Феномен русского умножения»

23. Энциклопедия юного математика для среднего и старшего школьного возраста/ Сост.А.П.Савин.-М.: Педагогика,1985.-352с.

24. Корнеева А.А. Философия и лад/ А.А.Корнеева// Наука.-2001.-№ 4.-с.11-23

25. Бортникова И. Цифра, счисление, число/И.Бортникова//Наука.-2003.-№ 3.-с.11-23

26. Журнал П/С приложение «Математика»-2007.-№44

27. Энциклопедия юного астронома для среднего и старшего школьного возраста/ сост. Н.П.Ерпылёв.-М.:Педагогика, 1980.-352с.

28. Детская энциклопедия для среднего и старшего школьного возраста в 12т. Т.2 Мир небесных тел./Академия педагогических наук СССР. – 3-е изд.-М.:Педагогика, 1972.-480с.

multiurok.ru

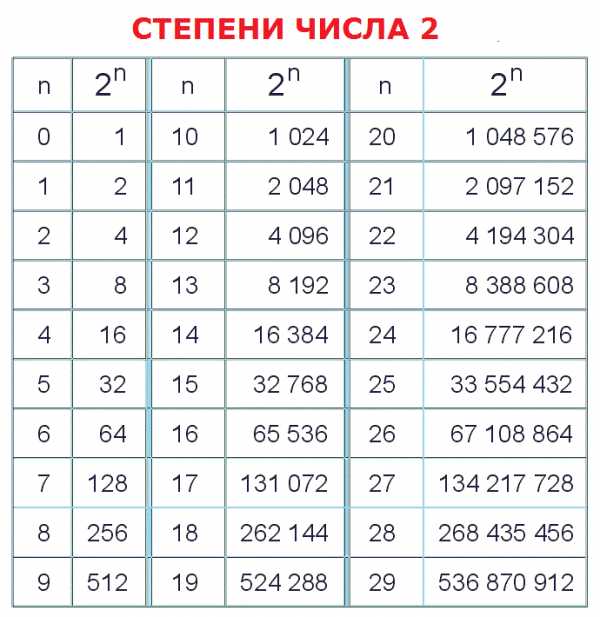
ТАБЛИЦА ПИФАГОРА — ФОРМУЛЫ по МАТЕМАТИКЕ

ПОДЕЛИТЕСЬ: // (function() { if (window.pluso)if (typeof window.pluso.start == «function») return; if (window.ifpluso==undefined) { window.ifpluso = 1; var d = document, s = d.createElement(‘script’), g = …

СМОТРИТЕ ещё:

Таблица квадратов 0 1 2 3 4 5 6 7 8 9 0 0 1 4 9 16 25 36 49 64 81 1 100 121 144 169 196 225 256 289 324 361 2 400 441 484 529 576 625 676 729 784 841 3 900 961 1024 1089 1156 1225 1296 1369 1444 1521 4 1600 1681 1764 1849 1936 2025 2116 2209 2304 2401 5 2500 2601 2704 2809 2916 3025 3136 3249 3364 3481 6 3600 3721 3844 3969 4096 4225 4356 4489 4624 4761 7 4900 5041 5184 5329 5476 5625 5776 5929 6084 6241 8 6400 6561 6724 6889 7056 7225 7396 7569 7744 7921 9 8100 8281 8464 8649 8836 9025 9216 9409 9604 9801   Если Вы только начинаете учить сложение, вычитание, умножение, деление, то есть считать, то можно перейти на ТРЕНАЖЕР и проверить свою технику счета.

СМОТРИТЕ ещё:

Чтобы просмотреть числа в этой таблице, кликните по ней мышкой, таблица увеличиться. Аналогично, уменьшаем. ПРОДОЛЖЕНИЕ Ниже эта же таблица простых чисел, но напечатана в ворде: Простые числа — это целое положительное число больше …

СМОТРИТЕ ещё:

КВАДРАТОМ ЧИСЛА а называется произведение двух множителей, каждый из которых равен а. РЕКОМЕНДУЮ: Очень хорошо знать НАИЗУСТЬ таблицу квадратов от 1 до 20 или даже до 30! Знание таблицы поможет вам при решении …

СМОТРИТЕ ещё:

КУБОМ ЧИСЛА а называется произведение трех множителей, каждый из которых равен а. Эта таблица поможет вам при извлечении кубических корней, при решении задач на нахождение объемов тел.   ЖЕЛАТЕЛЬНО ЗНАТЬ НАИЗУСТЬ ПЕРВЫЙ СТОЛБИК!   Таблица кубов 0 1 2 3 4 5 6 7 8 9 0 0 1 8 27 64 125 216 343 512 729 1 1000 1331 1728 2197 2744 3375 4096 4913 5832 6859 2 8000 9261 10648 12167 13824 15625 17576 19683 21952 24389 3 27000 29791 32768 35937 39304 42875 46656 50653 54872 59319 4 64000 68921 74088 79507 85184 91125 97336 103823 110592 117649 5 125000 132651 140608 148877 157464 166375 175616 185193 195112 205379 6 216000 226981 238328 250047 262144 274625 287496 300763 314432 328509 7 343000 357911 373248 389017 405224 421875 438976 456533 474552 493039 8 512000 531441 551368 571787 592704 614125 636056 658503 681472 704969 9 729000 753571 778688 804357 830584 857375 884736 912673 941192 970299 ПОДЕЛИТЕСЬ: //    

СМОТРИТЕ ещё:

Таблица факториалов чисел от 1 до 50   1! = 1 2! = 2 3! = 6 4! = 24 5! = 120 6! = 720 7! = 5040 8! = 40320 9! = 362880 10! = 3628800 11! = 39916800 12! = 479001600 13! = 6227020800 14! = 87178291200 15! = 1307674368000 16! = 20922789888000 17! = 355687428096000 18! = 6402373705728000 19! = 121645100408832000 20! = 2432902008176640000 21! = 51090942171709440000 22! = 1124000727777607680000 23! = 25852016738884976640000 24! = 620448401733239439360000 25! = 15511210043330985984000000 26! = 403291461126605635584000000 27! = 10888869450418352160768000000 28! = 304888344611713860501504000000 29! = 8841761993739701954543616000000 30! = 265252859812191058636308480000000 31! = 8222838654177922817725562880000000 32! = 263130836933693530167218012160000000 33! = 8683317618811886495518194401280000000 34! = 295232799039604140847618609643520000000 35! = 10333147966386144929666651337523200000000 36! = 371993326789901217467999448150835200000000 37! = 13763753091226345046315979581580902400000000 38! = 523022617466601111760007224100074291200000000 39! = 20397882081197443358640281739902897356800000000 40! = 815915283247897734345611269596115894272000000000 41! = 33452526613163807108170062053440751665152000000000 42! = 1405006117752879898543142606244511569936384000000000 43! = 60415263063373835637355132068513997507264512000000000 44! = 2658271574788448768043625811014615890319638528000000000 45! = 119622220865480194561963161495657715064383733760000000000 46! = 5502622159812088949850305428800254892961651752960000000000 47! = 258623241511168180642964355153611979969197632389120000000000 48! = 12413915592536072670862289047373375038521486354677760000000000 49! = 608281864034267560872252163321295376887552831379210240000000000 50! = 30414093201713378043612608166064768844377641568960512000000000000      

СМОТРИТЕ ещё:

Таблица умножения чисел от 1 до 20 × 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 3 3 6 9 12 15 18 21 24 27 30 33 36 39 42 45 48 51 54 57 60 4 4 8 12 16 20 24 28 32 36 40 44 48 52 56 60 64 68 72 76 80 5 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 6 6 12 18 24 30 36 42 48 54 60 66 72 78 84 90 96 102 108 114 120 7 7 14 21 28 35 42 49 56 63 70 77 84 91 98 105 112 119 126 133 140 8 8 16 24 32 40 48 56 64 72 80 88 96 104 112 120 128 136 144 152 160 9 9 18 27 36 45 54 63 72 81 90 99 108 117 126 135 144 153 162 171 180 10 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 11 11 22 33 44 55 66 77 88 99 110 121 132 143 154 165 176 187 198 209 220 12 12 24 36 48 60 72 84 96 108 120 132 144 156 168 180 192 204 216 228 240 13 13 26 39 52 65 78 91 104 117 130 143 156 169 182 195 208 221 234 247 260 14 14 28 42 56 70 84 98 112 126 140 154 168 182 196 210 224 238 252 266 280 15 15 30 45 60 75 90 105 120 135 150 165 180 195 210 225 240 255 270 285 300 16 16 32 48 64 80 96 112 128 144 160 176 192 208 224 240 256 272 288 304 320 17 17 34 51 68 85 102 119 136 153 170 187 204 221 238 255 272 289 306 323 340 18 18 36 54 72 90 108 126 144 162 180 198 216 234 252 270 288 306 324 342 360 19 19 38 57 76 95 114 133 152 171 190 209 228 247 266 285 304 323 342 361 380 20 20 40 60 80 100 120 140 160 180 200 220 240 260 280 300 320 340 360 380 400   Если Вы только начинаете учить сложение, вычитание, умножение, деление, то есть считать, то можно перейти на ТРЕНАЖЕР и проверить свою технику счета.  

СМОТРИТЕ ещё:

lyudmilanik.com.ua