Определение иррационального числа: Иррациональные числа — урок. Алгебра, 8 класс.

Содержание

Иррациональные числа: определение, примеры

Иррациональные числа известны людям с глубокой древности. Еще за несколько веков до нашей эры индийский математик Манава выяснил, что квадратные корни некоторых чисел (например, 2) невозможно выразить явно.

Данная статья является своего рода вводным уроком в тему «Иррациональные числа». Приведем определение и примеры иррациональных чисел с пояснением, а также выясним, как определить, является ли данное число иррациональным.

Само название «иррациональные числа» как бы подсказывает нам определение. Иррациональное число — это действительное число, которое не является рациональным. Другими словами, такое число нельзя представить в виде дроби mn, где m — целое, а n — натуральное число.

Определение. Иррациональные числа

Иррациональные числа — это такие числа, которые в десятичной форме записи представляют собой бесконечные непериодические десятичные дроби.

Для обозначения множества иррациональных чисел используется символ

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Навигация по статьям

Предыдущая статья

Пределы

Следующая статья

Общее уравнение плоскости

Арифметические операции над действительными числами
Взаимно обратные числа
Вычитание десятичных дробей
Вычитание натуральных чисел
Вычитание натуральных чисел

Все темы по математике

Дипломные работы
Курсовые работы
Рефераты
Контрольные работы
Отчет по практике
Все предметы

Узнать подробнее

Две практические работы нужно сделать только й вариант в практич работе и й вариант в практич работе

Вид работы:
Практическая работа
Выполнена:
20 февраля 2023 г.
Стоимость:
1 600 руб

Заказать такую же работу

Тема фотометрические методы анализа нужно отразить нефелометрический

Заказать такую же работу

Профессиональные компьютерные программы

Заказать такую же работу

Опасные природные процессы и явления Сложные природные условия

Вид работы:
Реферат
Выполнена:
21 января 2023 г.
Стоимость:
1 400 руб

Заказать такую же работу

Контрольная работа

Вид работы:
Контрольная работа
Выполнена:
16 января 2023 г.
Стоимость:
1 400 руб

Заказать такую же работу

Техническая механика Контрольных заданий

Вид работы:
Контрольная работа
Выполнена:

4 января 2023 г.
Стоимость:
2 700 руб

Заказать такую же работу

Смотреть все работы по механике

Билет 4 Определение иррационального числа

Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть которое не может быть представленным в виде дроби , где m — целое число, n — натуральное число. О существовании иррациональных чисел, точнее отрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа .

Множество иррациональных чисел обычно обозначается заглавной латинской буквой «i» в полужирном начертании без заливки — . Таким образом: , т.е. множество иррациональных чисел есть разность множеств вещественных и рациональных чисел.

Если множество рациональных чисел дополнить множеством иррациональных чисел, то вместе они оставят множество действительных чисел. Множество действительных чисел обычно обозначают буквой R; используют также символическую запись (-∞, +∞) или (-∞, ∞).

Множество действительных чисел можно описать так: это множество конечных и бесконечных десятичных дробей; конечные десятичные дроби и бесконечные десятичные периодические дроби — рациональные числа, а бесконечные десятичные непериодические дроби — иррациональные числа.

Каждое действительное число можно изобразить точкой на координатной прямой. Верно и обратное: каждая точка координатной прямой имеет действительную координату. Математики обычно, говорят так: между множеством R действительных чисел и множеством точек координатной прямой установлено взаимно однозначное соответствие. Координатная прямая есть геометрическая модель множества действительных чисел; по этой причине для координатной прямой часто используют термин числовая прямая.

Вдумайтесь в этот термин: не кажется ли он вам противоестественным? Ведь число — объект алгебры, а прямая — объект геометрии. Нет ли тут «смешения жанров»? Нет, все логично, все продумано. Этот термин в очередной раз подчеркивает единство различных областей математики, дает возможность отождествления понятий «действительное число» и «точка на координатной (числовой) прямой».

Обратите внимание: координатной прямой вы пользовались начиная с 5-го класса. Но, оказывается, в ваших знаниях был вполне оправданный пробел: не для любой точки координатной прямой вы сумели бы найти координату — просто учитель оберегал вас от такой неприятности.

Рассмотрим пример. Дана координатная прямая, на ее единичном отрезке построен квадрат (рис. 100), диагональ квадрата OB отложена на координатной прямой от точки О вправо, получилась точка D. Чему равна координата точки D? Она равна длине диагонали квадрата, т. е. . Это число, как мы теперь знаем, не целое и не дробь. Значит, ни в 5-м, ни в 6-м, ни в 7-м классе координату точки D вы бы найти не смогли. Потому мы до сих пор и говорили «координатная прямая», а не «числовая прямая».

Заметим, что был еще один оправданный пробел в ваших знаниях по алгебре. Рассматривая выражения с переменными, мы всегда подразумевали, что переменные могут принимать любые допустимые значения, но только рациональные, ведь других-то не было. На самом деле переменные могут принимать любые допустимые действительные значения. Например, в тождестве

в роли a и b могут выступать любые числа, не обязательно рациональные. Этим мы уже пользовались в конце предыдущего урока. Этим же мы пользовались и в уроке 18 «Преобразование выражений, содержащих операцию извлечения квадратного корня»— в частности, в примерах 6, 7, 8 из этого урока.

Для действительных чисел a, b, c выполняются привычные законы:

и т.д.

Выполняются и привычные правила:

произведение (частное) двух положительных чисел — положительное число;

произведение (частное) двух отрицательных чисел — положительное число;

произведение (частное) положительного и отрицательного числа — отрицательное число.

Действительные числа можно сравнивать друг с другом, используя следующее определение.

Определение. Говорят, что действительное число a больше (меньше) действительного числа b, если их разность а — b — положительное (отрицательное) число. Пишут a > b (a < b).

Из этого определения следует, что всякое положительное число a больше нуля (поскольку разность a — 0 = a — положительное число), а всякое отрицательное число b меньше нуля (поскольку разность b — 0 = b — отрицательное число).

Итак,

a > 0 означает, что a — положительное число;

a < 0 означает, что a — отрицательное число;

a > b означает, что a — b — положительное число, т. е. a — b > 0;

a < b означает, что a — b — отрицательное число, т.е. a — b < 0.

Наряду со знаками строгих неравенств (>, <) используют знаки нестрогих неравенств:

означает, что a больше нуля или равно нулю, т. е. a — неотрицательное число (положительное или 0), или что a не меньше нуля;

означает, что a меньше нуля или равно нулю, т. е. a — неположительное число (отрицательное или 0), или что a не больше нуля;

a-b>=0

a<=b означает, что a меньше или равно b, т. е. a — b — неположительное число, или что a не больше b; .

a-b<=0

Например, для любого числа a верно неравенство ; для любых чисел a и b верно неравенство .

Впрочем, для сравнения действительных чисел необязательно каждый раз составлять их разность и выяснять, положительна она или отрицательна. Можно сделать соответствующий вывод, сравнивая записи чисел в виде десятичных дробей. Геометрическая модель множества действительных чисел, т. е. числовая прямая, делает операцию сравнения чисел особенно наглядной: из двух чисел a, b больше то, которое располагается на числовой прямой правее. Таким образом, к сравнению действительных чисел нужно подходить достаточно гибко, что мы и используем в следующем примере.

Евдокс Книдский | Греческий математик и астроном

Год рождения:: около 395 г. до н.э. или 390 г. до н.э. Книд

Умер:: около 342 г. до н.э. или 337 г. до н.э. Книд

Предметы изучения:: иррациональное число метод истощения пропорциональность космическое движение звезда

Просмотреть весь связанный контент →

Евдокс Книдский (род. ок. 395–390 до н. э., Книд, Малая Азия [сейчас в Турции] — умер ок. 342–337 до н. э., Книд), греческий математик и астроном, значительно расширивший пропорции теории, способствовал идентификации созвездий и, таким образом, развитию наблюдательной астрономии в греческом мире и создал первую сложную геометрическую модель движения небесных тел. Он также писал по географии и участвовал в философских дискуссиях в Академии Платона. Хотя ни одно из его сочинений не сохранилось, его вклад известен из многих дискуссий на протяжении всей древности.

Жизнь

По словам историка III века н.э. Диогена Лаэртиуса (источника большинства биографических подробностей), Евдокс изучал математику у Архита из Тарента и медицину у Филистиона из Локры. В возрасте 23 лет он посещал лекции в Афинах, возможно, в Платоновской академии (открыта в г. ок. г. 387 г. до н. э.). Через два месяца он уехал в Египет, где обучался у священников 16 месяцев. Зарабатывая на жизнь учителем, Евдокс затем вернулся в Малую Азию, в частности в Кизик на южном берегу Мраморного моря, прежде чем вернуться в Афины, где он связался с Академией Платона.

Викторина «Британника»

Наука: правда или вымысел?

Аристотель сохранил взгляды Евдокса на метафизику и этику. В отличие от Платона, Евдокс считал, что формы существуют в воспринимаемых вещах. Он также определил добро как то, к чему стремятся все вещи, что он отождествлял с удовольствием. В конце концов он вернулся в свой родной Книд, где стал законодателем и продолжал свои исследования до своей смерти в возрасте 53 лет. Последователи Евдокса, включая Менехма и Каллиппа, процветали как в Афинах, так и в Кизике.

Математик

Вклад Евдокса в раннюю теорию пропорций (равных отношений) формирует основу для общего описания пропорций, содержащегося в Книге V Евклида « Элементов » ( ок. 300 г. до н. э.). Там, где предыдущие доказательства пропорции требовали отдельной обработки линий, поверхностей и тел, Евдокс предоставил общие доказательства. Однако неизвестно, насколько более поздние математики могли внести свой вклад в форму, найденную в Элементах . Он определенно сформулировал принцип деления пополам, согласно которому при наличии двух величин одного и того же вида можно непрерывно делить большую величину по крайней мере наполовину, чтобы построить часть, которая меньше меньшей величины.

Точно так же теория Евдокса о несоизмеримых величинах (величины, не имеющие общей меры) и метод исчерпания (его современное название) повлияли на Книги X и XII Элементов соответственно. Архимед ( ок. 285–212/211 до н. э.), в О сфере и цилиндре и в Методе выделил для похвалы два доказательства Евдокса, основанные на методе исчерпывания: что объемы пирамид и конусы составляют одну треть объема призмы и цилиндра соответственно с теми же основаниями и высотами. Различные следы предполагают, что доказательство последнего Евдоксом началось с предположения, что конус и цилиндр соизмеримы, прежде чем свести случай несоизмеримости конуса и цилиндра к соизмеримому случаю. Поскольку современное понятие действительного числа аналогично древнему понятию отношения, этот подход можно сравнить с 19Определения действительных чисел в терминах рациональных чисел в 19-м веке. Евдокс также доказал, что площади кругов пропорциональны квадратам их диаметров.

Евдокс также, вероятно, в значительной степени ответственен за теорию иррациональных величин формы a ± b (найденную в Элементах , Книга X), основанную на его открытии, что отношения стороны и диагонали правильного вписанный в окружность пятиугольник до диаметра окружности не попадает в классификации Теэтета Афинского ( с. 417–369 до н. э.). Согласно Эратосфену из Кирены ( ок. 276–194 до н. э.), Евдокс также внес вклад в решение проблемы удвоения куба, то есть в построение куба, объем которого вдвое превышает объем данного куба.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту.

Астроном

В двух работах, Феномены и Зеркало , Евдокс схематически описал созвездия, фазы неподвижных звезд (даты, когда они видны) и погоду, связанную с разными фазами. Через поэму Арата ( с. 315–245 до н. э.) и комментарий к поэме астронома Гиппарха ( ок. 100 до н. э.), эти произведения оказали непреходящее влияние в древности. Евдокс также обсуждал размеры Солнца, Луны и Земли. Возможно, он создал календарь восьмилетнего цикла ( Oktaëteris ).

Возможно, самая большая известность Евдокса связана с тем, что он первым попытался в О скоростях построить геометрическую модель движения Солнца, Луны и пяти планет, известных в древности. Его модель состояла из сложной системы из 27 взаимосвязанных геоконцентрических сфер, по одной для неподвижных звезд, по четыре для каждой планеты и по три для Солнца и Луны. Каллипп, а затем Аристотель модифицировали модель. Подтверждение Аристотелем ее основных принципов гарантировало непреходящий интерес в эпоху Возрождения.

Евдокс также написал этнографический труд («Круг земли»), фрагменты которого сохранились. Вполне вероятно, что Евдокс также разделил сферическую Землю на знакомые шесть частей (северную и южную тропическую, умеренную и арктическую зоны) в соответствии с делением небесной сферы.

Наследие

Евдокс — самый изобретательный греческий математик до Архимеда. Его работа формирует основу для самых продвинутых дискуссий в элементах Евклида 9.0026 и заложил основу для изучения Архимедом объемов и поверхностей. Теория пропорций — первая полностью сформулированная теория величин. Хотя большинство астрономов, по-видимому, отказались от его астрономических взглядов к середине 2 века до н. Неудовлетворенность модификацией этого принципа Птолемеем (где он отделил центр равномерного движения от центра круга движения) мотивировала многих астрономов средневековья и эпохи Возрождения, включая Николая Коперника (1473–1543).

Генри Росс Менделл
Ричард Дедекинд | немецкий математик
Ричард Дедекинд
Смотреть все медиа
Дата рождения:
6 октября 1831 г. Брауншвейг Германия
Умер:
12 февраля 1916 г. (84 года) Брауншвейг Германия
Предметы изучения:
Дедекинд огранка гипотеза континуума идеальный иррациональное число настоящий номер
Просмотреть все связанные материалы →
Рихард Дедекинд , полностью Юлий Вильгельм Рихард Дедекинд , (родился 6 октября 1831, Брауншвейг, герцогство Брауншвейг [Германия] — умер 12 февраля 1916, Брауншвейг), немецкий математик, разработавший серьезное переопределение иррациональных чисел с точки зрения арифметических понятий. Хотя его трактовка идей бесконечности и того, что составляет действительное число, не была полностью признана при его жизни, она продолжает оказывать влияние на современную математику.
Дедекинд был сыном юриста. Посещая гимназию Мартино-Катаринеум в 1838–1847 годах в Брауншвейге, он сначала интересовался в первую очередь химией и физикой. Однако в Каролинском колледже в 1848–1850 годах он обратился к исчислению, алгебре и аналитической геометрии, что помогло ему получить квалификацию для изучения высшей математики в Геттингенском университете под руководством математика Карла Фридриха Гаусса.
Викторина «Британника»
Числа и математика
После двух лет самостоятельного изучения алгебры, геометрии и эллиптических функций Дедекинд служил приват-доцентом («неоплачиваемый лектор») в 1854–1858 годах в Геттингенском университете, где в своих лекциях он представил, вероятно, для впервые изучил теорию уравнений Галуа и посетил лекции математика Петера Густава Лежена Дирихле. Этот опыт привел Дедекинда к мысли о необходимости переопределения иррациональных чисел с точки зрения арифметических свойств. Геометрический подход побудил Евдокса в 4 веке до н.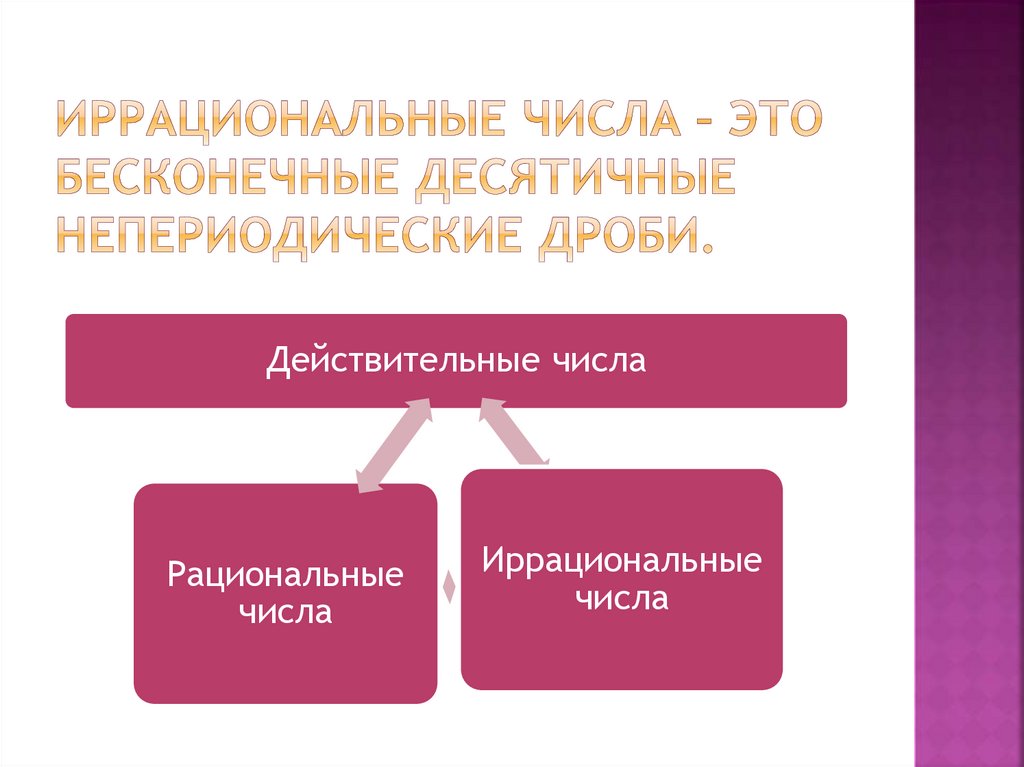
В 1858 году Дедекинд поступил на факультет Цюрихского политехнического института, где проработал пять лет. В 1862 году он поступил в Высшую техническую школу в Брауншвейге, где оставался в относительной изоляции до конца своей жизни.
Преподавая там, Дедекинд развил идею о том, что как рациональные, так и иррациональные числа могут образовывать континуум (без пробелов) действительных чисел, при условии, что действительные числа имеют отношение один к одному с точками на прямой. Он сказал, что тогда иррациональное число будет тем граничным значением, которое разделяет два специально сконструированных набора рациональных чисел.
Дедекинд понял, что характер континуума должен зависеть не от количества точек на отрезке (или континууме), а скорее от того, как линия поддается разделению. Его метод, теперь называемый разрезом Дедекинда, состоял в разделении всех действительных чисел в ряду на две части так, чтобы каждое действительное число в одной части было меньше, чем каждое действительное число в другой. Такой разрез, соответствующий данному значению, определяет иррациональное число, если ни в одной из частей нет ни наибольшего, ни наименьшего; тогда как рациональное определяется как разрез, в котором одна часть содержит наименьшую или наибольшую. Таким образом, Дедекинд определил бы квадратный корень из 2 как уникальное число, делящее континуум на два набора чисел так, что все члены одного набора больше, чем члены другого, или разрез, или деление, разделяющее ряд чисел на две части, так что один набор содержит все числа, квадраты которых больше 2, а другой набор содержит все числа, квадраты которых меньше 2.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Дедекинд разработал арифметическую интерпретацию иррациональных чисел в 1872 году в своей книге Stetigkeit und Irrationale Zahlen (англ. пер., «Непрерывность и иррациональные числа», опубликованной в Essays on The Theory of Numbers ). ). Он также предположил, как и немецкий математик Георг Кантор двумя годами позже, что множество — совокупность объектов или компонентов — является бесконечным, если его компоненты могут быть расположены во взаимно-однозначном отношении с компонентами одного из его компонентов. подмножества. Дополнив геометрический метод анализа, Дедекинд внес существенный вклад в современное понимание бесконечно большого и бесконечно малого.
Во время отпуска в Интерлакене, Швейцария, в 1874 году Дедекинд встретил Кантора. Дедекинд сочувственно выслушал только что опубликованное Кантором изложение революционной идеи множеств, которое впоследствии стало заметным в преподавании современной математики. Поскольку оба математика разрабатывали очень оригинальные концепции, такие как теория чисел и анализ, которые не сразу были приняты их современниками, и поскольку оба не имели должного профессионального признания, между ними возникла прочная дружба.
Продолжая свои исследования свойств и взаимосвязей целых чисел, то есть идеи числа, Дедекинд опубликовал Über die Theorie der ganzen Alexandriaischen Zahlen (1879; «К теории алгебраических целых чисел»).
No related posts.