Определение синуса, косинуса и тангенса, котангенса угла
Теорема Пифагора
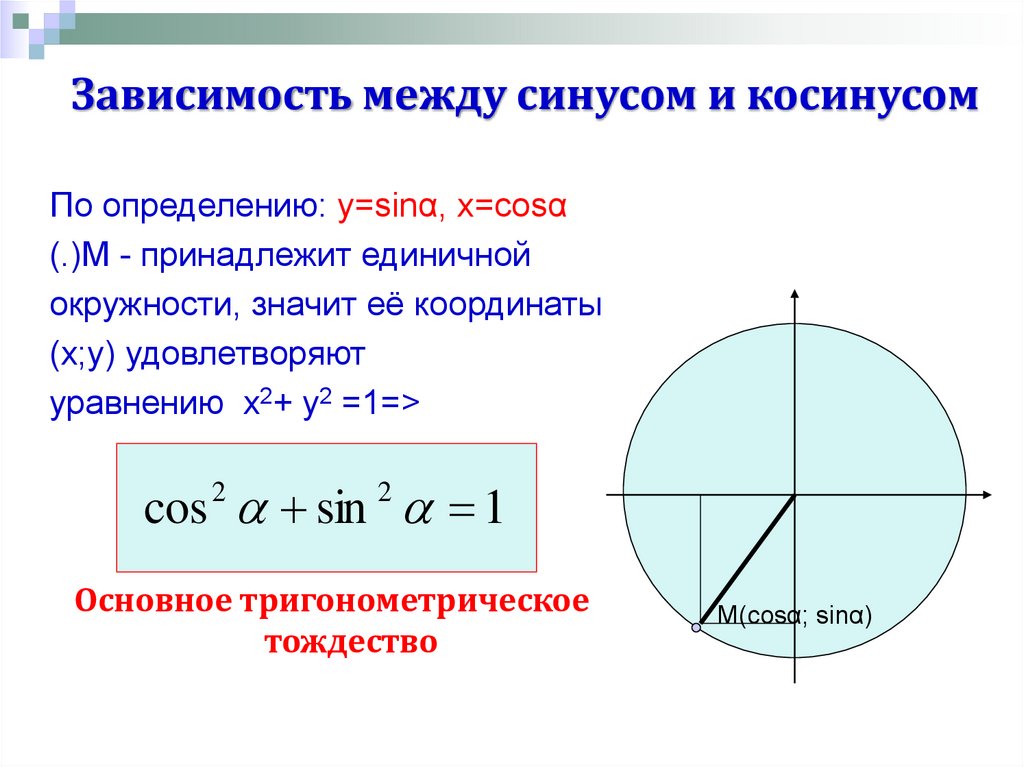
sin2a+cos2a=1
знаки синуса и косинуса
равенство углов равнобедренного треугольника
синус, косинус, тангенс углов a и –a
sin(-a)=sina
cos(-a)=cosa
формула расстояния между двумя точками
формулы сложения
формулы приведения
сумма и разность синусов, сумма и разность косинусов
синус и косинус двойного угла
синус и косинус половинного угла
понижение степени
Рис. 7 Структурно-логическая схема тригонометрической функции
На рисунке 7
изображена СЛС тригонометрической
функции представляющая структуру
освоенного содержания обучения.
Анализируя СЛС, демонстрирующие взаимосвязь степенной, показательной и логарифмической функций (см. рис.8) можно отметить, что определения функций являются исходными УЭ и на наш взгляд должны быть обязательно включены в объем запоминаемого содержания обучения. Свойства показательной и логарифмической функций являются следствиями свойств степенной функции, поэтому к первичным УЭ можно отнести именно свойства степенной функции.
Рис. 8 СЛС, демонстрирующие взаимосвязь УЭ степенной, показательной и логарифмической функций
На
основе структурно-логических схем были
построены таблицы, где выделены операции
(или логические шаги), которые необходимо
выполнить для получения формулы.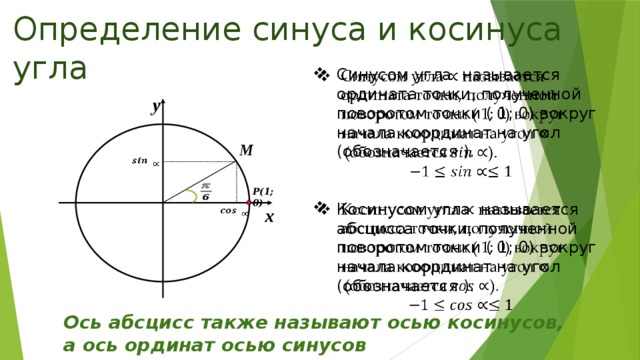
Затем был проведен сравнительный анализ утвержденного обязательного минимума основных образовательных программ полного общего образования и содержания признанных тестов достижений (ЕГЭ и ЦТ).
На основании полученных результатов можно отметить следующее:
все элементы минимума содержания отображены в школьной программе и исключений нет;
в указанной совокупности тестов достаточно часто используются учебные элементы формально не входящие в обязательный минимум содержания, например, теорема Пифагора;
не все элементы минимума содержания используются в отдельных батареях тестов;
часть элементов содержания не используется в исследованных батареях представленных выше тестовых систем;
в задачах есть примеры выхода за пределы обязательного минимума содержания;
количество применяемых учебных элементов больше числа заданий;
имеет место не эквивалентность вариантов по содержанию, что противоречит условию стандартизации тестов.
Выделенные в результате анализа структурно-логических схем учебные элементы содержания были максимально однозначно описаны и проанализированы на частотность использования в тестах достижений ЕГЭ и ЦТ [32, 33, 41]. Смысл частотного анализа – определить долю (процент) использования УЭ в анализируемых заданиях тестов.
Поскольку правильно выполненные операции, действия с этими УЭ определяют успешность выполнения теста в целом, частотность использования этих УЭ, независимо от степени осознанности их включения в задания тестов, пропорциональна значимости усвоения данных УЭ.
Представим теперь описание объекта, процедуры и результатов частотного анализа тестов ЦТ и ЕГЭ.
Конкретно, проведен
частотный анализ следующих тестовых
заданий: ЕГЭ 2001г. — 10 вариантов по 25
заданий в каждом [57]; ЕГЭ 2002г. –
демонстрационный вариант — 25 заданий
[58]; ЕГЭ 2003г. – демонстрационный вариант
— 30 заданий [59]; ЦТ 1999г.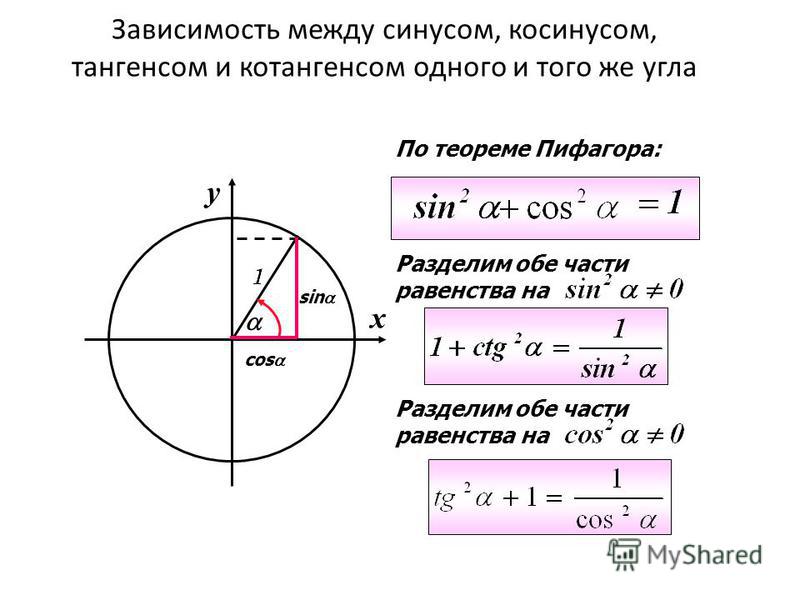
Решая проблему однозначности выделения, описания рассматриваемых УЭ, мы, отказавшись от предлагаемой в процедуре ЕГЭ их классификации, выделили перечень УЭ на основе СЛС представления функций в комплектах учебников школьной математики и разработанных СЛС, представляющих структуру освоенного знания (см. табл. Приложения 2). При этом ввели следующее описание УЭ:
Степенная функция – любая, используемая в тестовых заданиях и в их решении, функция вида: хs, s – действительное число, не равное нулю или единице, а х > 02.
Показательная функция – любая, используемая в тестовых заданиях и в их решении, функция вида: ах , где а и х действительные величины, а ≥ 0.
Логарифмическая функция – любая, используемая в тестовых заданиях и в их решении, функция вида: logаx, где а и х действительные, положительные величины.
Тригонометрические функции соответствуют своему традиционному для школьной математики геометрическому определению, в котором х – действительное число, cosx, sinx, tgx, ctgx – соответствующие тригонометрические функции.
свойства функций, для однозначности представляемые их аналитическим выражением.
Для определения частотности использования в тестах самих функций и их конкретных свойств прорешены все задачи в представленных выше вариантах и составлена таблица (См. приведенную в качестве примера обобщенную таблицу 1).
Таблица 1.
Частотность использования элементарных функций в тестах Централизованного тестирования и Единого государственного экзамена
Сред. в % | ЦТ 99 | ЦТ 00 | ЦТ 02 | ЕГЭ 01 | ЕГЭ 02 | ЕГЭ 03 | Сред. | Ст. Откл (S) |
Степенная функция | 71,82 | 86 | 78,50 | 69,60 | 68,00 | 70,00 | 74,29 | 8,47 |
Показательная функция | 5,45 | 8,35 | 9,59 | 12,80 | 16,00 | 17,00 | 11,62 | 4,38 |
Логарифмическая функция | 9,09 | 13,63 | 9,09 | 16,40 | 20,00 | 13,52 | 4,11 | |
Тригонометрическая функция | 15,45 | 20,55 | 18,18 | 30,40 | 24,00 | 20,00 | 21,69 | 4,89 |
Всего: | 101,81 | 130,55 | 115,36 | 140,20 | 120,00 | 127,00 | 121,12 | 7,01 |
в % Первая строка в
списке УЭ таблицы 1 — «Наличие степенной
функции» объединяет все описанные выше
представления степенной функции и,
традиционно выделяемые в школьной
математике корни степени n.
Конкретные
задания могут содержать УЭ не только
одной функции, поэтому их суммарный
процент превышает 100%.
В таблицах частотности по вариантам (см. таблицу 2): в строках содержатся описания УЭ школьной программы, а в столбцах – частотность использования данного УЭ в анализируемом варианте теста. При этом:
Таблица 2.
Определение синуса, косинуса и тангенса угла
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
ГАПОУ СО «Асбестовский политехникум»
Преподаватель: Максимова Е.
В.
Синусом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к гипотенузе:
sin A=
с
Косинусом острого угла прямоугольного
треугольника называется отношение
прилежащего катета к гипотенузе:
cos A=
Тангенсом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к прилежащему
катету:
tg A=
А
в
Определение синуса и косинуса
B
Δ
ОМА :
ОМ 1
ОА х;
АМ ОВ у
cos х
sin у
cos
OА х
х
OМ 1
sin
AМ у
у
OМ 1
По теореме Пифагора :
sin 2 cos 2 1
M cos ; sin
B
y
x
A
cos
sin
ctg
tg
sin
cos
у
М (x; y)
1
О
с
ь
-1
с
и
н
у
с
о
в
+
α
0
1 М (1;0)
Ось косинусов
̶
х
Окружность радиуса 1
с центром в начале координат,
на которой задана
точка М — начало отсчета
для измерения углов,
и направление
положительного обхода,
называется единичной
(тригонометрической)
окружностью
sin α = у
Синусом угла α называется
̶1
ордината (у) точки,
полученной поворотом точки
(1; 0) вокруг
Косинусом угла α называется абсцисса
(х) начала
точки,
координат
угол α
полученной поворотом точки (1;
0) вокругна
начала
координат на угол α
cos α = x
Для любого угла α существует:
1) синус этого угла и притом единственный;
2) косинус этого угла и притом единственный
Значит, есть
функции
sin α и cos α
Y
( — ; +)
II
I
O
(-;-)
III
( +; +)
X
IV
(+;-)
Таблица знаков синуса и косинуса
I
II
четверть четверть
cos t
sin t
+
+
+
III
четверть
IV
четверть
—
+
—
Таблица значений
синуса и косинуса
α
0
sinα
0
1
cosα
1
0
cos
cos
cos
cos
180
270
90
0000===10
–1
0
sin
sin
sin
sin
270
180
90
00000===0–1
10
y
1
π
—
90o 2
(0;1)
Используя точку,
соответствующую
углу α, запишите
синус и косинус угла,
+
sin α = у
π180o ( ̶ 1;0)
-1
cos α = x
(1;0) 0o 0
1 360o
2πx
0
(0; ̶ 1) -1
270o3π
—
2
Определение тангенса
Тангенсом угла α называется отношение
синуса угла α к его косинусу.
В
Δ
КОС :
C
M
КС КС
tg
КС
ОК
1
K
sin
tg
cos
линия tg
Определение котангенса
Котангенсом угла α называется отношение
косинуса угла α к его синусу.
линия сtg
В
ΔODN :
ctg
N
D
NД NД
NД
ОN
1
cos
сtg
sin
M
Тригонометрия на ладони
English Русский Правила
Косинус Определение и значение | Dictionary.com
- Основные определения
- Викторина
- Примеры
- Британский
- Научный
Показывает уровень сложности слова.
[ koh-sahyn ]
/ ˈkoʊ saɪn /
Сохранить это слово!
Показывает уровень оценки в зависимости от сложности слова.
сущ.
Тригонометрия.
- (в прямоугольном треугольнике) отношение стороны, прилежащей к данному углу, к гипотенузе.
- синус дополнения данного угла или дуги. Сокращение: cos
Математика. (действительного или комплексного числа x) функция cos x, определяемая бесконечным рядом 1 − (x2/2!) + (x4/4!) − + …, где ! обозначает факториал. Сокращение: cosCompare sine (по умолчанию 3), факториал (по умолчанию 1).
ВИКТОРИНА
ВЫ ПРОЙДЕТЕ ЭТИ ГРАММАТИЧЕСКИЕ ВОПРОСЫ ИЛИ НАТЯНУТСЯ?
Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик. Удачи!
Вопрос 1 из 7
Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок.
Начало косинуса
1625–35; <Новый латинский cosinus. См. co-, sine
Слова рядом с cosine
cosign, cosignatory, cosigner, Cosimo, Cosimo I, cosine, COSLA, cos салат, cosm-, косметический, косметический
Dictionary.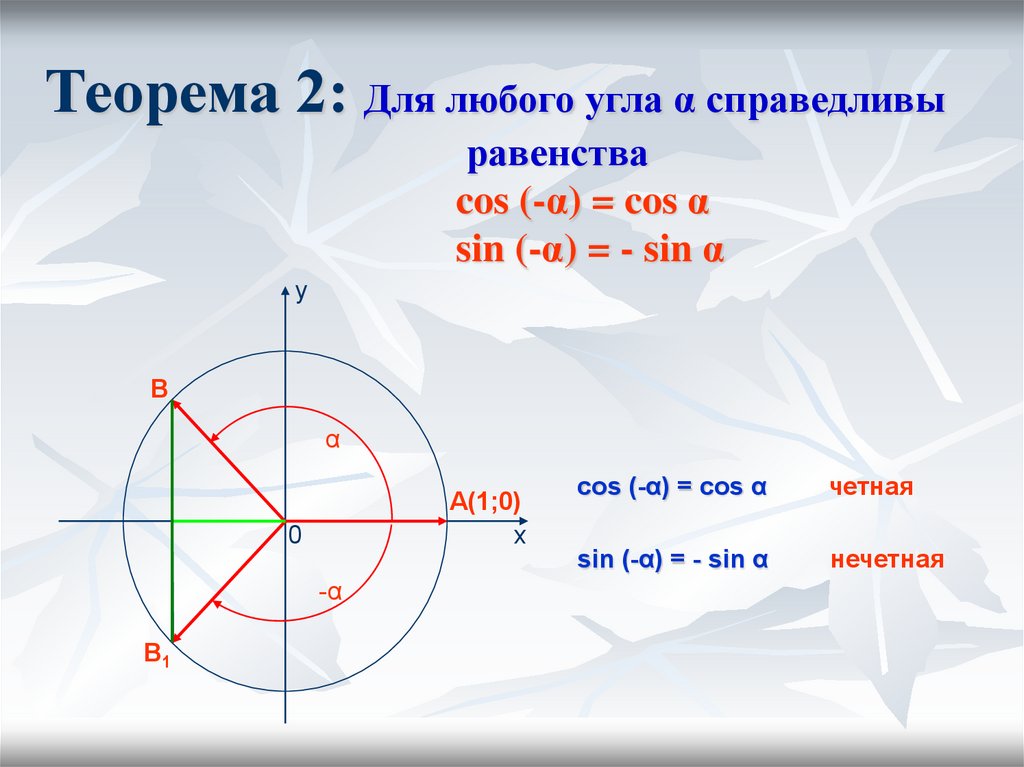
com Unabridged
На основе Random House Unabridged Dictionary, © Random House, Inc., 2022
Как использовать косинус в предложении
Благодаря показателю степени функции косинуса эта функция делает некоторые странные вещи, когда N меньше 1.
Можете ли вы сложить куб?|Зак Висснер-Гросс|11 февраля 2022 г.|FiveThirtyEight
Переменные не представляют буквально сами измерения углов, а вместо этого заменяют комплексные числа, связанные с косинусами углов.
Тетраэдрические решения, наконец, доказаны спустя десятилетия после компьютерного поиска|Кевин Хартнетт|2 февраля 2021 г.|Журнал Quanta
И, усевшись рядом с Дирриком, он начал объяснять тайны синуса, косинуса и тангенса.
Вяленая и мокрая рыба|Антон Бернхард Элиас Нильсен
Синус и косинус мне придется использовать в последней части моей лекции.
Приложение к журналу Scientific American, Vol. XXI., № 531, 6 марта 1886 г. | Разные
Подобно функциям синуса и косинуса, эллиптические функции имеют теоремы сложения, например.
Энциклопедия Нью-Грешэма|Разное
Тем не менее, я не держу зла на синус и косинус, которые я по-прежнему высоко ценю.
Жизнь мухи|Дж. Анри Фабр
Приведенные выше девять наклонений косинуса, как мы видели, связаны шестью уравнениями.
Encyclopaedia Britannica, 11th Edition, Volume 11, Slice 6|Various
Определения косинуса в Британском словаре
косинус
/ (ˈkəʊˌsaɪn) /
существительное (угла)
тригонометрическая функция, которая в прямоугольном треугольнике представляет собой отношение длины прилежащей стороны к длине гипотенузы; синус дополнения. Сокращение: cos
Слово Происхождение косинуса
C17: от нового латинского cosinus; см. co-, sine 1
Collins English Dictionary — Complete & Unabridged 2012 Digital Edition © William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins Издатели 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Научные определения косинуса
косинуса
[косинь]
Отношение длины прилежащего острого угла к длине стороны прямоугольного треугольника на длину гипотенузы.
Абсцисса конечной точки дуги единичной окружности с центром в начале декартовой системы координат, дуга имеет длину x и измеряется против часовой стрелки от точки (1, 0), если x положительно, или по часовой стрелке, если x равно отрицательный.
Функция числа x, равная косинусу угла, мера которого в радианах равна x.
Научный словарь American Heritage® Авторские права © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Определение: Синус — ProofWiki
Содержание
- 1 Определение
- 1.1 Определение из треугольника
- 1.2 Определение из круга
- 1.3 Реальные числа
- 1.4 Комплексные числа
- 2 См. также
- 3 Историческая справка
- 4 Лингвистическая записка
- 5 источников
Определение
Определение из треугольника
В приведенном выше прямоугольном треугольнике нас интересует угол $\theta$.
Синус от $\angle \theta$ определяется как $\dfrac {\text{Противоположный}} {\text{Гипотенуза}}$.
Определение из окружности
Синус угла прямоугольного треугольника можно продолжить до полной окружности следующим образом:
Рассмотрим единичную окружность $C$, центр которой находится в начале декартовой плоскости.
Пусть $P = \tuple {x, y}$ — точка на $C$ в первом квадранте, где $\theta$ — это угол, образуемый $OP$ с $x$- ось.
Пусть $AP$ — перпендикуляр из $P$ к оси $x$.
Тогда синус $\theta$ определяется как длина $AP$.
Следовательно, в первом квадранте синус 9{2 п + 1 } } {\ парен {2 п + 1}!} + \ cdots \)
См. также
- Эквивалентность определений синуса угла
- Определение: косинус
- Определение: Функция касания
- Определение: Котангенс
- Определение:Функция секущей
- Определение:Косеканс
- Определение:Гиперболический синус
- Определение: Обратный синус
- Свойства функции реального синуса
- Результаты о функции синуса можно найти здесь.
Гиппарх из Никеи впервые составил таблицы, в которых указаны длина дуги окружности и длина хорды, образующей ее, для различных углов, опирающихся на дугу. Однако он фактически не определил понятие синуса как такового.
sine впервые обсуждался Арьябхатой Старшим под именем ardha-jyā , что означает полухорд .
Символ $\sin$ для синуса, по-видимому, был изобретен Уильямом Отредом в его работе $1657$ Trigonometrie , хотя некоторые авторы приписывают его Эйлеру.
О sine первоначально писал Арьябхата Старший под именем ardha-jyā .
Слово jyā на санскрите означает тетива , а в математическом контексте означает хорду окружности.
Таким образом, слово ardha-jyā буквально означает полуаккорд . Позже первая часть слова, как правило, опускалась, в результате чего оставалось слово jyā .
Когда слово jyā было переведено на арабский язык, оно интерпретировалось как jiba .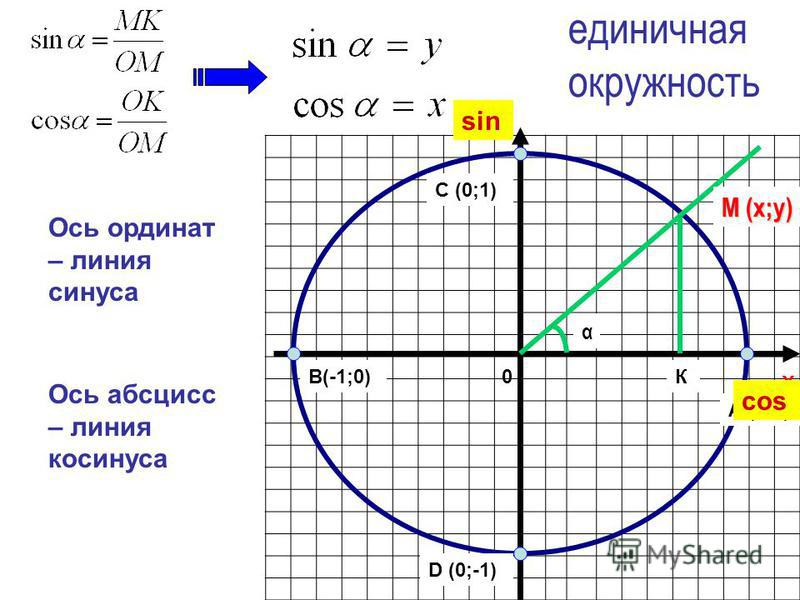
Гласные в арабском языке опущены, осталось слово jb . Слово jiba на арабском языке бессмысленно.
Когда Роберт Честерский приехал переводить эти произведения в 12 веке, он интерпретировал jb как слово jaib , что означает карман или сгиб (в одежде).
Это он перевел на латынь как синус , который имеет несколько значений, из которых кратность — одно, а кривая , обмотка или залив — другие.
Некоторые источники приписывают этот неверный перевод Джерарду Кремонскому, но, похоже, он следовал за Робертом, чей перевод за 1145$ имеет приоритет.
Слово sine произносится так же, как английское слово sign .
$\sin x$ озвучено синус (из) $x$ .
Источники
- 1989 г.: Эфраим Дж. Боровски и Джонатан М. Борвейн: Математический словарь : Ввод: Синус
- 2008: Ян Стюарт: Укрощение бесконечности .