Определение смежного угла: Свойства смежных углов — ответ на Uchi.ru

Могут ли смежные углы быть равными. Смежные углы. Полные уроки — Гипермаркет знаний. Смежные углы – основные свойства

В процессе изучения курса геометрии понятия “угол”, “вертикальные углы”, “смежные углы” встречаются достаточно часто. Понимание каждого из терминов поможет разобраться в поставленной задаче и правильно ее решить. Что такое смежные углы и как их определять?

Смежные углы – определение понятия

Термин “смежные углы” характеризует два угла, образованных общим лучом и двумя дополнительными полупрямыми, лежащими на одной прямой. Все три луча выходят из одной точки. Общая полупрямая является одновременно стороной как одного, так и второго угла.

Смежные углы – основные свойства

1. Исходя из формулировки смежных углов, нетрудно заметить, что сумма таких углов всегда образует развернутый угол, градусная мера которого равна 180°:

• Если μ и η являются смежными углами, то μ + η = 180°.
• Зная величину одного из смежных углов (например, μ), можно легко вычислить градусную меру второго угла (η), используя выражение η = 180° – μ.

2. Данное свойство углов позволяет сделать следующий вывод: угол, являющийся смежным прямому углу, также будет прямым.

3. Рассматривая тригонометрический функции (sin, cos, tg, ctg), основываясь на формулах приведения для смежных углов μ и η справедливо следующее:

• sinη = sin(180° – μ) = sinμ,
• cosη = cos(180° – μ) = -cosμ,
• tgη = tg(180° – μ) = -tgμ,
• ctgη = ctg(180° – μ) = -ctgμ.

Смежные углы – примеры

Пример 1

Задан треугольник с вершинами M, P, Q – ΔMPQ. Найти углы, смежные углам ∠QMP, ∠MPQ, ∠PQM.

• Продлим каждую из сторон треугольника прямой.
• Зная о том, что смежные углы дополняют друг друга до развернутого угла, выясняем, что:

смежным для угла ∠QMP будет ∠LMP,

смежным для угла ∠MPQ будет ∠SPQ,

смежным для угла ∠PQM будет ∠HQP.

Пример 2

Величина одного смежного угла составляет 35°. Чему равна градусная мера второго смежного угла?

• Два смежных угла в сумме образуют 180°.
• Если ∠μ = 35°, то смежный ему ∠η = 180° – 35° = 145°.

Пример 3

Определить величины смежных углов, если известно, что градусная мера одного из низ втрое больше градусной меры другого угла.

• Обозначим величину одного (меньшего) угла через – ∠μ = λ.
• Тогда, согласно условию задачи, величина второго угла будет равна ∠η = 3λ.
• Исходя из основного свойства смежных углов, μ + η = 180° следует

λ + 3λ = μ + η = 180°,

λ = 180°/4 = 45°.

Значит первый один угол ∠μ = λ = 45°, а второй угол ∠η = 3λ = 135°.

Умение апеллировать терминологией, а также знание основных свойств смежных углов поможет справиться с решением многих геометрических задач.

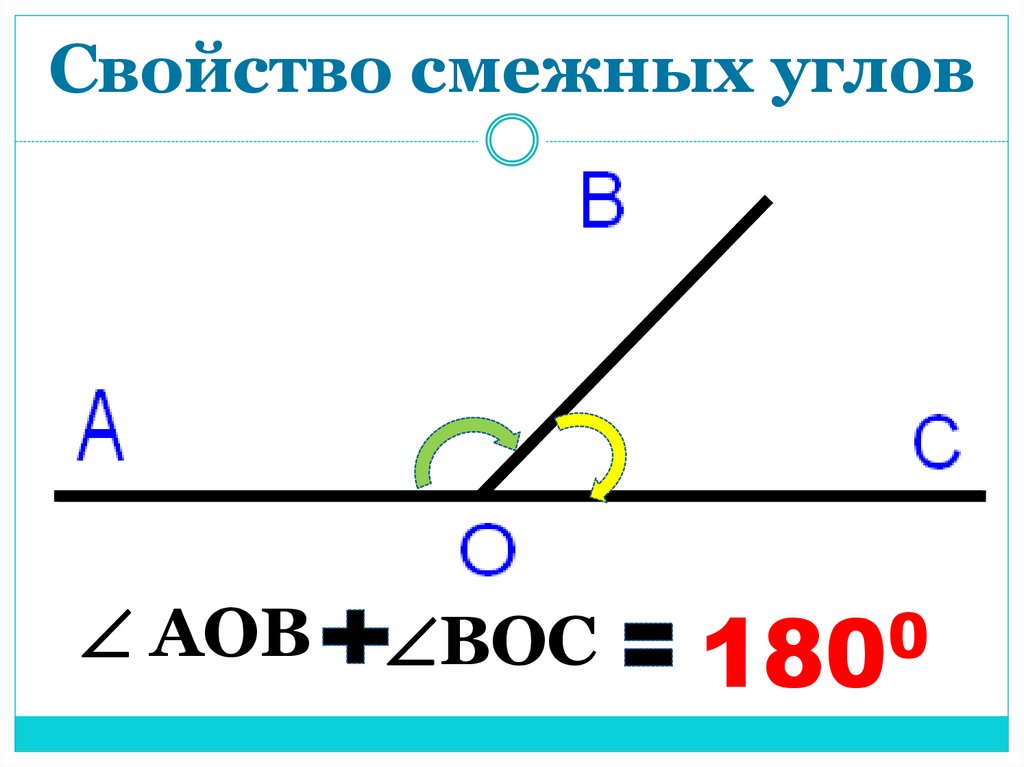
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.

Сумма смежных углов равна 180°

Теорема 1. Сумма смежных углов равна 180°.

Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .

Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.

Вертикальные углы равны

Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).

Теорема 2. Вертикальные углы равны.

Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.

Отсюда заключаем, что ∠ АОВ = ∠ COD.

Следствие 1. Угол, смежный с прямым углом, есть прямой угол.

Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные).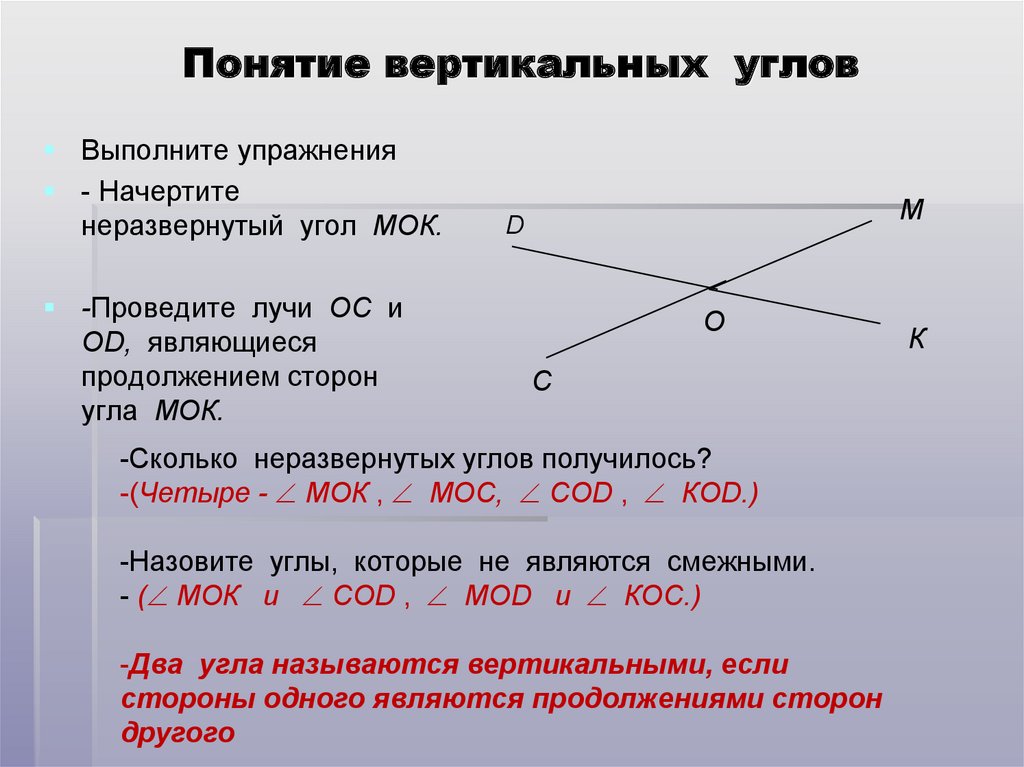 В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.

Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.

АН — перпендикуляр к прямой

Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.

Чертежный угольник

Справедлива следующая теорема.

Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).

Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.

Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».

Пример 1. Один из смежных углов равен 44°. Чему равен другой?

Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.

Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?

Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.

∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.

Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.

Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.

Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.

Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.

Вопрос 1. Какие углы называются смежными?
Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.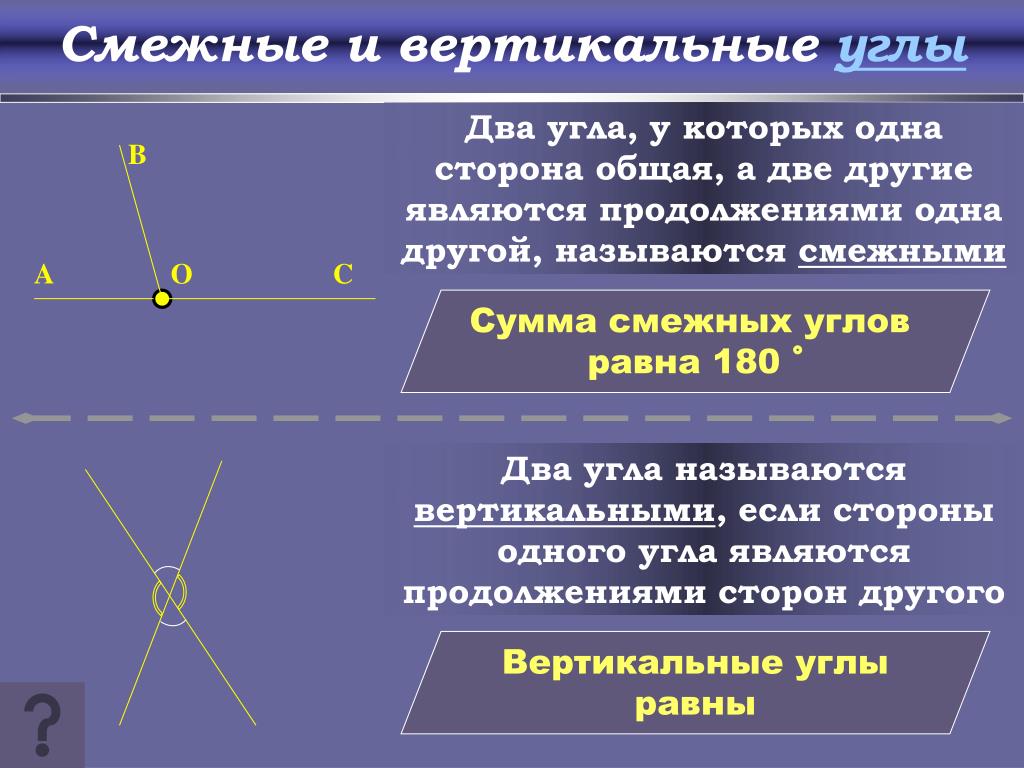

На рисунке 31 углы (a 1 b) и (a 2 b) смежные. У них сторона b общая, а стороны a 1 и a 2 являются дополнительными полупрямыми.

Вопрос 2. Докажите, что сумма смежных углов равна 180°.
Ответ. Теорема 2.1. Сумма смежных углов равна 180°.
Доказательство. Пусть угол (a 1 b) и угол (a 2 b) — данные смежные углы (см. рис.31). Луч b проходит между сторонами a 1 и a 2 развёрнутого угла. Поэтому сумма углов (a 1 b) и (a 2 b) равна развёрнутому углу, т. е. 180°. Что и требовалось доказать.

Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны.
Ответ.

Из теоремы 2.1 следует, что если два угла равны, то смежные с ними углы равны.
Допустим, углы (a 1 b) и (c 1 d) равны. Нам нужно доказать, что углы (a 2 b) и (c 2 d) тоже равны.

Сумма смежных углов равна 180°. Из этого следует, что a 1 b + a 2 b = 180° и c 1 d + c 2 d = 180°. Отсюда, a 2 b = 180° — a 1 b и c 2 d = 180° — c 1 d. Так как углы (a 1 b) и (c 1 d) равны, то мы получаем, что a 2 b = 180° — a 1 b = c 2 d. По свойству транзитивности знака равенства следует, что a 2 b = c 2 d. Что и требовалось доказать.

Вопрос 4. Какой угол называется прямым (острым, тупым)?
Ответ. Угол, равный 90°, называется прямым углом.
Угол, меньший 90°, называется острым углом.
Угол, больший 90° и меньший 180°, называется тупым.

Вопрос 5. Докажите, что угол, смежный с прямым, есть прямой угол.
Ответ. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом, есть прямой угол: x + 90° = 180°, x= 180° — 90°, x = 90°.

Вопрос 6. Какие углы называются вертикальными?

Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.

Вопрос 7. Докажите, что вертикальные углы равны.
Ответ. Теорема 2.2. Вертикальные углы равны.
Доказательство. Пусть (a 1 b 1) и (a 2 b 2)- данные вертикальные углы (рис.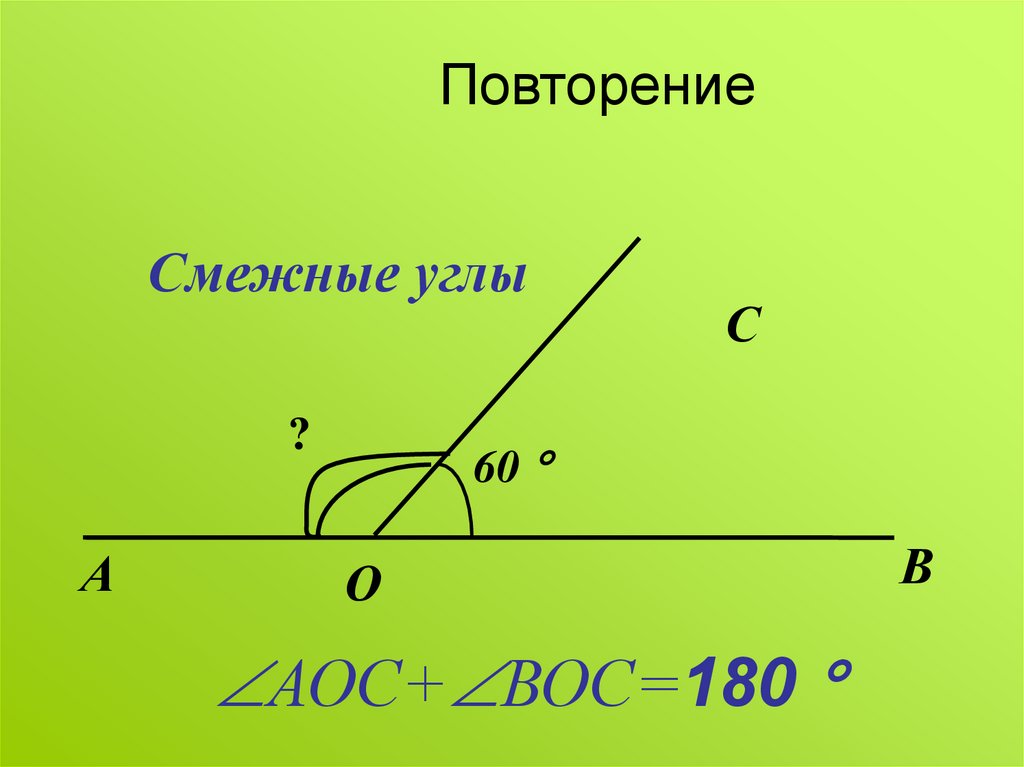 34). Угол (a 1 b 2) является смежным с углом (a 1 b 1) и с углом (a 2 b 2). Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a 1 b 1) и (a 2 b 2) дополняет угол (a 1 b 2) до 180°, т.е. углы (a 1 b 1) и (a 2 b 2) равны. Что и требовалось доказать.

Вопрос 8. Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые.
Ответ. Предположим, что прямые AB и CD пересекают друг друга в точке O. Предположим, что угол AOD равен 90°. Так как сумма смежных углов равна 180°, то получаем, что AOC = 180°-AOD = 180°- 90°=90°. Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.

Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых?
Ответ.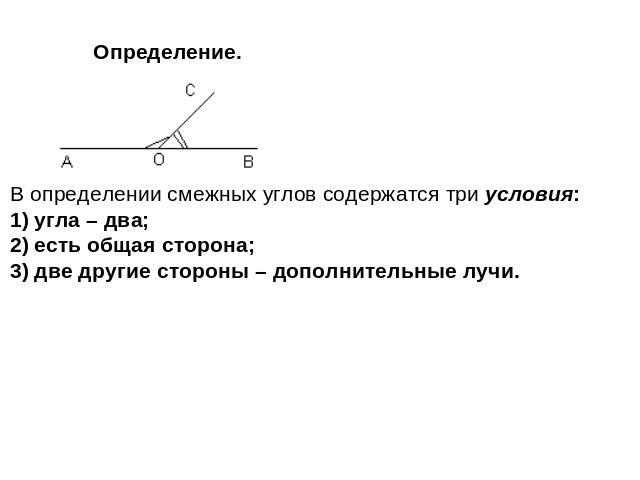 Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком \(\perp\). Запись \(a\perp b\) читается: «Прямая a перпендикулярна прямой b».

Вопрос 10. Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Ответ. Теорема 2.3. Через каждую прямую можно провести перпендикулярную ей прямую, и только одну.

Доказательство. Пусть a — данная прямая и A — данная точка на ней. Обозначим через a 1 одну из полупрямых прямой a с начальной точкой A (рис. 38). Отложим от полупрямой a 1 угол (a 1 b 1), равный 90°. Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.

Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c 1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b 1 .
Углы (a 1 b 1) и (a 1 c 1), равные каждый 90°, отложены в одну полуплоскость от полупрямой a 1 . Но от полупрямой a 1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не быть другой прямой, проходящей через точку A и перпендикулярной прямой a. Теорема доказана.

Вопрос 11. Что такое перпендикуляр к прямой?
Ответ. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.

Вопрос 12. Объясните, в чём состоит доказательство от противного.
Ответ. Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.

Вопрос 13. Что называется биссектрисой угла?
Ответ. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.

Что такое смежный угол

Угол – это геометрическая фигура (рис.1), образованная двумя лучами OA и OB (стороны угла), исходящими из одной точки O (вершина угла).

СМЕЖНЫЕ УГЛЫ — два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла.

Смежные углы — (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.

рис. 2

На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые.

рис. 3

На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C.

Теорема о смежных углах

Теорема: сумма смежных углов равна 180°

Доказательство:
Углы a1b и a2b смежные (см. рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.

Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол.

Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.

Определение 1. Углом называется часть плоскости, ограниченная двумя лучами с общим началом.

Определение 1.1. Углом называют фигуру, состоящую из точки — вершины угла — и двух различных полупрямых, исходящих из этой точки, — сторон угла.
Например, угол ВОС на рис1 Рассмотрим сначала две пересекающиеся прямые. При пересечении прямые образуют углы. Есть частные случаи:

Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.

Определение 3. Прямой угол — это угол величиной в 90 градусов.

Определение 4. Угол, меньший 90 градусов, называется острым углом.

Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом.
пересекающиеся прямые.

Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными.

Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами.
На рисунке 1:
смежные: 1 и 2; 2 и 3; 3 и 4; 4 и 1
вертикальные: 1 и 3; 2 и 4
Теорема 1. Сумма смежных углов равна 180 градусов.
Для доказательства рассмотрим на рис. 4 смежные углы АОВ и ВОС. Их суммой является развернутый угол АОС. Поэтому сумма данных смежных углов равна 180 градусов.

рис. 4

Связь математики с музыкой

«Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и, что между ними размещается все, что человечество создало в области науки и искусства.»
Г. Нейгауз
Казалось бы, искусство — весьма отвлеченная от математики область. Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика — самая абстрактная из наук, а музыка — наиболее отвлеченный вид искусства.
Консонанс определяет приятное для слуха звучание струны
В основе этой музыкальной системы были два закона, которые носят имена двух великих ученых — Пифагора и Архита. Вот эти законы:
1. Две звучащие струны определяют консонанс, если их длины относятся как целые числа, образующие треугольное число 10=1+2+3+4, т.е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
2. Частота колебания w звучащей струны обратно пропорциональна ее длине l .
w = a: l ,
где а — коэффициент, характеризующий физические свойства струны.

Так же предложу вашему внимаю забавную пародию про спор двух математиков =)

Геометрия вокруг нас

Геометрия в нашей жизни имеет немаловажное значение. Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились. Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов. Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.

Задание 1.

1. Вот на столе на книжной подставке стоит книга. Какой угол она образует?
2. А вот ученик работает за ноутбуком. Какой угол вы видите здесь?
3. Какой угол образует фото рамка на подставке?
4. Как вы думаете, возможно ли, чтобы два смежных угла были равными?

Задание 2.

Перед вами изображена геометрическая фигура. Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.

Задание 3.

Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке.

Решение задач

1) Даны два угла, относящиеся друг к другу как 1: 2, а смежные с ними — как 7: 5. Нужно найти эти углы.
2) Известно, что один из смежных углов больше другого в 4 раза. Чему равны смежные углы?
3) Необходимо найти смежные углы, при условии, что один из них на 10 градусов больше от второго.

Математический диктант на повторение ранее выученного материала

1) Выполните рисунок: прямые a I b пересекаются в точке А. Отметьте меньший из образованных углов цифрой 1, а остальные углы – последовательно цифрами 2,3,4; дополняющие лучи прямой а — через а1 и а2, а прямой b — через b1 i b2.
2) Пользуясь выполненным рисунком, впишите нужные значения и объяснения в места пропусков в тексте:
а) угол 1 и угол …. смежные, поскольку…
б) угол 1 и угол …. вертикальные, поскольку…
в) если угол 1 = 60°, то угол 2 = …, потому что…
г) если угол 1 = 60°, то угол 3 = . .., потому что…

Решите задачи:

1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°?
2. На рисунке найдите все пары смежных углов. А теперь вертикальных углов. Назовите эти углы.

3. Нужно найти угол, когда он втрое больше, чем смежный с ним.
4. Две прямые пересеклись между собой. В результате этого пересечения образовались четыре угла. Определите величину любого из них, при условии что:

а) сумма 2-х углов из четырех 84°;
б) разность 2-х углов из них равна 45°;
в) один угол в 4 раза меньше чем второй;
г) сумма трех из данных углов равна 290°.

Итог урока

1. назовите углы, которые образуются при пересечении 2-х прямых?
2. Назовите все возможные пары углов, находящихся на рисунке, и определите их вид.

Домашнее задание:

1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго.
2. Найдите углы, которые образуются при пересечении 2-х прямых, при условии, что один из углов равняется сумме 2-х других углов, смежных с ним.
3. Необходимо найти смежные углы, когда биссектриса одного из них образует со стороной второго угол, который больше чем второй угол на 60°.
4. Разница 2-х смежных углов равна трети от суммы этих двух углов. Определите величины 2-х смежных углов.
5. Разница и сумма 2-х смежных углов относятся как 1: 5 соответственно. Найдите смежные углы.
6. Разница двух смежных составляет 25% от их суммы. Как относятся величины 2-х смежных углов? Определите величины 2-х смежных углов.

Вопросы:

1. Что такое угол?
2. Какие бывают типы углов?
3. Какая особенность смежных углов?

Предмети > Математика > Математика 7 класс

Каждый угол, в зависимости от его величины, имеет своё название:

Вид угла	Размер в градусах	Пример
Острый	Меньше 90°
Прямой	Равен 90°. На чертеже прямой угол, обычно обозначают символом , проведённым от одной стороны угла до другой.
Тупой	Больше 90°, но меньше 180°
Развёрнутый	Равен 180° Развёрнутый угол равен сумме двух прямых углов, а прямой угол составляет половину развёрнутого угла.
Выпуклый	Больше 180°, но меньше 360°
Полный	Равен 360°

Два угла называются смежными , если у них одна сторона общая, а две другие стороны составляют прямую линию:

Углы MOP и PON смежные, так как луч OP — общая сторона, а две другие стороны — OM и ON составляют прямую.

Общая сторона смежных углов называется наклонной к прямой , на которой лежат две другие стороны, только в том случае, когда смежные углы не равны между собой. Если смежные углы равны, то их общая сторона будет перпендикуляром .

Сумма смежных углов равна 180°.

Два угла называются вертикальными , если стороны одного угла дополняют до прямых линий стороны другого угла:

Углы 1 и 3, а также углы 2 и 4 — вертикальные.

Вертикальные углы равны.

Докажем, что вертикальные углы равны:

Сумма ∠1 и ∠2 составляет развёрнутый угол. И сумма ∠3 и ∠2 составляет развёрнутый угол. Значит, эти две суммы равны:

∠1 + ∠2 = ∠3 + ∠2.

В этом равенстве слева и справа есть по одинаковому слагаемому — ∠2. Равенство не нарушится, если это слагаемое в левой и в правой части опустить. Тогда мы получаем.

Теорема ⭐ о сумме углов треугольника: определение, доказательство, следствие

Формулировка теоремы о сумме углов треугольника

Треугольник может иметь различные углы — острые, прямой, тупой, — но сумма их величин не может превышать 180 градусов. Эта закономерность отражена в теореме, доказательство которой имеет несколько вариантов.

Теорема 

Сумма углов в треугольнике всегда равна 180 о.

Данная теорема является одной из основных, рассматриваемых на уроках геометрии.

Рассмотрим рисунок с треугольником ABC:

Источник: izamorfix.ru

Треугольник имеет углы: A, B, C. Это углы внутренние. Складывая их величины, неизменно получаем 180о. При этом не имеет значения, данный треугольник равнобедренный, равносторонний или прямоугольный.

Исходя из такого свойства, треугольник не может иметь два тупых угла, поскольку их сумма будет более 180о.

Смысл теоремы о сумме углов треугольника был известен еще в Древнем Египте, его установили эмпирическим путем, т.е. путем наблюдения. Однако вероятно, что в то время отсутствовало доказательство этого утверждения. Его можно обнаружить в трудах Прокла, когда он давал комментарии к «началам» Евклида.

В книге № 1 евклидовских «Начал» приведено иное доказательство данной теоремы, чем принято сейчас. Оно опирается на соответствующий чертеж.

Примечание 1

Рассматриваемая теорем приписывается не только Евклиду, но и Пифагору. Она много раз подвергалась сомнению в неевклидовой геометрии.

Доказательство теоремы

Продолжим рассмотрение треугольника ABC из предыдущего раздела.

Для доказательства теоремы проведем дополнительную прямую линию так, чтобы она была параллельна стороне AC и проходила через вершину треугольника B (угол 2).

Источник: izamorfix.ru

Таким образом, в районе угла B образовалось три угла (№№ 4, 2, 5). Из рисунка видно, что их сумма равняется 180о.

На данном рисунке имеются накрест лежащие углы: №1 и №4. Их образование произошло при пересечении прямой AB двух параллельных прямых AC и α. Углы №3 и №5 — также накрест лежащие. Только образованы они при пересечении прямой BC двух параллельных прямых AC и α.

Углы №1 и №4, а также №3 и №5 попарно равны.

Поскольку сумма углов №№ 4, 2, 5 равна 180о, а углы №4 можно заменить №1, а №5 — №3, сумма углов №№ 1, 2, 3 также равна 180о.

Такое доказательство опирается на свойства углов, образованных при пересечении двух параллельных прямых третьей.

Следствие из теоремы

Формулировка теоремы о сумме углов треугольника имеет несколько следствий. Среди них:

1. Если в треугольнике один из углов прямой, то сумма прочих двух углов равна 90о. Свойство вытекает из обычного алгебраического действия. Обозначим углы прямоугольного треугольника A, B, C. Допустим, что C=90о. Тогда (A+B)=180о+90о.
2. Для равнобедренного прямоугольного треугольника характерно, что каждый из его острых углов равен 45о.
3. Треугольник, у которого равны длины всех трех сторон, имеет равные углы — 60о.
4. Углы любого треугольника либо все являются острыми, либо острых два, а третий равен 90о либо больше 90о (тупой).
5. Сумма двух внутренних углов, которые не смежны с внешним, равна величине этого внешнего угла.

Классификация треугольников по видам углов

Рассматривая треугольники, как многоугольники с тремя вершинами, в геометрии выделяют их следующие разновидности:

1. Остроугольный треугольник (все три вершины представляют собой острые углы).
2. Прямоугольный (одна из вершин составляет 90о). Стороны, которые образуют данный угол, — катеты, а сторона, противолежащая углу в 90о, — гипотенуза.
3. Тупоугольный (одна из вершин представлена тупым углом, а две другие — острыми).

В зависимости от особых характеристик сторон треугольника, существует еще одна классификация:

1. Треугольник с тремя равными сторонам — равносторонний.
2. Треугольник с двумя равными сторонами — равнобедренный.

Приведенная классификация подразумевает существование определенных признаков у каждой из названных групп. Эти признаки приходят на помощь в решении задач, когда нужно доказать особенности каких-либо геометрических фигур. Так:

1. Больший угол всегда расположен напротив большей стороны.
2. Равные углы всегда расположены так, что напротив них — равные стороны.
3. Любой треугольник (равносторонний, равнобедренный, тупоугольный, прямоугольный и т. п.) имеет 2 острых угла.
4. Любой внешний угол всегда по размеру превышает внутренний и равен сумме прочих, не смежных с ним, углов.

Для прямоугольного треугольника существуют еще несколько свойств, вытекающих из его определения и изложенных в учебниках по геометрии:

1. Напротив катетов всегда расположены острые углы.
2. Гипотенуза всегда превышает по своей длине любой из катетов, однако меньше их суммы.
3. Тот катет, напротив которого находится острый угол величиной 30о, равен половине длины гипотенузы.
4. Сумма квадратов катетов равна квадрату гипотенузы. Данное свойство доказывается теоремой Пифагора.

Примечание 2

Существуют отдельные свойства для равнобедренного треугольника. Его высота, проведенная в направлении основания, совпадает с медианой и биссектрисой того угла, который расположен между равными сторонами. Кроме того, она совпадает с осью симметрии треугольника, проведенной по основанию.

Пояснение на примерах

Рассмотрим особенности треугольников, приведенные выше, на примерах.

Упражнение 1

Сколько градусов составляет один из углов треугольника, если величины других 25о и 42о?

Решение:

Исходя из теоремы о сумме углов в треугольнике, производим следующие вычисление:

180о-(25о+42о)=113о.

Следовательно, данный треугольник тупоугольный.

Упражнение 2

Известно, что в треугольнике один из углов равен сумме двух других. К какому виду треугольников относится данная геометрическая фигура?

Решение:

Обозначим угол, равный сумме двух других углов, за X. Тогда X+2X/2=180 Путем математических действий приходим к уравнению следующего вида: 2X=180, откуда X=90о.

Ответ: данный треугольник имеет прямой угол, поэтому является прямоугольным.

Упражнение 3

Дан треугольник ABC. В нем угол C на 15о больше, чем угол A, а угол B — на 30о его меньше. Найти величину каждого из углов.

Решение:

Обозначим X величину угла A. Тогда угол C=X+15, B=X-30

 

Источник: wiki.eduvdom.com

Используем свойство суммы углов треугольника и составляем уравнение:

X+(X+15)+(X-30)=180

3X-15=180

3X=195

X=65

Ответ: угол A=65о, угол B=65-30=35о, угол C=65+15=80о.

Для проверки можно сложить величины полученных результатов: 65+35+80=180о. Следовательно, задача решена верно. 

Упражнение 4

Про треугольник ABC известно, что угол A составляет 60о, угол B — 80о. Из угла A на сторону BC опущена биссектриса, образовав треугольник ACD. Каких величин углы имеет данный треугольник?

Источник: wiki.eduvdom.com

Решение:

Исходя из определения биссектрисы, мы знаем, что это луч, который начинаясь в вершине угла треугольника и деля его на два равных угла, пересекает противоположную сторону в определенной точке.

Поскольку биссектриса делит угол A пополам, образованный  угол DAB равен 30о, а угол ADC=30+80=110о (поскольку это внешний угол треугольника).

Исходя из правила, что сумма углов в треугольнике равна 180о, проводим математическое действие:

Угол C=180-(110+30)=40о

Ответ: Угол C равен 40о.

Упражнение 5

В треугольнике ABC известна величина одного угла: A = 40о. Известно, что также что угол, смежный с углом B, составляет 70о. Определить величины всех углов.

Решение:

Источник: multiurok. ru

Решение задания заключается в уравнении. Обозначим величину угла C за X. Тогда

(X+40o+(180o-70o))=180o

X+150o=180o

X=30o

Данный вариант решения основан на том свойстве, что если сумма смежных углов равна 180о (а именно это мы видим на рисунке относительно угла B), то величина каждого из них равна 180о минус величина смежного угла.

Ответ: Величина угла C = 30о, угла B — 110о.

Проверочным действием является операция сложения всех известных и найденных величин углов: 110о+30о+40о=180о.

Упражнение 6

В треугольнике ABC известен угол A (40о). Кроме того, по условию этот треугольник равносторонний (AC=BC). Найти величины двух оставшихся углов.

Решение:

Источник: multiurok.ru

Известно утверждение, что в равностороннем треугольнике величины углов прилегающих к этим сторонам, равны. Следовательно, углы B и A равны. Используя теорему о сумме углов в треугольнике, принимая величину угла C за X, составляем равенство:

2*40о+X=180о

X=100о

Ответ: Величина угла B равна 40о, угла C — 100о. Следовательно, треугольник является тупоугольным.

Смежное определение и значение — Merriam-Webster

соседний ə-jā-sᵊnt 

1

а

: недалеко : ближний

город и пригороды

б

: имеющие общую конечную точку или границу

смежные участки

смежные стороны треугольника

с

: непосредственно перед или после

2

двух углов : с общей вершиной и одной стороной

рядом наречие

Синонимы

• примыкающие
• рядом с
• граничит с
• совпадающий
• смежный
• фланговый
• заподлицо
• окантовка
• присоединение
• рядом
• соседний
• плинтус
• прикосновение
• verging

Просмотреть все синонимы и антонимы в тезаурусе

Примеры предложений

Гарриманы владели двумя большими соседними домами на N Street, один для себя и один для картин Аверелла Гарримана. — Ларри Макмертри, 9 лет.0077 New York Times Review of Books , 23 октября 2003 г.

Услышание неожиданных аккордов было связано с магнитной активностью в области левого полушария, известной как зона Брока, и в прилегающей ткани правого полушария. — Брюс Бауэр, Science News , 5 мая 2001 г.

Коридоры, особенно соседние со спутниковым телефоном, были переполнены журналистами, жадными до освещения захвата Талибаном… — Михаил Игнатьев, 9 лет.0077 Житель Нью-Йорка , 24 марта 1997 г.

Продолжая копать в этом месте и в пяти соседних областях, они нашли 19 черепов, пять яиц, более 150 челюстей и сотни зубов, конечностей и фрагментов костей. — Натали Энджер, , время , 8 октября 1984 г.

их дом рядом с лесопарком

Недавние примеры в Интернете Количество мирных жителей в Славянске и , прилегающий к Краматорск, удвоились с тех пор, как достигли дна после прошлогодней массовой эвакуации, по словам региональных властей, достигнув более 50 000 и 80 000 соответственно. — Сергей Корольчук, Washington Post , 18 февраля 2023 г. Стачел Басси, основательница компании Hope Buss, которая управляет деревней Надежды, сказала, что медицинская помощь будет важна для людей, находящихся на прилегающей территории под открытым небом. — Рэй Джонсон, 9 лет.0077 The Courier-Journal , 26 января 2023 г. Место в Голливуде также планируется открыть в апреле, а в Санта-Монике — в мае. В центре города помещение рядом с окном откроется этим летом как кафе с возможностью перекусить. — Стефани Брейостафф, писатель, Los Angeles Times , 11 января 2023 г. Кухня и прилегающих к ней помещений станут фоном для переноса винтажных и бывших в употреблении предметов, от буфетных шкафов до столовой посуды и настенного декора, в более современные дома. — Кристина Макгирк, 9 лет.0077 Better Homes & Gardens , 10 января 2023 г. Изношенные ковры были вырваны для полированных бетонных полов, а кухня была перемещена из тесного угла у черного входа в более просторное помещение площадью 194 квадратных фута , примыкающее к столовой . —Майкл Снайдер Мартин Моррелл, New York Times , 29 ноября 2022 г. Основная спальня имеет встроенные элементы и смежных 9Офис 0078. — Лия Пикард, WSJ , 17 ноября 2022 г. «Джетс» были первой командой, которой пришлось использовать соседнее помещение общественного катка в качестве раздевалки. — Хосе М. Ромеро, , Республика Аризона, , 28 октября 2022 г. Офицеры обнаружили, что вход в магазин был осуществлен через смежных пустых площадей здания по адресу 1408 Berlin Turnpike. —Майк Мавредакис, 9 лет.0077 Хартфорд Курант , 25 октября 2022 г. Узнать больше

Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «смежный». Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.

История слов

Этимология

Среднеанглийский, заимствованный из англо-французского agisaunt, adjesant, заимствованный из латинского смежный-, adjacens, причастие настоящего времени adjacēre «находиться рядом, граничить», от ad- ad- + jacēre «лгать», стативное производное от основы jacere «бросать» — подробнее при входе в самолет 3

Первое известное употребление

15 век, в значении, определенном в смысле 1a

Путешественник во времени

Первое известное использование рядом с было в 15 веке

Другие слова того же века эффект смежности

соседний

аджаг

Посмотреть другие записи поблизости

Процитировать эту запись «Соседний.

» Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/adjacent. По состоянию на 27 февраля 2023 г. прилагательное

соседний ə-ˈjās-ᵊnt 

1

: лежащий рядом или рядом : имеющий общую границу или точку

поле , прилегающее к дороге

2

: имеющее общую вершину или вершину и сторону

смежные углы

смежные стороны прямоугольника

смежные наречие

Еще от Merriam-Webster на

смежных

Английский: Перевод смежный для говорящих на испанском языке

Britannica English: перевод смежный для говорящих на арабском языке

Последнее обновление: 20 фев 2023 — Обновлены примеры предложений

Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы!

Merriam-Webster без сокращений

эрзац

См. Определения и примеры »

Получайте ежедневно по электронной почте Слово дня!

---

Что появилось раньше?

• горячий прием или холодный прием ?

• горячий дубль холодный прием

Прослушайте слово и напечатайте его. Сколько вы можете получить правильно?

ПРОЙДИТЕ ТЕСТ

Сможете ли вы составить 12 слов из 7 букв?

ИГРАТЬ

слов запрос — Как вы называете это соседнее положение?

спросил 2 года, 8 месяцев назад

Изменено 2 года, 7 месяцев назад

Просмотрено 2к раз

Допустим, вы находитесь в классе. Ты красный квадрат. Как назвать положение желтых мест по отношению к вам?

Я думал использовать «следующий», но я думаю, что это не относится к местам впереди и позади красного квадрата.

Я также думал об «окружении», но это включало бы зеленые квадраты по углам.

Пример предложения:

Одноклассник, который издевается над Марком, должен сидеть __

• слово-запрос
• фраза-запрос

1

Желтые квадраты «смежны» с красными квадратами.

Откуда: https://www.merriam-webster.com/dictionary/adjacent

Определение смежных 1a: недалеко : РЯДОМ с городом и прилегающими пригородами б: имеющие общую конечную точку или граничащие с соседними участками смежные стороны треугольника c: непосредственно предшествующий или следующий за

В данном случае подходящим определением является «b», «имеющий общую конечную точку или границу».

17

В данном конкретном случае я бы, наверное, сказал: «Одноклассник, который издевается над Марком, должно быть, сидит на одном из четырех соседних мест».

Выражение «четыре соседних места» делает предложение однозначным и позволяет избежать использования слова «ортогонально», которое является техническим термином, который, как я полагаю, должен знать каждый носитель языка.

0

Их ортогонально примыкает к красному квадрату .

Зеленые квадраты по углам красного квадрата — это смежные по диагонали .

https://english.stackexchange.com/questions/164704/is-there-one-word-for-both-horizontal-or-vertical-but-not-diagonal-adjacency/164759

Если вы хотите быть очень общие и вызывают последующий шквал уточняющих вопросов от вашей предполагаемой аудитории о включении диагонально смежных квадратов, вы могли бы сказать, что они границы или примыкают к красному квадрату.

5

Вы можете использовать несколько слов, включая:

• смежный
• вокруг
Я бы предпочел

Смежный — обратите внимание, что это слово имеет более конкретное значение в математике, но в английской грамматике может означать «рядом с» в в любом направлении , в том числе в стороны, спереди или сзади. Само по себе «рядом с» имеет тенденцию означать слева или справа.

Ваше предложение «окружить» звучит не совсем правильно, так как рисунок стульев на вашем изображении не является кругом, а именно это и означает — образовывать круг вокруг. «Окружающий» является синонимом «окружающего», но конкретно не означает форму круга.

2

«Одно место от Марка» также обозначает места с каждой стороны, спереди и сзади. Это не исключает диагонально смежные сиденья.

Еще никто не говорил об этом, так что я скажу.

Нет ничего плохого в «следующем».

 Одноклассник, который издевается над Марком, должно быть, сидит рядом с ним.
 

Это совершенно нормальный, приемлемый, повседневный английский язык, который будет прекрасно понят и совсем не покажется неловким или странным. Это прекрасно применимо как к сиденьям впереди и сзади, так и к сиденьям по бокам. Без рисунка говорящий также может считать четыре угловых стола «соседними» по отношению к центральному, но это не так важно.

Я думаю, что остальные ответы делают это намного сложнее, чем нужно.

4

Немедленно

Можно сказать, что эти позиции непосредственно окружают центральную точку

Если мы посмотрим на определения «Немедленно», мы увидим:

Отсутствие промежуточного объекта или пространства; ближайший или следующий

и

Имеющие прямую опору

Это становится более ясным, если мы удалим пространство между объектами на изображении.