Средняя линия треугольника. Свойства средней линии треугольника.
- Альфашкола
- Статьи
- Средняя линия треугольника
Определение
\(AM = MC ; BN = NC =>\)
\(MN || AB\)
\(MN = \frac{AB }{ 2}\)
Теорема. Свойства средней линии треугольника.
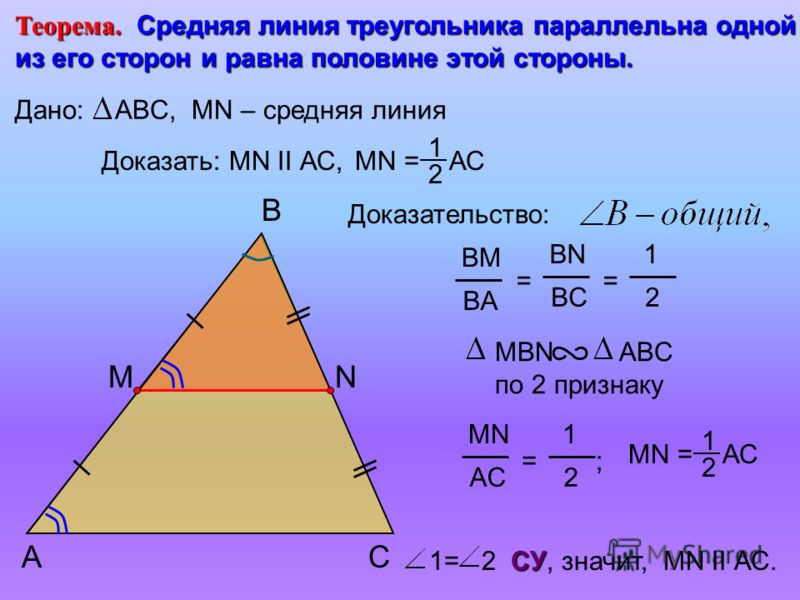
Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине:
\(MN\parallel AC;\)
\(MN = \frac{1}{2}AC\)
Деление отрезка на равные части
Разделим данный отрезок \(AB\) на \(5\) равных частей.
Пусть \(p\)-произвольный луч с началом \(A\) и \(p\) не лежит на \(АВ\).
Нарисуем пять последовательно равных треугольников.
\(АА_1 = А_1А_2 = A_2A_3 = A_3A_4 = A_4A_5\)
Соединим \(A_5\) с \(B\) и нарисуем линии через \(A_4, A_3, A_2\) и \(A_1\), которые параллельны \(A_5B\). Они пересекают \(AB\) соответственно в точках \(B_4, B_3, B_2\) и \(B_1\). Эти точки делят отрезок \(AB\) на пять равных частей.
\(А_1B_1 ||А_2B_2 ||A_2B_2 || A_3B_3 ||A_4B_4 ||A_5B_5 ||A_6B_6\)
И \(AB_1 = B_1B_2 = B_2B_3 = B_3B_4 = B_4B_5=B_5B_6\)
Понятно, что если \(AB\) разделить на другое количество равных частей, то у нас получится тоже самое.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Анна Фёдоровна Ринкман
Репетитор по математике
Стаж (лет)
Образование:
Коми государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 1-4 классов и русскому языку 1-6 классов.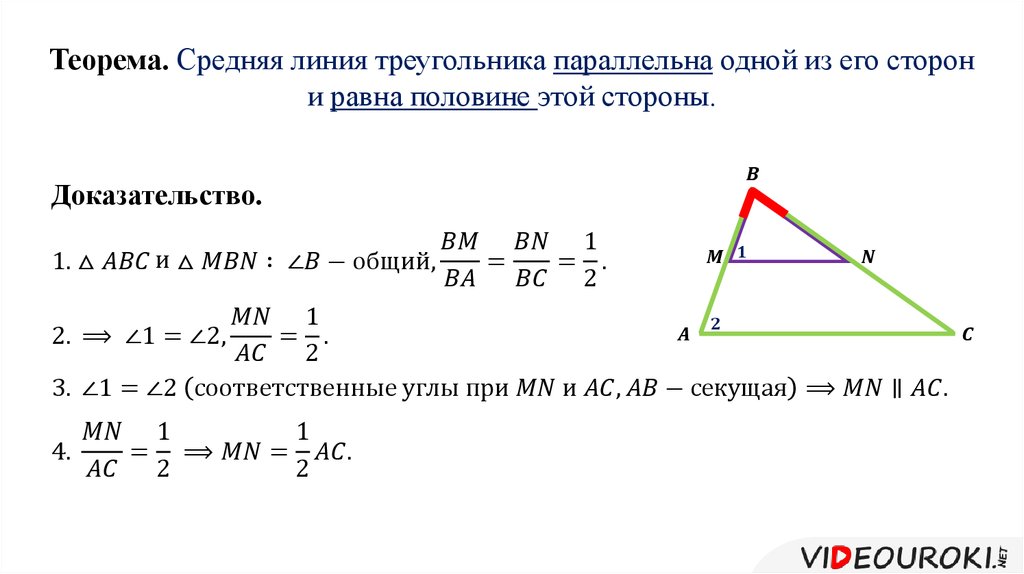
Помогаю дошкольникам и ученикам младшей школы легко и доступно понять учебный материал. Работала по программе Л. Г. Петерсон. Терпеливо и творчески нахожу подход к каждому ученику.
Сергей Николаевич Овчаренко
Репетитор по математике
Стаж (лет)
Образование:
Кубанский Государственный Университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов. Математика — это орудие, с помощью которого человек познает мир и покоряет его.
Зульашет Мовсуровна Гадаева
Репетитор по математике
Стаж (лет)
Образование:
Чеченский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по русскому языку для 5-9 классов. Подготовка к ОГЭ. РКИ.
Русский язык-красивый, богатый и мелодичный язык. У меня есть профильное образование + опыт работы + хорошие результаты учеников.
Похожие статьи
- Теорема Виета
- Декартова прямоугольная система координат, координаты точек
- Как легко разделить на 0,1; 0,01; 0,001
- Иррациональные уравнения: примеры с решениями
- ЕГЭ по математике, базовый уровень.
Планиметрия. Прямоугольный треугольник (вариант 1) - Решаем ОГЭ. Задание №16
- Безопасное лето: 9 способов защитить ребенка от паразитов
- Разнообразие детского рациона: разные источники белков, жиров и углеводов
Планиметрия. Прямоугольный треугольник (вариант 1)Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Презентация по геометрии Средняя линия треугольника (8 класс) доклад, проект
8 класс
Урок геометрии
Дан ∆ АВС, прямая XY параллельна прямой AC.
Доказать, что угол 1 равен углу 2.
Устная работа
Прямая АВ параллельна прямой CD, AD и BD секущие.
Доказать, что ∆ АОВ ~ ∆ DOС
C
D
A
B
O
Средняя линия треугольника
Тема урока:
ЦЕЛИ УРОКА:
дать определение средней линии треугольника,
доказать теорему о средней линии треугольника,
решать задачи, используя определение и свойство средней линии.
С
В
А
М
N
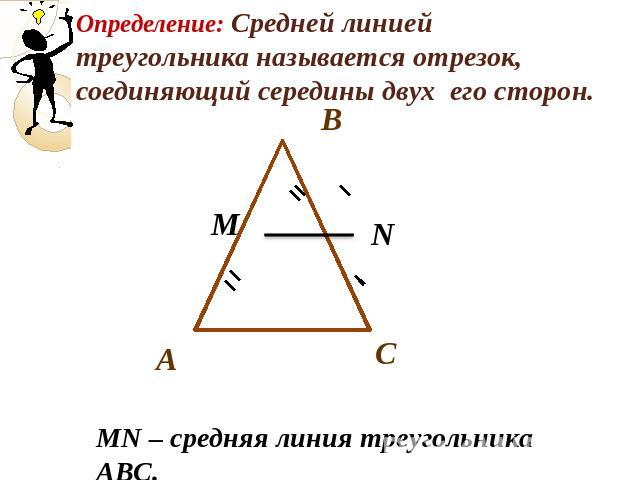
МN – средняя линия треугольника АВС.
Определение: Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
AM = MB
BN = NC
На каком рисунке изображена средняя линия треугольника ?
а)
г)
б)
в)
Устно:
г
Сколько средних линий имеет треугольник?
Задание.
Постройте произвольный треугольник и проведите в нем средние линии.
DF, DE, EF –средние линии ∆ АВС
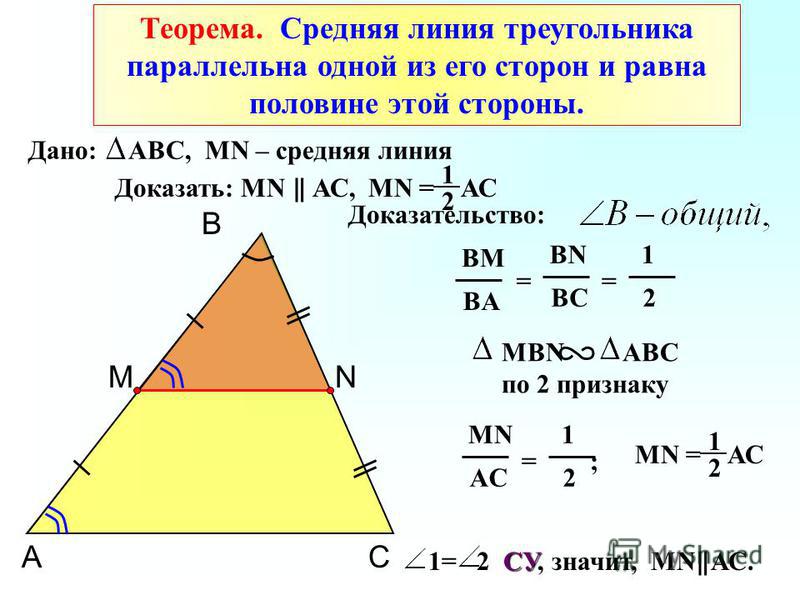
Теорема: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
С
В
А
М
N
Дано: ΔАВС, МN – средняя линия.
Доказать: МN || АС, МN =½ АС
Доказательство:
ΔАВС ~ ΔВМN,
т.к. ВМ:ВА = ВN:ВС=1:2 и угол В – общий.
2. Угол ВМN равен углу ВАС,
а они соответственные при прямых МN и АС и секущей АВ. Значит, МN || АС.
3. Т.к. ВМ:ВА =1:2, то и МN:АС=1:2.
Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины
1.
Сколько треугольников вы видите?
2. Есть ли равные треугольники? Почему?
Устно:
3. Сколько параллелограммов на рисунке?
∆ADF, ∆ DBE, ∆ ECF, ∆ DEF, ∆ ABC
∆ADF= ∆ DBE= ∆ ECF= ∆ DEF
ADEF, DBEF, ECFD
2) Задача
3,5
A
B
C
N
M
3
4
Дано: MN || AC.
Найти: Р∆АВС
1) п.62 (стр.146), № 565, 566
Домашнее задание:
Средняя линия треугольника. Свойство медианы треугольника
Цель : совершенствовать навыки решения задач на применение теоремы о средней линии треугольника и свойства медианы треугольника
1. Сколько треугольников вы видите?
2. Есть ли равные треугольники? Почему?
Устно:
3.
Сколько параллелограммов на рисунке?
∆ADF, ∆ DBE, ∆ ECF, ∆ DEF, ∆ ABC
∆ADF= ∆ DBE= ∆ ECF= ∆ DEF
ADEF, DBEF, ECFD
Являются ли отрезки EF и CD средними линиями ∆ АВС и ∆MNK?
EF является
CD не является
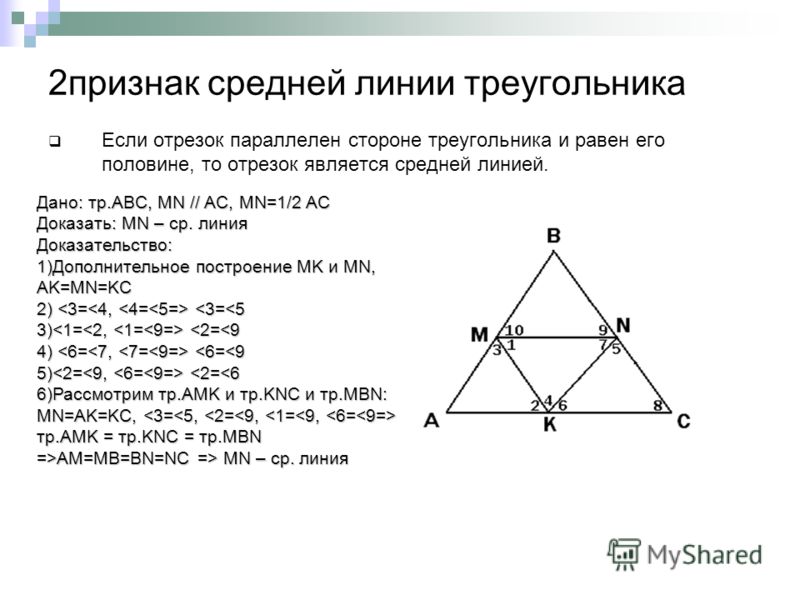
Отрезок MN является средней линией треугольника …
в)
Задача 1 ( ГИА 2013)
Средняя линия равностороннего треугольника АВС равна 8 см. Найти периметр этого треугольника.
А
В
С
Р ∆ АВС = 48 см
A
B
C
M
Дано: S∆ABC = 40 см²
Найти: SΔMNK
K
N
Задача 2
SΔ MNK =10 см²
Найти площадь треугольника, если высота, проведенная к одной из его сторон, равна 10, а средняя линия, параллельная этой стороне, равна 5.
Задача 3 ( ГИА 2013)
Н
SΔ АВС =50 см²
№567
А
В
С
D
М
N
P
Q
MNPQ –параллелограмм?
A
B
C
M
K
N
Какую часть от площади ∆АВС составляет площадь каждого из треугольников?
Какую часть от периметра ∆АВС составляет периметр каждого из треугольников?
Решите задачу:
О- точка пересечения диагоналей параллелограмма ABCD, Е и F – середины сторон АВ и CD , ОЕ=4 см, OF= 5 см. Найдите периметр ABCD.
Вычислите медианы треугольника со сторонами 25 см, 25 см, 14 см.
Решите задачи самостоятельно
ABCD-параллелограмм с периметром 28 см.
О- точка пересечения диагоналей. Найдите расстояние от середины CD, если расстояние от точки О до середины ВС равно 3 см.
Вычислите медианы треугольника со сторонами 25 см, 25 см, 14 см.
Какие новые знания получены на уроке?
Что называют средней линией треугольника?
Сформулируйте теорему о средней линии треугольника.
Подведем итог
2) Задача
3,5
A
B
C
N
M
3
4
Дано: MN || AC.
Найти: Р∆АВС
1) п.62 (стр.146), № 571, 564
Домашнее задание:
Моё настроение
Отличное!
Все понятно!
Непонятное!
Есть над чем подумать…
Спасибо за внимание!!!
Треугольник.
Медиана, биссектриса, высота, средняя линия.теория по математике 🎲 планиметрия
ОпределениеТреугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.
Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.
Виды треугольников по углам
Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.
| Остроугольные | Тупоугольные | Прямоугольные |
| Остроугольным треугольником называется треугольник, у которого все три угла острые. На рисунке показан такой остроугольный треугольник АВС. | Тупоугольным называется треугольник, у которого есть тупой угол. В треугольнике может быть только один тупой угол. На рисунке показан треугольник такого вида, где угол М – тупой. | Прямоугольным называется треугольник, у которого есть угол, равный 900 (прямой угол).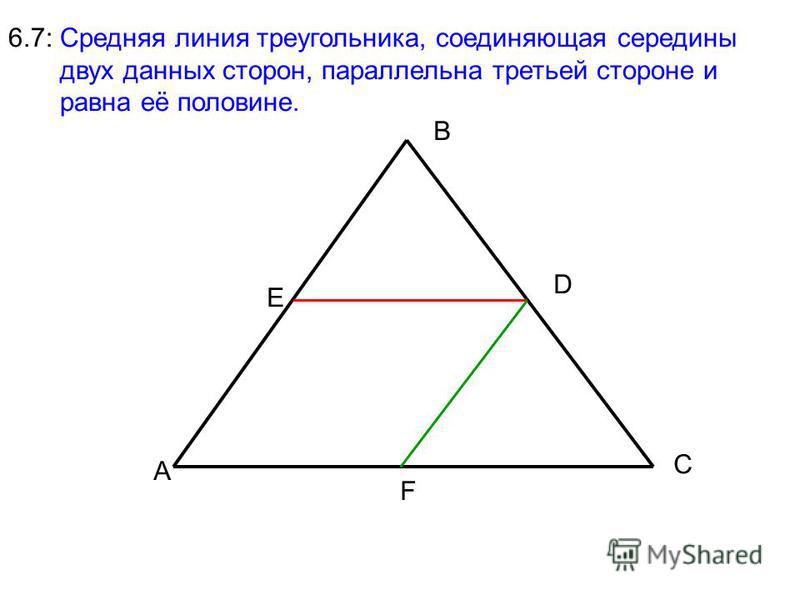 На рисунке угол С равен 900. Такой угол в любом прямоугольном треугольнике – единственный. |
Виды треугольников по сторонам
Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.
| Разносторонний | Равнобедренный | Равносторонний |
| Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС. | Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС. | Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС. |
Медиана
ОпределениеОтрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.
По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.
Биссектриса
ОпределениеБиссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.
В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD1, EE1 и CC1.
По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.
Высота
ОпределениеВысота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.
На рисунке показаны высоты треугольника АВС: АН1, ВН2 и СН3.
По рисунку видно, что высоты треугольника пересекаются в одной точке.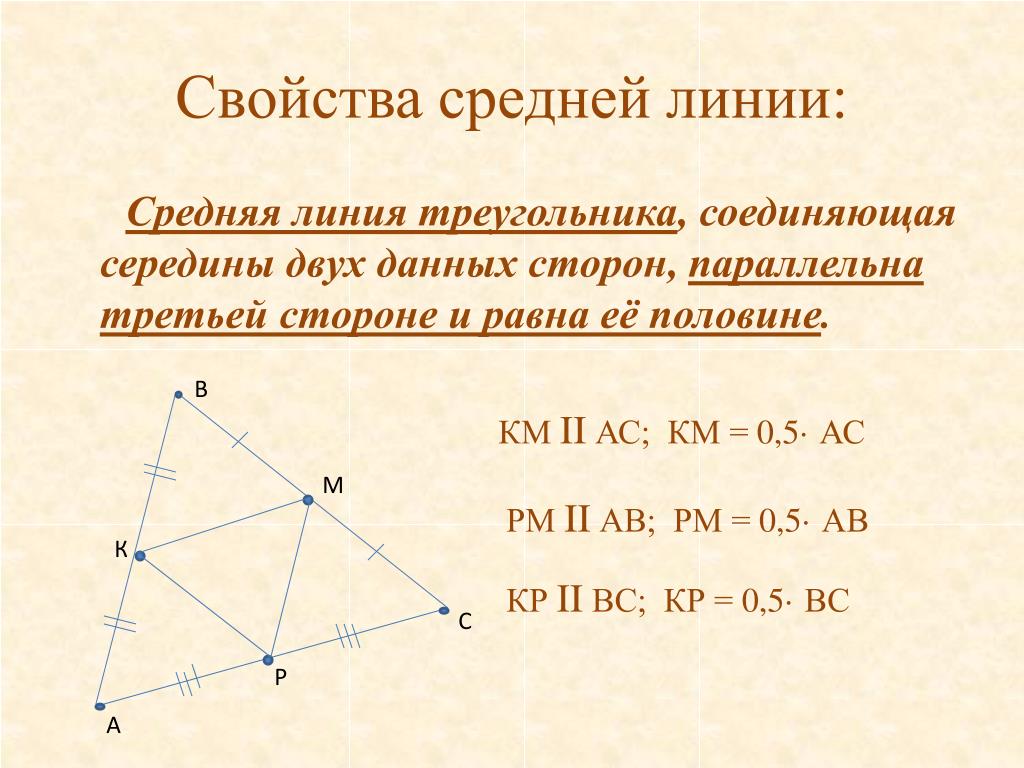
Это также справедливо для любого треугольника.
Средняя линия
ОпределениеСредней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.
Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.
Задание 25OM21R В треугольнике АВС известны длины сторон АВ=36, АС=54, точка О – центр окружности, описанной около треугольника АВС. Прямая ВD, перпендикулярная прямой АО, пересекает сторону АС в точке D.
Найдите СD.Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.
При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 900.
Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.
Составим отношение сторон:
AEAB..=ABAF.. откуда по свойству пропорции АВ2=АЕ∙АF
Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.
Составим отношение сторон:
AEAD..=ACAF.. ; откуда выразим AD=AE∙AFАC..=AE∙AFAC..
Теперь рассмотрим наши два полученных равенства: АВ2=АЕ∙АF и AD=AE∙AFAC..
Видим, что 362=АЕ∙АF (подставили вместо АВ значение 36), также у нас известно, что АС=54.
Найдем из второго равенства AD=AE∙AFAC..=36254..=24
Теперь найдем CD=AC-AD=54-24=30
Ответ: 30pазбирался: Даниил Романович | обсудить разбор | оценить
Задание 18OM21RНа клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.
Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
Ответ: 4pазбирался: Даниил Романович | обсудить разбор | оценить
Задание 15OM21RВ треугольнике АВС известно, что угол ВАС равен 840, АD – биссектриса. Найдите угол ВАD.
Ответ дайте в градусах.
Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 840:2=420
Ответ: 42pазбирался: Даниил Романович | обсудить разбор | оценить
Даниил Романович | Просмотров: 5.9k | Оценить:
Центроид треугольника — определение, различия, свойства, примеры
Центроид треугольника является точкой пересечения медиан треугольника. Прежде чем понять суть параллелизма, давайте обсудим медианы треугольника. Медианы — это отрезки, проведенные от вершины к середине противоположной стороны вершины. Каждая медиана треугольника делит треугольник на два меньших треугольника с равными площадями. Точка пересечения медиан треугольника называется 9.0003 центроид . Центроид всегда лежит внутри треугольника, в отличие от других точек совпадения треугольника.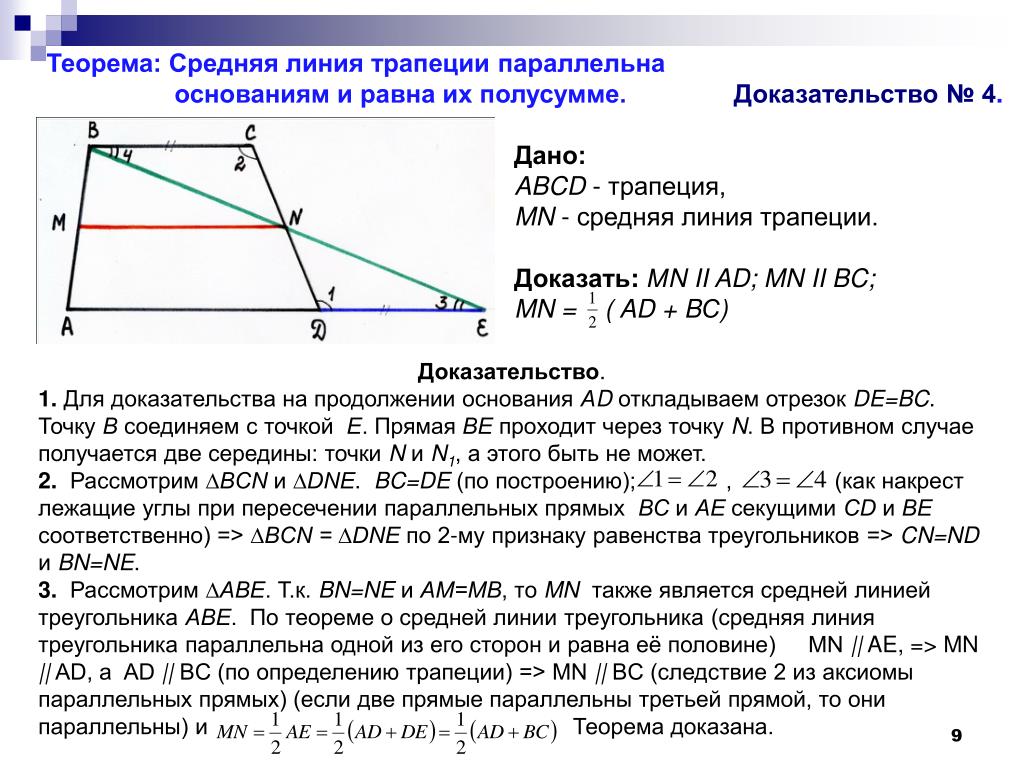
В этой статье мы рассмотрим понятие центроида треугольника, также обычно называемого центроидом, а также его формулу и свойства. Давайте узнаем больше о центроиде треугольника вместе с несколькими решенными примерами и практическими вопросами.
| 1. | Что такое центр тяжести треугольника? |
| 2. | Свойства центроида треугольника |
| 3. | Центроид треугольника Формула |
| 4. | Разница между ортоцентром и центроидом треугольника |
| 5. | Разница между центром и центром тяжести треугольника |
| 6. | Часто задаваемые вопросы о центроиде треугольника |
Что такое центроид треугольника?
Центр тяжести треугольника образуется при пересечении трех медиан треугольника. Это одна из четырех точек совпадения треугольника.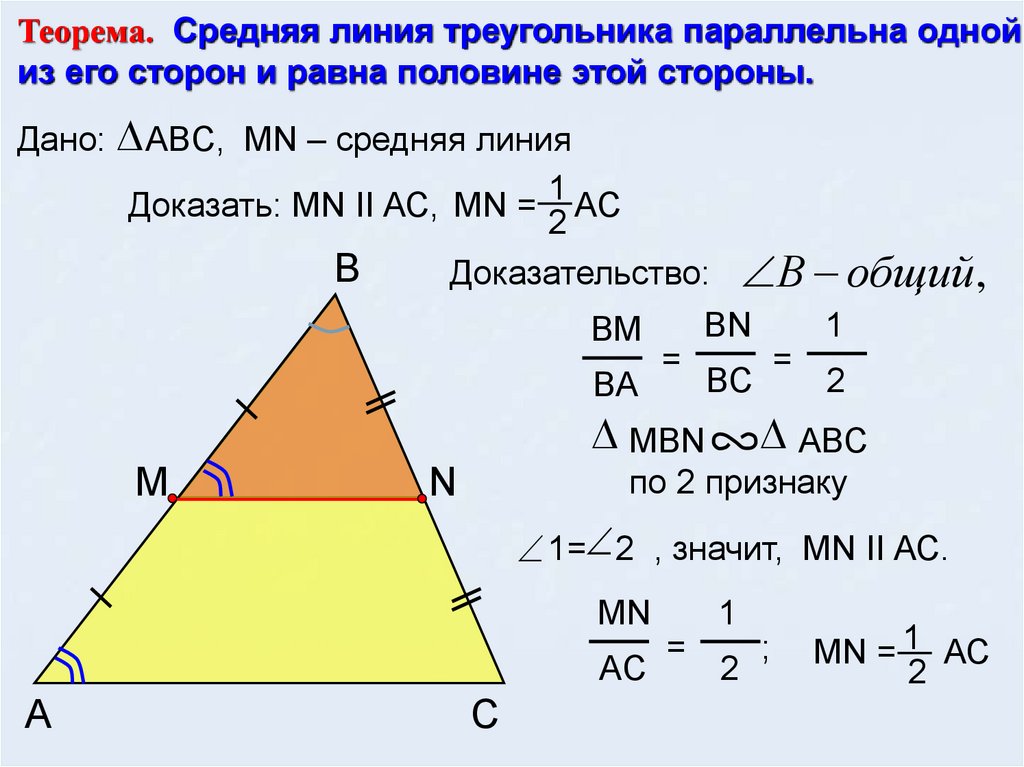
Медианы треугольника строятся при соединении вершин треугольника с серединами противоположных сторон треугольника. Обратите внимание на следующий рисунок, на котором показан центр тяжести треугольника.
Свойства центроида треугольника
Следующие точки показывают свойства центроида треугольника, которые очень помогают отличить центроид от всех других точек параллелизма.
- Центр тяжести также известен как геометрический центр объекта.
- Центроид треугольника — это точка пересечения всех трех медиан треугольника.
- Медианы делятся центроидом в соотношении 2:1.
- Центр тяжести треугольника всегда находится внутри треугольника.
Центроид формулы треугольника
Формула центра тяжести треугольника используется для нахождения центра тяжести треугольника с использованием координат вершин треугольника. Координаты центра тяжести треугольника можно вычислить, только если известны координаты вершин треугольника.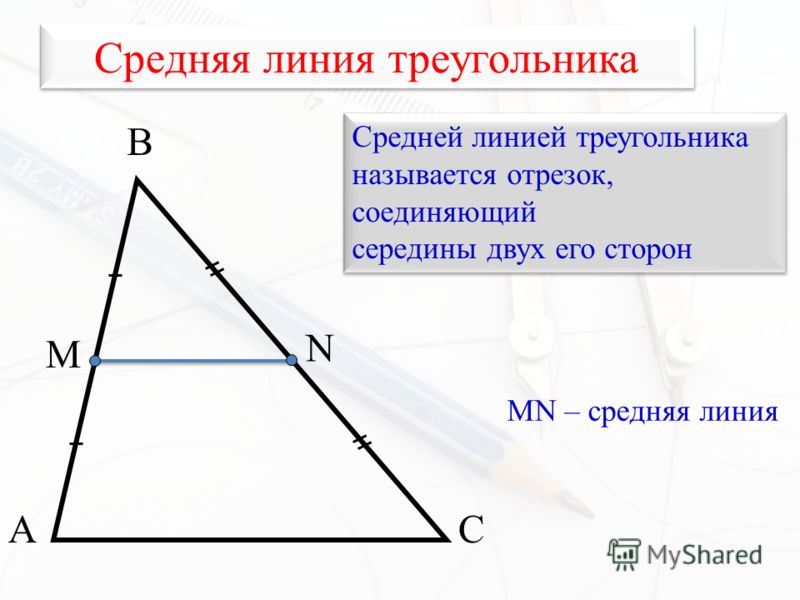
Формула для центра тяжести треугольника:
C(x,y) = (x 1 + x 2 + x 3 )/3, (y 1 + y 2 + y 3 )/3
где x 1 , x 2 и x 3 — координаты x вершин треугольника; а y 1 , y 2 и y 3 являются y-координатами вершин треугольника.
Обратите внимание на следующий рисунок, на котором вершины треугольника показаны в виде координат.
Разница между ортоцентром и центром тяжести треугольника
Существуют различные типы различий между ортоцентром и центром тяжести треугольника. Основные три различия между ортоцентром и центроидом треугольника объясняются в таблице ниже:
| Ортоцентр | Центроид |
|---|---|
| Ортоцентр — это точка пересечения высот. | Центроид — это точка пересечения медиан. |
| Может лежать вне треугольника | Всегда лежит внутри треугольника. |
| Не существует определенного отношения, на которое он делит высоты. | Медианы делятся центроидом в соотношении 2:1. |
Разница между центром и центром тяжести треугольника
Центроид и центр тяжести имеют различные типы различий между собой в зависимости от типа треугольника, в котором он находится. Важные различия между ортоцентром и центром тяжести треугольника объясняются в таблице, приведенной ниже:
| Инцентр | Центроид |
|---|---|
| Центр вписанной точки — это точка пересечения биссектрис угла. | Центроид — это точка пересечения медиан. |
| Всегда лежит внутри треугольника. | Всегда лежит внутри треугольника. |
Не существует определенного соотношения, на которое делит биссектрисы угла. | Медианы делятся центроидом в соотношении 2:1. |
Важные замечания по центроиду треугольника
- Центроид треугольника — это точка пересечения медиан треугольника.
- Он всегда лежит внутри треугольника.
- Centroid делит медианы в соотношении 2:1.
Связанные статьи
- Точка параллелизма
- Циркумцентр
- Высота треугольника
Центр тяжести треугольника Примеры
Пример 1: Если координаты вершин треугольника заданы как (4,3), (6,5) и (5,4), найдите положение центра тяжести треугольника.
Решение:
Чтобы найти центр тяжести треугольника, заданы следующие параметры:
(x 1 , y 1 ) = (4, 3)
(x 2 , y 2 )= (6, 5)
(x 3 , y 3 ) = (5, 4)
Формула центра тяжести 9007 0002 треугольник = C(x,y) = ((x 1 + x 2 + x 3 )/3, (y 1 + y 2 + y 3 )/3)
= ((4 + 6 + 5)/3, (3 + 5 + 4)/3)
= (15/3, 12/3)
= (5, 4)
Ответ: центр тяжести треугольника (5 , 4).
Пример 2: Определите центр тяжести прямоугольного треугольника, используя формулу центроида, если вершины треугольника равны (0,5), (5,0) и (0,0).
Решение:
Чтобы найти центр тяжести треугольника, заданы следующие параметры: 2 ) = (5,0)
(х 3 , у 3 ) = (0,0)
Используя формулу центроида,
C(x,y) = ((x 1 + x 2 + x 3 )/3, (y 1 + y 2 + y 28 y 2
18 )/3)
= ((0 + 5 + 0)/3, (5 + 0 + 0)/3)
= (5/3 , 5/3)
Ответ: Центр тяжести треугольник равен (5/3, 5/3).
Пример 3: Вершины треугольника равны (1, 2), (h, −3) и (−4, k), а координаты центра треугольника равны (5, –1). Найдите значение h и k.
Решение: . x 3 , y 3 ) = (–4, k)
Используя формулу центроида треугольника, мы имеем
C(x,y) = ((x 1 + x 2 + x 3 )/3, (у 1 + у 2 + у 3 )/3)
⇒ (5, -1) = ((1 + h – 4)/3, (2 — 3) + k)/3)
⇒ (5, -1) = ( (-3 + h)/3, (-1 + k)/3 )
⇒ (h — 3)/3 = 5 и (k — 1)/3 = -1
⇒ h — 3 = 15 и k — 1 = -3
⇒ h = 18 и k = -2
Ответ: Значения h и k равны h = 18 и k = -2.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Забронировать бесплатный пробный урок
Практические вопросы по центроиду треугольника
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о центроиде треугольника
Что такое центр тяжести треугольника?
Центр тяжести треугольника образуется при пересечении трех медиан треугольника. Это одна из четырех точек совпадения треугольника.
Какая формула для центроида треугольника?
Формула, используемая для вычисления центра тяжести треугольника: C(x,y) = ((x 1 + х 2 + х 3 )/3, (у 1 + у 2 + у 3 )/3), где, х 1 , 0 2 9 0 8 , 0 2 9 0 8 , 0 2 9 0 8 , 1 0 2 9 0 8 x 3 — «х-координаты» вершин треугольника; а y 1 , y 2 и y 3 — координаты y вершин треугольника.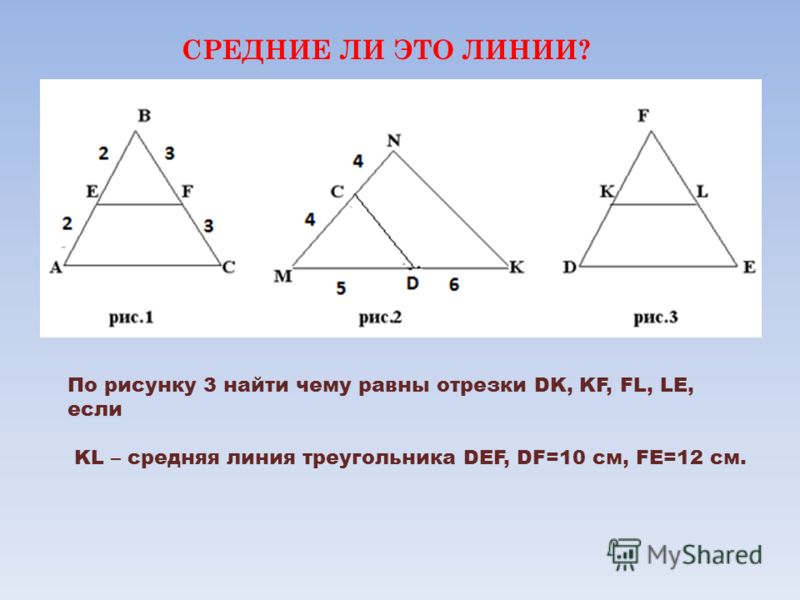
Каковы свойства центроида треугольника?
Центр тяжести треугольника образуется при пересечении трех медиан треугольника. Свойства центроида следующие:
- Центр тяжести также известен как геометрический центр объекта.
- Это точка пересечения всех трех медиан треугольника.
- Медианы делятся центроидом в соотношении 2:1.
- Центр тяжести треугольника всегда находится внутри треугольника.
Как проще всего найти центр тяжести треугольника?
Чтобы найти центр тяжести треугольника, нужно выполнить три основных шага:
- Определите и перечислите все три координаты каждой вершины.
- Сложите координаты x всех трех вершин и разделите сумму на 3.
- Сложите координаты y всех трех вершин и разделите сумму на 3.
Это будет центроид данного треугольника.
Где находится центроид любого заданного треугольника?
Центроид — это пересечение медиан треугольника.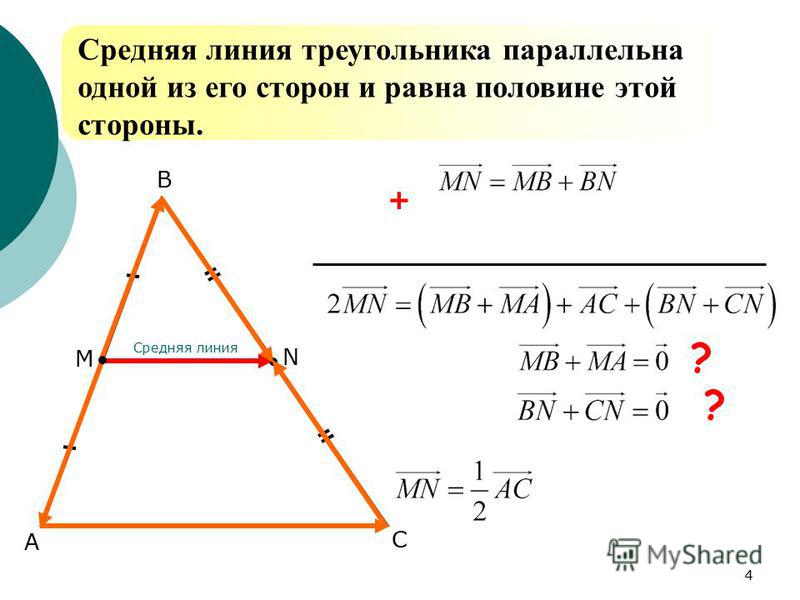
Если мы построим медианы треугольника, точка пересечения медиан будет центром тяжести треугольника. Он находится внутри треугольника.
Как найти центр тяжести треугольника, зная вершины?
Если нам известны вершины треугольника, мы используем следующую формулу для вычисления центра тяжести треугольника. Формула для центра тяжести треугольника:
C(x,y) = ((x 1 + x 2 + x 3 )/3, (y 1 + y 2 + y 3 )/3), где x 1 , x 2 и x 3 — «х-координаты» вершин треугольника; и у 1 , y 2 и y 3 — координаты y вершин треугольника.
Как найти центр тяжести треугольника?
Мы можем построить медианы треугольника и отметить точку их пересечения как центроид или мы можем использовать формулу, чтобы найти центр тяжести треугольника.
Какая связь между ортоцентром, центром окружности и центроидом треугольника?
Ортоцентр, центр описанной окружности и центроид всегда лежат на прямой линии, известной как линия Эйлера.
Центроид всегда находится между ортоцентром и центром описанной окружности треугольника. В равностороннем треугольнике ортоцентр, центр описанной окружности и центр тяжести лежат в одной и той же точке внутри треугольника. Для тупоугольного треугольника ортоцентр и центр описанной окружности лежат вне треугольника, а центр тяжести лежит внутри треугольника.
Центры треугольников
Центры треугольниковТреугольные центры
Кристина Данбар, UGA
В этом задании мы будем исследовать 4 различных центра треугольника: центроид, окружной центр, ортоцентр и инцентр.
ЦЕНТРОИД
Центроид треугольника построен по
Взяв любой заданный треугольник и соединив середины каждого
катет треугольника в противоположную вершину. Сегмент линии
образованная соединением этих точек, называется медианой.
Вы видите три медианы в виде пунктирных линий на рисунке ниже.
Какой бы формы ни был ваш треугольник, центроид всегда будет внутри треугольника. Ты можете посмотреть приведенный выше пример остроугольного треугольника или приведенный ниже примеры тупоугольного треугольника и прямоугольного треугольника, чтобы убедиться, что В этом случае.
Центроид является центром треугольника это можно представить как центр масс . Это это точка балансировки, которую следует использовать, если вы хотите сбалансировать треугольник на кончике карандаша, например.
Если у вас есть блокнот геометра и вы хотите хотите увидеть построение GSP центроида, нажмите здесь, чтобы скачать это.
ОКРУЖНОЙ ЦЕНТР
Центр описанной окружности является центром окружности
так что все три вершины окружности находятся на одинаковом расстоянии
вдали от центра окружности.
Таким образом, центр описанной окружности
точка, образующая начало окружности, в которой все три вершины
треугольника лежат на окружности. Таким образом, радиус
Окружность — это расстояние между центром описанной окружности и любой из
три вершины треугольника. Его можно найти, найдя середину
каждой стороны треугольника и построить прямую, перпендикулярную
к этой ноге в ее середине. Где пересекаются все три линии
является центром окружности.
Центр описанной окружности не всегда находится внутри треугольника. На самом деле он может быть вне треугольника, как в случае тупоугольный треугольник, или он может попасть в середину гипотенузы прямоугольного треугольника. Смотрите фотографии ниже для примеров этого.
Вы видите, что хотя центр описанной окружности вне треугольника в случае тупоугольного треугольника это равноудалены от всех трех вершин треугольника.
Если у вас есть блокнот геометра и вы хотите
хотите увидеть построение GSP центра окружности, нажмите
здесь
скачать его.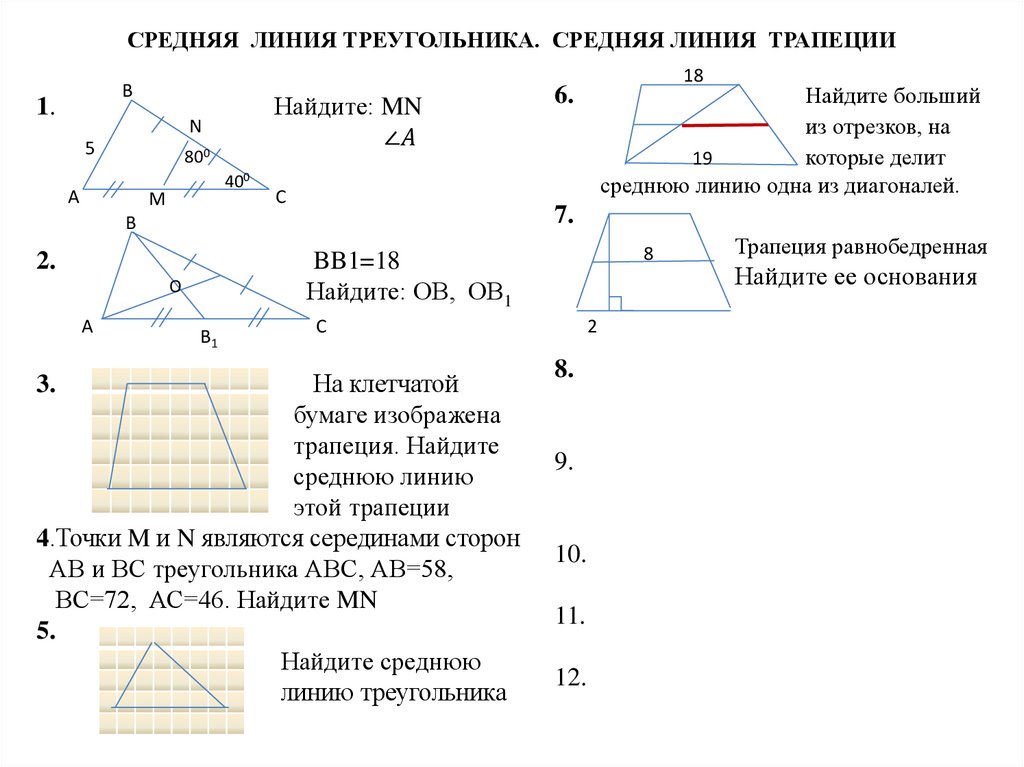
ОРТОЦЕНТР
Ортоцентр — это центр треугольника созданный из нахождения высот каждой стороны. Высота треугольника создается путем удаления линии из каждой вершины, которая перпендикулярна противоположной стороне. Высота над уровнем моря треугольник иногда называют высотой. Помните, высоты треугольника не проходят через середины катетов, если у вас есть особый треугольник, как равносторонний треугольник.
Как и центр описанной окружности, ортоцентр не должны быть внутри треугольника. Ознакомьтесь с кейсами тупоугольного и прямоугольного треугольников ниже. В тупоугольном треугольнике, ортоцентр выходит за пределы треугольника. В прямоугольном треугольнике ортоцентр приходится на вершину треугольника.
Если у вас есть блокнот геометра и вы хотите
хотите увидеть построение GSP ортоцентра, нажмите
здесь
скачать его.
ИНЦЕНТР
Incenter — это последний центр треугольника, который мы будет расследовать. Это точка, образующая начало окружности, вписанной внутрь треугольника. Как и центроид, центр всегда находится внутри треугольника. Он построен путем пересечения биссектрис трех углов вершины треугольника. Радиус окружности получается опустив перпендикуляр из центра вписанной стороны на любой из треугольников ноги. Ниже он показан красной пунктирной линией.
Чтобы увидеть, что инцентр на самом деле всегда внутри треугольника, давайте посмотрим на тупоугольный треугольник и прямоугольный треугольник.
Если у вас есть блокнот геометра и вы хотите
хотели бы увидеть строительство GSP инцентра, нажмите здесь, чтобы
скачать это.
Существует интересная связь между центр тяжести, ортоцентр и центр описанной окружности треугольника.
- Центр тяжести, ортоцентр и центр описанной окружности все падают по прямой.
- Центроид всегда находится между ортоцентром и центр окружности.
- Расстояние между центроидом и ортоцентр всегда в два раза больше расстояния между центроидом и центр окружности.
- В тупоугольных треугольниках центр описанной окружности всегда вне треугольника против наибольшего угла. Ортоцентр всегда находится вне треугольника, противоположного самому длинному нога, на той же стороне, что и наибольший угол.
- Единственный раз, когда все три этих центра
падение в том же месте в случае равностороннего треугольника.
На самом деле в этом случае центр инцентрации приходится на то же место, что и
Что ж.
Если у вас есть блокнот геометра и вы хотите хотели бы увидеть конструкции GSP всех четырех центров, нажмите здесь скачать его. В этом файле также есть все центры вместе на одной картинке, а также равносторонний треугольник. Это может быть использован для создания всех изображений выше.
ПЕРЕЙДИТЕ к Заданию 5: GSP Скрипты.
Разносторонний треугольник Определение — математика 7-го класса
Овладейте семью столпами школьной успеваемости
Улучшите свои оценки и снизьте стресс .
Двое детей катаются на лыжах за лодкой. У ребенка А есть веревка длиной 45 футов, а у ребенка В — веревка длиной 50 футов. Если они останутся на расстоянии 10 футов друг от друга, какой из следующих треугольников получится? Isosceles,Scalene,Equilateral
Плотники закладывают фундамент дома и используют старый прием.
Они создают треугольник, используя кусок пиломатериала длиной 3,4 и 5 футов. Эта комбинация создает угол 90 градусов для фундамента. Какой из следующих треугольников был создан? Равнобедренный, Равносторонний, Масштаб
Речевые задачи на разносторонний треугольник
* У разностороннего треугольника три стороны разной длины, что дает три угла с разными угловыми размерами.
*Как и у всех треугольников, сумма углов разностороннего треугольника составляет 180 градусов.
*Прямоугольный треугольник может быть разносторонним, но не равнобедренный, потому что у него две равные стороны.
*Вершина разностороннего треугольника — это точка, в которой две прямые пересекаются и образуют угол. Как и всякий треугольник, разносторонний имеет три вершины.
*Любая сторона разностороннего треугольника может быть основанием.
*A 30-60-90 прямоугольный треугольник – это разносторонний треугольник; однако 45-45-90 – нет.
*Разносторонние не имеют линии симметрии . Если вы можете сложить изображение или объект, и обе стороны точно совпадают, то вы можете провести «линию симметрии».
* Высота измеряется путем проведения перпендикулярной линии от основания до противоположной вершины.
*В зависимости от используемой базы может быть три разных высоты.
*Три высоты разностороннего треугольника пересекаются в точке, называемой ортоцентром.
ортоцентр
Ах, разносторонний треугольник
Расшифровка Moo.Math
7
7 Сегодня мы говорим о разносторонних треугольниках. Разносторонний треугольник – это треугольник, у которого все три угла различны. Итак, давайте рассмотрим два примера. Я собираюсь отметить эти треугольники 3 дюйма, 4 дюйма и 5 дюймов. Все три стороны имеют разную длину. Вот этот треугольник помечен так, что все три стороны одинаковы.
Метка сбоку представляет собой равные длины. На самом деле это равносторонний треугольник. Теперь давайте посмотрим на разносторонний треугольник на основе углов. У вас есть угол сорок пять градусов, угол сорок пять градусов и угол девяносто градусов, а здесь у вас есть угол 60 градусов, угол 30 градусов и угол девяносто градусов. Итак, исходя из углов, какой из этих углов является разносторонним? Вот этот (обводит треугольник 60, 30, 90 градусов), потому что все три угла различны или все три стороны различны. В другом треугольнике эти два угла одинаковы, что означает, что эти две стороны одинаковы, поэтому этот треугольник на самом деле называется равнобедренным треугольником. Итак, давайте посмотрим на правила. Определение: все стороны имеют разную длину и все углы имеют разную меру. Итак, наши 3, 4, 5 — это наш пример. Надеюсь, это видео было полезным.
Разносторонний треугольник
Этот Разносторонний треугольник имеет три стороны разной длины
Прямоугольный треугольник может быть разносторонним треугольником
Этот разносторонний треугольник имеет три угла разных размеров, что создает три разные длины сторон.
Нахождение внешнего угла треугольника0002 30 60 90 Треугольники
Нахождение площади треугольника
Что такое разносторонний треугольник?
Площадь Славен -треугольника
Найдите площадь Скалуеновой треугольник Использование 1/2 Основание x Высота
Высота
. Любая сторона 70002 Высота
. . Однако, если задана высота, основание будет перпендикулярно высоте
Нахождение периметра скальенового треугольника
Высота Неизвестно
Если высота Неизвестно, вы можете использовать Формула цапеля
Высота Неизвестно
Найдите Perimeter of A
0
0
09. a +b+c
(Другими словами, просто добавьте длины всех трех сторон.)
Несимметричные треугольники в реальной жизни
Несимметричный треугольник
Ферма крыши
Разносторонние треугольники используются в строительстве, автомобильных рамах, велосипедных рамах, мостах и многих других областях.