Свойства высот треугольника. Ортоцентр — подготовка к ЕГЭ по Математике
Анна Малкова
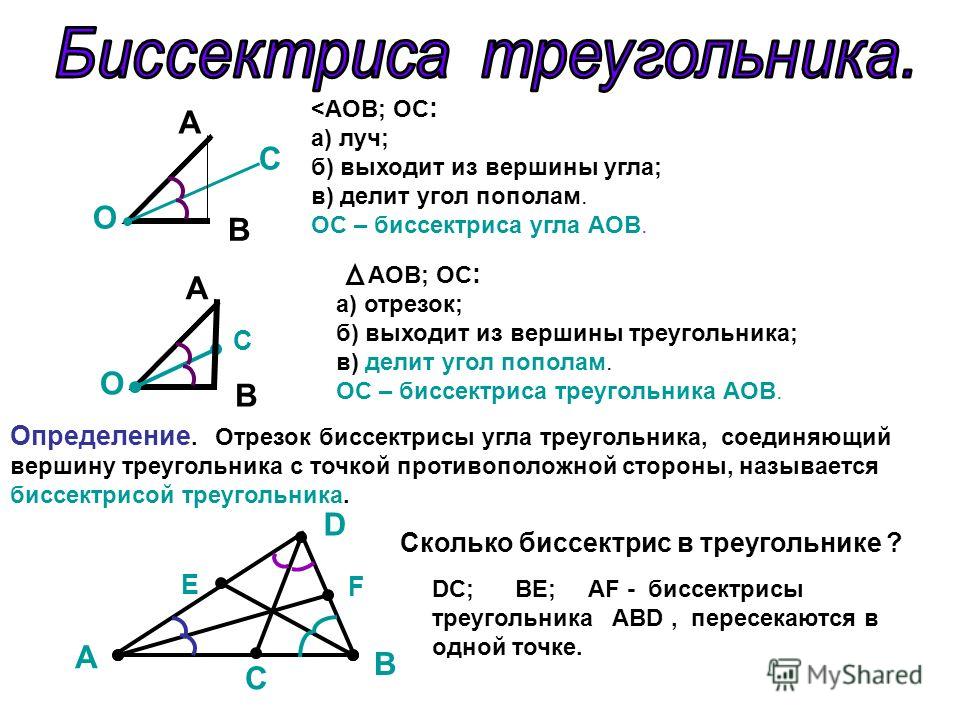
Схема 1. В треугольнике АВС проведены высоты АМ и СК.
Н – точка пересечения высот треугольника (ортоцентр), Н=АМ∩СК
Запомните этот рисунок. Перед вами – схема, из которой можно получить сразу несколько полезных фактов.
1. Треугольники МВК и △АВС, подобны, причем коэффициент подобия
, если , и , если
- Четырехугольник АКМС можно вписать в окружность. Эта вспомогательная окружность поможет решить множество задач.
- Четырехугольник ВКМН также можно вписать в окружность.
- Радиусы окружностей, описанных вокруг треугольников АВС, АНС, ВНС и АВН, равны.
- ,где R – радиус описанной окружности .
Докажем эти факты по порядку.
1) Заметим, что на рисунке есть подобные треугольники. Это АВМ и СВК, прямоугольные треугольники с общим углом В, и они подобны по двум углам
Мы получили, что в треугольниках МВК и АВС стороны, прилежащие к углу В, пропорциональны.
2) Докажем, что вокруг четырехугольника АКМС можно описать окружность. Для этого необходимо и достаточно, чтобы суммы противоположных углов четырехугольника АКМС были равны .
Пусть ∠ACB=∠BKM=γ (поскольку треугольники МВК и АВС подобны), тогда
– как смежный с углом ВКМ. Получили, что , и это значит, что четырехугольник AKMC можно вписать в окружность.
3) Рассмотрим четырехугольник KBMH. Его противоположные углы ВКН и ВМН — прямые, их сумма равна , и значит, четырехугольник КВМН можно вписать в окружность.
4) По теореме синусов, радиус окружности, описанной вокруг треугольника АВС,
Радиус окружности, описанной вокруг треугольника АНС,
Мы помним, что . Значит, синусы углов АВС и АНС равны, и радиусы окружностей, описанных вокруг треугольников АВС и АНС равны.
5) Докажем, что ,где R – радиус описанной окружности . Поскольку четырехугольник КВМН можно вписать в окружность и углы ВКН и ВМН – прямые, отрезок ВН является диаметром этой окружности.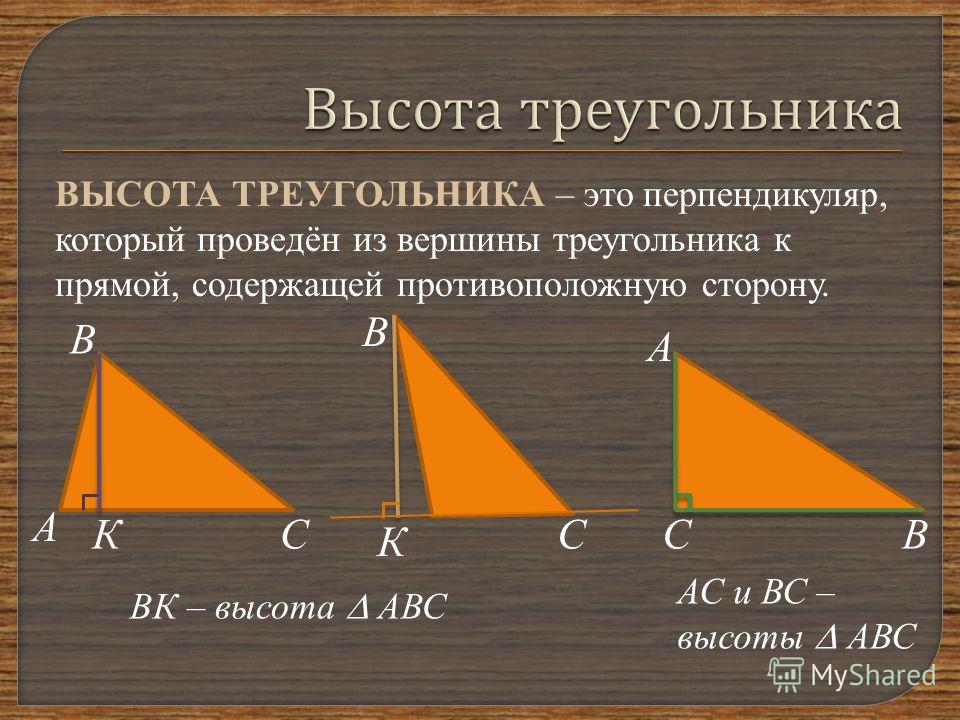
Диаметр окружности, описанной вокруг треугольника АВС, равен Поскольку треугольники МВК и АВС подобны, отношение диаметров описанных вокруг них окружностей равно . Получили, что
Задача ЕГЭ по теме «Высоты треугольника» (Профильный уровень, №16)
2. В остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и
а) Докажем, что
(по двум углам). Запишем отношение сходственных сторон:
Но это значит, что (по углу и двум сторонам), причем .
— смежный с углом ,
,
,четырехугольник ABNK можно вписать в окружность.
(опираются на одну дугу).
б) Найдем , если и
По теореме синусов,
Свойства высоты треугольника — справочник для студентов и школьников
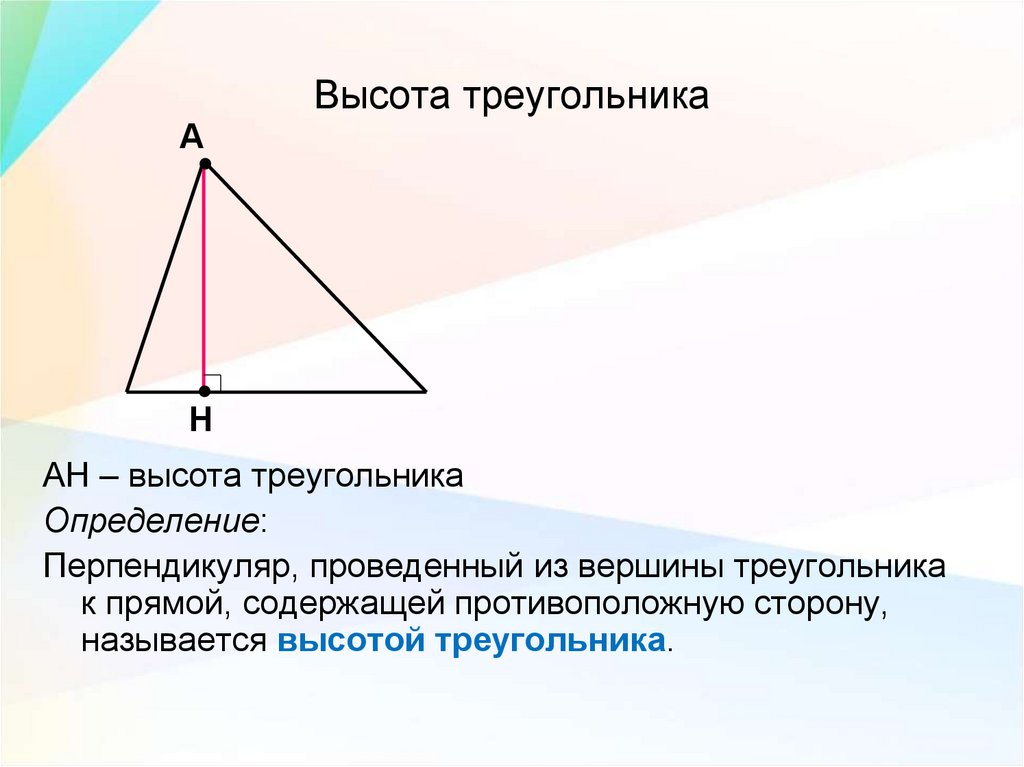
ОПРЕДЕЛЕНИЕ
Высота треугольника, взятого из заданной вершины, называется перпендикуляром, отброшенным от этой вершины к противоположной стороне или ее продолжению.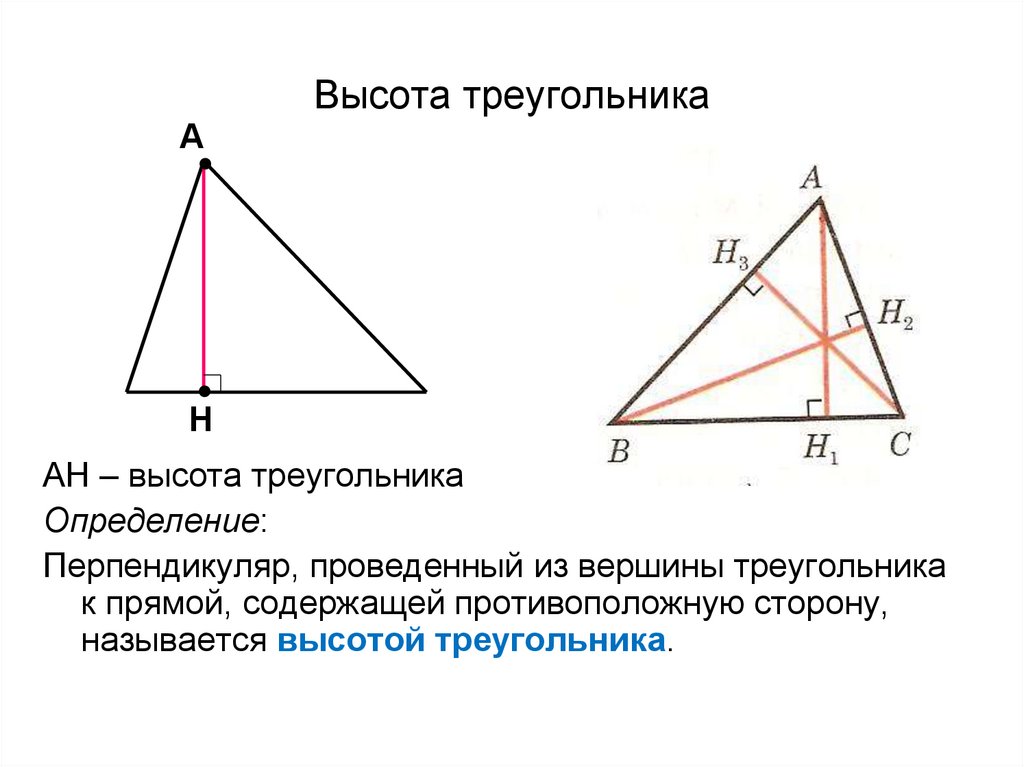
{2}}=\sqrt{117} \mathrm{см}
\)
Затем мы найдем область треугольника \(\ \mathrm{ABC} \):
\(\ S_{A B C}=\frac{1}{2} A B \cdot B C=\frac{2 \sqrt{13} \sqrt{117}}{2}=\sqrt{1521} \mathrm{см} \)
\(\ S_{A B C}=\sqrt{1521} \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Свойства медианы треугольника Свойства биссектрисы треугольника Свойства прямоугольного треугольника Свойства равностороннего треугольника
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПодпишись на рассылку, чтобы не пропустить информацию об акциях
2\).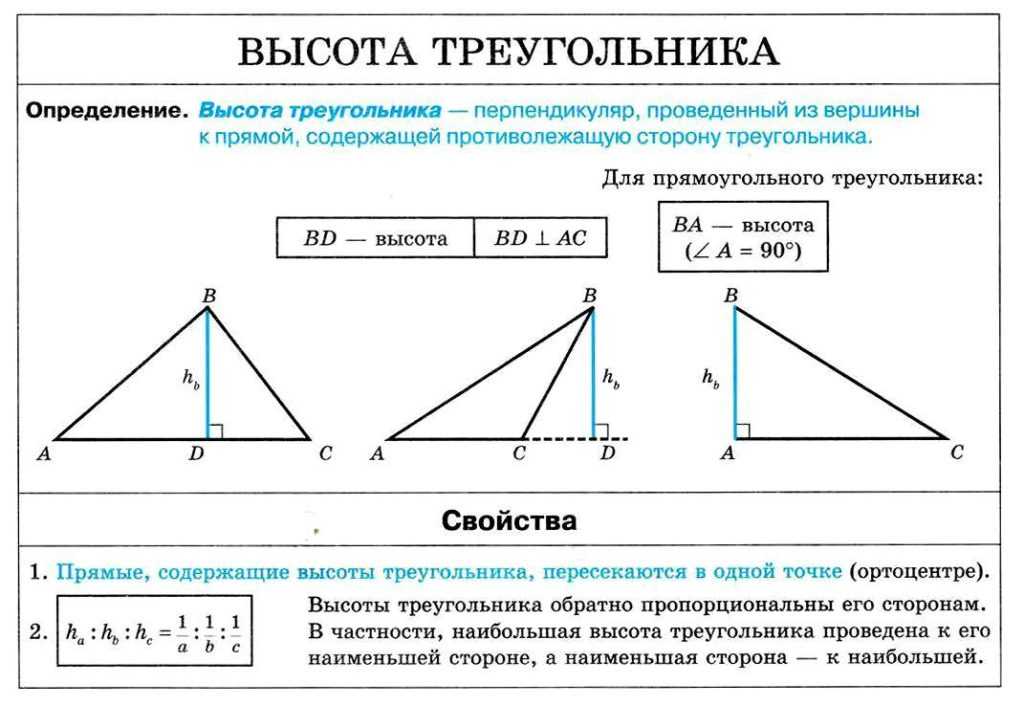
Предположим, вам нужно знать, как найти высоту треугольника △ABC по трем сторонам {6,7,8}.
Этот вопрос задают некоторые сдающие GMAT. Они знают, что им понадобится высота, чтобы найти площадь, поэтому они беспокоятся: как я найду эту высоту.
Короткий ответ: забудьте об этом!
Высота треугольника: какая высота?
Я не хочу быть легкомысленным. Просто, во-первых, «высота» треугольника — это его высота. Любой треугольник имеет три высоты, а значит, имеет три высоты! Сбивает с толку? Я знаю, извини.
Видите ли, любая сторона может быть базой. Из любой вершины можно провести линию, перпендикулярную противоположному основанию — это высота до этого основания.
Любой треугольник имеет три высоты и три основания.
Вы можете использовать любую пару высота-основание, чтобы найти площадь треугольника по формуле \(A= \frac{1}{2}bh\).
На каждой из диаграмм выше треугольник ABC одинаков.
Зеленая линия — это высота, «высота», а сторона с красным перпендикулярным квадратом на ней — это «база». Все три стороны треугольника получают поворот.
Нахождение высоты
Зная длины трех сторон треугольника, единственным способом найти высоту и площадь только по сторонам будет тригонометрия , что выходит далеко за рамки GMAT.
Вы НЕ несете 100% ответственности за знание того, как выполнять эти вычисления. Это несколько уровней продвинутого материала, помимо математики, которую вам нужно знать. Не беспокойтесь об этом.
На практике, если задача GMAT требует, чтобы вы вычислили площадь треугольника, им пришлось бы
Единственным исключением будет прямоугольный треугольник — в прямоугольном треугольнике, если один из катетов — это основание, а другой — высота, высота, поэтому найти площадь прямоугольных треугольников особенно легко.
Что нужно знать
Вам необходимо знать базовую геометрию.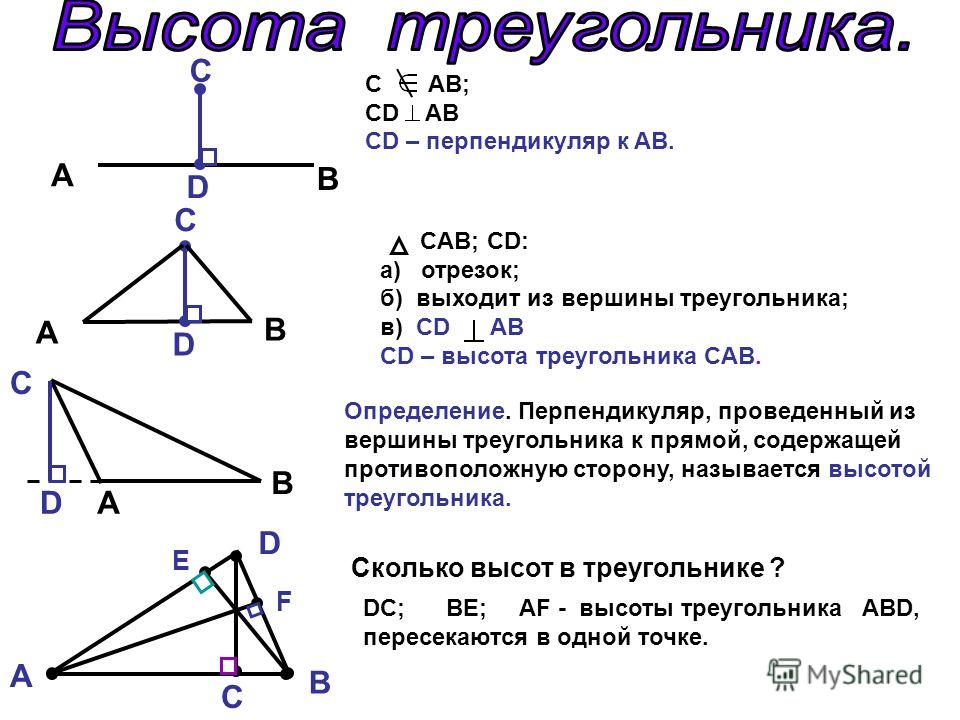
Да, помимо этого есть масса математических вычислений, и еще много чего вы могли бы знать о треугольниках и их свойствах, но вы ни за что из этого не несете ответственности. Вам просто нужно знать базовую геометрию треугольников, включая формулу:
Если треугольник не является прямоугольным, вы абсолютно не обязаны знать, как найти высоту — она всегда будет дана, если вам это нужно.
Вот вам бесплатный практический вопрос.
Две стороны треугольника имеют длину 6 и 8. Какие из следующих возможных площадей треугольника?
2
12
24
Щелкните здесь, чтобы получить ответ и видео-объяснение!
Некоторые предостережения «больше, чем вам нужно знать»
- Если вы не хотите знать по этой теме ничего, что вам абсолютно не нужно для GMAT, пропустите этот раздел !
- Технически, если вы знаете три стороны треугольника, вы можете найти площадь по так называемой формуле Герона, но это больше, чем ожидает от вас GMAT.
- Если один из углов треугольника тупой, то высоты до любого основания, примыкающего к этому тупому углу, лежат вне треугольника.
- Супертехнически, высота — это не отрезок, проходящий через вершину, перпендикулярную противоположному основанию, а отрезок, проходящий через вершину, перпендикулярную линии, содержащей противоположное основание.
На диаграмме выше в треугольнике △DEF одна из трех высот DG, которая идет от вершины D до бесконечной прямой линии, содержащей сторону EF. Это формальность, которую GMAT не проверяет и не ожидает от вас.
Если все три стороны треугольника — приятные положительные целые числа, то, по всей вероятности, фактическое математическое значение высот будет безобразным десятичным числом.
Многие источники подготовки к GMAT и преподаватели в целом замалчивают это, а для облегчения решения задач дают вам хорошее положительное целое число и для высоты над уровнем моря.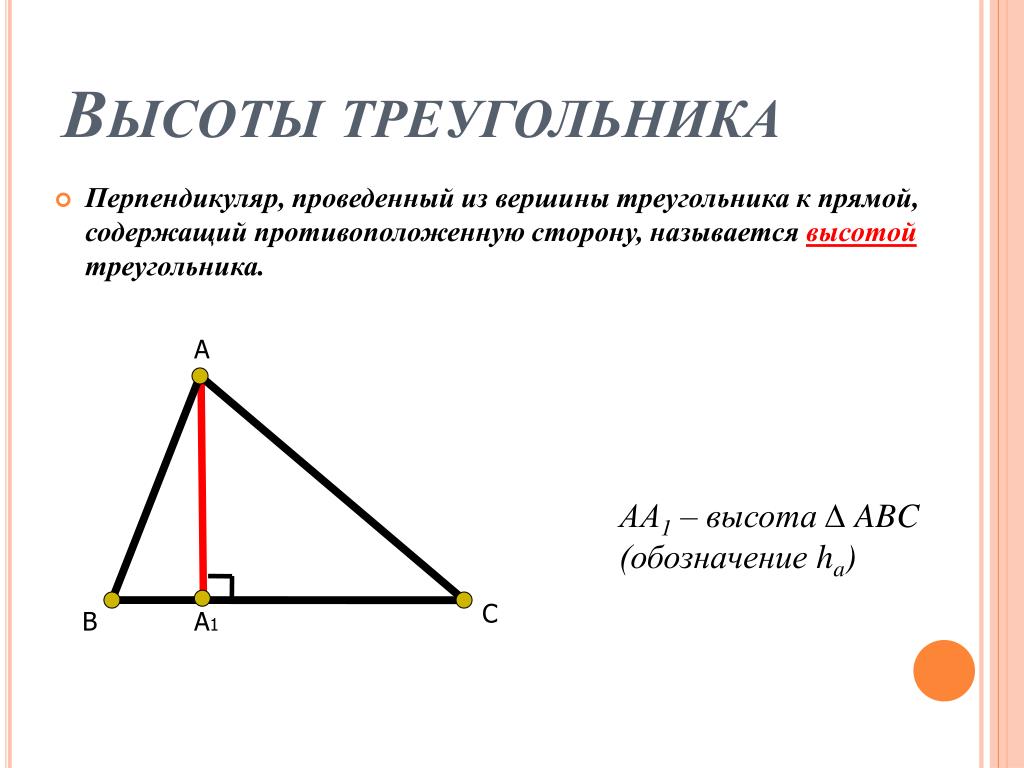
Помните этот треугольник △ABC сверху?
Например, реальное значение высоты от C до AB в треугольнике 6-7-8 равно:
Мало того, что вы 100% НЕ ожидаете, что знает, как найти это число, но и большинство составителей практических вопросов GMAT избавят вас от уродливых подробностей и просто скажут, например, высота = 5.
Это позволяет очень легко вычислить площадь.
Да, технически это ложь во спасение, но она избавляет бедных студентов от кучи уродливой десятичной математики, которой им не нужно заниматься.
На самом деле учителя математики всех уровней делают это постоянно — маленькая белая математическая ложь, чтобы избавить учеников от деталей, которые им знать не нужно.
Насколько я могу судить, люди, которые пишут сам GMAT, являются сторонниками истины во всех ее проявлениях и даже не занимаются «упрощением вещей для студента» — чистой ложью.
Они, скорее всего, обойдут всю проблему, например, сделав все соответствующие длины переменными или что-то в этом роде.
Еда на вынос
Все еще со мной?
Вот что вам нужно знать о треугольниках в день экзамена GMAT:
- \(Площадь =\frac{1}{2}bh\)
- Вам нужно знать только высоту прямоугольных треугольников на GMAT
- Если это не прямоугольный треугольник, вам будет дана высота
- Знаешь все три угла и две стороны? Используйте теорему Пифагора
Если вам нравится больше бесплатных ресурсов (а кому нет?) или вам просто интересно, каким будет содержание теста GMAT, ознакомьтесь с нашим Полным руководством.
Вот это.
Если у вас есть какие-либо вопросы, дайте мне знать в комментариях ниже. И да, я прочитал каждую из них!
Автор
← Предыдущий
Следующий →
Как найти высоту треугольника
Обновлено 24 апреля 2017 г.
Автор Damon Verial
Размеры и характеристики варьируются от одного треугольника к другому, что затрудняет прямое вычисление высоты фигуры.
Студенты должны определить лучший способ найти высоту, основываясь на том, что они знают о треугольнике. Например, когда вы знаете углы треугольника, может помочь тригонометрия; когда вы знаете площадь, базовая алгебра дает высоту. Проанализируйте имеющуюся у вас информацию, прежде чем разрабатывать план игры по нахождению высоты треугольника.
Площадь истерия
Иногда вы знаете площадь и основание треугольника, но не знаете его высоту. В этом случае вы можете манипулировать уравнением площади треугольника, чтобы получить его высоту. Уравнение площади треугольника: A = (1/2) * b * h, где A — площадь, b — основание, а h — высота. Используя алгебру, вы можете получить только h: разделите обе части на b, а затем умножьте обе части на 2, чтобы получить h = 2A / b. Подставьте площадь и основание в это уравнение, чтобы найти высоту треугольника. Например, если ваш треугольник имеет площадь 36 и основание 92 = 16. Извлеките квадратный корень из обеих сторон, чтобы получить a = 4.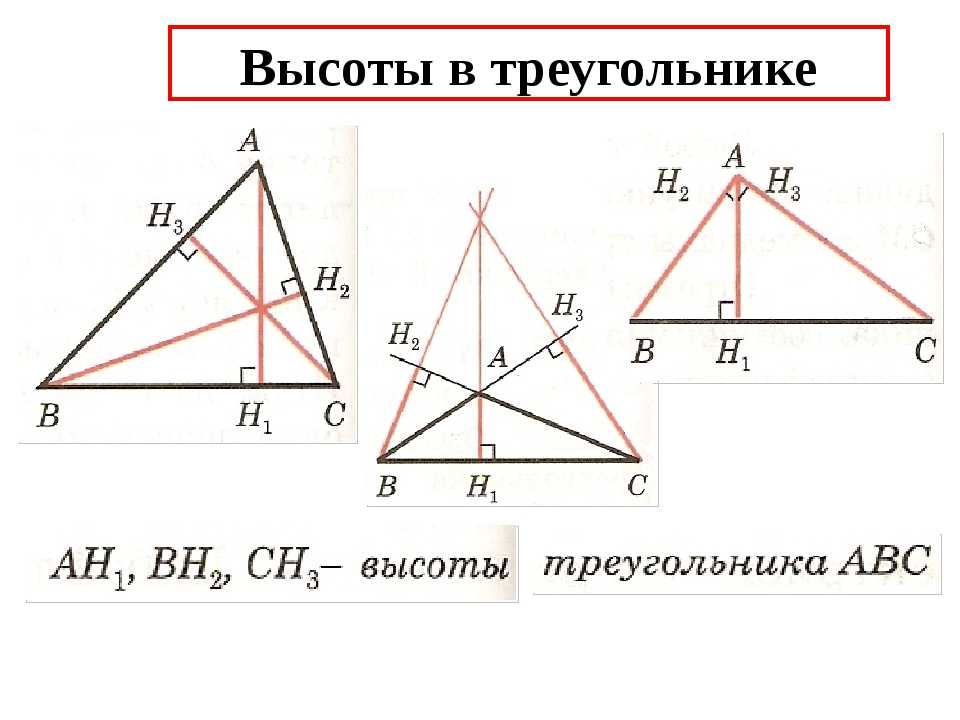
Высота свисает из угла
Поскольку вы можете нарисовать прямоугольный треугольник внутри любого треугольника, вы также можете использовать тригонометрические тождества, чтобы найти высоту треугольник. Если вы знаете угол между высотой и гипотенузой треугольника, вы можете составить уравнение tan(a) = x / b_, где a — угол, x — высота, а b_ — половина основания. Подставьте значения. Например, если ваш угол равен 30 градусам, а ваше основание равно 6, вы получите уравнение tan(30) = x/3. Решение для x дает x= 3 * tan(30). Поскольку тангенс угла 30 градусов равен sqrt(3)/3, уравнение упрощается и дает высоту x = sqrt(3).
Еще одна формула
Формула Герона позволяет найти высоту треугольника, сначала вычислив его половину периметра. Формула Герона гласит, что полупериметр треугольника равен сумме сторон треугольника, деленной на 2, или s = (a+b+c)/2, где a, b и c — стороны треугольника.