Определенный интеграл, примеры решений
Определенный интеграл от функции на промежутке обозначается и равен разности двух значений первообразной функции, вычисленных при и (формула Ньютона-Лейбница):
Геометрический смысл определенного интеграла. Определенный интеграл есть площадь криволинейной трапеции ограниченной графиком функции , осью и прямыми и (рис. 1), то есть
Для вычисления определенных интегралов подходят все методы, которые используются для нахождения неопределенных интегралов.
Примеры
ПРИМЕР 1| Задание | Вычислить интеграл
|
| Решение | Преобразуем подынтегральное выражение
Разобьем интеграл от суммы на сумму интегралов и вынесем за знак интеграла константы:
Полученные интегралы являются табличными, вычислим их:
|
| Ответ |
| Задание | Вычислить интеграл
|
| Решение | Вынесем константу за знак интеграла и вычислим полученный табличный интеграл:
|
| Ответ |
| Задание | Вычислить интеграл
|
| Решение | Сделаем замену , при этом пределы интегрирования изменятся: и . Подставляя все это в исходный интеграл, получим:
|
| Ответ |
| Задание | Вычислить интеграл
|
| Решение | Внесем под знак дифференциала, тогда
Подставляя все в исходный интеграл, получим:
|
| Ответ |
| Задание | Вычислить площадь криволинейной трапеции ограниченной функцией , осью и прямыми и . |
| Решение | Сделаем рисунок (рис. 2).
По геометрическому смыслу определенного интеграла нахождение площади заданной криволинейной трапеции сводится к вычислению интеграла
Вычислим этот интеграл: (кв. ед.) |
| Ответ |
Определённый интеграл и методы его вычисления
В каждой главе будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где 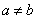 ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
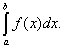
Как видно на графиках внизу (приращение первообразной функции обозначено 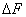 ), определённый
интеграл может быть как положительным, так и отрицательным числом
), определённый
интеграл может быть как положительным, так и отрицательным числом
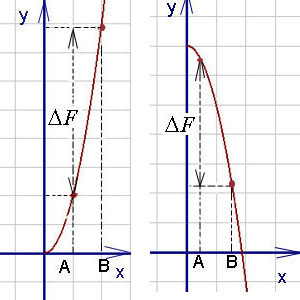
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,
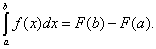 (38)
(38)
Равенство (38) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) кратко записывают так:
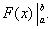
Поэтому формулу Ньютона-Лейбница будем записывать и так:
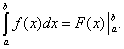 (39)
(39)
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Поэтому
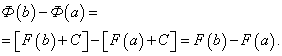
Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.
Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего предела b, далее — значение нижнего предела a и вычисляется разность F(b) — F(a). Полученное число и будет определённым интегралом..
При a = b по определению принимается
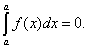
Пример 1. Вычислить определённый интеграл
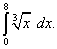
Решение. Сначала найдём неопределённый интеграл:
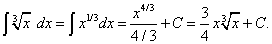
Применяя формулу Ньютона-Лейбница к первообразной
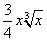
(при С = 0), получим
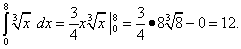
Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).
Пример 2. Вычислить определённый интеграл
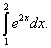
Решение. Используя формулу
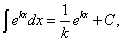
получим
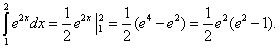
Найти определённый интеграл самостоятельно, а затем посмотреть решение
Теорема 1. Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е.
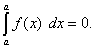
Это свойство содержится в самом определении определённого интеграла. Однако его можно получить и по формуле Ньютона-Лейбница:
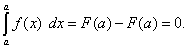
Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е.
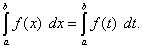 (40)
(40)
Пусть F(x) – первообразная для f(x). Для f(t) первообразной служит та же функция
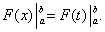
На основании формулы (39) последнее равенство означает равенство интегралов
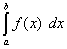
и
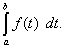
Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла, т.е.
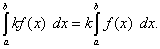 (41)
(41)
Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций
, т.е.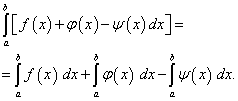 (42)
(42)
Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если
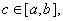
то
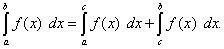 (43)
(43)
Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.
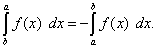 (44)
(44)
Теорема 7
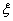 внутри его, т.е.
внутри его, т.е.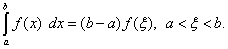 (45)
(45)
Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
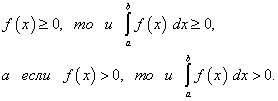
Теорема 9. Если верхний предел интегрирования больше нижнего и функции 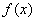 и
и 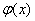 непрерывны, то неравенство
непрерывны, то неравенство
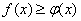
можно почленно интегрировать, т.е.
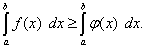 (46)
(46)
Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.
Пример 5. Вычислить определённый интеграл
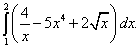
Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим
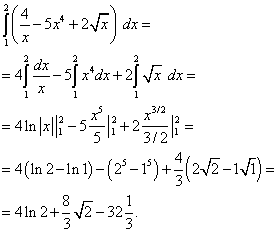
Пусть f(x) – непрерывная на отрезке [a, b] функция, а F(x) – её первообразная. Рассмотрим определённый интеграл
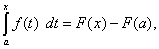 (47)
(47)
где
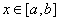 ,
,
а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х, которую обозначим через Ф(х), т.е.
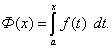 (48)
(48)
Докажем, что функция Ф(х) является первообразной для f(x) = f(t). Действительно, дифференцируя Ф(х), получим
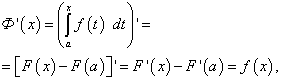
так как F(x) – первообразная для f(x), а F(a) – постояная величина.
Функция Ф(х) – одна из бесконечного множества первообразных для f(x), а именно та, которая при x = aобращается в нуль. Это утверждение получается, если в равенстве (48) положить x = aи воспользоваться теоремой 1 предыдущего параграфа.
При выводе формулы интегрирования по частям было получено равенство u dv = d (uv) – v du. Проинтегрировав его в пределах от a до b и учитывая теорему 4 параграфа этой статьи о свойствах определённого интеграла, получим
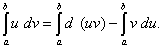
Как это следует из теоремы 2 параграфа о свойствах неопределённого интеграла, первый член в правой части равен разности значений произведения uv при верхнем и нижнем пределах интегрирования. Записав эту разность кратко в виде
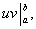
получаем формулу интегрирования по частям для вычисления определенного интеграла:
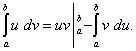 (49)
(49)
Пример 6. Вычислить определённый интеграл
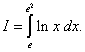
Решение. Интегрируем по частям, полагая u = ln x, dv = dx; тогда du = (1/x)dx, v = x. По формуле (49) находим

Найти определённый интеграл по частям самостоятельно, а затем посмотреть решение
Перейдём к вычислению определённого интеграла методом замены переменной. Пусть
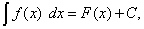
где, по определению, F(x) – первообразная для f(x). Если в подынтегральном выражении произвести замену переменной
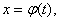
то в соответствии с формулой (16) можно записать
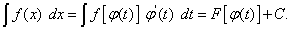
В этом выражении
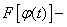
первообразная функция для
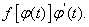
В самом деле, её производная, согласно правилу дифференцирования сложной функции, равна
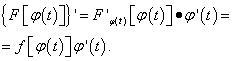
Пусть α и β – значения переменной t , при которых функция
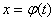
принимает соответственно значения aи b, т.е.
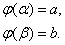
Тогда
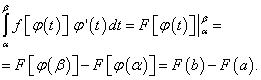
Но, согласно формуле Ньютона-Лейбница, разность F(b) – F(a) есть
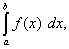
поскольку F(x) – первообразная для f(x).
Итак,
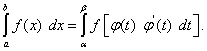 (50)
(50)
Это и есть формула перехода к новой переменной под знаком определённого интеграла. С её помощью определённый интеграл
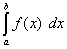
после замены переменной
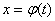
преобразуется в определённый интеграл относительно новой переменной t. При этом старые пределы интегрирования a и b заменяются новыми пределами 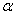 и
и 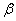 . Чтобы найти новые пределы, нужно в уравнение
. Чтобы найти новые пределы, нужно в уравнение
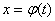
поставить значения x = aи x = b, т.е. решить уравнения
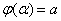
и
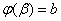
относительно 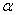 и
и 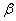 . После нахождения новых пределов интегрирования вычисление определённого интеграла сводится к применению формулы Ньютона-Лейбница к интегралу от новой переменной t. В первообразной функции, которая получается в результате нахождения интеграла, возвращаться к старой переменной нет необходимости.
. После нахождения новых пределов интегрирования вычисление определённого интеграла сводится к применению формулы Ньютона-Лейбница к интегралу от новой переменной t. В первообразной функции, которая получается в результате нахождения интеграла, возвращаться к старой переменной нет необходимости.
При вычислении определённого интеграла методом замены переменной часто бывает удобно выражать не старую переменную как функцию новой, а, наоборот, новую – как функцию старой.
Пример 9. Вычислить определённый интеграл
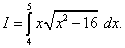
Решение. Произведём замену переменной, полагая
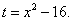
Тогда dt = 2x dx, откуда x dx = (1/2) dt, и подынтегральное выражение преобразуется так:
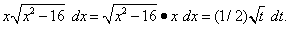
Найдём новые пределы интегрирования. Подстановка значений x = 4 и x = 5 в уравнение
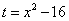
даёт
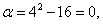
а
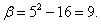
Используя теперь формулу (50), получим
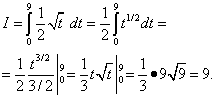
После замены переменной мы не возвращались к старой переменной, а применили формулу Ньютона-Лейбница к полученной первообразной.
Найти определённый интеграл заменой переменной самостоятельно, а затем посмотреть решение

Начало темы «Интеграл»
Продолжение темы «Интеграл»
Поделиться с друзьями
Определенный интеграл, теория и примеры
Например.
Детальный разбор понятия «Определенный интеграл»
Рассмотрим функцию , определенную и непрерывную на некотором отрезке . Выполним разбиение заданного отрезка с помощью точек на частичных отрезков , ,…, . На каждом частичном отрезке выберем произвольную точку и вычислим значение заданной функции в ней. Умножим полученное значение на длину соответствующего частичного отрезка: . Составим сумму всех таких произведений:
Такая сумма называется интегральной суммой функции на отрезке .
Пусть – длина наибольшего частичного отрезка: . Если предел интегральной суммы , когда максимальный диаметр разбиения , не зависит ни от способа разбиения отрезка на частичные отрезки, ни от выбора точек в них, то число называется определенным интегралом от заданной функции на отрезке и обозначается , то есть
Здесь числа и называются соответственно верхним и нижним пределами интегрирования; – подынтегральная функция; – подынтегральное выражение; – переменная интегрирования; – область или отрезок интегрирования.
Примеры решения задач
Функция называется интегрируемой на отрезке , если для нее на этом отрезке существует определенный интеграл .
| Понравился сайт? Расскажи друзьям! | |||
Определенный интеграл. Примеры решений — Мегаобучалка
Для того, чтобы научиться решать определенные интегралы необходимо:
1) Уметь находить соответствующие неопределенные интегралы.
2) Уметь вычислить определенный интеграл.
Как видите, для того, чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому, если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще не совсем закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений.
В общем виде определенный интеграл записывается так:
Что прибавилось по сравнению с неопределенным интегралом?
Прибавились пределы интегрирования.
Нижний предел интегрирования стандартно обозначается буквой a.
Верхний предел интегрирования стандартно обозначается буквой b.
Отрезок [a; b] включает граничные точки и называется отрезком интегрирования.
Что такое определенный интеграл? Можно посмотреть в учебниках про диаметр разбиения отрезка, предел интегральных сумм и т. д., но урок носит практический характер. Поэтому скажем, что определенный интеграл – это, прежде всего, самое что ни на есть обычное ЧИСЛО.
Есть ли у определенного интеграла геометрический смысл?Есть. И очень хороший. Самая популярная задача вычисления определённого интеграла – вычисление площади с помощью определенного интеграла.
Что значит решить определенный интеграл?Решить определенный интеграл – это значит, найти число, равное приращению первообразной функции на отрезке [a; b].
Как решить определенный интеграл?С помощью знакомой со школы формулы Ньютона-Лейбница:
.
Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.
Этапы решения определенного интеграла следующие:
1) Сначала находим первообразную функцию F(X) (неопределенный интеграл). Обратите внимание, что константа C в определенном интеграле никогда не добавляется.
Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись
?
Это подготовка для применения формулы Ньютона-Лейбница.
2) Подставляем значение верхнего предела в первообразную функцию: F(b).
3) Подставляем значение нижнего предела в первообразную функцию: F(a).
4) Рассчитываем (без ошибок!) разность F(b)-F(a), то есть, находим число, равное приращению первообразной (от подынтегральной) функции на отрезке [a; b].
Готово.
Всегда ли существует определенный интеграл? Нет, не всегда существует всё, что мы напишем в виде определённого интеграла. Например, интеграла
не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции и значения под квадратным корнем не могут быть отрицательными. А вот менее очевидный пример:
.
Такого интеграла тоже не существует на всём отрезке [-2; 3], так как в точках
,
этого отрезка подынтегральная функция f(x) = tg(x) не существует.
Для того, чтобы определенный интеграл существовал на данном отрезке, необходимо, чтобы подынтегральная функция была непрерывной на отрезке интегрирования.
Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования. Бывает так, что подолгу мучаешься с нахождением трудной первообразной, а когда наконец-то ее находишь, то ещё и ломаешь голову над вопросом: «что за ерунда получилась?». Например, если получилось примерно так:
???!!!
то нельзя подставлять отрицательные числа под корень! Если для решения в контрольной работе, на зачете или экзамене Вам предложен несуществующий интеграл вроде
,
то нужно дать ответ, что интеграла не существует и обосновать – почему.
Может ли определенный интеграл быть равен отрицательному числу?Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл, коим отведена отдельная лекция.
Может ли нижний предел интегрирования быть больше верхнего предела интегрирования?Может, и такая ситуация реально встречается на практике. Интеграл
преспокойно вычисляется по формуле Ньютона-Лейбница.
Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.
В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:
Например, в определенном интеграле перед интегрированием
целесообразно поменять пределы интегрирования на «привычный» порядок:
.
В таком виде интегрировать значительно удобнее.
Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:
Это справедливо не только для двух, но и для любого количества функций.
В определенном интеграле можно проводить замену переменной интегрирования, правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.
Для определенного интеграла справедлива формула интегрирования по частям: .
Пример 1
Вычислить определенный интеграл
.
Решение:
(1) Выносим константу за знак интеграла.
(2) Интегрируем по таблице с помощью самой популярной формулы
.
(3) Используем формулу Ньютона-Лейбница
.
Сначала подставляем в x3 верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.
Пример 2
Вычислить определенный интеграл
.
Это пример для самостоятельно решения, решение и ответ в конце урока.
Пример 3
Вычислить определенный интеграл
.
Решение:
.
(1) Используем свойства линейности определенного интеграла.
(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.
(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница.
СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряем на третьем слагаемом:
,
т. к. очень часто машинально пишут
.
Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, так:
.
Здесь устно использованы правила линейности, устно проинтегрированы табличные интегралы. Получилась всего одна скобка с отчёркиванием пределов:
(в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию мы сначала подставили 4, затем –2, опять же выполнив все действия в уме.
При втором способе существует повышенный риск допустить ошибку в вычислениях, поэтому студенту-чайнику лучше использовать первый способ, чтобы не терять знаки.
Несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная.
находится в одной скобке.
Исчисление I — Вычисление определенных интегралов
Онлайн-заметки ПавлаНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Проблемы с практикой
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Определение определенного интеграла
- Правило замещения для определенных интегралов
- Разделы
- Применение производных инструментов
- Приложения интегралов
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Алгебра и триггерный обзор
- Распространенные математические ошибки
- Праймер комплексных чисел
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Notes Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Полная книга — Только проблемы
- Полная книга — Решения
- Текущая глава — Только проблемы
- Текущая глава — Решения
- Текущий раздел — Только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузок
- Полная книга
- Текущая глава
- Текущий раздел
- Прочие товары
- Получить URL для загружаемых элементов
- Распечатать страницу в текущем виде (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- Алгебра
- Отборочные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- Полиномы
- Факторинговые многочлены
- Рациональные выражения
- Комплексные числа
- Решение уравнений и неравенств
- Отборочные
Определенные интегралы
Возможно, вам сначала захочется прочитать «Введение в интеграцию»!
Интеграция
Integration можно использовать для поиска областей, объемов, центральных точек и многих полезных вещей. Но его часто используют, чтобы найти область под графиком функции следующим образом: | ||
Область может быть найдена путем добавления срезов, ширина которых приближается к нулю : И есть Правила интеграции, которые помогают нам получить ответ. |
Обозначение
Символ «Интеграл» — стильная буква «S» (от «Сумма», идея суммирования срезов):
После символа интеграла мы помещаем функцию, интеграл которой мы хотим найти (называемую интегралом).А затем закончите с dx , чтобы обозначить, что срезы идут в направлении x (и приближаются к нулю по ширине).
Определенный интеграл
Определенный интеграл имеет начальное и конечное значения: другими словами, существует интервал [a, b].
a и b (называемые пределами, границами или границами) помещаются внизу и вверху буквы «S», например:
| Определенный Интегральный (от a до b ) | Неограниченный Интегральный (без конкретных значений) |
Мы находим Определенный интеграл, вычисляя неопределенный интеграл при a и b , затем вычитая:
Пример: что такое
Нам нужен определенный интеграл , от 1 до 2, из 2x dx
Сначала нам нужно найти Indefinite Integral .
Используя правила интегрирования, находим, что ∫2x dx = x 2 + C
Теперь посчитайте, что при 1 и 2:
- При x = 1: ∫2x dx = 1 2 + C
- При x = 2: ∫2x dx = 2 2 + C
Вычесть:
(2 2 + C) — (1 2 + C)
2 2 + К — 1 2 — К
4-1 + C — C = 3
И «C» отменяется… так что с определенными интегралами мы можем игнорировать C .
Результат:
Проверить : с такой простой формой попробуем еще вычислить площадь по геометрии:
А = 2 + 4 2 × 1 = 3
Да, у него есть площадь 3.
(Ура!)
Обозначение : Мы можем показать неопределенный интеграл (без + C) внутри квадратных скобок с пределами a и b после, например:
Пример (продолжение)
Хороший способ показать свой ответ:
Давайте попробуем другой пример:
Пример:
Определенный интеграл, от 0.От 5 до 1.0, из cos (x) dx:
(Примечание: x должен быть в радианах)
Неопределенный интеграл : ∫ cos (x) dx = sin (x) + C
Мы можем игнорировать C для определенных интегралов (как мы видели выше) и получаем:
= грех (1) — грех (0,5)
= 0,841 … — 0,479 …
= 0,362 …
И еще один важный пример:
Пример:
Определенный интеграл от 0 до 1 от sin (x) dx:
Неопределенный интеграл : ∫ sin (x) dx = −cos (x) + C
Поскольку мы начинаем с 0, можем ли мы просто вычислить интеграл при x = 1?
−cos (1) = −0.540 …
Что? Это минус ? Но на графике это выглядит положительно.
Ну … мы сделали ошибку !
Поскольку нам нужно вычесть интеграл при x = 0 . Не стоит предполагать, что он равен нулю.
Итак, давайте сделаем это правильно, вычтя одно из другого:
грех (x) dx
= [−cos (x)]= −cos (1) — (−cos (0))
= -0,540 … — (-1)
= 0.460 …
Так лучше!
Но у нас может быть отрицательные области , когда кривая ниже оси:
Пример:
Определенный интеграл от 1 до 3 от cos (x) dx:
Обратите внимание, что некоторые из них положительные, а некоторые отрицательные.
Определенный интеграл даст чистое значение .
Сделаем расчеты:
= грех (3) — грех (1)
= 0.141 … — 0,841 …
= −0,700 …
Таким образом, отрицательного больше, чем положительного, с чистым результатом -0,700 ….
Итак, нам нужно запомнить одну важную вещь:f (x) dx = (Площадь выше оси x) — (Площадь ниже оси x)
Попробуйте интегрировать cos (x) с разными начальными и конечными значениями, чтобы увидеть, как работают положительные и отрицательные значения.
Положительная область
Но иногда мы хотим, чтобы вся область обрабатывалась как положительное значение (без вычитания части ниже оси).
В этом случае мы должны вычислить площади отдельно , как в этом примере:
Пример: Какова общая площадь между y = cos (x) и осью x, от x = 1 до x = 3?
Это похоже на тот пример, который мы только что сделали, но теперь мы ожидаем, что вся площадь положительна (представьте, что нам нужно было это нарисовать).
Итак, теперь мы должны делать детали отдельно:
- Один для области над осью x
- Один для области ниже оси x
Кривая пересекает ось x при x = π / 2, поэтому мы имеем:
От 1 до π / 2:
cos (x) dx
= грех (π / 2) — грех (1)= 1 — 0.841 …
= 0,159 …
От π / 2 до 3:
cos (x) dx
= грех (3) — грех (π / 2)= 0,141 … — 1
= -0,859 …
Последний выходит отрицательным, но мы хотим, чтобы он был положительным, поэтому:
Общая площадь = 0,159 … + 0,859 … = 1,018 …
Это сильно отличается от ответа в предыдущем примере.
непрерывный
О да, функция, которую мы интегрируем, должна быть непрерывной между a и b : без дырок, скачков или вертикальных асимптот (где функция направлена вверх / вниз в сторону бесконечности).
Пример:
Вертикальная асимптота между a и b влияет на определенный интеграл.
Недвижимость
Область выше — область ниже
Интеграл добавляет площадь над осью, но вычитает площадь ниже, для «чистого значения»:
f (x) dx = (Площадь выше оси x) — (Площадь ниже оси x)
Добавление функций
Интеграл от f + g равен интегралу от f плюс интеграл от g :
f (x) + g (x) dx =
ф (х) dx +
.Исчисление I — Определение определенного интеграла
Онлайн-заметки ПавлаНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Проблемы с практикой
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Проблема области
- Вычисление определенных интегралов
- Разделы
- Применение производных инструментов
- Приложения интегралов
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Алгебра и триггерный обзор
- Распространенные математические ошибки
- Праймер комплексных чисел
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Notes Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Полная книга — Только проблемы
- Полная книга — Решения
- Текущая глава — Только проблемы
- Текущая глава — Решения
- Текущий раздел — Только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузок
- Полная книга
- Текущая глава
- Текущий раздел
- Прочие товары
- Получить URL для загружаемых элементов
- Распечатать страницу в текущем виде (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- Алгебра
- Отборочные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- Полиномы
- Факторинговые многочлены
- Рациональные выражения
- Комплексные числа
- Решение уравнений и неравенств
- Решения и наборы решений
- Линейные уравнения
- Приложения линейных уравнений
- Уравнения с более чем одной переменной
- Квадратные уравнения — Часть I
- Квадратные уравнения — Часть II
- Квадратные уравнения: сводка
- Приложения квадратных уравнений
- Уравнения, сводимые к квадратичным в форме
- Уравнения с радикалами
- Линейные неравенства
- Полиномиальные неравенства
- Рациональные неравенства
- Уравнения абсолютных значений
- Отборочные
Определенные интегралы
Определенный интеграл функции тесно связан с первообразной и неопределенным интегралом функции. Основное отличие состоит в том, что неопределенный интеграл, если он существует, является вещественным числовым значением, в то время как последние два представляют бесконечное количество функций, которые отличаются только константой. Взаимосвязь между этими понятиями будет обсуждаться в разделе, посвященном фундаментальной теореме исчисления, и вы увидите, что определенный интеграл будет иметь приложения ко многим задачам исчисления.Развитие определения определенного интеграла начинается с функции f ( x ), которая непрерывна на отрезке [ a, b ]. Данный интервал разделен на подинтервалы « n », которые, хотя и не обязательно, могут быть взяты равной длины (Δ x ). Произвольное значение домена, x i , выбирается в каждом подынтервале, и определяется его последующее значение функции, f ( x i ).Определяется произведение каждого значения функции на соответствующую длину подынтервала, и эти произведения « n » складываются для определения их суммы. Эта сумма называется суммой Римана и может быть положительной, отрицательной или нулевой, в зависимости от поведения функции на закрытом интервале. Например, если f ( x )> 0 на [ a, b ], то сумма Римана будет положительным действительным числом. Если f ( x ) <0 на [ a, b ], тогда сумма Римана будет отрицательным действительным числом.Сумма Римана функции f ( x ) на [ a, b ] выражается как

Таким образом, сумму Римана можно представить как «сумму n произведений».
Пример 1: Оцените сумму Римана для f ( x ) = x 2 на [1,3], используя четыре подинтервала равной длины, где x i — правое конечная точка на подынтервале и (см. рисунок).
Рисунок 1 Сумма Римана с четырьмя частями.
Поскольку подынтервалы должны быть равной длины, вы обнаружите, что

Сумма Римана для четырех подинтервалов равна

Если количество подинтервалов многократно увеличивать, то в результате длина каждого подинтервала будет становиться все меньше и меньше. Это можно переформулировать следующим образом: если количество подынтервалов неограниченно увеличивается ( n → + ∞), то длина каждого подынтервала приближается к нулю (Δ x → + ∞).Этот предел суммы Римана, если он существует, используется для определения определенного интеграла функции на [ a, b ]. Если f ( x ) определено на закрытом интервале [ a, b ], то определенный интеграл из f ( x ) от a до b определяется как

, если это ограничение выходит за пределы.
Функция f ( x ) называется подынтегральным выражением, а переменная x является переменной интегрирования.Числа a и b называются пределами интегрирования, с a — нижним пределом интегрирования, а b — верхним пределом интегрирования.
Обратите внимание, что символ ∫, используемый с неопределенным интегралом, является тем же самым символом, который ранее использовался для неопределенного интеграла функции. Причина этого станет более очевидной в нижеследующем обсуждении фундаментальной теоремы исчисления. Кроме того, имейте в виду, что определенный интеграл — это уникальное действительное число и не представляет бесконечное количество функций, которые являются результатом неопределенного интеграла функции.
Вопрос о существовании предела суммы Римана важно рассмотреть, поскольку он определяет, существует ли определенный интеграл для функции на отрезке. Как и в случае с дифференцированием, между непрерывностью и интегрированием существует значительная взаимосвязь, которую можно резюмировать следующим образом: если функция f ( x ) является непрерывной на отрезке [ a, b ], то определенный интеграл от f ( x ) на [ a, b ] существует, а f считается интегрируемым на [ a, b ].Другими словами, непрерывность гарантирует существование определенного интеграла, но обратное не всегда верно.
К сожалению, тот факт, что определенный интеграл функции существует на отрезке, не означает, что значение определенного интеграла легко найти.
Некоторые свойства полезны при решении задач, требующих применения определенного интеграла. Некоторые из наиболее распространенных свойств:
1. 
2. 
3. , где c — постоянная
, где c — постоянная
4. 
5. Правило суммы: 
6. Правило разницы: 
7. Если 
8. Если 
9. Если 
10. Если a, b, и c — любые три точки на закрытом интервале, то

11. Теорема о среднем значении для определенных интегралов: если f ( x ) непрерывно на закрытом интервале [ a, b ], то по крайней мере одно число c существует в открытом интервале ( a , b ) такая, что

Значение f ( c ) называется средним или средним значением функции f ( x ) на интервале [ a, b ] и

Пример 2: Оценить

Пример 3: Учитывая, что 

Пример 4: Учитывая, что 

Пример 5 Вычислить 

Пример 6: Учитывая, что  оценивает
оценивает 

Пример 7: Учитывая, что  оценивает
оценивает  .
.

Пример 8: Учитывая, что  , оцените
, оцените  .
.

Пример 9: Учитывая, что  найти все c значений, которые удовлетворяют теореме о среднем значении для данной функции на закрытом интервале.
найти все c значений, которые удовлетворяют теореме о среднем значении для данной функции на закрытом интервале.
По теореме о среднем значении

Поскольку  находится в интервале (3,6), заключение теоремы о среднем значении выполняется для этого значения c .
находится в интервале (3,6), заключение теоремы о среднем значении выполняется для этого значения c .
Основная теорема исчисления
Фундаментальная теорема исчисления устанавливает связь между неопределенными и определенными интегралами и вводит технику вычисления определенных интегралов без использования сумм Римана, что очень важно, поскольку вычисление предела суммы Римана может быть чрезвычайно трудоемким и трудоемким. Утверждение теоремы: Если f ( x ) непрерывно на интервале [ a, b ], а F ( x ) является любой первообразной f ( x ) по [ a, b ], затем 
Другими словами, значение определенного интеграла функции на [ a, b ] — это разность любой первообразной функции, вычисленной на верхнем пределе интегрирования, за вычетом той же первообразной, вычисленной на нижнем пределе интегрирования.Поскольку константы интегрирования одинаковы для обеих частей этой разности, они игнорируются при вычислении определенного интеграла, потому что они вычитают и дают ноль. Помня об этом, выберите постоянную интегрирования равной нулю для всех определенных интегральных вычислений после примера 10.
Пример 10: Оценить 
Поскольку общая первообразная x 2 равна (1/3) x 3 + C , вы обнаружите, что

Пример 11: Оценить 
Поскольку первообразная sin x — cos x , вы обнаружите, что

Пример 12: Оценить 
(потому что  , (первообраз
, (первообраз  , и вы обнаружите, что
, и вы обнаружите, что

Пример 13: Вычислить 
Поскольку первообразная x 2 -4 x + 1 равна (1/3) x 3 -2 x 2 + x , вы обнаружите, что 
Определенная интегральная оценка
Многочисленные методы, которые можно использовать для вычисления неопределенных интегралов, также могут использоваться для вычисления определенных интегралов.Методы подстановки и замены переменных, интегрирования по частям, тригонометрических интегралов и тригонометрической замены проиллюстрированы в следующих примерах.
Пример 14: Оценить 
Используя метод замещения с

пределы интегрирования можно преобразовать из значений x в соответствующие им значения u . Когда x = 1, u = 3 и когда x = 2, u = 6, вы обнаружите, что

Обратите внимание, что когда метод подстановки используется для вычисления определенных интегралов, нет необходимости возвращаться к исходной переменной, если пределы интегрирования преобразованы в новые значения переменных.
Пример 15: Оценить 
Используя метод подстановки с u = sin x + 1, du = cos x dx , вы обнаружите, что u = 1, когда x = π, и u = 0, когда x = 3π / 2; следовательно,

Обратите внимание, что вам никогда не приходилось возвращаться к тригонометрическим функциям в исходном интеграле, чтобы вычислить определенный интеграл.
Пример 16: Вычислить 
Использование интеграции по частям с

вы обнаружите, что

Пример 17: Вычислить 
Использование интеграции по частям с

Пример 18: Вычислить 


Пример 19: Вычислить  .
.

Пример 20: Вычислить  .
.
Поскольку подынтегральное выражение содержит форму a 2 + x 2 ,

Рисунок 2 Диаграмма для примера 20.

Пример 21: Вычислить 
Поскольку корень имеет вид 

Рисунок 3 Диаграмма для примера 21.

