| Определить эквивалентное сопротивление цепи
Задача 3.12.
Определить эквивалентное сопротивление цепи, в которой XL=XC=R=10 Ом.
Задача 3.13.
Чему равно эквивалентное сопротивление цепи?
Задача 3.14.
При каком соотношении величин ток I на входе цепи опережает по фазе напряжение U?
3.6. Цепь синусоидального тока при смешанном соединении элементов.
Для цепей синусоидального тока справедливы все формулы расчета цепей постоянного тока, но в комплексной форме. Поэтому методика расчета цепей при смешанном соединении элементовсводится к постепенному упрощению схемы путем замены отдельных участков эквивалентными сопротивлениями, в результате чего определяется эквивалентное сопротивление всей цепи.
Решить задачи:
Задача 3.15.
Для электрической цепи, представленной на рисунке, найти полное сопротивление Z всей цепи при ХL=5 Ом, R=XC=10 Ом.
Задачи 3.16.
Найти комплексное сопротивление Z всей цепи при ХL=10 Ом, R=20 Ом, XC=5 Ом.
Задача 3.17.
Определить характер нагрузки цепи, если ХL=R=XC.
3.7. Мощность цепи синусоидального тока.
3.7.1. Мгновенная мощность – произведение мгновенных значений напряжения и тока, т. е. p=u*i.
Распишем её для отдельных элементов цепи, приняв начальную фазу для напряжения φu=0:
— цепь с резистивным (активным) элементом (см. рис. 3.5,а):
Рис. 3.10
Мгновенная мощность имеет две составляющие: постоянную и переменную , изменяющуюся по косинусоидальномузакону с удвоенной частотой.
В этой цепи мгновенная мощность всегда положительная, и энергия в цепи передается в одном направлении от источника к приемнику, где она полностью (необратимо) преобразуется в другие виды энергии (рис. 3.10).
— цепь с индуктивным элементом
(см.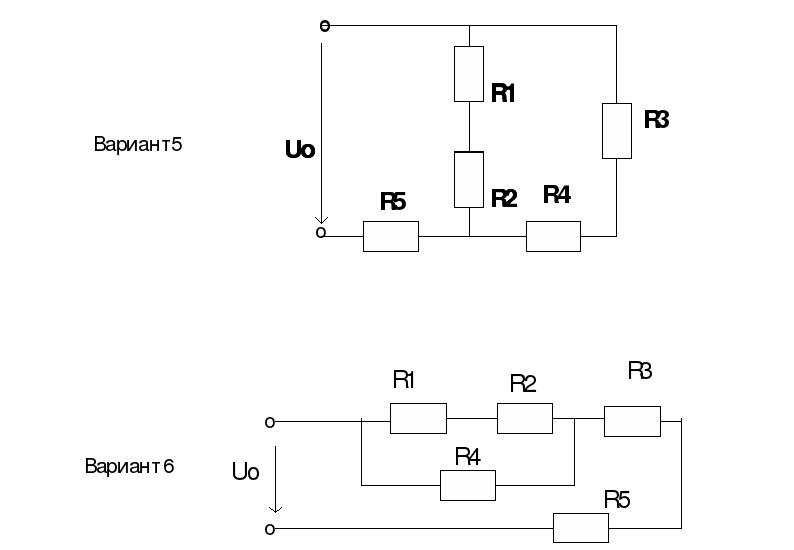
рис. 3.6a )Мгновенная мощность – переменная, изменяется по синусоидальному закону с удвоенной частотой. При возрастании тока i по абсолютной величине мгновенное значение мощности p>0, в это время происходит накопление энергии в магнитном поле индуктивности. При уменьшении тока i по абсолютной величине p<0 и в это время индуктивность становится источником электроэнергии (рис 3.11).
Рис 3.11
— цепь с емкостным элементом(см. рис. 3.7,а)
Мгновенная мощность – переменная, изменяющаяся по синусоидальному закону с удвоенной частотой. При возрастании тока по абсолютной величине мгновенное значение мощности p<0, в это время емкость становится источником электроэнергии. При уменьшении тока по абсолютной величине p>0, в это время происходит накопление энергии в электрическом поле емкости (рис 3.12).
Рис 3.12
3.7.2. Активная мощность – мощность необратимых преобразований электрической энергии на участке цепи за период:
Из формулы следует, что средняя за период мощность не равна нулю, если участок цепи имеет активное сопротивление.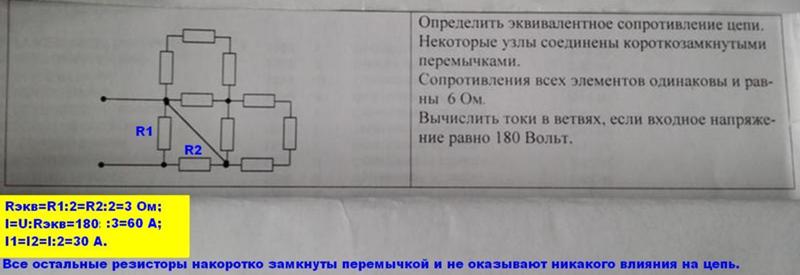
3.7.3. Реактивная мощность – мощность реактивных элементов полейpP=pL+pC в среднем за период равна нулю, но в течение четверти периода она положительна, что означает накопление энергии в магнитном поле катушки или электрическом поле конденсатора, а в течение следующей четверти периода – отрицательная, что соответствует обратному процессу.
Таким образом, имеет место процесс колебания энергии, но необратимых преобразований энергии (при отсутствии активной мощности) нет.
3.7.4. Полная мощность. Под полной мощностью участка цепи понимается максимально возможная мощность при заданных значениях тока I и напряжения U.
Необходимость введения понятия мощности заключается в том, что при конструировании любых электрических устройств их рассчитывают на определенное номинальное напряжение Uном и на определенный номинальный ток Iном, а их произведение Sном=UномIном дает максимально возможную мощность данного устройства (именно она указывается в паспорте большинства электрических устройств переменного тока).
Связь между различными мощностями:
Для облегчения запоминания этих формул можно обратить к так называемому треугольнику мощности (рис 3.13).
Рис 3.13
3.7.5. Коэффициент мощности.
Коэффициент мощности показывает, какая часть электрической энергии необратимо преобразуется в другие виды энергии, в том числе используется для выполнения полезной работы.
Для повышения коэффициента мощности применяются меры, которые сводятся или к уменьшению реактивной мощности QL или к ее компенсации мощностью QC.
Решить задачу.
Задача 3.18.
Выбрать схему, которая является рациональной для увеличения cosφ, где Ском – компенсирующая емкость, Rпр, Lпр – активное и индуктивное сопротивление приемника соответственно.
2. Способы соединения сопротивлений и расчет эквивалентного сопротивления электрической цепи
Сопротивления в
электрических цепях могут быть соединены
последовательно, параллельно, по
смешанной схеме и по схемам «звезда»,
«треугольник».
Электрическая цепь с последовательным соединением элементов
Рис. 2.1
Рис. 2.2
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 2.1).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
или ,
откуда следует
(1.6).
Таким образом, при
последовательном соединении элементов
цепи общее эквивалентное сопротивление
цепи равно арифметической сумме
сопротивлений отдельных участков.
Следовательно, цепь с любым числом
последовательно включенных сопротивлений
можно заменить простой цепью с одним
эквивалентным сопротивлением (рис. 2.2). После этого расчет цепи сводится
к определению тока I всей цепи по закону
Ома ,
и по вышеприведенным формулам рассчитывают
падение напряжений , , на соответствующих участках электрической
цепи (рис.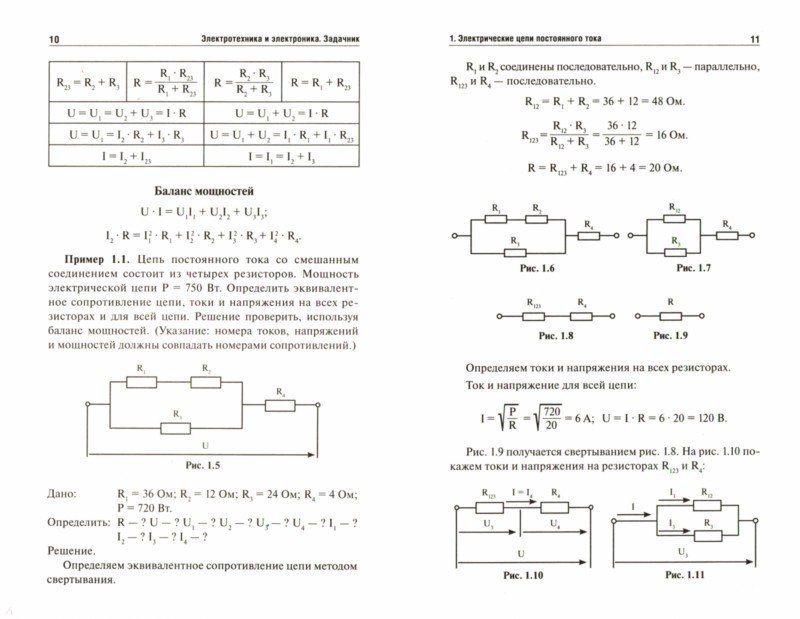
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 2.3).
Рис. 2.3
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
, т.е. ,
откуда следует, что
(1.7).
В том случае, когда параллельно включены два сопротивления и , они заменяются одним эквивалентным сопротивлением
(1.
8).
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
.
По мере роста числа параллельно включенных потребителей проводимость цепи возрастает, и наоборот, общее сопротивление уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 2.3)
.
Отсюда следует, что
,т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется
такое соединение, при котором в цепи
имеются группы параллельно и последовательно
включенных сопротивлений.
Рис. 2.4
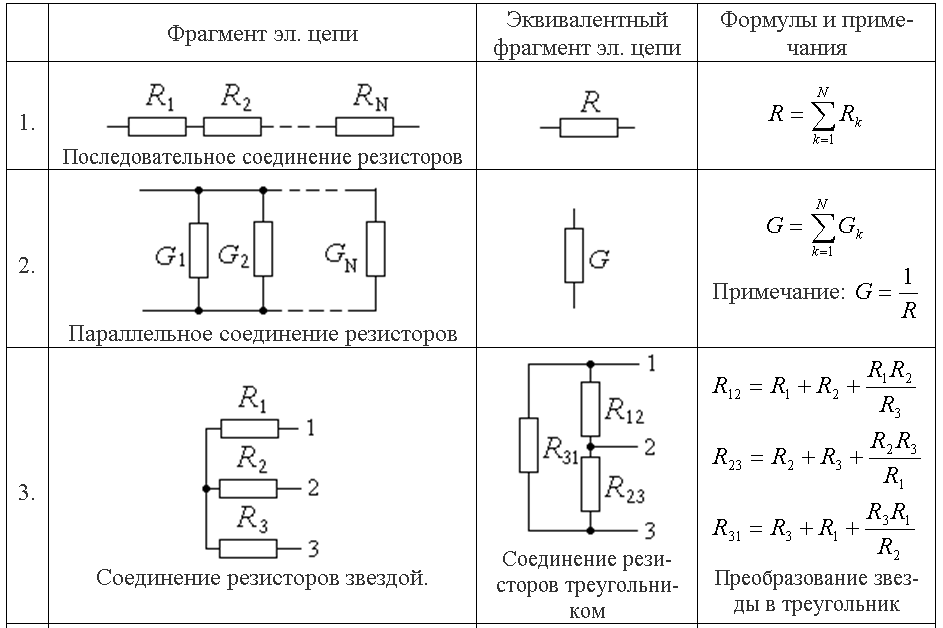
Для цепи, представленной на рис. 2.4, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: . Сопротивления и , R5 включены параллельно, тогда сопротивление участка цепи равно:
.
В этом случае исходную схему (рис. 2.4) можно представить в следующем виде (рис. 2.5):
Рис. 2.5
На схеме (рис. 2.5) сопротивление и соединены последовательно, и тогда сопротивление участка цепи равно:
.
Тогда схему (рис. 2.5) можно представить в сокращенном варианте (рис. 2.6):
Рис. 2.6
На схеме (рис. 2.6) сопротивление и соединены параллельно, тогда сопротивление участка цепи равно:
.
Схему (рис. 2.6) можно представить в упрощенном варианте (рис. 2.7), где сопротивления и включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 2.4) будет равно:
Рис. 2.8
В результате преобразований исходная схема (рис. 2.4) представлена в виде схемы (рис. 2.8) с одним сопротивлением . Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
Соединение элементов электрической цепи по схемам «звезда» и «треугольник»
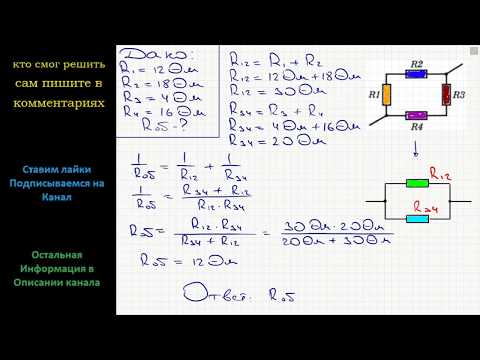
В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 2.9). Сопротивления , , , включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.
Рис.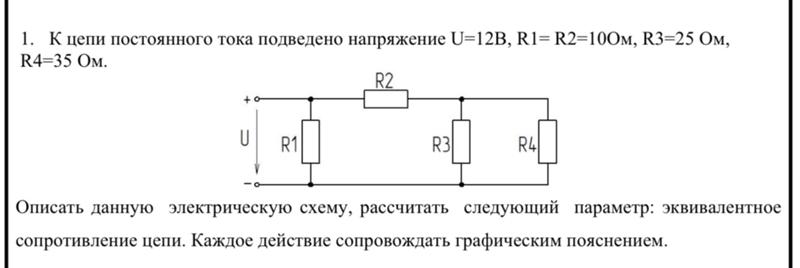
2.9
Рис. 2.10
В мостовой схеме сопротивления , , и , , соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника звездой (рис. 2.10). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:
, , (1.9)
Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:
, , (1.10)
После проведенных преобразований (рис. 2.10) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 2.9)
.
6.2 Резисторы, включенные последовательно и параллельно. Введение в электричество, магнетизм и электрические цепи
ЦЕЛИ ОБУЧЕНИЯ
К концу раздела вы сможете:
- Определение термина эквивалентное сопротивление
- Рассчитать эквивалентное сопротивление резисторов, соединенных последовательно
- Рассчитать эквивалентное сопротивление резисторов, соединенных параллельно
В разделе «Ток и сопротивление» мы описали термин «сопротивление» и объяснили базовую конструкцию резистора.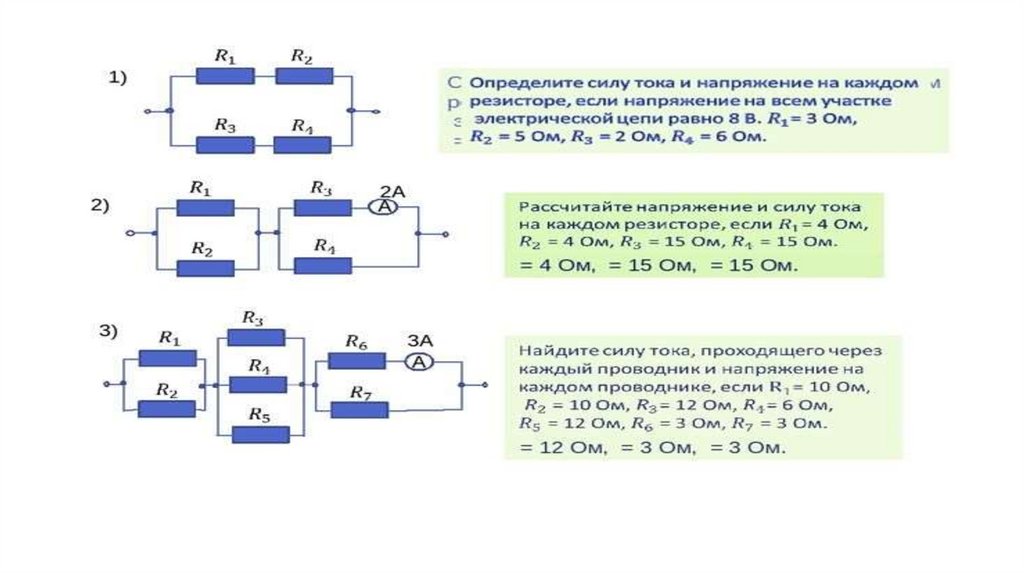
По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где . Большинство схем имеют более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, выдаваемый батареей, зависит от эквивалентное сопротивление Ом цепи.
Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от того, как они соединены. Простейшими сочетаниями резисторов являются последовательное и параллельное соединения (рис. 6.2.1). В последовательной схеме выходной ток первого резистора протекает на вход второго резистора; следовательно, ток в каждом резисторе одинаков. В параллельной цепи все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала, и токи через каждый резистор могут быть разными, в зависимости от резистора.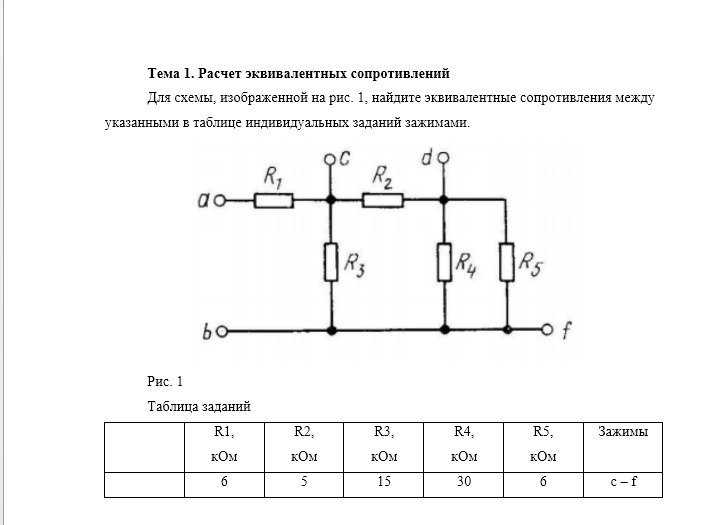
Сумма отдельных токов равна току, протекающему в параллельных соединениях.
(рис. 6.2.1)
Рисунок 6.2.1 (a) При последовательном соединении резисторов ток в каждом резисторе одинаков. б) при параллельном соединении резисторов напряжение на каждом резисторе одинаково.Резисторы серии
Резисторы называются последовательными, если ток течет через резисторы последовательно. Рассмотрим Рисунок 6.2.2, на котором показаны три последовательно соединенных резистора с приложенным напряжением, равным . Поскольку существует только один путь для протекания зарядов, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме сопротивлений отдельных элементов.
(рис. 6.2.2)
Рисунок 6.2.2 (a) Три резистора, подключенные последовательно к источнику напряжения. (b) Исходная схема сводится к эквивалентному сопротивлению и источнику напряжения. На рисунке 6.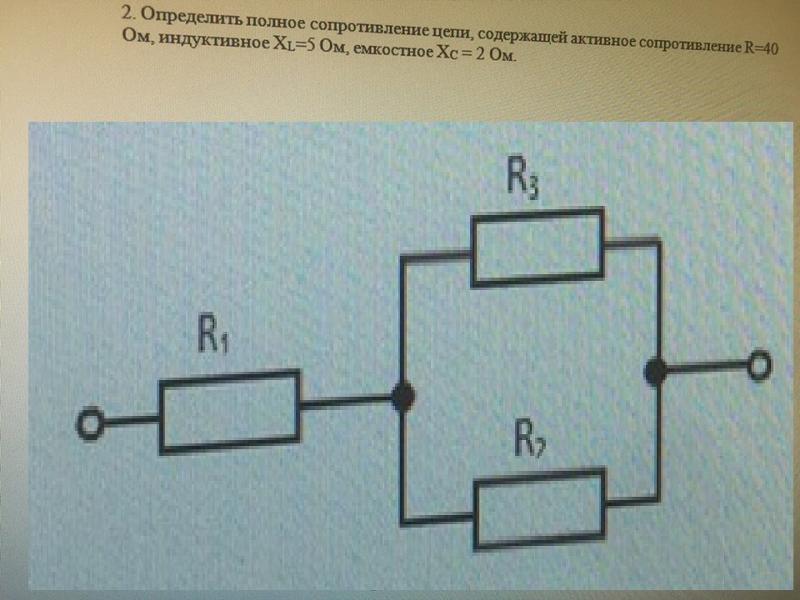
2.2 ток, поступающий от источника напряжения, протекает через каждый резистор, поэтому ток через каждый резистор одинаков. Ток в цепи зависит от напряжения, подаваемого источником напряжения, и сопротивления резисторов. Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии при протекании тока через каждый резистор. Согласно закону Ома, падение потенциала на резисторе при протекании через него тока рассчитывается по уравнению , где — ток в амперах () и — сопротивление в омах (). Поскольку энергия сохраняется, а напряжение равно потенциальной энергии на один заряд, сумма напряжения, приложенного к цепи источником, и падений потенциала на отдельных резисторах вокруг петли должна быть равна нулю:
Это уравнение часто называют петлевым законом Кирхгофа, который мы рассмотрим более подробно далее в этой главе. Для Рисунка 6.2.2 сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю:
Поскольку ток через каждый компонент одинаков, равенство можно упростить до эквивалентного сопротивления, которое представляет собой просто сумму сопротивлений отдельных резисторов.
Любое количество резисторов может быть соединено последовательно. Если резисторы соединены последовательно, эквивалентное сопротивление равно 90 016 Ом.
(6.2.1)
Одним из результатов последовательного соединения компонентов является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп соединены последовательно и одна лампочка перегорает, все остальные лампы гаснут.
ПРИМЕР 6.2.1
Эквивалентное сопротивление, ток и мощность в последовательной цепи
Батарея с напряжением на клеммах подключена к цепи, состоящей из четырех и одного резисторов, соединенных последовательно (рис. 6.2.3). Предположим, что батарея имеет незначительное внутреннее сопротивление. а) Рассчитайте эквивалентное сопротивление цепи. б) Рассчитайте ток через каждый резистор. в) Рассчитайте падение потенциала на каждом резисторе. г) Определите общую мощность, рассеиваемую резисторами, и мощность, отдаваемую батареей.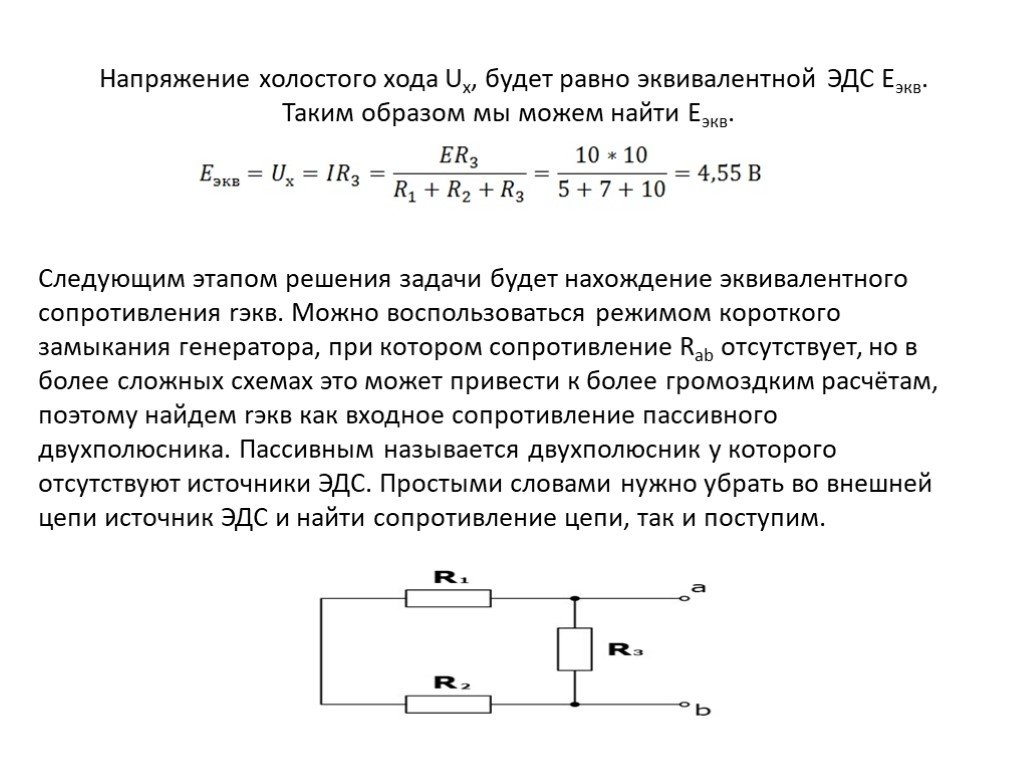
(рис. 6.2.3)
Рисунок 6.2.3 Простая последовательная цепь с пятью резисторами.Стратегия
В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений. Сила тока в цепи определяется по закону Ома и равна напряжению, деленному на эквивалентное сопротивление. Падение потенциала на каждом резисторе можно найти по закону Ома. Мощность, рассеиваемую каждым резистором, можно найти с помощью , а общая мощность, рассеиваемая резисторами, равна сумме мощностей, рассеиваемых каждым резистором. Мощность, выдаваемую аккумулятором, можно найти с помощью .
Решение
а. Эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений:
б. Ток в цепи одинаков для каждого резистора в последовательной цепи и равен приложенному напряжению, деленному на эквивалентное сопротивление:
в. Падение потенциала на каждом резисторе можно найти по закону Ома:
Обратите внимание, что сумма падений потенциала на каждом резисторе равна напряжению, выдаваемому батареей.
д. Мощность, рассеиваемая резистором, равна , а мощность, отдаваемая батареей, равна :
Значение
Есть несколько причин, по которым мы будем использовать несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи. Возможно, резистора нужного размера нет в наличии, или нам нужно отводить выделяющееся тепло, или мы хотим минимизировать стоимость резисторов. Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть заметной.
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 6.2
Некоторые цепочки миниатюрных праздничных огней закорачивают, когда перегорает лампочка. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи. «Короткое замыкание» похоже на наложение куска провода на компонент. Луковицы обычно сгруппированы в серии из девяти луковиц.
Если перегорает слишком много лампочек, шунты со временем открываются. Что вызывает это?
Кратко перечислим основные характеристики последовательно соединенных резисторов:
Сопротивления серии- суммируются, чтобы получить эквивалентное сопротивление:
- Один и тот же ток протекает через каждый резистор последовательно.
- Отдельные последовательно соединенные резисторы не получают общее напряжение источника, а делят его. Общее падение потенциала на последовательных резисторах равно сумме падений потенциала на каждом резисторе.
Параллельные резисторы
На рис. 6.2.4 показаны резисторы, подключенные параллельно к источнику напряжения. Резисторы параллельны, когда один конец всех резисторов соединен непрерывным проводом с пренебрежимо малым сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с пренебрежимо малым сопротивлением. Падение потенциала на каждом резисторе одинаково.
Ток через каждый резистор можно найти с помощью закона Ома, согласно которому напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы соединены параллельно, так что каждая подсистема использует полное напряжение источника и может работать совершенно независимо. То же самое относится и к проводке в вашем доме или любом здании.
(рис. 6.2.4)
Рисунок 6.2.4 (a) Два резистора, подключенные параллельно к источнику напряжения. (b) Исходная схема сводится к эквивалентному сопротивлению и источнику напряжения.Ток, протекающий от источника напряжения на Рисунке 6.2.4 , зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и входит в соединение или узел, где цепь разделяется, протекая через резисторы и . По мере того как заряды текут от батареи, некоторые из них проходят через резистор, а некоторые — через резистор. Сумма токов, втекающих в соединение, должна быть равна сумме токов, вытекающих из соединения:
Это уравнение называется правилом пересечения Кирхгофа и будет подробно обсуждаться в следующем разделе.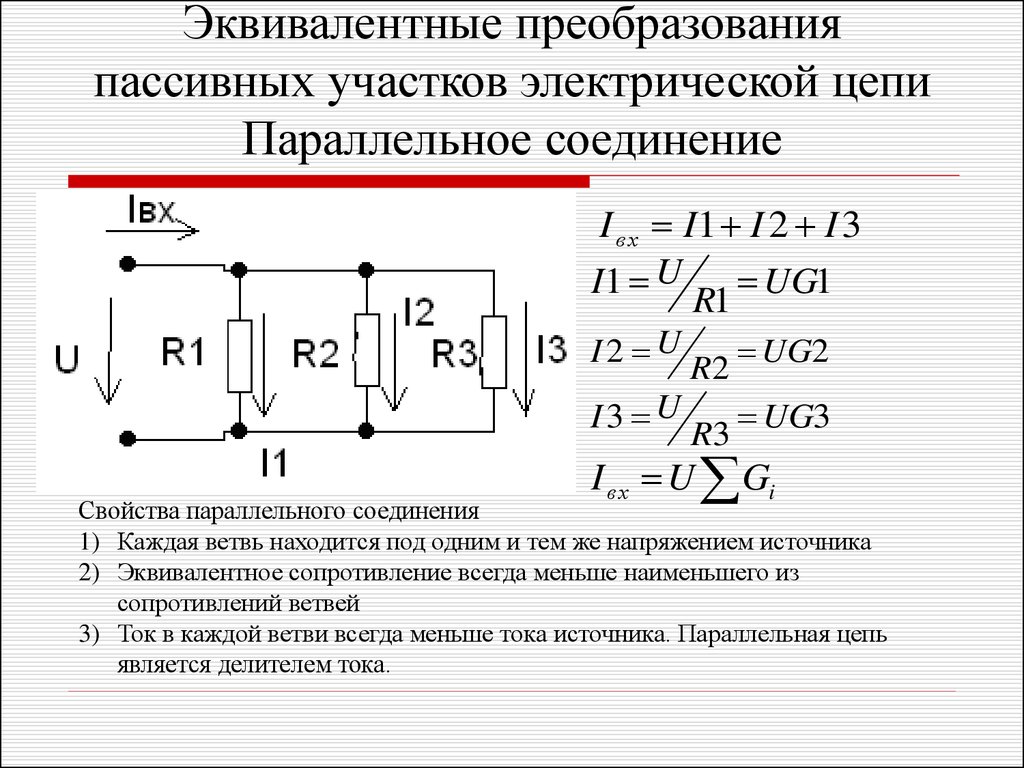
На Рисунке 6.2.4 правило соединения дает . В этой цепи есть два контура, что приводит к уравнениям и Обратите внимание, что напряжения на параллельных резисторах одинаковы (), а ток суммируется:
Обобщая любое количество резисторов, эквивалентное сопротивление параллельного соединения связано с сопротивлением отдельных резисторов в 9 раз.0016
(6.2.2)
Это соотношение приводит к эквивалентному сопротивлению, которое меньше, чем наименьшее из отдельных сопротивлений. Когда резисторы соединены параллельно, от источника протекает больший ток, чем по каждому из них по отдельности, поэтому общее сопротивление меньше.
ПРИМЕР 6.2.2
Анализ параллельной цепи
Три резистора , и соединены параллельно. Параллельное соединение подключается к источнику напряжения. а) чему равно сопротивление? б) Найдите ток, подаваемый источником в параллельную цепь. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна выходному току источника.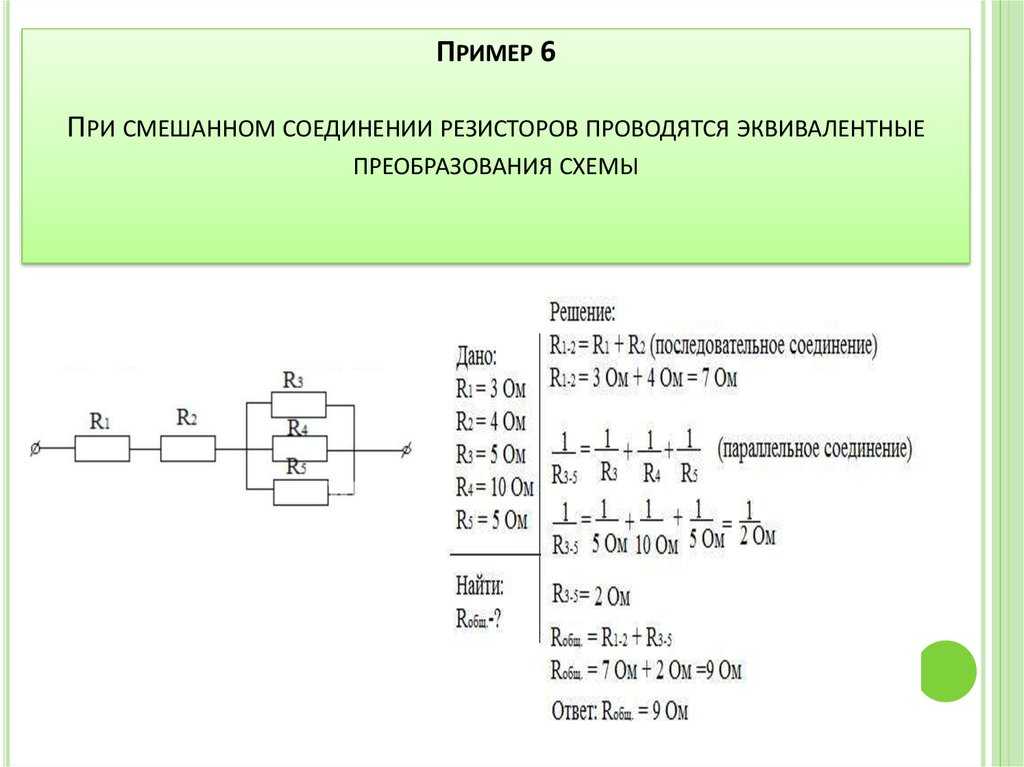
г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия
(a) Общее сопротивление для параллельной комбинации резисторов находится с помощью .
(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
(b) Ток, подаваемый источником, можно найти из закона Ома, заменив полное сопротивление на .
(c) Отдельные токи легко рассчитать по закону Ома, поскольку на каждый резистор подается полное напряжение. Общий ток представляет собой сумму отдельных токов: .
(d) Мощность, рассеиваемая каждым резистором, может быть найдена с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны. Возьмем , так как на каждый резистор подается полное напряжение.
(e) Суммарная мощность также может быть рассчитана несколькими способами, используйте .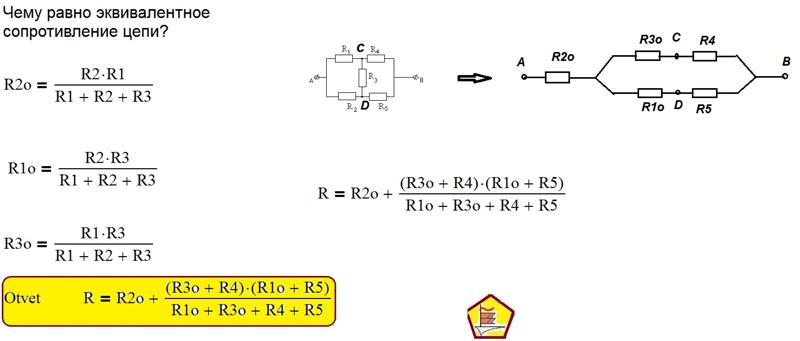
Решение
а. Общее сопротивление для параллельной комбинации резисторов находится с помощью уравнения 6.2.2. Ввод известных значений дает
Общее сопротивление с правильным количеством значащих цифр равно . Как и предполагалось, меньше наименьшего индивидуального сопротивления.
б. Полный ток можно найти из закона Ома, подставив полное сопротивление. Это дает
Ток для каждого устройства намного больше, чем для тех же устройств, соединенных последовательно (см. предыдущий пример). Цепь с параллельными соединениями имеет меньшее общее сопротивление, чем резисторы, соединенные последовательно.
в. Отдельные токи легко рассчитать по закону Ома, так как на каждый резистор подается полное напряжение. Таким образом,
Аналогично,
и
Общий ток представляет собой сумму отдельных токов:
д. Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.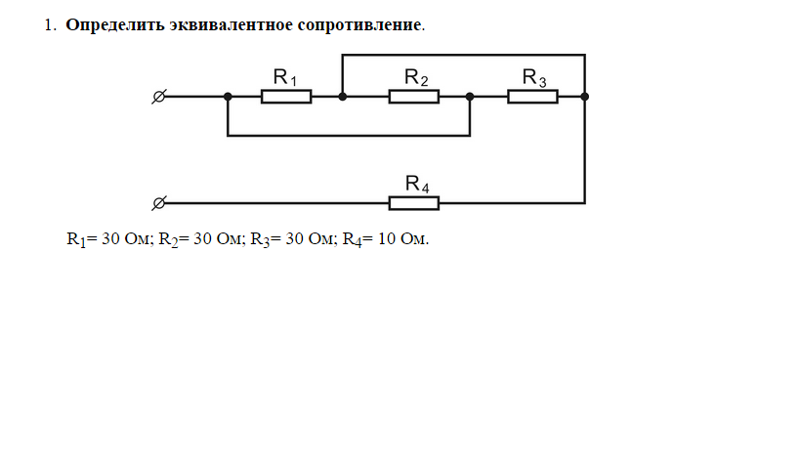
Возьмем , так как на каждый резистор подается полное напряжение. Таким образом,
Аналогично,
и
эл. Суммарная мощность также может быть рассчитана несколькими способами. Выбор и ввод общей текущей доходности
Значение
Суммарная мощность, рассеиваемая резисторами, также равна:
Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, отдаваемой источником.
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 6.3
Рассмотрим одинаковую разность потенциалов, приложенную к тем же трем резисторам, соединенным последовательно. Будет ли эквивалентное сопротивление последовательной цепи выше, ниже или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи больше, меньше или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая резистором, включенным последовательно, будет отличаться от мощности, рассеиваемой резисторами, включенными параллельно?
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 6.
4Как бы вы использовали реку и два водопада для моделирования параллельной конфигурации двух резисторов? Как разрушается эта аналогия?
Подытожим основные характеристики резисторов при параллельном включении:
- Эквивалентное сопротивление находится из
и меньше любого отдельного сопротивления в комбинации.
- Падение потенциала на каждом параллельном резисторе одинаково.
- Параллельные резисторы не получают суммарный ток каждый; они его делят. Ток, входящий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый параллельный резистор.
В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Возможно, вы помните, что в разделе «Емкость» мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно. Схемы часто содержат как конденсаторы, так и резисторы.
В таблице 6.2.1 обобщаются уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательных и параллельных соединений.
(таблица 6.2.1)
| Комбинация серии | Параллельная комбинация | |
|---|---|---|
| Эквивалентная емкость | ||
| Эквивалентное сопротивление | Таблица 10. |
1
(c) Шаг 2: На уменьшенной схеме показаны резисторы, соединенные параллельно, с эквивалентным сопротивлением . (d) Этап 3: Уменьшенная схема показывает, что и включены последовательно с эквивалентным сопротивлением , которое равно эквивалентному сопротивлению . (e) Уменьшенная схема с источником напряжения с эквивалентным сопротивлением . Это приводит к току от источника напряжения.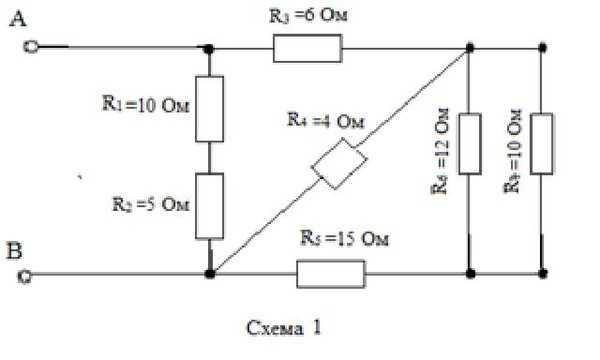
5(d). Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно. Эти два резистора можно привести к эквивалентному сопротивлению, которое является эквивалентным сопротивлением цепи:
Мощность, рассеиваемая резисторами, равна
Затем используйте этот результат, чтобы найти эквивалентное сопротивление последовательного соединения с .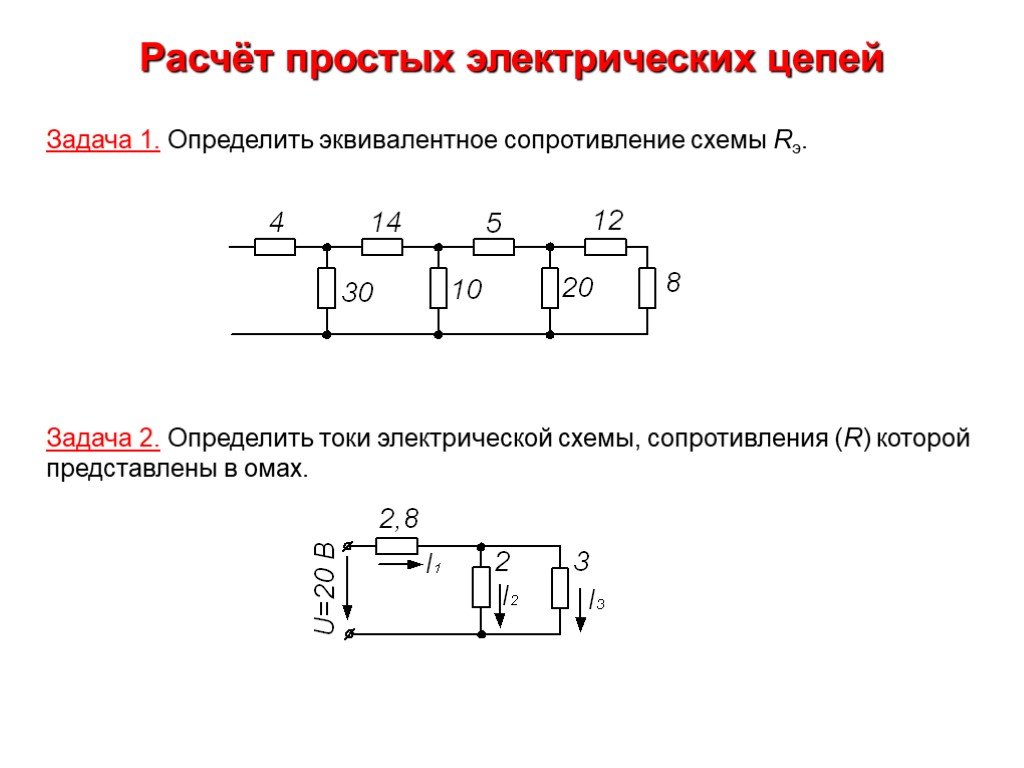
Когда сопротивление проводов велико, это может существенно повлиять на работу устройств, представленных и .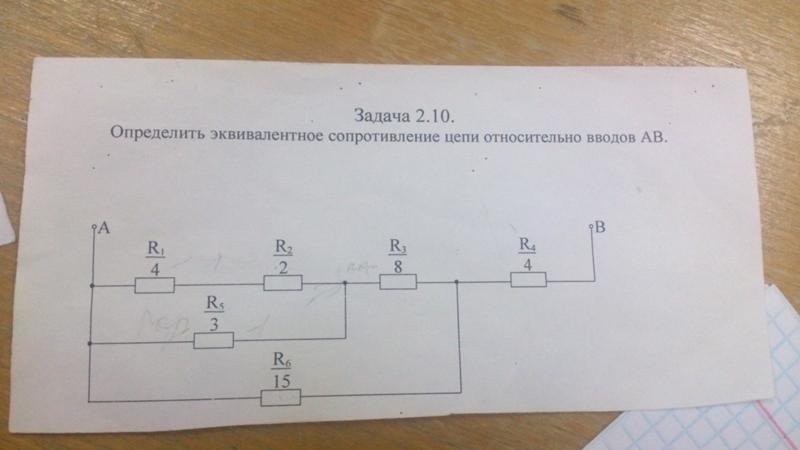
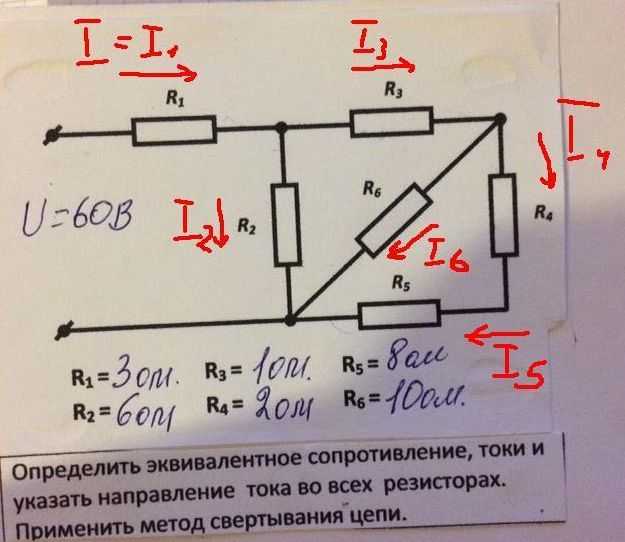Есть один список для серий и другой для параллельных.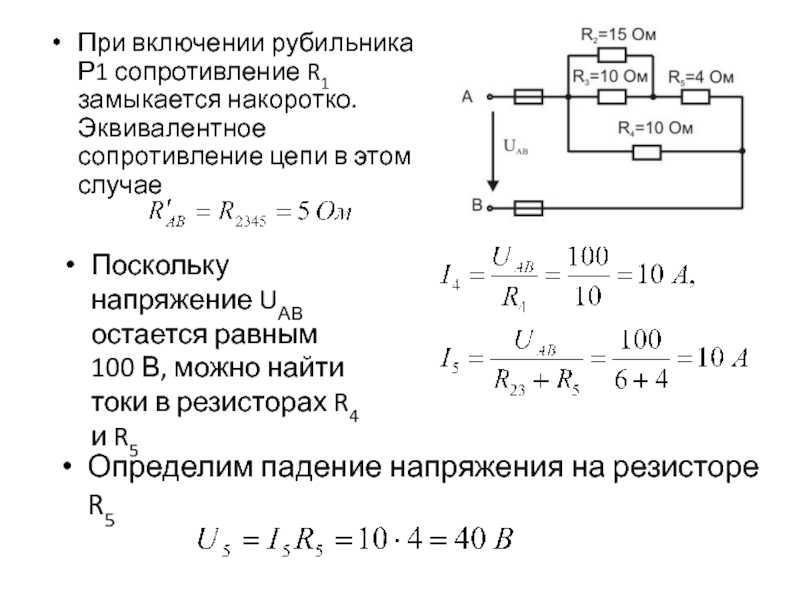
Так как , ток через каждый будет . Мощность, рассеиваемая резисторами, равна сумме мощностей, рассеиваемых каждым резистором: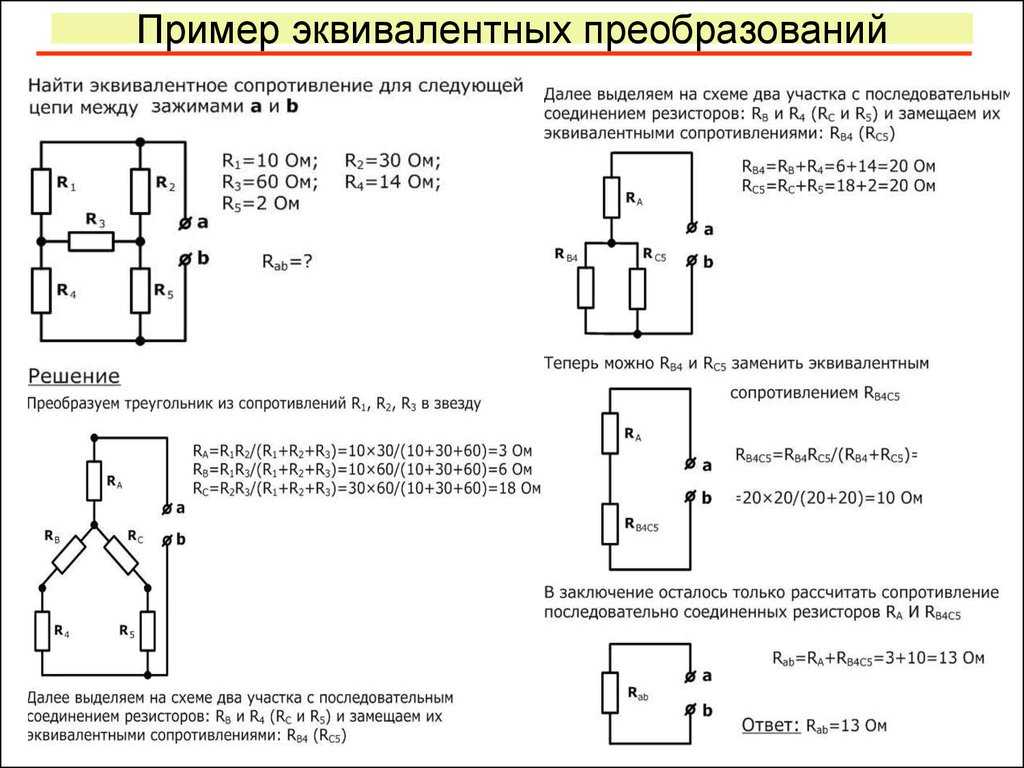 
org/contents/
