Определитель матрицы для чайников: Линейная алгебра для чайников

Указывает на заметку

• Умножение матриц некоммутативно, что означает A * B ≠ B * A
• Умножение матриц является ассоциативным, что означает A * (B * C) = (A * B) * C
• Существование A * B не подразумевает существование B * A
• Сложность операции умножения (A * B) составляет O (m * n * p), где m * n и n * p — порядок A и B соответственно
• Порядок матрицы C, вычисляемой как A * B, равен m * p, где m * n и n * p — порядок A и B соответственно.

В следующем издании этой статьи мы увидим больше операций, которые могут быть выполнены над матрицами, например, Инверсия матрицы, определитель матрицы, сопряжение матрицы и т. Д.

Мы также увидим, как эти матрицы действительно помогают в областинейронные сетии обработка изображений.

Матрицы имеют огромное значение почти во всех алгоритмах машинного обучения изКНН(Алгоритм ближайшего соседа) вплоть доСлучайные Леса,

Оригинальная статья

Критерий Гурвица — Теория автоматического управления для чайников

Подборка по базе: МАГИСТРЫ Varlashkina_T.I._Kravcova_G.F. Экономическая теория (Ми, Доклад-презентация и дискуссия Тема 1. Современные индивидуальн, Лекция. Теория З. Фрейда.pdf, Экспертные методы управления качеством.docx, Гибкие технологии управления персоналом.docx, Контрольная работа Документационное обеспечение управления.docx, Scilab ЛабПрактикум и теория.docx, ПЗ №1 Настройка ОС Windows. Панель управления ОС Windows.docx, ИПЗ теория соц работы кузьмина ценности.pptx, Экономич. теория .docx 1   …   6   7   8   9   10   11   12   13   14 Критерий Гурвица. Все корни полинома ) (s ∆ имеют отрицательные вещественные части то- гда и только тогда, когда все n главных миноров матрицы n H (определителей Гурвица) поло- жительны. Вспомним, что для устойчивости полинома необходимо, чтобы все его коэффициенты бы- ли положительными. Поэтому достаточно проверить только 1 − n первых определителей Гур- вица. Например, для 5 = n речь идет об определителях 0 1 1 > = a D , 0 2 0 3 1 2 > = a a a a D , 0 0 3 1 4 2 0 5 3 1 3 > = a a a a a a a a D , 0 0 0 0 0 4 2 0 5 3 1 4 2 0 5 3 1 4 > = a a a a a a a a a a a a D © К.Ю. Поляков, 2008 58 Раскрывая определитель матрицы 5 H по последнему столбцу, получаем 4 5 5 5 det D a H D = = . Так как 0 5 > a , из условия 0 4 > D сразу следует 0 5 > D Таким образом, условия устойчивости сводятся к нескольким неравенствам. Это очень удобно для систем низкого порядка. Например, для 2 = n необходимое и достаточное условие устойчивости – положительность всех коэффициентов полинома. Для 3 = n характеристиче- ский полином имеет вид 3 2 2 1 3 0 ) ( a s a s a s a s + + + = ∆ , поэтому условия Гурвица определяются матрицей ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 3 1 2 0 3 1 3 0 0 0 a a a a a a H ( 0 0 > a ). Полином устойчив, если все коэффициенты положительны и 0 3 0 2 1 2 0 3 1 2 > − = = a a a a a a a a D . (49) Рассмотрим систему, в которой объект и регулятор задаются передаточными функциями: ) 1 )( 1 ( 1 ) ( 2 1 + + = s T s T s P , s K s C = ) ( С помощью критерия Гурвица можно определить, при каких значениях K замкнутая система (с отрицательной обратной связью) устойчива. Передаточная функция замкнутой системы равна ) ( ) ( ) ( 1 ) ( ) ( ) ( s K s P s C s P s C s W ∆ = + = , где характеристический полином имеет вид K s s T T s T T K s s T s T s + + + + = + + + = ∆ 2 2 1 3 2 1 2 1 ) ( ) 1 )( 1 ( ) ( Необходимое условие устойчивости дает 0 > K . Применяя критерий Гурвица для системы третьего порядка (49), получаем 2 1 2 1 2 1 1 1 T T K T KT T T + ⇒ > + Таким образом, система устойчива при 2 1 1 1 0 T T K + Теперь предположим, что модель системы задана в пространстве состояний: ) ( ) ( ) ( ) ( ) ( ) ( t u D t x C t y t u B t x A t x ⋅ + ⋅ = ⋅ + ⋅ = & Как проверить ее устойчивость? Используя результаты раздела 3.7, построим передаточную функцию D B A sI C s W + − = −1 ) ( ) ( Характеристический полином этой системы (знаменатель ) (s W ), определяется формулой ) det( ) ( A sI s − = ∆ , где det обозначает определитель квадратной матрицы. Чтобы определить, устойчива ли систе- ма, нужно применить к этому полиному критерий Гурвица. + – x C(s) P(s) y u объект регулятор e © К.Ю. Поляков, 2008 59 6.5.2. Критерий Найквиста Критерий Найквиста позволяет определить устойчивость замкнутой системы, построив частотную характеристику разомкнутой системы. Пусть ) (s L – передаточная функция разомк- нутой системы, а ) ( ω j L – ее частотная характеристика. Для простоты сначала будем считать, что разомкнутая система устойчива и не содержит интег- рирующих звеньев, то есть ∞ ≠ = K L ) 0 ( , где K – некоторое число. Для каждой частоты ω значение ) ( ω j L – это комплексное число, которое можно изобра- зить точкой на комплексной плоскости. При изменении частоты от 0 до ∞ из этих точек скла- дывается годограф Найквиста – некоторая кривая, которая начинается в точке ) 0 ; (K на веще- ственной оси и заканчивается в начале координат (если ) (s L – строго правильная функция, то есть степень ее числителя меньше степени знаменателя). Можно доказать, что система устой- чива тогда и только тогда, когда годограф ) ( ω j L не охватывает точку ) 0 ; 1 ( − . На рисунке слева годограф не охватывает эту точку (и замкнутая система устойчива), а на рисунке справа – охва- тывает (система неустойчива). Выражение «система находится на границе устойчивости» означает, что частотная харак- теристика проходит через точку ) 0 ; 1 ( − . В этом случае для некоторой частоты ω мы имеем 1 ) ( = ω A и ° − = 180 ) ( ω φ . Это говорит о том, что после прохождения контура величина сигнала меняет знак, сохраняя абсолютную величину (энергию), то есть устанавливаются незатухающие колебания. Частота c ω , для которой 1 ) ( = c A ω , называется частотой среза. Для устойчивой системы значение фазы на частоте среза должно быть больше, чем ° −180 ; в этом случае годограф не охватит точку ) 0 ; 1 ( − Re Im K 1 − ° − = = 180 ) ( 1 ) ( ω φ ω A Re Im K 1 − Re Im K 1 − + – x L(s) y e © К.Ю. Поляков, 2008 60 Если передаточная функция ) (s L имеет полюса в точке 0 = s (то есть обращается в бес- конечность в этой точке), ситуация усложняется. Теперь годограф начинается не на веществен- ной оси, а приходит из бесконечности. Тогда в контур необходимо включить не только полу- ченную кривую, но и часть окружности бесконечного радиуса от вещественной оси до годогра- фа в порядке обхода по часовой стрелке. Если функция ) (s L имеет k полюсов в точке 0 = s , нужно добавить k секторов по ° 90 . На рисунках показаны годографы Найквиста устойчивых систем, в которых функция ) (s L имеет соответственно 1 и 2 полюса в точке 0 = s . Эти годо- графы не охватывают точку ) 0 ; 1 ( − Если в системе есть запаздывание на время τ , на любой частоте появляется дополнитель- ный сдвиг фазы на τω − (без изменения амплитуды). Это значит, что каждая точка годографа поворачивается на некоторый угол против часовой стрелки. На рисунке синяя линия – частотная характеристика системы без запаздывания, а крас- ная – аналогичная характеристика для системы с запаздыванием. Видно, что запаздывание при- вело к неустойчивости системы (годограф охватил критическую точку ) 0 ; 1 ( − ). Таким образом, система может потерять устойчивость из-за «медленного» датчика. Можно говорить о том, что запаздывание всегда ухудшает устойчивость системы, и этот факт важно учитывать при про- ектировании. Если ) (s L имеет полюса с положительной вещественной частью (разомкнутая система неустойчива), нужно считать, сколько раз годограф пересекает ось абсцисс левее точки ) 0 ; 1 ( − Причем переходы «сверху вниз» считаются положительными, а переходы «снизу вверх» — от- рицательными. Re Im K 1 − Re Im K 1 − c ω Re Im 1 − Re Im 1 − © К.Ю. Поляков, 2008 61 Для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы раз- ница между числом положительных и отрицательных переходов была равна 2 / l , где l – число неустойчивых полюсов функции ) (s L . Начальная точка на оси абсцисс левее точки ) 0 ; 1 ( − счи- тается за половину перехода. На рисунке показаны годографы устойчивых систем для случая 1 = l Частотная характеристика начинается на вещественной оси левее точки ) 0 ; 1 ( − . На рисун- ке слева годограф сначала идет вниз (половина положительного перехода) и больше нигде не пересекает ось абсцисс левее точки ) 0 ; 1 ( − , поэтому разница переходов равна 2 / 2 / 1 l = и замк- нутая система устойчива. На правом рисунке частотная характеристика сначала идет вверх (считаем это за половину отрицательного перехода), а затем переходит в нижнюю полуплоскость (положительный пере- ход). Разница снова равна 2 / 2 / 1 l = и система устойчива. 6.5.3. Критерий Найквиста для ЛАФЧХ Критерий Найквиста часто используется для логарифмических частотных характеристик. Сначала предположим, что передаточная функция разомкнутой системы не имеет неустойчи- вых полюсов. Как мы уже знаем, для анализа устойчивости наиболее важно поведение частот- ной характеристики в районе частоты среза c ω , где 1 ) ( = c A ω и 0 ) ( lg 20 ) ( = = c c m A L ω ω . Для устойчивой системы значение фазы на частоте среза должно быть больше, чем ° −180 . На гра- фике представлены три фазовых характеристики устойчивых систем. Кривая 1 соответствует случаю, когда в разомкнутой системе нет интеграторов (и фазовая характеристика начинается с нуля), кривая 2 – системе с одним интегратором, а кривая 3 – c двумя. Если разомкнутая система имеет неустойчивые звенья, нужно считать переходы фазовой характеристики через линию ° − = 180 ) ( ω φ левее частоты среза. Здесь положительным считает- ся переход снизу вверх, а отрицательным – сверху вниз. Если фазовая характеристика начина- ется на линии ° − = 180 ) ( ω φ (на нулевой частоте), это считается за половину перехода. Для ус- тойчивой системы разность между числом положительных и отрицательных переходов должна быть равна 2 / l , где l – число неустойчивых полюсов передаточной функции ) (s L ω m L c ω ω φ ° −180 0 0 ° − 90 1 2 3 Re Im 1 − K 2 1 − 1 + Re Im 1 − K 2 1 + © К.Ю. Поляков, 2008 62 6.6. Переходный процесс Хорошо спроектированная система должна не только быть устойчивой и поддерживать заданную точность в установившемся режиме, но и плавно переходить на новый режим при изменении заданного значения выхода (уставки). Качество переходных процессов обычно оце- нивается по переходной характеристике (реакции системы на единичный ступенчатый входной сигнал). В первую очередь нас интересует, насколько быстро заканчивается переход на другой ре- жим (время переходного процесса п t ). Оно определяется как время, через которое регулируе- мая величина «входит в коридор» шириной ∆ 2 вокруг установившегося значения ∞ y . Это зна- чит, что при п t t > значение выхода отличается от установившегося не более, чем на ∆ . Обычно величина ∆ задается в процентах от установившегося значения, чаще всего 2% или 5%. Заме- тим, что для апериодического звена с постоянной времени T время переходного процесса рав- но T t п 3 = (с точностью 5%). Другая важная характеристика – перерегулирование σ – показывает, на сколько процен- тов максимальное значение выхода max y превышает установившееся значение 12 ∞ y : % 100 max ⋅ − = ∞ ∞ y y y σ Иногда удается обеспечить нулевое перерегулирование (апериодический переходный процесс, как у апериодического звена). Нужно помнить, что увеличение быстродействия обычно приво- дит к увеличению перерегулирования. Вы уже знаете, что устойчивость линейной системы определяется полюсами ее переда- точной функции ) (s W , однако на переходные процесс влияют и нули, причем в некоторых слу- чаях очень существенно. Для примера рассмотрим передаточную функцию 2 2 ) 1 ( ) / 1 ( ) 1 ( 1 ) ( + + = + + = s a s a s as s W , где a может принимать как положительные, так и отрицательные значения. Такая передаточная функция имеет нуль в точке a s / 1 − = . Нули, на- ходящиеся в левой полуплоскости (при 0 > a ) часто называют устойчивыми (по аналогии с по- люсами), а нули в правой полуплоскости (при 0 a ) – неустойчивыми. Очевидно, что при 0 = a мы получаем апериодическое звено второго по- рядка. Теперь построим переходные характери- стики этого звена при разных значениях a . Заме- тим, что при любом a установившееся значение выхода равно 1 ) 0 ( = W 12 Понятие «перерегулирование» обычно вводится для случая, когда установившееся значение выхода больше ну- ля, хотя, в принципе, оно может быть и отрицательным – тогда перерегулирование показывает, насколько «ниже» установившегося значения ушла переходная функция в точке минимума. t y п t 0 ∞ y ∆ 2 t y п t 0 ∞ y max y ∆ 2 y 0 t 5 = a 2 = a 0 = a 2 − = a 5 − = a © К. Ю. Поляков, 2008 63 По графикам видно, что при нулевом значении a переходный процесс – апериодический. При 0 > a (устойчивый нуль) наблюдается перерегулирование, причем оно тем больше, чем больше модуль a. При отрицательных значениях a в переходном процессе есть недорегулирова- ние. Это значит, что в первый момент времени регулируемая переменная начинает изменяться в сторону, противоположную заданному значению. 6.7. Частотные оценки качества Качество системы можно оценивать не только во временнóй области (переходный про- цесс во времени), но и в частотной (по частотной характеристике). Из частотных оценок наибо- лее важны запасы устойчивости. Дело в том, что поведение реального объекта всегда несколь- ко отличается от принятой модели, более того, динамика может меняться во времени, напри- мер, когда корабль расходует топливо в ходе рейса. Поэтому недостаточно спроектировать просто устойчивую систему, нужно, чтобы система сохранила устойчивость при некоторых из- менениях параметров объекта и регулятора в сравнении с расчетными, то есть, обладала запа- сами устойчивости. Обычно арссматривают запасы устойчивости по амплитуде и по фазе. Запас устойчиво- сти по амплитуде m g – это дополнительное усиление контура, которое необходимо, чтобы вы- вести систему на границу области устойчивости. Эта величина измеряется в децибелах. Запас по амплитуде вычисляется по формуле g m A g 1 lg 20 = , где 1 g A – значение амплитудной характеристики на частоте g ω , где фазовая характеристика равна ° −180 . В практических зада- чах нужно обеспечивать запас по амплитуде не менее 6 дБ. Запас устойчивости по фазе m φ – это дополнительный сдвиг фазы («поворот» частотной характеристики против часовой стрелки), который необходим для того, чтобы вывести систему на границу устойчивости. Он определяется на частоте среза c ω , где 1 ) ( = c A ω . Запас по фазе должен быть не менее ° 30 Если в системе есть запаздывание на время τ , каждая точка годографа частотной характеристики дополнительно поворачивается против часовой стрелки на угол, равный τω для частоты ω . Поэтому запасы устойчивости (как по ам- плитуде, так и по фазе) уменьшаются. На рисунке синяя ли- ния соответствует системе без запаздывания, а красная – той же системе с запаздыванием. Видно, что во втором случае запасы устойчивости существенно меньше. Re Im K 1 − c ω g A m φ Re Im 1 − K © К.Ю. Поляков, 2008 64 Запасы устойчивости легко определяются по логарифмических частотным характеристикам: Заметим, что запас по амплитуде может быть равен бесконечности, если фазовая характеристи- ка не пересекает линию ° −180 К сожалению, в некоторых случаях классические запасы устойчивости (по амплитуде и фазе) дают не совсем верное представление о том, насколько система действительно близка к границе устойчивости. Поэтому в качестве единой характеристики иногда используют крат- чайшее расстояние γ от годографа до точки 0) ; 1 ( − Еще одна аналогичная характеристика называется 1   …   6   7   8   9   10   11   12   13   14

Определитель матрицы

Матрица представляет собой массив из множества чисел. Для

Определитель можно рассматривать как функцию, входом которой является квадратная матрица, а выходом — число. Если $n$ — это количество строк и столбцов в матрице (помните, что мы имеем дело с квадратными матрицами), мы можем назвать нашу матрицу $n \times n$ матрицей. Самая простая квадратная матрица — это матрица $1 \times 1$, которая не очень интересна, поскольку содержит только одно число. Определитель матрицы $1 \times 1$ — это само это число.

При увеличении сложности следующая квадратная матрица представляет собой $2 \times 2$ матрица, которую мы можем записать как \начать{выравнивать*} \оставил[ \begin{массив}{cc} а и б\\ CD \конец{массив} \Правильно]. \конец{выравнивание*}

Вычислим определитель этой матрицы следующим образом. Мы продолжаем по первой строке, начиная с левого верхнего компонента $a$. Мы умножить компоненту $a$ на определитель «подматрицы» формируется путем игнорирования строки и столбца $a$. В этом случае эта подматрица матрица $1 \times 1$, состоящая из $d$, и ее определитель просто $д$. Таким образом, первый член определителя равен $ad$.

Далее переходим ко второму компоненту первой строки, т.е. правая верхняя компонента $b$. Умножаем $b$ на определитель подматрица, образованная игнорированием строки и столбца $b$, т. е. $c$. Итак, следующий член определителя равен $bc$. Общий определитель это просто первый член $ad$

Хорошо, это было много работы для простого факта. Большинство студентов не есть проблемы с запоминанием определителя матрицы $2 \times 2$ без такой чепухи. Причина прохождения этого процесса должен был упростить вычисление определителя $3 \times 3$ (и больше).

Вычислим определитель матрицы $3 \times 3$ \начать{выравнивать*} \оставил[ \begin{массив}{ccc} а и б и в \\ д и д и ж \\ г и ч и я \конец{массив} \Правильно] \конец{выравнивание*} точно таким же образом. Проходим по первой строке и умножаем каждой компоненты определителем подматрицы, образованной игнорированием строку и столбец этого компонента.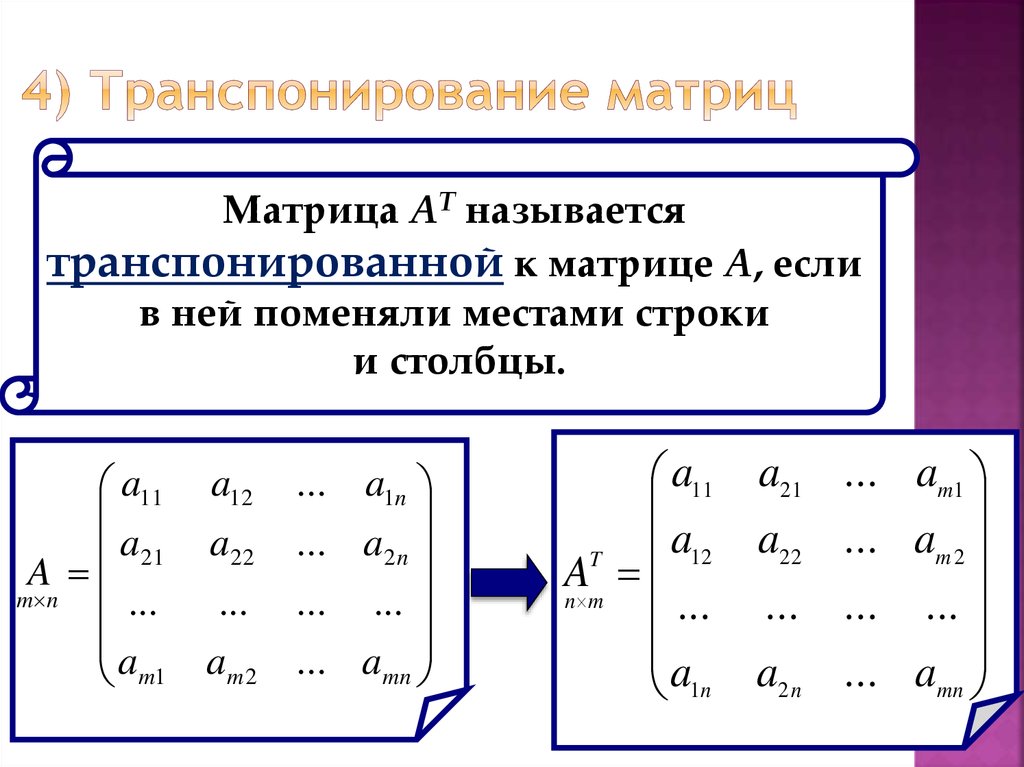

Теперь мы можем записать определитель матрицы $3 \times 3$. \начать{выравнивать*} \det\влево(\влево[ \begin{массив}{ccc} а и б и в \\ д и д и ж \\ г и ч и я \конец{массив} \верно-верно) &= a \det \left(\left[ \begin{массив}{cc} д и ж\\ Здравствуй \конец{массив} \верно-верно) -b \det\влево(\влево[ \begin{массив}{cc} д и ж\\ г и я \конец{массив} \верно-верно) +c \det \влево(\влево[ \begin{массив}{cc} д и е \\ г и ч \конец{массив} \верно-верно)\\ &=a(ei-fh) — b(di-fg) + c(dh-eg)\\ &=aei +bfg + cdh -afh -bdi -ceg \конец{выравнивание*}

Теперь, я думаю, вы могли бы запомнить окончательную формулу за 3 доллара. \times 3$ определитель. Но я предпочел бы использовать синаптическую связь моего мозга связи, чтобы сделать что-то более полезное. На самом деле, я боюсь, если я пытался запомнить это, я мог забыть что-то еще важное, например как сочетать одинаковые термины в алгебре.

Описанная выше процедура обобщается на более крупные определители. Например, чтобы вычислить определитель матрицы $4 \times 4$, у нас будет четыре члена, каждый из которых будет содержать определитель $3 x 3$. Если бы мы расширили все эти термины, используя приведенную выше формулу для определителя $3 \times 3$, вы можете себе представить, что у нас была бы довольно уродливая формула. Это слишком грязно, чтобы записывать. Но если надо, то можно. Однако обычно такие уродливые и скучные расчеты мы перекладывали на компьютер.

Ключевой факт, который следует помнить : определитель представляет собой одно число, вычисленное из матрицы.

Альтернативное обозначение

Мы часто записываем определитель $2 \times 2$ как $\left| \begin{массив}{cc} а и б\\ CD \end{array}\right|$ или определитель $3 \times 3$ как \начать{выравнивать*} \влево| \begin{массив}{ccc} а и б и в \\ д и д и ж \\ г и ч и я \конец{массив} \право|. \конец{выравнивание*} Это обозначение легче написать, чем исходное обозначение выше, поэтому мы будем часто использовать его.

Однако обратите внимание, что в этом случае вертикальные линии не среднее абсолютное значение. Определитель может быть отрицательным. В математике, нам нравится использовать одни и те же символы для обозначения разных вещей, это нормально, если это ясно из контекста. Поскольку абсолютный значение массива чисел бессмысленно, нотация однозначный.

линейная алгебра — Как интуитивно понять определитель?

Задавать вопрос

Спросил 12 лет, 2 месяца назад

Изменено 5 месяцев назад

Просмотрено 154k раз

$\begingroup$

На моем уроке линейной алгебры мы только что говорили об определителях. До сих пор я хорошо понимал материал, но теперь я очень запутался. Я понимаю, что когда определитель равен нулю, матрица не имеет обратной. Я могу найти определитель матрицы $2\times 2$ по формуле. Наш учитель показал нам, как вычислить определитель матрицы $n \times n$, разбив ее на определители меньших матриц. Видимо есть способ суммирования по куче перестановок. Но нотация действительно сложна для меня, и я действительно не знаю, что с ними происходит. Может ли кто-нибудь помочь мне интуитивно понять, что такое детерминант и как связаны все эти его определения?

• линейная алгебра
• матрицы
• определитель
• интуиция

$\endgroup$

9

$\begingroup$

Ваши проблемы с определителями довольно распространены. Их также трудно хорошо научить по двум основным причинам, которые я вижу: формулы, которые вы изучаете для их вычисления, запутаны и сложны, и нет «естественного» способа интерпретировать значение определителя, способ сначала легко интерпретировать производные, которые вы делаете в исчислении, как наклон касательной. Трудно поверить в такие вещи, как условие обратимости, которое вы изложили, когда даже неясно, что означают числа и откуда они берутся.

Вместо того, чтобы показывать, что многие обычные определения одинаковы, сравнивая их друг с другом, я собираюсь указать некоторые общие свойства определителя, которые, как я утверждаю, достаточны для того, чтобы однозначно определить, какое число вы должны получить, когда подставите его. заданная матрица. Тогда неплохо проверить, что все определения определителя, которые вы видели, удовлетворяют тем свойствам, которые я укажу.

Первое, о чем следует подумать, если вы хотите, чтобы «абстрактное» определение определителя объединило все остальные, — это то, что это не массив чисел с чертами сбоку. На самом деле нам нужна функция, которая принимает N векторов (N столбцов матрицы) и возвращает число. Предположим, что мы сейчас работаем с реальными числами. 92} \rightarrow \mathbb{R}$, затем $$ \det(a \vec v_1 +b \vec w_1 , \vec v_2 ,\ldots,\vec v_n ) = a \det(\vec v_1,\vec v_2 ,\ldots,\vec v_n) + b \det(\vec w_1, \vec v_2, \ldots,\vec v_n),$$ и соответствующее условие в каждом другом слоте.

Я утверждаю, что этих фактов достаточно, чтобы определить уникальную функцию , которая принимает N векторов (каждый длиной N) и возвращает действительное число, определитель матрицы, заданной этими векторами. Я не буду этого доказывать, но покажу вам, как это помогает при некоторых других интерпретациях определителя.

В частности, есть хороший геометрический способ представить определитель. Рассмотрим единичный куб в N-мерном пространстве: набор N векторов длины 1 с координатами 0 или 1 в каждой точке. Определитель линейного преобразования (матрицы) T представляет собой -значный объем области, полученный применением T к единичному кубу . (Не беспокойтесь слишком сильно, если вы пока не знаете, что означает «подписанная» часть).

Как это следует из нашего абстрактного определения?

Ну, если вы примените идентичность к единичному кубу, вы получите единичный куб. А объем единичного куба равен 1,

Если вы растянете куб на постоянный коэффициент только в одном направлении, новый объем будет таким же постоянным. И если вы сложите два блока вместе, выровненных в одном направлении, их общий объем будет суммой их объемов: все это показывает, что имеющийся у нас объем со знаком является линейным по каждой координате, если рассматривать его как функцию входных векторов.

Наконец, когда вы переключаете два вектора, определяющих единичный куб, вы меняете ориентацию. (Опять же, к этому можно вернуться позже, если вы не знаете, что это значит).

Таким образом, есть способы думать о детерминанте, не используя символы. Если вы изучали многомерное исчисление, вы могли бы подумать, с помощью этого геометрического определения определителя, почему определители (якобиан) появляются, когда мы меняем координаты при интегрировании. Подсказка: производная — это линейная аппроксимация связанной функции, и рассмотрите «дифференциальный элемент объема» в вашей исходной системе координат. {a\;b}_{c \;d}\Большой|$ либо: вы можете попробовать это, чтобы получить представление о вещах.

$\endgroup$

23

$\begingroup$

Определитель можно представить как объем. Думайте о столбцах матрицы как о векторах в начале координат, образующих края перекошенного прямоугольника. Определитель дает объем этой коробки. Например, в двух измерениях столбцы матрицы являются ребрами ромба.

Вы можете вывести алгебраические свойства из этой геометрической интерпретации. Например, если два столбца линейно зависимы, в вашем блоке отсутствует измерение, поэтому он был сведен до нулевого объема.

$\endgroup$

3

$\begingroup$

В дополнение к ответам, приведенным выше, определитель представляет собой функцию из набора квадратных матриц в действительные числа, которая сохраняет операцию умножения: \begin{уравнение}\det(AB) = \det(A)\det(B) \end{уравнение} таким образом, он переносит $некоторую$ информацию о квадратных матрицах в гораздо более знакомый набор действительных чисел.

Некоторые примеры:

Функция определителя отображает единичную матрицу $I$ в единичный элемент действительных чисел ($\det(I) = 1$.)

Какое действительное число имеет обратное мультипликативное число , а не ? Число 0. Итак, какие квадратные матрицы , а не имеют мультипликативные обратные? Те, которые отображаются в 0 детерминантной функцией.

Что такое определитель обратной матрицы? Обратный определитель, конечно. (и т. д.)

Это свойство определителя «сохранять операции» объясняет некоторые значения функции определителя и дает мне определенный уровень «интуиции» в работе с матрицами.

$\endgroup$

2

$\begingroup$

Вот запись моей лекции о геометрическом определении определителей:

Геометрическое определение определителей

В ней есть элементы из ответов Джейми Бэнкса и Джона Кука, и она неторопливо вдается в детали.

$\endgroup$

2

$\begingroup$

Я тоже нахожу наиболее интуитивным способ обращения с детерминантами во внешней алгебре. Определение дано на стр. 46 книги Ландсберга «Тензоры: геометрия и приложения». Два примера ниже расскажут вам все, что вам нужно знать. 92$ определяется

$$\begin{pmatrix}x\\y\end{pmatrix}\mapsto\begin{pmatrix}a&b\\c&d\end{pmatrix}\begin{pmatrix}x\\y\end{ pmatrix}.$$

Если вы определяете стандартный базисный вектор как $e_1=\begin{pmatrix}1\\0\end{pmatrix}$ и $e_2=\begin{pmatrix}0\\1\end{pmatrix }$, вы можете затем определить $f$ значениями, которые он принимает на базисных векторах: $f(e_1)=ae_1+ce_2$ и $f(e_2)=be_1+de_2$.

Линейный оператор $f$ расширяется до бивекторов с помощью $$f(e_1\клин e_2)=f(e_1)\клин f(e_2).$$

Затем вы можете написать

$$f(e_1\wedge e_2)=(ae_1+ce_2)\wedge(be_1+de_2)=(ad-bc)e_1\wedge e_2,$$

, где я использовал дистрибутивность и антикоммутативность произведения клина (последнее влечет $a\wedge a=0$ для любого вектора $a$). Итак, мы получаем определитель в виде скалярного множителя в приведенном выше уравнении, то есть

$$f(e_1\wedge e_2)=\det(A)\,e_1\wedge e_2.$$

Та же процедура работает для Матрицы 3 на 3, вам просто нужно использовать тривектор. Допустим, вам дано $$B=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32} &a_{33}\end{pmatrix}.$$ 93$

$$\begin{pmatrix}x\\y\\z\end{pmatrix}\mapsto \begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{ 22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix} \begin{pmatrix}x\\y\\z\end{pmatrix},$$

, для которого мы есть

$$g(e_1)=a_{11}e_1+a_{21}e_2+a_{31}e_3,\quad g(e_2)=a_{12}e_1+a_{22}e_2+a_{32 }e_3,\quad g(e_3)=a_{13}e_1+a_{23}e_2+a_{33}e_3$$

на стандартной основе $e_1=\begin{pmatrix}1\\0\\0 \end{pmatrix}$, $e_2=\begin{pmatrix}0\\1\\0\end{pmatrix}$, $e_3=\begin{pmatrix}0\\0\\1\end{pmatrix}$ . Оператор $g$ распространяется на тривекторы по формуле $$g(e_1\клин e_2\клин e_3)=g(e_1)\клин g(e_2)\клин g(e_3),$$

, что дает

$$g(e_1\клин e_2\клин e_3)=(a_{11}e_1+a_{21}e_2+a_{31}e_3)\клин(a_{12}e_1+a_{22 }e_2+a_{32}e_3)\wedge(a_{13}e_1+a_{23}e_2+a_{33}e_3). $$

Если затем следовать правилам $\wedge$, таким как дистрибутивность, антикоммутативность и ассоциативность, вы получаете $$g(e_1\клин e_2\клин e_3)=\det(B)\, e_1\клин e_2\клин e_3.$$

Это работает точно так же в более высоких измерениях.

$\endgroup$

1

$\begingroup$

Для протокола попробую дать ответ на этот старый вопрос, так как думаю, что к уже сказанному можно добавить кое-что.

Несмотря на то, что в основном это всего лишь (сложные) выражения, определители могут быть загадочными при первом знакомстве. Естественно возникают следующие вопросы: (1) как они определяются вообще?, (2) каковы их важные свойства?, (3) почему они существуют?, (4) почему нас это должно волновать? и (5) почему становится ли их выражение настолько огромным для больших матриц?

Поскольку определители $2\times2$ и $3\times3$ легко определяются явно, вопрос (1) можно подождать. Хотя (2) имеет много ответов, наиболее важными для меня являются следующие: определители обнаруживают (обращаясь в 0) линейную зависимость $n$ векторов в размерности $n$, и они представляют собой выражение в координатах этих векторов (а не, например, алгоритм). Если у вас есть семейство векторов, которые зависят (или хотя бы один из них зависит) от параметра, и вам нужно знать, для каких значений параметров они линейно зависят, то попытка использовать, например, исключение Гаусса для обнаружения линейной зависимости может работать к проблеме: могут потребоваться предположения о параметре, чтобы гарантировать, что какой-то коэффициент отличен от нуля, и даже тогда деление на него дает очень беспорядочные выражения. При условии, что количество векторов равно размерности $n$ пространства, взятие определителя немедленно преобразует вопрос в уравнение для параметра (которое можно или нельзя решить, но это другой вопрос). Именно так получают уравнение в задачах на собственные значения, если вы их видели. Это дает первый ответ на (4). (Но после того, как вы привыкнете к ним, вы сможете делать с детерминантами намного больше.)

Что касается вопроса (3), то загадка того, почему детерминанты вообще существуют, может быть уменьшена, если рассмотреть ситуацию, когда имеется $n-1$ заданных линейно независимых векторов, и спросить, когда окончательный неизвестный вектор $\vec x $ останется независимым от них, с точки зрения своих координат. Ответ состоит в том, что обычно так и будет, фактически всегда, если только $\vec x$ не окажется в линейной области $S$ этих $n-1$ векторов, которая является подпространством размерности $n-1$. Например, если $n=2$ (с одним заданным вектором $\vec v$), ответ будет «если только $\vec x$ не является скалярным кратным $\vec v$». Теперь, если представить себе фиксированную (не нулевую) линейную комбинацию координат $\vec x$ (технический термин — линейная форма на пространстве), то она станет $0$ именно тогда, когда $\vec x$ находится в некотором подпространстве размерности $n-1$. Если повезет, это может быть точно линейный отрезок $S$. (На самом деле здесь нет никакой удачи: если продолжить $n-1$ векторов еще одним вектором до базиса, то выражение $\vec x$ в этом базисе и взятие его конечной координаты задаст такую ​​линейную форму; как бы вы ни можете проигнорировать этот аргумент, если вы не особенно подозрительны.) Теперь важное наблюдение заключается в том, что такая линейная комбинация не только существует, но и ее коэффициенты могут быть приняты равными выражений в координатах наших $n-1$ векторов. Например, в случае $n=2$, если положить $\vec v={a\choose b}$ и $\vec x={x_1\choose x_2}$, то линейная комбинация $-bx_1+ax_2$ делает задание (оно становится равным 0 именно тогда, когда $\vec x$ является скалярным числом, кратным $\vec v$), а $-b$ и $a$ явно являются выражениями в координатах $\vec v$. На самом деле это линейных выражений. При $n=3$ с двумя заданными векторами выражения для коэффициентов линейной комбинации более сложны, но их все же можно записать в явном виде (каждый коэффициент есть разность двух произведений координат, по одному из каждого вектора). n$!

Однако нам нужно выражение, которое становится равным $0$, когда векторы линейно зависимы. Теперь волшебство (вроде как) состоит в том, что даже кажущееся гораздо более слабым требование, чтобы выражение стало $0$, когда два последовательных вектора среди $n$ равны , гарантирует это, и, кроме того, это почти навязывает форму нашего выражения на нас. Полилинейные формы, удовлетворяющие этому требованию, называются знакопеременными. Я пропущу (простые) аргументы, но чередующаяся форма не может включать термины, которые принимают одни и те же координаты любых двух разных векторов, и они должны менять знак всякий раз, когда меняются роли двух векторов (в частности, они не могут быть симметричными относительно векторов, даже если понятие линейной зависимости симметрично; обратите внимание, что уже $ -bx_1+ax_2$ не симметричен относительно перестановки $(a,b)$ и $(x_1,x_2)$). Таким образом, любой член должен включать каждую из координат $n$ один раз, но не обязательно по порядку: он применяет перестановок координат $1,2,\ldots,n$ к последовательным векторам. Более того, если терм включает одну такую ​​перестановку, то любой терм, полученный путем перестановки двух позиций в перестановке, также должен встречаться с противоположным коэффициентом. Но любые две перестановки могут быть преобразованы друг в друга повторной заменой двух позиций; таким образом, если какие-то члены вообще существуют, то должны быть члены для всех $n!$ перестановок, и все их коэффициенты равны или противоположны. Это объясняет вопрос (5), почему определитель является таким огромным выражением, когда $n$ велико.

Наконец, факт существования определителей оказывается непосредственно связанным с тем, что знаки могут быть связаны со всеми перестановками таким образом, что перестановка элементов всегда меняет знак, являющийся частью ответа на вопрос (3). Что касается вопроса (1), то теперь мы можем сказать, что определитель однозначно определяется как $n$-линейное знакопеременное выражение в элементах $n$ векторов-столбцов, содержащее член, состоящий из произведения их координат $1, 2,\ldots,n$ в таком порядке (диагональный член) с коэффициентом $+1$. Явное выражение представляет собой сумму по всем $n!$ перестановкам, соответствующий член получается путем применения этих координат в порядке перестановки и со знаком перестановки в качестве коэффициента. О вопросе (2) можно сказать еще много, но я остановлюсь здесь.

$\endgroup$

$\begingroup$

Верхняя внешняя степень $n$-мерного векторного пространства $V$ одномерна. Его элементы иногда называют псевдоскалярами, и они представляют собой ориентированные элементы $n$-мерного объема.

Линейный оператор $f$ на $V$ может быть расширен до линейного отображения на внешней алгебре по правилам $f(\alpha) = \alpha$ для $\alpha$ скаляра и $f(A \ клин B) = f(A) \клин f(B), f(A + B) = f(A) + f(B)$ для лопастей $A$ и $B$ произвольного класса. Общая информация: некоторые авторы называют это расширение внешний морфизм . Расширенная карта будет сохранять класс; т. е. если $A$ — однородный элемент внешней алгебры степени $m$, то $f(A)$ также будет иметь степень $m$. (Это можно проверить по свойствам расширенной карты, которую я только что перечислил.)

Все это означает, что линейная карта на внешней алгебре $V$, однажды ограниченная верхней внешней степенью, сводится к умножению на константу: определитель исходного линейного преобразования. Поскольку псевдоскаляры представляют ориентированные элементы объема, это означает, что определитель является именно фактором, с помощью которого карта масштабирует ориентированные объемы.

$\endgroup$

2

$\begingroup$

Здесь есть отличные ответы, очень подробные.

Здесь я даю более простой ответ, также обсуждаемый в Википедии. Думайте о определителе как о площади (в 2D; в 3D это будет объем и т. д.) параллелограмма, состоящего из векторов:

Имейте в виду, что площадь параллелограмма равна основанию $ \times$ высота . Проделав некоторые трюки со скалярным произведением, мы получим определитель:

$$ \begin{vmatrix} а и б \\ CD \end{vmatrix} = ad — bc = Area_{параллелограмм} $$

Вы можете разместить единичные векторы для каждого измерения, чтобы проверить единичную матрицу, увидев, что: $$ \begin{vmatrix} 1 и 0 \\ 0 и 1 \end{vmatrix} = ad — bc = 1 \times 1 — 0 \times 0 = 1 $$

Это объем с матрицей 3 на 3 и будет равен 1 во всех случаях, так как недиагональные элементы удаляют любой эффект от единственного значение, способствующее объему, как диагональное произведение единиц. В некоторых контекстах понимается, что система координат не изменяется.

Думая в этих терминах, мне также легче думать об сингулярных матрицах: невозможность взять обратную матрицу с определителем 0 теперь «кажется» попыткой делить на 0, так как я могу думать об определителе как «скалярное значение» матрицы. Это может не помочь другим, но если это поможет вам, отлично!

$\endgroup$

2

$\begingroup$

Если у вас есть матрица

• $H$ то вы можете рассчитать корреляционную матрицу с 9H$) = Произведение всех собственных значений $\lambda$

То есть, если у вас есть $3\times3$ матрица $H$, то $G$ тоже $3\times3$, что дает нам три собственных значения.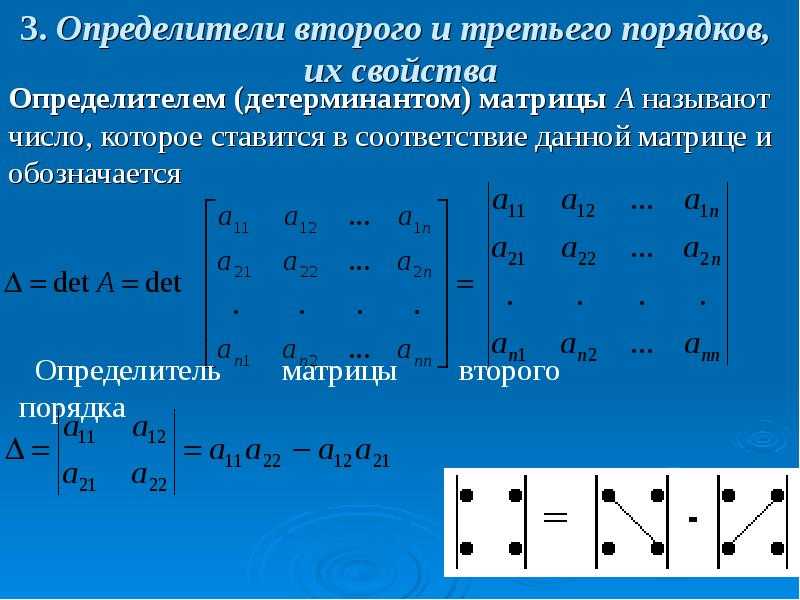 Произведение этих собственных значений равно объему прямоугольного параллелепипеда. С каждым дополнительным измерением/собственным значением кубоид получает дополнительное измерение.

$\endgroup$

$\begingroup$

(Я думал сделать это комментарием, но подумал, что он может заслужить больше внимания, чем получит комментарий. Голоса за и против покажут, прав я или нет).

Дополнение о знаке определителя

Мне понравился принятый ответ Джейми, но я был разочарован тем, что он не дал дополнительных объяснений о знаке определителя и понятии «вращение» или «ориентация» вектор. Ответ от Марка Ван Леувена больше комментирует это, но, возможно, этого недостаточно для всех — по крайней мере, для меня — чтобы понять, что означает для матрицы изменение ориентации пространства, которое она преобразует. Поэтому я погуглил этот вопрос и в итоге нашел следующее объяснение, которое я нахожу превосходным и доступным:

http://mathinsight. org/determinant_linear_transformation#lintrans3D

$\endgroup$

$\begingroup$

Хотя уже есть несколько отличных ответов, я думаю, что есть один аспект, который еще недостаточно освещен. А именно, учитывая, что матрицу можно рассматривать как представление линейного преобразования в данном базисе, что говорит нам определитель матрицы о данном преобразовании?

Предположим, у нас есть фигура в нашем векторном пространстве, любая форма , с единственным ограничением, что имеет четко определенный объем. Теперь мы можем спросить, что делает данное линейное преобразование с объемом этой формы?

Итак, первое, что мы замечаем, это то, что если мы возьмем направление, любое направление, и растянем фигуру вдоль этого направления с положительным коэффициентом, оставив все ортогональные направления неизменными, объем также будет умножен на этот коэффициент. Кроме того, если мы «растянем» фигуру с коэффициентом $0$ (сделав ее плоской), то после этого она явно будет иметь объем $0$, так что это правило хорошо распространяется и на этот пограничный случай.

Более того, если мы повернем фигуру (или оставим ее как есть), объем тоже не изменится. Обратите внимание, что не изменять громкость означает умножать громкость на единицу.

Обратите внимание, что все вышеперечисленное не зависит от формы, а является свойством только преобразования. Поэтому имеет смысл присвоить каждому такому преобразованию $T$ функцию, назовем ее $\det T$, которая сообщает нам коэффициент, который мы должны применить к объему, чтобы получить объем изображения.

Конечно, если мы делаем несколько таких преобразований подряд, и каждое умножает объем на определенный коэффициент, то умножаются и коэффициенты. То есть, $$\det(T_1T_2) = (\det T_1)(\det T_2).$$

Теперь, присмотревшись к вышеизложенному, мы видим, что мы еще не охватили все возможные преобразования. Мы рассмотрели все те преобразования, которые можно выполнить с помощью комбинаций растяжения и вращения, но мы еще не знаем, что делать при зеркальном отображении. Давайте рассмотрим конкретный случай зеркального отражения в одном направлении, то есть изменение знака одного направления на противоположное и сохранение всех остальных. Назовем это зеркальное преобразование $M$.

Ну, на первый взгляд кажется очевидным, что делать: Зеркальное отображение не изменяет объем любой формы, поэтому $\det M=1$, верно? Но затем заметим, что когда мы пишем doen $M$, это действительно растягивается с коэффициентом $-1$. Поскольку мы всегда умножаем, от этого множителя $-1$ всегда можно избавиться, применив абсолютное значение в конце. Но имеет ли этот фактор геометрический смысл?

Ну, есть много форм, которые не идентичны своему зеркальному отображению, и оказывается, что если вы хотите непрерывно преобразовывать их в свое зеркальное отображение посредством линейных преобразований, вам всегда нужно проходить через форму с объем $0$. Так что знак действительно несет геометрическую информацию, так что хранить ее также имеет смысл с геометрической точки зрения.

Поскольку все линейные преобразования могут быть получены последовательностями одномерных растяжений, вращений и одномерных зеркальных преобразований, мы теперь полностью определили значение $\det T$ для любого преобразования. Также интуитивно понятно, что оно хорошо определено (если мы достигнем одного и того же преобразования разными способами, оно все равно повлияет на объем фигур точно так же).

Теперь, когда мы определили влияние на преобразование, мы можем посмотреть, что оно означает для матрицы.

Очевидно, что диагональная матрица является произведением растяжек/отражений в координатных направлениях, поэтому определитель диагональной матрицы является просто произведением ее диагональных элементов. Замена двух столбцов или строк матрицы означает зеркальное отражение в соответствующем диагональном направлении до или после применения исходного преобразования, поэтому дает коэффициент $-1$. Если матрица необратима (столбцы линейно зависимы), изображение будет иметь нулевой объем, поэтому определитель равен $0$. И стандартные базисные векторы отображаются в столбцы вектора, поэтому единичный куб, натянутый на базисные векторы, будет отображаться в параллелепипед, натянутый на вектор-столбцы, объем которого, следовательно, будет задан как $|\det A|$.

$\endgroup$

1

$\begingroup$

Один из способов трактовки определителя, который проясняет связь между всеми упомянутыми вами различными понятиями, заключается в следующем:

Для векторного пространства $E$ размерности $n$ над полем $K$ и базиса $B =(b_1,…,b_n)$ $E$, определитель есть единственная (отличная от нуля) знакопеременная полилинейная $n$-форма $\phi$ $E$, удовлетворяющая условию $\phi(b_1,… ,b_n)=1$.

Это просто означает, что определитель представляет собой функцию $\phi$, которая принимает набор $(x_1,. ..,x_n)$ из $n$ векторов из $E$ и возвращает скаляр из поля $K$, так что

(1) $\phi$ линеен по каждой из $n$ переменных $(x_1,…,x_n)$ (многолинейно)

(2) если два из $x_i$ равны, то $\phi(x_1,…,x_n)=0$ ($\phi$ «переменная»)

(3) Оказывается, множество функций $\phi$, удовлетворяющих двум указанным выше все свойства кратны друг другу. Поэтому мы выбираем базис $B$ из $e$ и говорим, что определитель — это функция $\phi$, удовлетворяющая вышеуказанным свойствам, которая отображает $B$ в $1$.

Конечно, сразу не очевидно, что такая функция $\phi$ существует и единственна! 9n$, а базис $B$ — каноническим.

Оказывается, определитель удовлетворяет чудесному свойству $det(x_1,…,x_n) \neq 0$ тогда и только тогда, когда $(x_1,…,x_n)$ является базисом.

Теперь… даны $n$ векторов $x_1,…,x_n$, такие что координаты в базисе $B$ вектора $x_i$ равны $(a_{i,1},…,a_ {i,n})$ можно показать, что определитель $n$-векторов $x_1,…,x_n$ равен

$\sum_{\sigma \in S_n} sgn(\sigma) a_{1,\sigma(1)}. ..a_{n,\sigma(n)}$

, который должен быть вам знаком как выражение определителя в терминах перестановок. Здесь $S_n$ — симметрическая группа, т. е. множество перестановок $\{1,2,..,n\}$ и $sgn(\sigma)$ — сигнатура перестановки $\sigma$.

Чтобы связать определитель набора из $n$ векторов с определителем матрицы, заметим, что матрица $A=(a_{i,j})$ — это именно та матрица, у которой векторы-столбцы равны $ х_1,…,х_n$.

Таким образом, когда мы берем определитель матрицы, на самом деле мы вычисляем функцию с точки зрения $n$ векторов-столбцов. Ранее мы говорили, что эта функция отлична от нуля тогда и только тогда, когда $n$ векторов образуют базис, другими словами, тогда и только тогда, когда матрица имеет полный ранг, т. е. тогда и только тогда, когда она обратима.

Таким образом, абстрактное определение определителя как функции, которая отображает набор векторов в скалярное поле (при этом подчиняясь некоторым хорошим свойствам, таким как линейность), эквивалентно функции от матриц к скалярному полю, которая отлична от нуля точно, когда матрица обратима . Более того, эта функция оказывается мультипликативной! (Следовательно, ограничение этой функции на множество обратимых матриц дает гомоморфизм групп из $(Gl_n(K), \times)$ в $(K/\{0\},*)$.

Выражение определителя матрицы через перестановки может быть использовано для получения многих известных вам хороших свойств, например