| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
через диаметр и радиус.
Терминология, основные формулы и характеристика фигурыОкружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
π — 3.14
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.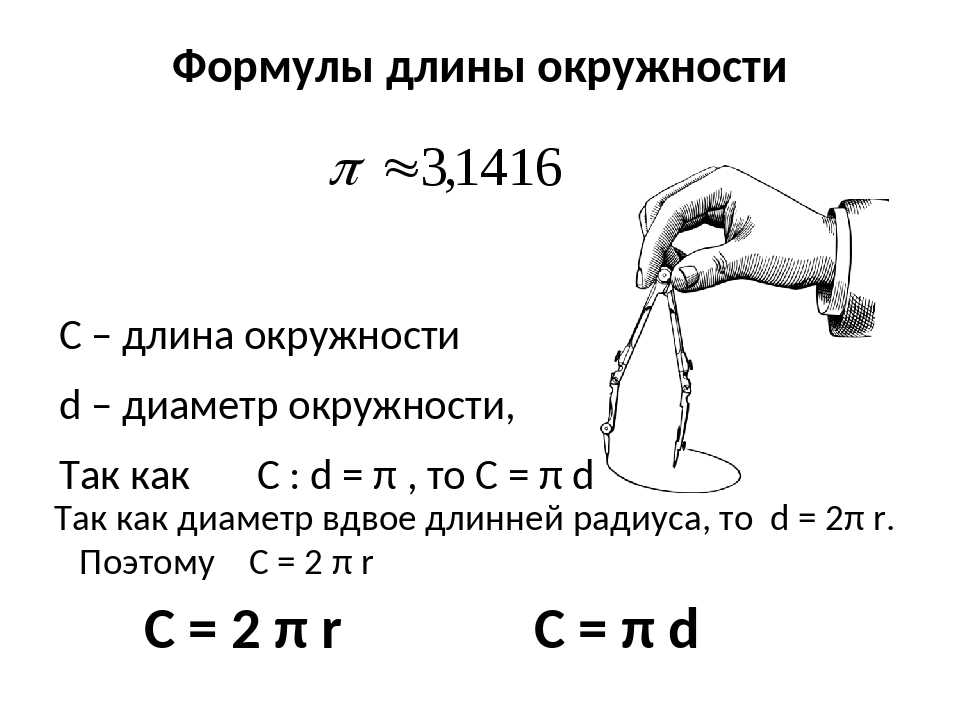
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 62,8 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Инструкция
Сначала надо исходные данные к задаче. Дело в том, что ее условии не может быть явно сказано, какова радиуса окружности .
Вместо этого в задаче может быть дана длина диаметра окружности . Диаметр окружности — отрезок, который объединяет между собой две противоположные точки окружности , проходя через ее центр. Проанализировав определения окружности , можно сказать, что длина диаметра удвоенной длине радиуса.
Теперь можно принять радиус окружности равным R. Тогда для длины окружности необходимо воспользоваться формулой:
L = 2πR = πD, где L — длина окружности , D — диаметр окружности , который всегда в 2 раза радиуса.
Обратите внимание
Окружность можно вписать в многоугольник, либо описать вокруг него. При этом, если окружность вписана, то она в точках касания со сторонами многоугольника будет делить их пополам. Чтобы узнать радиус вписанной окружности, нужно поделить площадь многоугольника на половину его периметра:
R = S/p.
Если окружность описана вокруг треугольника, то ее радиус находится по следующей формуле:
R = a*b*c/4S, где a, b, c — это стороны данного треугольника, S — площадь треугольника, вокруг которого описана окружность.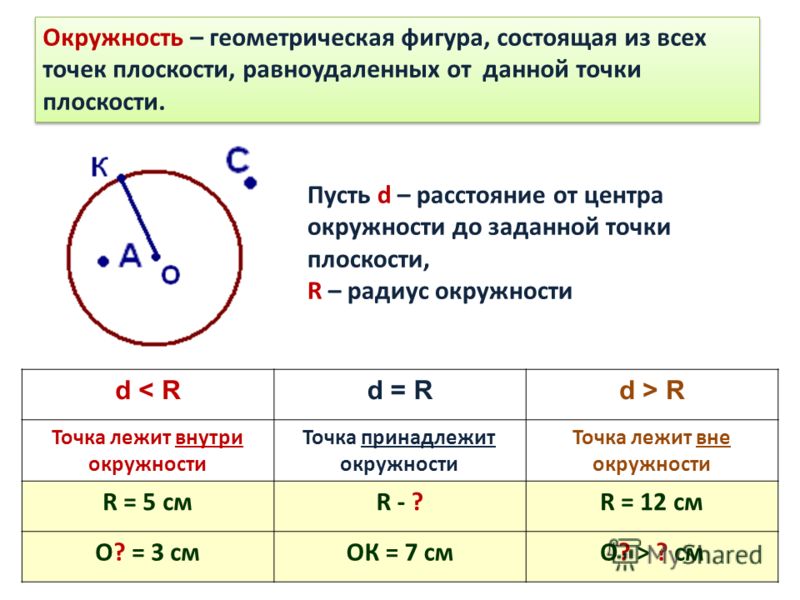
Если требуется описать окружность вокруг четырехугольника, то это можно будет сделать при соблюдении двух условий:
Четырехугольник должен быть выпуклым.
В сумме противоположные углы четырехугольника должны составлять 180°
Полезный совет
Помимо традиционного штангенциркуля, для начертания окружности можно применять и трафареты. В современных трафаретах включены окружность разных диаметров. Данные трафареты можно приобрести в любом магазине канцтоваров.
Источники:
- Как найти длину окружности?
Окружность — замкнутая кривая линия, все точки которой находятся на равном расстоянии от одной точки. Эта точка — центр окружности, а отрезок между точкой на кривой и ее центром называется радиусом окружности.
Инструкция
Если через центр окружности провести прямую линию, то ее отрезок между двумя точками пересечения этой прямой с окружностью называется диаметром данной окружности. Половина диаметра, от центра до точки пересечения диаметра с окружность — это радиус
Если окружность разрезать в произвольной точке, выпрямить и измерить, то полученная величина является длиной данной окружности.Начертите несколько окружностей разным раствором циркуля. Визуальное сравнение позволяет сделать вывод, что больший диаметр очерчивает больший круг, ограниченный окружностью с большей длиной. Следовательно, между диаметром окружности и ее длиной существует прямо пропорциональная зависимость.
По физическому смыслу параметр «длина окружности» соответствует , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
При увеличении числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Зависимость между длиной окружности L и ее диаметром D постоянна. Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью.
Нас окружает множество предметов. И многие из них имеют круглую форму. Она задана им для удобного использования. Взять, например, колесо. Если бы оно было изготовлено в форме квадрата, то как бы катилось по дороге?
Для того чтобы изготовить предмет круглой формы, нужно знать, как выглядит формула длины окружности через диаметр. Для этого сначала определим, что же представляет собой это понятие.
Круг и окружность
Окружностью является множество точек, которые размещены на равном расстоянии от основной точки — центра. Это расстояние называется радиусом.
Расстояние между двумя точками на данной линии называется хордой. Помимо того, если хорда проходит через основную точку (центр), тогда она называется диаметром.
А теперь рассмотрим, что такое круг. Совокупность всех точек, которые находятся внутри очертания, называется кругом.
Что такое длина окружности?
После того как мы рассмотрели все определения, мы можем высчитывать диаметр окружности. Формула будет рассмотрена немного позже.
Для начала мы попробуем измерить длину очертания стакана. Для этого мы обмотаем его ниткой, затем ее измерим линейкой и узнаем приблизительную длину воображаемой линии вокруг стакана. Потому что размер зависит от правильного измерения предмета, а данный способ не является надежным. Но тем не менее сделать точные измерения вполне возможно.
Для этого опять вспомним о колесе. Неоднократно мы видели, что если увеличить спицу в колесе (радиус), то увеличится и длина обода колеса (окружности). И так же при уменьшении радиуса окружности уменьшается и длина обода.
Если внимательно проследить за этими изменениями, то увидим, что длина воображаемой круглой линии пропорциональна ее радиусу. И данное число является постоянным. Дальше рассмотрим, как определяется диаметр окружности: формула для этого применится в примере ниже.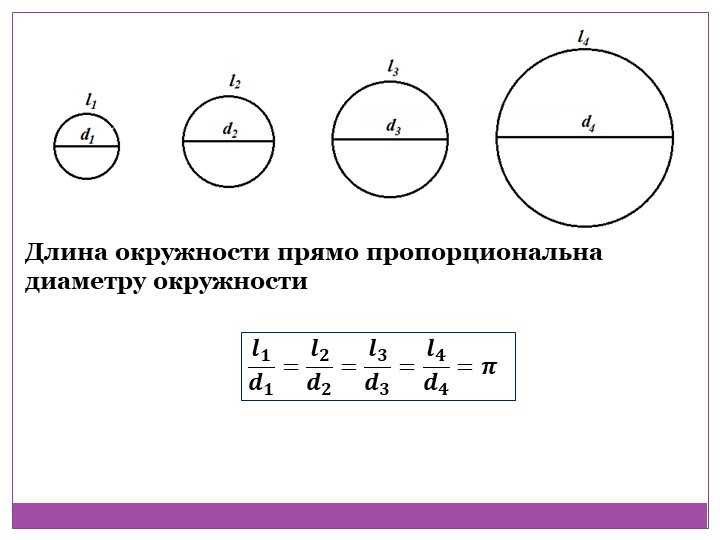
И рассмотрим ее, следуя шаг за шагом.
Формула окружности через диаметр
Поскольку длина очертания пропорциональна к радиусу, то и соответственно пропорциональна диаметру. Поэтому ее длину мы условно означим буквой C, диаметр — d. Поскольку соотношение длины очертания и диаметра — постоянное число, то его можно определить.
Проделав все подсчеты, мы определим число, которое приблизительно равно 3,1415… По той причине, что при подсчетах конкретное число не получилось, то обозначим его буквой π . Этот значок нам пригодится для того, чтобы была выведена формула длины окружности через диаметр.
Проведем воображаемую линию через центральную точку и измерим расстояние между двумя крайними. Это и будет диаметр. Если будем знать диаметр окружности, формула для определения длины ее самой будет выглядеть так: C = d * π .
Если мы будем определять длину разных очертаний, то если известен их диаметр, формула будет применена одна и та же. Поскольку знак π — это приблизительное исчисление, то и было решено умножать диаметр на 3,14 (число, округленное до сотых).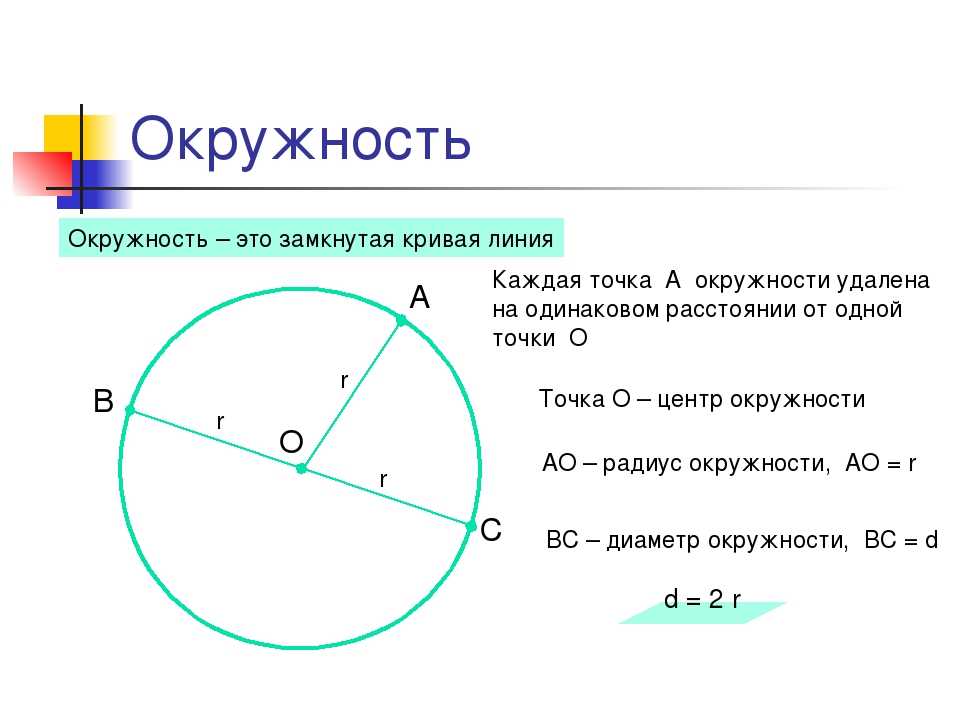
Как вычислить диаметр: формула
На этот раз попробуем с помощью данной формулы вычислить другие величины, помимо длины очертания. Чтобы вычислить диаметр по длине окружности, формула используется та же. Только для этого ее длину делим на π . Это будет выглядеть так d = C / π .
Рассмотрим, как эта формула действует на практике. К примеру, нам известна длина очертания колодца, следует вычислить его диаметр. Измерить его невозможно, поскольку из-за погодных условий нет доступа к нему. А задача у нас — изготовить крышку. Что будем делать в таком случае?
Нужно воспользоваться формулой. Возьмем длину очертания колодца — к примеру, 600 см. В формулу ставим конкретное число, а именно С = 600 / 3,14. В результате мы получим приблизительно 191 см. Округлим результат до 200 см. Затем с помощью циркуля рисуем круглую линию с радиусом в 100 см.
Поскольку очертание с большим диаметром нужно чертить соответствующим циркулем, то такой инструмент можно изготовить самому.
Для этого возьмем рейку нужной длины и на каждом конце вбиваем по гвоздю. Устанавливаем один гвоздь в заготовку и слегка его вбиваем, для того чтобы он не сдвинулся с намеченного места. А с помощью второго чертим линию. Приспособление очень простое и удобное.
Современные технологии позволяют для вычисления длины очертания использовать онлайн-калькулятор. Для этого нужно всего лишь ввести диаметр окружности. Формула будет применена автоматически. Так же можно вычислять длину окружности с помощью радиуса. Кроме того, если вы знаете длину окружности, онлайн-калькулятор вычисляет радиус и диаметр с помощью данной формулы.
Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.
Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :
S = πr 2
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7: 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 | 7 2 | = 3,14 | 49 | = | 153,86 | = 38,465 (см 2) |
| 4 | 4 | 4 | 4 |
Задача 3.
Найти радиус круга, если его площадь равна 12,56 м 2 .
Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:
r = √S : π
следовательно радиус будет равен:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πДлину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом.
Это отношение и обозначается буквой π .
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
И круг — геометрические фигуры, взаимосвязанные между собой. есть граничная ломаная линия (кривая) круга ,
Определение. Окружность — замкнутая кривая, каждая точка которой равноудалена от точки, называемой центром окружности.
Для построения окружности выбирается произвольная точка О, принятая за центр окружности, и с помощью циркуля проводится замкнутая линия.
Если точку О центра окружности соединить с произвольными точками на окружности, то все полученные отрезки будут между собой равны, и называются такие отрезки радиусами, сокращенно обозначаются латинской маленькой или большой буквой «эр» (r или R ).
Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Отрезок, соединяющий две точки окружности и проходящий через ее центр, называется диаметром. Диаметр состоит из двух радиусов , лежащих на одной прямой. Диаметр обозначается латинской маленькой или большой буквой «дэ» (d или D ).
Правило. Диаметр окружности равен двум ее радиусам .
d = 2r
D = 2R
Длина окружности вычисляется по формуле и зависит от радиуса (диаметра) окружности. В формуле присутствует число ¶, которое показывает во сколько раз длина окружности больше, чем ее диаметр. Число ¶ имеет бесконечное число знаков после запятой. Для вычислений принято ¶ = 3,14.
Длина окружности обозначается латинской большой буквой «цэ» (C ). Длина окружности пропорциональна ее диаметру. Формулы для расчета длины окружности по ее радиусу и диаметру:
C = ¶d
C = 2¶r
- Примеры
- Дано: d = 100 см.
- Длина окружности: C = 3,14 * 100 см = 314 см
- Дано: d = 25 мм.
- Длина окружности: С = 2 * 3,14 * 25 = 157 мм
Секущая окружности и дуга окружности
Всякая секущая (прямая линия) пересекает окружность в двух точках и делит ее на две дуги. Величина дуги окружности зависит от расстояния между центром и секущей и измеряется по замкнутой кривой от первой точки пересечения секущей с окружностью до второй.
Дуги окружности делятся секущей на большую и малую, если секущая не совпадает с диаметром, и на две равные дуги, если секущая проходит по диаметру окружности.
Если секущая проходит через центр окружности, то ее отрезок, расположенный между точками пересечения с окружностью, есть диаметр окружности, или самая большая хорда окружности.
Чем дальше секущая расположена от центра окружности, тем меньше градусная мера меньшей дуги окружности и больше — большей дуги окружности, а отрезок секущей, называемый хордой , уменьшается по мере удаления секущей от центра окружности.
Определение.
Кругом называется часть плоскости, лежащая внутри окружности.
Центр, радиус, диаметр окружности являются одновременно центром, радиусом и диаметром соответствующего круга.
Так как круг — это часть плоскости, то одним из его параметров является площадь.
Правило. Площадь круга (S ) равна произведению квадрата радиуса (r 2 ) на число ¶.
- Примеры
- Дано: r = 100 см
- Площадь круга:
- S = 3,14 * 100 см * 100 см = 31 400 см 2 ≈ 3м 2
- Дано: d = 50 мм
- Площадь круга:
- S = ¼ * 3,14 * 50 мм * 50 мм = 1 963 мм 2 ≈ 20 см 2
Если в круге провести два радиуса к разным точкам окружности, то образуется две части круга, которые называется секторами . Если в круге провести хорду, то часть плоскости между дугой и хордой называется сегментом окружности .
Формулы длины дуги. Длина дуги формула.
- Статьи
- Формулы длины дуги
org/ListItem»>АльфашколаДлина дуги — это расстояние вдоль части окружности, которая образует дугу. \(NM-\)длина дуги.
Измерение дуги в градусах
Длину окружности можно рассчитать следующим образом. Надо вычислить длину окружности, а затем умножить на меру дуги и
разделить полученный результат на \(360°\). Не забываем мера дуги равна величине центрального угла. Формулы длины дуги окружности:
\(L=\frac{2π r n}{360°}=\frac{π r n}{180°} \)
где \(r\)-радиус окружности, а \(n\)-мера дуги (или центрального угла) в градусах.
Радиус дуги r:
Центральный угол в радиусах n:
Если измерение дуги (или центрального угла) задано в радианах, то формула для длины дуги окружности является произведением радиуса и измерения дуги.
\(L= r × n\)
Радиус дуги r:
Мера дуги n:
где \(r\)-радиус окружности, а \(n\)-мера дуги (или центрального угла) в градусах.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Елена Вячеславовна Гришаева
Репетитор по математике
Стаж (лет)
Образование:
Рязанский государственный педагогический университет имени С. А. Есенина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор для 5-10 классов.
Выстрою с учеником его индивидуальное занятие, исходя из знаний математики. Не все задачи решаются моментально, но мы вместе будем искать самые быстрые и понятные пути решения.
Юлия Геннадьевна Ючко
Репетитор по математике
Стаж (лет)
Образование:
Минский государственный лингвистический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-9 классов. Я фанат английского языка. Хочу, чтобы и мои ученики выучили английский язык даже так же как и я и даже лучше! Коммуникативная методика, преподавание с креативом и энергией, индивидуальный подход к каждому ученику.
Елена Ивановна Качанова
Репетитор по математике
Стаж (лет)
Образование:
Витебский государственный педагогический институт им. С.М. Кирова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-8 классов. На своих уроках я применяю элементы современных образовательных технологий: здоровьесберегающие технологии, личностно-ориентированный подход, игровые технологии, технологии уровневых дифференциаций, проектное обучение, технологии проблемного обучения, также комбинирую несколько образовательных технологий в одном уроке.
С радостью жду Вас на своих занятиях!
Похожие статьи
- Признаки делимости (Часть 1)
- Площадь сферы
- Обратные тригонометрические функции
- Геологический факультет МГУ: вступительные экзамены
- Как перевести граммы в тонны?
- Иррациональные уравнения: примеры с решениями
- Задачи с прикладным содержанием (вариант 4)
- Можно ли разрешать детям пропускать занятия без причины?
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Окружность круга: определение, формулы и примеры
Окружность круга определяется как общая протяженность границы круга.
Окружность круга также известна как периметр круга. С точки зрения математических формул, периметр круга является результатом постоянного члена π и диаметра/радиуса круга. В этой статье об окружности круга вы узнаете определение, формулу, связанные термины и способы получения окружности с решенными примерами.
Окружность представляет собой круглую замкнутую структуру, все ее граничные точки равноудалены от фиксированной точки, называемой центром. Рассмотрим пример человека, бегущего по круглому саду или круглому парку. Граница, окружающая этот парк, является окружностью этого конкретного круга. Посмотрите на приведенное ниже изображение:
Окружность круга Определение Известная нам окружность описывается как форма, в которой все местоположения равноудалены от точки в центре. Определение длины окружности в математике — это расстояние по окружности. Это одномерная линейная оценка границы любой двумерной круглой поверхности.
Узнайте больше об ортогональных окружностях в этой связанной статье. периметр круга.
Отношение между диаметром и окружностью равно \(C=\pi D,\ \pi=\frac{C}{D}\)
Где \( \pi=\frac{22}{7}или\ 3.14\) и d – диаметр окружности.
Подробную информацию о круговой диаграмме см. здесь.
Формула длины окружности кругаКруг представляет собой двумерную фигуру, занимающую площадь и периметр. Периметр круга также называется окружностью, которая является мерой окружности. Площадь круга – это область, окруженная им в двумерной плоскости.
Длина окружности (или) периметра круга в единицах радиуса=\(2\pi R\)
Здесь R — радиус круга, π равно 3,14 или \(\frac{22}{7 }\)
Кроме того, Окружность в терминах диаметра=\(\pi D\)
Здесь D — диаметр окружности.
Окружность/периметр является линейной величиной, и ее единицы измерения такие же, как единицы длины. Если мы откроем круг и создадим из него прямую линию, то его диапазон будет окружностью. Обычно он измеряется в единицах, таких как см или единица м.
Узнайте больше о геометрических фигурах здесь.
Как найти длину окружности?Хотя окружность круга является его длиной, ее нельзя определить с помощью шкалы, как это обычно делается для других многоугольников, таких как квадраты, треугольники и прямоугольники. Это связано с изогнутой формой круга. Мы можем оценить длину окружности с помощью следующих подходов.
Подход 1: Мы можем проследить путь окружности с помощью нити и пометить точки на нити. Длину нити позже можно откалибровать с помощью обычной линейки. Например, рассмотрим, если нам дали круглую тарелку и спросили о ее окружности.
Шаг 1: Теперь, используя описанный выше подход; мы можем взять нить и вращать ее вокруг круглой пластины.
Шаг 2: Затем отметьте начальную и конечную точки на резьбе.
Шаг 3: Наконец, измерьте длину нити (от начальной до конечной точки), используя шкалу для окружности.
Подход 2: Точный способ узнать длину окружности в геометрии — вычислить ее. Поэтому для определения длины окружности мы используем формулу, включающую радиус или диаметр окружности и значение Пи (π).
Начнем с того, что если нам дан радиус и нужно рассчитать длину окружности, то необходимо выполнить следующий процесс:
Предположим, что радиус любого случайного круга равен 28 см, тогда мы можем получить длину окружности, выполнив следующие шаги:
Шаг 1: Проверяем выданные нам данные, здесь нам выдаются с радиусом.
Шаг 2: Примените формулу: \(C=2\pi r\). (Здесь C=длина окружности, r=радиус и π=22/7)
Шаг 3: Подставляя значения в формулу, получаем нужный ответ.
Шаг 4: \(C=2\pi r=2\times\frac{22}{7}\times28=176\text{ см}\)
Аналогичным образом, если нам дано диаметр, мы можем выполнить следующие шаги.
Рассмотрим диаметр любого случайного круга, равный 7 см, и тогда задается длина окружности:
Шаг 1: Проверьте предоставленные нам данные, здесь нам дан диаметр.
Шаг 2: Примените формулу: \(C=\pi D\). (Здесь C=длина окружности, D=радиус и π=22/7 или 3,14)
Шаг 3: Подставляя значения в формулу получаем нужный ответ.
Шаг 4: \(C=\pi D=\frac{22}{7}\times7=22\text{ см}\)
Окружность к диаметруОкружность к диаметру для данного круг — это соотношение, используемое для определения стандартного определения числа Пи (π).
C= πd
Разделите обе части на d.
C/d = π
Если мы разделим обе части уравнения (C= πd) на диаметр (d), мы получим значение, примерно равное π.
Здесь C=длина окружности и d=диаметр.
Это означает, что если нам известен диаметр, мы можем получить длину окружности, используя приведенное выше соотношение.
Узнайте больше об уравнении окружности здесь.
Решенные примеры на окружности окружностиПри всем знании определения и формулы пришло время попрактиковаться в некоторых решенных примерах для того же самого:
Решенный пример 1: Найдите длину окружности, радиус которой 21 см.
Решение: Дано: Радиус окружности\(=21\см.\) 92\)
Решено Пример 3 : Найдите длину окружности, диаметр которой равен 14 см.
Решение: Дано: Диаметр круга = 14 см.
⇒ Длина окружности =\(\pi D\ =\frac{22}{7}\times 14\ \text{cm}=44\ \text{cm}\)
Проверьте некоторые формулы среднего здесь.
Решено Пример 4 : Окружность валика 440см. Определить радиус ролика.
Решение: Окружность ролика = 440 см
⇒ Окружность круга = \(2\pi r\)
⇒ \(C=440=2\times\frac{22}{7}\times R\ )
⇒ R=70 см, а так как диаметр=2r, диаметр=2* 70=140 см
Мы надеемся, что приведенная выше статья об окружности поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы о длине окружностиВ.1 Какова формула длины окружности?
Ответ 1 Формула длины окружности выглядит следующим образом: \(2\pi R\)
Q.2 Что такое длина окружности?
Ответ 2 Окружность – это измерение окружности. Другими словами, можно сказать, что это периметр круга.
Q.
3 Как рассчитать длину окружности?
Ответ 3 Длину окружности можно рассчитать через радиус и диаметр следующим образом: Окружность (или) периметр окружности через радиус =\(2\pi R\)
с точки зрения диаметра=\(\pi D\)
Q.4 Каков периметр круга?
Ответ 4 Периметр круга есть не что иное, как длина окружности круга.
Q.5 Что такое символ окружности?
Ответ 5 Окружность представлена буквой «C». Окружность эквивалентна периметру фигуры, например параллелограмма.
Скачать публикацию в формате PDF| Площадь круга: изучите расчет площади с помощью формулы диаметра, окружности, прямоугольников и треугольников | |||||||||||||
| Площадь треугольника: изучите формулы, методы, сокращения здесь! | |||||||||||||
| Среднее значение в математике: определение, статистика с типами, формулами и ключевыми терминами | |||||||||||||
| Концепции человеческого развития ООН: подходы, показатели, ИЧР | |||||||||||||
Основы окружающей среды: факторы поддержания жизни, циклы окружающей среды 902 974 902 974 906 902 974 Экологические циклы 906Окружность круга – определение и формула Когда вы видите мяч, внешняя периферия мяча, видимая вам, является окружностью мяча. Окружность круга — ОпределениеДлина окружности — это длина границы окружности . Если мы разрежем круг и выпрямим его, длина границы будет мерой окружности круга. Окружность состоит из множества точек, расположенных на равном расстоянии от одной центральной точки. Эта точка известна как центр окружности . Расстояние между центром и любой точкой окружности называется радиусом окружности. Радиус является постоянной величиной. Это не меняется. Диаметр окружности — это максимальное расстояние между любыми двумя точками на окружности. Это в два раза больше радиуса. Формула длины окружностиОкружность окружности измеряется в таких единицах длины, как метр, сантиметр и т. д. Формула для расчета окружности: Окружность = 2πR Где R — радиус окружности, π ( pi) является постоянной величиной. Значение π = 3,1415926535897… π или пи — это греческая буква. Это очень важная константа в математике. Он дает отношение длины окружности к диаметру круга или отношение длины окружности к удвоенному радиусу. Для любого заданного круга это отношение останется равным π. Это константа, поэтому какими бы ни были длина окружности и радиус, отношение будет равно π. π — иррациональное число, поэтому его нельзя записать в виде конечного десятичного числа. Его значение равно 3,14159.26535… Его значение идет до бесконечных десятичных разрядов. Но использование бесконечного числа сделает вычисления практически невозможными. Вопрос: Найдите длину окружности, если радиус равен 14 см. (используйте π = 22/7) Ответ: R(дано) = 14 см Окружность = 2πR = 2 * 22/7 * 14 = 88 см Вопросы:1. Если длина окружности равна 24 см, найдите радиус этой окружности. 2. Найдите длину окружности, если радиус равен 22 см. (используйте π = 22/7). 3. Найдите длину окружности, если радиус равен 36 см. (используйте π = 3,14). 4. Если длина окружности 120 см, найдите радиус этой окружности. 5. Если длина окружности равна 68 см, найдите радиус этой окружности. Основные компоненты окружности1. Центр окружности: Центром окружности называется центральная точка окружности, от которой все расстояния до этой точки равны. 2. Диаметр: Хорда или линия, проходящая через центр окружности, называется диаметром. Диаметр считается самой длинной хордой в окружности. Диаметр в два раза больше радиуса. 3. Радиус: Постоянное расстояние от его центра называется радиусом окружности. Компоненты круга Площадь кругаПлощадь круга — это площадь, ограниченная окружностью. Это площадь внутри окружности. Окружность — единственная длина. Его ширина равна нулю. Он одномерный. Область не является одномерной. Формула для расчета площади круга: Площадь = πR 2 Где R — радиус круга, π — константа. Здесь снова значение π не является конечным. Поэтому для упрощения расчетов можно использовать π = 3,14 или π = 22/7. Если нам нужно вычислить длину окружности, площадь которой задана, мы сначала найдем радиус по площади, а затем подставим его в формулу для длины окружности. Из площади, чтобы получить радиус, мы должны сначала разделить на π, а затем найти из него квадратный корень. Это даст нам радиус. Затем просто введите значение радиуса в формулу для длины окружности, чтобы найти длину окружности. Можно также найти площадь круга, если известна длина окружности. Для этого сначала мы должны разделить длину окружности на π, а затем на 2. Это даст нам радиус. Затем введите радиус в формулу площади, чтобы вычислить площадь. Свойства кругаОкружность состоит из некоторых свойств i) Внешняя линия круга равноудалена от центра. ii) Диаметр круга делит его на 2 равные части и проходит через центр. iii) Круги разного размера или радиуса подобны. iv) Диаметр окружности равен наибольшей хорде и равен удвоенному радиусу. Решенный Пример длины окружностиВ 1. Какова длина окружности с радиусом 7 см? Ответ: Окружность или $\mathrm{C}=2 \pi \mathrm{r}=2 \times \pi \times \mathrm{r}=2 \times \dfrac{22}{7} \times 7= 44 \mathrm{~cm}$ В 2. ЗаключениеВот так мы вычисляем длину окружности и понимаем ее отличие от площади. Это одномерная физическая величина, которую легко понять и вычислить, если проследить, как определяется формула. Сосредоточьтесь на решенных примерах и начните использовать формулу, чтобы лучше понять концепцию. Формула нахождения длины окружности через радиус. Как найти длину окружности по диаметру и радиусу. Терминология, основные формулы и характеристика фигурыТаким образом, длина окружности ( C ) может быть вычислена путем умножения константы π на диаметр ( D ), или путем умножения π на удвоенный радиус, так как диаметр равен двум радиусам. Отсюда формула длины окружности будет выглядеть так: C = πD = 2πR где C — длина окружности, π — постоянная, D — диаметр окружности, R — это радиус окружности. Поскольку окружность является границей окружности, длину окружности также можно назвать длиной окружности или периметром окружности. Задачи на длину окружностиЗадание 1. Найдите длину окружности, если ее диаметр равен 5 см. Так как длина окружности π умножаем на диаметр, тогда длина окружности круга диаметром 5 см будет равна: C ≈ 3,14 5 = 15,7 (см) Задача 2. Найдите длину окружности, радиус которой равен 3,5 м. Сначала найдите диаметр окружности, умножив длину радиуса на 2: D = 3,5 2 = 7 (м) Теперь найдите длину окружности, умножив π на диаметр: С ≈ 3,14 7 = 21,98 (м) Задача 3. Найдите радиус окружности, длина которой 7,85 м. Чтобы найти радиус круга, зная его длину, разделите длину окружности на 2. π Площадь круга Площадь круга равна произведению числа π в квадрат радиуса. S = pr 2 где S площадь круга, а r радиус круга. Поскольку диаметр круга в два раза больше радиуса, радиус равен диаметру, деленному на 2: Задачи на площадь кругаЗадача 1. Найдите площадь круга, если его радиус равен 2 см. Так как площадь круга равна π умножить на радиус в квадрате, то площадь круга радиусом 2 см будет равна: S ≈ 3,14 2 2 = 3,14 4 = 12,56 (см 2) Задача 2. Найдите площадь круга, если его диаметр равен 7 см. Сначала найдите радиус окружности, разделив ее диаметр на 2: 7:2=3,5(см) Теперь вычислим площадь круга по формуле: S = pr 2 ≈ 3,14 3,5 2 = 3,14 см 12,25 3,25 = 8,26 ) Эту задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
Задача 3. Чтобы найти радиус круга, зная его площадь, разделите площадь круга на π , а затем извлеките квадратный корень из результата: r = √ S : π , поэтому радиус будет: r ≈ √12,56: 3,14 = √4 = 2 (м) ЧислоπОкружность окружающих нас предметов можно измерить с помощью сантиметровой ленты или веревки (нити), длину которой затем можно измерить отдельно. Но в некоторых случаях трудно или почти невозможно измерить окружность, например, внутреннюю окружность бутылки или просто нарисованную на бумаге окружность. В таких случаях можно вычислить длину окружности, если известна длина ее диаметра или радиуса. Чтобы понять, как это можно сделать, возьмем несколько круглых предметов, у которых можно измерить и длину окружности, и диаметр. Вычисляем отношение длины к диаметру, в результате получаем следующий ряд чисел: Отсюда можно сделать вывод, что отношение длины окружности к ее диаметру является постоянной величиной для каждой отдельной окружности и для всех круги в целом. Используя эти знания, вы можете использовать радиус или диаметр круга, чтобы найти его длину. Например, чтобы вычислить длину окружности радиусом 3 см, нужно радиус умножить на 2 (так мы получим диаметр), а полученный диаметр умножить на π . Наконец, с числом π мы узнали, что длина окружности радиусом 3 см равна 18,84 см. Инструкция Сначала необходимо исходные данные к заданию. Дело в том, что в его условии нельзя явно сказать, что такое радиус окружностей . Вместо этого в задаче можно задать длину диаметра кругов . Диаметр окружности отрезка, соединяющего две противоположные точки окружности проходят через его центр. Проанализировав определения окружностей , можно сказать, что длина диаметра вдвое больше длины радиуса. Теперь радиус окружностей можно принять равным R. Тогда для длины окружностей нужно использовать формулу: примечание Окружность может быть вписана в многоугольник или описана вокруг него. При этом если окружность вписанная, то она разделит их пополам в точках соприкосновения со сторонами многоугольника. Чтобы найти радиус вписанной окружности, нужно площадь многоугольника разделить на половину его периметра: Полезный совет Помимо традиционного штангенциркуля, для рисования круга можно использовать трафареты. В современные трафареты входит круг разного диаметра. Эти трафареты можно приобрести в любом канцелярском магазине. Источники:
Окружность — замкнутая кривая линия, все точки которой находятся на равном расстоянии от одной точки. Эта точка является центром окружности, а отрезок между точкой на кривой и ее центром называется радиусом окружности. Инструкция Если через центр окружности проведена прямая, то ее отрезок между двумя точками пересечения этой прямой с окружностью называется диаметром этой окружности. Половина диаметра, от центра до точки пересечения диаметра с окружностью, составляет радиус Нарисуйте несколько кругов с помощью различных растворов компаса. Визуальное сравнение приводит к выводу, что больший диаметр очерчивает большую окружность, ограниченную окружностью большей длины. Следовательно, существует прямо пропорциональная зависимость между диаметром круга и его длиной. По физическому смыслу соответствует параметру «длина окружности», ограниченная ломаной линией. Если в окружность вписан правильный n-угольник со стороной b, то периметр такой фигуры P равен произведению стороны b на число сторон n: P = b*n. Сторону b можно определить по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписан n-угольник. С увеличением числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Отношение между длиной окружности L и ее диаметром D постоянно. Отношение L/D=n*Sin(π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «пи» и выражаемой бесконечной десятичной дробью. Для расчетов без использования вычислительной техники принято значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для круга разделите его длину на π = 3,14. Окружность — это изогнутая линия, охватывающая окружность. Окружность имеет несколько характеристик, на основании которых производятся расчеты, связанные с этой геометрической фигурой. К ним относятся: диаметр, радиус, площадь и окружность. Эти характеристики взаимосвязаны, то есть для их расчета достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле, можно найти длину окружности, диаметр и ее площадь.
Как найти длину окружности? Теперь давайте узнаем. Окружность: формулаДля обозначения этой характеристики выбрана латинская буква p. Архимед также доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле значение p равно πd, то есть длине окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, ту же формулу длины окружности можно записать как p=2πr. Рассмотрим применение формулы на примере простых задач: Задание 1У основания Царь-колокола диаметр 6,6 метра. Чему равна окружность основания колокола?
Ответ: Окружность основания колокола 20,7 метра. Задача 2Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли 6370 км. Какова длина круговой орбиты спутника?
Ответ: длина круговой орбиты спутника Земли 42013,2 км. Методы измерения длины окружностиРасчет длины окружности на практике применяется нечасто. Причиной этого является приблизительное значение числа π. В быту для нахождения длины окружности используют специальный прибор — курвиметр. На окружности отмечают произвольную точку отсчета и ведут прибор от нее строго по линии, пока снова не достигнут этой точки. Как найти длину окружности? Нужно только иметь в виду простые формулы для расчетов. Здесь одной строки недостаточно, нужно знать специальные формулы. Единственное, что от нас требуется, это определить диаметр или радиус окружности. Формулы, которые должен знать каждый Еще почти 4000 лет назад ученые обнаружили удивительную зависимость: если длину окружности разделить на ее диаметр, то получится одно и то же число, равное примерно 3,14. Это значение было названо именно с этой буквы в древнегреческом языке, началось слово «периметр» и «окружность». На основании открытия, сделанного древними учеными, можно вычислить длину любой окружности: Где Р означает длину (периметр) окружности, D — диаметр, P — число «Пи». Длина окружности также может быть рассчитана через ее радиус (r), который равен половине длины диаметра. Вот вторая формула, которую нужно запомнить: Как найти диаметр круга? Представляет хорду, проходящую через центр фигуры. Способ 1: вписать прямоугольный треугольник в окружность Вычислить длину окружности не составит труда, если мы найдем ее диаметр. Нужно нарисовать окружность, где гипотенуза будет равна диаметру окружности. Для этого необходимо иметь под рукой линейку и угольник, иначе ничего не получится. Способ 2: вводим любой треугольник На стороне круга отмечаем любые три точки, соединяем их — получаем треугольник. Важно, чтобы центр круга лежал в районе треугольника, это можно сделать на глаз. К каждой стороне треугольника проводим медиану, точка их пересечения будет совпадать с центром окружности. А когда мы знаем центр, мы можем легко провести диаметр с помощью линейки. Этот способ очень похож на первый, но может быть использован при отсутствии квадрата или в случаях, когда нет возможности рисовать на фигуре, например, на тарелке. Пример задачи
1. Труднее найти длина окружности по диаметру Итак, давайте сначала рассмотрим этот вариант. Пример: Найдите длину окружности диаметром 6 см . Воспользуемся приведенной выше формулой для длины окружности, но сначала нам нужно найти радиус. Для этого делим диаметр 6 см на 2 и получаем радиус окружности 3 см. |
Итак, простыми словами, Окружность не что иное, как периметр круга или эллиптического объекта. Эта концепция доставляет удовольствие не только в обучении, но и в обучении. В этой статье мы представляем вам очень важную и интересную концепцию геометрии, которая представляет собой Окружность круга .
Поэтому для расчетов можно использовать π = 22/7. Это упрощает расчеты. Мы также можем принять значение π = 3,14. Для еще большего упрощения можно принять значение π = 3.
Какова длина окружности, диаметр которой равен 6 см? 9{2}$
Формула нахождения площади круга :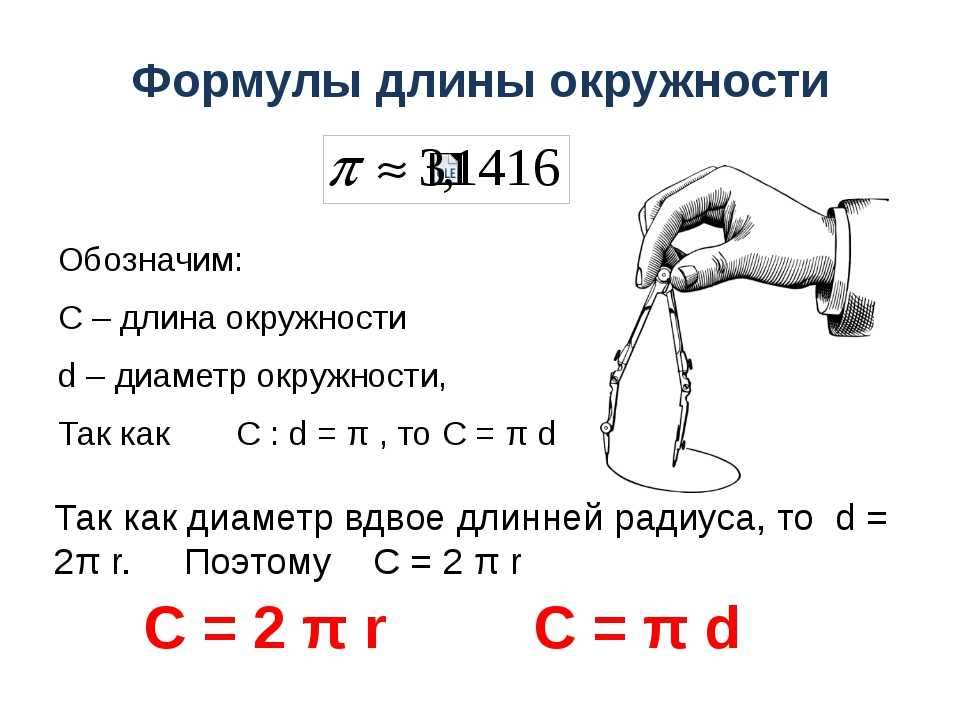
Найдите радиус круга, если его площадь равна 12,56 м2.
Это отношение обозначается буквой π .
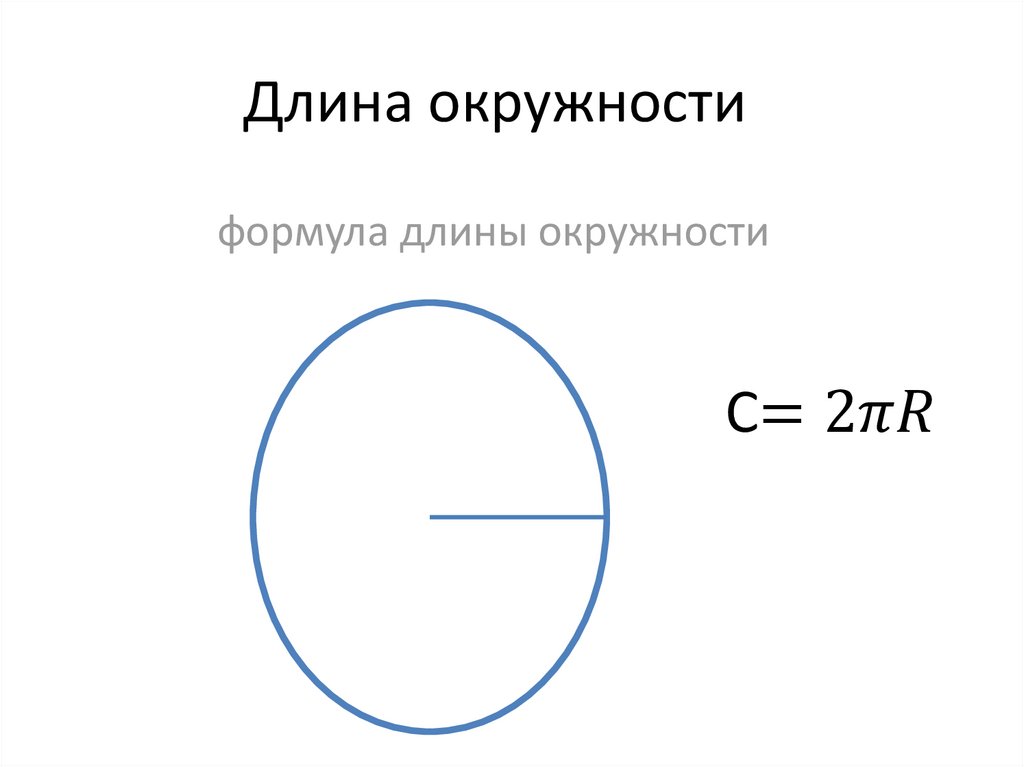
В геометрии фигуры плоские, поэтому определение относится к двумерному изображению. Предполагается, что все точки этой кривой находятся на равном расстоянии от центра окружности.
Поэтому хорда, проходящая через него, также называется диаметром.
В некоторых заданиях эти величины указаны. Но что, если у нас нет ничего, кроме рисунка? Без проблем. Диаметр и радиус можно рассчитать с помощью обычной линейки. Теперь приступим к самому основному.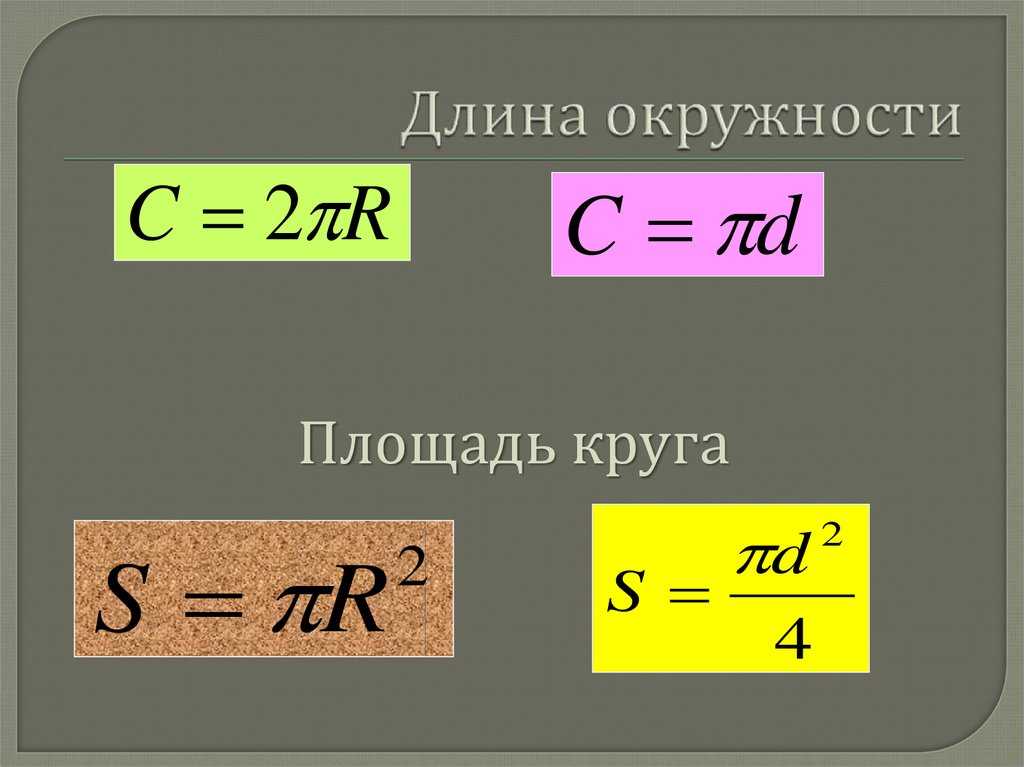
При этом он соединяет две самые удаленные точки окружности. Исходя из этого, вы можете самостоятельно начертить диаметр (радиус) и измерить линейкой его длину.
Необходимо взять лист бумаги с прямыми углами. Прикладываем лист к окружности так, чтобы одна вершина его угла соприкасалась с краем окружности. Далее отметьте точками места пересечения сторон бумаги с линией окружности. Соединяем эти точки карандашом и линейкой. Если у вас нет ничего под рукой, просто сложите бумагу. Эта линия будет равна длине диаметра.