Как рассчитать площадь и периметр помещения и в каких случаях следует ее знать?
Любое важное начинание надо просчитывать заранее, ремонт не исключение. Поскольку затраты предстоят большие, надо их оптимизировать и уменьшить по максимуму, особенно, если хочется сделать что-то дорогостоящее, например натяжные потолки с несколькими уровнями. Если покупать материалы «на глазок», легко можно ошибиться – купить или слишком много или придется идти в магазин и докупать недостающие стройматериалы. Для того, чтобы не купить лишнего дорогого стройматериала и сэкономить семейный бюджет, надо знать, как рассчитать площадь помещения. Вот с этого то и начнем.
В каких случаях нужны расчеты?
Расчет квадратных метров обязателен, если в проекте установить подвесные потолки. Для наглядности посмотрим, что нужно для гипсокартонных конструкций. Площадь комнаты рассчитывается, чтобы закупить гипсокартон в нужном количестве, а периметр надо знать для покупки пристенного профиля для установки обрешетки. Гипсокартон и профиля берем с запасом примерно 15-20% на обрезку, ведь не всегда можно изобразить на бумаге точный эскиз расположения на потолке гипсокартона или декоративных панелей.
Гипсокартон и профиля берем с запасом примерно 15-20% на обрезку, ведь не всегда можно изобразить на бумаге точный эскиз расположения на потолке гипсокартона или декоративных панелей.
Для заказа натяжного потолка делать расчет квадратуры комнаты требуется, что запланировать будущие траты и проконтролировать фирму-установщика в правильности их расчетов. Фирма, изготавливающая натяжные потолки обычно указывает цену за квадратный метр и плюсует работу по установке. Зная площадь и стоимость квадрата, можно легко определить конечную цену.
Вычислить площадь требуется даже для банальной покраски пола или потолка, чтобы знать, сколько закупать краски. Важно купить нужное количество краски, иначе если не хватит, а краску в магазине колорировали, то можно не угадать с цветом. Примерный расход краски на метр квадратный поверхности указывается на банке.
Пример расчета потребности в краске:
Квадратура пола составляет 30 м2
расход краски согласно данным на упаковке – 0,20 кг/м2
30 х 0,2 = 6 кг
Полагается брать краску свыше расчетного количества на 10%.
Поэтому получаем 6 + 10% = 6,6 кг. Это подойдет ведро 7 кг или приближенная расфасовка в зависимости от вида краски.
Как посчитать площадь комнаты
Если вы владелец небольшой прямоугольной комнаты, то большого труда вычислить квадратуру комнаты это не составит. Достаточно вспомнить школьный курс геометрии. А что делать, если на месте потолка сложный многоугольник или имеются всевозможные ниши или выступы?
Прямоугольная комната
Приступаем к расчетам. Повторение – мать учения, поэтому для тех, кто забыл, как считать площадь комнаты и ее периметр, напомним курс пятого класса. К примеру, имеем типовую прямоугольную комнату с шириной равной 2,5м и длиной, равной 4 м. Тогда, площадь равна длине, умноженной на ширину, или 2,5 х 4 =10 м2 . Периметр в нашем примере равен сумме длин всех сторон или 2,5 + 4 + 2,5 + 4 = 13м. Значит для натяжного потолка вам надо заказать пленку размером 10 м2 и приобрести профилей суммарной длины 18 + 20% (на обрезку) = 15,6 м. Естественно, при покупке багетов надо округлить суммарную длину до значения, кратного длине одной планки. Если в магазине имеется двухметровый профиль, то потребуется купить 16 м или 8 планок.
Если в магазине имеется двухметровый профиль, то потребуется купить 16 м или 8 планок.
Комната сложной формы
Очень часто в домах старой постройки встречаются комнаты с нишами, выступами, встроенными кладовками. Нам предстоит решить задачку посложнее, но оказывается все просто. Потребуется лист в клетку или простой, на котором мы нарисуем эскиз комнаты с приблизительным сохранением пропорций. Далее измеряем метраж прямых стен и записываем на эскизе рядом с соответствующими линиями, обозначающими стены.
А вот теперь порисуем. Эскиз надо разбить на прямоугольники при помощи угольника и линейки, соблюдая прямые углы. Причем, одной из сторон прямоугольника должна быть измеренная полная стена. Теперь надо вычислить квадратные метры каждого из нарисованных прямоугольников и суммировать их. Периметр вычислить в любом случае проще – просто складываем длины всех стен и закоулочков.
Расчет площади многогранной комнаты
Что делать, если в комнате есть «срезанные» или не прямые углы? Нам предстоит задача в три действия, но сначала опять же замеряем все стены, не забывая про скосы, и рисуем эскиз. Вот, как этот к примеру.
Вот, как этот к примеру.
Теперь начинается чистая геометрия. Первое действие – принимаем наш скос за гипотенузу прямоугольного треугольника, соединяем катеты. Остается применить формулу для вычисления прямоугольного треугольника, которая выглядит следующим образом: S = катет х катет /2. Катет у нас вычисляется так: известная длина стены равная 1,75 м (см. чертеж) минус противоположная стена 1,18 м. Получаем 0.57 м. Аналогично вычисляем другой катет, используя длины других противоположных стен.
Исходя из этого найдем площадь треугольника 0,57 х 0,57 / 2 = 0.57 м2
Второе действие – разделение комнаты на два прямоугольника без учета уже посчитанного треугольника. См. рисунок.
Далее повторяем расчеты в предыдущем примере для комнаты с нишей. Затем останется сложить площади всех полученных простых фигур, и получим квадратуру помещения.
В заключение
Не стоит скрупулезно обмерять и высчитывать все значения. В любом случае будет погрешность около 5%, но сколь либо серьезно это значение не влияет на расчеты. Можно не брать во внимание небольшие скругления углов. Если надо рассчитать площадь стен для закупки отделочных материалов, то действуем по первому примеру с правильным прямоугольником, вычитая площадь окон и дверей. В наших домах стандартная высота потолков может разниться в каждом из углов, поэтому берем большее значение с учетом обрезки. Пусть лучше будет небольшой запас, чем потом думать, как выйти из ситуации. Удачи вам в ремонте!
Можно не брать во внимание небольшие скругления углов. Если надо рассчитать площадь стен для закупки отделочных материалов, то действуем по первому примеру с правильным прямоугольником, вычитая площадь окон и дверей. В наших домах стандартная высота потолков может разниться в каждом из углов, поэтому берем большее значение с учетом обрезки. Пусть лучше будет небольшой запас, чем потом думать, как выйти из ситуации. Удачи вам в ремонте!
Калькулятор вычисления периметра и площади геометрических фигур
Определение периметра и площади геометрических фигур — важная задача, которая возникает при решении многих практических или бытовых задач. Если вам требуется поклеить обои, установить забор, рассчитать расход краски или кафеля, то вам обязательно придется иметь дело с геометрическими расчетами.
Для решения перечисленных бытовых вопросов вам потребуется работать с самыми разными геометрическими фигурами. Мы представляем вам каталог онлайн-калькуляторов, которые позволяют вычислить параметры наиболее популярных плоских фигур. Рассмотрим их.
Рассмотрим их.
Круг
Окружность — это множество точек на плоскости, которые равноудалены от центра на некоторое расстояние, называемое радиусом. Многие считают круг и окружность синонимами, однако это не так. Круг — это часть плоскости, ограниченная окружностью. Вы можете отыскать периметр и площадь круга, но у окружности найти можно только длину, так как она представляет собой кривую, не имеющую площади. Длина окружности или периметр круга находятся по простой формуле:
l = 2 pi × R,
где R – радиус фигуры.
Площадь круга рассчитывается согласно следующему выражению:
S = pi R2
Круги часто встречаются в реальной жизни. В основном это основания цилиндрических и конических деталей, а также просто круглые поверхности, например, круглые столики, диски, грампластинки или катушки. Вид окружности имеют колеса, обручи или кольца. В трехмерной реальности окружность превращается в сферу, а круг — в шар. Форму этих геометрических тел имеют многие реальные и природные объекты. Благодаря своей эффективности круг охватывает максимальную площадь при минимальном периметре. Именно поэтому форму шара имеют капли, снежные комья, метеориты или планеты.
Благодаря своей эффективности круг охватывает максимальную площадь при минимальном периметре. Именно поэтому форму шара имеют капли, снежные комья, метеориты или планеты.
Треугольник
Треугольник — первая гармоничная фигура на плоскости, ограниченная тремя отрезками. Свойства треугольника известны людям с античных времен: изучение фигуры стартовало в Древнем Египте и не завершено до сих пор. Огромный вклад в изучение свойств фигуры внесли Евклид, Эйлер и Лобачевский, но даже сегодня продолжается работа над поиском замечательных точек треугольника, которых на данный момент найдено более 6 тысяч. Для определения периметра фигуры достаточно сложить длины всех сторон треугольника по формуле:
P = a + b + c,
где a, b, c – стороны.
Для вычисления площади треугольника используется 5 различных формул плюс нахождение площади через определенный интеграл. Самое простое выражение для вычисления площади:
S = 0,5 a × h,
где a — сторона треугольника, h — его высота.
Наш калькулятор позволяет отыскать площадь или периметр треугольника, зная разные комбинации нескольких параметров, таких как углы, стороны или радиусы связанных окружностей.
Треугольники не слишком распространены в реальной повседневности. В природе они практически не встречаются, за исключением кристаллических решеток некоторых молекул или формы ушей у рыси. А вот в технике, геометрии и прикладных науках треугольник — царь и бог. Наибольшее применение находит следующий тип фигуры.
Прямоугольный треугольник
Прямоугольный треугольник — особая вариация фигуры, у которой две стороны обязательно образуют прямой угол. Эти стороны называются катетами, а противолежащая им сторона — гипотенузой. Соотношение катетов и гипотенузы лежит в основе евклидовой геометрии — эти соотношения определяются теоремой Пифагора. Изучение свойств прямоугольного треугольника положило начало одному из важных разделов математики — тригонометрии, которая используется в самых разных прикладных сферах от компьютерных игр до океанографии.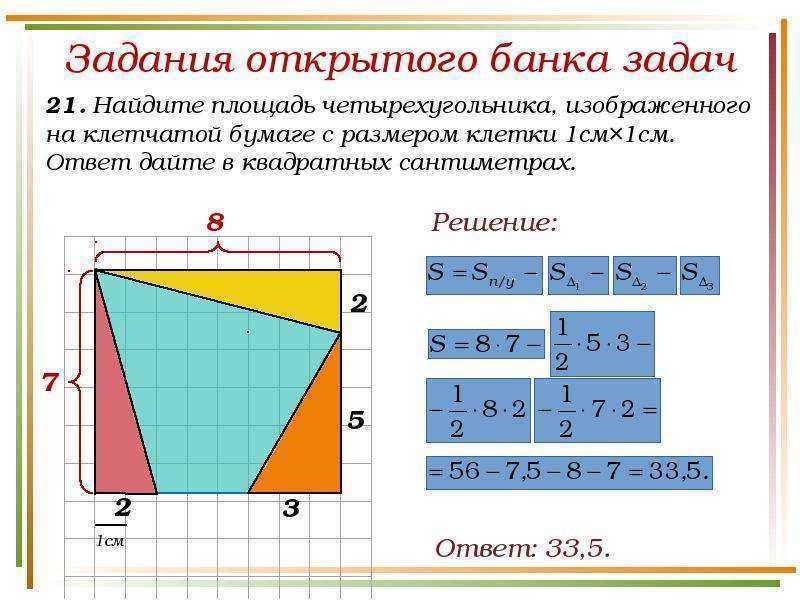
Формулы для вычисления периметра и площади прямоугольного треугольника ничем не отличаются от формул для обычных вариаций данной фигуры или вытекают из них.
Трапеция
Трапеция, как и слово трапеза, по-гречески означают «стол». Это плоская фигура, ограниченная четырьмя прямыми, две из которых параллельны, а две — нет. По сути, это выпуклый четырехугольник, поэтому параллелограмм и прямоугольник считаются частными случаями трапеции. В общем случае все стороны трапеции имеют разную длину, и для вычисления периметра используется формула:
P = a + b + c + d,
a, b, c и d – стороны четырехугольника.
Площадь фигуры определяется как:
S = 0,5 (a + b) × h,
где a и b – параллельные стороны трапеции, h – высота.
Трапеция очень часто встречается в рукотворном мире. Грани многих предметов имеют вид этого четырехугольника, а буквально трапецеидальную форму имеют такие объекты как автомобильные окна, паруса, скаты крыш или юбки.
Параллелограмм
Параллелограмм — это элегантный четырехугольник, пары сторон которого параллельны друг другу. Любой четырехугольник становится параллелограммом, если его противолежащие стороны параллельны, диагонали в точке пересечения разделяются пополам, а противоположные углы равны. Для вычисления периметра параллелограмма используется простая формула, которая иллюстрирует сумму попарно равных сторон:
Любой четырехугольник становится параллелограммом, если его противолежащие стороны параллельны, диагонали в точке пересечения разделяются пополам, а противоположные углы равны. Для вычисления периметра параллелограмма используется простая формула, которая иллюстрирует сумму попарно равных сторон:
P = 2 (a + b).
Площадь параллелограмма не зависит от величины его углов, и находится по следующей формуле:
S = a × h.
Параллелограммы часто встречаются в реальной жизни: это грани многих призматических объектов, очертания полей, спортивных площадок или клумб. Форму параллелограммов имеют практически все отделочные материалы: плитка, кафель, гипсокартон, паркет. Такое разнообразие обусловлено тем, что частными случаями параллелограмма являются прямоугольник, ромб и квадрат, формулы для определения периметров и площадей которых аналогичны или выводятся из теоремы Пифагора.
Частные случаи
Ромб — четырехугольник с одинаковыми сторонами. Параллелограмм становится ромбом в случаях, если его диагонали пересекаются под углом 90 градусов и являются биссектрисами своих углов.
Прямоугольник — это параллелограмм с прямыми углами. Кроме того, параллелограмм считается прямоугольником, если его стороны и диагонали отвечают условиям теоремы Пифагора.
Квадрат — это параллелограмм, у которого все стороны равны и все углы равны. Диагонали квадрата полностью повторяют свойства диагоналей прямоугольника и ромба, что делает квадрат уникальной фигурой, которая характеризуется максимальной симметрией.
Многоугольник
Правильный полигон — это выпуклая фигура на плоскости, которая имеет равные стороны и равные углы. В зависимости от количества сторон многоугольники имеют собственные названия:
- пять сторон — пентагон;
- шесть — гексагон;
- восемь — октагон;
- двенадцать — додекагон.
И так далее. Геометры шутят, что круг — это многоугольник с бесконечным количеством углов. Наш калькулятор запрограммирован на определение периметров и площадей только правильных многоугольников. Он использует общие формулы для всех правильных полигонов. Для вычисления периметра используется формула:
Для вычисления периметра используется формула:
P = n × a,
где n – количество сторон многоугольника, a – длина стороны.
Для определения площади используется выражение:
S = n/4 × a2 × ctg(pi/n).
Подставляя соответствующее n, мы можем подобрать формулу для любого правильного многоугольника, к которым также относятся равносторонний треугольник и квадрат.
Многоугольники имеют большое распространение в реальной жизни. Так форму пятиугольника имеет здание министерства обороны США — Пентагон, гексагона — пчелиные соты или кристаллы снежинки, октагона — дорожные знаки. Кроме того, многие простейшие, например радиолярии, имеют форму правильных полигонов.
Примеры из реальной жизни
Давайте рассмотрим пару примеров использования нашего калькулятора в реальных расчетах.
Покраска забора
Покраска поверхностей и расчет краски — это одни из самых очевидных бытовых задач, в которых требуются минимальные математические расчеты. Если нам нужно покрасить забор, высота которого составляет 1,5 метра, а длина 20 метров, то сколько потребуется банок краски? Для этого нужно узнать суммарную площадь забора и расход лакокрасочных материалов на 1 квадратный метр. Мы знаем, что расход эмали составляет 130 грамм на метр. Теперь определим площадь забора, используя калькулятор для вычисления площади прямоугольника. Она составит S = 30 квадратных метров. Естественно, что забор мы будем красить с обеих сторон, поэтому площадь для покраски увеличится до 60 квадратов. Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.
Мы знаем, что расход эмали составляет 130 грамм на метр. Теперь определим площадь забора, используя калькулятор для вычисления площади прямоугольника. Она составит S = 30 квадратных метров. Естественно, что забор мы будем красить с обеих сторон, поэтому площадь для покраски увеличится до 60 квадратов. Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.
Отделка бахромой
Пошив одежды — еще одна отрасль, в которой необходимы обширные геометрические познания. Пусть нам надо отделать бахромой платок, который представляет собой равнобедренную трапецию со сторонами 150, 100, 75 и 75 см. Для вычисления расхода бахромы нам потребуется узнать периметр трапеции. В этом нам и пригодится онлайн-калькулятор. Введем эти данные ячейки и получим ответ:
P = 400
Таким образом, нам понадобится 4 м бахромы для отделки платка.
Заключение
Плоские фигуры составляют реальный мир вокруг. Мы часто задавались в школе вопросом, пригодится ли нам геометрия в будущем? Выше приведенные примеры показывают, что математика постоянно используется в повседневной жизни. И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей. Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.
И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей. Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.
Можно ли по периметру вычислить площадь прямоугольника? – Обзоры Вики
Делим периметр пополам. Вычтите длину одной стороны из половины периметра, эта разница и будет длиной другой стороны. Перемножьте эти стороны вместе, и это будет площадь прямоугольника.
Отсюда можно ли найти площадь по периметру? Какова его площадь? Разделите периметр на 4: это дает вам длину одной стороны. Затем возведите эту длину в квадрат: это даст вам площадь.
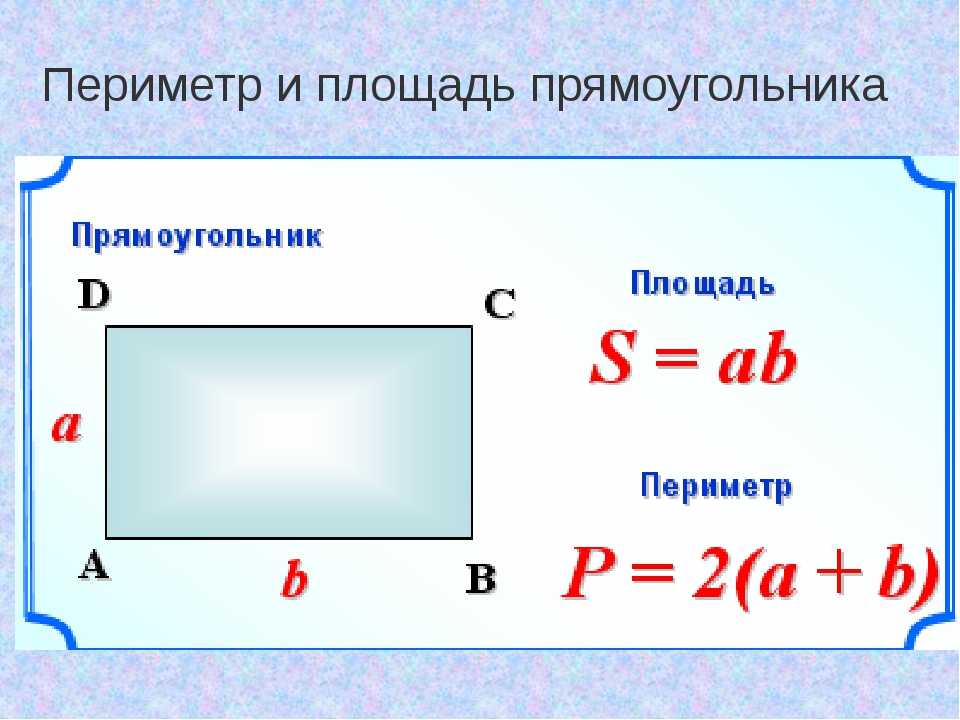
Какая формула площади прямоугольника? Чтобы найти площадь прямоугольника, нам просто нужно умножить его длину на ширину. Площадь — это просто произведение ширины прямоугольника на высоту. Формула для вычисления площади прямоугольника представлена в виде. Площадь = ш × в.
Площадь — это просто произведение ширины прямоугольника на высоту. Формула для вычисления площади прямоугольника представлена в виде. Площадь = ш × в.
По какой формуле вычисляется периметр прямоугольника?
Формула периметра прямоугольника гласит, что Р = (Д + Ш) × 2, где P обозначает периметр, L обозначает длину, а W обозначает ширину. Когда вам даны размеры прямоугольной формы, вы можете просто подставить значения L и W в формулу, чтобы найти периметр.
Какие формулы площади и периметра? Таблица формул площади и периметра
| цифры | Формула площади | Переменные |
|---|---|---|
| Площадь прямоугольника | Площадь = l × w | l = длина w = ширина |
| Площадь Квадрата | Площадь = а 2 | a = стороны квадрата |
| Площадь треугольника | Площадь = 1/2 ш × в | b = основание h = высота |
| Площадь круга | Площадь = πr 2 | r = радиус круга |
• 30 сентября 2020 г.
Что такое параметр прямоугольника? Периметр прямоугольника — это общее расстояние от его внешней границы. Он вдвое больше суммы его длины и ширины и рассчитывается по формуле: Периметр = 2 (длина + ширина).
Как найти периметр двух прямоугольников?
Умножьте сумму длины и ширины на два.
После того, как вы сложили длину и ширину прямоугольника, вы можете найти его периметр, умножение на два.
Также Что такое периметр и площадь квадрата и прямоугольника? Периметр прямоугольника равен P=2b+2h, где b — основание (или ширина), а h — высота (или длина). Если прямоугольник является квадратом со сторонами длиной s, формула для периметра будет Psquare=2s+2s=4s, а формула площади будет Квадрат=s⋅s=s2.
Что такое единицы площади и периметра?
Единицы периметра такие же, как и длины, т.е. м, см, мм и т.д.. Площадь: помимо плоскости, заключенной в простую замкнутую фигуру, называется плоской областью, а измерение замкнутой плоской области называется ее площадью. Площадь измеряется в квадратных единицах.
Площадь измеряется в квадратных единицах.
Существуют ли прямоугольники с одинаковым периметром? прямоугольники размеры 8 × 2 и 5 × 5 имеют одинаковый периметр (20) но разные районы. Увеличение площади связано с увеличением минимального периметра. Четырехугольник с наименьшим периметром для данной площади является квадратом. и а = 2(1+ г) г .
Чему равна площадь периметра квадрата?
Площадь квадрата = сторона × сторона = сторона² квадратных единиц
Следовательно, периметр квадрата будет равен: Периметр = 4 x сторона = 4 √Единицы площади. Таким образом, мы можем найти периметр квадрата, зная его площадь.
Все ли прямоугольники площадью 24 единицы имеют одинаковый периметр?
так.. это не может быть одинаковым. периметры могут быть одинаковыми, но площадь не может быть.
Периметр прямоугольника равен площади? Существуют разные единицы измерения периметра и площади. в тех же единицах, что и длина сторон прямоугольника или квадрата тогда как единица площади возведена в квадрат.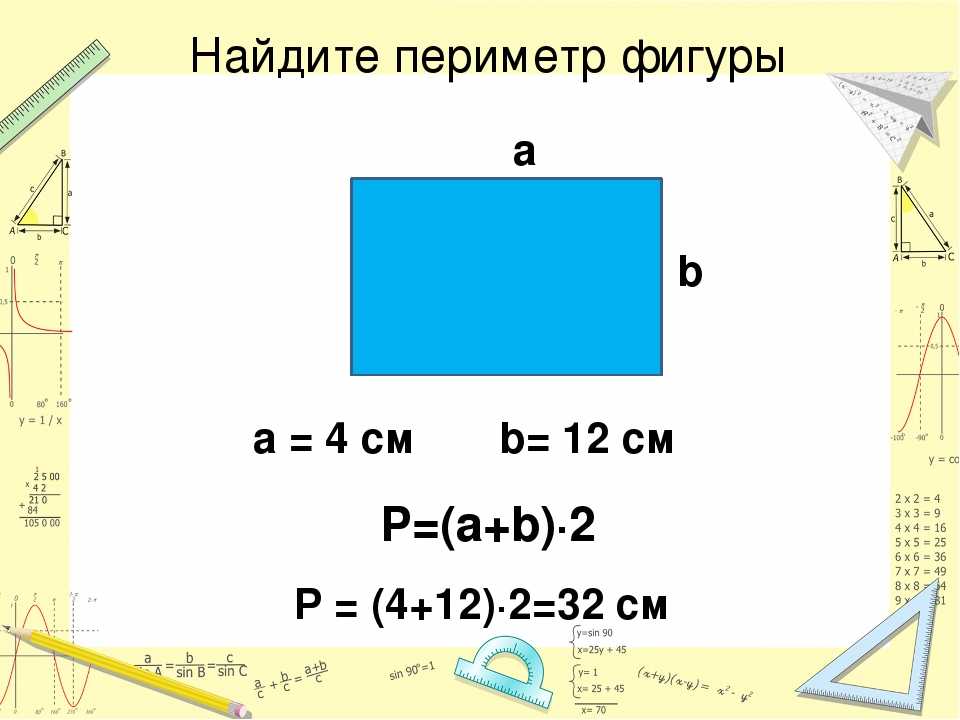
Можно ли нарисовать прямоугольники с одинаковым периметром, но разными площадями? Цель: Учащиеся узнают, что несколько прямоугольников могут имеют одинаковый периметр, но их площадь может быть разной.
Чему равна площадь квадрата и прямоугольника?
Квадратный. Площадь = а2. а = длина стороны. Прямоугольник. Площадь = ш × ч.
Площадь и периметр квадрата одинаковы? Ответ: Площадь одного квадрат равен квадрату длины его стороны а периметр квадрата в 4 раза больше длины его стороны.
Какова площадь квадрата 12 см?
Таким образом, площадь квадрата 144 см2.
Как два разных прямоугольника могут иметь периметр 24 см? На разных прямоугольниках используйте размеры 1″x11″, затем 2″x10″, затем 3″x9″, затем 4″x8″, затем 5″x7″, затем квадрат 6″x6″. (Квадрат — это тоже прямоугольник.) Все эти прямоугольники имеют одинаковый периметр. Это 24″.
Почему прямоугольники с одинаковым периметром имеют разную площадь?
Любые прямоугольник всегда будет иметь больше этих блоков, выставленных наружу, чем прямоугольник. квадрат той же площади. Это доказывает, что прямоугольник всегда будет иметь больший периметр, чем квадрат той же площади. Это означает, что если прямоугольник и квадрат имеют одинаковый периметр, прямоугольник должен иметь меньшую площадь.
квадрат той же площади. Это доказывает, что прямоугольник всегда будет иметь больший периметр, чем квадрат той же площади. Это означает, что если прямоугольник и квадрат имеют одинаковый периметр, прямоугольник должен иметь меньшую площадь.
Какие фигуры имеют одинаковую площадь и периметр? Двумерная равная фигура (или идеальная форма) тот, площадь которого численно равна его периметру. Например, прямоугольный треугольник со сторонами 5, 12 и 13 имеет площадь и периметр, оба имеют безразмерное числовое значение 30.
Как найти площадь и периметр одинаковыми?
Как перевести площадь в периметр? Связь между площадью и периметром квадрата заключается в том, что периметр в 4 раза больше квадратного корня из площади. Чтобы получить периметр из площади квадрата, умножьте квадратный корень из площади на 4 . Периметр всегда измеряется в линейных единицах, которые выводятся из квадратных единиц площади.
Периметр всегда измеряется в линейных единицах, которые выводятся из квадратных единиц площади.
Чем равны площадь и периметр?
В геометрии площадь — это двумерное пространство или область, занимаемая замкнутой фигурой, а периметр — это расстояние вокруг замкнутой фигуры, т. е. длина границы. Две фигуры могут иметь одинаковый периметр, но разные площади или могут иметь одинаковую площадь, но разные периметры. …
Что такое единицы площади?
Площадь — это площадь поверхности, которую может покрыть двумерная фигура, измеряемая в квадратных единицах. Единицей площади в СИ является квадратный метр (м2), которая является производной единицей.
Аннотация Этот урок предназначен для изучения математических понятий длины, периметра и площади. Эти действия и обсуждения могут быть использованы для развития понимания учащимися этих математических понятий. ЦелиПо окончании данного занятия учащиеся будут:
СтандартыУпражнения и обсуждения на этом уроке касаются следующих Стандарты НКТМ: Геометрия Анализировать характеристики и свойства двух- и трехмерных геометрических формы и разработать математические аргументы о геометрических соотношениях
Измерения Применять соответствующие методы, инструменты и формулы для определения измерений
Требования к учащимся
Подготовка учителейСтудентам понадобятся:
Основные терминыЭтот урок знакомит учащихся со следующими терминами посредством обсуждений:
План урока
|
Периметр и площадь | Предварительная алгебра | Периметр, площадь и объем
Дополнительные темы
по периметру и площадиПопулярные учебные пособия
по периметру и площадиКак найти длину прямоугольника, если известны его ширина и площадь?
Как найти длину прямоугольника, если известны ширина и площадь? Этот урок покажет вам, как!
Какая формула для периметра прямоугольника?
Какова формула периметра прямоугольника? Этот учебник покажет вам, как найти эту формулу!
Как найти периметр фигуры?
К вам когда-нибудь подходил человек на улице, вручал фигуру и просил найти ее периметр? Посмотрите этот урок, и в следующий раз вы будете готовы!
Как найти периметр прямоугольника?
Найти периметр прямоугольника так же просто, как сложить все его стороны! В этом учебном пособии вы пройдете шаги, необходимые для нахождения периметра прямоугольника.

Что такое площадь?
Площадь — это количество места, которое занимает фигура! Этот урок знакомит с площадью и объясняет, как мы находим площадь фигуры.
Как найти ширину прямоугольника, если известны его длина и периметр?
Пытаетесь вычислить недостающую длину стороны прямоугольника? Есть периметр и длина другой стороны? Затем вы можете использовать эту информацию и формулу для периметра прямоугольника, чтобы найти недостающую длину! Этот урок покажет вам, как!
Как найти площадь прямоугольника?
Чтобы найти площадь прямоугольника, умножьте длину на ширину! Этот урок покажет вам, как найти площадь прямоугольника. Проверьте это!
Как найти площадь треугольника?
Как найти площадь треугольника? Знать длину основания и высоту? Затем просто возьмите эти значения, подставьте их в формулу площади треугольника и решите! В этом руководстве показано, как это сделать.

Как найти площадь параллелограмма?
Ищете площадь параллелограмма? Получили длину основания и высоту? Затем подставьте эти значения в формулу площади параллелограмма и решите. Этот урок проведет вас через весь процесс!
Как найти площадь трапеции?
Хотите найти площадь трапеции? Если у вас есть длина каждого основания и высота, вы можете использовать их, чтобы найти площадь. В этом уроке вы увидите, как определить эти значения и подставить их в формулу площади трапеции. Тогда посмотрите, как упростить, чтобы получить ответ!
Как найти высоту треугольника, если известны площадь и основание?
Хотите найти высоту треугольника? Уже знаете площадь и длину основания? Затем вы можете использовать формулу площади треугольника, чтобы найти недостающее измерение! Посмотрите этот урок, чтобы узнать, как это сделать!
Как найти основание параллелограмма, если известны площадь и высота?
Хотите найти длину основания параллелограмма? Уже знаете площадь и высоту? Затем вы можете использовать формулу площади параллелограмма, чтобы найти недостающее измерение! Посмотрите этот урок, чтобы узнать, как это сделать!
Как найти высоту трапеции, если известны площадь и основания?
Хотите найти высоту трапеции? Уже знаете площадь и длину обоих оснований? Затем вы можете использовать формулу площади трапеции, чтобы найти недостающее измерение! Посмотрите этот урок, чтобы узнать, как это сделать!
Как найти площадь составной фигуры?
Составные фигуры — это всего лишь замаскированная комбинация более простых фигур! В этом уроке вы увидите, как разбить составную фигуру на более простые фигуры.
 Затем посмотрите, как найти площадь каждой из этих отдельных фигур, чтобы найти площадь всей составной фигуры. Смотрите весь процесс в этом уроке!
Затем посмотрите, как найти площадь каждой из этих отдельных фигур, чтобы найти площадь всей составной фигуры. Смотрите весь процесс в этом уроке!Что такое составная фигура?
Вы когда-нибудь замечали, что некоторые фигуры выглядят как комбинация нескольких других фигур? Фигуры такого типа называются составными фигурами. Этот урок знакомит вас с составными фигурами и показывает, как разбить составную фигуру на несколько фигур. Взглянем!
Какая формула площади прямоугольника?
Пытаетесь найти площадь прямоугольника? Есть формула, которая может помочь! Посмотрите этот урок, чтобы узнать о формуле площади прямоугольника.
Какая формула площади треугольника?
Знаете ли вы, что формулу площади треугольника можно найти, используя формулу площади параллелограмма? В этом уроке вы увидите, как это делается! Взглянем!
Какая формула площади параллелограмма?
Параллелограммы и прямоугольники очень похожи.
 На самом деле, вы можете превратить параллелограмм в прямоугольник, чтобы найти формулу площади параллелограмма! Посмотрите этот урок, чтобы увидеть, как это делается!
На самом деле, вы можете превратить параллелограмм в прямоугольник, чтобы найти формулу площади параллелограмма! Посмотрите этот урок, чтобы увидеть, как это делается!Какая формула площади трапеции?
Пытаетесь вычислить формулу площади трапеции? Вы можете начать с создания параллелограмма из двух трапеций. Затем используйте формулу площади параллелограмма, чтобы вычислить формулу площади одной трапеции. Этот урок покажет вам, как!
Площадь и периметр: разговоры учащихся о математике
Исследования показывают, что учащиеся лучше всего учатся, когда они сотрудничают и говорят о математике. Мои 25 с лишним лет в классе говорят мне, что это действительно так, но я сделаю еще один шаг и заявлю, что математический дискурс также может повысить уровень вовлеченности, мотивации и волнения. Я решил поделиться некоторыми подробностями о некоторых недавних работах в области и по периметру в моем классе, чтобы посмотреть, смогу ли я показать вам, что я имею в виду. Ресурсы, используемые на этих фотографиях, — это мои действия по области и периметру и мои карты задач по области и периметру.
Ресурсы, используемые на этих фотографиях, — это мои действия по области и периметру и мои карты задач по области и периметру.
Работа в парах с разделением обязанностей
Одна из первых задач по области и периметру, которую я выполняю, — это работа в парах, так как я хочу подготовить почву для нескольких вещей. Во-первых, во время этого модуля мы работаем почти ПОЛНОСТЬЮ совместно. Во-вторых, я хочу, чтобы ученики осознали силу второй пары глаз! Мы усердно работали над этой задачей, и я дал каждому партнеру разные задачи: один отвечал за «построение» прямоугольников, а другой отвечал за запись.
Я позвал свою группу «записывающих», чтобы помочь им стать экспертами в разнице между дюймами и квадратными дюймами, и сказал им, что они несут ответственность за использование правильного языка на протяжении всего урока. Я позвал «строителей», чтобы сказать им, что их работа состоит в том, чтобы ПОПРОСИТЬ у своего партнера предложения, а затем довести их до конца. Было очень весело ходить и подслушивать, как они работали, выполняя свою работу!
(Примечание: меня часто спрашивают, где я беру эти плитки. Я использую их для МНОГИХ вещей… они из пеноматериала, они недорогие и тихие! Моя партнерская ссылка ниже, если вы хотите их увидеть…)
Я использую их для МНОГИХ вещей… они из пеноматериала, они недорогие и тихие! Моя партнерская ссылка ниже, если вы хотите их увидеть…)
Сложность работы в больших группах
Давайте будем честными. Работа в парах достаточно сложна для младших школьников. При этом мне ДЕЙСТВИТЕЛЬНО нравится время от времени подталкивать их к работе с большими группами, чтобы мы могли обсудить с ними проблемы. Для решения этой задачи по области и периметру ученики работали в командах по ШЕСТЬ (я знаю!). Правила? Они должны были решить задачу (которая включала в себя разработку формы площадью 24 квадратных дюйма, которая уместилась бы на определенной сетке), И никакие два члена команды не могли иметь одинаковый периметр. Это означало, что им нужно поговорить. Это означало, что им нужно было задавать вопросы. Наконец, это означало, что им, возможно, придется давать и брать.
Я дал им лист бумаги для записи их решения ПОСЛЕ того, как они все работали вместе, чтобы убедиться, что каждый член команды справился с задачей. Потребовалось некоторое обучение, чтобы быть уверенным… но, когда мы закончили, у нас была отличная дискуссия о проблемах работы в больших командах, «взаимных уступках», необходимых для того, чтобы каждый голос был услышан, и так далее. Я не часто это делаю, но это был отличный форум для изучения работы в больших группах!
Потребовалось некоторое обучение, чтобы быть уверенным… но, когда мы закончили, у нас была отличная дискуссия о проблемах работы в больших командах, «взаимных уступках», необходимых для того, чтобы каждый голос был услышан, и так далее. Я не часто это делаю, но это был отличный форум для изучения работы в больших группах!
Повторение инструкций по улучшению фокусировки
Еще один способ заставить учащихся говорить о математике — попросить их повторить указания перед заданием. Поскольку многие из наших проектов по территории и периметру состояли из нескольких этапов, я просил партнеров уделить минуту, чтобы поговорить, прежде чем мы начнем, чтобы убедиться, что они понимают задачу, ожидания и то, как начать работу. Было здорово иметь возможность прояснить эти вещи ДО того, как они начали работать! Эти студенты говорили о том, как решить задачу, показанную в следующем разделе.
Знакомство с различными стилями обучения
Этот проект — один из моих любимых. Большая часть работы, которую я делаю с площадью и периметром, очень «практическая», но эта, в частности, требует, чтобы студенты «построили» прямоугольники, а затем создали художественное представление. Студенты, которые «видят» математику по-другому, часто очень преуспевают в этом, и тот факт, что они «строят» прямоугольники, измеряя длину стороны, а затем собирая прямоугольник, действительно помогает закрепить концепцию периметра.
Большая часть работы, которую я делаю с площадью и периметром, очень «практическая», но эта, в частности, требует, чтобы студенты «построили» прямоугольники, а затем создали художественное представление. Студенты, которые «видят» математику по-другому, часто очень преуспевают в этом, и тот факт, что они «строят» прямоугольники, измеряя длину стороны, а затем собирая прямоугольник, действительно помогает закрепить концепцию периметра.
Мне также нравится, как много диалогов происходит между учащимися… от предоставления отзывов о решении математической задачи и уточнения направлений до помощи в физическом формировании прямоугольников. Это, безусловно, совместные усилия, и мне нравится наблюдать за тем, как эти действия их вовлекают. Это действительно освобождает меня для ОБУЧЕНИЯ и коучинга, когда они работают.
Карточки с заданиями, доказательство мышления и многое другое
По мере продвижения нашего изучения площади и периметра пришло время использовать мои карточки с заданиями на площадь и периметр, чтобы проверить, действительно ли учащиеся усваивают математику. Опять же, мы начали с партнеров, которые работали и обсуждали математику, но я позволил им выбрать уровень сложности. Эти карточки с заданиями имеют прямоугольную форму… некоторые с видимыми квадратами… некоторые «открытые» формы… и некоторые неправильные формы, чтобы учащиеся могли попробовать свои силы в разделении на рабочие прямоугольники. Обсуждение было УДИВИТЕЛЬНЫМ, и затем мы собрались вместе, чтобы обсудить некоторые из стратегий, которые использовали студенты. Когда пришло время оценивать, я просто начал вытаскивать некоторые из своих бланков для выхода из области и периметра, чтобы посмотреть, что ученики могут делать самостоятельно, и я давал разные бланки в начале каждого урока в течение примерно 5 дней. Это действительно помогло мне понять, на ком сосредоточить свое преподавательское время.
Опять же, мы начали с партнеров, которые работали и обсуждали математику, но я позволил им выбрать уровень сложности. Эти карточки с заданиями имеют прямоугольную форму… некоторые с видимыми квадратами… некоторые «открытые» формы… и некоторые неправильные формы, чтобы учащиеся могли попробовать свои силы в разделении на рабочие прямоугольники. Обсуждение было УДИВИТЕЛЬНЫМ, и затем мы собрались вместе, чтобы обсудить некоторые из стратегий, которые использовали студенты. Когда пришло время оценивать, я просто начал вытаскивать некоторые из своих бланков для выхода из области и периметра, чтобы посмотреть, что ученики могут делать самостоятельно, и я давал разные бланки в начале каждого урока в течение примерно 5 дней. Это действительно помогло мне понять, на ком сосредоточить свое преподавательское время.
Демонстрация математических работ для повышения гордости и обсуждения
Я думаю, само собой разумеется, что когда учащиеся видят свою работу на выставке, это показывает, что мы ценим то, что они сделали.

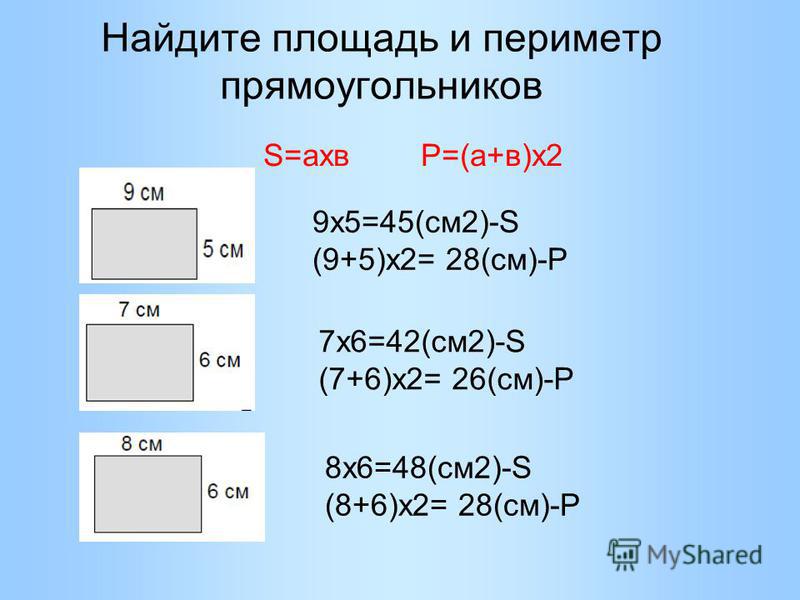
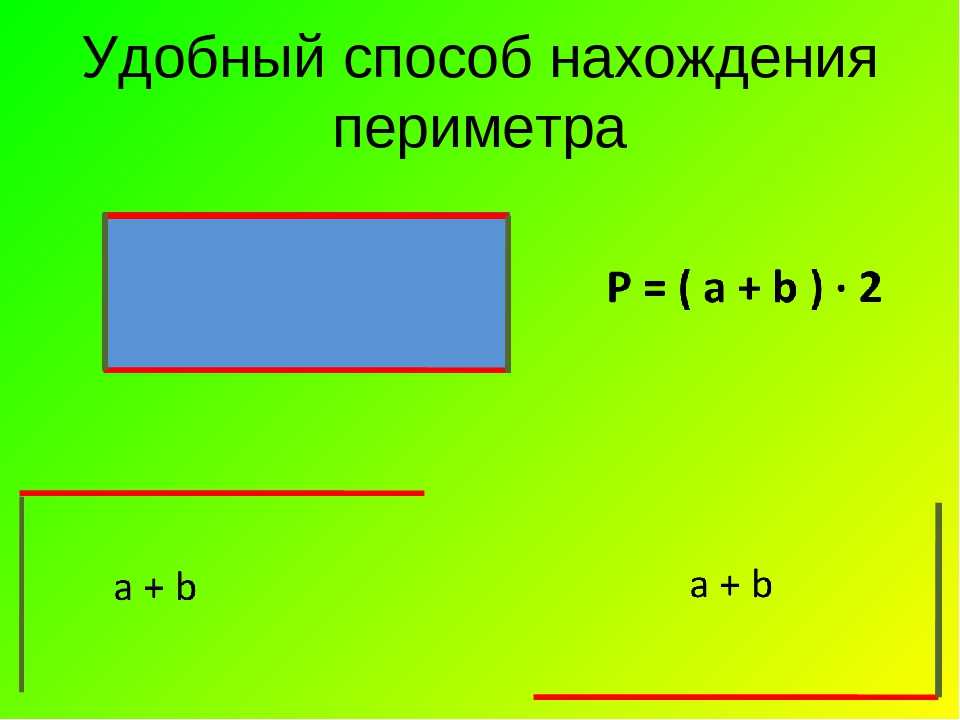



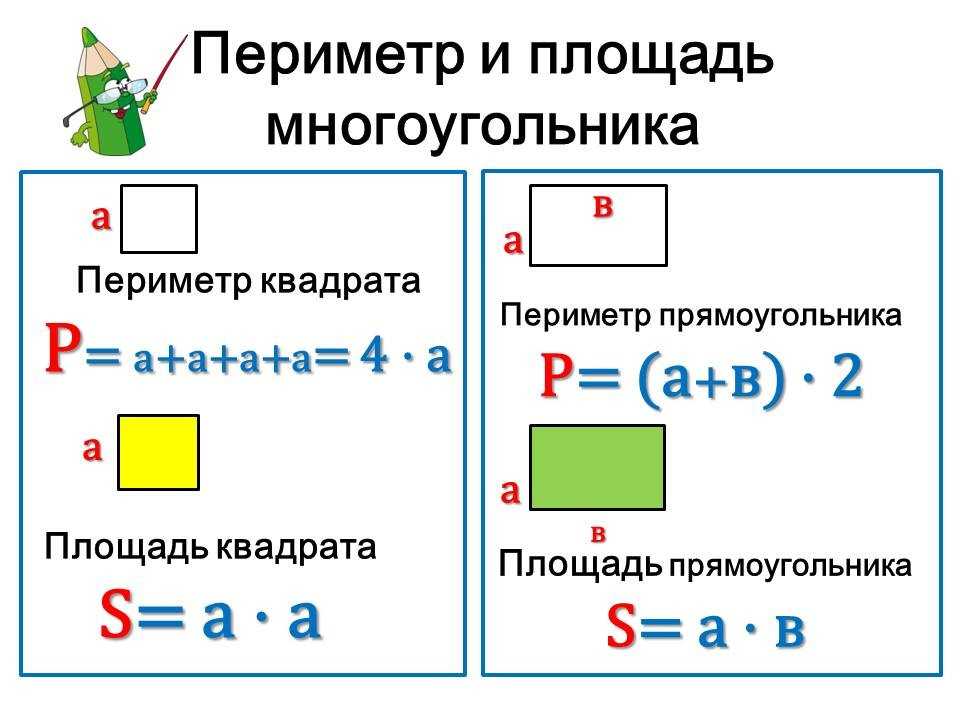 Они не смогут победить вас, если вы воспользуетесь формулой 1/2 * основание * высота. Они начнут спрашивать, как вы это делаете. Показать им. Постройте треугольник, пусть они вычислят площадь. Затем пусть они найдут основание и высоту. Затем используйте формулу. Они будут шокированы.
Они не смогут победить вас, если вы воспользуетесь формулой 1/2 * основание * высота. Они начнут спрашивать, как вы это делаете. Показать им. Постройте треугольник, пусть они вычислят площадь. Затем пусть они найдут основание и высоту. Затем используйте формулу. Они будут шокированы. Следите за вопросами в комнате и убедитесь, что студенты находятся на правильном веб-сайте.
Следите за вопросами в комнате и убедитесь, что студенты находятся на правильном веб-сайте.
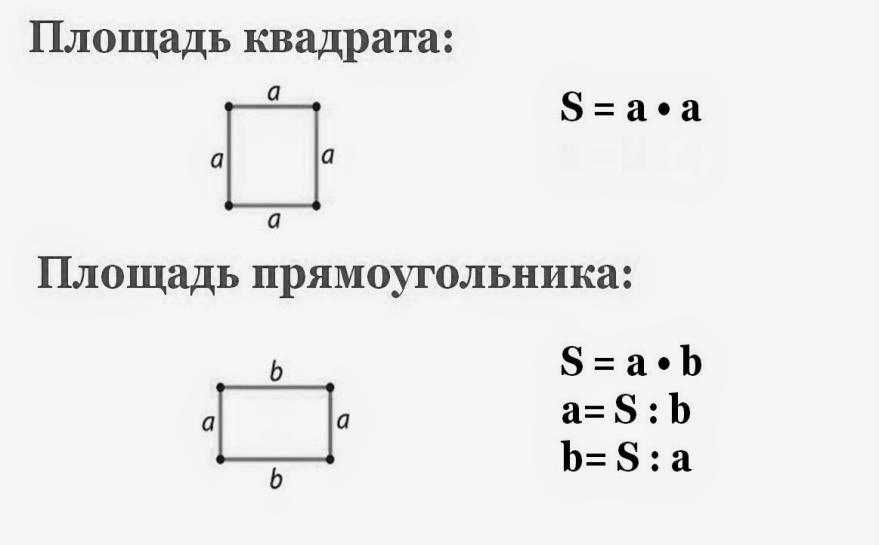
 Затем посмотрите, как найти площадь каждой из этих отдельных фигур, чтобы найти площадь всей составной фигуры. Смотрите весь процесс в этом уроке!
Затем посмотрите, как найти площадь каждой из этих отдельных фигур, чтобы найти площадь всей составной фигуры. Смотрите весь процесс в этом уроке!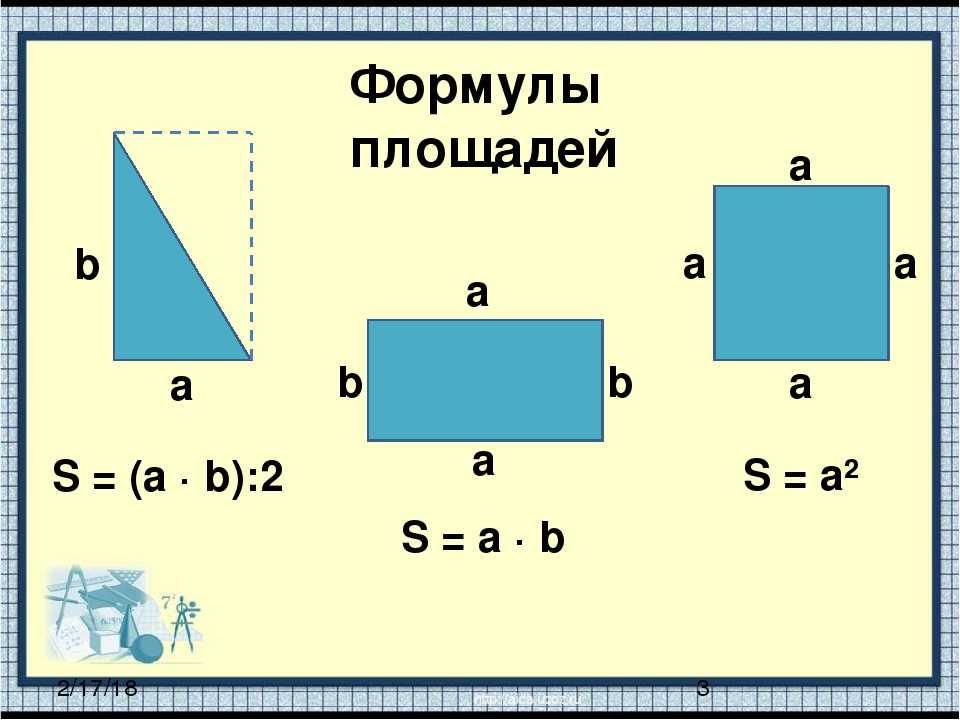 На самом деле, вы можете превратить параллелограмм в прямоугольник, чтобы найти формулу площади параллелограмма! Посмотрите этот урок, чтобы увидеть, как это делается!
На самом деле, вы можете превратить параллелограмм в прямоугольник, чтобы найти формулу площади параллелограмма! Посмотрите этот урок, чтобы увидеть, как это делается!