Факторный анализ (Окунь. Я.)
Факторный анализ (Окунь. Я.)
ОглавлениеПРЕДИСЛОВИЕ К РУССКОМУ ПЕРЕВОДУГлава первая.  ОБЩАЯ ХАРАКТЕРИСТИКА ФАКТОРНОГО АНАЛИЗА КАК НАУЧНОГО МЕТОДА ОБЩАЯ ХАРАКТЕРИСТИКА ФАКТОРНОГО АНАЛИЗА КАК НАУЧНОГО МЕТОДАГлава вторая. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ФАКТОРНОГО АНАЛИЗА 1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ 2. КОРРЕЛЯЦИЯ Глава третья. НЕКОТОРЫЕ ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ФАКТОРНОГО АНАЛИЗА 1. ИНТЕРПРЕТАЦИЯ КОРРЕЛЯЦИИ 2. НЕКОТОРЫЕ ОСНОВНЫЕ ЗАВИСИМОСТИ И ПОНЯТИЯ МНОГОФАКТОРНОГО АНАЛИЗА б. ВАЖНЕЙШИЕ ПОНЯТИЯ, СВЯЗАННЫЕ С ДИСПЕРСИЕЙ в. МАТРИЦА КОРРЕЛЯЦИИ И МАТРИЦА ФАКТОРОВ г. ОСНОВНЫЕ УРАВНЕНИЯ ФАКТОРНОГО АНАЛИЗА 3. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ НЕКОТОРЫХ ОСНОВНЫХ ЗАВИСИМОСТЕЙ б. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ КОРРЕЛЯЦИОННОЙ МАТРИЦЫ в. КОНФИГУРАЦИЯ ВЕКТОРОВ г. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ФАКТОРНОЙ МАТРИЦЫ д. РАНГ КОРРЕЛЯЦИОННОЙ МАТРИЦЫ И ОСИ КООРДИНАТ е. n-МЕРНОЕ ПРОСТРАНСТВО ж. НЕЗАВИСИМОСТЬ ПОЛОЖЕНИЯ СИСТЕМЫ КООРДИНАТ ОТ КОНФИГУРАЦИИ ВЕКТОРОВ з. ПРОСТРАНСТВО ОБЩИХ ФАКТОРОВ И ПРОСТРАНСТВО ТЕСТОВ и. ТРЕХМЕРНЫЕ МОДЕЛИ Глава четвертая. ЦЕНТРОИДНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ФАКТОРОВ 2. ОСНОВЫ РАСЧЕТА ФАКТОРНЫХ НАГРУЗОК В ЦЕНТРОИДНОМ МЕТОДЕ 3.  ПРОИСХОЖДЕНИЕ НАЗВАНИЯ «ЦЕНТРОИДНЫЙ МЕТОД» ПРОИСХОЖДЕНИЕ НАЗВАНИЯ «ЦЕНТРОИДНЫЙ МЕТОД»4. ОПРЕДЕЛЕНИЕ НАГРУЗОК ПЕРВОГО ОБЩЕГО ФАКТОРА 5. ОПРЕДЕЛЕНИЕ НАГРУЗОК СЛЕДУЮЩИХ ФАКТОРОВ 6. НЕКОТОРЫЕ СПЕЦИФИЧЕСКИЕ ПРОБЛЕМЫ ЦЕНТРОИДНОГО МЕТОДА б. ИЗМЕНЕНИЕ ЗНАКОВ ПЕРЕМЕННЫХ в. ПРОВЕРКА РАСЧЕТОВ В ЦЕНТРОИДНОМ МЕТОДЕ Глава пятая. ВРАЩЕНИЕ СИСТЕМЫ КООРДИНАТ 2. ПРОСТАЯ СТРУКТУРА 3. ПРОЦЕДУРА ВРАЩЕНИЯ В ТРЕХМЕРНОМ СЛУЧАЕ 4. ОСНОВНЫЕ СПОСОБЫ ПРОВЕРКИ ПРАВИЛЬНОСТИ РАСЧЕТОВ В ПРОЦЕССЕ ВРАЩЕНИЯ Глава шестая. ИНТЕРПРЕТАЦИЯ ФАКТОРОВ Глава седьмая. ДРУГИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ФАКТОРОВ 2. МНОГОФАКТОРНЫЙ АНАЛИЗ И КОНЦЕПЦИЯ СПИРМЭНА 3. ГЛАВНЫЕ РАЗНОВИДНОСТИ МЕТОДОВ ОПРЕДЕЛЕНИЯ ФАКТОРОВ Глава восьмая. РАЗЛИЧНЫЕ ТЕХНИКИ ПРОВЕДЕНИЯ ФАКТОРНОГО ЭКСПЕРИМЕНТА 3. ТЕХНИКИ Р И О 4. СРАВНЕНИЕ ТЕХНИК R, Q, Р И О Глава девятая. ЗАВИСИМЫЕ ФАКТОРЫ И ФАКТОРЫ ВЫСШИХ ПОРЯДКОВ 2. ФАКТОРЫ БОЛЕЕ ВЫСОКИХ ПОРЯДКОВ Глава десятая. ОСНОВНЫЕ ПРИНЦИПЫ ОРГАНИЗАЦИИ ИССЛЕДОВАНИЙ МЕТОДАМИ ФАКТОРНОГО АНАЛИЗА 2.  СТЕПЕНЬ ТРУДНОСТИ ТЕСТОВ СТЕПЕНЬ ТРУДНОСТИ ТЕСТОВ3. ПРОЦЕДУРА ОЦЕНКИ РЕЗУЛЬТАТОВ И СКОРОСТЬ ИХ ДОСТИЖЕНИЯ 4. ПРОБЛЕМА МОТИВАЦИИ 5. ОБСЛЕДУЕМАЯ ГРУППА 6. ПРАВИЛЬНАЯ ОРГАНИЗАЦИЯ ЭКСПЕРИМЕНТА 7. НАУЧНЫЙ ОТЧЕТ ЗАКЛЮЧЕНИЕ ВАЖНЕЙШИЕ ТЕРМИНЫ, ВСТРЕЧАЮЩИЕСЯ В ФАКТОРНОМ АНАЛИЗЕ ПРИЛОЖЕНИЕ К РУССКОМУ ИЗДАНИЮ ФАКТОРНЫЙ АНАЛИЗ СООТВЕТСТВИЙ 3. АКСИОМЫ И ОПРЕДЕЛЕНИЯ РАССТОЯНИЯ 4. ПРЕДСТАВЛЕНИЕ ЗНАЧЕНИЙ ПРИЗНАКА J В ПРОСТРАНСТВЕ RM 5. ПРОЕКЦИЯ ИССЛЕДУЕМОГО СКОПЛЕНИЯ ТОЧЕК НА ПРОСТРАНСТВО МАЛОЙ РАЗМЕРНОСТИ БИБЛИОГРАФИЯ |
Линейная алгебра — Свободный Университет
О курсе
В курсе будут рассказаны основные понятия и концепции современной линейной алгебры. Я постараюсь изложить линейную алгебру не в стандартном варианте, когда, фактически, одни и те же вещи рассказываются несколько раз, а последовательно — усложняя используемые понятия и добавляя дополнительное оснащение и структуры в рассматриваемые пространства. Мы пойдем от понятия векторного пространства к различным вариантам их оснащения (сопряженное пространство, скалярное произведение, метрика и т.д.). Хотя таким образом усвоение курса может быть более трудным, однако это даст возможность слушателям составить более структурирование понимание курса и подготовит к дальнейшему освоению других разделов математики: дифференциальных уравнений, функционального анализа и т.д..
Мы пойдем от понятия векторного пространства к различным вариантам их оснащения (сопряженное пространство, скалярное произведение, метрика и т.д.). Хотя таким образом усвоение курса может быть более трудным, однако это даст возможность слушателям составить более структурирование понимание курса и подготовит к дальнейшему освоению других разделов математики: дифференциальных уравнений, функционального анализа и т.д..
Первые 3 раздела ориентированы на всех, кому нужна линейная алгебра: программистов, специалистов по data science, экономистов и т.д.. Два последних раздела можно считать более продвинутыми, они расчитаны в первую очередь на студентов естественно-научных специальностей. Основной ход лекций будет дополнен дополнительными, которые призваны рассказать о важных сопутствующих математических понятиях.
Помимо лекций также будут семинарские занятия с решением задач и разбором теории.
Чему вы научитесь?
Будут освоены основные понятия линейной алгебры: как теоретически, так и практически.
* Линейные функционалы. Композиции линейных операторов и умножение матриц. Обратные матрицы. n$, полиномы, плоскость и трехмерное пространство, матрицы. Понятие линейного оператора.
n$, полиномы, плоскость и трехмерное пространство, матрицы. Понятие линейного оператора.
* Подпространства. Базисы, размерность, линейные оболочки. Дополнение базиса подпространства. Фактор-пространство. Определитель, ранг матрицы.
* Линейные операторы. Матричная запись линейного оператора (изоморфизм между пространством матриц и пространством линейных операторов, его зависимость от выбора базиса).Дополнительная лекция: комплексные числа, алгебраические уравнения.
02
* Собственные векторы, собственные подпространства. Теорема Гамильтона-Кэли.
* Инвариантые подпространства, корневые подпространства. Нильпотентные операторы.
* Теорема о жордановой нормальной форме. Описание с помощью ЖНФ различных классов операторов: проекторы, нильпотентные операторы, решение уравнений, функции от матриц. Теорема Вейера.
Теорема Вейера.Дополнительная лекция: Оценка сложности алгоритмов, вычисления.
03* Билинейные и квадратичные формы. Сигнатура, Скалярное произведение. Критерий Сильвестра, теорема Якоби.
* Алгебра Грассмана, детерминант.
* Метрика. Изометрии, ортогональные матрицы.
* Матричные нормы (операторная, Фробениуса).
* Алгебра операторов. Псевдообратные матрицы. Сопряженные операторы.
* Декомпозиции: LU, SVD разложения и другие.
* Алгебры Ли.Дополнительная лекция: теория групп, матричные группы
04
* Сопряженные пространства, линейные функционалы.
* Тензоры, алгебра тензоров. Перевод рассмотренных ранее конструкций на тензорный язык.
* Разложимые тензоры, координаты тензора.
* Внешнее и внутреннее произведение.
Дополнительная лекция — комплекс де Рама.
05
* Категории, группоиды. Основные примеры категорий.
* Функторы, кофункторы, естественные отображения.[1] Винберг Э.Б., Курс алгебры
скачать программу
[2] Ильин В.А., Позняк Э.Г., Линейная алгебра
[3] Кострикин А.И., Манин Ю.И., Линейная алгебра и геометрия
[4] Кострикин А.И., Введение в алгебру
[5] Ленг С., Алгебра
[6] Маклейн Дж., Категории для работающего математика
[7] Арутюнов А.А., Ершов А.В., Дополнительные задачи по ли-
нейной алгебре
[8] S. Axler., Linear Algebra Done Right
[9] А.В. Ершов, ТензорыПоступающим
Как подать заявку на курс?
Будьте в курсе новостей и событий университета
Спасибо! Будем держать вас в курсе 😉
матриц — Каково значение определителей в линейной алгебре?
спросил
Изменено 2 месяца назад
Просмотрено 8к раз
$\begingroup$
В некоторой литературе по линейной алгебре определители играют решающую роль и подчеркиваются в предыдущих главах (см.
 книги Антона и Рорреса и Лея). Однако в другой литературе он полностью игнорируется вплоть до последних глав (см. Гилберта Стрэнга).
Насколько большое значение мы должны придавать теме детерминантов? Я склонен использовать его для нахождения линейной независимости векторов и мог бы расширить это до нахождения обратного, но я думаю, что Джордан Гаусса и LU могут быть проще для обратного. Есть ли у него другие применения в линейной алгебре.
Существуют ли области, в которых детерминанты используются и оказывают реальное влияние? Существуют ли реальные приложения определителей?
Есть ли действительно хороший мотивирующий пример или объяснение, которое заинтересует учащихся в этой теме?
Где в линейной алгебре следует размещать определители? Как я уже сказал в своем комментарии, в одной литературе он находится в начале, а в другой — в конце. Мне нравится идея проверки независимости векторов с помощью определителей, поэтому думаю, что их следует размещать перед независимостью векторов. Что вы думаете? Если вы преподаете курс линейной алгебры, где вы размещаете эту тему.
книги Антона и Рорреса и Лея). Однако в другой литературе он полностью игнорируется вплоть до последних глав (см. Гилберта Стрэнга).
Насколько большое значение мы должны придавать теме детерминантов? Я склонен использовать его для нахождения линейной независимости векторов и мог бы расширить это до нахождения обратного, но я думаю, что Джордан Гаусса и LU могут быть проще для обратного. Есть ли у него другие применения в линейной алгебре.
Существуют ли области, в которых детерминанты используются и оказывают реальное влияние? Существуют ли реальные приложения определителей?
Есть ли действительно хороший мотивирующий пример или объяснение, которое заинтересует учащихся в этой теме?
Где в линейной алгебре следует размещать определители? Как я уже сказал в своем комментарии, в одной литературе он находится в начале, а в другой — в конце. Мне нравится идея проверки независимости векторов с помощью определителей, поэтому думаю, что их следует размещать перед независимостью векторов. Что вы думаете? Если вы преподаете курс линейной алгебры, где вы размещаете эту тему.
- линейная алгебра
- матрицы
- образование
$\endgroup$
3
$\begingroup$
Вы наблюдаете смещение акцента с детерминант. Это не означает, что они не важны; напротив, они очень важны — подумайте, например, о замене формулы переменной в множественных интегралах — но, введя их слишком рано в курсы линейной алгебры и потратив слишком много времени на их свойства, мы побудили студентов использовать определители. где их использование нецелесообразно, например, при решении линейных систем. Вы найдете самые крайние случаи в старых учебниках по линейной алгебре, вводя определители по их закрытой формуле, которая требует порядка $n!$ операций для вычисления $n\times n$ определителя. 9n$ — скалярное число, кратное детерминантной функции. Фактически, детерминантная функция является уникальной полилинейной альтернирующей функцией, когда оценка на матрице идентичности, рассматривая столбцы как векторы, дает единицу.

Определитель появляется в удивительном количестве мест и уже по одной этой причине важен. Я думаю, что это может быть отличным местом, чтобы представить идею о том, что математические объекты не обязательно важны из-за того, что они есть, а скорее свойства, которым они удовлетворяют (например, универсальные свойства). Если вы считаете, что линейная алгебра — хорошее место для введения основных понятий абстрактной математики, я думаю, что определитель делает это довольно хорошо. Описание определителя, приведенное выше, достаточно элементарно, чтобы любой, кто занимается линейной алгеброй, мог его понять, и доказательство последующих теорем об определителях проходит значительно легче с этой характеристикой, чем попытка вычислить ее с помощью комбинаторной формулы.

$\endgroup$
1
$\begingroup$
Это довольно неформальный ответ.
Определители в основном помогают описать природу решений линейных уравнений. Определитель действительной матрицы — это просто некоторое действительное число, говорящее вам об обратимости матрицы и, следовательно, сообщающее вам о линейных уравнениях, заключенных в матрице.
Ненулевой определитель эквивалентен тому, что матрица обратима, что эквивалентно соответствующим наборам линейных уравнений, имеющим ТОЧНО одно решение.
Нулевой определитель означает, что матрица НЕ обратима. В этом случае соответствующие системы линейных уравнений могут либо иметь бесконечно много решений, либо вообще не иметь их (в зависимости от чисел в правой части).
Так что определитель действительно полезен везде, где возникают линейные уравнения.
 Например, при проверке линейной независимости это то же самое, что требовать существования ЕДИНСТВЕННОГО решения системы линейных уравнений (то есть решения с нулевым вектором). Это то же самое, что определитель матрицы не равен нулю, как обсуждалось выше. Следовательно, линейная зависимость должна быть такой же, как и определитель, равный нулю (чтобы могли быть ненулевые решения уравнений, т. Е. Чтобы некоторые из векторов действительно можно было заставить нетривиально складываться, чтобы дать один из других) .
Например, при проверке линейной независимости это то же самое, что требовать существования ЕДИНСТВЕННОГО решения системы линейных уравнений (то есть решения с нулевым вектором). Это то же самое, что определитель матрицы не равен нулю, как обсуждалось выше. Следовательно, линейная зависимость должна быть такой же, как и определитель, равный нулю (чтобы могли быть ненулевые решения уравнений, т. Е. Чтобы некоторые из векторов действительно можно было заставить нетривиально складываться, чтобы дать один из других) .$\endgroup$
1
$\begingroup$
Забавно, что никто не упомянул, что определитель матрицы nxn с действительными элементами является гиперобъемом параллелоэдра со знаком, порожденным n столбцами матрицы. Это означает, что det = 0 (т. е. гиперобъем = 0) тогда и только тогда, когда столбцы матрицы линейно зависимы.
 Возможно, будет полезно поразмыслить над связью между этой интерпретацией определителя и данным ранее определением (единственная n-линейная альтернирующая функция столбцов матрицы, равная 1 при вычислении на единичной матрице), а также над тем, почему определитель появляется в формуле замены переменной для кратных интегралов.
Возможно, будет полезно поразмыслить над связью между этой интерпретацией определителя и данным ранее определением (единственная n-линейная альтернирующая функция столбцов матрицы, равная 1 при вычислении на единичной матрице), а также над тем, почему определитель появляется в формуле замены переменной для кратных интегралов.$\endgroup$
$\begingroup$
Определитель важен, потому что, среди прочего, приводит к характеристическому многочлену матрицы.
В самом деле — заметьте, что $Ax = \lambda x$, $x \ne 0$ тогда и только тогда, когда $p(\lambda) := \det(\lambda I_n — A) = 0$.
$\endgroup$
$\begingroup$
Детерминанты находят применение в реальном мире, поскольку кодируют определенные геометрические свойства преобразования. Во-первых, у них есть способ кодирования информации о том, как объемы изменяются по отношению к преобразованию.
 3$ с каноническими базисными векторами, которые определяют куб $1\times 1 \times 1$. Если я масштабирую любые координаты, скажем, первую, так что мы получаем прямоугольную призму $2 \times 1 \times 1$, а объем удваивается. На самом деле я могу масштабировать первую координату на что угодно, и это эквивалентно умножению объема на число. То же самое верно для второй и третьей координаты.
3$ с каноническими базисными векторами, которые определяют куб $1\times 1 \times 1$. Если я масштабирую любые координаты, скажем, первую, так что мы получаем прямоугольную призму $2 \times 1 \times 1$, а объем удваивается. На самом деле я могу масштабировать первую координату на что угодно, и это эквивалентно умножению объема на число. То же самое верно для второй и третьей координаты.Это означает, что объем масштабируется линейно по каждой координате, но у нас нет способа интерпретировать отрицательные числа, поскольку отрицательные объемы не имеют особого смысла. Однако нам не нужно интерпретировать негативы как отрицательные объемы, просто обычный объем, но с изменением ориентации. Отсюда вы недалеко от определителя, поскольку чередующаяся полилинейная карта является естественным выбором. Не очевидно, что полная полилинейность работает для объема при рассмотрении сдвиговых преобразований, но она помогает.
Однако математически геометрические свойства менее интересны, чем алгебраические.
 В частности, мне нравится, что определители дают вам групповой гомоморфизм $\det: GL_n(\mathbb{F}) \rightarrow \mathbb{F}$, и я также думаю, что это действительно здорово, что он отображает все делители нуля в кольце $n \times n$ матриц также равны $0$. Это как бы сворачивает векторное пространство обратно в поле, из которого оно пришло в аккуратном маленьком пакете.
В частности, мне нравится, что определители дают вам групповой гомоморфизм $\det: GL_n(\mathbb{F}) \rightarrow \mathbb{F}$, и я также думаю, что это действительно здорово, что он отображает все делители нуля в кольце $n \times n$ матриц также равны $0$. Это как бы сворачивает векторное пространство обратно в поле, из которого оно пришло в аккуратном маленьком пакете.Вероятно, наиболее важную роль детерминанты играют в отношении характеристического многочлена, который возникает при вычислении собственных векторов и собственных значений. Теорема Кэли-Гамильтона является важным результатом в этом направлении, что делает детерминанты особенно важными в этом отношении.
Что касается того, куда бы я поместил детерминанты, то я предпочитаю метод Стрэнга откладывать их. Их лучше всего понимать как чередующуюся полилинейную форму, и эти свойства дают вам все инструменты, необходимые для их расчета, если вы понимаете линейность. Тензорное произведение также будет полилинейным, поэтому детерминант обеспечивает простое введение в эту основную идею.
 Между этим и характеристическим полиномом я чувствую, что слишком важно пропускать определители, даже для студентов, которые переходят к инженерии или естественным наукам. Здесь есть нечто большее, чем просто простая формула для расчета объемов, но сам по себе важный математический объект.
Между этим и характеристическим полиномом я чувствую, что слишком важно пропускать определители, даже для студентов, которые переходят к инженерии или естественным наукам. Здесь есть нечто большее, чем просто простая формула для расчета объемов, но сам по себе важный математический объект.$\endgroup$
линейная алгебра — использование определителей
Определитель — это значение, связанное с квадратной матрицей.
Вот это вам о многом говорит, не так ли? Давайте попробуем сделать его более интуитивным, «почему это существует» и «как это работает».
Первое, что вам нужно знать, это то, что он не обязательно должен существовать. Матрицы тоже. И ничего. Но это полезная концепция, которая помогает нам решать проблемы, которые повторялись много раз, и было сочтено благоразумным дать ей имя. Как будто было разумно построить концепцию матриц, чтобы помочь с системами линейных уравнений. Видите ли, все, что делают математики, — это эффективное и стильное решение задач.
 Да, мы любим стиль. И в ходе нашего исследования некоторые значения и расчеты окажутся согласованными и очень полезными. И очень значимый по контексту. И мы дадим им имена и сделаем их нашими друзьями. Или инструменты.
Да, мы любим стиль. И в ходе нашего исследования некоторые значения и расчеты окажутся согласованными и очень полезными. И очень значимый по контексту. И мы дадим им имена и сделаем их нашими друзьями. Или инструменты.В первые дни, до того, как математики открыли элегантность матриц для решения систем линейных уравнений, определители были связаны с самими системами линейных уравнений. Их имя на самом деле является подделкой — оно буквально определяет , имеет ли система уникальное решение (ни чрезмерное, ни недостаточное). И математика показала, что это значение должно быть любым, кроме $0$, чтобы оставаться верным. Иметь уникальное решение. После этих первых детских шагов многие математики добавили к фундаменту исходных теория и концепция определителя процветали по мере того, как люди решали все больше и больше проблем. Я постараюсь не пугать вас подробностями, вы можете разобраться самостоятельно.
Определитель используется многими контекстно-зависимыми способами.


 n$, полиномы, плоскость и трехмерное пространство, матрицы. Понятие линейного оператора.
n$, полиномы, плоскость и трехмерное пространство, матрицы. Понятие линейного оператора. Теорема Вейера.
Теорема Вейера.
 книги Антона и Рорреса и Лея). Однако в другой литературе он полностью игнорируется вплоть до последних глав (см. Гилберта Стрэнга).
Насколько большое значение мы должны придавать теме детерминантов? Я склонен использовать его для нахождения линейной независимости векторов и мог бы расширить это до нахождения обратного, но я думаю, что Джордан Гаусса и LU могут быть проще для обратного. Есть ли у него другие применения в линейной алгебре.
Существуют ли области, в которых детерминанты используются и оказывают реальное влияние? Существуют ли реальные приложения определителей?
Есть ли действительно хороший мотивирующий пример или объяснение, которое заинтересует учащихся в этой теме?
Где в линейной алгебре следует размещать определители? Как я уже сказал в своем комментарии, в одной литературе он находится в начале, а в другой — в конце. Мне нравится идея проверки независимости векторов с помощью определителей, поэтому думаю, что их следует размещать перед независимостью векторов. Что вы думаете? Если вы преподаете курс линейной алгебры, где вы размещаете эту тему.
книги Антона и Рорреса и Лея). Однако в другой литературе он полностью игнорируется вплоть до последних глав (см. Гилберта Стрэнга).
Насколько большое значение мы должны придавать теме детерминантов? Я склонен использовать его для нахождения линейной независимости векторов и мог бы расширить это до нахождения обратного, но я думаю, что Джордан Гаусса и LU могут быть проще для обратного. Есть ли у него другие применения в линейной алгебре.
Существуют ли области, в которых детерминанты используются и оказывают реальное влияние? Существуют ли реальные приложения определителей?
Есть ли действительно хороший мотивирующий пример или объяснение, которое заинтересует учащихся в этой теме?
Где в линейной алгебре следует размещать определители? Как я уже сказал в своем комментарии, в одной литературе он находится в начале, а в другой — в конце. Мне нравится идея проверки независимости векторов с помощью определителей, поэтому думаю, что их следует размещать перед независимостью векторов. Что вы думаете? Если вы преподаете курс линейной алгебры, где вы размещаете эту тему.


 Например, при проверке линейной независимости это то же самое, что требовать существования ЕДИНСТВЕННОГО решения системы линейных уравнений (то есть решения с нулевым вектором). Это то же самое, что определитель матрицы не равен нулю, как обсуждалось выше. Следовательно, линейная зависимость должна быть такой же, как и определитель, равный нулю (чтобы могли быть ненулевые решения уравнений, т. Е. Чтобы некоторые из векторов действительно можно было заставить нетривиально складываться, чтобы дать один из других) .
Например, при проверке линейной независимости это то же самое, что требовать существования ЕДИНСТВЕННОГО решения системы линейных уравнений (то есть решения с нулевым вектором). Это то же самое, что определитель матрицы не равен нулю, как обсуждалось выше. Следовательно, линейная зависимость должна быть такой же, как и определитель, равный нулю (чтобы могли быть ненулевые решения уравнений, т. Е. Чтобы некоторые из векторов действительно можно было заставить нетривиально складываться, чтобы дать один из других) .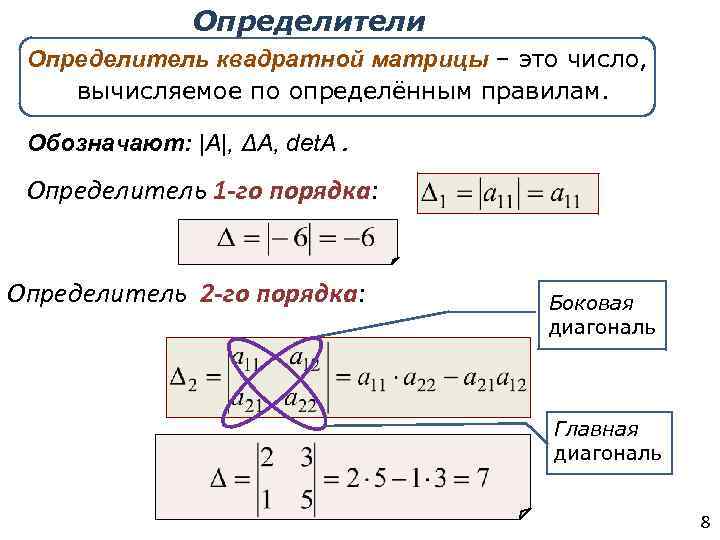 Возможно, будет полезно поразмыслить над связью между этой интерпретацией определителя и данным ранее определением (единственная n-линейная альтернирующая функция столбцов матрицы, равная 1 при вычислении на единичной матрице), а также над тем, почему определитель появляется в формуле замены переменной для кратных интегралов.
Возможно, будет полезно поразмыслить над связью между этой интерпретацией определителя и данным ранее определением (единственная n-линейная альтернирующая функция столбцов матрицы, равная 1 при вычислении на единичной матрице), а также над тем, почему определитель появляется в формуле замены переменной для кратных интегралов. 3$ с каноническими базисными векторами, которые определяют куб $1\times 1 \times 1$. Если я масштабирую любые координаты, скажем, первую, так что мы получаем прямоугольную призму $2 \times 1 \times 1$, а объем удваивается. На самом деле я могу масштабировать первую координату на что угодно, и это эквивалентно умножению объема на число. То же самое верно для второй и третьей координаты.
3$ с каноническими базисными векторами, которые определяют куб $1\times 1 \times 1$. Если я масштабирую любые координаты, скажем, первую, так что мы получаем прямоугольную призму $2 \times 1 \times 1$, а объем удваивается. На самом деле я могу масштабировать первую координату на что угодно, и это эквивалентно умножению объема на число. То же самое верно для второй и третьей координаты. В частности, мне нравится, что определители дают вам групповой гомоморфизм $\det: GL_n(\mathbb{F}) \rightarrow \mathbb{F}$, и я также думаю, что это действительно здорово, что он отображает все делители нуля в кольце $n \times n$ матриц также равны $0$. Это как бы сворачивает векторное пространство обратно в поле, из которого оно пришло в аккуратном маленьком пакете.
В частности, мне нравится, что определители дают вам групповой гомоморфизм $\det: GL_n(\mathbb{F}) \rightarrow \mathbb{F}$, и я также думаю, что это действительно здорово, что он отображает все делители нуля в кольце $n \times n$ матриц также равны $0$. Это как бы сворачивает векторное пространство обратно в поле, из которого оно пришло в аккуратном маленьком пакете. Между этим и характеристическим полиномом я чувствую, что слишком важно пропускать определители, даже для студентов, которые переходят к инженерии или естественным наукам. Здесь есть нечто большее, чем просто простая формула для расчета объемов, но сам по себе важный математический объект.
Между этим и характеристическим полиномом я чувствую, что слишком важно пропускать определители, даже для студентов, которые переходят к инженерии или естественным наукам. Здесь есть нечто большее, чем просто простая формула для расчета объемов, но сам по себе важный математический объект. Да, мы любим стиль. И в ходе нашего исследования некоторые значения и расчеты окажутся согласованными и очень полезными. И очень значимый по контексту. И мы дадим им имена и сделаем их нашими друзьями. Или инструменты.
Да, мы любим стиль. И в ходе нашего исследования некоторые значения и расчеты окажутся согласованными и очень полезными. И очень значимый по контексту. И мы дадим им имена и сделаем их нашими друзьями. Или инструменты.