Каково отношение длины окружности к диаметру радиуса круга? – Обзоры Вики
Все круги похожи, и «длина окружности, разделенная на диаметр», дает одно и то же значение независимо от их радиуса. Эта величина представляет собой отношение длины окружности к ее диаметру и называется π (Пи).
Следовательно, когда длина окружности и площадь круга численно равны, то диаметр численно равен? Следовательно, диаметр окружности является 4.
Какая связь между окружностью и радиусом? Окружность круга равно пи, умноженному на диаметр. Диаметр в два раза больше радиуса, поэтому уравнение для длины окружности с использованием радиуса равняется двойному радиусу в пи.
Дополнительно Почему длина окружности равна отношению ее радиуса? Наше отношение — длина окружности к радиусу. Длина окружности по радиусу равна в два раза больше радиуса . Тогда радиус равен . С этим соотношением мы замечаем, что у нас есть с обеих сторон.
Каково отношение радиуса к длине окружности любого круга, используя 3.
2) = 2/R..
Длина и площадь круга одинаковы, тогда радиус круга равен единице тире?
∴Радиус=2 единицы.
Площадь круга равна диаметру? Круг не является квадратом, но площадь круга (количество внутреннего пространства, заключенного в круге) измеряется в квадратных единицах. … Тем не менее, только с диаметр, или половину диаметра (радиус), или даже только длину окружности (расстояние вокруг), можно вычислить площадь любого круга.
Если периметр круга равен периметру квадрата, то отношение их площадей равно? 14:11.
Что такое длина окружности и диаметр круга?
Окружность — это длина одного полного круга по кругу., а диаметр — это длина отрезка прямой, разрезающего круг пополам.
Также как диаметр связан с окружностью? Мы узнали, что окружность — это расстояние по окружности, а диаметр — это расстояние по окружности, проходящей через центр. … Чтобы найти длину окружности по диаметру, ты умножаешь диаметр на пи. Чтобы найти диаметр по окружности, нужно длину окружности разделить на число Пи.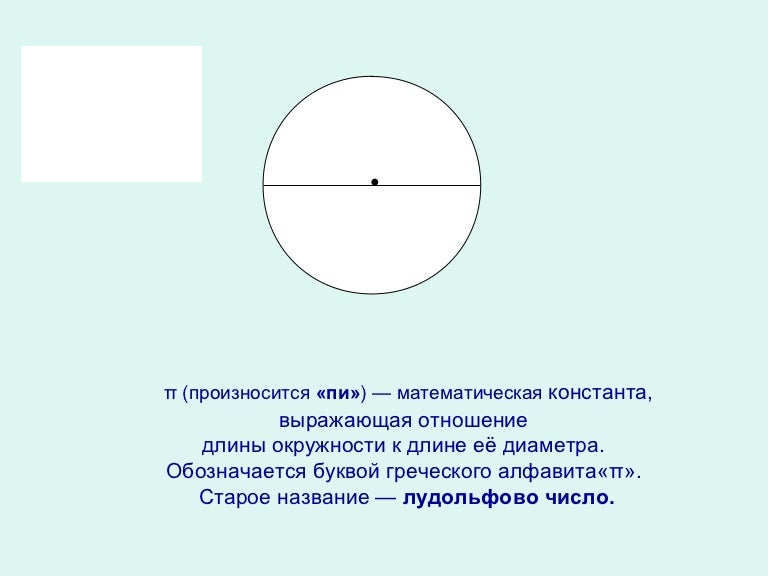
Что больше радиус или длина окружности?
Радиус — это самое короткое слово и самая короткая мера. Диаметр дольше. Окружность самый длинный.
Почему длина окружности 2 pi r? Отсюда следует, что отношение окружность: радиус, что равносильно высказыванию отношения окружность: диаметр, постоянно для любой окружности. Если эта константа равна некоторому числу π, то длина окружности = π × диаметр или длина окружности = 2π. × радиус. Значит доказано.
Каково отношение длины окружности к площади окружности, если радиус равен r?
Таким образом, отношение длины окружности радиуса r к ее площади равно 2: р.
Каково отношение длины окружности к площади окружности, если радиус равен R?
Таким образом, отношение длины окружности радиуса r к ее площади равно 2: р.
При каком значении радиуса r площадь и периметр круга равны? Периметр круга равен 2πr, где r — радиус круга. Следовательно, если r равно 2 единицам тогда площадь и периметр круга будут численно равны.
2) = 2 * 3.14 * r (где r = радиус круга), дает значение у тебя есть 2.
Тогда равны ли длина окружности и периметр квадрата?
Следовательно, Площадь круга > Площадь квадрата.
Могут ли круг и квадрат иметь одинаковый периметр? Формула периметра квадрата и периметра круга дана 4a и 2πr соответственно. … Площадь квадрата и круга находится по формулам a2 и πr2 соответственно.
Что больше периметр меньшего квадрата или длина окружности?
Следовательно, длина окружности равна 2πr; периметр квадрата равен 4s. Следовательно, окружность круг меньше периметра квадрата.
%d0%b4%d0%bb%d0%b8%d0%bd%d0%b0%20%d0%be%d0%ba%d1%80%d1%83%d0%b6%d0%bd%d0%be%d1%81%d1%82%d0%b8 in Polish — Russian-Polish Dictionary
Sample translated sentence: Еще 10 минут на 20 подъемов. ↔ Jeszcze 10 minut i będzie 20.
Glosbe Translate
Google Translate
+ Add translation Add
Currently we have no translations for %d0%b4%d0%bb%d0%b8%d0%bd%d0%b0%20%d0%be%d0%ba%d1%80%d1%83%d0%b6%d0%bd%d0%be%d1%81%d1%82%d0%b8 in the dictionary, maybe you can add one? Make sure to check automatic translation, translation memory or indirect translations.
Add example Add
Declension Stem
Насколько же это было уместно, ведь выпускники назначались служить в 20 стран мира!
I rzeczywiście, absolwenci otrzymali przydziały do 20 krajów świata!
jw2019Еще 10 минут на
Jeszcze 10 minut i będzie 20.
OpenSubtitles2018.v3Командир отряда 81-го гвардейского бомбардировочного авиационного полка (1-я гвардейская бомбардировочная авиационная дивизия, 6-й гвардейский бомбардировочный авиационный корпус, 2-я воздушная армия, 1-й Украинский фронт) гвардии капитан Пётр Абрамов особенно отличился при выполнении боевых заданий по доставке оружия, боеприпасов и продовольствия партизанам Белоруссии и Украины.
Dowodził oddziałem 81 pułku lotnictwa bombowego 1 Gwardyjskiej Dywizji Lotnictwa Bombowego 6 Gwardyjskiego Korpusu Lotnictwa Bombowego 2 Armii Powietrznej 1 Frontu Ukraińskiego w stopniu kapitana, szczególnie zasłużył się przy dostarczaniu broni, zapasów i żywności dla partyzantów Białorusi i Ukrainy.
Я знала, как высоко Бог ценит человека и его тело, но даже это не останавливало меня. Дженнифер, 20 лет
Wiedziałam, że Bóg każe nam dbać o ciało, ale to mnie nie powstrzymało” (20-letnia Jennifer).
jw2019Впоследствии Бог прописал этот порядок в соглашении Закона, которое заключил с народом Израиль при посредстве Моисея (Исх 20:8—11; Вт 5:12—15).
Później zostało przez Boga usankcjonowane przepisami Prawa nadanego narodowi izraelskiemu za pośrednictwem Mojżesza (Wj 20:8-11; Pwt 5:12-15).
jw2019Спорим на 20 баксов, что ты не сможешь провести целый день одна.
Założę się o 20 dolców, że nie spędzisz całego dnia sama.
OpenSubtitles2018.v3Когда мы помогаем другим, мы и сами в какой-то мере испытываем счастье и удовлетворение, и наше собственное бремя становится легче (Деяния 20:35).
Kiedy wysilamy się na rzecz drugich, pomagamy nie tylko im, ale także sami doświadczamy szczęścia i zadowolenia, dzięki którym łatwiej nam dźwigać nasze ciężary (Dzieje 
20 Слова Иисуса из Матфея 28:19, 20 показывают, что креститься следует тем, кто сделался Его учеником.
20 Słowa Jezusa z Ewangelii według Mateusza 28:19, 20 wskazują, że ochrzczeni mają być ci, którzy zostali jego uczniami.
jw2019Речь и обсуждение со слушателями, основанные на «Сторожевой башне» от 15 июля 2003 года, с. 20.
Przemówienie połączone z udziałem obecnych, oparte na materiale ze Strażnicy z 15 lipca 2003 roku, strona 20.
jw2019Спустя почти 40 лет, ко времени проведения второй переписи, число мужчин в племени Манассии возросло до 52 700, что было на 20 200 больше, чем в племени Ефрема (Чс 26:28—34, 37).
Gdy niemal 40 lat później przeprowadzono drugi spis ludności, liczba mężczyzn z tego plemienia wzrosła do 52 700 i przewyższyła liczbę mężczyzn w plemieniu Efraima o 20 200 (Lb 26:28-34, 37).
jw2019Ну, в то время, мы говорим о 80-х, в то время это было модно.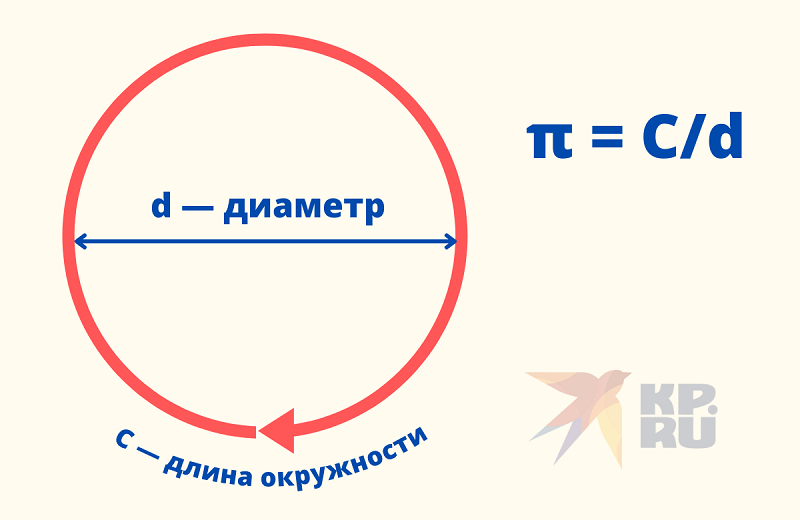
Cóż, na tamte czasy, mówimy o latach 80-tych, były bardzo modne.
OpenSubtitles2018.v3Он уехал 20 минут назад.
Wyszedł 20 minut temu.
OpenSubtitles2018.v3Хенаро сказал, что он ждал бы около меня, даже если бы на это ему понадобилось бы 20 лет.
Genaro powiedział mi kiedyś, że czekałby na mnie nawet dwadzieścia lat.
Literature20 Я приведу их в землю, о которой клялся их предкам+, в землю, где течёт молоко и мёд+, и они будут есть+ досыта, разжиреют+ и повернутся к другим богам+.
+ 20 Bo zaprowadzę ich do ziemi, co do której przysiągłem ich praojcom,+ która opływa w mleko i miód,+ i będą jeść,+ i nasycą się, i utyją,+ i zwrócą się do innych bogów,+ i będą im służyć, a mną wzgardzą i złamią moje przymierze.
jw2019Я был женат 20 лет.
Byłem żonaty przez 20 lat.
OpenSubtitles2018.v3Из остатков содержимого желудка Никольс выделил 20 миллиграммов.
Z resztek treści żołądka wyosobnił Nickolls 20 miligramów.
LiteratureОни стреляли снарядами М-8 (калибр 82-мм) и М-13 (калибр 132-мм).
Strzelały pociskami M–8 (kalibru 82 mm) albo M–13 (kalibru 132 mm).
Literature20 Оставлена родителями, но любима Богом
20 Opuszczona przez rodziców — kochana przez Boga
jw2019 Майкл Алекс Шервуд погиб в 20:55 13 августа.Michael Alex Sherwood zginął 13 sierpnia o ósmej pięćdziesiąt pięć.
LiteratureУ меня в 20:30 очень важная встреча.
Mam ważne spotkanie dziś o 8:30.
OpenSubtitles2018.v3Она ушла минут 20 назад.
Wyszła 20 minut temu.
OpenSubtitles2018.v3Ты сейчас рванул с 20 до 150 километров за 2 секунды!
Właśnie przeszedłeś od 10 do 111 w dwie sekundy.
OpenSubtitles2018.v3Когда в 80-х годах люди якудзы увидели, как легко брать ссуды и «делать» деньги, они создали компании и занялись операциями с недвижимым имуществом и куплей-продажей акций.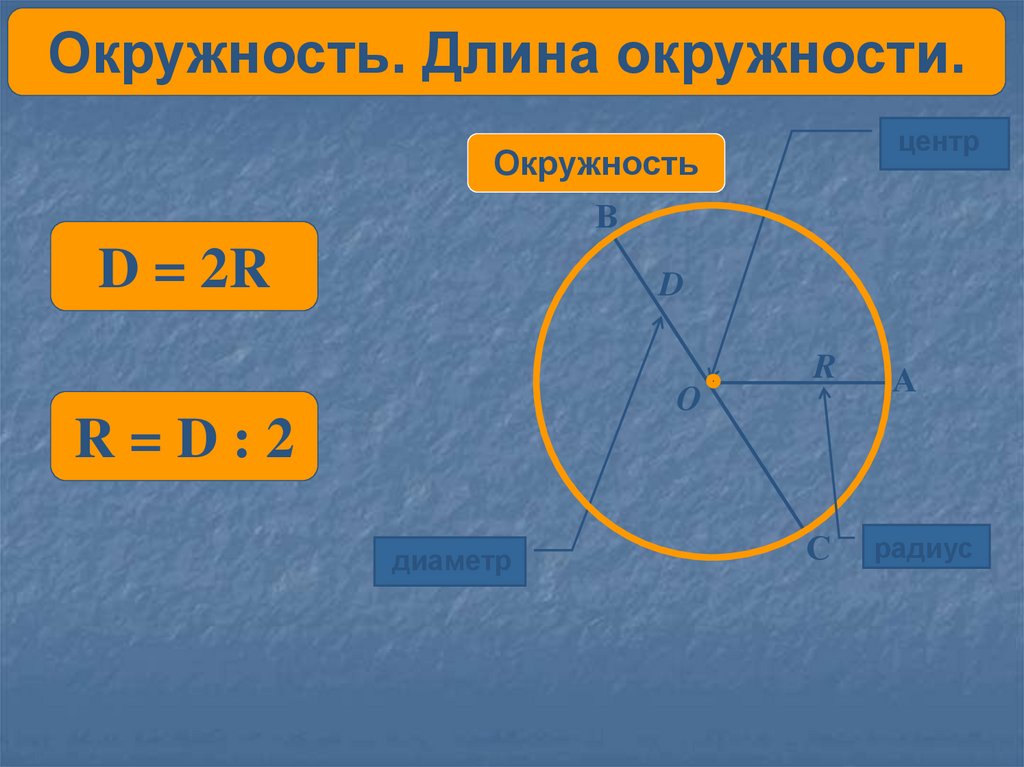
W latach osiemdziesiątych możliwość dużych zarobków za pożyczone pieniądze skłoniła yakuzę do zakładania przedsiębiorstw i zajęcia się handlem nieruchomościami oraz spekulacjami giełdowymi.
Обычно проводят связь между этим древним городом и современной Газой (Газза, Азза), расположенной примерно в 80 км к З.-Ю.-З. от Иерусалима.
Starożytna Gaza z reguły jest kojarzona ze współczesnym miastem o tej nazwie (Ghazza, ʽAzza), leżącym ok. 80 km na zach. pd. zach. od Jerozolimy.
jw2019Искренне беспокоясь о Павле, который находился в заключении в Риме, они помогали ему справляться с трудностями, поддерживая его материально (Фп 4:15—20).
Kiedy był więziony w Rzymie, szczerze się nim interesowali i pomagali mu znieść ucisk, wspierając go materialnie (Flp 4:15-20).
jw2019 The most popular queries list: 1K, ~2K, ~3K, ~4K, ~5K, ~5-10K, ~10-20K, ~20-50K, ~50-100K, ~100k-200K, ~200-500K, ~1Mгеометрия — Доказательство того, что каждый круг имеет отношение $\pi$
спросил
Изменено 6 лет, 4 месяца назад
Просмотрено 3к раз
$\begingroup$
Мы знаем, что отношение длины окружности к ее диаметру равно $\pi$, но можно ли это доказать для каждой окружности? Или это аксиома?
- геометрия
- аксиомы
$\endgroup$
16
$\begingroup$
Это довольно деликатный вопрос.
Во-первых, независимость отношения длины окружности к диаметру от радиуса окружности верна не для всех геометрий. На самом деле это характеристика «плоских» геометрий или, если использовать стандартный термин, евклидовых геометрий. Например, довольно легко видеть, что это отношение не является постоянным для кругов на сфере. Кроме того, при использовании любой из нескольких моделей гиперболической плоскости соотношение в гиперболической плоскости также не является постоянным.
Далее, понятие длины кривой очень тонкое и требует хорошего определения. Проблема с длиной заключается в том, что она очень чувствительна к небольшим изменениям и не является непрерывной (в том смысле, что для кривых, которые равномерно сходятся к данной кривой, длины кривых не обязательно должны сходиться к длине предельной кривой). Это делает приближение длины кривой геометрическими средствами тонким и подверженным ошибкам.
Один из надежных способов продолжить работу — принять определение длины графика дифференцируемой функции $f:[a,b]\to \mathbb R$, равное $\int _a^b\sqrt{1 +f'(x)^2}dx$.
2 }$. Подставьте это к определению длины, и вы получите $2r\pi $. Таким образом, окружность линейна по радиусу, поэтому при делении на диаметр всегда получается константа. (Чтобы сделать этот аргумент более строгим, нужно также доказать, что длина инвариантна к переносу, так что любой круг можно перевести так, чтобы его центр находился в начале координат).
Примечание: Древние греки по-разному рассуждали о константе $\pi$, поскольку у них не было нашего современного определения длины. Я не уверен, насколько они были осведомлены о тонкостях понятия длины. Возможно, лучше сначала рассмотреть площадь, а не длину. Тогда $\pi$ можно определить как отношение площади круга радиуса $r$ к квадрату радиуса. Доказательство того, что это отношение не зависит от радиуса, снова использует интегралы, но для измерения площади под графиком, а не длины графика. 9n$-угольник имеет длину, пропорциональную диаметру окружности, можно утверждать, что длина окружности также должна быть пропорциональна ее диаметру.
Таким образом, отношение длины окружности к ее диаметру должно быть постоянным.
$\endgroup$
5
$\begingroup$
Можно доказать, что отношение $\frac{\text{окружность}}{\text{диаметр}}$ одинаково для всех кругов, независимо от того, насколько они велики или малы; другими словами, это отношение является постоянным числом. Для обозначения этого постоянного числа используется символ $\pi$. Нам нужен специальный символ, потому что нет другого хорошего способа записать число, поскольку оно трансцендентно. Вы можете легко записать приблизительные значения, такие как $\tfrac{22}{7}$ или 3,14159.265, но это только примерно , равных $\pi$, а не точно $\pi$.
Короче говоря, тогда $\pi$ равно , определяемому как отношение $\frac{\text{окружность}}{\text{диаметр}}$. Используя ваш термин, это «аксиома».
Я предполагаю, что ваши знания математики довольно элементарны, поэтому я дал вам элементарный ответ, который игнорирует некоторые тонкие вопросы.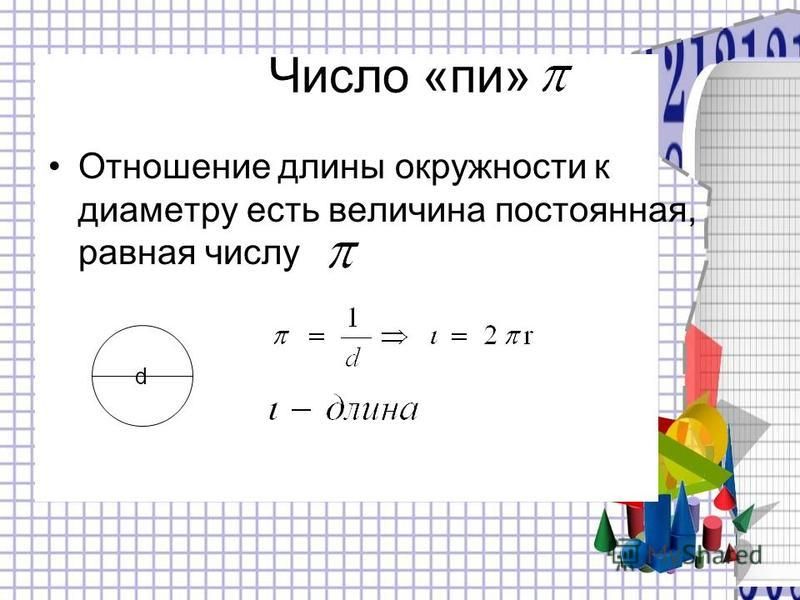
Например, я предположил, что мы работаем со стандартной плоской евклидовой геометрией и что у нас есть работоспособное интуитивное представление о том, что означает «длина».
$\endgroup$
5
Почему отношение длины окружности к ее диаметру всегда равно пи?
Математика Геометрия Философия Логика
Хеллен Дж.
спросил 09.08.20Почему отношение длины окружности к ее диаметру всегда равно пи?
Есть ли исключения?
Подписаться І 1
Подробнее
Отчет
5 ответов от опытных наставников
Лучший Новейшие Самый старыйАвтор: ЛучшиеНовыеСамыеСтарые
Нихил С. ответил 10.08.20
Репетитор
Новое в Византе
Репетитор по математике в старших классах и колледжах — все предметы
Посмотреть таких репетиторов
Смотрите таких репетиторов
Как было сказано в других ответах, число π часто определяется как π=C/d, где C — длина окружности, а d — диаметр окружности.
Ваши вопросы, кажется, подразумевают: « A круг? Но откуда мы знаем, что это то же самое для всех кругов?» Это хороший вопрос! Причина в том, что все круги аналогичны . Поскольку отношения сторон в подобных треугольниках одинаковы, отношение длины окружности к ее диаметру всегда равно π 9.0005
Я не «доказываю» этот факт, потому что доказательство зависит от того, с каких предположений вы начинаете. Раз уж вы спросили, есть ли исключения, стоит упомянуть об интересном результате. В обычной системе евклидовой геометрии π всегда является одним постоянным числом, как обсуждалось выше. Но в других системах геометрии он может иметь и другие значения. Если интересно, есть замечательная статья на эту тему Корнелии Ван Котт: https://www.maa.org/sites/default/files/pdf/awards/mathhorizons.23.3.24.pdf
Голосовать за 1 Понизить
Подробнее
Отчет
Дуглас Б.
ответил 10.08.20
Репетитор
4.9 (83)
Высшее образование и математика в колледже: ясно и по существу
См. таких репетиторов
Смотрите таких репетиторов
Окружность точно соответствует диаметру. Таким образом, каким бы большим или маленьким ни был круг, соотношение будет одинаковым.
Голосовать за 1 Понизить
Подробнее
Отчет
Деннис С. ответил 10.08.20
Репетитор
5,0 (352)
Преподаватель математики на пенсии
Смотрите таких репетиторов
Смотрите таких репетиторов
Посмотрите на формулу длины окружности
C = число пи • d
C = длина окружности
d = диаметр
Если диаметр умножить на любое число
длина окружности также будет умножена на то же число .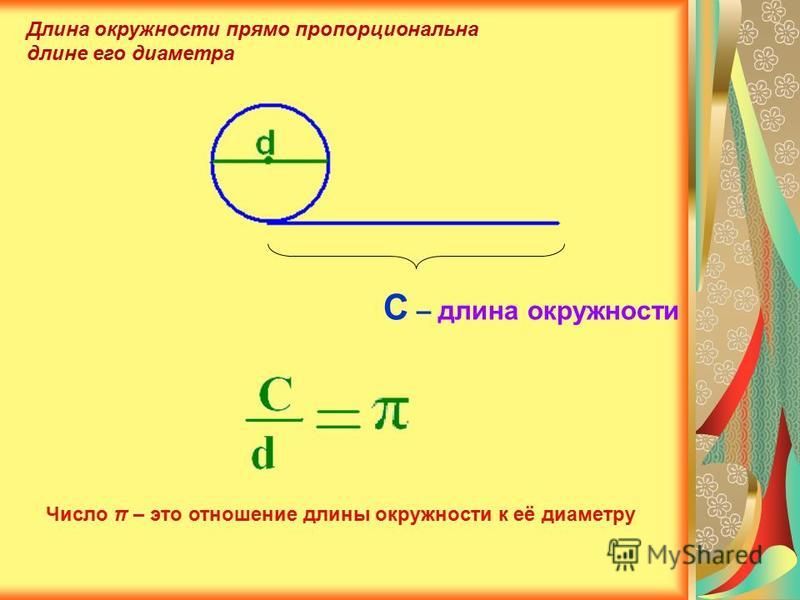
Для любого круга, если вы разделите длину окружности на диаметр, вы всегда получите число пи
Голосовать за 0 Понизить
Подробнее
Отчет
Марк М. ответил 10.08.20
Репетитор
5,0 (264)
Учитель математики – высококвалифицированный специалист NCLB
Об этом репетиторе ›
Об этом репетиторе ›
длина окружности = π x диаметр для всех окружностей.
Голосовать за 0 Понизить
Подробнее
Отчет
Дэвид В. ответил 10.08.20
Репетитор
4.
7
(90)
Опытный Профессор
Об этом репетиторе ›
Об этом репетиторе ›
Пожалуйста, начните с определения из ∏:
∏ = (длина окружности) / (диаметр окружности)
Поскольку это определение для ∏ , исключений нет.
Символ отношения длины окружности к его диаметру был необходим, потому что это отношение очень часто встречается в математике. Была выбрана греческая буква ∏ (пи).
ПРИМЕЧАНИЕ. Использование C=∏d или C=2∏r для демонстрации того, что это всегда верно, означает просто применение определения.
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.