Вычисление определителя методом Гаусса с выбором главного элемента
ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ МЕТОДОМ ГАУССА С ВЫБОРОМ ГЛАВНОГО ЭЛЕМЕНТА.
Одновременно с решением системы линейных алгебраических уравнений
можно вычислить определитель матрицы А.
Пусть в процессе исключения найдено распожение
т.е. построены матрицы L и U . Тогда
и, таким образом, произведение диагональных елементов матрицы L (ведущих, главных елементов метода исключения) равно определителю матрицы РА. Поскольку матрицы РА и А отличаются только перестановкой строк, определитель матрицы РА может отличаться от определителей матрицы А только знаком.
А именно,
Таким образом, для вычисления определителя необходимо знать, сколько перестановок было осуществлено в процессе сключения.
Если матрица А выроджена, то при использовании метод Гаусса с выбором главного элемента по столбцу на некотором шаге исключения К все элементы которого столбца, находящиеся ниже главной диагонали и на ней, окажутся равными нулю.
ОБРАЩЕНИЕ МАТРИЦ.
Нахождение матрицы, обратной матрице А , еквивалентно решению матричного уравнения
(1)
где Е — единичная матрица, X — искомая квадратная матрица.
Уравнение (1) можно записать в виде системы уравнений
(2)
где
Можно заметить, что система (2) распадается на m независимых систем уравнений с одной и той же матрицей А , но с различными правыми частями. Эти системы имеют
вид ( фиксируем j ) :
(3)
где у вектора — столбца равна единице j-та компонента и равны нулю остальные компоненты.
Например, для матрицы второго порядка система (2) распадается на две независимые системы:
Для решения систем (3) используется метод Гаусса ( обычный или с выбором главного элемента).
Рассмотрим применение метода Гаусса без выбора главного элемента. Поскольку все системы (3) имеют одну и ту же матрицу А , достаточно один раз совершить прямой ход метода Гаусса, т.е. получить разложение A=LU и запомнить матрицы L i U .
Обратный ход осуществляется путем решения систем уравнений
с треугольными матрицами L и U.
При осуществлении обратного хода можно сократить число действий, принимая во внимание специальный вид правых частей системы (4).
Запишем подробнее первые j-1 уравнений системы (4):
Учитывая невырожденность матрицы L ( т.е.
отсюда получаем
При этом оставшиеся уравнения системы (4) имеют вид
Отсюда последовательно находятся неизвестные по формулам:
Можно показать, что общее число действий умножения и деления, необходимое для обращения матрицы указанным способом, порядка . Тем самым обращение матрицы требует не намного больше времени, чем решение системы уравнений.
Метод Гаусса презентация, доклад
Лекция N7
Тема:
Метод Гаусса
Решение систем линейных уравнений.
Метод Гаусса
Пример.
1) Составим расширенную матрицы системы
2) Приведем матрицу к ступенчатому виду
3) Составим новую систему
Система имеет единственное решение
Можно было продолжить преобразования, и привести систему к виду Гаусса.
Теорема Кронекера-Капелли.
Примеры
Пример 1.
Исследовать на совместность и решить систему методом Гаусса.
Система имеет бесконечное множество решений. Найдем число свободных неизвестных
В этом примере система имеет бесконечное множество решений.
Запишем некоторые из них:
Пример 2. Исследовать на совместность и решить систему методом Гаусса.
Система несовместна (по теореме Кронекера-Капелли)
Мы рассмотрели два метода решения систем линейных уравнений:
1) Метод Крамера
2) Метод Гаусса
Метод Крамера предполагает вычисление определителей. Мы вычисляли определители 3-его порядка разложением по элементам первой строки.
Пример.
Способ 1.
-4
5
Способ 2.
1) Определитель не изменится, если поменять строки на соответствующие столбцы
Свойства определителей
2) Если у определителя 2 одинаковые строки или столбца, то он равен нулю.
3) Если у определителя нулевая строка или столбец, то он равен нулю.
4) Если две строки (столбца) поменять местами, то знак определителя изменится на противоположный.
Свойства определителей
5) Общий множитель строки (столбца) можно выносить за знак определителя.
6) Определитель не изменится, если к элементам строки (столбца) прибавить элементы другой строки (столбца), умноженные на число.
Пример.
Вычислить:
(т.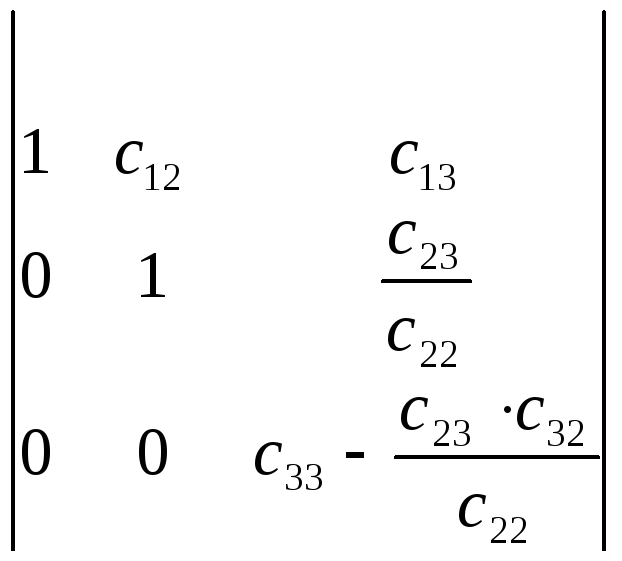
к. две одинаковые строки)
Пусть дана матрица
Определителем второго порядка, соответствующим данной матрице, называется число
Определитель обозначают символом
Таким образом,
Числа называются элементами определителя
Пример
Приведем свойства определителя второго порядка
1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами, т.е.
2. При перестановке двух строк (или столбцов) определитель изменит знак на противоположный, т.е.
3. Определитель с двумя одинаковыми строками (или столбцами) равен нулю.
4. Общий множитель всех элементов строки (или столбца) можно выносить за знак определителя:
5.
6. Если к элементам какой-либо строки (или столбца) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, то определитель не изменит своей величины, т.е.
Рассмотрим матрицу
Определитель третьего порядка
Определителем третьего порядка называют число
Назовем минором, соответствующим данному элементу определителя третьего порядка, определитель второго порядка, полученный из данного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент. Например, минор
соответствующий элементу есть определитель
Назовем алгебраическим дополнением
Например,
Правило.
Определитель третьего порядка равен сумме попарных произведений элементов какой-либо его строки (или столбца) на их алгебраические дополнения
Пример
Вычислить
Разлагаем по 1-му столбцу
Можно разлагать по 2-ой строке
Все свойства определителей 2-ого порядка остаются справедливыми для определителей 3-его порядка.
Свойства
Пример
Вычислить
т.к. совпадают первая и вторая строки.
Все свойства определителей 2-ого и 3-его порядков сохраняются для определителей высших порядков.
Определители высших порядков
Пример
Понятие обратной матрицы вводится только для квадратных матриц.
Обратная матрица
Опр.
Матрица называется обратной к
матрице , если
— единичная матрица
Теорема. Для того, чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы матрица A была невырожденной, т.е. чтобы её определитель был отличен от нуля.
Рассмотрим
Составим матрицу из алгебраических дополнений
Составим новую матрицу поменяв местами строки и столбцы (матрица называется транспонированной).
Составим матрицу, обратную матрице второго порядка
Здесь
Тогда
Пример.
то A – невырожденная, и, следовательно, существует обратная матрица
Вычисляем алгебраические дополнения:
Свойства
Примеры
Вычислить определитель произведения
1.
2.
По свойству 1
Домашнее задание
1. Проверить, что,
действительно
Домашнее задание
2.
Вычислить
Скачать презентацию
линейная алгебра — определитель большой матрицы с правилом Гаусса?
Задавать вопрос
спросил
Изменено 10 лет, 7 месяцев назад
Просмотрено 6к раз
$\begingroup$
$$A=\begin{pmatrix} 1 и -1 и 0 и 2 \\ 2 и 1 и 0 и 0 \\ 1 и 1 и 2 и 2 \\ 0 и 0 и 1 и 1 \\ \end{pmatrix}$$
С помощью метода нижнего определителя я получил $det(A)=-2$, но моя задача состоит в том, чтобы использовать метод Гаусса, чтобы найти определитель.
Я знаю, что для треугольной матрицы $B$ $det(B)=\prod b_{ii}$ т.е. след (произведение диагональных вещей). Теперь я могу превратить это в треугольную матрицу Гаусса Джордана, но я пока не могу понять, что означает решение определителя с помощью метода Гаусса или правила Гаусса, как бы вы это ни называли? Я нахожусь на странице 741 XI.5:4, здесь (не на английском), это должна быть тривиальная проблема, но я остановился на этом.
ERR: в чем проблема, пытаясь использовать GE?
- линейная алгебра
- матрицы
- определитель
$\endgroup$
4
$\begingroup$
Выполнение исключения Гаусса на
$$ А=\begin{pmatrix}
1 и -1 и 0 и 2 \\
2 и 1 и 0 и 0 \\
1 и 1 и 2 и 2 \\
0 и 0 и 1 и 1 \\
\end{pmatrix}$$
мы получаем
$$
\begin{pmatrix}
1 и -1 и 0 и 2 \\
0 и ? & ? & ? \\
0 & 0 & ? & ? \\
0 & 0 & 0 & ? \\
\end{pmatrix}$$
которое имеет определитель (см.
свойство 9здесь):
$$ 1 \раз ?\раз ? \ раз ? = -2 $$
Поскольку это вопрос (домашнее задание) , я позволю вам заполнить все пробелы.
$\endgroup$
4
$\begingroup$
Я думаю, это может помочь: Det через исключение Гаусса. Если вы вычислили треугольную матрицу с помощью метода Гаусса Жордана, все, что вам нужно, это соблюдать следующие 2 правила при применении исключения:
- Перестановка двух строк меняет знак определителя.
- При умножении строки на скаляр определитель умножается на этот скаляр.
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Исключение по Гауссу: Определитель матрицы с использованием прямого исключения: Пример: Youtube
Одновременные линейные уравнения: Исключение по Гауссу: Определитель Матрица с использованием прямого исключения: Пример: Youtube
./../../background.jpg»>ИСКЛЮЧЕНИЕ ГАУССА (ГЛАВА 04.06)
Определитель матрицы с использованием прямого исключения: Пример
По Аутар Кау
|
./../../../images/background.jpg»>Узнайте на примере, как найти определитель матрица с использованием прямых шагов исключения Гаусса.
В этом видео вы узнаете, как найти определитель матрицы с использованием прямых шагов исключения Гаусса с пример.
Наивное исключение Гаусса: Теория: Часть 1 из 2 [YOUTUBE 10:27] [СТЕНОК]
Наивное исключение Гаусса: теория: часть 2 из 2 [YOUTUBE 2:22] [СТЕНОК]
Наивный метод исключения Гаусса: Пример: Часть 1 из 2 (Выбывание вперед) [YOUTUBE 10:49] [СТЕНОК]
Наивный метод исключения Гаусса: Пример: часть 2 из 2 (обратная замена) [YOUTUBE 6:40] [СТЕНОК]
Подводные камни наивного исключения Гаусса Метод: [ЮТУБ 7:20] [СТЕНОК]
Наивное исключение Гаусса: округление Проблемы с ошибками: Пример: часть 1 из 3 [YOUTUBE 7:20] [СТЕНОК]
Наивное исключение Гаусса: округление Проблемы с ошибками: Пример: Часть 2 из 3 [YOUTUBE 7:40] [СТЕНОК]
Наивное исключение Гаусса: округление Проблемы с ошибками: Пример: часть 3 из 3 [YOUTUBE 8:07] [СТЕНОК]
Исключение по Гауссу с частичным Разворот: теория [YOUTUBE 10:39] [СТЕНОК]
Исключение по Гауссу с частичным Поворот: Пример: часть 1 из 3 (выбывание вперед) [YOUTUBE 7:15] [СТЕНОК]
Исключение по Гауссу с частичным Поворот: Пример: часть 2 из 3 (выбывание вперед) [YOUTUBE 10:08] [СТЕНОК]
Исключение по Гауссу с частичным Поворот: Пример: часть 3 из 3 (обратная замена) [YOUTUBE 6:18] [СТЕНОК]
Исключение по Гауссу с частичным Сводка: ошибки округления Проблемы: пример: часть 1 из 3 [YOUTUBE 8:58] [СТЕНОК]
Исключение по Гауссу с частичным Сводка: Проблемы с округлением: Пример: Часть 2 из 3 [YOUTUBE 8:17] [СТЕНОК]
Исключение по Гауссу с частичным Сводка: Проблемы с округлением: Пример: часть 3 из 3 [YOUTUBE 5:48] [СТЕНОК]
Определитель матрицы с использованием форварда Метод исключения: Фон [YOUTUBE 5:17] [СТЕНОК]
Определитель матрицы с использованием форварда Метод исключения: Пример [YOUTUBE 10:07] [СТЕНОК]
./../../../images/background.jpg»>АУДИТОРИЯ | НАГРАДЫ | ЛЮДИ | ТРЕК | РАСПРОСТРАНЕНИЕ | ПУБЛИКАЦИИ | ||
Авторские права:
Университет
Южной Флориды, 4202 E Fowler Ave, Tampa, FL 33620-5350. Все права защищены. Вопросы, предложения или
комментарии, контакт kaw@eng. | ||
