Определитель транспонированной матрицы равен определителю матрицы: 08. Свойства определителей

08. Свойства определителей

Определение 9. Транспонированием A матрицы называется такое ее преобразование, при котором строки матрицы становятся ее столбцами с теми же самыми номерами.

Матрица транспонированная матрице A обозначается символом :

.

Свойство 1. Определитель транспонированной матрицы равен определителю исходной матрицы, т. е. .

Доказательство. ОПределителя матрицы А есть алгебраическая сумма N! произведений вида

(11)

Где в каждое произведение входит по одному элементу из каждой строки и каждого столбца матрицы A, со знаком равным знаку подстановки

.

Так как сомножители произведения (11) также находятся по одному в каждом столбце и каждой строке матрицы , то каждое произведение определителя матрицы A входит в определитель матрицы . Отсюда. так как количество слагаемых в и в одинаково, следует, что и в состоят из одних и тех же слагаемых.

Для того, чтобы показать, что знаки произведений равны, составим подстановку для произведения (11) в (учитываем, что строки матрицы А стали столбцами матрицы с теми же номерами). Она равна подтановке:

.

Подстановки иИмеют одинаковое число инверсий, четность и знак.

Таким образом и суммы одних и тех же произведений и поэтому . Свойство доказано.

Замечание 1. Из свойства 1 вытекает, что строки и столбцы матрицы Равноправны, т. е., если какое-нибудь свойство доказано для строк, то оно будет справедливо и для столбцов и обратно. Поэтому дальнейшие свойства формулируются и доказываются только для строк. В дальнейшем под строками и столбцами определителя понимаются строки и столбцы соответствующей матрицы.

Свойство 2. Если в матрице поменять местами две строки, то абсолютная величина определителя не меняется, а знак определителя меняется на противоположный.

Доказательство. Пусть даны исходный и преобразованный определитель:

. (12)

Определитель Получается из определителя D перестановкой I-й и J-й строк (точками обозначены все остальные строки, которые в D и Совпадают. Требуется доказать, что D= -.

ОПределитель D есть алгебраическая сумма N! произведений вида

, (13)

Где в каждое произведение входит по одному элементу из каждой строки и каждого столбца определителя D, со знаком равным знаку подстановки

.

Так как сомножители произведения (13) также находятся по одному в каждом столбце и каждой строке определителя , то каждое произведение определителя D входит в определитель . Отсюда, так как количество слагаемых в D и одинаково, следует, что D и состоят из одних и тех же произведений, Для того, чтобы показать, что

D= —, достаточно показать, что каждое произведение (13) определителях D и Имеет противоположные знаки. Знак произведения (13) в определителе равен знаку подстановки:

(учитываем, что элемент Лежит в определителе в J-й строке в-м столбце, элемент — в I-й строке и в -м столбце).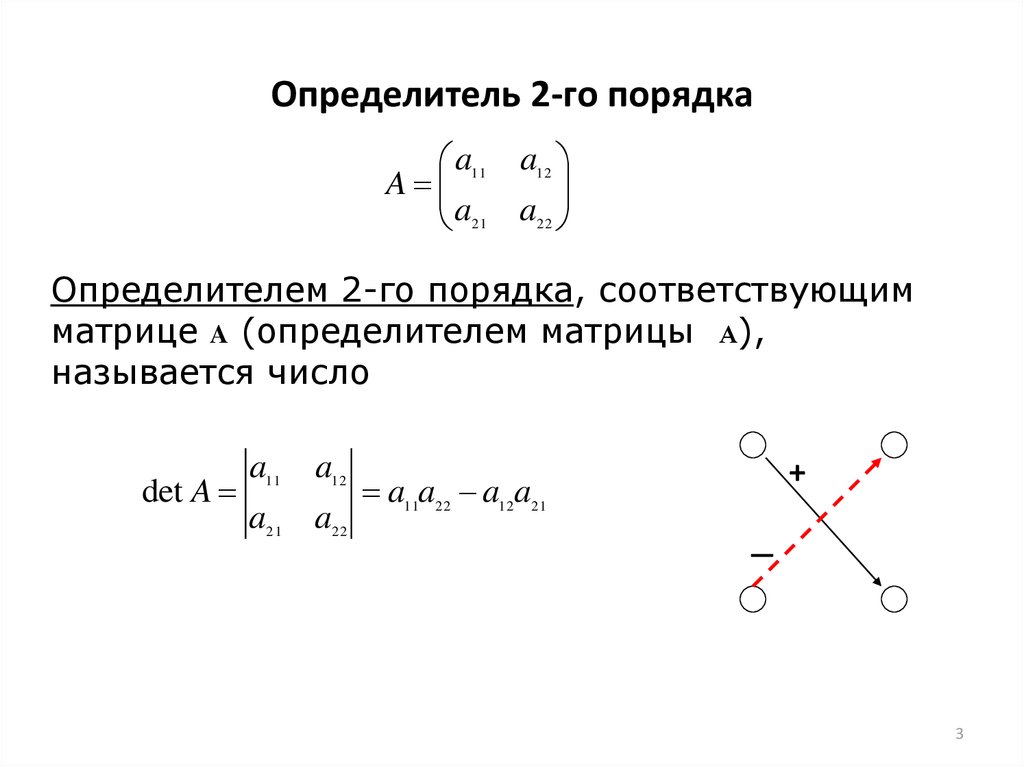 У подстановок и Совпадают вторые строки, а первая строка подстановки Получена из первой строки подстановки транспозицией элементов I и J . Поэтому в силу теоремы 2 подстановки и Имеют противоположную четность и знак. Отсюда образом произведение (13) входит в определители D и с противоположным знаком. Таким образом определители D и суммы одних и тех же произведений, но с противоположными знаками и D= —. . Свойство доказано.

Свойство 3. Если в определителе есть две одинаковые строки, то определитель равен нулю

.

Доказательство. Пусть в определителе D I-я строка равна j-й строке. Переставим I-ю и J-ю строки местами и получим определитель (см.(13)). По свойству 2 D= —. Так как I-я и J-я строки равны, то D= . Из этих равенств находим, что D= 0. Свойство доказано.

Свойство 4. Если в определителе есть нулевая строка, то определитель равен нулю.

Доказательство. Пусть в определителе I-я строка нулевая. По определению определителя он равен алгебраической сумме произведений вида:

.

В каждое произведение входит нулевой элемент I-й строки и поэтому оно равно нулю. Следовательно, и определитель равен нулю. Свойство доказано.

Свойство 5. Если все элементы какой-нибудь строки определителя представлены в виде двух слагаемых, то определитель равен сумме двух определителей, в первом из которых элементы отмеченной строки равны соответствующим первым слагаемым, во втором — вторым слагаемым.

Пусть все элементы I-й строки представлены в виде ; J=1,2,…,N. Тогда свойство перепишется в виде:

=

= .

Доказательство. По формуле (8) находим

= .

Свойство доказано.

Замечание 2. Индукцией по m легко доказать, что свойство 5 справедливо для случая, когда каждый элемент i-й строки сумма m слагаемых, .

Свойство 6. Если все элементы какой-нибудь строки определителя имеют общий множитель, то его можно вынести за знак определителя, т. е., если элементы какой-нибудь строки определителя умножить на число k, то и сам определитель умножится на число k.

.

Доказательство.

По формуле (8) находим

Свойство доказано.

Свойство 7. Если в определителе есть две пропорциональны строки, то он равен нулю.

Доказательство. Пусть I-я и J-я строки определителя пропорциональны, т. е. . Вынося из J-й общий множитель K за знак определителя, получим определитель с двумя равными строками, который равен нулю. Поэтому и исходный определитель равен нулю. Свойство доказано.

Свойство 8. Если к какой-нибудь строке определителя прибавить другую строку, умноженную на число k, то определитель от этого не изменится.

Доказательство. Пусть к I-й строке определителя прибавили ее J-ю строку, умноженную на число K . Тогда по свойствам 5 и 7 получаем:

Свойство доказано.

Определение 10. Говорят, что I-я строка матрицы

A есть линейная комбинация остальных строк определителя, если существуют такие числа , что каждый элемент I-й строки есть сумма попарных произведений этих чисел на соответствующие элементы остальных строк матрицы, т. е.

Свойство 9. Если какая-нибудь строка определителя есть линейная комбинация остальных строк определителя, то определитель равен нулю.

Доказательство. Если I-я строка определителя есть линейная комбинация остальных строк определителя, то по замечанию 2 определитель равен сумме n-1 определителей с пропорциональными строками, и по свойству 7 все такие определители равны нулю. Тогда и исходный определитель равен нулю. Свойство доказано.

< Предыдущая		Следующая >

Свойства определителей — ПриМат

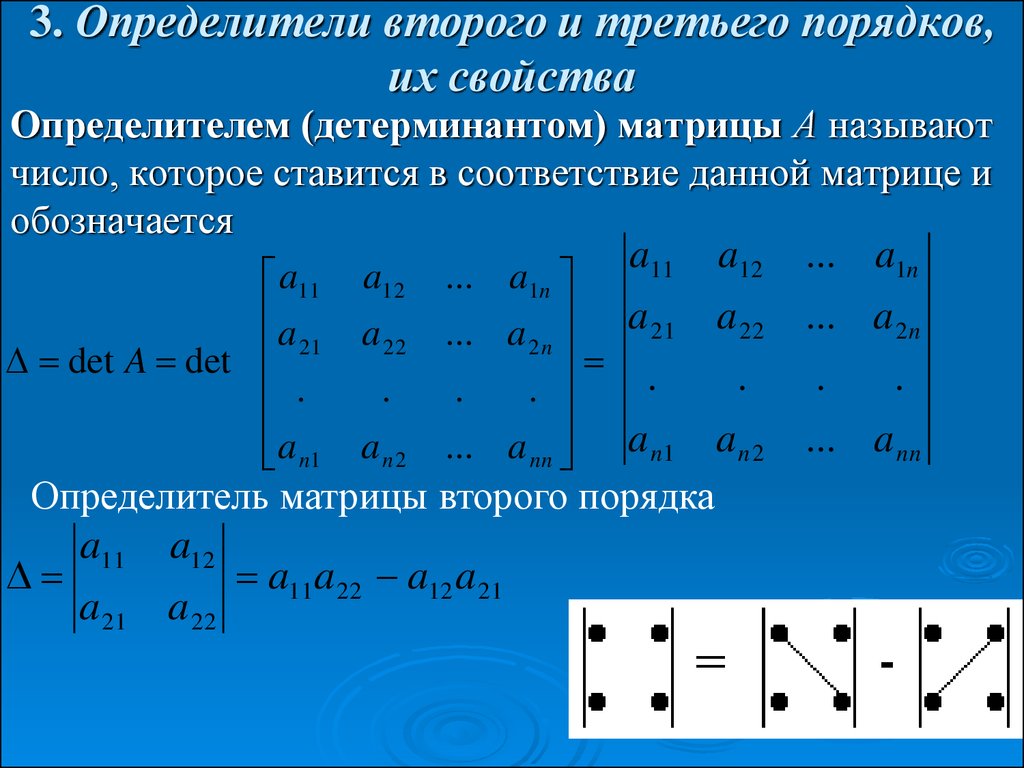
Рассмотрим свойства определителей, на основе которых можно существенно облегчить их вычисление:

Определитель транспонированной матрицы равен определителю начальной матрицы: $\det A = \det A^{T}$.

Доказательство

Действительно, брать произведения элементов по одному из каждой строки и по одному из каждого столбца исходной матрицы — то же самое, что делать это по отношению к транспонированной матрице. Далее, номера строк для исходной матрицы — это номера столбцов для транспонированной, а номера столбцов исходной матрицы — суть номера строк транспонированной. Поэтому каждое слагаемое входит в состав определителя исходной матрицы и определителя транспонированной с одним и тем же множителем.

[свернуть]

Транспозиция (замена) двух строк (столбцов) матрицы — меняет знак определителя $$\det A = \begin{vmatrix} a_{11} & … & a_{1n} \\ .&.&. \\ a_{i1} & … & a_{in} \\ a_{j1} & … & a_{jn} \\ .&.&. \\ a_{n1} & … & a_{nn} \end{vmatrix} = -\begin{vmatrix} a_{11} & … & a_{1n} \\ .&.&. \\ a_{j1} & … & a_{jn}\\ a_{i1} & … & a_{in} \\ .&.&. \\ a_{n1} & … & a_{nn} \end{vmatrix}.$$

Доказательство

Действительно, по Теореме №$2$ о транспозиции — транспозиция меняет четность элементов перестановки. При перестановке двух строк, каждый элемент меняет знак, значит и сам определитель меняет знак.

[свернуть]

Умножение всей строки (столбца) на некий элемент $\alpha$ является аналогичным умножению всего определителя на этот элемент. Определитель с нулевой строкой (столбцом) равен нулю: $$ \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1 j} & \cdots & a_{1 n} \\a_{21} & a_{22} & \cdots & a_{2 j} & \cdots & a_{2 n} \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\\alpha a_{i 1} & \alpha a_{i 2} & \cdots & \alpha a_{i j} & \cdots & \alpha a_{i n} \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\a_{n 1} & a_{n 2} & \cdots & a_{n j} & \cdots & a_{n n}\end{vmatrix}= \alpha \cdot\begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1 j} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 j} & \cdots & a_{2 n} \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{i 1} & a_{i 2} & \cdots & a_{i j} & \cdots & a_{i n} \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\a_{n 1} & a_{n 2} & \cdots & a_{n j} & \cdots & a_{n n}\end{vmatrix}. $$

Доказательство

Пусть на $\alpha$ умножаются все элементы $i$-той строки. Каждый член определителя содержит $1$ элемент из этой строки, поэтому всякий член определителя приобретает общий множитель $\alpha$, а это значит что и сам определитель умножается на $\alpha$.

[свернуть]

Если все элементы $i$-той строки (столбца) матрицы определителя разбить в сумму двух строк: $$a_{i j}=b_{j}+c_{j}, \quad j=1, \ldots, n$$ то и саму матрицу можно будет разбить на две, у которых все строки (столбцы) кроме $i$-той — такие же как у первой матрицы, а $i$-тая строка состоит из $b_{j}$ в первой матрице определителя, и из элементов $c_{j}$ во втором.

Доказательство

Действительно, любой член матрицы определителя можно представить в виде произведения: $$\begin{aligned}a_{1 \alpha_{1}} a_{2 \alpha_{2}} \ldots a_{i \alpha_{i}} \ldots a_{n \alpha_{n}}&=a_{1 \alpha_{1}} a_{2 \alpha_{2}} \ldots\left(b_{\alpha_{i}}+c_{\alpha_{i}}\right)\ldots a_{n \alpha_{n}}=\\&=a_{1 \alpha_{1}} a_{2 \alpha_{2}} \ldots b_{\alpha_{i}} \ldots a_{n \alpha_{n}}+a_{1\alpha_{1}} a_{2 \alpha_{2}} \ldots c_{\alpha_{i}} \ldots a_{n\alpha_{n}}. \end{aligned}.$$ Объединяя первые слагаемые этого выражения, мы получим матрицу определителя, где в первой матрице в $i$-той строке вместо элементов $a_{i j}$ стоят элементы$b_{j} .$ Соответственно вторые слагаемые составляют матрицу определителя, с элементами $c_{j}$ таким образом: $$\begin{vmatrix}a_{11} & a_{12} & \cdots & a_{1 n} \\a_{1}+c_{1} & b_{2}+c_{2} & \dots & b_{n}+c_{n} \\a_{n 1} & a_{n 2} & \dots & a_{n n}\end{vmatrix}=$$$$=\begin{vmatrix}a_{11} & a_{12} & \dots a_{1 n} \\b_{1} & b_{2} & \dots & b_{n} \\a_{n 1} & a_{n 2} & \dots & a_{nn}\end{vmatrix}+\begin{vmatrix}a_{11} & a_{12} & \dots & a_{1 n} \\c_{1} & c_{2} &\dots & c_{n} \\a_{n 1} & a_{n 2} & \dots & a_{n n}\end{vmatrix}.$$

[свернуть]

Определитель верхней (нижней) треугольной матрицы есть произведение элементов ее главной диагонали $$\begin{vmatrix}a_{11} & a_{12} & a_{13} & \cdots & a_{1 n} \\0 & a_{22} & a_{23} & \cdots & a_{2 n} \\0 & 0 & a_{33} & \cdots & a_{3 n} \\\cdots & \cdots & \cdots & \cdots & \cdots \\0 & 0 & 0 & \cdots & a_{n n}\end{vmatrix}=a_{11} \cdot a_{22} \cdot a_{33} \cdot \ldots \cdot a_{n n}. $$

Доказательство

Действительно, так как определитель есть произведение одного из элементов строки (столбца) его матрицы, то у первого столбца единственным будет $a_{11}$, во втором столбце — $a_{22}$ т.к. у первой строки $a_{11}$, третьим элементом — только $a_{33}$, далее аналогично.

[свернуть]

Если в матрице определителя одна строка будет результатом ее сложения с другой строкой и умножения на число, определитель не изменится . $$\begin{vmatrix}a_{11}& \cdots & \cdots & \cdots & a_{1n} \\ \cdots & \cdots & \cdots & \cdots & \cdots & \\ a_{i 1} & a_{i 2} & a_{i 3} & \cdots & a_{i n} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{j 1} & a_{j 2} & a_{j 3} & \cdots & a_{j n} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{n1}& \cdots & \cdots & \cdots & a_{nn}\end{vmatrix}=$$$$=\begin{vmatrix}a_{11}& \cdots & \cdots & \cdots & a_{1n} \\\cdots & \cdots & \cdots & \cdots & \cdots \\ a_{i 1} & a_{i 2} & a_{i 3} & \cdots & a_{i n} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{k 1}+k a_{i 1} & a_{k 2}+k a_{i 2} & a_{k 3}+k a_{i 3} & \cdots & a_{k n}+k a_{i n} \\ \ldots & \ldots & \ldots & \ldots & \ldots\\ a_{n1}& \cdots & \cdots & \cdots & a_{nn}\end{vmatrix}\cdot$$

Доказательство

Этот определитель можно представить в виде суммы определителей (по $4$ свойству), в итоге получится $2$ определителя, один из которых будет равен нулю, из-за равенства двух строк, а второй будет исходным.

[свернуть]

Вычислить определитель $$\det A=\begin{vmatrix}6 & 1 & 6 \\12 & 2 & 12 \\9 & 2 & 5\end{vmatrix}.$$

Решение

Выносим $2$ из второй строки определителя: $$\det A = \begin{vmatrix}6 & 1 & 6 \\12 & 2 & 12 \\9 & 2 & 5\end{vmatrix} = 2\begin{vmatrix}6 & 1 & 6 \\6 & 1 & 6 \\9 & 2 & 5\end{vmatrix} = 0.$$ Видим что у определителя две равных строки соответственно определитель равен нулю

[свернуть]

Вычислить определитель$$\det A =\begin{vmatrix}12& 5 & 1 & 5 & 19 \\0 & 8 & 2 & 12 & 9 \\0 & 0 & 4 & 27 & 41 \\0 & 0 & 0 & 5 & 13 \\ 0 & 0 & 0 & 0 & 7\end{vmatrix}$$

Решение

По пятому свойству, определитель треугольной матрицы равен произведению элементов главной диагонали: $$\det A=\begin{vmatrix}12& 5 & 1 & 5 & 19 \\0 & 8 & 2 & 12 & 9 \\0 & 0 & 4 & 27 & 41 \\0 & 0 & 0 & 5 & 13 \\ 0 & 0 & 0 & 0 & 7\end{vmatrix}=12\cdot8\cdot4\cdot5\cdot7=13440. $$

[свернуть]

Проверьте, будет ли определитель транспонированной матрицы равен исходной:$$\begin{Vmatrix}3 & 3 & -1 \\4 & 1 & 3 \\1 & -2 & -2\end{Vmatrix}.$$

Решение

$$\begin{vmatrix}3 & 3 & -1 \\4 & 1 & 3 \\1 & -2 & -2 \end{vmatrix}=$$$$=(-6)-(-18)-(-24) + 8 + 9 — (-1)=54$$$$\begin{vmatrix}3 & 4 & 1 \\3 & 1 & -2 \\-1 & 3 & -2 \end{vmatrix}=(-6)-(-18)-(-24)+8+9- (-1)=54.$$ Действительно, определитель транспонированной матрицы равен исходной

[свернуть]

Вычислите определитель треугольной матрицы: $$\begin{Vmatrix}3 & 0 & 0 \\4 & 1 & 0 \\1 & -2 & -2 \end{Vmatrix}.$$

Решение

Воспользуемся пятым свойством: $$\begin{vmatrix}3 & 0 & 0 \\4 & 1 & 0 \\1 & -2 & -2 \end{vmatrix} = 3\cdot1\cdot-2 = -6$$

Вычислите определитель: $$\begin{vmatrix}6 & 5 & 9 & 3 \\2 & 1 & 0 & 4 \\0 & 0 & 0 & 0 \\ 1 & 12 & 8 & 2 \end{vmatrix}. $$

Решение

[свернуть]

По $3$ свойству, матрица определителя, содержащая нулевую строку равна нулю. Ответ $\det A=0$

[свернуть]

Смотрите также

1. Конспект Белозерова Г.С. по алгебре — Глава IV.
2. Курош А.Г. Курс высшей алгебры М.: Наука, 1968, издание 9, глава 1, §4, «Определители n-го порядка»
3. В.Воеводин Линейная алгебра М.: Наука, 1980, глава 7, §62, «Матрицы и определители» — стр 201

Свойства Определителей

Проверьте себя на знание материала «Свойства Определителей»

1.3. Свойства определителей

gif»>	1.3. Свойства определителей			Высшая математика > 1. Элементы линейной алгебры > 1.3. Свойства определителей
	Определение 1 Матрица, полученная из данной матрицы  заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной по отношению к данной, и обозначается: .   Свойство 1 Определитель транспонированной матрицы равен определителю исходной.   Свойство 2 Если в определителе поменять местами две строки (столбца), то определитель поменяет знак.   Свойство 3  Определитель с двумя пропорциональными (в частности, равными) строками (столбцами) равен нулю.   Свойство 4 Если в определителе строка (столбец) целиком состоит из нулей, то определитель равен нулю.   Свойство 5 Общий множитель всех элементов какой либо строки (столбца) можно вынести за знак определителя.   Свойство 6 Правило сложения определителей: , т.е. если каждый элемент некоторой строки (столбца) представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, причем в одном из них соответствующая строка (столбец) состоит из первых слагаемых, а в другом — из вторых слагаемых, остальные же строки (столбцы) — те же, что и в исходном определителе.   Свойство 7 Определитель не изменится, если ко всем элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число: .   Определение 2 Верхней треугольной матрицей называется матрица вида: .   Определение 3 Нижней треугольной матрицей называется матрица вида: .   Определение 4 Диагональной матрицей называется матрица вида: . Свойство 8 Определитель диагональной, треугольной (верхней и нижней) матрицы равен произведению диагональных элементов.   Определение 5 Минором элемента определителя  называется определитель, получаемый из данного определителя вычеркиванием -ой строки и-ого столбца. Обозначается: . Замечание 1 Минор — это определитель, порядок которого на единицу меньше, чем у исходного.   Определение 6 Алгебраическим дополнением элемента определителя  называется число: , где  — соответствующий минор.   Пример 1 Дан определитель: . Вычислить  и   Решение Так как нужно вычислить минор и алгебраическое дополнение элемента , вычеркиваем в определителе вторую строку и третий столбец: . Тогда: , . Замечание 2 Так как знак перед минором в алгебраическом дополнении определяется только местом элемента в определителе, то правило выбора знаков выглядит следующим образом: .   Теорема разложения Определитель равен сумме произведений элементов какой — либо строки (столбца) на их алгебраические дополнения. Это означает, что если взять в определителе -ую строку, то его величину можно вычислить по следующей формуле: . Такой способ вычисления определителя называется разложением его по элементам -ой строки (аналогично определяется разложение определителя по элементам -ого столбца).   Пример 2 Вычислить определитель: , разложив его по элементам первого столбца.   Решение 1 способ . 2 способ Используя 7-ое свойство, обратим некоторые элементы первого столбца в ноль. Это упростит вычисление определителя. Умножим первую строку на (-3) и прибавим ко второй строке, затем умножим первую строку на (-7) и прибавим к третьей строке: . Заметим, что вторая строка имеет общий множитель (-2), а третья — (-1). Поэтому, применяя дважды 5-ое свойство, получим: . В первом столбце остался лишь один элемент, отличный от нуля. Тогда, разложив определитель по элементам первого столбца, получим: .   Свойство 10 Сумма произведений элементов какой — либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю. Например, сумма произведений элементов первой строки определителя на алгебраические дополнения соответствующих элементов второй строки равна нулю: .
					gif»>

Свойства определителей. Обратная матрица (Лекция №13)

1. Если квадратная матрица A^T является транспонированной матрицей A, то их определители совпадают |A^T | = |A|, т.е. определитель не меняется, если заменить его строки столбцами и обратно, например, для определителя третьего порядка .

   Доказательство проводится проверкой, т.е. сравнением обеих частей записанного равенства. Вычислим определители, стоящие слева и справа:

2. При перестановке 2-х строк или столбцов определитель изменит знак на противоположный, сохраняя абсолютную величину, т.е., например,

   Доказательство проводится аналогично доказательству свойства 1 сравнением обеих частей. Проведём его для определителя второго порядка.

   .

   Для определителя третьего порядка проверьте самостоятельно.

3. Если определитель имеет две одинаковые строки или столбца, то он равен нулю. Например, .

   Действительно, если переставить здесь 2-ю и 3-ю строки, то по свойству 2 этот определитель должен изменить знак, но сам определитель в данном случае не меняется, т.е. получаем |A| = –|A| или |A| = 0.

4. Общий множитель строки или столбца можно выносить за знак определителя. Например, .

   Доказательство проводится проверкой, как и свойство 1. (Самостоятельно)

5. Если все элементы какой–либо строки или столбца определителя равны нулю, то сам определитель равен нулю. (Доказательство – проверкой).
6. Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель можно представить в виде суммы 2-х определителей по формуле, например,

   .

   Доказательство — проверкой, аналогично свойству 1.

7. Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель не изменит своей величины. Например,

   .

   Докажем это равенство, используя предыдущие свойства определителя.

   Эти свойства определителей довольно часто используются при вычислении определителей и в различных задачах.

АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ И МИНОРЫ

Пусть имеем определитель третьего порядка: .

Минором, соответствующим данному элементу a_ij определителя третьего порядка, называется определитель второго порядка, полученный из данного вычёркиванием строки и столбца, на пересечении которых стоит данный элемент, т.е. i-ой строки и j-го столбца. Миноры соответствующие данному элементу a_ij будем обозначать M_ij.

Например, минором M₁₂, соответствующим элементу a₁₂, будет определитель , который получается вычёркиванием из данного определителя 1-ой строки и 2-го столбца.

Таким образом, формула, определяющая определитель третьего порядка, показывает, что этот определитель равен сумме произведений элементов 1-ой строки на соответствующие им миноры; при этом минор, соответствующий элементу a₁₂, берётся со знаком “–”, т.е. можно записать, что

.

(1)

Аналогично можно ввести определения миноров для определителей второго порядка и высших порядков.

Введём ещё одно понятие.

Алгебраическим дополнениемэлемента a_ij определителя называется его минор M_ij, умноженный на (–1)^i+j.

Алгебраическое дополнение элемента a_ij обозначается A_ij.

Из определения получаем, что связь между алгебраическим дополнением элемента и его минором выражается равенством A_ij = (–1)^i+jM_ij.

Например,

Пример. Дан определитель . Найти A₁₃, A₂₁, A₃₂.

Легко видеть, что используя алгебраические дополнения элементов, формулу (1) можно записать в виде:

.

Аналогично этой формуле можно получить разложение определителя по элементам любой строки или столбца.

Например, разложение определителя по элементам 2-ой строки можно получить следующим образом. Согласно свойству 2 определителя имеем:

Разложим полученный определитель по элементам 1-ой строки.

.

(2)

Отсюда т.к. определители второго порядка в формуле (2) есть миноры элементов a₂₁, a₂₂, a₂₃. Таким образом, , т.е. мы получили разложение определителя по элементам 2-ой строки.

Аналогично можно получить разложение определителя по элементам третьей строки. Используя свойство 1 определителей (о транспонировании), можно показать, что аналогичные разложения справедливы и при разложении по элементам столбцов.

Таким образом, справедлива следующая теорема.

Теорема (о разложении определителя по заданной строке или столбцу). Определитель равен сумме произведений элементов какой–либо его строки (или столбца) на их алгебраические дополнения.

Всё вышесказанное справедливо и для определителей любого более высокого порядка.

Примеры.

1. Вычислить определитель , раскладывая его по элементам 2-го столбца.

2. Вычислить определитель, используя его свойства. Прежде чем раскладывать определитель по элементам какой–либо строки, сводя к определителям третьего порядка, преобразуем его, используя свойство 7, сделав в какой–либо строке или столбце все элементы, кроме одного, равными нулю. В данном случае удобно рассмотреть 4-й столбец или 4-ю строку:

ОБРАТНАЯ МАТРИЦА

Понятие обратной матрицы вводится только для квадратных матриц.

Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A^-1 и удовлетворяющая условию . (Это определение вводится по аналогии с умножением чисел)

Справедлива следующая теорема:

Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.

Доказательство:

1. Необходимость. Пусть для матрицы A существует обратная матрица A^-1. Покажем, что |A| ≠ 0.

   Прежде всего заметим, что можно доказать следующее свойство определителей .

   Предположим, что |A| = 0. Тогда . Но с другой стороны . Полученное противоречие и доказывает, что |A| ≠ 0.

2. Достаточность. Для простоты доказательство проведём для случая матрицы третьего порядка. Пусть и |A| ≠ 0.

   Покажем, что в этом случае обратной матрицей будет матрица

   , где A_ij алгебраическое дополнение элемента a_ij.

   Найдём AB=C.

   Заметим, что все диагональные элементы матрицы C будут равны 1. Действительно, например,

   Аналогично по теореме о разложении определителя по элементам строки можно доказать, что c₂₂ = c₃₃ = 1.

   Кроме того, все недиагональные элементы матрицы C равны нулю. Например,

   Следовательно, AB=E. Аналогично можно показать, что BA=E. Поэтому B = A^-1.

Таким образом, теорема содержит способ нахождения обратной матрицы.

Если условия теоремы выполнены, то матрица обратная к матрице находится следующим образом

,

где A_ij — алгебраические дополнения элементов a_ij данной матрицы A.

Итак, чтобы найти обратную матрицу нужно:

1. Найти определитель матрицы A.
2. Найти алгебраические дополнения A_ij всех элементов матрицы A и составить матрицу , элементами которой являются числа A_ij.
3. Найти матрицу, транспонированную полученной матрице , и умножить её на – это и будет .

   Аналогично для матриц второго порядка, обратной будет следующая матрица .

Примеры.

1. Найти матрицу, обратную данной . Сделать проверку.

   |A| = 2. Найдем алгебраические дополнения элементов матрицы A.

   Проверка:

   .

   Аналогично A∙A^-1 = E.

2. Найти элементы и матрицы A^-1 обратной данной

   .

   Вычислим |A| = 4. Тогда .

   .

3. . Найдем обратную матрицу.

определение и свойства (11 шт)

Содержание:

• Определение
• Свойства определителей

Определение

Квадратной матрице $ A=\left( \begin{array}{cccc}{a_{11}} & {a_{12}} & {\dots} & {a_{1 n}} \\ {a_{21}} & {a_{22}} & {\dots} & {a_{2 n}} \\ {\ldots} & {\cdots} & {\cdots} & {\cdots} \\ {a_{n 1}} & {a_{n 2}} & {\dots} & {a_{n n}}\end{array}\right) $ $n$-го порядка ставиться в соответствие число $ |A|=\operatorname{det} A=\left| \begin{array}{cccc}{a_{11}} & {a_{12}} & {\dots} & {a_{1 n}} \\ {a_{21}} & {a_{22}} & {\dots} & {a_{2 n}} \\ {\ldots} & {\ldots} & {\ldots} & {\ldots} \\ {a_{n 1}} & {a_{n 2}} & {\dots} & {a_{n n}}\end{array}\right| $, называемое определителем матрицы или детерминантом. {3} \cdot|A|=8 \cdot|A|=8 \cdot 3=24 $

Ответ. $ |B|=24 $

4  Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.

$$ \left| \begin{array}{ccc}{b_{11}+c_{11}} & {b_{12}+c_{12}} & {b_{13}+c_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right|=\left| \begin{array}{ccc}{b_{11}} & {b_{12}} & {b_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right|+\left| \begin{array}{ccc}{c_{11}} & {c_{12}} & {c_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right| $$

5  Если две строки определителя поменять местами, то определитель поменяет знак.

Пример

$ \left| \begin{array}{ll}{1} & {1} \\ {2} & {3}\end{array}\right|=-\left| \begin{array}{ll}{2} & {3} \\ {1} & {1}\end{array}\right| $

6  Определитель с двумя равными строками равен нулю.

Пример

$ \left| \begin{array}{rrr}{1} & {2} & {3} \\ {1} & {0} & {-7} \\ {1} & {2} & {3}\end{array}\right|=0 $

7  Определитель с двумя пропорциональными строками равен нулю.

Пример

$ \left| \begin{array}{rrr}{1} & {2} & {3} \\ {-1} & {2} & {2} \\ {2} & {4} & {6}\end{array}\right|=\left| \begin{array}{ccc}{1} & {2} & {3} \\ {-1} & {2} & {2} \\ {2 \cdot 1} & {2 \cdot 2} & {2 \cdot 3}\end{array}\right|=0 $

8  Определитель, содержащий нулевую строку, равен нулю.

Пример

$ \left| \begin{array}{rrr}{1} & {-1} & {0} \\ {0} & {0} & {0} \\ {2} & {3} & {1}\end{array}\right|=0 $

9  Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.

Пример

Пусть задан определитель третьего порядка $ \left| \begin{array}{rrr}{1} & {-1} & {0} \\ {1} & {0} & {-1} \\ {2} & {3} & {1}\end{array}\right| $ . Прибавим ко второй строке определителя третью его строку, при этом значение определителя не измениться:

$$ \left| \begin{array}{rrr}{1} & {-1} & {0} \\ {1} & {0} & {-1} \\ {2} & {3} & {1}\end{array}\right|=\left| \begin{array}{ccc}{1} & {-1} & {0} \\ {1+2} & {0+3} & {-1+1} \\ {2} & {3} & {1}\end{array}\right|=\left| \begin{array}{rrr}{1} & {-1} & {0} \\ {3} & {3} & {0} \\ {2} & {3} & {1}\end{array}\right| $$

10  Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.

Пример

$ \left| \begin{array}{rrrr}{1} & {0} & {3} & {0} \\ {0} & {2} & {4} & {1} \\ {0} & {0} & {5} & {1} \\ {0} & {0} & {0} & {-1}\end{array}\right|=1 \cdot 2 \cdot 5 \cdot(-1)=-10 $

11  Определитель произведения матриц равен произведению определителей: $ |A \cdot B|=|A| \cdot|B| $

Читать дальше: минор и алгебраическое дополнение.

Когда определитель матрицы равен 1?

Содержание

• — Почему определитель не меняется при Транспонировании?
• — Что произойдет с определителем матрицы при перестановке двух столбцов?
• — Когда меняется определитель матрицы?
• — Что называется определителем матрицы?
• — Как изменится определитель Если в квадратной матрице поменять местами какие либо две строки или столбца )?
• — Как изменится определитель Если в квадратной матрице поменять местами какие либо две строки или столбца?
• — Что называется определителем?
• — В каком случае определитель матрицы равен 0?
• — Как называется операция перемены местами строк и столбцов матрицы?
• — Когда определитель равен нулю?
• — Какая разница между матрицей и определителем?
• — Как вычислить определитель квадратной матрицы?
• — Что такое определитель матрицы простыми словами?
• — В чем смысл определителя матрицы?
• — Что происходит с определителем при Транспонировании матрицы?

Определитель единичной матрицы равен единице: det(E) = 1. … Определитель матрицы не изменится, если к какой-то его строке или столбцу прибавить линейную комбинации других строк или столбцов. Если поменять местами две строки или два столбца матрицы, то определитель матрицы поменяет знак.

Почему определитель не меняется при Транспонировании?

При транспонировании матрицы ее определитель не меняется. 2. Если все элементы какого-либо столбца (строки) определителя равны нулю, то определитель также равен нулю. Это свойство очевидно, так как каждое слагаемое содержит по одному и только одному сомножителю из каждого столбца (строки).

Что произойдет с определителем матрицы при перестановке двух столбцов?

Если в определителе переставить местами любые две строки или два столбца, то определитель изменяет свой знак на противоположный.

Когда меняется определитель матрицы?

При перестановке любых двух строк, определитель меняет знак. Если в определителе есть две одинаковые строки, то он равен нулю.

Что называется определителем матрицы?

Определителем квадратной матрицы третьего порядка

Минором любого элемента матрицы (определителя) называется определитель, который получен из данного вычеркиванием той строки и того столбца, которым принадлежит данный элемент.

Как изменится определитель Если в квадратной матрице поменять местами какие либо две строки или столбца )?

Если поменять местами две строки (столбца) определителя, то знак определителя изменится на противоположный.

Как изменится определитель Если в квадратной матрице поменять местами какие либо две строки или столбца?

Где ‑ элементы первого столбца матрицы (9.2), а их алгебраические дополнения . Свойство 2. Если поменять местами две строки или два столбца матрицы , то ее определитель изменит знак на противоположный.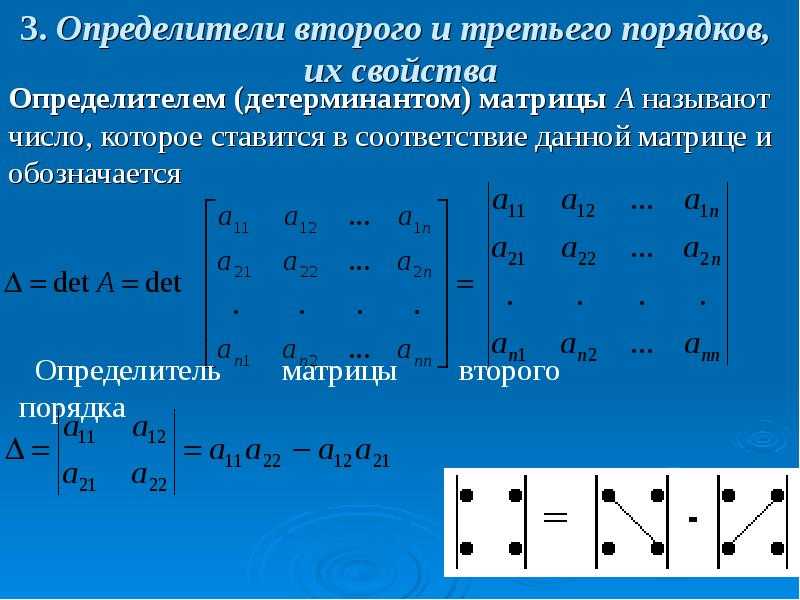

Что называется определителем?

Высшая математика — определителем. Определителем первого порядка называется число, равное единственному элементу матрицы: A ={a}, detA = |A| = a.

В каком случае определитель матрицы равен 0?

Определитель матрицы, содержащий нулевую строку (столбец), равен нулю. Определитель матрицы равен нулю если две (или несколько) строк (столбцев) матрицы линейно зависимы. Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить другую строку (столбец), умноженную на некоторое число.

Как называется операция перемены местами строк и столбцов матрицы?

Определение: Если матрица перестановок получена из единичной матрицы перестановкой местами двух строк (или двух столбцов), то такая матрица называется элементарной матрицей перестановок (англ. Elementary permutation matrix).

Когда определитель равен нулю?

Определитель матрицы равен нулю, если две или несколько строк или столбцов матрицы линейно зависимы. При транспонировании значение определителя матрицы не меняется: det(A) = det(AT).

Какая разница между матрицей и определителем?

Матрица — это сетка чисел, символов или выражений, которая организована в формате строк и столбцов. Определитель — это число, которое связано с квадратной матрицей. … Матрица определяется количеством строк и столбцов. Например, матрица с 2 строками и 3 столбцами называется матрицей 2 × 3.

Как вычислить определитель квадратной матрицы?

Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения.

Что такое определитель матрицы простыми словами?

Определение. Определитель матрицы — это алгебраическая сумма слагаемых, составленных следующим образом. Каждое слагаемое — это произведение элементов матрицы, взятых по одному из каждой строки и каждого столбца, умноженное на (−1) в степени количество инверсий: … От перестановки множителей произведение чисел не меняется.

В чем смысл определителя матрицы?

Определитель матрицы стоит искать для того, например, чтобы узнать, обратима ли она. Узнавать, обратима ли матрица, нужно для того, чтобы решить: обращать её таки — а это сложная алгоритмическая задача — или нет. Обращать матрицы нужно для вычисления коэффициентов линейной регрессии.

Что происходит с определителем при Транспонировании матрицы?

Определитель транспонированной матрицы равен определителю исходной матрицы: Это свойство вытекает из определения детерминанта и выражает равноправие строк и столбцов определителя. … Если в определителе переставить местами любые две строки или два столбца, то определитель изменяет свой знак на противоположный.

Интересные материалы:

Как часто нужно менять УФ лампы?
Как часто нужно подтверждать кмс?
Как часто нужно совершать резервное копирование?
Как часто нужно вязать кота сфинкса?
Как часто заводят Кремлёвские куранты?
Как чистить губку для тонального крема?
Как чистить и смазывать цепь велосипеда?
Как чистить репу?
Как читается Marc Jacobs?
Как дать себе права админа в Minecraft?

Матрицы – транспонирование, детерминанты и увеличение (видео)

TranscriptPractice

Здравствуйте и добро пожаловать в это видео о матричных манипуляциях! В этом видео мы рассмотрим:

• Транспонирование матриц
• Нахождение определителей матриц
• Увеличение матриц

Небольшое предисловие, прежде чем мы начнем. Вообще говоря, чем больше матрицы, с которыми вы работаете, тем утомительнее становится работа. С одной стороны, это может быть хорошей практикой, чтобы получить лучшее концептуальное понимание того, что делают матрицы, поскольку они являются частью интересной области математики. Но, с другой стороны, когда размер превышает 3 x 3 или около того, количество времени и бумаги, необходимых для некоторых операций вручную, становится довольно большим. Определенно рекомендуется какая-то технология.

Одним из способов манипулирования матрицами является транспонирование их.
Транспонирование матрицы обозначается буквой T. Таким образом, транспонирование [A] равно [A] ^T .
Чтобы транспонировать матрицу, отразите все элементы по главной диагонали. Другими словами, строка 1 оригинала становится столбцом 1 транспонированной матрицы, строка 2 оригинала становится столбцом 2 транспонированной матрицы и так далее.

Чаще всего вы будете транспонировать квадратные матрицы. Давайте посмотрим на пару примеров:

Неквадратные матрицы также можно транспонировать:

Иногда транспонирование матрицы дает равную матрицу. Рассмотрим [M] и [N] здесь:

[M] и [N] являются симметричными . [M]=[M] ^T и [N]=[N] ^T .

Еще одна вещь, которую мы можем делать с матрицами, — вычислять их определители. Определители (которые всегда являются одним числом) можно найти только при работе с квадратными матрицами.
Определитель [A] может быть обозначен как det(A) или |A|.

Чтобы найти определитель матрицы 3 x 3, мы начнем с умножения элементов в верхней строке на определители матриц 2 × 2, созданных с использованием четырех элементов, не входящих в строку или столбец исходного элемента. Итак, если мы начнем с a, мы затем умножим его на определитель [e, f, h, i], потому что это четыре элемента, не входящие в строку или столбец a. Затем мы будем чередовать наши знаки, поэтому, поскольку эта первая часть положительна, мы вычтем вторую часть нашего уравнения. На этот раз мы начнем с b. Мы умножим b на определитель [d, f, h, i], потому что это четыре элемента, не включенные в строку или столбец b. Наконец, мы добавим последнюю часть нашего уравнения. Помните, мы делаем это, потому что у нас чередуются знаки: положительный, отрицательный, положительный. Итак, у нас есть c умноженный на определитель [d, e, g, h]. Теперь мы можем упростить это еще больше, поскольку мы уже знаем, как найти определители матриц 2 x 2, поэтому наше окончательное уравнение будет выглядеть так.

Определители можно найти для квадратной матрицы любого размера, но это операция, где доступ к технологии может сэкономить много времени. Обычно нас не столько заботит вычисление определителя, сколько то, что он говорит нам о матрице.

Иногда бывает необходимо дополнить матриц . Увеличение матрицы означает объединение столбцов двух отдельных матриц в одну матрицу, которой можно манипулировать как единой. Обратите внимание, что количество строк в обеих матрицах должно совпадать, чтобы увеличить их.

Обозначение увеличения — полоса. Например, если мы хотим найти увеличение матрицы A и матрицы C, мы должны сделать это: Помните, что черта означает увеличение. Итак, мы начинаем с матрицы А и просто копируем ее вниз: 1, 2, 3, 4. Затем, поскольку мы дополняем ее матрицей С, мы поднимаемся сюда и видим, что у нас есть 7, 8. Все, что мы мы собираемся добавить это в конец нашей другой матрицы: 7, 8. Это даст нам нашу расширенную матрицу.

Теперь давайте увеличим матрицу A и матрицу D. Итак, увеличение D выглядит так: помните, начните с A и просто скопируйте его. Затем мы просто добавляем D в конец A. Итак, минус 3, минус 4, 6, 2
Вот и все! Вот как вы увеличиваете матрицы.

Спасибо за просмотр и удачной учебы!

Вопрос №1:

 
Найдите транспонирование матрицы ниже.
\(\begin{bmatrix}
4&5&6\\
-1&2&9\\
4&-7&1
\end{bmatrix}\)

\(\begin{bmatrix}
4&-1&4\\
5&2&-7\\
6&9&1
\end{bmatrix}\)

\(\begin{bmatrix}
3&-1&3\\
5&1&-7\\
2&9&1
\end{bmatrix}\)

\(\begin{bmatrix}
4&-1&4\\
1&2&-7\\
6&0&1
\end{bmatrix}\)

\(\begin{bmatrix}
4&-1&4\\
0&2&-7\\
0&0&1
\end{bmatrix}\)

Показать Ответ

Ответ:

Для транспонирования матрицы элементы отражаются по главной диагонали. Это означает, что \(5\) и \(-1\) поменяются местами, \(6\) и \(4\) поменяются местами, а \(9\) и \(-7\) поменяются местами.
\(\begin{bmatrix}
\bf4&5&6\\
-1&\bf2&9\\
4&-7&\bf1
\end{bmatrix}\) становится
\(\begin{bmatrix}
4&-1&4\\
5&2&-7\\
6&9&1
\end{bmatrix}\)

Скрыть ответ

Вопрос №2:

 
Какая матрица даст равную матрицу при транспонировании?

\(\begin{bmatrix}
4&6&2\\
6&5&3\\
2&3&7
\end{bmatrix}\)

\(\begin{bmatrix}
3&5&7\\
2&3&3\\
5&4&3
\end{bmatrix}\)

\(\begin{bmatrix}
0&0&02\ \\
5&4&3
\end{bmatrix}\)

\(\begin{bmatrix}
3&0&0\\
1&7&8\\
3&2&6
\end{bmatrix}\)

Show Answer

Answer:

\(\begin{bmatrix}
\bf4&6&2\\
6&\bf5&3\\
2&3&\bf7
\end{bmatrix}\)

Исходная матрица симметрична. Это означает, что при отражении элементов по главной диагонали новая матрица идентична исходной матрице.

Скрыть ответ

Вопрос №3:

 
Вычислите определитель следующей матрицы: 5\)

\(-4\)

\(-3\)

\(-2\)

Показать Ответ

Ответ:

Формулу \(ad-bc\) можно использовать для вычисления определителя матрицы. В исходной матрице \(a=1,b=5,c=2,\) и \(d=7\). Когда эти значения подставляются в формулу, \(ad-bc\) становится \((1)(7)-(5)(2)\), что упрощается до \(7-10\) или \(- 3\).

Скрыть ответ

Вопрос №4:

 
\(\begin{bmatrix}
R|Y
\end{bmatrix}\)
Черта между R и Y обозначает обозначение _________________.

сокращение строк

определители

транспонирование

увеличение

Показать ответ

Ответ:

Символ полосы указывает на увеличение. Увеличение матрицы означает объединение столбцов в единую матрицу, которой можно манипулировать как единой.

Скрыть ответ

Вопрос №5:

 
Увеличить матрицу E и матрицу K.0005

[K]
\(\begin{bmatrix}
7\\
0\end{bmatrix}\)

[E|K]
\(\left[\begin{matrix}
4&5\\
2&1 \end{matrix}
\left|\,\begin{matrix}7\\1\end{matrix}\right.\right]\)

[E|K]
\(\left[\begin{matrix }
3&5\\
2&1\end{matrix}
\left|\,\begin{matrix}7\\0\end{matrix}\right.\right]\)

[E|K]
\( \left[\begin{matrix}
7&3\\
2&1\end{matrix}
\left|\,\begin{matrix}5\\0\end{matrix}\right.\right]\)

[E|K]
\(\left[\begin{matrix}
2&1\\
3&7\end{matrix}
\left|\,\begin{matrix}0\\5\end{matrix}\ right.\right]\)

Показать ответ

Ответ:

Увеличение матриц происходит, когда столбцы двух отдельных матриц объединяются в единую матрицу, которой можно манипулировать. Количество строк должно быть одинаковым, чтобы матрицы увеличивались.

Скрыть ответ

 

Вернуться к Algebra II Videos

521365

Транспонирование матрицы — значение, свойства, примеры

Транспонирование матрицы — один из наиболее распространенных методов преобразования матриц в матричных понятиях в линейной алгебре. Транспонирование матрицы получается путем замены строк на столбцы и столбцов на строки для данной матрицы. Это особенно полезно в приложениях, где необходимо получить обратные и сопряженные матрицы.

В этой статье давайте узнаем о транспонировании матрицы, ее определении, свойствах и решенных примерах.

1.	Что такое транспонирование матрицы?
2.	Порядок транспонирования матрицы
3.	Транспонирование квадратной матрицы
4.	Свойства транспонирования матрицы
5.	Транспонирование горизонтальной и вертикальной матрицы
6.	Транспонирование симметричной матрицы
7.	Транспонирование диагональной матрицы
8.	Транспонирование транспонированной матрицы
9.	Определитель транспонирования матрицы
10.	Связь между сопряженной и транспонированной матрицей
11.	Часто задаваемые вопросы о транспонировании матрицы

Что такое транспонирование матрицы?

Транспонирование матрицы получается путем преобразования ее строк в столбцы (или, что то же самое, ее столбцов в строки). Прямоугольный массив чисел или функций, расположенных в виде строк и столбцов, называется матрицей. Этот массив чисел называется элементами или элементами матрицы.

Здесь для матрицы A элементы первой строки записаны в первый столбец новой матрицы, а элементы второй строки записаны во второй столбец новой матрицы. И эта новая матрица обозначается как A ^T , что является транспонированием заданной матрицы A.

Транспонирование символа матрицы

В линейной алгебре транспонирование матрицы на самом деле является оператором, который переворачивает матрицу по диагонали, переключая строку и столбец индексы матрицы B и создание другой матрицы. Транспонирование матрицы B часто обозначается как B’ или B ^T . Иногда они также обозначаются как B ^tr или Б ^т . Если матрица B имеет порядок m×n, то транспонированная матрица B’ имеет порядок n×m.

Порядок транспонирования матрицы

Порядок матрицы представляет количество строк и столбцов в данной матрице. Все горизонтальные линии элементов называются строками матрицы, обозначаемой буквой n, а вертикальные линии элементов называются столбцами матрицы, обозначаемой буквой m.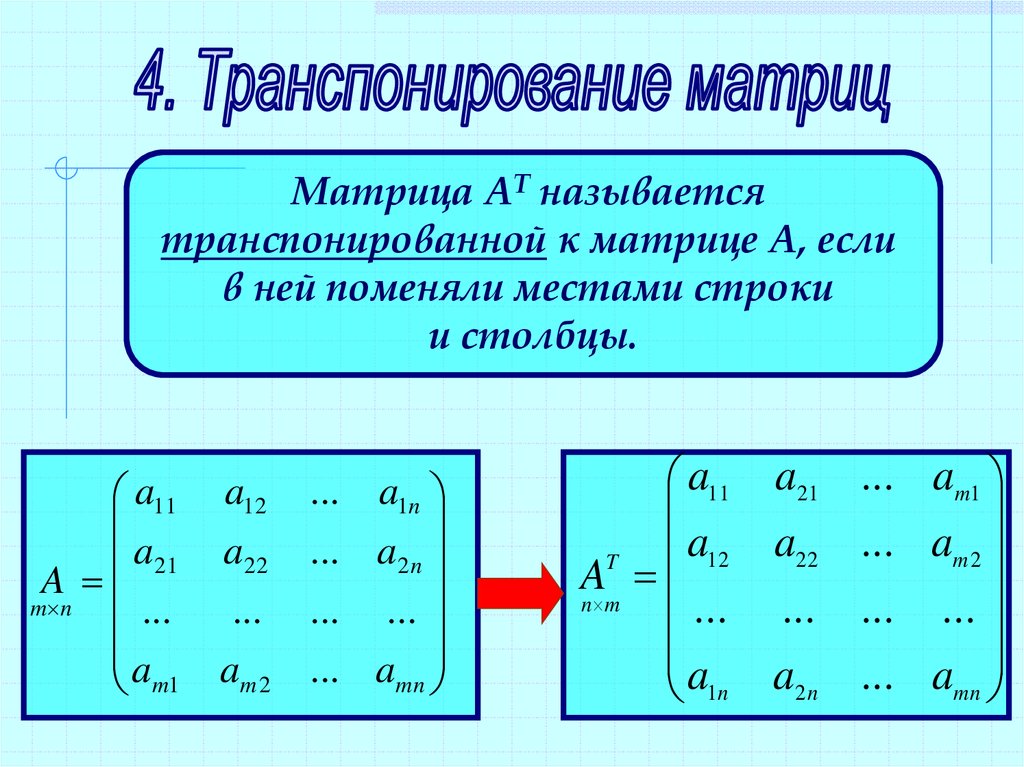 Вместе они представляют порядок матрицы, который записывается как n × м. А -й порядок транспонирования данной матрицы записывается как m x n.

Давайте проверим приведенный ниже пример, чтобы лучше понять, как найти транспонирование матрицы.

A = \(\left[\begin{массив}{ll}
-2&5&6\
5 и 2 и 7
\end{array}\right]\)

В приведенном выше примере мы видим, что задана матрица порядка 2 × 3. Элементы первой строки [-2, 5, 6] записаны в первом столбце , а элементы второй строки [5, 2, 7] записываются во второй столбец, чтобы получить транспонированную матрицу. Транспонирование матрицы A равно A ^T и имеет порядок 3 x 2.

A ^T = \(\left[\begin{array}{ll}
-2 и 5\
5 и 2 \\6 и 7
\конец{массив}\справа]\)

Транспонирование квадратной матрицы

Матрица, полученная из данной матрицы B после замены или обращения ее строк в столбцы и столбцов в строки, называется транспонированием матрицы B. Рассмотрим транспонирование квадратных матриц 2 × 2 и 3 × 3.

Транспонирование матрицы 2 × 2

Рассмотрим матрицу 2 × 2 C, после перестановки строк и столбцов результирующая транспонированная матрица C ^T выглядит так:

Таким же образом можно найти транспонирование матрицы A как:

\(A=\left[\begin{array}{ll}
1&-2\
3 и -4
\end{array}\right]\)

После перестановки строк и столбцов результирующая транспонированная матрица A ^T выглядит так:

A ^T = \(\left[\begin{array}{ll}
1 и 3 \
-2 и -4
\end{array}\right]\)

Транспонирование матрицы 3 × 3

Рассмотрим матрицу 3 × 3 C:

\(C = \left[\begin{array}{ccc}
c_{11} и c_{12} и c_{13} \\
c_{21} и c_{22} и c_{23} \\
c_{31} и c_{32} и c_{33}
\end{array}\right] \)

После перестановки строк и столбцов результирующая транспонированная матрица C ^T выглядит так:

C ^T = \(\left[\begin{array}{ccc}
c_{11} и c_{21} и c_{31} \\
c_{12} и c_{22} и c_{32} \\
c_{13} и c_{23} и c_{33}
\end{array}\right] \)

Таким же образом мы можем найти транспонирование матрицы A как:

\(A = \left[\begin{array}{ccc}
1&2&-3\
4&-5&6\
7 и 8 и -9
\end{массив}\right] \)

После перестановки строк и столбцов результирующая транспонированная матрица A ^T выглядит так:

A ^T = \(\left[\begin{array}{ccc}
1 и 4 и 7 \
2&-5&8\
-3 и 6 и -9
\конец{массив}\справа] \)

Свойства транспонирования матрицы

Транспонирование матрицы используется в некоторых линейных преобразованиях, поскольку они раскрывают некоторые важные свойства преобразования. Давайте узнаем о некоторых важных свойствах транспонирования матрицы:

• Квадратная матрица B порядка n × n считается ортогональной матрицей только тогда, когда B ^T × B = B × B ^T = I, здесь I — единичная матрица.
• Квадратная матрица B порядка n × n считается симметричной матрицей, если ее транспонирование равно самой себе. т. е. В ^Т = В.
• Квадратная матрица B порядка n × n считается кососимметричной матрицей, только если ее транспонирование равно отрицательному. т. е. В ^Т = -Б.
• Транспонирование суммы/разности (B ± C) ^T есть сумма/разность транспонирования матриц B и C, т. е. B ^T ± C ^T = (B ± C) ^T .
• Транспонирование обратимой матрицы B также обратимо, и его инверсия на самом деле является транспонированием обратной исходной матрицы B. Это можно представить как: (B ^T ) ^-1 = (B ^-1 ) ^Т .
• Транспонирование при применении к матрице имеет более высокий приоритет, чем операции умножения и сложения, т. е.
  CB ^T = C(B ^T ) и
  С + Д ^Т = С + (Д ^Т )

Аддитивное свойство транспонирования матрицы

Рассмотрим две матрицы B и C, транспонирование суммы (B + C) ^T представляет собой сумму транспонирования матриц B и C. Это можно представить как ( Б + В) ^Т = Б ^Т + С ^Т . Рассмотрим пример:

B = \(\left[\begin{array}{ll}
2 и 3\
1 и 0
\end{массив}\right]\)

C = \(\left[\begin{массив}{ll}
4&-2\
3 и 5
\end{массив}\right]\)

B + C = \(\left[\begin{массив}{ll}
(2+4) & (3-2) \\
(1+3) и (0+5)
\end{массив}\right]\) = \(\left[\begin{массив}{ll}
6 и 1 \
4 и 5
\end{массив}\right]\)

(B+C) ^T = \(\left[\begin{array}{ll}
6 и 4\
1 и 5
\end{array}\right]\)

Теперь возьмем транспонирование матриц отдельно,

B ^T = \(\left[\begin{array}{ll}
2 и 1 \
3 и 0
\end{массив}\right]\)

C ^T = \(\left[\begin{array}{ll}
4 и 3 \
-2 и 5
\end{массив}\right]\)

B ^T + C ^T =\(\left[\begin{array}{ll}
(2+4) & (1+3) \\
(3-2) и (0+5)
\end{массив}\right]\) = \(\left[\begin{массив}{ll}
6 и 4 \
1 и 5
\end{массив}\right]\)

B ^T + C ^T = \(\left[\begin{array}{ll}
6 и 4 \
1 и 5
\end{array}\right]\)

Из приведенного выше примера видно, что сумма остается одинаковой в обоих случаях. Таким образом, операция транспонирования учитывает сложение.

Транспонирование горизонтальной и вертикальной матрицы

Матрица считается горизонтальной, если количество строк в матрице меньше количества столбцов в этой матрице. И матрица считается вертикальной, когда количество столбцов в матрице меньше, чем количество строк в этой матрице. Рассмотрим горизонтальную матрицу P и вертикальную матрицу Q как:

P = \(\left[\begin{array}{ll}
1 и 2 и 3 \\
4 и 5 и 6
\end{массив}\right]\)

P ^T = \(\left[\begin{массив}{ccc}
1 и 4 \
2 и 5 \
3 и 6
\end{массив}\right] \)

Q = \(\left[\begin{массив}{ccc}
1 и 4 \
2 и 5 \
3 и 6
\end{массив}\right] \)

Q ^T = \(\left[\begin{array}{ll}
1 и 2 и 3 \\
4 и 5 и 6
\end{array}\right]\)

Из приведенных выше двух примеров мы можем видеть, что транспонирование горизонтальной матрицы P приводит к вертикальной матрице P ^T и транспонирование вертикальной матрицы Q дает горизонтальную матрицу Q ^T .

Транспонирование симметричной матрицы

Квадратная матрица порядка n × n считается симметричной тогда и только тогда, когда она симметрична относительно своей диагонали. Квадратная матрица C размера n x n считается симметричной тогда и только тогда, когда C ^T = C. Рассмотрим две заданные симметричные матрицы A и B:

A = \(\left[\begin{array}{ll}
2&-1\
-1 и 2
\end{массив}\right]\)

A ^T = \(\left[\begin{array}{ll}
2&-1\
-1 и 2
\end{массив}\right]\)

B = \(\left[\begin{массив}{ccc}
2 и 3 и 6 \
3 и 4 и 5 \
6 и 5 и 9
\end{массив}\right] \)

B ^T = \(\left[\begin{array}{ccc}
2 и 3 и 6 \
3 и 4 и 5 \
6 и 5 и 9
\end{array}\right] \)

Из приведенного выше примера видно, что после транспонирования двух матриц A и B они равны своим исходным матрицам, т. Е. A = A ^T и B = В ^Т .

Транспонирование диагональной матрицы

Квадратная матрица порядка n × n считается диагональной матрицей тогда и только тогда, когда все ее элементы, кроме диагональных, равны нулю. Рассмотрим две заданные диагональные матрицы C и D:

C = \(\left[\begin{массив}{ll}
5&0\
0 и -5
\end{массив}\right]\)

C ^T = \(\left[\begin{array}{ll}
5&0\
0 и -5
\end{массив}\right]\)

D = \(\left[\begin{массив}{ccc}
1&0&0\
0&2&0\
0 и 0 и 3
\end{массив}\right] \)

D ^T = \(\left[\begin{array}{ccc}
1&0&0\
0&2&0\
0 и 0 и 3
\end{array}\right] \)

Из приведенных выше двух примеров видно, что две диагональные матрицы C и D остаются диагональными матрицами даже после применения транспонирования.

Транспонирование транспонированной матрицы

Транспонирование транспонированной матрицы само по себе. т. е. для любой матрицы B (B ^T ) ^T = B. Рассмотрим здесь два примера:

C = \(\left[\begin{array}{ll}
1&-2\
3 и -4
\end{массив}\right]\)

C ^T = \(\left[\begin{array}{ll}
1 и 3 \
-2 и -4
\end{массив}\right]\)

(C ^T ) ^T = \(\left[\begin{array}{ll}
1&-2\
3 и -4
\end{массив}\right]\)

D = \(\left[\begin{массив}{ccc}
1&2&-3\
4&-5&6\
7 и 8 и -9
\end{массив}\right] \)

D ^T = \(\left[\begin{array}{ccc}
1 и 4 и 7 \
2&-5&8\
-3 и 6 и -9
\end{массив}\right] \)

(D ^T ) ^T = \(\left[\begin{array}{ccc}
1&2&-3\
4&-5&6\
7 и 8 и -9
\end{array}\right] \)

Из приведенных выше двух примеров видно, что транспонирование уже транспонированной матрицы дает исходную матрицу.

Определитель транспонирования матрицы

Определитель транспонированной матрицы A равен определителю самой матрицы A. т. е. det A = det A ^T для любой квадратной матрицы A. Для получения дополнительной информации вы можете нажать здесь.

Связь между сопряженной и транспонированной матрицей

Сопряженная квадратная матрица B является транспонированной кофакторной матрицей C исходной B. Связь между сопряженной исходной матрицей B и транспонированной кофакторной матрицей C может быть представлена ​​как adj(B) = ( В) ^Т . Рассмотрим этот пример:

Рассмотрим матрицу 2×2 D:

D = \(\left[\begin{array}{ll}
3 и 6 \
-4 и 8
\end{array}\right]\)

Младшая матрица M может быть представлена ​​как:

\(M=\left[\begin{array}{ll}
8&-4\
6 и 3
\end{array}\right]\)

Матрица кофакторов C может быть представлена ​​как:

\(C=\left[\begin{array}{ll}
8 и 4 \
-6 и 3
\end{array}\right]\)

Транспонирование C ^T матрицы кофакторов может быть показано как:

adj(D) = C ^T = \(\left[\begin{array {ll}
8&-6\
4 и 3
\end{array}\right]\)

Важные примечания по транспонированию матрицы:

• Транспонирование матрицы на самом деле является оператором, который переворачивает матрицу по ее диагонали путем переключения индексов строки и столбца матрицы B и изготовление другой матрицы.
• Транспонирование матрицы B часто обозначается либо B’, либо B ^T . Иногда их также обозначают как B ^tr или B ^t .
• Если матрица B имеет порядок m x n, то транспонированная матрица B’ имеет порядок n x m.

☛ Статьи по теме:

• Калькулятор матриц
• Формула матрицы
• Калькулятор диагональной матрицы
• Калькулятор матрицы транспонирования

Часто задаваемые вопросы о транспонировании матрицы

Что означает транспонирование матрицы?

Транспонирование матрицы — это матрица, полученная после замены или преобразования ее строк в столбцы (или столбцов в строки). Транспонирование B обозначается как B ^T .

Как найти транспонирование матрицы?

Транспонирование любой заданной матрицы можно вычислить, поменяв местами ее строки и столбцы. Рассмотрим матрицу 2 × 2 B:

\(A=\left[\begin{массив}{ll}
1&-2\
3 и 7
\end{array}\right]\)

После перестановки строк и столбцов результирующая транспонированная матрица C ^T выглядит так:

A ^T = \(\left[\begin{array}{ ll}
1 и 3 \
-2 и 7
\end{array}\right]\)

Что такое свойство сложения при транспонировании матрицы?

Согласно аддитивному свойству транспонирования матрицы, для двух матриц B и C транспонирование суммы (B + C) ^T представляет собой сумму транспонирований матриц B и C. Это можно представить как (B + C) ^T = B ^T +C ^T .

Что такое свойство умножения транспонирования матрицы?

Согласно свойству умножения транспонирования матрицы, транспонирование при применении к матрице имеет более высокий приоритет, чем операции умножения и сложения, т. е. CB ^T = C(B ^T ) и C + D ^T = С + (Д ^Т )

Каковы различные свойства транспонирования матрицы?

Вот различные свойства транспонирования матрицы:

• Квадратная матрица B порядка n × n считается ортогональной матрицей только тогда, когда B × B ^T = I, здесь I тождество матрица.
• Квадратная матрица B порядка n × n считается кососимметричной матрицей только тогда, когда она транспонирована B ^T = -B, т. е. равна своей отрицательной.
• Транспонирование разности (B — C) ^T — это разность транспонирования матриц B и C. B ^T — C ^T = (B — C) ^T
• Транспонирование обратимой матрицы B также обратимо, а ее инверсия B ^-1 на самом деле является транспонированием обратной исходной матрицы B. Это можно представить как: (B ^T ) ^-1 = (Б ^-1 ) ^Т .
• Транспонирование при применении к матрице имеет более высокий приоритет, чем операции умножения и сложения, т. е. CB ^T = C(B ^T ) и C + D ^T = C + (D ^T )

Что является определителем транспонирования матрицы?

Определитель транспонированной квадратной матрицы порядка n×n равен определителю матрицы, т.е. |B ^T | = |В|.

Что такое транспонирование квадратной матрицы?

Для любой квадратной матрицы порядка n×n транспонирование применяется к матрице следующим образом. Рассмотрим матрицу 2 × 2 C:

\(C=\left[\begin{массив}{ll}
с_{11} и с_{12} \\
c_{21} и c_{22}
\end{array}\right]\)

После перестановки строк и столбцов результирующая транспонированная матрица C ^T выглядит так:

C ^T = \(\left[\begin{array}{ ll}
с_{11} и с_{21} \\
c_{12} и c_{22}
\end{array}\right]\)

Как найти обратную матрицу методом транспонирования?

Вот шаги, которые нужно выполнить, чтобы вычислить обратную матрицу D с помощью метода транспонирования:

• Найдите определитель |D|. Если |Д| = 0, то обратное не существует. Только если |D| ≠ 0, существует обратное.
• Найдите минорную матрицу M всех элементов матрицы D
• Найдите матрицу кофакторов C всех минорных элементов матрицы M
• Найдите прил D путем транспонирования матрицы кофакторов C
• Затем найдите обратную матрицу D как D ^-1 = (1/|D|) × adj(D)
• Проверьте правильность обратного выражения, проверив его как D × D ^-1 = I, где I — единичная матрица.

Транспонирование — линейная алгебра

Все ресурсы по линейной алгебре

4 диагностических теста 108 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущий 1 2 3 4 5 Далее →

Справка по линейной алгебре » Операции и свойства » Транспонирование

Возможные ответы:

Правильный ответ:

Объяснение:

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Объяснение:

Сообщить об ошибке

Верно или неверно: Транспонирование матрицы с шестью строками и семью столбцами имеет семь строк и шесть столбцов.

Возможные ответы:

Неверно

Верно

Правильный ответ:

Верно

Объяснение:

Транспонирование матрицы меняет местами строки и столбцы, поэтому количество строк в исходной матрице равно количеству столбцов в транспонированном, и наоборот. Следовательно, матрица с шестью строками и семью столбцами имеет семь строк и шесть столбцов.

Сообщить об ошибке

Что из следующего равно ?

Возможные ответы:

Транспонирование  не существует.

Правильный ответ:

Объяснение:

Транспонирование матрицы меняет местами строки и столбцы. Таким образом, первый столбец содержит те же элементы по порядку, что и первая строка , и т.  д. С 9 0005

следует, что

Сообщить об ошибке

Пусть и – любые две матрицы одинаковой размерности.

Верно или ложно:

Должен содержать это .

Возможные ответы:

Неверно

Верно

Правильный ответ:

Верно

Объяснение:

Транспонирование суммы двух матриц действительно равно сумме их транспонирования. Давайте посмотрим на случай «два на два» — это рассуждение можно обобщить.

 и 

Транспонирование матрицы меняет местами строки и столбцы. Таким образом, первый столбец содержит те же элементы по порядку, что и первая строка , и т. д. Следовательно, 

 и .

матриц добавляются сроком сроком, поэтому

, транспонирование суммы исходных матриц, можно найти с первого добавления матриц. от суммы:

Действительно, .

Сообщить об ошибке

 является матрицей три на три с определителем 0.

Истинно, ложно или неопределенно:  не имеет транспонирования.

Возможные ответы:

Неверно

Верно

Не определено

Правильный ответ:

Неверно

Объяснение:

Каждая матрица имеет транспонирование независимо от значения ее определителя; найти транспонирование — вопрос перестановка  элементов – понятие, не зависящее от определителя, – так, чтобы его строки были столбцами транспонированного, и наоборот.

Сообщить об ошибке

 является матрицей два на два, такой что

Каким из следующих может быть  ?

Возможные ответы:

Правильный ответ:

Объяснение:

Так как это матрица два на два, мы допустим

,

, где , , и  представляют действительные значения.

Транспонирование матрицы меняет местами строки и столбцы. Таким образом, первый столбец содержит те же элементы по порядку, что и первая строка , и т. д. Следовательно,

и

Добавить две матрицы срок:

С

или, эквивалентно,

Следующее должно иметь:

,

Следующее:

,

Следующее:

,

Следующее:

,

Следующее:

Следующее.0005

или

,

или

и

,

или, эквивалентно,

.

Следовательно, любая матрица вида

для некоторого действительного числа сделает утверждение правильным. Единственным выбором, соответствующим этому образцу, является матрица

.

 

 

Сообщить об ошибке

 является невырожденной квадратной матрицей.

Истина, ложь или неопределенность:  является невырожденной квадратной матрицей. 9

Верно Объяснение:

Квадратная матрица невырожденна, т. е. имеет обратную, тогда и только тогда, когда ее определитель равен 0.

Пусть   матрица-столбец. Тогда транспонирование равно матрице строк

.

Произведение матрицы-строки и матрицы-столбца, каждая из которых имеет одинаковое количество элементов, является последовательной матрицей, единственным элементом которой является сумма квадратов элементов, поэтому

Определитель одиночной матрицы является ее единственным элементом, так же как и квадратная матрица с ненулевым определителем. Это доказывает, что может быть неособым для некоторого неквадрата.

Теперь пусть , единичная матрица два на два (или любая другая). — неособая квадратная матрица, и , поэтому

.

Это доказывает, что может быть неособым для некоторого квадрата.

Следовательно, если , невозможно определить, является ли матрица неособой квадратной.

Сообщить об ошибке

 является верхней треугольной матрицей.

Верно или неверно:  не может быть верхней треугольной матрицей.

Возможные ответы:

Верно

Неверно

Правильный ответ:

Неверно

Пояснение:

Единичная матрица любой размерности служит контрпримером, доказывающим ложность утверждения. Изучите тождество «три на три»

— верхняя треугольная матрица, все элементы которой выше главной диагонали — нули. Транспонирование — матрица, образованная перестановкой строк и столбцов, — это она сама. Таким образом,  является верхнетреугольной матрицей, транспонирование которой также является верхнетреугольной.

Сообщить об ошибке

 и  являются нижними треугольными квадратными матрицами. Какой из следующих должен следовать из этого?

Возможные ответы:

 вырожденная матрица, но не обязательно нулевая матрица.

 является диагональной матрицей, но не обязательно единичной или нулевой матрицей.

 – нулевая матрица.

 

 – невырожденная матрица, но не обязательно единичная.

 является единичной матрицей

Правильный ответ:

— диагональная матрица, но не обязательно единичная или нулевая матрица.

Объяснение:

Пусть это матрица три на три; это рассуждение распространяется на квадратные матрицы всех размеров.

 является нижней треугольной матрицей, поэтому все элементы над ее главной (сверху слева вниз справа) диагональю равны нулю; то есть

.

, транспонирование , представляет собой матрицу, образованную путем переключения строк со столбцами, поэтому

.

Тем не менее,  нижний треугольник также; как следствие 

,

и

.

Это показывает, что матрица  должна быть диагональной, то есть такой, на главной диагонали которой находятся только нули.

Сообщить об ошибке

← Предыдущая 1 2 3 4 5 Следующая →

Уведомление об авторских правах

Все ресурсы по линейной алгебре

4 Диагностические тесты 108 практических тестов Вопрос дня Карточки Учитесь по концепции

Свойства определителя

Марко Табога, доктор философии

В этой лекции мы выведем несколько полезных свойств определитель.

Чтобы полностью понять эту лекцию, вам нужно запомнить основные результаты, полученные в лекции о определитель элементарная матрица.

Оглавление

1. Определитель треугольной матрицы

2. Транспонирование определителя не меняет

3. Определитель матрицы с нулевой строкой или колонкой составляет ноль

4. Определение сингулярной матрицы составляет ноль

5. Детерминанты из продукта. Продукт

6. Degrinant of Inverse

7. 1111111111111111111111111111111111111111111111111111111111111111111111111111111112.

   Эффект умножения матрицы на скаляр

8. Эффект умножения строки или столбца на скаляр

9. Линейность в строках и столбцах

10. Определитель и ЛУ-разложение

Определитель треугольной матрицы

Первый результат касается определителя треугольная матрица.

Предложение Позволять быть треугольная матрица (верхняя или нижняя). Тогда определитель равно произведению его диагонали записей:

Доказательство

Предположим, что нижний треугольный. Обозначим через множество всех перестановок первый натуральные числа. Позволять быть перестановкой, в которой числа отсортированы в порядке возрастания. Соотношение четно и его знак потому что не содержит инверсии (см. лекцию о признак перестановки). Тогда определитель это здесь в ногу мы воспользовались тем, что для всех перестановок кроме в продуктвовлекает хотя бы одна запись выше главной диагонали, равная нулю. Последний факт можно доказать от противного. Предположим, что продукт включает только элементы на главной диагонали или под ней, и хотя бы один элемент под ней (в противном случае ). Тогда для все , но неравенство должно быть строгим хотя бы для одного . Предположим, что неравенство является строгим для . Тогда у нас есть за . Другими словами, перестановка должен содержать различные натуральные числа, меньшие или равные , что явно невозможно. На этом доказательство заканчивается от противного. Таким образом, мы доказали предложение для нижних треугольных матриц. Доказательство для верхнего треугольных матриц почти идентичны (нам нужно только поменять местами неравенства на последнем шаге).

Следствие из приведенного выше предложения следует.

Предложение Позволять быть единичной матрицей. Тогда

Доказательство

Единичная матрица диагональна. Следовательно, он треугольный и его определитель равен произведению его диагонали записи. Все последние равны . Как следствие, определитель равно .

Транспозиция не изменяет определитель

Следующее предложение устанавливает элементарное, но важное свойство определитель.

Предложение Позволять – квадратная матрица, и обозначим ее транспонирование через . Тогда

Доказательство

Обозначим через множество всех перестановок первого натуральные числа. Для любой перестановки , есть обратная перестановка такой что для . Если получается путем выполнения последовательности транспозиции, то получается путем выполнения противоположных транспозиций в обратном порядке. Таким образом, число транспозиций одинаково и, как следствие, имеем, что По используя понятие обратной перестановки, определитель можно легко вычислить как следует: где: в ногу мы использовали определение транспонировать; в ногу мы установили и, как следствие, .

Определитель матрицы с нулевой строкой или столбцом равен нулю

Следующее свойство, хотя и довольно интуитивное, часто используется для доказательства других свойства определителя.

Предложение Позволять быть квадратной матрицей. Если имеет нулевую строку (т. е. строку, все элементы которой равны нулю) или нулевую столбец, то

Доказательство

Это свойство можно доказать с помощью значение определительДля каждая перестановка , у нас есть что потому что произведение содержит по одной записи из каждой строки (столбца), но одна из строк (столбцы) содержит только нули. Следовательно,

Определитель сингулярной матрицы равен нулю

Сейчас мы сформулируем одно из наиболее важных свойств определитель.

Предложение Позволять быть квадратной матрицей. затем обратим тогда и только тогда, когда а также она сингулярна тогда и только тогда, когда

Пруф

Матрица строка эквивалентна уникальному матрица в уменьшенном эшелоне рядов форма (RREF). С а также эквивалентны по строкам, мы имеем там являются элементарными матрицами. Более того, по свойства определители элементарных матриц, имеем этоНо определитель элементарной матрицы отличен от нуля. Следовательно, где является отличной от нуля константой. Если обратим, является единичной матрицей и Если единственное число, имеет по крайней мере одну нулевую строку, потому что единственная квадратная матрица RREF, не имеющая нуля rows — единичная матрица, а последняя по строкам эквивалентна только невырожденные матрицы. Выше мы доказали, что матрицы, имеющие нулевую строку имеют нулевой определитель. Таким образом, если единственное число, иКому Таким образом, мы доказали, что все обратимые матрицы имеют ненулевой определитель, и все сингулярные матрицы имеют нулевой определитель. Поскольку матрица либо обратимое или единственное число, два логических следствия («если и только если») следить.

Определитель произведения равен произведению определителей

Следующее предложение показывает, что определитель произведения двух матриц равно произведению их определителей.

Предложение Позволять а также быть двумя матрицы. Тогда

Доказательство

Если одна из двух матриц вырожденная (т. е. не полный ранг), то их произведение единственное число потому что как объяснялось в лекции под названием Матричный продукт и классифицировать. Следовательно, а также по крайней мере один из или же равно нулю, поэтому чтоТаким образом, утверждение в предложении истинно, если хотя бы одна из двух матриц единственное число. Если ни одно из них не единственное, то мы можем записать их как произведения элементарный матрицы:где а также являются элементарными матрицами. Так как определитель произведения элементарных матриц равен произведениям их определителей, имеем чтоТаким образом, мы доказали, что утверждение в предложении верно и в случае когда две матрицы невырожденные.

Определитель обратного

Предыдущее предложение позволяет нам легко найти определитель обратного матрицы.

Предложение Позволять быть обратимая матрица. Затем

Доказательство

Так как имеют этоНо определитель произведения равен произведению детерминанты: и В качестве а следствие, кроме того, определитель обратимой матрицы отличен от нуля, так что мы можем разделите обе части приведенного выше уравнения на а также получить

Эффект умножения матрицы на скаляр

В этом подразделе представлено легко доказуемое утверждение о умножение матрицы скаляром. Прежде чем читать доказательство, попробуйте доказать его себя в качестве упражнения.

Предложение Позволять быть матрица. Тогда для любого скаляра ,

Доказательство

Это предложение легко доказывается с помощью определение определитель.

Эффект умножения строки или столбца на скаляр

Это свойство аналогично предыдущему.

Предложение Позволять быть матрица. Позволять быть скаляром. Позволять быть матрицей, полученной из путем умножения строки (или столбца) на . Затем,

Доказательство

Предположим, -й ряд был умножен на . По определению определитель: если вместо этого -й столбец умножается на , тот же результат верен, потому что транспозиция не меняет определитель.

Линейность в строках и столбцах

Определитель линейен по строкам и столбцам матрицы.

Предложение Позволять быть матрица. Обозначим через в -й ряд . предположим, где а также два векторы и а также два скаляра. Обозначим через матрица, полученная из заменив с . Обозначим через матрица, полученная из заменив с . Затем

Доказательство

По определению определителя мы есть

предложение Позволять быть матрица. Обозначим через в -й столбец . предположим, где а также два векторы и а также два скаляра. Обозначим через матрица, полученная из заменив с . Обозначим через матрица, полученная из заменив с . Затем

Доказательство

Это следствие предыдущего предложение (линейность в столбцах) и того факта, что транспозиции делают не менять определитель.

Определитель и LU-разложение

Один из самых простых и удобных способов вычисления определителя квадратная матрица основан на LU разложениегде , а также матрица перестановок, a нижняя треугольная и верхняя треугольная матрицы соответственно. Мы можем писатьи детерминанты , а также легко вычислить:

• если количество перестановок строк, необходимых для получения из единичной матрицы четно; в противном случае, ;

• равно произведению диагональных элементов потому что нижняя треугольная;

• равно произведению диагональных элементов потому что имеет верхнюю треугольную форму.

Как цитировать

Пожалуйста, указывайте как:

Taboga, Marco (2021). «Свойства определителя», Лекции по матричной алгебре. https://www.statlect.com/matrix-алгебра/determinant-properties.

Транспонирует ли определитель изменения?

Автор вопроса: Деннис Кинг

Оценка: 5/5 (69 голосов)

Доказательство по индукции того, что транспонирование матрицы не меняет ее определитель .

Что происходит, когда вы переставляете определитель?

Определитель транспонированной квадратной матрицы равен определителю матрицы, то есть |At| = |А| . … Тогда ее определитель равен 0. Но ранг матрицы такой же, как и ранг ее транспонирования, поэтому At имеет ранг меньше n и ее определитель также равен 0.

Изменяется ли определитель при инверсии?

Определитель обратной обратимой матрицы является обратным определителя : det(A ^{— 1} ) = 1 / det(A) [6.2. … Подобные матрицы имеют одинаковый определитель; то есть, если S обратим и имеет тот же размер, что и A, то det(S A S ^{— 1} ) = det(A).

Изменяют ли определитель операции со строками?

Вычисление определителя с использованием операций со строками

Если поменять местами две строки матрицы, определитель меняет знак . Если из другой строки вычесть кратное одной строки, значение определителя не изменится.

Умножаются ли определители?

Когда мы переставляем две строки матрицы, определитель умножается на −1 .

Определитель транспонирования | Преобразования матриц | линейная алгебра | Академия Хана

Найдено 21 связанных вопросов

Что такое формула определителя?

Определитель: |A| знак равно a (ei — fh) — b (di — fg) + c (dh — eg) . Определитель A равен «a умножить на e x i минус f x h минус b умножить на d x i минус f x g плюс c умножить на d x h минус e x g». Это может показаться сложным, но если вы внимательно наблюдаете за узором, это действительно просто!

Изменяется ли определитель при умножении строки?

Если мы добавим строку (столбец) матрицы A, умноженную на скаляр k, к другой строке (столбцу) матрицы A, , то определитель не изменится . Если поменять местами две строки (столбца) в A, определитель изменит знак.

Изменяет ли определитель скалярного умножения?

Если умножить скаляр на матрицу A, то значение определителя изменится в раз ! Это имеет смысл, так как мы вольны выбирать, по какой строке или столбцу мы будем расширять определитель.

В чем разница между матрицей и определителем?

Разница между матрицей и определителем: … Матрица — это группа чисел, но определитель — это уникальное число, связанное с этой матрицей . В матрице количество строк не обязательно должно быть равно количеству столбцов, тогда как в определителе количество строк должно быть равно количеству столбцов.

Как узнать, равен ли определитель 0?

Если две строки или два столбца идентичны, определитель равен нулю . Если матрица содержит либо строку нулей, либо столбец нулей, определитель равен нулю.

Что происходит, когда определитель равен 0?

Когда определитель матрицы равен нулю, объем области со сторонами, заданными ее столбцами или строками, равен нулю , что означает, что матрица, рассматриваемая как преобразование, переводит базисные векторы в линейно зависимые векторы, определяющие 0 объем.

Могут ли две разные матрицы иметь одинаковый определитель?

Таким образом, обе матрицы имеют одинаковое значение определителя . Следовательно, мы можем сказать, что две различные матрицы могут иметь одно и то же значение детерминанта.

Может ли определитель быть отрицательным?

Да, определитель матрицы может быть отрицательным числом . По определению определителя определителем матрицы является любое действительное число. Таким образом, он включает в себя как положительные, так и отрицательные числа вместе с дробями.

Является ли транспонирование тем же, что и инверсия?

Транспонированная матрица — это матрица, в которой строки и столбцы поменялись местами. Матрица , обратная матрице , является такой матрицей, что и равна единичной матрице.

Транспонирование всегда обратимо?

Поскольку ATA является квадратной матрицей, это означает, что ATA обратим .

Является ли определитель дистрибутивным по отношению к умножению?

определитель: Уникальная скалярная функция над квадратными матрицами, дистрибутивная при умножении матриц, полилинейная в строках и столбцах и принимающая значение 1 для единичной матрицы. Его аббревиатура — «дет».

Сколькими способами можно разложить определитель 3 на 3?

Существует шесть способов разложения определителя третьего порядка, соответствующих каждой из трех строк (R1, R2 и R3) и трех столбцов (C1, C2 и C3), и каждый способ дает одно и то же значение. Замечание. В общем случае, если A = kB, где A и B — квадратные матрицы порядка n, то |A| = kn |B|, n = 1, 2, 3.

Что происходит, когда определитель равен 1?

Если определитель матрицы равен 0, матрица называется вырожденной, а если определитель равен 1, матрица называется унимодулярной .

Как переключение строк влияет на определитель?

Перестановка этих строк не меняет определитель, но в то же время меняет его знак . Единственное число, которое не меняется при изменении знака, — это 0, поэтому определитель должен быть равен 0. Значение определителя с двумя равными строками должно быть равно 0.

Изменяется ли определитель при масштабировании матрицы?

Определитель умножается на масштабный коэффициент .

При перестановке строк и столбцов значение определителя?

Если поменять местами любые две строки (или два столбца) определителя, значение определителя равно , умноженному на -1 . |А| . Если две строки (или столбца) определителя совпадают, то значение определителя равно нулю.

Может ли определитель быть комплексным?

Определитель — это функция , которая сопоставляет квадратной матрице элемент поля, на котором она определена (обычно действительные или комплексные числа).

Что такое определитель примера?

Определитель представляет собой квадратный массив чисел (записанный парой вертикальных линий), который представляет определенную сумму произведений . Ниже приведен пример определителя 3 × 3 (в нем 3 строки и 3 столбца). Результатом умножения, а затем упрощения элементов определителя является одно число (скалярная величина).

Похожие вопросы

• 28Был ли 5mld перенесен в ирландию?
• 30Что такое транспонированная матрица?
• 30Какой ты мои мысли не можешь транспонировать?
• 22Похожи ли транспонированные матрицы?
• 40Was означает транспонирование?
• 24В симметричной матрице транспонировать?
• 26Зачем транспонировать песню?
• 32Что транспонировать матрицу?
• 43Определитель транспонирования один и тот же?
• 26Каковы свойства транспонирования матрицы?

Реклама

Популярные вопросы

• 22Как называется дабба по-английски?
• 22Использует ли embase термины сетки?
• 15Где находятся серии?
• 37Подходит ли подвал для дома?
• 35Кто является крупнейшей тектонической плитой?
• 36Были ли конфискованы золотые украшения в 1933 году?
• 27Сирень растет в тени?
• 41Когда были изготовлены галоши?
• 15Габила книш не содержит глютена?
• 37Когда отсчитывался первый год?

Определитель матрицы — 2×2, 3×3, 4×4.

..

Каталин Дэвид

Определение

Определитель квадратной матрицы A — это целое число, полученное с помощью ряда методов с использованием элементов матрицы.

Обозначение

Пусть $ А = \begin{pматрица} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \end{pmatrix}$

$дет(А) = \влево|А\вправо| знак равно \begin{vmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \end{vmatrix}$

Свойства определителя

1. Если в матрице есть строка или столбец со всеми элементами, равными 0 , то определитель равен 0 .

   Пример 12
   $\begin{vmatrix} 1 и 4 и 2\\ 0 и 0 и 0\\ 3 и 9& 5 \end{vmatrix}= 0$ или же $\begin{vmatrix} 1 и 4 и 0\\ 4 и 2 и 0\\ 3 и 9 и 0 \end{vmatrix}=0$

2. Если матрица имеет две равные строки или два равных столбца , то ее определитель равен 0 .

   Пример 13
   $\begin{vmatrix} 1 и 4 и 2\\ 1 и 4 и 2\\ 3 и 9 и 5 \end{vmatrix}= 0$ или же $\begin{vmatrix} 1 и 4 и 1\\ 4 и 2 и 4\\ 3 и 9 и 3 \end{vmatrix}=0$

3. Если матрица имеет две пропорциональные строки или два пропорциональных столбца , тогда его определитель равен 0 .

   Пример 14
   $\begin{vmatrix} 1 и 4 и 2\\ 2 и 8 и 4\\ 3 и 9 и 5 \end{vmatrix}= 0$ (первые две строки пропорциональны)
   или
   $\begin{vmatrix} 8 и 4 и 7\\ 4 и 2 и 3\\ 18 и 9 и 8 \end{vmatrix}=0$ (первые два столбца пропорциональны)

4. Если строка или столбец является суммой или разностью других строк, соответственно столбцов затем определитель равен 0 .

   Пример 15
   $\begin{vmatrix} 1 и 4 и 2\\ 7 и 2 и 3\\ 8 и 6 и 5 \end{vmatrix}= 0$     $R_{1} +R_{2} =R_{3}$ или

   $ \begin{vmatrix} 9 и 12 и 3\\ 1 и 8 и 7\\ 5 и 7 и 2 \end{vmatrix}=0$     $C_{1}+C_{3}=C_{2}$

5. В определителе мы можем отдельно выносить целые числа из строк и столбцов.

   Пример 16
   В определителе
   $\begin{vmatrix} 3 и 9 и 12\\ 5 и 1 и 8 \\ 7 и 4 и 2 \end{vmatrix}$, мы умножаем 3 из строки 1 $(R_{1})$ и получаем:
   $3 \cdot \begin{vmatrix} 1 и 3 и 4\\ 5 и 1 и 8\\ 7 и 4 и 2 \end{vmatrix}$, то мы выносим 2 из столбца 3 $(C_{3})$:
   $6\cdot \begin{vmatrix} 1 и 3 и 2\\ 5 и 1 и 4\\ 7 и 4 и 1 \end{vmatrix}$

6. В определителе мы можем прибавлять или вычитать строки или столбцы к другим строкам, соответственно столбцам и значение определителя остается прежним.

   Пример 17
   $\begin{vmatrix} 1 и 5\\ 3 и 8 \end{vmatrix}$ $\xlongequal{R_{1}+R_{2}} \begin{vmatrix} 4 и 13\\ 3 и 8 \end{vmatrix}$
   Пример 18
   $\begin{vmatrix} 1 и 5\\ 3 и 8 \end{vmatrix}$ $\xlongequal{C_{1}+C_{2}} \begin{vmatrix} 6 и 5\\ 11 и 8 \end{vmatrix}$

7. В определителе мы можем складывать или вычитать несколько строк или столбцов.

   Пример 19
   $\begin{vmatrix} 1 и 5\\ 3 и 8 \end{vmatrix}$ $\xlongequal{2R_{1}+3R_{2}} \begin{vmatrix} 11 и 34\\ 3 и 8 \end{vmatrix}$

   Пример 20
   $\begin{vmatrix} 1 и 5\\ 3 и 8 \end{vmatrix}$ $\xlongequal{5C_{1}-C_{2}} \begin{vmatrix} 0 и 5\\ 7 и 8 \end{vmatrix}$

8. Определитель матрицы равен определителю ее транспонирования.
9. Определитель произведения двух квадратных матриц равен произведению определителей данных матриц.

Минор матрицы

Определитель, полученный путем удаления некоторых строк и столбцов в квадратной матрице, называется минором этой матрицы.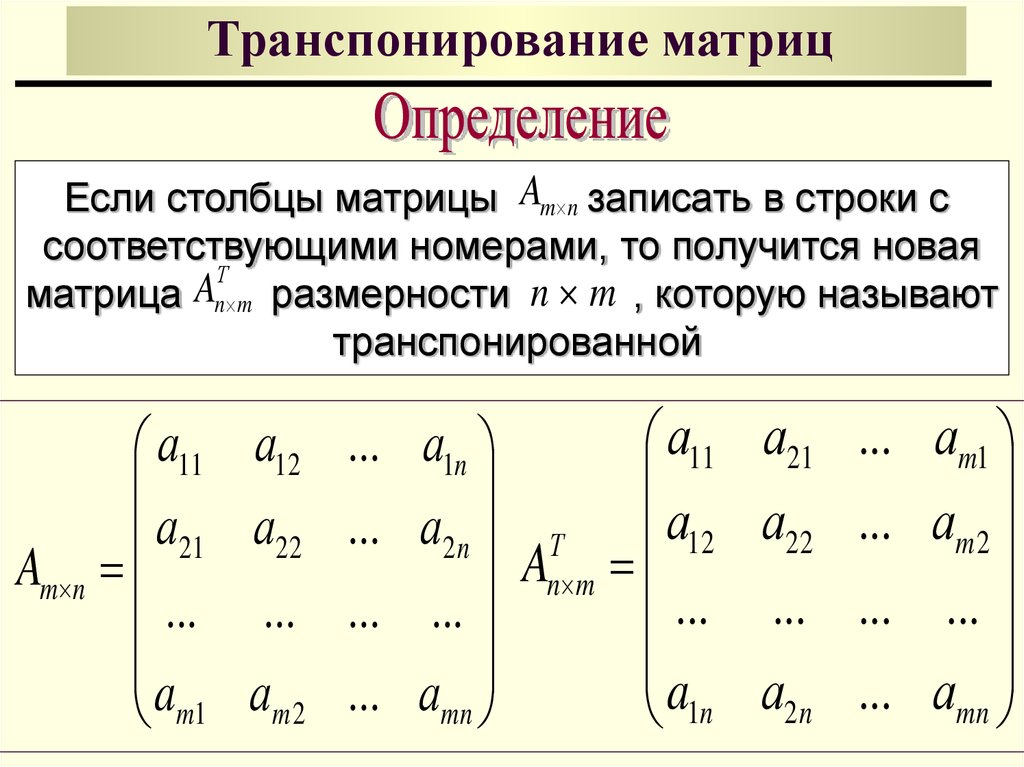

Пример 21
$A=\begin{pmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \end{pmatrix}$

Один из миноров матрицы A равен $\begin{vmatrix} 1 и 4\\ 5 и 3 \end{vmatrix}$ (получено удалением строки 3 и столбца 3 из матрицы A)

Другой минор $\begin{vmatrix} 1 и 2 \\ 6 и 1 \end{vmatrix}$ (получено удалением строки 2 и столбца 2 из матрицы A)

Пример 22
$B=\begin{pmatrix} 2 и 5 и 1 и 3\\ 4 и 1 и 7 и 9\\ 6 и 8 и 3 и 2\\ 7 и 8 и 1 и 4 \end{pматрица} $

Один из миноров матрицы B равен $ \begin{vmatrix} 1 и 7 и 9\\ 8 и 3 и 2\\ 8 и 1 и 4 \end{vmatrix}$ (получено удалением строки 1 и столбца 1 из матрицы B)

Еще один несовершеннолетний $\begin{vmatrix} 1 и 7 \\ 8 и 3 \end{vmatrix}$ (получено удалением строк 1 и 4 и столбцов 1 и 4 из матрицы B)

Позволять $A= \begin{pmatrix} а_{1,1} и а_{1,2} и а_{1,3} и . & . & a_{1,n}\\ а_{2,1} и а_{2,2} и а_{2,3} и . & . & а_{2,n}\\ а_{3,1} и а_{3,2} и а_{3,3} и . & . & а_{3,n}\\ . & . & . & . & .& .\\ a_{n,1} & a_{n,2} & a_{n,3} & . & . & Анна} \end{pmatrix}$

Мы можем связать минор $\Delta_{i,j}$ (полученный удалением строки i и столбца j) с любым элементом $a_{i,j}$ матрицы A.

Пример 23
$ A = \begin{pmatrix} 4 и 7\\ 2 и 9 \end{pmatrix}$

Нам нужно определить минор, связанный с 2. Так как этот элемент находится в строке 2, столбце 1, то 2 равно $a_{2,1}$.

Мы должны удалить строку 2 и столбец 1 из матрицы A, в результате чего получится

Минор числа 2 равен $\Delta_{2,1} = 7$.

Пример 24
$B=\begin{pmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \end{pmatrix}$

Нам нужно определить минор, связанный с 7. Так как этот элемент находится в строке 2, столбце 3, то 7 равен $a_{2,3}$.

Мы должны исключить строку 2 и столбец 3 из матрицы B, в результате чего получится

Минор числа 7 равен $\Delta_{2,3}= \begin{vmatrix} 1 и 4\\ 6 и 2 \end{vmatrix}$

Пример 25
$C=\begin{pmatrix} 2 и 5 и 1 и 3\\ 4 и 1 и 7 и 9\\ 6 и 8 и 3 и 2\\ 7 и 8 и 1 и 4 \end{pmatrix}$

Нам нужно определить минор, связанный с 5. Поскольку этот элемент находится в строке 1 столбца 2, то 5 равно $a_{1,2}$.

Мы должны исключить строку 1 и столбец 2 из матрицы C, в результате чего получится

Минор числа 5 равен $\Delta_{1,2}= \begin{vmatrix} 4 и 7 и 9\\ 6 и 3 и 2\\ 7 и 1 и 4\\ \end{vmatrix}$

Кофактор элемента матрицы

Пусть $A=\begin{pmatrix} а_{1,1} и а_{1,2} и а_{1,3} и . & . & a_{1,n}\\ а_{2,1} и а_{2,2} и а_{2,3} и . & . & а_{2,n}\\ а_{3,1} и а_{3,2} и а_{3,3} и . & . & а_{3,n}\\ . & . & . & . & .& .\\ a_{n,1} & a_{n,2} & a_{n,3} & . & . & Анна}\\ \end{pmatrix}$ 9{7}\cdot\Delta_{2,5}= -\Delta_{2,5} $ соответствует элементу $ a_{2.5}$

Приказ определителя

Порядок определителя равен количеству строк и столбцов.

Пример 26
$\begin{vmatrix} 1 и 4\\ 6 и 2\\ \end{vmatrix}$ (у него 2 строки и 2 столбца, поэтому его порядок равен 2)

Пример 27
$\begin{vmatrix} 4 и 7 и 9\\ 6 и 3 и 2\\ 7 и 1 и 4\\ \end{vmatrix}$ (у него 3 строки и 3 столбца, поэтому его порядок равен 3)

Вычисление определителя матрицы

Определитель матрицы равен сумме произведений элементов любой строки или столбца и их сомножителей.

$\слева| А\право| знак равно \begin{vmatrix} а_{1,1} и а_{1,2} и а_{1,3} и . & . & a_{1,n}\\ а_{2,1} и а_{2,2} и а_{2,3} и . & . & а_{2,n}\\ а_{3,1} и а_{3,2} и а_{3,3} и . & . & а_{3,n}\\ . & . & . & . & .& .\\ a_{n,1} & a_{n,2} & a_{n,3} & . & . & Анна}\\ \end{vmatrix}$ 9{3}\cdot\Delta_{1,2}=a_{1,1}\cdot\Delta_{1,1}-a_{1,2}\cdot\Delta_{1,2}$

Однако $ \Delta_{1,1}= a_{2,2} $ и $ \Delta_{1,2}=a_{2,1}$

$ \ влево | А\право| =a_{1.1} \cdot a_{2,2}- a_{1.2} \cdot a_{2,1}$

$\цвет{красный}{ \begin{vmatrix} а и б\\ CD \end{vmatrix} =a \cdot d — b \cdot c}$

Пример 28
$\begin{vmatrix} 2 и 5\\ 3 и 8 \end{vmatrix} =2 \cdot 8 — 3 \cdot 5 = 16 -15 =1$

Пример 29{4}\cdot\Delta_{1,3}=$ $a_{1,1}\cdot\Delta_{1,1}-a_{1.2}\cdot\Delta_{1,2}+a_{1.3}\cdot\Delta_{1,3}$

$\Дельта_{1,1}= \begin{vmatrix} а_{2,2} и а_{2,3}\\ а_{3,2} и а_{3,3} \end{vmatrix} = а_{2,2}\cdot а_{3,3}-a_{2,3}\cdot а_{3,2}$

$\Дельта_{1,2}= \begin{vmatrix} а_{2,1} и а_{2,3}\\ а_{3,1} и а_{3,3} \end{vmatrix} = а_{2,1}\cdot а_{3,3}-a_{2,3}\cdot а_{3,1}$

$\Дельта_{1,3}= \begin{vmatrix} а_{2,1} и а_{2,2}\\ а_{3,1} и а_{3,2} \end{vmatrix} = а_{2,1}\cdot а_{3,2}-a_{2,2}\cdot а_{3,1}$

$\влево| А\право| =a_{1,1}\cdot( a_{2,2}\cdot a_{3,3}-a_{2,3}\cdot a_{3,2})-a_{1,2}\cdot( a_{2,1}\cdot a_{3,3}-a_{2,3}\cdot a_{3,1})+$ $a_{1,3}\cdot(a_{2,1}\cdot а_{3,2}-а_{2,2}\cdot а_{3,1})=$ $a_{1,1}\cdot a_{2,2}\cdot a_{3,3}-a_{1,1}\cdot a_{2,3}\cdot a_{3,2}-a_{1 ,2}\cdot a_{2. 1}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3,1}+$ $a_{1,3}\ cdot a_{2,1}\cdot a_{3,2}-a_{1,3}\cdot a_{2,2}\cdot a_{3,1}=$ $\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3, 1}+a_{1,3}\cdot a_{2,1}\cdot a_{3,2}-}$ $\color{red}{(a_{1,1}\cdot a_{2,3}\cdot a_{3,2}+a_{1,2}\cdot a_{2,1}\cdot a_{3 ,3}+a_{1,3}\cdot a_{2,2}\cdot a_{3,1})}$

Чтобы быстрее достичь последнего отношения, мы можем использовать следующий метод.

Сначала перепишем первые две строки под определителем следующим образом.

$\begin{vmatrix} \color{red}{a_{1,1}} & a_{1,2} & a_{1,3}\\ \color{red}{a_{2,1}} & \color{red}{a_{2,2}} & a_{2,3}\\ \color{red}{a_{3,1}} & \color{red}{a_{3,2}} & \color{red}{a_{3,3}} \end{vmatrix}$
$\hspace{2мм}\begin{массив}{ccc} a_{1,1} & \color{red}{a_{1,2}} & \color{red}{a_{1,3}}\\ a_{2,1} & a_{2,2} & \color{red}{a_{2,3}}\\ \end{массив}$

Мы умножаем элементы на каждой из трех красных диагоналей (главная диагональ и нижняя) и суммируем результаты:
$\color{red}{a_{1,1}\cdot a_{2,2}\ cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1,3}+a_{3,1}\cdot a_{1,2}\cdot a_{2 ,3}}$

$\begin{vmatrix} \color{red}{a_{1,1}} & \color{red}{a_{1,2}} & \color{blue}{a_{1,3}}\\ \color{red}{a_{2,1}} & \color{blue}{a_{2,2}} & \color{blue}{a_{2,3}}\\ \color{blue}{a_{3,1}} & \color{blue}{a_{3,2}} & \color{blue}{a_{3,3}} \end{vmatrix}$
$\hпробел{2мм} \begin{массив}{ccc} \color{blue}{a_{1,1}} & \color{blue}{a_{1,2}} & \color{red}{a_{1,3}}\\ \color{blue}{a_{2,1}} & \color{red}{a_{2,2}} & \color{red}{a_{2,3}}\\ \end{массив}$

Мы умножаем элементы на каждой из трех синих диагоналей (второстепенная диагональ и нижняя) и суммируем результаты:

$\color{синий}{a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1, 1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1}}$

Если мы вычтем два отношения, мы получим формулу определителя:

$\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1, 3}+a_{3,1}\cdot a_{1,2}\cdot a_{2,3}-}$ $\color{red}{(a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1 ,1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1})}$

Пример 30
$A=\begin{pmatrix} 1 и 4 и 3 \\ 2 и 1 и 5\\ 3 и 2 и 1\\ \end{pmatrix}$

$\begin{vmatrix} 1 и 4 и 3 \\ 2 и 1 и 5\\ 3 и 2 и 1\\ \end{vmatrix}$
$\hspace{2мм}\begin{массив}{ccc} 1 и 4 и 3\\ 2 и 1 и 5\\ \end{массив}$

$ = 1\cdot1\cdot1 + 2\cdot2\cdot3 + 3\cdot4\cdot5 — (3\cdot1\cdot3 + 5\cdot2\cdot1 + 1\cdot4\cdot2) =$ $1 + 12 + 60 -(9 + 10 + 8)=73-27=46$

Пример 31
$A=\begin{pmatrix} 3 и 5 и 1 \\ 1 и 4 и 2\\ 7 и 1 и 9\\ \end{pmatrix}$

$\begin{vmatrix} 3 и 5 и 1 \\ 1 и 4 и 2\\ 7 и 1 и 9\\ \end{vmatrix}$
$\hspace{2mm}\begin{массив}{ccc} 3 и 5 и 1\\ 1 и 4 и 2\\ \end{массив} $

$= 3\cdot4\cdot9 + 1\cdot1\cdot1 + 7\cdot5\cdot2 — (1\cdot4\cdot7 + 2\cdot1\cdot3 + 9\cdot5\cdot1) =$ 108$ + 1 + 70 -(28 + 6 + 45)=79-79=100$

Существуют определители, элементами которых являются буквы. Их легче вычислить, используя свойства определителей. Например, мы вычисляем определитель матрицы, в которой есть одни и те же элементы в любой строке или столбце, но переупорядоченные.

$\begin{vmatrix} а и б и в \\ такси\\ б и в и а \end{vmatrix}$ $ \xlongequal{C_{1}+C_{2}+C_{3}} \begin{vmatrix} а + б + с и б и с\\ с + а + б & а & ​​б \\ б + в + а и в и а \end{vmatrix} = (а + б + с) \cdot \begin{vmatrix} 1 и б и в\\ 1 и а и б\\ 1 и с и а \end{vmatrix}$ 9{2} \end{vmatrix}= $

$\begin{vmatrix} а-в и б-в \\ (а-с) (а+с) и (б-с)(б+с) \end{vmatrix}=$ $(а-в)(б-в)\begin{vmatrix} 1 и 1\\ а+с и б+с \end{vmatrix}=$

$=(a-c)(b-c)[(b+c)-(a+c)]=$ $(a-c)(b-c)(b+c-a-c)=(a-c)(b-c)(b-a)$

Вычисление определителя 4×4

Для вычисления определителей 4х4 используем общую формулу.

Перед применением формулы с использованием свойств определителей:

1. Проверяем, выполняется ли какое-либо из условий для того, чтобы значение определителя было равно 0.
2. Мы проверяем, можем ли мы выделить любую строку или столбец.
3. Проверяем, является ли определитель матрицей Вандермонда и имеет ли он те же элементы, но переупорядоченные, в любой строке или столбце.

В любом из этих случаев воспользуемся соответствующими методами вычисления определителей 3×3. Мы модифицируем строку или столбец, чтобы заполнить его 0, за исключением одного элемента. Определитель будет равен произведению этого элемента и его кофактора. В этом случае кофактор представляет собой детерминант 3×3, который рассчитывается по специальной формуле.

Пример 33
$\begin{vmatrix} 1 и 3 и 9 и 2\\ 5 и 8 и 4 и 3\\ 0 и 0 и 0 и 0\\ 2 и 3 и 1 и 8 \end{vmatrix}$

Заметим, что все элементы в строке 3 равны 0, поэтому определитель равен 0.

Пример 34
$\begin{vmatrix} 1 и 3 и 1 и 2\\ 5 и 8 и 5 и 3\\ 0 и 4 и 0 и 0\\ 2 и 3 и 2 и 8 \end{vmatrix}$
Заметим, что $C_{1}$ и $C_{3}$ равны, поэтому определитель равен 0.

Пример 35
$\begin{vmatrix} 1 и 3 и 9 и 2\\ 5 и 8 и 4 и 3\\ 10 и 16 и 18 и 4\\ 2 и 3 и 1 и 8 \end{vmatrix}$
Заметим, что строки 2 и 3 пропорциональны, поэтому определитель равен 0.

Пример 36
$\begin{vmatrix} \цвет{красный}{4} & 3 & 2 & 2\\ 0 и 1 и -3 и 3\\ 0 и -1 и 3 и 3\\ 0 и 3 и 1 и 1 \end{vmatrix}$

Поскольку в столбце 1 есть только один элемент, отличный от 0, мы применяем общую формулу, используя этот столбец. Кофакторы, соответствующие элементам, равным 0, не нужно вычислять, потому что произведение их и этих элементов будет равно 0.

=
$=4(1\cdot3\cdot1 +(-1)\cdot1\cdot3+3\cdot(-3)\cdot3$ $-(3\cdot3\cdot3+3\cdot1\cdot1 +1\cdot( -3)\cdot(-1)))$ $=4(3-3-27-(27+3+3))=4\cdot(-60)=-240$

Пример 37
$\begin{vmatrix} 4 и 3 и 2 и 2\\ 0 и 1 и 0 и -2\\ 1 и -1 и 3 и 3\\ 2 и 3 и 1 и 1 \end{vmatrix}$

Чтобы изменить строки так, чтобы в них было больше нулей, мы оперируем столбцами и наоборот. Мы выбираем строку или столбец, содержащие элемент 1, потому что мы можем получить любое число путем умножения.

Мы замечаем, что в строке 2 уже есть два элемента, равных 0. Мы делаем только один другой 0, чтобы вычислить только сомножитель 1.

$\begin{vmatrix} 4 и 3 и 2 и 2\\ 0 и 1 и 0 и -2\\ 1 и -1 и 3 и 3\\ 2 и 3 и 1 и 1 \end{vmatrix} \xlongequal{C_{4}+2C_{2}}$ $\begin{vmatrix} 4 и 3 и 2 и 8\\ 0 & \цвет{красный}{1} & 0 & 0\\ 1 и -1 и 3 и 1\\ 2 и 3 и 1 и 7 \end{vmatrix}=$ $=$
9{2+2}\cdot \begin{vmatrix} 4 и 2 и 8\\ 1 и 3 и 1\\ 2 и 1 и 7 \end{vmatrix}=$
$=4\cdot3\cdot7 + 1\cdot1\cdot8 + 2\cdot2\cdot1$ $-(8\cdot3\cdot2 + 1\cdot1\cdot4 + 7\cdot2\cdot1) = $ 84$ + 8 + 4- 48-4-14=30$

Пример 38
$\begin{vmatrix} 1 и -2 и 3 и 2\\ 2 и 3 и 1 и -1\\ 3 и 3 и 3 и 3\\ -1 и 4 и 2 и 1\\ \end{vmatrix}$

Мы можем разложить 3 из строки 3:
$3\cdot \begin{vmatrix} 1 и -2 и 3 и 2\\ 2 и 3 и 1 и -1\\ 1 и 1 и 1 и 1\\ -1 и 4 и 2 и 1\\ \end{vmatrix}$ 9{3+4}\cdot$ $=(-1)\cdot \begin{vmatrix} -1 и -4 и 1\\ 3 и 4 и 2 \\ -2 и 3 и 1\\ \end{vmatrix}$
$=-((-1)\cdot 4\cdot 1 +3 \cdot 3\cdot1 + (-2)\cdot (-4)\cdot 2$ $- (1\cdot 4 \cdot (-2) + 2\cdot 3\cdot (-1) + 1\cdot (-4)\cdot3))$ $=-(-4 + 9 + 16 + 8 + 6 + 12) =-47 $

Пример 39
$\begin{vmatrix} 2 и 5 и 1 и 4\\ 4 и 1 и 6 и 3\\ 5 и 3 и 7 и 2\\ 1 и 0 и 2 и 4 \end{vmatrix}$

В этом примере мы можем использовать последнюю строку (которая содержит 1) и можем сделать нули в первом столбце. 9{4+1}\cdot \begin{vmatrix} 5 и -3 и -4\\ 1 и -2 и -13\\ 3 и -3 и -18 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 5 и -3 и -4\\ 1 и -2 и -13\\ 3 и -3 и -18 \end{vmatrix}$

Мы умножаем -1 из столбца 2 и -1 из столбца 3.
$ (-1)\cdot(-1)\cdot(-1)\cdot \begin{vmatrix} 5 и 3 и 4\\ 1 и 2 и 13\\ 3 и 3 и 18 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 5 и 3 и 4\\ 1 и 2 и 13\\ 3 и 3 и 18 \end{vmatrix}=$ $-[5\cdot 2\cdot 18 + 1\cdot 3\cdot 4+ 3\cdot 3\cdot 13 — (4\cdot 2\cdot 3\cdot + 13\cdot 3\cdot 5 + 18\cdot 3 \cdot 1)]=$ $-(180+12+117-24-195-54)=36$

Пример 40
$\begin{vmatrix} 4 и 7 и 2 и 3\\ 1 и 3 и 1 и 2\\ 2 и 5 и 3 и 4\\ 1 и 4 и 2 и 3 \end{vmatrix}$

В столбце 3 стоит 1, поэтому мы обнулим строку 2.

$\begin{vmatrix} 4 и 7 и 2 и 3\\ 1 и 3 и 1 и 2\\ 2 и 5 и 3 и 4\\ 1 и 4 и 2 и 3 \end{vmatrix}$ $\xlongequal{C_{1}-C_{3}, C_{2}-3C_{3},C_{4}-2C_{3}} \begin{vmatrix} 2 и 1 и 2 и -1\\ 0 и 0 и \цвет{красный}{1} и 0 \\ -1 и -4 и 3 и -2\\ -1 и -2 и 2 и -1 \end{vmatrix}=$ $=1\cdot(-1)^{2+5}\cdot \begin{vmatrix} 2 и 1 и -1\\ -1 и -4 и -2\\ -1 и -2 и -1 \end{vmatrix}$

Мы умножаем -1 из строки 2 и -1 из строки 3.

No related posts.