Определители третьего порядка
Высшая математика / Практикум по аналитической геометрии
Выражение вида
называется определителем третьего порядка.
Определитель третьего порядка имеет девять элементов, три строки, три столбца, две диагонали — главную и побочную.
Рис.1
Формула (1) показывает, что в раскрытом виде определитель содержит шесть членов. Для их определения существуют простые способы. Рассмотрим два из них.
Способ I. Выписываем все элементы определителя в том же порядке, как они расположены в определителе, и приписываем справа первые два столбца определителя:
Способ II. Возьмем со знаком плюс произведение элементов, стоящих на главной диагонали определителя, а также произведения элементов, стоящих на двух параллельных к ней линиях, содержащих по три элемента.
Произведения же элементов, стоящих на побочной диагонали и на двух параллельных к ней линиях, содержащих по три элемента, возьмем со знаком минус.
Алгебраическая сумма этих шести произведений дает значение определителя третьего порядка.
Пример. Вычислить определитель:
Решение.
Способ III. Способ разложения определителя по элементам какой-либо строки или столбца.
Если в определителе третьего порядка вычеркнуть одну строку и один столбец, на пересечении которых стоит некоторый элемент, то оставшиеся элементы образуют определитель второго порядка, который называется минором определителя Δ, соответствующим этому элементу. Например, минором определителя
соответствующим элементу будет определитель второго порядка
Чтобы вычислить определитель третьего порядка, нужно каждый элемент строки или столбца, по которым разлагается определитель, умножить на его минор, взятый со знаком плюс или минус в зависимости от того, будет ли сумма номеров зачеркнутых строки и столбца четным или нечетным числом. Например,
Например,
— разложение определителя Δ по первому столбцу.
Пример. Вычислить определитель
Решение.
Основные свойства определителей третьего порядка.
Свойство 1. Величина определителя не изменится, если за¬писать столбцы вместо строк, а строки вместо столбцов.
Свойство 2. При перестановке двух столбцов или строк определитель меняет знак.
Свойство 3. Чтобы умножить определитель на какое-нибудь число, достаточно умножить на это число все элементы какой-нибудь одной строки или какого-нибудь одного столбца.
Свойство 4. Если в определителе имеются две одинаковых строки или два одинаковых столбца, то он равен нулю.
Свойство 5. Величина определителя не изменится, если к элементам некоторого ряда прибавить элементы параллельного ряда, предварительно умножив их на постоянный множитель.
Определители матриц первого, второго и третьего порядков
Содержание Определитель квадратной матрицы первого порядка Определитель квадратной матрицы второго порядка Схема вычисления определителя второго порядка Примеры вычисления определителей второго порядка Определитель квадратной матрицы третьего порядка Правило треугольников нахождения определителя третьего порядка Примеры вычисления определителей третьего порядка
Используя специальное правило каждой квадратной матрице можно поставить в соответствие число, которое будем называть определителем (детерминантом) и обозначать или или
Определителем квадратной матрицы первого порядка называется число
Заметим, что здесь выражение означает определитель, хоть внешне очень похоже на запись модуля числа Таким образом, определитель матрицы первого порядка равен единственному элементу этой матрицы, например для матриц
и
определители
и
Определителем квадратной матрицы второго порядка
называется число
Таким образом, для того, что вычислить определитель матрицы 2-го порядка нужно умножить элементы главной диагонали матрицы и от полученного произведения вычесть произведение элементов побочной диагонали матрицы.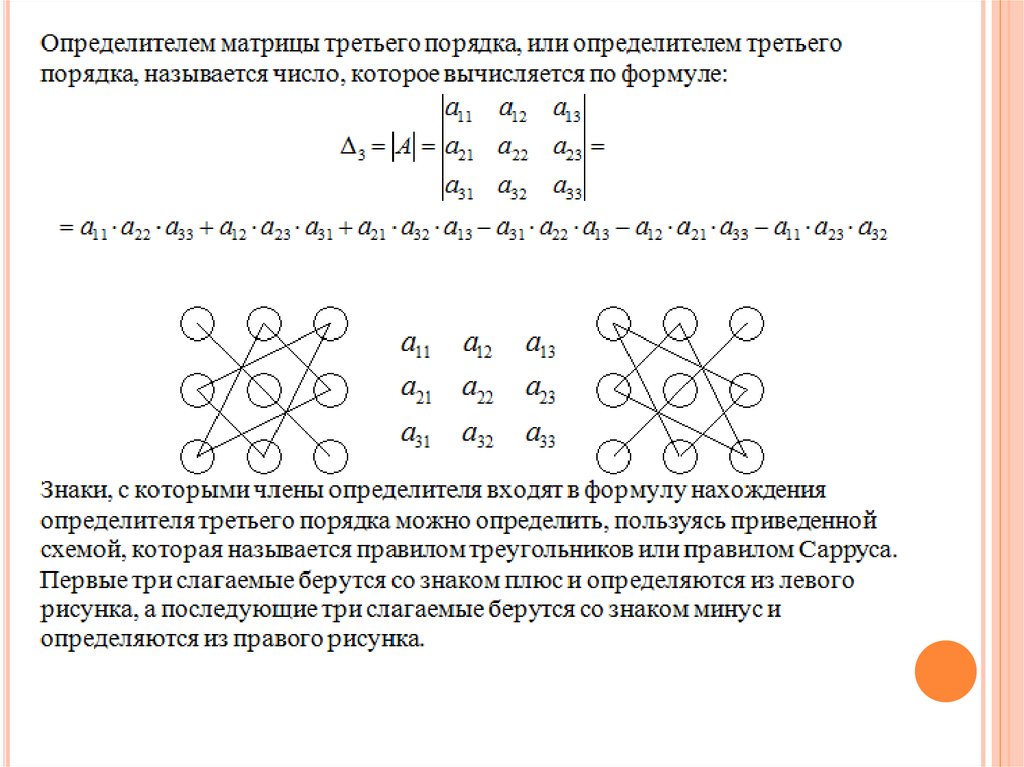 Схема вычисления определителя второго порядка представлена на рис. 1.
Схема вычисления определителя второго порядка представлена на рис. 1.
Рис. 1
Рассмотрим примеры, где требуется вычислить определитель второго порядка. У матриц
определители
Определителем квадратной матрицы третьего порядка
называется число
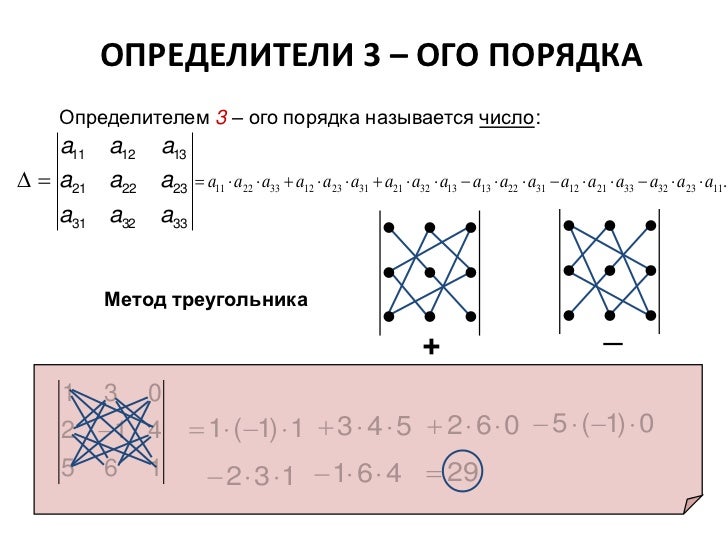
Как видим, для того чтобы вычислить определитель матрицы третьего порядка необходимо использовать достаточно сложную для запоминания формулу, однако, заучивать ее вовсе не обязательно. Гораздо легче понять и запомнить схему вычисления определителя третьего порядка (рис. 2) (ее еще называют правилом треугольников). Используя эту схему решаются задачи на вычисление определителей матриц 3×3, и с ее помощью всегда можно восстановить формулу нахождения определителя 3-го порядка.
Рис. 2
Как видно из схемы (рис. 2), для того чтобы найти определитель третьего порядка необходимо вычислить 6 чисел, каждое из которых представляет собой произведение трех чисел. Для нахождения первого числа требуется найти произведение элементов главной диагонали, второе и третье числа представляют собой произведения элементов, находящихся в вершинах равнобедренных треугольников (см. рис. 2), чьи основания параллельны главной диагонали матрицы. Аналогично, четвертое число в схеме есть произведение элементов второй (побочной) диагонали матрицы, а пятое и шестое числа находятся как произведения элементов-вершин равнобедренных треугольников с основаниями параллельными второй диагонали матрицы. Затем следует сложить первые три числа и из этой суммы вычесть сумму чисел с номерами 4 — 6.
Для нахождения первого числа требуется найти произведение элементов главной диагонали, второе и третье числа представляют собой произведения элементов, находящихся в вершинах равнобедренных треугольников (см. рис. 2), чьи основания параллельны главной диагонали матрицы. Аналогично, четвертое число в схеме есть произведение элементов второй (побочной) диагонали матрицы, а пятое и шестое числа находятся как произведения элементов-вершин равнобедренных треугольников с основаниями параллельными второй диагонали матрицы. Затем следует сложить первые три числа и из этой суммы вычесть сумму чисел с номерами 4 — 6.
Рассмотрим пример вычисления определителя матрицы третьего порядка. Определитель
Определители
В примечаниях «Введение в определители» мы поймем значение определителей и матриц и научимся вычислять определитель матрицы 3×3 и определитель матрицы 2×2.
Что такое матрица?
- Элементы матрицы называются элементами.
- Матрица может быть описана как прямоугольный массив чисел, расположенных в строках и столбцах.

- Матрица или матрицы (во множественном числе) могут использоваться для записи данных, зависящих от двух параметров, описания линейного уравнения или отслеживания коэффициентов линейного преобразования.
- Например, система линейных уравнений —
p1x + q1y = c1 и p2x + q2y = c2 может быть представлена как
|p1 q1||x y|=|c1 c2|
|p2 q2|
- Понятие матриц применяется в различных разделах математики, статистики, экономики, физики и техники.
Что такое определитель?
- В словаре английского языка определитель относится к элементу, который определяет или идентифицирует ценность или характер чего-либо.
- В математике каждой квадратной матрице порядка n можно поставить в соответствие действительное или комплексное число. Это действительное или комплексное число называется определителем квадратной матрицы A.
- Важно знать, что только квадратные матрицы могут иметь определители.
- Например, если X = p q r s , то определитель X будет обозначаться как X = p q r s =det X .

- Определители используются для определения того, имеет ли система из n уравнений решение.
- Есть несколько свойств определителей. Некоторые важные свойства определителей:0008
- Значение определителя не меняется даже при перестановке строк и столбцов матрицы.
- Знак определителя меняется, если поменять местами любые две строки или столбца этого определителя.
- Значение определителя равно нулю, если элементы любых двух строк и столбцов одинаковы.
История определителей
- Многие считают, что японский математик Секи Кова был первым, кто открыл определители. Секи Кова, которого также называли японским Ньютоном, был математиком и писателем периода Эдо. Ему приписывают создание основ японской математики. В 1683 году Кова в своей книге «Кай Фукудай но Хо» продемонстрировал свою идею детерминантов.
- Примерно в то же время немецкий математик Готфрид Лейбниц написал об определителях как способе решения линейных уравнений в письме Гийому де Лопиталю.

- Теоремы и свойства для вычисления определителей матриц еще больше обсуждались другими математиками в последующие столетия.
- Колин Маклюрин был английским математиком в 18 веке. Его книга «Трактат по алгебре» содержала правило Крамера и указывала способы определения четырех одновременных квадратных уравнений.
Определитель матрицы 1×1
- Определитель квадратной матрицы 1×1 — это просто число внутри матрицы.
- Например, пусть X = [x] — квадратная матрица 1×1. Тогда определитель X будет сам x.
Определитель 2 × 2 матрицы
DET (x) = x = = (P × S) — (Q × R)
Например, давайте рассчитывать определятель матрицы
.0072 Q = |2 3|
|5 9|
Det (Q) = Q =
= (2 × 9) – (3 × 5)= 18 – 15 = 3
Так как Det (A) = A = y2 – (y + 1) ( y – 1) = y2 – (y2 – 1) = y2 – y2 + 1 = 1
Следовательно, Det (A) = 1
Определитель матрицы 3×3
X=
3 Определитель матрицы 3 × 3 можно вычислить, раскладывая ее строки или столбцы. Следовательно, есть шесть способов вычисления 3×3. Определитель можно вычислить по 3 строкам и 3 столбцам и всегда давать один и тот же результат.
Следовательно, есть шесть способов вычисления 3×3. Определитель можно вычислить по 3 строкам и 3 столбцам и всегда давать один и тот же результат.
Определитель X можно вычислить, разложив его по первой строке.
Следовательно, p × (-1) (1+1) | т и |
| ш х |
На шаге 2 второй элемент строки 1, q, умножается на (-1)1+2, и определитель получается удалением элементов строки 1 и столбца 2. Результирующее уравнение будет иметь вид — q × (-1)1+2 × |s u|
| v х|
На шаге 3 третий элемент строки 1, r, умножается на (-1) 1+3, а определитель получается удалением элементов первой строки и третьего столбца. Полученное уравнение: r × (-1) 1+3 |s t |
|
Следовательно, X = (-1)2 p (t x – u w) + (-1)3 q (s x – u v) + (-1)4 r (s w – t v),
X= p t x – p u w – q s x + q u v + r s w – rt v… пусть это будет уравнение 1.
Точно так же определитель X можно вычислить по его второй и третьей строкам. Следует отметить, что значение определителя останется прежним, когда его разложат на первую, вторую и третью строки.
Расширение по столбцу 1.
Аналогично расширению по строке 1 будет три уравнения.
Уравнение 1 = p (-1)1+1
Уравнение 2 = s (-1)2+1
Уравнение 3 = v (-1)3+1
Следовательно, X = p (-1)2
+ s(-1)3
+ v(-1)4
r t),
= p t x – p u w – s q x + s r w + v q u – v r t… пусть это будет уравнение 2.
Определение значения X путем расширения строк 1,
X= 3 (56-20) – 4(63-10) + 5(18-8),
= 3 (36) – 4(53) + 5(10),
= 108 – 212 + 50 = -54
Определение значения X путем расширения столбца 2,
X = -4 (63 – 10) + 8 (21 – 5) – 2 (30 – 45),
= -4 (53) + 8 (16) – 2(-15),
= -212 + 128 + 30 = -54
Определитель X будет определен как-
Калькулятор матрицы детерминантов
- определителя онлайн с помощью онлайн-калькулятора матрицы определителя.
 Такие сайты, как Matrix Reshish, бесплатно вычисляют определитель матриц комплексных чисел.
Такие сайты, как Matrix Reshish, бесплатно вычисляют определитель матриц комплексных чисел. - Такие калькуляторы определителей матриц могут вычислять определитель даже неквадратных матриц и матриц, содержащих дроби и десятичные дроби.
Заключение
На этом мы завершаем нашу статью о введении в определители. Детерминанты обычно подразделяются на детерминанты первого порядка, определители второго порядка и определители третьего порядка. В математике концепция определителей используется для получения аналогичной формулы для нахождения решения системы из n уравнений с n неизвестными.
Свойства определителей – объяснение, важные свойства, примеры решений и часто задаваемые вопросы
В линейной алгебре определитель – это уникальное число, которое можно получить из квадратной матрицы. Детерминанты матрицы говорят, что K представлен как det (K) или, |K| или det K. Детерминанты и их свойства полезны, поскольку они позволяют нам получать те же результаты с различными и более простыми конфигурациями элементов. Определитель считается важной функцией, поскольку он удовлетворяет некоторым дополнительным свойствам определителей, которые выводятся из следующих условий.
Определитель считается важной функцией, поскольку он удовлетворяет некоторым дополнительным свойствам определителей, которые выводятся из следующих условий.
Мультипликативность; det (XY) = det (X) det (Y)
Инвариантность при транспонировании det (X) = det (Xt).
Инвариантность при операциях над строками; если X’ — это матрица, образованная суммированием кратного любой строки другой строке, то det (X) = det (X’).
Произошла смена знака при замене строк. Если X’ — это матрица, полученная путем перестановки двух строк местами, то det (X’) = -det (x)
Что называют детерминантами?
Определитель квадратной матрицы — это значение, определяемое элементами матрицы. В матрице 2×2. Детерминанты рассчитываются по формуле
В матрице 2×2. Детерминанты рассчитываются по формуле
Det \[ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \]
Более крупные матрицы имеют более сложные формулы.
Детерминанты имеют различные применения в математике. Например, они используются в формулах шнурков для вычисления площади, что полезно в качестве условия коллинеарности, поскольку три коллинеарные точки определяют треугольник, равный 0. Определитель также используется в исчислениях с несколькими переменными (в основном в Якобине) и в вычислениях. векторное произведение векторов.
Чем определитель отличается от матрицы?
Это вопрос, над которым постоянно размышляют многие студенты, а также в конечном итоге смешивают понятия на экзамене и теряют оценки. Хотя оба они важны с практической точки зрения, основными ключевыми различиями между ними являются:
В матрице набор чисел заключен в квадратные скобки, тогда как в определителе числа заключены в две черты
Количество строк и столбцов в матрице всегда одинаково.
 Это не относится к детерминантам
Это не относится к детерминантамДетерминанты помогают определить значения неизвестных переменных с помощью правила Крамера, тогда как матрицы используются для математических операций, таких как сложение, вычитание и т. д. Некоторые основные свойства определителей приведены ниже:
Если In — единичная матрица порядка m × m, то det(I) равно 1
Если Матрица XT транспонирована Матрице X, то det (XT) = det (X)
Если Матрица X-1 является обратной Матрице X, то det (X-1) = \[\ frac{1}{det (X)}\] = det(X)-1
Если две квадратные матрицы x и y имеют одинаковый размер, то det (XY) = det (X) det (Y)
Если матрица X сохраняет размер a × a, а C — константа, то det (CX) = Ca det (X)
Если A, B и C — три положительно полуопределенные матрицы одинакового размера, то следующее уравнение выполняется вместе со следствием det (A+B) ≥ det(A) + det (B) для A,B, C ≥ 0 det (A+B+C) + det C ≥ det (A+B) + дет (B+C)
В треугольной матрице определитель равен произведению диагональных элементов.

Определитель матрицы равен нулю, если каждый элемент матрицы равен нулю.
Формула Лапласа и матрица сопряжений.
Важные свойства определителей
Существует 10 широко используемых важных свойств определителей. Эти свойства облегчают расчеты, а также помогают в решении разного рода задач. Описание каждого из 10 важных свойств определителей приведено ниже.
Reflection Property
All-zero Property
Proportionality
Switching property
Factor property
Scalar multiple properties
Sum property
Triangle property
Определитель матрицы кофакторов
Свойство инвариантности
Каждое из этих свойств подробно обсуждается ниже:
1.
 Свойство отражения
Свойство отраженияСвойство отражения определителей определяет, что определители не изменяются, если строки преобразуются в столбцы, а столбцы преобразуются в строки.
2. Свойство All-Zero
Определители будут эквивалентны нулю, если каждый член строк и столбцов равен нулю.
3. Пропорциональность (свойство повторения)
Если каждый член строк или столбцов подобен столбцу какой-либо другой строки (или столбца), то определитель эквивалентен нулю.
4. Свойство переключения
Перестановка любых двух строк (или столбцов) определителя меняет его знаки.
5. Свойство фактора
Если определитель \[\Delta\] становится равным 0 при рассмотрении значения x = α, то (x -α) рассматривается как фактор \[\Delta\].
6.
 Скалярное множественное свойство
Скалярное множественное свойствоЕсли все элементы строки (или столбцов) определителя умножаются на ненулевую константу, то определитель умножается на аналогичную константу.
7. Свойство суммы
\[ \begin{vmatrix} j_{1} + k_{1} & l_{1} & m_{1}\\ j_{2} + k_{2} & l_{ 2} & m_{2}\\ j_{3} + k_{3} & l_{3} & m_{3} \end{vmatrix} = \begin{vmatrix} j_{1} & l_{1} & m_ {1}\\ j_{2} & l_{2} & m_{2}\\ j_{3} & l_{3} & m_{3} \end{vmatrix} + \begin{vmatrix} + k_{1 } & l_{1} & m_{1}\\ + k_{2} & l_{2} & m_{2}\\ + k_{3} & l_{3} & m_{3} \end{vmatrix} \]
8. Свойство треугольника
Если каждый член определителя выше или ниже главной диагонали содержит нули, то определитель эквивалентен произведению диагональных членов. Это
\[ \begin{vmatrix} x_{1} & x_{2} & x_{3}\\ 0 & y_{2} & y_{3}\\ 0 & 0 & z_{3} \end {vmatrix} = \begin{vmatrix} x_{1} & 0 & 0 \\ x_{2} & y_{2} & 0 \\ x_{3} & y_{3} & z_{3} \end{vmatrix } = X_{1}Y_{2}Z_{3}\]
9.
 Определитель матрицы кофакторов 9{2}\]
Определитель матрицы кофакторов 9{2}\]В приведенных выше определителях матрицы кофакторов Cij обозначает кофактор элементов aij в \[\Delta\].
10. Свойство инвариантности
\[ \begin{vmatrix} a_{1} & b_{1} & c_{1}\\ a_{2} & b_{2} & c_{3}\\ a_{ 3} & b_{3} & c_{3} \end{vmatrix} = \begin{vmatrix} a_{1} + \alpha b_{1} + \beta c_{1} & b_{1} & c_{1 } \\ a_{2} + \alpha b_{2} + \beta c_{2} & b_{2} & c_{2} \\ a_{3} + \alpha b_{3} + \beta c_{3 } & b_{3} & c_{3} \end{vmatrix} \]
Это означает, что определитель остается неизменным под действием терма \[C_{i} \rightarrow C_{i} + \alpha C_{j} + \beta C_{k} \], где j и k не эквивалентны на i или математическая операция терма \[R_{i} \rightarrow R_{i} + \alpha R_{j} + \beta R_{k} \], где j и k не эквивалентны i.
Примеры Задачи на свойства определителей
Некоторые важные примеры свойств определителей приведены ниже:
1.
 Используя свойства определителей, докажите, что 9{2}) \]
Используя свойства определителей, докажите, что 9{2}) \]Решение: С помощью инвариантности и скалярных кратных свойств Определителя мы можем доказать указанный выше Определитель.
\[ \Delta = \begin{vmatrix} x & y & z \\ y & z & x \\ z & x & y \end{vmatrix} = \begin{vmatrix} x + y + z & y & z \\ y + z + x & z & x \\ z + x + y & z & y \end{vmatrix}\] Работа\[ C_{[1]} \rightarrow C_{[1]} + C_{ [1]} + C_{[1]}\]
\[ = (x + y + z) \begin{vmatrix} 1 & y & 0 \\ 1 & z & x \\ 1 & x & y \ end{vmatrix} = (x + y + z) \begin{vmatrix} 1 & y & z \\ 0 & z — y & x — z \\ 1 & x — y & y — z \end{vmatrix}\ ] 9{2}) \]
2. Используя свойства определителей, докажите, что
\[ \begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{ vmatrix} = \begin{vmatrix} b & h & e \\ a & g & d \\ c & i & f \end{vmatrix} \]
Решение: перестановка строк и столбцов по диагоналям с помощью свойство отражения, а затем, используя свойство переключения определения, мы можем получить желаемый результат.
9{2} \]
= \[ \begin{vmatrix} b & h & e \\ a & g & d \\ c & i & f \end{vmatrix} = \begin{vmatrix} b & h & e \\ a & g & d \\ c & i & f \end{vmatrix} \] = R.H.S
Забавный факт: вам может быть очень интересно узнать, что определители были введены великим математиком и физиком Гауссом в свою книгу Disquisitiones arithmeticae, когда говорил о квадратных уравнениях в 1801 году. Он разработал ее как способ определения решений квадратных уравнений. Таким образом, это очень старая концепция, которая по сей день сохраняет столь высокий уровень важности. В этом красота математики, она никогда не стареет!
Время викторины
1. Согласно свойствам детерминантов, значение детерминанта равна нулю, если строка составляет
, умноженное на строку
, умноженная на колонку 9000
.

Разделено на столбец
2. Определители матрицы в матрицах представлены
Вертикальными линиями вокруг матрицы.
Горизонтальные линии вокруг Матрицы
Bracket around Matrix
None of the above
3. The Matrix product XY= O, then
X = O and Y = O
X = O or Y = O
x — Null Matrix
Ни один из вышеперечисленных
4.





 Такие сайты, как Matrix Reshish, бесплатно вычисляют определитель матриц комплексных чисел.
Такие сайты, как Matrix Reshish, бесплатно вычисляют определитель матриц комплексных чисел. Это не относится к детерминантам
Это не относится к детерминантам
 Свойство отражения
Свойство отражения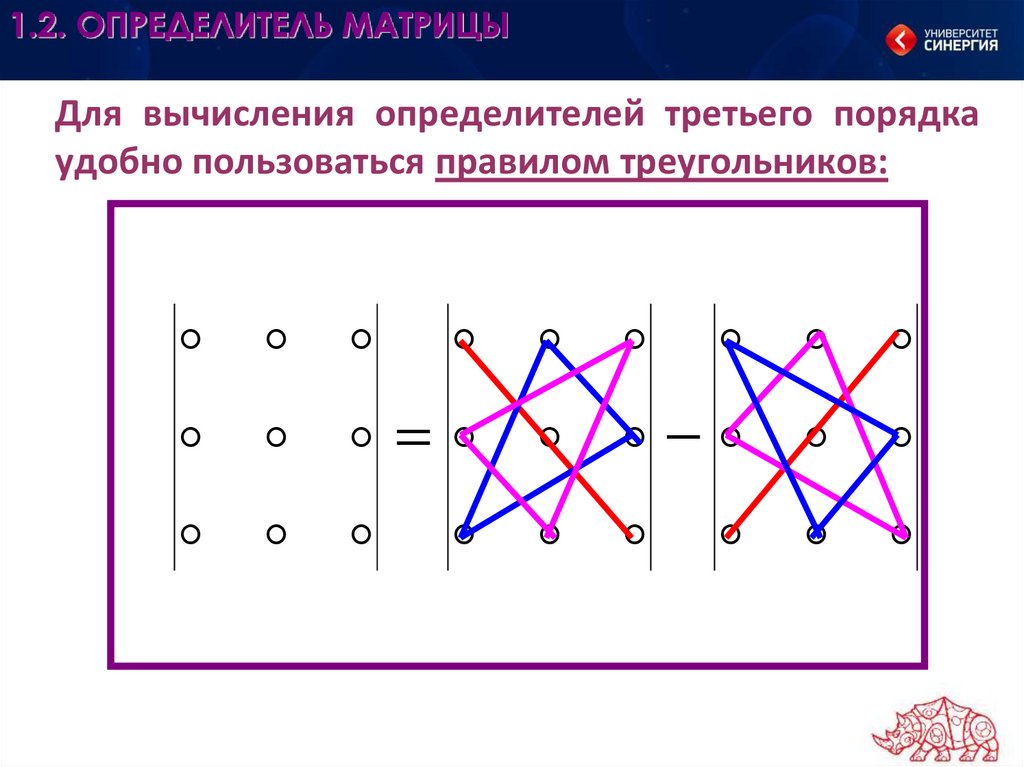 Скалярное множественное свойство
Скалярное множественное свойство Определитель матрицы кофакторов 9{2}\]
Определитель матрицы кофакторов 9{2}\] Используя свойства определителей, докажите, что 9{2}) \]
Используя свойства определителей, докажите, что 9{2}) \]

