НОУ ИНТУИТ | Лекция | Что такое граф? Определения и примеры
< Лекция 11 || Лекция 12: 12 || Лекция 13 >
Аннотация: Введение. Представления. Связность и расстояние. Остовные деревья. Клики. Изоморфизм. Планарность.
Ключевые слова: анализ, значение, Конечный граф, множества, ребро, инцидентно вершинам, граф, вершина, ориентированный, ориентированно из вершины, орграфами, неориентированном графе, петлей, ребра параллельны, простым, Матрица смежностей, соединений, матрица, орграф, кратные ребра, Матрица весов, взвешенным графом, вес ребра, стоимость, расстояние, надежность, вес, список ребер, представление, метка, Структура смежности, последователем, предшественник, вершины, соседи, список, Мультимножество, слово, поле, списки смежности, матрица инцидентности, смежны, ребра смежны, Простой путь, путь, длиной пути, кратчайшим путем, Замкнутый путь, циклом, ациклическим, подграф, индуцированный подмножеством, Неориентированный граф, связен, Ориентированный граф, (тривиально) связным, связной компонентой, компонентой, Несвязный граф, компонент, сильно связный подграф, Связный граф, точкой сочленения, разделяющей вершиной, разделимым, двусвязный, двусвязной компонентой, блок, граф связный, кратчайший путь, ациклический, деревом, лесом, дерево, остовные деревья, остовное дерево, остовном лесом, Лес, называется минимумом оставных деревьев, минимальное остовное дерево, жадный алгоритм, алгоритм, алгоритм ближайшего соседа, полный граф, кликой, подмножество, определение, Клик, поиск, изоморфными, отношение, изоморфизм, планарный граф
Введение
intuit.ru/2010/edi»>Множество самых разнообразных задач естественно формулируется в терминах графов. Так, например, могут быть сформулированы задачи составления расписаний в исследовании операций, анализа сетей в электротехнике, установления структуры молекул в органической химии, сегментации программ в программировании, анализа цепей Маркова в теории вероятностей. В задачах, возникающих в реальной жизни, соответствующие графы часто оказываются так велики, что их анализ неосуществим без ЭВМ. Таким образом, решение прикладных задач с использованием теории графов возможно в той мере, в какой возможна обработка больших графов на ЭВМ, и поэтому эффективные алгоритмы решения задач теории графов имеют большое практическое значение. В «Алгоритмы на графах» и «Калейдоскоп из комбинаторных алгоритмов» лекциях мы излагаем несколько эффективных алгоритмов на графах и используем их для демонстрации некоторой общей техники решения задач на графах с помощью ЭВМ.
Конечный граф состоит из конечного множества вершин и конечного множества ребер . Каждому ребру соответствует пара вершин: если ребро
соответствует ребру , то говорят, что инцидентно вершинам и . Граф изображается следующим образом: каждая вершина
представляется точкой и каждое ребро представляется отрезком линии, соединяющим его
концевые вершины. Граф
называется ориентированным, если
пара вершин , соответствующая каждому ребру, упорядочена. В
таком случае говорят, что ребро ориентированно
из вершины в вершину , а направление обозначается стрелкой
на ребре. Мы будем называть ориентированные графы орграфами. В неориентированном графе концевые вершины каждого ребра не упорядочены, и ребра не имеют направления. Ребро называется петлей, если оно начинается и кончается в одной и той же вершине.
Говорят, что два ребра
параллельны, если они имеют одну и ту же пару концевых вершин (и
если они имеют одинаковую ориентацию в случая ориентированного графа).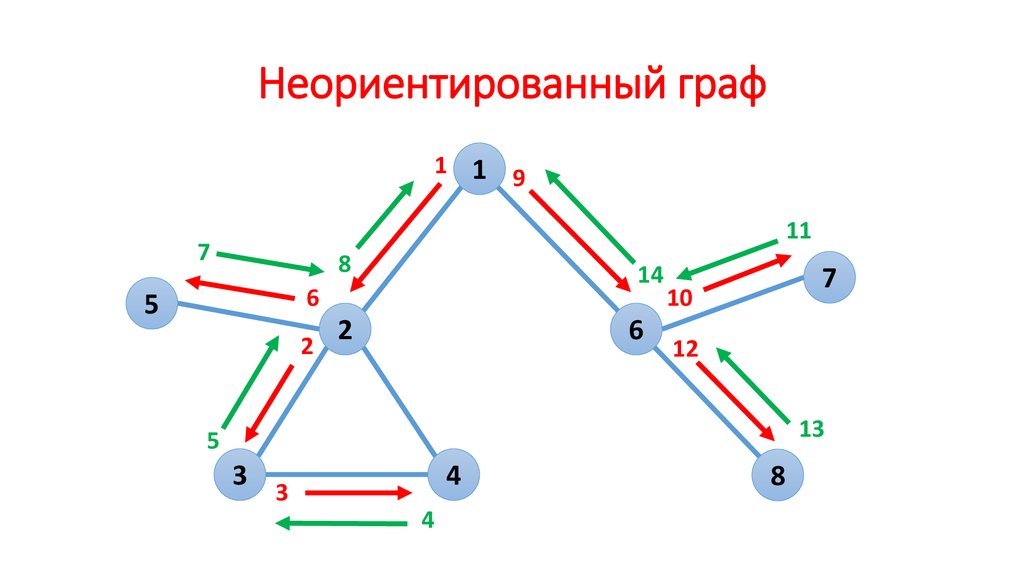
Представления
Наиболее известный способ представления графа на бумаге состоит в геометрическом изображении точек и линий. В ЭВМ граф должен быть представлен дискретным способом, причем возможно много различных представлений. Простота использования, так же как и эффективность алгоритмов на графе, зависит от подходящего выбора представления графа. Рассмотрим различные структуры данных для представления графов.
Матрица
смежностей. Одним из наиболее распространенных
машинных представлений простого графа является матрица смежностей или соединений.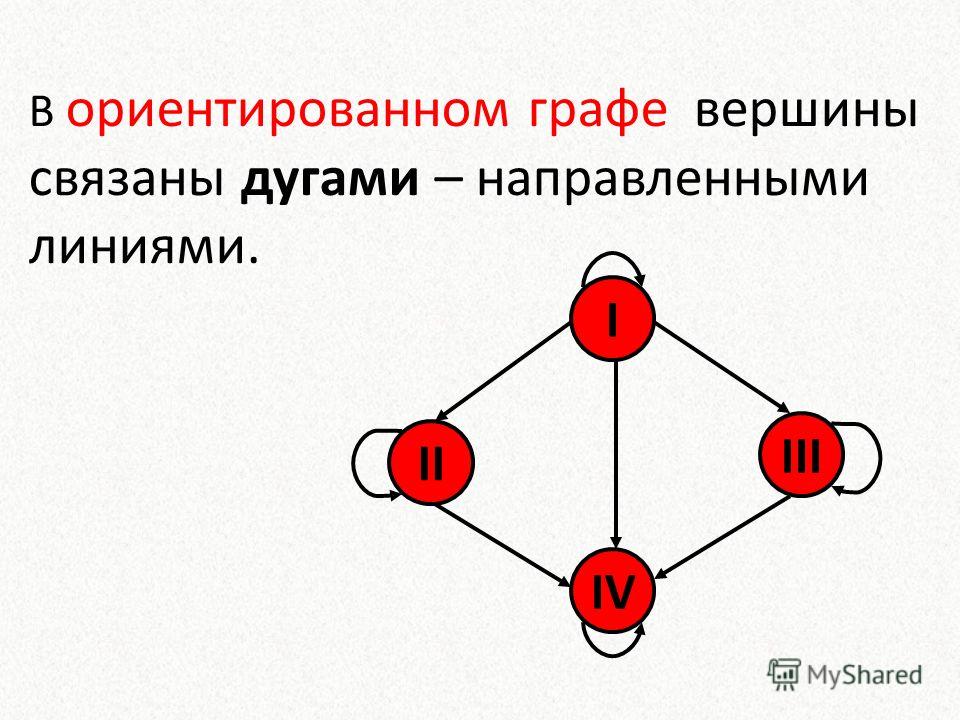
Рис. 12.1. Ориентированный граф и его матрица смежностей
Заметим, что в матрице смежностей петля может быть представлена соответствующим единичным диагональным элементом. Кратные ребра можно представить, позволив элементу матрицы быть больше 1, но это не принято, так как обычно удобно представлять каждый элемент матрицы одним двоичным разрядом.
Для задания матрицы смежностей требуется
двоичных разрядов. У неориентированного графа матрица смежностей симметрична, и
для ее представления достаточно хранить только верхний треугольник. В
результате экономится почти 50% памяти, но время вычислений может при этом немного
увеличиться, потому что каждое обращение к должно быть
заменено следующим: if then else .
Матрица весов. Граф, в котором ребру сопоставлено число , называется взвешенным графом, а число называется весом ребра . В сетях связи или транспортных сетях эти веса представляют некоторые физические величины, такие как стоимость, расстояние, эффективность, емкость или надежность соответствующего ребра. Простой взвешенный граф может быть представлен своей матрицей весов , где есть вес ребра, соединяющего вершины и . Веса несуществующих ребер обычно полагают равными или 0 в зависимости от приложений. Когда вес несуществующего ребра равен 0, матрица весов является простым обобщением матрицы смежностей.
Список ребер. Если
граф является разреженным, то возможно, что более
эффектно представлять ребра графа парами вершин. Это представление можно
реализовать двумя массивами и . Каждый
элемент в массиве есть метка вершины, а -е ребро графа выходит из
вершины и входит в вершину . Например, орграф,
изображенный на рис. 12.1, будет представляться следующим
образом:
Каждый
элемент в массиве есть метка вершины, а -е ребро графа выходит из
вершины и входит в вершину . Например, орграф,
изображенный на рис. 12.1, будет представляться следующим
образом:
Ясно, что при этом легко представимы петли и кратные ребра.
Структура смежности.
В ориентированном графе вершина называется последователем другой
вершины , если существует ребро, направленное
из в . Вершина называется тогда предшественником . В случае неориентированного графа две вершины называются соседями,
если между ними есть ребро. Граф может быть описан его структурой смежности, то
есть списком всех последователей (соседей) каждой вершины; для каждой
вершины задается — список всех последователей
(соседей) вершины . В большинстве алгоритмов на графах
относительный порядок вершин, смежных с вершиной в ,
не важен, и в таком случае удобно считать мультимножеством (или множеством,
если граф является простым) вершин, смежных
с .
Adj(v) 1: 6 2: 1, 3, 4, 6 3: 4, 5 4: 5 5: 3, 6, 7 6: 7: 1, 6
Если для хранения метки вершины используется одно машинное слово, то структура смежности ориентированного графа требует слов. Если граф неориентированный, нужно слов, так как каждое ребро встречается дважды.
Матрица инцидентности — задает граф : ,
если ребро выходит из вершины , ,
если ребро входит в вершину , и в остальных случаях.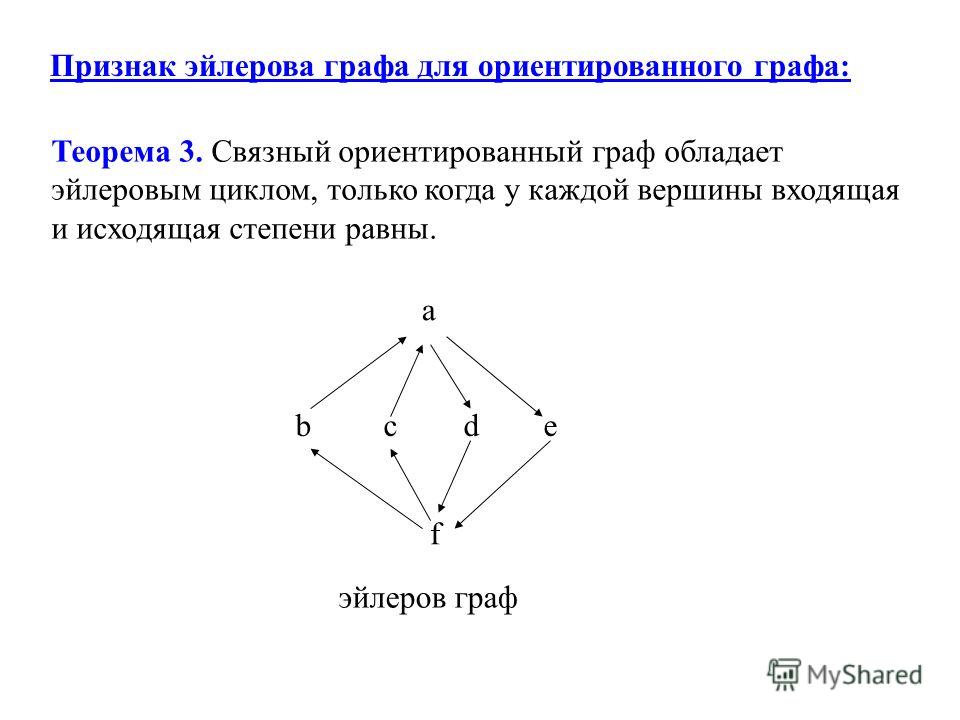
Связность и расстояние
Говорят, что вершины и в графе смежны, если существует ребро, соединяющее их. Говорят, что два ребра смежны, если они имеют общую вершину. Простой путь, или для краткости, просто путь, записываемый иногда как , — это последовательность смежных ребер , в которой все вершины различны, исключая, возможно, случай . В орграфе этот путь называется ориентированным из в , в неориентированном графе он называется путем между и . Число ребер в пути называется длиной пути. Путь наименьшей длины называется кратчайшим путем. Замкнутый путь называется циклом. Граф, который не содержит циклов, называется ациклическим.
Подграф графа есть граф, вершины и ребра которого лежат в . Подграф , индуцированный подмножеством множества вершин графа , — это подграф, который получается в результате удаления всех вершин из и всех ребер, инцидентных им.
intuit.ru/2010/edi»>Неориентированный граф связен, если существует хотя бы один путь в между каждой парой вершин и . Ориентированный граф связен, если неориентированный граф, получающийся из путем удаления ориентации ребер, является связным. Граф, состоящий из единственной изолированной вершины, является (тривиально) связным. Максимальный связный подграф графа называется связной компонентой или просто компонентой . Несвязный граф состоит из двух или более компонент. Максимальный сильно связный подграф называется сильно связной компонентой.Иногда недостаточно знать, что граф связен; нас может интересовать,
насколько «сильно связен» связный граф. Например, связный граф может
содержать вершину, удаление которой вместе с инцидентными ей ребрами разъединяет оставшиеся
вершины. Такая вершина называется точкой сочленения или разделяющей вершиной. Граф, содержащий точку сочленения, называется разделимым.
Граф без точек сочленения называется двусвязным или неразделимым.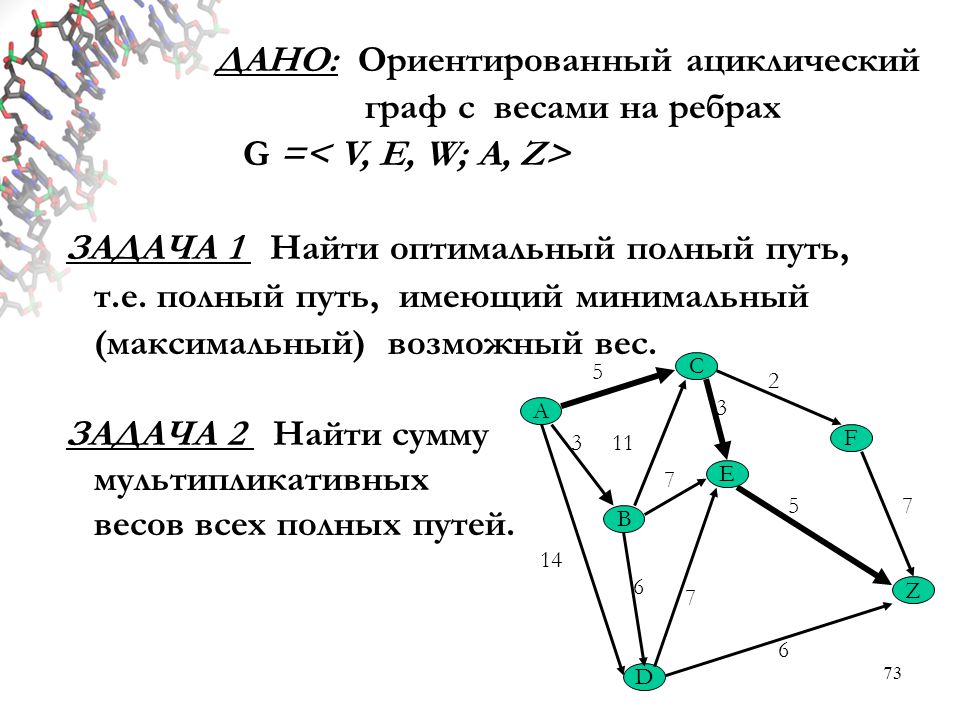 Максимальный двусвязный подграф графа называется двусвязной компонентой или блоком.
Максимальный двусвязный подграф графа называется двусвязной компонентой или блоком.
Большинство основных вопросов о графах касается связности, путей и расстояний. Нас может интересовать вопрос, является ли граф связным; если он связен, то может оказаться нужным найти кратчайшее расстояние между выделенной парой вершин или определить кратчайший путь между ними. Если граф несвязен, то может потребоваться найти все его компоненты. В нашем курсе строятся алгоритмы для решения этих и других подобных вопросов.
Дальше >>
< Лекция 11 || Лекция 12: 12 || Лекция 13 >
Алгоритмы на графах — Часть 0: Базовые понятия / Хабр
Как оказалось тема алгоритмов интересна Хабра-сообществу. Поэтому я как и обещал, начну серию обзоров «классических» алгоритмов на графах.
Так как публика на Хабре разная, а тема интересна многим, я должен начать с нулевой части. В этой части я расскажу что такое граф, как он представлен в компьютере и зачем он используется.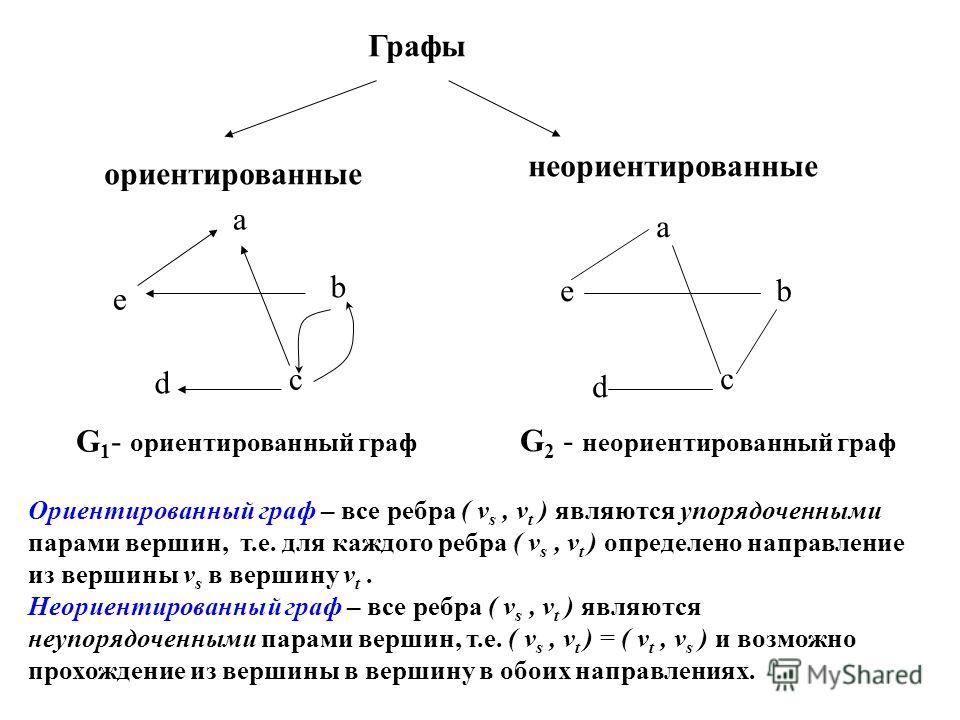 Заранее прошу прощения у тех кто это все уже прекрасно знает, но для того чтобы объяснять алгоритмы на графах, нужно сначала объяснить что такое граф. Без этого никак.
Заранее прошу прощения у тех кто это все уже прекрасно знает, но для того чтобы объяснять алгоритмы на графах, нужно сначала объяснить что такое граф. Без этого никак.
В математике, Граф — это абстрактное представление множества объектов и связей между ними. Графом называют пару (V, E) где V это множество вершин, а E множество пар, каждая из которых представляет собой связь (эти пары называют рёбрами).
Граф может быть ориентированным или неориентированным. В ориентированном графе, связи являются направленными (то есть пары в E являются упорядоченными, например пары (a, b) и (b, a) это две разные связи). В свою очередь в неориентированном графе, связи ненаправленные, и поэтому если существует связь (a, b) то значит что существует связь (b, a).
Пример:
Неориентированный граф: Соседство (в жизни). Если (1) сосед (3), то (3) сосед (1).См рис. 1.а
Ориентированный граф: Ссылки. Сайт (1) может ссылаться на сайт (3), но совсем не обязательно (хотя возможно) что сайт (3) ссылается сайт (1). См рис. 1.б
Степень вершины может быть входящая и исходящая (для неориентированных графов входящая степень равна исходящей).
Входящая степень вершины v это количество ребер вида (i, v), то есть количество ребер которые «входят» в v.
Исходящая степень вершины v это количество ребер вида (v , i), то есть количество ребер которые «выходят» из v.
Это не совсем формальное определение (более формально определение через инцидентность), но оно вполне отражает суть
Путь в графе это конечная последовательность вершин, в которой каждые две вершины идущие подряд соединены ребром. Путь может быть ориентированным или неориентированным в зависимости от графа. На рис 1.а, путем является например последовательность [(1), (4), (5)] на рис 1. б, [(1), (3), (4), (5)].
б, [(1), (3), (4), (5)].
У графов есть ещё много разных свойств (например они могут быть связными, двудольными, полными), но я не буду описывать все эти свойства сейчас, а в следующих частях когда эти понятия понадобятся нам.
Существует два способа представления графа, в виде списков смежности и в виде матрицы смежности. Оба способа подходят для представления ориентированных и неориентированных графов.
Матрица смежности
Этот способ является удобным для представления плотных графов, в которых количество рёбер (|E|) примерно равно количеству вершин в квадрате (|V|2).
В данном представлении мы заполняем матрицу размером |V| x |V| следущим образом:
A[i][j] = 1 (Если существует ребро из i в j)
A[i][j] = 0 (Иначе)
Данный способ подходит для ориентированных и неориентированных графов. Для неориентированных графов матрица A является симметричной (то есть A[i][j] == A[j][i], т.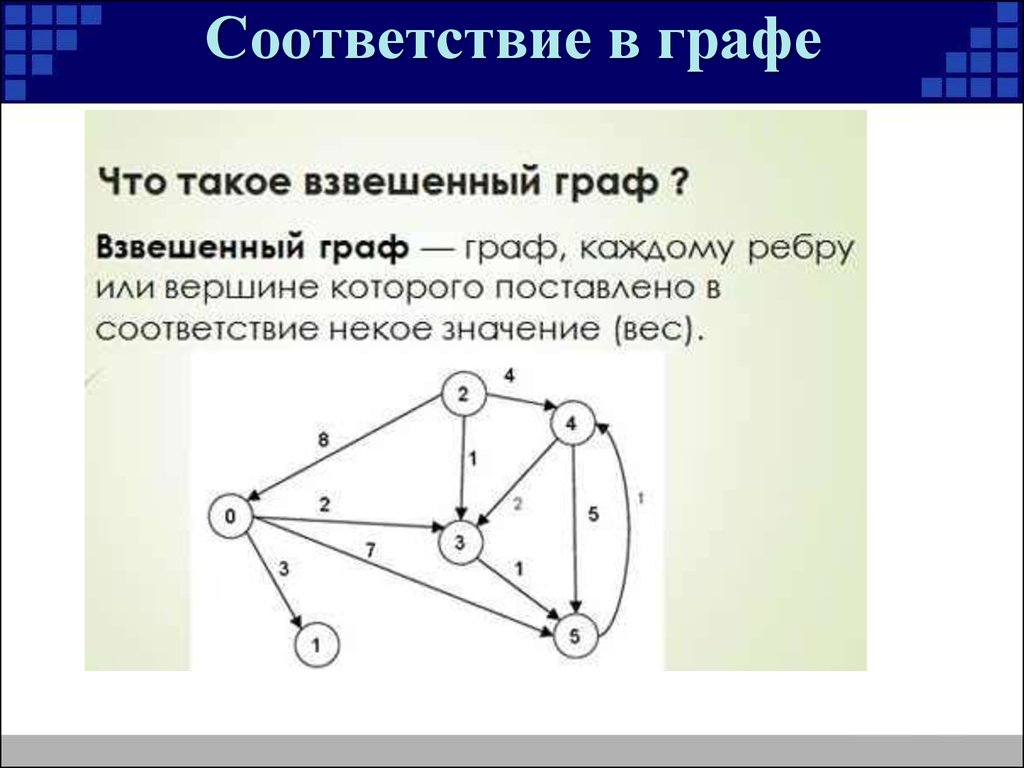 к. если существует ребро между i и j, то оно является и ребром из i в j, и ребром из j в i). Благодаря этому свойству можно сократить почти в два раза использование памяти, храня элементы только в верхней части матрицы, над главной диагональю)
к. если существует ребро между i и j, то оно является и ребром из i в j, и ребром из j в i). Благодаря этому свойству можно сократить почти в два раза использование памяти, храня элементы только в верхней части матрицы, над главной диагональю)
Понятно что с помощью данного способа представления, можно быстро проверить есть ли ребро между вершинами v и u, просто посмотрев в ячейку A[v][u].
С другой стороны этот способ очень громоздкий, так как требует O (|V|2) памяти для хранения матрицы.
На рис. 2 приведены представления графов из рис. 1 с помощью матриц смежности.
Списки смежности
Данный способ представления больше подходит для разреженных графов, то есть графов у которых количество рёбер гораздо меньше чем количество вершин в квадрате (|E| << |V|2).
В данном представлении используется массив Adj содержащий |V| списков. В каждом списке Adj[v] содержатся все вершины u, так что между v и u есть ребро. Память требуемая для представления равна O (|E| + |V|) что является лучшим показателем чем матрица смежности для разреженных графов.
Память требуемая для представления равна O (|E| + |V|) что является лучшим показателем чем матрица смежности для разреженных графов.
Главный недостаток этого способа представления в том, что нет быстрого способа проверить существует ли ребро (u, v).
На рис. 3 приведены представления графов из рис. 1 с помощью списков смежности.
Те кто дочитал до этого места, наверное задали себе вопрос, а где же собственно я смогу применить графы. Как я и обещал я буду стараться приводить примеры. Самый первый пример который приходит в голову это социальная сеть. Вершинами графа являются люди, а ребрами отношения (дружба). Граф может быть неориентированным, то есть я могу дружить только с теми кто дружит со мной. Либо ориентированным (как например в ЖЖ), где можно добавить человека в друзья, без того чтобы он добавлял вас. Если же он да добавит вас вы будете «взаимными друзьями». То есть будет существовать два ребра: (Он, Вы) и (Вы, Он)
Ещё одно из применений графа, которое я уже упоминал это ссылки с сайта на сайт.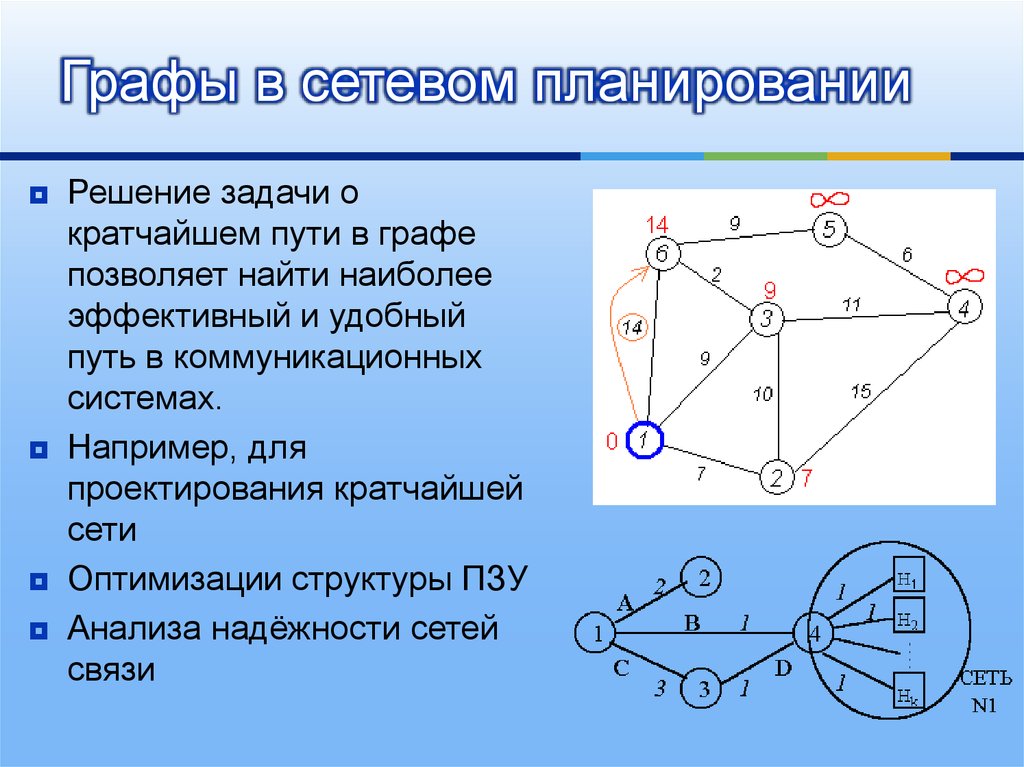 Представим Вы хотите сделать поисковую систему и хотите учесть на какие сайты есть больше ссылок (например сайт A), при этом учитывать сколько сайтов ссылается на сайт B, который ссылается на сайт A. У вас будет матрица смежности этих ссылок. Вы захотите ввести какую то систему подсчёта рейтинга, которая делает какие то подсчёты на этой матрице, ну, а дальше… это Google (точнее PageRank) =)
Представим Вы хотите сделать поисковую систему и хотите учесть на какие сайты есть больше ссылок (например сайт A), при этом учитывать сколько сайтов ссылается на сайт B, который ссылается на сайт A. У вас будет матрица смежности этих ссылок. Вы захотите ввести какую то систему подсчёта рейтинга, которая делает какие то подсчёты на этой матрице, ну, а дальше… это Google (точнее PageRank) =)
Это небольшая часть теории которая понадобится нам чтобы для следующих частей. Надеюсь вам было понятно, а главное понравилось и заинтересовало читать дальнейшие части! Оставляйте свои отзывы и пожелания в комментариях.
BFS — Алгоритм поиска в ширину
Кормен, Лайзерсон, Риверст, Штайн — Алгоритмы. Построение и анализ. Издательство Вильямс, 2007.
Словарь терминов теории графов
Граф — статья в английской Википедии
Статья это кросс-пост из моего блога — «Programing as is — записки программиста»
______________________
Текст подготовлен в Хабра Редакторе
Направленный граф в структуре данных
Обзор
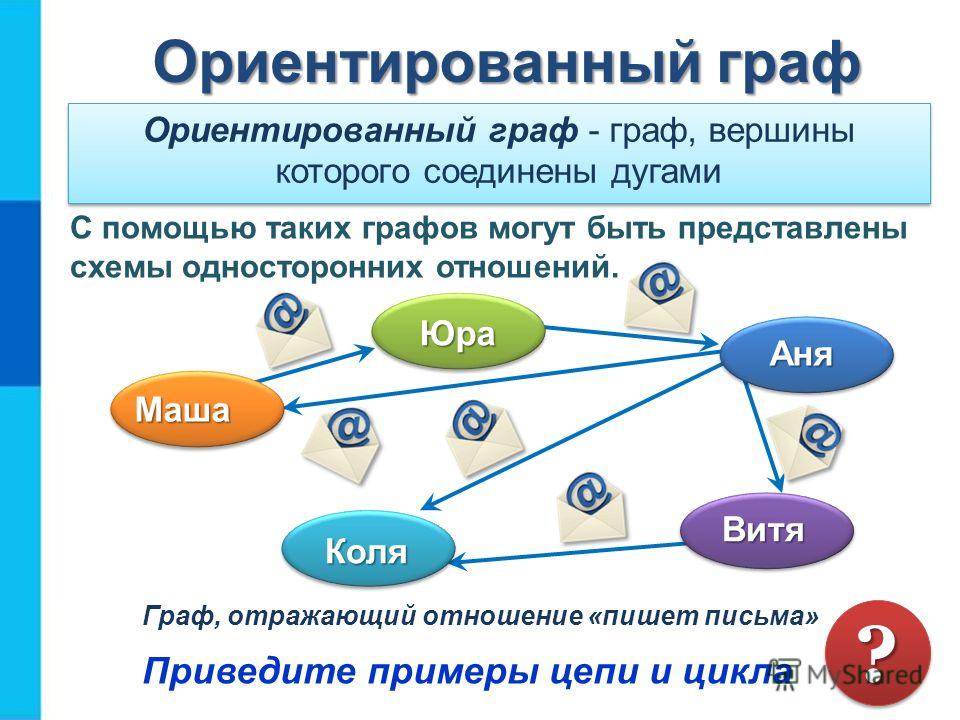
Граф — это нелинейная структура данных. Он состоит из нескольких узлов, также называемых вершинами. Вершины графа соединены ребрами. Граф, в котором с каждым ребром связано определенное направление, называется ориентированным графом. Направленные графы из теории графов широко используются для решения математических задач, социальных сетей, приложений, цифровой навигации, аэрокосмической промышленности и т. д.
Он состоит из нескольких узлов, также называемых вершинами. Вершины графа соединены ребрами. Граф, в котором с каждым ребром связано определенное направление, называется ориентированным графом. Направленные графы из теории графов широко используются для решения математических задач, социальных сетей, приложений, цифровой навигации, аэрокосмической промышленности и т. д.
Scope
В этой статье мы обсудим:
- Что такое структура данных ориентированного графа.
- Общие термины в графиках.
- Реализация ориентированного графа.
- Как пройти по ориентированному графу.
- Пример структуры данных ориентированного графа.
Что такое ориентированный граф в структуре данных?
Ориентированный граф — это структура данных, которая хранит данные в вершинах или узлах. Эти вершины могут быть соединены и направлены ребрами. Одна вершина направлена к другой вершине через ребро между ними.
Упорядоченная пара, P = (V, A), где «V» — набор узлов, а «A» — набор ребер.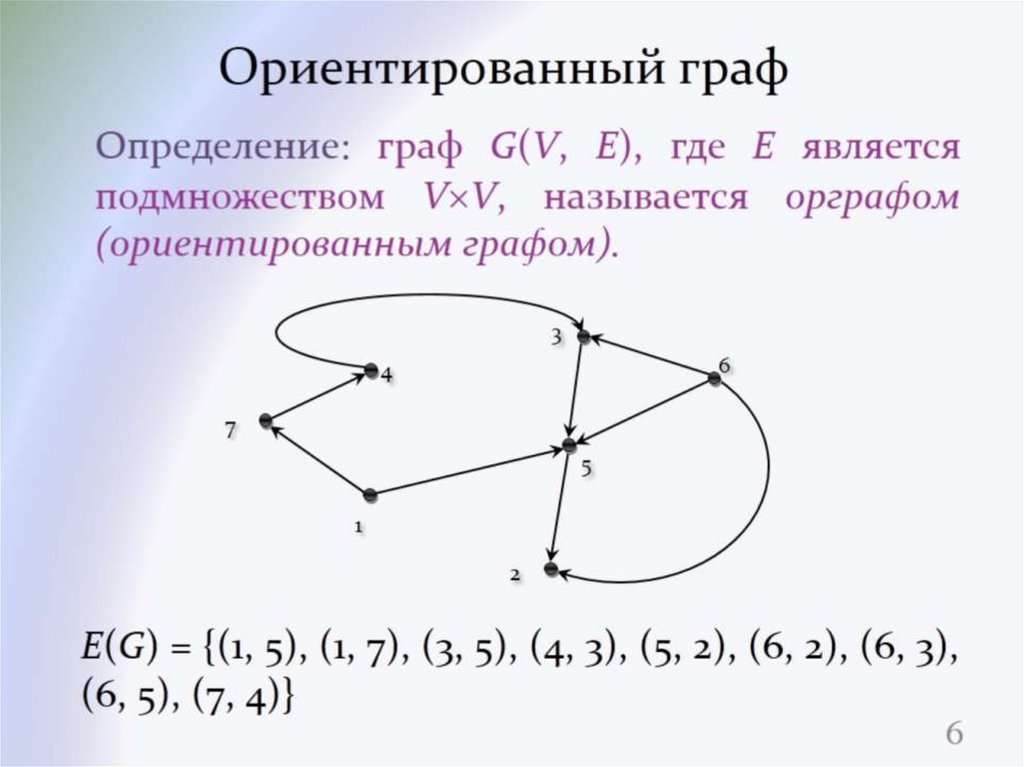 Мы используем эти элементы, то есть узлы и ребра, для создания структуры данных ориентированного графа. Каждое ребро в ориентированном графе имеет одно конкретное направление. Направление ребра между узлами «n1» и «n2» будет либо от n1 к n2, либо наоборот.
Мы используем эти элементы, то есть узлы и ребра, для создания структуры данных ориентированного графа. Каждое ребро в ориентированном графе имеет одно конкретное направление. Направление ребра между узлами «n1» и «n2» будет либо от n1 к n2, либо наоборот.
Терминология графов
Путь
Путь от узла m к узлу n представляет собой последовательность ребер, которые можно пройти, чтобы начать с m и достичь n.
Простой путь
Если все вершины пути различны, то путь называется простым путем.
Замкнутый путь
Если первая и последняя вершины пути совпадают, то говорят, что путь закрыт.
Тропа
Тропа — это открытый путь, в котором нет повторяющихся ребер. Вершины в следе могут повторяться, но все ребра в следе различны.
Цикл
Непустой путь называется циклом, если он начинается и заканчивается в одном и том же узле.
Связный граф
Граф называется связным, если существует минимум один путь между любыми двумя различными вершинами.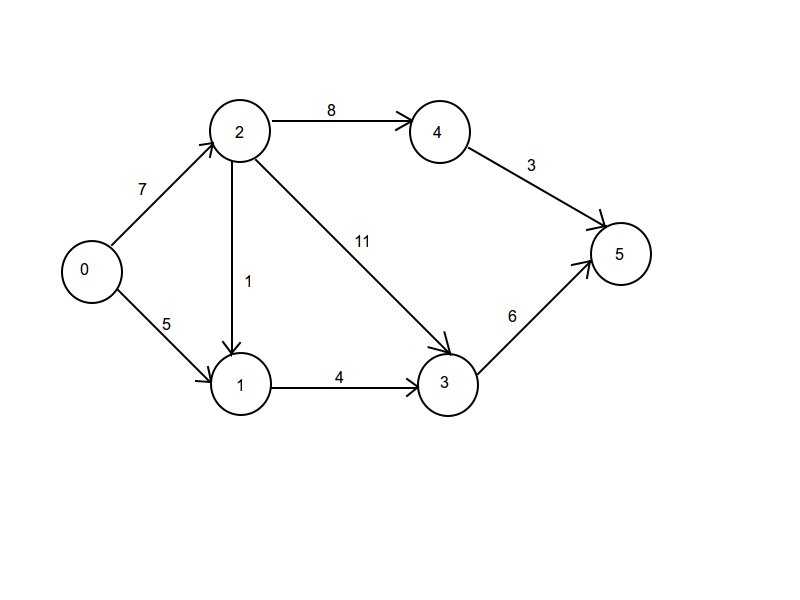
Взвешенный граф
Это граф, в котором каждому ребру присвоено значение веса. Вес ребра может обозначать его абсолютную важность, относительный приоритет, длину и т. д.
Смежные узлы
В графе два узла, соединенных ребром, называются соседними узлами или соседями друг к другу.
Степень узла
Количество ребер, соединенных с узлом, называется степенью узла. Если узел изолирован, то его степень равна 0.
Как реализован граф
Существует 2 способа реализации графов на компьютере:
1. Матричное представление смежности
2. Представление в виде связанного списка
Представление матрицы смежности
В этом представлении матрица используется для хранения и хранения данных графа.
Матрица смежности для невзвешенного ориентированного графа
Размер используемой матрицы n\*n. Здесь n — количество узлов.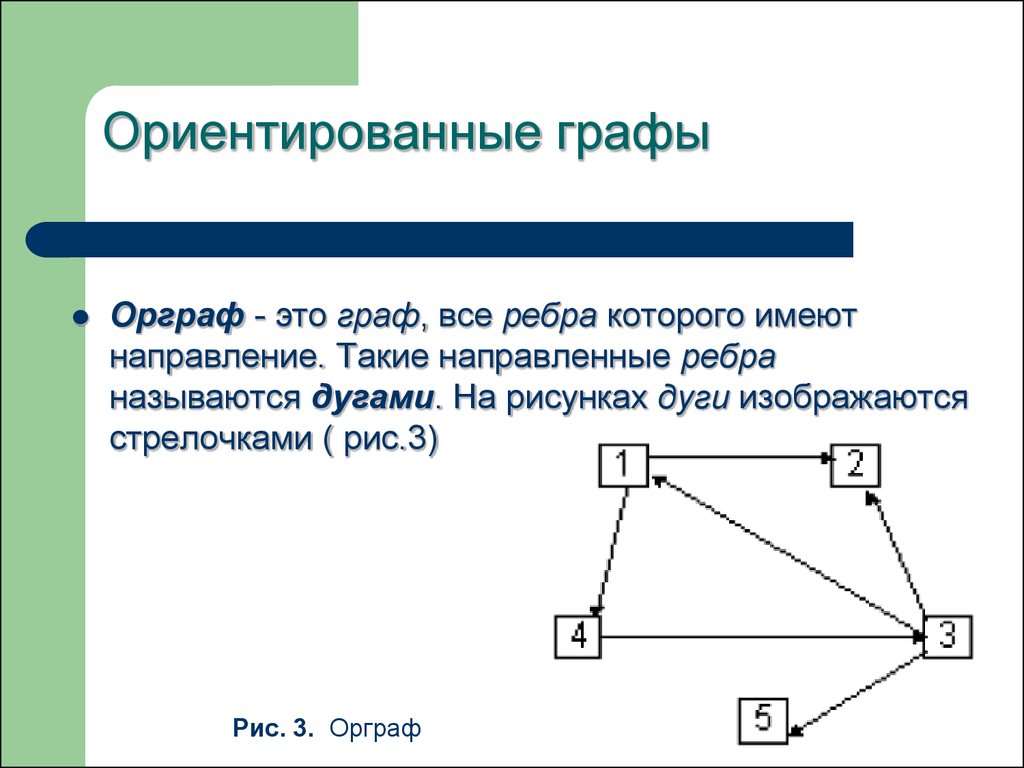 Значение в любой позиции (i,j) в матрице определяет, существует ли ребро от i-го узла до j-го узла. Ниже приведена схема ориентированного графа и его матрицы смежности.
Значение в любой позиции (i,j) в матрице определяет, существует ли ребро от i-го узла до j-го узла. Ниже приведена схема ориентированного графа и его матрицы смежности.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | 0 | 1 | 0 | 1 | 0 |
| B | 0 | 0 | 1 | 0 | 0 |
| C | 0 | 0 | 0 | 1 | 0 |
| D | 0 | 0 | 0 | 0 | 1 |
| E | 1 | 0 | 0 | 0 | 0 |
Матрица смежности для взвешенного направленного графа
Матрица аналогична матрице невзвешенного графа.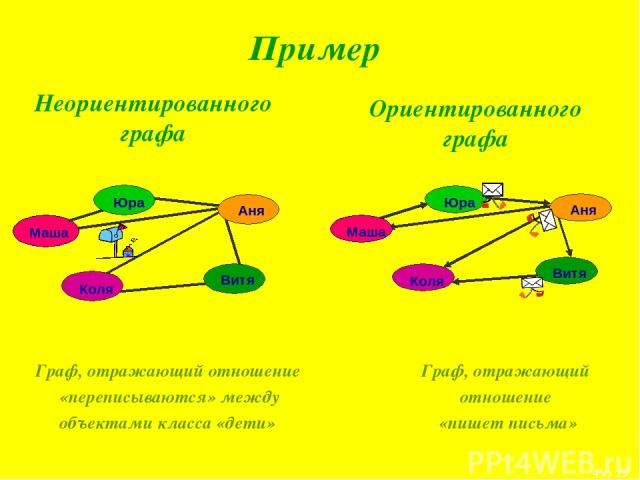 Чтобы приспособить представление веса ребер, было разработано много методов.
Чтобы приспособить представление веса ребер, было разработано много методов.
Наиболее распространенный метод — зафиксировать одно значение, указывающее на отсутствие ребра от вершины i до узла j. Одно подходящее значение равно 0. Другие значения (1,2,3,…, -1,-2,-3…) могут представлять наличие ребра, а также его вес.
Представление списка смежности
В этом представлении связанный список реализован для хранения и хранения данных графа в памяти компьютера.
Список смежности для невзвешенного ориентированного графа На диаграмме впереди показан направленный невзвешенный граф.
Следующая диаграмма представляет собой представление списка смежности ориентированного невзвешенного графа из приведенной выше диаграммы.
На рисунке выше мы можем заметить, что для каждой вершины графа есть узел связанного списка. Соседи n1, n2, n3… любого ребра i представлены связным списком, смонтированным в i. Этот список содержит всех соседей n1, n2, n3. .. элемента i.
.. элемента i.
Список смежности для взвешенного графа
Представление списка смежности направленного взвешенного графа аналогично представлению невзвешенного ориентированного графа. Предположим, что есть вершина i, в которой смонтирован список ее соседей v1, v2, v3… Узел связанного списка j-го соседа вершины i, vj будет содержать следующие 3 элемента:
- Значение соседней вершины в [дж].
- Вес ребра от текущей вершины графа i до соседней вершины j.
- Указатель, указывающий на узел связанного списка следующей соседней вершины графа (v[j+1]). Если дополнительных соседних вершин графа не существует, следующий указатель указывает на ноль.
На следующей диаграмме показан ориентированный взвешенный граф.
На следующей диаграмме показано представление списка смежности показанного выше графа.
Как пройти по ориентированному графу?
Существует два способа обхода ориентированного графа:
- BFS (поиск в ширину)
- DFS (поиск в глубину)
BFS
BFS (поиск в ширину) — это алгоритм обхода, предназначенный для обхода графа, начиная с корневого узла графа и исследуя все остальные соседние узлы. Затем процесс повторяется для всех соседей.
Затем процесс повторяется для всех соседей.
На графике любой заданный узел может быть выбран в качестве корневого узла при реализации BFS. Состояние любой вершины во время обхода либо посещено, либо непосещено. Узел помечается как посещенный после его изучения. Узел, помеченный как посещенный, не проходит дальше. Это помогает в работе с петлями и циклами.
Алгоритм
Шаги алгоритма для BFS следующие:
- Создайте очередь FIFO (First In First Out) и нажмите корень. в этом.
- Отметить посещенный корень.
- Повторите следующие шаги, пока очередь не пуста:
- Извлеките элемент из очереди и обработайте его.
- Пометить всех непосещенных соседей как посещенных и поместить их в очередь.
- КОНЕЦ
Сложность алгоритма BFS
Временная сложность BFS равна O(n), где n — количество узлов. Потому что мы исследуем каждый узел в графе ровно один раз.
Пространственная сложность BFS также равна O(n), так как в каждый момент времени максимальное количество узлов, присутствующих в очереди, может достигать n — общего количества узлов в графе.
DFS
DFS (поиск в глубину) — это рекурсивный подход, реализованный для обхода графа. Он реализован для посещения всех вершин графа или дерева с начальным узлом и идет все глубже и глубже, пока не будет найден целевой узел или узел без дочерних элементов (называемый листовым узлом). Структура данных стека может использоваться для реализации алгоритма DFS из-за его рекурсивного характера.
Алгоритм
Ниже приведены шаги, необходимые для обхода ориентированного графа методом поиска в глубину:
- Создайте стек LIFO (последним пришел — первым вышел) и поместите в него корень.
- Отметить посещенный корень.
- Повторите следующие шаги, пока стек не пуст:
- Извлечение элемента из стека.

- Пометить всех непосещенных соседей как посещенные и поместить их в стек.
- Извлечение элемента из стека.
- КОНЕЦ.
Сложность алгоритма поиска в глубину
Временная сложность DFS равна O(n), где n — количество узлов. Потому что мы исследуем каждый узел в графе ровно один раз.
Пространственная сложность DFS также равна O(n), так как одновременно максимальное количество узлов, присутствующих в стеке, может достигать n — общего количества узлов в графе.
Пример ориентированного графа в структуре данных
Простой пример ориентированного графа можно рассматривать как матрицу A, содержащую ребра между 5 различными вершинами (A, B, C, D и E).
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | 0 | 0 | 10 | 0 | 15 |
| B | 0 | 0 | 0 | 0 | 0 |
| C | 0 | 0 | 0 | 0 | 0 |
| D | 0 | 5 | 20 | 0 | 0 |
| E | 0 | 0 | 0 | 15 | 0 |
Now from the above matrix , можно построить граф с ребрами, направленными от строки к столбцу.
Если для конкретной ячейки есть 0, то это означает, что нет границы между строкой этой ячейки и столбцом ячейки. Кроме того, кроме 0, если есть целое число, это означает, что между строкой и столбцом этой ячейки есть ребро, а число в этой ячейке является весом ребра.
Заключение
- Ориентированный граф — это структура данных, которая хранит данные в вершинах или узлах, и эти узлы или вершины соединены и также направлены ребрами (одна вершина направлена к другой вершине через ребро), которые могут иметь некоторый вес.
- Направленный граф также называют орграфом или ориентированной сетью.
- Количество ребер, с которыми соединен узел, называется его степенью. Если узел изолирован, то его степень равна 0, .
- В матричном представлении матрица смежности используется для хранения и хранения графа.
- В списочном представлении реализован смежный связанный список для хранения и хранения данных графиков в памяти компьютера.

- В список смежности, благодаря реализации связанного списка, добавление вершины становится очень простым.
- Существует два способа перемещения по графу: BFS и DFS.
- Временная сложность BFS зависит от структуры данных, используемой для реализации графа. Сложность BFS равна O(V+E).
- DFS (поиск в глубину) — это рекурсивный подход, реализованный для обхода графа.
- Структура данных стека используется для реализации алгоритма DFS из-за его рекурсивного характера.
- Временная сложность алгоритма DFS также равна O(V+E), где количество ребер равно E, а количество вершин равно V.
5.11 Направленные графы
Ориентированный граф ,
также называется диграфом ,
граф, в котором ребра имеют направление. Этот
обычно обозначается стрелкой по краю; более формально, если $v$
и $w$ — вершины, ребро — неупорядоченная пара $\{v,w\}$, а
направленное ребро, называемое 9+_i$. Прогулка по в орграфе — это
последовательность $v_1,e_1,v_2,e_2,\ldots,v_{k-1},e_{k-1},v_k$ такая, что
$e_k=(v_i,v_{i+1})$; если $v_1=v_k$, это
закрытая прогулка или схема. -}f(e),
$$
для всех $v$, кроме $s$ и $t$.
$\квадрат$
-}f(e),
$$
для всех $v$, кроме $s$ и $t$.
$\квадрат$
Мы хотим присвоить значение потоку, равному чистому потоку из источник. Поскольку транспортируемое вещество не может «собираться» или «начинаться» в любой вершине, отличной от $s$ и $t$, кажется разумно, что это значение также должно быть чистым потоком в цель.
Прежде чем доказывать это, введем некоторые новые обозначения. Предположим, что $U$ представляет собой набор вершин в сети с $s\in U$ и $t\notin U$. Позволять $\overrightharpoon U$ — множество дуг $(v,w)$ с $v\in U$, $w\notin U$, а $\overleftharpoon U$ — множество дуг $(v,w)$ с $v\notin U$, $w\in долларов США. 9-}f(e)$. A максимальный расход в сети есть любой поток $f$, значение которого является максимальным среди всех потоков. $\квадрат$
Далее мы пытаемся формализовать понятие «узкого места». целью показать, что максимальный поток равен количеству, которое может пройти через самое узкое место.
Определение 5.11.5 Разрез в сети — это
множество $C$ дуг со свойством, что каждый путь из $s$ в $t$
использует дугу в $C$, то есть если дуги в $C$ удалены из
сети нет пути от $s$ до $t$.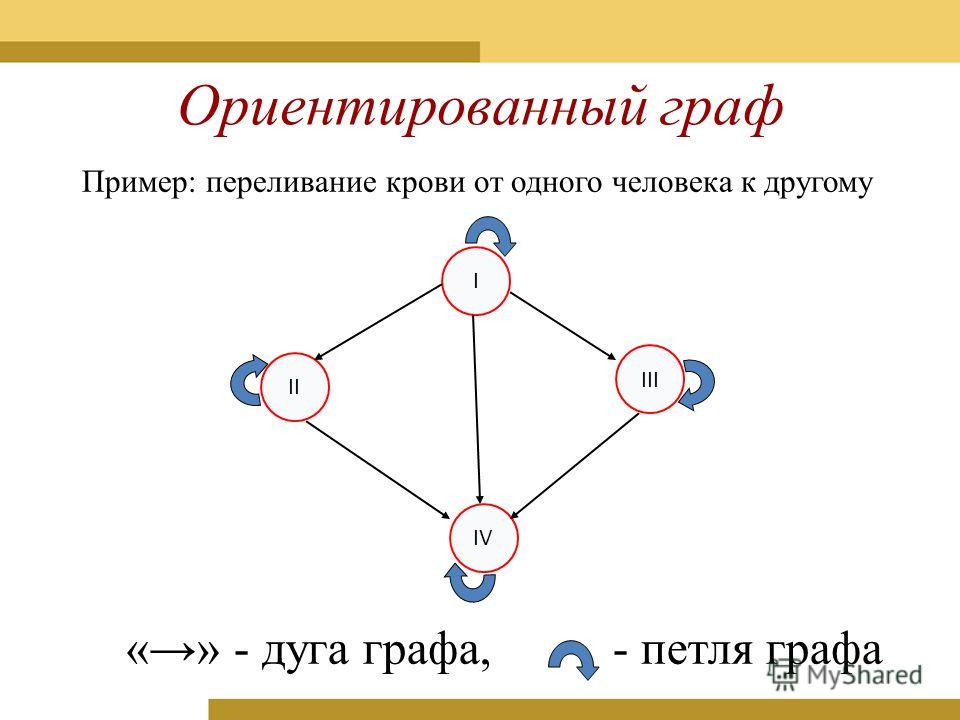 Емкость разреза, обозначаемая $c(C)$, равна
$$\sum_{e\in C} c(e).$$
Минимальный разрез – это разрез с минимальной производительностью. Разрез $C$ минимален, если нет
cut правильно содержится в $C$.
$\квадрат$
Емкость разреза, обозначаемая $c(C)$, равна
$$\sum_{e\in C} c(e).$$
Минимальный разрез – это разрез с минимальной производительностью. Разрез $C$ минимален, если нет
cut правильно содержится в $C$.
$\квадрат$
Обратите внимание, что минимальный разрез — это минимальный разрез. Ясно, что если $U$ — множество вершин, содержащих $s$, но не содержащих $t$, то $\overrightharpoon U$ — разрез.
Лемма 5.11.6. Предположим, что $C$ — минимальное сечение. Тогда есть множество $U$ содержащий $s$, но не $t$ такой, что $C=\overrightharpoon U$.
Доказательство. Пусть $U$ — множество вершин $v$, для которых существует путь из $s$ в $v$, не используя дуги в $C$.
Предположим, что $e=(v,w)\in C$. Поскольку $C$ минимально, существует путь $P$
из $s$ в $t$, используя $e$, но не используя другую дугу в $C$. Таким образом, существует
путь из $s$ в $v$, не используя ни одной дуги из $C$, поэтому $v\in U$. если есть
путь из $s$ в $w$ без использования дуги $C$, то по этому пути следует
часть $P$, начинающаяся с $w$, — это путь от $s$ до $t$
без дуги в $C$.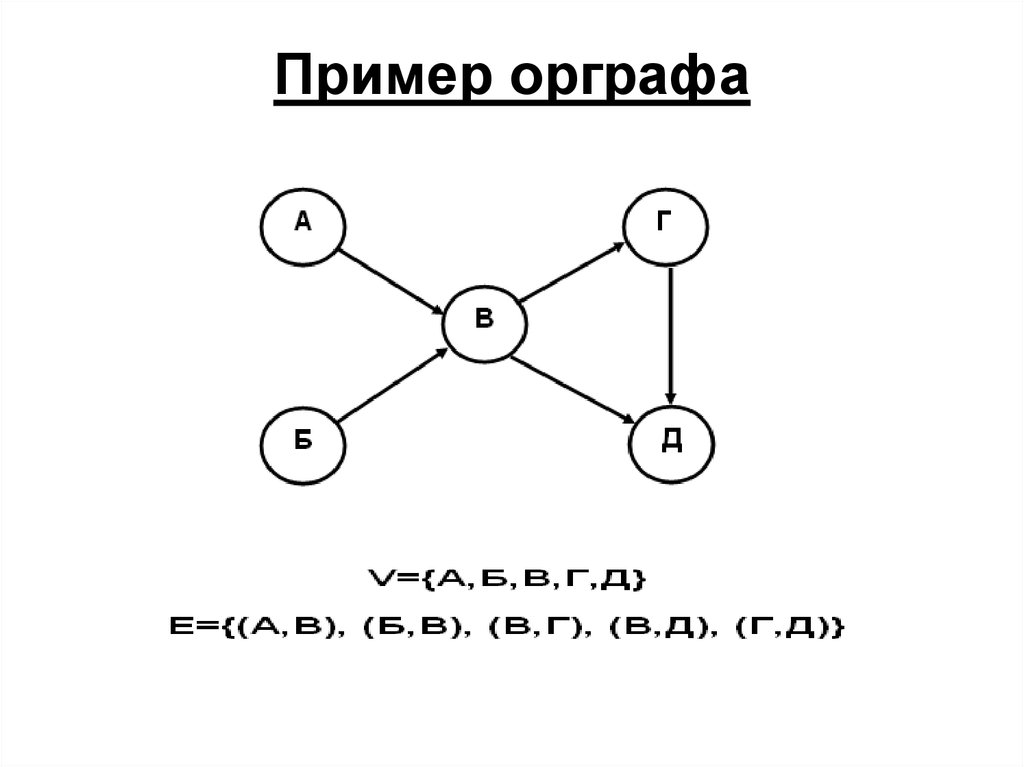 Это означает, что существует путь из $s$ в $t$
не используя дуги в $C$, противоречие. Таким образом, $w\notin U$ и, следовательно,
$e\in\overrightharpoon U$. Следовательно, $C\subseteq \overrightharpoon U$.
Это означает, что существует путь из $s$ в $t$
не используя дуги в $C$, противоречие. Таким образом, $w\notin U$ и, следовательно,
$e\in\overrightharpoon U$. Следовательно, $C\subseteq \overrightharpoon U$.
Предположим, что $e=(v,w)\in \overrightharpoon U$. Тогда $v\in U$ и $w\notin U$, поэтому каждый путь из $s$ в $w$ использует дугу в $C$. С $v\in U$ существует путь из $s$ в $v$, не использующий ни одной дуги из $C$, и этот путь, за которым следует $e$, является путем от $s$ до $w$. Следовательно, дуга $e$ должен находиться в $C$, поэтому $\overrightharpoon U\subseteq C$.
Мы показали, что $C=\overrightharpoon U$. $\qed$
Теперь мы можем доказать версию важная теорема о максимальном потоке и минимальном разрезе.
Теорема 5.11.7. Предположим, что в сети все пропускные способности дуг являются целыми числами. Тогда
значение максимального расхода равно пропускной способности минимального
резать. Более того, существует максимальный поток $f$, для которого все $f(e)$ являются
целые числа.
Доказательство. Сначала покажем, что для любого потока $f$ и разреза $C$ $\val(f)\le c(C)$. Достаточно показать это для минимального разреза $C$, а по лемме 5.11.6 мы знаем, что $C=\overrightharpoon U$ для некоторого $U$. Используя доказательство по теореме 5.11.3 имеем: $$ \val(f) = \sum_{e\in\overrightharpoon U} f(e)-\sum_{e\in\overleftharpoon U}f(e) \le \sum_{e\in\overrightharpoon U} f(e) \le \sum_{e\in\overrightharpoon U} c(e) = c (\ overrightharpoon U). $$ Теперь, если мы найдем поток $f$ и разрежем $C$ с $\val(f)=c(C)$, отсюда следует, что $f$ — максимальный поток, а $C$ — минимальный разрез. Мы представляем алгоритм, который создаст такие $f$ и $C$.
Для потока $f$, который изначально может быть нулевым потоком, $f(e)=0$ для все дуги $e$, выполните следующие действия:
0. Пусть $U=\{s\}$.
Повторяйте следующие два шага, пока в $U$ не будут добавлены новые вершины.
1. Если существует дуга $e=(v,w)$ с $v\in U$ и $w\notin U$, и $f(e)
2. Если существует дуга $e=(v,w)$ с $v\notin U$ и $w\in U$,
и $f(e)>0$, добавьте $v$ к $U$.
Если существует дуга $e=(v,w)$ с $v\notin U$ и $w\in U$,
и $f(e)>0$, добавьте $v$ к $U$.
Когда это завершается, либо $t\in U$, либо $t\notin U$. Если $t\in U$ существует последовательность различных вершины $s=v_1,v_2,v_3,\ldots,v_k=t$ такое, что для каждого $i$ $1\le i0$. Обновите поток, добавив $1$ к $f(e)$ для каждого из первых, и вычитая $1$ из $f(e)$ для каждого из последних. Этот новый поток $f’$ по-прежнему является потоком: в первом случае, поскольку $f(e)0$, $f'(e)\ge 0$. Это легко проверить, что для каждой вершины $v_i$ $1
В конце концов, алгоритм завершается с $t\notin U$ и потоком $f$.
Из этого следует
что для каждого $e=(v,w)$ с $v\in U$ и $w\notin U$ $f(e)=c(e)$,
и для каждого $e=(v,w)$ с $v\notin U$ и $w\in U$ $f(e)=0$.
Вместимость разреза $\overrightharpoon U$ равна
$$\sum_{e\in\overrightharpoon U} c(e).$$
Значение потока $f$ равно
$$
\sum_{e\in\overrightharpoon U} f(e)-\sum_{e\in\overleftharpoon U}f(e)=
\sum_{e\in\overrightharpoon U} c(e)-\sum_{e\in\overleftharpoon U}0=
\sum_{e\in\overrightharpoon U} c(e).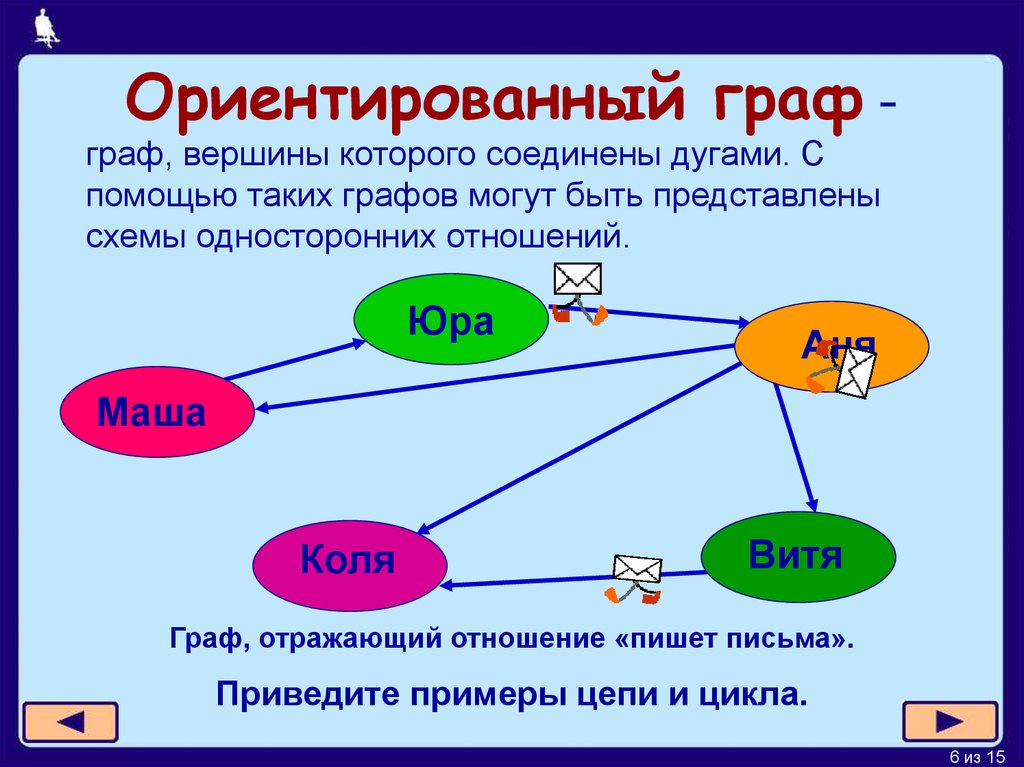 $$
Таким образом, мы нашли поток $f$ и разрезали $\overrightharpoon U$ так, что
$$
\val(f) = c(\overrightharpoon U),
$$
по желанию.
$\qed$
$$
Таким образом, мы нашли поток $f$ и разрезали $\overrightharpoon U$ так, что
$$
\val(f) = c(\overrightharpoon U),
$$
по желанию.
$\qed$
Теорема о максимальном потоке и минимальном разрезе верна, когда пропускная способность положительные действительные числа, хотя, конечно, максимальное значение потока в этом случае не обязательно будет целым числом. Это несколько больше трудно доказать; доказательство включает пределы.
Мы уже доказали, что в двудольном графе размер максимальное паросочетание равно размеру минимального вершинного покрытия, теорема 4.5.6. Это оказывается по сути, частный случай теоремы о максимальном потоке и минимальном разрезе.
Следствие 5.11.8 В двудольном графе $G$ размер максимального паросочетания одинаков как размер минимального вершинного покрытия.
Доказательство. Предположим, что части $G$ равны $X=\{x_1,x_2,\ldots,x_k\}$ и
$Y=\{y_1,y_2,\ldots,y_l\}$. Создайте сеть следующим образом:
ввести две новые вершины $s$ и $t$ и дуги $(s,x_i)$ для всех $i$
и $(y_i,t)$ для всех $i$. Для каждого ребра $\{x_i,y_j\}$ в $G$ пусть
$(x_i,y_j)$ — дуга. Пусть $c(e)=1$ для всех дуг $e$. Теперь значение
максимальный расход равен пропускной способности минимального разреза.
Для каждого ребра $\{x_i,y_j\}$ в $G$ пусть
$(x_i,y_j)$ — дуга. Пусть $c(e)=1$ для всех дуг $e$. Теперь значение
максимальный расход равен пропускной способности минимального разреза.
Пусть $C$ — минимальное сечение. Если $(x_i,y_j)$ — дуга $C$, заменить ее по дуге $(s,x_i)$. Это все еще разрез, так как любой путь из $s$ в $t$ включая $(x_i,y_j)$, должен включать $(s,x_i)$. Таким образом, мы можем предположить что $C$ содержит только дуги вида $(s,x_i)$ и $(y_i,t)$. Сейчас легко увидеть, что $$K=\{x_i\vert (s,x_i)\in C\}\cup\{y_i\vert (y_i,t)\in C\}$$ является вершинным покрытием $G$ того же размера, что и $C$.
Пусть $f$ — максимальный поток, такой что $f(e)$ — целое число для всех $e$,
и $\val(f)=c(C)$,
что возможно по теореме о максимальном потоке и минимальном разрезе. Рассмотрим множество
ребер
$$M=\{\{x_i,y_j\}\vert f((x_i,y_j))=1\}.$$
Если $\{x_i,y_j\}$ и
$\{x_i,y_m\}$ принадлежат этому множеству, то поток из вершины $x_i$
не менее 2, но есть только одна дуга в $x_i$, $(s,x_i)$, с
емкость 1, что противоречит определению потока. Аналогично, если
$\{x_i,y_j\}$ и $\{x_m,y_j\}$ входят в этот набор, тогда поток
в вершину $y_j$ не менее 2, но из
$y_j$, $(y_j,t)$, емкостью 1, тоже противоречие. Таким образом, $M$ является
соответствие. Более того, если $U=\{s,x_1,\ldots,x_k\}$, то значение
поток
$$
\sum_{e\in\overrightharpoon U}f(e)-\sum_{e\in\overleftharpoon U}f(e)=
\sum_{e\in\overrightharpoon U}f(e)=|M|\cdot1=|M|.
$$
Таким образом, $|M|=\val(f)=c(C)=|K|$, значит, мы нашли паросочетание и вершину
обложка такого же размера. Отсюда следует, что $M$ — максимальное паросочетание
$K$ — минимальное вершинное покрытие.
$\qed$
Аналогично, если
$\{x_i,y_j\}$ и $\{x_m,y_j\}$ входят в этот набор, тогда поток
в вершину $y_j$ не менее 2, но из
$y_j$, $(y_j,t)$, емкостью 1, тоже противоречие. Таким образом, $M$ является
соответствие. Более того, если $U=\{s,x_1,\ldots,x_k\}$, то значение
поток
$$
\sum_{e\in\overrightharpoon U}f(e)-\sum_{e\in\overleftharpoon U}f(e)=
\sum_{e\in\overrightharpoon U}f(e)=|M|\cdot1=|M|.
$$
Таким образом, $|M|=\val(f)=c(C)=|K|$, значит, мы нашли паросочетание и вершину
обложка такого же размера. Отсюда следует, что $M$ — максимальное паросочетание
$K$ — минимальное вершинное покрытие.
$\qed$
Пример 5.11.1 Связность в орграфах оказывается чуть больше
сложнее, чем связность в графах. Диграф это
подключен, если
лежащий в основе граф
связанный. (Основной граф орграфа создается путем удаления
ориентация дуг для создания ребер, то есть замена каждой
дуга $(v,w)$ ребром $\{v,w\}$. Даже если орграф простой,
лежащий в основе граф может иметь несколько ребер.) Орграф сильно
связно, если для каждой вершины $v$
и $w$ есть обход от $v$ до $w$.

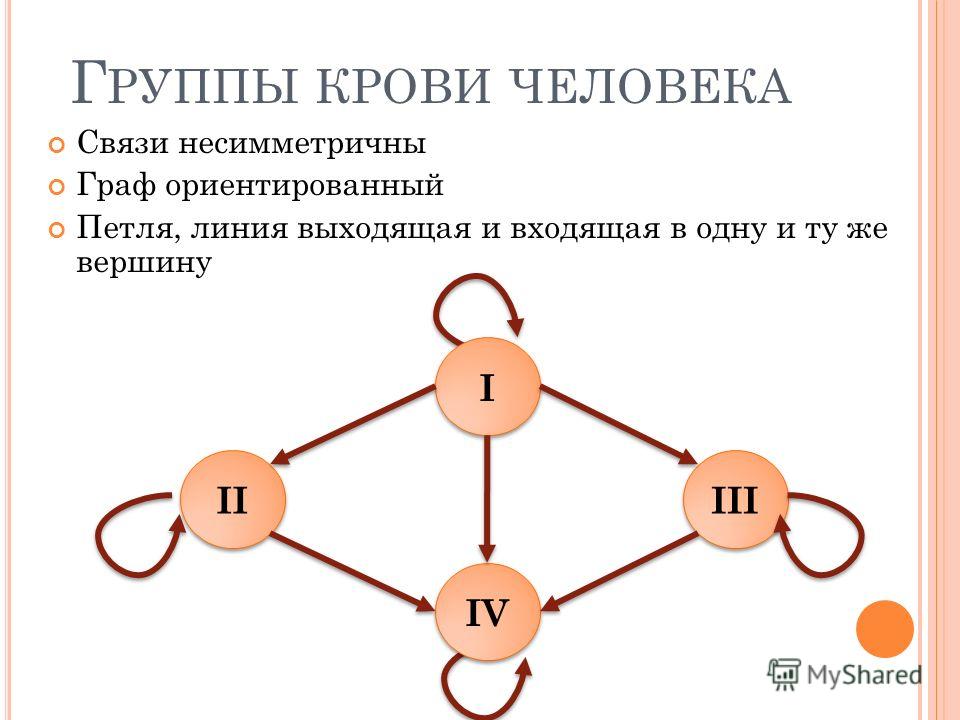 См рис. 1.а
См рис. 1.а