Ортогональные проекции вектора на прямую и плоскость — ПриМат
Зададим в трехмерной декартовой прямоугольной системе координат две точки $B_1$ и $B_2,$ определяющие вектор $\overline{B_1B_2}\left(\alpha_1, \beta_1, \gamma_1\right).$ Опустим из них перпендикуляры на плоскость $xy$ и получим точки $B_{1xy}$ и $B_{2xy}:$
Заметим, что прямые $B_1B_{1xy}$ и $B_2B_{2xy}$ параллельны оси аппликат, которая в свою очередь перпендикулярна плоскости $xy.$ Поэтому тот факт, что мы работаем именно в прямоугольной декартовой системе очень важен, так как в противном случае проекции не будут ортогональными. Итак, точки $B_{1xy}$ и $B_{2xy}$ определяют вектор $\overline{B_{1xy}B_{2xy}},$ который является ортогональной проекцией $\overline{B_1B_2}$ на плоскость $xy.$ Обозначим его следующим образом: $$\overline{B_{1xy}B_{2xy}} = pr_{xy}\overline{B_1B_2}.$$
Рассмотрим некоторые свойства проекций. Для этого возьмем еще один произвольный вектор $\overline{A_1A_2}\left(\alpha_2, \beta_2, \gamma_2\right)$ и для векторов $\overline{B_1B_2}$ и $\overline{A_1A_2}$ определим операции сложения и умножения на константу: $$\overline{B_1B_2}+\overline{A_1A_2} = \left(\alpha_1+\alpha_2, \beta_1+\beta_2, \gamma_1+\gamma_2\right),$$ $$\lambda\overline{B_1B_2} = \left(\lambda\alpha_1, \lambda\beta_1, \lambda\gamma_1\right),$$ $$\lambda\overline{A_1A_2} = \left(\lambda\alpha_2, \lambda\beta_2, \lambda\gamma_2\right).
Используя материалы второй статьи, найдем координаты проекций векторов на плоскость $xy:$ $$pr_{xy}\overline{B_1B_2} = \left(\alpha_1, \beta_1, 0\right),$$ $$pr_{xy}\overline{A_1A_2} = \left(\alpha_2, \beta_2, 0\right).$$
Тогда можно описать следующие свойства: $$pr_{xy}\left(\overline{B_1B_2}+\overline{A_1A_2}\right) = pr_{xy}\overline{B_1B_2}+pr_{xy}\overline{A_1A_2} = \left(\alpha_1+\alpha_2, \beta_1+\beta_2, 0\right),$$ $$pr_{xy}\left(\lambda\overline{B_1B_2}\right) = \lambda pr_{xy}\left(\overline{B_1B_2}\right) = \left(\lambda\alpha_1, \lambda\beta_1, 0\right),$$ $$pr_{xy}\left(\lambda\overline{A_1A_2}\right) = \lambda pr_{xy}\left(\overline{A_1A_2}\right) = \left(\lambda\alpha_2, \lambda\beta_2, 0\right).$$
При построении проекции вектора на координатную ось, все рассуждения остаются аналогичными.
Найти отношение длин вектора $\overline{AB}\left(8, -5, -2\right)$ и его ортогональной проекции на плоскость $yz.$
Решение
Найдем длину вектора $\overline{AB}:$ $$\left|\overline{AB}\right| = \sqrt{64+25+4} = \sqrt{93}.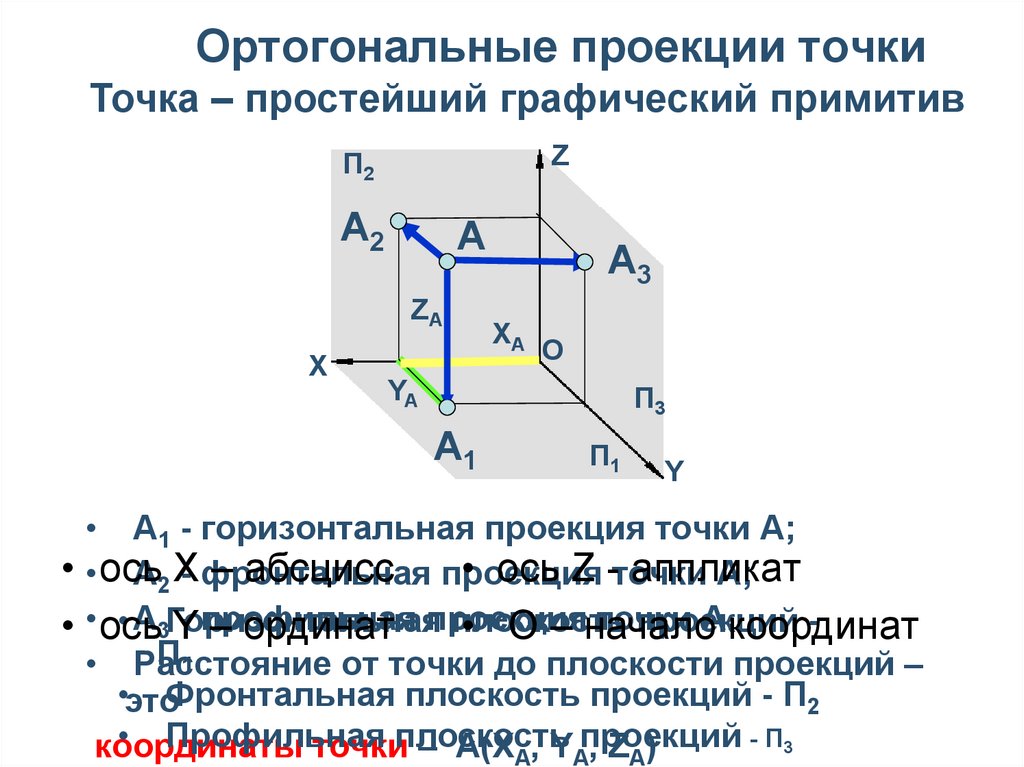 $$ Ортогональная проекция этого вектора имеет следующие координаты: $$pr_{yz}\left(\overline{AB}\right) = \left(0, -5, -2\right).$$ Найдем длину проекции: $$\left|pr_{yz}\left(\overline{AB}\right)\right| = \sqrt{25+4} = \sqrt{29}.$$ Имеем: $$\frac{\left|\overline{AB}\right|}{\left|pr_{yz}\left(\overline{AB}\right)\right|} = \frac{\sqrt{93}}{\sqrt{29}}.$$
$$ Ортогональная проекция этого вектора имеет следующие координаты: $$pr_{yz}\left(\overline{AB}\right) = \left(0, -5, -2\right).$$ Найдем длину проекции: $$\left|pr_{yz}\left(\overline{AB}\right)\right| = \sqrt{25+4} = \sqrt{29}.$$ Имеем: $$\frac{\left|\overline{AB}\right|}{\left|pr_{yz}\left(\overline{AB}\right)\right|} = \frac{\sqrt{93}}{\sqrt{29}}.$$
[свернуть]
- Воеводин В.В. Линейная алгебра. М.: Наука, 1994, Глава 3, $§$ 25, «Некоторые задачи» (стр. 83-85)
- Ильин В.А., Позняк Э.Г. Аналитическая геометрия. М.: ФИЗМАТЛИТ, 2004, $§$ 3, пункт 1, «Понятие направленного отрезка в пространстве. Проекция направленного отрезка на ось» (стр. 17)
© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Валентин Малявко (8), Елизавета Савицкая (8), Игорь Любинский (8), Юлия Стерлянко (8), Денис Стехун (8), Александр Базан (7), Анна Чалапчий (7), Константин Берков (7), Олег Шпинарев (7), Людмила Рыбальченко (6), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2),
Проекции вектора
Проекции вектораВ.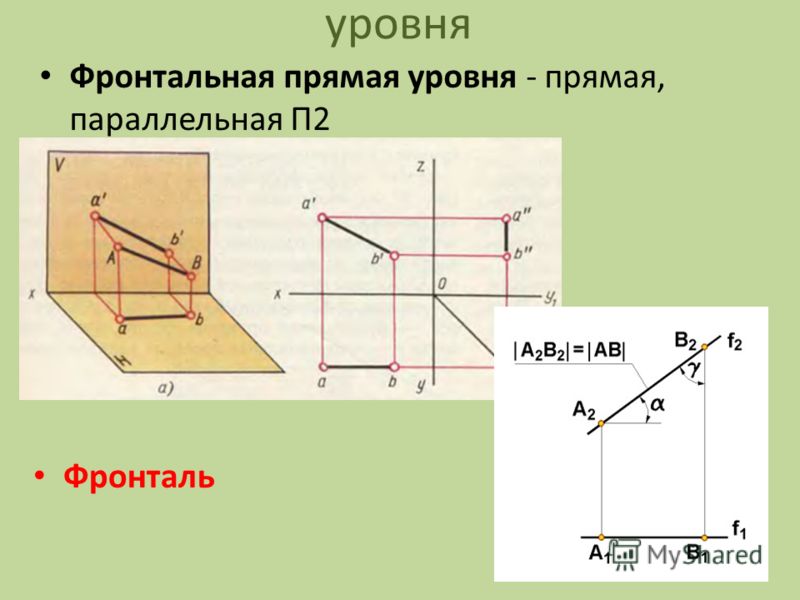 Г. Автор. Векторная и тензорная алгебра для будущих физиков и
техников
Г. Автор. Векторная и тензорная алгебра для будущих физиков и
техников
Суперобложка / Обложка / Содержание
|
От автора Введение Векторы .Геометрическое определение вектора .Алгебраические операции над направленными отрезками ..Сложение направленных отрезков ..Умножение направленных отрезков на число .Проекции вектора ..Параллельное проектирование вектора в пространстве ..Параллельное проектирование вектора в пространстве …Проекция точки на плоскость …Проекция вектора на плоскость ..Ортогональная проекция вектора в пространстве …Ортогональная проекция вектора на плоскость . .Метод координат ..Коллинеарные векторы ..Компланарные векторы ..Векторы в трехмерном геометрическом пространстве ..Линейная зависимость векторов и размерность пространства .Декартова система координат ..Различные формы записи векторов ..Линейные операции над векторами в координатной форме ..Скалярное умножение векторов …Свойства скалярного умножения …Скалярное умножение в декартовых координатах ..Некоторые примеры использования скалярного умножения .Измерение площадей и объемов ..Площадь параллелограмма, построенного на векторах ..Свойства определителя второго порядка ..Задачи на применение определителей . ..Определитель третьего порядка и его свойства ..Векторное произведение векторов ..Векторное умножение векторов базиса декартовой системы координат На подступах к тензорам .Преобразования координат .Скалярное умножение векторов в произвольных косоугольных координатах .Метрический тензор .Взаимный координатный базис .Ковариантные и контравариантные координаты вектора .Площадь и объем в косоугольных координатах ..Индексная форма записи для выражений с определителями ..Символы Веблена ..Свойства символов Веблена ..Тензор Леви-Чивиты ..Операция векторного умножения в произвольных косоугольных координатах .Линейные преобразования или операторы . ..Примеры линейных операторов .Доказательство теоремы об определителе Тензоры .Определение тензора .Общие определения алгебраических операций с тензорами .Примеры на применение тензоров в физике ..Тензор инерции ..Тензор напряжений .Задачи ..Задачи на тождественные преобразования Методические комментарии Литература |
|
.Проекции вектора
Слово
«проекция» происходит от латинского «projectio«
– бросание вперед. Идея этого понятия возникла, видимо, при
наблюдении теней, которые отбрасывают освещенные предметы (рис.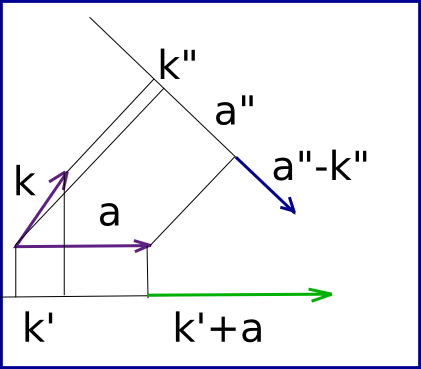 4).
4).
Способ проекции, изображенный на рис. 4 называется центральной проекцией. Если источник света А отнести достаточно далеко, то мы получим параллельную проекцию. Параллельная проекция обладает рядом полезных качеств, в силу чего находит широкое применение в инженерной практике. Мы тоже в дальнейшем будем говорить только о параллельной проекции, опуская ее полное название.
..Параллельное проектирование вектора в плоскости
Рассмотрим для начала наиболее простой, но тем не менее важный для понимания, частный случай – проектирование объектов целиком расположенных в плоскости на прямую, также расположенную в этой же плоскости. Направление проектирования зададим при помощи вектора .
На рис. 5 показаны проекции точки A,
отрезка BC и вектора
на прямую L.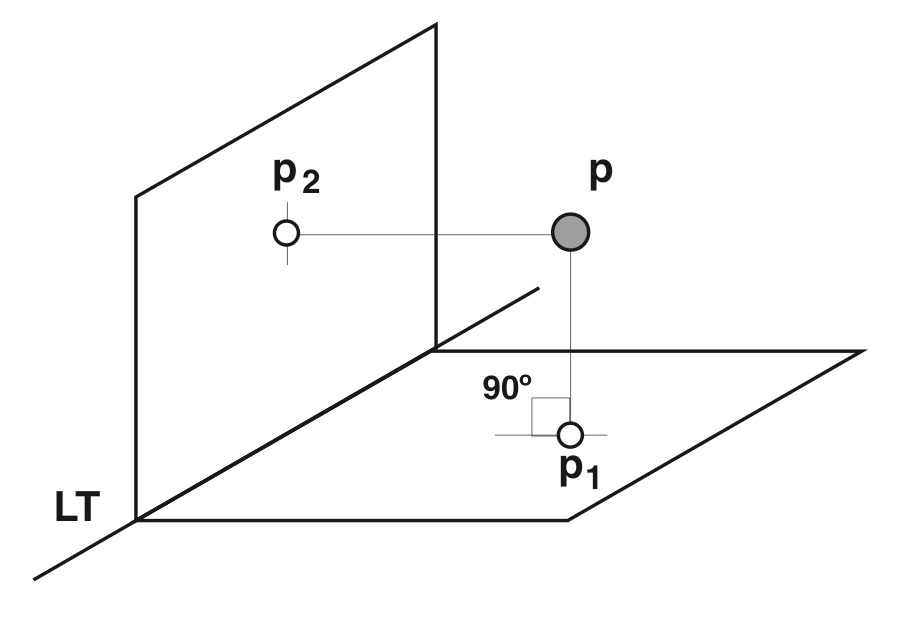
Из рисунка видно, что проекцией точки A на прямую L является точка , проекцией отрезка BC является отрезок , а проекцией вектора является вектор .
Параллельную проекцию вектора на прямую L по направлению будем обозначать .
Теперь дадим необходимые определения.
Определение проекции точки (10)
Пусть точка A,
прямая L, и
вектор
лежат в одной плоскости. Проекцией точки A
на прямую L в направлении
вектора
в этом случае будем называть точку
,
которая является результатом пересечения прямой L
и прямой, проведенной через точку A
в направлении вектора
.
Определение проекции вектора на прямую (11)
Пусть вектор , прямая L, и вектор лежат в одной плоскости. Проекцией вектора на прямую L в направлении вектора в этом случае будем называть вектор , равный вектору . Точки и при этом являются проекциями начала и конца вектора на прямую L.
Для векторов, лежащих на одной прямой, возможны лишь два направления: либо в одну, либо в другую сторону – третьего не дано. В этом случае само понятие вектора становится излишним, и можно вполне обойтись лишь алгебраическим значением – числом со знаком. Правда, для этого на прямой необходимо сначала задать одно из направлений в качестве положительного.
Определение направленной оси (12)
Прямая, с заданным на ней положительным направлением, называется
направленной осью или просто осью.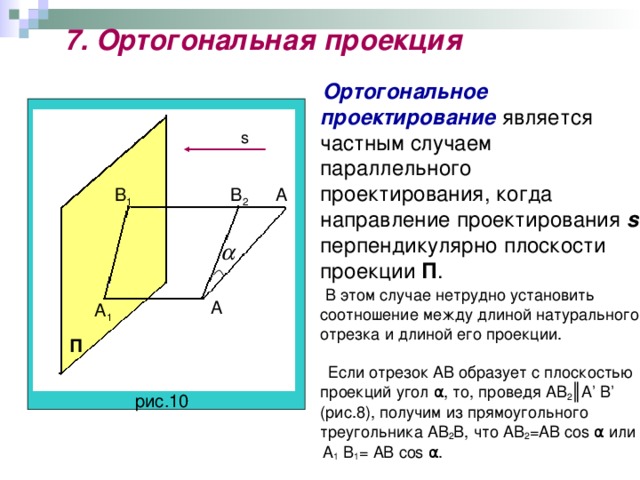
Определение алгебраического значения проекции вектора на направленную ось (13)
Алгебраическим значением проекции вектора на направленную ось называется модуль проекции вектора на эту ось, взятый со знаком «+», если направление проекции вектора совпадает с положительным направлением оси, и со знаком «–», в противном случае.
Обозначать алгебраическое значение проекции вектора на ось будем точно так же, как проекцию вектора на прямую, только без «векторной» черты сверху, например: .
Проекция вектора на ось – это вектор. Алгебраическое значение проекции вектора на ось – это число. Последнее название является исключительно громоздким, но пользуясь тем, что из контекста обычно всегда ясно, о чем идет речь – о числе или о векторе – и то и другое будем, в тех случаях, когда это не вызывает недоразумений, называть просто проекцией вектора.
Теорема о проекции суммы векторов на ось
Проекция суммы векторов на ось равна сумме их проекций.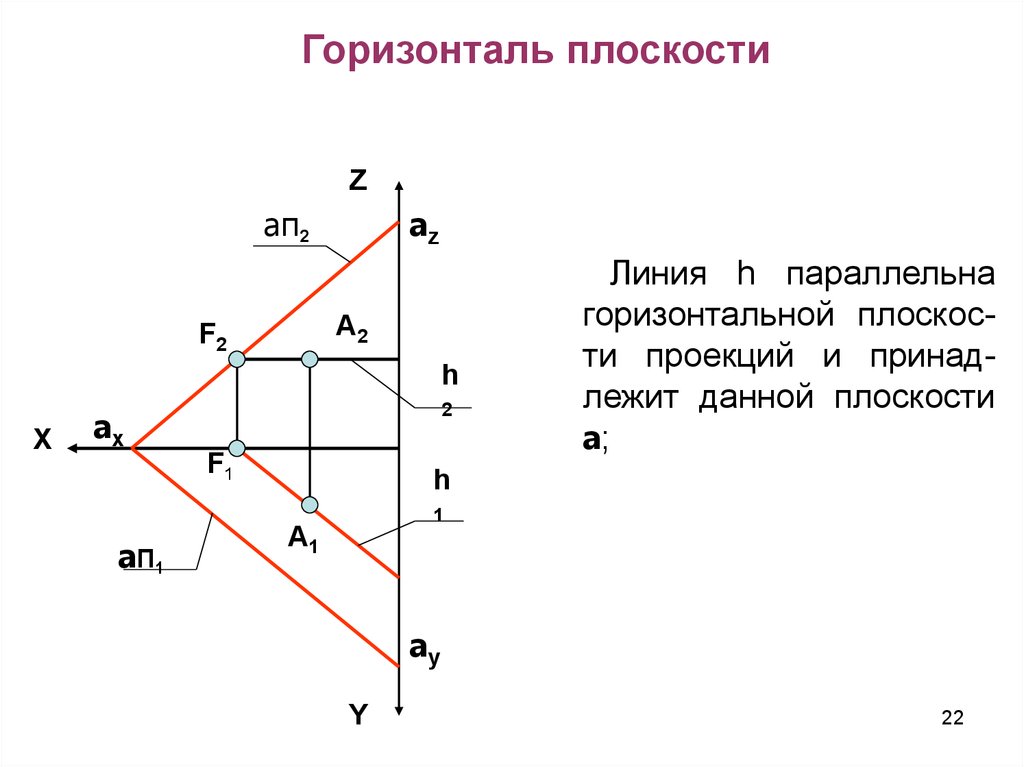
В данном случае из контекста теоремы неясно, о какого типа проекциях идет речь. Но к счастью, данная теорема справедлива и для векторной проекции и для алгебраической. А вот доказательства для этих случаев будут различные. Для начала докажем теорему для векторных проекций. Рассмотрим для определенности сумму четырех векторов (рис. 6).
Из рис. 6 видно, что:
,
,
в соответствии с правилами сложения векторов.
С другой стороны:
;
;
;
;
.
Следовательно,
.
Тот же самый результат может быть получен для любого количества векторов, что дает нам право записать теорему в общем виде:
.
Теперь мы можем доказать теорему об алгебраических значениях
проекций. Пусть
– единичный вектор, совпадающий с направлением оси
.
Такой вектор обычно называется ортом-вектором. Тогда векторную
проекцию произвольного вектора
на ось
можно записать как:
,
где s означает знак.
Пусть
– единичный вектор, совпадающий с направлением оси
.
Такой вектор обычно называется ортом-вектором. Тогда векторную
проекцию произвольного вектора
на ось
можно записать как:
,
где s означает знак.
Поскольку , то
. Но модуль проекции вектора на ось, взятый с соответствующим знаком, – это и есть по определению алгебраическая величина проекции вектора на ось. Следовательно, .
Запишем теперь обе формулировки доказанной нами теоремы в символической форме:
|
; |
(1) |
|
. |
(2) |
Как видим, и в символической записи эти две теоремы очень похожи, но
разница, тем не менее, есть.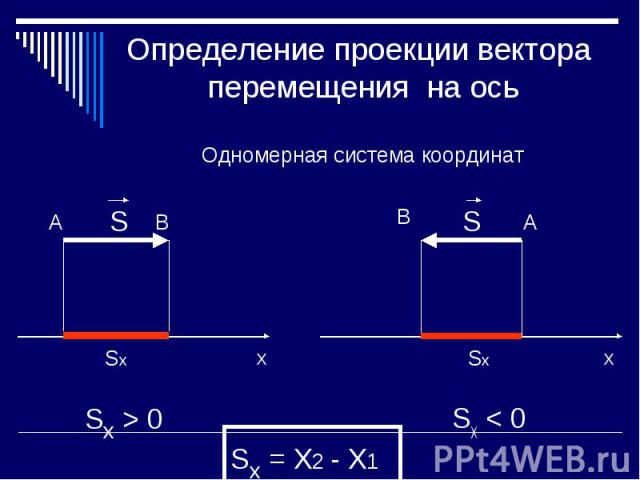 В первом случае справа и слева от знака
равенства стоят векторы, а во втором – числа.
В первом случае справа и слева от знака
равенства стоят векторы, а во втором – числа.
Вообще то, эта теорема относится к той категории теорем, в которых то, что требуется доказать, гораздо более очевидно, чем само доказательство. Так или иначе, теорема полезная, и в дальнейшем она нам еще пригодится.
К оглавлению
линейная алгебра — Почему это называется «Ортогональная проекция»? Почему не просто «Проекция»?
$\begingroup$
Прямо сейчас мы изучаем разложение векторов, но что-то я не понимаю, как называются эти штуки
Например, в тексте параллельный компонент y называется ортогональной проекцией у на и . Это не имеет смысла для меня. Почему слово «ортогональный» вообще там? Я думаю, что понимаю, почему они используют «ортогональный» для z, но для меня это не имеет смысла, когда они могут просто назвать его «ортогональным»
- линейная алгебра
$\endgroup$
$\begingroup$
Как объясняет ответ Билла, мы можем разложить каждый вектор в исходном пространстве, используя карту проекции.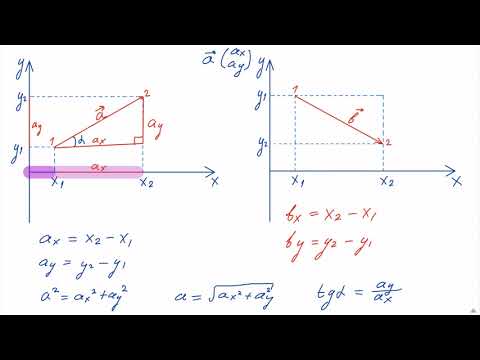 Это дает интуитивно понятную геометрическую интерпретацию ортогональных проекций.
Это дает интуитивно понятную геометрическую интерпретацию ортогональных проекций.
Если $p:V\to W$ — $\color{Green}{ортогональная}$ проекция вниз на подпространство, то слои (прообразы) каждой точки $w\in W$ перпендикулярны основанию (подпространство $W$). С $\dim V=2$ и $\dim W=1$: 92}w$ и $b = v — a = v — \mathrm{proj}_w(v)$. У нас есть
- $v=a+b$
- $a$ параллелен $w$
- $a$ и $b$ ортогональны (просто проверьте, что $a \;\cdot\; b=0$).
Существуют и другие «проекции», для которых $v=a+b$ и $a$ параллельно $w$. Например: пусть $a=w$ и $b=v-w$. Тогда $v=w+(v-w)=a+b$ и $a=w$ параллелен сам себе (т.е. $w$). Но в общем случае $v-w$ и $w$ не ортогональны.
$\endgroup$
4
$\begingroup$
На самом деле мы можем спроецировать любой вектор в базисе следующим образом:
Если $v_1,\ldots, v_n$ является базисом вашего векторного пространства, то проекция вектора $a_1 v_1 + \ldots + a_n v_n$ на $a_n$ относительно этого базиса равна $a_n v_n$. Обратите внимание, что проекция зависит от выбора базиса.
Обратите внимание, что проекция зависит от выбора базиса.
Если бы вы взяли ортогональный базис, содержащий $u$, то определение ортогональной проекции совпадало бы с приведенным выше, более общим, определением проекции.
$\endgroup$
$\begingroup$
Я изучал линейную алгебру по тому же учебнику и столкнулся с той же дилеммой. Я решил, что слово «ортогональный» в ортогональной проекции относится к тому, как некоторый вектор v проецируется на подпространство W. Если вы представляете проекцию, происходящую как растянутый процесс с точкой, представленной v , движущейся прямо к W по кратчайшему пути, то движение точки ортогонально W. Это контрастирует с «неортогональной» или «диагональной» проекцией, в которой проекция точки не ортогональна W. , Надеюсь, это поможет — это сработало для меня!
$\endgroup$
$\begingroup$
Потому что линия, по которой ваша исходная точка перемещается в проективную плоскость, ортогональна проективной плоскости.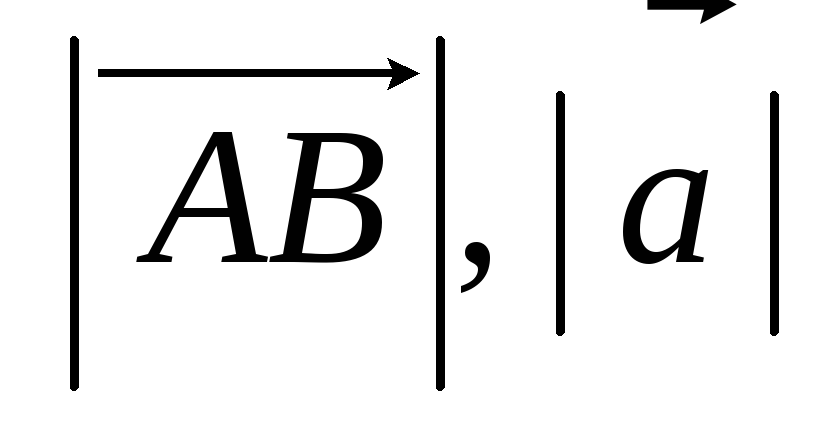 В этом контексте синонимом ортогонального является перпендикуляр, что, я думаю, является более распространенным и понятным словом.
В этом контексте синонимом ортогонального является перпендикуляр, что, я думаю, является более распространенным и понятным словом.
$\endgroup$
1
$\begingroup$
Рассмотрим пример трехмерного вектора, спроецированного на двухмерную плоскость (назовем ее базой). Чтобы проекция была ортогональной, вектор и его проекция на основание должны лежать в плоскости, перпендикулярной основанию, т. е. если вы представляете вектор как ряд точек, каждая из них должна падать перпендикулярно на основание, как показано на рисунке. фото ниже (извините за плохой рисунок).
Ортогональная проекция
Теперь представьте, что плоскость (и вектор) слегка повернуты влево, и вектор, и его проекция по-прежнему лежат на плоскости, но плоскость уже не перпендикулярна основанию. В этом случае проекция не является ортогональной.
Надеюсь, это поможет.

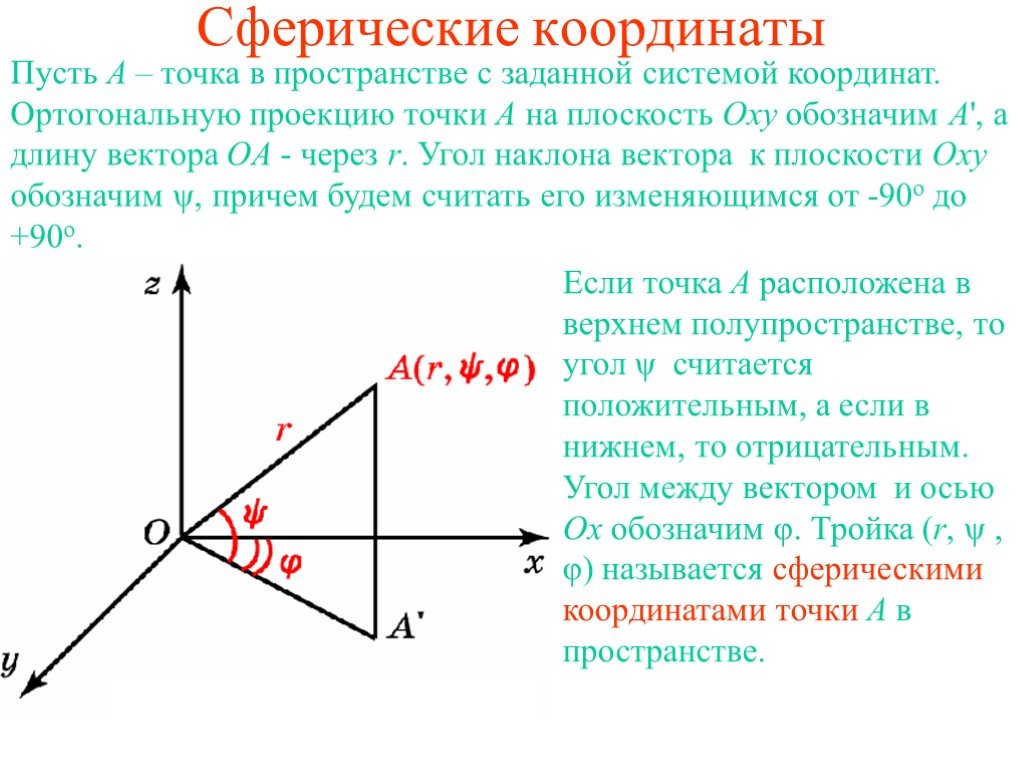 ..Ортогональная проекция вектора на прямую и направленную ось
..Ортогональная проекция вектора на прямую и направленную ось
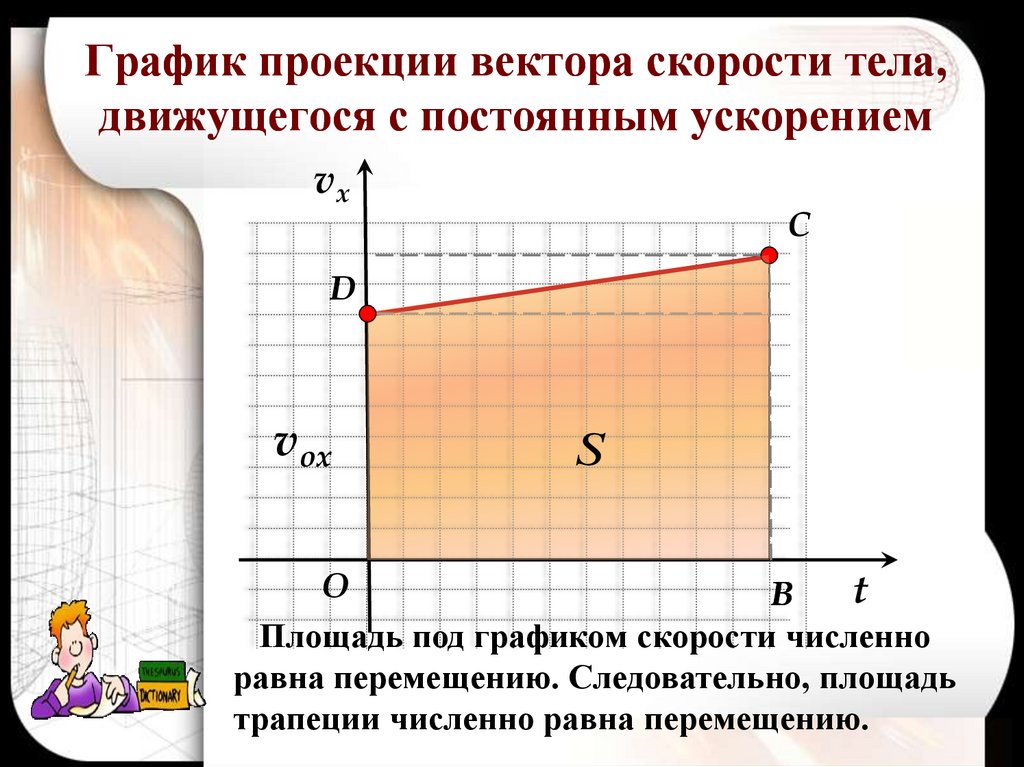 .Объем параллелепипеда, построенного на векторах
.Объем параллелепипеда, построенного на векторах
 Линейный оператор и его матрица
Линейный оператор и его матрица